Abstract
The evolution of the capillary breakup of a liquid jet under large excitation amplitudes in a parameter regime relevant to inkjet printing is analysed using three-dimensional numerical simulations. The results exhibit a reversal of the breakup length of the jet occurring when the velocity scales associated with the excitation of the jet and surface tension are comparable, and an inversion of the breakup from front-pinching to back-pinching at sufficiently large excitation amplitudes. Both phenomena are shown to be associated with the formation of vortex rings and a local flow obstruction inside the jet, which modify the evolution of the jet by locally reducing or even reversing the growth of the capillary instability. Hence, this study provides a mechanism for the well-known breakup reversal and breakup inversion, which are both prominent phenomena in inkjet printing. An empirical similarity model for the reversal breakup length is proposed, which is shown to be valid throughout the considered range of characteristic parameters. Hence, even though the fluid dynamics observed in capillary jet breakup with large excitation amplitudes are complex, the presented findings allow an accurate prediction of the behaviour of jets in many practically relevant situations, especially continuous inkjet printing.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The surface-tension-driven (capillary) breakup of liquid jets has been a very active topic of research since Savart (1833) reported the first systematic experimental observations of this phenomenon. Years later, Plateau (1873) identified surface tension as the driving mechanism of this instability, and Rayleigh (1879) was the first to predict the growth rate of the instability by means of a linear stability analysis. This linear stability analysis and its extensions to viscous flows (Weber 1931; Chandrasekhar 1961) have proven to be powerful tools to describe the capillary breakup of liquid jets. However, this analysis is based on the assumption that a jet is excited by an instability wave with a small (infinitesimal) amplitude, and does not consider the internal flow field within the jet.
The capillary breakup of a liquid jet in real engineering applications, such as inkjet printing, spray atomisation or the production of powders is, however, strongly influenced by nonlinear mechanisms arising from a finite excitation amplitude and the inertia of the jet. Nonlinear effects lead, for example, to the formation of satellite droplets (Rutland and Jameson 1970, 1971), and increase the short wavelength limit of the capillary instability with increasing excitation amplitude (Nayfeh 1970). Yuen (1968) showed that secondary waves, which develop as the instability grows to a finite amplitude, can lead to the formation of satellite droplets, even if the excitation is purely sinusoidal. The formation of satellite drops, which is an impediment to many engineering applications, can be delayed or completely avoided by applying a large excitation amplitude (Vassallo and Ashgriz 1991). The capillary breakup of liquid jets and filaments is also strongly dependent on the viscosity of the liquid (Schulkes 1996; Notz and Basaran 2004; Castrejón-Pita et al. 2012; Hoepffner and Paré 2013). For liquids with high viscosity the pressure field inside the liquid filament is dominated by the Laplace pressure resulting from surface tension (Schulkes 1996), while capillary and inertial effects dominate for fluids with low viscosity. Jets with intermediate viscosity, i.e. with an Ohnesorge number (formally defined in Sect. 2) in the range \(0.01< {Oh} < 1\), are known to feature complex fluid dynamics Eggers and Villermaux (2008). In fact, this operating range is very relevant to various engineering applications, including inkjet printing (Calvert 2001; Derby 2010).
The study of the breakup of harmonically excited jets is currently of great interest because two phenomena associated with large excitation amplitudes are not completely understood. For inkjet printing, in which the length of the liquid jet is preferred to be small and the formation of satellite drops is undesirable, large excitation amplitudes are routinely used. Based on linear stability analysis (Rayleigh 1879; Weber 1931), the breakup length (defined as the shortest distance from the nozzle to the tip of the continuous jet) is controlled by the initial amplitude of the instability, predicting a monotonic decrease of the breakup length with increasing excitation amplitude. In practical applications and laboratory experiments (Lopez et al. 1999; Kalaaji et al. 2003; Castrejón-Pita et al. 2011, 2013), however, it is often observed that the breakup length eventually stabilises and then increases if the excitation amplitude is increased further. This phenomenon, often referred to as breakup reversal, stands in obvious contradiction to the available theory. The second phenomenon which is still poorly understood, is focused on the shape of the breakup region, as it transitions from front-pinching to back-pinching, i.e. a droplet can either break away from the jet at its front or back. This transition is often called breakup inversion, and directly determines with which of its neighbouring drops a satellite drop merges with or whether a satellite drop remains as an individual drop (Pimbley and Lee 1977). Both the reversal and the inversion of breakup are regularly controlled in industrial applications to manipulate and control the breakup length of the jet as well as the formation of satellite droplets. However, since the majority of theoretical studies have focused on simplified models that assume small excitation amplitudes, or neglect the complex hydrodynamics ensuing from large excitation amplitudes, little is known about the origin of these phenomena.
In 2003, Kalaaji et al. (2003) observed an increasing breakup length on jets excited at large amplitudes, without providing an explanation. Cervone et al. (2010) conducted direct numerical simulations (DNS) of jets with large excitation amplitudes, but their analysis focused on numerical aspects, and on the influence of the wavenumber, rather than studying the excitation amplitude itself. Given the fact that complex flow structures are often neglected in linear stability analysis, one expects that this would fail to predict an increasing breakup length at large excitation amplitudes, as a more detailed knowledge of the velocity field in the jet is essential for understanding the underpinning physical phenomena. Recently, McIlroy and Harlen (2019) presented a first theoretical and numerical analysis of the breakup reversal and inversion using a one-dimensional slender-jet model as well as axisymmetric simulations using an Euler-Lagrange finite-element method. Their results show a clear reversal of the breakup, whereby the breakup length stagnates or even increases with increasing excitation amplitude, as well as an inversion of the breakup. Their analysis is limited to a narrow range of excitation amplitudes and fluid properties and the results do not explain the origin of the breakup reversal and inversion. In addition, there have only been few attempts to experimentally determine the internal velocity field of liquid jets away from the nozzle (Castrejón-Pita et al. 2011, 2012).
This article analyses the capillary breakup of liquid jets that are subject to large excitation amplitudes using three-dimensional numerical simulations. The aim of this analysis is to elucidate the origin of breakup reversal and breakup inversion of liquid jets subject to large excitation amplitudes in a parameter regime relevant to industrial applications. To this end, the breakup length and time of the jet, the flow field inside the jet, as well as the influence of gravity on the jet breakup are investigated for periodically excited jets in a parameter regime for which previous studies reported breakup reversal and inversion to be prominent, especially for Ohnesorge numbers between 0.01 and 1 (Kalaaji et al. 2003; McIlroy and Harlen 2019). Based on the presented results, a similarity model for the reversal breakup length is devised, which greatly simplifies the comparison and analysis of capillary jet breakup with large excitation amplitudes, and which facilitates the prediction of the behaviour of jets in many practically relevant situations.
2 Parametrisation and Scaling
A circular liquid jet with radius \(r_0\) and velocity U is considered, as schematically shown in Fig. 1. The initial instability has a wavelength \(\lambda = 2\pi r_0/\kappa\), and a dimensionless wavenumber \(\kappa = k r_0\), where k is the wavenumber. To facilitate the analysis and discussion of the results presented in Sect. 4, the capillary breakup of the liquid jet is described by the theoretical (linear) analysis of the dominating instability mechanism, i.e. the Rayleigh-Plateau instability, and based on its hydrodynamic energy balance.
The dispersion relation of the temporal growth of the Rayleigh-Plateau instability for a cylindrical liquid jet subject to an axisymmetric excitation and viscous stresses is given by Chandrasekhar (1961)
where \(I_0\) and \(I_1\) are the modified Bessel functions of the zeroth and first kind, respectively. The left-hand side of Eq. (1) represents the inviscid contributions, as originally derived by Rayleigh (1879), and the right-hand side represents the viscous contributions, with \(\xi ^2 = (k^2 + \omega \rho /\mu ) r_0^2 = \kappa ^2 + \omega t_{\mu }\), where \(\omega\) is the temporal growth rate of the instability, \(\rho\) is the liquid density and \(\mu\) is the liquid viscosity. The governing timescales are the capillary timescale
which represents the dispersion time due to surface tension over a distance \(r_0\), where \(\sigma\) is the surface tension coefficient, and the viscous timescale
which represents the time required for momentum to diffuse over a distance \(r_0\). Since \(I_1/I_0\) is always positive, the instability grows (\(\omega > 0\)) for \(0< \kappa < 1\), whereas the dispersion relation becomes purely imaginary, and the instability decays, for \(\kappa > 1\). In the context of the present study, it is interesting to note that the linear stability analysis implies a logarithmically reducing breakup time for increasing excitation amplitude.
The dispersion relation, Eq. (1), shows that the growth of the instability is governed by the Ohnesorge number, given as
which represents the transient balance between dispersive (surface tension) and dissipative (viscous stresses) effects that are relevant to the propagation of short interfacial waves (Denner 2016), in this case the Rayleigh-Plateau instability. The Ohnesorge number has been successfully applied to categorise the capillary breakup of jets into different characteristic regimes (Weber 1931; von Ohnesorge 1936; Castrejón-Pita et al. 2015).
The hydrodynamics of a liquid jet are governed by four mechanisms: inertia, viscous stresses, gravity and surface tension. The relative importance of these governing mechanisms may be quantified by their representative pressure scales (i.e. energy per unit volume), which are the inertial scale \(p_\rho = \rho U^{2}\), the viscous scale \(p_\mu = \mu U/r_0\), the gravity scale \(p_{g} = g \rho r_0\), where g is the gravitational acceleration, and the capillary scale \(p_\sigma = \sigma /r_0\). Comparing these pressure scales leads to the Weber number
which represents the relative importance of inertia and surface tension, the Reynolds number
which compares inertia and viscous stresses, and the Froude number
which compares inertia and gravity. Spatial stability analysis for the capillary breakup of a semi-infinite jet suggests breakup similarity with respect to the Weber number (Keller et al. 1973), which can be reformulated as \(\text {We} = U^2/u_\sigma ^2\), where \(u_\sigma =r_0/t_\sigma\) is the capillary velocity at which a liquid sheet or filament retracts due to surface tension (Taylor 1959; Culick 1960) (frequently referred to as the Taylor-Culick velocity).
3 Methods
Numerical simulations of the entire three-dimensional two-phase system, including both bulk phases as well as the fluid interface, are conducted by resolving all relevant scales in space and time, employing the numerical framework described in Sect. 3.1 and applying the simulation setup detailed in Sect. 3.2. The motivation for conducting three-dimensional simulations rather than axisymmetric two-dimensional simulations is to capture any azimuthal instabilities that may occur, in particular with respect to vortex rings, which are known to be susceptible to azimuthal instabilities (Widnall and Sullivan 1973).
Assuming a Cartesian coordinate system, the incompressible, isothermal flow is governed by the momentum equations
and the continuity equation
where t represents time, \({\mathbf {u}}\) is the velocity, p is the pressure, \({\varvec{\tau }} = \mu ({\varvec{\nabla }} {\mathbf {u}} + {\varvec{\nabla }} {\mathbf {u}}^\mathrm {T})\) is the stress tensor of the considered Newtonian fluids, \({\mathbf {g}}\) is the gravitational acceleration and \({\mathbf {f}}_\sigma\) is the volumetric force that represents the surface tension acting at the fluid interface.
The Volume-of-Fluid (VOF) method (Hirt and Nichols 1981) is adopted to capture the interface between the immiscible bulk phases. The local volume fraction of both phases in each mesh cell is represented by the colour function \(\gamma\), defined as \(\gamma = 1\) for the liquid jet and \(\gamma =0\) for the surrounding fluid, with the fluid interface located in mesh cells with \(0< \gamma < 1\). The colour function \(\gamma\) is advected with the underlying flow by the advection equation
3.1 Numerical Framework
The simulations are conducted using a fully-coupled pressure-based algorithm for interfacial flows (Denner and van Wachem 2014). The governing Eqs. (8) and (9) are discretised using a second-order finite-volume method with collocated variable arrangement (Denner et al. 2020), whereby the fluxes though the cell faces are computed using a momentum-weighted interpolation (Bartholomew et al. 2018). The advection equation (10) for the colour function is discretised using a compressive VOF method (Denner and van Wachem 2014). Assuming the force due to surface tension can be represented as a volume force acting in the interface region, the surface force per unit volume is described by the Continuum Surface Force (CSF) model (Brackbill et al. 1992) as
where \(\mathbf {{\hat{m}}} = \nabla \gamma / |\nabla \gamma |\) is the normal vector of the fluid interface and \(\chi = - \nabla \cdot \mathbf {{\hat{m}}}\) is the curvature of the fluid interface. The surface tension coefficient \(\sigma\) is assumed to be constant. In order to mitigate the impact of numerical artefacts in the vicinity of the fluid interface, the artificial viscosity model proposed by Denner et al. (2017) is applied with an interface viscosity of \(\mu _\Sigma = \min \{\sigma \Delta t |\nabla \gamma |, \, 3 \mu \}\), where \(\Delta t\) denotes the time-step applied in the simulations, which is sufficiently small as to not affect the predicted breakup length of the jet, as demonstrated by Denner et al. (2017).
The VOF-based method in conjunction with the CSF model used in this work does not require explicitly defined kinematic or traction boundary conditions at the gas-liquid interface. These conditions are satisfied implicitly at the discrete level, as discussed in detail in the seminal work of Brackbill et al. (1992). Furthermore, since we assume that the surface tension coefficient is constant, the traction at the gas-liquid interface reduces to a trivial no-slip condition.
3.2 Simulation Setup
The jet is simulated in a three-dimensional cylindrical domain with an axial length of \(L_z = 60 \, r_0 -120 \, r_0\) (chosen based on the expected breakup length \(L_{b}\) of the jet) and a radius of \(L_r = 10 \, r_0\), shown in Fig. 2. The jet is resolved with 29 cells per diameter \(d_0=2 \, r_0\) in the radial direction, 52 cells in the azimuthal direction and \(104.7 - 132.6\) cells per wavelength \(\lambda\) in the axial direction, similar to the work of Delteil et al. (2011). The applied computational time-step \(\Delta t\) satisfies a Courant number of \(\text {Co} = |{\mathbf {u}}| \Delta t/\Delta x \le 0.25\) as well as the dynamic capillary time-step constraint (Denner and van Wachem 2015). The density \(\rho\), surface tension coefficient \(\sigma\), and the initial radius \(r_0\) of the simulated jets for the various cases considered in this study are given in Table 1, and the viscosity \(\mu =\text {Oh} \sqrt{\sigma \rho r_0}\) of the liquid jet follows from the considered Ohnesorge number \(\text {Oh}\). Note that, for \(\text {Oh} = 0.1\), case J1 has the properties of an aqueous glycerol solution with a glycerol concentration of \(\approx 76\%\) per weight at room temperature. While some of these other properties might not represent real fluids, the resulting Oh and We numbers are within the range of industrial interest, and within the range where the reversal is known to appear. The density and viscosity ratios to the outer fluid surrounding the jet are \(\rho /\rho _{o} = 10^3\) and \(\mu /\mu _{o}=10^2\), respectively, which is typical for practical gas-liquid flows.
Three-dimensional cylindrical computational domain with \(L_r = 10 \, r_0\) and \(L_z = 80 \, r_0\) as well as the computational mesh in the cross-section of the cylinder. The colour of the jet represents the normal vector of the fluid interface and is used to better visualise the liquid jet in this figure
The axial velocity of the jet at the inlet of the computational domain for radial position \(r \le r_0\) is \(u_{z,\text {in}} = U [1 + \delta _0 \sin {(2 \pi f t)}]\), where \(\delta _0\) is the excitation amplitude and \(f = \kappa U/ (2 \pi r_0)\) is the excitation frequency. The velocity is zero at the inlet boundary for \(r>r_0\), and the gradient of the velocity normal to the boundary is assumed to be zero at all other boundaries. The pressure at the circumferential boundary is fixed to the ambient pressure, while the pressure is extrapolated from the closest cell centre to the domain boundaries that are oriented perpendicular to the axial jet direction.
The dimensionless wavenumber is \(\kappa =0.7\) in the majority of the presented cases, which corresponds, approximately, to the fastest growing mode of the Rayleigh-Plateau instability (Rayleigh 1879) and for which the temporal and spatial linear stability analyses are (for practical purposes) equivalent (Keller et al. 1973). Thus, the phase velocity of the capillary instability can be assumed to be equal to the jet velocity (Keller et al. 1973; González and García 2008), which simplifies the analysis of the capillary jet breakup.
Initially, the cylindrical liquid jet extends through the entire domain at a uniform velocity U, with the surrounding gas being at rest and simulations were run until the jet breakup attained a periodic behaviour. Breakup is, in general, defined in our simulations when the computational cell between the continuous jet and the broken-off droplet is void of liquid.
3.3 Validation
The dimensionless breakup time \(t_{b}/t_\sigma\) of a capillary jet subject to a dimensionless radius perturbation with amplitude \(\eta _0\) is
from which the dimensionless breakup length, under the assumption \(L_{b} = U \, t_{b}\), follows as
The breakup length in the simulations is defined as the shortest continuous length of the jet, when the periodic behaviour of the jet is fully developed. Based on the mechanical energy of the perturbation, Moallemi et al. (2016) proposed a relationship between a dimensionless radius perturbation \(\eta _0\) and the dimensionless velocity perturbation \(\delta _0\), given as \(\eta _0 = 3\delta _0/2\).
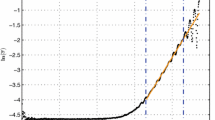
A water jet (\(\rho = 997 \, {kg} \, {m}^{-3}\), \(\mu = 9 \times 10^{-4} \, {Pa} \, {s}\)) in air (\(\rho _{o} = 1.18 \, {kg} \, {m}^{-3}\), \(\mu _{o} = 1.85 \times 10^{-5} \, {Pa} \, {s}\)) is considered, with surface tension coefficient \(\sigma = 0.073 \, {N} \, {m}^{-1}\), dimensionless perturbation wavenumber \(\kappa = 0.697\) and Ohnesorge number \(\text {Oh} = 9.43 \times 10^{-3}\). Applying a dimensionless perturbation amplitude of \(\delta _0 = 0.15\), a very good agreement between the results obtained with the applied numerical framework and the breakup lengths predicted by the linear stability analysis of Chandrasekhar (1961), Eq. (1), is observed in Fig. 3a. This demonstrates that the chosen simulation setup is able to capture all relevant physical mechanisms governing the capillary breakup.
For a constant Weber number of \(\text {We}=14.8\), the breakup length predicted with the applied numerical framework for different perturbation amplitudes \(\delta _0\) is in good agreement with the results reported by Moallemi et al. (2016) and with the result of the linear stability analysis given in Eq. (1). However, for \(\delta _0 \gtrsim 0.2\) an increasing discrepancy between the numerical results and the linear stability analysis can be observed in Fig. 3b, akin to the breakup reversal discussed in Sect. 1 and investigated in detail in Sect. 4.
4 Results
The presented cases focus on the parameter regime \(0.01 \le \text {Oh} \le 0.2\) and \(20 \le \text {We} \le 200\) where the breakup reversal and inversion are most prominent (McIlroy and Harlen 2019), for which the flow is laminar, with \(22 \le \text {Re} \le 1000\), and which is particularly relevant for inkjet printing applications (Calvert 2001; Derby 2010). The excitation velocity \(\Delta u_0 = \delta _0 U\) of the jet, the spatial development of the instability and the local variations in the cross section of the liquid jet lead to a complex flow field at large excitation amplitudes. First, the breakup length of jets in different excitation regimes is investigated in Sect. 4.1. The flow features that occur as a result of large excitation amplitudes are analysed in Sect. 4.2, and the influence of gravity is studied in Sect. 4.3. Finally, an empirical similarity model for the reversal breakup length of a given jet is proposed in Sect. 4.4.
4.1 Breakup Length
The dimensionless breakup length \(L_{b}/r_0\), as a function of excitation amplitude \(\delta _0\), without the influence of gravity (\(\text {Fr}=\infty\)), is shown in Fig. 4 for cases with different characteristic parameters (\(\text {We}\) and \(\text {Oh}\)). Breakup reversal is observed for most cases shown in Fig. 4, albeit with different “strengths” and at different excitation amplitudes. To this end, the reversal breakup length, \(L_b^*\), at which breakup reversal is observed is indicated in Fig. 4. Comparing jets with different fluid properties, the dimensionless breakup length \(L_{b}/r_0\), including the observed breakup reversal, is in excellent agreement for a given set of characteristic parameters (\(\text {We}\), \(\text {Oh}\), \(\kappa\), \(\delta _0\)) across the wide range of considered excitation amplitudes \(\delta _0\), as seen in Figs. 4a, b and f. The results presented in Figs. 4 and 5 show that a smaller excitation frequency \(f = \kappa \, U/(2 \, \pi \, r_0) = \kappa \sqrt{\text {We} \, u_\sigma ^2} / (2 \, \pi \, r_0)\), i.e. smaller \(\kappa\) or smaller \(\text {We}\), leads to a large increase of the breakup length after breakup reversal. Similar observations were reported in the experimental work of Castrejón-Pita et al. (2011). In addition, the breakup reversal is particularly pronounced at the intermediate Ohnesorge number \(\text {Oh}=0.1\), which is in good agreement with previous experimental measurements reported by Kalaaji et al. (2003), where the breakup reversal is particularly distinct for \(\text {Oh} = 0.083\), as well as the numerical work of McIlroy and Harlen (2019), who focused their analysis on \(\text {Oh} = 0.122\).
The dimensionless breakup time \(t_{b}/t_\sigma\) as a function of the excitation Weber number,
which relates the kinetic energy introduced by the excitation velocity to surface tension, is shown Fig. 6. When the excitation velocity is comparable to the capillary velocity, \(\text {We}_\delta \approx 1\), the breakup time is dependent on the viscosity as well as the velocity of the jet. Breakup reversal is observed only in this regime, see Fig. 6, indicating that the jet speed, the viscosity and surface tension all play a role in the reversal dynamics. For small excitation Weber numbers, \(\text {We}_\delta \ll 1\), surface tension dominates the breakup of the jet, which is the regime for which the linear stability analysis of Rayleigh (1879) was originally derived, under the assumption of an infinitesimal excitation amplitude and negligible inertial effects. On the other hand, if the excitation Weber number is large, \(\text {We}_\delta \gg 1\), the kinetic energy introduced by the excitation dominates the breakup of the jet, with surface tension and viscosity having a marginal influence; the jet ultimately breaks for very large excitation amplitudes.
Dimensionless breakup time \(t_{b}/t_\sigma\) as a function of the excitation Weber number \(\text {We}_\delta\), Eq. (14), for jets with different Ohnesorge number \(\text {Oh}\), and with \(\text {Fr}=\infty\) and \(\kappa = 0.7\)
4.2 Flow Features
The observations associated with the breakup discussed in the previous sections indicate that breakup reversal is strongly related to the properties of the jet as well as the flow field inside the jet.
Full contours of the dimensionless relative axial velocity \((u_z-U)/u_\sigma\) (upper half) and the vorticity (lower half) in the axisymmetric plane for jets (\(\text {We} = 50\), \(\text {Oh} = 0.1\), \(\text {Fr} = \infty\), \(\kappa = 0.7\)) with different excitation amplitudes \(\delta _0\), shown at the same time t. The scale at the bottom is the dimensionless axial distance \(z/r_0\) from the nozzle
Large differences in the flow field of the jet can be observed by changing the amplitude \(\delta _0\) of the velocity excitation. Figure 7 shows contours of the relative axial velocity \((u_z-U)/u_\sigma\) and the vorticity for the same jet (\(\text {We} = 50\), \(\text {Oh} = 0.1\), \(\text {Fr} = \infty\), \(\kappa = 0.7\)) with different \(\delta _0\). As the instability grows and the radii of the necks of the jet reduce, the flow in the necks accelerates and exits the necks into the adjacent drop. At a relatively small excitation amplitude, e.g. \(\delta _0=0.1\), and hence a small excitation velocity \(\Delta u_0\), the flow exiting the upstream neck (with reference to a given drop) closely follows the interface as it enters the drop, without forming a recirculation. At large excitation amplitudes, however, the flow exiting the upstream neck of the liquid jet does not follow the interface, because the diameter of the jet increases rapidly as the flow enters the drop, which is particularly pronounced for \(\delta _0 = 0.3\) in Fig. 7. This can be clearly seen by the streamlines shown in Fig. 8, which form closed paths, indicating the development of a vortex in a two-dimensional axisymmetric plane, and a vortex ring in three dimensions. This vortex ring is significantly smaller at small excitation amplitudes, as seen in Fig. 7. It has previously been shown that the generation of vorticity by the presence of curved surfaces and the formation of vortex rings during the thinning of capillary threads slow down the collapse of the neck and may facilitate an escape from end-pinching (Notz and Basaran 2004; Hoepffner and Paré 2013; Kamat et al. 2020). Moreover, the presence of surfactants plays a crucial role during this escape phenomena, due to the extra action that Marangoni stresses may offer during the generation of vorticity, particularly for low Ohnesorge numbers (Kamat et al. 2020). This is particularly important in real applications, as real inks and paint formulations will likely contain surfactants that may lead to even more complex reversal mechanisms.
Streamlines of the relative axial velocity \(u_z-U\) and contours of the pressure field in the axisymmetric plane through a drop (situated at \(z \approx 13 d_0\)) of the jet with \(\text {We} = 50\), \(\text {Oh} = 0.1\), \(\text {Fr} = \infty\), \(\kappa = 0.7\), and \(\delta _0=0.3\). The jet moves from the left to the right in the figure
The flows exiting the upstream and downstream necks into the drop collide with each other, forming a stagnation point, as observed in Fig. 8. This stagnation point is present irrespective of the excitation amplitude, but its position inside the drop changes, moving towards the downstream neck for increasing excitation amplitudes. Although the flows exiting both the upstream and the downstream necks have approximately the same relative velocity magnitude \(|u_z-U|\), as seen in Fig. 7, the upstream neck has a larger diameter and consequently, the associated flow carries more momentum than the flow through the downstream neck. As a result, the flow from the upstream neck penetrates much further into the drop and obstructs the flow exiting the downstream neck, as seen in Fig. 7. This obstruction of the flow can also be clearly observed in Fig. 8, where the flow exiting the downstream neck is deflected radially outwards by the flow coming from the upstream neck.
Hence, two distinct flow features can be identified for jets with large excitation amplitudes: (i) the development of a vortex ring and (ii) an obstruction of the flow exiting the downstream neck. These flow features influence the spatial development of the capillary instability, as evident by the evolution of the neck radii for the case with \(\text {We} = 50\), \(\text {Oh} = 0.1\), \(\text {Fr} = \infty\) and \(\kappa = 0.7\) shown in Fig. 9. Since this jet is dominated by inertia (Oh \(< 1\)), for a small excitation the neck radius is initially proportional to \(\tau ^{2/3}\) (Castrejón-Pita et al. 2015), where \(\tau = (t_\text {b} - t)/t_\sigma\) is the dimensionless time remaining to pinch-off, followed by a transition to the inertial-viscous regime with \(r/r_0 = 0.0304\tau /\)Oh (Eggers 1993). The jet with \(\delta _0 = 0.1\) is in very good agreement with these theoretical scalings, as observed in Fig. 10, and, hence, can be considered as a benchmark against which to compare the results of the larger excitation amplitudes.
4.2.1 Vortex Ring
The collapse of the upstream neck, shown in Fig. 9a, proceeds as expected based on theoretical considerations for the moderate excitation amplitude of \(\delta _0 = 0.1\). However, the collapse of the upstream neck is significantly slower for large excitation amplitudes (\(\delta _0 = 0.2\) and \(\delta _0 = 0.3\)), where the vortex ring observed in Fig. 7 is more pronounced than for \(\delta _0 = 0.1\). The collapse of the upstream neck is slowed down particularly at \(10 \, r_0 \le z \le 25 \, r_0\), as observed in Fig. 9a, which corresponds to the section where the vortex ring is most pronounced, see Fig. 7. The radius of the upstream neck of the jet excited with \(\delta _0 =0.3\) is even being “overtaken” by the neck of the jet with \(\delta _0=0.2\). It is worth recalling, that the breakup length of the jet should be logarithmically reducing with increasing excitation amplitude according to linear theory (Keller et al. 1973).
The vortex ring and its observed impact are very similar to the experimental and computational observations reported by Hoepffner and Paré (2013) for a recoiling filament, which showed that such a vortex ring slows down the collapse of the neck, and hence, delays or even suppresses the breakup of the filament. Hoepffner and Paré (2013) observed this vortex ring only at intermediate Ohnesorge numbers \(0.003< {Oh} < 1\). This observation agrees with the particularly distinct breakup reversal for \({Oh} \approx 0.1\), as noted in Sect. 4.1. At \({Oh} < 0.01\), the viscosity is too small for shear layers and the ensuing vortex ring to form and outgrow the instability, while for \(\text {Oh} > 1\) shear stresses dissipate most of the kinetic energy introduced by the excitation velocity. In addition, a shear layer originates from the zero velocity specified at the inlet boundary for \(r > 0\) but, as observed in Fig. 7, it quickly subsides, not having a discernible influence on the breakup reversal and inversion.
Although vortex rings are susceptible to azimuthal instabilities (Widnall and Sullivan 1973), the flow in all considered jets remains fully axisymmetric. This is significant for the practical exploitation of large excitation amplitudes, as the growth of azimuthal instabilities to finite size can lead to violent breakup of the liquid jet.
4.2.2 Flow Obstruction
The obstruction of the flow coming from the downstream neck as it enters the drop leads to a growth rate reduction of the instability. As observed in Fig. 9b, for large excitation amplitudes the radius of the downstream neck increases as the jet evolves; the fluid in the downstream neck cannot evacuate the collapsing neck fast enough, because it is blocked by the flow exiting the upstream neck, as observed clearly in Fig. 8.
This obstruction of the flow through the downstream neck causes breakup inversion, i.e. a transition from front-pinching (pinching of the downstream neck) to back-pinching (pinching of the upstream neck), which is observed in all studied cases, above a threshold excitation amplitude, as seen for instance in Table 2. Pinch-off is also explicitly indicated in Fig. 9 by a solid circle, illustrating the breakup inversion. Similar observations were made experimentally by Castrejón-Pita et al. (2011). If the flow in a given drop on the liquid jet is symmetric with respect to the plane that is oriented perpendicular to the axial direction of the jet (as in a static filament), the downstream neck would pinch first, since it has had more time to develop the capillary instability than the upstream neck. This is observed at relatively small excitation amplitudes, e.g. \(\delta _0=0.1\) in Figs. 7 and 9b, where the flow remains sufficiently symmetric for a given filament until close to pinching. This symmetry is quickly lost when the excitation amplitude increases, since the flow entering the drop through the upstream neck increases, see Fig. 7, which eventually results in the aforementioned obstruction of the flow at the downstream neck, and the associated impediment of the collapse of the downstream neck. Consequently, breakup inversion is observed at sufficiently large excitation amplitudes. In addition to the transition from front-pinching to back-pinching, McIlroy and Harlen (2019) also observed a transition back to front-pinching at even higher excitation amplitudes. In the parameter regime considered here, a transition back to front-pinching is not observed.
4.3 The Influence of Gravity
The influence of gravity has so far been neglected in the interest of simplicity. Assuming gravity is oriented in the streamwise direction of the jet, gravity accelerates the jet, which leads to a spatially varying jet velocity, jet diameter and instability wavelength.
In practice, the dynamic behaviour of the jet is qualitatively very similar to the case without gravity discussed in the previous sections. The breakup length as a function of the excitation amplitude \(\delta _0\) for the same jet of case J1 (\(\text {We} = 50\), \(\text {Oh} = 0.1\), \(\kappa = 0.7\)) with different gravitational accelerations, \(g \in \{0,9.81\} \, \text {m}\, \text {s}^{-2}\) (\(\text {Fr} \in \{\infty ,14.81\}\)), is shown in Fig. 11. Note that for the properties of case J1, given in Table 1, the jet with \(\text {Oh} = 0.1\) corresponds to an aqueous glycerol solution with approximately \(76 \%\) glycerol concentration per weight. With and without gravity, the breakup length attains a local minimum for \(0.20 \lesssim \delta _0 \lesssim 0.25\), and a local maximum for \(0.35 \lesssim \delta _0 \lesssim 0.4\), as observed in Fig. 11. The corresponding spatial evolution of the radii of the necks upstream and downstream of each drop shows a similar picture, see Fig. 12; the instability of both jets develops in a very similar fashion for \(z \lesssim 15 r_0\), while for \(z \gtrsim 15 r_0\) both jets exhibit a comparable qualitative behaviour that is shifted in space for the jet with \(g=9.81 \, \text {m}\, \text {s}^{-2}\) by the gravitational acceleration.
As seen in Fig. 13, for a Froude number \(\text {Fr} \gg 1\), i.e. when the kinetic energy of the jet dominates over the gravity potential energy, the breakup length of the jet is well approximated by
where \(L_{b}^{(g=0)}\) is the breakup length in the absence of gravity (\(g=0\)). The approximation defined by Eq. (15) has an error smaller than \(3 \%\) using the breakup time \(t_{b}\) obtained from the simulation. Because the instability propagates approximately with velocity U for \(\kappa =0.7\) (Keller et al., (1973; González and García, 2008), the breakup length is \(L_{b} \simeq U \, t_{b}\). With this assumption, Eq. (15) can be rearranged as
from which the breakup time follows as one of the roots. Thus, the jet is merely stretched by the continuous acceleration imposed by gravity, but the hydrodynamics remain largely unchanged.
Computed breakup length of jets (\(\text {Oh} = 0.1\), \(\kappa = 0.7\), \(\delta _0 = 0.1\)) with different Weber numbers \(\text {We}\) as a function the Froude number \(\text {Fr}\), compared against the prediction of Eq. (15)
For jets typically considered in experimental studies and practical applications, the influence of gravity is small, with \(\text {Fr} \gg 1\) (Goedde and Yuen 1970; Derby 2010; Calvert 2001; Kalaaji et al. 2003; Castrejón-Pita et al. 2011; Bruce 1976; Cline and Anthony 1978; Chaudhary and Maxworthy 1980). The accurate parametrisation of the breakup length for \(\text {Fr} \gg 1\) by the correlation proposed in Eq. (15) suggests that jets of practical relevance are merely stretched by the continuous acceleration as a result of gravity and are described reliably by only considering the balance of kinetic energy and gravity potential energy.
4.4 Reversal Breakup Length
Despite the complex flow features inside liquid jets subject to large excitation amplitudes identified in the previous sections, the breakup length, the breakup time, and the flow field are reliably parametrised for a given set of characteristic parameters. With a view on practical applications, this raises the question whether it is possible to find a simple empirical correlation to predict the reversal breakup length based only on the fluid properties, size and speed of the liquid jet. For instance, the reversal breakup length of an inkjet is of particular interest to continuous inkjet technology, as it allows to provide an improved and more consistent print quality (Castrejon-Pita et al., 2013).
Dimensionless reversal breakup length \(L_{b}^*/r_0\) as a function of the Weber number \(\text {We}\), for \(\kappa =0.7\) and constant Ohnesorge number \(\text {Oh}\). The reversal breakup length of the jet studied by McIlroy and Harlen (2019) is shown as a reference
Following the discussion in the previous sections, the Ohnesorge number, the Weber number and the dimensionless breakup length \(L_{b}/r_0\) are the relevant dimensionless groups of an excited liquid jet, under the assumption that gravitational effects are negligible. Similarity analysis stipulates that any dimensional group, defining here \(L_{b}^*/r_0\) as the shortest breakup length prior to reversal (see Fig. 4), can be written as a function of the remaining groups, i.e. \(L_{b}^*/r_0 = \phi (\text {We},\text {Oh})\). Based on the presented simulation results, these dimensionless groups are studied parametrically in the domain presented in Table 3. At constant \(\text {Oh}\), the reversal breakup length \(L_{b}^*/r_0\) follows a scaling of the form
as observed in Fig. 14. This correlation also matches the results reported by McIlroy and Harlen (2019). In contrast, at constant \(\text {We}\), shown in Fig. 14, the reversal breakup length follows the relationship
where \(C_i\) is a constant dependent on \(\text {We}\). Combining the evidence from Eqs. (17) and (18), the dimensionless reversal breakup length is given as
where the constant coefficients \(C_1\) and \(C_2\) are determined from the axial intercepts of Fig. 15, leading to
This empirical correlation describes the reversal breakup length of the liquid jet obtained from the simulations accurately, as observed in Fig. 16, for all considered jets. In addition, the reversal breakup length of the jet studied by McIlroy and Harlen (2019) is included in Fig. 16, which also shows excellent agreement with the proposed empirical correlation.
The currently available data does not, unfortunately, allow us to delineate a precise validity range of our empiric correlation. However, we observe a good agreement in the ranges \(0.15 \le \delta _0 \le 0.5\), \(5 \le\) We \(\le 200\) and \(0.01 \le\) Oh \(\le 0.2\). The correlation is not valid for the extreme cases of dripping (We \(\ll\) 1) and high viscosity (Oh \(\rightarrow \infty\)). In a dripping faucet there is no direct excitation (\(\delta _0 = 0.0\)), the flow is slow (We \(\ll\) 1) and, according to Ambravaneswaran et al. (2004), the breakup distance is \(L_b \approx 5 r_0\) and too short for the fastest growing Rayleigh-Plateau wavelength (\(\lambda = 9.8 r_0\)) to grow and pinch off the jet. For \(\mathrm {Oh} \gg 1\), the viscous (dissipative) timescale is small compared to the capillary (dispersive) timescale, effectively slowing down the growth of Rayleigh-Plateau instabilities. In fact, for \(\mathrm {Oh} \rightarrow \infty\) the Rayleigh-Plateau instability would not be able to form in finite time, as immediately evident by the linear stability analysis of Chandrasekhar (1961), see Eq. (1).
Nevertheless the results demonstrate that, for practical applications, the reversal breakup length can be predicted based only on the liquid properties, the jet radius, and the jet speed.
5 Conclusions
A computational study of the capillary breakup of liquid jets with large excitation amplitudes has been presented. Following the experimental and numerical observations of both a breakup reversal and a breakup inversion for large excitation amplitudes (Kalaaji et al. 2003; Castrejón-Pita et al. 2011, 2013; McIlroy and Harlen 2019), the aim of this study has been to elucidate the origin of these phenomena.
A vortex ring formed by the flow that exits the upstream neck of a given drop on the jet and an (often simultaneously occurring) obstruction of the flow exiting the downstream neck of the same drop, lead to a complex flow field within the jet, which has a significant influence on the evolution of the capillary instability at large excitation amplitudes. The vortex ring slows down the collapse of the upstream neck, whereas the obstruction delays, or even reverses, the collapse of the downstream neck. The result of this interaction is a breakup reversal and inversion for large excitation amplitudes. The prominence of breakup reversal and inversion for the studied parameters has been shown to be associated with the influence of the kinetic energy introduced by the excitation velocity and of viscous stresses; only for jets with an intermediate Ohnesorge numbers can the observed vortex rings form, which agrees with previous findings (Hoepffner and Paré, 2013). Furthermore, breakup reversal has been observed only when the excitation velocity and the capillary velocity scale are of similar magnitude, for \(\text {We}_\delta \approx 1\). The complex flow, and in particular the vortex ring, observed in jets with large excitation amplitudes remains fully axisymmetric and does not develop azimuthal instabilities. The influence of gravity on the capillary instability has been shown to be very small for jet properties typically encountered in laboratory experiments and engineering applications, and its impact on the breakup time and length can be quantified accurately.
Despite the complex fluid dynamics observed in capillary jet breakup with large excitation amplitudes, an empirical correlation has been proposed for the prediction of the minimum breakup length of the jet at which breakup reversal occurs, see Eq. (20), based only on the Weber and Ohnesorge numbers. This empirical correlation predicts the reversal breakup length of the liquid jet very accurately, greatly simplifying the design of engineering applications that benefit from minimising the breakup length of liquid jets, e.g. continuous inkjet printing, where large amplitudes can prevent satellite droplets and minimising the breakup length reduces the ambient exposure of the inkjet.
Future works on the topic of forced jets could explore the effect of the nozzle geometry, e.g. aspect ratio, on the breakup behaviour and include a more physical mechanism for the excitation, e.g. deformable walls as with a piezoelectric actuator in an inkjet system.
References
Ambravaneswaran, B., Subramani, H.J., Phillips, S.D., Basaran, O.A.: Dripping-jetting transitions in a dripping faucet. Phys. Rev. Lett. 93(3), 034501 (2004)
Bartholomew, P., Denner, F., Abdol-Azis, M.H., Marquis, A., van Wachem, B.: Unified formulation of the momentum-weighted interpolation for collocated variable arrangements. J. Comput. Phys. 375, 177–208 (2018)
Brackbill, J.U., Kothe, D.B., Zemach, C.: Continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354 (1992)
Bruce, C.A.: Dependence of ink jet dynamics on fluid characteristics. IBM J. Res. Dev. 20(3), 258–270 (1976)
Calvert, P.: Inkjet printing for materials and devices. Chem. Mater. 13(10), 3299–3305 (2001)
Castrejón-Pita, J.R., Castrejón-Garcia, R., and Hutchings, I.M.: High speed shadowgraphy for the study of liquid drops. In J. Klapp, A. Medina, A. Cros, and C.A. Vargas, editors, Fluid Dynamics in Physics, Engineering and Environmental Applications, pages 121–137. Springer, (2013)
Castrejón-Pita, A.A., Castrejón-Pita, J.R., Hutchings, I.M.: Breakup of liquid filaments. Phys. Rev. Lett. 108, 074506 (2012)
Castrejón-Pita, J.R., Hoath, S.D., Hutchings, I.M.: Velocity profiles in a cylindrical liquid jet by reconstructed velocimetry. J. Fluids Eng. 134, 011201 (2012)
Castrejón-Pita, J.R., Morrison, N.F., Harlen, O.G., Martin, G.D., Hutchings, I.M.: Experiments and Lagrangian simulations on the formation of droplets in drop-on-demand mode. Phys. Rev. E 83(3), 016301 (2011)
Castrejón-Pita, J.R., Baxter, W.R.S., Morgan, J., Temple, S., Martin, G.D., Hutchings, I.M.: Future, opportunities and challenges of inkjet technologies. Atom. Sprays 23(6), 541–565 (2013)
Castrejón-Pita, J.R., Castrejón-Pita, A.A., Thete, S.S., Sambath, K., Hutchings, I.M., Hinch, J., Lister, J.R., Basaran, O.A.: Plethora of transitions during breakup of liquid filaments. Proc. Nat. Acad. Sci. USA 112(15), 4582–4587 (2015)
Cervone, A., Manservisi, S., Scardovelli, R.: Simulation of axisymmetric jets with a finite element Navier-Stokes solver and a multilevel VOF approach. J. Comput. Phys. 229(19), 6853–6873 (2010)
Chandrasekhar, S.: Hydrodynamic and Hydromagnetic Stability. Clarendon Press, Oxford, England (1961)
Chaudhary, K.C., Maxworthy, T.: The nonlinear capillary instability of a liquid jet. Part 2. Experiments on jet behaviour before droplet formation. J. Fluid Mech. 96(02), 275 (1980)
Cline, H.E., Anthony, T.R.: The effect of harmonics on the capillary instability of liquid jets. J. Appl. Phys. 49, 3203 (1978)
Culick, F.E.C.: Comments on a ruptured soap film. J. Appl. Phys. 31, 1128 (1960)
Delteil, Julien, Vincent, Stéphane., Erriguible, Arnaud, Subra-Paternault, Pascale: Numerical investigations in Rayleigh breakup of round liquid jets with VOF methods. Comput. Fluids 50(1), 10–23 (2011)
Denner, F.: Frequency dispersion of small-amplitude capillary waves in viscous fluids. Phys. Rev. E 94, 023110 (2016)
Denner, F., van Wachem, B.: Fully-coupled balanced-force VOF framework for arbitrary meshes with least-squares curvature evaluation from volume fractions. Num. Heat Transf. Part B Fundam. 65(3), 218–255 (2014)
Denner, F., van Wachem, B.: Compressive VOF method with skewness correction to capture sharp interfaces on arbitrary meshes. J. Comput. Phys. 279, 127–144 (2014)
Denner, F., van Wachem, B.: Numerical time-step restrictions as a result of capillary waves. J. Comput. Phys. 285, 24–40 (2015)
Denner, F., Evrard, F., Serfaty, R., van Wachem, B.: Artificial viscosity model to mitigate numerical artefacts at fluid interfaces with surface tension. Comput. Fluids 143, 59–72 (2017)
Denner, F., Evrard, F., van Wachem, B.: Conservative finite-volume framework and pressure-based algorithm for flows of incompressible, ideal-gas and real-gas fluids at all speeds. J. Comput. Phys. 409, 109348 (2020)
Derby, B.: Inkjet printing of functional and structural materials: fluid property requirements, feature stability, and resolution. Ann. Rev. Mater. Res. 40(1), 395–414 (2010)
Eggers, J.: Universal pinching of 3D axisymmetric free-surface flow. Phys. Rev. Lett. 71(21), 3458–3460 (1993)
Eggers, J., Villermaux, E.: Physics of liquid jets. Rep. Prog. Phys. 71(3), 036601 (2008)
Goedde, E.F., Yuen, M.C.: Experiments on liquid jet instability. J. Fluid Mech. 40, 495–511 (1970)
González, H., García, F.J.: The measurement of growth rates in capillay jets. J. Fluid Mech. 619, 179–212 (2008)
Hirt, C.W., Nichols, B.D.: Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39(1), 201–225 (1981)
Hoepffner, J., Paré, G.: Recoil of a liquid filament: escape from pinch-off through creation of a vortex ring. J. Fluid Mech. 734, 183–197 (2013)
Kalaaji, A., Lopez, B., Attané, P., Soucemarianadin, A.: Breakup length of forced liquid jets. Phys. Fluids 15, 2469 (2003)
Kamat, P.M., Wagoner, B.W., Castrejón-Pita, A.A., Castrejón-Pita, J.R., Anthony, C.R., Basaran, O.A.: Surfactant-driven escape from endpinching during contraction of nearly inviscid filaments. J. Fluid Mech. 899, A28 (2020)
Keller, J.B., Rubinow, S.I., Tu, Y.O.: Spatial instability of a jet. Phys. Fluids 16(12), 2052 (1973)
Lopez, B., Soucemarianadin, A., Attané, P.: Break-up of continuous liquid jets: effect of nozzle geometry. J. Imag. Sci. Technol. 43, 145–152 (1999)
McIlroy, C., Harlen, O.G.: Effects of drive amplitude on continuous jet break-up. Phys. Fluids 31(6), 064104 (2019)
Moallemi, N., Li, R., Mehravaran, K.: Breakup of capillary jets with different disturbances. Phys. Fluids 28, 012101 (2016)
Nayfeh, A.H.: Nonlinear stability of a liquid jet. Phys. Fluids 13, 841–847 (1970)
Notz, P.K., Basaran, O.A.: Dynamics and breakup of a contracting liquid filament. J. Fluid Mech. 512, 223–256 (2004)
Pimbley, W.T., Lee, H.C.: Satellite droplet formation in a liquid jet. IBM J. Res. Dev. 21(1), 21–30 (1977)
Plateau, J.A.F.: Statique Expérimentale et Théorique Des Liquides Soumis Aux Seules Forces Moléculaires, vol. 2. Gauthier-Villars (1873)
Rayleigh, L.: On the Capillary Phenomena of Jets. Proceedings of the Royal Society of London 29(196–199), 71–97 (1879)
Rutland, D.F., Jameson, G.J.: Theoretical prediction of the sizes of drops formed in the breakup of capillary jets. Chem. Eng. Sci. 25(11), 1689–1698 (1970)
Rutland, D.F., Jameson, G.J.: A non-linear effect in the capillary instability of liquid jets. J. Fluid Mech. 46, 267–271 (1971)
Savart, F.: Constitution of a liquid jet flowing through a circular orifice in a thin diaphragm. Ann. Chim. Phys. 53, 337–386 (1833)
Schulkes, R.M.S.M.: The contraction of liquid filaments. J. Fluid Mech. 309, 277–300 (1996)
Taylor, G.I.: The dynamics of thin sheets of fluid. III. Disintegration of fluid sheets. Proc. Royal Soc. London 253, 313–321 (1959)
Vassallo, P., Ashgriz, N.: Satellite formation and merging in liquid jet breakup. Proc. Royal Soc. A Math. Phys. Eng. Sci. 433(1888), 269–286 (1991)
von Ohnesorge, W.: Die Bildung von Tropfen an Duesen und die Aufloesung fluessiger Strahlen. Zeitschrift fuer angewandte Mathematik und Mechanik 16(6), 355–358 (1936)
Weber, C.: Zum Zerfall eines Flussigkeitsstrahles. Zeitschrift fuer angewandte Mathematik und Mechanik 11(2), 136–154 (1931)
Widnall, S.E., Sullivan, J.P.: On the stability of vortex rings. Proc. Royal Soc. A Math. Phys. Eng. Sci. 332(1590), 335–353 (1973)
Yuen, M.-C.: Non-linear capillary instability of a liquid jet. J. Fluid Mech. 33, 151–163 (1968)
Acknowledgements
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), grant number 420239128, and the Engineering and Physical Sciences Research Council (EPSRC), Grant Numbers EP/P024173/1 and EP/S029966/1. AACP was financially supported by the Royal Society through a Research Fellowship, URF-R-180016, and an Enhancement Grant, RGF-EA-181002.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Denner, F., Evrard, F., Castrejón-Pita, A.A. et al. Reversal and Inversion of Capillary Jet Breakup at Large Excitation Amplitudes. Flow Turbulence Combust 108, 843–863 (2022). https://doi.org/10.1007/s10494-021-00291-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10494-021-00291-w