Abstract
A computational investigation of three configurations of the Delft Spray in Hot-diluted Co-flow (DSHC) is presented. The selected burner comprises a hollow cone pressure swirl atomiser, injecting an ethanol spray, located in the centre of a hot co-flow generator, with the conditions studied corresponding to Moderate or Intense Low-oxygen Dilution (MILD) combustion. The simulations are performed in the context of Large Eddy Simulation (LES) in combination with a transport equation for the joint probability density function (pdf) of the scalars, solved using the Eulerian stochastic field method. The liquid phase is simulated by the use of a Lagrangian point particle approach, where the sub-grid-scale interactions are modelled with a stochastic approach. Droplet breakup is represented by a simple primary breakup model in combination with a stochastic secondary breakup formulation. The approach requires only a minimal knowledge of the fuel injector and avoids the need to specify droplet size and velocity distributions at the injection point. The method produces satisfactory agreement with the experimental data and the velocity fields of the gas and liquid phase both averaged and ‘size-class by size-class’ are well depicted. Two widely accepted evaporation models, utilising a phase equilibrium assumption, are used to investigate the influence of evaporation on the evolution of the liquid phase and the effects on the flame. An analysis on the dynamics of stabilisation sheds light on the importance of droplet size in the three spray flames; different size droplets play different roles in the stabilisation of the flames.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Spray combustion is a highly challenging physical phenomenon involving multi-scale multi-phase processes in a reacting environment. The chemical length and time scales at which reaction occurs are very small compared to the integral length and time scales of the flow. The length scales at which the breakup of the liquid film issuing from the injector occur are also much smaller than those of the flow considered. Thus in order to perform large scale simulations, whilst operating at the optimum point between computational cost and accuracy, the extensive use of models is required. It is therefore important to understand the consequences of the modelling choices so as to better interpret the results and be aware of their predictive limitations.
If a simulation of any practical device is to be performed then Large Eddy Simulation (LES) provides a satisfactory degree of detail while keeping the computational cost reasonable. While Direct Numerical Simulation (DNS) studies may provide fundamental insights into MILD combustion regimes (van Oijen 2013; Minamoto and Swaminathan 2014), due to the very large computing requirements, especially for high Reynolds number flows, it is not currently feasible for industrial scale devices. In contrast the less expensive Reynolds Averaged Navier-Stokes (RANS) approach does not provide sufficient information on the interaction between the gas and the liquid phases.
In the present paper the Delft Spray in Hot-diluted Co-flow (DSHC) burner, used in one of the few detailed studies of Moderate or Intense Low-oxygen Dilution (MILD) combustion available, has been simulated. The experimental investigation was performed in TU Delft by Roekaerts et al. (Correia Rodrigues et al. 2015a, b), and provides a comprehensive characterisation of both the gaseous and liquid phase in terms of the velocity and temperature fields. Different co-flow temperatures are considered experimentally and present work describes the results of simulation of three cases measured.
The DSHC has been studied numerically at TU Delft by Roekaerts et al. (Ma et al. 2015; Ma and Roekaerts 2016a, b, c), Motaalegh Mahalegi and Mardani 2019 and by the authors (Gallot-Lavallée et al. 2016). The groups employ different approaches for modelling combustion. Roekaerts et al apply Flamelet Generated Manifolds (FGM), which is based on tabulation of the chemical mechanism in terms of two variables, mixture fraction and reaction progress variable. Hence the local temperature and chemical composition is ultimately based on the tabulated flamelets. The approach has been applied using both RANS and LES. In Motaalegh Mahalegi and Mardani (2019) the approach adopted is RANS, the EDC combustion model (with a skeletal chemical mechanism) and the Lagrangian tracking of droplets. In contrast Gallot-Lavallée et al. (2016) applied the stochastic fields method to solve the modelled transport equation for the joint pdf of the scalars (mass fractions and enthalpy) needed to describe reaction. The method allows for a comprehensive description of the chemical reaction mechanism used and no explicit assumptions regarding the mode of burning are required. It provides a more detailed description of the underlying chemical mechanisms. For the liquid phase Ma et al. (2015), Ma and Roekaerts (2016a), Ma and Roekaerts (2016b), Ma and Roekaerts (2016c) and Gallot-Lavallée et al. (2016) both used a Lagrangian point particle approach, and proposed a conditional injection method (Gallot-Lavallée et al. 2016; Ma and Roekaerts 2016a) to characterise he injection process. This requires assumptions regarding the distribution of droplet diameter at the injection location and adjustments are required on a case specific basis.
In the present work LES is applied with the stochastic fields method being used for the gas phase conjunction together with a Lagrangian point particle approach for the dispersed phase. The influence of sub-grid-scale (sgs) fluctuations on droplet dispersion are represented in a stochastic fashion as proposed by Bini and Jones (2008). The code used for this simulation is the in-house BOFFIN (Jones et al. 2002) which has previously been used to simulate a range of flames, for example a stratified flame (Brauner et al. 2016), gas turbine combustor (Jones et al. 2014, 2015), methanol spray flame (Jones et al. 2015) and the Sandia n-heptane spray flame (Gallot Lavallée and Jones 2016) amongst others.
The major aim of the present paper is to devise an injection model whereby the number of parameters needed to characterise the injector is minimised and the need to specify a droplet size and velocity distribution at the injection point is avoided. One possible alternative would be to adopt a complete and full multi-phase flow formulation. An example of such an approach is provided in Xiao et al. (2014a) and Xiao et al. (2014b) where an LES of a single drop and liquid jet breakup are considered. However, a full two-phase computation requires an extremely fine mesh and to combine this with a spray flame computation is likely to be prohibitively computationally expensive at the present time. As an alternative a simple primary droplet breakup model is combined with a probabilistic formulation of secondary breakup. The primary breakup model represents droplet formation via instabilities of the incoming fuel jet/sheet and provides an estimate of the resulting mean droplet size. Droplets of this size are then injected into the domain with a velocity determined by the fuel flow rate and the injector geometry; the subsequent secondary droplet breakup then being determined via a probabilistic formulation. The secondary breakup model is based on that proposed in Jones and Lettieri (2010). A similar approach using a different stochastic breakup model is described in Irannejad and Jaberi (2014). The influence of two equilibrium-based evaporation models, widely accepted in the literature Chen and Pereira (1996), are also investigated to provide an improved understanding of the dynamics of spray flame stabilisation. A preliminary study on a single droplet is used to provide insight into general characteristics of the models. In the spray flame the two models are compared in respect of the gaseous and liquid phase velocity fields and the flame structure and species production. The effect of the boundary conditions on flame stabilisation are also discussed.
In the first section of the paper a description of the mathematical models is provided, followed by the description of the experimental and numerical configuration. The results are then presented for a single droplet case and for the experimentally studied flames. A summary of the conclusions drawn follows.
2 Mathematical Modelling
Simulating a spray flame requires a careful choice of the different available modelling techniques in order to achieve accurate results whilst keeping the computational cost affordable. Specifically LES is adopted for the solution of the gas phase equations describing the evolution of the scalars and vector fields. In LES a spatial filter is applied to the equations of motion thereby filtering out the fine sub-filter scales from the equations. The method thus involves the direct simulation of large scale motions, which represent the most significant part of the energy spectrum, while the effects of the small, least energetic scales are modelled. Simple eddy viscosity models are conventionally adopted for the small sub-grid scale (sgs) fluctuations. Providing the Reynolds number, based on both viscosity and the sgs viscosity remains large, then the main role of the sgs model is to provide a mechanism for the dissipation of kinetic energy, (Wille 1997; Pope 2004). As a consequence results are relatively insensitive to the sgs closure model used and their direct influence on transport are negligible. The solution of the scalar fields is obtained via the use of the joint sgs-pdf solved by means of the stochastic field method. In this context the multi-phase flow is represented by the Lagrangian point particle approach, the atomisation process is accounted by a stochastic model for breakup.
2.1 Continuous Phase
2.1.1 Fluid Filtered Equations
In order to obtain the equations to be solved in LES, the equations of motion are filtered in order to separate the large scales from the small. The spatial filtering operator applied to a general function \(f = f ({\mathbf{x }},t)\) is defined in the physical space as:
where \(\varOmega\) is the integration domain, G is the filter function that must satisfy the normalisation property:
The density variations in the unresolved scales that arise in combusting flows can be treated through the use of density weighted, or Favre, filtering, defined by \({\tilde{f}} ({\mathbf {x}},t) = \overline{\rho f}/ \overline{\rho }\). With the inclusion of the contribution from the dispersed phase—treated as point sources— the application of the density weighted filtering operation to the equations of motion results in:
where \(\rho _g\) is the density of the gaseous phase, \(u_j\) is the gas phase velocity, \(\mu\) is the viscosity, p is the static pressure and \(e_{ij}\) is the strain tensor. It is noted that the use of the Favre filter operator results in Eq. (3) appearing in closed form. The terms \(\dot{m}\) and \(\dot{m}_{mom}\) represent sources of mass and momentum arising from evaporating spray. The sub-grid scale stress tensor \(\tau ^{sgs}_{ij} = \overline{\rho } \left( \widetilde{u_i u_j} - {\widetilde{u}}_i{\widetilde{u}}_j \right)\) is determined via the dynamically calibrated version of the Smagorinsky model proposed by Piomelli and Liu (1995).
2.1.2 Scalar Equations
In the present work the variation in thermodynamic pressure can be neglected and the unity Lewis (Le) number approximation is invoked so that a homologous equation for the species conservation and energy can be written:
where \(\phi _\alpha\) is the \(\alpha ^{th}\) scalar field, \({\mathscr {J}}^{sgs}\) is the sub-grid flux, \(\dot{m}_\alpha\) represents the rate of addition of mass of species \(\alpha\) to the continuous phase per unit volume through droplet evaporation and \(\sigma\) is the Prandtl or Schmidt number. The filtered form of the conservation equations for the chemical species contain the filtered net formation rate through chemical reaction, \(\overline{\rho _g \dot{\omega }_{\alpha }}\). The direct evaluation of this poses serious difficulties and the equation is not solved directly, instead a joint sgs-pdf evolution equation formulation is adopted.
The source terms appearing in the gas phase equations (3) and (4) are evaluated as: \(\bar{\dot{m}}=\frac{1}{{\varDelta }^{3}} \sum _{p=1}^{n}m^{(p)}\) where n is the number of droplets contained within the finite volume cell and \(m^{(p)}\) is the source term arising from the \(p^{th}\) droplet.
2.2 Sub-Grid Joint pdf
An exact equation describing the evolution of the joint sub-grid (more strictly the fine grained) pdf (\({P}_{\mathrm {sgs}}\)) defined as:
can be derived by standard methods, e.g. Gao and O’Brien (1993). Following the approach of Brauner et al. (2016) the resolved part of the convection and ‘molecular’ mixing are added to both sides of the equation so that the modelled form the equation becomes:
where \(\sigma _{sgs}\) is assigned the value 0.7 and \(\dot{\omega }_\alpha (\underline{\psi })\) is, in the case of chemical species, the net formation rate through chemical reaction. The terms on the rhs of equation represent sgs-transport of pdf and sgs micro-mixing respectively, which are represented by a Smagorinsky type gradient model and by the Linear Mean Square Estimation (LMSE) closure (Dopazo 1979). The micro-mixing constant \(C_d\) is 2.0 and the time-scale is given by \(\tau _{sgs}=\frac{\overline{\rho }\varDelta ^2}{\mu _{sgs}}\). The role of the micro-mixing term is to drive instantaneous chemical compositions or enthalpy of the \(n^{th}\) field towards their filtered mean value according to the sub-grid time scale. Equation (7) has the merit of becoming exact in the DNS limit or where sgs variations are negligible. In the present work this equation describing the evolution of the pdf is solved using the stochastic fields method.
2.3 Stochastic Field Method
The temporal evolution of the joint sgs-pdf is represented by an ensemble of N stochastic fields, with each field involving the \(N_s\) scalars, namely \(\xi _{\alpha }^{n} (\varvec{x},t)\) with \(1 \le n \le N\) and \(1 \le \alpha \le N_s\). In the present work the Itô formulation of the stochastic integral is adopted and the influence of the sgs fluctuations of the dispersed phase is neglected (Jones et al. 2016). Thus the fields evolves according to:
The stochastic fields given by Eq. (8) are not to be mistaken with any particular realisation of the real field, but rather form an equivalent stochastic system (both sets have the same one-point pdf, (Gardiner 1983)) smooth on the scale of the filter width. From the set of stochastic fields is possible to calculate the instantaneous mean field:
The liquid-phase contributions to Eq. (8) are evaluated via the spray equations, described below, using the continuous phase values of species concentrations and temperature.
2.4 Discrete Phase
The droplets are presumed to be sufficiently small as to be represented by point sources for the continuous phase and the spray is assumed ‘dilute’, (Jenny et al. 2012). Following the work of Bini and Jones (2008), a probabilistic representation of the spray is adopted. The spray pdf is described as a function of a set of macroscopic variables: the droplet radius, r, velocity \({\mathbf {v}}\), temperature \(\theta\). If, as is the present case, the breakup process is considered, the droplet number \({\mathscr {N}}\) is also to be included. In the present case the equation for the evolution of the corresponding joint pdf \({\bar{P}}_p(r,{\mathbf {v}}, \theta , n; {\mathbf {x}},t)\) is:
where \(a_j\) is the conditional particle acceleration, \(\dot{R}\) the conditional rate of change of the droplet size through evaporation, \(\dot{\varTheta }\) the conditional rate of change of droplet temperature caused by heat transfer from the surrounding gas phase, and \(\dot{\mathscr {N}}\) is the conditional rate of change of the number of droplets due to the breakup. Considering the state space \({\mathbf {\Phi }} = \left\{ {\mathbf {v}},r,\theta ,n \right\}\) to be a realisation of the sampling space \({\mathbf {\Psi }} = \left\{ v_j,R,\varTheta ,{\mathscr {N}}\right\}\), the rates of changes appearing Eq. (10) can be written in a general form as:
where the expectation of the rate of change of the state variable \(D\psi / Dt\) is conditioned upon \({\mathbf \Psi} = {\mathbf \Phi}\). The solution of the LES-pdf equations provides the deterministic instantaneous mean values of the scalar and velocity field of the gaseous phase at the droplet location. The particles are treated as point sources so that the fluctuations at the unresolved sub-grid-scales have an impact on the evolution of the droplets. The effect of the fluctuations of velocity and scalar fields such as temperature and mixture composition of the carrier phase must therefore be taken into account and modelled. To achieve this, Eq. (10) is first replaced with a set of stochastic differential equations as described in Bini and Jones (2007), which utilises a stochastic Markov model to represent the unresolved fluctuations. This stochastic particle approach (Jones and Sheen 1999; Bini and Jones 2007; Bini 2007) is consistent with the stochastic approach to the solution of the joint sub-grid pdf for the continuous phase.
2.4.1 Droplet Dispersion
The velocity of the droplets is obtained by the sum of deterministic contribution as formulated by Maxey and Riley (1983), and by a stochastic contribution as follow:
where \({\mathbf {V}}^{\left( p\right) }\) is the velocity of the \(p\)th particle, \(\widetilde{{\mathbf {U}}}\) is the filtered gas velocity at the droplet location, \(k_{sgs}\) is the unresolved kinetic energy of the gas phase, \(C_o\) is a model constant with an assumed value of unity, \({\mathbf {g}}\) is the gravitational acceleration, \(d{\mathbf{W }}_{t}\) represents the increment of the Wiener process and \(\tau _t\) is a sub-grid time scale which affects the rate of interaction between the droplet and turbulence dynamics, defined as: \({\tau _t}=\frac{\tau _p^{2\alpha }}{\left( {\frac{\varDelta }{{k_{sgs}}^{1/2}}}\right) ^{2\alpha -1}}\). The particle relaxation time, \(\tau _p\) is given by: \(\tau ^{-1}_{p} =\frac{3}{8}\frac{\rho _{f} C_{D}}{ \rho _{p} r_p} |{\mathbf {U}}-{\mathbf {V}}|\) where the drag coefficient \(C_{D}\) is obtained from Yuen and Chen (1976):
where Re is the Reynolds number based on the droplet diameter and the relative velocity of the droplet with respect to the gas phase. The sgs kinetic energy is obtained from: \(k_{sgs} = \left( 2 \varDelta \nu _{sgs} e_{ij} e_{ij}\right) ^{2/3}\) an expression derived using equilibrium arguments.
2.4.2 Droplet Breakup
The atomisation process that leads to a fluid film breaking up into droplets is certainly among the important challenges in spray simulations. One possible choice is to represent this phenomena by assuming an initial distribution of diameters based on empirical correlations, as reviewed in Lefebvre (1988), and use a conditional injection method to reproduce the specific characteristics of the injector. This approach has been previously applied to the simulation of the present experimental configuration using two different conditional injection models Gallot-Lavallée et al. (2016); Ma and Roekaerts (2016a). Both are based on a probabilistic injection process around the nominal injection angle, where the velocity of the droplet varies depending on the droplet size. However, the introduction of a suitable breakup model would allow the injection of droplets at a fixed size and angle, that will then break and disperse without any a priori assumptions regarding injection droplet size and velocity distributions.
A fuel injector is characterised by the injection of the liquid fuel in the form of a jet or sheet which becomes unstable and breaks up to form fragments of liquid of varied shapes and sizes (Lefebvre 1988; Gorokhovski and Herrmann 2008). The direct numerical simulation of this process requires a full multi-phase calculation and a mesh sufficiently fine to resolve it; an approach which is extremely computationally expensive. In the present work a simpler approach is adopted. The aim of the breakup model for primary atomisation is to reproduce the spray by specifying as few parameters as possible. Consequently the average diameter is calculated using the Linear Stability Analysis (LISA) (Senecal et al. 1999) model. The nominal injection angle is determined by the injector geometry and a normal distribution around that value is added to reproduce the oscillatory behaviour of the primary atomisation. The droplet velocity is determined by the fuel flow-rate.
The secondary breakup model used is the improved version of Noh et al. (Jones et al. 2016) of the previously proposed model by Jones and Lettieri (2010). The rate of change of the droplet number \(\dot{{\mathscr {N}}}\) in Eq. (10) is described with a discrete Poisson process; the distribution of the droplet sizes originated from the breaking event is described by a pdf that varies depending on the turbulence surrounding the droplet. The rate of change of the number of droplets through breakup (Lasheras et al. 2002) is given by:
where \(f(r,r_0)\) is the pdf of the size distribution of the daughter droplet arising from the breakup of a droplet of size \(r_0\), \(m(r_0)\) is the mean number of droplets originated from a droplet of size \(r_0\), the breakup event occurs at a frequency of \(\omega (\epsilon ,r_0)\), generating a probable number of daughter droplets \(n(r_0,t)\) in the range \(r_0 +dr\) at time t. The breakup frequency, function of the radius r and the dissipation of kinetic energy \(\epsilon\), is modelled to comprise a deterministic and stochastic contribution. The former due to the disruptive effect of aerodynamic forces and the latter to the fluctuations of the dissipation rate of turbulent kinetic energy. The expression used for \(\omega (\epsilon ,r)\) is:
where \(\sigma _s\) is the surface tension of the liquid phase, \(\beta = 8.2\), (Batchelor 1953) and \(K_g\) is assigned the value 2.0. The deterministic contribution to the breakup frequency is modelled to be the inverse of the breakup time scale (O’Rourke and Amsden 1987). The modelling of the stochastic part is based on the work from Martínez-Bazán et al. (1999) where the disruption of air bubbles in a turbulent water flow was investigated. It was observed that the frequency of the breakup events are dependent on the sgs dissipation of kinetic energy given by \(\epsilon = 2 \left( \mu + \mu _{sgs} \right) {\tilde{S}}_{ij} {\tilde{S}}_{ij}\). The model parameter \(K_g\) in the case of air bubbles was experimentally determined to be 0.25 and the methodology has been extended to the breakup of liquid jets in gas flow by Lasheras et al. (2002), Lasheras et al. (1998).
The pdf of the size distribution of the daughter droplets \(f(r,r_0)\) can be modelled following three approaches (Martínez-Bazán et al. 1999; Semiao et al. 1996; Babinsky and Sojka 2002): statistical models, phenomenological models based on the surface energy of a breaking droplet, and mixed models. Following the extended work of Martínez-Bazán et al. (2010) based on Martínez-Bazán et al. (1999), the following model is adopted:
where \(r*=r_1/r_0\) and \(\varLambda = r_c/r_0\). The critical radius \(r_c = [12\sigma /(\beta \rho )]^{3/5}\epsilon ^{-2/5}\) determines the threshold radius of the mother droplet \(r_0\) above which it experience breakup. The radii of the mass conserving daughter droplets \(r_1\) and \(r_2\) can be obtained using the inverse transform sampling method. However if the breakup problem is treated from a trajectory point of view then this would allow the daughter droplets to have trajectories independent of each other in the phase space. This would in turn require a continuous approach, leading to excessive computational costs. For this reason the breakup event is approximated as a discrete Poisson release process (Jones and Lettieri 2010). The number of broken droplets in a time interval \(t_0 + dt\) is then obtained from:
where \(N_t(r)\) is the number of droplets with diameter r at a given time t.
To summarise the model, if a droplet is injected in the computational domain with a nominal radius r, then providing this is larger than \(r_c\) and the time following injection \(\varDelta t\) is greater than the expected lifetime \(t_{break} = 1/\omega\) the droplet will breakup. The effective breakup frequency \(\omega\) is obtained by sampling a Poisson distribution with mean computed from the breakup frequency given by Eq.(15). The process will continue until the droplet radius becomes smaller than \(r_c\), the number of droplets generated in the breakup \(m(r_0)\) is computed as the sum of the number of daughter particles. The interested reader is referred to Jones et al. (2016), Noh (2016) for further details.
2.4.3 Droplet Evaporation
The evaporation of droplets has been extensively studied Miller et al. (1998) where they observed experimentally the evaporation of different liquid fuels and compared it numerically with several evaporation models. In many circumstances the equilibrium evaporation formulations are found to be comparable to the non-equilibrium. In this study, the droplet evaporation is described using two widely established evaporation models: the rapid-mixing or infinite conductivity model and its corrected version, Sirignano (1983) that incorporates the effect of Stefan flow on the heat and mass transfer. The first will be referred to as R-M and the second as A-S. The Biot number is small and the internal droplet temperature distribution may be assumed homogeneous. Thus phase equilibrium conditions may be presumed at the droplet surface (Faeth 1983). Under these assumptions the temperature \(\theta ^{(p)}\) and mass \(m^{(p)}\) of a single droplet i can be expressed as (Miller et al. 1998; Bini 2007):
where \(\theta _g\) is the carrier gas temperature at the \(p^{th}\) particle position, \(h_{fg}\) is the latent heat of evaporation, \(C_{p,g}\) and \(C_{p,\ell }\) are the gas and liquid heat capacities at constant pressure, \(Pr_g\) and \(Sc_g\) are the gas-phase Prandtl and Schmidt numbers while the Nusselt, \(Nu^*\) and Sherwood, \(Sh^*\) numbers appears in a modified form to account for convection of heat and mass transfer. In this context two different models are evaluated (Ranz and Marshall 1952; Clift et al. 2005); \(k_1\) is defined differently in the two models. The parameter \(f_2\) is a heat transfer correction due to the evaporation of the droplet, \(H_M\) represents the driving force for mass transfer, and \(H_{\varDelta \theta }\) represents an additional terms to correct the assumption of infinite liquid thermal conductivity. The two model selected differs to one another according to Table 1.
Where \(B_T\) and \(B_M\) are respectively the heat and mass transfer Spalding numbers, and \(C_{p,v}\) is the heat capacity of the vapour of the liquid phase. A brief description of the fundamental assumptions involved in the two methods is outlined below. Also, to take into account the sub-grid-scales fluctuations in the continuous phase, a stochastic vaporisation modification is added and is described later in the paper.
The models are found to be sensitive to the values of thermo-physical properties (Miller et al. 1998). The established \({1/3}^{rd}\) rule (Hubbard et al. 1975) is used to estimate the properties of the gas mixture, while the heat capacities and enthalpy (Burcat and Ruscic 2005) are obtained from JANAF polynomials; the other properties are estimated according to the kinetic theory of gases (Kuo 1986; Chung et al. 1988, 1984).
Rapid Mixing. This is the classical evaporation model (Spalding 1953; Godsave 1953), its main advantage is its simplicity of the implementation. No correction to the evaporation due to heat transfer or for Stefan flow is included and infinite thermal conductivity is assumed (\(H_{\varDelta \theta } = 0\)). A quasi-steady condition for the gas phase is also assumed (\(H_M = \ln (1 + B_M)\)) where the Spalding number is defined by \(B_M = \frac{Y_{f,\infty } -Y_{f,s}}{Y_{f,s}-1}\) with \(Y_f\) being gas-phase mass fractions. The Nusselt and Sherwood numbers are calculated using the Ranz and Marshall (1952).
Abramzon Sirignano. The Abramzon and Sirignano model (Sirignano 1989) is a revised version of the R-M model to include the effect of Stefan flow, the Spalding heat transfer number \(B'_T\) is modified as follow:
where \(F_M\) and \(F_T\) are given by:
In this case, according to Sirignano (1989), the Ranz-Marshall correlations can lead to an over estimation of mass transfer rates at low Reynolds numbers, therefore the correlation of Clift et al. (2005) is used. The method requires an iterative method for the determination of \(B'_T\) resulting in an increase in the computational cost, that is however limited as the algorithm converges, typically in a few iterations; for further details on the implementation of the method, refer to Noh (2016). Both models imply that the rate of change of droplet diameter increases rapidly as the droplets temperatures approach the saturation temperature—the rate of change approaches infinity as the saturation temperature is reached. As a consequence the droplets evaporate rapidly as the saturation temperature is approached and effectively disappear well before it is reached. A discussion on a simulation of the evaporation of a single droplet compared to experimental data will provide the basis for the interpretation of the results from the simulations of the lab-scale configuration. An important aspect of the two models is that the parameter \(k_1\) in the case of A-S differs from that of the case R-M.
Stochastic vaporisation modification. Following the work of Bini and Jones (2007), the influence of the sgs fluctuations on the evolution of the droplets is accounted for by a modification of the Sherwood number, and following (Gallot-Lavallée et al. 2016) the Nusselt number is modified in a similar fashion. This is achieved by separating \(Sh^*\) and \(Nu^*\) into a stochastic and deterministic component: \({\mathscr {A}}^* = {\mathscr {A}}^{det} + {\mathscr {A}}^{sgs}\) where the deterministic component is computed as previously discussed depending on the evaporation model selected. The stochastic component is constructed (consistent with the stochastic particle approach) by the use of a Wiener process that guarantees continuity, randomness and is physically realistic. The formulation is as follow:
where \({\mathscr {B}}_g\) is the gas phase Schmidt or Prandtl number as appropriate.
3 Experimental Configuration
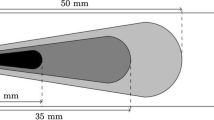
The burner simulated in this paper is the Delft Spray in a Hot-diluted Co-flow (DSHC) studied experimentally by Roekaerts at al. (Correia Rodrigues et al. 2015a, b). A schematic of the configuration is shown in Fig. 1. It comprises a cylindrical burner with 180 mm diameter in which a hot co-flow is generated by the combustion of lean fuel mixture Dutch Natural Gas (DNG) and air and the centreline a commercial hollow cone pressure swirl atomiser (WDA 0.5) produced by Delavan is used to inject liquid ethanol.
The nominal cone angle of the injector is \(\eta = 30^\circ\) and the injection pressure for the three cases is 1.2 MPa. A large number of cases were measured involving different co-flow temperatures, oxygen concentrations, fuel mass flow rate and velocity of the co-flow (Correia Rodrigues et al. 2015a, b). The cases simulated in the present study are shown in Table 2.
At the end of the co-flow generator (location referred as \(z=0\) indicated in Fig. 1) Laser Doppler Anemometry (LDA) was used to measure the axial and radial velocity components of the co-flow to provide detailed information on the boundary conditions. To characterise the droplets velocities and size simultaneously, a Phase Doppler Anemometry (PDA) measurement was performed allowing a direct comparison on a class-by-class size basis to be made. The temperature profiles were measured by means of Coherent Anti-Stokes Raman Scattering (CARS) technique both at \(z=0\) and in the spray flame. A flue gas analyser was employed to characterise the chemical species at the location \(z=0\).
4 Solution Method
The simulations are performed using the in-house code BOFFIN, a block structured highly parallelised code using MPI for inter-processor communication. It comprises a pressure based finite-volume incompressible formulation further details of which are provided in Jones and Prasad (2010). An approximate factorisation method is used for chemical reaction in which the time step is sub-divided to ensure that numerically accurate solutions are obtained. The discrete phase equations are solved using the method described in Bini and Jones (2008). In the present case eight stochastic fields are used, as it has previously been found that an increase of this value did not bring significant changes to time averaged results. The mesh used to encompass the cylindrical geometry was of height \(h=180~mm\) and diameter \(D =160~mm\) comprised 198 blocks with \(\sim 20,000\) elements in each with a total of \(\sim 4 \cdot 10^6\) nodes. The computational domain and mesh are shown in Fig. 2 where, a view from the bottom is also included.
The mesh is arranged so that a finer spacing of 0.2 mm is used in the central region, corresponding to the location of the injector. This provides for greater resolution of the atomisation process that occurs in this region. An exponential expansion in the radial direction up to 2 mm maintains an expansion ratio \(< 8\%\) to minimise commutation errors. In the axial direction (parallel to the flow) finer spacing of 0.2 mm is used in the vicinity of the injector while the coarser spacing of 4mm is used towards the outlet of the domain. The time-step is fixed at \(\varDelta t = 1\times 10^{-7}~s\). Simulations were carried out for 10 flow through times based on the bulk velocity and flame length to ‘wash-out’ the effects of initial conditions and statistics were then collected over further 15 flow through times. The reduced chemical mechanism for ethanol of Bhagatwala et al. (2014), involving 28 species, was used to describe reaction.
4.1 Boundary Conditions
The profiles for the inlet boundary conditions in the three cases in terms of chemical species, velocity and temperature were provided experimentally. At the outlet of the domain a zero gradient boundary condition is applied and at the walls a free slip condition is used. For the liquid phase boundary conditions no experimental information is available but only an estimate of the initial diameter and the velocity of the injected droplets is required and these are estimated using the LISA (Senecal et al. 1999) model resulting in an injected diameter of \(d_0 = 43~\mu m\) and axial velocity of \(\sim 28~m/s\). The nominal injection angle is fixed by the injector, and a normal distribution with a standard deviation (\(\sigma = 15^{\circ }\)), around that value is applied to reproduce the oscillatory behaviour of the primary atomisation. An instantaneous snapshot of the droplets under test-like conditions is presented, from a side view, in Fig. 3 and, from above the injector, in Fig. 4: in both figures the plotted size of the droplets is proportional to their physical size.
Plane sections of the domain orthogonal to the flow field at different axial locations. The droplets diameters are scaled on the physical diameters and the colour scheme follows the legend in Fig. 3
The figure refers to case \(H_{II}\) and serve to illustrate the simulated breakup process. In Fig. 3 shows results in a plane passing through the centerline and containing the injector with the bottom figure providing an expanded view to provide more insight on the region of initial breakup. Figure 4 presents horizontal sections orthogonal to the flow field at different axial locations.
All droplets are injected with the same diameter and the mean injection angle is also fixed but there is a small variation in the latter due to the normal distribution imposed. The size and velocity of injected droplets implies that they are roughly one diameter apart close to the injection point. After few millimetres the breakup process occurs, and the small daughter droplets tend to travel towards the centre of the spray whilst the larger ones maintain their original trajectory. This is mainly due to the momentum exchange with the gas phase that results in small droplets loosing momentum rapidly while the large droplets exhibit a ballistic behaviour. The phenomena is clearly visible in Fig. 4 where the droplets start to separate after 1 mm and at 4 mm a clear segregation is visible indicated by the sub-green droplets. These locations are far from the flame and as a consequence there is no direct interactions with it in this region. In the near injector region the diameter reduction is dominated by the breakup process but beyond this the diameters of most of the droplets fall below the critical value for breakup and evaporation appears to be dominant resulting in complete droplet evaporation beyond \(\sim 50~mm\) in this specific case.
5 Results
In this section a brief analysis for the case of a single evaporating droplet is presented to provide an insight on the performance of the different evaporation models. This is followed by a comparison of results of the simulations with the experimental data and the analysis of the results. The results are presented in three sections: the gaseous phase, the liquid phase and the flames.
5.1 Single Droplet Evaporation
In order to evaluate the performance of the different evaporation models, the evaporation of a single droplet in stagnant surroundings was computed and the results compared with the measurements of Saharin et al. (2012) taken using the cross wire technique. The droplets are ethanol and evaporate into an environment of 99.95% \(N_2\) in order to prevent the ignition of the evaporated fuel vapour. Two of the reported cases have been used for comparison. The first has an initial diameter of \(d_0 = 609~\mu m\) and temperature of \(T_0 = 473~K\) while the second has \(d_0 = 430~\mu m\), \(T_0 = 673~K\). The temporal evolution of the droplet diameter is measured by means of a high speed video camera. The droplet diameters studied are much larger than those to be found in a typical fuel injector where single droplet measurements are understandably not available. The computations are performed using the same algorithm as used in the LES code, although here it is applied to a single particle. The surrounding mixture is stagnant and represented by reference values as in the LES code. In a spray the evaporation results in an increase in the local mixture fraction and changes to the gas phase velocity, both of which are constrained in the single droplet case.
Both the R-M and A-S evaporation models are evaluated and the results are presented in Fig. 5, where the classical \(d^2\) law is observed both in the experiments and the computations.
Comparison of experimental Saharin et al. (2012) and simulated single droplet evaporation at different initial diameters and initial temperature. Left: initial diameter 609 \(\mu m\) and temperature 473 K. Right: initial diameter 430 \(\mu m\) and temperature 673 K
It is interesting to observe how the ethanol droplets deviate from a linear behaviour for small diameters. This is probably associated with the non perfect anhydrous composition of the droplets. Due to the high volatility of ethanol, water will be segregated and therefore evaporate at the end of the evaporation process. Furthermore, the accuracy of the cross-wire technique for very small droplets is not fully understood and can be a source of error. The results in Fig. 5 highlight how the R-M model over predicts the evaporation rates obtained experimentally, while the A-S model closely reproduces the measurements. At the higher temperature the evaporation process is very fast and the time scales are correspondingly much shorter. At the lower temperature the discrepancy is larger with both models though the diameter decay rate is reproduced more accurately by the A-S model over much of the diameter range. The study of the single droplet evaporation indicates that the A-S model is able to represent the measured evaporation rates more closely of the R-M model. The effects of the use of these to models in LES is discussed in the following sections.
5.2 Gaseous Phase
In this section the velocity profiles at different axial location for the three different cases are presented. The different radial profiles for the axial velocity are shown for case \(H_I\) in Fig. 6, for case \(H_{II}\) in Fig. 7, and for case \(H_{III}\) in Fig. 8.
The use of the two different evaporation models does not appear to influence the gas phase velocities appreciably. Only in the case \(H_I\) with the A-S model is there a somewhat larger dispersion of the axial velocity at the axial location \(z = 30~mm\).
The similarity of the profiles when comparing the two evaporation models is due to the fact that the interaction between the phases is greatest when the liquid volume fraction highest. This occurs in the region close to the injector where neither the dispersion nor the breakup is significant and for the three cases, a ‘double maximum’ in the axial velocity profile is observed. This is typical of the profile resulting from a hollow con injector. It is to be noted that the experimental velocity profiles displays a small asymmetry, which can be either due to a production defect in the injector or a measure of the uncertainty in the measurements. The comparisons with the experimental data show that the profile at the first measurement location is reproduced more accurately than those further downstream. Generally the comparisons, with the exception of \(H_I\) at \(z=30mm\), show a slight over-prediction in the velocity profiles that could be linked to an excessive dispersion of the droplets at downstream locations resulting in greater transfer of momentum to the gas phase. This does not appear likely, however, as the momentum exchange is not enhanced by the different evaporation rates of the two models. The experimental data for gas phase velocity are obtained using small fuel droplets, with Stokes behaviour, as a tracer. Thus some discrepancies could also be introduced at locations close to the flame because of the different intensity of the refraction of the droplets in this region. Given that the gas phase velocity profiles are a direct result of the injection of droplets the agreement between the simulations and experiments for the three cases is overall satisfactory. The acceleration of the gas phase is caused by the ‘drag’ forces exerted by the droplets, without which the velocity would remain essentially constant and equal to that of the co-flow.
5.3 Liquid Phase
The characteristics of the dispersed phase are discussed first in terms of the Sauter Mean Diameter (SMD). The SMD is the ratio of droplet volume and droplet area and it is defined as \(SMD = \sum d^3_{(p)}/\sum d^2_{(p)}\). The radial profiles of SMD at different locations for the three flames are shown in Fig. 9.
The inlet conditions for the dispersed phase for the three cases are identical and the mass flow rates are closely similar so that the difference that occur are because of the interaction with different gas phase conditions. The droplets appear to be distributed in a wider region and with greater values of SMD as the co-flow temperatures are reduced (ie \(H_{I} \rightarrow H_{III}\)) due to the correspondingly lower evaporation rates. At the first measurement location, the difference arising from the two models is negligible because the droplets are not exposed to a hot environment for sufficient time . However, at the axial location \(z = 20~mm\) and beyond the effect of the faster evaporation rate of R-M as compared to A-S is evident. The difference is probably related to the discrepancies evident in the preliminary study performed of a single droplet. However, when the evaporation rate is sufficiently large, the difference between the results of the two models becomes increasingly less important. The agreement of the simulations with the experiments does not seems to be significantly affected by the evaporation model except at the furthermost downstream location for cases \(H_{II}\) and \(H_{III}\). In these cases and location, the rapid mixing model results in an excessively rapid evaporation rate that reduces the SMD values too rapidly compared to the experimental data.
The axial velocity profiles for the different droplet classes at different downstream location for cases \(H_{I}\), \(H_{II}\) and \(H_{III}\) are presented in Figs. 10, 11, 12 .
The statistics are collected only when a droplet of the selected class size is present in the finite volume cell in order to reproduce the experimental measurement technique as closely as possible. Each of the columns denoted with \(d = d_{i}~\mu m\), refers to droplets with diameter \(d_i - 10~\mu m< d < d_i\). The differences in the velocity profiles with the two evaporation models is due to the difference in the change in momentum of the droplets and drag. In the case where the evaporation rate is more rapid, the diameter of droplets reduces correspondingly quicker. For lower diameter droplets this results in the R-M model giving overall a larger velocities per class size than would be the case if they exhibited a ballistic type behaviour.
The droplets with larger diameters (class \(40~\mu m\)) that survive at downstream locations are those that do not experience breakup—because of the breakup frequency—and they lose little axial momentum due to their larger inertia. However, the evaporation process results in a loss of mass and momentum so that the droplets decelerate because of the reduced diameter. A similar behaviour is observed for the class \(30~\mu m\) droplets, although the smallest of the reported classes ( \(20~\mu m\)) do not appear to change there nominal velocity substantially. This is partly due to the fact that those droplets are generated from the breakup of bigger, therefore faster moving, droplets. These resulting small droplets have initially a correspondingly high velocity but after a delay time reach an ‘equilibrium’ velocity. Also, the tracer-like behaviour of the small droplets is such that they tend to converge to the gas phase velocity. This droplet class has Stokes number, evaluated using the estimated local Kolmogorov time scale, \(St > 1\), but the difference in the velocities between the droplets and gas phase is relatively small. To provide an overall representation of the liquid phase, the mean axial and radial velocities for the complete liquid phase are presented in Fig. 13.
The profiles refer to different axial locations and to the three cases. The radial velocities are plotted in the same figure, but shifted by \(v_r = v_r - 10 [m/s]\) in the interest of clarity. Generally the agreement with the experimental data appears to be good for the first two measurement locations, where the results of the two evaporation models do not differ substantially both in terms of axial and radial velocities. The difference is most evident in the last reported measurement location (ie \(z = 30 mm\)). Here, the A-S model, with its lower evaporation rate, results in a larger axial velocity as compared to the R-M model. While the effect was not entirely evident in the class-by-class results, it is more apparent in the average liquid phase velocity, which provide a global representation. The effect of the choice of the different evaporation models thus appears to be clearer in the mean representation of the dispersed phase. The discrepancy between the models increases with increasing temperatures. In the case where the evaporation rate is faster the effect of the drag on the droplets gives rise to a larger loss of momentum. Therefore, a model that over-estimates the evaporation rates introduces, as a consequence the under prediction of the average liquid velocity.
5.4 Flames
The results of the simulations are discussed in terms of the different flames properties in this section. The effect of the different co-flow temperatures and the different evaporation models is examined by observation of the species concentration and temperature profiles. The combustion regime and the interaction between the spray and the flame are also discussed.
The temperature profiles for the three different flames and the two evaporation models at different axial locations are compared with the measured data in Fig. 14. The results for both models appear to be in reasonable overall agreement with the experimental data for cases \(H_I\) and \(H_{II}\), although appreciable local differences are evident. In case \(H_{III}\) the ignition process appears to be slightly delayed in the simulations resulting in an under prediction of the temperature peak at the first measurement location.
In the three cases a comparison between the evaporation models shows that the A-S model consistently results in a thickening of the flames compared to R-M model. This is almost certainly due to the longer life of the droplets when the A-S model is used so that the droplets tend to disperse more and deliver ethanol vapour to a wider region which in turn produces a wider region of flammable gas. With the R-M model the more rapid rate of evaporation gives rise to the fuel vapour being concentrated in a narrower region, thus reducing the reactivity. A convergence study involving mesh refinement and the influence of the stochastic fields showed an insensitivity to these parameters.
An instantaneous image of the temperature in a plane containing the injection axis is presented in Fig. 15 on which contours of mixture fraction, based on carbon element, are also shown.
As expected the values of mixture fraction arising from the R-M model are higher. However with the A-S model the fuel appears to be more evenly distributed resulting in the thickening of the reaction zone discussed above. Instantaneously pockets of high mixture fraction are generated and these are associated with the interaction of the droplets with the turbulent eddying structure of the gas phase. Overall the qualitative structure of the flames shown in Fig. 15 is consistent with the profiles of Fig. 14. An increasing value of the lift-off (estimated from the mean temperature and OH contours) is observed when reducing the co-flow temperature where the agreement between lift-off of the simulations and the experimental data is excellent for both the evaporation models, as summarised in Table 3.
It is interesting to observe that the choice of the evaporation model has only a marginal effect on the lift-off of the flame. The likely explanation for this is that the stabilisation process involves a premixed combustion regime that is linked more to the mixing problem rather than to the evaporation rate. In order to illustrate this an instantaneous plot of the flame index (FI) based on the fuel vapour is shown in Fig. 16.
The left half of each of the figures refers to the R-M model, while the right hand side refers to A-S model. The flame index, Yamashita et al. (1996) is defined as \(FI_{C_2H_5OH} = \nabla Y_{C_2H_5OH}\cdot \nabla Y_{O_2}\)) allows a distinction to be made between premixed and non-premixed burning, although in spray flames of the present type its use is subject to some uncertainty. If the index takes a positive value then the flame is premixed while a negative value indicates that the flame is non-premixed. There have been a number of DNS and LES studies involving Flame Index of lifted flames, for example Grout et al. (2011); Luo et al. (2011) where results indicate that the lifted base region may have both premixed and non-premixed structures.
The R-M model appears to be characterised by stronger gradients when compared to the A-S model. This is not surprising in the non-premixed region of the flame because of the correspondingly larger rate of formation of the fuel vapour. In the premixed region, corresponding to \(FI \ge 0\) where both fuel and oxygen are consumed, it appears that larger amounts of ethanol vapour lead to a larger reactivity of the mixture and therefore greater consumption of oxygen. The reduction of co-flow temperature (ie \(H_I \rightarrow H_{III}\)) causes a shift in the base of the reaction zone further upstream and the transition from non-premixed and premixed appears to be more smooth. It is observed that the location of the FI maxima is coincident with a strong transition from the inflow temperature to higher temperatures. However in this region the temperatures do not reach the fully burnt temperatures of the flame nor are they associated with OH production, typically associated with heat release. In Fig. 18 an instantaneous snapshot of the OH concentration together with the corresponding droplet distribution is shown. The figure exhibits a maximum in OH concentration that is not aligned with the maxima in the FI. However, it is associated with the maximum temperatures suggesting this to be the region with larger heat release.
Snapshots of OH concentration for the different cases \(H_I\), \(H_{II}\), and \(H_{III}\). Droplets distribution corresponding to the OH snapshot are superimposed, diameters are scaled on the real diameter and the colour scheme follows the one in Fig. 3. The left and right parts of the figures show results with the R-M (left) and A-S (right) models
Collecting together all the information presented above allows a better understanding of the flame formation and stabilisation processes. The first stage of the reaction zone is characterised by the addition of fuel via the evaporation of droplets that can be more or less intense depending on the evaporation model. This reduces the gas phase temperature because of the heat absorption related to the evaporation. The fuel vapour is added to the environment while oxygen concentration is reduced inducing a negative value of the FI associated with a non-premixed regime. When the mixing of the cold rich mixture with the hot co-flow causes the ethanol vapour to react with the oxygen, positive values of FI appear due to the negative gradients of both species in favour of intermediate products such as CO and \(CH_4\). The instantaneous snap-shot of the droplets of Fig. 18 shows that large droplets penetrate the region confined by the \(FI = 0\) line and supply fuel vapour at a higher temperature. This region is however low in oxygen as it has been consumed in the inner reaction zone closer to the centreline and correspondingly \(FI = 0\). When the fuel rich mixture mixes with the outer oxygen-rich region burning occurs, OH is produced and flame temperatures reach their adiabatic values. This is confirmed by the plotted temperature profiles and illustrated by the plots of mean (time average) heat release rates shown in Fig. 17 using the R-M model.
In Fig. 19 mixture fraction is plotted against temperature at the same location (\(z = 20~mm\)) for the three flames using both evaporation models. In order to provide a qualitative idea of the location of the different points of the scatter plot, a colour-map is added: red correspond to the centreline (\(r = 0\)) and blue to the co-flow (\(r = 40~mm\)). From the scatter plots it is possible to observe how the centreline (red) is characterised by low temperature and low Z values, while towards the side of the flame, local ignition processes occurs in the rich-mixture region. With increasing radius from the centreline a typical adiabatic flame profile is observed until \(Z_{st}\), where the temperature starts to decrease together with an increase in the richness of the mixture until it reaches the co-flow conditions. The lower co-flow temperatures reduce the mixing and the local ignition in the centreline region as it is observed by the lower dispersion of the scatter plots. The influence of the evaporation model here plays an important role. With the A-S model the dispersion is much larger than that arising from the R-M model. In case \(H_{III}\) it is also interesting to observe how the profile spans a much narrower range of mixture-fractions and no ignition phenomena occurs at high Z values. The flame appears to be located very close to \(Z_{st}\) which is due to the lower evaporation. Reducing the co-flow temperature further while using the A-S evaporation model would probably make the fuel supply too low producing local extinction phenomena.
Mixture-fraction—temperature scatter plot at \(z = 20 mm\) for the three flames. Upper row R-M model, lower row A-S model. The colour scheme represents the distance from the centreline (\(r = 0 mm\) red) and the co-flow (\(r = 40 mm\) blue). The dashed line represent the stoichiometric mixture fraction calculated to be 0.1
6 Conclusion
Three different configuration of the Delft Spray in Hot-diluted Co-flow have been studied. The LES Eulerian-stochastic field method coupled with the Lagrangian stochastic particle approach was found to reliably reproduce the measured data. The current work introduced the use of a stochastic breakup model in combination with a simple primary breakup model in order to minimise the parameters needed to characterise the injector and with the aim of providing more general approach hopefully applicable to larger number of injector configuration. The level of agreement achieved was found to be satisfactory and comparable to that previously obtained (Gallot-Lavallée et al. 2016) with estimated injector droplet size and velocity distributions. Given a specified fuel flow-rate however, with the present breakup model the only parameters that have been estimated are the diameter of the droplets injected, related to the injector orifice. No size or velocity distribution is needed and the breakup process is modelled. The droplet velocity at the injection point is determined by the fuel flow-rate and injector geometry.
Particular emphasis has also been put on the dependence of the LES results on two different evaporation models. A single droplet analysis comparing the infinite conductivity model and the corrected model of Abramzon and Sirignano with experimental data highlighted that the former model generally leads to an over-prediction of evaporation rates whilst the latter displays better overall agreement.
In the spray flame the two models were found to give very similar results at high temperatures but the differences become larger at low temperatures. The results of the simulations were compared with the measured the gas-phase velocity field, liquid phase average and class by class velocity fields, temperature profiles, OH profiles, FI profiles and mixture fraction-temperature scatter plot. Whilst marginal differences have been observed in the gas phase velocities, the dispersed phase showed some discrepancies in the non-size-class-specific quantities such as mean velocity and SMD. In these cases the enhanced evaporation of the infinite conductivity model reduces the SMD values at downstream locations thereby increasing their loss of momentum. The flames have similar lift-off heights but with the corrected evaporation model of Abramzon and Sirignano the reaction zone is thicker than that of the infinite conductivity model. Also the mixing process was found to be enhanced with the former model, as confirmed by the mixture fraction-temperature scatter plot.
The dynamics of the stabilisation of the flame were also investigated. The liquid ethanol spray is injected into the hot surrounds and begins to evaporate, thereby reducing the temperature locally. Due to the addition of fuel vapour and the associated local reduction of oxygen concentration the Flame Index takes negative values. When the mixture fraction levels become sufficiently large and the mixing with oxygen is sufficiently rapid reaction occurs between fuel and oxygen causing a change in the sign in the Flame Index so that it becomes positive. Intermediate species are created in this region and are stable until they are exposed to a richer oxygen region that shows high levels of OH concentration. Small droplets appears to be important for the supply of fuel vapour in the inner reaction zone indicated by the change in sign of the Flame index. The larger droplets, in contrast, penetrate this region and provide fuel region where high levels of OH are found. Overall a better overall agreement (although there are local discrepancies) was achieved with the corrected Abramzon and Sirignano evaporation model, consistent with the findings of Chen and Pereira (1996). The work provides validation of the stochastic breakup model for a pressure swirl atomiser, furnishes an improved insight on the DSHC stabilisation phenomena and demonstrates the effect of different evaporation models.
References
Babinsky, E., Sojka, P.: Modeling drop size distributions. Progr. Energy Combust. Sci. 28(4), 303–329 (2002)
Batchelor, G.K.: The Theory of Homogeneous Turbulence. Cambridge University Press, Cambridge (1953)
Bhagatwala, A., Chen, J.H., Lu, T.: Direct numerical simulations of HCCI/SACI with ethanol. Combust. Flame 161(7), 1826–1841 (2014)
Bini, M., Jones, W.P.: Large eddy simulation of particle laden turbulent flows. J. Fluid Mech. 614, 207–252 (2008)
Bini, M., Jones, W.P.: Particle acceleration in turbulent flows: a class of nonlinear stochastic models for intermittency. Phys. Fluids 19, 035,104 (2007)
Bini, M.: Large eddy simulation of particle and droplet laden flows with stochastic modelling of subfilter scales. Ph.D. thesis, Imperial College London (2007)
Brauner, T., Jones, W.P., Marquis, A.J.: Les of the cambridge stratified swirl burner using a sub-grid pdf approach. Flow Turbul. Combust. 96(4), 965–985 (2016)
Burcat, A., Ruscic, B.: Third Millenium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables. Argonne National Laboratory Argonne, IL (2005)
Chen, X.Q., Pereira, J.: Computation of turbulent evaporating sprays with well-specified measurements: a sensitivity study on droplet properties. Int. J. Heat Mass Transf. 39(3), 441–454 (1996)
Chung, T.H., Ajlan, M., Lee, L.L., Starling, K.E.: Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Eng. Chem. Res. 27(4), 671–679 (1988)
Chung, T.H., Lee, L.L., Starling, K.E.: Applications of kinetic gas theories and multiparameter correlation for prediction of dilute gas viscosity and thermal conductivity. Ind. Eng. Chem. Fund. 23(1), 8–13 (1984)
Clift, R., Grace, J.R., Weber, M.E.: Bubbles, drops, and particles. Courier Corporation (2005)
Correia Rodrigues, H., Tummers, M., van Veen, E., Roekaerts, D.: Effects of coflow temperature and composition on ethanol spray flames in hot-diluted coflow. Int. J. Heat Fluid Flow 51, 309–323 (2015)
Correia Rodrigues, H., Tummers, M.J., van Veen, E.H., Roekaerts, D.J.: Spray flame structure in conventional and hot-diluted combustion regime. Combust. Flame 162(3), 759–773 (2015)
Dopazo, C.: Relaxation of initial probability density functiond in turbulent convection of scalar fields. Phys. Fluids 22(1), 20–30 (1979)
Faeth, G.: Evaporation and combustion of sprays. Prog. Energy Combust. Sci. 9, 1–76 (1983)
Gallot Lavallée, S., Jones, W.P.: Large Eddy simulation of spray auto-ignition under EGR conditions. Flow Turbul. Combust. 96(2), 513–534 (2016)
Gallot-Lavallée, S., Jones, W., Marquis, A.: Large eddy simulation of an ethanol spray flame under mild combustion with the stochastic fields method. In: Proceedings of the Combustion Institute (2016)
Gao, F., O’Brien, E.: A large eddy simulation scheme for turbulent reacting flows. Phys. Fluids A 5, 1282–1284 (1993)
Gardiner, C.W.: Handbook of Stochastic Methods. For Physics, Chemistry and the Natural Science, Springer Series Synergetics, vol. 13. Springer (1983)
Godsave, G.: Studies of the combustion of drops in a fuel spray—the burning of single drops of fuel. In: Symposium (International) on Combustion, vol. 4, pp. 818–830. Elsevier (1953)
Gorokhovski, M., Herrmann, M.: Modeling primary atomization. Annu. Rev. Fluid Mech. 40(1), 343–366 (2008)
Grout, R.W., Gruber, A., Yoo, C.S., Chen, J.H.: Direct numerical simulation of flame stabilization downstream of a transverse fuel jet in cross-flow. Proc. Combust. Inst. 33(1), 1629–1637 (2011)
Hubbard, G., Denny, V., Mills, A.: Droplet evaporation: effects of transients and variable properties. Int. J. Heat Mass Transf. 18(9), 1003–1008 (1975)
Irannejad, A., Jaberi, F.: Large eddy simulation of turbulent spray breakup and evaporation. Int. J. Multiph. Flow 61, 108–128 (2014)
Jenny, P., Roekaerts, D., Beishuizen, N.: Modelling of of turbulent dilute spray combustion. Progr. Energy Combust. Sci. 38, 846–887 (2012)
Jones, W.P., Jurisch, M., Marquis, A.J.: Examination of an oscillating flame in the turbulent flow around a bluff body with large eddy simulation based on the probability density function method. Flow Turbul. Combust. 95(2–3), 519–538 (2015)
Jones, W.P., di Mare, F., Marquis, A.J.: Les-Boffin: Users Guide. Mechanical Engineering Department, Imperial College London, London (2002)
Jones, W.P., Marquis, A., Noh, D.: LES of a methanol spray flame with a stochastic sub-grid model. Proc. Combust. Inst. 35(2), 1685–1691 (2015)
Jones, W.P., Marquis, A., Vogiatzaki, K.: Large Eddy Simulation of spray combustion in a gas turbine combustor. Combust. Flame 161(1), 222–239 (2014)
Jones, W.P., Prasad, V.N.: Large Eddy simulation of the sandia flame series (D-F) using the Eulerian stochastic field method. Combust. Flame 157(9), 1621–1636 (2010)
Jones, W.P., Sheen, D.H.: A probability density function method for modelling liquid fuel sprays. Flow Turbul. Combust. 63, 379–394 (1999)
Jones, W.P., Lettieri, C.: Large eddy simulation of spray atomization with stochastic modeling of breakup. Phys. Fluids 22(11), x (2010). (115,106)
Jones, W.P., Marquis, A.J., Noh, D.: A stochastic breakup model for large eddy simulation of a turbulent two-phase reactive flow. In: Proceedings of the Combustion Institute (2016)
Kuo, K.K.: Principles of combustion. Wiley (1986)
Lasheras, J.C., Eastwood, C., Martınez-Bazán, C., Montanes, J.: A review of statistical models for the break-up of an immiscible fluid immersed into a fully developed turbulent flow. Int. J. Multiph. Flow 28(2), 247–278 (2002)
Lasheras, J., Villermaux, E., Hopfinger, E.: Break-up and atomization of a round water jet by a high-speed annular air jet. J. Fluid Mech. 357, 351–379 (1998)
Lefebvre, A.: Atomization and Sprays. CRC Press, Boca Raton (1988)
Luo, K., Pitsch, H., Pai, M.G., Desjardins, O.: Direct numerical simulations and analysis of three-dimensional n-heptane spray flames in a model swirl combustor. Proc. Combust. Inst. 33(2), 2143–2152 (2011)
Ma, L., Naud, B., Roekaerts, D.: Transported PDF Modeling of Ethanol Spray in Hot-Diluted Coflow Flame. Flow, Turbulence and Combustion (2015)
Ma, L., Roekaerts, D.: Modeling of spray jet flame under mild condition with non-adiabatic fgm and a new conditional droplet injection model. Combust. Flame 165, 402–423 (2016)
Ma, L., Roekaerts, D.: Structure of spray in hot-diluted coflow flames under different coflow conditions: a numerical study. Combust. Flame 172, 20–37 (2016)
Ma, L., Roekaerts, D.: Numerical study of the multi-flame structure in spray combustion. Proceedings of the Combustion Institute (2016)
Martínez-Bazán, C., Montañés, J., Lasheras, J.C.: On the breakup of an air bubble injected into a fully developed turbulent flow. part 2. size pdf of the resulting daughter bubbles. J. Fluid Mech. 401, 183–207 (1999)
Martínez-Bazán, C., Rodríguez-Rodríguez, J., Deane, G.B., Montañes, J., Lasheras, J.C.: Considerations on bubble fragmentation models. J. Fluid Mech. 661, 159–177 (2010)
Martínez-Bazán, C., Montañés, J.L., Lasheras, J.C.: On the breakup of an air bubble injected into a fully developed turbulent flow. part 1. breakup frequency. J. Fluid Mech. 401, 157–182 (1999)
Maxey, M.R., Riley, J.J.: Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids (1958–1988) 26(4), 883–889 (1983)
Miller, R.S., Hastard, K., Bellan, J.: Evaluation of equilibrium and non-equilibrium evaporation models for many-droplet gas-liquid flow simulations. Int. J. Multiph. Flow 24, 1025–1055 (1998)
Minamoto, Y., Swaminathan, N.: Scalar gradient behaviour in MILD combustion. Combust. Flame 161(4), 1063–1075 (2014)
Motaalegh Mahalegi, H..K., Mardani, A.: Investigation of fuel dilution in ethanol spray mild combustion. Appl. Therm. Eng. 159,113,898, (2019)
Noh, D.: A stochastic approach towards large eddy simulation of methanol/air spray flames. Ph.D. thesis, Imperial College London (2016)
O’Rourke, P.J., Amsden, A.A.: The Tab Method for Numerical Calculation of Spray Droplet Breakup. Tech. rep, SAE Technical Paper (1987)
Piomelli, U., Liu, J.: Large Eddy Simulation of rotating channel flows using a localized dynamic model. Phys. Fluids 7(4), 848–893 (1995)
Pope, S.B.: Ten questions concerning the large eddy simulation of turbulent flows. N. J. Phys. 6, (2004)
Ranz, W., Marshall, W.: Evaporation from drops—part(i) and part(ii). Chem. Eng. Prog. pp. 141–146 and 173–180 (1952)
Saharin, S., Chauveau, C., Moyne, L.L., Kafafy, R.: Vaporization characteristics of ethanol and 1-propanol droplets 22(3), 207–226 (2012)
Semiao, V., Andrade, P., da GraCa Carvalho, M.: Spray characterization: numerical prediction of Sauter mean diameter and droplet size distribution. Fuel 75(15), 1707–1714 (1996)
Senecal, P., Schmidt, D.P., Nouar, I., Rutland, C.J., Reitz, R.D., Corradini, M.: Modeling high-speed viscous liquid sheet atomization. Int. J. Multiph. Flow 25(6), 1073–1097 (1999)
Sirignano, W.: Fuel droplet vaporization and spray combustion theory. Prog. Energy Combust. Sci. 9, 291–322 (1983)
Sirignano, W.: Droplet vaporization models for spray combustion calculations. Int. J. Heat Mass Transf. 32, 1605–1618 (1989)
Spalding, D.B.: The combustion of liquid fuels. Fourth Symposium (International) on Combustion pp. 818–830 (1953)
van Oijen, J.: Direct numerical simulation of autoigniting mixing layers in MILD combustion. Proc. Combust. Inst. 34(1), 1163–1171 (2013)
Wille, M.: Large Eddy Simulation of Jets in Cross Flows. Ph.D. thesis, Imperial College of Science, Technology and Medicine, University of London (1997)
Xiao, F., Dianat, M., McGuirk, J.: LES of turbulent liquid jet primary breakup in turbulent coaxial air flow. Int. J. Multiph. Flow 60, 103–118 (2014)
Xiao, F., Dianat, M., McGuirk, J.J.: Large eddy simulation of single droplet and liquid jet primary breakup using a coupled level set/volume of fluid method. Atom. Sprays 24(4), 281–302 (2014)
Yamashita, H., Shimada, M., Takeno, T.: A numerical study on flame stability at the transition point of jet diffusion flames. In: Symposium (International) on Combustion, vol. 26, pp. 27–34. Elsevier (1996)
Yuen, M.C., Chen, L.W.: On drag of evaporating liquid droplets. Comb. Sci. Tech. 14, 147–154 (1976)
Acknowledgements
The authors appreciate the constructive discussions with Andrea Giusti and Philip Sitte.
Funding
This work was funded by General Electric Power (Switzerland) , the Engineering and Physical Sciences Research Council (EPSRC) [Grant Nos. EP/K026801/1 and EP/R029369/1] through the UK Consortium on Turbulent Reacting Flow (UKCTRF) and used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gallot-Lavallée, S., Jones, W.P. & Marquis, A.J. Large Eddy Simulation of an Ethanol Spray Flame with Secondary Droplet Breakup. Flow Turbulence Combust 107, 709–743 (2021). https://doi.org/10.1007/s10494-021-00248-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10494-021-00248-z