Abstract
The turbulent counter-flow flame (TCF) has proven to be a useful benchmark to study turbulence-chemistry interactions, however, the widely observed bulk flow fluctuations and their influence on the flame stability remain unclear. In the present work, premixed TCFs are studied numerically using a Large Eddy Simulation (LES) method. A transported probability density function (pdf) approach is adopted to simulate the sub-grid scale (sgs) turbulence-chemistry interactions. A solution to the joint sgs-pdf evolution equation for each of the relative scalars is obtained by the stochastic fields method. The chemistry is represented using a simplified chemical reaction mechanism containing 15 reaction steps and 19 species. This work compares results with two meshing strategies, with the domain inside nozzles included and excluded respectively. A conditional statistical approach is applied to filter out the large scale motions of the flame. With the use of digital turbulence, the velocity field in the flame region is well reproduced. The processes of local extinction and re-ignition are successfully captured and analysed together with the strain rate field, and local extinctions are found correlated to the turbulent structures in the reactant stream. The predicted probability of localised extinction is in good agreement with the measurements, and the influence of flame stoichiometry are also successfully reproduced. Overall, the current results serve to demonstrate the capability of the LES-pdf method in the study of the premixed opposed jet turbulent flames.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Turbulent flames involve complex mutual interactions between unsteady flows and chemical reactions over a variety of temporal and spatial scales, which poses a great challenge for combustion research. Numerical simulations can provide researchers with further understanding of the turbulence-chemistry interactions, as they have the abilities to overcome the difficulties associated with measurement techniques.
1.1 LES-pdf Method
The balance of accuracy and computing cost required for the accurate predictions of turbulent flames has led to a significant interest in Large-Eddy Simulations (LES) in recent years. With LES, the three-dimensional velocity field and energy-containing eddies are resolved temporally and spatially. These require a correct prescription of the boundary conditions, which can influence the overall simulation results significantly (Keating et al. 2004). However, it is impractical to have such comprehensive temporal datasets on the inflow conditions, since it relates to the structure and shape of the eddies and hence to the type of the flow and location in the field. Two simulation strategies are often selected: the upstream of the region of interest should be included in the simulation, or the inlet boundary conditions can be estimated with the use of synthetic turbulence generator (Klein et al. 2003).
As a modelling strategy for the sub-grid scales sgs scalar fields in the LES of reacting flows, a modelled evolution equation for the one-point joint filtered probability density function (pdf) is employed in the present work. It has the merit that chemical source terms appear in a closed form so that no additional modelling for the chemical reaction is required. The pdf equation is then solved using the LES stochastic fields method (Jones and Navarro-Martinez 2007), which provides solutions that are continuous but not differentiable in time and continuous and differentiable in space. Thus there are no spatially varying stochastic errors, a feature that allows the density and thus the pressure to be evaluated in a straight forward manner. The stochastic fields method in conjunction with LES has been successfully applied to simulate various flame configurations such as non-premixed flames, auto-ignition in methane and hydrogen flames and partially premixed flames with extinction, as well as spray flames (Gallot-Lavallée et al. 2017; Fredrich et al. 2019; Jones and Prasad 2011).
1.2 Turbulent Counter-Flow Flame Configuration
A variety of flame benchmarks have been established for numerical validations, and a particular set of flames are targets for the TNF (Turbulent Non-premixed Flames) Workshop which encourages discussions and collaborations of experimental and numerical research work on turbulent flames (Kempf 2007). As one of the target flames, turbulent counter-flow flames (TCFs) have been subjected to numerous investigations, with many attractive features such as simple flame shape, well-controlled boundaries and flexible operation modes etc.
In the context of early experimental studies, (Kostiuk et al. 1989, 1993a, b) examined a TCF with two axisymmetric premixed reactant streams, where the turbulence was generated by having the mixture flow pass through perforated plates in the nozzles. This turbulence generating scheme is preserved by the following experimentalists. First non-premixed and partially premixed TCFs were reported by Mastorakos et al. (Mastorakos et al. 1992a, b), where extinction limits and relative temperature characteristics were measured under selected conditions. It was observed in their work that partially premixing made flames more resistant to extinction, and this TCF was reproduced numerically by Jones and Prasetyo (1996) using a pdf-transport approach. Sardi et al. (1999) continued this work with the measurements of conditional scalar dissipation rates in an isothermal opposed jet, and results of this work were used for comparison in many numerical studies (Kempf et al. 2000; Eckstein et al. 2000). Korusoy and Whitelaw further performed the measurements of the velocity and strain rate of the isothermal flow-field with small separations of the nozzles (Korusoy and Whitelaw 2001, 2002). At Darmstadt University, (Geyer et al. 2005a, b) developed an opposed jet burner and performed a series of measurements of isothermal and premixed TCFs, including information on axial velocity, main species concentration, temperature, structure functions etc. These comprehensive descriptions of the flames provided information for the validation of LES by Geyer et al. (2005a). Böhm et al. (2007, 2009) performed simultaneous PIV/OH-LIF measurements of velocity and scalar fields. Furthermore, the flow field inside the nozzle was investigated by Böhm et al. (2010) with a transparent nozzle using high-speed PIV. It was found that close to the turbulent generating plate, turbulent kinetic energy was generated in the region of the jet breakup and during mutual interaction; the fluctuations then experienced strong decay leading to a more isotropic behaviour of the turbulence. Periodic fluctuations caused by vortex shedding were observed, and the corresponding frequency scaled with Reynolds number. Recently at Yale University and Sandia National Laboratories, (Coppola and Gomez 2009; Coriton et al. 2011, 2013) developed a TCF burner aimed at creating highly turbulent flames and investigating the extinction features. Pettit et al. (2011) reported collaborative works involving experimental and numerical investigations of diffusion flames with this burner. Tirunagari and Pope (2016); Tirunagari et al. (2016) studied the premixed mode of the burner numerically. The computational domain focused on the cylindrical domain between the two nozzles exit planes with the inlet boundary conditions achieved from a simulation of the iso-thermal case with the domain extended to the nozzle inlets.
Turbulent opposed jet configurations are known to be prone to large scale instabilities. These are likely to be associated with the impingement of the jets resulting in both longitudinal fluctuations and tilting of the gas mixing layer between the jets which easily observed by the naked eye during experiments or in snapshots of OH-PLIF images (Gomez 2011). Because of the close proximity of the jet outlets to the impingement plane these instabilities are likely to be influenced by the details of the inflowing jet turbulence and thus by the method used to generate turbulence upstream of the jet inlet, e.g. perforated plates or grids (Gomez 2011). The origins of the instabilities are not well understood but are not detected under laminar conditions. The instabilities affect the velocity field significantly and cause the discrepancy between experimental measurements and predictions, which is recognised by Geyer et al. (2005b) and Lindstedt et al. (2005). Coppola and his colleagues first studied this instability in an isothermal TCF using proper orthogonal decomposition (POD) (Coppola and Gomez 2010; Gomez 2011), which shows the existence of two modes of the oscillation of the mixing layer, namely an axial one and a precession one about the system axis. They also confirmed these large-scale, low-frequency instabilities are chaotic in nature and typically exhibit long length and time scales. The POD analysis is extended to the OH-LIF images under reacting conditions (Gomez 2011), which confirms the large-scale fluctuations of the mixing layer induce similar motions of the flame. These large scale motions are likely to have little influence on the detailed instantaneous flame structure. Hence, in the study of turbulence-flame interactions it is natural to seek methods to filter out the effects of these large-scale fluctuations. A conditional statistic algorithm was proposed and proved to be able to achieve this in Coppola and Gomez (2010), Gomez (2011) and allows study of turbulence-flame interactions. It is incorporated in the present work and is described in detail in Sect. 5.2.
1.3 Specific Objectives
In the present work, the Yale premixed TCF (Coriton et al. 2013) is studied numerically using the stochastic fields method. The burner system is presented schematically in Fig. 1, and detailed descriptions of it can be found in Coppola and Gomez (2009), Coriton et al. (2011). The present work aims to study the coupling effect of the turbulent flow field and the flame and to assess the predictive capabilities of the filtered probability density function/stochastic fields method in reproducing this premixed TCF. Particular attention is paid to the fluctuations of the flow field and local extinction and re-ignition phenomenon. Despite many previous studies of the TCF configuration, there is a limited availability of numerical studies of localised extinctions in premixed TCFs. Tirunagari and Pope (2017) visualised qualitatively local extinction events in a series of premixed TCFs using an LES method combined with a Lagrangian dynamic sgs model but providing little analysis. The paper is structured as follows: after the LES-pdf methodology is described in detail, the experimental configuration of the simulated premixed flame and the critical parameters for the simulation are discussed. Then numerical details are presented, followed by the discussion of results and comparison with experimental measurements. Finally, the paper concludes with the main findings and suggestions for future work.
2 Mathematical Formulation
2.1 Fluid Filtered Equations
In LES, a spatial filtering operation is performed to the governing equations to separate the larger scales from the smaller ones, so that the resulting filtered velocity field can be adequately resolved. The filtering operation of an instantaneous flow variable f at location \({\mathbf {x}}=(x_{1},x_{2},x_{3})\) can be written as:
which is defined over the entire three-dimensional integration domain \(\Omega\), and \(\Delta\) is the filter width (Vasilyev and Lund 1997). The density variations in reacting flows can be treated by introducing a density-weighted filtering operator (also known as Favre filtering operator) which shares the same property as the unweighted ones. A Favre filtering operation is defined as \(\tilde{f}={\overline{\rho f}}/{\overline{\rho }}\). Hence the filtered Navier–Stokes equations for low-Mach number, variable density flows can be written in the following form:
where \(\rho\) is the density of the flow, \(u_{j}\) is the flow velocity, p is the static pressure and \(e_{ij}\) is the rate of strain tensor. The filtered product \(\widetilde{u_{i} u_{j}}\) differs from the product of filtered velocities \(\widetilde{u_{i}} \widetilde{u_{j}}\), and the sub-grid scale (sgs) stress \(\tau ^{sgs}_{ij}\) is introduced, which is defined as:
where \(\tau ^{sgs}_{ij}\) is approximated via a Smagorinsky sgs viscosity in conjunction with the dynamic procedure of Piomelli and Liu (1995).
2.2 Scalar Equations
The filtered field equations for the chemical species and enthalpy are summarised as:
Equation (5) is the filtered field equation for the specific mole number of each of the \(N_{s}\) chemical species (\(n_{\alpha }\) is the \(\alpha\) -th species), and eq.(6) is for the enthalpy. Other symbols have their usual meanings. Fourier and Fick’s law are adopted for heat and species diffusion fluxes respectively:
where \(\sigma\) is the Prandtl or Schmidt number, which both are assumed to be equal and constant. Equations (5) and (6) are not solved directly in the present work so models for the sub-grid fluxes \({\mathscr {J}}^{sgs}_{\alpha ,j}\) and \({\mathscr {J}}^{sgs}_{h,j}\) are not required at this point.
Due to the difficulties encountered in evaluating the filtered values of the chemical source terms for the relative species, a joint sgs (or filtered fine-grained) pdf evolution formulation is introduced to solve the scalar transport equations. The joint sub-pdf (\({P}_{\mathrm {sgs}}\)) is defined as:
with \(f(\underline{\psi };{\mathbf {x}}',t)= \prod \limits _{\alpha =1}^{N_s}\delta \left[ \psi _{\alpha } - \xi _{\alpha }^{n}({\mathbf{x}}, t) \right]\) which represents a fine grained pdf and \(\psi _{\alpha }\) is the sample space for the scalar \(\phi _{\alpha }\). This filtered density function is essentially the probability density function of the random scalar variable \(\psi\) (see also (Pope 2000)).
An equation describing the evolution of the pdf can be derived by standard methods, eg by Gao and O’Brien Gao and O’Brien (1998). Following the approach of Brauner et al. Brauner et al. (2016) the resolved part of the convection and molecular mixing are added to both sides of the equation so that the modelled form the equation becomes:
where \(\dot{\omega }_{\alpha }(\underline{\psi })\) is the net formation rate through a chemical reaction for each reactive species, and this term doesn’t exist for the enthalpy equation. The first term on the right-hand side of (9) represents the closed sgs-pdf transport using a Smagorinsky type gradient model with \(\mu _{sgs}\) and \(\sigma _{sgs}\) representing the sub-grid scale diffusion coefficient and Schmidt number respectively, and \(\sigma _{sgs}\) is assigned the value 0.7. The last term on the right-hand side represents sgs micro-mixing which is closed by the Linear Mean Square Estimation (LMSE) closure (Dopazo 2008; Dopazo and O’Brien 2003), and the mixing time-scale is given by \(\tau _{sgs}=\overline{\rho }\Delta ^2/\mu _{sgs}\). The sgs mixing constant \(C_d\) is assigned the value of 2.0 Jones and Prasad (2010). The main advantage of the formulation is that the chemical reaction terms for the species appear in a closed form and that no combustion regime dependent modelling assumptions are invoked.
The equation describing the evolution of the pdf, (9), is solved using the stochastic fields method. \(\tilde{P}_{sgs}(\underline{\psi })\) is represented by an ensemble of N stochastic fields for each of the \(N_s+1\) scalars namely \(\xi _{\alpha }^{n}({\mathbf {x}},t)\) for \(1 \le n \le N, \ 1 \le \alpha \le N_s+1\). In the present work, the Itô formulation of the stochastic integral is adopted. The stochastic fields evolve according to:
where \(dW^{n}_{i}\) represents increments of a (vector) Wiener process, different for each field but independent of the spatial location \({\mathbf {x}}\).
3 Yale Premixed TCFs
The selected configuration is the premixed version of the Yale TCF burner, and a detailed description of it can be found in Coriton et al. (2013). As show in Fig. 1, both nozzles contain a convergent section terminated by a short straight pipe to the exit. The top nozzle (reactants side) is surrounded by a nitrogen co-flow with a bulk exit velocity of \(2.1 m\,s^{-1}\). This nozzle is identical to the nozzles applied in the study of non-premixed TCF in Pettit et al. (2011). The bottom nozzle is specifically designed to deliver a jet of combustion products with high temperature ended by a converging ceramic pipe with a wall thickness of 12.0mm.
The turbulence in the top stream is generated by forcing the reactants through a turbulence generating plate (TGP) enclosed inside the top nozzle. Different turbulent Reynolds numbers are achieved by varying the position of the TGP inside the nozzle, and in the present work the case with \(Re_{t} = 1050\) is studied. The volumetric flow rate of the reactant stream is kept constant at \(1.42 \cdot 10^{-3} m^{3}\cdot s^{-1}\), while the bulk momentum of the combustion product stream is adjusted to balance the bulk momentum of the upper flow. This allows the flame to stabilise near the mid-plane of the burner where an optical access and rich experimental data are easily available. The reactant flow composes of a mixture of \(CH_4/O_{2}/N_{2}\) with the reactant equivalence ratio \(\phi _u=0.85\), while the hot product stream is generated by a stoichiometric methane flame in the cylindrical chamber. The temperature of the burnt gas (\(T_{b}\)) can be varied by adjusting the \(O_{2}/N_{2}\) mole ratio of the premixed torch flame, and the studied condition is \(T_{b} = 1850 K\). The stoichiometry of the counter-flowing stream was found to have a great influence on flame stability (Coriton et al. 2016), and a study of such effect will be included in the future work. The average adverse velocity gradient is evaluated by the bulk strain rate, \(K_{bulk}\), defined as \(2V_{bulk}/d_{n}\), where \(d_{n}\) is the nozzle separation distance and \(V_{bulk}\) is the mean bulk inlet velocity of the upper nozzle. This velocity is kept unchanged as \(V_{bulk} = 11.2\) m/s. The simulated distance between the two nozzles is \(d_{n} = 16\) mm that corresponds to a strain rate of \(K = 1400 \mathrm{s}^{-1}\). The bulk velocity of the bottom flow is set to counterbalance the volumetric flow rate of the top flow.
These standard flow conditions for the present simulation are summarised in Table 1, where \(\phi\) represents equivalence ratio, Cp represents components, onr is oxygen to nitrogen ratio and the subscript t for top stream and b for bottom stream respectively.
4 Numerical Details
The work presented in this paper is performed using the in-house LES code, BOFFIN-LES, details of which are provided in Jones and Navarro-Martinez (2007). The chemical kinetics mechanism adopted for the oxidation of methane is the reduced mechanism purposed by Sung et al. (2001) based on GRI-Mech 3.0 mechanism. To reproduce the turbulence generated at the actual burner inlets in the experiments, an artificial inflow turbulence generator is applied. To prescribe meaningful fluctuations for boundary conditions rather than simple random data, (Klein et al. 2003) developed a synthetic turbulence inflow generator based on the use of digital filters, which was extended by di Mare et al. (2006). This approach generates turbulence structures correlated in time and space, with specified turbulent length and time scales. The present work compares the results of a Large Eddy Simulation with two meshes, M1 and M2 which are illustrated schematically in Fig. 2 with the details listed in Table 2. As shown in Fig. 2, M2 is practically identical to the portion of mesh M1 between nozzle exits.
The computational domain in M1 extends for 15 nozzle diameters in the axial direction, containing region between TGP and the inlet of the bottom duct. In the cross stream direction (x, z), both computational domains extend for 4 nozzle diameters in the region between two nozzle exits, which is aimed at reducing the influence of outlet boundary on the flow field in the regions of interest. The grid lines are gradually clustered towards the centre in both axial and radial directions where the best resolutions are achieved, and with a careful design, the grid number of M1 is limited to 2.9 million. The simulations were carried out with a constant time step of \(\Delta t = 1\times 10^{-6}\) s. The upper stream bulk velocity is 11.2 m/s, while the lower stream bulk velocity is about 38.2 m/s (summarised in Tirunagari et al. (2016)). The largest CFL number is monitored instantaneously and limited below 0.25. For both cases, a convergence study is first carried out, which confirms that an initialisation time of 8 flow-through times is enough for a statistically stationary flow to develop. The time-averaged results for the flow field are collected over a period of about 6 flow-through times. The total computational cost to perform an LES/PDF simulation for fully converging results is approximately 90,000 CPU-hours and 55,000 CPU-hours for M1 and M2 respectively.
Synthetic turbulence was applied at the inlet boundaries to represent the actual flow conditions in the experiments for both M1 and M2. The synthetic inflow turbulence generator involves the specification of the three turbulence levels, \(\bar{u^{'2}}\) and corresponding integral length scales. In the case M1 it was not possible to specify realistic values of these that resulted in the measured values at the nozzle exit being reproduced. The turbulence generator is based on the assumption that the spectra at inlet are described by that observed in the final period of decay of isotropic turbulence. While this is unrealistic in many cases the effects are inconsequential; the inflow turbulence interacts with mean shear, generating further turbulence which rapidly forgets its origin. However in the domain M1 there is no mean shear upstream of the nozzle so that the in-flowing turbulence relaxes to isotropy and dissipates over a distance comparable with the specified integral length scales. It is for this reason that the measured rms turbulence levels at the nozzle exit could not be reproduced. For both cases a single estimated and constant integral length scale was used. For M1, the turbulent length scale was estimated based on the TGP orifice geometry; for M2, the mean velocity at the nozzle exit planes obtained from the M1 simulations is applied and turbulence length scale was estimated to be the radius at the nozzle. For both cases, the magnitudes of the imposed turbulence was adjusted to give as close agreement as possible to the measured levels of rms velocity at the nozzles exits.
5 Results and Discussions
5.1 Instantaneous Snapshots
A non-reacting case is first established to verify the turbulent inlet boundary conditions and the applicability of the methodology, where the reactant flow is replaced by \(N_{2}\) flow at the same flow rate and inlet temperature. Contour plots of the instantaneous and mean axial velocity on the central plane from downstream of the TGP to bottom nozzle exit for M1 are shown in Fig. 3, together with a view of the axial velocity downstream of the TGP. From the mean velocity field in Fig. 3b, the axial symmetry of the axial flow field and the counter-flowing effect can be observed. Figure 3a presents the effect of feeding the gas stream through the star-shaped TGP and the development of the flow in the top nozzle. It can be seen that in the straight pipe, the jet begins to break up at about one diameter downstream of the TGP, with significant turbulent structures appearing in the shear layer. Due to the effect of mixing, the jet spreads in the cross-section direction as well. These features last until the jet reaches halfway of the converging pipe in the nozzle where the flow is significantly confined, and finally the flow becomes more homogenised and the size of turbulent eddies reduces greatly at the top nozzle exit. In the central region, the top jet encounter the bottom jet and the merged stream flows towards the outlet, with vortex shedding observed downstream. The simulated results inside the nozzle provide an opportunity to investigate the flow field generated by the perforated plate method and the interactions between the flow field and turbulent flame (in the reaction case) as most measurements only have access to the data outside of the nozzle.
The reacting case with standard flow conditions listed in Table 1 are set up for M1 and M2 respectively and one example is presented here to illustrate the general topology of the flame. Figure 4 displays snapshots of the mass fraction of \(CH_4\), OH, temperature and heat release rate (HRR) for M2, which provides an instantaneous visualisation of the flame. The turbulent premixed flame is identified by the region with high OH mass fraction signal shown in Fig. 4b. When traversing from bottom to top, three regions can be detected, namely the hot product region, the flame region and reactant region. The virtual boundary separating the flame region and the hot products is referred to as the gas mixing layer interface (GMLI), and the boundary between the flame region and the reactants is the turbulent flame front, which can also be denoted by the region with the high value of HRR shown in Fig. 4d. It can be observed that the flame front is significantly rolled up and corrugated, which is attributed to the turbulent fluctuations. Figure 5 illustrates the evolution of heat release for the two meshes, M1 and M2. Both cases exhibit the influence of large scale turbulent motions, although the effect is much larger for the smaller solution domain M2, almost certainly because of the larger inflow turbulence levels imposed (and consistent with the measured values) at the jet inlets for the smaller domain.
5.2 Conditional Statistic Approach
Schematic diagram of the gas mixing layer interface (GMLI) (Coriton et al. 2013) for fully intact flame front (a) and a local extinction case (b). Figures on the top are the sample OH-LIF images in a region between nozzle exits. The blue dashed lines denote the burner centre-line, and the red lines represent the GMLI and the flame front. The plots on the bottom are corresponding \(OH-LIF\) and \(|\nabla (OH-LIF)|\) signals. Plots of the progress variable c (blue lines) along the centre-line under the GMLI reference frame (the coordinated shown in red) are superimposed
As described in Sect. 1, the flame experiences large scale longitudinal fluctuations. In order to understand the flow-field and flame properties, a conditional statistical approach was defined based on a relative frame of reference. A detailed description can be found in Coriton et al. (2013) and is summarised here for convenience.
Figure 6 presents examples of a fully intact flame front a and a local extinction case b. The figures on the top show the \(OH-LIF\) field in a region between the nozzle exits, and the figures on the bottom show the corresponding profiles of \(OH-LIF\) signal and \(|\nabla (OH-LIF)|\) on the centre-line (denoted by the green dashed lines) at the same instance. The figures are rotated such the hot product stream is on the left and the reactant stream is on the right.
In both cases, the region on the left experiences a moderate OH-LIF signal value representing the OH content in the hot product stream. This region is hence designated as hot products. The region on the far right with OH-LIF signal value close to zero is labelled as the reactant region. In Fig. 6a, a region with high level of OH-LIF signals is found in between, which is caused by super-equilibrium OH concentration produced by the flame front. This region is designated as the flame region. In Fig. 6b, along the burner centerline, the OH-LIF signal reduce directly from the product stream value to the reactant stream value, indicating the flame is locally extinguished on the centre-line.
The GMLI is defined here, and is found by the following procedure. When traversing the gradient of OH-LIF (\(|\nabla (OH-LIF)|\)) profile along the centre-line from left to right, the first peak is defined as the GMLI position. In Fig. 6a, the location of the first peak is encountered when the OH-LIF signal increases from the hot product stream to the flame region; while in Fig. 6b, it occurs when OH-LIF signal decreases from the product stream to the reactant stream.
In the present study, the flame region is identified as the region to the right of the GMLI with the OH-PLIF signal exceeding a threshold value. The threshold value is \(5\%\) higher than the mean OH-LIF signal in the hot product stream and kept constant in all the cases. If a flame blue is present, the flame front is determined by the locations where the OH-LIF value crosses the threshold value Coriton et al. (2013). In Fig. 6b, OH-LIF signal remains under the threshold value, which is defined as a local extinction condition along the centre-line. The fresh product layer is hence defined as the separation between GMLI and flame front surface. When the flame is locally quenched, the GMLI and the flame front coincide resulting the fresh product layer thickness dropping to zero.
The probability of finding the fresh combustion products along the centerline is quantified by the following procedure: A binary progress variable, c, is defined with a value of unity in the combustion products region (the hot product counter-flowing stream and regions of fresh combustion product) and zero everywhere else. A local axial coordinate attached to the GMLI is then introduced, which is denoted by \(\Delta\). As shown in Fig. 6b, \(\Delta\) is parallel to the burner centre-line with an origin coincident with the instantaneous GMLI position and increases moving towards the reactants stream. Under this local coordinate, the contribution to c value from the counter-flowing product stream is excluded. In addition, the value of c in the burner reference frame can be affected by both of the localised extinctions and the variations of the position of the flame. Under \(\Delta\) coordinate, where the fluctuations of the GMLI is filtered out, \(c|\Delta\) is determined mainly by the flame topology and the flame brush thickness. The profiles of c in \(\Delta\) coordinate are shown by the blue plots in Fig. 6 for both cases. When the flame presents, \(c|\Delta\) equals 1 in the region between \(\Delta =0\) and the flame front; on the contrary, when the flame is locally quenched, \(c|\Delta\) equals 0 everywhere on the centre-line due to the absence of the turbulent flame front, which is the condition shown in Fig. 6b. Hence, the ensemble average of \(c|\Delta\), \(<c|\Delta>\), when approaching \(\Delta =0\) relates to the probability of detecting fresh combustion products, and its complement relates to the probability of local extinction.
5.3 Flow Field Study
The flow fields are examined qualitatively in this section. We first consider the velocity field based on the global coordinate system where it is important to remember that the unconditional rms velocities are affected by not only the turbulent eddies, but the large scale motions of the GMLI together with the flame, and the latter becomes more profound when approaching the GMLI. These combined effects are referred to as total fluctuations in the following analysis.
Figure 7 compares the mean and rms axial and radial velocity components for M1 and M2 with the experimental data. The velocities are normalised by the bulk velocity of the upper stream, \(V_{bulk}=11.2\) m/s, and the locations of the upper and the bottom nozzle outlets are at \(y=8\) mm and \(y=-8\) mm respectively. V is the axial velocity and U is the radial velocity components while the over-line denotes the mean velocity and subscript rms is for the corresponding rms velocity. The simulated mean velocities profiles are in good agreement with the experimental data for both the axial and radial components for M1 and M2. In the context of rms velocities, for M1, the axial rms velocity is under-predicted by 35% on the reactant side and the radial rms velocity is under predicted by around 45%. For M2, the axial rms velocity is well-reproduced at the nozzle exits, but under-prediction increases when approaching the central plane of the burner (y = 0). The largest discrepancy for the axial rms velocity is found around the stagnation plane (\(\overline{V}/V_{bulk} = 0\)), where \(\text { v'}_{rms}/V_{bulk}\) is under predicted by about 25%.
The normalised centre-line profiles of the conditional mean and rms axial and radial velocities compared with experimental data. \(\Delta\) coordinate represents the distance from the GMLI and increases in the direction of the upper nozzle.The green dashed lines denote the stain rates and will be explained in Sect. 5.4.1
To filter out the effects of the GMLI fluctuations on the flow field and to gain further insights into the turbulent fluctuations, we use a conditional statistical approach to study the flow field, and hence the velocity components are presented in the relative frame of the GMLI denoted by \(\Delta\). As shown in Fig. 8a, b, the simulated conditional mean velocities for both M1 and M2 are in good agreement with the measurements. At the GMLI, \({(\overline{V}|\Delta )}/V_{bulk}\) (normalised conditional mean axial velocity) has a value of zero, which indicates the stagnation plane coincides the GMLI on average. The rms velocities for M1 are again under predicted, which means the turbulence level in the flow is under predicted. These discrepancies are mainly due to insufficient resolution downstream of the TGP in the nozzle. For M2, we found good agreement with the predicted axial rms velocity and the measurements, which implies a good reproduction of the turbulent fluctuations generally. This is attributed to the realistic specification of synthetic turbulence at the nozzle exits, which is close to the region where these comparisons are made.
The above analysis is based on the conditional statistical approach which has been shown to have the ability to separate the GMLI fluctuations from the actual turbulent flow field. By comparing the results of M1 and M2, we conclude that with the selected turbulence generating method, M2 better reproduces the turbulent fluctuations. The observed large scale motions of the GMLI could be linked to the flow field inside the nozzle, especially the region downstream of the TGP where strong vortex shedding takes place. Böhm et al. (2010) reported periodic fluctuations of the flow field in the top nozzle caused by vortex shedding. However, the results of M1 are not sufficient to support this, since both the total fluctuations and turbulent fluctuations are under predicted. POD analysis of the LES results would be helpful to detect the coherent structure in the computed flow field, but the high computational cost makes the results unavailable in the present work.
5.4 Analysis of Flame Dynamics
5.4.1 Qualitative Analysis
We first examine the strain rate field by examining the profiles of the conditional mean velocities. Figure 7a shows that, the conditional mean axial velocity decreases with a moderate slope of \(K2 ~1100\,\mathrm{s}^{-1}\) for \(\Delta\) greater than 2 mm, and a sharp slop of \(K1~4000\,\mathrm{s}^{-1}\) within 1 mm of the GMLI. This suggests in general that the flame experiences a much higher strain rate than the global bulk strain rate estimate of \(K_{bulk}=1400\,\mathrm{s}^{-1}\) based on the exit velocity and the nozzle separation. The conditional mean radial velocity is nearly zero, which is expected due to the axial symmetry of the mean flow field.
In addition to the time mean rate of strain high velocity gradients can arise instantaneously with associated high local strain rates To characterise the dynamics of the flame, the linkage between local extinctions and local resolved rate of strain field is analysed. Figure 9 shows the instantaneous plots of OH mass fraction and strain rate magnitude, captured simultaneously.
Each OH mass fraction contour plot has the corresponding rate of strain field plotted below. These OH contours are plotted using a threshold value, which is selected to preserve the main features of the flame topology. Two continuous times series of OH mass fraction are displayed as examples, with \(t=0\) ms to \(t=0.5\) ms corresponding to a case of local extinction and \(t=1.2\) ms to \(t=1.9\) ms corresponding to a re-ignition process. The results of M2 are used for the analysis in this section and the images are rotated \(90^{\circ }\) with the product stream on the left and reactant stream on the right.
When tracking the strain rate magnitude along the flame front, the regions with high strain rate do not necessarily correlate with the location where local extinctions takes place. As can be observed in Fig. 9 at around \(z= -3\) mm, a pocket of reactant (denoted by a cyan circle) stretches into the reaction region gradually, pressing the flame front into the product stream. When the flame front meets the GMLI, local extinction takes place at around \(t=0.4\) ms. The extinction process seems to be, at most, very weakly correlated with local high strain rate. To support this, the vorticity magnitude, is computed. Four locations on the flame front (denoted by A, B C and D) at \(t=0.2\) ms are selected to represent different conditions: B and C are positions where extinctions occur, A and D are positions where combustion continues under different strain rate conditions. The vorticity magnitudes at these four positions are: \(3535.4\,\mathrm{s}^{-1}\), \(12,130.1\,\mathrm{s}^{-1}\), \(13,875.6\,\mathrm{s}^{-1}\) and \(7206.5\,\mathrm{s}^{-1}\) respectively. The high vorticity in the regions of flame extinction suggest that turbulent transport is the main cause of the extinction process in the present case. This turbulence induced local extinction process is observed in the experimental work (Coriton et al. 2013) and a similar process is observed in other turbulent flame configurations such as jet flames (Hult et al. 2005). A similar local extinction process to that observed above can be observed from \(t=0.2\) ms to \(t=0.4\) ms at around \(z= -3\) mm in the reacting region.
In Fig. 9 the plots from \(t=1.2\) to \(t=1.9\) ms illustrate a complete process of re-ignition. An ignition kernel (denoted by a red circle) first appears at \(t=1.3\) ms and grows rapidly and evolves as a result of flame propagation and convection. Consequently, at \(t=1.9\) ms, the ignited regions are connected and the flame is re-established. It has often been assumed that the extinguished regions would re-ignite when the local strain rate dropped below a threshold level (Kostiuk et al. 1993b). However in the present work, as can be observed from the strain rate field at \(t=1.3\) ms, the re-ignited kernels appear even in a region with relatively high local strain rates, and grow into burning ’islands’ at a consequence of turbulent transport. A more definitive study will require a further more detailed investigation into the temperature field as well as out-of-plane motions.
5.4.2 Conditional Statistical Analysis
To quantify the frequencies of the occurrence of regions of local extinction and re-ignition, the conditional approach discuss in Sect. 5.1 is adopted in this section to analyse the statistics of the progress variable.
First, in order to assess the influence of the sgs model contributions, the results of simulations with 1, 8 and 16 stochastic fields in the M2 case (denoted by M2-1, M2-8 and M2-16 respectively) are compared in Fig. 10a. The statistics for 1 and 8 fields are averaged over 6 flow-times, while due to the limited computing resource, the statistics of the 16-field simulation are averaged over 2 flow-through times, which is still ongoing. According to the results, it is observed preliminarily that 8-field and 16-field simulations reasonably well reproduce <\(c|\Delta\)>, as both sets of predictions are very similar. This indicates that 8 stochastic fields are sufficient to represent sgs chemistry effects for the case considered, which is consistent with the findings of Mustata et al. (2006).
The influence of different meshing strategies on flame behaviour is then investigated. Figure 10b compares the conditional mean progress variable in the M1 and M2 cases with 8 stochastic fields (named by M1-8 and M2-8 respectively). As presented in Fig. 10b, both M1 and M2 predict the evolution of \(<c|\Delta>\) with good accuracy, while a better agreement is found in M2 compared with the measurements. This is expected due to the better predicted conditional rms velocities achieved by M2. For M1, under-predictions of \(<c|\Delta>\) are found in the regions away from the GMLI, which indicates a low possibility of finding fresh combustion products there and, in general, a thinner reaction region in the simulations. This is mainly due to the under-predicted turbulence level in the flow field, which results in a weaker turbulent transport of the flame front.
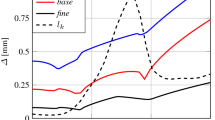
To understand the effects of flame stoichiometry on the local extinction, we study the flame with reactant equivalence ratio varied from \(\phi _{t} = 0.5\) to \(\phi _{t} = 1.0\), while other flow conditions remain the same as the standard conditions. The profiles of \(<c|\Delta>\) for M2 with \(\phi _{t} = 0.5, 0.7, 0.85\) and 1.0 are displayed in Fig. 11. The trend of the probability of detecting fresh combustion products is well reproduced for all the cases. As \(\phi _{t}\) decreases from 1.0 to 0.5, the conditional mean progress variable decreases significantly all the way.
As discussed in Sect. 5.1, the complement of the ensemble average of the progress variable at GMLI, \(1-<c|\Delta\)> at \(\Delta = 0\) specifies the probability of local extinction along the centre-line. Hence, the probability of localised extinction for \(\phi _{t} = 1.0, 0.85, 0.7\) and 0.5 are about 2% 3%, 40% and 72% respectively. For the very lean case \(\phi _{t} = 0.5\), <\(c|\Delta\)> drops to zero after \(\Delta = 2\,\hbox{mm}\), indicating that the flame is mostly extinguished and the turbulent flame brush thickness is less than 2mm most of the time. This can be explained by decreased laminar flame speeds in lean flames, and hence a smaller distance between the flame front and the GMLI, which is consistent with the laminar flame calculations in Coriton et al. (2013) and successfully reproduced here.
6 Conclusions
Premixed TCFs are studied using a LES-pdf method. With the conditional statistical method and the digital turbulence generating method used, the simulated results for the velocity fields in the regions between nozzle exits are in good agreement with the experimental data. The localised extinction processes are successfully captured by the simulations, and are found to be attributed to the turbulent eddies in the reactant stream. The predicted statistics of localised extinction are in good agreement with the experimental data, and the effect of reactant equivalence ratio on flame stability is successfully reproduced. The results reveal that a leaner flame is more prone to local extinction due to reduced flame speed. Overall, the results serve to demonstrate the capability and potential of the LES-pdf method in the study of this counter-flow flame. The future work will include the large domain simulation with POD analysis of the iso-thermal flow field to investigate the observed large scale fluctuations. The effect of main bulk strain rate and temperature of the counter-flowing bottom stream on the flame feature will be examined using LES-pdf method as well.
References
Böhm, B., Geyer, D., Dreizler, A., Venkatesan, K.K., Laurendeau, N.M., Renfro, M.W.: Simultaneous PIV/PTV/OH PLIF imaging: conditional flow field statistics in partially premixed turbulent opposed jet flames. Proc. Combust. Inst. 31(1), 709–717 (2007)
Böhm, B., Heeger, C., Boxx, I., Meier, W., Dreizler, A.: Time-resolved conditional flow field statistics in extinguishing turbulent opposed jet flames using simultaneous high-speed PIV/OH-PLIF. Proc. Combust. Inst. 32(2), 1647–1654 (2009)
Böhm, B., Stein, O., Kempf, A., Dreizler, A.: In-Nozzle Measurements of a Turbulent Opposed Jet Using PIV. Flow Turbul. Combust 85(1), 73–93 (2010)
Brauner, T., Jones, W.P., Marquis, A.J.: LES of the Cambridge stratified swirl burner using a sub-grid pdf approach. Flow Turbul. Combust 96(4), 965–985 (2016)
Coppola, G., Gomez, A.: Experimental investigation on a turbulence generation system with high-blockage plates. Exp. Thermal Fluid Sci. 33(7), 1037–1048 (2009)
Coppola, G., Gomez, A.: Experimental study of highly turbulent isothermal opposed-jet flows. Phys. Fluids 22, 105101 (2010)
Coriton, B., Frank, J.H., Hsu, A.G., Smooke, M.D., Gomez, A.: Effect of quenching of the oxidation layer in highly turbulent counterflow premixed flames. Proc. Combust. Inst. 33(1), 1647–1654 (2011)
Coriton, B., Frank, J.H., Gomez, A.: Effects of strain rate, turbulence, reactant stoichiometry and heat losses on the interaction of turbulent premixed flames with stoichiometric counter-flowing combustion products. Combust. Flame 160(11), 2442–2456 (2013)
Coriton, B., Frank, J.H., Gomez, A.: Interaction of turbulent premixed flames with combustion products: Role of stoichiometry. Combust. Flame 170(C), 37–52 (2016)
di Mare, L., Klein, M., Jones, W.P., Janicka, J.: Synthetic turbulence inflow conditions for large-eddy simulation. Phys. Fluids 18(2), 025107 (2006)
Dopazo, C.: Probability density function approach for a turbulent axisymmetric heated jet. Centerline evolution. Physics of Fluids 18(4), 397 (2008)
Dopazo, C., O’Brien, E.E.: Functional formulation of nonisothermal turbulent reactive flows. Phys. Fluids 17(11), 1968 (2003)
Fredrich, D., Jones, W.P., Marquis, A.J.: The stochastic fields method applied to a partially premixed swirl flame with wall heat transfer. Combust. Flame 205, 446–456 (2019)
Gallot-Lavallée, S., Jones, W.P., Marquis, A.J.: Large Eddy Simulation of an ethanol spray flame under MILD combustion with the stochastic fields method. Proc. Combust. Inst. 36(2), 2577–2584 (2017)
Gao, F., O’Brien, E.E.: A large-eddy simulation scheme for turbulent reacting flows. Phys. Fluids A 5(6), 1282–1284 (1998)
Geyer, D., Kempf, A., Dreizler, A., Janicka, J.: Turbulent opposed-jet flames: a critical benchmark experiment for combustion LES. Combust. Flame 143(4), 524–548 (2005)
Geyer, D., Kempf, A., Dreizler, A., Janicka, J.: Scalar dissipation rates in isothermal and reactive turbulent opposed-jets: 1-D-Raman/Rayleigh experiments supported by LES. Proc. Combust. Inst. 30(1), 681–689 (2005)
Gomez, A.: Highly turbulent counterflow flames: a laboratory-scale benchmark for turbulent combustion studies. In: Fall Technical Meeting of the Eastern States Section of the Combustion Institute (2011)
Hult, J., Meier, U., Meier, W., Harvey, A., Kaminski, C.F.: Experimental analysis of local flame extinction in a turbulent jet diffusion flame by high repetition 2-D laser techniques and multi-scalar measurements. Proc. Combust. Inst. 30, 701–709 (2005)
J Eckstein, J.Y.C., Chou, C.P., Janicka, J.: Modelling of turbulent mixing in opposed jet configuration: one-dimensional Monte Carlo probability density function simulation. Proc. Combust. Inst. 28, 141–148 (2000)
Jones, W.P., Navarro-Martinez, S.: Large eddy simulation of auto-ignition with a sub-grid probability density function method. Combust. Flame 150(3), 170–187 (2007)
Jones, W.P., Prasad, V.N.: Large Eddy Simulation of the Sandia Flame Series (D-F) using the Eulerian stochastic field method. Combust. Flame 157(9), 1621–1636 (2010)
Jones, W.P., Prasad, V.N.: LES-pdf simulation of a spark ignited turbulent methane jet. Proc. Combust. Inst. 33(1), 1355–1363 (2011)
Jones, W.P., Prasetyo, Y.: Probability density function modelling of premixed turbulent opposed jet flames. Symp. (Int.) Combust. 26(1), 275–282 (1996)
Keating, A., Piomelli, U., Balaras, E., Kaltenbach, H.J.: A priori and a posteriori tests of inflow conditions for large-eddy simulation. Phys. Fluids 16(12), 4696–4712 (2004)
Kempf, A.M.: LES validation from experiments. Flow Turbul. Combust 80(3), 351–373 (2007)
Kempf, A., Forkel, H., Chen, J.Y., Sadiki, A., Janicka, J.: Large-eddy simulation of a counterflow configuration with and without combustion. Proc. Combust. Inst. 28(1), 35–40 (2000)
Klein, M., Sadiki, A., Janicka, J.: A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 186(2), 652–665 (2003)
Korusoy, E., Whitelaw, J.H.: Opposed jets with small separations and their implications for the extinction of opposed flames. Exp. Fluids 31(1), 111–117 (2001)
Korusoy, E., Whitelaw, J.H.: Extinction and relight in opposed flames. Exp. Fluids 33(1), 75–89 (2002)
Kostiuk, L.W., Bray, K.N.C., Chew, T.C.: Premixed turbulent combustion in counter-flowing streams. Combust. Sci. Technol. 64(4–6), 233–241 (1989)
Kostiuk, L.W., Bray, K.N.C., Cheng, R.K.: Experimental study of premixed turbulent combustion in opposed streams. Part I—Non-reacting flow field. Combust. Flame 92(4), 377–395 (1993)
Kostiuk, L.W., Bray, K.N.C., Cheng, R.K.: Experimental study of premixed turbulent combustion in opposed streams. Part II reacting flow field and extinction. Combust. Flame 92(4), 396–409 (1993a)
Lindstedt, R.P., Luff, D.S., Whitelaw, J.H.: Velocity and strain-rate characteristics of opposed isothermal flows. Flow Turbul. Combust. 74, 169–194 (2005)
Mastorakos, E., Taylor, A.M.K.P., Whitelaw, J.H.: Extinction and temperature characteristics of turbulent counterflow diffusion flames with partial premixing. Combust. Flame 91(1), 40–54 (1992)
Mastorakos, E., Taylor, A.M.K.P., Whitelaw, J.H.: Scalar dissipation rate at the extinction of turbulent counterflow non-premixed flames. Combust. Flame 91(1), 55–64 (1992)
Mustata, R., Valiño, L., Jiménez, C., Bondi, S.: A probability density function Eulerian Monte Carlo field method for large eddy simulations: Application to a turbulent piloted methane/air diffusion flame (Sandia D). Combust. Flame 125(1–2), 88–104 (2006)
Pettit, M.W.A., Coriton, B., Gomez, A., Kempf, A.M.: Large-Eddy Simulation and experiments on non-premixed highly turbulent opposed jet flows. Proc. Combust. Inst. 33(1), 1391–1399 (2011)
Piomelli, U., Liu, J.: Large-eddy simulation of rotating channel flows using a localised dynamic model. Phys. Fluids 7(4), 839–848 (1995)
Pope, S.B.: Turbulent Flows. Cambridge University Press, Cambridge (2000)
Sardi, K., Taylor, A.M.K.P., Whitelaw, J.H.: Extinction of Turbulent Counterflow Flames under Periodic Strain. Combust. Flame 120, 265–284 (1999)
Sung, C.J., Law, C.K., Chen, J.Y.: Augmented reduced mechanisms for NO emission in methane oxidation. Combust. Flame 125(1–2), 906–919 (2001)
Tirunagari, R.R., Pope, S.B.: An investigation of turbulent premixed counterflow flames using large-eddy simulations and probability density function methods. Combust. Flame 166, 229–242 (2016)
Tirunagari, R.R., Pope, S.B.: Characterisation of extinction/re-ignition events in turbulent premixed counterflow flames using strain-rate analysis. Proc. Combust. Inst. 36, 1919–1927 (2017)
Tirunagari, R.R., Pettit, M.W.A., Kempf, A.M., Pope, S.B.: A simple approach for specifying velocity inflow boundary conditions in simulations of turbulent opposed-jet flows. Flow Turbul. Combust 98(1), 131–153 (2016)
Vasilyev, O.V., Lund, T. S.: A general theory of discrete filtering for LES in complex geometries. In: Annual Research Briefs of Centre for Turbulence Research, Stanford, pp. 41–50 (1997)
Acknowledgements
This research has been funded by Imperial College London and the China Scholarship Council (CSC). The work was supported by the Engineering and Physical Sciences Research Council (EPSRC) through the UK Consortium on Turbulent Reacting Flow (UKCTRF) and the simulations have been performed using the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gong, Y., Jones, W.P. & Marquis, A.J. Study of a Premixed Turbulent Counter-Flow Flame with a Large Eddy Simulation Method. Flow Turbulence Combust 106, 1379–1398 (2021). https://doi.org/10.1007/s10494-020-00240-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10494-020-00240-z