A Numerical Investigation of the Effects of Fuel Composition on the Minimum Ignition Energy for Homogeneous Biogas-Air Mixtures

Abstract

The minimum ignition energy (MIE) requirements for ensuring successful thermal runaway and self-sustained flame propagation have been analysed for forced ignition of homogeneous stoichiometric biogas-air mixtures for a wide range of initial turbulence intensities and CO₂ dilutions using three-dimensional Direct Numerical Simulations under decaying turbulence. The biogas is represented by a CH₄ + CO₂ mixture and a two-step chemical mechanism involving incomplete oxidation of CH₄ to CO and H₂O and an equilibrium between the CO oxidation and the CO₂ dissociation has been used for simulating biogas-air combustion. It has been found that the MIE increases with increasing CO₂ content in the biogas due to the detrimental effect of the CO₂ dilution on the burning and heat release rates. The MIE for ensuring self-sustained flame propagation has been found to be greater than the MIE for ensuring only thermal runaway irrespective of its outcome for large root-mean-square (rms) values of turbulent velocity fluctuation, and the MIE values increase with increasing rms turbulent velocity for both cases. It has been found that the MIE values increase more steeply with increasing rms turbulent velocity beyond a critical turbulence intensity than in the case of smaller turbulence intensities. The variations of the normalised MIE (MIE normalised by the value for the quiescent laminar condition) with normalised turbulence intensity for biogas-air mixtures are found to be qualitatively similar to those obtained for the undiluted mixture. However, the critical turbulence intensity has been found to decrease with increasing CO₂ dilution. It has been found that the normalised MIE for self-sustained flame propagation increases with increasing rms turbulent velocity following a power-law and the power-law exponent has been found not to vary much with the level of CO₂ dilution. This behaviour has been explained using a scaling analysis and flame wrinkling statistics. The stochasticity of the ignition event has been analysed by using different realisations of statistically similar turbulent flow fields for the energy inputs corresponding to the MIE and it has been demonstrated that successful outcomes are obtained in most of the instances, justifying the accuracy of the MIE values identified by this analysis.

1 Introduction

Localised forced ignition (e.g. spark or laser ignition) of homogeneous mixtures is of critical importance for the efficient use of fuel in Spark Ignition (SI) engines and industrial gas turbines. It is widely acknowledged that fossil fuels will predominantly be used to meet a major part of the energy demand for the foreseeable future for power generation and transportation applications. However, fossil fuel reserves are finite and thus eco-friendly alternative renewable fuels are becoming ever more important. One such alternative fuel is biogas, which can be used as either a compliment or a replacement for existing fossil fuels. Additionally, depending on the production method used, it can be a carbon–neutral fuel and due to the existing natural gas infrastructure, it can be easily stored and transported whilst also being used in conjunction with natural gas for power generation and transportation (Holm-Nielsen et al. 2009). Biogas is primarily composed of methane (CH₄) and carbon dioxide (CO₂), however, production of industrial quantities of biogas with a fixed composition may be hard due to its potential biological origins (Vasavan et al. 2018; Rasi et al. 2007). The composition of biogas is of critical importance, as large variations in CO₂ content can affect the ignition of the fuel, leading to adverse effects on the subsequent flame propagation (Lieuwen et al. 2008).

Due to the fundamental importance of localised forced ignition, several analytical (Espí and Liñán 2001, 2002; Champion and Deshaies 1986), experimental (Champion and Deshaies 1986; Ballal and Lefebvre 1975, 1979, 1981; Lefebvre and Ballal 2010; Huang et al. 2007; Shy et al. 2010, 2017aa, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b; Larsson et al. 2013; Mordaunt and Pierce 2014; Lafay et al. 2007; Galmiche et al. 2011; Zhen et al. 2013; Forsich et al. 2004; Biet et al. 2014; Mulla et al. 2016) and computational (Turquand d’Auzay et al. 2019a, b; Poinsot et al. 1996; Thiele et al. 2000; Kaminski et al. 2000; Klein et al. 2008; Patel and Chakraborty 2015, 2016a, b; Mastorakos 2009; Mastorakos 2017) studies have investigated this phenomenon in detail from different viewpoints. Espí and Liñán (2001, 2002) investigated ignition characteristics in quiescent homogeneous gaseous mixtures originating from a point ignition source, whilst analytical tools were developed to predict flame initiation by Champion and Deshaies (1986). These analytical studies (Espí and Liñán 2001, 2002; Champion and Deshaies 1986) provided key physical insights into the ignition phenomenon for both laminar and turbulent conditions, despite the fact they were carried out for laminar conditions. In-depth experimental studies have been carried out for a wide range of fuels such as propane-air, iso-octane, diesel oil and heavy fuel oil by Lefebvre and co-workers (Ballal and Lefebvre 1975, 1979, 1981; Lefebvre and Ballal 2010). These experimental studies (Ballal and Lefebvre 1975, 1979, 1981; Lefebvre and Ballal 2010) showed that the critical radius that the kernel needs to reach for successful self-sustained flame propagation to occur following thermal runaway, increases with increasing turbulence intensity but also increases with either an increase or a decrease in equivalence ratio ϕ with respect to the stoichiometric (i.e. ϕ = 1.0) mixture. This indicates that more energy is required to ignite fuel-lean or fuel-rich mixtures than that is needed for stoichiometric mixtures, and this behaviour becomes more prevalent with an increase in turbulence intensity. Huang et al. (2007) and Shy et al. (2010) analysed the minimum ignition energy (MIE) for homogeneous methane-air mixtures under homogeneous isotropic forced turbulence for different values of equivalence ratios and turbulence intensities u′/s_l (where u′ is the root-mean-square (rms) value of the turbulent velocity, and s_l is the unstrained laminar burning velocity of the homogeneous mixture in question). They observed the qualitatively similar variation of MIE with u′ and ϕ, that Lefebvre and co-workers (Ballal and Lefebvre 1975, 1979, 1981; Lefebvre and Ballal 2010) reported, but in addition to that a transition in the increase of the MIE with increasing turbulence intensity was observed beyond a critical value of turbulence intensity (u′/s_l)_crit. For u′/s_l < (u′/s_l)_crit, the MIE requirement increases gradually with an increase in turbulence intensity, but remains significantly smaller than the MIE for u′/s_l > (u′/s_l)_crit. The MIE requirement increases rapidly with increasing u′ for u′/s_l > (u′/s_l)_crit. Additionally, the effects of parameters other than turbulence intensity, such as spark gap distance, equivalence ratio, fuel type and pressure were also investigated by Shy and co-workers (Peng et al. 2013; Shy et al. 2017a, b; Jiang et al. 2018). Cardin et al. (2013a, b) have investigated the MIE variation using laser ignition for lean methane-air mixtures under isotropic homogeneous decaying turbulence and observed a transition of the MIE with increasing turbulence intensity, which Shy and co-workers (Shy et al. 2010, 2017a, b; Peng et al. 2013; Jiang et al. 2018) reported using a spark ignition system. Thus, it can be inferred that the transition of the MIE is independent of the ignition system and both experimental studies observed that the transition in MIE requirement occurred at Ka ~ 10, where Ka is the Karlovitz number. However, it must be mentioned that differences were observed for the critical turbulence intensity between the analyses by Shy et al. (2010, 2017a, b), Peng et al. (2013), Jiang et al. (2018) and Cardin et al. (2013a, b), which have been attributed to the different ignition apparatus, experimental setup and the integral length scale of the turbulence used in the respective analysis.

Larsson et al. (2013) experimentally investigated the MIE required for successful ignition across hydrocarbon fuels mixed with inert gases, due to industrial demand to ignite gas turbines using the fuel available on offshore plants. Methane and propane mixtures separately diluted with nitrogen and carbon dioxide were investigated, to find the maximum amount of inert gas concentration in each gas composition which could be successfully ignited. The variation of the MIE with increasing diluent percentage was also investigated by Larsson et al. (2013), with the turbulence and spark characteristics kept unaltered across all the experiments carried out. As the volumetric percentage of diluent (CO₂) in the fuel-blend increased, so did the MIE for the biogas mixture following a power-law trend. It was found that the successful ignition was possible up to a maximum of 25% CO₂ volumetric dilution in the fuel blend (CH₄ + CO₂). Studies by Mordaunt and Pierce (2014) and Lafay et al. (2007) for biogas/air mixtures in a gas turbine configuration reported a large modification of the reaction zone (Lafay et al. 2007) and a hindrance to flame kernel formation that can potentially lead to flame extinction (lean blow-out) (Mordaunt and Pierce 2014), due to the presence of CO₂ in the fuel mixture. Galmiche et al. (2011) also investigated the effects of CO₂ dilution up to a large level (5–40% by volume of the mixture) on localised forced ignition, and reported that CO₂ acts as a heat sink, and an increase in the amount of CO₂ in the mixture leads to an increase in the energy required for a successful ignition. Zhen et al. (2013) investigated the effects of diluting methane with nitrogen and carbon dioxide. It was reported that carbon dioxide had a more adverse effect than nitrogen on flame stabilisation, and a lower flame temperature was observed when carbon dioxide was the diluent. Forsich et al. (2004) conducted an experimental study on laser ignition of CH₄ mixtures diluted with CO₂, at pressures up to 3.0 MPa, and observed that biogas-air mixtures show a slower combustion process when compared to methane-air mixtures, which is attributed to the lower burning velocity of biogas-air mixtures. For similar air–fuel ratios, biogas-air mixtures exhibited a lower peak pressure and pollutant emission than methane-air mixtures, and this was attributed to the presence of CO₂. The presence of CO₂ slows the burning rate, as previously mentioned, but also acts as a heat sink due to it having a larger heat capacity than nitrogen, leading to slower propagating flames at a lower temperature. Further work by Biet et al. (2014) investigated the ignition of CH₄–CO₂-air mixtures at ultra-lean conditions under varying pressure using both laser and spark ignition systems, with a view towards the identification of the minimum pulse energy of the laser ignition system and the lower flammability limit. It was observed that the dilution of methane with carbon dioxide, increased the lower flammability range, whilst a laser ignition system was found to perform better than an electric spark system at high pressures. Mulla et al. (2016) also reported similar conclusions for the laser ignition of methane/air diluted with CO₂.

Localised forced ignition has also been investigated using Direct Numerical Simulations (DNS) to analyse the early stages of premixed flame kernel development as a result of localised forced ignition (Poinsot et al. 1996; Thiele et al. 2000; Kaminski et al. 2000; Klein et al. 2008; Patel and Chakraborty 2015). The effects of turbulence intensity on successful ignition have been numerically analysed by Patel and Chakraborty (2015), and it was reported that an increase of turbulence intensity with a fixed length scale has a detrimental effect on successful ignition. Patel and Chakraborty (2015) also investigated the effects of spark parameters such as the characteristic width of the energy deposition, spark duration, energy deposited and turbulence intensity for homogeneous mixtures for different equivalence ratios, and their findings were in good qualitative agreement with the experimental results by Ballal and Lefebvre (1975, 1979, 1981). Three-dimensional simple chemistry DNS was also used to investigate the influence of turbulence intensity, fuel Lewis number and mixture fraction gradient on ignition success and subsequent self-sustained combustion (Patel and Chakraborty 2016, b). An in-depth review on localised forced ignition for both homogeneous and inhomogeneous mixtures was provided by Mastorakos (2009, 2017), and interested readers are directed there for further information.

Of particular interest to this study is the transition of MIE from low to high turbulence intensities observed across a wide range of fuels, which was reported by Shy and co-workers (Huang et al. 2007; Shy et al. 2010, 2017a, b; Peng et al. 2013; Jiang et al. 2018) and Cardin et al. (2013a, b), and it was subsequently numerically replicated by Turquand d’Auzay et al. (2019a). Further work was undertaken by Turquand d’Auzay et al. (2019b) on the effects of varying turbulence intensity and dilution levels on the localised forced ignition of turbulent mixing layers of CH₄–CO₂–air, and the effects of CO₂ dilution reported were in agreement with those of previous experimental studies (Larsson et al. 2013; Mordaunt and Pierce 2014; Lafay et al. 2007; Galmiche et al. 2011; Zhen et al. 2013; Forsich et al. 2004; Biet et al. 2014; Mulla et al. 2016). However, to the best of the authors’ knowledge, existing experimental and numerical studies have investigated MIE variation for undiluted fuels such as methane and hydrogen but the MIE dependence on the volumetric percentage of the diluent present in compound fuels such as biogas is yet to be investigated. The present study aims to address this gap in the existing literature by utilising three-dimensional compressible DNS to investigate the variation of the MIE for premixed stoichiometric homogeneous CH₄–CO₂–air mixtures under decaying isotropic turbulence, with varying levels of CO₂ dilution. The MIE has been evaluated for, only a successful thermal runaway, and also a successful thermal runaway followed by self-sustained combustion once the ignitor has been switched off. A two-step chemical mechanism (Turquand d’Auzay et al. 2019b; Bibrzycki and Poinsot 2010; Selle et al. 2004; Westbrook and Dryer 1981), which captures the incomplete combustion of CH₄ in CO and H₂O and the equilibrium between the oxidation of CO and the dissociation of CO₂, is utilised to account for the effects of CO₂ dilution on the reaction kinetics. Thus, the objectives of the present study are to understand the effects that varying levels of dilution of the fuel with CO₂ have:

• (1) On the variation of the MIE requirements for successful ignition and subsequent flame propagation under different initial intensities of homogeneous isotropic decaying turbulence.

• (2) To investigate the effects that varying dilution levels have on the transition of the MIE between small and large values of turbulence intensity based on the physical insights gained from the DNS dataset.

The rest of the paper will be organised as follows. The mathematical background and numerical implementations pertaining to the current analysis are presented in the next two sections. The results are presented and subsequently discussed in the following section. Finally, the main findings are summarised, and conclusions are drawn.

2 Mathematical Background

In the interest of computational economy, a two-step chemical mechanism presented by Westbrook and Dryer (1981) has been used for the present analysis. The chemical mechanism used, accounts for 6 species (CH₄, O₂, CO₂, H₂O, CO and N₂) and is a compromise between single-step chemistry and more complex mechanisms. The three steps, which make up the chemical mechanism used in the present study, are shown below in Table 1. The first step accounts for the fuel oxidation, whilst the equilibrium between the oxidation of carbon monoxide and the dissociation of carbon dioxide is accounted for by the second and third steps. The rate constants used are expressed using an Arrhenius form equation as shown below (Poinsot and Veynante 2005):

$$ k_{j} = A_{j} \hat{T}^{{\beta_{j} }} \exp \left( { - E_{a,j} /R\hat{T}} \right) $$

(1)

where $A_{j}$ is the pre-exponential constant, $\beta_{j}$ is the temperature exponent, $E_{a,j}$ is the activation energy of the reaction (Poinsot and Edwards 2005) and $\hat{T}$ is the dimensional temperature. The reaction progress rates are then estimated by:

$$ Q_{j} = k_{j} \mathop \prod \limits_{l = 1}^{N} \left[ {X_{l} } \right]^{{n_{{l_{j} }} }} $$

(2)

where N is the number of species involved in the jth reaction and $n_{{l_{j} }}$ is the stoichiometric coefficient of species l in reaction j. The numerical values of the coefficients for this study are detailed in Table 1 and follow those proposed by the CERFACS 2s_CM2 mechanism (Bibrzycki and Poinsot 2010; Selle et al. 2004). In order to accurately capture the laminar flame speed dependence on equivalence ratio, the pre-exponential adjustment (PEA) proposed by Bibrzycki and Poinsot (2010) is used and tailored so that the unstrained laminar burning velocity obtained across the whole of the CH₄ flammability range (0.55 ≤ ϕ ≤ 1.55) closely matches the GRI-Mech 3.0 values (Smith et al. 2018).

Table 1 Attributes of the chemical mechanism used in this analysis

The combustion of biogas can be represented by the following global reaction:

$$ {\text{CH}}_{4} + 2\left( {{\text{O}}_{2} + 3.76{\text{N}}_{2} } \right) + {\text{a}} \cdot {\text{Diluent}} \to {\text{CO}}_{2} + 2{\text{H}}_{2} {\text{O}} + 7.52{\text{N}}_{2} + {\text{a}} \cdot {\text{Diluent}} $$

(3)

where the diluent is taken to be CO₂ for the present work. The biogas composition is described following the definition presented by Galmiche et al. (2011):

$$ \psi^{u} = \frac{a}{a + 1 + 2 + 7.52} = \frac{a}{a + 10.52} $$

(4)

where $\psi^{u}$ represents the dilution percentage which is the molar fraction of the diluent (CO₂) in the unburned gases and a represents the stoichiometric coefficient as shown in Eq. 3. Subsequently a separate definition for dilution percentage, $\psi^{f}$, based on the dilution of the fuel blend, can be defined as:

$$ \psi^{f} = \frac{a}{a + 1} $$

(5)

Thus, $\psi^{f}$ represents the molar fraction of the diluent present in the fuel blend (CH₄ + CO₂). The above chemical mechanism has been validated for both CH₄ and CH₄ + CO₂ mixtures, against other chemical mechanisms [GRI-Mech 3.0 (Smith et al. 2018) and 2s_CM2 (Bibrzycki and Poinsot 2010; Selle et al. 2004)] and experimental results (Galmiche et al. 2011), and for further details regarding the performance and validation of the mechanism, interested readers are directed to the recent work by Turquand d’Auzay et al. (2019b). It must be mentioned that the present chemical mechanism overestimates the laminar burning velocity for large values of $\psi^{u}$, and thus the present study has been conducted up to an intermediate level of dilution, with $\psi^{u} \le 0.10$, for which laminar burning velocity predictions are sufficiently accurate (Turquand d’Auzay et al. 2019b). The mixture composition is described in terms of the mixture fraction $\xi$, which is defined using Bilger’s definition (Bilger et al. 1980) as:

$$ \xi = \frac{{\beta - \beta_{O} }}{{\beta_{F} - \beta_{O} }} $$

(6)

where $\beta = 2Y_{C} /W_{C} + Y_{H} /2W_{H} - Y_{O} /W_{O}$ with $\beta_{O}$ and $\beta_{F}$ being the values of $\beta$ in the oxidizer and fuel streams respectively, with $Y_{k}$ and $W_{k}$ denoting the atomic mass fractions and molecular weights. The stoichiometric mixture fraction value is expressed as Bilger et al. (1980):

$$ \xi_{st} = - \frac{{\beta_{O} }}{{\beta_{F} - \beta_{O} }} $$

(7)

The extent of the completion of chemical reactions can be measured by a reaction progress variable c that increases monotonically from zero in the unburned mixture to unity in the products, and is defined here based on the fuel mass fraction as Patel and Chakraborty (2015):

$$ c = \frac{{\xi Y_{{F_{\infty } }} \left( {\psi^{u} } \right) - Y_{F} }}{{\xi Y_{{F_{\infty } }} \left( {\psi^{u} } \right) - max\left( {0,\frac{{\xi - \xi_{st} }}{{1 - \xi_{st} }}} \right)Y_{F\infty } \left( {\psi^{u} } \right) }} $$

(8)

where $Y_{{F_{\infty } }}$ is the mass fraction of fuel (CH₄) in the unburned reactants, whilst $\psi^{u}$ within brackets indicates values that correspond to that level of dilution. It must be mentioned that the progress variable can also be defined in terms of oxidizer mass fraction, however, the choice of progress variable definition does not affect the results presented later in this paper. For the present analysis, a stoichiometric homogeneous mixture (i.e. $\xi = \xi_{st}$) has been considered and the mixture fraction $\xi$ is not needed for the analysis of localised forced ignition of homogeneous mixtures, as carried out in this paper. However, $Y_{{F_{\infty } }} \left( {\psi^{u} } \right)$ changes with the variation of $\psi^{u}$ (e.g. $Y_{{F_{\infty } }} = 1.0,0.574,0.396$ and 0.237 for $\psi^{u} = 0,0.025,0.05$ and 0.10, respectively).

In line with previous computational studies that investigated localised forced ignition (Turquand d’Auzay et al. 2019b; Patel and Chakraborty 2015, 2016a, b) and subsequently the transition of MIE (Turquand d’Auzay et al. 2019a), several assumptions are made for the present study. In the present study, the Lewis number of all species is taken to be equal to unity. All species in the gaseous phase are taken to be perfect gases, and thus the perfect gas law is used for compressible flow DNS. Standard values were taken for the ratio of specific heats ($\gamma = C_{P}^{g} /C_{v}^{g} = 1.4$, where $C_{p}^{g}$ and $C_{v}^{g}$ are the gaseous specific heats at constant pressure and volume, respectively) and Prandtl number ($Pr = \mu C_{p}^{g} /\lambda = 0.7$, where $\mu$ is the dynamic viscosity and $\lambda$ is the thermal conductivity of the mixture in the gaseous phase). The species diffusion velocity is accounted for by using Fick’s law of diffusion.

In order to account for the effects of the localised forced ignition, an additional source term, $(q''' = A_{sp} exp\left( { - r^{2} /2R_{sp}^{2} } \right)$ with $r$ being the distance from the ignitor centre and $R_{sp}$ representing the characteristic radius of energy deposition) is added to the energy conservation equation, which is given by (Turquand d’Auzay et al. 2019a, b; Patel and Chakraborty 2016a, b):

$$ \frac{\partial }{\partial t}\rho e + \underbrace {{\frac{\partial }{{\partial x_{k} }}\rho u_{k} e}}_{{ - C_{1} }} = \underbrace {{ - \frac{\partial }{{\partial x_{k} }}u_{k} p}}_{{P_{1} }} + \underbrace {{\frac{\partial }{{\partial x_{k} }}\tau_{ki} u_{i} }}_{{D_{1} }} + \underbrace {{\frac{\partial }{{\partial x_{k} }}\left[ {\lambda \frac{{\partial \hat{T}}}{{\partial x_{k} }}} \right]}}_{{D_{2} }}\underbrace {{ - \frac{\partial }{{\partial x_{i} }}\rho \mathop \sum \limits_{k = 1}^{N} h_{s,k} Y_{k} V_{k,i} }}_{{D_{3} }} + \underbrace {{\dot{w}_{T} }}_{{P_{2} }} + \underbrace {{q^{{{\prime \prime \prime }}} }}_{{P_{3} }} $$

(9)

where $h_{s,k}$ is the specific enthalpy, p is the pressure, $\tau_{ki}$ is the viscous shear stress, $\dot{w}_{T} = |\dot{w}_{F} |H_{\phi }^{{\psi_{u} }}$ is the source term originating from heat release due to combustion (with $H_{\phi }^{{\psi_{u} }}$ is the heat of combustion for the dilution level of ${\psi^{u}}$,) and $e = \mathop \smallint \nolimits_{{T_{ref} }}^{{\hat{T}}} C_{V} d\hat{T} + u_{k} u_{k} /2$ is the specific stagnation internal energy. For the current analysis the term $\mathop \sum \nolimits_{k = 1}^{N} h_{s,k} Y_{k} V_{k,i} = C_{P} \left( {\hat{T} - T_{0} } \right)\mathop \sum \nolimits_{k = 1}^{N} Y_{k} V_{k,i} = 0$ vanishes as the specific heats at constant pressure and volume are taken to be identical for all the species for the sake of simplicity. The heat capacity of CO₂ is indeed higher than that of N₂ at low temperature (e.g. $\hat{T} = 300\;{\text{K}}$) where the difference is as high as 40%. However, their heat capacities become equal at $\hat{T} = 600\;{\text{K}}$, while the current analysis is carried out for a heat release parameter $\tau = \left( {T_{ad}^{0} - T_{0} } \right)/T_{0} = 3.0$ (where $T_{ad}^{0}$ and T₀ are the adiabatic flame temperature of the undiluted stoichiometric mixture and unburned gas temperature respectively), which corresponds to a preheating of $T_{0} = 590\;{\text{K}}$. This temperature was chosen to reduce the error made by using the assumption of equal $C_{p}$ for all species. Additionally, for higher values of the mixture temperature, the difference of the specific heat between the two species is at most 6%, which means that the errors introduced by the assumption of equal $C_{p}$ are likely to be small for this analysis. Furthermore, within the mixtures currently considered (which are predominantly composed of N₂ by 61% per mass in the pure fuel stream for the worst cases with $\psi^{u} = 0.10$), and the relatively low amount of CO₂ dilution (at most 28% by mass in the mixture for the worst cases with $\psi^{u} = 0.10$), the mixture specific heat would be very close to that of N₂, and thus the assumption of equal specific heat capacity can be used without much inaccuracy.

The constant $A_{sp}$ in the source term $q^{{{\prime \prime \prime }}} = A_{sp} exp\left( { - r^{2} /2R_{sp}^{2} } \right)$ is determined by a volume integration which leads to the total ignition power $\dot{Q}$ in the following manner:

$$ \dot{Q} = \mathop \smallint \limits_{V} q^{{{\prime \prime \prime }}} dV = a_{sp} \rho_{0} C_{p} \tau T_{0} \left( {\frac{4}{3}\pi \delta_{z}^{03} } \right)\left[ {\frac{{H\left( t \right) - H\left( {t - t_{sp} } \right)}}{{t_{sp} }} } \right] $$

(10)

where $a_{sp}$ is a parameter determining the total energy deposited by the ignitor, $\delta_{z}^{0}$ is the Zel’dovich flame thickness of the undiluted stoichiometric mixture ($\delta_{z}^{0} = D_{0} /s_{l}^{0}$, where $D_{0}$ is the unburned mass diffusivity of the reactants and $s_{l}^{0}$ is the unstrained laminar burning velocity of the undiluted stoichiometric mixture) and $H\left( t \right)$, and $H\left( {t - t_{sp} } \right)$ are Heaviside functions, which ensure that the ignitor is only active during $0 \le t \le t_{sp}$. The energy deposition duration $t_{sp}$, is expressed as $t_{sp} = b_{sp} t_{f} ,$ where $t_{f} = \delta_{z}^{0} /s_{l}^{0}$ is a characteristic timescale and the energy deposition parameter $b_{sp}$ is given a value of b_sp = 0.2 in the present study, which falls within its optimal range $\left( {0.2 \le b_{sp} \le 0.4} \right)$ (Ballal and Lefebvre 1979). For a shorter duration, strong shock waves that dissipate energy can be formed, and for a longer one, the temperature is wastefully dissipated outside of the energy deposition region. The details of the spark formation (momentum modification contribution, plasma and shock wave formation) are not considered in this analysis for simplicity and computational economy. In the present study, b_sp and R_sp and all other spark parameters are kept constant (i.e. $b_{sp} = 0.2$, $R_{sp} = 2.45\delta_{z}^{0}$) whilst only a_sp is varied until the minimum energy levels leading to either of the two following phenomena is found:

• 1. Ignition A successful ignition in this paper refers to a situation where the maximum temperature either attains or surpasses the adiabatic flame temperature corresponding to the diluted mixture (i.e. $T_{ad}^{{\psi^{u} }}$) during or after the energy deposition period regardless of subsequent flame behaviour. If the maximum temperature does not reach the adiabatic flame temperature, it is referred to as a misfire in the following discussion.

• 2. Self-sustained propagation A successful self-sustained propagation is obtained when the flame kernel burns without the aid of the ignitor after a successful ignition. It is determined by evaluating the temporal evolution of the burned gas volume (i.e. $V_{c \ge 0.9}$), that is, if the temporal derivative of the burned gas volume is positive at the end of the simulation time (i.e. t = 10.0 t_sp) or when the kernel leaves the computational domain, a successful self-sustained propagation is obtained, otherwise, it is considered failed or quenched.

It must be mentioned that a successful ignition does not necessarily give rise to successful self-sustained combustion. It will be demonstrated later, as the turbulence intensity increases, the energy required to simply ignite the mixture differs from the energy required to obtain self-sustained combustion under the same turbulent conditions. Thus, it was deemed necessary to investigate both events. Thus, finding the MIE consists of finding the values of a_sp which are sufficient to either (i) produce at least a successful thermal runaway or (ii) ensure a successful thermal runaway and subsequent flame propagation once the ignitor is switched off. The stochasticity of the ignition phenomenon is a key aspect (Turquand d’Auzay et al. 2019a; Mastorakos 2009; Mastorakos 2017) and cannot be overlooked. To determine the MIE experimentally (Huang et al. 2007; Shy et al. 2010, 2017a, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b), one first needs to estimate the amount of energy needed to achieve just about more than 0% probability of successful ignition, and the energy required to achieve 100% ignition. To obtain these values many experimental realisations are needed, and once these ‘upper’ and ‘lower’ limits have been ascertained, the energy which leads to 50% ignition probability is taken to be the measure of the MIE. This is done by keeping the energy input unaltered for numerous turbulence realisations to ascertain if a successful (0%) or unsuccessful (100%) event will occur, in order to determine these thresholds. This approach is used in experiments as the energy can be kept unaltered whilst the turbulence realisation cannot. In total, for only one turbulence intensity in an experimental study, tens or hundreds of runs are carried out to determine the MIE value (Huang et al. 2007; Shy et al. 2010, 2017a, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b). However, this method cannot be followed using DNS due to the exorbitantly expensive computational cost associated with such a task. Admittedly, the experimental approach is the optimal method, however the computational method adopts an alternative approach. The use of DNS allows for the turbulent realisation to be kept unaltered, whilst only the input energy is varied. It is worth noting that in an experimental scenario a successful thermal runway (i.e. temperature locally assuming a value either equal to or above the adiabatic flame temperature) is always obtained at the spark location but this is not guaranteed in this computational method because a misfire can happen without any thermal runaway when the energy input is not sufficient (Patel and Chakraborty 2015, 2016a). Therefore, the situations described by (i) and (ii) have been distinguished in this analysis following the previous analysis by Turquand d’Auzay et al. (2019a). It is also worth noting that the terminology ‘ignitability’ and ‘successful ignition’ in the context of experimental analyses (Huang et al. 2007; Shy et al. 2010, 2017a, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b) translate to “successful ignition with subsequent “self-sustained flame propagation” for the current DNS analysis.

In order to analyse the effects of stochasticity, additional simulations have been carried out under different realisations of statistically identical conditions of the initial turbulent flow field (i.e. $u^{{\prime }} /s_{l}^{0}$ and l_t). Subsequently, the amount of energy required to achieve both (i) and (ii) for the first turbulent realisation (henceforth referred to as S01) was tested on the two other turbulent realisations (referred to as S02 and S03 respectively) to analyse the stochasticity of the ignition phenomenon. This method keeps the computational cost (time and storage) to a manageable level (e.g. the current analysis required approximately 570 DNS cases at a cost of 5.85 × 10⁶ core hours). It is worth noting that the MIE requirements are evaluated based on only one turbulent realisation (i.e. realisation S01) due to the computational cost arising from needing multiple simulations to ascertain the MIE for a certain case. This inherently means that successful thermal runaway and self-sustained flame propagation are always obtained for one of the turbulent realisations (henceforth will be mentioned as realisation S01) for the stochasticity analysis associated with the MIE values. This, in turn, raises questions regarding the statistical significance of the MIE values obtained computationally from realisation S01. The methodology followed in this study ensures that the ignitability for this MIE value has to be above 0% and falls within the 0 to 100% ignition probability range, as a successful event has been observed for a random turbulent realisation. Subsequently, it has to be ascertained the range of ignitability where the reported MIE value falls for the statistically identical conditions for the same energy input. To address this aspect, two further turbulent realisations (henceforth refereed to S02 and S03) were considered in this analysis. As a successful event was observed for one of these two added realisations for all turbulence intensities, it further reinforces that the ignition probability is above 0% for the reported value of the MIE. Additionally, with the observation of an unsuccessful event, it can be confirmed that the reported MIE value corresponds to the ignition probability greater than 0% and smaller than 100%. To aid with the understanding of this concept, it is useful to refer to the experimental work by Cardin et al. (2013a) where a histogram of event outcomes against deposited energy has been presented. The MIE values reported in the present study, and for the reasons outlined above, correspond to the successful events on the histogram presented by Cardin et al. (2013a) for each turbulence intensity investigated.

It is impossible to make an estimation of the ignition probability for the reported MIE values based on only three statistically independent realisations because the minimum number of realisations and energy levels required for each turbulence intensity would be similar to that required in an experimental analysis. Additionally, as the ignition probability has been found to vary linearly with the deposited energy (Cardin et al. 2013a), whereas the qualitative trends of normalised MIE are not expected to vary significantly regardless of the value of ignition probability associated with the MIE values reported here.

As this analysis is one of the first attempts to analyse the MIE variation with turbulence intensity for premixed biogas-air mixtures using DNS, a number of assumptions have been made for the purpose of simplification. Therefore, it is useful to revisit the key assumptions and their implications on the findings before moving on to the discussion of the results. The key assumptions made in this analysis are:

• The biogas is considered to be made up of a mixture of CH₄ and CO₂. A two-step mechanism involving incomplete combustion of CH₄ to CO and an equilibrium reaction between the oxidation of CO to CO₂ and dissociation of CO₂ to CO has been considered to represent biogas-air combustion. It has been demonstrated elsewhere (Turquand d’Auzay et al. 2019b) that this mechanism captures the laminar burning velocity variation with equivalence ratio with reasonable accuracy for the range of ${\psi^{u}}$ values considered here. This mechanism also qualitatively captures the reduction of the laminar burning velocity $s_{l}^{{\psi^{u} }}$ with increasing ${\psi^{u}}$ and the quantitative agreement with detailed chemistry results remain satisfactory for the range of ${\psi^{u}}$ (i.e. 0 ≤ ${\psi^{u}}$ ≤ 0.1) but the quantitative agreement deteriorates with increasing ${\psi^{u}}$. The interested readers are referred to Turquand d’Auzay et al. (2019b) for further information in this regard. It is recognised that the quantities such as ignition delay may not be accurately captured quantitatively by a two-step chemical mechanism. However, the present analysis deals with localised forced ignition and the ignition delay related to autoignition does not play a major role in this analysis apart from the identification of the critical turbulence intensity for the MIE transition. Thus, it can be expected that the results of this analysis will at least be qualitatively valid. Moreover, a two-step mechanism is likely to lead to a smaller value of MIE than the value obtained from detailed chemistry because the latter one includes endothermic reactions contributing to reduce the burned gases temperature. However, the variation of the MIE with turbulence intensity is determined by the competition between the chemical heat release and heat transfer rate from the hot gas kernel, which is not modified by the simplification of chemistry and thus the findings of this analysis are expected to be at least qualitatively valid. This will further be demonstrated later in this paper by indicating good agreement with the results of this paper with previous findings based on single step chemistry (Turquand d’Auzay et al. 2019a).

• The gaseous mixture is considered to be composed of perfect gases. The specific heat of all the species are considered to be identical. However, the mixture is considered to be preheated so that the error made by using the assumption of equal C_p across all species can be reduced. Moreover, the incurred error by this assumption is likely to be small for the range of ${\psi^{u}}$ (i.e. 0 ≤ ${\psi^{u}}$ ≤ 0.1) considered here because of the moderate mass fraction of CO₂ in the gaseous mixture.

• The Lewis number of all the species are considered to be unity for the sake of simplification. The use of a unity Lewis number assumption is likely to have an impact on the absolute values of the MIE, but this assumption will not modify the variations of the MIE with the variation of turbulence intensity (Patel and Chakraborty 2016a). The Lewis number values of CH₄, O₂, N₂, CO, CO₂ and H₂O are 0.98, 1.10, 1.04, 1.09,1.39 and 0.89, respectively and thus most constituents of the gaseous mixture have a Lewis number close to unity except for CO₂ and H₂O. However, given the moderate value of maximum possible mass fractions of CO₂ and H₂O (e.g. CO₂ at most 28% by mass in the mixture for the worst cases with ${\psi^{u}}$ = 0.10) for the range of ${\psi^{u}}$ (i.e. 0 ≤ ${\psi^{u}}$ ≤ 0.1) considered here, the effective Lewis number is expected to be close to unity irrespective of the method of its evaluation.

• Only the thermal aspect of the spark is considered in this analysis by considering a source term in the energy conservation equation which deposits energy for a stipulated period of time following several previous analyses (Turquand d’Auzay et al. 2019a, b; Patel and Chakraborty 2015, 2016a, b). However, this method neglects the initial shock wave produced by breakdown phase, which may lead to an underprediction of the flame kernel surface and subsequently to an underprediction of its MIE. Moreover, plasma physics which are also neglected in the present study, introduce radicals to the flame, which might have some influence on the MIE value. However, these simplifications will not modify the qualitative variations of the normalised MIE with the variation of turbulence intensity, which will be revealed later by the good agreement of simulation results with previous experimental results (Huang et al. 2007; Shy et al. 2010, 2017a, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b).

3 Numerical Implementation

The simulations have been carried out using the three-dimensional compressible DNS code SENGA + (Turquand d’Auzay et al. 2019a, b; Patel and Chakraborty 2015, 2016a, b) in three separately sized domains depending on the turbulence intensity investigated and whether the MIE for either ignition or propagation was being determined. For ignition across all turbulence intensities investigated, the computational domain is taken to be 44δ ⁰_z  × 44δ ⁰_z  × 44δ ⁰_z or 4.8l_t × 4.8l_t × 4.8l_t, and subsequently when self-sustained propagation was investigated a larger domain of 66δ ⁰_z  × 66δ ⁰_z  × 66δ ⁰_z or 7.4l_t × 7.4l_t × 7.4l_t has been used for low to medium turbulence intensities (i.e. u′/s ⁰_l  < 13.50), whilst for high turbulence intensities (i.e. u′/s ⁰_l  > 13.50) investigated, a domain of size 89δ ⁰_z  × 89δ ⁰_z  × 89δ ⁰_z or 9.9 l_t × 9.9l_t × 9.9l_t has been used. The domain sizes have been chosen in such a manner to accommodate the development of the kernel in the computational domain for as long as possible. The domains are discretised by Cartesian grids of 352 × 352 × 352, 540 × 540 × 540 and 720 × 720 × 720, respectively, with cells of uniform size ∆x, ensuring at least 10 grid points across the undiluted thermal flame thickness $\delta_{th}^{0} = \left[ {T_{ad}^{0} - T_{0} } \right]/max\left( {\left| {\nabla \hat{T}} \right|_{L} } \right) < \delta_{th}^{{\psi^{u} }}$. It also ensures $\eta_{k} > \Delta x$, where η_k is the Kolmogorov length scale. For these simulations, all the boundaries of the domain are taken to be partially non-reflecting and specified using the modified Navier-Stokes Characteristic Boundary Conditions (NSCBC) technique (Sutherland and Kennedy 2003). For partially non-reflecting boundaries the wave amplitude variations coming to the boundaries from the interior of the domain are calculated from the primitive variables available from the solution, whereas the wave amplitude variations coming into the domain are estimated by a linear relaxation technique. The gradients of shear stresses, mass flux and conduction heat flux in the boundary normal direction are considered to be zero for partially non-reflecting boundaries (Sutherland and Kennedy 2003). Interested readers are referred to Sutherland and Kennedy (2003) for further information regarding the specification of the partially non-reflecting boundary condition using the NSCBC technique. The spatial differentiation and time advancements have been carried out using high order finite difference (10th order central difference for the internal grid points and the order of differentiation gradually decreases to 2nd order one-sided scheme at the boundaries) and 3rd order low storage explicit Runge–Kutta schemes (Wray 1990), respectively. The flame-turbulence interaction takes place under decaying isotropic homogeneous turbulence. A well-known pseudo-spectral method (Rogallo 1981) is used to initialise the turbulent velocity fluctuations by an incompressible, homogeneous isotropic field with prescribed values of root-mean-square (rms) values u′ and integral length scale l_t. The initial integral length scale is kept constant throughout the study at $l_{t} /\delta_{z}^{0} = 9.0$, and it remains comparable with previous computational studies of localised ignition (Turquand d’Auzay et al. 2019a; Klein et al. 2008; Patel and Chakraborty 2015, 2016a, b). A summary of the initial values of normalised rms turbulent velocity (i.e. u′/s ⁰_l and $l_{t} /\delta _{z}^{{\psi^{u}}}$), normalised integral length scale (i.e. $l_{t} /\delta _{z}^{{\psi^{u}}}$ and $l_{t} /\delta_{th}^{{\psi^{u} }}$), normalised Kolmogorov length scale (i.e. $\eta_{k} /\delta_{th}^{{\psi^{u} }}$), Damköhler number $Da = l_{t} s_{l}^{{\psi^{u} }} /u^{{\prime }} \delta_{z}^{{\psi^{u} }}$, Karlovitz number $Ka = \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{1.5} \left( {l_{t} /\delta_{z}^{{\psi^{u} }} } \right)^{ - 0.5}$ and the ratio of eddy turnover time $t_{e} = l_{t} /u^{{\prime }}$ to the energy deposition time $t_{sp}$ are exemplarily provided in Table 2 for $\psi^{u} = 0.05$. The values of $s_{l}^{{\psi^{u} }} /s_{l}^{0} ,$ $\left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right)/\left( {T_{ad}^{0} - T_{0} } \right)$, $\delta_{l}^{{\psi^{u} }} /\delta_{l}^{0}$, $l_{t} /\delta_{th}^{{\psi^{u} }}$ and $l_{t} /\delta _{z}^{{\psi^{u}}}$ for different values of $\psi^{u}$ are also listed in Table 2.

Table 2 Initial values of normalised rms turbulent velocity $\left( {{\text{i}}.{\text{e}}.\;u^{{\prime }} /s_{l}^{0} \;{\text{and}}\;u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right),$ normalised integral length scale $\left( {{\text{i}}.{\text{e}}.\; l_{t} /\delta_{z}^{\psi^{u}} \;{\text{and}}\;l_{t} /\delta_{th}^{{\psi^{u} }} } \right),$ normalised Kolmogorov length scale $\left( {{\text{i}}.{\text{e}}.\;\eta_{k} /\delta_{th}^{{\psi^{u} }} } \right),$ Damköhler number $Da = l_{t} s_{l}^{{\psi^{u} }} /u^{{\prime }} \delta_{z}^{{\psi^{u} }} ,$ Karlovitz number $Ka = \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{1.5} \left( {l_{t} /\delta_{z}^{{\psi^{u} }} } \right)^{ - 0.5}$ and the ratio of eddy turn over time $t_{e} = l_{t} /u^{{\prime }}$ to the energy deposition time t_sp for ${\psi^{u}}$ = 0.05, and the values of $s_{l}^{{\psi^{u} }} /s_{l}^{0} ,\;\left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right)/\left( {T_{ad}^{0} - T_{0} } \right),\;\delta_{l}^{{\psi^{u} }} /\delta_{l}^{0} ,\;l_{t} /\delta_{th}^{{\psi^{u} }}$ and $l_{t} /\delta_{z}^{\psi^{u}}$ for different values of ${\psi^{u}}$

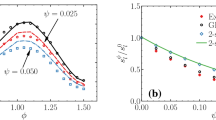
The present study investigates the MIE behaviour for four different levels of dilution $\psi^{u} = 0.0,0.025,0.05$ and 0.10 (alternatively $\psi^{f} = 0.0,0.21,0.36$ and 0.54), where $\psi^{u} = 0.0$ (alternatively $\psi^{f} = 0.0$) indicates a pure methane-air mixture. The mixture in all cases is considered to be perfectly premixed with an equivalence ratio of unity, and the initial mass fractions of oxidizer, methane and carbon dioxide can be recovered for each dilution percentage investigated from the definition of $\psi^{u}$ in conjunction with Eq. 3. The ratio $l_{t} /\delta_{z}^{0}$ is kept constant, however when the respective flame thickness for the diluted mixture $\delta_{z}^{{\psi^{u} }}$ is used, the ratio $l_{t} /\delta_{z}^{{\psi^{u} }}$ decreases with increasing dilution percentage as shown in Fig. 1, as the presence of CO₂ thickens the flame and reduces laminar burning velocity.

Fig. 1

Variation of $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ with $u^{{\prime }} /s_{l}^{0}$ (dots), and variation of $l_{t} /\delta_{z}^{{\psi^{u} }}$ with $l_{t} /\delta_{z}^{0}$ (lines), across all cases investigated

The cases investigated here have been designed in such a manner that the rms turbulent velocity u′ is kept unaltered, whilst the level of dilution in the fuel-blend is subject to change, specifically due to the difficulty of producing industrial quantities of biogas with a fixed composition $\psi^{u}$, and this approach is consistent with the experimental work by Larsson et al. (2013). This, in turn, means that even if u′ and $l_{t}$ are kept constant, the ratios of $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ and $l_{t} /\delta_{th}^{{\psi^{u} }}$ change with the variation of the mixture composition for the stoichiometric mixture, as shown in Fig. 1, and this has a significant influence on the MIE variation. The DNS simulations, which are used to evaluate the MIE only for successful thermal runaway, have been carried out for at least $t = 2.0t_{sp}$, whilst the simulations for successful propagation, have been carried out till $t = 10.0t_{sp}$, or until the kernel exits the domain. For each value of u′ across all dilution percentages investigated, several simulations have been carried out with different values of the ignition energy parameter a_sp to estimate the MIE to a precision of about 1.0% of the corresponding laminar MIE value for ignition, whilst for ensuring self-sustained flame propagation the MIE was sought with an accuracy of 2-4% of the corresponding laminar MIE value for the specific realisation investigated. The simulation time of $t = 10.0t_{sp}$ used in the present study remains comparable to that used in previous analyses (Turquand d’Auzay et al. 2019a, b; Klein et al. 2008; Patel and Chakraborty 2015, 2016, b).

4 Results and Discussion

In order to allow for direct comparison between cases with different dilution fractions, the MIE is normalised based on the MIE obtained for the respective $\psi^{u}$ under laminar conditions, and is calculated as $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{i/p} = \left( {E_{i/p} } \right)_{{{{\psi }}^{u} }} /\left( {E_{p} } \right)_{{{{\psi }}^{u} }}^{\text{L}}$ where $E_{i/p} = \left( {a_{sp} } \right)\rho_{0} C_{p} \tau T_{0} \left( {4/3\pi (\delta_{z}^{0}})^{3} \right)$ is the MIE and the subscripts i and p indicate values sufficient just for thermal runaway and also for self-sustained flame propagation following thermal runaway, respectively. The subscript $\psi^{u}$ indicates the dilution level, whilst the superscript L refers to laminar quiescent condition. The values of $\left( {a_{sp} } \right)_{{{{\psi }}^{u} }}^{\text{L}} = \left( {E_{p} } \right)_{{{{\psi }}^{u} }}^{\text{L}} /[\rho_{0} \left( {4\pi /3} \right)(\delta_{z}^{0} )^{3} C_{p} \left( {T_{ad}^{0} - T_{0} } \right)]$ for different dilution percentages $\psi^{u}$ are listed in Table 3. It is important to note that $\delta_{z}^{{\psi^{u} }}$ increases, whereas $\left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right)$ decreases with increasing $\psi^{u}$ (see Table 2) and thus the quantity $\left( {a_{sp}^{'} } \right)_{{{{\psi }}^{u} }}^{\text{L}} = \left( {E_{p} } \right)_{{{{\psi }}^{u} }}^{\text{L}} /[\rho_{0} \left( {4\pi /3} \right)(\delta_{z}^{{\psi^{u} }} )^{3} C_{p} \left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right)]$ may not show a monotonic trend with the variation of $\psi^{u}$ and therefore it becomes difficult to compare the relative magnitudes of $\left( {E_{p} } \right)_{{{{\psi }}^{u} }}^{\text{L}}$ from the values of $\left( {a_{sp}^{{\prime }} } \right)_{{{{\psi }}^{u} }}^{\text{L}}$. By contrast, $[\rho_{0} \left( {4\pi /3} \right)(\delta_{z}^{0} )^{3} C_{p} \left( {T_{ad}^{0} - T_{0} } \right)]$ does not change with $\psi^{u}$ and thus $\left( {a_{sp} } \right)_{{{{\psi }}^{u} }}^{\text{L}}$ provides the relative magnitudes of $\left( {E_{p} } \right)_{{{{\psi }}^{u} }}^{L}$ in the simplest form, and thus allows for the comparison of the MIE values with relative ease. Therefore, the values of $\left( {a_{sp} } \right)^{\text{L}}$ are provided in Table 3 and the value of $\left( {a_{sp}^{{\prime }} } \right)_{{{{\psi }}^{u} }}^{\text{L}} = \left( {E_{i/p} } \right)_{{{{\psi }}^{u} }}^{\text{L}} /\left[ {\rho_{0} \left( {4\pi /3} \right)(\delta_{z}^{{\psi^{u} }} )^{3} C_{p} \left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right)} \right]$ can be estimated from the information provided in Table 3 and the values of $\left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right)/\left( {T_{ad}^{0} - T_{0} } \right)$ and $\delta_{z}^{{\psi^{u} }} /\delta_{z}^{0}$ values listed in Table 2.

Table 3 The MIE normalised by the energy required bring a sphere of radius $\delta_{z}^{0}$ from T⁰ to T ⁰_ad for self-sustained flame propagation for laminar quiescent mixtures for different values of ${\psi^{u}}$

To understand the effect that varying levels of dilution have on the thermal runaway and subsequent flame propagation, it is instructive to examine the temporal evolutions of maximum temperature under laminar conditions across the different dilution levels investigated in this analysis. The temporal evolutions of the maximum value of non-dimensional temperature $T_{norm} = \left( {\hat{T} - T_{0} } \right)/\left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right)$ under laminar conditions for different dilution percentages $\psi^{u}$ are shown in Fig. 2 for an input ignition energy which is the MIE for $\psi^{u} = 0.025$. It can be seen from Fig. 2 that an increase of $\psi^{u}$ leads to a decrease in the maximum value of $T_{norm}$. Figure 2 further shows that thermal runaway takes place only for the cases with $\psi^{u} = 0.0$ and $\psi^{u} = 0.025$, and the maximum value of $T_{norm}$ surpasses its value corresponding to the respective adiabatic flame temperature $\left( {T_{norm} > 1.0} \right)$ at $t/t_{sp} = 2.3$ for the undiluted cases and at $t/t_{sp} = 4.0$ for the case with $\psi^{u} = 0.025$, whilst for the higher dilution percentages, $T_{norm}$ decreases after the end of the energy deposition duration $\left( {t/t_{sp} = 1.0} \right),$ and results in a misfire.

Fig. 2

Temporal evolutions of the maximum value of $T_{norm}$ under laminar conditions with ${\psi^{u}}$ = 0.0, 0.025, 0.05 and 0.10 as indicated by the legend for input energy equal to the MIE for ${\psi^{u}}$ = 0.025 under laminar conditions

The temporal evolutions of $(T_{norm} )_{max}$ for the cases with $\psi^{u} = 0.0\;{\text{and}}\;\psi^{u} = 0.025$ in Fig. 2 are indicative of autoignition, as the thermal runaway occurs after the end of the energy deposition duration, and this behaviour is consistent with previous findings by Turquand d’Auzay et al. (2019a). As all the cases presented in Fig. 2 are laminar and an identical amount of energy is being deposited into the mixture, an increase in $\psi^{u}$ leads to misfire, highlighting the ‘heat sink effect’ of CO₂ (Turquand d’Auzay et al. 2019b). This, in turn, suggests that the MIE is expected to increase with increasing $\psi^{u}$ for a given value of $u^{{\prime }} /s_{l}^{0}$, and this will be demonstrated and discussed later in this paper. Thermal runaway due to autoignition after the energy deposition period has also been observed for the MIE corresponding to $\psi^{u} = 0.05$ and $0.10$ under laminar conditions, and the temporal evolutions of $(T_{norm} )_{max}$ for the MIE for $\psi^{u} = 0.05$ and 0.10 are qualitatively similar to the profile shown for $\psi^{u} = 0.025$ in Fig. 2. It is also worth noting that the time delay $\left( {t \approx 4.0t_{sp} } \right)$ for $(T_{norm} )_{max}$ to surpass the adiabatic flame temperature (i.e. $T_{norm} = 1.0$) for $\psi^{u} = 0.025$ is nearly double in comparison to the time delay $\left( {t \approx 2.3t_{sp} } \right)$ observed for the corresponding undiluted methane-air mixture. This illustrates the detrimental effects of CO₂ dilution on ignition delay, along with the slower combustion process for the diluted mixture when compared to undiluted methane-air mixtures, which is also in agreement with experimental findings (Galmiche et al. 2011).

To further investigate the effects of $\psi^{u}$ and initial turbulence intensity on the ignition event, the isosurfaces of different values of $T_{norm}$ at $t/t_{sp} = 0.5,1.0,1.5,2.0,2.5$ are presented in Fig. 3. The cases selected for the comparison were chosen to have almost identical $u^{{\prime }} /s_{l}^{{\psi^{u} }} \left( { \approx 10.75} \right)$ for all $\psi^{u}$ values investigated in the present study. It can be seen from Fig. 1 that despite $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ being nearly the same value $\left( { \approx 10.75} \right)$ across all the cases, the turbulence intensities are $u^{{\prime }} /s_{l}^{0} = 10.75, 9.5, 8.5$ and 6.0 for $\psi^{u} = 0.0, 0.025, 0.05$ and 0.10 cases, respectively. Observing the temporal evolutions of the $T_{norm}$ isosurfaces in Fig. 3, it can be inferred that despite $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ being very similar, the ignition kernels become increasingly wrinkled and elongated owing to increases of $u^{{\prime }} /s_{l}^{0}$ with decreasing $\psi^{u}$ (right to left). It is worth noting that the hot gas kernel is expected to be roughly spherical at early times (i.e. $t\sim t_{sp}$) because the shape of the hot gas kernel is determined by the diffusion of the deposited thermal energy but Fig. 3 clearly shows a departure from the pure spherical shape as time elapses due to the interaction with turbulence. The moderate level of wrinkling of temperature isosurfaces in Fig. 3 arises due to the fact that the eddy turnover time $t_{e} = l_{t} /u^{{\prime }}$ remains greater than the energy deposition time $t_{sp}$ for all cases considered here (see Table 2). All cases exhibit a $T_{norm} = 1.0$ isosurface by $t = 2.0t_{sp}$ (i.e. successful thermal runaway), except for the case with $\psi^{u} = 0.05$ where the $T_{norm} = 1.0$ isosurface appears at $t = 2.5t_{sp}$. However, at $t = 2.50t_{sp}$, the hot gas kernel in the case with $\psi^{u} = 0.025$ starts quenching with the volume corresponding to $T_{norm} = 1.0$ being absent, whereas hot gas kernels for the other cases exhibit $T_{norm} = 1.0$ isosurfaces, which also exhibit growths in size within the time duration shown in Fig. 3. However, the growth of the hot gas kernel following thermal runaway does not necessarily lead to self-sustained flame propagation and a long mode of failure to achieve self-sustained flame propagation (Mastorakos 2009) can be obtained when the input energy for ensuring just thermal runaway is less than the energy required to ensure self-sustained propagation $\left( {{\text{i}}.{\text{e}}.\;\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{\text{p}} > \left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{\text{i}} } \right),$ as is the case for all the diluted cases shown in Fig. 3.

Fig. 3

Isosurfaces of (yellow) $T_{norm} = 0.1$, (light green) 0.5 and (purple) 1.0 with the energy deposition region indicated by the wireframe sphere, obtained for $\left( {\varGamma_{{\psi^{u} }} } \right)_{i}$ with $u^{{\prime }} /s_{l}^{{\psi^{u} }} \approx 10.50$ for ${\psi^{u}}$ = 0.0, 0.025, 0.05 and 0.10 (left to right) and for t/t_sp = 0.5, 1.0, 1.5, 2.0 and 2.5 (top to bottom). The black lines are all perpendicular to each other and meet at the centre of the energy deposition region, which is also the centre of the domain

These results might superficially seem counter-intuitive as the undiluted case and the case with the highest amount of CO₂ dilution are exhibiting growths in the volume of the regions corresponding to $T_{norm} \ge 1.0$ with time, whereas the other cases exhibit signs of flame quenching. In order to explain this behaviour, it is also important to account for the amount of deposited ignition energy. The normalised MIE $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{i}$ is 1.106, 1.085, 1.06 and 1.026 for the cases with $\psi^{u} = 0.0, 0.025, 0.05$ and 0.10, respectively for the conditions shown in Fig. 3. Using the values presented in Table 3, the values of $\left( {E_{i} } \right)_{{{{\psi }}^{u} }}$ are $\left\{ {3.90,3.85,3.85, 3.90} \right\} \times \left[ {\rho_{0} \left( {4\pi /3} \right)(\delta_{z}^{0} )^{3} C_{p} \left( {T_{ad}^{0} - T_{0} } \right)} \right]$ for $\psi^{u} = \left\{ {0.0, 0.025, 0.05,0.10} \right\}$, respectively for the cases shown in Fig. 3. These values are close to each other for the $\psi^{u}$ values considered in Fig. 3, and thus a wide variety of outcomes for the ignition kernels are expected to be obtained for almost equal ignition energy input due to the stochastic nature of the ignition phenomenon. The flame kernel for the $\psi^{u} = 0.025$ case exhibits an indication of eventual flame quenching by $t = 3.0t_{sp}$, whereas the region corresponding to $T_{norm} = 1.0$ is absent by $t/t_{sp} = 3.0$, for the $\psi^{u} = 0.05$ case indicating flame quenching similarly to the $\psi^{u} = 0.025$ case. For the $\psi^{u} = 0.10$ case, the hot gas kernel continues to grow during $t_{sp} \le t \le 3.0t_{sp}$ under $u^{\prime}/s_{l}^{\psi } \approx 10.75$ $\left( {u^{{\prime }} /s_{l}^{0} = 6.0} \right)$ before the flame eventually quenches as the energy deposited to achieve a successful thermal runaway is equal to 75% of the energy requirement for ensuring self-sustained flame propagation $\left( {{\text{i}}.{\text{e}}.\;\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{i} = 0.75\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p} } \right).$ However, for the case with $\psi^{u} = 0.0$, the hot gas kernel ensued from thermal runaway will go on to successfully propagate without the aid of external energy addition as $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{i}$ is equal to $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{\text{p}}$ for the value of $u^{{\prime }} /s_{l}^{0}$ considered in Fig. 3. From the above observations, it can be surmised that the level of CO₂ dilution in the mixture and turbulence intensity $u^{{\prime }} /s_{l}^{0}$ interact with each other and play a significant role in deciding whether successful ignition will occur and determining the fate of the ignited hot gas kernel.

The temporal evolution of the non-dimensional temperature $T_{norm} = 0.7$ isosurfaces coloured by the normalised reaction rate magnitude of the fuel $\left( {\left| {\dot{\omega }_{{Y_{{CH_{4} }} }} } \right| \times \delta_{z}^{0} /\rho_{0} s_{l}^{0} } \right)$ at different time instants (i.e. t/t_sp = 4.0, 6.0 and 8.0) are exemplarily shown in Fig. 4 for the MIE for self-sustained flame propagation for different dilutions (i.e. ${\psi^{u}}$ = 0.0, 0.025, 0.05 and 0.10) in the case of initial turbulence intensity of $u^{{\prime }} /s_{l}^{0} = 8.50$. It can be seen from Fig. 1 that $u^{{\prime }} /s_{l}^{\psi^{u}}$ values for a given value of $u^{{\prime }} /s_{l}^{0}$ increase with increasing ${\psi^{u}}$ and thus the biogas cases are subjected to greater values of $u^{{\prime }} /s_{l}^{\psi^{u}}$ than 8.50 and this trend increases with increasing ${\psi^{u}}$. It can be seen from Fig. 4 that the flame kernels become increasingly deformed under turbulent motion. Figure 4 further demonstrates that the high-temperature kernel moves away from the original ignitor location and can also become fragmented at later times. This suggests that turbulent flow conditions away from the ignitor location also play a key role in determining the possibility of successful self-sustained flame propagation. Furthermore, a comparison between the cases shown in Fig. 4 reveals that larger volumes of the high-temperature zone are obtained for higher values of $\psi^{u}$, whereas the normalised fuel reaction rate magnitude decreases with increasing ${\psi^{u}}$. An increase in ${\psi^{u}}$ decreases the mass fractions of fuel and oxidiser, which leads to a decrease of $\left| {\dot{\omega }_{{Y_{{CH_{4} }} }} } \right| \times \delta_{z}^{0} /\rho_{0} s_{l}^{0}$. The heat release rate within the flame kernel needs to exceed the heat transfer from the hot gas kernel to allow for self-sustained flame propagation once the ignitor is switched off and the possibility of the heat transfer rate dominating over the heat release rate increases for a larger surface to volume ratio. As the reaction rate magnitudes are smaller for higher values of ${\psi^{u}}$, the hot gas kernels need to be bigger to have a smaller surface area to volume ratio to ensure self-sustained flame propagation unassisted by the external energy addition. This is reflected in the larger volume of the hot gas kernel for higher values of ${\psi^{u}}$ in Figs. 3 and 4. Moreover, the necessity to have a larger volume of the high-temperature region for higher values of ${\psi^{u}}$ for the MIE suggests that the demand for the MIE is expected to increase with increasing ${\psi^{u}}$. Although turbulent cases are shown in Fig. 4, the aforementioned conclusions are valid for both laminar and turbulent conditions. It can indeed be seen from Table 3 that $\left( {E_{p} } \right)_{{{{\psi }}^{u} }}^{L}$ increases with increasing ${\psi^{u}}$.

Fig. 4

Isosurfaces of $T_{norm} = 0.7$ coloured by the normalised reaction rate magnitude of the fuel $\left( {\left| {\dot{\omega }_{{Y_{{CH_{4} }} }} } \right| \times \delta_{z}^{0} /\rho_{0} s_{l}^{0} } \right)$ obtained for their respective $\left( {\varGamma_{{\psi^{u} }} } \right)_{p}$ with $u^{{\prime }} /s_{l}^{0} = 8.50$ for ${\psi^{u}}$ = 0.0, 0.025, 0.05 and 0.10 (top to bottom) and for t/t_sp = 4.0, 6.0 and 8.0 (left to right) with the energy deposition region indicated by the translucent blue sphere

The variations of the MIE values of biogas-air mixtures normalised by the MIE for self-sustained flame propagation of the laminar quiescent undiluted mixture $\left( {E_{i} } \right)_{{{{\psi }}^{u} }} /\left( {E_{p} } \right)_{{{{\psi }}^{u} = 0.0}}^{\text{L}}$ and $\left( {E_{p} } \right)_{{{{\psi }}^{u} }} /\left( {E_{p} } \right)_{{{{\psi }}^{u} = 0.0}}^{\text{L}}$ are shown as functions of $u^{{\prime }} /s_{l}^{0}$ and $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ in Fig. 5a and b, respectively. The variation of $\left( {E_{i/p} } \right)_{{{{\psi }}^{u} }} /\left( {E_{p} } \right)_{{{{\psi }}^{u} = 0.0}}^{\text{L}}$ with $Ka = \left( {u^{{\prime }} /s_{l}^{{{{\psi }}^{\text{u}} }} } \right)^{3/2} \left( {l_{t} /\delta_{z}^{{\psi^{u} }} } \right)^{ - 1/2}$ is shown in Fig. 5c, which does not appreciably change the level of collapse of data for different values of ${\psi^{u}}$ in comparison to that shown in Fig. 5b. Thus, the variation of $\left( {E_{i/p} } \right)_{{{{\psi }}^{u} }} /\left( {E_{p} } \right)_{{{{\psi }}^{u} = 0.0}}^{\text{L}}$ with $Ka$ will not be considered further in this paper.

Fig. 5

Variation of the MIE values for ensuring just thermal runaway (empty circles) and self-sustained flame propagation (filled diamonds) for biogas-air mixtures normalised by the MIE required to obtain successful propagation for the undiluted laminar case $\left( {{\text{i}}.{\text{e}}.\;\left( {E_{i/p} } \right)_{{\psi^{u} }} /\left( {E_{p} } \right)_{{\psi^{u} = 0.0}}^{L} } \right)$ for different values of (a) $u^{{\prime }} /s_{l}^{0}$, (b) $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ and (c) $Ka$

It can be seen from Fig. 5 that $\left( {E_{i/p} } \right)_{{{{\psi }}^{u} }}$ increases with increasing ${\psi^{u}}$ and this behaviour is consistent for all $u^{{\prime }} /s_{l}^{0}$. This behaviour is found to be qualitatively consistent with both experimental and numerical findings of Larsson et al. (Larsson et al. 2013) for a gas turbine combustor. A comparison between Fig. 5a and b reveals that the energy requirement for just ensuring thermal runaway is significantly smaller than that needed for ensuring self-sustained flame propagation for large values of u′ beyond the critical turbulence intensity (i.e. $\left( {u^{\prime}/s_{l}^{0} } \right) > \left( {u^{\prime}/s_{l}^{0} } \right)_{crit}$). The corresponding critical turbulence intensity $\left( {u^{\prime}/s_{l}^{{\psi^{u} }} } \right)_{crit}$, can be obtained by using the ratios $s_{l}^{{\psi^{u} }} /s_{l}^{0}$ (see Table 2). The trends presented in Fig. 5 are consistent with the observations made in previous studies for undiluted fuel–air mixtures (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b) and also with the findings of Figs. 3 and 4. Moreover, the transition in the normalised MIE demand $\left( {E_{i/p} } \right)_{{{{\psi }}^{u} }}$ with increasing u′ for $\left( {u^{{\prime }} /s_{l}^{0} } \right) > \left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ is consistent with previous experimental (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b) and computational (Turquand d’Auzay et al. 2019a) findings. The increase in the energy requirement with increasing ${\psi^{u}}$ is attributed to the decreases in burned gas temperature and heat release rate with increasing dilution level. To further investigate the transition of the MIE requirements with increasing rms turbulent velocity u′ for $\left( {u^{{\prime }} /s_{l}^{0} } \right) > \left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ and the influences of ${\psi^{u}}$ on it, the normalised MIE $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{i/p}$ is plotted as a function of $u^{{\prime }} /s_{l}^{0}$ in Fig. 6.

Fig. 6

Variation of the normalised MIEs (a, b) $\left( {\varGamma_{{\psi^{u} }} } \right)_{i}$ and (c, d) $\left( {\varGamma_{{\psi^{u} }} } \right)_{p}$ with (a, c) $u^{{\prime }} /s_{l}^{0}$ and (b, d) $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ for different dilution levels ${\psi^{u}}$

It can be seen from Fig. 6 that the normalised critical turbulence intensities $\left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ and $\left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)_{crit}$ for the MIE for self-sustained flame propagation decrease with increasing ${\psi^{u}}$ (i.e. pink to red to blue to black markers in Fig. 6). The values of $\left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ and $\left( {u^{\prime } /s_{l}^{{\psi^{u} }} } \right)_{crit}$ are compared with previous experimental findings by Shy et al. (2010), Cardin et al. (2013a, b) and computational findings by Turquand d’Auzay et al. (2019a) in Table 4. It is worth noting that the $\psi^{u} = 0.0$ cases (black markers) indicate stoichiometric undiluted methane-air mixtures. The present authors previously investigated the behaviour of the MIE transition for premixed stoichiometric methane-air mixtures with near-identical simulation parameters as in the present study, but a single step chemical mechanism was used (Turquand d’Auzay et al. 2019a). However, in the present study with the two-step chemical mechanism, the transition has been observed for $\left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit} \approx 15.0$ for $\psi^{u} = 0.0$, whilst for the study with the single-step mechanism (Turquand d’Auzay et al. 2019a) the transition was obtained at $\left( {u^{\prime } /s_{l}^{0} } \right)_{crit} \approx 11.5$ for $\psi^{u} = 0.0$. This difference originates due to the different chemical mechanisms used in these studies, and $\left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ for $\psi^{u} = 0.0$ found in the present study matches the experimental value reported by Shy et al. (i.e. $\left( {u^{\prime}/s_{l} } \right)_{crit} \approx 15.0$) for the stoichiometric mixture (Shy et al. 2010). Additionally, the present critical turbulence intensity is in the same range as the value that was reported by Cardin et al. (2013a, b) for lean methane-air mixtures $\left( {{\text{i}}.{\text{e}}.\;\left( {u^{{\prime }} /s_{l} } \right)_{crit} = 7.0 - 11.0} \right).$ The Karlovitz number $Ka = \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)_{crit}^{3/2} \left( {l_{t} /\delta_{z}^{{\psi^{u} }} } \right)^{ - 1/2}$ for the critical turbulence intensity for the MIE transition varies between 10.0 to 19.0 for the cases considered here, and this range of Karlovitz number is consistent with previous experimental findings (Shy et al. 2010; Cardin et al. 2013a, b). The agreement in order of magnitude for the critical turbulence intensity and Karlovitz numbers between the present study and the previous experimental findings (Shy et al. 2010; Cardin et al. 2013a) is encouraging, despite the difference in equivalence ratio. It has already been demonstrated in Fig. 2 that thermal runaway occurs after the energy deposition period $\left( {{\text{i}}.{\text{e}}.\;t \gg t_{sp} } \right)$ due to autoignition for small values of turbulence intensity $\left( {{\text{i}}.{\text{e}}.\; \left( {u^{{\prime }} /s_{l}^{0} } \right) < \left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit} } \right).$ The prediction of the autoignition process (e.g. autoignition delay) depends on the choice of chemical mechanism and therefore the differences in critical turbulence intensity values between single and two-step chemical mechanisms arise due to the differences in autoignition behaviours. It is worth noting that the autoignition delay cannot be accurately predicted without a detailed chemical mechanism and therefore the differences in $\left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ and $\left( {u^{\prime } /s_{l}^{{\psi^{u} }} } \right)_{crit}$ values obtained from single and two-step chemical mechanisms should be considered with caution. However, the qualitative behaviour of the variation of $(\varGamma_{{\psi^{u} }} )_{i/p}$ with $u^{\prime } /s_{l}^{0} \left( {{\text{or}}\;u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)$ remains unaltered by the choice of the chemical mechanism. In fact, the following discussion will illustrate the scaling of $(\varGamma_{{\psi^{u} }} )_{p}$ with $u^{\prime } /s_{l}^{0} \left( {{\text{or}}\;u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)$ remains independent of the choice of chemical mechanism.

Table 4 Values of normalised critical turbulence intensities $\left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ and $\left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)_{crit}$ for self-sustained flame propagation, obtained from DNS data along with previous experimental findings by Shy et al. (2010), Cardin et al. (2013a) and computational findings of Turquand d’Auzay et al. (2019a)

It can be seen from the log–log plot in Fig. 6 that the normalised MIE $\varGamma_{{\psi^{u} }}$ for a given dilution level ${\psi^{u}}$ can be approximated by a power-law of the form $(\varGamma_{{\psi^{u} }} )_{i} \propto \left( {u^{\prime } /s_{l}^{0} } \right)^{{n_{i} }}$ and $(\varGamma_{{\psi^{u} }} )_{p} \propto \left( {u^{\prime } /s_{l}^{0} } \right)^{{n_{p} }}$ (or alternatively form $(\varGamma_{{\psi^{u} }} )_{i} \propto \left( {u^{\prime } /s_{l}^{{\psi^{u} }} } \right)^{{n_{i} }}$ and $(\varGamma_{{\psi^{u} }} )_{p} \propto \left( {u^{\prime } /s_{l}^{{\psi^{u} }} } \right)^{{n_{p} }}$ because $s_{l}^{0} /s_{l}^{{\psi^{u} }}$ is a constant for a given value of ${\psi^{u}}$), which are shown by the dashed lines in Fig. 6. The values of the power-law exponents n_i and n_p for different values of ${\psi^{u}}$ are summarised in Table 5. As can be seen from the relevant values in Table 5, n_i and n_p values are of the same small order of magnitude (~ 10⁻²) and are quite similar $\left( {{\text{i}}.{\text{e}}.\;n_{\text{i}} \approx n_{\text{p}} } \right)$ for $\left( {u^{{\prime }} /s_{l}^{0} } \right) < \left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit} .$ The small differences between n_i and n_p that arise for $\left( {u^{{\prime }} /s_{l}^{0} } \right) < \left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit} ,$ are due to the different number of data points that are used for obtaining n_i and n_p because the MIE transition for just thermal runaway takes place at a different turbulence intensity from that for self-sustained flame propagation. The similarity between n_i and n_p for $\left( {u^{{\prime }} /s_{l}^{0} } \right) < \left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ is also reinforced by Fig. 5, where the energy requirements are shown to be near-identical for ignition and propagation in these cases, thus implying that the corresponding slopes should exhibit similar behaviour. It can be seen from Fig. 6 that the trendlines for estimating n_p are in excellent agreement with the data points, which are sufficient in number to provide confidence that the slope on the log–log plot has been adequately captured.

Table 5 Values of power-law exponents n_i and n_p obtained from DNS data for $({\varvec{\Gamma}}_{{\varvec{\psi}^{\varvec{u}} }} )_{\varvec{i}} \propto \left( {\varvec{u^{\prime}}/\varvec{s}_{\varvec{l}}^{0} } \right)^{{\varvec{n}_{\varvec{i}} }}$ $\left( {{\text{alternatively}}\;(\varGamma_{{\psi^{u} }} )_{i} \propto \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{{n_{i} }} } \right)$ and $(\varGamma_{{\psi^{u} }} )_{p} \propto \left( {u^{{\prime }} /s_{l}^{0} } \right)^{{n_{p} }}$ $\left( {{\text{alternatively}}\;(\varGamma_{{\psi^{u} }} )_{p} \propto \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{{n_{p} }} } \right)$

It can be seen from Table 4 that the critical turbulence intensity where the MIE transition occurs is different for different values of ${\psi^{u}}$. Thus, the variation of $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ with $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ for different values of ${\psi^{u}}$ do not completely collapse even though the power law exponent n_p exhibits similar values for the different dilution levels. However, the extent of collapse of the variation of $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ with $u^{{\prime }} /s_{l}^{{\psi^{u} }}$ for different values of ${\psi^{u}}$ is relatively better than the variation of $\left( {{{\varGamma }}_{MIE}^{{\psi^{u} }} } \right)_{p}$ with $u^{{\prime }} /s_{l}^{0}$ (see Fig. 6).

It can be seen that $n_{p} > n_{i}$ for all values of ${\psi^{u}}$, which is consistent with the greater energy demand to ensure the successful self-sustained flame propagation without any external assistance in comparison to the energy demand for just obtaining thermal runaway (which is referred to as ignition in this analysis). The values of n_p obtained from previous experimental findings by Shy et al. (2010), Cardin et al. (2013a) and computational findings by Turquand d’Auzay et al. (2019a) are summarised in Table 6. It can be seen from Tables 5 and 6 that the exponent n_p for $\psi^{u} = 0.0$ is found to be 2.20 (i.e. n_p = 2.2) for $\psi^{u} = 0.0$, which is in good agreement with the corresponding value (i.e. n_p = 2.0) reported by Turquand d’Auzay et al. (2019a). A comparison between Tables 5 and 6 reveals that a good agreement is found with the experimental findings by Cardin et al. (2013a). Moreover, Table 5 reveals that n_p varies between 1.7 and 2.2 (i.e. n_p = 1.7–2.2). This range of n_p is consistent with the experimental values reported by Cardin et al. (2013a). However, a much larger value of n_p was previously reported by Shy and his co-workers (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018). The quantitative disagreements that arise between the experimental studies by Shy and his co-workers (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018) and with the current DNS (and also previous DNS analysis by Turquand d’Auzay et al. (2019a)) can be attributed to differences in the (i) measurement of the energy deposited, (ii) integral length scales between the experimental and DNS studies and the use of forced turbulence by Shy and co-workers (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018), as opposed to decaying turbulence used in the DNS studies (Turquand d’Auzay et al. 2019a), and also in the experiments by Cardin et al. (2013a, b). In experiments, the exact amount of energy deposited to the gaseous mixture cannot be measured as precisely as it is in the case of DNS (no heat losses, plasma formation, and shock wave in the numerical results) (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018) but the uncertainty regarding the energy input in laser ignition (Cardin et al. 2013a, b) is likely to be smaller than in spark ignition. At this point it is imperative to highlight the fact that for the present computational study, the turbulence parameters and characteristics are very similar to those reported by Cardin et al. (2013a, b). As previously mentioned, the experimental work by Cardin et al. (2013a, b) utilises decaying turbulence at comparable intensities and a laser ignition system, which provides more accurate estimation of the depositing energy into the flammable mixture than for the spark ignition system. Thus, the agreement in order of magnitude between computational and experimental studies for both the critical turbulence intensity and exponent n_p, despite the difference in equivalence ratio is encouraging despite several assumptions made for the purpose of this computational analysis.

Table 6 Values of the power-law exponent n_p after the transition has occurred for self-sustained flame propagation, from experimental findings by Shy et al. (2010), Cardin et al. (2013a), computational findings of Turquand d’Auzay et al. (2019a), and the present DNS Data

It is worth noting that the competition between the chemical heat release rate and heat transfer rate from the hot gas kernel determines the fate of the ignited hot gas kernel in the absence of external energy added by the ignitor. The heat transfer has an adverse effect on the likelihood of both ignition and subsequent self-sustained propagation, and it increases with increasing turbulent eddy diffusivity $D_{t}$, which scales with rms turbulent velocity u′ (i.e. $D_{t} \sim u^{\prime}l_{t}$). Under forced turbulence u′ does not decay with time and thus the heat transfer from the hot gas kernel does not decrease with time but under decaying turbulence, the heat transfer from the hot gas kernel decreases with the decay in $D_{t}$ with time. This implies that the MIE under forced turbulence would have to be greater than the values found under decaying turbulence, as the higher heat transfer from the hot gas kernel would result in a misfire or flame quenching if the MIE for decaying turbulence were used for forced turbulence. Therefore, the DNS results would probably be in better agreement with the experimental results presented by Shy and co-workers (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018) if forced turbulence were to be used in place of the current use of decaying turbulence.

The differences between the definitions of successful ignition between experimental and the current DNS analysis may also contribute to the differences between n_p values obtained from the current investigation and the experimental observations by Shy and co-workers (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018). However, despite the differences between the current decaying turbulence DNS results with experimental findings for forced turbulence (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018), the transition of the MIE with increasing turbulence intensity has been qualitatively captured in this study. Furthermore, the power-law exponent n_p for the MIE scaling for self-sustained flame propagation has been found to be in good agreement with the experimental findings for laser ignition of lean methane-air mixtures under decaying turbulence (Cardin et al. 2013a, b) and also with previous computational findings (Turquand d’Auzay et al. 2019a) $\left( {{\text{i}}.{\text{e}}.\; \left( {\varGamma_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{{\prime }} /s_{l}^{0} } \right)^{2} \;{\text{or}}\;\left( {\varGamma_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{2} } \right)$ for the undiluted stoichiometric homogeneous CH₄-air mixture based on single-step chemistry, which suggested n_p = 2.0. It is also worth noting that here n_p has been estimated based on a modest number of data points, so there is a small degree of uncertainty in the n_p values presented in Table 6. Therefore, considering the narrow range of n_p around 2.0 (i.e. 1.70 < n_p < 2.20), it can be inferred that $\left( {\varGamma_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{\prime } /s_{l}^{0} } \right)^{2} \;\left( {{\text{or}}\;\left( {\varGamma_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{\prime } /s_{l}^{{\psi^{u} }} } \right)^{2} } \right)$ may also be valid for biogas-air mixtures. It has already been demonstrated in Fig. 2 that thermal runaway takes place during the energy deposition period (i.e. $0 \le t \le t_{sp}$) for high values of $u^{\prime}/s_{l}^{0}$ and during this period the value of $(T_{norm} )_{max}$ remains high enough to yield an extremely small ignition delay, which is not significantly affected by the choice of chemical mechanism and therefore the scaling $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{{\prime }} /s_{l}^{0} } \right)^{2} \;\left( {{\text{or}}\;\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{2} } \right)$ does not change between single- and two-step chemical reactions for undiluted stoichiometric homogeneous CH₄-air mixture. The small range of n_p around 2.0 (i.e. $1.70 < n_{p} < 2.20$) can be explained in the following manner.

The heat release must overcome the overall heat transfer rate from the kernel initiated by thermal runaway in order to ensure that it propagates without the assistance of any external energy source. Thus, one gets the following relation under the critical condition in the absence of any mean advection (Turquand d’Auzay et al. 2019a; Klein et al. 2008):

$$ \mathop \smallint \limits_{V} \dot{w}_{T} dV\sim \rho_{0} s_{l}^{{\psi^{u} }} A_{T} \left( {Y_{Fu} - Y_{Fb} } \right)H_{\phi }^{{\psi^{u} }} \sim q_{eff} A_{p} $$

(11)

where the heat release rate $\dot{w}_{T}$ is taken to scale with $\rho_{0} s_{l}^{{\psi^{u} }} \left( {Y_{Fu} - Y_{Fb} } \right)H_{\phi }^{{\psi^{u} }} {{\varSigma '}}$ with ${{\varSigma '}}$ being the flame surface area to volume ratio (Klein et al. 2008), $H_{\phi }^{{\psi_{u} }}$ is the heat of combustion for the dilution level of $\psi^{u}$, $A_{T}$ is the actual flamelet area and $A_{p}$ is the projected flame surface. In Eq. 11, $q_{eff}$ is the effective diffusive thermal flux which can be taken to scale as (Turquand d’Auzay et al. 2019a):

$$ q_{eff} \sim \rho_{0} C_{p} \left( {D + D_{t} } \right)\left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right)/R_{crit} $$

(12)

where $D_{t}$ is the eddy diffusivity, and henceforth it will be considered that $D_{t} \gg D$ because turbulent diffusion is expected to be much stronger than the molecular diffusion rate. In Eq. 12, $R_{crit}$ is the critical radius of the hot gas kernel and one needs $R > R_{crit}$ for self-sustained propagation without the assistance of external energy addition. Otherwise, the flame eventually quenches for $R < R_{crit}$ (Klein et al. 2008). Upon using $C_{p} \left( {T_{ad}^{{\psi^{u} }} - T_{0} } \right) = H_{\phi }^{{\psi^{u} }} \left( {Y_{Fu} - Y_{Fb} } \right)$ in eq. 12 one gets (Turquand d’Auzay et al. 2019a; Klein et al. 2008):

$$ R_{crit} \sim \frac{{u^{{\prime }} l_{t} }}{{S_{L}^{{\psi^{u} }} \left( {A_{T} /A_{p} } \right)}} $$

(13)

where the turbulent diffusivity is scaled as $D_{t} \sim u^{{\prime }} l_{t}$ and the quantity $A_{T} /A_{p}$ is by definition is the wrinkling factor ${{\varXi }}$ which is often scaled using a power-law as ${{\varXi }}\sim \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{{n_{{{\varXi }}} }}$ (Muppala et al. 2005; Kobayashi and Kawazoe 2000) with $0 < n_{{{\varXi }}} < 1$. This suggests that Eq. 13 can be rewritten as:

$$ R_{crit} \sim \delta_{z}^{0} \left( {l_{t} /\delta_{z}^{0} } \right)\left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{{1.0 - n_{{{\varXi }}} }} $$

(14)

As the MIE can be taken to scale with the energy required to raise the temperature of the mass of the gas of radius $R_{crit}$ from unburned gas conditions to the adiabatic flame temperature $\left( {{\text{i}}.{\text{e}}.\;E_{p} \sim \rho_{0} \left( {4\pi R_{crit}^{3} /3} \right)C_{p} \left( {T_{ad}^{{\psi_{u} }} - T_{0} } \right)} \right),$ the normalised MIE, $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ can be taken to scale as:

$$ \left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p} \sim \left( {l_{t} /\delta_{z}^{0} } \right)^{3} \left( {u^{{\prime }} /s_{l}^{0} } \right)^{{3 - 3n_{{{\varXi }}} }} \left( {s_{l}^{0} /s_{l}^{{\psi^{u} }} } \right)^{{3 - 3n_{{{\varXi }}} }} \;{\text{or}}\;\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{{\prime }} /s_{l}^{{\psi^{u} }} } \right)^{{3 - 3n_{{{\varXi }}} }} \;{\text{or}}\;\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{{\prime }} /s_{l}^{0} } \right)^{{3 - 3n_{{{\varXi }}} }} $$

(15)

It can be seen from Fig. 1 that the ratio $s_{l}^{0} /s_{l}^{{\psi^{u} }}$ and $\delta_{z}^{0} /\delta_{z}^{{\psi^{u} }}$ are constants for a given biogas composition and thus the scaling given by Eq. 15 does not change with CO₂ dilution but the multiplicative constant for proportionality changes with the variation of $\psi^{u}$. Moreover, it is worth noting that the scaling given by Eq. 15 is independent of the choice of the chemical mechanism, which is consistent with the good agreement of n_p between the current results and the previous findings based on single-step chemistry (Turquand d’Auzay et al. 2019a). Under decaying turbulence, the values of u′/s ⁰_l and $l_{t} /\delta_{z}^{0}$ change with time but in the timescale of ignition, these values have been found not to change significantly from their initial values. Several analyses on turbulent premixed combustion (Abdel-Gayed and Bradley 1977; Abdel-Gayed et al. 1984; Bradley 1992; Bradley 2002; Bray 1990; Nivarti and Cant 2017; Ahmed et al. 2019) reported the bending effect where the wrinkling factor ${{\varXi }}$ varies linearly (i.e. $n_{{{\varXi }}} \approx 1.0$) with u′ for small turbulence intensities, whereas for large turbulence intensities, ${{\varXi }}$ becomes less sensitive to the changes in u′ with $n_{{{\varXi }}} < 1$. A value of $n_{{{\varXi }}} \approx 1.0$ is consistent with small values of n_p for small turbulence intensities (see Table 5). Equation 15 suggests that $n_{{{\varXi }}} = 1/3$ yields $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{\prime}/s_{l}^{0} } \right)^{2}$ for large values of u′/s ⁰_l . Several previous studies reported ${{\varXi }}\sim \left( {u^{\prime}/s_{l}^{{\psi^{u} }} } \right)^{0.3 - 0.4}$, which also suggests $n_{p} = 1.8 - 2.1$ according to Eq. 15. In the present analysis, explicit filtering of the DNS data using a Gaussian filter kernel is utilised to estimate $n_{{{\varXi }}}$ from the slope of the linear part of the variation of $\log \left[ {\mathop \smallint \limits_{V} \overline{{\left| {\nabla c} \right|}} dV/\mathop \smallint \limits_{V} \left| {\nabla \bar{c}} \right|dV} \right]$ with $\log {{\Delta }}$ as done in several previous analyses (Chakraborty and Klein 2008; Gao et al. 2014; Klein and Chakraborty 2019), where the overbar indicates the LES filtering operation and Δ is the filter width. The variations of $\log \left[ {\mathop \smallint \limits_{V} \overline{{\left| {\nabla c} \right|}} dV/\mathop \smallint \limits_{V} \left| {\nabla \bar{c}} \right|dV} \right]$ with $\log {{\Delta }}$ have been presented in several previous studies (Chakraborty and Klein 2008; Gao et al. 2014; Klein and Chakraborty 2019). The variation of $\log \left[ {\mathop \smallint \limits_{V} \overline{{\left| {\nabla c} \right|}} dV/\mathop \smallint \limits_{V} \left| {\nabla \bar{c}} \right|dV} \right]$ with $\log {{\Delta }}$ obtained in this analysis is qualitatively similar to the results presented in several previous analyses (Chakraborty and Klein 2008; Gao et al. 2014; Klein and Chakraborty 2019) and thus not shown here for the sake of conciseness. However, the averaged values of $n_{{{\varXi }}}$ from all $\left( {u^{{\prime }} /s_{l}^{0} } \right) > \left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ cases for a given value of ${\psi^{u}}$ using the variations of $\log \left[ {\mathop \smallint \limits_{V} \overline{{\left| {\nabla c} \right|}} dV/\mathop \smallint \limits_{V} \left| {\nabla \bar{c}} \right|dV} \right]$ with $\log {{\Delta }}$ are reported in Table 7. A comparison between the n_p and $n_{{{\varXi }}}$ values from Tables 5 and 7 respectively reveals that n_p remains close to $\left( {3 - 3n_{{{\varXi }}} } \right)$, which also validates the scaling given by Eq. 15 and explains why $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p} \propto \left( {u^{{\prime }} /s_{l}^{0} } \right)^{2}$ roughly holds for a range of different mixture compositions irrespective of the value of CO₂ dilution ${\psi^{u}}$. Further discussion on the bending phenomenon and the parameterisation of ${{\varXi }}$ in terms of the power-law exponent $n_{{{\varXi }}}$ for hot gas kernels are beyond the scope of this analysis. However, the scaling estimate given by Eq. 15 and its apparent agreement with the computationally obtained normalised MIE $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ offers an alternative perspective for the transition in MIE. It is worth noting that n_p has been estimated independently of $n_{{{\varXi }}}$, and as n_p is estimated based on a limited number of sample points due to computational limitations, the differences between n_p and $(3 - 3n_{{{\varXi }}} )$ according to the values reported in Tables 5 and 7 should be treated as statistical errors.

Table 7 Values of $n_{\varXi }$ from all $\left( {u^{{\prime }} /s_{l}^{0} } \right) > \left( {u^{{\prime }} /s_{l}^{0} } \right)_{crit}$ cases for different values of ${\psi^{u}}$ using the variations of $\log \left[ {\mathop \smallint \limits_{V} \overline{{\left| {\nabla c} \right|}} dV/\mathop \smallint \limits_{V} \left| {\nabla \bar{c}} \right|dV} \right]$ with $\log {\varvec{\Delta}}$

The stochasticity of the ignition phenomenon is a key element, and the findings for the stochasticity analysis are summarised in Fig. 7 in terms of the number of successful ignition events for the ignition energy input corresponding to $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{i}$. It can be seen from Fig. 7 that successful thermal runaway has been obtained for at least two out of the three turbulent realisations for all values of u′/s ⁰_l and the values of $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{i}$ reported here can be taken to be reasonably accurate. Figure 7 further suggests that a 100% success rate in terms of ignition was observed for realisations S01 and S02, whilst a successful ignition (i.e. a thermal runaway) was only observed for u′/s ⁰_l  = 1.0 and 2.50 for the realisation S03 and these observations hold across all values of ${\psi^{u}}$ and u′/s ⁰_l investigated here. In the present approach, the only difference between different turbulent realisations arises principally due to thermal diffusion rate because the fuel composition encountered by the hot gas kernel is the same across realisations, and thus the contributions of P₂ and P₃ in the energy conservation equation (i.e. Eq. 9) are expected to be quantitatively similar between the different realisations during the energy deposition duration (i.e. t < t_sp) before the thermal runaway takes place. The differences in heat transfer behaviour from the hot gas kernel for different turbulence realisations for a given energy input corresponding to $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{i}$ decide if the thermal runaway takes place or not. For small turbulence intensities, thermal runaway takes place after the energy deposition period (i.e. t > t_sp) as a result of autoignition (see Fig. 2). Thus, the turbulence realisations, which lead to high magnitudes of heat transfer rate precludes the possibility of thermal runaway either during the energy deposition period or after the energy deposition period as a result of autoignition. The magnitudes of thermal diffusion rate D₂ from the hot gas kernel supersedes the combined contributions of heat release and external energy addition (i.e. P₂ + P₃) in the energy conservation equation in the realisation S03 for u′/s ⁰_l  > 2.50 to lead to misfire (Turquand d’Auzay et al. 2019a) (not shown here).

Fig. 7

Number of successful events out of three different turbulent realisations (S01, S02, S03) across all turbulent cases for ${\psi^{u}}$ = 0.0, 0.025, 0.05 and 0.10 for the input ignition energy corresponding to $\left( {\varGamma_{{\psi^{u} }} } \right)_{i}$

The stochasticity analysis of self-sustained flame propagation has been conducted only for a limited number of turbulence intensities because of the high computational cost associated with it. The outcomes of the stochasticity analysis for self-sustained flame propagation for three initial turbulence intensities (u′/s ⁰_l  = 4.0, 8.50 and 11.0) are exemplarily shown in Fig. 8. It can be seen from Fig. 8 that successful self-sustained flame propagation is obtained for at least for two realisations (i.e. for S01 and S02 realisations) for the ignition energy input corresponding to $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ for all the initial turbulence intensities (u′/s ⁰_l  = 4.0, 8.50 and 11.0) shown in this figure. This suggests that $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ values have been estimated with reasonable accuracy in this analysis. It can be seen from Fig. 8 that for the energy input corresponding to $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$, a failed propagation following successful thermal runaway occurs in the case of S03 realisation for initial turbulence intensities of $u^{{\prime }} /s_{l}^{0} = 8.50$ and 11.0 for biogas-air mixtures with ${\psi^{u}}$ = 0.025, 0.05 and 0.1, and also for the initial turbulence intensity of $u^{{\prime }} /s_{l}^{0} = 11.0$ for ${\psi^{u}}$ = 0.0. The present findings for the undiluted mixture (i.e. ${\psi^{u}}$ = 0.0) are consistent with previous findings by Turquand d’Auzay et al. (2019a) who investigated the same range of $u^{{\prime }} /s_{l}^{0}$. It was demonstrated in Fig. 4 that the hot kernel moves and elongates to a different location from the original ignitor location for large turbulence intensities and thus non-local effects become increasingly important with increasing $u^{{\prime }} /s_{l}^{0}$. The budget of the terms in the energy conservation equation (Eq. 9) was presented in Turquand d’Auzay et al. (2019a) and the same qualitative behaviour has been observed here. Therefore, the energy budget plots for the cases considered here are not explicitly shown here but the main findings are summarised. After the energy deposition period, the heat release rate, P₂, and thermal diffusion rate, D₂, act as the leading order terms in the energy conservation equation (i.e. Eq. 9) (Turquand d’Auzay et al. 2019a). In order to have successful flame propagation without the aid of external energy addition, the combined contribution of the heat release rate and thermal diffusion rate (i.e. P₂ + D₂) for all the non-dimensional temperature $T_{norm}$ isosurfaces in the reaction zone needs to be positive in a mean sense (Turquand d’Auzay et al. 2019a) in order to ensure the growth of the hot gas kernels. By contrast, the hot gas kernel shrinks in size for negative mean values of (P₂ + D₂) within the reaction zone. For the S03 realisation, the hot gas kernel, which ensued from thermal runaway, gets convected to a region where the local conditions give rise to large negative values of D₂. These large magnitudes of D₂ overcome the positive values of P₂ in the reaction zone in the case of S03 realisation, and as a result, the reaction zone shrinks in size and eventually disappears, prompting quenching of the hot gas kernel (Turquand d’Auzay et al. 2019a). As the magnitude of heat release rate P₂ decreases with increasing ${\psi^{u}}$, the negative values of D₂, whose magnitudes are determined by the local turbulence statistics, are more likely to overcome the heat release rate for high values of ${\psi^{u}}$. This is reflected in the failure to obtain successful self-sustained flame propagation for initial $u^{{\prime }} /s_{l}^{0} = 8.5$ in the case of $\psi^{u} = 0.025,0.05$ and 0.10 for the S03 realisation, whereas successful flame propagation is obtained for the undiluted mixture (i.e. ${\psi^{u}}$ = 0.0). It is worth noting that $u^{{\prime }} /s_{l}^{{{{\psi }}^{\text{u}} }}$ values increase with increasing ${\psi^{u}}$ for a given value of $u^{{\prime }} /s_{l}^{0}$ (see Fig. 1) and $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ and $\left( {E_{p} } \right)_{{{{\psi }}^{u} }} /\left( {E_{p} } \right)_{{{{\psi }}^{u} = 0.0}}^{\text{L}}$ values increase significantly with an increase in ${\psi^{u}}$ (see Figs. 5 and 6). Thus, the hot gas kernel generated by external energy addition is bigger for higher values of ${\psi^{u}}$ for the MIE input for self-sustained flame propagation. Thus, the surface to volume ratio of the hot gas kernel at the end of energy deposition decreases with increasing ${\psi^{u}}$. The ratio of the magnitudes of the heat transfer rate to heat release rate decreases with the decreasing surface to volume ratio. Therefore, the smaller surface to volume ratio values for higher values of ${\psi^{u}}$ may compensate for the weaker heat release rates for larger extents of CO₂ dilution and thus the frequency of obtaining unsuccessful events does not change significantly with increasing ${\psi^{u}}$ in Fig. 8.

Fig. 8

Number of successful events out of three different turbulent realisations (S01, S02, S03) across selected turbulent cases for ${\psi^{u}}$ = 0.0, 0.025, 0.05 and 0.10 for the input ignition energy corresponding to $\left( {\varGamma_{{\psi^{u} }} } \right)_{p}$

5 Conclusions

The minimum ignition energy (MIE) of stoichiometric biogas-air mixtures with varying levels of CO₂ dilution have been numerically evaluated under homogeneous isotropic decaying turbulence for a wide range of initial turbulence intensities using three-dimensional DNS. An increase in mole fraction of CO₂ in the CH₄/CO₂ blend increases the MIE demand significantly which is in good qualitative agreement with previous experimental results (Larsson et al. 2013). The variation of the MIE with turbulence intensity exhibits a transition such that the energy demand increases significantly above a threshold value of turbulence intensity for both successful ignition and self-sustained flame propagation for all CO₂ dilution levels. This behaviour has been found to be consistent with previous numerical (Turquand d’Auzay et al. 2019a) and experimental (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b) findings. The threshold value of turbulence intensity for the aforementioned transition decreases with an increasing level of CO₂ dilution. However, the range of the critical turbulence intensity values for the MIE transition has been found to be consistent with previous experimental (Huang et al. 2007; Shy et al. 2010, 2017, b; Peng et al. 2013; Jiang et al. 2018; Cardin et al. 2013a, b) and numerical (Turquand d’Auzay et al. 2019a) findings. The MIE for self-sustained propagation assumes considerably higher values than the MIE requirement for only successful thermal runaway and the scaling for the normalised MIE for self-sustained flame propagation $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ for undiluted stoichiometric methane-air mixture has been found to be roughly valid even for the stoichiometric biogas-air mixtures. Scaling analysis and flame wrinkling statistics have been utilised to explain the increase of the normalised MIE for self-sustained flame propagation $\left( {{{\varGamma }}_{{\psi^{u} }} } \right)_{p}$ with increasing turbulence intensity $u^{{\prime }} /s_{l}^{0}$ following a power-law with its exponent being roughly the same for biogas-mixtures irrespective of the level of CO₂ dilution. It has been found that unsuccessful events can still be obtained for some turbulent flow realisations even for the MIE inputs for both thermal runaway and self-sustained flame propagation due to the stochastic nature of localised forced ignition events. However, the frequency of successful events is found to be higher than the unsuccessful outcomes indicating reasonable accuracy of the MIE values reported here. The physical reasons behind the stochasticity of the ignition and flame propagation events for the MIE values have been explained in terms of the competition between the heat release and thermal diffusion rates. The aforementioned findings are unlikely to be influenced by the choice of chemical mechanism, thermophysical transport properties, energy deposition modelling and the equivalence ratio of the mixture, as discussed earlier in the context of assumptions made for this analysis. For example, the results for the undiluted mixture (i.e. ${\psi^{u}}$ = 0.0) for the present two-step chemical mechanism did not change significantly in comparison to a previous analysis with single-step chemistry (Turquand d’Auzay et al. 2019a). However, further analyses in the presence of detailed chemistry, and non-unity equivalence ratio will be necessary. Moreover, this analysis and the previous numerical investigation on the MIE transition (Turquand d’Auzay et al. 2019a) have been conducted for fuel–air mixtures without differential diffusion effects of heat and mass and this gap in the existing literature will form the basis for future investigations by relaxing the assumptions related to identical specific heats and unity Lewis number.