1 Introduction

European Directives are coming into force setting increasingly stringent emission limit values (ELVs) for regulating emissions from, e.g. combustion processes. Hydrogen chloride (HCl) is a harmful gas which is released to the atmosphere, e.g. from fossil or biofuel power plants or waste incinerators. Currently, HCl gas emissions from the industry are covered by the Industrial Emissions Directive 2010/75/EU. Here, HCl measurements are referred to wet chemistry methods. Advanced diagnostic techniques are needed to support monitoring and enforcement of ELVs in European legislation for regulating HCl emissions (http://empir.npl.co.uk/impress/), and to replace the wet chemistry methods.

Regarding quality control measurements of HCl, there is no good and validated source for stable HCl gas standards to calibrate commercial HCl sensors, and there is no HCl CMCs (calibration and measurement capabilities) for concentration under 10 μmol/mol (ppm). The nature of combustion leads to product gases at elevated temperatures. The product gases need to be transported elsewhere, e.g. for particulate filtration or pollutant removal, which is realized, e.g. via exhaust gas ducts, which very often have a significantly lower temperature than the exhaust gas. Thermal coupling and exchange of heat of gas and the duct wall unavoidably generate thermal gradients inside the duct, which are dependent on gas and wall temperature, the gas residence time at a certain temperature level, thermal conductivity of gas and duct, and many other parameters. Combustion optimization, e.g. by control loops to minimize pollutant levels often request dynamic pollutant concentration measurements in the exhaust gas. If this is done via a gas sampling process it requires gas sample conditioning, i.e. significant cooling, as well as removal of particulate and/or condensates, which causes increasing risks of systematic, unwanted modifications of the sampled gas. For highly reactive and strongly adsorbing target species (e.g. like HCl), gas sampling can become too costly, too error prone and even more or less impossible due to the inability to control the sampling-initiated changes of the gas probe.

Optical, frequently laser-based, analytical methods based on spectral absorption of the target molecule (laser absorption spectroscopy) (Ebert and Wolfrum 2001; Schulz et al. 2007) offer key features for combustion emission measurements such as high sensitivity, excellent chemical selectivity and compatibility with online in situ measurement capabilities, allow sampling-free gas sensing, e.g. by trans-illumination of the gas duct exploiting, e.g. narrow-band spectral losses caused by small target molecules. One of the most widely used optical technique for combustion diagnostics is laser absorption spectroscopy, in particular tunable diode laser absorption spectroscopy (TDLAS) (Sepman et al. 2019; Teichert et al. 2003; Qu et al. 2015, 2016). The TDLAS measurement process is described by the Lambert–Beer law. As the “total” absorption signal is “generated” along the entire path between laser and detector, and thus reflects the spatial integration of each incremental path element, absorption techniques are often also called “line-of-sight” techniques (LOS: the line between the laser and the detector).

Direct tunable diode laser absorption spectroscopy (dTDLAS) is a variant of TDLAS which combines this spectroscopic technique with a proprietary, first-principles approach to directly yield traceable, absolute gas species concentrations without any reference-gas-based calibration (Ortwein et al. 2010; Buchholz et al. 2014; Buchholz and Ebert 2018). dTDLAS spectrometers are often implemented as sampling-free, open-path sensors (Teichert et al. 2003).

For spatially heterogeneous distributions of the target species (in an otherwise physically homogenous gas sample) LOS methods have the advantage that they essentially measure the “spatially averaged” concentration along the path. This can be a big advantage if the target species is unevenly distributed in the gas duct, as it avoids local sampling artefacts known from extractive sampling lines. It also avoids the need to determine a “representative” gas extraction point. However, the by far most frequent scenario is more complicated: Not only the target species concentration but also the physical boundary conditions of the target species (in particular gas temperature or gas matrix composition) are spatially heterogeneous too, which can have strong implications on the spectroscopy of the LOS signal.

Fundamentally, the dTDLAS evaluation requires spatial homogeneity in gas temperature and matrix gas composition (Qu and Schmidt 2015; Sepman et al. 2017; Bürkle et al. 2018). If the homogeneity requirement is not fulfilled, which is typically the case in industrial applications, the question needs to be answered, what systematic deviation arises and how can those be quantified and minimized (Ouyang and Varghese 1989; Goldenstein et al. 2013). In particular spatial gas temperature variations (e.g. from thermal boundary layers (BL) near walls) along the LOS of the spectrometer need to be carefully considered. In this case the spectral signature of the target species is locally influenced by the local boundary conditions and the LOS technique does not spatially integrate the gas concentration anymore. Instead, a systematically shifted (weighted), “apparent local gas concentration” which contains information on the spatial temperature dependence and the gas matrix-dependence of the spectral absorption of the probed absorption feature becomes effective and leads to systematic deviations from the ideal response. The local weighing factors, however, depend on the selection of the individual absorption line, its temperature and matrix gas coefficient, the absolute values of the (average) gas temperature and the (average) matrix composition and the magnitude of the relative spatial variability of temperature and the matrix gas, which makes it in most cases impossible for a standard user to measure, estimate or correct the systematic deviations caused by these effects. In particular if the user does not know the exact spectral wavelength of the target line used in the spectrometer.

Sampling-free in situ LOS sensors like commercial TDLAS instruments when applied to heterogenous situations in general need to be carefully characterized (e.g. wrt. the temperature dependence of the transition line) by the manufacturer or end-user in order to quantify the effects of spatial heterogeneities of the target species and the physico-chemical boundary conditions.

This however is usually neither done by the manufacturer nor the user of such a device as the required spectral data usually not made available by the manufacturer. In addition, the user often lacks detailed information on the magnitude and the temporal stability of the BL at the sampling location. Further the user would need the exact instrument wavelength, the (often manufacturer proprietary) spectral parametrization and information on the signal evaluation process used. This severe lack of information makes it impossible to quantify or at least estimate the systematic deviations (and its variability) of the open-path LOS TDLAS instrument.

In order to address these issues and to derive good estimates for possible systematic deviations caused by these problems as described above, we propose the use of approximate, assumed BL properties in realistic application scenarios in combination with a dTDLAS-instrument with a full physical model and complete set of spectral parameters for the target absorption line. In addition to our previous case studies (Qu et al. 2018) for CO2-dTDLAS and CO-dTDLAS, this work focuses on a new 3.6 µm mid-IR HCl spectrometer which has a better sensitivity compared to the previous 1.74 µm HCl-TDLAS systems (Ortwein et al. 2010; Bjoroey et al. 1996; Masusaki et al. 1999; Corsi et al. 1999). The transition line strength of the probed HCl absorption line at 3.6 µm is more than ten times stronger than the lines in the NIR range.

To better understand thermal BL effects, our simple, previous, step-change, two-temperature-zone simulation model has been improved. A third “transition zone” with a continuous, linear temperature growth was introduced into the simulation model, while the principle of the simulation method stays the same as that in our previous paper (Qu et al. 2018). This new continuous three-zone model can better represent for the real scenarios, and provides more precise estimation of systematic deviations due to realistic thermal BL.

The idea of developing the simulation model is to provide a tool that can calculate/quantify the BL effect of any first principles dTDLAS-based spectrometer even under difficult conditions as long as there are some good assumptions/knowledge on the shape and depth of the BL, e.g. from a fluid dynamics approach.

In this paper, we first introduce the measurement principle and the first principles HCl spectrometer, followed by a description of the implemented simulation model on this HCl spectrometer and corresponding results on heterogeneity effects. Note that as the principle of the simulation method has already been validated before (Qu et al. 2018, 2020), here we use it as a toolbox to quantify the BL effects.

2 Method

Tunable diode laser absorption spectroscopy (Nwaboh et al. 2017; Ebert et al. 2005) In TDLAS, the wavelength λ of a tunable laser is rapidly scanned across a narrow region of the optical spectrum covering one or a low number of absorption lines. The intensity of the laser light, I(λ), focused onto a photodetector after passing through the absorbing medium can be described by the Lambert–Beer law:

$$I\left( \lambda \right) = E\left( t \right) + I_{0} \left( \lambda \right) \cdot T_{r} \left( t \right) \cdot { \exp }\left[ { - S\left( T \right) \cdot g\left( {\lambda - \lambda_{0} } \right) \cdot N \cdot L} \right]$$
(1)

with the background emission E(t) at time t, incident laser intensity I0(λ) at wavelength λ, and the broadband transmission losses Tr(t) by matrix gas effects and dust particles along the path (Ebert et al. 2005). Note that laser current is intentionally tuned below laser threshold to measure the background signal at the beginning of each scan to deduce the background correction E(t). The exponential term includes the line strength S(T) at gas temperature T, the area-normalized line shape function g(λ − λ0) (centred at wavelength λ0), the absorber number density N and the absorption path length L. Applying the ideal gas law to Eq. 1 yields the gas concentration X of the target species (Nwaboh et al. 2013)

$$X = \frac{{k_{\text{B}} \cdot T \cdot A_{\text{line}} }}{{S\left( T \right) \cdot L \cdot p_{\text{total}} }}$$
(2)

where kB is the Boltzmann constant, ptotal is the total pressure of the gas sample, and Aline is the area underneath the absorption line determined by spectral integration of the measured absorption line on a linearized wavenumber axis. The spectral integration is realized by fitting a Voigt profile to the absorbance spectrum. The wavenumber axis is linearized before the concentration measurements using a Fabry–Perot etalon as a frequency “ruler”. Note that the number density N in Eq. 1 is converted to concentration X (amount fraction of the substance) in Eq. 2.

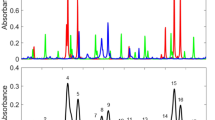
Line selection The selection process of appropriate spectral transition lines is critical for the performance of a laser absorption spectrometer. A careful line selection procedure should be used to find lines with sufficient absorption line strength, good isolation from interfering molecules, low relative temperature sensitivity, and the availability of a commercial laser source. For combustion flue gas measurements, with high amount of water (H2O) and CO2 present in the hot gas flow, many HCl lines suffer from severe spectral interference by the dense H2O absorption spectrum. Hence, it is decisive to select an optimal, spectrally unobscured HCl transition with a sufficiently strong line strength. In Fig. 1, spectra are simulated for the following conditions: gas temperature at 300 K and 450 K, 1013 hPa pressure, 1 m path length, H2O: 20 vol%, CO2: 20 vol%, HCl: 10 ppm, (as there is no CO absorption line in this spectral window, CO is not included in Fig. 1). In the selected spectral range, there are two strong HCl lines (the weaker one is H37Cl, the stronger one, HCl P5 line at 2775.76 cm−1 is selected as our targeted line. Here, the interference by CO or CO2 is negligible, and the H2O spectral influence is getting smaller at 450 K (Fig. 1b) which is preferable for hot flue gases measurements.

Fig. 1
figure 1

Simulated HCl spectra in a typical combustion matrix gas in the spectral range of 2760–2785 cm−1 (based on HITRAN spectral data (Rothman et al. 2013)) at different temperatures, a at a gas temperature of 300 K, b at a gas temperature at 450 K. The assumed matrix gas composition of a typical combustion product gas is H2O: 20 vol%, CO2: 20 vol%, HCl: 10 ppm at 1 atm (1013 hPa) and 1 m path length

Full size image

Line temperature dependence To develop a TDLAS spectrometer for combustion diagnostics, it is essential to study the temperature dependence of the target line. Figure 2a shows two forms of the temperature dependence of the targeted HCl transition line, one is the number density normalized temperature dependence S(T) with the unit of cm−1/mol cm−2 (left axis), it is the same unit as the HITRAN database (Rothman et al. 2013) provides, the other axis is S(T)/T with the unit of cm−1/mol cm−2 K (right axis). When the gas concentration X is to be measured, the temperature dependence of S(T)/T (red curve in Fig. 2a) is used to analyse the temperature dependence of the target signal. For an absorber number density measurement (N, in Eq. 1), the number density normalized temperature dependence S(T) (blue curve in Fig. 2a) is used to calculate the temperature effect on the line strength. In the temperature range shown in Fig. 2a, S(T)/T is decreasing as the temperature is increasing, this means that the spectrometer sensitivity will decrease with temperature. Figure 2b shows the line strength temperature sensitivity (can be called as line strength temperature coefficient) at different temperature, it reflects the relative line strength variation (in  %) when the temperature changes by 1 K. It is calculated from the slope of the S(T)/T (red curve in Fig. 2a) divided by S(T)/T. In Fig. 2b, the line strength temperature coefficient changes at different temperatures from 0.08%/K to 0.22%/K over the full temperature range. The most sensitive temperature region with the largest T-coefficient is around 400 K. For example, the sensitivity is around 0.2%/K at 600 K in Fig. 2b, and hence, there will be about 2% concentration deviation when the temperature error is 10 K’, this means if we have a 10 K temperature “misinterpretation (i.e. incorrect or insufficient temperature measurement, especially when there is a temperature gradient along the LOS)” in the measurement, it converts into a systematic concentration deviation of up to 2% at 600 K. Knowing the temperature fluctuation, the HCl concentration uncertainty by the temperature ‘misinterpretation’ can be estimated from the line strength sensitivity curve. However, this estimation is only valid for spatially uniform conditions.

Fig. 2
figure 2

a Temperature behaviour of the line strength for the selected HCl P5 transition in the fundamental 1-0 band, (the P5 line strength S(T) = 2.886 × 10−19 cm−1/mol cm−2, the lower-state energy E0 = 312.73 cm−1). b Relative temperature coefficient in % change of S(T)/T per change in temperature in K

Full size image

3 Experiment

Set up A schematic of the new HCl spectrometer set-up is shown in Fig. 3. A 3.6 µm interband cascade laser (ICL) (Nanoplus GmbH) is used to scan across the P5 HCl absorption line in the HCl 1-0 fundamental band. The wavelength scan is achieved by varying the laser current with a 140 Hz triangular wave generated by a function generator (Agilent, 33220A). The laser injection current is supplied by a low-noise laser current driver (Thorlabs, LDC8002), while the laser temperature is stabilized by a Peltier-element operated by a Peltier driver (Thorlabs TEC8020). The laser beam was directed through a 77 cm gas cell with Brewster-angled windows and then focused onto a photodetector (VIGO, PVI-4TE-5). The inner surface of the gas cell was passivated by a commercial SilcoNert 2000 coating (Silcotek Corporation). The nonlinear dynamic wavelength tuning of the laser was determined experimentally in separated previous experiment by using an optical etalon—a wavenumber “ruler” (not shown in Fig. 3), and used to transfer the signal from a linear temporal onto a linearized wavenumber axis. The detector signal was sampled with 18-bit resolution at 600 kHz by a DAQ (National Instruments, PXI-6289). The gas temperature, respectively, the gas pressure, inside the gas cell are continuously measured by a PT100 resistor and a MKS Baratron sensor, respectively.

Fig. 3
figure 3

Schematic of the experimental HCl dTDLAS set-up

Full size image

HCl in CO2 measurements To evaluate the performance of the HCl spectrometer and its capability for measuring HCl in combustion environments, e.g. oxyfuel exhaust gas, the TDLAS spectrometer was tested by measuring HCl/CO2 gas mixtures (115 ppm HCl in CO2, static mixture from Linde). HCl is a highly reactive and corrosive gas which can cause strong adsorption wall losses in static gas scenarios. To suppress these systematic effects a dynamic measurement scheme was applied: Here, a constant flow of gas was introduced to the cell to balance the losses by adsorption or chemical reactions. The gas flow (200 sccm) was controlled by a mass flow controller (MFC). The gas cell was operated at room temperature. According to Fig. 2b, a 1 K temperature error at 297 K would lead into a systematic relative concentration deviation of 0.12%. Our temperature measurement uncertainty was about 0.2 K which corresponds to relative HCl concentration deviation of 0.024%.

Figure 4a and b show a typical measured, single shot raw signal (captured within t = 0.007 s) after background light offset subtraction (see E(t) in Eq. 1), as well as the absorption signal fitted with a Voigt line shape profile. Figure 4c shows the fitting residual between the measured data and the fitted Voigt profile. It is also common to normalize the residual noise equivalent absorption coefficient (optical density 1σ = 8 × 10−4) with respect to the path length and the square root of the temporal measurement bandwidth, which yields in this case 8.7 × 10−7cm−1·Hz−1/2, while in our previous NIR HCl-TDALS system (Ortwein et al. 2010), the normalized residual noise equivalent absorption coefficient was 1.3 × 10−6cm−1·Hz−1/2.

Fig. 4
figure 4

a Typical measured raw signal after laser offset subtraction. b The measured HCl P5 line spectrum at 21 °C, 954 hPa, 77 cm path length, gas sample HCl in CO2 and the fitted Voigt profile. c The fitting residual between measured data and simulated spectrum

Full size image

Despite the Silconert coating, we additionally conditioned and passivated the cell by purging a HCl gas mixture (115 ppm HCl in CO2, static mixture from Linde) at 200 sccm through the cell for over 1 h as shown in Fig. 5a. The effect of the successful passivation can be seen in the second filling, where the equilibrium concentration was reached much faster, in less 1000 s. During the first filling, the HCl signal didn’t reach the final equilibrium level within 4000 s as shown in Fig. 5a. The explanation of this behaviour is that the first filling passivated the surface of the cell thereby causing additional loss of HCl. After the passivation was concluded the subsequent fillings showed negligible HCl losses.

Fig. 5
figure 5

a HCl concentration XHCl measured in pure CO2 with the HCl-dTDLAS spectrometer as a function of time. The first two filling cycles of the cell are shown. The faster and better adaptation to the reference value of the gas mixture indicates the need for cell passivation, to minimize adsorption/desorption and chemical reaction effects. b Allan deviation plot for the time series marked (two-end-arrow) in (a)

Full size image

The measured, stable HCl concentration at the end of the second filling after passivation was 115.9 ± 0.5 ppm. The precision and stability of the spectrometer were investigated by means of the Allan deviation (Werle 2011) as shown in Fig. 5b. The Allen deviation-based precision improves with increasing integration time, as white noise is reduced by increased averaging. For long averaging time periods of 1000 s and beyond the precision gets limited by long-term instabilities like drifts. At 1 s time resolution a precision of 2 ppm HCl can be deduced, while at 110 s averaging time, a precision of 0.17 ppm (i.e. 170 ppb) was demonstrated with our HCl spectrometer at room temperature and a slightly reduced pressure of 320 hPa, to improve the chemical selectivity. The concentration of the gas standard of 115 ppm, hence, can be detected with a SNR of about 1000.

4 Thermal Boundary Layer Effect Simulation

In our previous study (Qu et al. 2018) our first approximate BL model was a binary, step-change BL assumption (two-temperature-zone model) with only a single homogenous cold zone near the wall and a hot zone in the core of the duct. The spectral simulation model to describe this situation and to quantify the effects of a cold BL and the accuracy of the dTDLAS instrument was experimentally verified for the case of the CO2 molecule using two separately controlled absorption gas cells trans-illuminated consecutively by the laser beam. It is obvious that the step-change in temperature is unrealistic in that sense such an infinitively steep gradient will never persist inside a free gas flow. Instead the unavoidable mixing and interaction of the gas flow will “soften” the edge leading to a “smooth” variation between the two (temperature) regions. A detailed description of the BL would be a parametrization which ensures continuity in absolute values as well as the first and second spatial derivatives, which however requests too many parameters to describe the transition zone scenario. This would also cause very significant work to experimentally derive this information from the real application scenario, nor is a well-controlled experimental laboratory realization of a temperature transition region realistic as this also requires the preparation, implementation and validation of spatially resolved temperature measurement techniques which far beyond the scope of this study. On the other hand, it is a good alternative to further refine the simulation model, whose spectroscopic submodels have been validated in the previous CO study (Qu et al. 2020) and can be adopted to allow for continuous temperature variations.

Hence, we have chosen an obvious but computationally more simple refinement of the simulation model which is a three-layer simulation with two distinct temperature regions (hot centre + cold wall) and a linear transition zone in-between to allow continuous parameter variation. Most important simulation parameters are therefore the absolute values of the parameters in the wall and the core layer, as well the thickness of the three layers. A graphical representation of the new three-layer model is shown in Fig. 6a for the case of a temperature gradient.

Fig. 6
figure 6

a Schematic drawing of a three-zone temperature distribution across the flue gases from combustion process, thermal boundary thickness ΔL. b Simulated concentration with different calculation temperatures for a fixed BL thickness. c Simulated concentration deviations for different calculation temperatures with different BL thickness

Full size image

The parameters which describe the new model are the cold zone near the wall with Tcold and L1, BL or transition zone with thickness ΔL where temperature is assumed to vary linearly along the spatial coordinate, and a hot zone in the core of the duct with Thot and L2. To investigate the thermal BL effects, the basic idea is to derive the concentration from a simulated path-integrated spectrum with temperature gradients along LOS and to apply the same fitting evaluation to the simulated integrated spectrum. Note that all submodels of this approach have the same principle as the validated model (Qu et al. 2018), only the temperature along the LOS part of the transition zone is varied. In order to selectively evaluate the respective parameter influence, the HCl concentration along the laser beam path was assumed to have a constant-uniform distribution. This is an extremely valuable possibility which only a simulation approach can generate, which also justifies why we preferred the simulation over a potential experimental realization of a transition layer.

It is typical for real-world situations that only very scare heterogeneity data are available, e.g. temperature information for local intrusive point measurements, e.g. with thermocouples is available, i.e. the cold(er) wall temperature and/or the higher core temperature (Qu et al. 2018). Nevertheless, it is of high importance that the user of LOS laser spectrometers (e.g. dTDLAS but also WMS and similar principles) must understand which temperature information/choice of measurement point has which effect on the extracted dTDLAS species concentration and how systematic or statistic uncertainties of the temperature measurement influence the final result. Also, it is important to better understand (and minimize) the spectroscopic effects associated by line broadening which are influenced by the local physico-chemical boundary conditions. These questions can be evaluated with the new three-zone model.

In principle the user has multiple possibilities to measure gas temperatures, which generate with different technical complications: Most simple and robust is the duct wall temperature or a point gas temperature measurement in the cold layer. Technically, more demanding is a point measurement in the hot gas region as these sensors often experience fouling and have to be corrected for radiation effects. Even better would be to have a cold-hot-point measurement which also allows to determine a two-zone mean average temperature. Even better, but already almost impossible to permanently realize in a technical environment would be a real path-averaged temperature, which could be realized potentially via a dedicated LOS temperature sensor. Path-averaged temperatures are straight forward to realize in a simulation, which is why we use this number as “ideal” reference in order to allow a relative comparison with the other approaches.

Figure 6 explains the “different” temperature choices which are used in Eq. 2. These are the path-averaged temperature Tave = ∑LiTi/∑Li, the maximum temperature along the LOS Thot, the two-zone mean temperature Tmean = (Thot + Tcold)/2 as well as the lowest Tcold.

Generating the line integrated spectrum and fitting this with the dTDLAS code we can evaluate, compare and quantify the effect of the different temperature measurement choices which is shown in Fig. 6b and c. The deviation is defined as the discrepancy between the derived concentration and the “true” initial concentration used to simulate the path-integrated spectrum. Figure 6b shows the simulated deviations of a fixed thermal BL thickness ΔL = 20 cm with varying temperature difference ΔT (with fixed Tcold = 300 K, L1 = 20 cm, L2 = 60 cm, total path length L = 100 cm). The deviation is derived with respect to the temperature ‘choice’ as well as the magnitude of the temperature difference ΔT between hot and cold zone used for concentration calculation in Eq. 2.

Another important parameter is the thermal BL thickness whose effect on the dTDLAS concentration measurements is shown in Fig. 6c, with fixed Tcold = 300 K and Thot = 900 K, the total path length (L = 100 cm) and the path length ratio (L2(cold) = 3×L1(hot)) are also fixed. In the transition-zone, the temperature increased linearly from Tcold to Thot. Here, to separate temperature from matrix effects all simulations considered that the HCl distribution along the LOS was uniform. When ΔL = 0, it becomes to the previous two-zone temperature model with ΔT = 600 K. Using the experimentally validated two-zone simulation model (Qu et al. 2018), same results were obtained by this modified three-zone model. In the condition of ΔL/L = 1, the “transition-zone” extends over the whole path. The temperature Tcold at the starting point increases linearly to Thot at the ending point. In this condition, Tave equals to Tmean, that’s why the red (Tave) and black (Tmean) curves are overlapping at ΔL/L = 1 as shown in Fig. 6c.

As seen from the simulation results, if the measured spectra were analysed by using Thot, the system deviation will increase while the BL thickness increasing as shown by blue curve in Fig. 6c. When using Tave for calculation (red line in Fig. 6b, c), the deviation is smaller comparing with other calculated temperatures in most conditions. In real scenarios, however first, the real-time in situ path-averaged temperature Tave is tedious and costly to measure, second, it is highly unlikely to repeat such path-averaged temperature measurement often enough to cover dynamic changes of the BL. This means in most cases Tave is technically unavailable. Nevertheless, it is for us a reference case how small the deviation could get if “better” temperature information (i.e. Tave) would have been available for a dTDLAS spectral evaluation. Even though the studied scenarios are highly specific and somewhat artificial, it is important to understand that systematic deviations of the measured concentration of a few percent to even beyond 10% are realistic, they are thus outside the precision range of typical commercial laser sensors which normally claim 1% and sometimes up to 0.1% accuracy. In view of the described problems, this seems unrealistic to specify the precision of a (open-path, cross duct) TDLAS spectrometer without any/little knowledge on the shape and magnitude of the BL in the given application. It is also unclear and certainly unknown to the user of a commercial instrument if the spectral line choice by the instrument developer was such, that these BL effects are reduced or even strongly enhanced.

TDLAS applications under spatially heterogeneous conditions are quite common, but neither is the heterogeneity characterized, nor modelled, nor is the spectral line data revealed and the spectral evaluation transparent enough so that the systematic effects can be estimated or quantified. Standardization should therefore be developed so that users are given, e.g. the transition line data used. Further the measured temperature should be carefully selected to minimize the deviation, and better knowledge of thermal BL is needed. Using the simulation model shown here, it is easy to quantify the systematic deviation levels by knowing the measured transition line and estimated BL information.

5 Conclusions

In the paper we present a novel first-principles HCl spectrometer especially for applications in CO2-rich exhaust gases, e.g. from combustion or even oxyfuel combustion processes. It is operated on the P5 line in the HCl 1-0 fundamental band and offers an absolute concentration response without a need for previous or regular calibration exercises and thus can serve as an instrument-defined optical gas standard (OGS). We tested and validated the new spectrometer under well-controlled laboratory conditions, i.e. for gas matrix effects and detection limits.

Secondly, we developed and applied an improved version of our spectral simulation model to evaluate the magnitude and parameter dependence of the BL effects which are to a certain extent present in all real-world scenarios and which are very difficult to evaluate, to avoid or to compensate by users of commercial optical LOS sensors like TDLAS spectrometers.

To improve this situation, we expanded our previous two-zone, step-change BL simulation method by adding a linear temperature transition zone to better represent thermal BL in real-world scenarios and has applied this model to the newly developed HCl-dTDLAS system. This simulation method can be used to evaluate whether the transition line is suitable for certain heterogeneous conditions within acceptable deviations. Additionally, it is important to report the measurements uncertainty/deviation, especially for legal metrology. Our simulation model can be used by dTDLAS spectrometer users (as well as instrument developers) to calculate systematic deviations of their concentration measurements caused by BL, and the similar results as shown in Fig. 6 can be obtained by just adding the BL information and line parameters of the target molecule into the model.

The new mid-IR HCl spectrometer shown in this paper together with the heterogeneity effects simulation model lays the foundation to become a first optical HCl reference technique which can fulfil the European legislation for HCl monitoring from combustion emissions. Further simulations will be performed to extend the method to more complex gas matrixes and to describe severe composition heterogeneities.