Numerical Study of Quenching Distances for Side-Wall Quenching Using Detailed Diffusion and Chemistry

Abstract

The numerical investigation of quenching distances in laminar flows is mainly concerned with two setups: head-on quenching (HOQ) and side-wall quenching (SWQ). While most of the numerical work has been conducted for HOQ with good agreement between simulation and experiment, far less analysis has been done for SWQ. Most of the SWQ simulations used simplified diffusion models or reduced chemistry and achieved reasonable agreement with experiments. However, it has been found that quenching distances for the SWQ setup differ from experimental results if detailed diffusion models and chemical reaction mechanisms are employed. Side-wall quenching is investigated numerically in this work with steady-state 2D and 3D simulations of an experimental flame setup. The simulations fully resolve the flame and employ detailed reaction mechanisms as well as molecular diffusion models. The goal is to provide data for the sensitivity of numerical quenching distances to different parameters. Quenching distances are determined based on different markers: chemiluminescent species, temperature and OH iso-surface. The quenching distances and heat fluxes at the cold wall from simulations and measurements agree well qualitatively. However, quenching distances from the simulations are lower than those from the experiments by a constant factor, which is the same for both methane and propane flames and also for a wide range of equivalence ratios and different markers. A systematic study of different influencing factors is performed: Changing the reaction mechanism in the simulation has little impact on the quenching distance, which has been tested with over 20 different reaction mechanisms. Detailed diffusion models like the mixture-averaged diffusion model and multi-component diffusion model with and without Soret effect yield the same quenching distances. By assuming a unity Lewis number, however, quenching distances increase significantly and have better agreement with measurements. This was validated by two different numerical codes (OpenFOAM and FASTEST) and also by 1D head-on quenching simulations (HOQ). Superimposing a fluctuation on the inlet velocity in the simulation also increases the quenching distance on average compared to the reference steady-state case. The inlet velocity profile, temperature boundary condition of the rod and radiation have a negligible effect. Finally, three dimensional simulations are necessary in order to obtain the correct velocity field in the SWQ computations. This however has only a negligible effect on quenching distances.

1 Introduction

The behavior of chemically reacting flows is decisively influenced by the presence of walls. This applies to numerous technologically and scientifically important processes, such as the formation of pollutants in combustion systems or the formation of deposits in power and process engineering. Thus, processes close to the wall have a strong influence on the development of new technological concepts. Examples are the development of engines, gas turbines, power plants and the process engineering industry. Despite their great importance, the underlying individual mechanisms and their interaction are not sufficiently known.

Most engineering applications of combustion processes with high power densities, for instance in gas turbines, internal combustion engines or aero engines, take place in enclosed chambers in which the flames propagate in the vicinity of walls and interact with them up to the point of extinction. Among other things, two mechanisms that are highly relevant for all combustion processes are significantly determined by the flow near the wall. First, a number of pollutants, especially unburnt hydrocarbons, carbon monoxide and soot, are preferably formed in areas close to the wall. For example, depending on the thermodynamic conditions, over 50% of the unburnt hydrocarbons in engine combustion come from the area close to the wall (Alkidas 1999), since the sharply falling temperature leads to quenching of reaction processes. Secondly, the changes in the reaction processes on differently designed walls have a decisive influence on the stability behavior of combustion systems (Güralp et al. 2006). The situation with respect to flame quenching and pollutant formation in modern engines is additionally exacerbated by the downsizing trend, which leads to higher wall-surface to volume ratios of the combustion chamber. Since the formation and oxidation of soot can be described with a radical mechanism (Appel et al. 2000; Frenklach and Wang 1991), it is not surprising that the strongly temperature-dependent processes are also strongly influenced by the presence of cold walls.

First systematic investigations have been carried out by Blanc et al. (1947, (1948), Elbe and Lewis (1948), Harris et al. (1948) as well as by Friedman and Johnston (1950) already in the middle of the last century. The authors determined quenching distances under various flame and wall conditions. Since then, extensive experimental (Lu et al. 1991; Ezekoye et al. 1992; Bellenoue et al. 2003; Sotton et al. 2005; Kim et al. 2006; Boust et al. 2007; Labuda et al. 2011; Mann et al. 2014; Dreizler and Böhm 2015; Suckart et al. 2016; Rißmann et al. 2017; Jainski et al. 2017a, b, 2018; Kosaka et al. 2018; Häber and Suntz 2018; Kosaka et al. 2019) and numerical (Poinsot et al. 1993; Bruneaux et al. 1996; Popp and Baum 1997; Hasse et al. 2000; Andrae et al. 2002; Singh 2004; Chauvy et al. 2010; Proch and Kempf 2015; Ganter et al. 2017; Heinrich et al. 2018a, b; Strassacker et al. 2018, 2019) studies on flame–wall interactions (FWI) have been carried out in recent years. Even though almost seven decades have been spent on the investigation of flame quenching near (cold) walls, which has improved the understanding of the flame–wall interaction substantially, one is far from having a quantitative understanding of the phenomena. For the most part, this may be attributed to the circumstance that a multitude of influencing factors contribute to the extinction of the flame near the wall, e.g. fuel type, stoichiometry (in the case of a premixed flame), pressure, wall material, wall temperature and flow conditions.

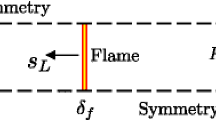
Wall quenching can be broadly divided into head-on quenching (HOQ), where flame propagation is perpendicular to the wall, and side-wall quenching (SWQ), with the flame burning parallel to the wall. The quenching distance is an important parameter to describe flame wall interactions. It measures how far the flame approaches the wall and it is directly related to the heat exchange between the flame and the wall (Poinsot et al. 1993; Bellenoue et al. 2003; Boust et al. 2007; Sotton et al. 2005; Kosaka et al. 2018). The maximum heat flux from the combustion zone to the cold wall increases with decreasing quenching distance. Various factors have a significant influence on the quenching distance and thus on the flame–wall interaction. For example, it is well known (Jainski et al. 2017b; Häber and Suntz 2018; Bellenoue et al. 2003; Blanc et al. 1947; Kosaka et al. 2018) that the quenching distance changes systematically as a function of fuel and equivalence ratio and that it strongly depends on the marker used to evaluate it. Studies on the effect of surface temperature and material have shown that the flame–wall interaction at low surface temperatures (<500 K) is governed solely by the heat losses to the wall (Kim et al. 2006; Miesse et al. 2004; Yang et al. 2011, 2013; Saiki et al. 2015). Furthermore, the quenching distance and wall heat flux systematically change as a function of wall surface temperature in sidewall and head-on configurations (Popp and Baum 1997; Ezekoye et al. 1992; Hasse et al. 2000; Jainski et al. 2017b; Kosaka et al. 2018). At the point of flame–wall interaction, the heat flux to the wall increases with increasing wall surface temperature accompanied by a decreasing quenching distance, hence, confirming correlations derived earlier by, for example, Poinsot et al. (1993) or Boust et al. (2007).

The quenching distance is commonly expressed in its normalized form as the quenching Peclet number, $Pe_q=d_q/\delta _f$, which allows a convenient comparison between different fuels and mixture compositions, see e.g. Poinsot et al. (1993), Boust et al. (2007). Here $d_q$ is the quenching distance and $\delta _f=a/s_l$ the diffusive flame thickness, where a is the thermal diffusivity and $s_l$ the laminar flame speed. For head-on quenching (HOQ), the Peclet number is typically in the range $Pe_q \sim 2.6{-}2.9$ (Poinsot et al. 1993; Bruneaux et al. 1996; Popp and Baum 1997; Hasse et al. 2000; Sotton et al. 2005; Boust et al. 2007; Chauvy et al. 2010; Mann et al. 2014; Rißmann et al. 2017). Absolute quenching distances, for example for stoichiometric methane/air mixtures, are on the order of $d_q \sim 0.17{-}0.20\,\hbox {mm}$. For the same conditions, the wall heat flux is ${\dot{Q}}_{wall} \sim 500\,\hbox {kW}/\hbox {m}^2$, with a normalized heat flux of $\varPhi _q={\dot{Q}}_{wall}/{\dot{Q}}_\varSigma =0.4{-}0.6$, where ${\dot{Q}}_\varSigma$ is the so-called flame power (Poinsot et al. 1993; Popp and Baum 1997; Hasse et al. 2000; Sotton et al. 2005; Boust et al. 2007; Mann et al. 2014). Generally, in the HOQ case, there is quite a good qualitative and quantitative agreement between experiment and simulation.

For the side-wall quenching (SWQ) configuration, quenching distances and Peclet number ($Pe_q \sim 7$) are about twice as large compared to the HOQ configuration (Bellenoue et al. 2003; Boust et al. 2007; Jainski et al. 2017b; Kosaka et al. 2018; Häber and Suntz 2018). Accordingly, wall heat fluxes are also lower by a factor of about two. Up until now, however, there is no comprehensive comparison between experiments and detailed numerical simulations of the side-wall quenching configuration, especially using different species concentration profiles and temperature profiles to evaluate quenching distances and wall heat fluxes for a wide variety of conditions. In this work, an experimental SWQ setup (Jainski et al. 2017b; Häber and Suntz 2018) is investigated. In the setup, an atmospheric V-shaped flame stabilized by a rod, which acts as a flame anchor, interacts with an isothermal wall at one side. Previously, Heinrich et al. performed 2D and 3D simulations of the same setup using tabulated chemistry and a unity Lewis number assumption (Heinrich et al. 2018a). The reported Peclet numbers were in very good agreement with experimental values. Preliminary calculations with detailed reaction chemistry and detailed molecular diffusion, however, showed a systematic and up to now unreported deviation from the experimental values. Specifically, quenching distance and wall heat flux in the detailed SWQ simulations were much closer to the HOQ configuration.

The focus of this work therefore lies on applying detailed reaction mechanisms and molecular transport to perform fully resolved simulations of the flame structure during flame–wall interaction. The aim is to explore possible causes for the observed and unresolved differences between experiment and simulation using extensive parameter studies. We will show that these differences are independent of the numerical code used, the reaction mechanisms and the fuel. The diffusion model has by far the greatest influence, but an acceptable quantitative agreement between simulation and experiment is only observed with a unity Lewis number assumption. Section 2 introduces the experimental setup. The simulation setups are described in Sect. 3. In Sect. 4, quenching distances are evaluated from the simulations in terms of different markers and compared to the experimental ones. Additionally, other quantities like heat flux at the cold wall and the flow field are compared as well. Sect. 5 presents results of a grid independence study. To further investigate the sensitivity of the quenching distance in the simulation to different parameters, simulations of 1D head-on quenching (HOQ) are performed in Sect. 6. This allows to conduct parameter studies with less computational effort and to systematically evaluate the influence of reaction mechanisms, diffusion models and wall temperatures on quenching distances. Finally, the influence of oscillating inflow and overall fluid velocity on the quenching distances is discussed.

2 Experimental Setup

Flame quenching near cold walls is studied using a generic side-wall quenching (SWQ) burner setup developed by Dreizler and co-workers (Jainski et al. 2017b; Kliewer and Patterson 2016). In the following, we will give a brief overview of the experimental setup and the measured quantities. For details, please refer to the references given in this section. Figure 1 illustrates the burner configuration used in our investigations. A detailed description of the experimental setup can be found in (Jainski et al. 2017b; Häber and Suntz 2018). The premixed fuel/air mixture enters the burner from the bottom and exits the burner through a Morel-shaped quadratic nozzle with an exit area of $40\times 40\,\hbox {mm}^{2}$. A circular ceramic rod ($D=1\,\hbox {mm}$, AL23, Friatec AG) placed 16 mm downstream of the nozzle exit anchors the V-shaped flame. One branch of the flame interacts with a temperature stabilized wall, which is aligned parallel to the initial, vertical major flow direction. Wall and ceramic rod are spaced 10 mm apart. A co-flow of pure nitrogen encloses the central fuel/air flow. Table 1 lists the operating conditions of the sidewall-quenching burner. The coordinate system is defined such that z is along the vertical direction (parallel to the cold wall), being zero at the nozzle exit. The x -axis is perpendicular to the wall surface, with its origin at the wall and being positive towards the ceramic rod.

Fig. 1

Side-view of the experimental setup of the side-wall quenching (SWQ) burner

Table 1 Operating conditions of the SWQ-burner. See Jainski et al. (2017b), Häber and Suntz (2018) for more details

Inside the plenum of the burner, the flow is homogenized by a honeycomb structure and two packages of fine meshes. A converging nozzle provides a laminar top-hat velocity profile at the quadratic burner outlet. The remaining axial velocity fluctuations are below 1% (Jainski et al. 2017b). Since the wall is not placed flush on the edge of the outlet nozzle but directly in the outlet stream, the pointed lower edge of the wall is exposed directly to the homogeneous velocity of the top-hat profile. The boundary layer then forms along the wall downstream. For this reason, most of the simulations described below use a constant velocity across the inlet (the influence of a different inlet profile is explored in Sect. 5).

As an example, Figs. 2 and 3 show particle imaging velocimetry (PIV) measurements of the cold flow close to the nozzle exit and wall. The nozzle exit is at $z=0\,\hbox {mm}$ and the wall at $x=0\,\hbox {mm}$. PIV measurements were performed using a double-pulse Nd:YAG laser (Spectra Physics, Quanta Ray, PIV-200, 532 nm) and a double-frame camera (LaVision, Imager sCMOS). Vector fields were calculated using the DaVis software package (LaVision, Version 10) with a $32 \times 32$ pixel window size (50% overlap) and a spatial resolution of the vector field of 0.16 mm. Figure 2 shows a 2D-image of the z-component of the mean velocity field in a plane perpendicular to the wall and Fig.3 displays cross-sections 3 mm and 20 mm above the nozzle exit (gray dashed lines in Fig. 2). The x-component is negligible compared to the z-component. Close to the nozzle exit ($z=3\,\hbox {mm}$), the flow profile is still very close to the top-hat profile, although the wall edge slightly disturbs the velocity field. Further downstream the boundary layer starts to develop along the wall.

Fig. 2

Vertical component of the velocity field in a plane perpendicular to the wall and close to the burner exit ($z=0\,\hbox {mm}$) and wall ($x=0\,\hbox {mm}$). The right edge of the nozzle exit is at $x=30\,\hbox {mm}$

Fig. 3

Top: cross-sections of the velocity field 3 mm and 20 mm above the nozzle exit (gray dashed lines in Fig. 2). Bottom: RMS fluctuations of the velocity component

The design of the burner (converging nozzle downstream of a large volume plenum) promotes acoustic Helmholtz resonances (Schuller et al. 2003). The resonance frequency of the burner setup is $\sim 100\,\hbox {Hz}$ (Jainski et al. 2017a, b). Figure 3 also shows the root-mean-squared (RMS) value of the velocity fluctuations of the z-component with an average value of ${\bar{u}}_{z,rms}=0.07\,\hbox {m/s}$. The influence of the Helmholtz resonance and the consequences of the associated velocity fluctuations are evaluated in Sect. 6.7.

All measurements cited and reported here were obtained on two independent but identical burner configurations set up by two research groups and complementary but different measurement techniques are utilized for determining the quenching distances as well as the wall heat fluxes. Although partly different fuels, mixture compositions, wall materials and wall temperatures were used at the two setups, the data presented here relate almost exclusively to the same operating conditions. Specifically, the various quenching distances are based on three completely different optical methods: (a) planar laser-induced fluorescence (PLIF) imaging of OH radicals (Jainski et al. 2017b) (b) the chemiluminescence of the electronically excited OH* and CH* radicals (Häber and Suntz 2018) and (c) point-wise gas phase temperature measurements using coherent anti-Stokes Raman spectroscopy (CARS) (Kosaka et al. 2018). Simultaneously, wall surface temperatures were measured using one-dimensional phosphor thermometry (Kosaka et al. 2018). Wall heat fluxes were then estimated from measured gas and wall surface temperatures using a linear approximation of Fourier’s law (Kosaka et al. 2018). In addition, and new in this work, wall heat fluxes have also been measured using commercial heat flux sensors (greenTEG gSKIN XM 26) mounted on the back side of the 2 mm thick wall (Fig. 1). Due to the size of the heat flux sensors ($4.4\,\hbox {mm}\times 4.4\,\hbox {mm}$) and the heat conduction within the wall parallel to the z-direction, the spatial resolution is limited, but the heat flux sensors provide an independent validation of the magnitude of the flame-side wall heat fluxes. The position of the heat flux sensors was varied relative to the flame front in the z-direction to obtain more data points at different heights above the burner. The heat flux sensors have been calibrated in-place using a home-built heat source with a well defined surface heat flux (not shown here for brevity).

3 Numerical Setup

3.1 Numerical Solver

Our in-house solver (Zirwes et al. 2019b, 2018) implemented in the open-source CFD framework OpenFOAM (Weller et al. 2017) in version v1712 is used for the simulations of the SWQ and HOQ in the following sections. It is coupled to the open-source library Cantera (Goodwin et al. 2017) in version 2.5.0a2 in order to compute detailed molecular diffusion coefficients from either the multi-component or mixture-averaged model (Kee et al. 2005) and to utilize finite rate chemistry from detailed reaction mechanisms.

The governing equations for reacting flows are solved in their fully compressible formulation: Conservation of mass

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \nabla \cdot \left( \rho \mathbf {u}\right) =0 \end{aligned}$$

(1)

where $\rho$ is the density, t time and $\mathbf {u}$ the fluid velocity. Conservation of momentum

$$\begin{aligned} \frac{\partial \left( \rho \mathbf {u}\right) }{\partial t}+\nabla \cdot \left( \rho \mathbf {u}\mathbf {u}\right) =-\nabla p + \nabla \cdot \left( \mu \left( \nabla \mathbf {u}+\left( \nabla \mathbf {u}\right) ^T-\frac{2}{3}{I}\nabla \cdot \mathbf {u}\right) \right) \end{aligned}$$

(2)

with I the unit tensor, p the pressure and $\mu$ the dynamic viscosity. For each species k, a transport equation is solved:

$$\begin{aligned} \frac{\partial \left( \rho Y_k\right) }{\partial t} + \nabla \cdot \left( \rho (\mathbf {u}+\mathbf {u}_{c,k})Y_k\right) = {\dot{\omega }}_k -\nabla \cdot \mathbf {j}_k \end{aligned}$$

(3)

$Y_k$ is the mass fraction of species k, ${\dot{\omega }}_k$ its reaction rate and $\mathbf {u}_{c,k}$ the correction velocity in case of mixture-averaged diffusion. For the mixture-averaged model, the diffusive mass flux is computed from

$$\begin{aligned} \mathbf {j}_k=-\rho D_{k}\nabla Y_k \end{aligned}$$

(4)

where $D_{k}$ is the mixture-averaged diffusion coefficient for computing the diffusive mass flux of species k based on the mass fraction gradient (Kee et al. 2005). In case of the multi-component formulation, the diffusive mass flux is computed from:

$$\begin{aligned} \mathbf {j}_k=-\rho \sum _{j\ne k}\left( {D_{k,j}Y_j}\right) \nabla Y_k-\rho M_k\sum _{j\ne k}\left( {D_{k,j}Y_j}\right) \nabla \left( \frac{1}{{\bar{M}}}-\frac{Y_k}{M_k}\right)+\rho\frac{M_k}{\bar{M}}\sum_{j\ne k}D_{k,j}\nabla Y_j -\frac{D_{T,k}}{T}\nabla T \end{aligned}$$

(5)

$D_{k,i}$ is the multi-component diffusion coefficient of species k into species i, $M_k$ is the molar mass of species k and ${\bar{M}}$ the mean molecular weight of the mixture. The formulation given in Eq. (5) is equivalent to the one given in Kee et al. (2005), but allows to discretize the first term on the right hand side implicitly. The last term on the right hand side is the diffusive mass flux due to the Soret effect, with $D_{T,k}$ being the thermodiffusion coefficient of species k. Mass diffusion due to pressure gradients is generally neglected in this work.

Conservation of energy is formulated in terms of total enthalpy $h_{\mathrm {tot}}$:

$$\begin{aligned} \frac{\partial \left( \rho h_{\mathrm {tot}}\right) }{\partial t} + \nabla \cdot \left( \rho \mathbf {u}h_{\mathrm {tot}}\right) =\nabla \cdot \left( \lambda \nabla T\right) -\sum _k\nabla \cdot \left( h_{s,k}\mathbf {j}_k\right) +\frac{\partial p}{\partial t}-\sum _k h^{\circ }_k{\dot{\omega }}_k+{\dot{q}}_{\mathrm {rad}} \end{aligned}$$

(6)

$\lambda$ is the heat conductivity of the mixture, T the temperature, $h_{s,k}$ the sensible enthalpy of species k, $h_k^\circ$ the standard enthalpy of formation and ${\dot{q}}_{\mathrm {rad}}$ the heat flux due to radiation.

The governing equations are solved with the finite volume method (FVM). For all simulations in this work, spatial gradients are discretized using a fourth order interpolation method and time is discretized implicitly using the second order backward Euler method. The Courant-Friedrich-Lewy number is limited to $\mathrm {CFL}\approx 0.1$ for all simulations. The pressure-velocity coupling is achieved by the pressure implicit split operator technique. For more information about the solver and the governing equations see Zirwes et al. (2019a, b), Zhang et al. (2017).

3.2 Computational Domain

The simulation setup is built to resemble the experimental setup described in the previous section and all simulations are performed until the steady-state solution is attained for the flame branch near the cold wall.

Fig. 4

Computational domain showing the V-shaped flame and the quenching near the cold wall on the left. Right: zoom near the rod where the flame anchors

Figure 4 on the left shows the temperature field from the 2D simulation for the methane-air flame at an equivalence ratio of $\phi =1$. The unburnt fuel-air mixture enters the domain from the inlet at the bottom at 1 atm and 293 K and a velocity of 1.52 m/s. This velocity is lower than in the experiments (see Table 1) to match the experimental flame length, because flow divergence effects cannot be taken into account in the 2D setup (for more information see Heinrich et al. 2018a). The boundaries on the right and at the top are outlets. The boundary on the left is a cold wall with a fixed temperature of 293 K. A rod with a diameter of 1 mm and a fixed surface temperature of 293 K acts as the flame anchor resulting in a V-shaped flame. In total, the domain has a width of 60 mm and a height of 150 mm.

The computational mesh consists of 6.4 million cells and is refined toward the region where the flame quenching occurs as well as the rod. Near the cold wall, the mesh has an equidistant cell size of $10\,\mu \hbox {m}$. The 3D setup has the same mesh topology and cell sizes as the 2D domain but is extended in the third direction by 100 mm. In total, it consists of 65 million cells, where the flame branch near the cold wall is discretized with equidistant cells of $10\,\mu \hbox {m}$. The front and back boundary conditions are open to allow the gas flow to escape the computational domain. The other boundary conditions are the same as in the 2D setup except the inflow velocity is the same as in the experiments (1.9 m/s) because flow divergence effects are fully captured in 3D. The GRI 3.0 reaction mechanism (Smith et al. 1995) is used for methane and the UCSD mechanism (Williams 2018) for propane, both extended by additional reaction pathways for chemically exited OH* and CH* radicals (Kathrotia et al. 2012) and the mechanism by Kee et al. (2005) for the 3D simulations due to the lower computational cost compared to GRI 3.0 but similar results for the quenching distances (see Sect. 6.2).

The flow inside the domain is laminar. The flow around the rod shows a small region of flow recirculation but mostly behaves like a creeping flow ($Re \approx 100$) as shown in Fig. 4. The figure shows the streamlines and the temperature field in the vicinity of the rod for the steady-state solution. Because the surface temperature of the rod is fixed at 293 K in the simulation, the flame does not stabilize directly at the rod but stabilizes in the low velocity region directly downstream of the rod.

4 Results

The 2D simulations for the side-wall quenching have been performed for five methane equivalence ratios from lean to rich and three propane equivalence ratios. Quenching distances based on different markers can be compared to the experiments. Additionally, heat flux measurements at the cold wall are available Kosaka et al. (2018) too. If not stated otherwise, the numerical results are obtained from the mixture-averaged diffusion model and the GRI 3.0 reaction mechanism. For a detailed discussion on the effect of different diffusion models and reaction mechanisms, see Sect. 6.

Fig. 5

Example for the quenching distance from the simulation resulting from different markers (OH*, CH* and temperature iso-surfaces, and an iso-surface based on the OH gradient) from a methane flame (left) and propane flame (right). The thin, black dashed line shows the position of the maximum heat release rate. The colored circles mark the position where the respective iso-lines are closest to the cold wall. $h_{\mathrm {max}}$ is the height where the heat flux from the flame to the wall has its maximum

The quenching distances are obtained from different markers (species concentrations or temperature), which yield different values for the quenching distance. This is illustrated in Fig. 5 for a methane and a propane flame. The following definitions are evaluated and discussed:

• the distance between the cold wall and the iso-line of the OH* or CH* concentrations for which the intensity (mole fraction) drops to 50% of its maximum value in a freely propagating flame with the same equivalence ratio (Häber and Suntz 2018)

• the iso-line of the gradient of OH intensity (mole fraction) at a value of half the maximum value from the freely propagating 1D flame, which approximately corresponds to the maximum of the second spatial derivative of the OH intensity (Jainski et al. 2017b)

• the iso-contour of temperature that corresponds to the temperature at the maximum gradient of the heat release rate in a freely propagating flame (Kosaka et al. 2018).

Fig. 6

Direct comparison between experimental measurements and 2D simulation results of profiles normal to the wall at different heights for the methane/air flame at $\phi =1$. Top: temperature profiles. Bottom: OH profiles

A direct comparison between experimental measurements and 2D simulation results for the methane/air case at $\phi =1$ is shown in Fig. 6. At the top of Fig. 6, temperature profiles normal to the wall (x direction) are plotted at the height of the quenching point $z=h_{max}$ (center) as well as 1 mm below (left figure) and above (right figure) that point, showing reasonable agreement. At the bottom of Fig. 6, profiles of the normalized OH intensity from OH-LIF are plotted together with the normalized OH concentration from the 2D simulation. While the agreement is comparatively well far away from the wall ($x>2\,\hbox {mm}$), there are noticeable differences near the wall.

This discrepancy near the wall is further analyzed in Fig. 7 in terms of the quenching distances. On the left of Fig. 7, the minimal distance to the cold wall is shown of the iso-lines defined by the markers described above for the different methane flames. This minimal distance to the wall is defined as the quenching distance $d_q$. Obviously, the quenching distance is not a single unique number, because it strongly depends on the species or marker selected in the measurements or simulations. Results from experiments using different measurement techniques (filled circles, solid lines) such as chemiluminescence (Häber and Suntz 2018), OH-LIF (Jainski et al. 2017b) and CO-CARS (Jainski et al. 2017b; Kosaka et al. 2018) are compared with corresponding quenching distances obtained from the 2D and 3D simulations (open circles, dashed lines). The accuracy of the measured quenching distances is typically less than $\pm 0.04\,\hbox {mm}$ (Häber and Suntz 2018; Jainski et al. 2017b; Kosaka et al. 2018).

Fig. 7

Left: Quenching distances based on different markers for methane flames from the experiment (filled markers, solid lines) (Häber and Suntz 2018; Jainski et al. 2017b; Kosaka et al. 2018) and simulation (open markers, dashed lines). Right: Results of quenching distances for the propane flames

The qualitative trend of the dependence of quenching distance on equivalence ratio from the simulations agrees well with the experiments for all markers. However, in order to obtain the quantitative agreement shown in Fig. 7, the quenching distances from the simulation have to be multiplied by a factor of 1.8. This factor is the same for all equivalence ratios and all markers, indicating that the relative ordering of the quenching distances obtained from different markers as well as their ratio is the same in the experiments and simulations. It should be noted that the experimentally determined quenching distances are based on three completely independent experimental techniques and have been obtained independently in two research groups. The quenching distances from the simulation performed with OpenFOAM also agree well with results from the academic CFD code FASTEST (Schäfer and Stosic 1994), which was used to investigate methane flames (Ganter et al. 2017) (not shown here). The very good agreement between experiment and simulation therefore not only confirms the independent measurements, but it also suggests that the numerical simulations successfully capture qualitatively the relative dependence of quenching distances to equivalence ratio of the side-wall quenching configuration. Only the absolute values deviate by a constant factor.

For the propane flames, agreement between simulation and experiment is also very good quantitatively if scaled by a constant factor (Fig. 7 on the right). It is interesting to note that this is the same factor as for the methane flames, although a different reaction mechanism and fuel is used in this case. A comparison of quenching distances for fuel-rich propane flames is not possible with the current simulation setup because fuel-rich propane flames do not stabilize at the rod but are driven downstream in the simulation due to the rod being colder in the simulation (293 K) than in the experiment (the rod is not actively cooled in the experiments). An additional simulation has been conducted where the rod is assumed to be perfectly adiabatic. Having a perfectly cold rod and a perfectly adiabatic rod covers both extreme cases, where the experimental condition lies in-between. In case of the adiabatic rod, the flame stabilizes directly at the rod instead of in the downstream region (see Fig. 4). This has a slight influence on the flame height. Due to the rod being far away from the point of quenching, the highest observed difference in the quenching distance was $5\,\mu \hbox {m}$.

Fig. 8

Measured (Kosaka et al. 2018) and simulated heat fluxes ${\dot{q}}$ along the cold wall (z-direction) where $h_{max}$ is the flame height and $z-h_{max}=0$ is the location of maximum heat flux at the wall

A comparison between simulated and measured (Kosaka et al. 2018) heat flux at the cold wall is presented in Fig. 8, where the experimentally determined heat flux normal to the wall surface is compared to the simulation for methane-air flames at three equivalence ratios. Experimentally, wall heat fluxes were determined by a combination of wall surface and gas phase temperature measurements 0.1 mm away from the surface (Kosaka et al. 2018). The results from the simulations show good qualitative agreement and yield even good quantitative agreement if divided by the same constant factor of 1.8. In other words, the simulation consistently underestimates the quenching distance by almost a factor of two and therefore, the wall heat flux should be overestimated by a similar amount due to the connection between heat release rate and quenching distance (Boust et al. 2007). This is exactly what we observe (see Fig. 7), which implies that the absolute deviation of quenching distance and wall heat flux between experiment and simulation are inherently consistent. Again, only the absolute values are off by the same factor. The uncertainty in the experimental quenching distances is less than $\pm 50\,\mu \mathrm {m}$ for the OH-LIF and temperature isoline data (Jainski et al. 2017b; Kosaka et al. 2018) and about $\pm 70\,\mu \hbox {m}$ for the chemiluminescence data (Häber and Suntz 2018). However, since the scaling factor is the same for all experimental methods, we consider measurement errors as the cause of the discrepancy between experiment and simulation to be unlikely.

Fig. 9

Measured signals of the heat flux sensors on the back side of the 2 mm thick wall and simulated heat fluxes ${\dot{q}}$ for methane-air flames at five different equivalence ratios. $h_{max}$ is the flame height and $z-h_{max}=0$ is the location of maximum heat flux at the wall

While Fig. 8 contains the wall heat fluxes estimated from the gas phase and wall surface temperatures, Fig. 9 shows the heat fluxes obtained using commercial heat flux sensors (red dots). In order to minimize the influence of the sensors on the thermal properties of the wall and due to the permissible temperature range, the heat flux sensors were mounted on the side of the wall facing away from the flame. As previously mentioned, the spatial extent of the sensors and the heat conduction parallel to the wall surface limit the spatial resolution and lead to a significant broadening of the peak heat flux compared to the wall surface facing the flame. Figure 9 also contains simulated heat fluxes (lines) extracted from the 2D calculations. For the comparison, the heat flux on the back side of the wall was calculated based on the simulated front-side heat fluxes in Fig. 8, taking into account the 2D heat conduction in the wall as well as the size of the sensor and assuming a constant temperature of $T=293\,\hbox {K}$ on the back surface. Similar to Fig. 8, the simulated heat fluxes were divided by a factor of 1.8. Overall, the signals of the heat flux sensors and the simulated heat fluxes show a good qualitative agreement. In addition, the peak heat fluxes between experimental and scaled simulated heat fluxes are within 15% of each other. Thus, the heat flux sensors offer an independent validation of the experimentally determined wall heat fluxes in Fig. 8.

The fact that the simulations consistently reproduce the dependence of the quenching distances and wall heat fluxes as a function of quenching marker, equivalence ratio and fuel, and that only the absolute values deviate from the experiment by an identical factor, indicates that there is a systematic error either in the experiments or in the simulations. In the following, we will therefore investigate the dependence of the flame–wall interaction on a variety of factors and their influence on the simulated quenching distances; including the reaction mechanism, the spatial dimension (2D or 3D), the diffusion model (mixture averaged, multi-component, $Le=1$) and transient effects due to inflow fluctuations. It should be noted that this discrepancy between simulation and measurements is not present for the head-on quenching setup (Sect. 6), where quenching distances between experiment and simulation compare quantitatively well without any correction.

5 Grid Independence Study

To rule out that the difference between simulation and experiments is caused by the grid resolution, a grid independence study has been conducted for the SWQ case. The mesh used in all simulations so far has a region of equidistant resolution of $10\,\mu \hbox {m}$ over the whole length of the cold wall and which extends 0.75 cm perpendicular to it. Other meshes with equidistant resolution of $\varDelta x=5\,\mu \hbox {m}$, $20\,\mu \hbox {m}$ and $40\,\mu \hbox {m}$ are considered for the grid study. Figure 10 shows results for the quenching distance $d_q$ obtained from the temperature marker for methane/air at $\phi =1$ with the reaction mechanism by Kee et al. (2005) (red dots). The difference between the coarsest and the finest mesh in $d_q$ is about 3%. The dashed black line shows the experimentally measured quenching distance.

The resolution of boundary layers is estimated with $y^+=\frac{0.5\varDelta x u_{\tau }}{\nu }$. For the mesh with $10\,\mu \hbox {m}$ resolution, $y^+=0.11$. Even for the coarsest mesh with $\varDelta x=40\,\mu \hbox {m}$, $y^+$ is still 0.45. Therefore, boundary layers are fully captured by the meshes.

To ensure that the flow is fully resolved and laminar, additional simulations with the WALE (Nicoud and Ducros 1999) sub-grid turbulence model (instead of no sub-grid model) have been performed on the mesh with $\varDelta x=10\,\mu \hbox {m}$ and the coarsest mesh with $40\,\mu \hbox {m}$ (blue crosses in Fig. 10). Quenching distances are slightly increased by using the turbulence model, but the change is less than 0.5% and therefore negligible.

Another simulation on the $\varDelta x=10\,\mu \hbox {m}$ mesh is conducted which includes radiation. The model considers radiation for $\hbox {H}_2\hbox {O}$, $\hbox {CO}_2$ (Barlow et al. 2001) and CO, $\hbox {H}_2$ (Liu and Rogg 1991) and assumes an optically thin gas due to the atmospheric conditions. The quenching distance is slightly increased, but the difference is only about 1%, so that radiation at atmospheric conditions is negligible for the quenching distances.

Lastly, a simulation is performed on the $\varDelta x=10\,\mu \hbox {m}$ mesh, where instead of a constant flow velocity at the inlet $u_z=1.52\,\hbox {m/s}$ (as shown in Sect. 2) a pipe flow profile is used:

$$\begin{aligned} u_z=\frac{3}{2}u_{\mathrm {bulk}}\left( 1-\frac{(x-L)^2}{L^2}\right) \end{aligned}$$

(7)

with $L=20\,\hbox {mm}$, $x\in [0,40]\,\hbox {mm}$ and $u_{\mathrm {bulk}}=1.52\,\hbox {m/s}$. Although this has an impact on the quenching distance, the difference is only about 8%. Therefore, it can be concluded that the distance from the inlet to the point of quenching is large enough, so that the boundary layers along the cold wall can develop independently of the velocity profile set at the inlet.

Fig. 10

Quenching distances $d_q$ from 2D simulations of SWQ on meshes with different cell size $\varDelta x$. The black dashed line shows the experimental result. Additionally, simulation results with the WALE turbulence model (instead of no turbulence model in the base simulations), using a radiation model and using a pipe flow profile at the inlet instead of a constant inlet velocity are included

6 Sensitivity of the Simulated Quenching Distance

In this section, different parameters are varied to show how sensitive the quenching distances from the simulation are to these parameters. If not stated otherwise, the quenching distances are evaluated using the temperature iso-surface as marker, which corresponds to the temperature at the maximum gradient of the heat release rate in a freely propagating flame.

6.1 Flow Velocity and 2D vs. 3D Effects

Most of the results presented in Sect. 4 are from the 2D simulation setup. However, due to the non-isothermal character of the reacting flow and the lack of closed boundaries in the y-direction, the experimental setup in Fig. 1 is, strictly speaking, not a 2D-problem. The gas expansion downstream of the flame causes a flow divergence in the y-direction, which is not captured by the 2D simulations (Heinrich et al. 2018a). On the other hand, the flow field upstream of the flame and near the wall is influenced much less by the dimensionality than downstream of the flame. In order to investigate if and what influence the flow field downstream of the flame has on the flame–wall interaction, we have also performed 3D calculations for selected conditions.

The main difference between the 2D and 3D setup is, that the bulk flow velocity at the inlet is reduced from 1.9 m/s for the 3D case to 1.52 m/s for the 2D case or 80% of the experimental setup, in order to achieve the same flame height between 2D simulation, 3D simulation and experiment.

Fig. 11

Field of the magnitude of the fluid velocity from PIV measurements (Jainski et al. 2018) and the 2D and 3D simulations

Figure 11 shows the velocity magnitude field from PIV measurements (Jainski et al. 2018) as well as 2D and 3D simulations. It can be seen that the velocities in the 2D case are much higher due to the missing flow divergence in 2D. The same effect is shown in Fig. 12, where the velocity component parallel to the cold wall is plotted along horizontal lines at specific and constant values of $z-z_0$. While the 2D simulations overestimate the velocity locally, the results from the 3D simulation are closer to the PIV measurements, confirming previous studies (Jainski et al. 2018).

Fig. 12

Flow velocity component parallel to the cold wall plotted along horizontal lines from the 2D and 3D simulations as well as PIV measurements

In the 3D setup, it is assumed that a homogeneous gas flow enters the domain over the whole inlet plane. In the experiment, there is a nozzle for methane/air and a surrounding nozzle for a nitrogen co-flow, that is not included in the simulation, which might lead to the differences in Fig. 12. However, regardless of the agreement between experimental and numerical flow fields, the flow field is fundamentally different in the 3D case compared to the 2D case. Nonetheless, quenching distances are nearly unaffected so that the details of the flow field are an unlikely cause for the observed differences of the quenching distances. In Fig. 7, the star-shaped symbols represent the quenching distance from the 3D simulation, which agree well with the 2D results. If the same inlet velocity is used for the 2D simulations as in the 3D case and the experiments, the flame length increases by about 20%, while the quenching distances remain approximately the same (within 5%). Therefore, the effect of the velocity field or inlet velocity on the quenching distance only plays a subordinate role and experimental uncertainties regarding the mass flow rate are not able to explain the deviation of quenching distances between simulation and experiment.

6.2 Reaction Mechanism

In the previous section, the GRI 3.0 (Smith et al. 1995) reaction mechanism was used for the 2D simulation of the methane flames, the UCSD (Williams 2018) mechanism for the 2D propane flames and the Kee mechanism (Kee et al. 2005) for the 3D methane flame.

In order to study how the quenching distance changes with different reaction mechanisms, 1D head-on quenching (HOQ) simulations are conducted, which allow to test many different reaction mechanisms for a canonical test case.

Fig. 13

Position of temperature and OH iso-surface, global maximum of heat release rate (HRR) and heat flux at the cold wall over time during the HOQ. The cold wall is located at $d=0$. The case is propane-air at $\phi =1$

The computational domain consists of 10,000 cells with a total length of 2 cm, resulting in an equidistant resolution of $2\,\mu \hbox {m}$. The right boundary is a cold wall at 300 K and the left boundary an outlet with zero gradient for all solution variables and a fixed pressure of 1 atm. The initial solution is given by a freely propagating stationary one-dimensional premixed flame with an equivalence ratio of $\phi =1$, which is calculated using Cantera in a preprocessing step. Temperature and species mass fraction profiles are mapped to the computational domain so that the burnt part of the flame is on the left at the outlet and the unburnt gas on the right where the cold wall is located. The position of the flame front, identified by the maximum heat release rate, is located 1 cm from the wall so that the flame propagates towards the cold wall. The gas velocity is initially set to zero throughout the domain. The diffusion model is the mixture-averaged model (Kee et al. 2005) (see also Sect. 6.3).

An example of the HOQ process is shown in Fig. 13. The flame first freely propagates toward the cold wall ($d=0\,\hbox {mm}$) as shown by the constant value of the heat release rate, zero heat flux at the wall and decreasing value of the position of the temperature and OH marker. As the flame comes close to the cold wall, the heat release rate sharply drops and the position of the temperature and OH iso-surfaces reach a minimum distance to the cold wall. At the same time, the heat flux at the cold wall reaches its maximum value.

Fig. 14

Quenching distances of methane and propane flames at $\phi =1$ from different reaction mechanisms and using the iso-thermal contour as marker for the HOQ setup

Figure 14 shows the quenching distances from different reaction mechanisms for methane and propane flames. In total, 20 reaction mechanisms for methane are investigated: Kee et al. (2005), sk17 Sankaran et al. (2007), drm22 and drm19 (Kazakov and Frenklach 1994), GRI1.2, GRI3.0 and a skeletal mechanism with 30 species (skeletal30) (Smith et al. 1995), Lu13/Lu19 (Lu and Law 2008), USC C3 (Davis et al. 1999), HyChem (Wang et al. 2018), USC C1/C3 (Qin et al. 2000), Meoh (Li et al. 2007), Najm (Zádor and Najm 2012), Valorani (Valorani et al. 2006), UCSD (Williams 2018) and USC Mech II (Wang et al. 2007), GRI2.11 (Bowman et al. 1995) and Lindstedt and Skevis (1997); Lindstedt et al. (1994). In addition, a new reduced mechanism (reduced CRECK) was obtained ad hoc from the CRECK kinetic mechanism (Ranzi et al. 2012), 1911 version. Starting from a core $\hbox {C}_0$–$\hbox {C}_3$ mechanism obtained by combining the $\hbox {H}_2$/$\hbox {O}_2$ and $\hbox {C}_1$/$\hbox {C}_2$ subsets by Metcalfe et al. (2013), and $\hbox {C}_3$ from Burke et al. (2015), the reduction methodology implemented in the DoctorSMOKE++ software (Stagni et al. 2016), coupling flux analysis (Pepiot-Desjardins and Pitsch 2008) and sensitivity analysis (Niemeyer et al. 2010) was adopted. Considering the operating conditions of interest for the flame–wall interaction, reaction states were sampled in 0D reactors at starting conditions of $p = 1\,\hbox {atm}$, $0.75\le \phi \le 1$ and variable temperatures. The final mechanism contains 26 species and 195 reactions and is included in the supplementary materials. For the propane flames, seven mechanism are used: GRI3.0 (Smith et al. 1995), Peters (2001), Poinsot (Haworth et al. 2000), UCSD (Williams 2018), USC C1 C3 (Qin et al. 2000), USC C3 (Davis et al. 1999) and USC Mech II (Wang et al. 2007). The marker based on temperature as discussed above is tracked over time and its position is recorded. The quenching distance is given by the minimum distance to the wall that this iso-surface reaches. In Fig. 14, the quenching distances from the simulations are shown directly without scaling.

Also shown in Fig. 14 are results from the 2D simulations for SWQ using GRI 3.0 (star) as well as the measurements (empty symbols) (Jainski et al. 2017b; Kosaka et al. 2018). Although both detailed and reduced mechanisms are employed, the difference in quenching distance resulting from the different reaction mechanisms is only about $\pm 25\,\mu \hbox {m}$. This is in contrast to the diffusion models, where using simplified diffusion models leads to significantly different quenching distances (see Sect. 6.3). The measured HOQ quenching distances (black triangle and diamond) agree well with the simulated quenching distances (colored circles). The quenching distances from the simulations for all investigated cases correspond to Peclet numbers $Pe=d_q/\delta_f$ of 2.6 to 2.9, with the flame thickness $\delta_f=a/s_l$, where a is the thermal diffusivity of the unburnt gas composition and $s_l$ the laminar flame speed. These values also fit well to HOQ Peclet numbers from the literature, which lie between 2.6 and 3.5 (Dreizler and Böhm 2015; Boust et al. 2007; Bruneaux et al. 1996; Poinsot et al. 1993; Sotton et al. 2005; Mann et al. 2014; Popp and Baum 1997; Hasse et al. 2000; Chauvy et al. 2010). Similarly, normalized wall heat fluxes $\varPhi _q=Q_W/Q_\varSigma$ agree well between simulation and experiment in the HOQ case and are in the order of $\varPhi _q \approx 0.4$ (Dreizler and Böhm 2015; Boust et al. 2007; Bruneaux et al. 1996; Poinsot et al. 1993; Sotton et al. 2005; Mann et al. 2014; Popp and Baum 1997; Hasse et al. 2000; Chauvy et al. 2010). Here $Q_W$ is the maximum wall heat flux at the quench point and $Q_\varSigma$ is the so-called flame power.

The experimentally measured quenching distances (wall heat fluxes) for the SWQ setup are approximately a factor of two higher (lower), compared to the HOQ case, corresponding to Peclet numbers of $Pe\approx 7$ (Bellenoue et al. 2003; Boust et al. 2007; Jainski et al. 2017b; Kosaka et al. 2018; Häber and Suntz 2018) and normalized wall heat fluxes of $\varPhi _q \sim 0.2$ (Jainski et al. 2017b; Kosaka et al. 2018). By contrast, the simulated values in the SWQ and HOQ setup are almost identical.

Overall, the variations between the different mechanisms in terms of the quenching distance are practically negligible, but the type of quenching mechanism (head-on vs. side-wall) has a huge impact on the experiment that is not reflected in the simulations.

6.3 Diffusion Model

All presented simulation results so far were calculated using the mixture-averaged diffusion model. In this model, binary diffusion coefficients for each species are computed from kinetic gas theory and a mixture-averaged diffusion coefficient based on the binary coefficients is computed for each species based on the Hirschfelder-Curtiss approximation (Kee et al. 2005). A more rigorous diffusion model is the multi-component diffusion model, which calculates a diffusion coefficient for each species pair depending on the current mixture composition (Kee et al. 2005). This model is computationally much more expensive than the mixture-averaged one. The multi-component model also allows to evaluate the diffusion coefficients for the Soret diffusion. On the other hand, a much more simple diffusion model is based on assuming a unity Lewis number Le. In this model, all species have the same diffusion coefficient D.

Fig. 15

Quenching distances based on the temperature marker from the SWQ setup using the GRI 3.0 reaction mechanism (left) and the HOQ setup using the Kee reaction mechanism (right) for different diffusion models

Figure 15 shows results of the quenching distance from the SWQ and HOQ simulations using the different diffusion models. While the mixture averaged and multi-component (with and without Soret diffusion) model agree within 1%, the unity Lewis number assumption yields significantly higher quenching distances. These results from OpenFOAM are also consistent with previously published data obtained with the CFD code FASTEST (Ganter et al. 2017) for SWQ of methane flames.

Fig. 16

Profiles perpendicular to the cold wall through the quenching of the SWQ setup for a methane-air flame of a temperature, b local Lewis number, c local equivalence ratio and d mass fraction of $\hbox {H}_2\hbox {O}_2$

In the unity Lewis number model, the diffusion coefficient of each species is computed from

$$\begin{aligned} D_k=D=a=\frac{\lambda }{\rho c_p} \end{aligned}$$

(8)

where a is the thermal diffusivity, $c_p$ the isobaric heat capacity and $\lambda$ the heat conductivity. It should be noted that only the computation of the diffusion coefficients are affected by the unity Lewis number model; the heat conductivity and viscosity are computed exactly as in the mixture-averaged model. Figure 16 shows profiles of different quantities along a line perpendicular to the cold wall through the quenching point of the SWQ setup for methane/air at $\phi =1$ using the GRI 3.0 reaction mechanism. The cold wall is located at $x=0\,\hbox {mm}$. Using the unity Lewis number model (Fig. 16a), a less steep rise of the temperature profile is achieved, which leads to the higher quenching distances. Figure 16b shows the local Lewis numbers computed from Bechtold and Matalon (Bechtold and Matalon 2001)

$$\begin{aligned} Le_{BM}=1+\frac{(Le_E-1)+(Le_D-1)A}{1+A} \end{aligned}$$

(9)

which reduces for $\phi =1$ to

$$\begin{aligned} Le_{BM}=\frac{1}{2}(Le_{\mathrm {O}_2}+Le_{\mathrm {CH}_4}) \end{aligned}$$

(10)

An alternative effective Lewis number is computed for the mixture from

$$\begin{aligned} Le_{eff}=\frac{a}{\sum _kX_kD_k} \end{aligned}$$

(11)

where $X_k$ is the mole fraction of the k-th species. Because this case is a methane/air flame at $\phi =1$, the Lewis number of the mixture is close to unity. Near the wall, however, the local stoichiometry reduces slightly for the mixture-averaged diffusion model (Fig. 16b). For the unity Lewis number model, the local stoichiometry stays constant due to all species having the same diffusion coefficient. This also affects species concentrations close to the wall, where the largest deviations were found for the mass fraction of $\hbox {H}_2\hbox {O}_2$ (Fig. 16d).

Fig. 17

Measured temperature profile perpendicular to the wall at the point of quenching ($z=h_{flame}$). Simulated results with the unity Lewis number model and mixture averaged diffusion model are shown as lines for the SWQ case with methane/air at $\phi =1$

Using the unity Lewis number model not only brings the quenching distances closer to the experimental results, but also yields better agreement with the measured temperature profiles. Figure 17 shows measured and simulated temperature profiles perpendicular to the cold wall at the point of quenching. With the unity Lewis number model, the results agree better with the experimental data. These results are not expected, since the unity Lewis number model constitutes a less accurate diffusion model compared to the mixture-averaged or multi-component one. In contrast to the HOQ case, where all gradients are normal to the flame front, diffusion in the SWQ case has a tangential component. Therefore, there might be a need for more research to find a better way of computing normal and tangential diffusive fluxes in the presence of steep gradients within the boundary layers and flame stretch (Luo et al. 2020; Zhang et al. 2020) at the cold wall under quenching conditions.

6.4 Wall Temperature

Because the quenching distances are affected by the wall temperature, HOQ simulations have been performed for varying gas and wall temperatures. Figure 18 shows, that the quenching distance decreases almost linearly with the gas and wall temperature (Kosaka et al. 2018; Hasse et al. 2000). These results show that the difference between the quenching distances from the simulation and experiment are not due to an uncertainty in the wall temperature, because even uncertainties as big as 40 K would not explain the factor of 1.8. In contrast, the experimental uncertainties for the wall temperature are $<7.5\,\hbox {K}$ (Kosaka et al. 2018).

Fig. 18

Quenching distances based on the temperature marker for methane flames at $\phi =1$ from the HOQ setup for different wall temperatures

6.5 Conjugate Heat Transfer

In Sect. 6.4, the wall temperature was considered constant in the HOQ setup. In this subsection, the 2D SWQ configuration for methane/air at $\phi =1$ with the mixture-averaged transport model and reaction mechanism by Kee et al. is performed with conjugate heat transfer. The wall is modeled to be stainless steel with a thickness of 2 mm, as used in the experiment. The grid resolution normal to the wall is 20 $\upmu$m. In the experiment, the back-side of the wall is cooled by water. In the simulation, the back-side of the wall is assumed to be fixed at 293 K. Near the quenching point, the wall temperature reaches its maximum value of 330 K, which is an increase of about 37 K. The effect of considering the heat conduction within the wall on the quenching distances, however, is negligible: the quenching distance is slightly reduced from 200 $\upmu$m, when assuming a constant wall temperature of 293 K, to 198 $\upmu$m when considering conjugate heat transfer, when using the temperature marker to compute the quenching distance (Fig. 19).

Fig. 19

Simulation result including conjugate heat transfer for methane/air at $\phi =1$, showing the region near the quenching point. The OH mass fraction field at the top shows the flame in the fluid domain, while the temperature field at the bottom shows the solid domain of the wall. White lines illustrate temperature contours while the black lines show the grid resolution in the solid domain. Material data from Martienssen and Warlimont (2009)

6.6 Surface Reactions

Surface chemistry has been investigated by Strassacker et al. (2018). They found no significant influence of heterogeneous reactions on methane flames at 1 bar. On the basis of the investigations by Strassacker further simulations of 1D HOQ and 2D SWQ were performed taking catalytic wall reactions into account. The results, however, do not show a significant influence on the wall thermo-chemical state for the methane case (not shown here). Even for more complex hydrogenated fuels, in particular dimethyl ether (DME), the influence of these catalytic wall reactions is small and only present for specific species, e.g. $\hbox {CH}_2$O. Similar results have been found by Häber et al. (2017), where surface reactions do not play a significant role in the particle ignition process of methane flames at atmospheric conditions for a wide range of wall materials. Therefore, surface reactions are unlikely to cause the observed discrepancies.

6.7 Transient Effects

One difference between the experimental and numerical setup is, that the simulation assumes a flame that is perfectly in steady-state. In the experimental setup, however, a Helmholtz resonance frequency of $\sim 100\,\hbox {Hz}$ is present (Jainski et al. 2017a), which leads to a fluctuation of the flame tip or quenching point in flow direction. This fluctuation is typically about $\pm 150\,\mu \hbox {m}$ (Jainski et al. 2017b, a) or $\pm 500\,\mu \hbox {m}$ (RMSD) (Häber and Suntz 2018), depending on the setup. Only in extreme cases of very fuel lean ($\phi < 0.76$) or very fuel rich mixtures ($\phi > 1.3$) that fluctuation might be as high as $\pm 1.5\,\hbox {mm}$ (peak-to-peak) (Häber and Suntz 2018). In order to capture the effect in the simulation, the inlet flow is modified to oscillate harmonically with $u_z=u_{z,0}(1+a\sin (2\pi f t))$, where $u_z$ is the inflow velocity and $f=100$ Hz. Two cases are considered: one case, where the amplitude is based on the experimentally measured fluctuation of $a=0.037$ ($u_{z,\mathrm {rms}}=0.07\,\hbox {m/s}$), and another case, where the amplitude is chosen as a much more extreme value of $a=0.2$ or $u_{z,\mathrm {rms}}=0.30\,\hbox {m/s}$.

Because the distance from the flame anchor (rod) to the quenching point is relatively large, the flame oscillates periodically but not harmonically. A snapshot of the flame during the oscillation is shown in Fig. 20, where an instability with a characteristic length scale develops on the flame branch near the cold wall.

Fig. 20

Snapshot of the flame in terms of the temperature field during the oscillation with $a=0.2$. Because of the large distance between the rod and the quenching point, an instability can develop on the flame branch near the cold wall

Fig. 21

Quenching distance based on the temperature marker for the oscillating 2D methane-air flame at $\phi =1$ using the Kee reaction mechanism over time. The black dahsed line shows the quenching distance from the experiment, the mean quenching distance from the instantaneous temperature data $\overline{d(t)}$, and the quenching distance when applying the temperature marker to the mean temperature field $d({\bar{t}})$ from the two cases with $u_{\mathrm {rms}}=0.30\,\hbox {m/s}$ and $u_{\mathrm {rms}}=0.07\,\hbox {m/s}$

Figure 21 shows the instantaneous quenching distances (solid lines) based on the temperature marker during five oscillation periods. Although the quenching distance $d_q(t)$ is affected by the transient flow, it oscillates by less than $\pm 0.05\,\hbox {mm}$. The oscillation amplitude of the flame perpendicular to the wall is almost the same for both cases. Therefore, even large oscillation amplitudes at the inlet likely cannot explain the deviation of quenching distance from the experiment. Please note that the experimental quenching distance in Fig. 21 is obtained for instantaneous snapshots of OH-LIF, not for time averaged measurements. On average, the quenching distance based on the temperature marker $\overline{d_q(t)}\approx 0.21\,\hbox {mm}$ is slightly higher than in the steady-state case, but again much lower than the experimental value of 0.37 mm (compare Fig. 7). However, if the quenching distances are determined not from the instantaneous temperature fields but from the mean temperature field, the apparent quenching distance $d_q({\bar{t}})$ is significantly higher.

The reason for this is not the oscillation of the quenching distance itself, but rather the oscillation of the flame height, which smears out the temperature and species profile in the temporal average. Because the oscillation of the flame length has a much higher amplitude for $u_{\mathrm {rms}}=0.3\,\hbox {m/s}$ compared to 0.07 m/s, the mean temperature field is much more smeared out for $u_{\mathrm {rms}}=0.3\,\hbox {m/s}$. This leads to higher apparent quenching distances, and in the case of $u_{\mathrm {rms}}=0.3$ even higher than the experimental value.

Therefore, if the experimental measurements capture a time-averaged view of the flame, the resulting quenching distance might be too high. However, the oscillation amplitude of the inlet velocity ($a=20\,\%$) or of the flame height ($h\ \pm 50\,\hbox {mm}$) in the simulations is many times greater than in the experiment. The time-averaged quenching distance based on oscillation amplitudes closer to the ones seen in the experiment is therefore much lower as shown in Fig. 21.

The quenching distances reported by Häber and Suntz (2018) based on chemiluminescence measurements are indeed averaged over a rather long exposure time (up to 100 ms) to facilitate a telecentric imaging with an exceptionally large depth of field necessary to image a 2D projection of the flame. So we might expect the reported quenching distances for $\hbox {OH}^*$ and $\hbox {CH}^*$ to be a little higher than the instantaneous values. But that is not the case for the OH-LIF data (Jainski et al. 2017b) and CARS temperature profiles (Kosaka et al. 2018; Jainski et al. 2017b). Although the temperature determination via CARS is a single-point measurement, an OH-LIF image was simultaneously recorded with each point in order to determine the position of the acquisition point relative to the flame front (internal reference system). That is, the fluctuation of the flame height has implicitly already been taken into account in the OH-LIF and CARS data. Thus, the good relative agreement of the experimental and simulated quenching distances in Fig. 7 makes it unlikely that (a) the $\hbox {OH}^*$ and $\hbox {CH}^*$ quenching distances are largely overestimated and (b) that the oscillation of flame height and quenching distance is the sole cause of the observed deviation of the absolute values between experiment and simulation. Much higher oscillation amplitudes than what is observed in the experimental setup would be required to achieve quenching distances based on the averaged temperature field that can explain the difference between experiment and simulation. Therefore, the Helmholtz resonance frequency in the experimental setup or transient effects in general cannot explain this difference.

7 Conclusion

Detailed numerical simulations of an experimentally investigated side-wall quenching setup have been performed. The simulations are able to fully resolve the flame structure as well as the flow field and boundary conditions with a resolution of $10\,\mu \hbox {m}$. A systematic parameter study has been conducted to reveal the sensitivity of a large variety of influencing factors on quenching distances in the presence of detailed diffusion and chemistry.

2D simulations show that quenching distances from different markers based on OH, OH*, CH* and temperature yield the same trends as the experiments for methane and propane as well as all tested equivalence ratios. In order to achieve quantitative agreement, the quenching distances from the simulation have to be increased by a constant factor. It is interesting to note that this constant factor is the same for methane and propane, for all equivalence ratios and all different markers used to define the quenching distance. Wall heat fluxes at the cold wall are also consistent and show good agreement with measurements if they are reduced by the same constant factor.

While using the simple unity Lewis number diffusion model yields quenching distances that are closer to the experimental results in both the OpenFOAM and FASTEST codes, detailed diffusion models lead to significantly lower quenching distances. The simple unity Lewis number diffusion model also yields better agreement with measured temperature profiles near the cold wall. This might suggest that the current formulation of diffusion coefficients in detailed diffusion models is not suitable to compute accurate normal and tangential diffusive fluxes in regions of large gradients in boundary layers under quenching conditions. Apart from the diffusion model, the sensitivity of the quenching distances to a large number of different parameters has been investigated in the presence of detailed diffusion for the SWQ setup. The inlet velocity affects the flame length and general velocity field but only plays a minor role on quenching distances. An increase of inlet velocity by 20% leads to quenching distances changing by less than 5%. Performing the simulation in 3D instead of 2D yields velocity fields that are closer to the measured values but does not affect the quenching distances. The dependence of quenching distances on different reaction mechanisms was investigated numerically using one-dimensional head-on quenching setups with 20 different reaction mechanisms including detailed, skeletal and reduced mechanisms (a new reduced mechanism based on the CRECK model is included in the supplementary material) which show negligible influence on quenching distances. Different detailed diffusion models also do not affect the quenching distances. Letting the flame oscillate with a fixed frequency leads to increased quenching distances, both on average and based on the averaged temperature field, but the velocity oscillation amplitudes required for reaching the measured quenching distances are too high to explain the difference. Radiation effects as well as the effect of heat conduction within the wall are negligible.

The aforementioned factors were shown to not be the reason for the systematic difference in the quenching distances (by a constant factor) from the experiment, which are obtained by three different measurement techniques and separately by two research groups, and the simulations, which are obtained by two different CFD codes (OpenFOAM and FASTEST). The results, however, allow to rule out a large range of factors as cause for the difference. The unresolved discrepancy suggests that the current simulation methods and models may not yet be sufficient for the small-scale phenomena near the wall.