Simulation of the Self-Ignition of a Cold Premixed Ethylene-Air Jet in Hot Vitiated Crossflow

Abstract

The aim of this paper is to analyze the self-ignition of a jet flame in hot vitiated cross flow using Large Eddy Simulation with analytically reduced chemistry. A rich premixed ethylene-air mixture ($\phi = 1.2$) at 300 K is injected into a hot vitiated crossflow at 1500 K. The simulated reacting flow steady-state was validated against experiments in previous publications and the focus of the present work is the transient self-ignition of the jet. It is shown that spontaneous ignition occurs at very lean mixture fractions in the form of reacting patches in the windward jet mixing layer. These patches grow, laterally wrap the jet and extend into the recirculation region. Chemical explosive mode analysis is performed to identify the chemically active regions that are precursors of the patches undergoing spontaneous ignition. It is shown that the self-ignition occurs at very lean fuel concentrations regions, which are leaner and hotter than the most reactive mixture fraction of the jet and crossflow. This is explained by the fact that the scalar dissipation is significantly lower in these very lean regions. Ultimately, the peak heat release moves toward the richer regions and an autoignition cascade governs the steady state flame anchoring.

1 Introduction

The jet in crossflow (JICF) configuration has been widely studied over the past 80 years, see Margason (1993), due to its significant technological interest. This configuration generates a complex flow field allowing for fast mixing rates of 2 streams. This is useful in lean combustion technology, for instance, where a compact mixing section upfront of the flame is highly desirable. The JICF configuration has been extensively used in aeronautic and power applications (Karim et al. 2017; Pennell et al. 2017), examples include fuel and dilution air injection at staged combustors and effusion holes for turbine blade cooling (Marr et al. 2012; Roa et al. 2012). Most of the research in the literature focuses on non-reacting JICF, see the reviews from Karagozian (2010), and Mahesh (2013). Less is known about reactive JICF (RJICF), where experimental studies have been mainly conducted for non-premixed configurations with jets being composed of pure fuel or N$_2$-diluted fuel, e.g. Sidey and Mastorakos (2015), and Steinberg et al. (2013). Fleck et al. (2013) showed ignition kernels that do not always anchor the flame. Sullivan et al. (2014) proposed autoignition as flame stabilization mechanism after measuring ignition location of the same order of those obtained from 0-D reactor simulations. In contrast, only few studies on jet configurations with fuel premixed with oxidizer are available, e.g. Schmitt et al. (2013), Kolb et al. (2016), and Pinchak et al. (2019). Pinchak et al. (2019) investigated experimentally a RJIJCF configuration of premixed ethylane-air. They determined that for crossflow temperatures of 900 K, the flame stabilization mode was controlled by propagation rather than autoignition. The problem of flame ignition using Large Eddy Simulations (LES) has been investigated in several papers, e.g. forced ignition (Lacaze et al. 2009; Triantafyllidis et al. 2009), or self-ignition in coflow gaseous (Han et al. 2016; Cao et al. 2005; Gordon et al. 2007) and spray flames (Eyssartier et al. 2013). One can also refer to LES studies of non-premixed, e.g. Weinzierl et al. (2017) used a NOx model to predict emissions; and premixed, e.g Schulz et al. (2019), Schulz and Noiray (2019), RJICF configurations. The problem of ignition has also been studied with direct numerical simulations (DNS) (Lapointe et al. 2015; Krisman et al. 2017). For instance, Lyra et al. (2015) investigated a rich hydrogen RJICF configuration using joint DNS and experiments observing significant differences between the structure and stability mechanism of windward and leeward flames. Kolla et al. (2012) simulated by DNS a RJICF and studied the blowout phenomenon dynamics due to kinematic imbalance between flame propagation speed and flow normal velocity.

Investigating the self-ignition of premixed jets in vitiated crossflow is relevant for modern combustion technologies and is the subject of the present work. In fact, due to increasing renewable energy sources which provide intermittent energy supply, a higher flexibility in power generation systems is demanded. Such demand has to be met under the constrain of stricter pollutant emissions regulation. Hence, more advanced technology is required for more operationally and fuel flexible power generation systems. To meet these needs, industrial research and development focuses on new staged combustion concepts, some of them involving premixed fuel-air jets in RJICF configurations. These technology developments raise fundamental questions on the nature of the combustion process in these configurations. In their recent experimental work, Wagner et al. (2015, 2017a, b) used $\text {OH}$ and $\text {CH}_2\text {O}$ planar laser induced fluorescence (PLIF) simultaneously with high-speed particle image velocimetry (PIV) to investigate a premixed $\text {C}_2\text {H}_4$-Air RJICF. They investigated the windward and the leeward regions of the flame intersecting in the central plane, and they showed that the flame is lifted on the windward side of the jet, and is anchored at the jet root on the leeward side. They came to the conclusion that autoignition due to mixing between jet and crossflow is likely to play an important role in flame stabilization. However autoignition regions are hard to identify by experimental means, as autoignition takes place at the shortest autoignition times $\tau _{\text {AI}}$, i.e. at the most reactive mixture fraction (Mastorakos et al. 1997) where the mixture tends to be very lean (Schulz et al. 2017), scalar dissipation rates are low, and fuel concentrations are very challenging to detect experimentally. To address this issue, a numerical study from Schulz et al. (2019), Schulz and Noiray (2019) simulated, with LES, exactly the same test case to investigate more thoroughly the flame stabilization mechanism. They used analytically reduced chemistry (ARC) and chemical explosive mode analysis (CEMA) to capture the non-trivial autoignition chemistry. This study corroborated that autoignition drives the flame stabilization at the windward flame side in the form of an autoignition-cascade. This phenomenon takes place along the windward mixing layer of the jet and starts at its root: the heat release peak shifts progressively from the leaner outer side to the richer inner side of the mixing layer. This peak grows in intensity along the jet trajectory until an apparently lifted flame becomes visible. This cascade is associated with the convective and diffusive transfer of the heat released by auto-igniting fluid parcels. In the downstream part of the windward mixing layer, the flame is not located at the most reactive mixture fractions which would be deduced from a chemically frozen pure mixing simulation.

The studies mentioned previously focus on the analysis of flame stabilization for a fully established flame that has reached a steady state, i.e. they focus on the phenomenon that sustains an existing flame in the jet. The autoignition-cascade explains flame sustainability, however no conclusions can be drawn about the establishment of such flame. There is not abundant research in the literature about the characteristics of the ignition process and the flame appearance, i.e. the process that leads to a transition between a non-reactive JICF to a RJICF (the transient ignition process). This numerical study aims to address this knowledge gap by building up on the work of Wagner et al. (2015, 2017a, b), followed by Schulz et al. (2019), Schulz and Noiray (2019). The main goal is to study the evolution of the flow leading to the appearance of the flame, using a numerical LES approach with analytically reduced chemistry and chemical explosive mode analysis, and to link these observations with the conclusions reached in previous studies about flame stabilization.

2 Numerical Method

2.1 RJICF Configuration

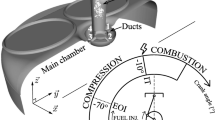
The geometry employed in this study, see Fig. 1, is based on the experimental setup from Wagner et al. (2015, 2017a, b). It consists of a rectangular channel with an overall length of 190 mm and a cross section of 76.2 mm width and 38.1 mm height. The jet inlet is centered at the bottom wall, at a distance of 110 mm from the crossflow inlet. The jet outlet has a diameter of $d=9.53$ mm and a total pipe length of $\sim 2d$ was chosen to ensure jet trajectory independence from pipe length, see Schulz et al. (2019), whereas in the experimental setup this length amounts to $\sim 33d$.

Experiments in Wagner et al. (2015, 2017a, b) were performed at atmospheric pressure. The crossflow contained the burned products of a $\text {C}_3\text {H}_8$-Air mixture at equivalence ratio $\phi _{\text {cf}}=0.87$, temperature $T_{\text {cf}}=1500$ K measured at the jet location with uncertainties of $\pm 15$ K and bulk velocity of $u_{\text {cf}}=7.6$ m/s. To compute the crossflow composition a 1-D freely-propagating flame simulation was performed using Cantera Goodwin et al. (2009) with the detailed AramcoMech2.0 mechanism. Intermediate species were neglected, the effect was demonstrated to be of the same order of magnitude as the temperature uncertainties, see Schulz et al. (2019). The jet consisted of a cold mixture of $\text {C}_2\text {H}_4$-Air at $\phi _{\text {j}}=1.2$, temperature of $T_{\text {j}} = 300$ K and velocity $u_{\text {j}}=9.96$ m/s, leading to a jet-to-crossflow momentum ratio

$$\begin{aligned} J = \frac{\rho _{\text {j}} u_{\text {j}}^2}{\rho _{\text {cf}} u_{\text {cf}}^2}=8.7, \end{aligned}$$

(1)

where $\rho _{\text {j}}$, $u_{\text {j}}$ and $\rho _{\text {cf}}$, $u_{\text {cf}}$ stand for density and bulk velocity of jet and crossflow respectively.

Fig. 1

Computational mesh and sketch of the RJICF configuration. Refinement of $\Delta x_{\text {min}} = 0.2$ mm applied to region from windward side to recirculation zone

2.2 Large Eddy Simulations Model

Large eddy simulations (LES) were performed using the software AVBP (Gicquel et al. 2011), an explicit cell-vortex code for CFD analysis of unsteady turbulent reacting flows. The Standard Smagorinsky model was used for the sub-grid Reynolds stress tensor, with a Smagorinsky coefficient of 0.18. The two-step Taylor-Galerkin convection scheme (TTGC) was used, giving third-order accuracy in space and time. A time step of $\sim 5\times 10^{-8}$ s was reached based on the acoustic CFL condition. Navier-Stokes characteristic boundary conditions (NSCBC) (Poinsot and Lelef 1992) were used at inlets and outlet. The crossflow inlet was set to a flat velocity profile with no turbulence, whereas the jet inlet was set to a turbulent velocity profile with $u'/u_{\text {j}}=0.1$. The boundary conditions on the jet pipe walls were set to adiabatic with a fixed temperature of 300 K, albeit on the domain walls heat-loss $\dot{q}=(T_{\text {w}}-T_{\infty })/R_{\text {w}}$ was used. A reference $T_{\infty }=300$ K and thermal resistance $R_{\text {w}}=0.02$ K/W result in a wall temperature of $T_{\text {w}}=700$ K. A wall velocity/temperature coupled model based on Van Driest transformation was used, since the mesh resolution is not sufficient to resolve the boundary layers. The initial solution was set to a fully developed non-reactive JICF configuration flowfield where the ethylene was removed from the jet mixture. The reactive mixture entered the domain through the jet inlet pipe at the simulation starting point so that the full transition from non-reactive JICF to reactive JICF configurations could be studied.

Four different grid sizes were tested in Schulz et al. (2019) ranging from $\Delta x=0.2-1.0$ mm to test mesh convergence. It was shown that a cell size of $\Delta x=0.2$ mm ensures grid independence in terms of jet trajectory and velocity. The current mesh, Fig. 1, is based on the mesh from Schulz et al. (2019) which was validated using Pope’s criterion (Pope 2000) that at least $80\%$ of the turbulent kinetic energy should be resolved. A further refinement of this mesh is done in this study, with $\Delta x=0.2$ mm covering not only the windward flame region, but the whole volume from the flame windward side to the recirculation region downstream from the jet ($\sim 35$ mm total length), i.e. the region where the flame sits and the transient ignition process develops, see Fig. 1. This unstructured computational mesh contains 23.7 million tetrahedral cells and a total amount of 45,600 CPU-hours were necessary to simulate 10 ms of flow-through time.

The Dynamic Thickened Flame (DTF) model is used, applying a dynamic thickening on the flame front to a minimum of 4.5 cells while keeping a constant laminar flame speed $s_{\text {L}} = 0.75$ m/s. The model from Colin et al. (2000) was used to simulate the wrinkling of the flame front on the sub-grid scale. In Schulz et al. (2017) it has been demonstrated that the thickening factor has a delaying effect over the auto-ignition time $\tau _{\text {AI}}$. It is demonstrated in Schulz and Noiray (2019) that the DTF model does not delay autoignition for cell sizes of $\Delta x=0.2$ mm, i.e. the characteristic mesh size used on the flame development region.

2.3 Analytically Reduced Chemistry Scheme

LES was performed using the analytically reduced chemistry (ARC) scheme derived by Felden et al. (2018) from the detailed (Narayanaswamy et al. 2014) kinetic scheme for ethylene-air combustion. The detailed scheme comprises 164 transported species whereas the ARC contains 18. The reduction tool YARC was used (Pepiot-Desjardins and Pitsch 2008a, b), performing a 2-step reduction. Firstly, species and reactions are reduced resulting in a 29 species scheme. Next, a quasi steady state approximation (QSS) is applied to 11 of these species, leaving $\hbox {N}_2$, H, $\hbox {H}_2$, O, OH, $\hbox {O}_2$, $\hbox {H}_2\hbox {O}_2$, $\hbox {H}_2\hbox {O}$, CO, $\hbox {CH}_3$, $\hbox {CH}_2\hbox {O}$, $\hbox {CO}_2$, $\hbox {CH}_4$, $\hbox {C}_2\hbox {H}_2$, $\hbox {C}_2\hbox {H}_4$, $\hbox {C}_2\hbox {H}_6$ and $\hbox {CH}_2\hbox {CO}$ as the final transported species. A validation of this ARC scheme is available in Schulz et al. (2019), Schulz and Noiray (2019).

2.4 Chemical Explosive Mode Analysis

CEMA is a diagnostic tool developed by Lu et al. (2010) to identify local ignition and extinction behavior of turbulent flames (Luo et al. 2012; Shan et al. 2012). It is based on concepts from computational single perturbation (CSP) theory (Lam 1993) and it characterizes locally the combustion modes at play in reactive flows. Reactive flows are described in the Eulerian coordinate system by a set of PDEs of the form

$$\begin{aligned} \frac{D \mathbf{y} }{Dt} = \mathbf{g} (\mathbf{y} ) \equiv \varvec{\omega }(\mathbf{y} ) + \mathbf{s} (\mathbf{y} ), \end{aligned}$$

(2)

where D/Dt is the material derivative, and $\mathbf{y}$ is the vector of local thermo-chemical state variables, such as temperature and species concentrations. The source term of the equation $\mathbf{g} (\mathbf{y} )$, can be decomposed into chemical source terms $\varvec{\omega } (\mathbf{y} )$, and non-chemical source terms $\mathbf{s} (\mathbf{y} )$, that include all diffusive and mixing effects.

The CEMA method is based on the eigenvalue analysis of the chemical source term of the governing equation (2). The local chemical information is completely encoded in the Jacobian matrix, $\mathbf{J} _{\omega }$, of the chemical source term $\varvec{\omega } (\mathbf{y} )$. Hence, the eigenmodes of this matrix define the chemical modes of the system. The transport equation of such source term reads,

$$\begin{aligned} \frac{D \varvec{\omega }(\mathbf{y} )}{Dt} = \mathbf{J} _{\omega }\frac{D \mathbf{y} }{Dt} = \mathbf{J} _{\omega }(\varvec{\omega } + \mathbf{s} ), \quad \varvec{J}_{\omega } = \frac{\delta \varvec{\omega }}{\delta \mathbf{y} }. \end{aligned}$$

(3)

The eigendecomposition of $\varvec{J}_{\omega }$ yields

$$\begin{aligned} \lambda _e = \mathbf{b} _e \cdot \mathbf{J} _{\omega } \cdot \mathbf{a} _e, \end{aligned}$$

where $\lambda _e$ are the eigenvalues, and $\mathbf{b} _e$ and $\mathbf{a} _e$ are the left and right eigenvectors respectively. In general, $\lambda _e$ contains complex eigenvalues that indicate the presence of oscillatory modes, where the real part corresponds to the inverse of time scales of the explosion, and the imaginary part corresponds to the oscillation frequency. CEMA only takes into account the real parts of $\lambda _e$. The chemical explosive mode (CEM) is defined locally as the eigenmode of the Jacobian $\varvec{J}_{\omega }$ exhibiting the eigenvalue $\lambda _e$ with the largest positive real part (Lu et al. 2010; Luo et al. 2012).

The existence of CEM implies explosive nature of the local mixture, i.e. its propensity to ignite under isolated conditions. If several eigenmodes have associated positive eigenvalues, the CEM is defined at each gridpoint as the mode associated to the highest local positive eigenvalue, i.e. ignition is controlled by the fastest CEM. A recent extension of the CEMA analysis incorporates the local contribution of the diffusion source terms (Xu et al. 2019), and it is therefore important to stress that these terms are not accounted for in the present work.

Fig. 2

Sequence showing sudden addition of $\hbox {C}_2\hbox {H}_4$ to the air stream forming the JICF, from left to right $t=0, 1, 2, 3$ ms. Green: isosurface $Y_{\text {O}_2}=0.1$. Blue: isosurface $Y_{\text {C}_2\text {H}_4}=2\times 10^{-3}$

3 Transient Ignition

Figure 2 shows a 3D evolution of the flowfield from the initial conditions at $t=0$ ms (left) up to $t=3$ ms of flow-through time (right). Firstly, the non-reactive JICF configuration can be observed as an isosurface of oxygen mass fraction $Y_{\text {O}_2}=0.1$ where the jet only contains air and the fuel has not yet been released. Next, the reactive mixture ($\text {C}_2\text {H}_4$-Air at $\phi = 1.2$) is introduced in the domain through the jet pipe. A blue isosurface of ethylene mass fraction $Y_{\text {C}_2\text {H}_4}=2\times 10^{-3}$ that ascends through the jet pipe can bee seen. The aim of Fig. 2 is to show the dynamic transition from non-reactive to reactive JICF configuration while maintaining the jet flow structure. In the next sections the presence of the non-reactive mixture will not be shown in the figures. It is emphasized that the jet structure does not start with the release of reactive mixture, but rather that it is present in the flowfield before as a non-reactive JICF. As previously mentioned, the aim is to study the transient ignition process of such configuration.

Figure 3 shows the average heat release rate $\dot{q}_{\text {av}}$ of the overall domain in time. During approximately the first 1.5 ms of simulation, the reactive mixture is fully confined inside the jet pipe and the heat release rate remains low as no reaction has yet occurred. At around $t\sim 1.5$ ms the reactive mixture enters the crossflow $(T_{\text {cf}} = 1500 \hbox {K})$. Up to $t\sim 3\,\hbox {ms}$ the reactive mixture $(T_{\text {j}} = 300\,\hbox {K})$ heats up due to pure mixing effects, immediately before the reaction starts. From $t\sim 3$ to $t\sim 7\,\hbox {ms}\,\dot{q}_{\text {av}}$ grows exponentially due to chemical reactions until reaching a peak at $t\sim 7.2\,\hbox {ms}$ and from there it starts decreasing until convergence with the steady state is reached and the RJICF stabilizes.

Two sequences of the domain development can be distinguished and are further analyzed. Firstly, the heat release outbreak sequence (circle stamps in Fig. 3), showing the first evidence of appearance of strong chemical reactions in the flow. It is concentrated at $t= 3\,\hbox {ms}$ and lasts approximately $\sim 1.5\,\hbox {ms}$. Secondly, the transient ignition sequence of the flame (triangle stamps in Fig. 3), spanning from the heat release outbreak phenomenon $(t= 3\,\hbox {ms})$ up to the stabilization of the flame $(t\sim 10\,ms)$.

Fig. 3

Evolution in time of $\dot{q}_{\text {av}}$ (left) and zoom at $t=3\,\hbox {ms}$ (right). Triangle stamps (a, b, c, d, e, f) refer to the transient ignition sequence. Circle stamps ($t_0=2.8\,\hbox {ms}$, $t_0+\Delta t$, $t_0+3\Delta t$, $t_0+7\Delta t$, $t_0+11\Delta t$, $t_0+15\Delta t$ with $\Delta t=0.1\,\hbox {ms}$) refer to the heat release outbreak sequence

Fig. 4

Instantaneous 3D contours of the RJICF heat release outbreak process, $t_0 = 2.8\,\hbox {ms}$ and $\Delta t = 0.1\,\hbox {ms}$. From top to bottom: front, back and lateral views of the jet. Flame visualized by heat release rate $\dot{q} = 2\times 10^6\,[\hbox {W}/\text {m}^3]$ (yellow) and jet visualized by ethylene mass fraction $Y_{\text {C}_2\text {H}_4}=2 \times 10^{-3}$ (colored by T) isosurfaces. See Fig. 3 for time instants

3.1 Heat Release Outbreak Sequence

Before the flame reaches the stable regime observed in Wagner et al. (2015, 2017a, b), Schulz et al. (2019), Schulz and Noiray (2019) the flow undergoes an ignition process composed of several phases. This section refers to the appearance of the first high $\dot{q}$ regions in the flow (they will be referred to as reaction kernels in the following paragraphs). These regions indicate that a strong exothermic reaction starts developing, a necessary previous step for ignition and flame appearance. Figure 4 shows instantaneous 3D jet contours at instants covering a time span of $\sim 1.5\,\hbox {ms}$ that starts at $t_0=2.8\,\hbox {ms}$ with the first appearance of a high-heat-release-rate region, i.e. the very first evidence detected of strong exothermic reaction. Jet contours are generated as isosurfaces of $Y_{\text {C}_2\text {H}_4}= 2 \times 10^{-3}$ (equivalent to a mixture fraction between jet and crossflow equal to $Z \approx 0.03$ where 1 is pure jet and 0 is pure crossflow) colored by temperature. Heat release rate is visualized with a plain yellow isosurface of $\dot{q} = 2\times 10^6 [\hbox {W}/\text {m}^3]$. This value has been chosen because the first high-$\dot{q}$ region that appears spontaneously and abruptly in the flowfield is of the same order, hence establishing a lower limit of heat release rate to consider the exothermic reaction.

In Fig. 4, at $t_0$ the first high-$\dot{q}$ kernels appear at the jet windward side location where the temperature of the reactive mixture has risen to values near the crossflow temperature, i.e. locations where mixing was strongest. High temperature values and very lean fuel concentration are the conditions for the lowest autoignition times (Schulz et al. 2019); this and the fact that the reaction kernel outbreaks spontaneously demonstrate that the triggering phenomenon is autoignition. At $t_0 + \Delta t$ new kernels appear uncorrelated with each other as the autoignition conditions are met, i.e. autoignition times at those locations fall below residence times. At the same time, due to the heat released and the associated increment in temperature, the reaction kernel from $t_0$ expands to the surroundings, triggering a chain reaction that grows along the windward side of the jet. In the following instants, these reaction kernels merge together and form an homogeneous high-$\dot{q}$ surface. This chain reaction has a similar behavior to the autoignition-cascade first introduced by Schulz et al. (2019), Schulz and Noiray (2019), however no flame is yet established in these early instants as the $\dot{q}$ values are well below the flame values presented in Schulz et al. (2019). At $t_0 + 7\Delta t$ the reaction surface reaches the lateral borders of the jet and starts wrapping up around it. Note that no reaction kernel has formed in the leeward side of the jet because the autoignition conditions are not met there. The temperature of the recirculation region is lower compared to the jet windward side ($\sim 500\,\hbox {K}$ difference) due mainly to recirculation of cold reactants from the jet, see Fig. 4. Hence, no autoignition can be established. At $t_0 + 15\Delta t$ the wrapping process is completed and the high-$\dot{q}$ surface is closed at the recirculation region. This suggests that from this instant the temperature in the recirculation region will increase, affecting the jet leeward side.

Fig. 5

Instantaneous contours at center section of the RJICF windward side (red frame). Showing: scalar dissipation rate $\chi$, heat release rate $\dot{q}$, temperature T, maximum shear stress $\tau ^{ss}_{max}$, and velocity magnitude $|\varvec{u}|$. Instantaneous snapshots at $t=t_0 + \Delta t$, $t_0+ 7\Delta t$, $t_0+ 15\Delta t$ where $t_0 = 2.8$ ms and $\Delta t = 0.1\,\hbox {ms}$. White isocontour shows ethylene mass fraction $Y_{\text {C}_2\text {H}_4}=5 \times 10^{-3}$, corresponding to the most reactive mixture fraction $Z_{mr}=0.07$. See Fig. 3 for time instants

A more detailed analysis of this heat release outbreak process is now performed by focusing on the reacting flow dynamics at the root of the windward shear layer of the jet. Figure 5 shows the following variables in the central plane at 3 selected instants ($t_0 + \Delta t$, $t_0 + 7\Delta t$ and $t_0 + 15\Delta t$): the scalar dissipation rate $\chi = 2D|\nabla Z|^2$ where D is the mass diffusivity, the heat release rate $\dot{q}$, the temperature T, the maximum shear stress $\tau ^{ss}_{max}$, and the velocity magnitude $|\varvec{u}|=(u_x^2+u_y^2+u_z^2)^{0.5}$. In this figure, the white isocontour represents the most reactive mixture fraction $Z_{mr}=0.07$ which corresponds to $Y_{\text {C}_2\text {H}_4}\approx 0.005$ and which was computed using Cantera Goodwin et al. (2009) by Schulz et al. (2019) for a 0-D reactor initially composed of a mixture between the hot vitiated air and the cold ethylene-air mixture. The $\dot{q}$ plot shows that, contrary to what would be expected, the first reaction kernels do not appear at the most reactive mixture region (white iso-line), but in regions with smaller fuel concentrations at $t_0 + \Delta t$, i.e. regions located closer to the crossflow with respect to the white iso-line. The underlying reason is that autoignition is a complex phenomenon very sensitive not only to mixture composition and temperature values, but also to the effects of turbulence, shear stresses and scalar dissipation rates. Arndt et al. (2013) showed that high values of strain rates can significantly alter the onset location of autoignition flames, and that this sensitivity increases at lower values of temperature. Indeed, the most reactive mixture region in Fig. 5 presents high scalar dissipation and shear stress, and relatively low temperatures $(\sim 600K)$. This, following the conclusions from Arndt et al. (2013), might increase autoignition delay times and prevent ignition there.

Firstly, Fig. 5 shows that the heat release outbreak occurs in regions where $\chi$ is low and temperature high. This is fully in line with the findings from Mastorakos et al. (1997) who investigated autoignition in inhomogeneous mixtures showing that it occurs in regions where scalar dissipation rates is low. Indeed, regions with higher $\chi$ have larger heat losses, which delay or prevent autoignition. At $t_0 + 7\Delta t$ the reaction kernel grows and expands through the very lean and low-$\chi$ region. At $t_0 + 15\Delta t$ the heat release rate is sufficiently high to overcome the heat losses associated with the scalar dissipation rate. Consequently, the autoignition kernel expands towards richer regions with higher values of $\chi$ due to the autoignition-cascade described in Schulz et al. (2019). Secondly, the shear stress also has a strong effect on the ignition location. At similar conditions as the one treated in this paper, Wagner et al. (2015, 2017a) experimentally observed a high correlation between strain rate distributions of different flames at the root of the windward flame, suggesting that strain rates have strong effect on the flame stabilization location. They showed that the windward flame root anchors in regions of optimum mean strain rates, that are located right at the edge of the shear layer near the crossflow. There, the strain rates are high but not as large as in the shear layer center. In fact, too high strain rates can inhibit autoignition because of too intense mixing and too short residence times; furthermore, too low strain rates also delay autoignition as mixing between the two streams is weakened. This means that there exists an optimal combination of local strain rate, temperature and mixture composition for which ignition will be promoted. Considering that strain rate and shear stress are proportional, with the dynamic viscosity $\mu$ as proportionality factor, our observations regarding the location of $\dot{q}$ with respect to $\tau ^{ss}_{max}$ during the early stage of the flame ignition in Fig. 5 are in line with the conclusions of Wagner et al. (2015) that were drawn from data recorded for a well established flame. The first reaction kernel at $t_0 + \Delta t$ is located in the outer edge of the shear layer where shear stresses are sufficiently high to ensure certain level of mixing and temperature increase, but not so high as to prevent or delay the ignition. Shortly after, the reaction region expands along the shear layer outer edge, where shear stresses are moderately high, see $t_0 + 7\Delta t$ and $t_0 + 15\Delta t$.

Fig. 6

Probability density functions of the strain rate $S_{xy}$ for the transient ignition sequence $t=$ 5, 7, 7.3, 7.8 and 10 ms (b, c, d, e and f respectively, corresponding to the time stamps of Fig. 3). Data was extracted from the flame region (where $\dot{q}>10^8\,\hbox {W}/\hbox {m}^3$) enclosed in a cuboid $(8.5\times 17.5\times 6\,\hbox {mm}^3)$ located at the jet windward side. In (f), the experimental results from Wagner et al. (2015) (red line) and the numerical results from Schulz et al. (2019) (black line), which were both extracted in the center plane of the windward flame, are also shown

The previous observations were made for the heat release outbreak sequence where the flame is not fully developed. Still, it was shown that they are in line with the conclusions of Wagner et al. (2015, 2017a) that apply for a fully stabilized flame. There, the windward flame edge stabilized at the jet root in the outer edge of the shear layer. To further corroborate and extend these conclusions, Fig. 6 shows the probability density function of the strain rate $S_{xy}=1/2(\delta u_x/\delta y + \delta u_y/\delta x)$ for the transient ignition sequence until flame stabilization occurs, and compares it to the results obtained by Wagner et al. (2015) and Schulz et al. (2019). The data for all instants was extracted from the high heat release region (where $\dot{q}>10^8\,\hbox {W}/\hbox {m}^3$) enclosed in a cuboid $(8.5\times 17.5\times 6\,\hbox {mm}^3)$ located at the root of the jet windward side. Note that instant (a) of the sequence ($t=3$ ms, see Fig. 3) is not included in the figure as it does not contain a high heat release region. The results show that for all the instants of the ignition process, the flame stabilizes in regions with a characteristic predominant strain rate value that remains rather constant $(\sim 1500\,\hbox {s}^{-1})$ during the whole ignition process. The magnitude of this value represents the optimal strain rate for flame stabilization, sufficiently high to ensure proper mixing between the two streams, but not too high as to prevent or delay ignition. In Fig. 6f, for which $t=10\,\hbox {ms}$, one has the fully developed jet flame, and a good agreement with the experiments (Wagner et al. 2015) and previous LES simulations (Schulz et al. 2019). It is worth mentioning that the histogram of the present work is made from data extracted in the cuboid centered on the central plane of the jet, while data considered in Wagner et al. (2015) and Schulz et al. (2019) were taken from the central plane only. It shows that the optimum strain rate does not significantly change $\pm 3\,\hbox {mm}$ from the central plane.

Fig. 7

Joint probability density functions of scalar dissipation rate $\chi$ vs maximum shear stress $\tau ^{ss}_{max}$ for the transient ignition sequence $t= 5$ (b), 7 (c), 7.3 (d), 7.8 (e), 10 (f) ms . See Fig. 3 for time instants. Data was extracted from the flame region (where $\dot{q}>10^8\,\hbox {W}/\hbox {m}^3$) enclosed in a 3D domain $(8.5\times 17.5\times 6\,\hbox {mm}^3)$ located at the jet windward side

Similarly, a joint probability density function of scalar dissipation rate $\chi$ vs maximum shear stress $\tau ^{ss}_{max}$ is presented in Fig. 7 for the transient ignition sequence. The data was extracted at the same instants and from the same domain as in Fig. 6. The results show that the region where heat release occurs corresponds to very low values of the scalar dissipation $(\chi \sim 0\,\hbox {s}^{-1})$ and a range of optimum shear stress ($\tau ^{ss}_{max} \sim [1000,4000]$ Pa), corroborating the findings of Fig. 5 (note the logarithmic scale of the colormap for the joint probability density function). Furthermore, it is shown here that these values do not significantly change during the ignition process. Note that these conclusions are valid in the base region of the windward side where the flame root anchors, i.e. valid at the flame stabilization location. It will be shown in the next section that, in the downstream direction of the jet, the fully developed flame crosses the shear layer and entrains the jet bulk flow.

3.2 Transient Ignition Sequence

Figure 8 shows 2D maps obtained from sections along the jet centerline of 3 different magnitudes: heat release rate $\dot{q}$, temperature T and ethylene mass fraction $Y_{\text {C}_2\text {H}_4}$. The heat release rate maps show 3 interesting features occurring in the flow field. Namely, heat release outbreak from the windward side, heating of the recirculation region, and ignition process with flame propagation and stabilization. Firstly, the heat release outbreak shown in the previous section is contained in plots a-b. At $t=7\,\hbox {ms}$ (c) the heat release region on the jet windward side extends across the shear layer towards much richer mixtures. There it presents higher $\dot{q}$ values associated with reaction of richer mixtures. Such mixtures comprise values up to $Y_{\text {C}_2\text {H}_4} \approx 0.04$ equivalent to $Z\approx 0.5$ that would not autoignite under pure mixing conditions. $\dot{q}$ reaches values close to $\approx 10^9\,[\hbox {W}/\text {m}^3]$, which can be easily differentiated in the plots. These high values of heat release are of the order of magnitude shown in Schulz et al. (2019) suggesting the appearance of the flame that extends from the jet windward side (lifted) and encloses the reactive jet upper end at $t=7\,\hbox {ms}$ (c). Advancing in time, the flame grows stronger (higher $\dot{q}$), and by $t=10\,\hbox {ms}$ (f) it closes around the jet and stabilizes in the leeward side jet root. Focusing on the plots where the flame is present (c-f) one can see that the temperature plots present a strong gradient of temperatures in the surrounding flame region that reaches values up to 2400 K. Comparing the $Y_{C_2H_4}$ maps against the $\dot{q}$ map, the flame tends to move closer to the jet center in the downstream direction, entering regions of high jet bulk velocity and high fuel mass fractions. The heat release region around the jet is perfectly continuous spanning from the jet root, but kernels/patches of higher $\dot{q}$ magnitude appear in the windward front (but not in the leeward front) due to the wrinkling of the flame. This is a consequence of vortex shedding from the jet pipe (see f).

Secondly, a weaker heat release rate region appears at the recirculation zone (see b) caused by the entrainment of reacting gas from the sides of the jet due to the wrapping process. The reaction is then triggered at the recirculation zone and stabilizes there due to the continuous input of reacting mixture. When the mixture ignites at the jet windward side, the heat release rate in the recirculation region increases as it is highly influenced by the jet front side due to the wrapping behavior. From then, it keeps a rather constant intensity even after the appearance of the flame at the jet leeward side. In the temperature maps the recirculation region (and the jet leeward side) presents 3 different stages, first it is cold when the wrapping process is not yet completed (a–b), second it gets warmer due to the stabilization of the heat release region there (c–e) and finally it reaches high temperatures once the flame leeward front is established (f). Finally, the peak of $\dot{q}_{\text {av}}$ at $t\sim 7.2\,\hbox {ms}$ in Fig. 3 is due to the accumulation of reactive mixture in the flowfield. Since the flame does not develop in the first instant, most of the mixture released to the flow is not burned and accumulates. After ignition the flame grows and reaches the unburned reactants causing the average heat release peak. As these pools of reactants (proportional to the jet volume) are consumed by combustion, $\dot{q}_{\text {av}}$ decreases until stabilization of the flame is reached.

Fig. 8

Instantaneous 2D maps at center section of the RJICF. From top to bottom: heat release rate $\dot{q}$, temperature T and ethylene mass fraction $Y_{\text {C}_2\text {H}_4}$. From left to right: time sequence at $t=3,\,5,\,7,\,7.3,\,7.8,\,10$ ms. Jet visualized by ethylene mass fraction $Y_{\text {C}_2\text {H}_4}=2 \times 10^{-3}$ isocontour (white). See Fig. 3 for time instants

3.3 Chemical Explosive Mode Analysis

The CEMA allows to identify chemically active regions in the flowfield. In the case of a fully established flame (as opposed to a transient igniting flame), the chemically active regions are also characterized by regions of high heat release. On the contrary, in a transient ignition process this might not be the case since the flow should become chemically active as a previous step before having a fully developed exothermic reaction. CEMA is able to detect the chemically active regions even before strong significant levels of heat released are reached. Figure 9 show instantaneous values of the normalized chemical explosive mode (left plot, $\lambda _e$), heat release ratio (center plot, $\dot{q}$), and the fuel mass fraction (right plot, $Y_{\text {C}_2\text {H}_4}$) at the beginning and end of the transient ignition sequence. The blue iso-contour on the $Y_{\text {C}_2\text {H}_4}$ map represents fuel mass fraction found at the most reactive mixture fraction defined by the mixing of the jet and the vitiated cross flow, i.e. $Z_{mr}=0.07$ and $Y_{\text {C}_2\text {H}_4}=5 \times 10^{-3}$ (Schulz et al. 2019). The red iso-contour shows the region with a normalized chemical explosive mode that represents highly reacting zones $(log_{10}(1+|Re(\lambda _e)|) \sim 4)$. Small values of the most explosive modes $(\lambda _e)$ suggest that the mixture is not in equilibrium, but its growth is very small, with time constants $(1/\lambda _e)$ longer than 1 s. On the contrary, for $1/\lambda _e \ll 1$ there is a fast exponential growth of the CEM.

Fig. 9

Instantaneous 2D maps at center section of the RJICF of normalized local chemical explosive mode $\lambda _e$ (left), heat release ratio $\dot{q}$ (center), and ethylene mass fraction $Y_{\text {C}_2\text {H}_4}$ (right). Two time sequences at $t=3$ (top) and 10 ms (bottom) are shown. Blue isocontour in $Y_{\text {C}_2\text {H}_4}$ map shows ethylene mass fraction $Y_{\text {C}_2\text {H}_4}=5 \times 10^{-3}$, corresponding to the most reactive mixture fraction $Z_{mr}=0.07$. Red isocontour shows ignition region with $log_{10}(1+|Re(\lambda _e)|)\sim 4$. See Fig. 3 for time instants

In the first instants $(t=3\,\hbox {ms})$, the fuel emerges from the jet exit and starts mixing with the hot crossflow products near the shear layer region. This leads to increasing temperatures of the mixture at small fuel concentrations due to pure mixing effects while heat release rate is still low. This can be observed in Fig. 5 in detail. As a result, these regions at the jet root become chemically active and are detected in the CEM map where one can observe two branches at windward and leeward sides. On the contrary, only a small patch in the windward side is visible in the heat release ratio map. The red iso-contour shows that in the initial instants the reaction zone appears at fuel mass fractions leaner than that of the most reactive mixture fraction $(Y_{\text {C}_2\text {H}_4}=5 \times 10^{-3})$, i.e. closer to the crossflow than to the jet flow with respect to the blue iso-contour. This is in line with the previous discussion where it was shown that small reacting kernels of low heat release are formed exclusively in very lean zones with high T and low $\chi$ at the windward side due to autoignition and pure mixing effects between the 2 streams. After the flame is fully stabilized $(t=10\,\hbox {ms})$, the most reactive regions (red isocontour) extend around the jet and in the downstream direction. An important difference is observed at the jet root, where the reaction occurs now at higher fractions of fuel, coincident with the most reactive mixture fraction levels, i.e. blue and red iso-contours are coincident in the jet root. Towards the jet downstream direction, the reaction entrains the jet stream to higher fuel mass fractions. The autoignition of these richer regions is characterized by higher heat release rates and higher flow reactivity as shown in Fig. 9. This findings are in line with the phenomenon of autoignition cascade (Schulz et al. 2019). Note that the highly reacting regions observed in the chemical explosive mode map are coincident with the high heat release zones with $\dot{q}\sim 10^9$. However, regions with smaller $\dot{q}$ are not captured as chemically active.

The results from the time evolution from $t=3\,\hbox {ms}$ (no flame), to $t=10\,\hbox {ms}$ (fully stabilized flame) show a “low-heat-release” autoignition phenomenon starting at the front root of the jet under very lean conditions. The heat released is advected and diffuses, increasing the local temperatures and decreasing the autoignition delay times. This leads to stabilization and growth of the reaction kernels, enclosing regions of higher fuel concentrations. The evolution in time and the shift of the jet-root reacting region from very lean to richer zones can be seen by comparing the relative locations between red and blue iso-contours at the jet root. As the fuel progresses in the jet downstream direction, the chemically active region (red iso-contours) extends in the same direction and grows in magnitude. We can see how the reaction zone wraps the jet starting from the root windward side. The CEMA post processing corroborates the findings from the previous section.

4 Conclusions

This study investigates the transient self-ignition process of a cold premixed ethylene-air jet in hot vitiated crossflow using large eddy simulation and analytically reduced chemistry. The equivalence ratio and temperature of the jet mixture are 1.2 and 300 K respectively. It is injected into a hot vitiated crossflow at 1500 K. The main finding of this numerical study is that the heat release outbreaks in the form of autoignition patches along the windward side of the jet base in regions of low scalar dissipation and moderate shear stress. Moreover, these regions are leaner than the most reactive mixture fraction, when the latter is computed from reactor simulations of mixtures of the hot vitiated cross flow and of the cold premixed air-ethylene jet. There, autoignition conditions are met, i.e. very lean mixture fractions, high temperature, low scalar dissipation rates, moderate shear, and low flow velocity. These patches initiate a process of heat release diffusion that make richer mixtures more reactive and lead to their expansion around the jet and to an exponential growth of heat release magnitude. These lateral reactive fronts ultimately wrap up the jet and finally merge in the leeward region where autoignition conditions are not found. From this point, the heat release along the jet windward side intensifies due to the autoignition-cascade phenomenon. Low heat release at the jet root diffuses downstream in the jet along and across the shear layer shifting the most reactive mixture fractions to higher values. This chain reaction allows the overall level of heat release rate on the windward side of the jet to exponentially grow and then saturate to the steady state level, creating a fully developed flame. It is also shown that this flame stabilizes at the jet root in the windward side in regions where scalar dissipation is low and shear is moderate, and that this is the case during the whole ignition process. These findings are complemented with a chemical explosive mode analysis, which shows that the reaction kernels start forming at the very lean locations of the jet windward side with low scalar dissipation and moderate shear.