Quantitative Flow Visualization of Slightly Underexpanded Microjets by Mach–Zehnder Interferometers

Abstract

The Mach–Zehnder interferometer with the finite fringe setting is applied for a shock-containing microjet issued from an axisymmetric convergent nozzle with an inner diameter of 1.0 mm at the exit. Experiments are performed at a nozzle pressure ratio of 3.0 to produce a slightly underexpanded sonic jet where the Reynolds number, based upon the diameter and flow properties at the nozzle exit, is $4.45 \times 10^4$. The reconstruction of the jet density field is performed using the Abel inversion method under the assumption of an axisymmetric flow as well as the Fourier transform method for the phase shift analyses of interferograms. The three-dimensional density field of a shock-containing microjet can be captured with a spatial resolution of 4 $\upmu$m, and the near-field shock structure inside the jet plume is shown in the density contour plot at the cross-section including the jet centerline. In addition, the density field of the microjet is illustrated with various techniques, including representation such as the vertical-knife-edge schlieren, the horizontal-knife-edge schlieren, the bright-field schlieren, and the shadowgraphy. In addition to experiments, the Reynolds averaged Navier–Stokes (RANS) simulation with the SST k–$\omega$ turbulence model is carried out to model the microjets, and a quantitative comparison with the experiments is performed. The jet centerline density profile obtained by the present experiment is quantitatively compared with those from the previous Mach–Zehnder interferometer, the background oriented schlieren, as well as the RANS simulation.

1 Introduction

Since the pioneering research of Scroggs and Settles (1996), there has been considerable experimental research on the subject of the dynamics of a supersonic microjet for the application of microscale devices. For detailed understanding the characteristics of a jet flow, it requires quantitative information of velocity, density, and temperature fields. However, it has been challenging to capture the fine-structures inside a supersonic microjet using a conventional visualization technique. The structures of supersonic microjets were systematically studied for the first time by Scroggs and Settles (1996), who made axisymmetric nozzles with exit Mach numbers ranging from 1.0 to 2.8 and two different inner diameters of 600 $\upmu$m and 1200 $\upmu$m at the nozzle exit. They measured the Pitot pressures along the jet centerline by impinging the jet upon at a plate, including a pressure port of 0.2 mm in diameter with a pressure sensor attached to the reverse side. Phalnikar et al. (2008) fabricated a micro Pitot probe with a pressure hole of 50 $\upmu$m in diameter, and later, Aniskin et al. (2013) developed one with an intake port of 12 $\upmu$m diameter. These two research groups performed the Pitot pressure measurements to study the size of shock cells and the supersonic core length of the microjet. However, the intrusive probe, including a Pitot probe, a static pressure tube, and a hot-wire anemometer, can only measure the flow parameters at discrete points. Such probes are also very sensitive to the flow alignment (John 1984). In addition, the intrusive probe can alter the flow fields since the presence of the probe located inside the flow can change the shock structures significantly. Recently, Mironov et al. (2019) investigated the influence of the Pitot tube diameter on the axial pressure distribution and the supersonic core length in an underexpanded microjet. They demonstrated that the Pitot pressure distribution along the centerline of the microjet is shifted in the downstream direction with respect to the curves, which are calculated for free microjets. In contrast, nonintrusive techniques such as the Laser Doppler and the Particle Image Velocimetry can be used for velocity measurements, however, these techniques often contain an inherent error because the tracer particles cannot necessarily follow a strong velocity gradient across a shock wave (Koike et al. 2006; Sakurai et al. 2015; Wernet 2016). Therefore, with complex shock-containing structures, a proper and homogeneous seeding is very difficult.

Schlieren techniques have been used for qualitative flow visualization in the past using line-of-sight integrations. However, integration and subsequent processing analyses can be now done with ease on conventional personal computers. Consequently, the schlieren-based quantitative techniques such as the moiré schlieren (Tabei et al. 1992) and the calibrated schlieren (Mariani et al. 2019) have been utilized to investigate supersonic jets. Moreover, the background-oriented schlieren (BOS) is one of recent approaches to provide three-dimensional quantitative flow visualization for external flows such as free jets, flows around an airfoil as well as internal flows including supersonic nozzles and diffusers (Settles and Hargather 2017). However, to the authors’ knowledge, only three papers (Venkatakrishnan 2005; Van Hinsberg and Rösgen 2014; Nicolas et al. 2017) have measured the density fields of macro-scale shock-containing jets, and there is little application of BOS for micro-scale shock-containing jets. More recently, Wernet and Stiegemeier (2017) have applied BOS for the micron-scale density field of a free jet issued from a small rocket engine. Another simpler optical technique for visualizing jet density fields comparable to BOS might be the rainbow schlieren deflectometry (Takano et al. 2016; Maeda et al. 2018; Agrawal and Wanstall 2018; Mariani et al. 2020). This technique is a modified approach based on the conventional color schlieren. The modification is made only by replacing the color filter in the schlieren cutoff plane with a rainbow filter having continuous color stripe distribution. Kolhe and Agrawal (2009) examined for the first time the density field of underexpanded microjets issued from an orifice injector of 500 $\upmu$m diameter at the exit by the rainbow schlieren deflectometry with a spatial resolution of 25 $\upmu$m.

Dam et al. (1998) developed a laser-based diagnostic tool to record gas densities and applied the UV laser Rayleigh scattering for a miniature jet. Graur et al. (2004) carried out density measurements using the high-sensitivity Raman spectroscopy to clarify the flow topology just behind a Mach disk in a microjet. Belan et al. (2008) employed an electron beam technique for determining density distributions in sections of a shock-containing jet issued from a micro-orifice. In addition, Schmid and Veisz (2012) utilized the Mach–Zehnder interferometer (MZI) to investigate the problem seen while generating microscopic supersonic jets for laser-plasma experiments. Franquet et al. (2015) have provided a comprehensive review on axisymmetric supersonic jets issued from orifices or nozzles, covering papers experimentally dealing with underexpanded jets. However, the structure and dynamical properties of axisymmetric underexpanded jets are still known only qualitatively, and there is little quantitative information on the dynamics of supersonic microjets.

Most recently, Sugawara et al. (2020) applied MZI for a microjet with a Mach disk to diagnose three-dimensional jet density fields and to reveal the flow topology of the shock system in the near-field region. As a counterpart of our previous studies, we pay a special attention on a supersonic microjet including “weak shocks”, through which total pressure losses are considered to be negligible. Some theoretical models about supersonic jets with weak shocks have been proposed (Tam et al. 1985; Tam 1988; Morris et al. 1989; Emami et al. 2009). However, experimental data to validate these theoretical models are still lacking in the current literature. In this study, in addition to experiments, the RANS simulations with the SST k–$\omega$ turbulence model have been performed to model a microjets with weak shocks, and we perform a mutual quantitative comparison with the present and previous experimental data for jet centerline density profiles.

2 Experimental Apparatus

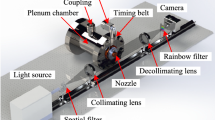
The experiments were conducted in a blowdown compressed air facility of the High-Speed Gasdynamics Laboratory at the University of Kitakyushu. A schematic diagram of the experimental apparatus with the Mach–Zehnder interferometer system is shown in Fig. 1. Ambient air is pressured by the compressor up to 1 MPa, and then stored in the high-pressure reservoir consisting of two storage tanks with a total capacity of 2 m$^3$ after being filtered and dried. The supply line from the reservoir can be connected to the plenum chamber through a coupling, as shown in Fig. 1. Hence, the high-pressure dry air from the reservoir is stagnated in the plenum chamber, and then discharged into the atmosphere through a test nozzle. In the present experiment, the plenum pressure is controlled and maintained constant at a value of $p_{\mathrm{os}}$ = 306 kPa ± 0.5 kPa during the testing by a solenoid valve, and the back pressure $p_{\mathrm{b}}$ is 102 kPa ± 0.5 kPa.

Fig. 1

Schematic drawing of experimental apparatus

As schematically shown in Fig. 2, the axisymmetric convergent nozzle with 6 mm and 1 mm in diameter at the inlet and exit was used as a test nozzle. The nozzle wall contour from the inlet to exit was designed based on a sinusoidal curve so as to realize smooth uniform flows at the inlet and exit. The nozzle was manufactured from a brass block using a cut-processing machine (Kitamura Machinery, Mycenter-3XG) with a positioning accuracy of ±2 $\upmu$m and a repeatability of ±1 $\upmu$m. The experiment was carried out at a nozzle pressure ratio (NPR) of 3.0 within an accuracy of 1.0 $\%$ to produce a slightly underexpanded free jet. The total temperature in the plenum chamber was equal to the room temperature ($T_{\mathrm{b}}$ = 300 ± 0.1 K) within an accuracy of about 0.1 centigrade during the experiment. To obtain density fields in a shock-containing microjet, quantitative flow visualization was made using the Mach–Zehnder interferometer system with a field of view of 50 mm diameter. The Reynolds number $Re_{d}$ at the nozzle exit is $Re_{d}$ = 4.45 $\times$ $10^4$ , which is calculated based on the assumption of an isentropic flow from the nozzle inlet to exit.

Fig. 2

Test nozzle

The Mach–Zehnder interferometer is an optical instrument of high precision and versatility (see Fig. 1) with the associated optical equipment that uses a blue semiconductor laser with a wavelength of 405 nm as a light source. The laser beam is expanded by a spatial filter with a pinhole of 50 $\upmu$m in diameter to make a coherent beam before collimated into a parallel beam, and then is split into reference and test beams by a beamsplitter (BS1). The beamsplitter reflects roughly half of the intensity of the wave front in one direction and transmits the rest in another direction. The reference beam passes through still air and travels to another beamsplitter (BS2) after being reflected at Mirror 1 (M1). The test beam passes through a refracted index field produced by a free jet that is issued from a test nozzle and also travels to BS2 after being reflected at Mirror 2 (M2). The two beams are combined before being focused by the imaging lens and then produce interferograms on the recording medium in a digital camera.

It is critical to accurately measure the wall shape at the nozzle exit section in order to investigate flow features of a jet issued from a micron-scale nozzle. To estimate the error of circularity for the wall shape, we obtained a digital image of the section by the laser scanning microscope (Olympus Model LEXT OLS4100) as shown with a linear scale in Fig. 3. After reading the image in a personal computer, the radial distances from a certain reference point to the wall periphery were measured at each angle of 20$^\circ$ with AutoCAD 2013 software.

Fig. 3

Digital image of nozzle exit section

Figure 4 illustrates a schematic drawing of the nozzle exit section where the black solid line represents the real wall shape, the blue and red solid lines are the minimum circumscribed and the maximum circles that are just sufficient to fit inside and to enclose the wall shape. In addition, the black dotted line shows the least-squared circle corresponding to the real wall shape. The origin (a, b) of the least-squares circle and the radius $r_{le}$ can be calculated as follows.

Fig. 4

Schematic drawing of nozzle exit section

In a Cartesian xy-coordinate system, the equation of a circle centered at (a, b) with a radius of r is expressed by $f(x, y)=(x-a)^2+(y-b)^2-r^2=0$. The objective function J is defined as follows:

$$\begin{aligned} J=\sum _{i=1}^N \left[ (x_i-a)^2+(y_i-b)^2-r^2\right] ^2 \end{aligned}$$

(1)

where $(x_i, y_i)$ is the measurement coordinate, and N is the number of the data points measured (N = 19 in this study). The least-squares method finds the optimal parameter values for a, b, and r in (1) by minimizing J. To find these optimal parameters, we need to solve the following three equations, which are obtained by taking derivatives of J respect to $\alpha$ (= $-2a$), $\beta$ ( = $-2b$), and $\gamma$ ( = $a^2 + b^2 - r^2$):

$$\begin{aligned} \frac{\partial J}{\partial \alpha }&= \sum \left[ 2x_i \left( x_i^2+y_i^2+\alpha x_i+\beta y_i+\gamma \right) \right] =0 \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial J}{\partial \beta }& = \sum \left[ 2y_i \left( x_i^2+y_i^2+\alpha x_i+\beta y_i+\gamma \right) \right] =0 \end{aligned}$$

(3)

$$\begin{aligned} \frac{\partial J}{\partial \gamma }& = \sum \left[ 2 \left( x_i^2+y_i^2+\alpha x_i+\beta y_i+\gamma \right) \right] =0 \end{aligned}$$

(4)

Accordingly, from combination of (2)–(4) , it follows that

$$\begin{aligned} \left[ \begin{array}{c} \alpha \\ \beta \\ \gamma \end{array}\right] =- \left[ \begin{array}{lll} \sum x_i^2 &{} \sum x_i y_i &{} \sum x_i \\ \sum x_i y_i &{} \sum y_i^2 &{} \sum y_i \\ \sum x_i &{} \sum y_i &{} \sum 1 \end{array}\right] ^{-1} \left[ \begin{array}{l} \sum \left( x_i^3+x_i y_i^2\right) \\ \sum \left( x_i^2 y_i+y_i^3\right) \\ \sum \left( x_i^2+y_i^2\right) \end{array}\right] \end{aligned}$$

(5)

by the matrix representation.

After inserting the nineteen measured coordinates, we obtained $a= -1.05$ $\upmu$m , $b=-0.494$ $\upmu$m, and $r=r_{le}=500.3$ $\upmu$m. The out-of-roundness or the error of circularity is defined as the radial distance ($r_{ci}-r_{in}$) between the minimum circumscribed circle (radius $r_{ci}$) and the maximum inscribed circle (radius $r_{in}$), which contains the profile of the surface at the section perpendicular to the axis of rotation. The variation of the wall periphery at the nozzle exit section against the polar angle $\theta$ is shown in Fig. 5. The precision error for the radius r of the least-squares circle becomes $\pm \,1.4$ $\upmu$m and it corresponds to around $\pm \,0.3$ $\%$ to the radius.

Fig. 5

Variation of wall periphery at nozzle exit section against polar angle

3 Reconstruction of Jet Density Fields

The method for reconstructing a jet density field consists of two steps. The first step is the acquisition of the values of fringe shifts from their original positions measured in the experiment, which is followed by the calculation of density values using the resulting fringe shifts. The former can be done using the Fourier transform method presented by Takeda et al. (1982) and the latter by Nestor and Olsen (1960) for the Abel inversion method under the assumption of an axisymmetric density field. The methodology of extracting the density field using both of the methods is described below.

Generally, the Mach–Zehnder interferometers can be arranged so as to produce finite fringe and infinite fringe patterns. In the infinite fringe method, each fringe occurs due to one wavelength shift in the optical path length as a result of changes in the flow field (Smits and Lim 2000). The finite fringe method can measure densities more minutely than the infinite fringe method by analyzing a fringe shift and is the method employed in the present work. In the finite fringe method, the mirrors and the beamsplitter are deliberately misaligned to produce an initial fringe pattern or a background fringe pattern of straight lines. The image is then processed using techniques for obtaining density fields by digital subtraction of the background fringe pattern from the deformed fringe pattern. In the present experiment, the background fringes were set in the horizontal orientation with respect to the nozzle axis by the appropriate adjustment of Mirror 2 shown in Fig. 1.

3.1 Wave Interaction Between Reference and Test Beams

When the test beam passes through a free jet with a variable refractive-index field, the background fringes are changed into the deformed fringe patterns. As shown in Fig. 6a, for simplicity, we first consider the reference and test beams after the beams pass through the BS2 (see Fig. 1) as plane waves. The coordinate x is the direction of the optical axis, in which the test beam propagates after being reflected at Mirror 2 as shown in Fig. 1. The coordinates y and z form the vertical plane perpendicular to the x direction. The reference beam $\Psi _1$ travels in the direction rotated at an angle $\eta$ around z axis, and the test beam $\Psi _2$ propagates in the positive direction of the x axis.

Fig. 6

Variation of background and deformed fringes by finite fringe setting

If the reference and test beams have the same phase $\varphi _0$ at $x = y = t = 0$ without being influenced by the refractive index fields, they can be expressed for a fixed $z = z_0$ as follows:

$$\begin{aligned} \Psi _1({{\mathbf{r}}},t)=a\exp {\left[ i({{\mathbf{k}}}_1 \cdot {\mathbf{r}}-\omega t+\varphi _0)\right] } \end{aligned}$$

(6)

$$\begin{aligned} \Psi _2({{\mathbf{r}}},t)=a\exp {\left[ i({{\mathbf{k}}}_2 \cdot {\mathbf{r}}-\omega t+\varphi _0)\right] } \end{aligned}$$

(7)

where $\omega$ and a are an angular frequency and an amplitude of light in still air, and t is the time. ${\mathbf{k}}_1$ and ${\mathbf{k}}_2$ are the wave vectors, and ${\mathbf{r}}$ is the position vector. They are given by

$$\begin{aligned} {{\mathbf{k}}}_1=\frac{2\pi }{\lambda _a}(\cos \eta ,-\sin \eta ,0), {{\mathbf{k}}}_2=\frac{2\pi }{\lambda _a}(1,0,0), {{\mathbf{r}}}=(x,y,z_0) \end{aligned}$$

(8)

Here, $\lambda _a$ is the wavelength of light in still air.

As shown in Fig. 6a, if the test wave undergoes a path difference $d= d(y, z_0)$ in propagation distance through changes in refractive index, the resultant test wave $\Psi _2^{'}$ becomes

$$\begin{aligned} \Psi _2^{'}({{\mathbf{r}}},t)=a\exp {\left[ i\left( {{\mathbf{k}}}_2 \cdot {{\mathbf{r}}}-\omega t+\varphi _0-\frac{2\pi }{\lambda _a}d\right) \right] } \end{aligned}$$

(9)

If $\Psi _1$ and $\Psi _2$ are superimposed on a recording medium located at $x = 0$, the resultant intensity field can be expressed as

$$\begin{aligned} g_r(y,z_0)& \equiv {} |\Psi _1({{\mathbf{r}}},t)+\Psi _2({{\mathbf{r}}},t)|^{2}\nonumber \\& = 2a^2+2a^2\cos \left[ ({{\mathbf{k}}}_2-{{\mathbf{k}}}_1)\cdot {{\mathbf{r}}}\right] \end{aligned}$$

(10)

This intensity varies in a sinusoidal form. Therefore, there are local maxima at the following conditions.

$$\begin{aligned} ({\mathbf{k}}_2-{\mathbf{k}}_{1})\cdot {\mathbf{r}}=2m\pi \end{aligned}$$

(11)

where m is integer.

Substitution of Eq. (8) into Eq. (11) leads to

$$\begin{aligned} y=y_m=\frac{m\lambda _a}{\sin \eta } \end{aligned}$$

(12)

This implies that the intensity distribution has the maximum brightness at the locations of $y = y_m$.

Using Eq. (12), the interval b between interferograms on the medium (x = 0) is given by

$$\begin{aligned} b=|y_{m+1}-y_m|=\frac{\lambda _a}{\sin \eta } \end{aligned}$$

(13)

The interval b becomes narrower with increasing $\eta$ for $0<\eta <\pi /2$, and it shows infinite fringe patterns for $\eta = 0$.

Similarly, from Eqs. (6) and (9), the intensity field experiencing changes in refractive index is given by

$$\begin{aligned} g(y,z_0)& = |\Psi _1({\mathbf{r}},t)+\Psi _2^{'}({\mathbf{r}},t)|^{2}\nonumber \\& = 2a^2+2a^2\cos \left[ ({\mathbf{k}}_2-{\mathbf{k}}_1)\cdot {\mathbf{r}}-\frac{2\pi }{\lambda _a}d\right] \end{aligned}$$

(14)

The comparison of Eqs. (10) and (14) shows that $g(y, z_0)$ can be translated by a phase

$$\begin{aligned} \Delta \varphi (y,z_0)=\frac{2\pi }{\lambda _a}d \end{aligned}$$

(15)

or it can be converted into the corresponding path difference

$$\begin{aligned} \Delta y=\frac{b\Delta \varphi (y,z_0)}{2\pi } \end{aligned}$$

(16)

as shown in Fig. 6b, c.

Substitution of Eq. (8) into Eq. (14) and considering Eq. (15) yields

$$\begin{aligned} g(y,z_0)=2a^2+2a^2\cos \left[ k_{0}y-\Delta \varphi (y,z_0)\right] \end{aligned}$$

(17)

on the recording medium where $k_0 = 2\pi /b$.

3.2 Fourier Transform Method

Typical profiles taken using a digital camera showing background and deformed fringe patterns are illustrated in Fig. 6b, c as lines of constant phase. The parallel and equally spaced fringes shown as blue solid lines in Fig. 6b are also referred to as the wedge fringes. The interval b in Fig. 6b denotes the distance between two successive crests of the background fringes, and it is a function of the intersection angle ($\eta$) between the reference and the test beams and the wavelength ($\lambda _a$) of the laser light used in the experiment, as shown in Eq. (13). The red dashed line in Fig. 6c shows the intensity profile $g(y, z_0)$ corresponding to the deformed fringe pattern at a particular axial position $z_0$ and it can be given by (Takeda et al. 1982; Yagi et al. 2017)

$$\begin{aligned} g(y,z_0)=g_0(y,z_0)+g_1(y,z_0)\cos {\left[ k_0y-\Delta \varphi (y,z_0)\right] } \end{aligned}$$

(18)

In this expression, $g_0(y, z_0)$ and $g_1(y, z_0)$ are used (see Eq. (17)). The phase shift $\Delta \varphi (y,z_0)$ only contains the desired information on the density field in the free jet. The intensity profile of the deformed fringe pattern expressed as Eq. (18) can be rewritten in the following expression:

$$\begin{aligned} g(y,z_0)& = g_0(y,z_0)+c(y,z_0)\exp (ik_0y)\nonumber \\&\quad +\, c^*(y,z_0)\exp (-ik_0y) \end{aligned}$$

(19)

with

$$\begin{aligned} c(y,z_0)=\frac{1}{2}g_1(y,z_0)\exp \left[ -i\Delta \varphi (y,z_0)\right] \end{aligned}$$

(20)

Here, i is the imaginary unit and the asterisk * denotes the complex conjugate.

The Fourier transform of Eq. (19) with respect to y is given by:

$$\begin{aligned} G(k,z_0)=G_0(k,z_0)+C(k-k_0,z_0)+C^*(k+k_0,z_0) \end{aligned}$$

(21)

where the capital letters denote the Fourier transforms of the respective primitive functions, and k is the spatial wave number in the y direction. Since the spatial variations of $g_0(y, z_0)$, $g_1(y, z_0)$, and $\Delta \varphi (y,z_0)$ are slow compared with the spatial frequency $k_0$ when the interval between fringes is sufficiently small, the Fourier spectra in Eq. (21) are separated by the wave number $k_0$ and have the three independent peaks as schematically shown in Fig. 7a. We make use of either of these two spectra on the carrier, say $C(k-k_0, z_0)$, and translate it by $k_0$ on the wave number axis toward the origin to obtain $C(k, z_0)$ as shown in Fig. 7b. The unwanted background variation $G_0(k, z_0)$ has been filtered out in this stage by the pertinent band pass filter.

Fig. 7

Fourier transform method for fringe pattern analysis

Applying the inverse Fourier transform of $C(k, z_0)$ with respect to the k to obtain $c(y, z_0)$ and taking the logarithm of Eq. (20) leads to

$$\begin{aligned} \ln c(y,z_0)=\ln \frac{g_1(y,z_0)}{2}-i\Delta \varphi (y,z_0) \end{aligned}$$

(22)

Consequently, the phase shift $\Delta \varphi (y,z_0)$ in the imaginary part of Eq. (22) can be completely separated from the unwanted amplitude variation $g_1(y,z_0)$ in the real part.

3.3 Abel Inversion Method

A free jet with an axisymmetric refractive index field is depicted in Fig. 8a. The refractive index n in the flow field depends only on the radial distance r from the centerline O ($x=y=0$) for a fixed axial distance $z_0$ measured from the nozzle exit plane, i.e.,

$$\begin{aligned} n&=n(r,z_0), \quad for \; 0 \le r \le R,\nonumber \\ n&=n_a, \quad for \; R < r \end{aligned}$$

(23)

where $n_a$ is the refractive index for the ambient air and R the radial distance to the jet boundary.

Fig. 8

Light beam passing through axisymmetric refractive index field

Refractive index values can be obtained directly from the measured fringe positions on a given cross section normal to the jet axis, and each measured cross section is independent of others. As illustrated in Fig. 8a, the optical path difference $\Lambda (y, z_0)$ of the test beam which passes through the field with and without the jet, can be expressed by

$$\begin{aligned} \Lambda (y,z_0)=2\int _y^R \frac{\left[ n(r,z_0)-n_a\right] }{\sqrt{r^2-y^2}}rdr \end{aligned}$$

(24)

The fringe shift $\Delta y$ at any location on a recording medium can be related to the $\Lambda (y, z_0)$ as follows:

$$\begin{aligned} \Delta y=\frac{b}{\lambda _0} \Lambda (y,z_0) \end{aligned}$$

(25)

where $\lambda _0$ is the wavelength of light in vacuum for the laser used. The use of the Gradstone–Dale relation

$$\begin{aligned} n(r,z)=1+K \rho (r,z) \end{aligned}$$

(26)

with combination of Eqs. (24) and (25) gives

$$\begin{aligned} \Delta y=\frac{2bK}{\lambda _0} \int _y^R \frac{\left[ \rho (r,z_0)- \rho _a\right] }{\sqrt{r^2-y^2}}rdr \end{aligned}$$

(27)

where K is the Gradstone–Dale constant and $\rho _a$ is the density of ambient air.

Once the fringe shifts for a fixed streamwise location $z_0$ are obtained by the Fourier transform method, the density field is found by inverting Eq. (27) using the Abel inversion (Sneddon 1972):

$$\begin{aligned} \rho (r,z_0)=\rho _a - \frac{\lambda _0}{\pi bK} \int _r^R \frac{1}{\sqrt{y^2-r^2}} \frac{d}{dy}(\Delta y)dy \end{aligned}$$

(28)

The integral in Eq. (28) is evaluated by using the algorithm proposed by Nestor and Olsen (1960) as follows:

$$\begin{aligned} \rho (r_k,z_0)=\rho _a - \frac{\lambda _0}{\pi ^2 K \Delta w} \sum _{n=k}^N B_{k,n} \Delta \varphi \left( y_n, z_0\right) \end{aligned}$$

(29)

where $r_k=k \Delta w$ (k = 0, 1, 2, ..., N) is the radial distance from the jet centerline, $\Delta w$ is the sampling interval, which is the same as the distance between neighboring pixels on the recording medium, N is the total number of intervals in the medium, $\Delta \varphi (y_n, z_0) = 2 \pi y_n / b$, $y_n \le y < y_{n+1},$ $y_n = n\Delta w,$ and

$$\begin{aligned} &B_{k,n}=-A_{k,n} \quad if \; n=k,\nonumber \\ &B_{k,n}=A_{k,n-1}-A_{k,n} \quad if \; n \ge k+1 \end{aligned}$$

(30)

with

$$\begin{aligned} A_{k,n}= \frac{\sqrt{(n+1)^2-k^2} - \sqrt{n^2-k^2}}{2n+1} \end{aligned}$$

(31)

Density values can be captured at the spatial resolution determined by the sampling interval. 30 interferogram pictures of a microjet were taken at a sampling frequency of around 1 Hz by a CMOS camera (The Imaging Source, DFK72BUC02) where an exposure time was set to be 100 $\upmu$s. Each picture was recorded as a JPEG RGB image (8-bit each color) at a resolution of 2592 $\times$ 1944 square pixels and then turned into an HSV image (8-bit each color) according to the hue (H)–saturation (S)–value (V) color model. Since the intensity distributions of interferograms recorded are represented by a single parameter V with an 8-bit grayscale image, the distributions of background and deformed fringes with 256 different possible intensities can be calculated from the Mach–Zehnder interferometer for the density-field in the free jet. The plane of focus was located in the nozzle axis. The spatial resolution for the present MZI system was measured as 4.1 $\upmu$m ± 130 nm based on the physical and imaged dimensions of the test nozzle before starting experiments. Since the fringe-interval, b, of the interferograms for the present MZI system is b = 24.6 $\upmu$m on the physical dimension, a wave corresponding to one wavelength in the intensity distribution of the interferograms can be constituted only around 6 data points” (b/$\Delta w$ = 6) when compared to the 256 (8 bit) grayscale level. Hence, the present MZI system has a high dynamic range for the fringe-shift analysis.

For each of 30 interferogram images obtained experimentally, the phase shifts at the upper and lower sides with respect to the jet centerline are averaged and then the reconstruction using the Abel inversion is performed for the averaged image. The same procedure is repeated for all the 30 interferogram images. It takes a few hours for performing 30 reconstruction using the in-house code with the commercial software LabVIEW2016. The average and standard deviation for the experiment are obtained over all the 30 reconstructed density fields.

4 Numerical Methods

Microjets from an axisymmetric convergent nozzle with an inner diameter of $D_e$ = 1 mm at the nozzle exit are calculated using the commercial CFD software, ANSYS Fluent Version 15.0. The flow is assumed to be symmetric with respect to the jet centerline (z-axis); therefore, only the upper half of the domain needs to be considered. The axisymmetric pressure based compressible RANS equations are numerically solved. More specifically, the Menter’s SST k–$\omega$ turbulence model is employed in the present study because of its robustness for a variety of CFD applications, including transonic and supersonic flows as well as shock-wave-boundary layer interactions (Franquet et al. 2015).

The inlet and far-field boundary conditions are identical to the experimental setup. The plenum pressure ($p_{os}$) and temperature upstream of the nozzle are 306 kPa and 300 K, respectively, and the back pressure ($p_b$) is set to the atmospheric pressure. The nozzle operating pressure ratio, NPR = $p_{os}$/$p_b$, is kept constant at 3.0. The dry air is assumed to be a perfect gas with a constant specific heat ratio of $\gamma$ = 1.4, and the coefficient of viscosity is calculated by using the Sutherland’s law. The solid walls including the nozzle wall are treated adiabatic and no-slip. We use the pressure outlet condition (i.e., $p_b$ is specified) for the top and right boundaries, which are located sufficiently far from the nozzle exit. The structured mesh is generated by the mapped face meshing function equipped with ANSYS Fluent, and the total mesh count is approximately 50 thousand elements. In our previous studies (Sugawara et al. 2020), we performed the grid sensitivity analysis and confirmed that the numerical solutions converged for this resolution. Inside the nozzle, the grid spacing smoothly reduces in the radial direction to capture the thin boundary layer. To capture the fine structures of the shock-containing microjets, we set a minimum mesh interval to around 2 $\upmu$m in the vicinity of the nozzle exit. (Note that the spatial measurement resolution of the density is around 4 $\upmu$m.) The number of iterations is 10,000, at which the residuals of all equations (species, momentum, energy, turbulent kinetic energy, k, and specific rate of dissipation, $\omega$) reduce by three orders of magnitude, and the solutions seem to sufficiently converge. Here, the CFL number is set to be 0.1. We use the differentiable function as the limiter of the MUSCL scheme to achieve the third-order accuracy in space. Note that using the high-order scheme, which satisfies a total-variation-diminishing (TVD) condition, is particularly important for this type of application. The time integration is performed using the three-stage Runge–Kutta method. It should be kept in mind that the previous study of Sugawara et al. (2020) for a microjet with a Mach disk, which was performed under a condition of NPR = 4.0, showed that there is an excellent quantitative agreement between the experiment and the simulation for three representative streamwise density profiles at the jet centerline, the lipline and the intermediate line between them.

5 Results and Discussion

5.1 Interferograms of Microjet with Weak Shocks

Since the MZI system with the finite fringe setting is not yet very common for measurements of compressible flow fields, it would be helpful to include the picture of the interference fringes as seen by the camera sensor.

Figure 9a shows an interferogram of an axisymmetric microjet (the flow direction is left-to-right), in which the ratio (NPR) of the plenum pressure to the back pressure is kept constant at NPR = 3.0 in such a manner that the nozzle is operated at a slightly underexpanded condition. Regardless of a somewhat high NPR, the shock-cell structure unique to an underexpanded free jet is clearly obscured in this optical representation. Parts A and B, enclosed by a red quadrangle in Fig. 9a, are the regions: one is far from the jet plume, and the other includes the shock cell structure. Figure 9b (an enlarged view of Part A in Fig. 9a) represents an image of the background fringe pattern. The interval between the parallel fringes corresponds to b in Fig. 6b. It is necessary to make the space between fringes as narrow as possible to avoid islands in the fringe pattern. Wide fringes move farther away from the original location than narrower fringes do. As a result, wide fringes cover the regions, which are considerably different from the optical retardations. This results in the creation of islands (Winckler 1948). An enlarged view of Part B in Fig. 9a is shown in Fig. 9c. Although it’s very difficult to discern shock systems in Fig. 9c, the effect on the interferograms can be slightly observed. It should be noted that fringe variations seen in the interferogram image are not symmetric with respect to the jet centerline. As illustrated in Fig. 8a, the optical path differences, $\Lambda (y, z_0)$, of the test beams passing through the areas across the jet centerline are the same in the case of axisymmetric flows. The corresponding fringe shift, $\Delta y$, then becomes $\Delta y = b\Lambda (y, z_0)/ \lambda _0$ from Eq. (25). This means that the fringes across the jet centerline are shifted in the same direction with the same magnitudes of displacement, i.e., density variations move the fringes perpendicular to themselves always in the same direction. Consequently, the fringes crowd on one side of the axis and expand at a symmetrical point on the other side of the axis, although density variations are the same at symmetrical points (Ladenburg et al. 1949). When experiments are performed using the interference fringes perpendicular to the jet centerline, axisymmetric interferograms could be obtained. In any case, it is not feasible to obtain more information on a detailed microjet structure from the interferogram of Fig. 9c alone.

Fig. 9

Typical interferograms by MZI with finite fringe setting

5.2 Density Field of Microjets with Weak Shocks

The density contour plot at the cross-section including the jet centerline of the microjet is shown in Fig. 10. The contour levels with an interval of $\rho /\rho _{\mathrm{b}}$ = 0.1 are shown at the top. Three red dashed lines parallel to the abscissa ($z/D_e$) correspond to the locations of the jet centerline ($r/D_e$ = 0), the lipline ($r/D_e$ = 0.5), and the intermediate line ($r/D_e$ = 0.25) between them. In the contour plot, we observe that the expansion and compression regions are repeatedly produced and that the edge location of the shear layer remains almost the same ($r/D_e$ = 0.5) until the end of the domain. The radial locations, at which the oblique shock in each shock-cell is reflected and expansion waves are formed, are shown as open circles in Fig. 10, These might be seen as the jet free boundaries. The compression regions of the first three shock-cells have two local maxima at locations away from the jet centerline. There is no Mach disk for the present pressure condition (NPR = 3.0), which is smaller than that (NPR = 3.32) of the measurements using Rayleigh scattering by Panda and Seasholtz (1999). Their experimental data also show no Mach disk. It should be noted that the conventional schlieren and shadowgraph pictures sometimes show the incident shock or barrel shock inside the first shock cell, but such a shock cannot be seen in the current density contour plot at the jet cross section. Therefore, what was considered to be the incident shock wave or barrel shock wave seen in the conventional pictures so far could be considered to be a compression wave for the present pressure condition, where there is a noticeable difference between density distributions integrated in the line-of-sight direction and that at the jet cross-section shown in Fig. 10. The present results are consistent with those of Panda and Seasholtz (1999)

The streamwise density profiles at radial distances of $r/D_e$ = 0, 0.25 and 0.5 are shown in Fig. 11a–c, where the experimental results are represented with the precision error bars. These radial locations are shown as the three horizontal red dashed lines in the contour plots of Fig. 10. The density value at the nozzle exit plane, which is estimated based on the assumption of one-dimensional isentropic flow from the nozzle inlet to the exit, is shown as a leftward arrow on a vertical axis as a reference. The solid dashed line parallel to the abscissa indicates the level of the ambient density $\rho _{\mathrm{b}}$ = 1.18 kg/m$^3$ ($\rho = \rho _{\mathrm{b}}$) in the present experiment. The solid line parallel to the abscissa indicates the level of the fully expanded jet density $\rho _{\mathrm{j}}$ = 1.62 kg/m$^3$ ($\rho _{\mathrm{j}} = 1.37 \rho _{\mathrm{b}}$), which is calculated with the assumption of the isentropic flow from the nozzle inlet to the ambient atmosphere of the nozzle exit. Note that the uncertainty bars shown on the density profiles of Fig. 11 only refer to density uncertainties, but not position uncertainties in the z direction. Therefore, the horizontal caps of the vertical error bars have no physical meaning.

Fig. 10

Density contour plot of microjet with weak shocks

Fig. 11

Streamwise density profiles of microjet with weak shocks

As a global feature, the density profile in Fig. 11a exhibits a representative property appearing in an underexpanded free jet, i.e., the flow expansion and compression are quasi-periodically repeated downstream responsible for the shock cell structures. In addition, the density rapidly decreases below the ambient level by expansion waves originating from the nozzle lip. The local minima in the density profiles gradually increase with increasing streamwise distance. While, the level of the local maxima remains almost constant till the third peak. This trend is in good agreement with the experimental result of Panda and Seasholtz (1999). Figure 11b shows the density profile at the radial location of $r/D_e$ = 0.25. As seen in the compression regions of the first and second shock cells, each compression region includes a gradual change followed by an abrupt rise in density. Figure 11c shows the streamwise density profile along the jet lipline ($r/D_e$ = 0.5). It shows some small bumps quasi-periodically appearing, which are marked as small black circles in the density contour plot of Fig. 10. These bumps are responsible for the reflection as expansion waves of oblique shocks at the free jet boundaries.

5.3 Various Visual Representation for Flow Field of Microjet

Conventional schlieren systems are based on the deflection of light beams crossing a refractive index field and a line-of-sight imaging technique allowing only a qualitative flow visualization. In the optical setting, a collimated light beam is deflected across a knife-edge or cutoff filter causing a change of light intensity in the direction perpendicular to the knife-edge (Settles 2001). It is often seen that we compare computational schlieren images with experimental ones in order to assess the accuracy of numerical predictions. In this case, we should be aware that the standard experimental schlieren pictures include the “integrated” information of the density gradient along the line-of-sight direction. Instead, numerical results might be typically taken at “the cross-section”.

Figure 12a–d illustrate the flow features at the cross-section including the jet centerline for the same flow field of the microjet obtained by using various visualization techniques such as (a) vertical-knife-edge schlieren, (b) horizontal-knife-edge schlieren, (c) bright-field schlieren and (d) shadowgraphy. All the visualization results as well as the vertical and horizontal axes are non-dimensionalized, as shown in Fig. 12. Figure 12a, b shows the streamwise and radial density gradients (the flow direction is left-to-right.) For the near-field shock wave structures, Fig. 12a clearly shows the degree of the streamwise compression or expansion. It can be recognized the quasi-periodical shock-cell structure as a consecutive pattern of the expansion and compression regions, which keep the similar shape in the streamwise direction. As seen in Fig. 10, there are some densely areas of the density contour lines around the jet lipline (r/$D_e$ = 0.5). Hence, Fig. 12b highlights the radial variation of the jet shear layers. The bright-field schlieren shown in Fig. 12c, which is also referred to as the circular-cutoff schlieren (Settles and Hargather 2017), express the magnitude of the density gradient vector, and it indicates the degree of compression and expansion in the every direction. In addition, this technique sometimes can effectively capture the flow topology of three-dimensional shock structure (Maeno et al. 2005; Li et al. 2018; Sugawara et al. 2020). As shown in Fig. 12d, the shadowgraph image displays the detailed structure of the small perturbations around the jet when compared with any of the schlieren images shown in Fig. 12a, b. Please note that the Abel inversion method seems to have difficulty in avoiding the inversion error near the jet centerline (r/$D_e$ $\sim$ 0.1), which causes some spurious wavy features in the density contour in Fig. 12.

Fig. 12

Various visual representation of microjet with weak shocks

About the distinction between the schlieren and the shadowgraph methods, Settles (2001) states that the second spatial derivative of the refractive index can be much larger than the first derivative in gas flows involving shock waves or turbulence. For weaker disturbances overall and gradual phenomena like expansion fans, however, the schlieren method holds the advantage of much higher sensitivity. Hadjadj and Kudryavtsev (2005) found numerically that the shadowgraph technique is very sensitive to small density variations owing to double differentiation of the gas density. Therefore, it can be useful for capturing fine flow features in detail. From these results, we may conclude that it is necessary to carefully choose the experimental results obtained by a different visualization technique to compare numerical results (note that a different technique has a large variety of range of the level of sensitivity shown at the top of each figure).

5.4 Comparison Among Jet Centerline Density Profiles from Quantitative Visualization Techniques and RANS

In Fig. 13, the centerline density profile obtained by MZI is quantitatively compared with those by other quantitative flow visualization methods under the exactly same nozzle operating condition (NPR = 3) with different exit diameters ($D_e$). The density profiles normalized by the ambient density $\rho _{\mathrm{b}}$ from Nakamura and Iwamoto (1996) as well as Nicolas et al. (2017) are superimposed on the current experimental data (blue line) and the numerical result (red line). In order to make it easier to view, the precision error bars are removed from our experimental result. For a better understating of the current experimental and numerical results, we would like to explain the assumptions and restrictions made for each methodology.

The density profiles, which are obtained by the present and previous MZI methods through the density reconstruction using the Abel inversion method, are measured under the assumption of an axisymmetric jet. In the process, Nakamura and Iwamoto (1996) performed the phase shift analysis by the Laplace transform method, in contrast with the Fourier transform method used in the present study. For the BOS method, the density profile was captured from the instantaneous three-dimensional density field reconstructed with the simultaneous schlieren pictures, which were taken by mounting 12 synchronized cameras around a test nozzle. In addition, it should be noted that the wall contour of the nozzle used in the present experiment has a sinusoidal curve profile over the range from the nozzle inlet to the exit as shown in Fig. 2, while Nakamura and Iwamoto (1996) employed a convergent nozzle with a curvature radius of 2$D_e$ (= 20 mm) at the nozzle exit. Nicolas et al. (2017) used the wall contour of the nozzle that converges in the downstream direction at a constant half angle of 30$^\circ$ and followed by a short straight duct so that a uniform sonic condition is realized at the nozzle exit.

Fig. 13

Comparison of measured and simulated jet centerline density profiles

As seen in Fig. 13, there is an excellent quantitative agreement between the density profiles obtained from the present and previous MZI methods over the whole region measured, regardless of different nozzle exit diameters. It is evident that the nozzle wall boundary layer is found to have a negligible influence on the density profile of the microjet. The density profiles obtained from both the present MZI method and RANS show an excellent quantitative agreement with each other, except the slight deviation observed in the downstream region of the fourth shock-cell due to the unsteady jet behavior presumably (Raman 1998). A distinctive double bump can be seen just in the downstream region of the first shock-cell or just in the upstream region of the second shock-cell in both the density profiles. Both density profiles are in good agreement in the shape and density value. There is a qualitative agreement between the density profiles obtained from the present MZI method and BOS over the entire region measured. As seen in the profiles from the present MZI method and RANS, the profile from BOS also exhibits a double bump. It is observed that both the curves from the present MZI method and BOS agree well within the region of the first shock-cell. The values at the local minima in each density profile, which correspond to the ends of the expansion regions in the shock-cells, gradually increase with increasing streamwise distance. On the other hand, the streamwise locations of the local minima, showing the end of the expansion region, and those of the local maxima, indicating the end of the compression region, are gradually deviated from each other with increasing streamwise distance. However, the density values at these corresponding local minima and maxima agree well with each other except for the second positive peak. Although we are unable to determine the cause of the deviation at this stage, it could be attributed to different characteristic of these visualization techniques.

6 Concluding Remarks

The flow structures of a microjet with weak shocks were investigated by the Mach–Zehnder interferometer with the finite-fringe setting. The Abel inversion and the Fourier transform methods were utilized to reconstruct the density field of the microjet. The flow features of the microjet were ascertained by using various flow visualization methods such as the vertical knife-edge schlieren, the horizontal knife-edge schlieren, the bright-field schlieren, and the shadowgraphy. We observe that the density field in the compression regions of the first three shock-cells has two local maxima at locations away from the jet centerline, which has not been reported by other studies. The visual representations with a high spatial resolution studied in this paper could be useful for assessing the accuracy of numerical simulations examining intricate flow structures such as an interaction between shock waves and shear layers or shock–vortex interactions. The RANS simulation with the SST k-$\omega$ turbulence model was performed to model microjets, and the predicted jet centerline density profiles are compared with the ones from present and previous experimental data (Nakamura and Iwamoto 1996; Nicolas et al. 2017). An excellent overall agreement is achieved among three profiles, and it is confirmed that the jet centerline density profiles are insensitive to a nozzle exit diameter. Also, we find insignificant effect of the nozzle wall boundary layer on the density profile. The predicted density profile exactly coincides with the data from the present MZI method till the third shock-cell in the sense that both the profiles exhibit a distinctive double bump between the first and second shock-cells.

As a comparison between the present MZI and BOS techniques, there is a very favorable overall agreement between the centerline density profiles particularly within the first shock cell. Although a deviation between the streamwise locations of the local minima and maxima in the density profiles obtained from both the techniques gradually increase streamwise distance, the local minima and maxima values agree well with each other except for the second positive peak. A double bump can be also seen in the profile from BOS. Considering simplicity of the present MZI method and its comparable accuracy to the conventional method we conclude that the current MZI method is significantly effective to examine the fine structures of the shock containing microjets and makes it possible to provide experimental data with a high accuracy. We believe that the experimental data presented in this paper would serve to be a useful database to validate other non-intrusive measurement techniques, numerical simulation codes as well as theoretical models for supersonic jets with weak shocks.