Skip to main content
SpringerLink
Log in

Pressure Drop for Gas and Polymer Aqueous Solution Two-Phase Flows in Horizontal Circular Microchannel

  • Published:
Flow, Turbulence and Combustion Aims and scope Submit manuscript

Abstract

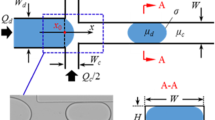
This study investigated pressure drop for gas and non-Newtonian liquid two-phase flows in a horizontal circular microchannel (0.25 mm I.D.) made of fused silica tube. Three kinds of polymer aqueous solutions (sodium carboxymethyl cellulose, xanthan gum and polyacrylamide) with different mass concentration were used as non-Newtonian liquids, while the nitrogen gas was used as the test gas. The flow conditions were varied in the range of the volumetric flux jL = 0.12–0.58 m/s for the liquid phase and the volumetric flux jG = 0.03–0.84 m/s for the gas phase. The flow patterns observed for these combinations of gas–liquid conditions were all slug flow or Taylor flow. In the preliminary experiment for single-phase liquid flows, Darcy friction factor data were obtained for non-Newtonian liquid as well as Newtonian one, and the obtained friction factor agreed with that for Hagen-Poiseuille flow by using generalized Reynolds number. The two-phase pressure drop varied depending on types of polymer because of the shear thinning effects of polymer solutions with the shear rate. In addition, the elasticity of polymer solutions depending on its molecular weight might affect the pressure drop characteristics. The experimental data of two-phase pressure drop have been compared with the result calculated by existing models. As the comparison results, the existing models predicted the present data if the appropriate correlations for homogeneous viscosity and two-phase friction multiplier needed in the models were used for each polymer aqueous solution. In addition, the unit cell model could correlate the pressure drop data if a fitting parameter changes against each polymer solution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Abbreviations

a, b :

Constant values in Eqs. (2) and (29) (−)

Bo :

Bond number

c :

Constant value in Eq. (26)

C :

Constant value in Eq. (15)

Ca :

Capillary number (−)

D :

Inner diameter (m)

j :

Volumetric flux (m/s)

K :

Consistency coefficient (Pa sn)

L :

Length (m)

n :

Flow index (−)

N conf :

Confined number

ΔP :

Pressure drop (N/m2)

Q :

Volume flow rate (m3/s)

Re :

Reynolds number (−)

u :

Velocity (m/s)

We :

Weber number

x :

Mass quality

X :

Lockhart–Martinelli parameter

y :

Distance from the wall (m)

α :

Void fraction (−)

β :

Gas volume flow fraction (−)

λ :

Darcy friction factor (−)

µ :

Viscosity (Pa s)

ρ :

Density (kg/m3)

σ :

Surface tension (N/m)

τ :

Wall shear stress (N/m2)

a :

Apparent

e, eff :

Effective

f :

Friction

L :

Liquid

G :

Gas

s, S :

Slug

SP :

Single-phase flow

TP :

Two-phase flow

UC :

Unit cell

B :

Bubble

References

  • Ali, M.I., Sadatomi, M., Kawaji, M.: Two-phase flow in narrow channels between two flat plates. Can. J. Chem. Eng. 71, 1411–1435 (1994)

    Google Scholar 

  • Awad, M.M., Muzychka, Y.S.: Effective property models for homogeneous two-phase flows. Exp. Thermal Fluid Sci. 33(1), 106–113 (2008)

    Article  Google Scholar 

  • Bandaru, S.V.S.R.K., Chhabra, R.P.: Pressure drop for single and two-phase flow of non-Newtonian liquids in helical coils. Can. J. Chem. Eng. 80, 315–321 (2002)

    Article  Google Scholar 

  • Beattie, D.R.H., Whalley, P.B.: A simple two-phase frictional pressure drop calculation method. Int. J. Multiphase Flow 8(1), 83–87 (1982)

    Article  Google Scholar 

  • Boger, D.V., Cable, P.J.: An anomalous effect in the measurement of normal stresses in polyacrylamide solutions. Rheol. Acta 16, 322–323 (1977)

    Article  Google Scholar 

  • Bretherton, F.P.: The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188 (1961)

    Article  MathSciNet  Google Scholar 

  • Chhabra, R.P., Farooqi, S.I., Richardson, J.F.: Isothermal two-phase flow of air and aqueous polymer solutions in a smooth horizontal pipe. Chem. Eng. Res. Des. 62, 22–32 (1984)

    Google Scholar 

  • Chisholm, D., Laird, A.D.K.: Two-phase flow in rough tubes. Trans. ASME 80(2), 276–286 (1958)

    Google Scholar 

  • Chung, P.M.-Y., Kawaji, M.: The effects of channel diameter on adiabatic two-phase flow characteristics in microchannels. Int. J. Multiphase Flow 30, 735–761 (2004)

    Article  Google Scholar 

  • Dukler, A.E., Wicks III, M., Cleveland, R.G.: Pressure drop and hold-up in two-phase flow. AIChE J. 10(1), 38–51 (1964)

    Article  Google Scholar 

  • Farooqi, S.I., Richardson, J.F.: Rheological behaviour of Kaolin suspensions in water and water glycerol mixtures: trans. IChemE 58, 116–124 (1980)

    Google Scholar 

  • Farooqi, S.I., Richardson, J.F.: Horizontal flow of air and liquid (Newtonian and non-Newtonian) in a smooth pipe. Part I: a correlation for average liquid holdup, Transactions of IChemE 60, 292–305 (1982)

    Google Scholar 

  • Fu, T., Ma, Y., Funfschilling, D., Li, H.Z.: Bubble formation in non-Newtonian fluids in a microfluidic T-junction. Chem. Eng. Process. 50, 438–442 (2011a)

    Article  Google Scholar 

  • Fu, T., Ma, Y., Funfschilling, D., Li, H.Z.: Gas–liquid flow stability and bubble formation in non-Newtonian fluids in microfluidic flow-focusing devices. Microfluid. Nanofluid. 10, 1135–1140 (2011b)

    Article  Google Scholar 

  • Hwang, Y.W., Kim, M.S.: The pressure drop in microtubes and the correlation development. Int. J. Heat Mass Transf. 49(11–12), 1804–1812 (2006)

    Article  Google Scholar 

  • Imaizumi, Y., Kunugi, T., Yokoike, T., Kawara, Z.: Viscoelastic fluid behaviors around a rising bubble via a new method of mesh deformation tracking. Chem. Eng. Sci. 120, 167–173 (2014)

    Article  Google Scholar 

  • Kandlikar, S.G.: Fundamental issues related to flow boiling in minichannels and microchannels. Exp. Therm. Fluid Sci. 26, 389–407 (2002)

    Article  Google Scholar 

  • Kawahara, A., Chung, P.M.-Y., Kawaji, M.: Investigation of two-phase flow pattern, void fraction and pressure drop in a microchannel. Int. J. Multiphase Flow 28, 1411–1435 (2002)

    Article  Google Scholar 

  • Kawahara, A., Sadatomi, M., Nei, K., Matsuo, H.: Experimental study on bubble velocity, void fraction and pressure drop for gas–liquid two-phase flow in a circular microchannel. Int. J. Heat Fluid Flow 30, 831–841 (2009)

    Article  Google Scholar 

  • Kawahara, A., Sadatomi, M., Nei, K., Matsuo, H.: Characteristics of two-phase flows in a rectangular microchannel with a T-junction type gas–liquid mixer. Heat Transf. Eng. 32, 585–594 (2011)

    Article  Google Scholar 

  • Kawahara, A., Sadatomi, M., Shimokawa, S.: Lengths of bubble and slug and pressure drop in gas–liquid slug flow in microchannels. Multiphase Sci. Technol. 24, 239–256 (2012)

    Article  Google Scholar 

  • Kawaji, M., Chung, P.M.-Y.: Unique characteristics of adiabatic gas-liquid flows in microchannels: diameter and shape effects on flow patterns, void fraction and pressure drop. In: Proceedings of 1st International Conference on Microchannels and Minichannels, pp. 115–128 (2003)

  • Kozicki, W., Chou, C.H., Tiu, C.: Non-Newtonian flow in ducts of arbitrary cross-sectional shape. Chem. Eng. Sci. 21, 665–679 (1966)

    Article  Google Scholar 

  • Kreutzer, M.T., Kapteijn, F., Moulijn, J.A., Kleijn, C.R., Heiszwolf, J.J.: Inertial and interfacial effects on pressure drop of Taylor flow in capillaries. AIChE J. 51(9), 2428–2440 (2005)

    Article  Google Scholar 

  • Lockhart, R.W., Martinelli, R.C.: Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Prog. 45(1), 39–48 (1949)

    Google Scholar 

  • Mansour, H.M., Kawahara, A., Sadatomi, M.: Experimental investigation of gas–non-Newtonian liquid two-phase flows from T-junction mixer in rectangular microchannel. Int. J. Multiphase Flow 72, 263–274 (2015)

    Article  Google Scholar 

  • McAdams, W.H.: Heat Transmission, 3rd edn. McGraw-Hill, New York (1954)

    Google Scholar 

  • Mishima, K., Hibiki, T.: Some characteristics of air–water two-phase flow in small diameter vertical tubes. Int. J. Multiphase Flow 22, 703–712 (1996)

    Article  Google Scholar 

  • Ohta, M., Yoshida, Y., Sussman, M.: A computational study of the dynamic motion of a bubble rising in Carreau model fluids. Fluid Dyn. Res. 42, 025501 (2010)

    Article  MathSciNet  Google Scholar 

  • Picchi, D., Correra, S., Poesio, P.: Flow pattern transition, pressure gradient, hold-up predictions in gas/non-Newtonian power-law fluid stratified flow. Int. J. Multiphase Flow 63, 105–115 (2014)

    Article  MathSciNet  Google Scholar 

  • Serizawa, A., Feng, Z.P., Kawara, Z.: Two-phase flow in microchannels. Exp. Therm. Fluid Sci. 26, 703–714 (2002)

    Article  Google Scholar 

  • Sontti, S.G., Atta, A.: Formation characteristics of Taylor bubbles in power-law liquids flowing through a microfluidic co-flow device. J. Ind. Eng. Chem. 65, 82–94 (2018)

    Article  Google Scholar 

  • Sousa, R.G., Reithmuller, M.L.A., Pinto, M.F.R., Campos, J.B.L.M.: Flow around individual Taylor bubbles rising in stagnant polyacrylamide (PAA) solutions. J. Non-Newton. Fluid Mech. 135, 16–31 (2006)

    Article  Google Scholar 

  • Tang, G.H., Lu, Y.B., Zhang, S.X., Wang, F.F., Tao, W.Q.: Experimental investigation of non-Newtonian liquid flow in microchannels. J. Non-Newton. Fluid Mech. 173–174, 21–29 (2012)

    Article  Google Scholar 

  • Yang, Z.C., Bi, Q.C., Liu, B., Huang, K.X.: Nitrogen/non-Newtonian fluid two-phase upward flow in non-circular microchannels. Int. J. Multiphase Flow 36, 60–70 (2010)

    Article  Google Scholar 

Download references

Acknowledgements

This study was partially supported by the Harada Memorial Foundation and KAKENHI (19K04172).

Author information

Authors and Affiliations

  1. Faculty of Advance Science and Technology, Kumamoto University, 2-39-1 Kurokami, Chuo-ku, Kumamoto City, 860-8555, Japan

    Akimaro Kawahara, Yukihiro Yonemoto & Yoichi Arakaki

Authors
  1. Akimaro Kawahara
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yukihiro Yonemoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yoichi Arakaki
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Akimaro Kawahara.

Ethics declarations

Conflict of interests

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kawahara, A., Yonemoto, Y. & Arakaki, Y. Pressure Drop for Gas and Polymer Aqueous Solution Two-Phase Flows in Horizontal Circular Microchannel. Flow Turbulence Combust 105, 1325–1344 (2020). https://doi.org/10.1007/s10494-020-00127-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10494-020-00127-z

Keywords

Search

Navigation