Abstract
In Lagrangian stochastic collision models, a fictitious particle is generated to act as a collision partner, with a velocity correlated to the velocity of the real colliding particle. However, most often, the fluid velocity seen by this fictitious particles is not accounted for in the generation of the fictitious particle velocity, leading to a de-correlation between the fictitious particle velocity and the local fluid velocity, which, after collision, leads to an unrealistic de-correlation of the real particle velocity and the fluid velocity as seen by the particle. This de-correlation, in turn, causes a spurious decrease of the particle kinetic energy, even though the collisions are assumed perfectly elastic. In this paper, we propose a new model in which the generated fictitious particle velocity is correctly correlated to both the real particle velocity and the local fluid velocity at the particle, hence preventing the spurious loss of the total particle kinetic energy. The model is suitable for small inertial particles. Two algorithms for integrating the collision frequency are also compared to each other. The models are validated using large eddy simulation (LES) of mono-dispersed particle-laden stationary homogeneous isotropic turbulence. Simulations are conducted with spherical particles with different turbulent Stokes number, \(St_t = [0.75 - 5.8]\), and volume fractions, \(\alpha _p = [0.014 - 0.044]\), and are compared to the results of the LES using a deterministic discrete particle simulation model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Turbulent two-phase flows are found in various environmental, biological and industrial processes. Typical examples are various, such as the break-up and coalescence of cloud droplets (Xue et al. 2008), collisions of blood cells (Chesnutt and Marshall 2009), and fluidized beds (van Wachem et al. 2001b), to name just a few. The complexity of the underlying physics are due to the multi-level of interactions occurring in such problems, such as particle-fluid and particle–particle interactions. When considering solid particles, the latter interaction is essentially reduced to analysing collisions, although other features such as fragmentation (Bruchmüller et al. 2011) may also be considered. In the case of particles, a collision occurs when the distance between two particles is equal to their average diameter.
In numerical simulations, the Lagrangian framework is commonly used to predict the behaviour of particles in turbulent gas-solid flows. The trajectories of individual particles are modelled by solving Newton’s second law, where various forces such as drag, gravity and the forces arising from collisions are typically taken into account to compute the motion of the particles. The particle solver is coupled with either Direct Numerical Simulation (DNS) or Large Eddy Simulation (LES), which are numerical tools to solve the dynamics of turbulent flows. The former may be more accurate, as it captures all the scales of the turbulence, but it is computationally very expensive for flows with a high Reynolds number. LES offers a good balance between accuracy and computational time. The level of coupling between the particles and the turbulent flow depends mainly on the volume fraction and mass loading (Balachandar and Eaton 2010). If the volume fraction is higher than about \(10^{-3}\), the interaction between particles, i.e. collisions, must be taken into account, and simulations are described as four-way coupled.
In the Lagrangian framework, particle collisions are handled in two steps : (1) the detection of colliding particles, and (2) the calculation of the post-collisional velocities. Two methods are typically found in the literature to solve the latter: the hard-sphere model (Maw et al. 1976) and the soft-sphere model (Cundall and Strack 1979). The soft-sphere model is also commonly referred to as discrete element model or distinct element model (DEM), and allows for enduring contact between two particles. In this work, the hard-sphere model is used, and is referred to as discrete particle simulation (DPS). In DPS, the particle collisions are assumed binary and instantaneous, and this model is therefore suitable for volume fractions up to values corresponding to moderately dense flows. At higher volume fractions the assumptions of binary and instantaneous collisions are no longer valid.
To numerically detect a collision, a straightforward method is to evaluate the distance between all particle pairs (Allen and Tildesley 1989). A basic implementation of this would require the checking of all particle pairs, therefore the computational cost scales as \({\mathscr {O}}(N_p^2)\). Using optimised techniques, this leads to a search cost of \({\mathscr {O}}(N_p\log (N_p))\) (Hopkins and Louge 1991), which is still computationally expensive for a large number of particles, hence the motivation for stochastic approaches, which typically have a cost of \({\mathscr {O}}(N_p)\) (Sommerfeld 1999).
Oesterle and Petitjean (1993) have proposed a stochastic Lagrangian model where, depending on the collision probability, a fictitious colliding particle partner is generated along the trajectory of a real particle. Following a rejection-acceptance method, a certain “random” collision can be selected to be carried out. In case a collision event occurs, a fictitious particle is generated, with a random velocity, which has an expectation equal to the local averaged particle velocity. A hard-sphere model is subsequently applied to compute the post-collisional velocity of the real particle. However, this model does not take into account the particle–particle velocity correlation existing between two colliding particles in a turbulent flow. Sommerfeld (1999) proposed an improved version of the model where the generated fictitious particle velocity is directly correlated to the real particle velocity. This model is referred to as the stochastic one particle (SOP) model. Although this model shows promising results, Although in this model the velocity of the fictitious particle is correlated to the velocity of the real particle, and there is thus an indirect coupling between the velocity of the fictitious particle and the fluid velocity, there is no direct correlation between the fictitious particle velocity and the fluid velocity. This means that the correlation between the velocity of the fluid and the velocity of the fictitious particle is too small. This leads to a spurious de-correlation between the real particle velocity and the local fluid velocity, which, in turn, decreases the particle kinetic energy. Berlemont et al. (2001) adapted a similar stochastic model for the tracking of multiple particles. To overcome the de-correlation of the fluid-particle velocity, they proposed an ad hoc method that modifies the post-collisional fluid velocity, so it then satisfies, on average, the fluid-particle velocity covariance. However, the distribution of collision properties, such as the angles, remained the same.
These stochastic approaches also rely on the evaluation of the collision rate, collision probability, or collision frequency (Zaichik et al. 2003). In the work of Sommerfeld (1999), a local collision frequency is computed based on the relative velocity between the real and fictitious particles. However, for homogeneous turbulence, there exist multiple models to evaluate the average, or global, collision frequency, which is proportional to the average of the relative velocity norm between colliding particles (Franklin et al. 2007). In order to correctly evaluate the global collision frequency, it is important to recognize the various physical mechanisms responsible for particle–particle collisions, such as shear induced collisions or turbulent induced particle agitation (Meyer and Deglon 2011). The work of Saffman and Turner (1956) focuses on the relative velocity induced by shear flow for zero-inertia particles, whereas Abrahamson (1975) worked on the collision frequency of inertial particles in vigorously turbulent flows. In his study, the velocities of colliding particles are assumed to be uncorrelated and follow a Gaussian distribution. However, colliding particle velocities are correlated to a certain degree, especially in the case of small particles, as their motion is driven by the same turbulent eddies. Lavieville et al. (1995) adopted a more general approach, assuming that the velocity distributions of the particle fluctuating velocities are Maxwellian. The fluid-particle velocity correlation distribution is also assumed a joint normal distribution. The final expression of the fluid-particle velocity correlation is derived by introducing a fluid-particle correlation coefficient. In their study with small, mono-dispersed particles, the correlation between the particle velocity and the local fluid velocity seen by the particle is taken into account in the computation of the collision frequency. The statistics of the fluid velocity seen by two colliding particles is the same, i.e. assuming particles smaller than the smallest turbulent scale. The results of Lavieville et al. (1995) are compared to LES and show generally good results, depending on the kinetic energy of the particles and their Stokes number. Pigeonneau (1998) has adopted a very similar theory and has extended this theory for slightly bigger particles and droplets, accounting for the fact that the fluid velocity as seen by the two particles in the collision are different. This is achieved by an extrapolation of the expression of the fluid statistics across the length of the particle, by accounting for the first term of the Taylor expansion in the expression.
Other correction terms have also been integrated in the collision frequency computation, such as the collision efficiency (Thomas et al. 1999) or the radial distribution function at contact (Sundaram and Collins 1997) which is used to integrate the effect of preferential concentration.
This paper presents a new fully correlated model for dealing with stochastic collisions in Euler–Lagrangian gas–solid flows. Although this model assumes that the velocity fluctuations of the particle and of the fluid as seen by the particle are normally distributed, we do not assume that the fluid-particle covariances are normally distributed, as in Lavieville et al. (1995) and Pigeonneau (1998). Using a Cholesky decomposition of the formulated covariance matrix and assuming that the dimensions behave independent, we propose an expression for the fictitious particle velocity which satisfies the solution of this covariance matrix. In our model, we assume the particles are small, so that we can take the statistics of the fluid velocity as seen by the particle to be the same for the real and the fictitious particle. The generated fictitious particle velocity is directly correlated to both the real particle velocity and the local fluid velocity seen. The spurious decrease of the particle kinetic energy is prevented, while the model ensures that the collision physics remain consistent, e.g. the distribution of collision angles depends on the particle inertia. Two different algorithms to evaluate the collision frequency in such stochastic models are also discussed and compared. LES simulations of stationary homogeneous isotropic turbulence are performed following the configuration of Lavieville et al. (1995). The stochastic model results are validated against deterministic LES–DPS simulations. The flows considered are dilute enough to apply the hard-sphere model but dense enough so to allow relevant statistics of collisions. Mono-dispersed solid particles are assumed perfectly elastic, i.e. with no loss of energy during collisions.
This manuscript is organised as follows. Section 2 presents the numerical methods used in the manuscript, including the fluid equations of motion, the fluid turbulence forcing, the particle equations of motion, the general collision model, and the implementation of the deterministic collision model. Section 2 also presents the framework of generating a fictitious particle for the stochastic collision framework and presents the stochastic one particle (SOP) model. Section 3 presents the newly proposed correlation stochastic one particle (CSOP) model. In Sect. 4 simulations of four cases of statistically homogeneous isotropic particle-laden turbulence are pursued, of which the results are discussed and the various treatments are compared. Finally, Sect. 5 draws the conclusions from this work.
2 Numerical Methods
The algorithm to predict gas-solid flow consists of three steps: (1) the Eulerian turbulent flow dynamics are resolved using direct numerical simulation (DNS) or a model for turbulence; (2) the particle dynamics are then evaluated via a particle-transport step; (3) the inter-particle collisions are treated and the particle post-collisional velocities computed. These will be shortly discussed below.
2.1 Fluid Phase Modelling
In this work, we will consider particles in a box of statistically homogeneous isotropic turbulence. Such a flow has been used for many studies over a time-span of more than 4 decades (Riley and Patterson 1974) and has been used to analyze the behaviour of turbulence (Lundgren 2003) as well as studying the behaviour of particles in such flows (Boivin et al. 1998).
The turbulence in the box will be generated and sustained by forcing (Mallouppas et al. 2013). As in this work the particle volume fraction and the exchange of momentum to the fluid are very low, they can both be safely neglected. However, the flow is sufficiently dense, that particle collisions cannot be neglected. Considering LES, the fluid phase governing equations are then given by
where the operator \({\widetilde{\cdot }}\) represents the filtering, \({\widetilde{v}}_{f,i}\) is the filtered fluid velocity in the i-direction, \({\widetilde{p}}\) is the filtered pressure, and \(f_j\) is the forcing term to sustain a turbulent flow (Mallouppas et al. 2013), \({\widetilde{\tau }}_{ij}\) is the filtered viscous stress tensor and \(\tau ^m_{ij}\) represents the sub-grid stresses. For an incompressible flow, the filtered viscous stress tensor is defined as
where \(\mu _f\) is the molecular, dynamic fluid viscosity. The forcing term (Mallouppas et al. 2013) sustains the kinetic energy of the homogeneous isotropic turbulence at a given turbulence kinetic energy, \(q_{f,wanted}^2\), and reads as
where \(q_f^2\) is the turbulence kinetic energy, \(\varDelta t\) the timestep, and \(v_{j,\text {triggered}}\) is a temporally correlated velocity field randomly triggered from a turbulence energy spectrum. The subscript wanted corresponds to the value which is aimed for, and the subscript computed corresponds to the currently determined value.
Following Boussinesq’s hypothesis, the sub-grid stresses are proportional to the local filtered rate of strain, \({\widetilde{S}}_{ij}\), through the sub-grid viscosity, \(\mu _{SGS}\), which is computed using the Smagorinsky model (Smagorinsky 1963)
where \(C_S\) is the Smagorinsky constant and \(\varDelta\) the filter width. Simulations are performed using an in-house CFD research code, MultiFlow (van Wachem et al. 2000). The Navier–Stokes equations are solved on a collocated grid. The variable discretization uses a central scheme for the advection term and a second order Euler scheme for the transient term. The velocity-pressure solver is fully implicit and coupled (Bartholomew et al. 2018; Denner and van Wachem 2014; Xiao et al. 2017).
2.2 Particle Phase Modelling
The equation of motion of particles has been derived from Newtons second law (Maxey and Riley 1983). Considering heavy particles, \(\rho _p \gg \rho _f\) where \(\rho _p\) and \(\rho _f\) are the particle and fluid density, respectively, considering that the particles are smaller than the smallest turbulent length scale, and neglecting gravity, the drag is the only relevant force, and the equation of motion of the particle is
where \(x_{p,i}\) and \(v_{p,i}\) are the particle position and velocity in the i-direction, respectively, \(v_{f@p,i}\) is the undisturbed fluid velocity as seen by the particle (Gatignol 1983), \(\tau _p\) is the particle momentum response time, which is a time scale measuring the time required for a particle to respond to a change in flow velocity and defined as (Crowe et al. 1998)
where \(d_p\) is the particle diameter and \(f_D\) is the particle drag function, which depends on the particle Reynolds number, where the particle Reynolds number is defined as
and the particle drag function as
where \(C_D\) is the drag coefficient of the particle given as (Schiller and Naumann 1933)
2.3 Hard-Sphere Collision Model
In a hard-sphere model, particles collide when their distance is equal to their averaged diameter. In the hard-sphere model, collisions are considered instantaneous and binary. From the conservation of momentum, the particle post-collisional velocities, \({v}_{p1}^{new}\) and \({v}_{p2}^{new}\), are computed as
where \({J_i}\) is the impulse exchange vector which, neglecting friction, is given as (van Wachem et al. 2001a)
where \(e_c\) is the coefficient of restitution (\(e_c=1\) in case of perfectly elastic particles), \({w_i} = {v}_{p1,i} - {v}_{p2,i}\) the relative velocity between the colliding particles, and \({k}_i\) the unit vector joining the colliding particle centres. Rotation of the particles is neglected, but can be easily accounted for.
2.4 Deterministic Discrete Particle Simulation
In a deterministic discrete particle simulation (DPS), collisions are treated by evaluating the potential collision time between each pair of particles in the domain. Therefore, this approach is also commonly referred to as event-driven (Mallouppas and van Wachem 2013). Once a minimum collision time has been established, all the particle positions are updated with this collision time. The particle positions are updated using a third order Taylor expansion in time, and the velocities are computed using a second order Taylor expansion in time,
where \(x_{p,i}^{n}\) and \(v_{p,i}^{n}\) are the position and velocity, respectively, of the particle p in the direction i at time level n, \(\varDelta t\) the timestep, and \(F_{i}^n\) the forces acting on the particle and its mass \(m_p\). In a LES–DPS simulation, the forces acting on each particle arise from the fluid drag forces. The interpolation of the fluid properties to the particles is performed with a third order polynomial interpolation (Mallouppas and van Wachem 2013).
Once the particles have been updated with the minimum collision time, two of the particles in the domain should be touching. The collision of the two touching particles is then handled with the model described in the previous section. In this algorithm, the collision time needs to be determined for each pair of particles, making it very expensive. Therefore, a stochastic collision model is very favourable.
2.5 Fictitious Collision Particle
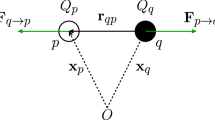
The inter-particle collisions in the hard-sphere model can be resolved deterministically or stochastically. A deterministic collision is found by comparing all pairs of particles in a domain, and determining if the pair of particles is separated by a distance which is the average diameter of the two particles. In a stochastic collision framework, the collision probability of each “real” particle in the domain is stochastically evaluated, and if appropriate, a fictitious particle, typically referred to as particle 2, is generated. Its position and velocity are subsequently determined from a stochastic model. A rejection-acceptance method is then used to determine whether the fictitious collision between the real and fictitious particles will occur or not. This is achieved by selecting a random number from a uniform distribution on [0,1]: a fictitious collision is executed if that random number is larger than the expected collision probability. If a collision should be executed, the generated random position of the fictitious particle follows the condition of uniform probability of finding the projected position, \({x}_{p_2,\perp }\), on the plane \(({t}^1, {t}^2)\) that is orthogonal to the relative particle velocity \({w} = {v}_{p1} - {v}_{p2}\), as shown in Fig. 1. An example of a stochastic model to determine the position and velocity of the fictitious particle is the stochastic one particle (SOP) model.
2.5.1 SOP Model
In the SOP model (Sommerfeld 2001), the fictitious particle velocity is estimated as
where \(\xi \sim {\mathscr {N}}(0,1)\) is a Gaussian random number of mean zero and a standard deviation equal to unity, \(\langle {v_p^2}\rangle = \frac{2}{3}q_p^2\) is the mean square particle fluctuating velocity and \(q_p^2\) is the particle kinetic energy. \(R_{pp}\) is the particle–particle velocity correlation of two colliding particles
To determine the particle–particle velocity correlation, there exist various models, such as the empirical formula proposed by Sommerfeld (2001), given as
where \(St_t\) is the turbulent Stokes number, defined as the ratio between, the particle response time, \(\tau _p\), and the Lagrangian integral time scale, \(T_L\).
3 New CSOP Model
In this section, a new model taking into account the particle–particle velocity correlation and the particle-fluid velocity correlation upon the velocity of the fictitious particle is introduced. This section is structured as follows. After deriving the expression for the velocity of the fictitious particle in the new correlated stochastic one particle (CSOP) model, Sect. 3.1 discusses how the position of the fictitious particle is determined. Section 3.2 discusses how to locally evaluate the collision probability and, subsequently, Sect. 3.3 discusses how the global collision probability is determined. Section 3.4 then compares the implications and implementation of the two approaches to determine the collision probability and compares the algorithms for this.
The SOP model, given by Eq. (15), is limited by the fact that the fictitious particle velocity, \({v}_{p2}\), is only correlated to the real particle velocity but not to the local fluid velocity. However, the motion of a particle in a flow is, depending on the particle and fluid properties, correlated to the turbulent flow transporting it. Neglecting the covariance term, \(\langle v_{f@p_2,i} v_{p_2,i} \rangle\), has been observed in previous work (Berlemont et al. 2001; Fede et al. 2015), and will lead to a decrease in particle kinetic energy when the flow statistics are stationary.
The idea of the new model, the correlated stochastic one particle (CSOP) model, is to extend Eq. (15) such that the fictitious particle velocity also depends on the local fluid velocity. Particles are assumed small enough, so that the stochastics of the fluid velocity as seen by both colliding particles is the same. The three variables which describe the problem, namely \({v}_{p_1}\), \({v}_{p_2}\) and \({v}_{f@p}\), form a tri-variate normal distribution. This assumption has been tested by analyzing the results of a deterministic LES–DPS simulation with a deterministic collision algorithm, and for the cases considered these variables are indeed described well by a Gaussian function, as shown in Fig. 2.
A covariance matrix can be formulated, which is defined as
where \(\langle {v_f^2}\rangle (=\langle v_{f@p}^2\rangle )\) is the local fluid velocity variance, and \(\sigma _{fp}\) and \(\sigma _{pp}\) are the fluid-particle and particle–particle covariances, respectively taken as
from which the particle-fluid, \(R_{fp}\), and particle–particle, \(R_{pp}\), correlations are computed as
The covariance matrix is based on a one-dimensional formalism, i.e. each dimension is assumed independent and can hence be treated independently,
Hereafter, the dimension subscripts i, j are omitted for simplicity.
From the covariance matrix, a stochastic representation of the three variables can be evaluated. A method to sample n random numbers from a multivariate normal distribution can be summarised as:
-
1.
Determine a matrix \({A}\) such that \({A}{A}^T = {\varSigma }\), where \({\varSigma }\) is the covariance matrix;
-
2.
Generate a vector \({z} = (z_1,...,z_n)\) with \(z_i \sim {\mathscr {N}}(0,1)\);
-
3.
Compute the sampled random variable vector \({x}\) as
$$\begin{aligned} {x} = {\mu } + {A}{z} \end{aligned}$$(24)where \(\mu _i = E(x_i)\) is the mean of the variable.
When considering homogeneous isotropic turbulence, the mean of the three variables (\({v}_{p_1}\),\({v}_{p_2}\),\({v}_{f@p}\)) is equal to zero. A convenient way to obtain \({A}\), is to apply a Cholesky decomposition of the covariance matrix, \({\varSigma }\), such that
where \({L}\) is a lower triangular matrix. This decomposition can be found, because \({\varSigma }\) is a symmetric matrix, and is also be positive semi-definite, because of the condition
Under the assumption of stationary homogeneous isotropic turbulence, the system to solve is
From the Cholesky decomposition of the 3x3 covariance matrix \(\varSigma\), the lower triangular matrix is obtained as
The positive semi-definite condition for \({\varSigma }\) (Eq. 26) ensures that the numerators of the bottom right element of \({L}\) are roots of positive numbers. As \(v_{p_1}\) and \(v_{f@p}\) are known variables in the problem, \(z_1\) and \(z_2\) can be computed as
and the random fictitious particle velocity, \(v_{p_2}\), can be stochastically evaluated as
where \(z_3 \sim {\mathscr {N}}(0,1)\). When the particle velocities are uncorrelated to the fluid velocity, i.e. \(R_{fp}= 0\), Eq. (15) of the SOP model is recovered.
3.1 Fictitious Particle Position
The methodology for generating the fictitious particle position is rigorously developed hereafter, and follows a similar procedure as previous works (Sommerfeld 2001; Berlemont et al. 2001). The methodology is sketched in Fig. 3. Because of the symmetry of collision between two particles, the projection of the impact point is uniform on the cross-sectional collision plane defined by the normal vector \({n} = -\frac{{w}}{|{w}|}\), where \({w}\) is the relative velocity between the two particles. Two uniform random numbers, \(\beta \in [0;1]\) and \(\alpha \in [0;2\pi ]\), are chosen to generate the random position of the fictitious particle.
Generation of the fictitious particle \(\mathbf {p_2}\) position (in blue). A spherical coordinate system (\({n},{t}^1,{t}^2\)) is build depending on the relative velocity between the two particles, \({w}\). Two uniform random numbers are generated, \(\beta \in [0;1]\) and \(\alpha \in [0;2\pi ]\), which ensure the symmetry condition of the collision impact point, \({\mathscr {C}}\), i.e. uniformity on the cross-sectional plane, \({\mathscr {S}}_\perp\). The angles \(\varPsi\) and \(\varPhi\) are derived as a function of \(\alpha\) and \(\beta\), and the position of \(\mathbf {p_2}\) is then computed. Note that the two particles are presented with different diameters for clarity
The coordinate system (\({n},{t}^1,{t}^2\)) is obtained by first setting the normal vector in the opposite direction of the relative velocity, \({n} = -\frac{{w}}{|{w}|}\). The two tangential vectors, \({t}^1\) and \({t}^2\), can be any chosen orthogonal vectors in the tangential plane, i.e. verifying \({n} \cdot {t}^1 = {n} \cdot {t}^2 = {t}^1 \cdot {t}^2= 0\). For instance, the following pair verifies these conditions:
In the new local coordinate system (\({n},{t}^1,{t}^2\)), the coordinates of point \({x}_{p2}\), the center of the fictitious particle \(p_2\), are defined as
where \(d_p\) is the particle diameter and the two spherical coordinate angles, \(\varPhi\) and \(\varPsi\), are expressed in terms of the random numbers \(\beta\) and \(\alpha\) as
Finally, in the global coordinate system, the position of the fictitious particle is computed as
Figure 4 shows the results obtained from LES–DPS on the projection of various particle positions during a collision on the tangential plane \(({t}_1,{t}_2)\). The points are uniformly distributed on the plane, confirming the uniform condition applied for the stochastic generation of the fictitious particle position.
3.2 Local Evaluation of the Collision Frequency
After a fictitious particle has been generated, the probability of the collision occurring between the real particle and the fictitious particle must be also determined. This probability is stochastically determined from the collision frequency. The collision frequency can be determined locally, around each real particle, or globally, for the whole system.
The local collision frequency can be directly determined from kinetic theory Lun et al. (1984), and it is computed for each real particle, \(p_1\), as Sommerfeld (2001)
where \(n_p({x}_{p_1})\) is the local number of particles per volume, \({v}_{p_2}\) is the generated fictitious particle velocity, obtained from a stochastic model, and \(g_0\) is the radial distribution function at contact, which is always greater or equal to one and it is introduced to take into account particle clustering effect on the collision frequency (Sundaram and Collins 1997; Reade and Collins 2000). In the present work, the cases studied are considered dilute and the particles are inertial enough not to show a very strong clustering behaviour, hence we assume \(g_0 = 1\) (van Wachem et al. 2001a). \(n_p({x}_{p_1})\) is evaluated by considering all direct neighbouring grid cells, and summing the number of particles divided by the considered volume, as shown in Fig. 5. However, to compute \(n_p({x}_{p_1})\) locally, the number of particles in the considered volume must be sufficiently large, in order to avoid a numerical preferential concentration effect, which tends to overestimate the collision frequency.
3.3 Global Evaluation of the Collision Frequency
Many models for evaluating the average, or global, collision frequency have been derived for homogeneous isotropic turbulent two-phase flows. Following the formalism of Chapman and Cowling (1990), from the particle velocity distribution function \(f^{(1)}_p({x}_{p_1},{v}_{p_1})\), the probability for a particle \(p_1\) to be located in the volume \(d{x}_{p_1}\) centred in \({x}_{p_1}\), with a velocity in the range \([{c}_{p_1},{c}_{p_1}+d{c}_{p_1}]\) is given as
For the cases considered in the paper, the particle velocity distribution function, \(f^{(1)}_p({x}_{p_1},{v}_{p_1})\), may be assumed Gaussian, so that
For the evaluation of binary collisions in mono-dispersed case, the probability of having two particles, \(p_1\) and \(p_2\), located at \({x}_{p_1}\) and \({x}_{p_2} = {x}_{p_1} + d_p {k}\), respectively, and with velocities within the range \({c}_{p_1} + d{c}_{p_1}\) and \({c}_{p_2} + d{c}_{p_2}\), respectively, is computed as (Lun et al. 1984)
where \(f^{(2)} _p({x}_{p_1},{v}_{p_1},{x}_{p_2},{v}_{p_2})\) is the particle-pair velocity distribution function and \({c}_{rel} = {c}_{p_1} - {c}_{p_2}\) is the relative velocity between the two particles. Using the isotropy condition, the average collision frequency, \(f_c\), is then derived as (Lavieville et al. 1995; Pigeonneau 1998)
where \(n_p\) the average number of particles per unit volume in the whole domain and \(g_0\) is the radial distribution function and is assumed to be equal to one. In case of very inertial particles (\(St_t \gg 1\)), the velocities of colliding particles are independent, such that, from chaos theory, one obtains
Integrating Eq. (41) in Eq. (40), the collision frequency is recovered as by Abrahamson (1975)
Lavieville et al. (1995) have developed an extended model for \(f^{(2)}_p({c}_{p_1},{c}_{p_2})\), which takes into account the correlation between the colliding particle velocities and the fluid velocity as seen by the particles. They assumed that particles are small enough so that the fluid velocity as seen by the two colliding particles is equal, and the conditional fluid velocity distribution function is also Gaussian. The correlated particle-pair velocity distribution function can then be expressed as
where the constants \(C_2\) and \(C_{12}\) are given as
Integrating Eq. (43) in Eq. (40) leads to the derivation of a correlated expression for the collision frequency and is given as
which is the global expression for the collision frequency.
3.4 Algorithm Comparison
In both the local and global algorithms, the probability of two particles colliding, \(P_{coll}\), is computed as (Oesterle and Petitjean 1993)
where \(\varDelta t\) is the timestep, and \(f_c\) is the collision frequency. In practice, the timestep is typically taken as the same timestep as used to solve the fluid, as long as the condition \(\varDelta t < \tau _c / 10\) is met (Berlemont et al. 2001), with \(\tau _c = 1 / f_c\) the collision time. Often, a first order approximation of Eq. (46) is found in papers Berlemont et al. (2001), Sommerfeld (2001), and reads as \(P_{coll} \approx f_c \varDelta t\). A rejection-acceptance method is applied to determine whether a collision will occur or not. This is achieved by generating a uniform random number, \(\chi\), between 0 and 1. If this number is smaller than the collision probability \(P_{coll}\), then a collision between the two particles is executed.
The two algorithms are summarised below. The global frequency algorithm (GFA) is independent of any individual particle property, i.e. all potential colliding partners have the same probability of collision. On the other hand, with the local frequency algorithm (LFA) the collision probability is directly proportional to the relative velocity between the real and generated fictitious particle. High relative velocity of potential colliding partners, hence, have a larger probability to collide. The LFA can also capture preferential concentration through the local evaluation of \(n_p\), and it is applicable outside of stationary homogeneous turbulence flows.
4 Results and Discussion
To validate the working of the newly proposed model for the stochastic inter-particle collision model, LES of stationary homogeneous isotropic turbulence are performed in a periodic cubic box of length \(L_{box}=0.128\) m with 64\(^3\) grid cells, laden with particles. The flow parameters follow the configuration set in the numerical work of Deutsch and Simonin (1991) on two-fluid model LES. The fluid density, \(\rho _f\), and dynamic viscosity, \(\mu _f\), are 1.17 kg m\(^{-3}\) and 1.72\(\cdot 10^{-5}\) Pa s, respectively. The forcing scheme of Mallouppas et al. (2013) is applied to sustain the turbulence kinetic energy, \(q_f^2\), which is fixed at 0.135 m\(^2\)s\(^{-2}\). Additional parameters of the forcing scheme can be found in Table 1. The Smagorinsky constant is set to be \(C_S = 0.12\).
The particle parameters are taken from Lavieville et al. (1995) and four different test cases are considered in this paper, which are summarised in Table 2. Particles are considered spherical, with a diameter of \(d_p = 6.56\cdot 10^{-4}\) m, and collisions are assumed purely elastic. The particle mean response time, \(\tau ^F_{fp} = \langle 1 / \tau _p \rangle ^{-1}\), the fluid Lagrangian integral time scale as seen by the particle, defined as \(\tau ^t_{f@p} = \int _0^\infty \frac{v_{f@p}(t+t_0)v_{f@p}(t_0)}{2q_{f@p}^2}dt\), and the fluid-particle correlation velocity, \(R_{fp}\), have been determined from the deterministic LES–DPS simulations. If the flow under consideration is statistically homogeneous, such as in homogeneous isotropic turbulence, \(R_{fp}\) is constant in the whole domain. However, if the flow is statistically steady in time but not in space, \(R_{fp}\) varies in space and can be determined by locally sampling the particle and fluid velocity. If the statistics of the flow are changing temporally, the local values of \(R_{fp}\) should also change in time, and a transport equation for this correlation will have to be solved (Simonin et al. 1993). The turbulent Stokes number values, \(St_t\), have been taken from the corresponding particles from the work of Sommerfeld (2001), in order to match the empirical model for the particle–particle correlation (Eq. 17). For the cases with inertial particles (Case III and Case IV), the number of particle per volume, \(n_p\), is determined globally with the local frequency algorithm.
The timestep of the fluid integration is \(\varDelta t_f = 6.75\cdot 10^{-4}\) s. For the stochastic collision models, sub-timesteps are performed on the frozen field for the particle transport and collisions. The particle integration timestep is taken as \(\varDelta t_p = \varDelta t_f / 10\), and the particle trajectories and velocities are integrated using the Verlet algorithm (Allen and Tildesley 1989). Collision statistics are collected after a time of \(10 T_{E} \simeq 0.25\) s.
Figure 6 compares the CPU time per iteration for the deterministic LES–DPS and the stochastic LES–CSOP simulations. It is noted that the computational effort associated with the CSOP model is about 10% more than that of the SOP model. two orders of magnitude faster, and the computational effort does not increase at the same rate with regard to the number of particles in the simulation domain. The results stress the advantages of a stochastic collision model for modelling of large-scale flows in the Euler–Lagrange framework.
Fluid-particle velocity covariance, \(q_{fp}\), normalized by the fluid kinetic energy seen by the particles, \(q_{f@p}\), as a function of the inverse Stokes number \(\eta _r\). The black-filled symbols correspond to the deterministic LES–DPS simulations, the grey-filled symbols to the CSOP model simulations, and the empty ones to the SOP model simulations. The black line corresponds to the theoretical expression of the velocity covariances given in Eq. (49)
4.1 Fluid-Particle Velocity Covariance Loss
During a perfectly elastic instantaneous collision, the sum of the fluid-particle covariances of the two particles is conserved, such that
In the SOP model, the last term of the RHS of Eq. (47) does not converge to the correct value, but to a lower value, as the fluid-particle velocity correlation is not directly taken into account during the generation of the fictitious particle velocity. The post-collisional fluid-particle correlation of the real particle, and \(\langle {v}_{p1}^{new} {v}_{f@p}\rangle\) will then decrease. Under the assumption that the fluid velocity as seen by two colliding particles is the same, the transport equation for the fluid-particle velocity covariance, \(q_{fp} = \langle {v}_{p} {v}_{f@p}\rangle\), is derived as (Fede et al. 2015)
which yields a theoretical expression for the fluid-particle velocity covariance normalized by the fluid kinetic energy as seen by the particle, as
where \(\eta _r = {\tau ^t_{f@p}}/{\tau ^F_{fp}}\) is the inverse Stokes number. Figure 7 shows the results of Eq. (49) compared to the simulation results obtained by the deterministic and two stochastic approaches using the global frequency algorithm, as a function of the inverse Stokes number, \(\eta _r\). The deterministic LES–DPS results accurately fit the theoretical prediction given by Eq. (49). The fluid-particle covariance loss is clearly seen when applying the SOP model. Because of the higher volume fraction, Case I and Case II (large \(\eta _r\)) experience a higher loss in the covariance. The CSOP model, on the other hand, accurately follows the LES–DPS and theoretical results. As the inverse Stokes number increases (the particles become lighter), there seems to be a slight overprediction of the fluid-particle covariance. This may be due to the assumption of \(g_0 = 1\), or because of the finite size of the particles.
Fluid-particle relative velocity distributions of colliding particles. The continuous lines correspond to the relative velocity between the real particle and the fluid velocity seen, and the dashed ones to the relative velocity between the fictitious particle and the same fluid velocity seen. The SOP and CSOP results are compared to LES–DPS
Figure 8 shows the real and fictitious particle-fluid relative velocity distribution, \(|{v}_{p_1} - {v}_{f@p}|\) (continuous lines) and \(|{v}_{p_2} - {v}_{f@p}|\) (dashed lines), respectively, for each of the four simulated cases. The results of the stochastic SOP and CSOP models are compared to the results of the deterministic LES–DPS simulations. The CSOP model presents a good prediction of the real particle-fluid relative velocity, whereas the SOP tends to overestimate \(|{v}_{p_1} - {v}_{f@p}|\), especially for the less inertial particles (Cases I and II). Moreover, the SOP model significantly overestimates the fictitious particle-fluid relative velocity, which highlights the decorrelation between the two variables \({v}_{p_2}\) and \({v}_{f@p}\). In the case of the CSOP model, the real and fictitious particle-fluid relative velocity distribution are equal for the larger inertial particle (Case III and IV), which confirms the assumption that the fluid velocity as seen by the particle is the same for both colliding particles.
4.2 Particle Kinetic Energy
Assuming perfectly elastic collisions, the particle kinetic equation for the particles in a box of statistically steady turbulence can be expressed as (Fede et al. 2015)
Hence, a loss in the velocity covariance, \(q_{fp}\), will lead to a loss in the total particle kinetic energy. Figure 9 shows the time evolution of the particle kinetic energy for each simulated case. For the stochastic models, no collisions are considered in the first 100 timesteps. After 100 timesteps, corresponding to a time of \(t=0.0675\) s, the stochastic collision algorithm is enabled. The results predicted by the CSOP model show that the particle kinetic energy is conserved, and reaches the same values as obtained from the deterministic LES–DPS for the four simulated cases. With the SOP model, the particle kinetic energy indeed decreases, which is non-physical.
4.3 Particle–Particle Correlation Model
All stochastic models require an empirical model to compute the particle–particle correlation, \(R_{pp}\), such as Eq. (17). Using the form of the particle-pair velocity distribution function in Eq. (43), the particle–particle correlation, \(R_{pp}\) can be expressed as
Zaichik et al. (2003) developed a model for the particle–particle correlation, which reads as
where \(f(d_p)\) is the longitudinal auto-correlation coefficient, which, in case of small particles (\(d_p \ll \lambda\)), is equal to one, and \(f_u\) is the response coefficient, given as
where \(\tau _T\) is the Taylor time scale. Following the models proposed by Zaichik et al. (2003), for the cases considered in this paper, z is equal to 0.4.
Figure 10 shows the particle–particle correlation as a function of the turbulent Stokes number. The two analytical models given in Eqs. (51) and (52), and the empirical model of Sommerfeld (2001) are compared to the results obtained with the deterministic LES–DPS simulations. The model of Zaichik et al. (2003) underestimates the particle–particle correlation for \(St_t > 1\), whereas the empirical model of Sommerfeld (2001) shows good prediction with regard to the results from LES–DPS, except for the high Stokes number case. The analytical model obtained from the particle-pair velocity distribution function (Eq. 51) also shows a good prediction of the particle–particle correlation. Assuming such a model, the generation of the fictitious particle velocity, Eq. (30), can be simplified to
The fictitious particle velocity is not directly correlated to the real particle velocity, and only one parameter, namely \(R_{fp}\), requires modelling.
4.4 Particle Relative Velocity Distribution
With the local frequency algorithm (LFA), the probability for a particle to collide with its fictitious partner is directly proportional to the norm of their relative velocity, \(|{w}| = |{v}_{p_1} - {v}_{p_2}|\). With the global frequency algorithm (GFA), the average relative velocity of colliding particles, \(\langle |{w}| \rangle\), in homogeneous isotropic turbulence has been modelled and is used to compute the collision frequency. Figure 11 shows the distribution of the relative velocity, \({w}\), obtained with the LFA and GFA, and compared to LES–DPS results. In all cases, the relative velocity obtained from the LFA is larger than the one obtained with the GFA, which is in better agreement with the LES–DPS results. As expected, the local evaluation of the collision frequency tends to prevent particles with small relative velocity to collide, as the probability of collision, \(P_{coll}\), tends to zero.
For inertial particle (Case III and Case IV), the GFA predicts relative velocity distributions similar to the ones obtained from LES–DPS. However, for less inertial particles (Case I and Case II), the GFA tends to overestimate the relative velocity. In the CSOP model, the fluid-particle velocity correlation, \(R_{fp}\), is computed for all particles in the domain, which is assumed to be equal to the fluid-particle velocity correlation of all colliding particles, \(R_{fp}^{coll}\). However, the fluid-colliding particle velocity correlation is smaller than the fluid-particle velocity correlation of all particles, as shown in Table 3 from LES–DPS results. This leads to an overestimation of the fluid-particle velocity covariance, \(q_{fp}\), and, in turn, the particle kinetic energy increases. As the average of the square of the relative velocity, \(\langle |{w}^2| \rangle\), is proportional to the particle kinetic energy, \(q_p^2\), an overestimation of the relative velocity is seen with the GFA compared to the results of the LES–DPS.
Another explanation for the overestimation of the relative velocity distribution obtained with the stochastic models comes from preferential concentration of particles (Reade and Collins 2000). Less inertial particles (Case I and Case II) are more likely to follow similar vortical structures (Wicker and Eaton 2001; Goto and Vassilicos 2008), thus the relative velocity of particles confined in clusters is expected to be smaller.
4.5 Particle–Particle Collision Angle Distribution
Berlemont et al. (2001) have tried to overcome the spurious particle kinetic energy loss in their Lagrangian particle tracking framework, by artificially modifying the fluid velocity as seen by the particle after the collision, in order to ensure the conservation of the fluid-particle covariance. However, they note that this method leads to an identical distribution of the collision angle regardless of the particle density, which is unrealistic.
The CSOP model accurately captures the collision angle as a function of the particle density, in the same way the SOP model does (Sommerfeld 2001). Figure 12 shows the results of the particle–particle collision angle for each cases, and compares the LFA and GFA results with LES–DPS. Inertial particles collide more randomly, as the mean collision angle approaches \(\pi /2\). As less inertial particles are more likely to follow the flow field, they collide with an angle close to zero.
The GFA is more accurate with regard to the LES–DPS results, but tends to predict higher values of the collision angle for Case I and Case II. The colliding angle of less inertial particles is expected to be reduced as they accumulate in cluster regions which explains the overestimation observed with the GFA. In the same way as for the relative velocity distribution, the LFA tends to prevent collisions with a small collision angle (\(\theta \sim 0\)) to occur, which leads eventually to the overestimation of the collision angle distribution.
4.6 Collision Frequency Comparison
A theoretical prediction of the collision frequency is obtained by integrating Eqs. (49) and (50) into Eq. (45) such that
If the particle velocity is considered uncorrelated to the fluid velocity, i.e. \(R_{fp}= 0\), the normalized collision frequency reads as
Figure 13 shows the normalized collision frequency obtained with the GFA and LFA and compares them to LES–DPS results. As expected, the GFA results are in accordance with the theoretical curve of the correlated collision frequency, Eq. (55), as the global collision frequency is derived from the same equations. For the cases with inertial particles (Case III and Case IV), the number of particles per volume, \(n_p\), is determined globally in both algorithms. Moreover for these cases, the computed normalized collision frequency is larger with the LFA and GFA than with the LES–DPS.
Square of the collision frequency, \(f_c^2 / (4\sqrt{\pi }d_p^2n_p)^{2}\), normalized by \(2q_{f@p}^2\). The local and global frequency algorithms results are compared to LES–DPS. The continuous and dashed lines represent the theoretical normalized collision frequency for the correlated (Eq. 55) and uncorrelated cases (Eq. 56), respectively
Although the LES–DPS and GFA results are in good agreement for Case II, there is a major divergence occurring for Case I. The GFA predicts a decreasing normalized collision frequency with increasing inverse Stokes number, \(\eta _r\), for \(\eta _r > 1\). However, the opposite is observed with the LES–DPS results. This is an effect of preferential concentration, as particles gathered in clusters tends to collide more often (Reade and Collins 2000), which is not captured by the theory behind the GFA. The LFA, on the other hand, shows a good prediction trend. Although the normalized collision frequency is overestimated in Case II, the normalized collision frequency computed in Case I is evaluated larger than in Case II. Preferential concentration effects are partly captured by the local evaluation of \(n_p\), although its accuracy is debatable as the LFA still over-evaluates the normalized collision frequency compared to LES–DPS.
Results such as the relative velocity and the collision angle distribution are determined more accurately with the GFA, but the LFA has the advantage of being applicable for any type of turbulent gas-solid flow, without analytical solutions or a priori knowledge of the collision frequency. A major feature to develop would be to integrate the effect of the correlated motion of the particles in the derivation of the collision frequency in the LFA. For instance, in their Monte–Carlo method, Fede et al. (2015) approximate the fluid and particle velocity probability density distributions into linear combinations of Dirac function which enables them to derive a correlated expression of the probability of collision between parcels of particles.
5 Conclusions
This paper presents a novel correlated stochastic model for particle collisions in the framework of Euler–Lagrange turbulent gas-solid flows. The correlated model ensures that the velocity of the fictitious particle is correctly correlated to both the real colliding particle velocity and to the local fluid velocity as seen by the particle. This prevents an unrealistic decorrelation between the particle and fluid velocity. Simulations of a particle-laden flow of stationary homogeneous isotropic turbulence are conducted, using the new model, and comparing its results with an existing stochastic model and a deterministic discrete particle model. The simulations are carried out with varying particle Stokes number \(St_t = [0.75 - 6.0]\) and particle volume fractions \(\alpha _p = [0.014 - 0.044]\). The results show that the simulations using the stochastic model are orders of magnitude less computational expensive as the deterministic collision model, whilst the physical predictions are very close to the deterministic model. The prediction of the fluid-particle velocity correlation and the particle kinetic energy variation in time, is much more accurate compared to other stochastic collision models.
This paper also studies the effect of the model to determine the probability of a collision occurring, and two algorithms to compute this probability are compared. Under the assumption of homogeneous and isotropic turbulence, the global algorithm computes a unique collision frequency that applies to all particle collisions, and depends only on averaged variables, such as the average particle kinetic energy. With the local algorithm, the collision frequency is proportional to the local relative velocity between the real and the fictitious particle, and varies for each collision event. Although the global algorithm shows slightly better predictions for the colliding particle relative velocity and collision angle distributions in a stationary homogeneous isotropic turbulence flow, it is only applicable if there is either an analytical model or an a priori knowledge of the collision frequency. On the other hand, the local frequency algorithm is much more flexible and can be applied for any given flow condition.
References
Abrahamson, J.: Collision rates of small particles in a vigorously turbulent fluid. Chem. Eng. Sci. 30(11), 1371–1379 (1975)
Allen, M.P., Tildesley, D.J.: The Computer Simulation of Liquids, vol. 42. Oxford University Press, Oxford (1989)
Balachandar, S., Eaton, J.K.: Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42(1), 111–133 (2010)
Bartholomew, P., Denner, F., Abdol-Azis, M., Marquis, A., van Wachem, B.: Unified formulation of the momentum-weighted interpolation for collocated variable arrangements. J. Comput. Phys. 375, 177–208 (2018)
Berlemont, A., Achim, P., Chang, Z.: Lagrangian approaches for particle collisions: the colliding particle velocity correlation in the multiple particles tracking method and in the stochastic approach. Phys. Fluids 13(10), 2946–2956 (2001)
Boivin, M., Simonin, O., Squires, K.D.: Direct numerical simulation of turbulence modulation by particles in isotropic turbulence. J. Fluid Mech. 375(1), 235–263 (1998)
Bruchmüller, J., van Wachem, B., Gu, S., Luo, K.H.: Modelling discrete fragmentation of brittle particles. Powder Technol. 208(3), 731–739 (2011)
Chagras, V.: Simulation eulérienne–lagrangienne d’écoulements gaz-solide non isothermes: interactions particules-turbulence, application aux écoulements en conduite. PhD thesis, Université Henri Poincaré (2004)
Chapman, S., Cowling, T.G.: The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction, and Diffusion in Gases. Cambridge Mathematical Library, 3rd edn. Cambridge University Press, Cambridge (1990)
Chesnutt, J., Marshall, J.: Effect of particle collisions and aggregation on red blood cell passage through a bifurcation. Microvasc. Res. 78(3), 301–313 (2009)
Crowe, C.T., Sommerfeld, M., Tsuji, Y.: Multiphase Flows with Droplets and Particles. CRC Press, Boca Raton (1998)
Cundall, P., Strack, O.D.L.: A discrete numerical model for granular assemblies. Géotechnique 29(1), 47–65 (1979)
Denner, F., van Wachem, B.: Fully-coupled balanced-force VOF framework for arbitrary meshes with least-squares curvature evaluation from volume fractions. Numer. Heat Transf. Part B Fundam. 65(3), 218–255 (2014)
Deutsch, E., Simonin, O.: Large eddy simulation applied to the motion of particles in stationary homogeneous fluid turbulence. Turbul. Modif. Multiph. Flows 110, 35–42 (1991)
Fede, P., Simonin, O., Villedieu, P.: Monte–Carlo simulation of colliding particles or coalescing droplets transported by a turbulent flow in the framework of a joint fluid–particle pdf approach. Int. J. Multiph. Flow 74, 165–183 (2015)
Franklin, C.N., Vaillancourt, P.A., Yau, M.K.: Statistics and parameterizations of the effect of turbulence on the geometric collision kernel of cloud droplets. J. Atmos. Sci. 64(3), 938–954 (2007)
Gatignol, R.: The Faxén formulas for a rigid particle in an unsteady non-uniform Stokes-flow. J. de Mécanique théorique et appliquée 2(2), 143–160 (1983)
Goto, S., Vassilicos, J.C.: Sweep-stick mechanism of heavy particle clustering in fluid turbulence. Phys. Rev. Lett. 100(5), 054503 (2008)
Hopkins, M., Louge, M.: Inelastic microstructure in rapid granular flows of smooth disks. Phys. Fluids A Fluid Dyn. 3, 47 (1991)
Lavieville, J., Deutsch, E., Simonin, O.: Large eddy simulation of interactions between colliding particles and a homogeneous isotropic turbulence field. In: Gas–Solid Flows ASME, vol. 228, pp. 347 (1995)
Lun, C.K.K., Savage, S., Jeffery, D.J., Chepurniy, N.: Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 140, 223–256 (1984)
Lundgren, T.S.: Linearly forced isotropic turbulence. Technical report, DTIC Document (2003)
Mallouppas, G., George, W.K., van Wachem, B.: New forcing scheme to sustain particle-laden homogeneous and isotropic turbulence. Phys. Fluids 25, 083304 (2013)
Mallouppas, G., van Wachem, B.: Large eddy simulations of turbulent particle-laden channel flow. Int. J. Multiph. Flow 54, 65–75 (2013)
Maw, N., Barber, J.R., Fawcett, J.N.: The oblique impact of elastic spheres. Wear 38(1), 101–114 (1976)
Maxey, M.R., Riley, J.R.J.: Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26(4), 883 (1983)
Meyer, C., Deglon, D.: Particle collision modeling—a review. Miner. Eng. 24(8), 719–730 (2011)
Moissette, S.: Étude Dynamique et Thermique Par Modélisation Eulérienne-Lagrangienne Des Effets Liés Aux Interactions Turbulence-Particules Dans Un Écoulement Gaz-Solide En Conduite Verticale Non-Isotherme. Nancy 1 (2001)
Oesterle, B., Petitjean, A.: Simulation of particle-to-particle interactions in gas solid flows. Int. J. Multiph. Flow 19(1), 199–211 (1993)
Pigeonneau, F.: Modeling and Numerical Computation of Droplet Collision in Laminar and Turbulent Flows. Université Pierre et Marie Curie - Paris VI, Theses (1998)
Reade, W.C., Collins, L.R.: Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12(10), 2530 (2000)
Riley, J.J., Patterson, G.S.: Diffusion experiments with numerically integrated isotropic turbulence. Phys. Fluids 17(2), 292 (1974)
Saffman, P.G., Turner, J.S.: On the collision of drops in turbulent clouds. J. Fluid Mech. 1(01), 16 (1956)
Schiller, L., Naumann, A.: Über die grundlegenden Berechnungen bei der Schwerkraftaufbereitung. Ver. Deut. Ing. 77, 318–320 (1933)
Simonin, O., Deutsch, E., Minier, J.: Eulerian prediction of the fluid/particle correlated motion in turbulent two-phase flows. Appl. Sci. Res. 51(1–2), 275–283 (1993)
Smagorinsky, J.: General circulation experiments with the primitive equations. I: the basic experiment. Month. Weather Rev. 91(3), 99–165 (1963)
Sommerfeld, M.: Inter-particle collisions in turbulent flows: a stochastic Lagrangian model. In: First Symposium on Turbulence and Shear Flow Phenomena, Begel House Inc (1999)
Sommerfeld, M.: Validation of a stochastic Lagrangian modelling approach for inter-particle collisions in homogeneous isotropic turbulence. Int. J. Multiph. Flow 27(10), 1829–1858 (2001)
Sundaram, S., Collins, L.R.: Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335(1997), 75–109 (1997)
Sungkorn, R., Derksen, J., Khinast, J.: Modeling of turbulent gas–liquid bubbly flows using stochastic Lagrangian model and lattice-Boltzmann scheme. Chem. Eng. Sci 66(12), 2745–2757 (2011)
Thomas, D., Judd, S., Fawcett, N.: Flocculation modelling: a review. Water Res. 33(7), 1579–1592 (1999)
van Wachem, B., Denner, F., Evrard, F.: A fully coupled multiphase flow solver (2000). www.multiflow.org. Accessed 02 Feb 2020
van Wachem, B., Schouten, J., van den Bleek, C., Krishna, R., Sinclair, J.: Comparative analysis of CFD models of dense gas–solid systems. AIChE J. 47(5), 1035–1051 (2001a)
van Wachem, B., Van der Schaaf, J., Schouten, J., Krishna, R., van den Bleek, C.: Experimental validation of Lagrangian–Eulerian simulations of fluidized beds. Powder Technol. 116(2), 155–165 (2001b)
Wicker, R.B., Eaton, J.K.: Structure of a swirling, recirculating coaxial free jet and its effect on particle motion. Int. J. Multiph. Flow 27(6), 949–970 (2001)
Xiao, C.-N., Denner, F., van Wachem, B.: Fully-coupled pressure-based finite-volume framework for the simulation of fluid flows at all speeds in complex geometries. J. Comput. Phys. 346, 91–130 (2017)
Xue, Y., Wang, L.-P., Grabowski, W.W.: Growth of cloud droplets by turbulent collision-coalescence. J. Atmos. Sci. 65(2), 331–356 (2008)
Zaichik, L.I., Simonin, O., Alipchenkov, V.M.: Two statistical models for predicting collision rates of inertial particles in homogeneous isotropic turbulence. Phys. Fluids 15(10), 2995 (2003)
Acknowledgements
Open Access funding provided by Projekt DEAL. We would like to thank Dr. Gregor Zimmermann, Dr. Jörg Schulenburg and Daniel Hasemann for their support with the HPC and computing systems at the Otto-von-Guericke-Universität Magdeburg.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
van Wachem, B., Curran, T. & Evrard, F. Fully Correlated Stochastic Inter-Particle Collision Model for Euler–Lagrange Gas–Solid Flows. Flow Turbulence Combust 105, 935–963 (2020). https://doi.org/10.1007/s10494-020-00111-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10494-020-00111-7