Discovery of Algebraic Reynolds-Stress Models Using Sparse Symbolic Regression

Abstract

A novel deterministic symbolic regression method SpaRTA (Sparse Regression of Turbulent Stress Anisotropy) is introduced to infer algebraic stress models for the closure of RANS equations directly from high-fidelity LES or DNS data. The models are written as tensor polynomials and are built from a library of candidate functions. The machine-learning method is based on elastic net regularisation which promotes sparsity of the inferred models. By being data-driven the method relaxes assumptions commonly made in the process of model development. Model-discovery and cross-validation is performed for three cases of separating flows, i.e. periodic hills (Re=10595), converging-diverging channel (Re=12600) and curved backward-facing step (Re=13700). The predictions of the discovered models are significantly improved over the k-ω SST also for a true prediction of the flow over periodic hills at Re=37000. This study shows a systematic assessment of SpaRTA for rapid machine-learning of robust corrections for standard RANS turbulence models.

1 Introduction

The capability of Computational Fluid Dynamics (CFD) to deliver reliable prediction is limited by the unsolved closure problem of turbulence modelling. The workhorse for turbulence modelling in industry are the Reynolds-Averaged Navier-Stokes (RANS) equations using linear eddy viscosity models (LEVM) [1]. The lower computational costs compared to high-fidelity approaches, e.g. Large-Eddy (LES) or Direct Numerical Simulations (DNS), come at the price of uncertainty especially for flows with separation, adverse pressure gradients or high streamline curvature. Data-driven methods for turbulence modelling based on supervised machine learning have been introduced to leverage RANS for improved predictions [2,3,4]. In [5], the source terms of the Spalart-Allmaras were learnt from data using a single hidden layer neural network, which served as a first feasibility study. In [6], a factor was introduced to correct the turbulent production in the k-equation of the k-ω model. This term was found via inverse modelling and served to train a Gaussian process. While this approach has been extended and applied to industrially relevant flows such as airfoils in [7, 8] it still relies on the Boussinesq assumption. In [9], a deep neural network was trained to predict a_ij given input only from a baseline linear eddy viscosity simulation and thus replacing the turbulence model instead of augmenting it. The network was designed to embed Galilean invariance of the predicted a_ij. This concept of physics-informed machine learning was extended, e.g., in [10] using random forest regression. Despite the success of the data-driven approaches a drawback is their black box nature, which hampers the understanding of the physics of the resulting models in order to derive new modelling ideas from it.

Recently, a method has been introduced using genetic-programming (GEP) based symbolic regression to derive Explicit Algebraic Reynolds-stress Models (EARSM) directly from high-fidelity data [11, 12]. EARSM, first introduced by [13] and further developed by [14], are nonlinear extensions of LEVM and are commonly derived by projecting Reynolds-stress models (RSM) onto a set of tensorial polynomials [15, 16]. These models are numerically more robust than RSM at similar computational costs as LEVM [17], but do not show superior predictive capabilities for all kinds of flows [15]. The data-driven GEP method retains the input quantities used to derive EARSM, but replaces the commonly used projection method to find the formal structure of the model by an evolutionary process, which makes it an open-box machine learning approach. The advantage of such a data-driven method is that instead of relying on assumptions made during the development of an EARSM, a model is inferred directly from data. While such a model might not provide an universal approach for all kinds of flows as commonly aimed for in physical modelling, it serves as a pragmatic tool to correct the flow at hand. For cases exhibiting similar flow physics, e.g. separation, it has also been shown that the discovered models provide suitable corrections indicating the predictive potential of a data-driven approach.

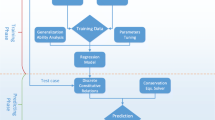
Due to the non-deterministic nature of GEP it discovers for each run another model with a different mathematical form, e.g. other terms and/or other values for coefficients, with varying complexity. It is reported that the models using only a few nonlinear terms show a low training and prediction error as well as high numerical robustness for industrially relevant flow cases [18, 19]. Therefore, we instead introduce a new deterministic symbolic regression method SpaRTA (Sparse Regression of Turbulent Stress Anisotropy), for which we constrain the search towards sparse algebraic models using sparsity-promoting regression techniques [20, 21]. SpaRTA combines functions from a predefined library of candidates without any random recombination. It consists of four steps: (i) building a library of candidate functions, (ii) model selection using sparse-regression techniques, (iii) inference of model coefficients and (iv) cross-validation of the resulting models, see Fig. 1. The first three steps are computationally very cheap also for high-dimensional problems and allow for rapid model discovery.

Fig. 1

Technical flow diagram of SpaRTA (Sparse Regression of Turbulent Stress Anisotropy)

The present study provides several novel concepts for data-driven modelling, which are organised as follows. In Section 2 we define additive model-form error terms within the k-ω SST LEVM model and use k-corrective-frozen-RANS, which is an extension of the method introduced in [12], to compute the model-form error from high-fidelity data. The novelty in this work is that we identify not only a correction of the stress-strain relation, but also one for the turbulent transport equations and thereby achieve excellent agreement with mean-fields of high-fidelity data. We also validate that the model-form error is successfully captured by adding the two terms to the solver and performing a CFD simulation. The k-corrective-frozen-RANS does not require any iterative optimisation procedure as compared to [6] and is therefore very efficient, but also limited to full-field data. In Section 3 we introduce the steps of SpaRTA. The details of the test cases, the CFD setup and the sources of the high-fidelity data are given in Section 4. In Section 5 SpaRTA is applied to the test cases, the discovered models are presented and the best models are chosen using cross-validation. Finally, conclusions are drawn in Section 6.

2 Model-Form Error of RANS Equations

In the following, we augment the baseline model, i.e. the linear eddy viscosity assumption and the turbulence transport equations of the k-ω SST, with additive terms accounting for the error due to the model-form. We introduce k-corrective-frozen-RANS, which is an extension of the method in [12], to extract these two types of error from high-fidelity data sources efficiently. Finally, we validate that the extracted terms reduce the error for given test cases.

2.1 Identification of additive model-form error from data

The incompressible and constant-density RANS equations read

$$ \begin{array}{@{}rcl@{}} \partial_{i} U_{i} &=& 0, \\ U_{j} \partial_{j} U_{i} &=& \partial_{j} \left[ -\frac{1}{\rho} P + \nu \partial_{j} U_{i} - \tau_{ij} \right], \end{array} $$

(1)

where U_i is the mean velocity, ρ is the constant density, P is the mean pressure and ν is the kinematic viscosity. The Reynolds-stress τ_ij is the subject of modelling. This symmetric, second-order tensor field can be decomposed into an anisotropic a_ij =2kb_ij and isotropic part $\frac {2}{3} k \delta _{ij}$

$$ \begin{array}{@{}rcl@{}} \tau_{ij} = 2k \left( b_{ij} + \frac{1}{3} \delta_{ij} \right), \end{array} $$

(2)

in which the baseline model, $b_{ij}^{o} = -\frac {\nu _{t}}{k} S_{ij}$, forms a linear relation between anisotropy and the mean-strain rate tensor S_ij via the scalar eddy viscosity ν_t. Commonly, ν_t is computed using a transport model such as k-ω SST [15], in which k is the turbulent kinetic energy and ω the specific dissipation rate.

In order to extract the model-form error in these models from high-fidelity data sources, we compute the residuals of the baseline turbulence model given the data. The residual for the constitutive relation is equivalent to an additive term $b^{\varDelta }_{ij}$ leading to an augmented constitutive relation

$$ \begin{array}{@{}rcl@{}} b_{ij} = -\frac{\nu_{t}}{k} S_{ij} + b^{\varDelta}_{ij}. \end{array} $$

(3)

To evaluate $b^{\varDelta }_{ij}$ it is necessary to estimate ν_t, therefore also ω needs to be specified. In [12, 22], ω was efficiently obtained by passively solving the ω transport equation given high-fidelity data for U_i, k and b_ij. The associated ν_t was then used to compute $b^{\varDelta }_{ij}$ with Eq. 3. This method is named frozen-RANS as only one equation is solved iteratively while the remaining variables are frozen [23, 24]. Despite the fact that $b^{\varDelta }_{ij}$ also alters the production of turbulent kinetic energy P_k, it is not evident that solving the k equation given the data and the frozen ω should lead to the same k as present in the data. Therefore, we introduce k-corrective-frozen-RANS for which we also compute the residual of the k equation alongside the computation of the frozen ω. The residual is equivalent to an additive correction term, which we define as R, leading to an augmented k-ω SST model

$$ \begin{array}{@{}rcl@{}} \partial_{t} k + U_{j} \partial_{j} k &=& P_{k} + R - \beta^{*} \omega k + \partial_{j} \left[ (\nu + \sigma_{k} \nu_{t}) \partial_{j} k \right], \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} \partial_{t} \omega + U_{j} \partial_{j} \omega &=& \frac{\gamma}{\nu_{t}} \left( P_{k} + R\right) - \beta \omega^{2} + \partial_{j} \left[ (\nu + \sigma_{\omega} \nu_{t}) \partial_{j} \omega \right] + CD_{k\omega}, \end{array} $$

(5)

in which the production of turbulent kinetic energy is augmented by $b^{\varDelta }_{ij}$ and bounded following Menter’s limiter [25]

$$ \begin{array}{@{}rcl@{}} P_{k} = \min \left( -2k(b_{ij}^{o} + b^{\varDelta}_{ij}) \partial_{j} U_{i}, 10 \beta^{*} \omega k\right). \end{array} $$

(6)

The corresponding eddy viscosity is $\nu _{t} = \frac {a_{1} k}{\max \limits (a_{1} \omega , SF_{2})}$. The other standard terms of k-ω SST read

$$ \begin{array}{@{}rcl@{}} CD_{k\omega} &=& \max \left( 2 \sigma_{\omega 2} \frac{1}{\omega}(\partial_{i} k)(\partial_{i} \omega), 10^{-10} \right), \\ F_{1} &=& \tanh\left[\left( \min \left[\max \left( \frac{\sqrt{k}}{\beta^{*} \omega y}, \frac{500\nu}{y^{2}\omega} \right), \frac{4\sigma_{\omega 2}k}{CD_{k\omega}y^{2}} \right] \right)^{4}\right],\\ F_{2} &=& \tanh \left[ \left( \max \left( \frac{2\sqrt{k}}{\beta^{*} \omega y}, \frac{500\nu}{y^{2} \omega} \right) \right)^{2} \right], \\ {\Phi} &=& F_{1}{\Phi}_{1} + (1-F_{1}){\Phi}_{2}, \end{array} $$

(7)

in which the latter blends the coefficients ${\Phi } \rightarrow ({\Phi }_{1}, {\Phi }_{2})$

$$ \begin{array}{@{}rcl@{}} \alpha = (5/9,0.44), \beta = (3/40,0.0828), \sigma_{k} = (0.85,1.0), \sigma_{\omega} = (0.5,0.856). \end{array} $$

(8)

The remaining terms are β^∗ =0.09,a₁ =0.31 and $S = \sqrt {2S_{ij}S_{ij}}$. For the iterative computation of the frozen ω the variables U_i, k and b_ij are kept frozen in Eqs. 4 and 5. At each iteration the term R is computed as the residual of Eq. 4 and fed back into Eq. 5. The equations are discretized using linear upwinding for the divergence terms and 2nd order central differencing for diffusion. The fields predicted by a baseline k-ω SST were used as initial condition for ω. For the cases studied the solver reaches convergence after a few hundred iterations. In order to validate that the resulting fields compensate the model-form error, $b^{\varDelta }_{ij}$ and R are added as static fields to a modified OpenFOAM solver [26] and a CFD simulation is performed starting from the baseline solution for the flow configurations described in Section 4, for which high-quality data is available. The mean-squared error between the high-fidelity data and the reconstructed velocity U_i as well as the Reynolds-stress τ_ij is low, see Table 1. Also the stream-wise velocity profiles shown in Fig. 2 demonstrate that the high-fidelity mean-flow data is essentially reproduced given $b^{\varDelta }_{ij}$ and R.

Table 1 Mean-squared error 𝜖 of reconstructed velocity U_i and Reynolds-stress τ_ij for different test cases with $b^{\varDelta }_{ij}$ and R added as static fields to the solver

Fig. 2

Stream-wise velocity component for propagated model-form error acquired using k-corrective-frozen-RANS

In [6, 8, 27] an inversion procedure was introduced to infer correction factors such as R from data. For this method the data can be scarce, e.g. single profiles of experiments. However, this method is built upon a computationally-intensive optimisation problem, whereas k-corrective-frozen-RANS only requires a single equation to be solved. This makes k-corrective-frozen-RANS a cost-efficient way to extract the model-form error, if full-field data of high-fidelity simulations is available.

2.2 Nonlinear eddy-viscosity models for $b^{\varDelta }_{ij}$ and R

In order to discover corrections for the model-form error $b^{\varDelta }_{ij}$ and R, we need to decide on a modelling ansatz. Within this mathematical framework the symbolic regression targets to find specific expressions as corrections models. In [13], a nonlinear generalisation of the linear eddy viscosity concept was proposed. This concept has been used in several works on data-driven turbulence modelling [2, 3]. The fundamental assumption is made that the anisotropy of the Reynolds-stress b_ij not only depends on the strain rate tensor $S_{ij} = \tau \frac {1}{2} (\partial _{j} U_{i} + \partial _{i} U_{j})$ but also on the rotation rate tensor $\varOmega _{ij}= \tau \frac {1}{2} (\partial _{j} U_{i} - \partial _{i} U_{j})$ with the timescale τ =1/ω. The Cayley-Hamilton theorem then dictates that the most general form of the anisotropic part of the Reynolds-stress can be expressed as

$$ \begin{array}{@{}rcl@{}} b_{ij}(S_{ij}, \varOmega_{ij}) = \sum\limits_{n=1}^{N} T_{ij}^{(n)} \alpha_{n}(I_{1}, ..., I_{5}), \end{array} $$

(9)

with ten nonlinear base tensors $T_{ij}^{(n)}$ and five corresponding invariants I_m. In the following, we only consider two-dimensional flow cases, for which the first three base tensors form a linear independent basis and only the first two invariants are nonzero [28]. Our set of base tensors and invariants reads

$$ \begin{array}{@{}rcl@{}} T_{ij}^{(1)} &=& S_{ij}, T_{ij}^{(2)} = S_{ik}\varOmega_{kj} - \varOmega_{ik}S_{kj}, \\ T_{ij}^{(3)} &=& S_{ik}S_{kj} - \frac{1}{3} \delta_{ij} S_{mn}S_{nm} \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} I_{1} &=& S_{mn}S_{nm}, I_{2} = \varOmega_{mn}\varOmega_{nm}. \end{array} $$

(11)

Using this set for Eq. 9 we have an ansatz, which only requires functional expressions for the coefficients α_n, to model $b^{\varDelta }_{ij}$. However, computing $b^{\varDelta }_{ij}$ using Eq. 3 requires a correct k as discussed in Section 2.1. This aspect is taken into account in the modelling ansatz for R, for which we take a closer look at the eddy viscosity concept.

Both linear and nonlinear eddy viscosity models provide expressions for the anisotropy b_ij based on a local relation between stress and strain. Due to the restriction of this local closure only the normal stresses $\frac {2}{3}k\delta _{ij}$ can account for nonlocal effects by transport equations for the turbulent quantities using convection and diffusion terms [15, 29]. The term R provides local information to correct the transport equations. Depending on the local sign of R it either increases or decreases the net production P_k locally. Hence, it acts as an additional production or dissipation term, which can overcome the error in k. We model it in a similar way to the turbulent production

$$ \begin{array}{@{}rcl@{}} R = 2kb^R_{ij} \partial_{j} U_{i}, \end{array} $$

(12)

which has the additional benefit that we can also use the framework of nonlinear eddy viscosity models to model R. Given the polynomial model (9) and the set of base tensors (10) and invariants (11) we are now left with the task of providing suitable expressions for α_n(I₁,I₂) for n =1,...,3 to overcome the model-form error.

In [12] models identified using genetic programming were modified such that any additional contribution of the first base tensor $T^{(1)}_{ij}$ in Eq. 9 was added with a positive sign for the computation of P_k. This ad-hoc correction was established based on physical reasoning to avoid very low production close to walls and led to significantly improved predictions. However, in contrast to [12] we have extracted two target terms $b^{\varDelta }_{ij}$ and R using k-corrective-frozen-RANS, which also make it possible to systematically study (i) how to obtain corrections models for each target individually and (ii) their combined effect on the predictions. Treating the two targets separately has the disadvantage that energy is not conserved, because Eq. 12 has no corresponding part in the momentum equation [30,31,32]. Also in literature several classical [33, 34] as well as more recent data-driven [6, 12] approaches exist, which violate conservation of energy. It has been shown that overcoming this inconsistency improves the predictive performance of the models [31]. Thus, a natural next step would be to combine both targets in order to find a single model accounting for the sources of model-form error on the level of the constitutive relation as well as within the turbulent transport equations. This requires a multi-objective version of the deterministic symbolic regression detailed below, which is beyond the scope of this paper.

3 Model Discovery Methodology

Deterministic symbolic regression constructs a large library of nonlinear candidate functions to regress data. It identifies the relevant candidates by adopting a sparsity constraint. Two fundamental methods have been proposed: Sparse identification of nonlinear dynamics (SINDy) [20, 35] and fast function extraction (FFX) [36]. Both methods were applied in several areas of physical modelling. In the following, we introduce the steps of the model discovery methodology SpaRTA based on FFX, for which a library is constructed using a set of raw input variables and mathematical operations. The model selection uses elastic net regression. Finally, for the inference of the model coefficients the stability requirements of a CFD solver are considered. An overview of SpaRTA is given in Fig. 1.

3.1 Building a library of candidate functions

The deterministic symbolic regression requires a library of candidate functions, from which a model is deduced by building a linear combination of the candidates. Hence, the library is an essential element of the entire methodology and needs to accommodate relevant candidates explaining the data. We rely on the nonlinear eddy viscosity concept and aim to find models for α_n in Eq. 9 given as primitive input features the invariants I₁ and I₂. For the present work we focus on a library, in which the primitive input features are squared and the resulting candidates are multiplied by each other leading to a maximum degree of 6. In addition to the two invariants we also include a constant function c to the set of raw input features. The resulting vector $\boldsymbol {{\mathcal{B}}}$ reads

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\mathcal{B}} &=& \left[ 1, I_{1}, I_{2}, {I_{1}^{2}}, {I_{2}^{2}}, {I_{1}^{2}} {I_{2}^{3}}, {I_{1}^{4}} {I_{2}^{2}}, I_{1} {I_{2}^{2}}, I_{1} {I_{2}^{3}}\right., \\ && \left. I_{1} {I_{2}^{4}}, {I_{1}^{3}} I_{2}, {I_{1}^{2}} {I_{2}^{4}}, {I_{1}^{2}} I_{2}, I_{1} I_{2}, {I_{1}^{3}} {I_{2}^{2}}, {I_{1}^{2}} {I_{2}^{2}} \right]^{T} \end{array} $$

(13)

with the cardinality of $\boldsymbol {{\mathcal{B}}}$, $|\boldsymbol {{\mathcal{B}}}|=16$.

For the library to regress models for $b^{\varDelta }_{ij}$ each function of $\boldsymbol {{\mathcal{B}}}$ is multiplied with each base tensor $T_{ij}^{(n)}$, leading to the library of tensorial candidate functions

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\mathcal{C}}_{b^{\varDelta}_{ij}} = \left[T^{(1)}_{ij}, T^{(2)}_{ij}, \hdots, {I_{1}^{2}} {I_{2}^{2}}T^{(3)}_{ij} \right]^{T}. \end{array} $$

(14)

In order to regress models for R the double dot product of each function in $\boldsymbol {\mathcal {C}}_{b^{\varDelta }_{ij}}$ with the mean velocity gradient tensor ∂_jU_i is computed, leading to

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\mathcal{C}}_{R} = \left[T^{(1)}_{ij}\partial_{j} U_{i}, \hdots, {I_{1}^{2}} {I_{2}^{2}}T^{(3)}_{ij}\partial_{j} U_{i} \right]^{T}. \end{array} $$

(15)

The two libraries $\boldsymbol {\mathcal {C}}_{b^{\varDelta }_{ij}}$ and $\boldsymbol {\mathcal {C}}_{R}$ are evaluated given the high-fidelity validation data for each test case and stored column-wise in matrices $\boldsymbol {C}_{b^{\varDelta }_{ij}}$ and C_R. In order to avoid large values, a candidate function is discarded from the library, if it contains values with a magnitude larger than 10⁵. Finally, the target data $b^{\varDelta }_{ij}$ and R are stacked to vectors.

3.2 Model selection using sparsity-promoting regression

Given the above defined libraries the task is to form a linear model to regress the target data Δ = b^Δ or R by finding the coefficient vector Θ

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\varDelta} = \boldsymbol{C}_{\varDelta} \boldsymbol{\varTheta}, \end{array} $$

(16)

which represents a large, overdetermined system of equations. When using ordinary least-squares regression a dense coefficient vector Θ is obtained, resulting in overly complex models, which are potentially overfitting the data given the large libraries Eqs. 14 and 15. Due to multi-collinearity between the candidates, C_Δ can be ill-conditioned, so that the coefficients may also display large differences in magnitude expressed in a large l₁-norm of Θ. Such models are unsuitable to be implemented in a CFD solver as they increase the numerical stiffness of the problem and impede convergence of the solution.

Following the idea of parsimonious models we constrain the search to models which optimally balance error and complexity and are not overfitting the data [35]. In principle, given a library a combinatoric study can be carried out, by performing an ordinary least-squares regression for each possible subset of candidates. Starting from each single candidate function individually, proceeding with all possible pairs up to more complex combinations. As the number of possible models grows exponentially with the number of candidates $I = 2^{|\boldsymbol {\mathcal {C}}_{\varDelta }|} -2$ this approach becomes already infeasible for the simple libraries Eqs. 14 and 15 with $|\boldsymbol {\mathcal {C}}_{\varDelta }| \approx 48$.

Hence, we follow [35, 36] and engage sparsity-promoting regularisation of the underlying least-squares optimisation problem. The model-discovery procedure is divided into two parts: (i) model selection and (ii) model inference, see Fig. 1. For the first step, the model selection, we use the elastic net formulation

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\varTheta} &=& \underset{\hat{\boldsymbol{\varTheta}}}{\arg \min} \left\|{ \boldsymbol{C}_{\varDelta} \hat{\boldsymbol{\varTheta}} - \boldsymbol{\varDelta}}\right\|_{2}^{2} + \lambda \rho \left\|{\hat{\boldsymbol{\varTheta}}}\right\|_{1} \\ &&+ 0.5 \lambda (1-\rho) \left\|{\hat{\boldsymbol{\varTheta}}}\right\|_{2}^{2}, \end{array} $$

(17)

which blends the l₁- and l₂-norm regularisation given the mixing parameter ρ ∈ [0,1] and the regularisation weight λ, to promote the sparsity of Θ [36, 37]. On its own, the l₁-norm, known as Lasso-regression, promotes sparsity by allowing only a few nonzero coefficients while shrinking the rest to zero. The l₂-norm, known as Ridge-regression, enforces relatively small coefficients without setting them to zero, but is able to identify also correlated candidate functions instead of picking a single one. By combining both methods, the elastic net can find sparse models with a good predictive performance. Besides the mixing parameter, also the regularisation parameter λ shapes the form of the model: For a very large λ the vector Θ will only contain zeros independent of ρ. The amount of nonzero coefficients increases for smaller λ values making the discovery of sparse models possible.

Given the elastic net regularisation method we need to specify suitable combinations of the weight λ and type of the regularisation ρ, for which the optimisation problem Eq. 17 is solved. Most commonly the optimal (λ,ρ) combination is found based on a strategy to avoid overfitting of the resulting models, e.g. using cross-validation [35], for which the data is split into a training and a test set. While the optimisation problem given a grid (λ,ρ) is solved on the former, only the model with the best performance evaluated on the latter survives. For the purpose of CFD a true validation of the models can only be performed once they are implemented in a solver and applied to a test case. In order to not overcharge the role of the training data from k-corrective-frozen-RANS at this stage of the methodology, we select a wide spectrum of models varying in accuracy and complexity using Eq. 17 instead of a single one. The validation task will be performed later using a CFD solver. Following [36] we use

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\rho} = [0.01, 0.1, 0.2, 0.5, 0.7, 0.9, 0.95, 0.99, 1.0]^{T}, \end{array} $$

(18)

which ensures that we cover a substantial range of different regularisation types. The upper limit of the regularisation weight is defined as $\lambda _{\max \limits } = \max \limits (|\boldsymbol {C}_{\varDelta }^{T} \boldsymbol {\varDelta }|) / (K \rho )$, because for any $\lambda >\lambda _{\max \limits }$ all elements in Θ will be equal to zero. The entire vector

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\lambda} = [\lambda_{0}, ..., \lambda_{\max}]^{T} \end{array} $$

(19)

is defined of having 100 entries between $\lambda _{0} = \xi \lambda _{\max \limits }$ with ξ =10^− 3 uniformly spaced using a log-scale as defined in [36]. This provides a search space (λ,ρ), the elastic net, which is large enough and has an appropriate resolution. At each grid point (λ_i,ρ_j) a vector $\boldsymbol {\varTheta }^{(i,j)}_{\varDelta }$ as a solution of Eq. 17 is found using the coordinate descent algorithm. The duration for the model selection step given the number of data points $K \sim 15000$ is of the order of a minute on a standard consumer laptop.

Solving Eq. 17 for different (λ_i,ρ_j) might produce $\boldsymbol {\varTheta }^{(i,j)}_{\varDelta }$ with the same abstract model form $\boldsymbol {\bar {\varTheta }}$, which means that the same entries are equal to zero. As the specific values of the coefficients will be defined in the next step, the selection step of SpaRTA concludes with filtering out the set of D unique abstract model forms $\boldsymbol {\mathcal {D}}_{\varDelta } = \left \{\boldsymbol {\bar {\varTheta }}_{\varDelta }^{d} \left | d = {1, ..., D}\right . \right \}$.

3.3 Model inference for CFD

The abstract models $\boldsymbol {\mathcal {D}}_{\varDelta }$ are found using standardised candidates, because the relevance of each candidate should not be determined by its magnitude during the model selection step. With the aim of defining a model with the correct units, we need to perform an additional regression using the unstandardised candidate functions for each subset determined by the abstract model forms in $\boldsymbol {\mathcal {D}}_{\varDelta }$, which is the purpose of the model inference step outlined in the following.

In [35, 38, 39] this was done using ordinary least-squares regression for problems in the domains of dynamical systems and biological networks. As mentioned above, the ability of the CFD solver, in which the models will be implemented, to produce a converged solution is sensitive to large coefficients, which has been reported in [11, 12, 22]. We take this additional constraint into account by performing a Ridge regression

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\varTheta}_{\varDelta}^{s,d} = \operatornamewithlimits{arg\ min}_{\hat{\boldsymbol{\varTheta}}_{\varDelta}^{s,d}} \left\|{ \boldsymbol{C}_{\varDelta}^{s} \hat{\boldsymbol{\varTheta}}_{\varDelta}^{s,d} - \boldsymbol{\varDelta}}\right\|_{2}^{2} + \lambda_{r} \left\|{\hat{\boldsymbol{\varTheta}}_{\varDelta}^{s,d}}\right\|_{2}^{2}, \end{array} $$

(20)

in which λ_r is the Tikhonov-regularisation parameter. The index s denotes the submatrix of C_Δ and the subvector of $\boldsymbol {\varTheta }_{\varDelta }^{d}$ consisting of the selected columns or elements respectively as defined in $\boldsymbol {\mathcal {D}}_{\varDelta }$. The elements of $\boldsymbol {\varTheta }_{\varDelta }^{d}$ associated with the inactive candidates are zero and are not modified during this step.

By using the l₂-norm regularisation the magnitude of the nonzero coefficients is shrunk [35, 40]. In general, low values for λ_r reduce the bias introduced through regularisation, but lead to larger coefficient values, and vice versa. Since shrinkage of the coefficients also reduces the influence of candidate functions with a lower magnitude compared to others, we need to find a trade-off between error of the model on the target data Δ and the likelihood that the model will deliver converged solutions when used in a CFD solver. The problem of finding such an optimum is that the latter aspect can only be answered retrospectively. Recently, this problem has been addressed in [41] by embedding CFD simulations in the search for correction models guided by genetic programming. While this increases the costs of the model search drastically, it also significantly increases the chance of delivering models with better convergence properties. Even though this procedure provides a strong indication, the identified models are also not guaranteed to converge a priori for any other test case outside the training set. Via testing using the cases in Section 4, we have identified 0.01 < λ_r < 0.1 able to deliver coefficients in a range balancing the error on the target data Δ and the likelihood to produce converged CFD solutions. Our efforts are based on an empirical observation, but do not guarantee a well-behaving numerical setup under all conditions. We have identified corrections of $b^{\varDelta }_{ij}$ as the only contribution which can do harm to the convergence properties for the given test cases. However, at this stage of the process we exclude models, if they are not converging on a given test case.

Finally, the resulting coefficient vector $\boldsymbol {\varTheta }_{\varDelta }^{d}$ is used to retrieve the symbolic expression of the models by a dot product with the library of candidate functions $\boldsymbol {\mathcal {C}}_{\varDelta }$ in Eqs. 14 and 15

$$ \begin{array}{@{}rcl@{}} M^{d}_{\varDelta} := \boldsymbol{\mathcal{C}}_{\varDelta}^{T} \boldsymbol{\varTheta}_{\varDelta}^{d}, \end{array} $$

(21)

which are implemented in the open-source finite-volume code OpenFOAM [26]. The divergence terms of the equations are discretised with linear upwinding and turbulent diffusion with 2nd order central differencing. In summary, the model discovery step of SpaRTA selects models utilising elastic net regression in Eq. 17 and further infers the coefficients of the selected models in Eq. 20. The latter process is guided by the aim to discover models complying with the restrictions of a CFD solver.

4 Test Cases and High-Fidelity Data

In order to apply SpaRTA we need full-field data of U_i, k and τ_ij, which we take from LES and DNS studies conducted by other researchers. We have selected three test cases of separating flows over curved surfaces in two-dimensions with similar Reynolds-numbers. For each case fine meshes are selected, which ensure that the discretisation error is much smaller compared to the error due to turbulence modelling.

Periodic hills (PH)

Flow over a series of hills in a channel. Initially proposed by [42] this case has been studied both experimentally as well as numerically in detail. We use LES data from [43] for Re =10595 (PH₁₀₅₉₅) to apply SpaRTA and test the performance of the resulting models. In addition, we also use experimental data from [44] at a much larger Re =37000 (PH₃₇₀₀₀) in order to test the models outside the range of the training data. The numerical mesh consists of 120 × 130 cells. Cyclic boundary conditions are used at the inlet and outlet. The flow is driven by a volume forcing defined to produce a constant bulk velocity.

Converging-diverging channel (CD)

A DNS study of the flow within a channel, in which an asymmetric bump is placed, exposed to an adverse pressure gradient was performed by [45] for Re =12600 (CD₁₂₆₀₀). The flow shows a small separation bubble on the lee-side of the bump, which is challenging for RANS to predict. The numerical mesh consists of 140 × 100 cells. The inlet profile was obtained from a channel-flow simulation at equivalent Re.

Curved backward-facing step (CBFS)

In [46] a LES simulation of a flow over a gently-curved backward-facing step was performed at Re =13700 (CBFS₁₃₇₀₀). Similar to PH also for this flow the mean effect of separation and reattachment dynamics is the objective. The numerical mesh consists of 140 × 150 cells. The inlet was obtained from a fully-developed boundary layer simulation.

Despite the simple geometries, the mean effect of the separation and reattachment dynamics of a flow on a curved surface is a challenging problem for steady-RANS approaches. Especially, PH serves as an important testbed for classical and data-driven approaches for turbulence modelling, e.g. [2, 47], but also the other two have been introduced with the purpose of closure investigation.

5 Discovered Models and Cross-Validation Using CFD

In the following, the method SpaRTA introduced in Section 3 is applied to the three test cases of Section 4. The models resulting from the model-discovery are presented and their mean-squared error on the training data is evaluated. In order to identify the models with the best predictive capabilities, we carry out cross-validation of the resulting models using CFD [40]: Models identified given training data of one case are used for CFD simulations of the remaining two case. For each case a single model is chosen as the best-performing one. Finally, the three resulting models are tested in a true prediction for the flow over periodic hills at Re =37000.

The goal of the model-discovery is to identify an ensemble of diverse models with small coefficients, varying in model-structure (complexity) and accuracy. Such an ensemble is better-suited for the cross-validation on unseen test cases, than a selection of the best models given only the training data. The sparse-regression for $b^{\varDelta }_{ij}$ applied to the three test cases resulted in 7 distinct models for PH₁₀₅₉₅ and 8 for CD₁₂₆₀₀ and CBFS₁₃₇₀₀. For R the model discovery resulted in 1, 3 and 4 distinct model forms for CBFS₁₃₇₀₀, PH₁₀₅₉₅ and CD₁₂₆₀₀ respectively. We identify $T^{(1)}_{ij}$, $I_{1}T^{(1)}_{ij}$ and $I_{2} T^{(1)}_{ij}$ as the relevant candidates to regress R, and models combining all three give the lowest error per test case. The ensembles of discovered models are shown in Figs. 3 and 4. Each row represents a model structure, the colours indicate the nonzero value of the coefficient corresponding to the chosen candidate function. If a candidate function is not selected the corresponding field is left blank. The result is a hierarchical spectrum of models regressing the training data varying in complexity and error.

Fig. 3

Model-structure of all discovered models using SpaRTA and mean-squared error on training data. The matrix (l.) shows the values of the active (coloured) candidate functions (x-axis) for each model M_i with model index i (y-axis). The mean-squared error between the frozen data $b^{\varDelta }_{ij}$ and the model is also shown (r.)

Fig. 4

Selected models and their mean-squared error evaluated on the training data R

Cross-validation tests how well models identified on training data perform on unseen test cases [40]. This assessment allows to determine the best-predictive models from a set. As stated above, the role of the frozen training data should not be overcharged, so that we cross-validate using CFD. By doing so, we can assess the validity of SpaRTA as a tool for model discovery as well as the predictive performance of the identified models outside of their training set. The found correction models regress $b^{\varDelta }_{ij}$ and R individually and can also be applied individually for predictions when implemented in the solver, i.e. a model correcting $b^{\varDelta }_{ij}$ can be used without a correction of R and vice-versa. We can also study their combined effect. For the cross-validation in the following, all models are applied to the three test cases, which requires 61, 48 and 75 simulations for the cases PH₁₀₅₉₅, CD₁₂₆₀₀ and CBFS₁₃₇₀₀ respectively.

In Fig. 5 the mean-squared error of each model on the velocity field 𝜖(U) normalised with the mean-squared error of the baseline 𝜖(U^o) is shown. The type of model, whether it is providing a correction both for $b^{\varDelta }_{ij}$ and R or for each one individually, and from which training data it originated, is emphasised by a unique marker form and color combination. Most of the models show a good or even substantial improvement over the baseline. But, for the set of models, only providing a correction for $b^{\varDelta }_{ij}$, not all lead to an improvement of the resulting velocity field. In contrast to that, if only a correction for R is deployed, the result is a consistent, substantial improvement across all test cases. Using both a model for $b^{\varDelta }_{ij}$ and R only provides a minor additional improvement for some cases. For the test case CBFS₁₃₇₀₀ using both corrections leads to a detrimental effect, the error increases for models identified on PH₁₀₅₉₅ and CD₁₂₆₀₀ data. Surprisingly, the best model per test case is not always identified on the associated training data. While this expectation holds for the cases CBFS₁₃₇₀₀ and CD₁₂₆₀₀ it is not true for PH₁₀₅₉₅, for which the other two training sets deliver significantly better performing models. In general, the data of CD₁₂₆₀₀ and CBFS₁₃₇₀₀ provide models, which are well performing on all test cases presented.

Fig. 5

Mean-squared error of velocity vector of each correction model normalised by the mean-squared error of the baseline k-ω SST. The colour indicates on which high-fidelity data the models have been identified. Full circles represent simulations using both corrections, while left-/right-filled circles represent simulations using only correction for R or $b^{\varDelta }_{ij}$ respectively

In Fig. 6, both the error and the model structure for the correction of $b^{\varDelta }_{ij}$ as well as for R is shown. The models are ordered according to the mean-squared error on the stream-wise velocity U. In line of the discussion of Fig. 5 three groups can be identified: a few models, which lead to an increased error compared to the baseline; a small group of models per test case, which are equal or similar to the baseline; and the great majority of models, which result in an improvement. It can be observed how the error in the velocity is significantly reduced once a correction of R is used. The best models correct the velocity up to 5 times better in mean-squared error than the k-ω SST baseline model. This leaves still room for further improvement compared to the error using the frozen data sets, see Table 1. But, especially for case CBFS₁₃₇₀₀ the result is already very close to the possible correction provided by the frozen data at least for U.

Fig. 6

The two matrices (l.) show the models M_i for $b^{\varDelta }_{ij}$ and R. The mean-squared error in velocity U normalised by the mean-squared error of the baseline k-ω SST model is also shown (right)

Given this cross-validation assessment we select models $\boldsymbol {M}^{(i)} = (M^{(i)}_{b^{\varDelta }}, M^{(i)}_{R} )^{T}$ based on the lowest 𝜖(U) per case

$$ \begin{array}{@{}rcl@{}} M^{(1)}_{b^{\varDelta}} &= & 0, \\ M^{(1)}_{R} &= & 0.39 T^{(1)}_{ij}, \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} M^{(2)}_{b^{\varDelta}} &= & 0.1 T^{(1)}_{ij} + 4.09 T^{(2)}_{ij}, \\ M^{(2)}_{R} &= & 1.39 T^{(1)}_{ij}, \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} M^{(3)}_{b^{\varDelta}} &= & 0\\ M^{(3)}{R} &= & 0.93 T^{(1)}_{ij}, \end{array} $$

(24)

for which further details on the corresponding training data and the rank of the model on each test case are given in Table 2. The models M⁽¹⁾ and M⁽³⁾ provide very simple correction of R and none for b^Δ. Also for M⁽²⁾ an equivalent model with a similar error using no correction for b^Δ could be found, see row number 20 in Fig. 6. Especially model M⁽³⁾ performs very well both on CBFS₁₃₇₀₀ (rank 1.) and PH₁₀₅₉₅ (5.). While the rank of the others varies more between the test cases, they are still within the set of well-performing models with 𝜖(U)/𝜖(U^o) < 0.5. Their predictions of stream-wise velocity U, k, the Reynolds-stress component τ_xy and the skin-friction coefficient C_f are shown in Figs. 7, 8, 9 and 10 for the three test cases. As already stated for the error evaluated on the entire domain discussed above, these three models show an improvement of the spatial distribution of the predicted quantities in comparison to the baseline prediction of k-ω SST. Especially the velocity is well-captured for all three. While k is better identified compared to the baseline, we still observe a discrepancy between the predictions and the data. For PH₁₀₅₉₅ the three models do not fit the complex spatial structure especially in the shear-layer, but together encapsulate the data for most of the profiles. For CD₁₂₆₀₀ the models are underestimating k for x < 7 and overestimate it further downstream. For CBFS₁₃₇₀₀ the models also underestimate on the curved surface, but fit the data better than the baseline for 3 < x < 5. The magnitude of the Reynolds-stress component τ_xy is underestimated on the curved surfaces of all test cases. For PH₁₀₅₉₅ the models fail to fit the complex spatial structure especially within the separated shear-layer behind the hill and on the hill itself. The skin friction coefficient C_f and the associated separation and reattachment points are better captured compared to the baseline k-ω SST for PH₁₀₅₉₅ and CBFS₁₃₇₀₀. For CD₁₂₆₀₀, we observe a small recirculation zone as reported in the literature using M⁽¹⁾, but too far down-stream. However, while the baseline k-ω SST drastically over-predicts this zone, M⁽²⁾ and M⁽³⁾ ignore it entirely.

Table 2 Best-predictive models with rank (index i,j,k in Fig. 6) and normalised error on velocity 𝜖(U)/𝜖(U^o) for different cases

Fig. 7

Predicted stream-wise velocity

Fig. 8

Predicted turbulent kinetic energy

Fig. 9

Predicted shear stress

Fig. 10

Predicted skin friction coefficient

Overall, the models agree well with the spatial data, which is in line with the global error on U in Table 2. To correct the velocity prediction sufficiently only a slight modification of the baseline k-ω SST model is necessary. A model for R using a scalar times $T^{(1)}_{ij}$ is sufficient for the given test cases. The resulting magnitudes of R and P_k are shown in Fig. 11. The enhanced production P_k due to a positively-signed R induces an increase of eddy viscosity, which makes the corrected model more dissipative compared to the baseline k-ω SST model. This is shown in Fig. 12 for the periodic hills at stream-wise position x =4.0. The result is an increase of shear-stress, which leads to shortening of the recirculation bubble [47]. Consequently, the increase of eddy viscosity follows the magnitude of the coefficients of the models, i.e. M⁽¹⁾ < M⁽³⁾ < M⁽²⁾.

Fig. 11

P_k (coloured) and R (grey) at x =4.0 for flow over periodic hills at Re =10595 using correction models

Fig. 12

Eddy viscosity profile at x =4.0 for flow over periodic hills at Re =10595 (coloured) and Re =37000 (grey) using correction models compared to baseline k-ω SST

In order to test how the models extrapolate to cases of larger Re, we predict the flow over periodic hills at Re =37000, see Fig. 13. Due to an increase of turbulence this case has a significantly shorter recirculation zone. For this true prediction throughout the domain the three models improve significantly compared to the baseline. Interestingly, the models M⁽²⁾ and M⁽³⁾ are providing a better fit of the data than M⁽¹⁾, which was performing better on the lower Re case. Also for this case, the eddy viscosity is significantly larger compared to the baseline model, see Fig. 12, inducing the same pattern as discussed above for PH₁₀₅₉₅.

Fig. 13

Predicted stream-wise velocity for flow over periodic hills at Re =37000 using correction models compared to baseline k-ω SST and experimental data of [44]

6 Conclusion and Extension

In this work SpaRTA was introduced to discover algebraic models in order to correct the model-form error within the k-ω SST. For this novel machine learning method two additive terms, on the level of the stress-strain relation $b^{\varDelta }_{ij}$ and within the turbulent transport equations R, were identified by means of k-corrective-frozen-RANS, for which the governing equations are evaluated given high-fidelity data of three cases of separating flows. It was validated that the computed terms are compensating the model-form error and reproduce the high-fidelity LES or DNS mean-flow data. Hence, k-corrective-frozen-RANS is a cost-efficient way to distill useful information directly from full-field data without the need of an inversion procedure.

Cross-validation of the discovered models using CFD was carried out to rank the models. While using both corrections for R as well es for $b^{\varDelta }_{ij}$ leads to an improvement of the predictions over the baseline, a correction only for R is already enough to achieve sufficient results for the velocity field. This also shows the potential for a multi-objective optimisation approach aiming to find models, which are correcting R and $b^{\varDelta }_{ij}$ together instead of separately. For the best performing models on each case both the global error on U as well as the spatial structure on U, k and τ_xy was coherent. The models also performed well for the periodic hills flow at a much larger Re-number (Re =37000). As the sparse regression is computationally inexpensive, SpaRTA allows for rapid discovery of robust and pragmatic models, i.e. a model trained for one flow may perform well for flows outside of the training range, but with similar features.

The necessary modification in order to improve the predictions of U is simple and in-line with common knowledge on eddy viscosity turbulence models for separating flows in 2D. But, the corrections are learnt directly from data without the aid of a priori knowledge. In other work it was shown that using more complex function approximators from the machine learning toolbox, e.g. neural networks or random forest, more details of the flow can be captured, e.g. on the hill’s crest of PH₁₀₅₉₅, which are missed by SpaRTA. However, the present systematic study has shown the capabilities of SpaRTA to discover effective corrections to k-ω SST at low costs. Further work will focus on the uncertainty of the inference step of SpaRTA. We will also apply SpaRTA to a larger variety of flow cases in order to show its potential for rapid model discovery of corrections for industrial purposes.