1 Introduction

Heat transfer augmentation has been an open question since the invention of the first Stirling engine in the early nineteenth century. Over the last 200 odd years various designs and techniques have been used to enhance the effective heat transfer between internal flow components such as heat transfer from a working fluid/solid to a passive fluid in solar thermal or nuclear applications. In thermal-hydraulics systems one of the main objectives is thus the effective heat transfer with minimum pressure drop across the working system. The current test-case consists of the flow through a wall-bounded pin matrix in a staggered arrangement with a heated bottom wall. In addition to the complex underlying flow physics, this case is close to several industrial configurations found in internal cooling of gas-turbine blades, electronic devices and nuclear thermal-hydraulics. The use of pin-fin-arrays has proved to be an effective technique in achieving enhanced rates of heat transfer in the past. Some of the earlier experimental studies done by [1,2,3,4] and more recently by [5,6,7,8,9] report a number of flow characteristics including the heat transfer and pressure loss coefficients through various configurations of pin-fin-arrays.

Of particular interest among these are the experiments of [5,6,7,8] which were chosen as test case for the 15th ERCOFTAC-SIG15/IAHR Workshop on Refined Turbulence Modelling held at Chatou in 2011. This particular test case was chosen for the workshop to assess and examine the suitability of various advanced modelling techniques/methods for flow and heat transfer calculations in complex, practice-relevant situations. The present work reported in this paper made a major contribution to this workshop [10] and the full set of current results can be accessed through the ERCOFTAC Knowledge Base Wiki;Footnote 1 later referred to as ERCOFTAC-KB-Wiki for simplicity. Various numerical studies conducted prior to the workshop, such as the Unsteady Reynolds-Averaged Navier-Stokes (URANS) calculations by [11, 12], and hybrid Reynolds-Averaged Navier Stokes/Large Eddy Simulation by [13] also formed the baseline for numerical contributions along with the experimental data of [5,6,7,8] for the workshop.

The aim of the present study is to evaluate different strategies for modelling turbulence in the pin-fin-array test case of the workshop. Of particular importance is the determination of the level of modelling necessary to predict the main characteristics of the flow and heat transfer. In the past, URANS has been shown to be able to reproduce 2D and 3D wakes of bluff bodies [14, 15], but heat transfer predictions in complex flows close to industrial configurations, such as the wall-bounded pin matrix, are still very challenging. LES is undoubtedly a good candidate for reproducing the physics of such flows accurately, but at a cost unaffordable for high Reynolds numbers, such that comparing LES with lower-cost URANS methods, is of great interest to industry.

The present paper starts with the description of the experimental and numerical test cases (Section 2), followed by discussion of numerical treatment given in Section 3. This will be followed by discussions of some of the main results in Sections 4 and 5; the full set of results can be found in the ERCOFTAC Knowledge Base Wiki.1

2 Test Case Description

2.1 Experimental setup

The experiments of [5,6,7] and [8] were conducted in a small bench top wind tunnel for a staggered pin-fin-array consisting of 8 rows with \(7\frac {1}{2}\) pins per row (see Fig. 1). Both the cross passage (S/D) and stream-wise (X/D) pin spacing ratios were equal to 2.5 while the pin height to diameter (H/D) ratio was equal to 2. The pin diameter (D) was chosen to be equal to 2.54 cm. The test section began at 7.75D upstream of the centerline of the first row of pins and ended 7.75D downstream of the centerline of the last row. The inlet total temperature and static pressure were measured on the centerline, 5D upstream of row 1, whereas the exit static pressure was measured 5D downstream of row 8. Tests were conducted at three Reynolds numbers: 3,000, 10,000, and 30,000 which were based on the maximum gap velocity (VG) and the pin diameter (D). The gap bulk velocity was determined between two adjacent pins of the same row. The readers are referred to the ERCOFTAC-KB-Wiki for further details about the experimental setup, results and data uncertainties. The remaining description will focus on the numerical test-case which is studied and on the data utilized for the present comparisons.

Fig. 1
figure 1

2D sketch of [8] experiment. (a) Complete experimental setup (b) Top view of the pin-fin configuration

Full size image

2.2 Computational setup

The computational domain shown in Fig. 2a, consisting of 8 by 2 pins, was used for all the simulations. The chosen domain is essentially a sub-domain of the experimental setup with the assumption of lateral (Y − axis) periodicity. All solid surfaces (pins, bottom and top walls) were set as no-slip solid walls. The inlet of the channel was set at a distance LU = 10D upstream of the center of the first row of pins, whereas the outlet was LD = 15D downstream of the center of the last row of pins (this gives Xinlet = − 10D and Xoutlet = 32.5D), respectively. Note that these two distances were both equal to 7.75D in the experimental setup but are not sufficient to perform reliable CFD calculations (see [16] and [17]), in particular the upstream distance, unless one represents the nozzle of the experiment which would lead to added computational costs. On the other hand, the height of the computational model was set to match the experimental set-up, H = 2D.

Fig. 2
figure 2

(a) Sketch of the complete computational domain (b) Row numbering and lines (A1, B and C) locations. i = 1,..,8. Line A1: (X = 2.5D(i − 1), Y = 0 if i is even and Y = 1.25D if i is odd, 0 ≤ Z ≤ 2D). Line B: (X = 2.5D(i − 1), − 0.75D ≤ Y ≤ 0.75D if i is even and 0.5D ≤ Y ≤ 2D if i is odd, Z = D). Line C : Centerline of the cylinder (Z = D), 00 at the leading edge (sense of rotation: counter clockwise with Z-axis from bottom to top wall)

Full size image

For the computations, the temperature was treated as a passive scalar with an imposed temperature at the inlet, and an imposed heat flux at the bottom wall with adiabatic conditions elsewhere. For the Large Eddy Simulations (LES), a uniform inflow velocity was imposed without any synthetic or precursor turbulence generation. Note that the reported inflow turbulence intensity in the experiment was about 1.4%. In fact, different inlet conditions would have certainly affected the flow around the first and the second rows but not around the subsequent rows. On the other hand, for URANS a uniform velocity and 5% turbulence intensity were imposed at the inlet. This latter condition triggers the production of the Reynolds stresses, mandatory for their development. Some tests (not reported herein) which were carried out without inlet turbulence showed that the computations degenerate to a solution where the Reynolds stresses vanish. However, preliminary tests also showed that the level of inlet turbulence intensity only affects the flow around the first two rows and that a value of 5% leads to results in better agreement with the measurements. The inlet condition for the dissipation rate (ε) in URANS was given by the standard relation used for internal flows

$$ \varepsilon=\frac{C_{\mu}^{3/4} k^{3/2}}{0.1 \kappa H} $$
(1)

where k is the turbulent kinetic energy, H = 2D (the height of the channel), κ = 0.42 and Cμ = 0.09. Isotropy of turbulence is assumed at the inlet for the Reynolds-stress model.

For the computations, a Cartesian co-ordinate system was used with X, Y and Z-axes in the stream-wise, span-wise (lateral) and wall-normal directions, respectively. 1-D profiles were drawn along lines A1, B & C (see Fig. 2b) for post-processing/comparisons. The main lines for the velocity components and the Reynolds stresses were A1 and B and the main line for the pressure coefficient was C (mid-span location). The exact positions of the lines were:

∙A1 –:

Line at mid-span (Y/D = 0) location between two adjacent pins of the same row along the channel height (Z-axis).

∙B –:

Surface to surface line between two adjacent pins of the same row at mid channel height (Z/D = 1.0) along the lateral (Y ) direction.

∙C –:

Circumferential line around the pin surface from 00 − 1800, at mid channel height (Z/D = 1.0). Angle zero (00) on the leading edge of the pins with a counter-clockwise orientation.

The local Nusselt number is given by Nu = qwD/(λ(Tw − Tref)) where λ is the thermal conductivity, and Tw & Tref are the time averaged temperatures at the wall and the reference value, respectively. Tref takes into account the increase in the bulk temperature of the fluid from the heated surface as it flows down the array (see [18]). Therefore, at a given X location, one gets: Tref = qwSh(X)/(ρCpV0Si), where Sh(X) is the heated surface from the inlet to X. [18] used an estimate of this surface Sh = (−Xinlet + X)Shtot/LX where Xinlet is the X coordinate of the inlet plane, Shtot the total heated surface (here the surface is from Xinlet to Xoutlet) and LX the total length of the domain (LX = Xoutlet − Xinlet). ρ, Cp and Si are the fluid density, the specific heat and the inlet surface area, respectively.

3 Numerical Treatment and Models

3.1 General description of the computations

All numerical simulations were performed using the Électricité de France (eDF) in-house open source solver Code_Saturne (http://code-saturne.org) [19]. The code is based on an unstructured collocated finite-volume approach for cells of any shape. It uses a predictor/corrector method with Rhie and Chow interpolation [20] and a SIMPLEC algorithm, [21] for the pressure correction. For LES, pure second-order central differencing scheme was applied for the velocity components whereas for the temperature a central difference scheme with a slope test was used. Here the slope test determines whether to use a pure central scheme or to use first-order upwinding based on limiting of the overshoots. It is worth mentioning here that the slope test is done locally both in time and space. The time-advancing scheme was second-order, based on Crank-Nicolson/Adams Bashforth (the scheme for diffusion including the velocity gradient was totally implicit, for convection semi-implicit and for diffusion including the transpose of the velocity gradient explicit). For URANS, a centered scheme with a slope test was used for the velocity components and the temperature, whereas a first-order upwind scheme was utilized for the turbulence quantities. The time-advancing scheme in this case was first-order Euler which needs substantially smaller time steps for stability reasons. However, the use of the first-order Euler scheme here is justified as it is substantially faster than a second-order semi-implicit scheme such as the one used for the LES simulations.

Three Reynolds numbers were computed: ReD = 3,000 only with LES, ReD = 10,000 with both LES and URANS and ReD = 30,000 only with URANS. For the test cases the experimental flow conditions are listed in Table 1. For the computations a Prandtl number of 0.71 was used with fluid thermal conductivity defined as λ = 1/(PrReD). The temperature was treated as a passive scalar with the inlet temperature set as 00 and the imposed heat flux set to unity. Zero-gradient boundary conditions were used for all the variables at the outlet and an implicit periodic condition was set in the lateral direction for all the variables. All the computations were run on EDF BlueGene/P and BlueGene/Q supercomputers using up to 4096 cores costing just under 3 million core Central Processing Unit (CPU) hours (approximately 45,000 kAU) for each LES simulation and around 2 million (approximately 30,000 kAU) for each URANS simulation.

Table 1 Experimental flow conditions
Full size table

3.2 Turbulence models

The LES implementation in Code_Saturne [22] is based on the dynamic Smagorinsky model [23] with Lilly’s minimization [24] in which the Smagorinsky constant CS is clipped below zero and above 0.065. This model has been successfully used for flows around bluff bodies and in turbo-machinery; please see the effect of clipping of CS in [25]. A turbulent Prandtl number of 0.5 was used when solving for the temperature with LES, see [26].

In the current study three low Reynolds number URANS models were chosen based on their availability and relative popularity in the heat transfer community: the k-ω-SST model [27], the ϕ-model [28] and the EB-RSM model [29].

The k-ω-SST model uses a blending between the standard k − ω and k − ε models. The ϕ-model uses the elliptic relaxation concept introduced by [30]. It is a stabilized version of the \(\overline {v^{2}}-f\) model [14], based on the variable \(\phi =\overline {v^{2}}/k\), where \(\overline {v^{2}}\) characterizes the energy of the wall-normal fluctuations and is used in the evaluation of the eddy viscosity. For the present study, in both eddy-viscosity models, a Simple Gradient Diffusion Hypothesis (SGDH) was used for the temperature equation with a turbulent Prandtl number of 0.9.

The EB-RSM model proposed by [31] and later modified by [29] is inspired by the elliptic relaxation concept for the Reynolds stresses. Instead of using six relaxation equations, it solves one elliptic equation for a parameter α which is equal to zero at the wall and goes to 1 far from the wall. This parameter is then used to blend near-wall and remote (away from the wall) regions for the redistribution and dissipation terms of the Reynolds-stress transport equations. In the current formulation the EB-RSM uses the Speziale, Sarkar and Gatski model [32] for the homogeneous part of the redistribution term. For the temperature equation a Generalized Gradient Diffusion Hypothesis (GGDH) approach is used with a constant of 0.23. In the present simulations the use of more advanced models such as the AFM (Algebraic Flux Model), the EB-AFM or the EB-GGDH [33] did not affect the results for global quantities such as the mean Nusselt number. This suggests that in the forced convection regime, good predictions of heat transfer can be obtained with simple models for temperature diffusion as long as the dynamics of the flow is accurately resolved.

3.3 Computational meshes

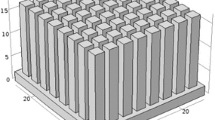
Figure 3 shows the zoomed in views of the mesh used for LES at ReD = 3,000. The mesh resolutions for the different computations are given in Table 2 (see table caption for details).

Fig. 3
figure 3

Computational mesh used for LES at ReD = 3,000

Full size image
Table 2 Mesh information
Full size table

Note that for URANS, only the parameters used for the finest grid are mentioned. The two coarser levels were obtained by coarsening the grid spacing by a factor of 2 in all the directions. Particular attention was paid to the grid refinement near the solid walls. Two meshes containing 18 million and 76 million cells were utilized in LES to simulate the two Reynolds numbers ReD = 3,000 and ReD = 10,000, respectively, ensuring that the non-dimensional wall distance of the first computational cell (n+) remained below 2 almost everywhere. Moreover, it was also carefully checked that the near-wall cells satisfy the usual refinement criteria. The current non-dimensional values of y+ ≈ 2 and Δz+ ≤ 40, clearly satisfy the resolved LES refinement criteria of y+ < 2, Δx+ = 50 − 150 and Δz+ = 15 − 40, [34, 35] (also see the wall treatment figures in the ERCOFTAC-KB-Wiki for further details).

An additional way to ensure that the mesh is sufficiently fine is to carry out simulations without using a subgrid-scale (sgs) model in order to quantify its effect on the solution. It was observed that the influence of the sgs model was very limited for the present level of mesh refinement (see the Sensitivity to the sub-grid scale model section and relevant figures in the ERCOFTAC-KB-Wiki for details).

3.4 Grid Convergence study for URANS

A separate grid convergence study was performed for all the three URANS models at the two higher Reynolds numbers. Here only the study performed for ReD = 10,000 with the EB-RSM model is presented for the grid convergence study as conclusions for all other models were similar. Three levels of refinement were used for all the models as described before.

Figure 4a and b show the mean stream-wise velocity and the pressure coefficient along the line B (pin mid-line) for the ReD = 10,000 case for row 3, respectively. As the computations were unsteady, the r.m.s. values, or more generally the Reynolds stresses were combined as the sum of the resolved and modelled parts: \(R_{ij} = R^{res}_{ij} + R^{mod}_{ij}\). These modelled and resolved parts are not shown in the current paper but can be downloaded from the ERCOFTAC-KB-Wiki database. It is observed from Fig. 4 that the coarse mesh results are very far from the experiments. However, the two finest meshes only show slight difference in profiles. Thus, the discussions in Sections 4 and 5 are based on the results obtained with the finest mesh (called here “very fine mesh”). In order to gain confidence in the finest mesh results, a further sensitivity study on the numerical discretization schemes with and without slope test was also performed. Based on the results it was concluded that the use of a centered scheme for the turbulent quantities did not affect the results. Other tests were also carried out such as introducing outer iterations for pressure/velocity coupling but none of them exhibited a noticeable effect on the results and are hence not reported here (please see the Sensitivity study to convection scheme on the ERCOFTAC-KB-Wiki database for detailed plots).

Fig. 4
figure 4

Grid convergence study: (a) Mean stream-wise velocity (b) mean pressure coefficient profiles along the pin mid-line (Line-B) obtained using EB-RSM at ReD = 10,000

Full size image

Table 3 summarizes the main computations for which results are reported in Sections 4 and 5. Note that all simulations were run for a substantially long period of time for the flow to fully develop. For the simulations a complete flow through pass was defined based on the time the flow took from the inlet of the domain to the outlet, TPass. Based on this, the total number of passes over which each of the individual cases were run (TotPass = TotalSimulationtime/TPass) and the number of passes over which the flow statistics were averaged (AvePass), are given in Table 3. The maximum local CFL number for each of the cases is also given in the same table which is less than 1 for all LES simulations and less than 2 for URANS.

Table 3 Parameters of the main computations which are reported in the current paper
Full size table

4 Results and Discussions (Global Quantities)

4.1 Pressure loss coefficient

In this section we discuss the measured values of the pressure loss coefficient in Ames et al. experiments as well as those obtained from the current numerical simulations at the three computed Reynolds numbers. The pressure loss coefficient is based on the total pressure drop from the inlet to the outlet of the domain and is defined as \(f={\Delta }{P}/(2\rho {V}^{2}_{BG} N)\), where N is the number of rows.

Figure 5a shows the computed pressure loss coefficient comparison with the measured values of Ames et al. and correlations of [36] and [2]

Fig. 5
figure 5

(a) Pressure loss coefficient (b) Average Nusselt number at the bottom wall

Full size image

Jacob [36]:

$$f = (0.25 + 0.1175/(P/D-1)^{1.08}) Re^{-0.16}$$

Metzger et al. [2]:

$$ \begin{array}{@{}rcl@{}} f = 0.317 {Re_{D}}^{-0.132} \text{for} Re_{D} < 10^{4} \\ f = 1.76 {Re_{D}}^{-0.318} \text{for} Re_{D} > 10^{4} \end{array} $$

Table 4 compares various computations to the experiments and gives the relative errors. LES shows a very good agreement with the [2] correlation and Ames et al. experimental results. The relative error is equal to 1% and 3% for the two computed Reynolds numbers, respectively. The EB-RSM model shows a satisfactory pressure loss coefficient at ReD = 10,000 (1% error) but the result is worse at ReD = 30,000 (where the error is 10%). The k-ω-SST model also exhibits globally good results (7% and 6% errors). On the other hand the ϕ-model gives the worst results with errors of 17% and 12% for the two Reynolds numbers, respectively. This will be further explained in Section 5.2 later. Wall resolved LES can thus be seen as an excellent candidate to obtain satisfactory pressure loss coefficients in the present configuration. It is important to note here that although the k-ω-SST model exhibits good results for the pressure loss coefficient, the physics of the present flow is not properly captured as will be shown later and thus one cannot rely on this model.

Table 4 Pressure loss coefficient for the different computations compared to Ames et al. experimental values
Full size table

4.2 Average Nusselt number comparisons

Figure 5b shows all comparisons between simulations, experiments provided by Ames et al. and the correlations of [4] and [2].

  1. VanFossen

    [4]: Nus = 0.153Re0.686

  2. Metzger et al.

    [2]: Nus = 0.079Re0.717

Note that the local experimental results have an uncertainty of ± 12%, ± 11.4%, and ± 10.5% for the 3,000, 10,000, and 30,000 Reynolds numbers, respectively, in the end-wall regions adjacent to the pins and ± 9% away from the pins. For the simulations, the total area of the bottom wall was used for the calculation of the average Nusselt number.

Table 5 compares the computations with the experiments and gives the relative errors. One can see that the two models using an eddy-viscosity (ϕ-model and k-ω-SST) are quite far from the experimental results, except for the ϕ-model at ReD = 30,000. However, as will be shown later, this model exhibits wrong physics. LES and EB-RSM yielded satisfactory values within the experimental error interval. The superiority of these two models will be discussed later when showing the results of the local normalized Nusselt number on the bottom wall. Ames and Dovrak [5] using standard Realizable k − ε and RNG k − ε models also found a substantial underestimation of the average Nusselt number when the pins were heated. Delibra et al. [11] used the URANS ζ − f model (which is very similar to the ϕ-model utilized in the present work) at the 10,000 and 30,000 Reynolds numbers and obtained average Nusselt numbers of 46.2 and 122.3, respectively. These values are also substantially different from the experimental results but it should be mentioned here that these values were obtained by using an imposed constant temperature at the wall. Using this boundary condition in the present work with the ϕ-model also led to higher values of the average Nusselt numbers (41 and 100, respectively, not shown here). This shows that imposing the temperature gives higher Nusselt numbers than the ones obtained by imposing the heat flux with this model. The effect of the temperature boundary condition was also tested with the LES at ReD = 10,000 and with the EB-RSM model at ReD = 30,000. The average Nusselt numbers were found to be equal to 46 and 115.2, respectively. Hence, clear conclusions concerning the effect of imposing the temperature instead of the heat flux at the bottom wall can be drawn for these two models which gave more realistic physics than the eddy-viscosity models. However, one can state that there is clearly a strong influence of the thermal boundary conditions on the results. Delibra et al. [37] also reported LES computations. However, the one carried out for ReD = 30,000 was fairly coarse with a short integration time and will thus not be considered here for comparisons. Furthermore, their LES at ReD = 10,000 gave an average Nusselt number of 44.3 with an error of 18% compared to the experiments of Ames et al. This led [13] to test a hybrid RANS/LES approach but the results were still less accurate than the ones obtained with their URANS approach based on the ζ − f model (see Table 5).

Table 5 Average Nusselt number comparison on the bottom wall for ReD = 3,000 (Exp.-Ames et al., DLES-[13], URANS*-[11])
Full size table

5 Results and Discussions (Local Quantities)

5.1 Mean velocity

Figure 6 displays the dimensional mean stream-wise velocity field in the mid-plane (Z = D). The wakes downstream of the cylinders are similar in LES and EB-RSM and are shorter downstream of the cylinders from row 4 on-wards. This was not observed at all for the ϕ-model and the k-ω-SST model. Furthermore, both eddy-viscosity models (EVM) over-predicted the pin adjacent gap velocities. One can thus conclude at this stage that the tested EVM models are not able to predict the present flow. Clearly, they predict too long and too weak recirculation regions behind the pins. It is well known that, in the case of wakes of infinite cylinders [14] or wall-mounted obstacles [15], the RANS models (steady state computations) cannot accurately predict the recirculation region, and that URANS can drastically improve the prediction by resolving a significant part of the large-scale unsteadiness, which is a major contributor to the mixing of momentum. It can be anticipated that the main difference between the EB-RSM and the eddy-viscosity models lies in the tendency of the latter to provide a steady solution because of their strongly diffusive character. It can also be argued that eddy-viscosity models tend to overestimate turbulent production close to stagnation points and thus overestimate the turbulent energy in the boundary layers around the cylinders and, consequently, in their wake. This hypothesis will be investigated below.

Fig. 6
figure 6

Dimensional mean stream-wise velocity (m/s) in the mid-plane z = D (a) ReD = 10,000 (b) ReD = 30,000

Full size image

Figure 7 shows the mean axial velocity component along line B of rows 3 and 5 for the different computations (for further row comparisons see the ERCOFTAC-KB-Wiki database). One observes from Fig. 7b that the EB-RSM model and LES predictions are very close to each other. In fact, for row 3, the EB-RSM model captures the near wall behavior even better than LES, as the peak value by LES is slightly overpredicted. For row 5, both LES and the EB-RSM model slightly overpredict the mean velocity near the pin. On the other hand, the eddy-viscosity models fail to capture the near-wall and the inter-gap flow behavior, see the underprediction at Y/D = 0.1 and Y/D = 0.75 in Fig. 7b, particularly for the row 3 profile.

Fig. 7
figure 7

Mean stream-wise velocity component along line B - LES and URANS computations (a) ReD = 3,000 (b) ReD = 10,000 (c) ReD = 30,000

Full size image

It is further observed that the two eddy-viscosity models exhibit a dramatic deficit of the mean axial velocity midway between the tubes, in accordance to the overestimation of the size of the recirculation regions as first observed in Fig. 6. On the other hand, LES and EB-RSM models perform well compared to the experimental data with a slight overestimation of the mean stream-wise velocity peaks close to the walls at several locations, in particular starting from row 3. Note that the convergence study shown in Section 3 proved that the refinement needed to obtain a convergent solution around pin 2 is very important (with the first two levels of refinement, a deficit in the central velocity was observed). This is an indication that the accurate reproduction of the large-scale unsteadiness is crucial in this flow: [38] showed that the correct reproduction of the unsteadiness of the wake of an obstacle requires a careful elimination of sources of numerical diffusion. This remark suggests that the origin of the failure of the eddy-viscosity models is in their inability to reproduce realistic large-scale unsteadiness.

Figure 8 shows the mean axial velocity component along line A1 for the highest Reynolds number case. It is observed that the two eddy-viscosity models severely underestimate the mean streamwise velocity, supporting the earlier observations made from Figs. 6 and 7. Both EVM models overpredict the length of the recirculation region behind each pin, such that the recovery of the boundary layer in between the subsequent pins is slowed down. In contrast, the RSM model provides a solution very close to the experimental profiles but slightly underestimates the velocity all along the A1 line. However, this must not be interpreted as a deficit of flow rate, which is conserved as the velocity underestimations on line A1 are compensated by overestimations elsewhere.

Fig. 8
figure 8

Mean stream-wise velocity component along line A1 - URANS computations at ReD = 30,000

Full size image

5.2 r.m.s velocity

The best way to gain insight into the very different behavior of the models is to investigate the relative contributions of the resolved and modelled parts of the velocity field to the total r.m.s velocities, as shown in Fig. 9. Here, the contribution of the subgrid scales is neglected for LES (as it is not explicitly evaluated in the present Smagorinsky model formulation). Since no synthetic turbulence is prescribed at the inlet, there is no resolved content before the first pin, and the resolved contribution rapidly develops after the first row. However, as observed from the figure, the flow reaches a fully developed state only around the last row, in accordance with the experiments. The EB-RSM model also exhibits a rapid development of the resolved motion, with r.m.s. levels of the same order of magnitude as those of LES. In addition, a smaller, but significant level of modelled stress contributes to the total fluctuations.

Fig. 9
figure 9

Resolved (left) and modelled (right) contributions to the dimensional r.m.s of the stream-wise velocity component (m/s) in the mid-plane (Z = D)- LES and URANS computations (a) ReD = 10,000 (b) ReD = 30,000

Full size image

From Fig. 9 it is further observed that the behavior of the two eddy-viscosity models (EVM) is completely different from LES and EB-RSM. For the EVM cases, the contribution of the resolved motion remains small compared to that of the modelled motion, up to at least row 4 and even up to row 7 for the k-ω-SST model. This result indicates that these models face difficulties to reproduce unsteadiness in the wake. As mentioned above, predicting the correct level of mixing in wakes dominated by large-scale vortex shedding, such as behind cylinders or wall-mounted obstacles [14, 15], requires a URANS solution with a very significant amount of resolved unsteadiness. This is the reason why the two eddy-viscosity models exhibit longer recirculation regions in Fig. 6 and consequently underestimate the mean stream-wise velocity in between the subsequent pins (Figs. 7 and 8). Note that at Re = 30,000, the ϕ-model remains steady all the way down to the last row. It is interesting to remark here that with a coarser mesh (not shown here), the ϕ-model rapidly developed unsteadiness. This is in agreement with the findings of [39]; in coarse RANS simulations, dispersive numerical errors (oscillations) can trigger an unsteady behavior, which can paradoxically improve the predictions. The present results show that on fine-enough grids, the solution of eddy-viscosity models remains steady for the first rows and only gradually develops unsteadiness on subsequent rows.

This difficulty to develop an unsteady content, compared to the EB-RSM, can be attributed to an overestimation of diffusion in the wake that prevents the growth of resolved fluctuations. A first possible explanation would be that turbulence is generated in excess by EVM models in the region of the stagnation point [40, 41]. For example, it is clear from Fig. 9, in the right-hand column, that the ϕ-model produces a high level of turbulence upstream of the first cylinder. Convection of this turbulence downstream may cause an overestimation of the turbulent diffusion in the wake. However, this stagnation point anomaly is, at least, partially corrected in the k-ω-SST model by the introduction of a production limiter: P = min(Pk,10ε), where Pk = 2νtSijSij is the standard production term derived from the Boussinesq relation [42]. Indeed, Fig. 9 shows that this model does not exhibit the same overestimation of turbulence production as the ϕ-model in the stagnation region. Therefore, another explanation is more convincing, even if the two problems can be combined: it appears in Fig. 9, particularly for the SST model, that the overestimation of production takes place mainly in the wake of the cylinders. Indeed, as shown by [43] for the case of a periodic flow (synthetic jet), the Boussinesq relation used in eddy-viscosity models, i.e., the linear relation between the turbulent anisotropy tensor and the mean strain tensor, is at the origin of a strong overestimation of the modelled turbulent production, and, consequently, of the modelled turbulent diffusion of momentum, when the deformation varies rapidly in space or time and the Reynolds stress tensor does not have time to follow this evolution. This overproduction bears some similarity to the problem of the stagnation point anomaly, since it is also to be traced to the use of the linear Boussinesq relation, but is active in other situations, far from the wall, when turbulence is out of equilibrium (see [44, 45] and [46]). For instance, in a 2D-flow, it can be easily shown [43] that the exact production of turbulent energy involves a factor of cos(2Θ), where Θ is the angle between the eigenvectors of the anisotropy tensor and those of the strain tensor (stress-strain lag), such that eddy-viscosity models, which assume Θ = 0, overestimate production. This can be generalized to 3D-flows by considering the so-called stress-strain lag parameter \(C_{as}=-a_{ij} S_{ij}/\sqrt {2S_{ij} S_{ij}}\) [46]. In the case of 2D tube bundles, a case very similar to the present pin-fin-array, it was shown, using experimental data of Simonin and Barcouda,Footnote 2 that the stress-strain misalignment is so strong that large regions of negative production (Θ > 45 deg) are observed in between subsequent tubes (see Fig. 2.17 of Viollet et al. [47]). The lack of consideration of this stress-strain lag prevents the large-scale unsteadiness to be captured in cylinder wakes [46], a problem that can be avoided by using a Reynolds-stress model [43].

Figure 10 shows the r.m.s. profiles of the stream-wise velocity along line B. Here again only the profiles along row 3 are shown and the remaining profiles can be accessed via the ERCOFTAC-KB-Wiki database. The quantity plotted in the figure is \(u^{\prime }=\sqrt {\overline {u_{1}^{\prime 2}}+\overline {R_{11}}}\), where \(u_{1}^{\prime }\) is the resolved streamwise velocity fluctuation and \(\overline {R_{11}}\) the time-averaged value of the stream-wise modelled Reynolds normal stress R11. LES and EB-RSM models perform very well compared to the experimental data. As mentioned earlier, it can be seen in Fig. 11 that for the stream-wise stresses, a major part of the total fluctuations of the EB-RSM model comes from the resolved part, which again shows that this model easily reproduces the large-scale unsteadiness appearing in the wake of the pins. However, in contrast with LES, the modelled part is not negligible. Figure 10 shows that the eddy-viscosity models severely underestimate the total stream-wise fluctuations, except in the central region. It is not expected from these models to provide very accurate r.m.s. velocities, since they are based on the Boussinesq relation, which is not designed to reproduce the individual normal stresses. However, the amplitude of u′ is underestimated by a factor of more than 2 close to the pin surfaces, which shows that a significant amount of turbulent energy is missing in this region. Figure 11 and more prominently the contours of Fig. 9 provide a rather enlightening explanation for this result. In contrast to the cylinder wake (regions far from the wall), where, as mentioned above, eddy-viscosity models yield a high level of modelled turbulent energy, it can be seen that the contribution of the modelled part close to the pin surfaces is of the same order of magnitude as that of the EB-RSM, but the resolved content remains very small, such that the total, including the resolved and modelled parts, is significantly underestimated. In particular, the near-wall peak, which is largely contributed by the resolved part for the EB-RSM, is completely missed by the eddy-viscosity models. This result is of course consistent with the contourplots of Fig. 9, and definitely supports the conclusion that the main issue with the eddy-viscosity models is their difficulty to grow unsteadiness in the wake of the pins, due to their over-diffusive character.

Fig. 10
figure 10

r.m.s of the stream-wise velocity component along line B - LES and URANS computations for row 3 (a) ReD = 3,000 (b) ReD = 10,000 (c) ReD = 30,000

Full size image
Fig. 11
figure 11

Resolved, \(u^{\prime }_{res}\) and modelled, \(u^{\prime }_{mod}\) contributions to the r.m.s of the stream-wise velocity component along line B - URANS computations (a) ReD = 10,000 (b) ReD = 30,000

Full size image

5.3 Mean pressure coefficient

Figure 12 shows the profiles of the mean pressure coefficient along the midline of pins 3 and 5 for the three Reynolds numbers. Profiles along other pins can be accessed via the ERCOFTAC-KB-Wiki database. Note that the experimental results have an uncertainty of ± 0.075 at ReD = 3,000 and of ± 0.025 at ReD = 10,000 and ReD = 30,000. LES results are in relatively good agreement with the experimental data. EB-RSM exhibits overall satisfactory results as well. In fact for ReD = 10,000 for Row 3, the EB-RSM prediction is even better than LES. This result is surprising at first glance, but it is important to emphasize that the LES does not have any fluctuating content at the inlet. Therefore, it takes some rows for the resolved turbulent energy to reach a level compatible with the experiments, in contrast to the EB-RSM for which the turbulence intensity at the inlet is 5%. This discrepancy is not observed at row 5, since the resolved energy content in the LES has developed.

Fig. 12
figure 12

Pressure coefficient along the line C- LES and URANS computations (a) ReD = 3,000 (b) ReD = 10,000 (c) ReD = 30,000

Full size image

On the other hand, both the eddy-viscosity models show less accurate results, in particular the ϕ-model. This is expected since the mean flow characteristics are not correctly reproduced, especially the size of the recirculation regions behind the pins, as seen and discussed before. It is also observed that for these models separation was delayed, which led to a weak prediction downstream of the pins. This can also be seen in the contour plots of the mean stream-wise velocity in Fig. 6. On the other hand, the ϕ-model comparisons are somewhat better for the deeper rows. It can, however, be noticed that at the highest Reynolds number the pressure recovery in general is not predicted very accurately by all the tested models; in addition to the local separation and reattachment, the strong vortex shedding from the sides of the pins make this condition the most difficult to predict with even the most advanced of the RANS closures.

5.4 Nusselt number on the bottom wall

Figure 13 shows the contours of the Nusselt number normalized by its average value over the bottom wall. LES computations exhibit an excellent behavior compared to the experimental results. The Nusselt number seems however overestimated at the locations of the horseshoe vortices and underestimated in the wake of the third row, in particular for the highest Reynolds number case. Recall here that the errors made on the average of the normalized Nusselt number were equal to 3% and 1% for the ReD = 3,000 and ReD = 10,000 cases, respectively.

Fig. 13
figure 13

Comparisons of the Local Nusselt number normalized by its average (Nus/Nusav) (a) ReD = 3,000 (b) ReD = 10,000 (c) ReD = 30,000

Full size image

For the two eddy-viscosity models, owing to the misprediction of the flow topology and the fluctuation level observed in previous sections, it is not surprising that both these models cannot predict the local quantities such as the Nusselt number properly. Moreover, it can be observed that for the k − ω-SST model, the contours are not fully symmetrical, even with a very long averaging time, which suggests the presence of very low frequencies that are probably not physical. On the other hand, the EB-RSM model exhibits a very satisfactory global behavior in particular at the highest Reynolds number. However, the Nusselt number is underestimated in the wake of the first cylinder as the unsteadiness is lower than that predicted by the LES. The prediction for the next rows is satisfactory although an overestimation of the heat transfer in the wake of the cylinders was observed for the last 4 rows.

Figure 14 shows the detailed profiles of the normalized Nusselt number at mid-span (Y/D = 0 plane). LES exhibits very good results in general, except in the wake of the first pin, where roughly halfway between the two pins, the maximum of the Nusselt number is overestimated for both the tested Reynolds numbers. The Nusselt number is also underestimated just after each pin, but this discrepancy is present for all the models and at all the tested Reynolds numbers. This suggests that the underestimation is not due to the turbulence modelling but rather due to the use of adiabatic conditions on the pin walls, which is not fully representative of the experimental setup.

Fig. 14
figure 14

Local Nusselt number normalized by its average (Nus/Nusav) at mid-span Y/D = 0 plane (a) ReD = 3,000 (b) ReD = 10,000 (c) ReD = 30,000

Full size image

The results provided by the URANS models are mixed. Clearly, the k-ω-SST is the least satisfactory model, since the results do not match the experiments anywhere. In the wake of the first pin, where turbulence is not yet fully developed, mixing is dominated by the large-scale unsteadiness, which is not reproduced by this model. In contrast, in the wake of the last two pins, turbulence has developed, as seen in Fig. 9, and the model overestimates turbulent mixing and heat transfer. The ϕ-model better reproduces the Nusselt number in the wake of the last pin, but, in accordance with what has been said earlier, the model does not reproduce the large-scale unsteadiness either, such that the mixing of momentum and heat is underestimated in the wakes of the first few pins. On the other hand the behaviour of the EB-RSM is globally comparable to that of LES, although after the first row, the Nusselt number is significantly underestimated.

6 Conclusions

Simulations were carried out for the flow through a wall-bounded pin matrix in a staggered arrangement with an imposed heat flux at the bottom wall, at various Reynolds numbers (3,000, 10,000, 30,000) based on the gap velocity and the diameter of the pins. Two LES simulations (with 18 and 76 million computational cells) and six URANS simulations (utilizing 17 and 29 million cells) were performed. For URANS, the ϕ-model, k-ω-SST model (both associated to the SGDH with a constant turbulent Prandtl number) and the EB-RSM model combined to the GGDH were used. For LES, the dynamic Smagorinsky model with Lilly’s minimization was used. Both global and local comparisons were drawn against experimental data of Ames et al. and hybrid model simulations of Delibera et al.

A global evaluation of the results was performed by computing pressure loss coefficients and average Nusselt numbers. For a more detailed evaluation, the mean pressure coefficient, the mean velocity profiles, r.m.s. of stream-wise velocity, resolved and modelled contributions to r.m.s. values and the Nusselt number at the bottom wall were computed for all the models.

For the global pressure loss coefficient, LES at ReD = 3,000 and ReD = 10,000 exhibited excellent comparisons with both experimental and analytical correlations. For the URANS models, it was observed that only the EB-RSM model produced reliable results but only for ReD = 10,000. For the higher ReD case of 30,000 none of the models seems to perform particularly well; the worst results were obtained by the eddy-viscosity models. For the average Nusselt number the current LES and EB-RSM results were again found to be in good agreement with the experiments for all the tested ReD numbers. Once again, the two eddy-viscosity models did not provide accurate results mainly due to their inability to reproduce the unsteadiness of the flow.

The detailed comparison of the results with the experiments and amongst the models is particularly interesting and the complete set of results can be accessed via the ERCOFTAC-KB-Wiki. It is observed that the models fall into two categories: those which are able to reproduce the unsteadiness of the wakes of the pins (LES and EB-RSM) and those which essentially provide a steady solution, at least for the first few rows (eddy-viscosity models). The correct reproduction of the global topology of the flow, in particular the length of the recirculation regions behind the pins, is closely related to the presence of a major unsteady contribution. This can be traced to the fact that the turbulent/unsteady structures which efficiently mix momentum in the wake of bluff bodies are the very large-scale structures, which are resolved by LES and EB-RSM, but not by the eddy-viscosity models. This is in line with several previous studies, such as [14] or [15], in which it was shown that the pure RANS models, i.e., RANS models used in a steady-state computation, are not able to correctly reproduce such wakes, while the same models used in URANS mode, i.e., in a time-dependent computation, provide excellent results.

Consequently, reproducing the characteristics of pin-fin-array flows, in which each row of pins is affected by the wake of the preceding row, requires a time-dependent computation in which the unsteadiness develops rapidly, starting from the first row. This behavior is not only observed for LES, but also for the Reynolds-stress model, for which the mixing is dominated by the resolved contribution. In contrast, EVM models face strong difficulties to develop unsteadiness at the first few rows, which severely affects the global predictions. Following previous studies [43,44,45], this issue can be related to the misalignment of the Reynolds-stress and mean strain tensors in non-equilibrium flows (stress-strain lag), such as cylinder wakes, which is ignored by the eddy-viscosity models; the resulting overestimation of modelled turbulence energy in the wake prevents the development of resolved unsteadiness.

In conclusion, for such a complex configuration, consisting of a staggered arrangement of wall-mounted obstacles, with heat transfer, LES can provide accurate and reliable solutions. URANS can provide an alternative solution, particularly attractive for high Reynolds numbers, for which LES can become prohibitively costly, but the choice of the RANS closure is crucial. Due to the importance of avoiding an overestimation of turbulent diffusion in the wakes of the pins, eddy-viscosity models should be avoided and a Reynolds-stress model, or, possibly, a lag eddy-viscosity model [46], should be used. For this case, in the forced convection regime, the model for the turbulent heat fluxes is not crucial; associated with the EB-RSM, which globally provides accurate flow dynamics, the Generalized Gradient Diffusion Hypothesis (GGDH) appears sufficient to reproduce the main heat transfer characteristics.