Abstract
Turbulent combustion models approximate the interaction between turbulence, molecular transport and chemical reactions. Among the many available turbulent combustion models, the present focus is the linear-eddy model (LEM) used as a subgrid combustion model for large eddy simulations. In particular this paper introduces a new LEM closure with the reaction-rate approach to close the filtered chemical source terms in the governing equations for species mass fractions and enthalpy. The new approach is tested using a non-premixed syngas flame and a bluff-body stabilized premixed flame problem. Simulation results are compared to data from a direct numerical simulation and experiments. This comparison shows that mean and rms quantities compare well with experiments and are in the range of previous simulation studies. These results are obtained with a pressure-based and unstructured computational-fluid-dynamics solver, an approach that is preferred in industry.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Turbulent combustion happens in combustion devices such as internal combustion engines and gas-turbine engines [1, 2]. It involves an interaction between highly non-linear chemical reactions, turbulence and molecular mixing. Turbulence is characterized by a broad range of scales in spacetime, ranging from the smallest Kolmogorov scales to the largest flow structures characterized by the scales of the flow geometry. Computational fluid dynamics (CFD) provides useful tools to study turbulent combustion. One such CFD tool is direct numerical simulations (DNS), which aims at fully resolving the flow physics. However, DNS is currently computationally affordable only for relatively simple problems. In contrast, CFD approaches for engineering problems approximate the above physics with turbulent combustion models. There are numerous turbulent combustion models available [2, 3] and several studies have compared them [4,5,6].
From a practical point of view it is desirable to have a turbulent combustion model that is generally valid, which means that it is predictive for both premixed and non-premixed combustion modes and independent of chemical time scales (fast/flamelet-type chemistry vs. non-fast chemistry). One such type of model is the transported probability-density-function (TPDF) method [43,44,45]. Another one is the linear-eddy model (LEM) of Kerstein [7] when used as a subgrid combustion model for large eddy simulations (LES) [8, 9], in which case it is called LES-LEM.
LEM was initially formulated as a scalar mixing model for non-reacting flows [7] and later extended to predict reactive flows [10]. LEM relies on a one-dimensional line on which all spatial and temporal scales are resolved, hence reducing computational cost relative to three-dimensional DNS while retaining high resolution. Modeling of turbulence is done via stochastic mapping events. Diffusion and reaction are represented with reactive-diffusive partial differential equations.
LES-LEM has been employed in a large variety of combustion problems [11,12,13,14,15,16,17,18,19,20,21,22,23]. McMurtry et al. [24] showed simulation results of turbulent scalar mixing. Non-premixed turbulent combustion simulations were done by Calhoon [25] and Menon and Calhoon [26], and premixed turbulent combustion by Smith [27] and Chakravarthy and Menon [28]. Spray combustion simulations were performed by Pannala and Menon [29], and by incorporating radiative heat loss and soot modeling by Zimberg et al. [30]. Predictions of a premixed turbulent methane/air flame were presented by Sankaran and Menon [31]. Sen and Menon employed artificial neural networks to speed up chemistry calculations [32, 33]. LES-LEM with a low-Mach-number numerical scheme was used to simulate the Sandia flame D by Ochoa et al. [34]. Choi and Menon applied LES-LEM for simulations of a cavity-stabilized combustor [35]. A few examples of simulation on reciprocating engines include work done in KIVA for simulating a direct injection spark ignition engine using LES-LEM [36], and an URANS-LEM method in order to investigate pressure histories in an automotive HCCI engine [37]. Martinez et al. [38, 39] studied turbulent combustion of hydrogen-enriched fuels. Lovett et al. [40] studied the flame structure of bluff-body stabilized flames. Srinivasan et al. [41] used LES-LEM for investigating combustion instabilities in a continuous variable resonance combustor (CVRC) and also performed spray combustion simulations [42].
Turbulent combustion models can be used in at least two different ways [3]. One is the so-called primitive-variable method in which the models provide closure for the filtered or averaged thermochemical quantities, i.e. the species mass fractions and an energy variable such as enthalpy or temperature. This method is perhaps the most popular one and is typically used with flamelets [2], transported-PDF methods [43,44,45], and in most previous LES-LEM studies as well. The other method is the reaction-rate approach in which the turbulent combustion model provides closure for the chemical source terms in the conservation equations of the thermochemical quantities, i.e. models of this type solve transport equations for all species and a form of the energy equation. Thus, this approach is computationally more expensive than the primitive-variable method. However, the approach can be regarded as more broadly applicable as it simplifies the inclusion of more physics into the modeling [3].
An additional advantage of using the reaction-rate approach is that it can potentially ease the use of more than one turbulent combustion model during a simulation. For example, consider a combustion problem involving a vigorously burning flame in some region in spacetime, a flame undergoing extinction-reignition in another region, and ignition in yet another region. This is a multi-physics combustion problem. Knowing the fact that turbulent combustion models can be more cost-effective (e.g. in terms of accuracy and computational cost) for a particular type of physics but not necessarily for other physics, it becomes desirable to use one particularly suitable model for one region in spacetime and other suitable models in other regions. The potential for such an approach to lead to more cost-effective combustion simulations is beginning to be recognized [46, 47]. This is the case not only in the combustion community but, for instance, in the multi-phase-flow community as well [48]. Within this hybrid framework, the primitive-variable method runs into the difficulty that turbulent combustion models handle the turbulent transport in different ways, as discussed shortly for the case of LEM. In comparison, the reaction-rate approach does not run into this problem as it solves for the conservation equations of the thermochemical quantities. Furthermore, the reaction-rate approach isolates modeling errors due to the turbulent combustion model in the chemical source terms, simplifying as well the comparison of errors from different models.
In the LEM framework, the reaction-rate approach could also help in reducing potential artifacts produced by the splicing algorithm. This algorithm, as clarified later, is used to transport the thermochemical quantities residing on the individual LEM domains between LES cells. It can result in a spatial distribution of scalars that may differ from the distribution that would be obtained by solving the filtered or averaged conservation equations. Thus, by solving such equations concurrently with the splicing, it is possible to make adjustment to the spatial distribution of a thermochemical quantity if such an inconsistency is considered unacceptably large.
The primitive-variable approach is standard for previous LES-LEM implementation so it is valuable then to explore how well a new LEM closure with the reaction-rate approach performs. Therefore, the present work and a parallel one [49] use LEM following the reaction-rate approach. The present work differs from this previous one in that it uses a significantly different code framework, and it retains the splicing algorithm instead of getting rid of it. Importantly, the latter feature allows the present approach to retain the time-history of the subgrid solution rather than disregard it, at the cost of making the code more complex. In principle this facilitates a more accurate modeling of highly unsteady phenomena, e.g. extinction and re-ignition. This potential capability, however, remains to be shown and is not addressed here. The present work makes use of unstructured meshes and a pressure-based approach, both of which are usual industry practice. The current paper is a major revision and expansion of a previous conference paper [50]. Common material is reprinted with permission from AIAA.
The present paper is arranged as follows. Section 2 introduces the new proposed methodology based on LEM. Thereafter, Section 3 compares predictions with this methodology with those from DNS and traditional LES-LEM for a syngas flame problem [51]. Section 4 compares simulation results with experiments for a bluff-body stabilized flame combustor called the Volvo combustor from now on [52,53,54]. These two test problems are selected since they have been used in the development of various turbulent combustion models and serve the purpose of determining whether the present approach works well. These tests, however, suffer from two serious shortcomings discussed later on. Due to these shortcomings, Section 5 presents a sensitivity study for high-Reynolds-number flames. Finally, simulation results are used to further explain how the present model works, and then the paper finishes with conclusions in Section 7.
2 Methodology
2.1 LES equations
The current work uses the OpenFOAM library version 2.3.1 [55, 56] and considers the following filtered conservation equations for global mass, momentum, sensible enthalpy, and species mass for gases that are variable density, viscous, heat-conducting and multiple-component and move at low-Mach-number speeds:
Here ρ denotes the density, p the pressure, ui is the velocity component in spatial direction i, h is the sensible enthalpy, and Yα is the mass fraction of the species α. The bar denotes conventional filtering and the tilde density weighted Favre filtering. \(\bar \tau _{ji}\), \(\bar q_{j}\), and \(\bar j_{\alpha ,j}\) are respectively the filtered viscous stress tensor, heat flux, and Fickian molecular flux of species α. Likewise, \(\tau _{ji}^{sgs}\), \(q_{j}^{sgs}\), and \(j_{\alpha ,j}^{sgs}\) are the subgrid viscous stress tensor, heat flux, and molecular flux of species α, all of which need closure. These conservation equations are complemented with the equation of state for ideal gases
where Wα is the molecular weight of species α and Rm is the universal gas constant. The averaged caloric equation of state is given as,
with hα(T) given by the NASA polynomials [57].
The terms \(\tau _{ij}^{sgs}\), \(q_{j}^{sgs}\), and \(j_{\alpha ,j}^{sgs}\) are the subgrid stress tensor, heat flux, and mass flux of species k. They are closed with
In the syngas flame problem, the SGS viscosity μsgs is computed with OpenFOAM’s implementation of the Smagorinsky model [58]
with Ck being a model constant (Ck = 0.02), Δ the cube root of a given finite volume, and ksgs the SGS kinetic energy obtained from
where a = Ce/Δ, \(b=2 \widetilde {S}_{kk} / 3\), \(c=2 C_{k} {\Delta } (\widetilde {S}_{ij} - \delta _{ij} \widetilde {S}_{kk} /3) \widetilde {S}_{ij}\), and Ce = 1.048. For incompressible flows, the constants Ck and Ce are related to the constant Cs of the typical implementation of the Smagorinsky model [59] through \(C_{s}=C_{k}^{3/4}C_{e}^{-1/4}\). For the Volvo combustor simulations, μsgs is computed with OpenFOAM’s implementation of Yoshizawa & Horiuti’s one-equation eddy model [60].
Closure of the averaged source terms \(\bar S_{h}\) and \(\bar S_{\alpha }\) is done as follows.
2.2 Closure of the chemical source terms with the no-model approach
With the no-model (also called the perfectly stirred reactor model) approach, the averaged chemical source term is given by:
where \(\bar C_{\alpha } = \bar \rho \tilde Y_{\alpha } / W_{\alpha }\) is the molar concentration of species α. It means that the chemical source term is simply evaluated using directly the filtered values of the resolved fields.
2.3 LEM subgrid modeling inside a LES cell
The LES-LEM model is composed of the following elements: the LES equations discussed before; the LEM modeling inside a LES cell; the exchange of information between the LEM and the LES; the LEM modeling “between” LES cells; and, for the current formulation the closure of \(\bar S_{h}\) and \(\bar S_{\alpha }\).
The hallmark feature of the LEM is a 1D domain resolving all scales [9] having an inflow on one end and an outflow at the other end. In LES-LEM, there is one 1D domain per computational LES cell, as shown in Fig. 1. All the cells of the LEM domain within a LES cell are uniformly initialized with the thermochemical conditions in that LES cell. The initial LEM domain length is chosen to be equal to the local LES mesh spacing Δ. The solution on the LEM domain time advances the conservation equations in their 1D form as:
where MLEM is the total mass in a LES cell, the summation (index i) is done over all cells of the LEM domain, the x coordinate is parallel to the 1D array, and ST is the heat-source term in the temperature equation. Constant pressure is assumed on the LEM which allows updating of the LEM density resulting in change of the LEM domain length. Here unity Prandtl and Lewis numbers are used to compute qx and jα,x.
LES-LEM simulations use a 1D domain (in black) consisting of a stack of LEM cells per computational LES cell (in red) [61]. Note that the LEM domains have no assigned orientation relative to the underlying coordinate system
Macromixing (subgrid turbulent stirring) is modelled by distorting the profiles of all scalar quantities according to
Here M(x) is a mapping operation known as the triplet map. The effect of the triplet map on a flow property profile defined in [x0,x0 + l] is to replace the profile with three compressed images of the original with the middle image flipped. This is how the rotational and compressive motions observed in the turbulent flows are represented in the LEM [62].
The triplet maps are parametrized by a location x0, a length l, and an eddy rate λ per unit domain length. They are implemented in a stochastic way by sampling x0 from a uniform distribution and l from
where lp and lmax are the smallest and the largest unresolved length-scales characterizing the turbulence, and are specified by the user. Here lp is taken as the Kolmogorov length-scale η, and lmax equals the local mesh spacing of the LES solver Δ. Implied in Eq. 17 are Kolmogorov’s scalings in the inertial subrange (e.g. the time-scale of an eddy τ scales as τ ∼ l2/3). An estimate for the Kolmogorov length-scale is given by
with Nη being a model constant, and ReΔ the subgrid Reynolds number:
where ν is the kinematic viscosity and usgs is the characteristic subgrid velocity fluctuation obtained from the LES subgrid turbulent kinetic energy \(\bar k_{sgs}\) as \(u_{sgs}=\sqrt {2\bar k_{sgs}/3}\).
The eddy rate λ per unit domain length with unit (length x time)-1 is obtained through an analogy between eddy sampling statistics and inertial range scaling laws and is computed via
with Cλ being a model constant. The average time interval between triplet maps is:
where lLEM is the LEM domain length and the actual eddy occurrences are sampled from a Poisson process. The sampling rejected the eddies that extend beyond the LEM domain boundary. The values of Cλ = 1 and Nη = 1.1 are used throughout unless said otherwise. These values were chosen to ensure that triplet maps are occurring during the simulation.
2.4 LES-LEM advection modeling
Another element of the present LES-LEM formulation is an algorithm that transfers the subgrid-scale quantities, i.e. those defined in the 1D arrays, between 1D arrays in the adjacent LES computational cells. The present work uses the splicing algorithm since it has proven to be robust for practical combustion implementations. The splicing algorithm cuts and pastes the end portions of the 1D arrays of the adjacent LES cells to emulate a Lagrangian type of mass transfer. Decisions of how much to cut and paste are based on values of the mass fluxes across the faces of LES computational cells. For example, if the mass flux at a given face of cell A is large and directed from cell A to cell B, a large portion of the 1D array in A will be cut and then pasted onto one of the two endpoints of the array in B. There is some arbitrariness, however, in how this is exactly done. If this mass flux were small, a small portion would be cut and pasted. Details about the splicing algorithm are given in [50, 64].
2.5 Closure of the chemical source terms with LEM
Figure 2 shows the coupling between the LES and the LEM subgrid combustion model. The LES provides information about the cell spacing Δ, the subgrid turbulent kinetic energy \(\bar k_{sgs}\), the time step of the simulation Δt and the pressure to the LEM. With this information, the LEM subgrid-scale simulation advances Eqs. 13–20 for the LES time interval Δt. The chemical source terms \(\bar S_{h}\) and \(\bar S_{\alpha }\) are obtained by taking the median or mean value along various LEM elements for the current LES time step. Mean values are calculated (e.g. for species mass fractions) with
where the summation (index i) is over the elements of the LEM array and Δxi denotes the non-uniform length of an individual LEM cell. The median source term, on the other hand, is calculated by first sorting the source term values of all the LEM elements in ascending order, and then picking up the middle value. Apparently, the chosen value can come from a different cell for each species. Comparison of predictions using the mean and the median is discussed later in Section 4.4. Although the use of the mean is intuitive, the median is considered here as well because it is a more robust measure since it prevents outliers. These source terms are then used in the LES conservation equations for the species mass fractions and sensible enthalpy. The temperature on the LES side is then calculated from the caloric equation of state, Eq. 6.
In the present implementation, the PISO algorithm [63] is used. It has an outer loop which starts with predicting a velocity (using Eq. 2), which is followed by an inner iterative loop to correct the velocity field using the outcome of a pressure Poisson equation obtained by fulfilling the continuity equation. In the inner iterative loop, the LES density is obtained from the equation of state Eq. 5. After splicing is done with the predicted LES mass flux, the LEM lines are restored back to the state before the predicted splicing was done, in order to do the splicing with the correct LES mass flux as described in [64].
The last step is to correct the temperatures and the species mass fractions in the LEM domains to take into account the fact that the convection due to the solution of Eqs. 1-4 differs from that of the splicing algorithm. The need for this step is discussed further in Section 6. There is not a unique way to conduct this correction, and the following algorithm is a result of trial and error and has been found to be robust, as demonstrated later.
The goal of this correction algorithm is to keep the Favre-averaged temperatures and species mass fractions from the LEM domains within some tolerance of those from the solution of Eqs. 1–4. LES quantities are not altered. Fig. 3 summarizes the correction for the temperature. A similar process is used for the species mass fractions.
Steps of correcting the temperature in a LEM domain. Here Ti is the temperature of LEM cell i and nLEM is the total number of LEM cells. The temperature difference \(T^{\prime }\) is a difference between the LES temperature \(\tilde T\) and the Favre-averaged LEM temperature \(\tilde T_{LEM}\). The notation += means addition assignment. This correction procedure is also used for the species mass fractions
The first step of the correction computes the difference T′ between the LES temperature \(\tilde T\) and the Favre-averaged LEM temperature \(\tilde T_{LEM}\), the latter of which is obtained via:
where Ti denotes the LEM cell temperature, and the summation (index i) is over all cells of the LEM array. In a second step, T′ is added to each Ti. This updates \(\tilde T_{LEM}\). If the new updated difference T′ is within a specified tolerance the correction is stopped, otherwise the updated difference T′ is added again to each Ti and the aforementioned steps are repeated.
At this point, a distinctive conceptual feature of the present closure must be highlighted. It is common in LES to make a sharp distinction between the closure of diffusive processes (micromixing) and reaction. This is evident by noticing that in Eqs. 1–4 separate closure is needed for, on one hand, \(\bar q_{j}\) and \(\bar j_{\alpha ,j}\), and, on the other hand, \(\bar S_{h}\) and \(\bar S_{\alpha }\). However, a more realistic picture is that diffusive and reacting processes are closely coupled at the subgrid level (meaning reaction and diffusive terms can be of the same order), for example, in some premixed flames. Now, with LEM \(\bar S_{h}\) and \(\bar S_{\alpha }\) are computed as explained above using a 1D structure that represents both reaction and diffusion. Thus, it is perhaps more accurate to say that the present closure, although given for \(\bar S_{h}\) and \(\bar S_{\alpha }\), is not a closure for subgrid reaction, but for subgrid reaction-diffusion processes, i.e. with proper resolution the LEM is capable of fully resolving flame structures in 1D. This is why the approach is termed a subgrid reaction-diffusion closure with LEM.
2.6 Numerical method
The conservation equations Eqs. 1–4 are solved with an adaptation of reactingFoam which is the standard solver of the OpenFOAM library for chemically reacting flow. This solver is transient, pressure-based and can handle unstructured meshes [64]. A low-Mach-number assumption is used as done in reactingLMFoam [65, 66] by splitting the pressure into a fluid-mechanical-induced pressure and a thermodynamic pressure, the latter of which is spatially constant and which is used to evaluate the equation of state. As a result, acoustic waves are eliminated from the solution. The OpenFOAM library has various temporal and spatial discretization options available. In the current work, the time discretization is done with a second-order backward-differencing scheme that uses the current and previous two time step values. OpenFOAM’s limited linear differencing scheme is used for the convective and diffusive fluxes.
3 Medium-Reynolds-Number Syngas Flame
3.1 Configuration
This Section considers a reacting, temporally-evolving, planar jet in a cuboid of size Lx × Ly × Lz studied with DNS by Hawkes et al. [51]. Fig. 4 shows a schematic of the jet. The fuel stream is an initially planar jet moving in the x-direction, with the oxidizer moving in the opposite direction on either side of the fuel stream. Turbulence is generated by shear at the interface between the two jets. The fuel is syngas, comprising 50% CO, 10% H2, and 40% N2 by volume. The oxidizer is composed of 25% O2 and 75% N2 by volume. Both fuel and oxidizer are initially at 500 K and react according to a skeletal mechanism for C1-kinetics [51]. The pressure is atmospheric. The characteristic jet velocity is U, and at t = 0 both streams have a velocity of U/2 in their respective directions. A characteristic length-scale of the problem is the jet height H, and a characteristic jet time scale is tj = H/U. Thus, a Reynolds number can be defined as Re = (UH)/νf, where νf is the kinematic viscosity of the pure fuel. The Damköhler number is defined as Da = χqtj, with χq being the quenching scalar dissipation rate for the flamelet solution. The size of the computational domain is given in terms of the characteristic length as Lx = 12H, Ly = 14H, and Lz = 8H. The (global) Mach number is M = U/(c1 + c2), where c1 = 476 ms− 1, and c2 = 445 ms− 1 are the sound speeds in the fuel and oxidizer streams respectively. Periodic boundary conditions are specified in the streamwise (x) and the spanwise (z) directions. The mesh spacing is uniform and equal in all directions.
For the simulations presented in this work, H = 0.96 mm, and U = 193 ms− 1, which correspond to case M of Hawkes et al. [51]. The jet Reynolds number is 4478, and the jet characteristic time is tj ∼ 5 μ s. The LES is set up closely following the setup used in the DNS study. However, whereas the DNS used a uniform mesh size of 768 × 896 × 512, the LES uses a mesh 8 times coarser, 96 × 112 × 64. The DNS mesh spacing corresponds roughly to the Kolmogorov length-scale.
In the DNS, combustion is started by superimposing a laminar flamelet solution and by using broadband turbulent velocity fluctuations. In the present LES, all fields are initialized by mapping the DNS initial condition onto the LES mesh. One more difference with the DNS is treatment of the boundary conditions at the ends of the vertical extent of the domain. Here Neumann boundary conditions are used with all quantities except pressure, which is set to an atmospheric value.
For the syngas jet, comparisons are presented here for two different simulations: a simulation with no turbulent combustion model (the no-model approach), and with the LES-LEM model. The LES-LEM simulations used the median source terms. Using the mean source terms produced almost identical results. The mesh used to simulate this jet is formed by uniform cubical control volumes. For the advective terms in the transport equations, a second-order center-difference scheme is used.
3.2 Comparison with DNS
Figure 5 shows the streamwise and spanwise spatially averaged mean and rms lateral temperature profiles obtained from the simulations. Fig. 6 shows the mixture fraction fields at the same instants. The largest discrepancies are seen at 10tj. This is likely due to the present use of a simplified molecular transport modeling (e.g., unity Lewis numbers for all species) since a preliminary no-model-approach simulation (not shown) not using this simplified modeling captures well the profiles at 10tj. The impact of more realistic molecular diffusion models will be investigated in the future. Nonetheless, overall the simulation results agree well with the DNS, which was the main purpose of evaluating the new implementation here. In addition, Figs. 5 and 6 show that for this case LES-LEM does not show a clear benefit over the no-model approach. One possible explanation is that the Reynolds number associated with this problem is not large enough for the detailed turbulent combustion models to fully kick in. This is further discussed in Section 6.
Spatially averaged mean and rms lateral profiles of temperature for the temporal syngas jet. at = 0 bt = 10tjct = 16tjdt = 20tjet = 30tjft = 40tj. (Black solid line: mean, no turbulent combustion model; blue solid line: mean, LES-LEM; ∘: mean, DNS; black dashed line: rms, no turbulent combustion model; blue dashed line: rms, LES-LEM; \(\Box \): rms, DNS.)
Spatially averaged mean and rms lateral profiles of the mixture fraction for the temporal syngas jet. at = 0 bt = 10tjct = 16tjdt = 20tjet = 30tjft = 40tj. (Black solid line: mean, no turbulent combustion model; blue solid line: mean, LES-LEM; ∘: mean, DNS; black dashed line: rms, no turbulent combustion model; blue dashed line: rms, LES-LEM; \(\Box \): rms, DNS.)
3.3 Comparison with traditional LES-LEM
In Figs. 7 and 8 the temperature and some of the major species are shown compared with the results of Sen et al. [33] who used the traditional LES-LEM. Overall the results obtained from the present simulation are at least as good as or slightly better than those of Sen et al. with the potential benefit of the new approach being more robust and flexible as explained before. It should be noted that Sen et al. used a non-uniform, stretched mesh with 192 × 224 × 128 cells as opposed to the use of 96 × 112 × 64 uniformly-spaced cells in the present work.
Mixture fraction-conditioned profiles of temperature and species mass fractions at 20tj for the temporal syngas jet. (Black solid line: present work; blue dashed line: LES-LEM of Sen et al. [33]; ∘: DNS.)
Mixture fraction-conditioned profiles of temperature and species mass fractions at 40tj for the temporal syngas jet. (Black solid line: present work; blue dashed line: LES-LEM of Sen et al. [33]; ∘: DNS.)
4 Volvo Combustor
The Volvo combustor is a standard test case for the evaluation of turbulent premixed combustion models which has been investigated extensively in the past. Here the case is used to compare the new LES-LEM implementation with experiments and other modeling approaches and to evaluate the impact of certain model parameters within LES-LEM on the simulation results.
4.1 Configuration
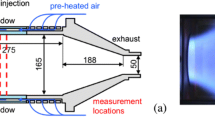
The experimental setup of the Volvo test problem [52,53,54] consists of a rectilinear channel, with an inlet section where air and (gaseous) propane mix before entering a honeycomb, and a downstream section where the premixed reactants burn in a flame that gets stabilized downstream of a wedge [52]. The cross section of the wedge is an equilateral triangle with side of 40 mm. The end of the downstream section is connected to a round exhaust duct with a cross sectional area about 3.4 times larger than that of the channel [67]. Unfortunately, the length of this exhaust section has not been documented in the open literature. Atmospheric conditions are used.
The computational domain used for the current work is shown in Fig. 9 and has the following geometric parameters: h1 = 40 mm, h2 = h1sin60, xmin = -820 mm, xmax = 680 mm, ymin = -60 mm, ymax = 60 mm, and a spanwise length of 40 mm. The honeycomb is ignored as done in previous CFD studies. The pressure gradient normal to the inlet plane is set to zero. No turbulent fluctuations are imposed at the inlet because the region of interest is downstream of the wedge which is responsible for generation of strong turbulence. All walls are modeled as no-slip and adiabatic, unless stated otherwise. At the outlet, velocity, temperature and species are set to a zero-normal-gradient condition or a fixed value, depending on the direction of the flow. Pressure is dealt with a similar way at the outlet. Cyclic boundary conditions are used in the z-direction, unless indicated otherwise. An unstructured hexahedral 3D mesh with 77400 cells is used with the simulation time step of 10− 6 s.
Of the various operating conditions of the Volvo test problems, the one considered for the present work is the so-called Case 1. In Case 1, the inlet conditions are 288 K, 17 m/s, and 0.61 equivalence ratio. Table 1 summarizes the various simulations conducted for the present study. Table 2 [68] shows the chemical kinetic model used in the present work.
4.2 Comparison with experiments
Figure 10 shows instantaneous temperature maps using the no-model approach (simulation 1 cf. Table 1) and the LES-LEM baseline case (simulation 2 cf. Table 1). Notice that immediately downstream of the flameholder the flame is symmetric (varicose) about the y = 0 plane. This agrees with experiments (cf. Fig. 9 in Sjunnesson et al. [54]) and many other simulation studies. However, the transition towards an asymmetric (sinusoidal) flame shape further downstream agrees with some simulation studies (Fig. 4b in Moller et al. [69], Fig. 8a in Fureby [70] and Fig. 3 in Comer et al. [71]) and disagrees with others where the flame is predominantly symmetric all the way towards the outlet (Fig. 4 in Giacomazzi et al. [72], Cocks et al. [73], and perhaps also Baudoin et al. [74]). This latter predominantly symmetric shape appears to be the physically correct one for the present boundary conditions because many of the most recent simulation studies show this shape [75,76,77,78,79]. The cause for the transition from symmetric to asymmetric flame shape seen in the present simulations may be the use of a low-Mach-number formulation instead of a fully-compressible one [77]. More importantly, since many studies diverge on whether the flame further downstream is symmetric or not, the fact that this portion of the flow (in a non-linear dynamics sense) is close to a bifurcation cannot be ruled out, in which case its accurate prediction is very difficult. Furthermore, it must be stressed that, from the open literature, it is unclear how the flame looks like close to the outlet in the experiments.
Spatial variations of mean quantities are shown in Figs. 11 and 12 for the no-model approach (simulation 1 cf. Tab. 1) and LES-LEM with Cλ = 1 (simulation 2 cf. Tab. 1) and Cλ = 10 (simulation 3 cf. Tab. 1). These quantities are averaged in the spanwise direction and over time, the latter of which is done for a time interval of 0.02 s. (Through trial and error this interval is found to be adequate to evaluate the mean quantities.) Overall, Figs. 11 and 12 show that the sensitivity to the type of model and LES-LEM model constant is small, although the best agreement with the experiments is given by the LES-LEM simulation with Cλ = 10. In Fig. 11, perhaps the largest disagreement between the experimental data and predictions is seen in the temperature profiles near the outlet. This disagreement could be due to the lack of near-wall mesh refinement in the present simulations, or due to the fact that the wall thermal boundary condition from the experiments is unknown. Nonetheless, the overall agreement between the simulations and experiments shown in Figs. 11 and 12 is within that seen in some simulation studies [70, 72,73,74, 80] but slightly less accurate as those seen in other studies [13, 81], the latter of which includes a previous LES-LEM study, which is compared to the current study in the Section 4.3.
Vertical profiles of mean quantities for the case 1 at different streamwise locations obtained with the no-model approach (red) and the LES-LEM with Cλ = 1 (blue) and Cλ = 10 (green), cf. Table 1. The experimental data is denoted with black circles. Here, U denotes the mean horizontal velocity, V the mean vertical velocity and Uin is the inlet velocity of 17 m/s
Figure 13 shows the vertical variation of rms quantities computed from the resolved fields using the no-model approach and the LES-LEM simulations. The largest discrepancy between simulations and experimental results happens close to the flameholder. This discrepancy is not surprising due to the rather coarse mesh used. In addition, Fig. 13 shows that the sensitivity of rms quantities to the choice of the turbulent combustion model and LES-LEM model constant is small, except for the rms values of the horizontal velocity at x/h = 9.4, where the LES-LEM model with Cλ = 10 gives the best agreement with experiments.
Vertical profiles of rms quantities for the case 1 at different streamwise locations obtained with the no-model approach (red) and the LES-LEM with Cλ = 1 (blue) and 10 (green), cf. Table 1. The experimental data is denoted with black circles
4.3 Comparison with traditional LES-LEM
Figure 14 shows the comparison of the results obtained from the present LES-LEM implementation with the LES-LEM study of Porumbel and Menon [13]. It can be seen that predictions from Porumbel and Menon seem to be slightly more accurate for this case. However, their study uses more than ten times the (LES) cells used in the present work. Thus, the present study puts LES-LEM model through a more stringent test since a larger portion of the inertial range physics is not directly resolved in the present study by the LES and needs to be captured by the one-dimensional LEM instead.
4.4 Sensitivity to model parameters
The splicing algorithm divides the mass fluxes into those related to the resolved velocity field and those due to the subgrid-scale (sgs) velocity field [64]. Figures 15 and 16 show that the sensitivity of the present predictions to using (simulation 2 cf. Table 1) or not using the sgs contribution (simulation 7 cf. Table 1) is small.
Vertical profiles of mean quantities for Case 1 at different streamwise locations obtained with LES-LEM for the baseline case (red), a case where combustion happens only where the temperature is large enough (green), and a case where the sgs contribution to the splicing is zero (blue), cf. Table 1. The experimental data is denoted with black circles
In terms of the effect of using the median or mean to compute the source terms, the effect of this choice was found to be negligible. This has been observed in another study as well [61].
Figures 15 and 16 also compare predictions between the baseline LES-LEM case (simulation 2 cf. Table 1) and a case where the source term calculations in Eqs. 14–15 is only done at locations where the resolved temperature is larger than 285 K (simulation 10 cf. Table 1). This simple change to the model formulation reduces the computational cost by a factor of 4.7 and provides predictions comparable to the baseline case, as can be seen in Figs. 15 and 16.
5 High-Reynolds-Number syngas Flame
The apparent insensitivity to the choice of turbulent combustion model seen above motivated the simulation of two cases not considered in the DNS study. Two simulations with an increased Reynolds number to demonstrate the influence of increased subgrid turbulence-chemistry interactions are shown here. Case M10 is case M of Hawkes et al. [51], which has been discussed in Section 3 already, but with all length-scales of the mesh multiplied by a factor of 10. This was done by scaling length of the mesh points by 10 in the 3 Cartesian directions, resulting in increasing size of the computational domain by 10 in all the 3 directions. The same is done for case M10U2 but, in addition, the initial velocity field is multiplied by a factor of 2. In cases M10 and M10U2 the Reynolds number is 44780 and 179120 respectively. The simulations of these cases use the same number of cells (in the 3 directions) as indicated above for the M case. So by increasing the length of each cell, the cell-based Reynolds number was increased. This also increased the LEM domain lengths.
For case M10, notice in Fig. 17 that no-model simulations show two reaction layers that appear to merge at the end of the simulation. In contrast, LEM simulations show that these layers merge by t = 30tj. This observation is consistent with a larger turbulent mixing between these layers, which in the case of LEM is represented with triplet maps and the splicing as clarified in Section 6. Furthermore, this merging seen in LEM but not in the no-model simulations is similar to that seen in LEM and not in eddy-breakup-model (EBU) simulations of reacting wakes [82, 83]. In these reacting wakes this merging is observed in the experiments.
Effect of the LEM turbulent combustion modeling on the three cases M, M10, and M10U2. For the case M10, the LEM (d) produces turbulent mixing between the reaction layers earlier as compared to the no-model approach (c). The two reaction layers in (d) merge at t = 30tj, while in (c) they merge at the end of simulations. For the case M10U2, the LEM (f) also produces merging of the two reaction layers earlier and a larger extinction region in spacetime is observed with the LEM (f) as compared to the no-model approach (e)
Moving to case M10U2, Fig. 17 shows that LEM produces a larger extinction region in spacetime (represented by the yellow region) than the no-model approach. This comparison is similar to the observation of stronger extinction, in the form of lift-off distance, seen in LEM simulations of a stagnation-point-combustor in comparison with EBU simulations [14]. Thus, these effects of LEM are consistent with those seen in other studies.
In view of the lack of DNS data for cases M10 and M10U2, however, it is not possible to judge whether the no-model approach or LEM provide more accurate predictions. Nonetheless, for the present purposes, the key message from Fig. 17 is that, in contrast to the previous results, the effect of the turbulent combustion model in cases M10 and M10U2 is profound since it affects the qualitative evolution of the flow. More investigation with LES-LEM focusing on high-Reynolds-number flames will follow in the future.
6 Discussion
An attempt is now made to explain the above apparent insensitivity to the turbulent combustion model, at least for the syngas DNS flame. In LEM the subgrid-scale interaction between turbulent motions, micromixing and reaction is captured in two ways. One is by using 1D conservation laws and triplet maps (“inside” a LES cell). In this case, high levels of turbulence are concomitant with a large number of eddies (triplet maps), Neddies, being implemented per LES time step. On the other hand, values of Neddies of near zero indicate that LEM behaves closely to the no-model approach. Note that Neddies is related to the μsgs through Eqs. 10, 19 and 20 since a higher λ implies higher values of Neddies. The second way the above interaction is captured in LEM is through the movement of LEM elements between adjacent LES cells (not “inside” a LES cell) due to the splicing. From this explanation, the low values of μsgs and spatially averaged (in xz plane) Neddies shown in Figs. 18a and 18b for case M suggest the LEM behaves in a no-model-approach way. In other words, the elements of LEM that represent the subgrid-scale interaction between turbulence and other physics are not active. In contrast, notice in Fig. 18 that for the cases M10 and M10U2 both μsgs and Neddies increase by an order of magnitude. (Note the change of the color scale.) In these cases the elements of LEM to model turbulence-chemistry interactions are active.
Having discussed how predictions from the present LES-LEM model compare with the experiments and a benchmark model (the no-model approach), attention is now drawn towards the design of such a LES-LEM model. For this purpose, Fig. 10 compares the effect of the correction step, cf. Figure 2. Notice in Fig. 10 that by not using this correction there was an artificial extinction of the flame. Thus, the correction step or some alternative is required. This is not surprising because the convection of species by the solution of Eq. 4 differs from that produced by the splicing in at least two ways. First, the solution of Eq. 4 numerically smears the species in a way that the splicing is not prone to because the splicing corresponds to diffusion-free advection in a Lagrangian way. Second, the splicing produces an artifact that the solution of Eq. 4 is not prone to. Such an artifact can be demonstrated with the following test problem of passive scalar advection.
This test problem uses a hexahedral computational domain of size 120× 120 ×8 mm discretized with 64× 64 ×8 hexahedral cells in which a non-reacting uniform flow is assumed from south-west to north-east with a velocity magnitude of 70.7 m/s. Since the problem is non-reacting, there is no transfer of information due to source terms from the LEM to the LES, cf. Figure 2. Initially a blob of a passive scalar sits as indicated in Fig. 19a in the center of the domain. It is important to note in Fig. 19 that the mesh is purposely coarse to exaggerate the effect of numerical diffusion and artifacts from the splicing, both of which can be reduced by refining the mesh (not shown here). In particular, notice that initially the blob is represented with only seven cells across its diameter. The flow has no initial fluctuations, and no turbulence-transport model is used, i.e. a pure advection problem is studied here. Figs. 19b-d show the resulting scalar field at a later time from three different approaches: the solution of Eqs. 1–4 (as usually done), the use of the splicing algorithm with no correction, and the use of splicing with the correction discussed above. In Figs. 19c-d the concentration of the passive scalar is computed as
where Yα denotes the mass fraction of the scalar α, and the summation (index i) is over the elements of the LEM array. First, it is evident by comparing Fig. 19b and c that the splicing distorts the shape of the blob in a way that should be considered an artifact. However, also notice that the numerical dissipation produced by the splicing is much less than that from the solution of Eqs. 1–4 (as usually done). This is a result of the fact that the splicing is a Lagrangian algorithm. Finally, a comparison of Figs. 19b and d shows that the present correction step does indeed correct for the splicing artifact just discussed. Thus, in problems such as this blob-convection test the present correction can be useful to prevent artifacts from the splicing. However, if the mesh is fine enough the splicing artifacts are small and the effect of the correction is negligible [61].
7 Summary and Conclusions
The present paper introduces a new LEM closure for LES with the reaction-rate approach. Using LEM in this way, instead of closing the filtered thermochemical quantities as traditionally done, offers some conceptual advantages. For example, this new closure facilitates the assessment of inconsistency due to the turbulence-transport model. Moreover, for the purpose of reducing computational cost, it simplifies the use of more than one turbulent combustion model within one simulation, which may well include the use of no-model in very refined regions.
Predictions with this new closure agree with DNS results for a syngas flame problem with an accuracy comparable to previous traditional LES-LEM simulations. Furthermore, present predictions for the Volvo combustor are within those of previous simulations, but not as accurate as those from simulations using meshes ten or more times finer than those used here.
In spite of the above promising results, LES-LEM does not show more accurate predictions over the no-model approach for low-Reynolds-number reactive turbulence. The level of turbulence, given by the Reynolds number for instance, in the DNS syngas flame and the Volvo tests are fairly low. This statement is supported by the fact that, at least in the syngas flames, while the LEM model is barely active in the DNS syngas flame (case M), it is very active in the higher-Reynolds-number syngas flames (cases M10 and M10U2). Unfortunately, there are no DNS nor experiments for these flames. Furthermore, the heat release rate in the DNS syngas flame and the Volvo tests is also low, in which case the effects of combustion (e.g., flow expansion) on the fluid dynamics is mild. This is a well known problem with the Volvo combustor and similar academic combustors [73].
In practice, however, much higher Reynolds numbers than those of the medium-Reynolds-number syngas flame and Volvo test case can occur, in particular in gas-turbine-engine combustors [84]. In principle LES-LEM is better suited for these problems, but this capability remains to be demonstrated. Thus, future work on its development should consider test problems closer to actual applications, problems such as the high-Reynolds-number, premixed jet burner of Dunn et al. [85], or the very-high-Reynolds-number, gas-turbine-like LM6000 [86, 87] or GE-E3 [88] combustors, and conduct careful comparisons with, say, the no-model approach at various levels of mesh refinement.
Finally, unlike traditional LES-LEM implementations, the present work demonstrates the use of LES-LEM in a pressure-based and unstructured CFD solver, an approach that is preferred in industry.
References
Turns, S.R.: An introduction to combustion. McGraw-Hill, New York (1996)
Peters, N.: Turbulent combustion. Cambridge University Press, Cambridge (2000)
Poinsot, T., Veynante, D.: Theoretical and numerical combustion. R. T. Edwards, Inc., Philadelphia (2005)
Gonzalez-Juez, E.D., Kerstein, A.R., Ranjan, R., Menon, S.: Advances and challenges in modeling high-speed turbulent combustion in propulsion systems. Progr. Energy Combust. Sci 60, 26–67 (2017)
Oefelein, J.C.: Analysis of turbulent combustion modeling approaches for aero-propulsion applications, AIAA paper 2015–1378 (2015)
Fureby, C.: A comparative study of large eddy simulation (LES) combustion models applied to the volvo validation rig, AIAA paper 2017–1575 (2017)
Kerstein, A.R.: A linear-eddy model of turbulent scalar transport and mixing. Combust. Sci. Technol 60(4-6), 391–421 (1988)
Menon, S., Kerstein, A.R., McMurtry, P.A.: A linear eddy mixing model for large eddy simulation of turbulent combustion. In: Galperin, B., Orszag, S.A. (eds.) Large eddy simulation of complex engineering and geophysical flows, pp 287–314. Cambridge University Press, Cambridge (1993)
Menon, S., Kerstein, A.R.: The linear-eddy model. In: Echekki, T., Mastorakos, E. (eds.) Turbulent combustion modeling, vol. 95, pp 221–247. Springer Series, New York (2011)
Kerstein, A.R.: Linear-eddy modelling of turbulent transport. Part 7. Finite-rate chemistry and multi-stream mixing. J. Fluid Mech 240, 289–313 (1992)
Menon, S., Sankaran, V., Stone, C.: Subgrid combustion modeling for the next generation National Combustion Code. NASA Tech. Rep 2003-212202 (2003)
Sankaran, V.: Subgrid combustion modeling for compressible two-phase reacting flow. Georgia Institute of Technology, Ph.D. thesis (2003)
Porumbel, I., Menon, S.: Large eddy simulation of bluff body stabilized premixed flame, AIAA Paper 2006–152 (2006)
Parisi, V.: Large eddy simulation of a non-premixed stagnation point reverse flow combustor. Georgia Institute of Technology, Master’s thesis (2006)
Undapalli, S.: Large eddy simulation of premixed and non-premixed combustion in a stagnation point reverse flow combustor. Georgia Institute of Technology, Ph.D. thesis (2008)
Sen, B.A., Menon, S.: Artificial neural networks based chemistry-mixing subgrid model for LES, AIAA Paper 2009–241 (2009)
Genin, F., Menon, S.: Simulation of turbulent mixing behind a strut injector in supersonic flow, AIAA Paper 2009–132 (2009)
Wey, T., Liu, N.: Assessment of turbulence-chemistry interaction models in the National Combustion Code (NCC) - Part I, AIAA Paper 2010–16098 (2010)
Liu, N., Wey, T.: On the TFNS subgrid models for liquid-fueled turbulent combustion, AIAA Paper 2014–3569 (2014)
Harvazinski, M.E., Huang, C., Sankaran, V., Feldman, T.W., Anderson, W.E., Merkle, C.L., Talley, D.G.: Coupling between hydrodynamics, acoustics, and heat release in a self-excited unstable combustor. Phys. Fluids 27(4), 045102 (2015)
Fureby, C., Zettervall, N., Kim, S., Menon, S.: Large eddy simulation of a simplified lean premixed gas turbine combustor. In: International symposium of turbulence and shear flow phenomena (2015)
Maxwell, B.M., Falle, S.A.E.G., Sharpe, G., Radulescu, M.I.: A compressible-LEM turbulent combustion subgrid model for assessing gaseous explosion hazards. J. Loss Prevention Process Industries 36, 460–470 (2015)
Li, S., Zheng, Y., Mira, D., Li, S., Zhu, M., Jiang, X.: A LES-LEM study of preferential diffusion processes in a partially premixed swirling combustor with synthesis gases. J. Eng. Gas Turbine Power 139, 031501 (2016)
McMurtry, P.A., Menon, S., Kerstein, A.R.: A linear eddy sub-grid model for turbulent reacting flows: Application to hydrogen-AIR combustion. Proc. Combust. Inst 24, 271–278 (1992)
Calhoon, W.H.: On subgrid combustion modeling for large-eddy simulations. Georgia Institute of Technology, PhD thesis (1996)
Menon, S., Calhoon, W.H.: Subgrid mixing and molecular transport modeling in a reacting shear layer. Proc. Combust. Inst 26, 59–66 (1996)
Smith, T.M.: Unsteady simulations of turbulent premixed reacting flows. Georgia Institute of Technology, PhD thesis (1998)
Chakravarthy, V.K., Menon, S.: Subgrid modeling of turbulent premixed flames in the flamelet regime. Turbul. Flow Combust. 65, 133–161 (2000)
Pannala, S., Menon, S.: Large eddy simulations of two-phase turbulent flows, AIAA Paper 1998–0163 (1998)
Zimberg, M.J., Frankel, S.H., Gore, J.P., Sivathanu, Y.R.: A study of coupled turbulent mixing, soot chemistry, and radiation effects using the linear eddy model. Combust. Flame 113, 454–469 (1998)
Sankaran, V., Menon, S.: Subgrid combustion modeling of 3-D premixed flames in the thin-reaction-zone regime. Proc. Combust. Inst 30, 575–582 (2005)
Sen, B.A., Menon, S.: Linear eddy mixing based tabulation and artificial neural networks for large eddy simulations of turbulent flames. Combust. Flame 157, 62–74 (2010)
Sen, B.A., Hawkes, E.R., Menon, S.: Large eddy simulation of extinction and reignition with artificial neural networks based chemical kinetics. Combust. Flame 157, 566–578 (2010)
Ochoa, J.S., Sanchez-Insa, A., Fueyo, N.: Subgrid linear eddy mixing and combustion modelling of a turbulent nonpremixed piloted jet flame. Flow, Turbul. Combust. 89, 295–309 (2012)
Choi, J.J., Menon, S.: Large eddy simulation of cavity-stabilized supersonic combustion, AIAA Paper 2009–5383 (2009)
Sone, K., Menon, S.: Effect of subgrid modeling on the in-cylinder unsteady mixing process in a direct injection engine. J. Eng. Gas Turbines Power 125(2), 435–443 (2003)
Steeper, R., Sankaran, V., Oefelein, J., Hessel, R.: Simulation of the effect of spatial fuel distribution using a linear-eddy model. SAE Technical Paper 2007-01-4131 (2007)
Martinez, D.M., Jiang, X., Moulinec, C., Emerson, D.R.: Numerical simulations of turbulent jet flames with non-premixed combustion of hydrogen-enriched fuels. Comput. Fluids 88, 688–701 (2013)
Martinez, D.M., Jiang, X., Moulinec, C., Emerson, D.R.: Numerical assessment of subgrid scale models for scalar transport in large-eddy simulations of hydrogen-enriched fuels. Int. J. Hydrogen Energy 39, 7173–7189 (2014)
Lovett, J.A., Ahmed, K., Bibik, O., Smith, A.G., Lubarsky, E., Menon, S., Zinn, B.T.: On the influence of fuel distribution on the flame structure of bluff-body stabilized flames. J. Eng. Gas Turbines Power 136(4), 041503 (2013)
Srinivasan, S., Ranjan, R., Menon, S.: Flame dynamics during combustion instability in a high-pressure, shear-coaxial injector combustor. Flow, Turbul. Combust. 94, 237–262 (2015)
Srinivasan, S., Kozaka, E.O., Menon, S.: A new subgrid breakup model for LES of spray mixing and combustion. In: Direct and large-eddy simulation VIII, pp. 333–338. ERCOFTAC, Springer Science and Business Media (2011)
Pope, S.B.: PDF methods for turbulent reactive flows. Prog. Energy Combust. Sci. 11(2), 119–192 (1985)
Haworth, D.C.: Progress in probability density function methods for turbulent reacting flows. Prog. Energy Combust. Sci. 36(2), 168–259 (2010)
Haworth, D.C., Pope, S.B.: Transported probability density function methods for Reynolds-averaged and large-eddy simulations. In: Echekki, T., Mastorakos, E. (eds.) Turbulent Combustion Modeling. Fluid Mechanics and Its Applications, vol. 95. Springer, Dordrecht (2011)
Pope, S.B.: Small scales, many species and the manifold challenges of turbulent combustion. Proc. Combust. Inst 34(1), 1–31 (2013)
Wu, H., See, Y.C., Wang, Q., Ihme, M.: A pareto-efficient combustion framework with submodel assignment for predicting complex flame configurations. Combust. Flame 162(11), 4208–4230 (2015)
Gada, V.H., Tandon, M.P., Elias, J., Vikulov, R., Lo, S.: A large scale interface multi-fluid model for simulating multiphase flows. Appl. Math. Model 44, 189–204 (2017)
Ranjan, R., Muralidharan, B., Nagaoka, Y., Menon, S.: Subgrid-scale modeling of reaction-diffusion and scalar transport in turbulent premixed flames. Combust. Sci. Technol 188(9), 1496–1537 (2016)
Gonzalez-Juez, E.D., Arshad, S., Oevermann, M., Menon, S.: Turbulent-combustion closure for the chemical source terms and molecular mixing using the linear-eddy model, AIAA Paper 2017–5080 (2017)
Hawkes, E.R., Sankaran, R., Sutherland, J.C., Chen, J.H.: Scalar mixing in direct numerical simulations of temporally evolving plane jet flames with skeletal CO/H2 kinetics. Proc. Combust. Inst 31(1), 1633–1640 (2007)
Sjunnesson, A., Nelson, C., Max, E.: LDA Measurements of velocities and turbulence in a bluff body stabilized flame. Proceedings of the 4th International Conference on Laser Anemometry, Cleveland, OH (1991)
Sjunnesson, A., Olovsson, S., Sjoblom, B.: Validation rig – A tool for flame studies. Volvo Flygmotor Internal Report VFA 33, 9370–308 (1991)
Sjunnesson, A., Henrikson, P., Lofstrom, C.: CARS measurements and visualization of reacting flows in a bluff body stabilized flame, AIAA Paper 1992–3650 (1992)
OpenFOAM: Software available at http://www.openfoam.org
Weller, H.G., Tabor, G., Jasak, H., Fureby, C.: A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys 12(6), 620–631 (1998)
NASA polynomials, available at http://combustion.berkeley.edu/gri-mech/data/nasa_plnm.html
Smagorinsky, J.: General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 91(3), 99–164 (1963)
Garnier, E., Adams, N., Sagaut, P.: Large eddy simulation for compressible flows. Springer, Berlin (2009)
Yoshizawa, A., Horiuti, K.: A statistically-derived subgrid-scale kinetic energy model for the large eddy simulation of turbulent flows. J. Phys. Soc. Japan 54, 2834–2839 (1985)
Gonzalez-Juez, E.D., Dasgupta, A., Arshad, S., Oevermann, M., Lignell, D.: Effect of the turbulence modeling in large-eddy simulations of nonpremixed flames undergoing extinction and reignition, AIAA Paper 2017–0604 (2017)
Kerstein, A.R.: One-dimensional turbulence: model formulation and application to homogeneous turbulence, shear flows, and buoyant stratified flows. J. Fluid Mech 392, 277–334 (1999)
Issa, R.I.: Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys 62(1), 40–65 (1986)
Arshad, S., Kong, B., Kerstein, A.R., Oevermann, M.: A strategy for large-scale scalar advection in large eddy simulations that use the linear eddy sub-grid mixing model. Intl. J. Numer. Methods Heat Fluid Flow, in press (2018)
Duwig, C., Nogenmyr, K., Chan, C., Dunn, M.J.: Large eddy simulations of a piloted lean premix jet flame using finite-rate chemistry. Combust. Theory Model 15(4), 537–568 (2011)
Fiorina, B., Mercier, R., Kuenne, G., Ketelheun, A., Avdiċ, A., Janicka, J., Geyer, D., Dreizler, A., Alenius, E., Duwig, C., et al.: Challenging modeling strategies for LES of non-adiabatic turbulent stratified combustion. Combust. Flame 162(11), 4264–4282 (2015)
Ma, F., Proscia, W., Ivanov, V., Montanari, F.: Large eddy simulation of self-excited combustion dynamics in a bluff-body combustor, AIAA Paper 2015–3968 (2015)
Angelberger, C., Veynante, D., Egolfopoulos, F., Poinsot, T.: Large eddy simulations of combustion instabilities in premixed flames, Annual Research Briefs Center Turbul. Research 61–82 (1998)
Möller, S., Lundgren, E., Fureby, C.: Large eddy simulation of unsteady combustion. Int. Symposium Combust 26(1), 241–248 (1996)
Fureby, C.: Large eddy simulation of combustion instabilities in a jet engine afterburner model. Combust. Sci. Technol 161(1), 213–243 (2000)
Comer, A.L., Huang, C., Rankin, B.A., Harvazinski, M.E., Sankaran, V.: Modeling and simulation of bluff body stabilized turbulent premixed flames, AIAA Paper 2016–1936 (2016)
Giacomazzi, E., Battaglia, V., Bruno, C.: The coupling of turbulence and chemistry in a premixed bluff-body flame as studied by LES. Combust. Flame 138(4), 320–335 (2004)
Cocks, P.A.T., Soteriou, M.C., Sankaran, V.: Impact of numerics on the predictive capabilities of reacting flow LES. Combust. Flame 162(9), 3394–3411 (2015)
Baudoin, E., Nogenmyr, K.J., Bai, X.S., Fureby, C.: Comparison of LES models applied to a bluff body stabilized flame. AIAA Paper 2009–1178 (2009)
Fureby, C.: A comparative study of large eddy simulation (LES) combustion models applied to the Volvo validation rig, AIAA Paper 2017–1575 (2017)
Drennan, S.A., Kumar, G., Liu, S.: Developing grid-convergent LES simulations of augmentor combustion with automatic meshing and adaptive mesh refinement, AIAA Paper 2017–1574 (2017)
Gonzalez-Juez, E.D.: Numerical simulations of thermoacoustic combustion instabilities in the Volvo combustor, AIAA Paper 2017–4686 (2017)
Wu, H., Ma, P.C., Lv, Y., Ihme, M.: MVP-workshop contribution: Modeling of Volvo bluff body flame experiment, AIAA Paper 2017–1573 (2017)
Sankaran, V., Gallagher, T.: Grid convergence in LES of bluff body stabilized flames, AIAA Paper 2017–1791 (2017)
Durand, L., Polifke, W.: Implementation of the thickened flame model for large eddy simulation of turbulent premixed combustion in a commercial solver, ASME Paper GT2007-281888 (2007)
Jones, W.P., Marquis, A.J., Wang, F.: Large eddy simulation of a premixed propane turbulent bluff body flame using the Eulerian stochastic field method. Fuel 140, 514–525 (2015)
Genin, F., Chernyavsky, B., Menon, S.: Large eddy simulation of scramjet combustion using a subgrid mixing/combustion model, AIAA Paper 2003–7035 (2003)
Menon, S., Seitzman, J., Shani, S., Gėnin, F., Thao, T., Miki, K., Segal, C., Thakur, A.: Experimental and numerical studies of mixing and combustion in scramjet combustors, AIAA Paper 2004–3826 (2004)
Gicquel, L.Y.M., Staffelbach, G., Poinsot, T.: Large Eddy Simulations of gaseous flames in gas turbine combustion chambers. Progr. Energy Combust. Sci. 38 (6), 782–817 (2012)
Dunn, M.J., Masri, A.R., Bilger, R.W.: A new piloted premixed jet burner to study strong finite-rate chemistry effects. Combust. Flame 151(1-2), 46–60 (2007)
Kim, W., Menon, S., Mongia, H.C.: Large-eddy simulation of a gas turbine combustor flow. Combust. Sci. Technol 143(1-6), 25–62 (1999)
Grinstein, F.F., Fureby, C.: LES studies of the flow in a swirl gas combustor. Proc. Combust. Inst 30(2), 1791–1798 (2005)
Miki, K., Moder, J., Liou, M.: Computational study of combustor-turbine interactions, AIAA Paper, 2017–4824 (2017)
Acknowledgements
The authors thank the Swedish Research Council Vetenskapsrådet and the Combustion Engine Research Center (CERC) for funding this project at Chalmers. Special thanks to Alan Kerstein and Venkateswaran Sankaran for helpful discussions. Thanks to Prof. Evatt Hawkes for kindly providing the DNS data used in the present study. Also thanks to the financial support from the Small-Business-Innovation-Research / Small-Business-Technology-Transfer (SBIR/STTR) project titled ‘Physical submodel development for turbulence combustion closure’, contract number FA9550-15-C-0044.
Funding
This study was funded by the Swedish Research Council Vetenskapsrådet, the Combustion Engine Research Center (CERC) at Chalmers University of Technology and the Small-Business-Innovation-Research / Small-Business-Technology-Transfer (SBIR/STTR) project titled ‘Physical submodel development for turbulence combustion closure’(contract number FA9550-15-C-0044).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Arshad, S., Gonzalez-Juez, E., Dasgupta, A. et al. Subgrid Reaction-Diffusion Closure for Large Eddy Simulations Using the Linear-Eddy Model. Flow Turbulence Combust 103, 389–416 (2019). https://doi.org/10.1007/s10494-019-00019-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10494-019-00019-x