Subgrid Reaction-Diffusion Closure for Large Eddy Simulations Using the Linear-Eddy Model

Abstract

Turbulent combustion models approximate the interaction between turbulence, molecular transport and chemical reactions. Among the many available turbulent combustion models, the present focus is the linear-eddy model (LEM) used as a subgrid combustion model for large eddy simulations. In particular this paper introduces a new LEM closure with the reaction-rate approach to close the filtered chemical source terms in the governing equations for species mass fractions and enthalpy. The new approach is tested using a non-premixed syngas flame and a bluff-body stabilized premixed flame problem. Simulation results are compared to data from a direct numerical simulation and experiments. This comparison shows that mean and rms quantities compare well with experiments and are in the range of previous simulation studies. These results are obtained with a pressure-based and unstructured computational-fluid-dynamics solver, an approach that is preferred in industry.

1 Introduction

Turbulent combustion happens in combustion devices such as internal combustion engines and gas-turbine engines [1, 2]. It involves an interaction between highly non-linear chemical reactions, turbulence and molecular mixing. Turbulence is characterized by a broad range of scales in spacetime, ranging from the smallest Kolmogorov scales to the largest flow structures characterized by the scales of the flow geometry. Computational fluid dynamics (CFD) provides useful tools to study turbulent combustion. One such CFD tool is direct numerical simulations (DNS), which aims at fully resolving the flow physics. However, DNS is currently computationally affordable only for relatively simple problems. In contrast, CFD approaches for engineering problems approximate the above physics with turbulent combustion models. There are numerous turbulent combustion models available [2, 3] and several studies have compared them [4,5,6].

From a practical point of view it is desirable to have a turbulent combustion model that is generally valid, which means that it is predictive for both premixed and non-premixed combustion modes and independent of chemical time scales (fast/flamelet-type chemistry vs. non-fast chemistry). One such type of model is the transported probability-density-function (TPDF) method [43,44,45]. Another one is the linear-eddy model (LEM) of Kerstein [7] when used as a subgrid combustion model for large eddy simulations (LES) [8, 9], in which case it is called LES-LEM.

LEM was initially formulated as a scalar mixing model for non-reacting flows [7] and later extended to predict reactive flows [10]. LEM relies on a one-dimensional line on which all spatial and temporal scales are resolved, hence reducing computational cost relative to three-dimensional DNS while retaining high resolution. Modeling of turbulence is done via stochastic mapping events. Diffusion and reaction are represented with reactive-diffusive partial differential equations.

LES-LEM has been employed in a large variety of combustion problems [11,12,13,14,15,16,17,18,19,20,21,22,23]. McMurtry et al. [24] showed simulation results of turbulent scalar mixing. Non-premixed turbulent combustion simulations were done by Calhoon [25] and Menon and Calhoon [26], and premixed turbulent combustion by Smith [27] and Chakravarthy and Menon [28]. Spray combustion simulations were performed by Pannala and Menon [29], and by incorporating radiative heat loss and soot modeling by Zimberg et al. [30]. Predictions of a premixed turbulent methane/air flame were presented by Sankaran and Menon [31]. Sen and Menon employed artificial neural networks to speed up chemistry calculations [32, 33]. LES-LEM with a low-Mach-number numerical scheme was used to simulate the Sandia flame D by Ochoa et al. [34]. Choi and Menon applied LES-LEM for simulations of a cavity-stabilized combustor [35]. A few examples of simulation on reciprocating engines include work done in KIVA for simulating a direct injection spark ignition engine using LES-LEM [36], and an URANS-LEM method in order to investigate pressure histories in an automotive HCCI engine [37]. Martinez et al. [38, 39] studied turbulent combustion of hydrogen-enriched fuels. Lovett et al. [40] studied the flame structure of bluff-body stabilized flames. Srinivasan et al. [41] used LES-LEM for investigating combustion instabilities in a continuous variable resonance combustor (CVRC) and also performed spray combustion simulations [42].

Turbulent combustion models can be used in at least two different ways [3]. One is the so-called primitive-variable method in which the models provide closure for the filtered or averaged thermochemical quantities, i.e. the species mass fractions and an energy variable such as enthalpy or temperature. This method is perhaps the most popular one and is typically used with flamelets [2], transported-PDF methods [43,44,45], and in most previous LES-LEM studies as well. The other method is the reaction-rate approach in which the turbulent combustion model provides closure for the chemical source terms in the conservation equations of the thermochemical quantities, i.e. models of this type solve transport equations for all species and a form of the energy equation. Thus, this approach is computationally more expensive than the primitive-variable method. However, the approach can be regarded as more broadly applicable as it simplifies the inclusion of more physics into the modeling [3].

An additional advantage of using the reaction-rate approach is that it can potentially ease the use of more than one turbulent combustion model during a simulation. For example, consider a combustion problem involving a vigorously burning flame in some region in spacetime, a flame undergoing extinction-reignition in another region, and ignition in yet another region. This is a multi-physics combustion problem. Knowing the fact that turbulent combustion models can be more cost-effective (e.g. in terms of accuracy and computational cost) for a particular type of physics but not necessarily for other physics, it becomes desirable to use one particularly suitable model for one region in spacetime and other suitable models in other regions. The potential for such an approach to lead to more cost-effective combustion simulations is beginning to be recognized [46, 47]. This is the case not only in the combustion community but, for instance, in the multi-phase-flow community as well [48]. Within this hybrid framework, the primitive-variable method runs into the difficulty that turbulent combustion models handle the turbulent transport in different ways, as discussed shortly for the case of LEM. In comparison, the reaction-rate approach does not run into this problem as it solves for the conservation equations of the thermochemical quantities. Furthermore, the reaction-rate approach isolates modeling errors due to the turbulent combustion model in the chemical source terms, simplifying as well the comparison of errors from different models.

In the LEM framework, the reaction-rate approach could also help in reducing potential artifacts produced by the splicing algorithm. This algorithm, as clarified later, is used to transport the thermochemical quantities residing on the individual LEM domains between LES cells. It can result in a spatial distribution of scalars that may differ from the distribution that would be obtained by solving the filtered or averaged conservation equations. Thus, by solving such equations concurrently with the splicing, it is possible to make adjustment to the spatial distribution of a thermochemical quantity if such an inconsistency is considered unacceptably large.

The primitive-variable approach is standard for previous LES-LEM implementation so it is valuable then to explore how well a new LEM closure with the reaction-rate approach performs. Therefore, the present work and a parallel one [49] use LEM following the reaction-rate approach. The present work differs from this previous one in that it uses a significantly different code framework, and it retains the splicing algorithm instead of getting rid of it. Importantly, the latter feature allows the present approach to retain the time-history of the subgrid solution rather than disregard it, at the cost of making the code more complex. In principle this facilitates a more accurate modeling of highly unsteady phenomena, e.g. extinction and re-ignition. This potential capability, however, remains to be shown and is not addressed here. The present work makes use of unstructured meshes and a pressure-based approach, both of which are usual industry practice. The current paper is a major revision and expansion of a previous conference paper [50]. Common material is reprinted with permission from AIAA.

The present paper is arranged as follows. Section 2 introduces the new proposed methodology based on LEM. Thereafter, Section 3 compares predictions with this methodology with those from DNS and traditional LES-LEM for a syngas flame problem [51]. Section 4 compares simulation results with experiments for a bluff-body stabilized flame combustor called the Volvo combustor from now on [52,53,54]. These two test problems are selected since they have been used in the development of various turbulent combustion models and serve the purpose of determining whether the present approach works well. These tests, however, suffer from two serious shortcomings discussed later on. Due to these shortcomings, Section 5 presents a sensitivity study for high-Reynolds-number flames. Finally, simulation results are used to further explain how the present model works, and then the paper finishes with conclusions in Section 7.

2 Methodology

2.1 LES equations

The current work uses the OpenFOAM library version 2.3.1 [55, 56] and considers the following filtered conservation equations for global mass, momentum, sensible enthalpy, and species mass for gases that are variable density, viscous, heat-conducting and multiple-component and move at low-Mach-number speeds:

$$ \frac{\partial \bar \rho}{\partial t} + \frac{\partial (\bar \rho \tilde u_{i} )}{\partial x_{i}} = 0 , $$

(1)

$$ \frac{\partial \bar \rho \tilde u_{i}}{\partial t} + \frac{\partial (\bar \rho \tilde u_{j} \tilde u_{i})} {\partial x_{j}} = - \frac{\partial \bar p}{\partial x_{i}} + \frac{\partial}{\partial x_{j}} \left( \bar \tau_{ji} + \tau_{ji}^{sgs} \right) , $$

(2)

$$ \frac{\partial \bar \rho \tilde h}{\partial t} + \frac{\partial (\bar \rho \tilde u_{j}\tilde h)} {\partial x_{j}} = - \frac{\partial}{\partial x_{j}} \left( \bar q_{j} + q_{j}^{sgs} \right) + \bar S_{h} , $$

(3)

$$ \frac{\partial \bar \rho \tilde Y_{\alpha}}{\partial t} + \frac{\partial (\bar \rho \tilde u_{j} \tilde Y_{\alpha})} {\partial x_{j}} = - \frac{\partial}{\partial x_{j}} \left( \bar j_{\alpha,j} + j_{\alpha,j}^{sgs} \right) + \bar S_{\alpha} . $$

(4)

Here ρ denotes the density, p the pressure, u_i is the velocity component in spatial direction i, h is the sensible enthalpy, and Y_α is the mass fraction of the species α. The bar denotes conventional filtering and the tilde density weighted Favre filtering. $\bar \tau _{ji}$, $\bar q_{j}$, and $\bar j_{\alpha ,j}$ are respectively the filtered viscous stress tensor, heat flux, and Fickian molecular flux of species α. Likewise, $\tau _{ji}^{sgs}$, $q_{j}^{sgs}$, and $j_{\alpha ,j}^{sgs}$ are the subgrid viscous stress tensor, heat flux, and molecular flux of species α, all of which need closure. These conservation equations are complemented with the equation of state for ideal gases

$$ \overline{p}=\overline{\rho}R_{m}\sum\limits_{\alpha=1}^{N} \frac{ \tilde{Y}_{\alpha} \tilde{T}} {W_{\alpha}} , $$

(5)

where W_α is the molecular weight of species α and R_m is the universal gas constant. The averaged caloric equation of state is given as,

$$ \tilde h = \tilde h (\tilde T) \ = {\sum}_{\alpha} \tilde{Y}_{\alpha} h_{\alpha} (\tilde{T}) $$

(6)

with h_α(T) given by the NASA polynomials [57].

The terms $\tau _{ij}^{sgs}$, $q_{j}^{sgs}$, and $j_{\alpha ,j}^{sgs}$ are the subgrid stress tensor, heat flux, and mass flux of species k. They are closed with

$$ \tau_{ij}^{sgs} = - 2 \mu^{sgs} \left( \widetilde{S}_{ij} - \frac{\delta_{ij}}{3} \widetilde{S}_{kk} \delta_{ij} \right) , $$

(7)

$$ q_{j}^{sgs} = - \frac{\mu^{sgs}}{\overline{\rho}} \frac{\partial \widetilde{h}_{s}}{\partial x_{j}} , $$

(8)

$$ j_{\alpha,j}^{sgs} = - \frac{\mu^{sgs}}{\overline{\rho}} \frac{\partial \widetilde{Y}_{\alpha}}{\partial x_{j}} . $$

(9)

In the syngas flame problem, the SGS viscosity μ^sgs is computed with OpenFOAM’s implementation of the Smagorinsky model [58]

$$ \mu^{sgs} = C_{k} \overline{\rho} {\Delta} \sqrt{k^{sgs}} , $$

(10)

with C_k being a model constant (C_k = 0.02), Δ the cube root of a given finite volume, and k^sgs the SGS kinetic energy obtained from

$$ k^{sgs} = \left( \frac{-b + \sqrt{b^{2} + 4ac}} {2a} \right)^{2} , $$

(11)

where a = C_e/Δ, $b=2 \widetilde {S}_{kk} / 3$, $c=2 C_{k} {\Delta } (\widetilde {S}_{ij} - \delta _{ij} \widetilde {S}_{kk} /3) \widetilde {S}_{ij}$, and C_e = 1.048. For incompressible flows, the constants C_k and C_e are related to the constant C_s of the typical implementation of the Smagorinsky model [59] through $C_{s}=C_{k}^{3/4}C_{e}^{-1/4}$. For the Volvo combustor simulations, μ^sgs is computed with OpenFOAM’s implementation of Yoshizawa & Horiuti’s one-equation eddy model [60].

Closure of the averaged source terms $\bar S_{h}$ and $\bar S_{\alpha }$ is done as follows.

2.2 Closure of the chemical source terms with the no-model approach

With the no-model (also called the perfectly stirred reactor model) approach, the averaged chemical source term is given by:

$$ \bar S_{\alpha} = S_{\alpha}(\bar C_{\alpha}, \tilde T) . $$

(12)

where $\bar C_{\alpha } = \bar \rho \tilde Y_{\alpha } / W_{\alpha }$ is the molar concentration of species α. It means that the chemical source term is simply evaluated using directly the filtered values of the resolved fields.

2.3 LEM subgrid modeling inside a LES cell

The LES-LEM model is composed of the following elements: the LES equations discussed before; the LEM modeling inside a LES cell; the exchange of information between the LEM and the LES; the LEM modeling “between” LES cells; and, for the current formulation the closure of $\bar S_{h}$ and $\bar S_{\alpha }$.

The hallmark feature of the LEM is a 1D domain resolving all scales [9] having an inflow on one end and an outflow at the other end. In LES-LEM, there is one 1D domain per computational LES cell, as shown in Fig. 1. All the cells of the LEM domain within a LES cell are uniformly initialized with the thermochemical conditions in that LES cell. The initial LEM domain length is chosen to be equal to the local LES mesh spacing Δ. The solution on the LEM domain time advances the conservation equations in their 1D form as:

$$ \sum\limits_{i} \rho_{i} {\Delta} x_{i} = M_{LEM} , $$

(13)

$$ \frac{\partial T}{\partial t} = - \frac{\partial q_{x}}{\partial x} + S_{T} . $$

(14)

$$ \frac{\partial Y_{\alpha}}{\partial t} = - \frac{\partial j_{\alpha,x}}{\partial x} + S_{\alpha} . $$

(15)

where M_LEM is the total mass in a LES cell, the summation (index i) is done over all cells of the LEM domain, the x coordinate is parallel to the 1D array, and S_T is the heat-source term in the temperature equation. Constant pressure is assumed on the LEM which allows updating of the LEM density resulting in change of the LEM domain length. Here unity Prandtl and Lewis numbers are used to compute q_x and j_α,x.

Fig. 1

LES-LEM simulations use a 1D domain (in black) consisting of a stack of LEM cells per computational LES cell (in red) [61]. Note that the LEM domains have no assigned orientation relative to the underlying coordinate system

Macromixing (subgrid turbulent stirring) is modelled by distorting the profiles of all scalar quantities according to

$$ T(x) \rightarrow T(M(x)) , Y_{\alpha}(x) \rightarrow Y_{\alpha}(M(x)) . $$

(16)

Here M(x) is a mapping operation known as the triplet map. The effect of the triplet map on a flow property profile defined in [x₀,x₀ + l] is to replace the profile with three compressed images of the original with the middle image flipped. This is how the rotational and compressive motions observed in the turbulent flows are represented in the LEM [62].

The triplet maps are parametrized by a location x₀, a length l, and an eddy rate λ per unit domain length. They are implemented in a stochastic way by sampling x₀ from a uniform distribution and l from

$$ f(l) = \frac{5}{3} \frac{l^{-8/3}}{l_{p}^{-5/3} - l_{max}^{-5/3}} , $$

(17)

where l_p and l_max are the smallest and the largest unresolved length-scales characterizing the turbulence, and are specified by the user. Here l_p is taken as the Kolmogorov length-scale η, and l_max equals the local mesh spacing of the LES solver Δ. Implied in Eq. 17 are Kolmogorov’s scalings in the inertial subrange (e.g. the time-scale of an eddy τ scales as τ ∼ l^2/3). An estimate for the Kolmogorov length-scale is given by

$$ \eta = N_{\eta} \frac{\Delta}{Re_{\Delta}^{3/4}} , $$

(18)

with N_η being a model constant, and Re_Δ the subgrid Reynolds number:

$$ Re_{\Delta} = \frac{u_{sgs} {\Delta}}{\nu} , $$

(19)

where ν is the kinematic viscosity and u_sgs is the characteristic subgrid velocity fluctuation obtained from the LES subgrid turbulent kinetic energy $\bar k_{sgs}$ as $u_{sgs}=\sqrt {2\bar k_{sgs}/3}$.

The eddy rate λ per unit domain length with unit (length x time)^-1 is obtained through an analogy between eddy sampling statistics and inertial range scaling laws and is computed via

$$ \lambda = \frac{54}{5} \frac{\nu Re_{\Delta}}{C_{\lambda} {\Delta}^{3}} \frac{\left( \frac{\Delta}{\eta} \right)^{5/3} -1} {1 - \left( \frac{\eta}{\Delta} \right)^{4/3}} , $$

(20)

with C_λ being a model constant. The average time interval between triplet maps is:

$$ {\Delta} t_{stir} = \frac{1}{\lambda {l_{LEM}}} , $$

(21)

where l_LEM is the LEM domain length and the actual eddy occurrences are sampled from a Poisson process. The sampling rejected the eddies that extend beyond the LEM domain boundary. The values of C_λ = 1 and N_η = 1.1 are used throughout unless said otherwise. These values were chosen to ensure that triplet maps are occurring during the simulation.

2.4 LES-LEM advection modeling

Another element of the present LES-LEM formulation is an algorithm that transfers the subgrid-scale quantities, i.e. those defined in the 1D arrays, between 1D arrays in the adjacent LES computational cells. The present work uses the splicing algorithm since it has proven to be robust for practical combustion implementations. The splicing algorithm cuts and pastes the end portions of the 1D arrays of the adjacent LES cells to emulate a Lagrangian type of mass transfer. Decisions of how much to cut and paste are based on values of the mass fluxes across the faces of LES computational cells. For example, if the mass flux at a given face of cell A is large and directed from cell A to cell B, a large portion of the 1D array in A will be cut and then pasted onto one of the two endpoints of the array in B. There is some arbitrariness, however, in how this is exactly done. If this mass flux were small, a small portion would be cut and pasted. Details about the splicing algorithm are given in [50, 64].

2.5 Closure of the chemical source terms with LEM

Figure 2 shows the coupling between the LES and the LEM subgrid combustion model. The LES provides information about the cell spacing Δ, the subgrid turbulent kinetic energy $\bar k_{sgs}$, the time step of the simulation Δt and the pressure to the LEM. With this information, the LEM subgrid-scale simulation advances Eqs. 13–20 for the LES time interval Δt. The chemical source terms $\bar S_{h}$ and $\bar S_{\alpha }$ are obtained by taking the median or mean value along various LEM elements for the current LES time step. Mean values are calculated (e.g. for species mass fractions) with

$$ \bar S_{\alpha} = \frac{{\sum}_{i} {{\Delta} x}_{i} S_{\alpha , i}}{{\sum}_{i} {{\Delta} x}_{i}} , $$

(22)

where the summation (index i) is over the elements of the LEM array and Δx_i denotes the non-uniform length of an individual LEM cell. The median source term, on the other hand, is calculated by first sorting the source term values of all the LEM elements in ascending order, and then picking up the middle value. Apparently, the chosen value can come from a different cell for each species. Comparison of predictions using the mean and the median is discussed later in Section 4.4. Although the use of the mean is intuitive, the median is considered here as well because it is a more robust measure since it prevents outliers. These source terms are then used in the LES conservation equations for the species mass fractions and sensible enthalpy. The temperature on the LES side is then calculated from the caloric equation of state, Eq. 6.

Fig. 2

Coupling between the LES and the LEM subgrid model

In the present implementation, the PISO algorithm [63] is used. It has an outer loop which starts with predicting a velocity (using Eq. 2), which is followed by an inner iterative loop to correct the velocity field using the outcome of a pressure Poisson equation obtained by fulfilling the continuity equation. In the inner iterative loop, the LES density is obtained from the equation of state Eq. 5. After splicing is done with the predicted LES mass flux, the LEM lines are restored back to the state before the predicted splicing was done, in order to do the splicing with the correct LES mass flux as described in [64].

The last step is to correct the temperatures and the species mass fractions in the LEM domains to take into account the fact that the convection due to the solution of Eqs. 1-4 differs from that of the splicing algorithm. The need for this step is discussed further in Section 6. There is not a unique way to conduct this correction, and the following algorithm is a result of trial and error and has been found to be robust, as demonstrated later.

The goal of this correction algorithm is to keep the Favre-averaged temperatures and species mass fractions from the LEM domains within some tolerance of those from the solution of Eqs. 1–4. LES quantities are not altered. Fig. 3 summarizes the correction for the temperature. A similar process is used for the species mass fractions.

Fig. 3

Steps of correcting the temperature in a LEM domain. Here T_i is the temperature of LEM cell i and n_LEM is the total number of LEM cells. The temperature difference $T^{\prime }$ is a difference between the LES temperature $\tilde T$ and the Favre-averaged LEM temperature $\tilde T_{LEM}$. The notation += means addition assignment. This correction procedure is also used for the species mass fractions

The first step of the correction computes the difference T^′ between the LES temperature $\tilde T$ and the Favre-averaged LEM temperature $\tilde T_{LEM}$, the latter of which is obtained via:

$$ \tilde T_{LEM} = \frac{{\sum}_{i} \rho_{i} {\Delta} x_{i} T_{i}}{{\sum}_{i} \rho_{i} {\Delta} x_{i}} , $$

(23)

where T_i denotes the LEM cell temperature, and the summation (index i) is over all cells of the LEM array. In a second step, T^′ is added to each T_i. This updates $\tilde T_{LEM}$. If the new updated difference T^′ is within a specified tolerance the correction is stopped, otherwise the updated difference T^′ is added again to each T_i and the aforementioned steps are repeated.

At this point, a distinctive conceptual feature of the present closure must be highlighted. It is common in LES to make a sharp distinction between the closure of diffusive processes (micromixing) and reaction. This is evident by noticing that in Eqs. 1–4 separate closure is needed for, on one hand, $\bar q_{j}$ and $\bar j_{\alpha ,j}$, and, on the other hand, $\bar S_{h}$ and $\bar S_{\alpha }$. However, a more realistic picture is that diffusive and reacting processes are closely coupled at the subgrid level (meaning reaction and diffusive terms can be of the same order), for example, in some premixed flames. Now, with LEM $\bar S_{h}$ and $\bar S_{\alpha }$ are computed as explained above using a 1D structure that represents both reaction and diffusion. Thus, it is perhaps more accurate to say that the present closure, although given for $\bar S_{h}$ and $\bar S_{\alpha }$, is not a closure for subgrid reaction, but for subgrid reaction-diffusion processes, i.e. with proper resolution the LEM is capable of fully resolving flame structures in 1D. This is why the approach is termed a subgrid reaction-diffusion closure with LEM.

2.6 Numerical method

The conservation equations Eqs. 1–4 are solved with an adaptation of reactingFoam which is the standard solver of the OpenFOAM library for chemically reacting flow. This solver is transient, pressure-based and can handle unstructured meshes [64]. A low-Mach-number assumption is used as done in reactingLMFoam [65, 66] by splitting the pressure into a fluid-mechanical-induced pressure and a thermodynamic pressure, the latter of which is spatially constant and which is used to evaluate the equation of state. As a result, acoustic waves are eliminated from the solution. The OpenFOAM library has various temporal and spatial discretization options available. In the current work, the time discretization is done with a second-order backward-differencing scheme that uses the current and previous two time step values. OpenFOAM’s limited linear differencing scheme is used for the convective and diffusive fluxes.

3 Medium-Reynolds-Number Syngas Flame

3.1 Configuration

This Section considers a reacting, temporally-evolving, planar jet in a cuboid of size L_x × L_y × L_z studied with DNS by Hawkes et al. [51]. Fig. 4 shows a schematic of the jet. The fuel stream is an initially planar jet moving in the x-direction, with the oxidizer moving in the opposite direction on either side of the fuel stream. Turbulence is generated by shear at the interface between the two jets. The fuel is syngas, comprising 50% CO, 10% H₂, and 40% N₂ by volume. The oxidizer is composed of 25% O₂ and 75% N₂ by volume. Both fuel and oxidizer are initially at 500 K and react according to a skeletal mechanism for C₁-kinetics [51]. The pressure is atmospheric. The characteristic jet velocity is U, and at t = 0 both streams have a velocity of U/2 in their respective directions. A characteristic length-scale of the problem is the jet height H, and a characteristic jet time scale is t_j = H/U. Thus, a Reynolds number can be defined as Re = (UH)/ν_f, where ν_f is the kinematic viscosity of the pure fuel. The Damköhler number is defined as Da = χ_qt_j, with χ_q being the quenching scalar dissipation rate for the flamelet solution. The size of the computational domain is given in terms of the characteristic length as L_x = 12H, L_y = 14H, and L_z = 8H. The (global) Mach number is M = U/(c₁ + c₂), where c₁ = 476 ms^− 1, and c₂ = 445 ms^− 1 are the sound speeds in the fuel and oxidizer streams respectively. Periodic boundary conditions are specified in the streamwise (x) and the spanwise (z) directions. The mesh spacing is uniform and equal in all directions.

Fig. 4

Schematic of the syngas jet configuration. Temperature contours at t = 40t_j are shown

For the simulations presented in this work, H = 0.96 mm, and U = 193 ms^− 1, which correspond to case M of Hawkes et al. [51]. The jet Reynolds number is 4478, and the jet characteristic time is t_j ∼ 5 μ s. The LES is set up closely following the setup used in the DNS study. However, whereas the DNS used a uniform mesh size of 768 × 896 × 512, the LES uses a mesh 8 times coarser, 96 × 112 × 64. The DNS mesh spacing corresponds roughly to the Kolmogorov length-scale.

In the DNS, combustion is started by superimposing a laminar flamelet solution and by using broadband turbulent velocity fluctuations. In the present LES, all fields are initialized by mapping the DNS initial condition onto the LES mesh. One more difference with the DNS is treatment of the boundary conditions at the ends of the vertical extent of the domain. Here Neumann boundary conditions are used with all quantities except pressure, which is set to an atmospheric value.

For the syngas jet, comparisons are presented here for two different simulations: a simulation with no turbulent combustion model (the no-model approach), and with the LES-LEM model. The LES-LEM simulations used the median source terms. Using the mean source terms produced almost identical results. The mesh used to simulate this jet is formed by uniform cubical control volumes. For the advective terms in the transport equations, a second-order center-difference scheme is used.

3.2 Comparison with DNS

Figure 5 shows the streamwise and spanwise spatially averaged mean and rms lateral temperature profiles obtained from the simulations. Fig. 6 shows the mixture fraction fields at the same instants. The largest discrepancies are seen at 10t_j. This is likely due to the present use of a simplified molecular transport modeling (e.g., unity Lewis numbers for all species) since a preliminary no-model-approach simulation (not shown) not using this simplified modeling captures well the profiles at 10t_j. The impact of more realistic molecular diffusion models will be investigated in the future. Nonetheless, overall the simulation results agree well with the DNS, which was the main purpose of evaluating the new implementation here. In addition, Figs. 5 and 6 show that for this case LES-LEM does not show a clear benefit over the no-model approach. One possible explanation is that the Reynolds number associated with this problem is not large enough for the detailed turbulent combustion models to fully kick in. This is further discussed in Section 6.

Fig. 5

Spatially averaged mean and rms lateral profiles of temperature for the temporal syngas jet. at = 0 bt = 10t_jct = 16t_jdt = 20t_jet = 30t_jft = 40t_j. (Black solid line: mean, no turbulent combustion model; blue solid line: mean, LES-LEM; ∘: mean, DNS; black dashed line: rms, no turbulent combustion model; blue dashed line: rms, LES-LEM; $\Box$: rms, DNS.)

Fig. 6

Spatially averaged mean and rms lateral profiles of the mixture fraction for the temporal syngas jet. at = 0 bt = 10t_jct = 16t_jdt = 20t_jet = 30t_jft = 40t_j. (Black solid line: mean, no turbulent combustion model; blue solid line: mean, LES-LEM; ∘: mean, DNS; black dashed line: rms, no turbulent combustion model; blue dashed line: rms, LES-LEM; $\Box$: rms, DNS.)

3.3 Comparison with traditional LES-LEM

In Figs. 7 and 8 the temperature and some of the major species are shown compared with the results of Sen et al. [33] who used the traditional LES-LEM. Overall the results obtained from the present simulation are at least as good as or slightly better than those of Sen et al. with the potential benefit of the new approach being more robust and flexible as explained before. It should be noted that Sen et al. used a non-uniform, stretched mesh with 192 × 224 × 128 cells as opposed to the use of 96 × 112 × 64 uniformly-spaced cells in the present work.

Fig. 7

Mixture fraction-conditioned profiles of temperature and species mass fractions at 20t_j for the temporal syngas jet. (Black solid line: present work; blue dashed line: LES-LEM of Sen et al. [33]; ∘: DNS.)

Fig. 8

Mixture fraction-conditioned profiles of temperature and species mass fractions at 40t_j for the temporal syngas jet. (Black solid line: present work; blue dashed line: LES-LEM of Sen et al. [33]; ∘: DNS.)

4 Volvo Combustor

The Volvo combustor is a standard test case for the evaluation of turbulent premixed combustion models which has been investigated extensively in the past. Here the case is used to compare the new LES-LEM implementation with experiments and other modeling approaches and to evaluate the impact of certain model parameters within LES-LEM on the simulation results.

4.1 Configuration

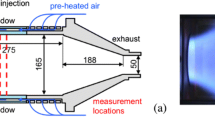
The experimental setup of the Volvo test problem [52,53,54] consists of a rectilinear channel, with an inlet section where air and (gaseous) propane mix before entering a honeycomb, and a downstream section where the premixed reactants burn in a flame that gets stabilized downstream of a wedge [52]. The cross section of the wedge is an equilateral triangle with side of 40 mm. The end of the downstream section is connected to a round exhaust duct with a cross sectional area about 3.4 times larger than that of the channel [67]. Unfortunately, the length of this exhaust section has not been documented in the open literature. Atmospheric conditions are used.

The computational domain used for the current work is shown in Fig. 9 and has the following geometric parameters: h₁ = 40 mm, h₂ = h₁sin60, x_min = -820 mm, x_max = 680 mm, y_min = -60 mm, y_max = 60 mm, and a spanwise length of 40 mm. The honeycomb is ignored as done in previous CFD studies. The pressure gradient normal to the inlet plane is set to zero. No turbulent fluctuations are imposed at the inlet because the region of interest is downstream of the wedge which is responsible for generation of strong turbulence. All walls are modeled as no-slip and adiabatic, unless stated otherwise. At the outlet, velocity, temperature and species are set to a zero-normal-gradient condition or a fixed value, depending on the direction of the flow. Pressure is dealt with a similar way at the outlet. Cyclic boundary conditions are used in the z-direction, unless indicated otherwise. An unstructured hexahedral 3D mesh with 77400 cells is used with the simulation time step of 10^− 6 s.

Fig. 9

Schematic of the Volvo test problem

Of the various operating conditions of the Volvo test problems, the one considered for the present work is the so-called Case 1. In Case 1, the inlet conditions are 288 K, 17 m/s, and 0.61 equivalence ratio. Table 1 summarizes the various simulations conducted for the present study. Table 2 [68] shows the chemical kinetic model used in the present work.

Table 1 Summary of the simulation settings for case 1

Table 2 Single step chemical reaction and five species mechanism for propane combustion for case 1 (rate constants are written as AT^b x exp(− E/RT); units are cm, mol, s, K, cal)

4.2 Comparison with experiments

Figure 10 shows instantaneous temperature maps using the no-model approach (simulation 1 cf. Table 1) and the LES-LEM baseline case (simulation 2 cf. Table 1). Notice that immediately downstream of the flameholder the flame is symmetric (varicose) about the y = 0 plane. This agrees with experiments (cf. Fig. 9 in Sjunnesson et al. [54]) and many other simulation studies. However, the transition towards an asymmetric (sinusoidal) flame shape further downstream agrees with some simulation studies (Fig. 4b in Moller et al. [69], Fig. 8a in Fureby [70] and Fig. 3 in Comer et al. [71]) and disagrees with others where the flame is predominantly symmetric all the way towards the outlet (Fig. 4 in Giacomazzi et al. [72], Cocks et al. [73], and perhaps also Baudoin et al. [74]). This latter predominantly symmetric shape appears to be the physically correct one for the present boundary conditions because many of the most recent simulation studies show this shape [75,76,77,78,79]. The cause for the transition from symmetric to asymmetric flame shape seen in the present simulations may be the use of a low-Mach-number formulation instead of a fully-compressible one [77]. More importantly, since many studies diverge on whether the flame further downstream is symmetric or not, the fact that this portion of the flow (in a non-linear dynamics sense) is close to a bifurcation cannot be ruled out, in which case its accurate prediction is very difficult. Furthermore, it must be stressed that, from the open literature, it is unclear how the flame looks like close to the outlet in the experiments.

Fig. 10

Case 1 instantaneous temperature maps with the no-model approach (top), the LES-LEM baseline case (center), and a LES-LEM case without the correction (bottom), cf. Table 1. This is Fig. 4 in Ref. [50] and it is reprinted with permission from AIAA

Spatial variations of mean quantities are shown in Figs. 11 and 12 for the no-model approach (simulation 1 cf. Tab. 1) and LES-LEM with C_λ = 1 (simulation 2 cf. Tab. 1) and C_λ = 10 (simulation 3 cf. Tab. 1). These quantities are averaged in the spanwise direction and over time, the latter of which is done for a time interval of 0.02 s. (Through trial and error this interval is found to be adequate to evaluate the mean quantities.) Overall, Figs. 11 and 12 show that the sensitivity to the type of model and LES-LEM model constant is small, although the best agreement with the experiments is given by the LES-LEM simulation with C_λ = 10. In Fig. 11, perhaps the largest disagreement between the experimental data and predictions is seen in the temperature profiles near the outlet. This disagreement could be due to the lack of near-wall mesh refinement in the present simulations, or due to the fact that the wall thermal boundary condition from the experiments is unknown. Nonetheless, the overall agreement between the simulations and experiments shown in Figs. 11 and 12 is within that seen in some simulation studies [70, 72,73,74, 80] but slightly less accurate as those seen in other studies [13, 81], the latter of which includes a previous LES-LEM study, which is compared to the current study in the Section 4.3.

Fig. 11

Vertical profiles of mean quantities for the case 1 at different streamwise locations obtained with the no-model approach (red) and the LES-LEM with C_λ = 1 (blue) and C_λ = 10 (green), cf. Table 1. The experimental data is denoted with black circles. Here, U denotes the mean horizontal velocity, V the mean vertical velocity and U_in is the inlet velocity of 17 m/s

Fig. 12

Streamwise profiles of the mean horizontal velocity at the y = 0 plane for the cases in Fig. 11. For the simulation numbers, cf. Table 1

Figure 13 shows the vertical variation of rms quantities computed from the resolved fields using the no-model approach and the LES-LEM simulations. The largest discrepancy between simulations and experimental results happens close to the flameholder. This discrepancy is not surprising due to the rather coarse mesh used. In addition, Fig. 13 shows that the sensitivity of rms quantities to the choice of the turbulent combustion model and LES-LEM model constant is small, except for the rms values of the horizontal velocity at x/h = 9.4, where the LES-LEM model with C_λ = 10 gives the best agreement with experiments.

Fig. 13

Vertical profiles of rms quantities for the case 1 at different streamwise locations obtained with the no-model approach (red) and the LES-LEM with C_λ = 1 (blue) and 10 (green), cf. Table 1. The experimental data is denoted with black circles

4.3 Comparison with traditional LES-LEM

Figure 14 shows the comparison of the results obtained from the present LES-LEM implementation with the LES-LEM study of Porumbel and Menon [13]. It can be seen that predictions from Porumbel and Menon seem to be slightly more accurate for this case. However, their study uses more than ten times the (LES) cells used in the present work. Thus, the present study puts LES-LEM model through a more stringent test since a larger portion of the inertial range physics is not directly resolved in the present study by the LES and needs to be captured by the one-dimensional LEM instead.

Fig. 14

Vertical profiles of mean quantities for the Case 1 at different streamwise locations obtained with the present LES-LEM study (red) and the LES-LEM of Porumbel and Menon (blue). The experimental data is denoted with black circles

4.4 Sensitivity to model parameters

The splicing algorithm divides the mass fluxes into those related to the resolved velocity field and those due to the subgrid-scale (sgs) velocity field [64]. Figures 15 and 16 show that the sensitivity of the present predictions to using (simulation 2 cf. Table 1) or not using the sgs contribution (simulation 7 cf. Table 1) is small.

Fig. 15

Vertical profiles of mean quantities for Case 1 at different streamwise locations obtained with LES-LEM for the baseline case (red), a case where combustion happens only where the temperature is large enough (green), and a case where the sgs contribution to the splicing is zero (blue), cf. Table 1. The experimental data is denoted with black circles

Fig. 16

Streamwise profiles of the mean horizontal velocity at the y = 0 plane for the cases in Fig. 15. For the simulation numbers, cf. Table 1

In terms of the effect of using the median or mean to compute the source terms, the effect of this choice was found to be negligible. This has been observed in another study as well [61].

Figures 15 and 16 also compare predictions between the baseline LES-LEM case (simulation 2 cf. Table 1) and a case where the source term calculations in Eqs. 14–15 is only done at locations where the resolved temperature is larger than 285 K (simulation 10 cf. Table 1). This simple change to the model formulation reduces the computational cost by a factor of 4.7 and provides predictions comparable to the baseline case, as can be seen in Figs. 15 and 16.

5 High-Reynolds-Number syngas Flame

The apparent insensitivity to the choice of turbulent combustion model seen above motivated the simulation of two cases not considered in the DNS study. Two simulations with an increased Reynolds number to demonstrate the influence of increased subgrid turbulence-chemistry interactions are shown here. Case M10 is case M of Hawkes et al. [51], which has been discussed in Section 3 already, but with all length-scales of the mesh multiplied by a factor of 10. This was done by scaling length of the mesh points by 10 in the 3 Cartesian directions, resulting in increasing size of the computational domain by 10 in all the 3 directions. The same is done for case M10U2 but, in addition, the initial velocity field is multiplied by a factor of 2. In cases M10 and M10U2 the Reynolds number is 44780 and 179120 respectively. The simulations of these cases use the same number of cells (in the 3 directions) as indicated above for the M case. So by increasing the length of each cell, the cell-based Reynolds number was increased. This also increased the LEM domain lengths.

For case M10, notice in Fig. 17 that no-model simulations show two reaction layers that appear to merge at the end of the simulation. In contrast, LEM simulations show that these layers merge by t = 30t_j. This observation is consistent with a larger turbulent mixing between these layers, which in the case of LEM is represented with triplet maps and the splicing as clarified in Section 6. Furthermore, this merging seen in LEM but not in the no-model simulations is similar to that seen in LEM and not in eddy-breakup-model (EBU) simulations of reacting wakes [82, 83]. In these reacting wakes this merging is observed in the experiments.

Fig. 17

Effect of the LEM turbulent combustion modeling on the three cases M, M10, and M10U2. For the case M10, the LEM (d) produces turbulent mixing between the reaction layers earlier as compared to the no-model approach (c). The two reaction layers in (d) merge at t = 30t_j, while in (c) they merge at the end of simulations. For the case M10U2, the LEM (f) also produces merging of the two reaction layers earlier and a larger extinction region in spacetime is observed with the LEM (f) as compared to the no-model approach (e)

Moving to case M10U2, Fig. 17 shows that LEM produces a larger extinction region in spacetime (represented by the yellow region) than the no-model approach. This comparison is similar to the observation of stronger extinction, in the form of lift-off distance, seen in LEM simulations of a stagnation-point-combustor in comparison with EBU simulations [14]. Thus, these effects of LEM are consistent with those seen in other studies.

In view of the lack of DNS data for cases M10 and M10U2, however, it is not possible to judge whether the no-model approach or LEM provide more accurate predictions. Nonetheless, for the present purposes, the key message from Fig. 17 is that, in contrast to the previous results, the effect of the turbulent combustion model in cases M10 and M10U2 is profound since it affects the qualitative evolution of the flow. More investigation with LES-LEM focusing on high-Reynolds-number flames will follow in the future.

6 Discussion

An attempt is now made to explain the above apparent insensitivity to the turbulent combustion model, at least for the syngas DNS flame. In LEM the subgrid-scale interaction between turbulent motions, micromixing and reaction is captured in two ways. One is by using 1D conservation laws and triplet maps (“inside” a LES cell). In this case, high levels of turbulence are concomitant with a large number of eddies (triplet maps), N_eddies, being implemented per LES time step. On the other hand, values of N_eddies of near zero indicate that LEM behaves closely to the no-model approach. Note that N_eddies is related to the μ^sgs through Eqs. 10, 19 and 20 since a higher λ implies higher values of N_eddies. The second way the above interaction is captured in LEM is through the movement of LEM elements between adjacent LES cells (not “inside” a LES cell) due to the splicing. From this explanation, the low values of μ^sgs and spatially averaged (in xz plane) N_eddies shown in Figs. 18a and 18b for case M suggest the LEM behaves in a no-model-approach way. In other words, the elements of LEM that represent the subgrid-scale interaction between turbulence and other physics are not active. In contrast, notice in Fig. 18 that for the cases M10 and M10U2 both μ^sgs and N_eddies increase by an order of magnitude. (Note the change of the color scale.) In these cases the elements of LEM to model turbulence-chemistry interactions are active.

Fig. 18

Effect of turbulent combustion modeling on the three cases M, M10, and M10U2 using LEM and C_λ = 1

Having discussed how predictions from the present LES-LEM model compare with the experiments and a benchmark model (the no-model approach), attention is now drawn towards the design of such a LES-LEM model. For this purpose, Fig. 10 compares the effect of the correction step, cf. Figure 2. Notice in Fig. 10 that by not using this correction there was an artificial extinction of the flame. Thus, the correction step or some alternative is required. This is not surprising because the convection of species by the solution of Eq. 4 differs from that produced by the splicing in at least two ways. First, the solution of Eq. 4 numerically smears the species in a way that the splicing is not prone to because the splicing corresponds to diffusion-free advection in a Lagrangian way. Second, the splicing produces an artifact that the solution of Eq. 4 is not prone to. Such an artifact can be demonstrated with the following test problem of passive scalar advection.

This test problem uses a hexahedral computational domain of size 120× 120 ×8 mm discretized with 64× 64 ×8 hexahedral cells in which a non-reacting uniform flow is assumed from south-west to north-east with a velocity magnitude of 70.7 m/s. Since the problem is non-reacting, there is no transfer of information due to source terms from the LEM to the LES, cf. Figure 2. Initially a blob of a passive scalar sits as indicated in Fig. 19a in the center of the domain. It is important to note in Fig. 19 that the mesh is purposely coarse to exaggerate the effect of numerical diffusion and artifacts from the splicing, both of which can be reduced by refining the mesh (not shown here). In particular, notice that initially the blob is represented with only seven cells across its diameter. The flow has no initial fluctuations, and no turbulence-transport model is used, i.e. a pure advection problem is studied here. Figs. 19b-d show the resulting scalar field at a later time from three different approaches: the solution of Eqs. 1–4 (as usually done), the use of the splicing algorithm with no correction, and the use of splicing with the correction discussed above. In Figs. 19c-d the concentration of the passive scalar is computed as

$$ \tilde Y_{\alpha} = \frac{{\sum}_{i} \rho_{i} Y_{\alpha, i}}{{\sum}_{i} \rho_{i}} , $$

(24)

where Y_α denotes the mass fraction of the scalar α, and the summation (index i) is over the elements of the LEM array. First, it is evident by comparing Fig. 19b and c that the splicing distorts the shape of the blob in a way that should be considered an artifact. However, also notice that the numerical dissipation produced by the splicing is much less than that from the solution of Eqs. 1–4 (as usually done). This is a result of the fact that the splicing is a Lagrangian algorithm. Finally, a comparison of Figs. 19b and d shows that the present correction step does indeed correct for the splicing artifact just discussed. Thus, in problems such as this blob-convection test the present correction can be useful to prevent artifacts from the splicing. However, if the mesh is fine enough the splicing artifacts are small and the effect of the correction is negligible [61].

Fig. 19

Scalar in the non-reacting blob-convection problem at an initial time (a) and at a later time as a result of: solving Eqs. 1-4 (b), the splicing algorithm (c), and the splicing algorithm with the present correction (d). This is Fig. 9 in Ref. [50] and it is reprinted with permission from AIAA

7 Summary and Conclusions

The present paper introduces a new LEM closure for LES with the reaction-rate approach. Using LEM in this way, instead of closing the filtered thermochemical quantities as traditionally done, offers some conceptual advantages. For example, this new closure facilitates the assessment of inconsistency due to the turbulence-transport model. Moreover, for the purpose of reducing computational cost, it simplifies the use of more than one turbulent combustion model within one simulation, which may well include the use of no-model in very refined regions.

Predictions with this new closure agree with DNS results for a syngas flame problem with an accuracy comparable to previous traditional LES-LEM simulations. Furthermore, present predictions for the Volvo combustor are within those of previous simulations, but not as accurate as those from simulations using meshes ten or more times finer than those used here.

In spite of the above promising results, LES-LEM does not show more accurate predictions over the no-model approach for low-Reynolds-number reactive turbulence. The level of turbulence, given by the Reynolds number for instance, in the DNS syngas flame and the Volvo tests are fairly low. This statement is supported by the fact that, at least in the syngas flames, while the LEM model is barely active in the DNS syngas flame (case M), it is very active in the higher-Reynolds-number syngas flames (cases M10 and M10U2). Unfortunately, there are no DNS nor experiments for these flames. Furthermore, the heat release rate in the DNS syngas flame and the Volvo tests is also low, in which case the effects of combustion (e.g., flow expansion) on the fluid dynamics is mild. This is a well known problem with the Volvo combustor and similar academic combustors [73].

In practice, however, much higher Reynolds numbers than those of the medium-Reynolds-number syngas flame and Volvo test case can occur, in particular in gas-turbine-engine combustors [84]. In principle LES-LEM is better suited for these problems, but this capability remains to be demonstrated. Thus, future work on its development should consider test problems closer to actual applications, problems such as the high-Reynolds-number, premixed jet burner of Dunn et al. [85], or the very-high-Reynolds-number, gas-turbine-like LM6000 [86, 87] or GE-E3 [88] combustors, and conduct careful comparisons with, say, the no-model approach at various levels of mesh refinement.

Finally, unlike traditional LES-LEM implementations, the present work demonstrates the use of LES-LEM in a pressure-based and unstructured CFD solver, an approach that is preferred in industry.