A DNS Study of Sensitivity of Scaling Exponents for Premixed Turbulent Consumption Velocity to Transient Effects

Abstract

3D Direct Numerical Simulations of propagation of a single-reaction wave in forced, statistically stationary, homogeneous, isotropic, and constant-density turbulence, which is not affected by the wave, are performed in order to investigate the influence of the wave development on scaling (power) exponents for the turbulent consumption velocity U_T as a function of the rms turbulent velocity u^′, laminar wave speed S_L, and a ratio L₁₁/δ_F of the longitudinal turbulence length scale L₁₁ to the laminar wave thickness δ_F. Fifteen cases characterized by u^′/S_L = 0.5,1.0,2.0,5.0, or 10.0 and L₁₁/δ_F = 2.1, 3.7, or 6.7 are studied. Obtained results show that, while U_T is well and unambiguously defined in the considered simplest case of a statistically 1D planar turbulent reaction wave, the wave development can significantly change the scaling exponents. Moreover, the scaling exponents depend on a method used to compare values of U_T, i.e., the scaling exponents found by processing the DNS data obtained at the same normalized wave-development time may be substantially different from the scaling exponents found by processing the DNS data obtained at the same normalized wave size. These results imply that the scaling exponents obtained from premixed turbulent flames of different configurations may be different not only due to the well-known effects of the mean-flame-brush curvature and the mean flow non-uniformities, but also due to the flame development, even if the different flames are at the same stage of their development. The emphasized transient effects can, at least in part, explain significant scatter of the scaling exponents obtained by various research groups in different experiments, thus, implying that the scatter in itself is not sufficient to reject the notion of turbulent burning velocity.

1 Introduction

When investigating premixed turbulent combustion, burning rate is commonly characterized using either turbulent flame (or displacement) speed S_T, i.e., the speed of a mean flame surface with respect to the local mean flow, or burning (or consumption) velocity U_T, i.e., the bulk mass rate of consumption of a reactant (or creation of a product), normalized using a mean flame surface area and the partial density of the reactant in the fresh mixture (or the partial density of the product in burned gas, respectively). Accordingly, as reviewed elsewhere [1,2,3], S_T and U_T were in the focus of experimental research into premixed combustion for many years. In particular, over the past decade, such measurements were conducted by various research groups, e.g., [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. However, values of U_T and S_T obtained from different experiments under similar conditions, i.e., comparable rms turbulent velocities u^′, close unburned gas temperatures, the same pressure, the same fuel, and the same equivalence ratio, are strongly scattered, e.g., see Fig. 4.11 in Ref. [22]. Furthermore, even scaling (power) exponents q_m in fits $U_{T}=b_{1}{\prod }_{m = 1}^{M} Q_{m}^{q_{m}}$ or $S_{T}=b_{2}{\prod }_{m = 1}^{M} Q_{m}^{q_{m}}$ to various experimental databases are scattered [3]. In these two expressions, M ≥ 3, Q₁ = u^′, Q₂ = S_L, and other Q_m are substituted with a ratio L/δ_F of an integral length scale L of turbulence to the laminar flame thickness δ_F = a/S_L, turbulent Reynolds number Re_t = u^′L/ν_u, Damköhler number Da = τ_T/τ_F, or Karlovitz number Ka = τ_F/τ_η. Factors b₁ and b₂ are typically constant, but, in some fits, they depend on the density ratio σ = ρ_u/ρ_b, Prandtl number Pr = ν/a, Schmidt number Sc = ν/D, or Lewis number Le = a/D. Here, τ_T = L/u^′, $\tau _{\eta } =\left (\nu _{u} / \bar {\varepsilon } \right )^{1 / 2}$, and τ_F = δ_F/S_L are eddy-turn-over, Kolmogorov, and laminar-flame time scales, D is the molecular diffusivity of a deficient reactant in a mixture, ν and a are the kinematic viscosity and heat diffusivity of the mixture, subscripts u and b designate fresh reactants and equilibrium products, respectively, ε = 2νS_ijS_ij is the dissipation rate, S_ij = 0.5 (∂u_i/∂x_j + ∂u_j/∂x_i) is the rate-of-strain tensor, u_i and x_i are components of the velocity vector u and spatial coordinates x, respectively, $\bar {Q}$ is the Reynolds-averaged value of a quantity Q, and the summation convention applies for repeated indexes.

It is worth stressing that not only results of earlier measurements, processed in Ref. [3], but also recent experimental data on S_T and U_T show significant scatter of the aforementioned scaling exponents. For instance, the scaling exponent q_v for S_T or U_T vs. the rms velocity u^′, e.g., $S_{T}\propto {u^{\prime }}^{q_{v}}$, was reported to be (i) less than unity [5, 7,8,9,10,11,12,13,14, 16, 19,20,21], e.g., q_v = 0.49 [16], q_v = 0.55 [21], q_v = 0.63 [8], (ii) equal to unity [6], or (iii) even equal to two [17]. The fitted values of the scaling exponent q_s for S_T or U_T vs. S_L range from 0.37 [8] to 0.74 [10]. The scatter is much more pronounced for the scaling exponent q_r for S_T or U_T vs. a ratio of L/δ_L, with both negative, e.g., q_r = − 0.37 [8], and positive, e.g., q_r = 0.25 [14], q_r = 0.5 [13], or even q_r = 1.35 [10], being reported.

There are two major, but fundamentally opposite standpoints regarding the significant scatter of experimental data on U_T, S_T, and the scaling exponents obtained from various flames using various methods. On the one hand, based on this scatter, the notions of U_T and S_T are sometimes put into question in the sense that they may not be extrapolated beyond a particular flame configuration used to evaluate them. Then, strictly speaking, research into turbulent burning velocity and flame speed is of minor fundamental value. On the other hand, while the scatter of measured U_T, S_T, and their scaling exponents seems to be a sufficient reason for expressing concern over the notions of these quantities, such a standpoint is not widely accepted and evaluation of U_T and S_T is still in the focus of experimental research into premixed combustion, e.g., see [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] and references quoted therein. Moreover, U_T and S_T are widely used in numerical simulations of turbulent flames, as reviewed elsewhere [3, 22,23,24,25]. To warrant such experimental and numerical investigations, it is necessary to assure that the aforementioned scatter does not prove that the notion of U_T or S_T should be limited to a particular flame configuration. Accordingly, it is necessary to reveal effects that (i) can cause the well-documented significant scatter of experimental data on U_T, S_T, and even the scaling exponents, but (ii) are consistent with a standpoint that the notion of U_T or S_T is of a fundamental value.

As far as the values of U_T and S_T are concerned, three such effects are well known. As shown [26,27,28,29,30,31] and reviewed [3, 22, 32] elsewhere, the quantitative scatter of available experimental data on U_T and S_T results, at least in part, from sensitivity of values of turbulent burning velocities and flame speeds to methods used to analyze raw experimental data and, in particular, to the choice of a mean flame surface within a thick mean flame brush. More specifically, first, U_T is sensitive to such a choice, because (i) areas of different mean flame surfaces can significantly differ from each other if the mean flame brush is thick and curved [28, 30, 31] and (ii) U_T is inversely proportional to the area used to normalize the bulk burning rate. Second, speeds of different mean flame surfaces can be substantially different due to non-uniformities of the mean flow of unburned gas within the thick flame brush, with such effects being well known in spatially diverging flows [26, 27]. Third, S_T characterizing different mean flame surfaces can be significantly different if the mean flame brush thickness δ_T grows with time or distance from a flame-holder [28], with such a growth of δ_T being well documented in a number of experiments with various premixed flames, as reviewed elsewhere [3, 22, 32], see also recent papers [10, 16, 33, 34]. While the focus of studies [3, 22, 26,27,28,29,30,31,32] was placed on the values of U_T and S_T, rather than the scaling exponents, a recent numerical work [35] has shown that the three aforementioned well-known effects can even cause substantial sensitivity of the scaling exponents q_v, q_s, and q_r to methods used to evaluate U_T or S_T by processing raw experimental data.

These three effects are relevant, respectively, to (i) U_T if the mean flame brush is curved, (ii) S_T if the mean flow of fresh reactants is not spatially uniform, e.g., the mean flow diverges or converges, and (iii) S_T if δ_T grows. However, none of these three well-known effects is relevant to turbulent burning velocity obtained from a statistically 1D planar turbulent premixed flame. In this simplest case, U_T is equal to properly normalized mean rate of a reactant consumption (or product creation), integrated along a straight line normal to a mean flame surface, with all mean flame surfaces being parallel to each other and having the same area. Therefore, U_T is well and unambiguously defined. It is sensitive neither to the choice of a mean flame surface nor to the growth of the mean flame brush thickness, with the mean flow of unburned reactants being spatially uniform in the considered case. Nevertheless, even in this simplest case associated with negligible role played by the aforementioned three well-known effects, there is another effect, which can also contribute to significant scatter of the scaling exponents for U_T. The major goal of present work is to emphasize substantial sensitivity of the scaling exponents to that effect.

More specifically, the paper aims at analyzing Direct Numerical Simulation (DNS) data obtained for various ratios of u^′/S_L and L/δ_F in the statistically 1D planar case in order to show that transient effects can yield a significant scatter of the scaling exponents q_v, q_s, and q_r for the turbulent consumption velocity even in such a case. As noted above, consideration of the statistically 1D planar case offers an opportunity to place the focus of the study on the transient effects by eliminating the three other relevant well-known effects discussed earlier. Moreover, the paper aims at demonstrating that the transient effects can manifest themselves in apparent sensitivity of the scaling exponents to flame configuration and measurement method. Other related research issues such as comparison of computed scaling exponents with theoretical or experimental results are beyond the major scope of the paper.

In the next section, statement of the problem and DNS attributes are summarized. In the third section, results are discussed, followed by conclusions.

2 Research Method

2.1 Statement of the problem

In order to place the focus of the study on the aforementioned transient effects and to isolate them from other phenomena as much as possible, the simplest relevant problem is addressed, i.e., we consider propagation of a statistically 1D planar (for the reasons discussed earlier) single-reaction wave in a constant-density turbulent flow, which is not affected by the wave. On the one hand, the invoked simplifications are very strong and make the studied problem substantially different from the problem of propagation of a premixed flame in a turbulent flow, because Lewis number and preferential diffusion, thermal expansion, complex chemistry and other effects can play an important role in the latter case, as reviewed, e.g., in Refs. [36,37,38,39] or shown in recent papers [40, 41]. Accordingly, from purely numerical perspective, the present simulations are inferior to modern DNS studies that allow for both thermal expansion and complex chemistry in intense (u^′/S_L ≫ 1) turbulence, e.g., [41,42,43,44,45,46,47]. However, the invoked assumptions are fully adequate to the qualitative goal of the present work. Indeed, if the transient effects are of significant importance under simple studied conditions, then, there are no solid reasons to disregard such effects under other, more realistic conditions.

On the other hand, the invoked simplifications allow us (i) to perform DNS by substantially varying both u^′/S_L and L/δ_F (in a range of L/δ_F > 1), which is necessary for studying the scaling exponents, but is still not feasible in the case of a complex chemistry, and (ii) to obtain reliable statistics for both fully-developed and developing waves by significantly increasing the number of samples using a method valid solely in a constant-density case, as discussed in Section 2.2.

It is also worth noting that, first, turbulent flame speeds evaluated using single-step and multi-step chemistry were recently compared in two independent DNS studies [46, 48]. Obtained results show that “mean turbulent flame properties such as burning velocity and fuel consumption can be predicted with the knowledge of only a few global laminar flame properties” [46, p.294] and “the global mechanism is adequate for predicting flame speed” [48, p.53]. Moreover, target-directed experiments [49] performed using the well-recognized Leeds fan-stirred bomb facility do not show a notable effect of combustion chemistry on turbulent flame speed either. Such effects are commonly expected to be of substantial importance when local combustion extinction occurs, but this phenomenon is beyond the scope of the present study.

Second, the assumption of a constant density, invoked to greatly improve statistical sampling, appears to be of minor importance for the goals of the present study for the following three reasons. (I) The vast majority of approximations of experimental data on U_T or S_T [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] do not invoke the density ratio σ, thus, implying a weak influence of σ on U_T or S_T. (II) Recent target-directed experiments [50], as well as earlier measurements [49], did not reveal a substantial influence of σ on U_T or S_T. (III) Recent DNS studies, e.g., [51, Figs. 10-11] or [52, Fig. 2a], do not indicate such an influence either.

Thus, DNS of propagation of a statistically 1D, planar, single-reaction wave in forced, constant-density, homogeneous, and isotropic turbulence was performed by numerically solving the following 3D Navier-Stokes

$$ \partial_{t}{\mathbf{u}+}\left( {\mathbf{u}\cdot \nabla} \right){\mathbf{u}=-}\rho^{\mathrm{-1}}\mathrm{\nabla} p\mathrm{+}\nu \mathrm{\nabla}^{2}{\mathbf{u}+\mathbf{f}} $$

(1)

and reaction-diffusion

$$ \partial_{t}c\mathrm{+\mathbf{u}\cdot \nabla} c\mathrm{=}D\mathrm{\nabla} ^{2}c\mathrm{+}W $$

(2)

equations, as well as ∇⋅u = 0, in a fully periodic rectangular box of a size of Λ_x ×Λ×Λ using a uniform cubic grid of N_x × N×N cells (N_x/N = Λ_x/Λ = 4) and an in-house solver [53] developed for low-Mach-number reacting flows. Here, ∂_t designates partial derivative with respect to time, p is the pressure, a vector-function f is used to maintain turbulence intensity by applying energy forcing at low wavenumbers [54], c is the reaction progress variable (c = 0 and 1 in reactants and products, respectively),

$$ W\mathrm{=}\frac{1}{\mathrm{1+}\tau} \frac{\mathrm{1-}c}{\tau_{R}}\exp\left[ \mathrm{-}\frac{Ze\left( \mathrm{1+}\tau \right)^{2}}{\tau \left( \mathrm{1+}\tau c \right)} \right] $$

(3)

is the reaction rate, τ_R is a constant reaction time scale, while parameters Ze = 6 and τ = 6 are counterparts of the Zel’dovich number $Ze={\mathrm {{\Theta }}_{a}\left (T_{b}-T_{u} \right )} / {T_{b}^{2}}$ and heat-release factor τ = σ − 1, respectively. Substitution of c = (T − T_u) / (T_b − T_u) into the exponent in Eq. 3 results in the classical Arrhenius law with the activation temperature Θ_a. Therefore, Eq. 3 offers an opportunity to mimic the behavior of the reaction rate in a flame by considering constant-density reacting flows.

As the state of the reacting mixture is characterized with a single scalar c, the simulated problem is associated with Le = 1 and Sc = Pr.

2.2 DNS attributes

Because the DNS attributes are discussed in detail elsewhere [55,56,57,58,59], we will restrict ourselves to a very brief summary of the simulations.

The boundary conditions were periodic not only in transverse directions y and z, but also in direction x normal to the mean wave surface [56]. This was possible, because (i) the thickness of the entire wave brush was significantly smaller than the length Λ_x of the computational domain in each simulated case at each instant and (ii) the c-field did not affect the velocity and pressure fields in the studied constant-density cases. Accordingly, Eq. 2 was not solved in narrow layers upstream and downstream of the wave brush, but the reaction progress variable was equal to zero and unity, respectively, within these layers, e.g., c (x_le − 𝜖Λ_x ≤ x < x_le, y, z, t) = 0. Here, 𝜖 ≪ 1 and x_le = x_le (t) is the axial coordinate of the reactant boundary of the layer where (2) was solved. Due to the wave propagation, the time derivative dx_le/dt was negative at all instances with the exception of instances when x_le (t) = 0. At these instances, (i) the identical reaction wave entered the computational domain through its right boundary (x = Λ_x) and (ii) c (x, t) dropped from unity to zero on the plane x = Λ_x (1 − 𝜖), but (2) was not solved in the vicinity of this plane. Such a method allowed us to strongly improve sampling statistics by simulating a number of cycles of wave propagation through the computational domain, but the method is justified only in the case of ρ =const and ν =const.

The initial turbulence field was generated by synthesizing prescribed Fourier waves [60] with an initial rms velocity u₀ and the forcing scale l₀ = Λ/4. The initial turbulent Reynolds number Re₀ = u₀l₀/ν was changed by changing the domain width Λ, with the numerical resolution Δx = Δy = Δz = Λ_x/N_x = Λ/N being the same in all cases. Subsequently, for each Re₀, a forced incompressible turbulent field was simulated by integrating (1) with the same forcing vector-function f [61]. In all cases, the velocity, length, and time scales showed statistically stationary behavior at $t>t^{\ast } = 3.5\tau _{T}^{0}= 3.5l_{0} / u_{0}$ [55, 56], the turbulence achieved statistical homogeneity and isotropy over the entire domain [55, 56], u^′≅u₀, and a ratio of L₁₁/Λ was about 0.12 [58]. Here, L₁₁ is the longitudinal length scale of the turbulence, evaluated at t > t^∗.

To obtain fully-developed statistics, i.e., mean characteristics of the statistically stationary stage of turbulent wave propagation, a planar wave c(x,0) = c_L (ξ) was released at x₀ = Λ_x/2 at t = 0 such that ${\int }_{-\infty }^{0} {c_{L}\left (\xi \right )d\xi } ={\int }_{0}^{\infty } {\left [ 1-c_{L}\left (\xi \right ) \right ]d\xi }$. Here, ξ = x − x₀ and c_L (ξ) is a pre-computed laminar wave profile. Subsequently, evolution of a long-living field c(x, t) was simulated by solving (2). Sampling of the fully developed statistics was started at $t=t^{\ast } = 3.5{\tau _{T}^{0}}$ and was performed over a time interval longer than $50{\tau _{T}^{0}}$. For that purpose, the time-dependent mean value $\hat {q}(x,t)$ of a quantity q(x, t) was evaluated by averaging DNS data over transverse coordinates, followed by computing the fully-developed profile of $\bar {q}(x)$ by averaging $\hat {q}(x,t)$ over time. Finally, x-coordinates were mapped to $\bar {c}(x)$-coordinates.

To study transient effects, the same pre-computed laminar-wave profiles c_L (ξ) were simultaneously embedded into the turbulent flow in M equidistantly separated planar zones centered around x_m/Λ_x = (m − 0.5)/M i.e., c_m (x, t₀) = c_L (ξ_m), where coordinates ξ_m = x − x_m were set using ${\int }_{-\infty }^{0} {c_{L}\left (\xi _{m} \right )d\xi _{m}} ={\int }_{0}^{\infty } {\left [ 1-c_{L}\left (\xi _{m} \right ) \right ]d\xi _{m}}$ and m was an integer number (1 ≤ m ≤ M = 30). Subsequently, evolutions of M transient fields c_m (x, t) were simulated by solving M independent (3), with these fields c_m (x, t) and the long-living field c (x, t) affecting neither each other nor the turbulence in the studied case of ρ =const and ν =const. Accordingly, all M transient fields c_m (x, t) were independent from each other, and the distance between iso-surfaces of two different transient fields did not affect computed results.

The transient simulations were run over $2{\tau _{T}^{0}}$ before being reset. Subsequently, at $t=t^{\ast } + 2j{\tau _{T}^{0}}$, where j ≥ 1, the flow was again populated by M new profiles of c_L (ξ) and the transient simulations were repeated. Time-dependent mean quantities $\overline {\overline {q^{t}}}(x,t)$ were evaluated by averaging DNS data over transverse coordinates and over the entire ensemble [m = 1,…, M and various time intervals $t^{\ast } + 2\left (j-1 \right ){\tau _{T}^{0}}\le t\le t^{\ast } + 2j{\tau _{T}^{0}}$] of the transient fields q_{m, j} (x, t). Then, x-coordinates were mapped to $\overline {\overline {c^{t}}}(xt)$-coordinates, as discussed in detail elsewhere [56].

Such a method (i.e., simulations of M independent transient fields) significantly increased the sampling counts for calculating transient statistics. It is worth remembering, however, that such a method can only be used for simulating processes that do not affect the flow, e.g., a constant-density reaction wave addressed here.

Both fully-developed and transient bulk consumption velocities were calculated by integrating the mean reaction rate along the normal to the mean reaction wave brush, i.e.,

$$ \overline {U_{T}} =\int\limits_{0}^{{\Lambda}_{x}} {\bar{{W}}(x,t)dx.} $$

(4)

$$ U_{T} (t)=\int\limits_{0}^{{\Lambda}_{x}} {\overline{\overline {W^{t}}} (x,t)dx.} $$

(5)

Various cases were set up by selecting a turbulent field and specifying the speed S_L and thickness δ_F = D/S_L of the laminar reaction wave, with the required reaction time scale τ_R in Eq. 3 being found in 1D pre-computations of the laminar wave. Because the reaction waves did not affect the flow, the choice of a turbulent field was independent of the choice of S_L and δ_F. Accordingly, three turbulence fields A (N_x = 256, Re₀ = 50, η/Δx = 0.68), B (N_x = 512, Re₀ = 100, η/Δx = 0.87), and C (N_x = 1024, Re₀ = 200, η/Δx = 1.07), characterized by different Λ, $l_{0}, {\tau _{T}^{0}},$and L₁₁, were generated and propagation of five different sets of reaction waves in each turbulence field was simulated. Within each set of waves, the speed S_L was varied, but the thickness δ_F retained the same value due to an appropriate adjustment of the Schmidt number Sc. Characteristics of all 15 cases are shown in Table 1, where η = (ν³/〈ε〉)^1/4 is the Kolmogorov length scale, Pe = u^′L₁₁/ (S_Lδ_F) is turbulent Péclet number, 〈ε〉 is the dissipation rate averaged over the computational domain and time at t > t^∗. Moreover, extra cases were designed to show weak sensitivity of computed results to grid resolution, L₁₁/Λ, etc., but these results are discussed elsewhere [57, 58].

Table 1 Studied cases

3 Results and Discussion

To reveal significant influence of transient effects on the scaling exponents referred to, the DNS data on both fully-developed $\bar {U_{T}}$ and developing U_T (t) turbulent consumption velocities were processed using the same method. More specifically, data on Y = {U_T/u^′, U_T/S_L, (U_T − S_L) /u^′, (U_T − S_L) /S_L} vs. X = {u^′/S_L, Da, Ka, Pe, (u^′/S_L) (L₁₁/δ_F) ^d} were approximated with Y = aX^b using least square fit.¹ In the case of X = (u^′/S_L) (L₁₁/δ_F) ^d, the power exponent d was varied from -4 to 4 with a step of 0.01 and the exponent that yielded the lowest value of 𝜖 = |1 −R²| was selected. Here,

$$ \mathrm{R}^{2}= 1-\frac{{\sum}_{k = 1}^{K} \left( Y_{k}-a{X_{k}^{b}} \right)^{2}} {{\sum}_{k = 1}^{K} \left( Y_{k}-\frac{1}{K}{\sum}_{l = 1}^{K} Y_{l} \right)^{2}} $$

(6)

is the coefficient of determination [62] and K = 15 is the number of studied cases. The aforementioned sets of expressions for X and Y were used to process the DNS results, because various fits to experimental data bases on U_T (or S_T) can be found in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22, 32], e.g., (U_T − S_L) /u^′ = f (Da) [2], U_T/u^′ = f (Da) [3, 14], U_T/u^′ = f (Ka) [3, 4, 9, 11], U_T/S_L = f (Re_t) [4, 13, 32], U_T/S_L = f (u^′/S_L) [5, 7, 12, 15, 21] (U_T − S_L) /S_L = f (u^′/S_L) [6, 16, 31], U_T/S_L ∝ (u^′/S_L) ^q (L/δ_F) ^d [3, 8, 10], etc., with functions f being different for different fits. Note that, for brevity, the same symbol U_T is used in all these expressions although flame speeds S_T were reported in some of the cited papers.

The present DNS data on the fully-developed consumption velocities are best fitted, see triangles in Fig. 1, with $\bar {U_{T}} / {u^{\prime }}\propto \left ({u^{\prime }} / S_{L} \right )^{-0.5}\left (L_{11} / \delta _{F} \right )^{0.6}$, i.e., the scatter 𝜖 = |1 −R²| is the lowest in this case. In Ref. [58], a larger number of cases was analyzed and $\bar {U_{T}} / S_{L}\propto {Pe}^{0.5}$ best fitted those data. For the present data, this fit is shown in circles in Fig. 1. Another fit to the present DNS data is plotted in squares in Fig. 1, because this fit is relevant to developing reaction waves, as will be discussed later. It is worth stressing that the DNS data on the fully-developed consumption velocity were already analyzed and compared with experimental data and theoretical results in Ref. [58]. Here, these DNS data are solely reported for comparison with the DNS data on the developing U_T. Accordingly, the reader interested in a more detailed discussion of the behavior of $\bar {U_{T}}$ is referred to Ref. [58].

Fig. 1

Approximations (lines) of DNS data (symbols) on the fully-developed turbulent consumption velocities. 1 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. a ratio of ${u^{\prime }} / S_{L}$ fitted with $\bar {U_{T}} / {u^{\prime }}\propto \left ({u^{\prime }} / S_{L} \right )^{-0.5}$, R² = 0.876; 2 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. turbulent Péclet number fitted with $\bar {U_{T}} / S_{L}\propto {Pe}^{0.5}$, R² = 0.977; 3 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. ratios of ${u^{\prime }} / S_{L}$ and L₁₁/δ_F fitted with $\bar {U_{T}} / {u^{\prime }}\propto \left ({u^{\prime }} / S_{L} \right )^{-0.5}\left (L_{11} / \delta _{F} \right )^{0.6}$, R² = 0.992

The DNS data on the developing consumption velocities were analyzed using three different methods. The simplest method consists in fitting the DNS data obtained at the same normalized wave-development time 𝜃 = t_d/τ_T. This method of the data processing mimics measurement of a turbulent consumption velocity, performed at certain distance z from flame-stabilization zone in a statistically stationary flame. Such turbulent consumption velocities were experimentally obtained, e.g., by Verbeek et al. [17] and by Sattler et al. [63] from V-shaped (rod-stabilized) flames. It is worth remembering that, as discussed in detail elsewhere [3, 22], development of a statistically stationary premixed turbulent flame occurs during advection of the flame element by the mean flow, similarly to development (decay) of statistically stationary turbulence behind a grid or to development (growth) of a statistically stationary turbulent mixing layer. In such cases, the flame (turbulence, or mixing layer, respectively) development time can roughly be estimated as follows t_d ≈ z/U, where U is the mean flow velocity in the z-direction. Accordingly, the normalized wave development time 𝜃 is equal to z/ (Uτ_T) in this case.

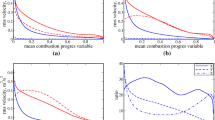
Certain representative results are shown in Fig. 2. At a low value of 𝜃, see Fig. 2a, the data are very well fitted with U_T/u^′∝ (u^′/S_L) ^− 0.99, see squares. Fitting with U_T/u^′∝ (u^′/S_L) ^− 0.99 (L₁₁/δ_F) ^− 0.1 does a little bit better job, see triangles, due to the use of the third fitting parameter. While circles in Fig. 2a might also look to be weakly scattered, this impression is wrong, as shown in insert. It indicates that a dependence of U_T/S_L on Pe is weakly pronounced at 𝜃 = 0.2. Thus, at low 𝜃, the consumption velocity is almost proportional to S_L and almost independent of u^′. Such a result could be claimed to be expected, because U_T (𝜃 = 0) = S_L, but, in any case, this result shows that transient effects can significantly change the scaling exponents.

Fig. 2

Approximations (lines) of DNS data (symbols) on developing turbulent consumption velocities evaluated for a𝜃 = 0.2, b𝜃 = 0.6, c𝜃 = 1, and d𝜃 = 2.0. 1 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. a ratio of ${u^{\prime }} / S_{L}$ fitted with U_T/u^′∝ (u^′/S_L) ^α, 2 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. turbulent Péclet number fitted with $U_{T} / S_{L}\propto {Pe}^{\beta }$, 3 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. ratios of ${u^{\prime }} / S_{L}$ and L₁₁/δ_F fitted with U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ. Insert shows solely data on $U_{T} / S_{L}\propto {Pe}^{\beta }$

When the normalized time 𝜃 is increased, scatter of the DNS data around U_T/u^′∝ (u^′/S_L) ^α and U_T/S_L ∝ Pe^β is increased and decreased, respectively, see squares and circles, respectively, in Fig. 2b, c, and d, as well as circles and triangles in Fig. 3a. Due to the use of an extra parameter, U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ fits to the DNS data well at all 𝜃, see squares in Fig. 3a, but the power exponents vary with increasing 𝜃. In particular, triangles-down and squares in Fig. 3b show that the scaling exponents γ and δ, respectively, increase with increasing 𝜃 (because γ < 0, its magnitude decreases) and tend to values yielded by the best fit to the DNS data on the fully-developed $\bar {U_{T}}$, see dashed and double-dashed-dotted lines, respectively. Scaling exponents α in U_T/u^′∝ (u^′/S_L) ^α and β in U_T/S_L ∝ Pe^β show the same trend, see circles and triangles-up, respectively, in Fig. 3b, but the scatter is increased and decreased, respectively, with increasing 𝜃, see circles and triangles, respectively, in Fig. 3a.

Fig. 3

a Coefficients of determination and b power exponents vs. normalized wave-development time. Symbols and lines show results obtained from developing and fully-developed reaction waves, respectively. 1 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. a ratio of ${u^{\prime }} / S_{L}$ fitted with U_T/u^′∝ (u^′/S_L) ^α and the power exponent α, 2 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. turbulent Péclet number fitted with $U_{T} / S_{L}\propto {Pe}^{\beta }$ and the power exponent β, 3 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. ratios of ${u^{\prime }} / S_{L}$ and L₁₁/δ_F fitted with U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ and the power exponent γ, 4 – the power exponent δ in U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ

Since the majority of measurements of turbulent burning velocity in V-shaped flames, e.g., [11, 16, 17], and, especially, in Bunsen (rim-stabilized) flames, e.g., [5, 10, 12, 15, 19, 21, 31], were performed by averaging experimental data over the entire flame volume or over a significant part of it, another method of processing the DNS data was also used in order to evaluate similarly averaged values of the developing U_T. For this purpose, let us consider a simple mean-reaction-wave surface that has a conical shape, with the cone base radius and height being equal to R and H, respectively. Such a simple configuration is akin to the shape of the mean surface of a Bunsen flame stabilized on a nozzle rim of a radius R.

Then, the volume-averaged consumption velocity 〈U_T〉 is equal to

$$ \langle U_{T}\rangle \mathrm{=}U\frac{R}{H} $$

(7)

where U is the mean flow velocity at the nozzle, i.e., at z = 0. Moreover, the bulk consumption velocity evaluated using the reactant flux through the nozzle, i.e., πR²U, should be equal to the bulk consumption velocity evaluated using the local value of U_T (z) and integrated over distance z from the nozzle. Consequently,

$$ \pi R^{2}U = 2\pi \frac{R}{H}{\int\limits_{0}^{H}} {U_{T} (z)zdz= 2\pi \frac{R}{H}(U\tau_{T} )^{2}\int\limits_{0}^{\theta_{\mathrm{m}}} {U_{T} (\theta )\theta d\theta = 2\pi RH\theta_{\mathrm{m}}^{-2} \int\limits_{0}^{\theta_{\mathrm{m}}} {U_{T} (\theta )\theta d\theta} } ,} $$

(8)

where 𝜃_m = H/ (Uτ_T) is the maximal normalized wave-development time. Comparison of Eqs. 7 and 8 shows that

$$ \langle U_{T} \rangle (\theta_{\mathrm{m}} )= 2\theta^{-2}\int\limits_{0}^{\theta_{\mathrm{m}}} {U_{T} (\theta )\theta d\theta} . $$

(9)

The volume-averaged 〈U_T〉(𝜃_m) evaluated by integrating U_T (𝜃) obtained in the DNS mimics turbulent burning velocity measured in experiments with statistically stationary Bunsen flames, e.g., [5, 10, 12, 15, 19, 21, 31]. If mixture composition, the rms turbulent velocity u^′, and the mean nozzle velocity U are varied in such experiments, but a ratio of u^′/U retains the same value, then, the maximal normalized flame-development time 𝜃_m = (H/U)/ (L₁₁/u^′) also retains the same value for the same H. Accordingly, evaluation of the scaling exponents for 〈U_T〉 at various constant 𝜃_m is relevant to such experiments.

Results of processing the set of 〈U_T〉(𝜃_m), which were evaluated using Eq. 9 and U_T (𝜃) extracted from the DNS data in all 15 cases A1-A5, B1-B15, and C1-C5, are shown in Figs. 4 and 5. These results look similar to results obtained for the instantaneous developing U_T (𝜃), which are reported in Figs. 2 and 3. The major difference consists of 〈U_T〉(𝜃_m) < U_T (𝜃), which is obvious, because the function U_T (𝜃) integrated in Eq. 9 is an increasing function. Thus, while the two methods of processing the same DNS data on U_T (𝜃) clearly show substantial influence of the wave development on the considered scaling exponents, the simulated effect does not mimic an influence of measurement method on the scaling exponents. Nevertheless, application of one more method to processing the same DNS data revealed the latter influence also.

Fig. 4

Approximations (lines) of DNS data (symbols) on developing volume-averaged turbulent consumption velocities evaluated for a𝜃 = 0.2, b𝜃 = 0.6, c𝜃 = 1.0, and d𝜃 = 2.0. 1 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. a ratio of ${u^{\prime }} / S_{L}$ fitted with U_T/u^′∝ (u^′/S_L) ^α, 2 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. turbulent Péclet number fitted with $U_{T} / S_{L}\propto {Pe}^{\beta }$, 3 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. ratios of ${u^{\prime }} / S_{L}$ and L₁₁/δ_F fitted with U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ. Insert shows solely data on 〈U_T〉/S_L ∝ Pe^β

Fig. 5

a Coefficients of determination and b power exponents vs. normalized wave-development time. Symbols and lines show results obtained from developing and fully-developed reaction waves, respectively. 1 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. a ratio of ${u^{\prime }} / S_{L}$ fitted with U_T/u^′∝ (u^′/S_L) ^α and the power exponent α, 2 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. turbulent Péclet number fitted with $U_{T} / S_{L}\propto {Pe}^{\beta }$ and the power exponent β, 3 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. ratios of ${u^{\prime }} / S_{L}$ and L₁₁/δ_F fitted with U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ and the power exponent γ, 4 – the power exponent δ in 〈U_T〉/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ

The third method applied to process the same DNS data on U_T (𝜃) is associated with an experiment with an expanding statistically spherical premixed turbulent flame. In such experiments, e.g., [4, 9, 13, 14, 18, 20], measurements are performed in a bounded range of the flame kernel radii R_f, with this range being independent on mixture composition, turbulence characteristics, pressure, and temperature. To mimic such measurements, we numerically integrated the following equation

$$ \frac{dr_{f}}{d\theta} \mathrm{=}u_{t}\left( \theta \right) $$

(10)

Here, r_f = R_f/L₁₁ is the mean wave radius normalized using L₁₁, and u_t (𝜃) = U_T (𝜃)/u^′ is taken from the DNS data. Subsequently, the DNS dependencies of U_T (𝜃) were transformed to U_T [r_f (𝜃)] using results of integration of Eq. 10 and the fits discussed earlier were applied to sets of 15 values of U_T [r_f (𝜃)] associated with the same wave “radius”r_f in different cases A1-A5, B1-B5, and C1-C5.

Obtained results are reported in Figs. 6 and 7. Data on U_T fitted (i) at the same normalized time, see Figs. 2, 3, 4 and 5, and (ii) at the same normalized wave radius r_f, see Figs. 6 and 7, show similar qualitative trends, but, in the latter case, the difference between the developing U_T and the fully-developed $\bar {U_{T}}$ is less pronounced. Accordingly, the scaling exponents that yield the best fits to the DNS data depend not only on the wave-development time, but also on a method (whether U_T is studied at the same 𝜃 or at the same r_f) used to compare data computed in different cases. These effects can cause significant variations of the scaling exponents q_v, q_s, and q_r for turbulent consumption velocity as a function of u^′, S_L, and L₁₁/δ_F, respectively, see Table 2 and note that values of 1 ≤ 𝜃 ≤ 2 or 1 ≤ r_f ≤ 2 are typical for various experiments with statistically stationary or expanding premixed turbulent flames, respectively. In particular, Table 2 shows that the transient effects result in increasing q_v and q_r, but decreasing q_s with wave-development time, see also the fully-developed scaling exponents reported in the right column titled with ∞.

Fig. 6

Approximations (lines) of DNS data (symbols) on developing turbulent consumption velocities evaluated for ar_f = 0.2, br_f = 0.6, cr_f = 1.0, and dr_f = 2.0. 1 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. a ratio of ${u^{\prime }} / S_{L}$ fitted with U_T/u^′∝ (u^′/S_L) ^α, 2 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. turbulent Péclet number fitted with $U_{T} / S_{L}\propto {Pe}^{\beta }$, 3 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. ratios of ${u^{\prime }} / S_{L}$ and L₁₁/δ_F fitted with U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ

Fig. 7

a Coefficients of determination and b power exponents vs. normalized wave-development time. Symbols and lines show results obtained from developing and fully-developed reaction waves, respectively. 1 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. a ratio of ${u^{\prime }} / S_{L}$ fitted with U_T/u^′∝ (u^′/S_L) ^α and the power exponent α, 2 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. turbulent Péclet number fitted with $U_{T} / S_{L}\propto {Pe}^{\beta }$ and the power exponent β, 3 – a ratio of $\bar {U_{T}} / {u^{\prime }}$ vs. ratios of ${u^{\prime }} / S_{L}$ and L₁₁/δ_F fitted with U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ and the power exponent γ, 4 – the power exponent δ in U_T/u^′∝ (u^′/S_L) ^γ (L₁₁/δ_F) ^δ

Table 2 Scaling exponents in $U_{T}\propto {u^{\prime }}^{q_{v}}S_{L}^{q_{s}}\left (L_{11} / \delta _{F} \right )^{q_{r}}$

More specifically, inspection of Table 2 shows that the scaling exponent q_s is significantly larger for the volume-averaged consumption velocity 〈U_T〉(𝜃), associated with Bunsen and V-shaped flames, when compared to the consumption velocity U_T [r_f (𝜃)] associated with expanding statistically spherical flames.² The opposite trend is well pronounced for the scaling exponent q_v. These results imply that development of premixed turbulent flames can affect the scaling exponents for burning velocity not only directly, but also indirectly. In other words, the scaling exponents obtained from premixed turbulent flames of different configurations may be different not only due to the well-known effects of the mean-flame-brush curvature and the mean flow non-uniformities, but also due to the flame development, even if the different flames are at the same stage of their development. Such effects can, at least in part, explain significant scatter of the scaling exponents reported in different papers.

The results presented above have the following implications. First, the transient effects should appropriately be taken into account when comparing experimental data reported by different research groups or when testing a model of premixed turbulent combustion. For instance, a widely accepted practice of assessment of such models consists in directly comparing the model expression for the fully-developed U_T (or the scaling exponents in the expression) with a fit to experimental data on U_T or S_T. However, this method ignores the transient effects and, therefore, appears to be flawed. When using experimental data to test a numerical model, a method of evaluation of turbulent flame speed or burning velocity in simulations should be as close as possible to the method adapted to measure the data.

Second, while experimental data obtained from expanding premixed turbulent flames convey some information on the transient effects, e.g., see Refs. [3, 9, 13, 14, 18, 20, 49, 50], development of U_T or S_T has yet been addressed in a few experimental investigations of statistically stationary premixed turbulent flames [17, 63]. Definitely, the issue requires further target-directed research. In particular, dependencies of the local values of U_T or/and S_T on distance from flame-stabilization zone should be measured in statistically stationary premixed turbulent flames.

Third, a phenomenological method of processing experimental data on S_T (R_f), obtained from expanding statistically spherical premixed turbulent flames, was proposed to be used in Ref. [64], where the method was also validated against seven experimental databases reported by six independent research groups. Subsequently, the method was theoretically substantiated [30] by assuming self-similarity of the mean structure of developing premixed turbulent flames [65, 66], with that assumption being well supported by various experiments discussed in detail elsewhere [3, 22, 67, 68]. On the contrary, a similar method has not yet been elaborated for statistically stationary premixed turbulent flames and this gap should be filled. To do so, a few model expressions for the transient U_T (𝜃), available in the literature, e.g., see Refs. [3, 69], could be used and, eventually, further developed. However, as already noted in the previous paragraph, results of measurements of the local U_T or S_T at different distances from flame-holder are strongly required for this purpose.

Finally, it is worth noting that the aforementioned model expressions for the transient U_T (𝜃) also predict variations in the scaling exponents during flame development. For instance, the following equation [70]

$$ \frac{U_{T}\left( \theta \right)}{U_{T}\left( \theta \mathrm{\to \infty} \right)}\mathrm{=}\left[ \mathrm{1+}\frac{1}{\theta} \left( \mathrm{e}^{\mathrm{-}\theta} \mathrm{-1} \right) \right]^{1 / 2} $$

(11)

which was developed within the framework of the Flame Speed Closure (FSC) model [22, 25] and was validated in RANS simulations [24, 25, 35, 71] of various experiments with statistically stationary premixed turbulent flames, predicts that q_v (𝜃→∞) = q_v (𝜃≪ 1) + 0.5 and q_L (𝜃→∞) = q_L (𝜃≪ 1) + 0.5 also. Here, q_L is the scaling exponent with respect to an integral length scale L. In other words, both scaling exponents increase during flame development, with the total increase in q_v or q_L being equal to 0.5. The same increasing trend is shown for q_v and q_r in Table 2, with the magnitude of the total increase being sufficiently close to 0.5 at least for the latter scaling exponent (and for q_v if U_T (𝜃) and 〈U_T〉(𝜃_m) are considered).

4 Conclusions

While turbulent consumption velocity U_T is well and unambiguously defined in the simplest case of a statistically planar 1D turbulent reaction wave, the wave development can significantly affect scaling exponents for U_T as a function of the rms turbulent velocity, laminar wave speed, and a ratio of the turbulence and laminar wave length scales. Moreover, the scaling exponents depend on a method used to compare values of U_T, i.e., the scaling exponents found by processing data obtained at the same wave-development time may be substantially different from the scaling exponents found by processing data obtained at the same wave size.