1 Introduction

Exhaust gas emissions in diesel engines nowadays have stringent regulations [1]. One of the methods which can reduce emissions in the engines is multiple-injection. Multiple-injection in diesel engines can be beneficial for exhaust after-treatment, reduction of unburned hydrocarbons at low temperatures combustions, and engine out soot reduction [2,3,4,5].

Studies on the multiple-injection need future investigations to understand better the mechanism behind the emission reduction. For example, for soot reduction, there are different explanations. O’Connor and Musculus in their review paper [2] categorized these explanations into three main categories, including enhanced mixing effect [6,7,8,9], increase temperature effect [10,11,12,13] and injection duration effect [14,15,16,17].

After the fuel is injected into the engine, it vaporizes rapidly, and after a short distance from the injector, the two-phase spray converts to a single phase gas jet [18, 19]. The vaporized fuel mixes with the air. Entrainment, which is the influx of ambient air into the jet can be increased by using different injection strategies. More entrainment causes better mixing of the injected fuel and ambient air. The soot forms in regions with high local mixture fraction. By better mixing, the fuel rich zones can be avoided.

In modern engines, combustion occurs mainly after the end of injection [18]. Based on this reason, in this work, the focus is on the improvement of mixing after the end of the injection. Han et al. in their experiment showed that while due to heat release in reacting jets, the magnitude of entrainment to the reacting jets is less than that to non-reacting jets, the variation of the entrainment along the jet streamline direction is, however, similar to non-reacting jets up to about 40 jet diameters downstream [20]. In this work, the focus is on the mixing improvement and for simplification, a non-reacting jet is studied.

In the study of injection strategies, the limits in engines must be considered. For example, modern common rail injection systems can achieve 1 ms dwell time between two injections [2, 21]. Even by considering these limits, many injection strategies can be designed. To be able to study the effect of each designing parameter, the other parameters must be kept constant. The load is assumed to be constant here, which means that the total amount of injected fuel is the same. The effect of the time duration between the first and the second injections are studied.

In this study the key questions are:(1) How much is mixing improved by splitting a single injection into two smaller injections? (2) By having a fixed total injection duration and a constant interval duration, when should the splitting take place to have less fuel-rich zones after the end of injections? (3) What is the fluid mechanic mechanism which potentially causes a better mixing of injected fuel and ambient air in multiple injections? (4) How does penetration length change in multiple-injection?

2 Case Specification and Numerical Method

As a baseline case for the validation of the numerical method and the solver, we have chosen the study of Hu, et al. [18]. They simulated a high-pressure single injection gas jet through a 1.35 mm diameter nozzle into the ambient air at atmospheric pressure and compared the results with an available experiment [22, 23]. In these experiments, the gas was injected for 4 ms and the mean axial velocity was measured along the centerline during and after the injection. The experiments reported an ensemble-average of velocity that was calculated from an ensemble of 100-500 measurements at each condition. The nearest data point that was measured in the experiments was at 2.9 mm from the nozzle. In the simulations, the inflowing mass flow rate was selected to match up the mean velocity at 2.9 mm. This gives a velocity of 90 m/s at the nozzle exit.

The computational domain is a cylinder with a diameter of 50D and a length of 100D, where D= 1.35 mm is the nozzle diameter (Fig. 1a). The nozzle is placed in the center of the domain base. A cylindrical O-grid mesh is used, which consists of 2.3 million cells (Fig. 1b). The grids are refined toward the nozzle exit and across the jet axis such that 80% of computational cells are located within the refinement cylinder 10D× 25D.

Fig. 1
figure 1

a Computational domain. Diameter= 50D and lenght= 100D, where D = 1.35 mm is the nozzle diameter. The length of axuluary pipe is 30D; b The grid near the nozzle. The red and blue surfaces are iso-countours of mixture fraction in the first injection and second injections, respectively

Full size image

It is known that the modeling of turbulent inlet velocity boundary conditions in LES requires an extra care. For example, treating a turbulent inlet velocity boundary condition with only imposing white noise fluctuations is inappropriate as such noises will quickly dissipate within a few nozzle diameter and will not develop into large-scale fluctuations. In this work to achieve an appropriate inlet boundary condition for the injector, in addition to the main domain, a long axillary pipe is simulated. Simulation results at the outlet of such axillary pipe, which are time-variant, are used as the inlet boundary condition for the main domain calculations.

OpenFOAM is used for numerical solution of spatially filtered Navier-Stokes (N-S) Equations for incompressible flow. Both temporal and spatial terms are discretized using implicit second-order schemes. Dynamic k-equation is used as the sub-grid scale (SGS) model in the LES. In addition to the N-S equations and the SGS k-equation, a mixture fraction transport equation is solved to trace injected gas.

$$ \frac{\partial\overline\rho{\tilde Z}}{\partial t}+\frac{\partial \overline{\rho} \tilde u_{j} \tilde Z}{\partial x_{j}}-\frac{\partial}{\partial x_{j}}\left[ {\overline{\rho D} \frac{\partial \tilde Z}{\partial x_{j}}+{\Phi}_{Z}^{sgs}}\right]= 0 $$
(1)

where Z is the mixture of the the injected gas, u is velocity, \(\phantom {\dot {i}\!}\rho \) is density and \(\phantom {\dot {i}\!}{\Phi }_{Z}^{sgs}\) is the subgrid mass flux. This equation enables us to study the mixing of the injected gas with the ambient air. Both temporal and spatial terms are discretized using implicit second-order schemes.

3 Results and Discussion

The validation of the simulation is done in two steps. Firstly, to check the grid independence, a steady jet flow is simulated and the result is compared with available experiments. Secondly, the same jet but with short single injection is simulated and the accuracy of the simulation of the transient jet is investigated. Once the accuracy of the numerical method and the computational setting are confirmed, the same settings are used to investigate multiple-injection cases.

3.1 Steady jet simulation for grid study

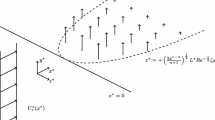
To examine the grid independence, a steady jet flow is simulated and the results are compared with the available experiment. To achieve the quasi-steady state in the simulation, the steady jet flow is simulated for 15 ms. The first 3 ms is considered as transient jet flow and after that time-averaged axial velocity along the centerline is calculated. The jet velocity at the nozzle exit in this simulation is set to 90 m/s. According to the literature [24], the time-averaged axial velocity along the axis of a steady jet is a linear function of the inverse of axial position:

$$ \frac{U_{0}(x)}{U_{j}}=\frac{B}{(x-x_{0})/D} $$
(2)

where x is the axial distance from the jet outlet, \(\phantom {\dot {i}\!}x_{0} \) is a virtual origin, \(\phantom {\dot {i}\!}U_{0}(x)\) is the average axial velocity at the center of the jet at x, \(\phantom {\dot {i}\!}U_{j}\) is velocity at x = 0, D is the nozzle diameter and B is an empirical constant which is independent of Reynolds number [25]. It must be mentioned that this equation is not valid in the initial development region of the jet.

We used different grids and calculated the B value. The topologies of the grids are the same, but the cell sizes are changed. Five different grids are employed, with the normalized averaged size of cells at the nozzle exit (Δh∗) ranging from 0.04 to 0.08. The baseline grid consists of 2.3 million cells and \(\phantom {\dot {i}\!}{\Delta } h^{*}= 0.046\) In Fig. 2 the results from different grids are compared to the experimental data of Hussein et al. [24]. The measured B in the experiment is 5.8 and with the baseline grid, the difference between the calculated B in CFD and experiment is 3.6%.

Fig. 2
figure 2

Calculated B factor (See Eq. 2). Δh∗ = Δh/D where Δh is the size of the cell in the injector outlet and D is the dimeter of the injector. By reducing the size of cells, the calculated B in LES converges to the measured value in the expriment in Ref. [24]

Full size image

In addition to axial profile the radial profile of the mean axial velocity is investigated. In a turbulent round jet, the radial profiles of the mean axial velocity in different axial positions beyond the developing region are self-similar [24, 25]. In other words, profiles of \(\phantom {\dot {i}\!}U(x,r)/U_{0}(x)\) as a function of \(\phantom {\dot {i}\!}r/(r_{1/2}(x))\) in different axial positions collapse into a single profile. \(\phantom {\dot {i}\!}U(x,r)\) and \(\phantom {\dot {i}\!}U_{0}(x)\) are axial velocity at \(\phantom {\dot {i}\!}(x,r)\) and \(\phantom {\dot {i}\!}(x,0)\) respectively, r is the radial distance from the axis, and r1/2(x) is the jet’s half-width radius, defined as:

$$ U(x,r_{1/2})=\frac{1}{2}U_{0}(x) $$
(3)

In Fig. 3 the radial profiles of the steady jet flow at different axial positions are compared with the results from Ref. [25]. As can be seen in this figure, all radial profiles are collapsed into a single curve, which indicates a self-similar velocity distribution across the jet axis.

Fig. 3
figure 3

Self-similarity of radial profiles of mean axial velocity in the steady jet at different downstream locations. The results are compared to the curve from Ref. [25]

Full size image

3.2 Validation of transient jet simulation

The transient jet flow case studied her is taken from the expriment [22] and simulations [18]. The jet has the same configuration as the steady flow discussed in Section 3.1, but a shorter injection duration. The inlet gas has a top-hat time profile, with an inlet velocity of 90 m/s for \(\phantom {\dot {i}\!}0<t<4\ ms\). The baseline grid is used in the present transient jet simulation. Each transient case can be divided into three phases, ramp up, quasi-steady, and ramp down periods. To be able to study multiple-injection, the simulation must be able to replicate these three phases. Figure 4 shows the ensemble-averaged centerline velocity at various downstream locations during and after the injection. Figure 4a shows the measurement in the experiments and Fig. 4b shows the results of Hu et al. [18], and Fig. 4c shows the present prediction. In the experiments, the ensemble-averaged velocity over 100-500 injection events is reported. In current work, to calculate the ensemble-averaged values, each calculation was repeated 20 times with a different instance of the inlet velocity boundary conditions generated from the axillary pipe, as discussed early. Figure 5 shows the distribution of the mass fraction of injected gas at \(\phantom {\dot {i}\!}t = 1.2\ ms\). While the large-scale eddies, can be observed in the single realization instantaneous field (Fig. 5a), the ensemble-average over 20 realizations (Fig. 5b) shows a symmetric distribution of variables and a smoother field.

As can be seen, the current results agree well with the experimental results. The velocity magnitude in the quasi-steady phase has been well predicted, with some minor under-predictions at a few locations, e.g., at \(\phantom {\dot {i}\!}x/D = 24.7\). These deviations are most likely due to the inconsistency in the injector boundary condition. It is noted that the injector used in the experiment had a complex geometry, whereas we used a simplified tube as a nozzle in these simulations. Nonetheless, the time history of the variations in the ramp up \(\phantom {\dot {i}\!}(0<t<2)\), quasi-steady \(\phantom {\dot {i}\!}(2<t<4)\) and ramp down \(\phantom {\dot {i}\!}(4<t<6)\) stages are captured reasonably well. This can be confirmed once we compare our results with the simulation results from Hu et al. [18] for the same conditions.

Fig. 4
figure 4

Ensemble-averaged centerline velocity at various downstream locations (x/D = 2.2,5.9,9.6,13.4,17.2,21.0,24.7) a Experiment [22], b LES (Hu et al. [18]), c LES (present study)

Full size image
Fig. 5
figure 5

Mass fraction of the injected gas at t = 1.2 ms. a LES instantaneous field; b Ensemble-averaged over 20 LES realizations

Full size image

As can be seen, the current results agree well with the experimental results. The velocity magnitude in the quasi-steady phase has been well predicted, with some minor under-predictions at a few locations, e.g., at \(\phantom {\dot {i}\!}x/D = 24.7\). These deviations are most likely due to the inconsistency in the injector boundary condition. It is noted that the injector used in the experiment had a complex geometry, whereas we used a simplified tube as a nozzle in these simulations. Nonetheless, the time history of the variations in the ramp up \(\phantom {\dot {i}\!}(0<t<2)\), quasi-steady \(\phantom {\dot {i}\!}(2<t<4)\) and ramp down \(\phantom {\dot {i}\!}(4<t<6)\) stages are captured reasonably well. This can be confirmed once we compare our results with the simulation results from Hu et al. [18] for the same conditions.

3.3 Specification of multiple-injection strategies

To define realistic injection strategies, real engine experiments in Ref. [4, 26] are considered. In Ref. [4], a single injection is split into a main 970 μs injection plus a short \(\phantom {\dot {i}\!}200\ \mu s\) post-injection. In Ref. [4], the actual start of the main and post-injections are -5 and 3 ATDC (after top-dead-center) respectively, and the engine speed is 1200 rpm. Based on this timing, cases 1-4 are defined in Table 1. In this table, cases a and b are the ones used in previous sections for the grid study and validation of simulation using the available experimental measurements. Case 1 is a single injection which is used as the baseline case, and cases 2 to 4 are double-injection. The mixing in different double-injection strategies will be compared with the single injection (case 1). In all four cases, the total time in which the air is injecting is constant. It means that the mass of injected air in all four cases are the same. The interval between two injections in double-injection cases is also the same. The only difference is how the single injection is split. Case 2 is a small pre-injection plus the main injection, case 3 consists of two equal injections and case 4 is the main injection plus a short post-injection. The main question is which strategy improves the mixing the most and how penetration length changes in different cases.

Table 1 Injection strategies (Cases a and b are only used for the grid study and validation of the simulation, using the availabe measurements)
Full size table

3.4 Mixture fraction distribution

In this section, we analyze the mixture fraction distribution to study the mixing performance of each strategy. At first, we show the probability density function (PDF) of mixture fraction after the end of injection, as an indication of the mixing performance of different splitting strategies. We shall further analyze the results by providing more results to explain the effects of injection duration and dwell time in each case.

Figure 6 is the histogram of the mixture fraction distribution at 0.5 ms after the end of the second injection. This figure is essentially a PDF distribution of the equivalence ratio in the domain. The rationale behind selecting 0.5 ms after the end of the second injection is the fact that modern direct injection systems are designed in such a way that main heat release from combustion occurs at least a few crank angles after the end of injection [18]. Therefore, the results of mixture fraction distribution after 0.5 ms from the end of the second injection in our study can potentially indicate the performance of different split injection strategies in real engines. In Fig. 6, the horizontal axis is the mixture fraction, and the vertical axis is the total mass of the region of the domain with a specific mixture fraction. As it can be seen in this figure, the results in cases 1, 2 and 3 are virtually the same, whereas the results in case 4 is substantially different in the fuel-lean side of the diagram, e.g., mixture fraction \(\phantom {\dot {i}\!}<\) 0.15. This means that after 0.5 ms from the end of the second injection, the splitting strategy of case 4 results a better mixing between injected mass and ambient air.

Fig. 6
figure 6

PDF of mixture fraction, 0.5 ms after the end of injection. (t = 1.7 ms for case 1 and t = 1.85 ms for case 2, 3 and 4)

Full size image

We further examine the local distribution of the mixture fraction in the time history of the shown snapshot results in Fig. 7. The results in this figure are from an ensemble-averaged of 20 realizations of flow fields. In all figures, an arbitrary iso-countor of \(\phantom {\dot {i}\!}Z = 0.15\) is also shown to better distinguish between regions with high and low levels of injected mass. The start of the second injection and the interaction between two injections are visible at \(\phantom {\dot {i}\!}t=\)0.5, 0.9 and 1.3 ms in cases 2, 3 and 4, respectively. Of particular interest, in this figure, is the results after \(\phantom {\dot {i}\!}t=\)1.35 ms, which is the end of the second injection for all double injection cases. These results are consistent with those of Fig. 6 and confirm the superior effect of a post-injection in case 4 on the mixing quality after the end of injection. For example, at \(\phantom {\dot {i}\!}t=\)1.5 and 1.7 ms, the iso-countor in case 4 has been stretched along the axial direction and it is slim and longer than those of the other cases. It can be seen that at \(\phantom {\dot {i}\!}t=\)1.9 ms the structure of the high-mixture-fraction zone in case 4 is quite different from that of the other cases. Interestingly, the region with a mixture fraction larger than 0.15 in case 4 has essentially vanished at \(\phantom {\dot {i}\!}t=\)2.1 ms, despite the fact that the total injected mass for all cases was the same and all cases had the same dwell timing. Results show that the onset of split injection plays an important role in the mixture formation processes, and a small post injection is much more efficient than a pre-injection or a long second injection.

Fig. 7
figure 7

Distribution of ensemble-average of mixture fraction for double injection cases. The white line on each plot is the iso-countour of Z = 0.15. a case 2; b case 3; c case 4

Full size image

To quantify the role of split injection in each injection strategy, we provide a plot of the variation of the mass in the system with a mixture fraction larger than 0.15 as a function of time in Fig. 8. This mass, \(\phantom {\dot {i}\!}m_{Z>0.15}\), is calculated based on Eq. 4 as below:

$$ m_{Z>0.15}={\int}_{Z>0.15}\rho Z dv $$
(4)

where \(\phantom {\dot {i}\!}\rho \) is the density, dv is the volume of the element, and the integral is calculated over the entire domain with mixture fraction larger than 0.15 (the region inside the white line boundary in Fig. 7). There are three major observations in this plot: (i) as long as the mass is injected the \(\phantom {\dot {i}\!}m_{Z>0.15}\) is increased, and during the injection pausing in double-injection cases (0.2 < t < 0.4 ms in case 2, \(\phantom {\dot {i}\!}0.6<t<0.8\ ms\) in case 3 and \(\phantom {\dot {i}\!}1<t<1.2\ ms\) in case 4) it decreases. As it can be seen the decrease rate of the mass during the dwell time in cases 3 and 4 are much higher than case 2; (ii) the peak of \(\phantom {\dot {i}\!}m_{Z>0.15}\) for cases 3 and 4 is smaller than cases 1 and 2. This implies that a pre-injection is not as effective as an injection splitting with a late dwell timing in reducing the mass of the fuel-rich regions; (iii) after the end of the second injection, the slope of decreasing of the \(\phantom {\dot {i}\!}m_{Z>0.15}\) in case 4 is higher than other cases. This is consistent with the results in Figs. 6 and 7, and confirms the above discussed superior effects of a post-injection.

Fig. 8
figure 8

The mass of high-mixture-fraction zone (4) as a function of time. The vertical axis is normalized by the total mass of injection, which is a constant value. In this plot Z = 0.15 is considered as a threshold for calculation of the high-mixture-fraction zone

Full size image

3.5 The underlying mechanisms

In this section, we explain the underlying mechanism of the observations made in the previous section. We distinguish between two different mechanisms ”tail-entrainment mechanism” and ”area/volume ratio mechanism” and describe the role of each of them.

3.5.1 Tail-entrainment mechanism

Figure 9a and b show the snapshots of mixture fraction distribution in case 4 at the end of first injection (t = 1 ms), and during the interval (at t = 1.1 ms) respectively. The solid white line is the iso-countor line of mixture fraction corresponding to 0.05, which is about the stoichiometric mixture fraction of hydrocarbon fuel-air mixture. The shown vectors are velocity vectors in ambient air. The influx of ambient air vectors toward the fuel rich region after the end of the first injection can be seen in Fig. 9b. During the interval, in the absence of injection and with this amount of influx of ambient air, the mixture fraction of injected air decreases drastically. Hu et al. [18] also observed this mechanism for a single injection and explained that in the ramp-down phase of a single injection the air entrainment into the jet increases.

In double injection, the tail-entrainment mechanism happens twice, once at the end of each injection. This mechanism explains the observation (i) and (ii) in cases 3 and 4. The high entrainment from the tail of the first injection during the interval reduces the mass of high-mixture-reaction zone. However, in case 4 which has a very short first injection, the injection ends at the beginning of ramp-up phase of the injection. (See Fig. 4c considering that the first injection in case 2 ends at \(\phantom {\dot {i}\!}t = 0.2\ ms\).) Therefore, for this very short injection, the tail-entrainment mechanism is weak and as can be seen in Fig. 8 the reduction of mass of high-mixture-fraction zone in case 2 during \(\phantom {\dot {i}\!}0.2<t<0.4\ ms\) is lower than that in case 3 and 4 during \(\phantom {\dot {i}\!}0.6<t<0.8ms\) and \(\phantom {\dot {i}\!}1<t<1.2ms\), respectively.

Fig. 9
figure 9

Snapshot of distribution of mixture fraction of injected gas in case 4. Ensemble-average of 20 LES realizations. The solid lines are the iso-countor line of mixture fraction of 0.05. The vectors are velocity vectors of ambient air. a t = 1 ms; b t = 1.1 ms

Full size image

3.5.2 Area/volume ratio effect

When a jet is split into two smaller jets, the area of the jet increases. This increase of the area can be identified by comparing the results in Fig. 7 at \(\phantom {\dot {i}\!}t = 0.9\ ms\) for case 3 and those of other cases at the same instant. In addition to this point, the split of an injection makes the jet narrower and this also increases the area/volume ratio of the jet, for instance, at \(\phantom {\dot {i}\!}t = 1.1\ ms\) for case 3 or \(\phantom {\dot {i}\!}t = 1.5\ ms\) for case 4. This increase in the area of the jet leads to a better mixing with ambient air as we call this effects the “area/volume ratio mechanism”.

Figure 10 shows the ratio of the area of the high-mixture-fraction zone to its volume, by considering \(\phantom {\dot {i}\!}Z = 0.15\) as the boundary of this zone. It can be seen the ratio, during \(\phantom {\dot {i}\!}0.2<t<0.7\ ms\) in case 2, \(\phantom {\dot {i}\!}0.7<t<1.5\ ms\) in case 3, and \(\phantom {\dot {i}\!}t>1.2\ ms\) in case 4 is higher than that of the single injection case. When the second injection penetrates into the first injection and they collapses into a single injection the “area/volume ratio” effects vanishes. In case 4, the splitting has occurred in the late part of the injection and the effect of this mechanism after the end of injection explains the observation (iii). The higher area/volume ratio after the end of injection in case 4 leads to a high reduction of mass of high-mixture-fraction zone in case 4 in comparison to the other cases in Fig. 8, after the end of injections.

Fig. 10
figure 10

Ratio of area of the high-mixture-fraction zone to its volume. Z = 0.15 is considered as the boundary of the this zone

Full size image

3.6 Penetration

Figure 11 shows the penetration length in different cases. Here, \(\phantom {\dot {i}\!}Z = 0.01\) is considered as a threshold for mixture fraction at the outer boundary of the jet. The time history of the penetration length for all cases are almost the same as a single injection case, indicating that a split injection does not alert the overall penetration length.

Fig. 11
figure 11

Penetration length in different cases

Full size image

4 Conclusion

A large-eddy simulation was performed for four injection strategies including one single injection and three multiple injections. The total duration of injections and interval durations in multiple strategies were kept the same, and the effect of splitting timing was studied. The result shows that enhancement of the influx of the ambient air at the end of each injection improves the mixing between the injected mass and the ambient gasses. In a double injection strategy, this “tail-entrainment mechanism” at the end of the first injection increases mixing and reduces the mass of high-mixture-fraction zone. In cases with a very short first injection, this effect is much weaker.

In addition to this mechanism, splitting a single injection into two smaller one increases the surrounding area of the jet. This “area/volume ratio mechanism” can potentially improve the mixing quality between the jet and the ambient. However, results show that this mechanism vanishes, rapidly. Therefore, in order to obtain a sensible mixing enhancement at the end of injection, the splitting timing should be retarded toward the end of the injection period. Consideration of these two mechanisms is of great importance for designing an effective injection strategy in advanced combustion engines where it is desirable to obtain a combustion phasing after the end of fuel injection.