1 Introduction

Artificial intelligence has achieved excellent breakthroughs in the fields of intelligent control, target detection, driverless vehicles, and fault diagnosis in recent years [1,2,3,4]. The rapid development of deep learning technology benefits mainly from rich training data, innovative algorithms, and the improved performance of computing equipment. Among these factors, the richness of training data can directly affect the performance of deep learning models. However, in some industries, like medical and financial institutions, data barriers can be formed because data privacy makes it difficult for multiple research institutions to conduct collaborative learning through data sharing. Federated learning (FL) is a new privacy-protected distributed framework that allows a cluster of devices (local clients) to collaboratively learn a global shared model coordinated by a central server without exposing their private data [5,6,7]. Therefore, the FL framework reduces a substantial amount of the privacy risk and cost associated with conventional centralized training. Recently, this framework has attracted great attention in a variety of industries.

With the extension of the existing research, FL still faces various challenges, among which communication cost is a critical issue [8, 9]. In typical FL, only model parameters, rather than raw data, are transmitted between the client and the cloud server. A modern neural network architecture may have millions of model parameters, resulting in each iterative use requiring a high bandwidth [10]. In addition, FL requires multiple iterations to achieve greater model accuracy, resulting in a higher amount of communication overhead in the whole training process [11]. Finally, the resource-constrained edge devices participating in the training lead to limited bandwidth between clients and the cloud server, particularly during uplink transmission. The communication cost becomes a bottleneck for FL with limited bandwidth. Therefore, improving the efficiency of FL communication is a crucial factor in promoting its development [12].

While FL no longer requires collecting raw data from clients, the privacy implied by the data is not guaranteed [13]. To train the FL model, the client must upload the model parameters or gradients, which are essentially mappings to the raw data under specific rules and contain almost all the data information. Many attack models have demonstrated that data information can be derived from the model parameters or gradients. Such attacks are either disguised as models for training participants or come directly from the server, and the attack models are divided into refactoring attacks [14], inference attacks [15], and eavesdropping attacks [16]. Hence, safeguarding each client in FL from such advanced privacy attacks without a completely trusted server presents a significant challenge that requires immediate attention [8].

A wide range of studies have been conducted on FL communication efficiency and privacy protection. Among them, the methods for improving communication efficiency include mainly the quantization method [17], compression method [11], and communication delay method [18]. The privacy protection methods include mainly differential privacy (DP) [19, 20], secure multiparty computation (SMC) [21] and homomorphic encryption (HE) [22, 23]. However, few studies consider both communication efficiency and privacy protection in FL. In this paper, we propose a novel FL framework with communication-efficient and privacy-preserving (FLCP) that reduces the required level of communication overhead and provides a formal guarantee of privacy without assuming a fully trusted server. A novel adaptive weight compression algorithm is proposed to improve communication efficiency. The typical gradient compression algorithm may affect the training model’s convergence rate and accuracy. In addition, since the data distribution of FL is non-IID and unbalanced, the traditional compression algorithm is unsuitable for the FL setting. Thus, to take full advantage of the performance of the compression algorithm, it is necessary to set a reasonable compression rate [24]. Based on the fixed compression rate algorithm, the compression rate is adaptively adjusted by our method in the dynamic perception model’s training stage, so that each client enjoys a unique compression rate. We also introduce a communication delay method, by which communication efficiency is improved by increasing the degree of local computation to reduce the degree of communication frequency [18, 25]. This is the first study to describe a compression scheme applied to FL with consideration of actual FL characteristics. To protect clients’ privacy without a completely trusted server, we design a lightweight encryption protocol that incorporates local DP to provide provable privacy protection while maintaining the performance of the training model.

The main contributions of this paper are summarized as follows:

  1. 1)

    We propose a novel FL framework called the FLCP for training on distributed data without a trusted server, with communication efficiency and privacy protection. This method possesses robustness and can tolerate arbitrary clients dropping out during the training process with a negligible loss of accuracy.

  2. 2)

    We develop a novel adaptive weight compression FedAvg algorithm (AWC-FedAvg) aimed at reducing overall communication costs. Specifically, the AWC-FedAvg method adaptively adjusts the compression rate based on the non-IID and unbalanced data distributions in FL.

  3. 3)

    We develop a hybrid protocol that combines lightweight HE and DP to ensure full protection for the model training process and its results. Specifically, our enhanced lightweight HE protocol, with reduced ciphertext operation volume, facilitates the widespread implementation of FL. Additionally, the DP system, based on the Laplace mechanism, preserves the confidentiality of local updates, effectively safeguarding clients’ privacy against adversarial collisions.

  4. 4)

    We conduct an analysis of the FLCP in terms of convergence analysis and privacy guarantees at the theoretical level. Moreover, we evaluate its performance extensively. The results show that compared with the baseline method, the FLCP has superior convergence while maintaining model accuracy, significantly improving training and communication efficiency.

The remainder of this paper is as follows. In Section 2, related works are discussed, and a comprehensive comparison to the existing approaches is conducted. Next, the research background and preliminaries are presented in Section 3. Then, we introduce the FLCP in Section 4. Afterward, a theoretical analysis of the FLCP is conducted in terms of its convergence analysis and privacy guarantees in Section 5. In Section 6, experimental evaluations are performed. Finally, Section 7 concludes the paper.

2 Related work

2.1 Communication efficiency in FL

At present, the training framework for FL is based mainly on the parameter server. Each time a compute node completes an iteration, the generated gradients or model parameters need to be synchronized to the parameter server, which brings about a high level of communication overhead when synchronizing either gradients or model parameters. The solutions for improving the communication efficiency of distributed machine learning include primarily communication delay, compression, and quantization methods. The communication delay method attempts to reduce communication frequency f to improve communication efficiency. Federated averaging (FedAvg) was proposed by McMahan et al. [5] to decrease communication bit-width. In the FedAvg method, instead of communicating with the server after each iteration, the client performs several iterations of stochastic gradient descent (SGD) to compute the updates. The gradient compression algorithm plays a vital role in reducing the communication overhead of FL. Strom et al. [26] first proposed that clients upload only the gradient with a larger absolute value than the fixed threshold in the training process. This method provides a compression rate of as many as 3 orders of magnitude when performing an acoustic modeling task. However, for the threshold, it is not easy to select a suitable value in practice because different model architectures and layers may vary greatly. Later, P. Luo et al. [27] proposed an adaptive gradient compression algorithm. Unlike Strom’s scheme, the adaptive gradient compression algorithm no longer relies on a fixed threshold to select gradients. Instead, the gradients are sorted according to their absolute values, and then an appropriate proportion of the gradients is adaptively selected for uploading in descending order of magnitude. Furthermore, Nori et al. [28] proposed an enhanced FL scheme that jointly and dynamically adjusts the local update frequency and compression rate to minimize the learning error. Y. Mao et al. [29] proposed an efficient communication FL framework with an adaptive quantization gradient (AQG), which adaptively adjusts the quantization level according to the update of local gradients to reduce any unnecessary transmission.

Table 1 Comparison of functionality with existing models
Full size table
Fig. 1
figure 1

System architecture of FL

Full size image

2.2 Privacy protection in FL

In response to the leakage of private data in FL, some privacy protection methods have been proposed, including mainly encryption-based privacy protection methods represented by secure multiparty computing (SMC) and homomorphic encryption (HE) and disturbance-based privacy represented by differential privacy (DP). SMC involves two or more participants holding private data and obtaining the output through joint computation, which meets the security characteristics of correctness, privacy, and fairness. To ensure communication between the device and the cloud server, Keith et al. [32] introduced an SMC protocol based on secret sharing, applicable within the parameter aggregation process of FL. HE schemes can guarantee that specific mathematical operations performed on the ciphertext have the same effect on the plaintext. Moreover, Ma et al. [33] proposed a multikey HE protocol for secure aggregation in FL, ensuring the privacy of shared gradients within an incompletely trusted environment. This method effectively addresses the privacy-security concern without compromising model accuracy. However, since data encryption requires many computing resources, this method is unsuitable for the training of deep learning models in large-scale data environments. Aono et al. [22] proposed encrypting the gradients generated by each client in FL to ensure the local data privacy security of multiple participants in the training. Since the computation amount of gradient encryption is directly related to the amount of training data, this method increases the model training time and degree of computational consumption and does not take the bias term into account. DP technology refers to introducing randomness into the model training process, that is, adding a certain degree of random noise to make the output and actual results have a certain degree of deviation to prevent the attacker from reasoning. Stacey et al. [30] proposed a privacy protection scheme combining DP and SMC for the FL model, protecting data privacy while achieving a high degree of accuracy.

2.3 Function comparison

The functional advantages of the FLCP are analyzed compared to those of the state-of-the-art FL approaches with communication efficiency and privacy preservation, i.e., FL with differential privacy (NbAFL) [19], hybrid approach to privacy protection FL (TP-SMC) [30], robust and communication efficiency FL (RCEFL) [11] and privacy-preserving federated deep learning (PPFDL) [31], as listed in Table 1. Specifically, NBAFL utilizes DP to ensure the confidentiality of each client’s local gradient, but this approach does not guarantee model accuracy, and the default aggregation result is a publicly available parameter. TP-SMC proposes a hybrid security protocol for FL, which combines DP and SMC to provide high-level privacy protection and reduce the amount of injected noise. RCEFL proposes a sparse ternary compression framework that is robust to dropping out and that can improve communication efficiency and support FL environments but does not provide privacy protection. PPFDL additively incorporates HE and Yao’s garbled circuits, ensuring the high level of security of the information related to the client. However, PPFDL neither guarantees the confidentiality of the model parameters in a collusion attack nor provides excellent communication efficiency during the training process. Table 1 illustrates that none of the abovementioned state-of-the-art methods can completely solve the challenges of communication efficiency and privacy protection. Contrastingly, our proposed FLCP mitigates the abovementioned attacks by integrating HE and DP and improves communication efficiency through a compression algorithm.

3 Background and preliminaries

This section first describes the architecture and the threat model of the FLCP system and then discusses the primary cryptographic techniques that constitute the FLCP. Finally, this section illustrates the essential implementation steps of HE and introduces the basic principles and properties of DP.

Table 2 Summary of mathematical symbols
Full size table

3.1 Federated learning system

We consider an FL system consisting of n clients and a cloud server, as shown in Fig. 1. Let \(D_i = \{X_1^i , X_2^i , {...,X}_m^i \}\) denote the local dataset with m data points, held by client \(U_i\), where \(i \in \{ 1,2,...,n\}\). Under the server’s orchestration, the client uses local data to train the shared model \(\theta \) collaboratively. Because of the high amount of latency and privacy issues in the process of transmitting local data points to the central server, FL enables clients to retain data locally while training the model. Specifically, the model parameter \(\theta \) is trained by minimizing the global loss function,

$$\begin{aligned} \underset{\theta }{\min }\ f(\theta ) = \frac{1}{n}\sum \limits _{i = 1}^n {f_i} (\theta ) ~\mathrm{{with }} f_i (\theta ) = \frac{1}{m}\sum \limits _{X \in D{_i} } {l(\theta ,X)}, \end{aligned}$$
(3.1)

where \({l(\theta ,X)}\) denotes the loss function of model \(\theta \) at sampling point X and \(f_i\) is client i’s local empirical risk function. For ease of description, some main notations in this paper are summarized in Table 2.

In FL, a global shared model is collectively learned by n clients that possess different data structures under the central server’s orchestration. The training process of this model generally involves the following four stages: local training, model uploading, model aggregation and model broadcasting. For centralized training, computational costs are the main bottleneck, while communication costs dominate in FL. Since the local dataset is usually very small relative to the entire dataset, and the current smart devices on the edge have high-speed processors, the computing costs are nearly negligible. However, in cloud computing, the communication resources between the client and the server are usually limited, particularly for uplink transmission. Therefore, how to improve communication efficiency becomes the main challenge for FL. To solve this problem, an adaptive compression algorithm is proposed to improve communication efficiency during training. In addition, cryptographic methods are utilized to ensure the privacy of the transmission updates and model accuracy. Ultimately, both communication efficiency and privacy protection are achieved under our proposed scheme.

3.2 Threat model

The proposed scheme assumes that the clients and the cloud server are “honest-but-curious” semitrusted entities. In other words, all entities (clients and servers) faithfully follow the designed training scheme but may attempt to deduce private information from the shared message. Moreover, we also assume that an adversary colludes with the cloud server or clients. This situation means that corrupted participants may disclose sensitive information to other malicious entities. Furthermore, the opponent may also be the passive external aggressor. Although these adversaries can eavesdrop on all shared information during training, they do not actively interrupt the transmission of information or inject false information. Therefore, the security objective of our protocol is to protect clients’ privacy throughout the training process. According to the above privacy threat model, the following confidentiality requirements are developed:

  • Privacy security for local client parameters: An adversary, malicious cloud server or client, can utilize global parameters and shared model updates to recover sensitive client information, such as contribution and membership information. Therefore, the client’s local parameters need to be encrypted before being transmitted to the server to prevent the client’s private information from being leaked.

  • Privacy security for aggregated results: To make the training process non-discriminatory and fair, the reliability of each client ought to be kept confidential and cannot be inferred by other entities in the training process. Moreover, the aggregated result can be considered valuable intellectual property generated from multiple resources, potentially containing proprietary information about certain clients. As a result, the aggregation results are kept confidential from the opponent, except for those clients participating in training.

3.3 Homomorphic encryption

Based on the type and method of the supported mathematical operations, HE schemes can be divided into the following: partially HE algorithms that support a mathematical operation without limiting the number of operations; somewhat HE algorithms that support specific mathematical operations with a limited number of operations; and fully HE algorithms that support unlimited types of mathematical operations with unlimited operations. This research adopts the Paillier HE algorithm [34,35,36], which includes the following four steps:

1) KeyGen()\( \rightarrow \)(pk, sk): Randomly select two large prime numbers b and d randomly, satisfying \(gcd(pq,(b - 1)(d - 1)) = 1\). Calculate \(N = bd\), \(\lambda = lcm(b - 1,d - 1)\). Randomly select \(g \in Z_{N{^2}}^{*}\), then public key \(pk = (N,g)\), secret key \(sk = (\lambda )\).

2) Encryption(pk, m) \(\rightarrow \) C: Enter the public key pk and plaintext m. Randomly select \(r \in Z_{N{^2}}^{*}\), ciphertext \(C = g{^m} r{^N} (mod\, N{^2})\).

3) Decryption(sk, C) \(\rightarrow \) m: Enter the secret key sk and ciphertext information C, where \(L(x) = \frac{{x - 1}}{N}\). Calculate plaintext \(m = \frac{{L(C{^\lambda } (\bmod \, N{^2}))}}{{L(g{^\lambda } (mod\, N{^2}))}}\bmod N\).

4) Verification algorithm:

$$\begin{aligned} \begin{aligned}&E(m{_1}) \times E(m{_2})\\&= (g^{m{_1}} r_{1}^{N} (mod N{^2})) \times (g^{m{_2}} r_{2}^{N} (mod N{^2}))\\&= g^{m_{1} + m_{2}} {(r_{1} + r_{2})^{N}}(mod N^{2})\\&= E(m_{1} + m_{2}). \end{aligned} \end{aligned}$$
(3.2)

3.4 Differential privacy

Differential privacy (DP) is a cryptographic mechanism with powerful mathematical underpinnings, ensuring that the overall statistical information remains the same, regardless of changes in individual tuples. In 2008, Dwork et al. [37] proposed DP protection by injecting noise to make the query results of the two datasets undistinguishable.

Definition 1

A randomized query function F satisfies the \(\varepsilon \)-differential if for any adjacent databases D and \(\bar{D}\), and any \(S \subset Range(F)\),

$$\begin{aligned} |{\log \frac{{P[F(D) = S]}}{{P[F(\bar{D}) = S]}}} |\le \varepsilon . \end{aligned}$$
(3.3)

Parameter \(\varepsilon \) refers to the privacy budget, which indicates the current level of privacy protection. Generally, a smaller \(\varepsilon \) value provides a higher privacy protection level, but the training model under such a condition is less accurate.

Given the above DP mechanism, choosing a suitable noise level is a meaningful research issue that affects the client’s privacy security and the model’s convergence in the FL process.

4 Proposed FLCP

This section presents the FLCP to address communication overhead and privacy disclosure issues in FL. First, we outline how to use the AWC-FedAvg method to reduce the communication cost of the training model. Next, a hybrid approach is developed to protect the privacy of each client within the system. Finally, an overall algorithm including all of these components is proposed, and the system architecture of the FLCP is presented.

4.1 Improving communication efficiency with the AWC-FedAvg method

The FedAvg-based weight compression algorithm is proposed to reduce the amount of single communication traffic and communication time in this paper. Because the fixed compression rate adopted in the traditional compression algorithm affects the convergence rate and model accuracy, and the training data of FL are non-IID and unbalanced, this algorithm is not suitable for the FL setting. Therefore, it is necessary to set a reasonable compression rate to fully utilize the performance of the compression algorithm. The adaptive weight compression FedAvg (AWC-FedAvg) method is based on the Top-K compression algorithm [27], which adaptively adjusts the compression rate in the dynamic perception model’s training stage. The algorithm can appropriately increase or reduce the number of local update parameters according to the model’s training conditions and improve training efficiency while ensuring the training accuracy of the neural network model. Figure 2 illustrates the overall flow of the AWC-FedAvg algorithm, of which there are four fundamental stages: local update, compression weight, server aggregation update, and feedback regulation.

Fig. 2
figure 2

The overall flow of the AWC-FedAvg algorithm

Full size image

1) Local update: Once the cloud server initializes the model parameters, it randomly selects a set of r clients \(N_t\) to broadcast the model parameters to the local client. Then, the selected clients perform several local iterations and send the local update results to the cloud server. Specifically, let \(\theta _i^{(t,c)}\) be client i’s model at the c-th local iteration of the t-th round. In each local iteration \(c=\) 0,\(\ldots \),\(\lambda \)-1, client i updates the model by

$$\begin{aligned} \theta _i^{(t,c + 1)}\mathrm{{ = }}\theta _i^{t,c}\mathrm{{ - }}\eta g(\theta _i^{t,c}), \end{aligned}$$
(4.1)

where \(g(\theta _i^{t,c}) = \frac{1}{B}\sum \nolimits _{X \in D{_i}} \nabla l(\theta _i^{t,c},X )\) represents the mini-batch SGD computed on the basis of a batch of B sampling points \(X_i\) of the local dataset \(D_{i}\).

2) Compression weight: After several local SGD updates, the weight is compressed before uploading to the server. In this paper, the compression algorithm developed by P. Luo et al. [27] is improved, so the transmission data is decreased through transmitting Top-K weight parameters with adaptive compression rate, expressed as

$$\begin{aligned} \theta _{i}^{*} = To{p_{p }}(sort(\{ |{\theta _{1} } |,|{\theta _{2} } |,...,|{\theta _{n} } |\} )), \end{aligned}$$
(4.2)

where \(|{\theta _{n} } |\) is the absolute value of the weight, arranged in descending order. \({Top}_{p }\) chooses the weight of the largest p, which denotes the selection operator. p is the weight’s compression rate, which is given by

$$\begin{aligned} p = \frac{{size[compressed(\theta )]}}{{size[\theta ]}} \times 100\%, \end{aligned}$$
(4.3)

where \({size[compressed(\theta )]}\) represents the size of compressed model parameters, and \({size[\theta ]}\) represents the size of global model parameters. This method solves the problem that the weight is too small to be updated when the threshold is used as the cut-off point. In order to make full use of all the parameters of the iteration, AWC-FedAvg employs the residual accumulation method to accumulate small weights so that it can synchronize with the cloud server at a certain future moment without losing the model accuracy. The residual term is updated after each communication round by

$$\begin{aligned} R_{\tau } = \sum \nolimits _{t = 1}^{\tau } {(\theta _{i} - \theta _{i}^{*} )} = R_{\tau - 1} + \theta _{i} - \theta _{i}^{*} , \end{aligned}$$
(4.4)

where \(R_{\tau }\) represents the residual term. Eventually, these weights become sufficiently large to transmit.

Algorithm 1
figure g

Adaptive adjustment of compression rate.

Full size image

3) Server aggregate update: The client compresses its local model parameters and uploads them to the cloud server. The global shared model is aggregated by

$$\begin{aligned} \varDelta \theta \leftarrow \frac{1}{{|{N_{t} } |}}\sum \nolimits _{i \in N{_t} } {\theta _{i}^{*} }. \end{aligned}$$
(4.5)

After the cloud server updates the global model by aggregating local parameters, it broadcasts the global shared model to the client.

4) Feedback regulation: As a critical step in the algorithm, feedback regulation refers to adaptively adjusting the compression rate of the present iteration based on the accumulated information. Algorithm 1 demonstrates the flow of the adaptive adjustment compression rate in which \(p_{\min } \) is the minimum compression rate, \(p_{\max } \) represents the maximum compression rate, and \(\delta \) denotes the accuracy deviation. The weight compression algorithm is designed with the sigmoid function, and its compression rate update is expressed as

$$\begin{aligned} p \leftarrow p_{\max } - \frac{{2(p_{\max } - p_{\min } )}}{{1 + e^{|\mu |* \delta } }}, \end{aligned}$$
(4.6)

where \(\mu \) represents the change in accuracy. Since the focus only lies on the trend of accuracy change, instead of the positive and negative fluctuations of accuracy change, the compression algorithm takes the absolute value of the accuracy change. The deviation of the accuracy change is denoted as \(\delta \). It is a certain constant and is employed to control the sensitivity of the compression rate variation. Specifically, the larger \(\delta \) makes the compression rate become more sensitive to the trend of accuracy change and the compression rate change become faster.

Finally, the client updates the compression rate p through feedback regulation, and waits to enter the next cycle. The details are formalized in Algorithm 2. The proposed method’s strength lies in adaptively adjusting the compression rate of each iteration through the model performance. This algorithm is applied to each client. Based on the data distribution of different clients, the client can enjoy a specific compression rate, which makes the training convergence faster and the convergence accuracy higher.

Algorithm 2
figure h

Adaptive Weight Compression FedAvg (AWC-FedAvg).

Full size image

4.2 Improving security performance with the FLCP

4.2.1 Preventing privacy leakage with differential privacy

The above approach to reducing communication overhead can effectively prevent the direct leakage of client information by saving the raw data locally. However, this approach cannot prevent more advanced attacks such as [15] and [38], which infer sensitive information from the local dataset by eavesdropping on the message traffic between the client and the server. According to the proposed threat model, the client and the server are semi-trusted “honest-but-curious” entities, and malicious adversaries outside the system may collude with the honest client to eavesdrop on the sent model parameters. These attackers can receive the latest global shared model \(\varDelta \theta \) that the cloud server sends to the client and the local model \(\theta _{i}^{*} \) that the client sends to the cloud server, which contain private information from the client’s dataset. Our security goal is to protect against the disclosure of these two types of private information.

Within our setting, a straightforward approach is the use of the Laplace mechanism. Specifically, each client \(i \in N_{t}\) adds proper Laplace noise into the local model parameters before uploading the information, and the local model update is shown in (4.7). Thus, in this case, the adversary does not acquire private information about the individual sample in \(D_t\) based on the obtained model parameters.

$$\begin{aligned} \bar{\theta }_i^ * \leftarrow \theta _{i}^{*} + Lap(\frac{{\varDelta f}}{ \varepsilon }). \end{aligned}$$
(4.7)

Here, \(\varDelta f\) denotes global sensitivity, expressed as the maximum value of \({|{f(D) - f(\bar{D})} |_1}\) for adjacent datasets D and \(\bar{D}\). \(Lap(\frac{{\varDelta f}}{ \varepsilon })\) is the random variable sampled from the Laplace distribution that satisfies \(Pr[Lap(\frac{{\varDelta f}}{\varepsilon }) = x] = \frac{\varepsilon }{{2\varDelta f}}\, e{^{\frac{{ - |x |\varepsilon }}{{\varDelta f}}}} \) [39]. In our scheme, function f calculates each client’s weight during one epoch.

4.2.2 Secure aggregation scheme

Although the Laplace mechanism can be used to implement DP, the model parameters uploaded in each iteration are plaintext and are, thus, still exposed to the adversary, resulting in the disclosure of private information. In fact, the server merely requires that the average of the local model be obtained. Therefore, the privacy leakage of the client can be reduced by concealing the client’s local model and limiting the server to merely obtaining the aggregation results of the encrypted local models without affecting the training process. In brief, this approach can be implemented through a secure aggregation scheme, in which the server merely obtains the aggregation results of the encrypted local model without knowing the local model of each client. Thus, the FL privacy protection communication scheme proposed in [22] is adopted to establish different TLS/SSL secure channels between the client and the server. In addition, a lightweight encryption protocol is developed based on HE, which contributes to alleviating the high levels of calculation and communication overhead needed for all communication rounds.

In our setup, the secure aggregation scheme hides clients’ individual information, restores the sum of clients’ individual information in each round, and keeps clients’ communication costs low [25]. Therefore, the proposed secure aggregation scheme consists of the following main steps:

1) Initialization: Considering the security parameter \(\rho \), the secret key sk is generated and allocated to each client, which includes two large prime numbers b, d (\(|b |= |d |\mathrm{{ = }}\rho \)). The public parameter is \(N=bd\).

2) Encryption phase: Subsequently, the local weights \(\theta _{i} \) are encrypted with secret key b, d, that is, calculate \({\theta _{i,b}} \equiv {\theta _i}\,\bmod \,{\hspace{0.55542pt}} \,b\), \({\theta _{i,d}} \equiv {\theta _i}\,\bmod \,{\hspace{0.55542pt}} d\). Since we have \(1 \equiv \mathrm{{ }}{b^{ - 1}}b\,\bmod \,{\hspace{0.55542pt}} \,d\), \(1 \equiv \mathrm{{ }}{d^{ - 1}}d\,\bmod \,{\hspace{0.55542pt}} \,b\), the local client computes the ciphertext like this:

$$\begin{aligned} {C_i} = \mathrm{{ }}{d^{ - 1}}d\theta _{i,b}^b + \mathrm{{ }}{b^{ - 1}}b\theta _{i,d}^d\,\bmod \,{\hspace{0.55542pt}} \,N, \end{aligned}$$
(4.8)

where \(b^{-1}\) and \(d^{-1}\) represent the reciprocal of b and d, respectively. The encrypted local updates \(C_i\) from the clients participating in the training are transmitted to the server.

3) Aggregation phase: After obtaining the encrypted updates of the clients, given its computing power, the cloud server aims to perform the aggregation operation as follows:

$$\begin{aligned} \begin{aligned}&{C_{agg}} = \sum \limits _{i = 1}^n {{C_i}} \\&= {d^{ - 1}}d\sum \limits _{i = 1}^n {{\theta ^b}_{i,b}} + {b^{ - 1}}b\sum \limits _{i = 1}^n {{\theta ^d}_{i,d}} \,\bmod \,{\hspace{0.55542pt}} N\\&= {d^{ - 1}}d{(\sum \limits _{i = 1}^n {{\theta _{i,b}}} )^b} + {b^{ - 1}}b{(\sum \limits _{i = 1}^n {{\theta _{i,d}}} )^d}{\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} N. \end{aligned} \end{aligned}$$
(4.9)

Afterwards, the server starts to communicate with the local clients and releases the encrypted global updates \(C_{agg}\) to avoid the adversary’s attack.

4) Decryption phase: After the local clients receive the encrypted global updates \(C_{agg}\), each client starts the decryption operation by

$$\begin{aligned} \begin{array}{l} {C_{agg}}{\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} b = {d^{ - 1}}d{(\sum \limits _{i = 1}^n {{\theta _{i,b}}} )^b} + {b^{ - 1}}b{(\sum \limits _{i = 1}^n {{\theta _{i,d}}} )^d}{\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} b\\ = {d^{ - 1}}d{(\sum \limits _{i = 1}^n {{\theta _{i,b}}} )^b}{\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} b\\ = {d^{ - 1}}d{(\sum \limits _{i = 1}^n {{\theta _{i,b}}} )^{b - 1}}(\sum \limits _{i = 1}^n {{\theta _{i,b}}} ){\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} b\\ = (\sum \limits _{i = 1}^n {{\theta _{i,b}}} ){\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} b\\ = {\theta _{agg,b}}{\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} b. \end{array} \end{aligned}$$
(4.10)

In the same way,

$$\begin{aligned} \begin{array}{l} {C_{agg}}{\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} d = {d^{ - 1}}d{(\sum \limits _{i = 1}^n {{\theta _{i,b}}} )^b} + {b^{ - 1}}b{(\sum \limits _{i = 1}^n {{\theta _{i,d}}} )^d}{\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} {\hspace{0.55542pt}} d\\ = (\sum \limits _{i = 1}^n {{\theta _{i,d}}} ){\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} d\\ = {\theta _{agg,d}}{\hspace{0.55542pt}} \,\bmod \,{\hspace{0.55542pt}} d. \end{array} \end{aligned}$$
(4.11)

This formula applies Euler Theorem and \(gcd\Big [\Big ( \sum \nolimits _{i = 1}^n {{\theta _{i,b}}}\Big ),\) \(b \Big ] = 1\). According to the above operation, the local clients obtain the decrypted result model \( \theta _{agg}\) by utilizing the Chinese Remainder Theorem (CRT) as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta _{agg} \equiv { \theta }_{agg,b} \bmod \,b,\\ \theta _{agg} \equiv { \theta }_{agg,d} \bmod \,d. \end{array}\right. } \end{aligned}$$
(4.12)

Compute the congruence expressions:

$$\begin{aligned} \theta _{agg} = \mathrm{{ }}{M_b}d{\theta _{agg,b}} + \mathrm{{ }}{M_d}b{\theta _{agg,d}}\,\bmod \,N, \end{aligned}$$
(4.13)

where \({M_b}d \equiv 1\bmod \,b\) and \(\mathrm{{ }}{M_d}b \equiv 1\bmod \,d\). Due to \(gcd(b,d) = 1\), it is easy to calculate \({M_b}\) and \({M_d}\). It is worth noting that since our proposed secure aggregation scheme requires only that each client encrypts the local model parameters using the same public key and uploads them to the cloud server, when the client drops out, the decryption is not affected. By comparing the TP-SMC [30] and PPFDL [31] encryption schemes, it is shown that the training process affects the subsequent ciphertext operation if any client fails to upload data. Therefore, the FLCP is robust to clients dropping out during training and is proven to have a higher degree of model accuracy than do the TP-SMC and PPFDL in Section 6. Furthermore, since the sender and receiver are identical in our system, our secure aggregation further removes the ciphertext component, supporting the usage of this system in large-scale scenarios. Finally, clients update the local parameter based on the global shared model.

Fig. 3
figure 3

System architecture of FLCP

Full size image

4.3 The overall scheme of FLCP

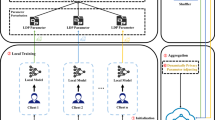
In this paper, the trainers in FL, including computers, mobile phones, smart devices, etc., are collectively taken as clients. We construct the FLCP framework, which contains several clients and a cloud server, as shown in Fig. 3. The clients and cloud servers are “honest-but-curious” semi-trusted entities, by which all entities (clients and servers) will faithfully follow the designed training protocol but may attempt to deduce private information from the shared messages. On account of the issue of privacy, most clients are reluctant to expose their data to cloud servers and other clients, but they want to learn high-precision models from the data combination. In particular, the client trains the model on the local dataset in a synchronous manner, then compresses the updated model parameters and transmits them to the server in ciphertext form. According to the property of HE, the server aggregates the encrypted local model and broadcasts the aggregation results calculated on the ciphertext to the client to update the local model. Through multiple rounds of communication, the client finally obtains a global model that meets the convergence requirements without explicitly disclosing individual datasets.

The overall protocol of FLCP is summarized in Algorithm 3. Our protocol involves T communication rounds, and in each round, a group of clients is selected to execute \(\lambda \) local iterations. Specifically, at each round \(t = 0,..., T\), the server initially selects \(r \le n\) clients uniformly and randomly, denoted as \(N_t\). Then the server broadcasts its current shared model parameters \(\theta ^t\) to the clients \(N_t\), and each client \(i \in N_{t} \) executes \(\lambda \) local iterations in their local dataset \(D_i\) according to (4.2). After \(\lambda \) local iterations, the clients in \(N_t\) compress weights by \({p\% }\) and upload an encrypted local model \(C_i\) to the server. Finally, the server aggregates the encrypted messages to compute the next global model, and the procedure is repeated for T rounds.

Algorithm 3
figure i

FLCP algorithm.

Full size image

5 Theoretical analysis

In this section, the convergence of the FLCP is first analyzed under the condition of the use of the periodic averaging method and the adaptive compression method. Then, a rigorous security analysis of the FLCP is conducted.

5.1 Convergence analysis

The convergence bounds for the FLCP with non-convex losses are presented. To deduce the convergence bounds of the model, we require the following assumptions.

Assumption

  1. 1.

    (Smoothness) Let’s assume that a function \(f:\mathbb {R}^d \rightarrow \mathbb {R}\) is L-smooth, for any \(\textrm{x},\textrm{y} \in \mathbb {R}\), we have \(f(\mathrm{{y}}) \le f(\mathrm{{x}}) + \left\langle {\nabla f(\mathrm{{x}}),\mathrm{{y - x}}} \right\rangle \mathrm{{ + }}\frac{L}{2}{\left\| {\mathrm{{x - y}}} \right\| }^{2} \).

  2. 2.

    (Unbiased gradient) For any \(i, \textrm{x} \in \mathbb {R}^d \), \(\mathbb {E}\left[ {\nabla f_{i} (\textrm{x})} \right] = \nabla f(\textrm{x})\).

  3. 3.

    (Second moments and bounded variances) For any \(i, \,\textrm{x} \in \mathbb {R}^d \), there exit positive constants \(\sigma \) and G, \( \mathbb {E}{\left\| {\nabla f_{i} (\textrm{x})} \right\| ^2} \le G^{2} \), \( \mathbb {E}\left[ {{{\left\| {\nabla f_{i} (\textrm{x}) - \nabla f(\textrm{x})} \right\| }^2}} \right] \le {\sigma ^2}\).

  4. 4.

    (Compression operator) For a constant \(\alpha \in \left( {0,1} \right] \), a compression operator \({Top}_{p} : \mathbb {R}^d \rightarrow \mathbb {R}^d\) that for all \(\textrm{x} \in \mathbb {R}^d \), \( \mathbb {E}\left\| {\mathrm{{x}} - {Top}_{p} (\textrm{x})} \right\| \le \left( {1 - \alpha } \right) {\left\| \textrm{x} \right\| }^{2} \).

where L represents the Lipschitz constant, implying that the loss function f is L-smooth. Conditions 2 and 3 in the assumption regarding the bias and variance of the mini-batch gradients are customary for SGD methods. Condition 4 in the assumption denotes selecting p out of d coordinates, and p coordinates with the highest magnitude values (\(To{p_p}\)) give \(\alpha = \frac{p}{d}\).

The protocol involves K iterations, and during iteration k, each client i calculates the stochastic gradient \(g(\theta _{i}^{k} )\) in its local dataset and updates the current model \(\theta _{i}^{k} \). In addition, the residual accumulation method is adopted, and the errors generated in each iteration are accumulated in the memory of each client and compensated in future updates. This updating method is the key to maintaining model accuracy, which provides clients with a controlled way to use both the current update and the residual update from previous rounds of communication.

To facilitate the analysis of FLCP convergence, the update rule is redefined as

$$\begin{aligned} \begin{aligned}&{{\bar{\theta }}^{k + 1}} = {{\bar{\theta }}^k} - \eta \left[ {\frac{1}{n}\sum \limits _{i = 0}^n {g(\theta _i^k)} } \right] ,\\&R^{k\mathrm{{ + }}1} : = R^{k} + \sum \limits _{i = 1}^n {\eta \nabla f(\theta _i^k)} - \theta ^{*} , \end{aligned} \end{aligned}$$
(5.1)

where \({\overline{\theta }^k}\) is the averaged model at iteration k, and \(R^k\) is the residual term at iteration k.

Lemma 1

For every \(k \in \mathbb {Z}\) and fixed learning rate \(\eta \), the following holds for each client \(i \in \left[ n \right] \):

$$\begin{aligned} \mathbb {E}{\left\| {R^{k } } \right\| ^2} \le \frac{{4(1 - {\alpha ^2})}}{{{\alpha ^2}}}{\eta ^2}{G^2}. \end{aligned}$$
(5.2)

Proof

According to Conditions 3 and 4 in the assumption and the inequality \({\left\| {\mathrm{{a}} + \mathrm{{b}}} \right\| ^2} \le (1 + \beta ){\left\| \mathrm{{a}} \right\| ^2} + (1 + \frac{1}{\beta }){\left\| \mathrm{{b}} \right\| ^2}\) for every \(\beta > 0\) (taking any \(z > 1\) in the following), we have that

$$\begin{aligned} \begin{aligned}&\mathbb {E}{\left\| {R^{k + 1} } \right\| ^2} \le \left( {1 - \alpha } \right) \mathbb {E}{\left\| { R^{k} + \sum \limits _{i = 1}^n {\eta \nabla f(\theta _i^k)} } \right\| ^2}\\&\le (1 - \alpha )\left( {1 + \frac{{(z - 1)\alpha }}{z}} \right) \mathbb {E}{\left\| {{R^k}} \right\| ^2} + \\&(1 - \alpha )\left( {1 + \frac{z}{{(z - 1)\alpha }}} \right) \mathbb {E}{\left\| {\sum \limits _{i = 1}^n {\eta \nabla f(\theta _i^k)} } \right\| ^2}\\&\le \left( {1 - \frac{\alpha }{z}} \right) \mathbb {E}{\left\| {{R^k}} \right\| ^2} + \frac{{z(1 - \alpha ^{2} )}}{{(z - 1)\alpha }}{\eta ^2}{G^2}. \end{aligned} \end{aligned}$$
(5.3)

When (5.3) is expanded, we find that the upper bound of the residual is a geometric sum:

$$\begin{aligned} \begin{aligned}&\mathbb {E}{\left\| {R^{k + 1} } \right\| ^2} \le \frac{{z(1 - \alpha ^{2} )}}{{(z - 1)\alpha }}{\eta ^2}{G^2}\sum \limits _{j = 0}^\infty {{\left( {1 - \frac{\alpha }{z}} \right) }^{j} } \\&\le \frac{{z^{2} (1 - {\alpha ^2})}}{{(z - 1){\alpha ^2}}}{\eta ^2}{G^2}. \end{aligned} \end{aligned}$$
(5.4)

Inequality (5.4) is true for \(z > 1\), and when \(z = 2\), the value of the inequality is minimized. Taking \(z = 2\), we btain that

$$\begin{aligned} \mathbb {E}{\left\| {R^{k + 1} } \right\| ^2} \le \frac{{4(1 - {\alpha ^2})}}{{{\alpha ^2}}}{\eta ^2}{G^2}. \end{aligned}$$
(5.5)

Since the right-hand side of this inequality does not depend on k, it follows that \(\mathbb {E}{\left\| {R^{k } } \right\| ^2} \le \frac{{4(1 - {\alpha ^2})}}{{{\alpha ^2}}}{\eta ^2}{G^2}\) holds for every \(k \in K\). In addition, \({\overline{\theta }^k}\) is the average of the compression model, and the updated mean residual is \(\theta _i^k - {\bar{\theta }^k} = \frac{1}{n}\sum \limits _{i = 1}^n {{R^k}}\).

Theorem 1

Let \(f_i\) be L-smooth, each \(i \in \left[ n \right] \). For a constant \(\alpha \in \left( {0,1} \right] \), a compression operator \({Top}_{p} :\mathbb {R}^d \rightarrow \mathbb {R}^d\). Let \(\left\{ {\theta _i^k} \right\} _{k = 0}^{K - 1}\) be generated based on Algorithm 3, for fixed learning rate \(\eta \) . Then we have that

$$\begin{aligned} \begin{aligned}&\mathbb {E}\left[ {\frac{1}{{Kn}}\sum \limits _{k = 0}^{K - 1} {\sum \limits _{i = 1}^n {{{\left\| {\nabla f(\theta _i^k)} \right\| }^2}} } } \right] \le \frac{{4\left[ {f({{\bar{\theta }}^0}) - f^{*} } \right] }}{{\eta K}}\\&+ \frac{{2\eta {\sigma ^2}L}}{n} + \frac{{16(1 - {\alpha ^2})}}{{{n^2}{\alpha ^2}}}{L^2}{\eta ^2}{G^2}. \end{aligned} \end{aligned}$$
(5.6)

Proof

According to Condition 1 in the assumption, we have that

$$\begin{aligned} \begin{aligned}&f({{\bar{\theta }}^{k + 1}}) - f({{\bar{\theta }}^k})\\&\le \left\langle {\nabla f({{\bar{\theta }}^k}),{{\bar{\theta }}^{k + 1}} - {{\bar{\theta }}^k}} \right\rangle + \frac{L}{2}{\left\| {{{\bar{\theta }}^{k + 1}} - {{\bar{\theta }}^k}} \right\| ^2}\\&= - \eta \left\langle {\nabla f({{\bar{\theta }}^k}),{g^k}} \right\rangle + \frac{{{\eta ^2}L}}{2}{\left\| {{g^k}} \right\| ^2}\\&= - \eta \left\langle {\nabla f({{\bar{\theta }}^k}),{g^k}} \right\rangle + \frac{{{\eta ^2}L}}{2}{\left\| {{g^k} - {{\hat{g}}^k} + {{\hat{g}}^k}} \right\| ^2}\\&\overset{(a)}{\le }\ -\eta \left\langle {\nabla f({{\bar{\theta }}^k}),{g^k}} \right\rangle + {\eta ^2}L{\left\| {{g^k} - {{\hat{g}}^k}} \right\| ^2} + {\eta ^2}L{\left\| {{{\hat{g}}^k}} \right\| ^2}\\&= - \frac{\eta }{n}\sum \limits _{i = 1}^n {\left\langle {\nabla f({{\bar{\theta }}^k}),\nabla {f_i}(\theta _i^k)} \right\rangle } + {\eta ^2}L{\left\| {\frac{1}{n}\sum \limits _{i = 1}^n {\nabla f(\theta _i^k)} } \right\| ^2}\\&+ {\eta ^2}L{\left\| {{g^k} - {{\hat{g}}^k}} \right\| ^2}, \end{aligned} \end{aligned}$$
(5.7)

where \(g^k\) represents the average mini-batch gradients, \({\hat{g}}^k\) represents the average full-batch gradients, and inequality (a) is based on Jensen’s inequality. Taking the expectation of sampling at iteration k, based on the Lipschitz continuity of the gradients of local functions, we have that

$$\begin{aligned} \begin{aligned}&\mathbb {E}[f({{\bar{\theta }}^{k + 1}})] - \mathbb {E}[f({{\bar{\theta }}^k})]\\&\le - \frac{\eta }{2}{\left\| {\nabla f({{\bar{\theta }}^k})} \right\| ^2} - \frac{\eta }{2}{\left\| {\frac{1}{n}\sum \limits _{i = 1}^n {\nabla f(\theta _i^k)} } \right\| ^2}\\&+ \frac{\eta }{2}{\left\| {\nabla f({{\bar{\theta }}^k}) - \frac{1}{n}\sum \limits _{i = 1}^n {\nabla f(\theta _i^k)} } \right\| ^2}\\&+ {\eta ^2}L{\left\| {\frac{1}{n}\sum \limits _{i = 1}^n {\nabla f(\theta _i^k)} } \right\| ^2} + \frac{{{\eta ^2}{\sigma ^2}L}}{{2n}}\\&\le - \frac{\eta }{{2n}}\sum \limits _{i = 1}^n {\left( {{{\left\| {\nabla f({{\bar{\theta }}^k})} \right\| }^2} - {L^2}{{\left\| {{{\bar{\theta }}^k} - \theta _i^k} \right\| }^2}} \right) } \\&+ \frac{{2{\eta ^2}L - \eta }}{{2n}}\sum \limits _{i = 1}^n {{{\left\| {\nabla f(\theta _i^k)} \right\| }^2}} + \frac{{{\eta ^2}{\sigma ^2}L}}{{2n}}\\&\le - \frac{\eta }{{2n}}\sum \limits _{i = 1}^n {\left( {{{\left\| {\nabla f({{\bar{\theta }}^k})} \right\| }^2} + {L^2}{{\left\| {{{\bar{\theta }}^k} - \theta _i^k} \right\| }^2}} \right) } \\&+ \frac{{2{\eta ^2}L - \eta }}{{2n}}\sum \limits _{i = 1}^n {{{\left\| {\nabla f(\theta _i^k)} \right\| }^2}} + \frac{{{\eta ^2}{\sigma ^2}L}}{{2n}}\\&+ \frac{{\eta {L^2}}}{n}{\left\| {{{\bar{\theta }}^k} - \theta _i^k} \right\| ^2}. \end{aligned} \end{aligned}$$
(5.8)

We bound the first term in terms of \({\left\| {\nabla f(\theta _i^k)} \right\| }^2\) as:

$$\begin{aligned} \begin{aligned} {\left\| {\nabla f(\theta _i^k)} \right\| ^2}&\le 2{\left\| {\nabla f(\theta _i^k) - \nabla f({{\bar{\theta }}^k})} \right\| ^2} + 2{\left\| {\nabla f({{\bar{\theta }}^k})} \right\| ^2}\\&\le 2{L^2}\left\| {\theta _i^k - {{\bar{\theta }}^k}} \right\| ^2 + 2{\left\| {\nabla f({{\bar{\theta }}^k})} \right\| ^2}, \end{aligned} \end{aligned}$$
(5.9)

where Inequality (5.9) follows from the L-Lipschitz gradient. Based on this, the expression is rearranged as

$$\begin{aligned} \begin{aligned}&\frac{1}{n}\sum \limits _{i = 1}^n {\mathbb {E}{{\left\| {\nabla f(\theta _i^k)} \right\| }^2}} \le \frac{{4\left[ {\mathbb {E}[f({{\bar{\theta }}^k})] - \mathbb {E}[f({{\bar{\theta }}^{k + 1}})]} \right] }}{\eta }\\&+ \frac{{2\eta {\sigma ^2}L}}{n} + \frac{{4L}}{{{n}}}\mathbb {E}{\left\| {{{\bar{\theta }}^k} - \theta _i^k} \right\| ^2}. \\ \end{aligned} \end{aligned}$$
(5.10)

From Lemma 1 we get \(\mathbb {E}{\left\| {{{\bar{\theta }}^k} - \theta _i^k} \right\| ^2} \le \frac{{4(1 - {\alpha ^2})}}{{n{\alpha ^2}}}{\eta ^2}{G^2}\) and substitute it into formula (5.10) as

$$\begin{aligned} \begin{aligned}&\frac{1}{n}\sum \limits _{i = 1}^n {\mathbb {E}{{\left\| {\nabla f(\theta _i^k)} \right\| }^2}} \le \frac{{4\left[ {\mathbb {E}[f({{\bar{\theta }}^k})] - \mathbb {E}[f({{\bar{\theta }}^{k + 1}})]} \right] }}{\eta }\\&+ \frac{{2\eta {\sigma ^2}L}}{n} + \frac{{16(1 - {\alpha ^2})}}{{{n^2}{\alpha ^2}}}{L^2}{\eta ^2}{G^2}. \end{aligned} \end{aligned}$$
(5.11)

By taking a telescopic sum from \(k=0\) to \(k=K-1\), we obtain that

$$\begin{aligned} \begin{aligned}&\mathbb {E}\left[ {\frac{1}{{Kn}}\sum \limits _{k = 0}^{K - 1} {\sum \limits _{i = 1}^n {{{\left\| {\nabla f(\theta _i^k)} \right\| }^2}} } } \right] \le \frac{{4\left[ {f({{\bar{\theta }}^0}) - f^{*} } \right] }}{{\eta K}}\\&+ \frac{{2\eta {\sigma ^2}L}}{n} + \frac{{16(1 - {\alpha ^2})}}{{{n^2}{\alpha ^2}}}{L^2}{\eta ^2}{G^2}. \end{aligned} \end{aligned}$$
(5.12)

5.2 Security analysis

5.2.1 Security against the cloud server

After reviewing the training process of the above FL algorithm, the intermediate data obtained by the client and the cloud server are illustrated in Table 3, which shows that in FL training, each client can obtain the global model parameters through secret key decryption but cannot acquire other client model parameters \({\theta _{par}}\), gradient g, Predictionresults, and Loss. Moreover, the cloud server obtains the encrypted local model parameter \(Enc({\theta _{par}})\) and the encrypted global model parameter \(Enc({\theta _{global}})\). The cloud server does not have a secret key and cannot decrypt the parameter data.

Table 3 Data information obtained by the participant and parameter server
Full size table

As shown in Fig. 3, the central server averages the model parameters uploaded by clients and updates the global parameters of the neural network model. Moreover, the validity of the ciphertext calculation formula in the figure is guaranteed by the property of the HE scheme.

Definition 2

(CPA-Security) [40]. For the HE scheme in this work, we describe the chosen plaintext attacks (CPA) as a game between adversary \(\mathscr {A}\) and challenger \(\mathscr {C}\):

  • Initialization. \(\mathscr {C}\) creates the CPA system and sends the generated public parameters pp and the key pairs (pk, sk) to \(\mathscr {A}\).

  • Challenge. Adversary \(\mathscr {A}\) selects two plaintexts \(m_0\) and \(m_1\) with the same length and sends them to \(\mathscr {C}\). Challenger \(\mathscr {C}\) selects \(b \in \{ 0,1\} \) at random and computes \({C^ * } = \mathrm{{Enc}}\left( {pk, m_{b} } \right) \). Then the challenge ciphertext \(C^ *\) is returned to \(\mathscr {A}\).

  • Guess. Adversary \(\mathscr {A}\) guesses whether the plaintext encrypted in the previous step of challenger \(\mathscr {C}\) is \(m_0\) or \(m_1\), and outputs the guess result, which is recorded as \(b^\prime \). If \({b^\prime }=b\), the adversary attack succeeds.

The advantage of an adversary attack can be defined as the following function:

$$\begin{aligned} \mathrm{{Adv}}_{\mathscr {A}}^{\mathrm{{CPA}}}(\kappa ) = |{\Pr [b = {b^\prime }] - \frac{1}{2}} |, \end{aligned}$$
(5.13)

where \(\kappa \) denotes the length of the encryption scheme key. HE scheme is secure against the chosen plaintext attacks (CPA-secure) if the advantage of an adversary attack is negligible in \(\kappa \).

Theorem 2

Our protocol does not leak information from the datasets to an “honest-but-curious” parameter server as long as the HE scheme is CPA-secure.

Proof

It is assumed that adversary \(\mathscr {A}\) can compromise the cloud server and participants other than \(\gamma \) and \(\nu \) in each round of aggregation and query their secret key \({\left\{ {{sk}_{i} } \right\} _{i \ne \gamma ,i \ne \nu }}\). Then, \(\mathscr {A}\) encrypts the plaintext \(m_{i} \) of arbitrarily appointed participant i \(\left( {i \ne \gamma ,i \ne \nu } \right) \) using the secret key \({sk}_{i} \). Even if \(\mathscr {A}\) can obtain the key \({SK}_{c} \) and the ciphertext of the participant, it can merely obtain the sum of \(m_{\gamma } \) and \(m_{\nu }\). In other words, \(\mathscr {A}\) still fails to identify the ciphertext of \(\gamma \) and \(\nu \) from the random values. If \(\mathscr {A}\) can identify the ciphertext of \(\gamma \) and \(\nu \) from the random values, then the advantage of an adversary attack is not negligible in \(\kappa \). That is, \(\mathscr {A}\) can solve the decision-augmented learning with error (LWE) problem, which is difficult in reality. As a result, our encryption protocol is CPA-secure, safeguarding the client’s data from compromise.

5.2.2 Security against the cloud server and compromised clients

The adversary may compromise with some clients by stealing the system’s private keys and the honest clients’ privacy. Thus, DP is utilized to provide strict privacy protection and prove that the local perturbation model satisfies different privacy requirements.

Theorem 3

The local model preserves \(\varepsilon \)-differential privacy. For any two adjacent datasets D and \(\bar{D}\),

$$\begin{aligned} |{\log \frac{{P({\bar{\theta }_i^ * } |D |) }}{{P({\bar{\theta }_i^ * } |{\bar{D}} |) }}} |\le \varepsilon . \end{aligned}$$
(5.14)

Proof

Let \(\chi \) be the noise injected into \(\theta \) and \(\chi \sim Lap(\frac{{\varDelta f }}{\varepsilon })\). We have

$$\begin{aligned} \begin{aligned} P(\bar{\theta }_i^*|D |)&= P\left[ {\mathrm{{ }}{f_i}(D) + \chi = t} \right] \\&= P[\chi = t - {f_i}(D)] \\&= \frac{\varepsilon }{{2\varDelta f}}\exp (\frac{{ - |{t - \mathrm{{ }}{f_i}(D)} |}}{{\varDelta f}}). \end{aligned} \end{aligned}$$
(5.15)

Similarly,

$$\begin{aligned} P(\bar{\theta }_i^*|{\overline{D} } |) = \frac{\varepsilon }{{2\varDelta f}}\exp (\frac{{ - |{t - \mathrm{{ }}{f_i}(\overline{D} )} |}}{{\varDelta f}}). \end{aligned}$$
(5.16)

Thus,

$$\begin{aligned} \begin{aligned} \frac{{P(\bar{\theta }_i^ * |D |)}}{{P(\bar{\theta }_i^ * |{\bar{D}} |)}}&= \frac{{P\left[ {f_{i} (D) + \chi = t} \right] }}{{P\left[ {f_{i} (\bar{D}) + \chi = t} \right] }}\\&= \frac{{\exp (\frac{{ - \varepsilon |{t - f_{i} (D)} |}}{{\varDelta f}})}}{{\exp (\frac{{ - \varepsilon |{t - f_{i} (\bar{D})} |}}{{\varDelta f}})}}\\&= \exp (\frac{{\varepsilon (|{t - f_{i} (\bar{D})} |- |{t - f_{i} (D)} |)}}{{\varDelta f}})\\&\le \exp (\frac{{|{f_{i} (\bar{D}) - f_{i} (D)} |}}{{\varDelta f}}) \le \exp (\varepsilon ). \end{aligned} \end{aligned}$$
(5.17)

Thus, perturbation of local updates preserves \(\varepsilon \)-DP, and the proposed security scheme tolerates the server to collude with any client, but no valuable information can be inferred.

6 Experiments

This section mainly conducts experiments to evaluate FLCP performance. We first briefly describe the experimental setup. Then, the influence of the key factors in the FLCP on convergence is studied. Finally, the performance of the FLCP is compared with several baseline approaches in terms of model accuracy, training time, and communication efficiency.

6.1 Experimental setup

To evaluate the performance of the FLCP, all clients are allowed to run a unified convolutional neural network (CNN), which includes two convolutional layers, an average pooling layer, and two fully connected layers. MNIST [41] and CIFAR-10 [42] are used as benchmarks. The former includes 60,000 training examples and 10,000 testing examples, each of which is a \(28 \times 28\) size gray-level image, while the latter contains 50,000 training examples and 10,000 testing examples, consisting of 10 classes of \(32 \times 32\) images with three channels (RGB). To simulate the FL setting, we assume that there are 12 clients in the system. Each local client’s dataset is assigned an approximately identical distribution by randomly shuffling and evenly partitioning the training dataset. Several state-of-the-art FL approaches with communication efficiency and privacy preservation, including NbAFL [19], TP-SMC [30], RCEFL [11], and PPFDL [31] listed in Table 1, as well as the well-known classical FL algorithm FedAvg [5], are selected as baselines for comparing the performance of our proposed scheme.

Table 4 Configuration details of cloud server and client modules
Full size table

Comprehensive information about the cloud server and client module configurations in the experimental scenario is provided in Table 4. All clients have sufficient computing power to run the encryption and decryption algorithms. The compression and privacy protection algorithms are simulated in the Python3 language, and we use the PyTorch library. The parameters of the neural network model are encrypted and decrypted by using the open-source Paillier library.

6.2 Convergence property

In this subsection, the influence of several key factors on the convergence characteristics of the scheme is studied. Moreover, the influence of the key factors with different values on the degree of convergence is compared.

6.2.1 Impact of compression rate p

To test the properties of the adaptive compression algorithm in the FLCP, we compare it with fixed compression rates of \(0.00\%\) (uncompressed), \(99.00\%\), \(99.60\%\), and \(99.99\%\) under the same conditions. In the adaptive compression algorithm, the minimum compression rate \(p_{\min } \) is set to \(99.00\%\), and the maximum compression rate \(p_{\max } \) is set to \(99.99\%\). The variation in the degrees of training loss between the fixed compression rate scheme and the adaptive compression scheme under the condition that the model is trained with the early stop strategy is illustrated in Fig. 4.

Fig. 4
figure 4

Change comparison in training loss

Full size image
Table 5 Comparison of accuracy and total time
Full size table
Fig. 5
figure 5

Convergence of the training loss and the model accuracy on MNIST dataset

Full size image

Figure 4 illustrates that the adaptive compression algorithm smooths the model convergence curve because the model’s training loss decreases rapidly during the initial training stage, making a relatively large compression rate adoption suitable. When the convergence rate reaches a higher level, the model’s training loss decreases more slowly, prompting an adaptive adjustment of the compression rate to a smaller value. In terms of the iteration number, the convergence of the adaptive compression scheme is comparable to that of the fixed \(99.00\%\) compression and uncompression schemes, and it can reach the optimum in fewer iteration cycles. In addition, adaptive compression, \(99.00\%\) compression, and uncompressed schemes can converge with better accuracy. Thus, our experiments demonstrate that the adaptive compression algorithm performs better in terms of model convergence and iteration number.

Table 5 intuitively compares the performance of the fixed compression rate and adaptive compression algorithms in terms of accuracy and total time. The total training time of the model is composed of the accumulated time across iterative rounds. In terms of accuracy, the adaptive compression algorithm maintains the model’s accuracy at a high level (\(99.07\%\)), which is close to the uncompressed accuracy level. In terms of total training time, the adaptive compression algorithm performs better than other control groups, significantly improving training efficiency. In particular, the total time of the adaptive compression algorithm is reduced by approximately \(91\%\) compared to that of the uncompressed algorithm. Therefore, our experiments have proven that the adaptive gradient compression algorithm ensures model accuracy and can converge to the optimum in the shortest time, thus improving the speed of model training.

6.2.2 Impact of local iteration number \(\lambda \) and privacy budget \(\varepsilon \)

This part shows the degree of the FLCP’s convergence regarding communication round number T under different settings of privacy budget \(\varepsilon \) and local iteration number \(\lambda \). As shown in Figs. 5 and 6, we conduct experiments with different numbers of privacy budgets and local iterations on the MNIST and CIFAR-10 datasets, respectively, to evaluate the convergence of the FLCP. Specifically, we demonstrate the testing accuracy and the training loss concerning communication round number T when \(\varepsilon \mathrm{{ = }}\left\{ {2,4,8} \right\} \). For each case, we set 4 diverse values of the local iteration, i.e., \(\lambda =\{ 1,5,10,\) \(20\}\).

Fig. 6
figure 6

Convergence of the training loss and the model accuracy on CIFAR-10 dataset

Full size image
Fig. 7
figure 7

Comparison of model accuracy on MNIST and CIFAR-10 datasets

Full size image
Table 6 Model accuracy with different numbers of clients dropping out
Full size table
Fig. 8
figure 8

Comparison of training time on MNIST and CIFAR-10 datasets

Full size image

For the MNIST dataset experiments, the testing accuracy and training loss usually first sharply then slowly change. As the privacy budget \(\varepsilon \) increases, the size of the testing accuracy curve increases, and the training loss curve of the CNN converges to a lower bound, indicating that the size of the privacy budget \(\varepsilon \) has some influence on testing accuracy. This finding corresponds to the FLCP’s convergence, where a higher privacy budget \(\varepsilon \) produces a smaller convergence error but provides a lower privacy security level. For specific privacy budget settings, the initial training loss decreases significantly with the increasing local iteration \(\lambda \) and eventually reaches a lower stationary point, which shows that a larger \(\lambda \) value implies a minor convergence error. When \(\lambda \mathrm{{ = 20}}\), we observe that the training loss decreases to the lowest value after utilizing approximately 70 iterations, and then it grows with an increasing number of iterations. The reason for this is that continuous training introduces additional noise to the well-trained model after the loss reaches a stationary point; thus, the size of the training loss curve increases. Similar trends have been observed for the CIFAR-10 dataset experiments. Different privacy budget values \(\varepsilon \) have different effects on accuracy. A smaller privacy budget \(\varepsilon \) can provide a stronger DP guarantee, but it also results in a loss of precision. However, the FLCP adopts a security aggregation protocol that achieves a high level of accuracy at the same security level. It is noted that a reasonable number of local iterations \(\lambda \) is critical for model training. The local update number \(\lambda \) is too small, and additional rounds of communication are thus needed to aggregate the updates. Conversely, the local update number \(\lambda \) is too large, and it is difficult for the loss function to converge.

6.3 Comparison of model accuracy, training time and communication efficiency

This subsection primarily compares the FLCP with the benchmark methods introduced in the experimental setup in three aspects: model accuracy, training time, and communication efficiency. To better evaluate the results, two common baselines are added. The first approach is stand-alone training, which trains the model only on local datasets without collaborating with other clients and has the most robust degree of privacy preservation. The second approach is centralized dataset training, which ignores privacy issues but has the highest degree of model accuracy.

Table 7 Time of encryption and decryption
Full size table
Fig. 9
figure 9

Total ciphertext size of different transmission approaches in an iteration

Full size image

6.3.1 Model accuracy

To evaluate model performance, we compare the accuracy of the resulting models of these methods, as shown in Fig. 7. It can be observed that the centralized training method possesses the highest model accuracy (\(99.4\%\) in MNIST and \(97.8\%\) in CIFAR-10), while the stand-alone method has the lowest model accuracy (\(91.6\%\) in MNIST and \(89.3\%\) in CIFAR-10). As a naive FL algorithm, FedAvg’s model accuracy is slightly lower than that of other recent FL results. RCEFL adopts the low-precision quantization method to improve communication efficiency, which causes an inevitable loss of precision. In addition, we can observe distinct trends depending on whether a specific privacy-preserving method is employed to safeguard the privacy of the training process and resultant model. Among these trends, the accuracy of methods utilizing encryption-based protocols (such as FLCP, PPFDL, and TP-SMC) is higher than that of those methods merely utilizing the DP protocol (such as NBAFL) because the noise injected by the latter decreases the degree of model accuracy. This finding shows the cost of guarding against the inference risks of the model. Furthermore, to prove that the FLCP is more robust to clients dropping out than the PPFDL and TP-SMC methods, we tested the model accuracy for different numbers of clients dropping out, and the results are shown in Table 6. As the number of clients dropping out increases, the model accuracy of the PPFDL and TP-SMC models decreases significantly, while that of the FLCP method remains almost unaffected. When the number of clients dropping out is \(\textbf{D}=5\), the model accuracy of the FLCP, PPFDL, and TP-SMC methods on the MNIST dataset are \(99.21\%\), \(98.75\%\), and \(97.80\%\), respectively, indicating that the FLCP is more robust to clients dropping out. The FLCP and PPFDL methods have the highest accuracy among all the privacy preservation methods, slightly lower than that of the centralized method, indicating that the FLCP has little effect on model accuracy. The pivotal factor of our approach is its ability to reduce noise by using encryption techniques. Hence, we demonstrate that the approach combining DP protection and HE can achieve a higher degree of model precision while protecting the privacy of inputs and outputs.

6.3.2 Training time

These methods are compared and analyzed in terms of training time, as shown in Fig. 8. It is noted that the trend of the training time curves of different methods increases with the epoch. The FedAvg method takes the longest among all algorithms (36.5 minutes on MNIST and 33.7 minutes on CIFAR-10). Moreover, it is observed that the runtime of encryption-based methods such as FLCP, TP-SMC, and PPFDL is longer than that of methods without encryption, such as NbAFL and RCEFL, because the ciphertext operation increases the training. Among these algorithms, the TP-SMC’s training time is the longest, since each global update requires additional communication rounds and demands each client’s participation in the training. We evaluate the time consumed by the client to perform encryption and decryption. The experimental results are shown in Table 7, demonstrating that the time consumed by ciphertext operations is closely related to the number of updated model parameters. When the number of model parameters is 36,800, the time taken by the client for encryption and decryption is 46.8 milliseconds (ms) and 44.3 ms, respectively. The FLCP adopts a parameter compression algorithm that significantly reduces the number of updated model parameters. Compared to PPFDL and TP-SMC with secure aggregation schemes, the training time of the FLCP (28.4 minutes on MNIST and 25.7 minutes on CIFAR-10) is significantly less than that of PPFDL (34.3 minutes on MNIST and 31.9 minutes on CIFAR-10) and TP-SMC (35.8 minutes on MNIST and 32.6 minutes on CIFAR-10). This finding demonstrates the effectiveness of our proposed optimization approach concerning model training.

6.3.3 Communication efficiency

The experiment in this paper is carried out on a simulated FL framework, and thus, we measure network communication efficiency by comparing the volume of encryption parameters exchanged during transmission. Given that only encryption-based approaches involve transmitting encrypted parameters, we merely compare the FLCP, PPFDL, and TP-SMC. Figure 9 shows the total volume of ciphertext transmitted under various encryption-based methods in a global epoch. The orange bar indicates the initial ciphertext volumes of the model parameters, and the blue bar represents the subsequent ciphertext volumes, containing the multiplied ciphertext, partially decrypted ciphertext, and global parameters. In Fig. 9, it can be seen that compared to PPFDL and TP-SMC, the FLCP decreases the transmitted ciphertext volume of MNIST by \(87\%\) and that of CIFAR-10 by \(89\%\) on average, because it has a smaller initial ciphertext size than those of the other approaches due to the adaptive compression algorithm implemented in the FLCP. Therefore, our approach plays a significant role in improving communication efficiency.

7 Conclusion

This paper proposes a novel approach, namely, the federated learning framework with communication-efficient and privacy-preserving (FLCP), which can reduce communication costs and enhance privacy protection within FL settings. Specifically, we design an adaptive compression algorithm to improve communication efficiency and combine HE and DP to prevent privacy leakage. Compared to current compression methods, the FLCP adaptively compresses uploaded parameters based on the actual data distribution characteristics of the client, reducing communication overhead and ensuring superior model convergence. In addition, our proposed FLCP adopts a lightweight HE combined with DP to significantly mitigate security threats to local clients, providing a higher level of privacy security during the training process, even if the adversary colludes with the client. The experimental results on the MNIST and CIFAR-10 datasets indicate that the proposed FLCP is effective in terms of model accuracy and training efficiency. In the following studies, we will examine the performance of the FLCP in complex training tasks such as multitask learning for high-dimensional datasets.