A new bargaining solution for finite offer spaces

Abstract

The bargaining problem deals with the question of how far a negotiating agent should concede to its opponent. Classical solutions to this problem, such as the Nash bargaining solution (NBS), are based on the assumption that the set of possible negotiation outcomes forms a continuous space. Recently, however, we proposed a new solution to this problem for scenarios with finite offer spaces de Jonge and Zhang (Auton Agents Multi-Agent Syst 34(1):1–41, 2020). Our idea was to model the bargaining problem as a normal-form game, which we called the concession game, and then pick one of its Nash equilibria as the solution. Unfortunately, however, this game in general has multiple Nash equilibria and it was not clear which of them should be picked. In this paper we fill this gap by defining a new solution to the general problem of how to choose between multiple Nash equilibria, for arbitrary 2-player normal-form games. This solution is based on the assumption that the agent will play either ‘side’ of the game (i.e. as row-player or as column-player) equally often, or with equal probability. We then apply this to the concession game, which ties up the loose ends of our previous work and results in a proper, well-defined, solution to the bargaining problem. The striking conclusion, is that for rational and purely self-interested agents, in most cases the optimal strategy is to agree to the deal that maximizes the sum of the agents’ utilities and not the product of their utilities as the NBS prescribes.

1 Introduction

Automated negotiation is a research area that deals with autonomous agents that are purely self-interested, but nevertheless need to cooperate to ensure beneficial outcomes [13]. A typical example is the scenario in which a buyer and a seller are negotiating the price of a car. Although the seller would prefer to get paid the highest possible price, she should also take into account that the price has to be low enough for the buyer to accept the offer.

In general, in automated negotiation, two or more agents may propose offers to each other, and may accept or reject the offers they receive from each other. Although a negotiating agent is self-interested, its proposals must also benefit the other agents because otherwise they would never accept any of these proposals.

The question which offer represents the ideal trade-off between an agent’s own utility and its opponent’s utility, is known as the bargaining problem. In the literature, many solutions to this problem have been proposed. Arguably the best known of these is the Nash bargaining solution (NBS) [32]. The problem with the NBS, however, is that it is based on the assumption that set of possible outcomes of the negotiation forms a convex set, so it does not apply to domains where the number of possible outcomes is finite.

This assumption of convexity is typically defended with two arguments. Firstly, it is often argued that one can always make the set of possible negotiation outcomes convex, by allowing ‘lotteries’ over outcomes. However, it is hard to imagine any real-life situation were negotiators would agree on a lottery ticket as the outcome of their negotiations. A second, more realistic, argument is that one can make any discrete set of offers convex by allowing monetary side-payments. Although we agree that there are many real-world scenarios where this is indeed a valid argument, we argue that there are still many other scenarios were such monetary payments are not possible. See, for example, the Automated Negotiating Agents Competitions (ANAC) [4], or see [23, 24] for a real-world application.

We therefore argue that there is a need for an alternative solution to the bargaining problem that applies to negotiation scenarios with only a finite number of possible offers.

Recently, we proposed such a solution [21], based on game-theoretical principles. Our idea was to model the negotiations as a normal-form game, which we called the concession game, and which could be a seen as a discrete variant to the game defined by Nash in [34]. We then argued that the solution of the bargaining problem can be found as a Nash equilibrium of this concession game. Unfortunately, this game typically has multiple Nash equilibria, so we left it as an open question how to choose between those equilibria. In this paper we fill this gap by describing a recipe to select the correct Nash equilibrium, resulting in a more refined version of the bargaining solution we proposed earlier.

The question which equilibrium a player should select when a game has multiple Nash equilibria, is known as the equilibrium selection problem. This is another problem that has also been studied extensively, and again there is no single solution that is generally accepted, because each of these solutions needs to make additional assumptions that are typically only justifiable in specific scenarios [17, 16, 12, 30, 38, 41, 31, 26]

Of course, just like any of these existing solutions, the new solution that we are proposing here also requires certain additional assumptions which may not always hold. In our case, we assume what we call the assumption of role-equifrequency, which means we assume that each ‘side’ of the game (i.e. ‘row-player’ and ‘column-player’) is played equally often, or with equal probability. While this may not always be true, it has the advantage that it is often relatively easy to reason whether or not this assumption holds in a given scenario.

The striking result of our analysis, is that under this assumption, the optimal strategy for a purely self-interested negotiator, is to aim for an agreement that maximizes the sum of the utilities, rather than the product.

In summary, this paper makes the following contributions:

• We present a new solution to the equilibrium selection problem for 2-player normal-form games.

• We use this solution to fill a gap in our earlier work in which we proposed a new solution to the bargaining problem for finite offer spaces.

• We show that this bargaining solution can, in many cases, be calculated efficiently.

The rest of this paper is organized as follows. In Section 2 we briefly discuss existing work on the bargaining problem and the equilibrium selection problem. In Section 3 we recall the definitions from existing work that are necessary to understand this paper. In Section 4 we prove a theorem that allows us to characterize the Nash equilibria of the concession game. In Section 5 we present our solution to the equilibrium selection problem, and prove that this solution is optimal, under the assumption of role equifrequency. In Section 6 we show how our bargaining solution can be calculated efficiently. Then, in Section 7 we present a number of examples to demonstrate our approach. In Section 8 we go into a more detailed discussion of a number of decisions and assumptions we have made throughout this paper. And finally, in Section 9 we summarize our conclusions and discuss future work.

The source code of our algorithm to calculate our bargaining solution is publicly available at: https://www.iiia.csic.es/~davedejonge/downloads.

2 Related work

The equilibrium selection problem has been studied extensively, but there is no single solution that is generally accepted, because every solution that has been proposed makes a number of additional assumptions that are typically only justifiable in specific scenarios. For example, very elaborate theories of equilibrium selection were developed in [17] and [16], which were largely based on the concept of risk dominance, which takes into account the risk that the opponent may not be perfectly rational or that the utility values may not be perfectly known. Furthermore, these existing approaches depend on a tracing procedure [12], which starts from some prior assumption over the chosen strategies, and then evolves to some unique Nash equilibrium, but it is not always clear why it would be rational for the opponent to follow exactly the same tracing procedure. Many other solutions have been proposed that are based on some evolutionary approach [30, 38, 41, 31, 26].

The bargaining problem is another problem that has been studied extensively. While the NBS seems to be the most widely accepted solution, it has been widely criticized in the literature, because some of its axioms are controversial [25]. Most notably, the axiom of ‘independence of irrelevant alternatives’ (see Section 8.4). Therefore, alternative solutions based on different axioms have been proposed, such as the Kalai-Smorodinsky solution [25], but their axioms remain equally controversial. Other attempts to overcome this issue discard the axiomatic approach altogether, and instead try to derive an optimal negotiation strategy [40], rather than just an optimal outcome, but they still require assumptions that are not always clearly justifiable, such as time-discounted utility functions.

Furthermore, various generalizations of the Nash bargaining solution have been proposed for non-convex domains [11, 18], but they still assume the offer space is continuous, rather than discrete. To the best of our knowledge, no one else has proposed any bargaining solution for negotiation domains with a finite offer space.

The simplest types of negotiation strategies that have been proposed in the literature are the so-called time-based strategies [13]. They base their decisions when to make which proposal only on time. More sophisticated agents, however, apply adaptive strategies that use machine learning techniques to predict, at run-time, how far the opponent is willing to concede, based on the offers received from that opponent. The adaptive agent then makes sure it will never propose or accept any offer with utility lower than the maximum utility the opponent is predicted to offer. A plethora of different machine learning techniques have been used for this, such as non-linear regression [45], Gaussian processes [44], wavelet decomposition [9], Bayesian learning [19, 43, 45], or reinforcement learning [27, 14]. Apart from learning at run-time, various authors have also proposed the use of machine learning techniques to learn from previous negotiation sessions [7, 42, 37]. While the authors of such agents do often use the NBS or social welfare to measure the performance measure for their approach, they rarely investigate whether their agents converge to a theoretically optimal solution when they negotiate against themselves. Other important types of strategy are Tit-for-Tat [13] and MiCRO [20].

Social welfare (i.e. the sum of the utilities of all agents) has often been used in the automated negotiation literature as a performance measure, but often only as a measure to assess the quality of some negotiation system as a whole, rather than the quality of an individual strategy [1, 8]. On the other hand, in [46] it was mentioned that social welfare can also be useful to measure the strength of individual strategies, because even a self-interested agent may prefer to optimize social welfare if that improves its long-term relationship with some specific other agent, which would allow it to achieve more individual utility in the future. For this reason, various editions of ANAC awarded a prize for the agents that scored highest social welfare [15, 2]. It should be noted, however, that in this paper we are not looking at the benefits of long-term relationships. We argue that a self-interested agent should aim to maximize the utility sum, even if it is sure that it will never interact with the same opponent ever again.

3 Preliminaries

In this section we discuss the relevant definitions and theorems from existing literature that are required to understand the rest of the paper.

3.1 Game theory

We here give the formal definition of a ‘game’ and of related concepts such as ‘strategies’ and ‘Nash equilibria’.

Definition 1

A normal-form game G (for two players) is a tuple $\langle \mathcal {A}_1, \mathcal {A}_2, u_1, u_2\rangle$, where $\mathcal {A}_1$ and $\mathcal {A}_2$ are two finite sets representing the actions of the two players, and $u_1, u_2$ are two utility functions $u_i : \mathcal {A}_1 \times \mathcal {A}_2 \rightarrow \mathbb {R}$.

We say an agent plays the role of player 1 (resp. 2) if it chooses an action from the set $\mathcal {A}_1$ (resp. $\mathcal {A}_2$) with the aim of maximizing the utility function $u_1$ (resp. $u_2$). We will call this agent $\alpha _1$ (resp. $\alpha _2$). In the literature, these roles are also often referred to as the row-player and the column-player, respectively.

A strategy $q$ for $\alpha _i$ in game G, is a map that assigns a probability value to each action $a\in \mathcal {A}_i$. That is, $q(a) \in [0,1]$, and $\sum _{a\in \mathcal {A}_i} q(a) = 1$. The set of all actions for which $q(a) > 0$ is called the support of $q$. A strategy is called a pure strategy if the size of its support is exactly 1, and it is called a mixed strategy if its support is greater than 1. A joint strategy $\vec {q} = (q_1, q_2)$ is a pair consisting of one strategy for each player. We may sometimes abuse terminology and refer to a strategy a, where a is actually an action, when we mean the pure strategy with support $\{a\}$.

For any player i and any joint strategy $\vec {q}= (q_1,q_2)$, we can define the utility value $u_i(q_1, q_2) \in \mathbb {R}$ as:

$$\begin{aligned} u_i(q_1, q_2) := \sum _{a\in \mathcal {A}_1}\sum _{a' \in \mathcal {A}_2} q_{1}(a)\cdot q_{2}(a')\cdot u_i(a,a'). \end{aligned}$$

(1)

We will sometimes use the notation $\vec {u}(q_1, q_2)$ or $\vec {u}(\vec {q})$ as a shorthand for $(u_1(q_1, q_2), u_2(q_1, q_2))$. If $(q_1, q_2)$ is a joint strategy then we say that $q_1$ is a best response to $q_2$ if for all other strategies $q'$ for player 1 we have: $u_1(q_1,q_2) \ge u_1(q',q_2)$. Similarly, $q_2$ is a best response to $q_1$ if for all other strategies $q'$ for player 2 we have: $u_2(q_1,q_2) \ge u_2(q_1,q')$. Furthermore, $(q_1, q_2)$ is called a Nash equilibrium if $q_1$ is a best response to $q_2$ and $q_2$ is a best response to $q_1$. Note that whenever we use the term ‘Nash equilibrium’, we are referring to an equilibrium of strategies that can be either mixed or pure. The question which equilibrium strategy a player should choose when a game has more than one Nash equilibrium, is known as the equilibrium selection problem.

While there is no generally accepted correct solution to the general equilibrium selection problem, there is clear solution for the subclass of symmetric games [10]. A symmetric game is a game $\langle \mathcal {A}_1, \mathcal {A}_2, u_1, u_2\rangle$, for which $\mathcal {A}_1 = \mathcal {A}_2$ and, for all $a, a' \in \mathcal {A}_1$ we have: $u_1(a, a') = u_2(a', a)$. If G is a symmetric game then a symmetric Nash equilibrium of G is a Nash equilibrium $(q_1, q_2)$ for which $q_1=q_2$. One can argue that in symmetric games players should behave symmetrically, and therefore that we should only be interested in symmetric Nash equilibria. Furthermore, it is known that every finite symmetric game has at least one symmetric Nash equilibrium [10, 33], and since a given symmetric equilibrium yields the the same utility to each player, the players should choose the symmetric equilibrium that maximizes their utility.

3.2 Automated negotiation

We here recall the main ideas and definitions from the literature on automated negotiation. We first present the definition of a ‘negotiation domain’, in Section 3.2.1, and then, in Section 3.2.2 we discuss what it means for a negotiation strategy to be ‘optimal’, and why this notion is important.

3.2.1 Definitions

In a classical scenario for automated negotiation two agents $\alpha _1$ and $\alpha _2$ have to make a deal together. The agents have a fixed amount of time to make proposals to one another according to some negotiation protocol [39]. That is, each agent may propose an offer $\omega$ to the other agent, from some given set of possible offers $\Omega$. The other agent may then either accept the proposal or reject it and make a counter proposal $\omega ' \in \Omega$. The agents continue making proposals to each other until either the deadline has passed, or one of the agents accepts a proposal made by the other. Each agent $\alpha _i$ has a utility function $U_i$ that assigns to each offer $\omega \in \Omega$ a utility value $U_i(\omega ) \in \mathbb {R}$, but which is not known to the other agent.¹ When an offer $\omega$ gets accepted the agents receive their respective utility values, $U_1(\omega )$ and $U_2(\omega )$ corresponding to this offer. On the other hand, if the negotiations fail because no proposal is accepted before the deadline, then each agent $\alpha _i$ receives a fixed utility value $rv_i \in \mathbb {R}$, known as its reservation value.

Definition 2

A finite bilateral negotiation domain N is a tuple

$\langle \Omega , U_1, U_2, rv_1, rv_2, \rangle$ where:

• $\Omega$ is a finite set of possible offers.

• $U_1$ and $U_2$ are two utility functions (one for each agent) which are maps from $\Omega$ to $\mathbb {R}$

• $rv_1$, $rv_2 \in \mathbb {R}$ are the reservation values of the respective agents.

An offer $\omega \in \Omega$ is said to be individually rational if $U_1(\omega ) > rv_1$ and $U_2(\omega ) > rv_2$. An offer $\omega$ is said to be dominated by another offer $\omega '$ if $U_1(\omega ') \ge U_1(\omega )$ and $U_2(\omega ') \ge U_2(\omega )$ and at least one of these two inequalities is strict. An offer $\omega$ is said to be Pareto-optimal if it is not dominated by any offer in $\Omega$. We will always assume (w.l.o.g.) that for any two offers $\omega \ne \omega '$ we have either $U_1(\omega ) \ne U_1(\omega ')$ or $U_2(\omega ) \ne U_2(\omega ')$.

We define the Pareto-set of a negotiation domain to be a sorted list $(\omega ^1, \omega ^2, \dots \omega ^n)$, containing exactly the offers in $\Omega$ that are Pareto-optimal and individually rational, and in which the offers are sorted in order of increasing utility for agent $\alpha _1$. That is:²

$$\begin{aligned} rv_1< U_1(\omega ^1)< U_1(\omega ^2)< \dots < U_1(\omega ^n) \end{aligned}$$

(2)

which, by Pareto-optimality, also implies:

$$\begin{aligned} U_2(\omega ^1)> U_2(\omega ^2)> \dots> U_2(\omega ^n) > rv_2 \end{aligned}$$

(3)

Definition 3

Let N be a negotiation domain. For any offer $\omega \in \Omega$, we define its utility vector as the pair $(U_1(\omega ), U_2(\omega ))$. Furthermore, we define the utility space of N as the set of all utility vectors of the offers in $\Omega$. That is, the set $\{(U_1(\omega ), U_2(\omega )) \in \mathbb {R}^2 \mid \omega \in \Omega \}$. Whenever we say that a negotiation domain N is convex, we mean that the utility space of N is a convex set.

When an agent $\alpha _i$ proposes or accepts an offer $\omega$ for which its utility $u_i(\omega )$ is less than for any other offer $\omega '$ it has proposed so far, we say the agent is conceding, or making a concession. When we say that one agent is willing to concede more than the other, we mean that the first agent is willing to accept a lower amount of utility from the final agreement than the other agent.

3.2.2 Optimal negotiation strategies

The main question in automated negotiation is how to decide which offers to propose or accept, and when. One might think that this could be answered by modeling negotiations as an extensive-form game, and then trying to find a subgame perfect equilibrium. However, it is hard to model negotiations in this way, because negotiations take place over continuous time (for a more in-depth discussion, see Section 8.2).

Instead, Nash took an entirely different approach. Rather than trying to derive the optimal negotiation strategy itself, he only derived the the final outcome of a negotiation between two agents that negotiate optimally. Once we know the answer to that question, we can implement a strategy that concedes to, but no further than, that offer. If both agents play such a strategy, then they can only come to exactly that agreement, and therefore it does not matter anymore how exactly they concede towards that deal.³

Nash formulated a number of axioms and argued that, if the agents apply an optimal negotiation strategy, they would agree upon an offer that satisfies those axioms. He then proved that the unique offer that satisfies those axioms is the one that that maximizes the product of the utilities of the two agents.

Definition 4

For any bilateral negotiation domain, its Nash bargaining solution (NBS) is defined as the offer $\omega _{ NBS } \in \Omega$ that satisfies:

$$\begin{aligned} \omega _{ NBS } := \mathop {\mathrm {arg\,max}}\limits _{\omega \in \Omega } \{(U_1(\omega )-rv_1)\cdot (U_2(\omega )-rv_2) \} \end{aligned}$$

However, one of the main assumptions underlying the NBS, is that the negotiation domain is convex. Without this requirement Nash’s proof is no longer valid, and the NBS may not even be well-defined, because there could be multiple offers that maximize the utility product.

It is important to stress here, that even if you know how to determine the theoretically optimal negotiation strategy, it is not easy to actually implement it, because it would depend on the opponent’s utility function, which is usually not known to the agent. Nevertheless, it is still very interesting and important to be able to define the optimal negotiation strategy. Firstly, because it may help researchers to determine how well a given negotiation strategy performs in comparison to the theoretically optimal one. Secondly, even if the opponent’s utility function is not exactly known, the agent may still have an approximate model of this utility function, obtained either at runtime [6], or beforehand, based on background knowledge of the domain [23]. Therefore, the agent could use this estimated opponent utility to at least approximate the theoretically optimal strategy.

3.3 The concession game

In [21] we proposed a new solution for the bargaining problem with finite offer spaces. That is, we modeled the question how far an agent should be willing to concede as a normal-form game, which we called the concession game. We here repeat the definition of this game, although it should be noted that we here use a slightly different definition than the one in our previous paper.

First, in Section 3.3.1, we explain the concession game by means of an example and then, in Section 3.3.2, we present the formal definition. Finally, in Section 3.3.3 we discuss what exactly it means to play a mixed strategy of the concession game.

3.3.1 Example

We here explain the concession game using an example from [21, 35].

Suppose the negotiation domain has two pareto-optimal offers, $\omega ^1$ and $\omega ^2$ which have utility vectors $(U_1(\omega ^1) , U_2(\omega ^1)) = (40, 60)$ and $(U_1(\omega ^2) , U_2(\omega ^2)) = (60, 40)$. Both agents have to choose which would be the very lowest utility they are willing to accept at the end of the negotiations. In this case, each agent has two options: to demand at least 40 utility points, or to demand at least 60 points. If both agents demand at least 60, then their demands are incompatible because there is no offer that yields 60 or more to both agents, so the negotiations fail and the agents will receive their respective reservation values. If $\alpha _1$ demands 60 while $\alpha _2$ demands 40, then the only feasible outcome is $\omega ^2$, so that will be the final agreement, and the agents will receive the respective utility values of $\omega ^2$. Vice versa, if $\alpha _1$ demands 40 while $\alpha _2$ demands 60 then the outcome will be $\omega ^1$. If both players only demand 40, then both $\omega ^1$ and $\omega ^2$ are feasible, so the outcome of the negotiation will depend on the details of their respective negotiation strategies. To abstract away such details, we will simply assume that in that case there is a 50% chance that they will agree on contract $\omega ^1$, and 50% chance it will be $\omega ^2$. The question which utility each agent should demand (40 or 60) can now be seen as a normal-form game, with a payoff matrix as displayed in Table 1, and the optimal strategy can be found by calculating its Nash equilibrium.

Table 1 Payoff matrix of the concession game $C_N$ corresponding to a very simple domain negotiation domain N with two offers $\omega ^1$ and $\omega ^2$ and utility vectors $(U_1(\omega ^1), U_2(\omega ^1)) = (40,60)$ and $(U_1(\omega ^2), U_2(\omega ^2)) = (60,40)$

3.3.2 Formal definition

We are now ready to present the formal definition of a concession game, which is just a generalization of the example above, to the case with n offers.

Definition 5

Let N be a negotiation domain with Pareto-set $(\omega ^1, \omega ^2 \dots \omega ^n)$ (where $\omega ^n$ is the offer that is most preferred by $\alpha _1$ and $\omega ^1$ is most preferred by $\alpha _2$), then the concession game $C_N$ corresponding to N is a normal-form game in which both players have the same set of actions $\mathcal {A}_1 = \mathcal {A}_2 = \{a^1, a^2, \dots , a^n\}$ and the utility functions $u_i$ are given as:

$$\begin{aligned} u_i(a^k, a^m) = {\left\{ \begin{array}{ll} rv_i &{} \text {if\ } k>m\\ U_i(\omega ^k) &{} \text {if\ } k=m\\ \frac{1}{1+m-k} \sum _{j=k}^m U_i(\omega ^j) &{} \text {if\ } k < m \end{array}\right. } \end{aligned}$$

(4)

Fig. 1

If player 1 plays action $a^7$, it means he is willing to accept $\omega ^7$, or any other offer that is better for him (i.e. $\omega ^{7}, \omega ^{8}, \omega ^9$, or $\omega ^{10}$). Similarly, if player 2 plays action $a^{3}$ it means she is willing to accept $\omega ^3$, or anything better for her (i.e. $\omega ^1$, $\omega ^2$, or $\omega ^3$). In that case there is no overlap between the acceptable offers, so no deal can be made

Fig. 2

If player 1 plays action $a^3$, it means he is willing to accept $\omega ^3, \omega ^4, \dots \omega ^{10}$, while, if player 2 plays action $a^{3}$ it means she is willing to accept $\omega ^1, \omega ^2, \dots \omega ^7$. In this case the offers $\omega ^3, \omega ^4, \dots \omega ^7$ are acceptable to both players, so any of these may become the accepted offer

Note that the lower case $u_i$ denotes the utility functions of the concession game $C_N$, while the upper case $U_i$ denotes the utility functions of the negotiation domain N. Furthermore, note that although each action $a^k$ of the game $C_N$ corresponds exactly to one offer $\omega ^k$ of the Pareto-set of N, we make a strict distinction between the two. Specifically, when an agent plays action $a^k$ it means that at the end of the negotiations that agent would be willing to propose or accept any offer that is better than or equal to $\omega ^k$, but will never propose or accept any offer that is worse than $\omega ^k$.

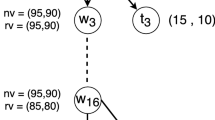
The intuition behind (4) is that if agent $\alpha _1$ chooses action $a^k$ and agent $\alpha _2$ chooses $a^m$, with $k>m$, then there is no offer that can satisfy both agents, so negotiations will fail and the agents receive their respective reservation values. For example, if $\alpha _1$ plays $a^7$ and $\alpha _2$ plays $a^{3}$ (see Fig. 1), it means that $\alpha _1$ is only willing to propose or accept offers $\omega ^{7}$, $\omega ^{8}$, $\omega ^{9}$ and $\omega ^{10}$, while $\alpha _2$ is only willing to propose or accept offers $\omega ^1$, $\omega ^2$, and $\omega ^3$. On the other hand, if $k < m$ it means that any offer $\omega ^j$ with $k \le j \le m$ is acceptable to both agents. We then assume that any of these offers have equal probability of being selected as the final outcome. For example, if $\alpha _1$ plays $a^{3}$ and $\alpha _2$ plays $a^{7}$ (see Fig. 2), it means that $\alpha _1$ is willing to propose or accept offers $\omega ^3, \omega ^4 \dots \omega ^n$, while $\alpha _2$ is willing to propose or accept offers $\omega ^1, \omega ^2 \dots , \omega ^{7}$. So, the offers from $\omega ^3$ to $\omega ^{7}$ are acceptable to both agents.

Finally, if $k = m$ then $\omega ^k = \omega ^m$ is the only acceptable offer, so indeed negotiations will end with $\omega ^k$ as the accepted offer and the agents receive $U_1(\omega ^k)$ and $U_2(\omega ^k)$ respectively (see Fig. 3).

Fig. 3

If both players play action $a^6$, then $\omega ^6$ is the only offer that is acceptable to both players

We should remark that this definition is slightly different from our original definition in [35]. That is, in that other paper we assumed, in the case of $k < m$, that the outcome would be either $\omega ^k$ or $\omega ^m$, while in this paper we assume that any other offer $\omega ^j$ in between them is also a feasible outcome. We think that this new definition more realistic.

Furthermore, we think it is important to stress the following:

Remark 1

The concession game is, in general, not a symmetric game.

Although the utility functions of the two players are both described by (4), the concession game is, in general, not symmetric, because the right-hand side of (4) depends on $U_i$, which is, in general, different for each agent.

In the rest of this paper we will use the notation $u_{i}^{k,m}$ as a shorthand for $u_i(a^k, a^m)$ and $U_{i}^{k}$ as a shorthand for $U_i(\omega ^k)$. The following two identities, which follow directly from (4), will be useful later on.

$$\begin{aligned} u_i^{k,k} = U_i^{k} \quad \text {for\ all\ } k. \end{aligned}$$

(5)

$$\begin{aligned} u_i^{k,m} = \frac{1}{1+m-k}\sum _{j=k}^m u_i^{j,j} \quad \text {if\ } k\le m. \end{aligned}$$

(6)

3.3.3 Execution of a strategy

Let us now discuss what it actually means for a negotiating agent to play a mixed strategy of the concession game.

Suppose that some negotiation domain N has a Pareto-set of size 10, so the Pareto-optimal offers are labeled as $\omega ^1, \omega ^2, \dots \omega ^{10}$. Furthermore, suppose that the strategy selected by our agent has support $\{a^5, a^6\}$. Then, agent $\alpha _1$ will start by making proposals $\omega ^{10}, \omega ^9, \dots$, etc. until reaching⁴$\omega ^6$. At that point, $\alpha _1$ will flip a coin (with probabilities weighted according to its mixed strategy) to determine whether to play $a^5$ or $a^6$, that is: whether to stick with $\omega ^6$ as its final offer, or to concede further to $\omega ^5$. In the first case $\alpha _1$ simply keeps repeating the offer $\omega ^6$, while in the second case it will need to decide when to make that final concession. The agent cannot propose $\omega ^5$ immediately, because that would give $\alpha _2$ enough time to react to it and and play the best reply against $a^5$, which would defeat the whole purpose of playing randomized strategy. Therefore, $\alpha _1$ should first keep repeating $\omega ^6$, and try to wait until the very last moment before making the final concession and propose $\omega ^5$. This also has the advantage that $\alpha _1$ can wait and see if $\alpha _2$ is willing to accept $\omega ^6$, before $\alpha _1$ proposes $\omega ^5$.

We will not go into the details of what exactly is ‘the last possible moment’ because it depends on the details of the negotiation protocol. In a round-based protocol this would be clear, but in a continuous-time protocol the agent would have to make an estimation of what the latest time would be at which it could safely make a proposal without risking that the message arrives too late.

4 The nash equilibria of the concession game

In this section we present our first new main result, namely a characterization of the Nash Equilibria of a concession game. Specifically, we show that any concession game has exactly one Nash equilibrium for every non-empty subset S of $\mathcal {A}$, so, in total, any concession game always has exactly $2^{|\mathcal {A}|}-1$ Nash equilibria. This claim is formalized by two theorems. Theorem 1 was already proved in [35], but for a slightly different definition of the concession game. Therefore, we here state it again and present an updated proof. Theorem 2, on the other hand, was only conjectured in [35], but not yet proven. So, the main contribution of this section is a proof of Theorem 2.

Before we can state and prove these theorems, we first need the following two lemmas, of which the proofs can be found in the Appendix.

Lemma 1

For any concession game $C_N$, if $k\le l< m$ then we have: $u_2^{k,m} < u_2^{k,l}$.

Lemma 2

Let $C_N$ be any concession game with actions $\mathcal {A}$, let S be any proper non-empty subset of $\mathcal {A}$ and let $a^k$ be any action that is not in S, i.e. $a^k \in \mathcal {A} \setminus S$. If one player plays a mixed strategy with support S, then playing $a^k$ is not a best response for the other player.

The proof of Lemma 2 is essentially the same as the proof that we presented earlier in [35]. However, since the definition of the concession game was slightly different in our previous paper, and since also our notation has changed, we think it is useful to present an updated proof. Furthermore, note that Lemma 3 and Theorem 1 are just reformulations of Lemma 2. Nevertheless we feel it is useful, for clarity, to state them separately.

Lemma 3

In any concession game, if one player chooses a mixed strategy with support S, then the best response for the opponent is a mixed strategy with support $S'$, where $S'$ is a subset of S.

Proof

This follows directly from Lemma 2. $\square$

Theorem 1

In any Nash equilibrium of a concession game, the strategies of both players have exactly the same support.

Proof

This follows directly from Lemma 3. $\square$

Theorem 1 says that any Nash equilibrium of a concession game can be identified with a single set of of actions $S \subseteq \mathcal {A}$, which is the support of both players’ strategies. Therefore, from now on whenever we refer to “an equilibrium with support S”, we mean a Nash equilibrium such that both players play a strategy with support S.

The following theorem says that the opposite also holds, and therefore that there is a one-to-one relationship between all the Nash equilibria of the concession game and all the non-empty subsets of $\mathcal {A}$.

Theorem 2

Let $\mathcal {A}$ be the set of actions of a concession game. Then, for any nonempty subset S of $\mathcal {A}$ there exists a Nash-equilibrium in which both players play a strategy with support S.

Proof

We already know from Lemma 3 that, for any arbitrary subset S of $\mathcal {A}$, if agent $\alpha _1$ chooses a mixed strategy $q_1$ with support S, then the best response for $\alpha _2$ is to play a mixed strategy with support $S' \subseteq S$. Thus, we only need to show that $\alpha _1$ can choose $q_1$ in such a way that $\alpha _2$ will be indifferent between all the elements of S (i.e. regardless of which action $a\in S$ agent $\alpha _2$ chooses, $\alpha _2$ will always receive the same expected utility). It is well-known in game theory (e.g. see [35]) that this then implies that any strategy $q_2$ for $\alpha _2$ with support S will be a best-response to $q_1$. Furthermore, from the symmetrical definition of the concession game, it then follows that $\alpha _2$ can also choose $q_2$ in such a way that $\alpha _1$ will be indifferent between all actions in S, which in turn implies that $q_1$ is also a best response to $q_2$, and thus we have constructed a Nash equilibrium in which both strategies have support S.

To simplify notation we will assume that S consists of a number of consecutive actions, i.e. $S =\{a^k,a^{k+1},a^{k+2}, \dots a^{m}\}$. The proof works just as well for subsets with non-consecutive actions, but we would then have to rename the actions. Furthermore, we will assume the reservation values $rv_i$ are zero. It is straightforward to adapt the proof to non-zero reservation values.

Let $q_1$ denote a strategy for $\alpha _1$ with support S, and let $u_2(q_1, a^l)$ denote the expected utility of $\alpha _2$ when $\alpha _1$ plays $q_1$, while $\alpha _2$ plays action $a^l$. Then we have:

$$ u_{2}(q_1,a^l) = \sum _{i=0}^{n} u_2(a^{i},a^{l})\cdot q_{1}(a^i) $$

Then, if we use $q_{1}^{i}$ as a shorthand for $q_{1}(a^i)$ and we make use of the fact that $q_{1}^{i}=0$ for all $a^i \not \in S$, we can rewrite this as:

$$\begin{aligned} u_{2}(q_1,a^l) = \sum _{i=k}^{m} u_2^{i,l}\cdot q_{1}^{i} \end{aligned}$$

(7)

Furthermore, noting that by (4) we have $u_{2}^{i,l} = rv_i = 0$ whenever $i>l$, we can rewrite this as:

$$\begin{aligned} u_{2}(q_1,a^l) = \sum _{i=k}^{l} u_2^{i,l}\cdot q_{1}^{i} \end{aligned}$$

(8)

As explained, we need to show that the values of $q_{1}^{i}$ can be chosen such that $\alpha _2$ is indifferent between all actions $a^l \in S$. In other words, we need the value of $u_{2}(q_1,a^l)$ to be the same for all $a^l \in S$. Combined with (8) this means that we have to show there is some value c such that the following set of equations can be satisfied simultaneously:

$$\begin{aligned} \sum _{i=k}^{l} u_2^{i,l}\cdot q_1^i = c \quad \text {for\ all\ } l \in \{ k,k+1,\dots , m\} \end{aligned}$$

(9)

Note that this is indeed a set of equations, one for each value of l. Specifically, these are $(m-k)+1$ equations with $(m-k)+2$ variables (the variables are $q_1^k, \dots q_1^m$ and c). In addition, since the variables $q_1^i$ are to be interpreted as probabilities, they should also obey the equation $\sum q_1^i = 1$, so in total we have an equal number of variables and equations. We can solve this by first picking an arbitrary positive value for c, and then solving the system of equations (9). Let’s denote the solution obtained in this way by $\hat{c}, \hat{q}_1^k, \hat{q}_1^{k+1}\dots \hat{q}_1^m$. We can then obtain a new solution to (9) by setting $q_1^i =\frac{\hat{q}_1^i}{\sum \hat{q}_1^i}$ and $c = \frac{\hat{c}}{\sum \hat{q}_1^i}$. Note that this is indeed a new solution to the same set of equations, and that the value of c is irrelevant anyway, since we merely want to prove that the left-hand side of (9) is the same for all l. This new solution clearly also satisfies $\sum q_1^i = 1$. Finally, since the $q_1^i$ are to represent probabilities, we must also show that $q_1^i>0$ for all $i \in \{k \dots m\}$.

We will now show by induction that (9) can indeed be solved this way. That is, we start by finding $q_1^k$ from the equation for $l=k$, and then we show that if for some integer t all $q_1^i$ with $i\le t$ are known, then we can use these values to determine $q_1^{t+1}$.

For $l=k$ (9) is: $u_2^{k,k} \cdot q_1^{k} = c$. This is easily solved as:

$$\begin{aligned} q_1^k = \frac{c}{u_2^{k,k}} \end{aligned}$$

(10)

and since both $c >0$ and $u_2^{k,k}>0$ we have that $q_1^k>0$.

Now, suppose that for some integer t we have found the values of $q_1^k, q_1^{k+1} \dots q_1^t$. Then, choosing $l = t+1$ in (9) we get: $\sum _{i=k}^{t+1} u_2^{i,t+1}\cdot q_1^i = c$, which can be rewritten as:

$$\begin{aligned} \sum _{i=k}^t u_2^{i,t+1}\cdot q_1^i \ \ + \ \ u_2^{t+1,t+1}\cdot q_1^{t+1} \quad = \quad c\ \end{aligned}$$

(11)

Note that we already have, by induction, that:

$$\begin{aligned} \sum _{i=k}^t u_2^{i,t}\cdot q_1^i \quad = \quad c \end{aligned}$$

(12)

We can equate the left-hand sides of (11) and (12) to get:

$$ \sum _{i=k}^t u_2^{i,t+1}\cdot q_1^i \ \ + \ \ u_2^{t+1,t+1}\cdot q_1^{t+1} \quad = \quad \sum _{i=k}^t u_2^{i,t}\cdot q_1^i $$

which can then be rewritten as:

$$\begin{aligned} q_1^{t+1}= & {} \frac{\sum _{i=k}^t u_2^{i,t}\cdot q_1^i - \sum _{i=k}^t u_2^{i,t+1}\cdot q_1^i}{u_2^{t+1,t+1}} \nonumber \\= & {} \frac{\sum _{i=k}^t ( u_2^{i,t} - u_2^{i,t+1} )\cdot q_1^i}{u_2^{t+1,t+1}} \nonumber \\= & {} \frac{\sum _{i=k}^t ( u_2^{i,t} - u_2^{i,t+1} )\cdot q_1^i}{U_2^{t+1}} \end{aligned}$$

(13)

Here, to get from the second line to the third line, we used (5) to rewrite the denominator. We now just need to show that this expression is positive. We can see this as follows. Firstly, we know that $U_2^{t+1} > 0$, from (3) and the assumption that $rv_2 = 0$. Secondly, we know by induction that $q_1^i>0$ for all $i\in \{k, k+1, \dots 1\}$. Finally, the fact that $( u_2^{i,t} - u_2^{i,t+1} ) > 0$ follows from Lemma 1. $\square$

Note that, as we explained in the proof, Equations (10) and (13) only yield the unnormalized probabilities, so in order to get the true probabilities, one still needs to divide them by $\sum _{j}q_1^j$. Also note that the result will be independent of the chosen value of c, because this value will be canceled out by this normalization.

For completeness, we mention that if we repeat the calculations in this proof with non-zero reservation values, then (10) and (13) become:

$$\begin{aligned} q_1^k= & {} \frac{c}{u_2^{k,k} - rv_2}\\ q_1^{t+1}= & {} \frac{\sum _{i=k}^t ( u_2^{i,t} - u_2^{i,t+1} )\cdot q_1^i}{U_2^{t-1}-rv_2}\\ \end{aligned}$$

5 Selecting the best equilibrium

In Section 4 we have seen that any concession game has exactly $2^{|\mathcal {A}|}-1$ different Nash equilibria. The question is now which one the players should choose. We therefore present a new solution to the equilibrium selection problem. Although we are mainly interested in its application to the concession game, this solution concept applies just as well to any other 2-player normal-form game.

Our solution is based on the assumption that, given some set of games, for any game in this class, our agent will be playing that game equally often in the role of player 1 as it will be playing that game in the role of player 2. We call this the assumption of role-equifrequency (AoRE).

We make the following claim, which we will formalize and prove in Section 5.6: Under the AoRE a perfectly rational and purely self-interested agent should choose its strategy corresponding to the Nash equilibrium that maximizes the sum of the utilities of the two players.

5.1 The assumption of role-equifrequency

Of course, the AoRE does not always hold, but we can think of three general scenarios where the AoRE can be assumed to be true:

• 1. Our agent is going to play one or more different games, and we know that each game will be repeated a number of times, and we know that for each of these games our agent will play each of the two roles equally often.

• 2. Our agent is going to play one or more different games, and we know that for each game our agent has a 50% chance of playing the role of player 1 and a 50% chance of playing as player 2.

• 3. Our agent is going to play one or more different games, but we have absolutely no knowledge whatsoever about how often our agent is going to play each role of each game.

A good example of the first scenario would be when you are implementing a chess-playing algorithm, because it would be reasonable to assume that this algorithm is going to play black equally often as white. Another example of the first (or second) scenario, would be a tournament setting such as the Automated Negotiating Agents Competition (ANAC) [5]. The third scenario may occur if one is implementing a general-purpose game-playing algorithm, for a broad class of games, rather than for any specific game (as in the research field of general game playing). In that case the designer of the algorithm may have no reason to believe, for any given game, that the agent will play that game as player 1 more often or less often than as player 2. It can therefore be argued that one can assign an equal probability to each role. This is known as the principle of indifference [36].

Apart from these three scenarios, one can also imagine situations in which the AoRE may not be perfectly true, but where it is still a reasonable approximation of reality.

On the other hand, the AoRE may not hold if an algorithm is specifically designed for one particular role in one specific domain. For example, when a negotiating agent represents a phone company that negotiates with its (human) customers on the price and contents of a phone contract. Since the agent always represents the phone company and never the customer, the AoRE clearly does not hold. In such situations our solution concept does not apply.

5.2 Multiple equilibria that maximize utility-sum

As we mentioned above, we claim that a rational agent should choose a Nash equilibrium that maximizes the sum of the players’ utilities (which will be proven below). The next question to answer, then, is how to break the tie if there are multiple such equilibria.

For example, suppose there are two such equilibria $\vec {q} = (q_{1}, q_{2})$ and $\vec {r} = (r_{1}, r_{2})$, with $u_1(\vec {q}) + u_2(\vec {q}) = u_1(\vec {r}) + u_2(\vec {r})$. An agent $\alpha _i$ playing this game cannot simply flip a coin and randomly choose between $q_{i}$ and $r_{i}$, because if it does that, then it is actually playing the strategy $\frac{1}{2}q_{i} + \frac{1}{2}r_{i}$, which may not even be an equilibrium strategy at all. Instead, we need some tie-breaking rule that allows us to deterministically choose one equilibrium. Secondly, we argue that this tie-breaking rule cannot be arbitrary, but has to be based on some rational criterion. After all, if our agent $\alpha _1$ picks an equilibrium $(q_1, q_2)$ without any rational justification, then there is no reason to believe the opponent $\alpha _2$ will pick the same equilibrium, so $\alpha _2$ might pick the other one $(r_1, r_2)$. But then the agents end up playing the joint strategy $(q_1, r_2)$ which, again, may not be an equilibrium at all, and which may actually yield very low utility to $\alpha _1$.

Fig. 4

A flowchart of our solution to the equilibrium selection problem

We argue that the most rational solution to break ties, is to pick the equilibrium that minimizes the absolute difference between the utilities of the two agents $|u_1(\vec {q}) - u_2(\vec {q})|$, because it can be considered the most ‘symmetrical’ solution. After all, if instead agent $\alpha _1$ picks an asymmetrical equilibrium that is very good for itself, but bad for the other agent $\alpha _2$, then it is reasonable to assume agent $\alpha _2$ reasons in the same way, and also picks an equilibrium that is very good for itself, but bad for $\alpha _1$. This, of course, means that the two agents pick different equilibria. So, the agents should neither pick the most selfish equilibrium, nor the most unselfish equilibrium. Instead, they should choose the solution that minimizes the utility-difference.

5.3 Degenerate equilibria

Even with the tie-breaking rule of the previous subsection, it could still happen that among those equilibria that maximize the utility-sum there are multiple equilibria that all minimize the absolute utility-difference. That would mean that for each of these equilibria $\vec {q}$ there is another equilibrium $\vec {r}$ for which the utility vector $\vec {u}(\vec {r})$ is either exactly the same as $\vec {u}(\vec {q})$, or is the ‘reflection’ of $\vec {u}(\vec {q})$ (e.g. $\vec {u}(\vec {q}) = (60, 40)$ and $\vec {u}(\vec {r}) = (40, 60)$).

Definition 6

For any pair of numbers $(a,b) \in \mathbb {R}^2$ we define its reflection to be the pair (b, a).

We say that such solutions are degenerate, and we argue that in that there is no rational and deterministic way to choose among several degenerate solutions. Therefore all degenerate solutions need to be discarded (in Section 8.1 we present a more detailed discussion about why this is necessary).

Definition 7

We say a Nash equilibrium $\vec {q}$ is degenerate if there exists at least one other Nash equilibrium $\vec {r}$ such that either they have identical utility vectors, or the utility vector of $\vec {r}$ is the reflection of the utility vector of $\vec {q}$. That is:

$$\begin{aligned} (u_1(\vec {q}), u_2(\vec {q})) = (u_1(\vec {r}), u_2(\vec {r})) \quad \text {or} \quad (u_1(\vec {q}), u_2(\vec {q})) = (u_2(\vec {r}), u_1(\vec {r})). \end{aligned}$$

5.4 Our solution to the equilibrium selection problem, summarized

In summary, our solution to the equilibrium selection problem works as follows (see also Fig. 4):

• 1. Calculate all Nash equilibria.

• 2. Discard those Nash equilibria that are degenerate. If the set of non-degenerate Nash equilibria is empty, then return without any result.

• 3. Among the non-degenerate equilibria, pick the equilibrium $\vec {q}$ that maximizes the utility-sum $u_1(\vec {q}) + u_2(\vec {q})$.

• 4. If there is more than one such equilibrium, break ties by choosing the one that minimizes the absolute utility-difference $|u_1(\vec {q}) - u_2(\vec {q})|$ (there can only be one such equilibrium, because otherwise it would be degenerate).

If all Nash equilibria are degenerate, then our solution concept does not return any result. However, this is a very extreme situation, and at this point it is not even clear to us whether this situation can even happen at all.

One could say that Step 3 picks the equilibrium that maximizes ‘social welfare’, and that Step 4 picks the one that maximizes ‘fairness’. However, we feel it is important to stress the following:

Remark 2

Our solution concept has nothing to do with social welfare maximization or fairness maximization. We argue that our solution concept is optimal for purely self-interested agents that do not care about social welfare or fairness.

Our only motivation for steps 3 and 4 is that they are optimal from a purely self-interested point of view, as we will show in Section 5.6. So, the fact that our solution concept happens to maximize social welfare and fairness is just a coincidental side effect, and not an intentional goal.

Furthermore, we should remark that other authors have also studied the maximization of social welfare for purely-self interested reasons. For example, in [46] the authors mentioned that it could be useful for the purpose of building social relationships with agents that you may encounter again in the future. However, we should stress that in our case we are not considering such social relationships. Our arguments still hold even if each opponent is only encountered once.

5.5 An exception

Although we argued above that all degenerate equilibria should be discarded, there is one situation where we can make an exception to this rule. That is, a degenerate Nash equilibrium $\vec {q}$ does not need to be discarded if the following two conditions are satisfied:

• There does not exist any equilibrium $\vec {r}$ for which $\vec {u}(\vec {r})$ is the reflection of $\vec {u}(\vec {q})$ (we say that $\vec {q}$ is only weakly degenerate).

• There is some possibility for the players to communicate.

In this case, the equilibria the agents have to choose between all have identical utility vectors, so the agents do not care which of them is selected, as long as they both select the same one. This means the agents could just use any arbitrary tie-breaking rule, as long as they coordinate with each other to ensure they both select the same equilibrium. For example, one agent could just pick an arbitrary equilibrium, announce it to the other agent, and the other agent then simply picks the same one. Note, however, that this only works for weakly degenerate equilibria, because otherwise one agent would prefer one equilibrium, while the other would prefer the other, so neither of the two agents would be willing to follow the choice of the other.

5.6 Optimality of our solution

In this section we formally show that, under the AoRE, our solution concept that we described above is, in a certain sense, optimal. The main idea behind our notion of optimality, is that we do not focus on what is the best strategy for an individual game, but instead we try to find the optimal algorithm that selects a strategy for any game G in some given class of games $\mathcal {G}$. Selecting such an algorithm can then itself be seen as a kind of game, and even though the games $G \in \mathcal {G}$ may not be symmetrical, the AoRE ensures that this ‘meta-game’, is in fact symmetrical, and we already know how to select an optimal Nash equilibrium for such games, as explained in Section 3.1.

We will here always assume that $\mathcal {G}$ is some set of 2-player normal-form games, and that $\mathcal {P}$ is function $\mathcal {G}\times \{1,2\} \rightarrow \mathbb {R}^+$. The value $\mathcal {P}(G,i) \in \mathbb {R}^+$ represents the frequency or probability that our algorithm will be playing game G as player i.

Definition 8

A strategy selection algorithm (SSA) T for $\mathcal {G}$ is an algorithm that can take as its input any pair (G, i) with $G \in \mathcal {G}$, and $i\in \{1,2\}$ and outputs a mixed strategy for player i in the game G. The set of all possible SSAs for $\mathcal {G}$ is denoted as $\mathcal {T}_\mathcal {G}$.

We will not give a precise formalization of the set $\mathcal {T}_\mathcal {G}$, but one could think of it as the set of all Turing machines that take as input a string representing a game G and a number i, and that output some string representing a strategy for player i in game G. One example of an SSA could be an implementation of the Lemke-Howson algorithm [29].

For any SSA we want to assign a score to it that represents how well it performs. This score depends on the frequency with which it plays each of the games in $\mathcal {G}$ in each role, and on the SSA applied by its opponents.

Definition 9

Let $\mathcal {G}$ be a set of games, and $\mathcal {P}$ be a function $\mathcal {G} \times \{1,2\} \rightarrow \mathbb {R}^+$. Furthermore, let T and $T'$ be two SSAs. Then we define two utility functions $\mathcal {U}_I$ and $\mathcal {U}_ II$, with respect to $\mathcal {P}$, as follows:⁵

$$\begin{aligned} \mathcal {U}_I(T,T') := \sum _{G\in \mathcal {G}} \mathcal {P}(G,1) \cdot u_1(T(G,1),T'(G,2))\nonumber \\ + \ \mathcal {P}(G,2) \cdot u_2(T'(G,1),T(G,2)) \end{aligned}$$

(14)

$$\begin{aligned} \mathcal {U}_ II (T,T') := \sum _{G\in \mathcal {G}} \mathcal {P}(G,1) \cdot u_2(T(G,1),T'(G,2))\nonumber \\ + \ \mathcal {P}(G,2) \cdot u_1(T'(G,1),T(G,2)) \end{aligned}$$

(15)

The expression $\mathcal {U}_I(T,T')$ represents the total expected utility that T would obtain when playing against $T'$, while $\mathcal {U}_{ II }$ represents the expected utility obtained by its opponent $T'$.

In (14) the term $u_1(T(G,1),T'(G,2))$ represents the expected utility obtained by T when it plays the role of player 1 in game G, while its opponent applies algorithm $T'$, and $u_2(T'(G,1),T(G,2))$ is the utility that T receives when it plays as player 2 in game G against an opponent that applies $T'$. Similarly, in the two corresponding terms in (15) represent the utility values obtained by $T'$ in those same games.

Furthermore, note that in both equations, the expression $\mathcal {P}(G,i)$ represents the probability or frequency that T will play the game G in the role of player i. That is, it refers to the SSA that appears as the first argument in $\mathcal {U}_I$ or $\mathcal {U}_ II$

Definition 10

We say that $\mathcal {P}$ satisfies the Assumption of Role-Equifrequency (AoRE) if for all games $G\in \mathcal {G}$ we have $\mathcal {P}(G,1) = \mathcal {P}(G,2)$.

Definition 11

Let $\mathcal {G}$ be some set of games and $\mathcal {P}$ some weight distribution over $\mathcal {G}\times \{1,2\}$. Then, the meta-game for $\mathcal {P}$, denoted $\Gamma _{\mathcal {P}}$, is a 2-player normal-form game, defined as follows:

• For both players, their set of actions is given by the set of SSAs for $\mathcal {G}$. That is: $\mathcal {A}_I = \mathcal {A}_{ II } = \mathcal {T}_\mathcal {G}$.

• The utility functions are given by $\mathcal {U}_I$ and $\mathcal {U}_ II$, as in Def. 9 (w.r.t. $\mathcal {P}$).

Note that we use roman numerals I and $II$ as indices for the players of the meta-game, in order to clearly distinguish them from the players 1 and 2 of the individual games $G \in \mathcal {G}$. To be clear: if some agent $\alpha$ plays the meta-game in the role of player I, it means that $\alpha$ will play each game G with probability (or frequency) $\mathcal {P}(G,1)$ as player 1, and with probability (or frequency) $\mathcal {P}(G,2)$ as player 2.

We feel we should stress the following:

Remark 3

Even though each game $G\in \mathcal {G}$ may be repeated several times, this does not mean the meta-game can be seen as a repeated game.

Note that according to Def. 8 an SSA only takes as its input the description of a single game plus the index of the role to play. This means it does not accept the history of any previously played games as its input. In other words, it does not remember any earlier games, so each game is played as an entirely new game, independent from anything that happened in previous games, and from any opponents it has played against before. Therefore, it is not playing a repeated game.

Lemma 4

If $\mathcal {P}$ satisfies the AoRE, then $\Gamma _\mathcal {P}$ is a symmetric game.

Proof

We need to show that for any T and $T'$ we have $\mathcal {U}_I(T,T') = \mathcal {U}_ II (T',T)$. Thanks to the AoRE we can define $\mathcal {P}(G) := \mathcal {P}(G,1) = \mathcal {P}(G,2)$, so we can rewrite (14) as:

$$\begin{aligned} \mathcal {U}_I(T,T') = \sum _{G\in \mathcal {G}} \mathcal {P}(G) \cdot \Big ( u_1(T(G,1),T'(G,2)) + u_2(T'(G,1),T(G,2))\Big ) \end{aligned}$$

Similarly, we can rewrite (15) as:

$$\begin{aligned} \mathcal {U}_ II (T',T) = \sum _{G\in \mathcal {G}} \mathcal {P}(G) \cdot \Big ( u_2(T'(G,1),T(G,2)) + u_1(T(G,1),T'(G,2))\Big ) \end{aligned}$$

These two expressions are indeed equal. $\square$

In the following, for any game $G \in \mathcal {G}$, we will use the notation $q\rightsquigarrow q'$ to denote that $q'$ is a best response to $q$, and $q\leftrightsquigarrow q'$ denotes that $(q, q')$ is a Nash equilibrium. Similarly, given some distribution $\mathcal {P}$, we will use the notation $T \Rightarrow T'$ to denote that SSA $T'$ is a best response to T in the meta-game $\Gamma _\mathcal {P}$, and $T \Leftrightarrow T'$ to denote that T and $T'$ form a Nash equilibrium of the meta-game $\Gamma _\mathcal {P}$.

Lemma 5

$T'$ is a best response to T iff for all games $G \in \mathcal {G}$ and all roles $i \in \{1,2\}$, the strategy $T'(G,i)$ selected by $T'$ is a best response to the strategy selected by T in the opposing role. That is:

$T \Rightarrow T'$ iff for all $G \in \mathcal {G}$ we have $T(G,1) \rightsquigarrow T'(G,2)$ and $T(G,2) \rightsquigarrow T'(G,1)$.

Proof

Suppose that $T \Rightarrow T'$ but there is some game $\hat{G}$ for which we do not have $T(\hat{G},1) \rightsquigarrow T'(\hat{G},2)$. This means that there is some other strategy $q$ for player 2 in game $\hat{G}$ for which $T(\hat{G},1) \rightsquigarrow q$. Let us now define a new SSA $T^\dagger$ as follows:

$$\begin{aligned} T^\dagger (G,i) = {\left\{ \begin{array}{ll} q&{} \text {if\ } (G,i) = (\hat{G},2) \\ T'(G,i) &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

It should be clear that if in (15) we replace $T'$ by $T^\dagger$ then all terms stay the same, except for the term $u_2(T(\hat{G},1) , T'(\hat{G},2))$, which will be replaced by the term $u_2( T(\hat{G},1) , q)$. And since $q$ is a best response to $T(\hat{G},1)$ the new term must be greater than the old term, so we have $\mathcal {U}_ II (T,T') < \mathcal {U}_ II (T,T^\dagger )$, which is in contradiction with the assumption that $T \Rightarrow T'$. This proves that we must have $T(G,1) \rightsquigarrow T'(G,2)$, and in a similar way we can show that $T(G,2) \rightsquigarrow T'(G,1)$ must also hold.

To prove the other direction, assume that for all G in $\mathcal {G}$ we have $T(G,1) \rightsquigarrow T'(G,2)$ and $T(G,2) \rightsquigarrow T'(G,1)$, while we do not have $T \Rightarrow T'$. So, there must be some $T^\dagger$ with $\mathcal {U}_ II (T,T') < \mathcal {U}_ II (T,T^\dagger )$. We see from (15) that this means there must be some game G such that either $u_2(T(G,1), T'(G,2)) < u_2(T(G,1), T^\dagger (G,2))$ or $u_1(T'(G,1), T(G,2)) < u_2(T^\dagger (G,1), T(G,2))$. But the first of these inequalities contradicts the assumption that $T(G,1) \rightsquigarrow T'(G,2)$, while the second contradicts $T(G,2) \rightsquigarrow T'(G,1)$. $\square$

Corollary 1

Two SSAs form a Nash equilibrium of the meta-game, if and only if for each game $G \in \mathcal {G}$ the strategies they select form a Nash equilibrium of G. That is:

$T \Leftrightarrow T'$ iff for all G in $\mathcal {G}$ we have: $T(G,1) \leftrightsquigarrow T'(G,2)$ and $T'(G,1) \leftrightsquigarrow T(G,2)$.

Proof

This follows directly from Lemma 5. $\square$

Lemma 6

For any $\mathcal {G}$ and any $\mathcal {P}$ that satisfies the AoRE, the meta-game $\Gamma _\mathcal {P}$ has at least one pure symmetric Nash equilibrium.

Proof

For each game $G \in \mathcal {G}$, pick a Nash equilibrium $(q_1,q_2)$ of that game. This equilibrium does not need to be symmetric, and its strategies do not need to be pure. Then, simply define $T(G, i) = q_i$. Note that by Corollary 1 we then have that (T, T) is a Nash equilibrium of $\Gamma _\mathcal {P}$, which is clearly symmetric. Furthermore, note that it is a pure equilibrium, despite the fact that the strategies selected by T may be mixed strategies. This is because in the definition of $\Gamma _\mathcal {P}$ each SSA T is considered to be a single action. $\square$

Definition 12

We say an SSA T is rational if the following two conditions both hold:

• T is a best response to itself (i.e. T vs. T forms a pure symmetric Nash equilibrium of the meta-game).

• for every game $G \in \mathcal {G}$ the Nash equilibrium (T(G, 1), T(G, 2)) is non-degenerate.

Note that if T is a best response to itself, then, by Corollary 1 the pair (T(G, 1), T(G, 2)) is indeed a Nash equilibrium of G.

Definition 13

Suppose that $\mathcal {P}$ satisfies the AoRE. Then we say T is an optimal SSA (w.r.t. $\mathcal {P}$) if it is rational and, in addition, the following condition also holds:

• For any other rational SSA $T'$ we have $\mathcal {U}_I(T,T) \ge \mathcal {U}_I(T',T')$.

Note that since, in this case, the meta-game $\Gamma _\mathcal {P}$ is symmetrical, this condition can be equivalently stated as $\mathcal {U}_ II (T,T) \ge \mathcal {U}_ II (T',T')$.

We are now ready to state the next main theorem of this paper, which implies that our solution concept, described in Section 5, is optimal in the sense of Definition 13.

Theorem 3

If $\mathcal {P}$ satisfies the AoRE, and T is a rational SSA such that for any $G\in \mathcal {G}$ the pair (T(G, 1) , T(G, 2)) is a Nash equilbrium that maximizes $u_1(\vec {q}) + u_2(\vec {q})$ among all non-degenerate Nash equilibria $\vec {q}$ of G, then T is an optimal SSA w.r.t. $\mathcal {P}$.

Proof

In this proof we will use the notation $\tau _i$ as a shorthand for T(G, i) and $\tau _i'$ as shorthand for $T'(G,i)$.

Suppose the contrary, i.e. that T is not optimal, which means there is some rational SSA $T'$ such that $\mathcal {U}_I(T,T) < \mathcal {U}_I(T',T')$. We then see from Equation (14) that there must be at least one game G for which we have:

$$\begin{aligned} {\begin{matrix} &{} \mathcal {P}(G,1) \cdot u_1(\tau _1,\tau _2) \quad + \quad \mathcal {P}(G,2) \cdot u_2(\tau _1,\tau _2) \quad < \\ &{} \quad \quad \mathcal {P}(G,1) \cdot u_1(\tau _1',\tau _2')\quad + \quad \mathcal {P}(G,2) \cdot u_2(\tau _1',\tau _2') \end{matrix}} \end{aligned}$$

and thanks to the AoRE we can remove the factors $\mathcal {P}(G,1)$ and $\mathcal {P}(G,2)$, so we get:

$$\begin{aligned} {\begin{matrix}&u_1(\tau _1,\tau _2) + u_2(\tau _1,\tau _2) \quad < \quad u_1(\tau _1',\tau _2') + u_2(\tau _1',\tau _2') \end{matrix}} \end{aligned}$$

Note that by Corollary 1 the pairs $(\tau _1,\tau _2)$ and $(\tau _1',\tau _2')$ are both Nash equilibria of G, and since T and $T'$ were both assumed rational, they are both non-degenerate. So, this inequality is in contradiction to the assumption that $(\tau _1,\tau _2)$ maximizes the utility-sum among all non-degenerate Nash equilibria. $\square$

6 A more efficient algorithm

In Section 4 we have seen that any concession game has $2^{|\mathcal {A}|} - 1$ equilibria. This means it would be intractable to calculate all of them, and therefore we cannot apply the solution to the equilibrium selection problem that we presented in Section 5 in a brute-force manner. Luckily, however, we will show in this section that, in the case of the concession game, we can apply our solution without explicitly calculating all equilibria.

Let S be any subset of $\mathcal {A}$. Then we define the two extreme points of S as the first and last element of S (viewed as a list, sorted as in (2)) respectively. For example, if $S = \{a^3, a^4, a^7,a^{12}\}$ then the extreme points are $a^3$ and $a^{12}$. Formally, $a^k$ and $a^m$ are the extreme points of S iff for all $a^l \in S$ we have $U_1(\omega ^k) \le U_1(\omega ^l) \le U_1(\omega ^m)$.

In the following, we will use the notation $u_i(S)$ to denote the expected utility for agent $\alpha _i$ when both players follow the equilibrium with support S.

We first need the following two lemmas, which are proven in the Appendix:

Lemma 7

For any concession game $C_N$, if $k\le l \le m$ then we have $u_1^{k,l} \le u_1^{k,m}$.

Lemma 8

For any concession game $C_N$, if $k\le l\le m$ then we have $u_2^{l,m} \le u_2^{k,m}$.

We can then use these two lemmas to prove the following important lemma.

Lemma 9

Let $C_N$ be a concession game with actions $\mathcal {A}$. Then for any subset S of $\mathcal {A}$ with extreme points $a^k$ and $a^m$, and for any $i\in \{1,2\}$ we have:

$$\begin{aligned} u_i(S) \le u_i^{k,m}. \end{aligned}$$

Proof

Let S be a set for which $a^k$ and $a^m$ are the extreme points (with $k<m$). For $u_1(S)$ we then have:

$$ u_1(S) \ \ = \ \ \sum _{a^l \in S} q_2^l\cdot u_1^{k,l} \ \ \le \ \ \sum _{a^l \in S} q_2^l\cdot u_1^{k,m} \ \ = \ \ u_1^{k,m} $$

Here, the first equation comes from (1), by fixing action $a^k$ for player 1 (which is allowed because in a Nash equilibrium each player is indifferent between the various actions in its support), and the inequality in the middle comes from Lemma 7.

In a similar way, using Lemma 8, we obtain:

$$\begin{aligned} u_2(S) \ \ = \ \ \sum _{a^l \in S} q_1^l\cdot u_2^{l,m}\ \ \le \ \ \sum _{a^l \in S} q_1^l\cdot u_2^{k,m} \ \ = \ \ u_2^{k,m} \end{aligned}$$

$\square$

Lemma 9 is useful, because it means that $u_1^{k,m} + u_2^{k,m}$ is an upper bound for the utility sum $u_1(S) + u_2(S)$, which can be calculated quickly without determining the actual Nash equilibrium corresponding to S. If this upper bound is lower than the utility-sum of any other support $S'$ that we have already calculated and that is non-degenerate, then we can immediately discard the equilibrium with support S, as well as any other equilibrium for which the support has the same extreme points.

Lemma 10

Let $C_N$ be a concession game with actions $\mathcal {A}$. Then, for any subset S of $\mathcal {A}$ there exists an action $a^t\in \mathcal {A}$ such that $u_1(S) + u_2(S) \le u_1^{t,t} + u_2^{t,t}$.

Proof

We denote the extreme points of S by $a^k$ and $a^m$. Furthermore, we define $a^t$ to be the action in S such that:

$$\begin{aligned} t = \mathop {\mathrm {arg\,max}}\limits _{j \in \{k, k+1, \dots , m\}} u_1^{j,j} + u_2^{j,j} \end{aligned}$$

Then we have:

$$\begin{aligned} u_1(S) + u_2(S)\le & {} u_1^{k,m} + u_2^{k,m}\\= & {} \frac{1}{m-k+1} \sum _{j=k}^m u_1^{j,j} + u_2^{j,j}\\\le & {} \frac{1}{m-k+1} \sum _{j=k}^m u_1^{t,t} + u_2^{t,t}\\= & {} (u_1^{t,t} + u_2^{t,t}) \cdot \frac{1}{m-k+1} \sum _{j=k}^m 1\\= & {} u_1^{t,t} + u_2^{t,t}\\ \end{aligned}$$

where the first line comes from Lemma 9, the second line is from (6), and the third line holds by our definition of t. $\square$

Lemma 10 implies that, to calculate our solution concept, most of the times we can ignore all subsets S with $|S |>1$, because for such subsets there will always be some action $a^t$ such that the Nash equilibrium with support $\{a^t\}$ will have a higher utility sum. The only case in which we cannot ignore such subsets, is when the equilibrium with support $\{a^t\}$ happens to be degenerate.

Theorem 4

Let $C_N$ be a concession game with actions $\mathcal {A}$. If there is a unique action $a^*\in \mathcal {A}$ that maximizes the utility sum $u_1(a,a) + u_2(a,a)$, then our solution concept can be calculated in linear time (i.e. in $O(|\mathcal {A}|)$) and it will return the Nash equilibrium with support $\{a^*\}$.

Proof

Clearly, to determine $a^*$ and to determine that it is unique, we only need to calculate the values $u_1(a,a) + u_2(a,a)$ for each $a\in \mathcal {A}$, so this can indeed be done in $O(|\mathcal {A}|)$. The fact that $\{a^*\}$ is indeed the solution follows from the fact that for any other subset S with $|S |= 1$ we know that it is dominated by $\{a^*\}$ (by definition of $a^*$), and for any subset S with $|S |> 1$, we know by Lemma 10 that it is dominated by some subset with $|S |= 1$ (namely $S = \{a^t\}$, with $a^t$ as in that Lemma). Furthermore, the fact that $a^*$ is unique implies that the equilibrium with support $\{a^*\}$ is non-degenerate. $\square$

Table 2 The expected utility vectors for the 7 Nash equilibria of the concession game corresponding to the Nice-or-Die negotiation domain

7 Examples

In this section we present two simple example negotiation domains and for both of them we calculate our optimal solution and compare it to the NBS. Furthermore, we calculate the optimal solutions of all domains that were used in ANAC 2012 and 2013, and show that they can be calculated quickly.

7.1 Utility-sum vs. Utility-product

We will now give a simple example that clearly shows how a negotiation algorithm that aims to maximize the utility-sum, performs better than an algorithm that aims to maximize the utility-product.

Imagine we have a negotiation domain with only two offers: $\Omega = \{\omega ^1, \omega ^2\}$, and the following utility functions:

$$\begin{aligned} U_{1}(\omega ^{1}) = 3 \quad&\quad U_{2}(\omega ^{1}) = 10 \\ U_{1}(\omega ^{2}) = 6 \quad&\quad U_{2}(\omega ^{2}) = \,\,6 \end{aligned}$$

Note that $\omega _1$ maximizes the utility-sum $(10 + 3 > 6+6)$, while $\omega ^2$ maximizes the utility-product $(6\cdot 6 > 10\cdot 3)$.

Furthermore, suppose that we have two agents, $\alpha$ and $\beta$, that will negotiate over this domain twice, once with $\alpha$ having utility function $U_1$ and once with $\beta$ having utility function $U_1$. In other words, they are playing the concession game twice, with their roles flipped between the two games, so the AoRE holds.

We then see that if the agents both applied a strategy that always aims to maximize the utility-product, then they would always agree on $\omega ^2$. So, in the first negotiation, agent $\alpha$ would receive $U_1(\omega ^2)$ and agent $\beta$ would receive $U_2(\omega ^2)$, which means they both receive 6 utility points. In the second negotiation, since the utility functions are now swapped, agent $\alpha$ would receive $U_2(\omega ^2)$ and agent $\beta$ would receive $U_1(\omega ^2)$. Again, this means they both receive 6 points, so, summed over both sessions, the two agents would each receive a total of 12 utility points.

On the other hand, if they both aimed to maximize the utility-sum, then they would always agree on $\omega ^1$. So, in the first negotiation $\alpha$ would receive $U_1(\omega ^1) = 10$ and $\beta$ would receive $U_2(\omega ^1) = 3$. In the second negotiation, $\alpha$ would receive $U_2(\omega ^1) = 10$ and $\beta$ would receive $U_1(\omega ^1) = 3$. This means that both agents would receive a total of 13 utility points.

Indeed, both agents are better off if they aim to maximize the utility sum, rather than the utility product.

7.2 The nice-or-die domain

The Nice-or-Die domain is a negotiation domain that has been used in several editions of ANAC [5, 46]. It has only three offers, with the following utility vectors:⁶$\vec {U}(\omega ^1) = (160\ ,\ 1000)$, $\vec {U}(\omega ^2)=(299\ ,\ 299)$ and $\vec {U}(\omega ^3) = (1000,\ 160)$. This domain is especially interesting because its Nash bargaining solution is not well-defined. After all, both $\omega ^1$ and $\omega ^3$ maximize the product of the agents’ utilities. We show that our solution concept, on the other hand, does yield a well-defined optimal solution.

Since the Nice-or-Die domain contains three offers, the corresponding concession game has $2^3-1 = 7$ Nash equilibria. Using (1), (10), and (13) we can calculate the utility vectors of each of these equilibria. The results are displayed in Table 2. We see that both $\{a^1\}$ and $\{a^3\}$ maximize the utility sum $1000 + 160 = 1160$, and they also both have the same utility difference $|1000-160 |= 840$. Therefore, these are degenerate solutions and we have to discard them. The next best equilibria are $\{a^1,a^2\}$ and $\{a^2, a^3\}$, but again they are degenerate so we have to discard them as well. Finally, the next best equilibrium is the one with support $\{a^2\}$, which yields an expected value of 299 utility points for each agent, so this is the final outcome of our solution concept.

7.3 The ANAC 2012 and 2013 domains

Apart from the Nice-or-Die domain, we have also calculated our solution concept for all other domains that were used in in ANAC 2012 and 2013 (with reservation values always set to 0). Thanks to Theorem 4 the calculation of the solution took, in all cases, no more than a fraction of a second (on a laptop with Intel Core i7-8750H@2.20GHz CPU and 32 GB RAM). We found that in most cases our solution concept yields exactly the same result as the Nash Bargaining solution. Therefore, in Table 3 we only show those few domains for which it was different (for clarity we display the utilities as values between 0 and 1,000). We also note that in all cases the support of the optimal solution had size 1. In other words, in each of these domains there is a single offer that can be considered the optimal solution, and there is no need to apply a mixed strategy.

Table 3 Size: the number of offers in the domain

8 Discussion

In this section we will go into a more in-depth discussion of a number of details that we mentioned earlier in the paper.

8.1 Degenerate equilibria

One point of critique that one might have against our approach, is the fact that we simply discard degenerate equilibria. Let us therefore explain our justification for this decision in a bit more detail.

Firstly, one should understand that the appearance of degenerate equilibria is a very extreme case, because it requires a perfect symmetry between the two equilibria. That is, they are only degenerate if the values of their utility vectors are exactly the same. For example, suppose we have two equilibria that yield utility vectors of (40, 60) and (60, 40), respectively. If we make even the slightest perturbation to one of these values, so that, for example, the first utility vector actually becomes $(40 + \epsilon ,60)$ for some very small value $\epsilon$, then they are no longer degenerate. Therefore, some might argue that degenerate equilibria are a purely theoretical phenomenon that cannot exist in practice, and therefore, that it does not matter what we do with degenerate solutions.

On the other hand, if one insists that perfectly symmetrical situations do exist, then one should also accept that in such a situation it is strictly impossible for any decision-making algorithm to make a rational choice between the options (otherwise the situation would not be perfectly symmetrical). Therefore, any choice between two degenerate equilibria should either be randomized, or based on some non-rational criterion.

To make this clearer, we will discuss a few possible ways an agent might choose between two degenerate equilibria $(q_1,q_2)$ and $(r_1,r_2)$ to avoid discarding them, but we will argue that none of these solutions is actually feasible:

• 1. The agent chooses randomly.

• 2. The agent uses some some criterion that is rational, but not based on the given utility values, to make a choice.

• 3. The agent uses an entirely arbitrary criterion, which is not based on any form of rationality, to make a choice.

• 4. The two agents jointly agree to apply some (arbitrary) tie-breaking criterion to make a choice.

The first of these options is not feasible, because if you flip a coin to choose between strategies $q_1$ and $r_1$, you are in reality playing an entirely different mixed strategy, namely the strategy $\frac{1}{2}\cdot q_1 + \frac{1}{2}\cdot r_1$, which may not even be an equilibrium strategy at all. And even if this does happen to be an equilibrium strategy, it means that the agent is actually choosing a different equilibrium, rather than any of the two degenerate equilibria. In other words, the agent has discarded the two degenerate equilibria after all.

If the second option was feasible, it would mean that the given utility functions $u_1$ and $u_2$ actually do not faithfully capture the rational decision-making process of the agent. In other words, the agent is in reality basing its decisions on a pair of alternative utility functions $u_1'$ and $u_2'$, which are slightly different from the given ones, and which break the tie between the two equilibria. But that would mean that the two equilibria only seemed degenerate because their values were expressed with the incorrect utility functions $u_1$ and $u_2$, while in reality they are not degenerate at all (w.r.t. $u_1'$ and $u_2'$). But then we still have not solved the problem of what to do if we encounter two equilibria that are truly degenerate (w.r.t. $u_1'$ and $u_2'$).

In the third case, one can imagine, for example, that the various actions of the game have names, and that whenever the agent has to choose between degenerate equilibria, it picks the one for which the support contains the action that comes first in alphabetical order. This criterion is only used to break the tie, and there is no rational justification to prefer that specific tie-breaker over any other one. To explain why this does not work, let us say that our agent selects strategy $q_1$. Now, since this choice was based on an arbitrary tie-breaking criterion, it would be impossible for the opponent to reason which strategy our agent has chosen. Therefore, the opponent will have to guess which strategy is its best response, so there is a 50% probability that the opponent will pick $q_2$, and 50% probability that the opponent will pick $r_2$. Alternatively, the opponent might also use an arbitrary tie-breaking criterion, but since our agent cannot know which one, from our agent’s point of view there will still be a 50% probability the opponent picks $q_2$, and 50% probability the opponent picks $r_2$. But that means that our agent’s best response to the opponent is neither $q_1$, nor $r_1$. Instead, our agent should actually pick the strategy that is a best response against $\frac{1}{2}\cdot q_2 + \frac{1}{2}\cdot r_2$. Therefore, if both agents are rational, neither of the two would actually choose their strategy using this non-rational criterion, because both agents would have reason to deviate to a different strategy. This means that, just as for point 1, the agents end up playing an entirely different equilibrium, which means they have effectively discarded the two degenerate equilibria after all.

The final option one might consider, is that the two agents could somehow jointly coordinate to pick the same equilibrium. For example, one agent could announce its selection so that the other can follow and select the same equilibrium, or they could in some way jointly agree which equilibrium to select. However, as we already explained in Section 5.5, this only works if the utility vectors of those equilibria are identical. Otherwise, there is one equilibrium that favors one agent, while another equilibrium favors the other agent. Given that the situation is perfectly symmetrical between the two agents, either both agents should be willing to accept the least favorable option, or neither of them. In the first case we still do not have any rational criterion to select the equilibrium, so the only way out would be for the two agents to flip a coin together, but as we argued in the Introduction, and also below in Section 8.3, that would violate one of the basic assumptions of our work. In the second case, neither of the two equilibria would be chosen by the agents, so again they are discarded after all.

8.2 Negotiations as an extensive-form game

In Section 3.2.2 we mentioned that negotiations are difficult to model as extensive-form games, because they take place in continuous time. We will here discuss this in some more detail.

Of course, one could try to model time as being composed of very small, but discrete, time steps. In order to make this a realistic model of actual continuous-time negotiations, those time steps would then need to be so small that a computer can practically no longer distinguish it from a continuous-time model. For example, each time step could be the length of one CPU cycle.

The problem, however, is that any theoretically derived solution for such an extensive-form game could be very difficult (if not impossible) to implement in practice. For example, a strategy might prescribe that a specific offer must be proposed in the last time step. But if that time step only lasts for a nanosecond, then this is obviously not feasible, because the time it takes for the algorithm to calculate which proposal should be made and execute all computational steps involved in the act of proposing it, would typically take longer than a nanosecond. Furthermore, one should take into account that in any realistic scenario the negotiators would likely exchange their proposals over a network, which means that one should take network latency into account, which is unpredictable and which therefore makes precise timing of a proposal very difficult.

An alternative is to model negotiations over much larger discrete steps. For example, in the main league of ANAC 2019 [3] negotiations were limited to no more than 1000 rounds. However, this means we would be studying an inherently different problem than continuous-time negotiations. Furthermore, it seems unrealistic to impose such a limit in a real-world negotiation, as it would be unfair for the agent that needs to make a decision in the last round, since it would only be able to accept or reject the last offer, while it would not be allowed to make any new proposals.

8.3 Randomized strategies vs. randomized agreements

In the Introduction we have argued against the use of lotteries or coin flips to make the offer space convex. However, later on, we did allow players to play mixed strategies. At first sight, this may seem contradictory, but we should make clear that these are two entirely different forms of randomization. Specifically, we oppose the use of randomized agreements, but we have nothing against randomized strategies.

The main difference, is that in the case of a randomized strategy it is a single agent alone that performs the coin flip to decide its strategy, and it is purely in the agent’s own interest to do so, because it allows it to be unpredictable to its opponent. Furthermore, the coin flip can be implemented in the source code of the agent itself, which means that the agent will not have any reason to distrust the fairness of the coin flip.

On the other hand, in the case of a randomized agreement, there are two agents involved that together decide to flip a coin to make a final decision. This is unsatisfactory, because no matter the outcome, there will always be one agent that will be unhappy with the outcome (if there was an outcome that made both agents happy, then they would not need to flip a coin). Furthermore, since there are two agents involved, the coin flip should be executed by an external algorithm, which should be trusted by both agents.

To give a more practical idea of the difference, note that randomized strategies are very common in real-world scenarios. One can think, for example, of border control units that each day pick a random location where they will patrol the border, or ticket controllers in a public transportation system that pick a random metro station on a random date to perform a surprise ticket control. On the other hand, it is much harder to imagine a real-world example of a randomized agreement. For example, it would be very strange for a car salesman to propose to the client to flip a coin to determine the price of a car.

8.4 Comparison between Our Solution and the NBS

We here discuss the differences between the NBS and our solution.

Nash argued that, given a negotiation domain N, if the two agents both negotiate optimally, then the outcome $o(N) \in \Omega$ they would agree upon, would satisfy the following axioms [32]:

• 1. o(N) is Pareto-optimal:

  $$\begin{aligned} \forall \omega \in \Omega : \quad U_1(o(N)) \ge U_1(\omega ) \quad \vee \quad U_2(o(N)) \ge U_2(\omega ) \end{aligned}$$

• 2. o(N) is independent of ‘irrelevant alternatives’:

  $$\begin{aligned}{} & {} \text {Let\ } N = (\Omega , U_1, U_2, rv_1, rv_2)\,\text {and}\\{} & {} N' = (\Omega ', U_1, U_2, rv_1, rv_2)\,\text {with}\,\Omega '\subset \Omega . \\{} & {} \text {Then, if\ }o(N) \!\in \! \Omega ', \text {\ then we must have:\ } o(N') \!=\! o(N). \end{aligned}$$

• 3. o(N) is invariant under any arbitrary positive linear transformation of the utility function and reservation value of either of the two agents:

  $$\begin{aligned} {\begin{matrix} &{} \text {Let\ } N = (\Omega , U_1, U_2, rv_1, rv_2) \text {\ and\ } N' = (\Omega , U_1', U_2', rv_1', rv_2') \\ &{} \text {such\ that:\ } U_1' = a\cdot U_1 + b \text {\ and\ } rv_1' = a\cdot rv_1 + b \\ &{} \text {and: \ \ \ \ \ \ \ \ } U_2' = c\cdot U_2 + d \text {\ and\ } rv_2' = c\cdot rv_2 + d \\ &{} \text {with\ } a,c\in \mathbb {R^+} \text {\ and\ } b,d\in \mathbb {R}. \\ &{} \text {Then:\ } o(N) = o(N') \end{matrix}} \end{aligned}$$

• 4. If the utility space is symmetrical, then o(N) should also be symmetrical:

  $$\begin{aligned} {\begin{matrix} &{} \text {If\ for\ every\ } \omega \in \Omega \text {\ there\ exists\ an\ offer\ } \omega ' \in \Omega \text {\ such\ that: } \\ &{} (U_1(\omega ) , U_2(\omega )) = (U_2(\omega ') , U_1(\omega ')) \quad \text {then:} \quad U_1(o(N)) = U_2(o(N)) \end{matrix}} \end{aligned}$$

On the other hand, our bargaining solution returns a set of offers $o(N) \subseteq \Omega$, which is to be interpreted as the support of a Nash equilibrium of the concession game $C_N$. It is defined by the following axioms:

• 1. The Nash equilibrium with support o(N) should be Pareto-optimal (among the set of all Nash equilibria of $C_N$).

• 2. The Nash equilibrium with support o(N) should be non-degenerate.

• 3. Among those equilibria that satisfy the previous two conditions, the equilibrium with support o(N) should maximize the utility-sum of the two players.

• 4. Among those equilibria that satisfy the previous three conditions, the equilibrium with support o(N) should minimize the absolute utility-difference.

Assuming the offer space is finite, and that $C_N$ has at least one non-degenerate equilibrium, this solution always returns a single well-defined solution. Furthermore, we have shown that if the AoRE holds, then this solution is theoretically optimal.

We have seen that, in most cases, our solution concept can be summarized as “the offer that maximizes the utility-sum of the two players", while the NBS is the offer that maximizes the utility-product. So, an important question is where this difference comes from. Of course, we have assumed that our offer space is finite while Nash assumed it was convex. However, this is not the actual reason for this difference. After all, we could imagine an offer space that is finite, but where the offers are so dense that it can be seen as approximately convex.

For example, if we take our example of Section 7.1, with two utility vectors (3, 10) and (6, 6), and we extend it by adding many offers with utility vectors that lie on the straight line between the two original ones. We can then easily see that (3, 10) still maximizes the utility-sum, while it does not maximize the utility product, because at least (6, 6) has a higher product.

The real reason for the difference, is that Nash assumes that the utility function of each player can be arbitrarily re-scaled, independently from the other agent (and many other approaches have made the same assumption [32, 17, 18, 11]). At first sight, this seems to make sense. After all, each player could measure their utility according to their own preferred scale. For example, if the payoff is monetary (such as in [28, 23]), then one agent might measure it in euros, while the other might measure it in dollars. The outcome should obviously not depend on the choice of unit or currency of either agent.

However, one should keep in mind that we make a distinction between the agent and the role this agent is playing. We still agree that each agent should be able to choose their own unit or currency, but since we are assuming the AoRE, each agent has to sum its utility over all games and all roles it has played. This, in turn, means that the agent has to measure the payoff for each role of each game in the same unit or currency. So, we can no longer assume that the optimal solution is invariant when we apply different linear transformations to the two respective utility functions. If we apply a linear transformation to the payoff of player 1, we should apply the same transformation also to the payoff of player 2. Note, however, that we still allow each agent to apply any arbitrary linear transformation, independently of other agents.

Formally, our solution concept satisfies the following property (compare this to the corresponding axiom for the NBS above):

$$\begin{aligned} {\begin{matrix} &{} \text {Let\ } N = (\Omega , U_1, U_2, rv_1, rv_2) \text {\ and\ } N' = (\Omega , U_1', U_2', rv_1', rv_2') \\ &{} \text {such\ that:\ } U_1' = a\cdot U_1 + b \text {\ and\ } rv_1' = a\cdot rv_1 + b \\ &{} \text {and: } U_2' = a\cdot U_2 + b \text {\ and\ } rv_2' = a\cdot rv_2 + b \\ &{} \text {with\ } a\in \mathbb {R^+}, \text {\ and\ } b\in \mathbb {R}. \\ &{} \text {Then:\ } o(N) = o(N') \end{matrix}} \end{aligned}$$

We did not mention this property in our list of axioms above, because we do not require this property to hold. We merely observe that it holds for our solution concept, as a consequence of the other axioms. Similarly, we do not require the axiom of independence of irrelevant alternatives to hold, but it turns out that our solution does satisfy it, at least in those domains where all equilibria are non-degenerate.

8.5 Optimality of MiCRO on the ANAC domains

In a recent paper [20] we argued that many of the negotiation domains that have been used for the ANAC competitions are too simplistic. We presented a very simple negotiation strategy, called MiCRO, and showed that if two agents both apply this strategy, then, in many of these domains, they always reach an agreement that coincides with the NBS. From this we concluded that MiCRO performs optimal on such domains.

However, this conclusion was based on the assumption that the NBS defines the ‘optimal solution’, which is of course in contradiction to our conclusion in this paper. Nevertheless, our conclusions about the ANAC domains and MiCRO remain valid, because, as we have seen in Section 7.3, in most ANAC domains the NBS also coincides with the optimal solution according to our definition.

9 Conclusions and future work

We have introduced a new solution to the equilibrium selection problem, based on the assumption of role-equifrequency, and have showed that under this assumption it is rationally optimal. Furthermore, we have used it to improve the bargaining solution that we proposed in earlier work. The surprising conclusion is, that in many cases this solution coincides with the maximum social welfare solution, even though we assume agents are purely self-interested, and do not care about social welfare.

There are several remaining questions that would be interesting to study further. The main weakness of this work is that we have assumed that if the two agents select their strategies such that there are multiple feasible agreements, then the actual outcome of the negotiation can be modeled as a random choice from a uniform probability distribution over the feasible agreements (see (4)). This seems a strong assumption and we can imagine that in reality this outcome may not be uniformly distributed. Therefore, we aim to generalize our assumptions, and instead assume the probability distribution can have any triangular shape.

Another important open question is whether our bargaining solution always returns a solution or not. We know that if all Nash equilibria are degenerate then it does not return any solution, but, as we already mentioned above, it is not yet clear to us whether that can actually happen in the case of the concession game.

Finally, it would be interesting to study under what conditions it is better to apply any of the existing solutions of the equilibrium selection problem, instead of ours, to the concession game (e.g. when the AoRE does not hold).

Appendix

We here present a number of proofs that we omitted from the main text.

1.1 Proof of Lemma 1

To prove:

For any concession game $C_N$, if $k\le l< m$ then we have: $u_2^{k,m} < u_2^{k,l}$.

Proof

We will show that $u_2^{k,l} - u_2^{k,m} > 0$. First, note that by (6) we can write:

$$\begin{aligned} u_2^{k,l} - u_2^{k,m} = \frac{1}{l-k+1} \sum _{j=k}^l u_2^{j,j} - \frac{1}{m-k+1} \sum _{j=k}^m u_2^{j,j} \end{aligned}$$

Then, if we split the second summation into two parts, we get:

$$\begin{aligned} u_2^{k,l} - u_2^{k,m} = \frac{1}{l-k+1} \sum _{j=k}^l u_2^{j,j} - \frac{1}{m-k+1} \sum _{j=k}^l u_2^{j,j} - \frac{1}{m-k+1} \sum _{j=l+1}^{m} u_2^{j,j} \end{aligned}$$

and then by taking the first two summations together:

$$\begin{aligned} u_2^{k,l} - u_2^{k,m} = (\frac{1}{l-k+1} - \frac{1}{m-k+1}) \sum _{j=k}^l u_2^{j,j} - \frac{1}{m-k+1} \sum _{j=l+1}^{m} u_2^{j,j} \end{aligned}$$

Note that since $l < m$ we have that $(\frac{1}{l-k+1} - \frac{1}{m-k+1}) > 0$. Furthermore, note that from (3) and (5) we have that if $j \le l$, then $u_2^{j,j} \ge u_2^{l,l}$. This means that, if we replace the $u_2^{j,j}$ in the first summation by $u_2^{l,l}$, then the new expression will be smaller than or equal to the original expression. Therefore, we have:

$$\begin{aligned} u_2^{k,l} - u_2^{k,m} \ge (\frac{1}{l-k+1} - \frac{1}{m-k+1}) \sum _{j=k}^l u_2^{l,l} - \frac{1}{m-k+1} \sum _{j=l+1}^{m} u_2^{j,j} \end{aligned}$$

Similarly, making use of the fact that if $j > l$, then $u_2^{j,j} < u_2^{l,l}$, but this time applying it to the second summation (and noting that there is a minus sign before the second summation), we get:

$$\begin{aligned} u_2^{k,l} - u_2^{k,m} > (\frac{1}{l-k+1} - \frac{1}{m-k+1}) \sum _{j=k}^l u_2^{l,l} - \frac{1}{m-k+1} \sum _{j=l+1}^{m} u_2^{l,l} \end{aligned}$$

Note that now, in both summations, the summand $u_2^{l,l}$ is constant (i.e. does not depend on the index j), so we can take it outside of the sum, and get:

$$\begin{aligned} u_2^{k,l} - u_2^{k,m} > (\frac{1}{l-k+1} - \frac{1}{m-k+1}) \cdot u_2^{l,l} \cdot \sum _{j=k}^l 1 - \frac{1}{m-k+1} \cdot u_2^{l,l} \cdot \sum _{j=l+1}^{m} 1 \end{aligned}$$

And finally, using straightforward algebra, we can re-write the right-hand side to get:

$$\begin{aligned} u_2^{k,l} - u_2^{k,m}> & {} (\frac{1}{l-k+1} - \frac{1}{m-k+1})\cdot u_2^{l,l} \cdot (l-k+1) - \frac{1}{m-k+1} \cdot u_2^{l,l} \cdot (m-l) \\= & {} \frac{l-k+1}{l-k+1} \cdot u_2^{l,l} - \frac{l-k+1}{m-k+1} \cdot u_2^{l,l} - \frac{m-l}{m-k+1} \cdot u_2^{l,l}\\= & {} 0 \end{aligned}$$

1.2 Proof of Lemma 2

To Prove:

Let $C_N$ be any concession game with actions $\mathcal {A}$, let S be any proper non-empty subset of $\mathcal {A}$ and let $a^k$ be any action that is not in S, i.e. $a^k \in \mathcal {A} \setminus S$. If one player plays a mixed strategy with support S, then playing $a^k$ is not a best response for the other player.

Proof

Suppose agent $\alpha _1$ is playing a mixed strategy q. The expected utility of $\alpha _2$, when playing $a^k$ is then given by:

$$\begin{aligned} u_2(q, a^k) = \sum _{i=1}^n q(a^i) \cdot u_2(a^i,a^k) \end{aligned}$$

(16)

We will prove that, if the support of q is S and if $a^k \not \in S$, then there is some other action $a^l$ for which $u_2(q, a^l) > u_2(q, a^k)$ (we should also prove a similar statement for $u_1$, but since the definition of the concession game is entirely symmetrical for the two players, it is obvious that an analogous proof works for $u_1$.). To prove this we will consider two separate cases, namely the case that $i>k$ for all $a^i\in S$, and the case that there is at least one $a^i\in S$ for which $i<k$ and .

Case 1 Suppose that for all $a^i\in S$ we have $i>k$. Note that if $i>k$ then by (4) we have $u_2(a^i, a^k) = rv_2$, while if $i\le k$ we have $a^i \not \in S$ and therefore $q(a^i) = 0$. We can then easily see from (16) that we have:

$$\begin{aligned} u_2(q, a^k) \le rv_2 \end{aligned}$$

(17)

Now let l be the smallest integer such that $a^l \in S$. Then we have:

$$\begin{aligned} {\begin{matrix} u_2(q, a^l) &{}= \sum _{i=1}^n q(a^i) \cdot u_2(a^i,a^l) \\ &{}= \sum _{i=l}^{n} q(a^i) \cdot u_2(a^i,a^l) \\ &{}= q(a^l)\cdot u_2(a^l, a^l) + \sum _{i=l+1}^{n} q(a^i)\cdot u_2(a^i, a^l)\\ &{}= q(a^l)\cdot u_2(a^l, a^l) + \sum _{i=l+1}^{n} q(a^i)\cdot rv_2\\ &{}> q(a^l)\cdot rv_2 + \sum _{i=l+1}^{n} q(a^i)\cdot rv_2\\ &{}= rv_2 \cdot \sum _{i=l}^{n} q(a^i) \\ &{} = rv_2 \end{matrix}} \end{aligned}$$

(18)

Here, the second line follows from the fact that if $i<l$ then $a^i \not \in S$ and therefore $q(a^i) = 0$. The fourth line follows from the fact that $u_2(a^i, a^l) = rv_2$ whenever $i>l$ (see (4)). To obtain the fifth line we have used that $u_2(a^l, a^l) = U_2(\omega ^l) > rv_2$ (see (3) and (4)). The last line follows again from the fact that $q(a^i) = 0$ for all $i<l$ and that the values $q(a^i)$ are probabilities, so they sum to 1. Combining (17) and (18) we see we have indeed that $u_2(q, a^l) > u_2(q, a^k)$.

Case 2 Now suppose there is at least one integer j such that $a^j\in S$ and $j<k$. Let l be the largest such integer. Since $u_2(a^i, a^k) = rv_2$ for all $i>k$, and $q(a^i)=0$ for all i with $l < i \le k$ we can rewrite Equation (16) as:

$$ u_2(q,a^k) = \sum _{i=0}^l q(a^i) \cdot u_2(a^i,a^k) + \sum _{i=k+1}^n q(a^i) \cdot rv_2 $$

Similarly, we have:

$$ u_2(q,a^l) = \sum _{i=0}^l q(a^i) \cdot u_2(a^i,a^l) + \sum _{i=k+1}^n q(a^i) \cdot rv_2 $$

If we now compare these two equations, we see that, in order to prove that $u_2(q,a^l) > u_2(q,a^k)$ we only need to show that for each $i \in \{1,2,\dots l\}$ we have $u_2(a^i,a^k) < u_2(a^i,a^l)$. But this is indeed the case, by Lemma 1. $\square$

1.3 Proof of Lemma 7

To prove:

For any concession game $C_N$, if $k\le l \le m$, then we have $u_1^{k,l} \le u_1^{k,m}$.

Proof

In the case that $l=m$, this obviously holds, so we only need to prove that it holds for $k\le l < m$. Specifically, we will show that in that case we have $u_1^{k,m} - u_1^{k,l} > 0$.

$$\begin{aligned} u_1^{k,m} - u_1^{k,l}= & {} \sum _{i=k}^m \frac{u_1^{i,i}}{m-k+1} - \sum _{i=k}^l\frac{ u_1^{i,i}}{l-k+1}\\= & {} \sum _{i=k}^{l} \frac{u_1^{i,i}}{m-k+1} + \sum _{i=l+1}^{m} \frac{ u_1^{i,i}}{m-k+1} - \sum _{i=k}^l \frac{u_1^{i,i}}{l-k+1}\\= & {} \sum _{i=l+1}^{m} \frac{u_1^{i,i}}{m-k+1} + (\frac{ 1}{m-k+1} - \frac{ 1}{l-k+1}) \sum _{i=k}^{l} u_1^{i,i}\\> & {} \sum _{i=l+1}^{m} \frac{u_1^{l,l}}{m-k+1} + (\frac{ 1}{m-k+1} - \frac{ 1}{l-k+1}) \sum _{i=k}^{l} u_1^{i,i}\\\ge & {} \sum _{i=l+1}^{m} \frac{u_1^{l,l}}{m-k+1} + (\frac{ 1}{m-k+1} - \frac{ 1}{l-k+1}) \sum _{i=k}^{l} u_1^{l,l}\\= & {} (l-m) \cdot \frac{ u_1^{l,l}}{m-k+1} + (\frac{ 1}{m-k+1} - \frac{ 1}{l-k+1}) \cdot (l-k+1)\cdot u_1^{l,l}\\= & {} \frac{l-m}{m-k+1} \cdot u_1^{l,l} + \frac{l-k+1}{m-k+1}\cdot u_1^{l,l} - \frac{l-k+1}{l-k+1}\cdot u_1^{l,l}\\= & {} 0 \end{aligned}$$

Here, the first line is from (6), and we have obtained the second line from the first one by splitting the first sum into two parts, one over the range $k, k+1 \dots l$ and another one over the range $l+1, l+2 \dots m$. To go from the third line to the fourth we have used that $u_1^{l,l} < u_1^{i,i}$, whenever $l<i$ (which follows from (2) and (5)). Next, to get the fifth line, we have used the opposite, namely that $u_1^{i,i}\le u_1^{l,l}$, whenever $i\ge l$. This is justified, because the factor $(\frac{1}{m-k+1} - \frac{1}{l-k+1})$ before the sum is negative (because $l<m$ and therefore $\frac{1}{m-k+1} < \frac{1}{l-k+1}$). So, if we replace the term $u_1^{i,i}$ in the second sum by something that is greater, the overall expression becomes smaller. The rest is straightforward algebra. $\square$

1.4 Proof of Lemma 8

To prove:

For any concession game $C_N$, if $k\le l\le m$, then we have: $u_2^{l,m} \le u_2^{k,m}$.

Proof

This is trivial in the case that $k=l$, so we will prove that if $k< l\le m$, then $u_2^{k,m} - u_2^{l,m}>0$

$$\begin{aligned} u_2^{k,m} - u_2^{l,m}= & {} \sum _{i=k}^m \frac{u_2^{i,i}}{m-k+1} - \sum _{i=l}^m\frac{ u_2^{i,i}}{m-l+1}\\= & {} \sum _{i=k}^{l-1} \frac{u_2^{i,i}}{m-k+1} + \sum _{i=l}^{m} \frac{ u_2^{i,i}}{m-k+1} - \sum _{i=l}^m \frac{u_2^{i,i}}{m-l+1}\\= & {} \sum _{i=k}^{l-1} \frac{u_2^{i,i}}{m-k+1} + (\frac{ 1}{m-k+1} - \frac{ 1}{m-l+1}) \sum _{i=l}^{m} u_2^{i,i}\\> & {} (l-k)\cdot \frac{u_2^{l,l}}{m-k+1} + (\frac{ 1}{m-k+1} - \frac{ 1}{m-l+1}) \sum _{i=l}^{m} u_2^{i,i}\\\ge & {} (l-k)\cdot \frac{u_2^{l,l}}{m-k+1} + (\frac{1}{m-k+1} - \frac{1}{m-l+1})\cdot (m-l+1) \cdot u_2^{l,l}\\= & {} \frac{l-k}{m-k+1}\cdot u_2^{l,l} + \frac{m-l+1}{m-k+1}\cdot u_2^{l,l} - \frac{m-l+1}{m-l+1} \cdot u_2^{l,l}\\= & {} 0 \end{aligned}$$

For the the details of this proof, see the proof of Lemma 7.