Skip to main content
SpringerLink
Log in

Geometric algebra-based multiscale encoder-decoder networks for 3D motion prediction

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

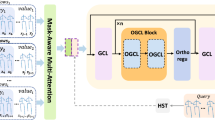
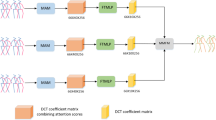
3D human motion prediction is one of the essential and challenging problems in computer vision, which has attracted extensive research attention in the past decades. Many previous methods sought to predict the motion state of the next moment using the traditional recurrent neural network in Euclidean space. However, most methods did not explicitly exploit the relationships or constraints between different body components, which carry crucial information for motion prediction. In addition, human motion representation in Euclidean space has high distortion and shows a weak semantic expression when using deep learning models. Based on these observations, we propose a novel Geometric Algebra-based Multiscale Encoder-Decoder network (GAMEDnet) to predict the future 3D poses. In the encoder, the core module is a novel multiscale Geometric Algebra-based multiscale feature extractor(GA-MFE) , which extracts motion features given the multiscale human motion graph. In the decoder, we propose a novel GA-Graph-based Gated Recurrent Unit (GAG-GRU) to sequentially produce predictions. Extensive experiments are conducted to show that the proposed GAMEDnet outperforms state-of-the-art methods in both short and long-term motion prediction on the datasets of Human 3.6M, CMU Mocap.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Algorithm 1
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availibility Statement

All data generated or analyzed during this study are included in this paper. The data of this work is available on request from the authors. The data of H3.6M and CMU Mocap are also available in the public repository.

References

  1. Alahi A, Goel K, Ramanathan V, Robicquet A, Fei-Fei L, Savarese S (2016) Social lstm: Human trajectory prediction in crowded spaces. Proc IEEE Conf Comput Vis Pattern Recogn, 961–971

  2. Bhattacharyya A, Fritz M, Schiele B (2018) Long-term on-board prediction of people in traffic scenes under uncertainty. Proc IEEE Conf Comput Vis Pattern Recognit, 4194–4202

  3. Boujebli M, Drira H, Mestiri M, Farah IR (2020) Rate-invariant modeling in lie algebra for activity recognition. Electronics 9(11). https://doi.org/10.3390/electronics9111888

  4. Bourached A, Griffiths RR, Gray R et al (2022) Generative model-enhanced human motion prediction[J]. Appl AI Lett 3(2):e63

    Article  Google Scholar 

  5. Cai H, Zheng VW, Chang KCC (2018) A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Trans Knowl Data Eng, 30(9):1616–1637

    Article  Google Scholar 

  6. Cai Y, Huang L, Wang Y, Cham TJ, Cai J, Yuan J, Liu J, Yang X, Zhu Y, Shen X et al (2020) Learning progressive joint propagation for human motion prediction. Eur Conf Comput Vis, 226–242. Springer

  7. Chaolong L, Zhen C, Wenming Z, Chunyan X, Jian Y (2018) Spatio-temporal graph convolution for skeleton based action recognition. Proc Thirty-Second AAAI Conf Artif Intell

  8. Chen S, Liu B, Feng C, Vallespi-Gonzalez C, Wellington C (2020) 3d point cloud processing and learning for autonomous driving: Impacting map creation, localization, and perception. IEEE Signal Proc Mag, 38(1):68–86

    Article  Google Scholar 

  9. Chiu HK, Adeli E, Wang B, Huang DA, Niebles JC (2019) Action-agnostic human pose forecasting. IEEE Winter Conference on Applications of Computer Vision (WACV), pp 1423–1432 . https://doi.org/10.1109/WACV.2019.00156

  10. Clevert D, Unterthiner T, Hochreiter S (2016) Fast and accurate deep network learning by exponential linear units (elus). In: 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, May 2-4, Conference Track Proceedings . arxiv:1511.07289

  11. Cong Thang P, Pham M, Tachibana K (2020) Human action recognition method based on conformal geometric algebra and recurrent neural network. Information and Control Systems 5. https://doi.org/10.31799/1684-8853-2020-5-2-11

  12. Fragkiadaki K, Levine S, Felsen P, Malik, J (2015) Recurrent network models for human dynamics. In: Proc IEEE Int Conf Comput Vis, 4346–4354

  13. Ghosh P, Song J, Aksan E, Hilliges O (2017) Learning human motion models for long-term predictions. International Conference on 3D Vision (3DV), pp 458–466. IEEE

  14. Gopalakrishnan A, Mali A, Kifer D, Giles L, Ororbia AG (2019) A neural temporal model for human motion prediction. Proc IEEE/CVF Conf Comput Vis Pattern Recognit, 12,116–12, 125

  15. Gui LY, Wang YX, Liang X, Moura JM (2018) Adversarial geometry-aware human motion prediction. Proceedings of the European Conference on Computer Vision (ECCV), 786–803

  16. Guo X, Choi J (2019) Human motion prediction via learning local structure representations and temporal dependencies. Proc AAAI Conf Artif Intell, 33:2580–2587

    Google Scholar 

  17. Hamill J, Knutzen KM (2006) Biomech basis Hum Mov,. Lippincott Williams & Wilkins

    Google Scholar 

  18. Hamilton WL, Ying R, Leskovec J (2017) Representation learning on graphs: Methods and applications. CoRR arXiv:1709.05584

  19. Ionescu C, Papava D, Olaru V, Sminchisescu C (2014) Human3.6m: Large scale datasets and predictive methods for 3d human sensing in natural environments. IEEE Trans Pattern Analysis and Mach Intell, 36(7):1325–1339. https://doi.org/10.1109/TPAMI.2013.248

  20. Jin X, Xiao H, Shen X, Yang J, Lin Z, Chen Y, Jie Z, Feng J, Yan S (2017) Predicting scene parsing and motion dynamics in the future. CoRR arxiv:1711.03270

  21. Kingma DP, Ba J (2015) Adam: A method for stochastic optimization. 3rd International Conference on Learning Representations, ICLR, San Diego, CA, USA, May 7-9, Conference Track Proceedings. arxiv:1412.6980

  22. Kipf TN, Welling M (2016) Semi-supervised classification with graph convolutional networks. CoRR abs/1609.02907. arxiv:1609.02907

  23. Kuroe Y (2011) Models of clifford recurrent neural networks and their dynamics. The Int Joint Conf Neural Netw, pp 1035–1041. https://doi.org/10.1109/IJCNN.2011.6033336

  24. Li C, Zhang Z, Lee WS, Lee GH (2018) Convolutional sequence to sequence model for human dynamics. Proc IEEE Conf Comput Vis Pattern Recognit, 5226–5234

  25. Li M, Chen S, Zhao Y, Zhang Y, Wang Y, Tian Q (2020) Dynamic multiscale graph neural networks for 3d skeleton based human motion prediction. Proc IEEE/CVF Conf Comput Vis Pattern Recognit, 214–223

  26. Li M, Chen S, Zhao Y, Zhang Y, Wang Y, Tian Q (2021) Multiscale spatio-temporal graph neural networks for 3d skeleton-based motion prediction. IEEE Trans Image Process, 30:7760–7775. https://doi.org/10.1109/TIP.2021.3108708

    Article  MathSciNet  Google Scholar 

  27. Liu Q, Cao W (2022) Geometric algebra graph neural network for cross-domain few-shot classification. Appl Intell, 1–14

  28. Liu X, Li Y, Xia R (2020) Rotation-based spatial-temporal feature learning from skeleton sequences for action recognition. SIViP, 14. https://doi.org/10.1007/s11760-020-01644-0

  29. Mao W, Liu M, Salzmann M (2020) History repeats itself: Human motion prediction via motion attention. Eur Conf Comput Vis, Springer 474–489

  30. Mao W, Liu M, Salzmann M, Li H (2019) Learning trajectory dependencies for human motion prediction. Proc IEEE/CVF Int Conf Comput Vis, 9489–9497

  31. Mao W, Liu M, Salzmann M, Li H (2021) Multi-level motion attention for human motion prediction. Int J Comput Vis, 129(9):2513–2535

    Article  Google Scholar 

  32. Martinez J, Black MJ, Romero J (2017) On human motion prediction using recurrent neural networks. Proc IEEE Conf Comput Vis Pattern Recognit, pp 2891–2900

  33. Men Q, Ho ESL, Shum HPH, Leung H (2021) A quadruple diffusion convolutional recurrent network for human motion prediction. IEEE Trans Circ Syst Video Technol, 31(9):3417–3432. https://doi.org/10.1109/TCSVT.2020.3038145

    Article  Google Scholar 

  34. Pavllo D, Grangier D, Auli M (2018) Quaternet: A quaternion-based recurrent model for human motion. arXiv preprint arXiv:1805.06485

  35. Pearson J, Bisset D (1994) Neural networks in the clifford domain. In: Proceedings of 1994 IEEE International Conference on Neural Networks (ICNN’94), 3:1465–1469. https://doi.org/10.1109/ICNN.1994.374502

  36. Pei H, Wei B, Chang KCC, Lei Y, Yang B (2020) GEOM-GCN: GEOMETRIC GRAPH CONVOLUTIONAL NETWORKS[C]. The 8th International Conference on Learning Representations, ICLR 2020. The accessed date is 14 Feb 2020

  37. Rivera-Rovelo J, Bayro-Corrochano E (2006) Medical image segmentation using a self-organizing neural network and clifford geometric algebra. The IEEE Int Joint Conf Neural Netw Proc, pp 3538–3545. https://doi.org/10.1109/IJCNN.2006.247362

  38. Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G (2009) The graph neural network model. IEEE Trans Neural Netw, 20(1):61–80. https://doi.org/10.1109/TNN.2008.2005605

    Article  Google Scholar 

  39. Tang J, Zhang J, Yin J (2022) Temporal consistency two-stream cnn for human motion prediction. Neurocomputing 468:245–256

    Article  Google Scholar 

  40. Veličković P, Cucurull G, Casanova A, et al (2018) Graph attention networks[C]. International Conference on Learning Representations. The accessed date is 16 Feb 2018

  41. Wang B, Adeli E, Chiu Hk, Huang DA, Niebles JC (2019) Imitation learning for human pose prediction. Proc IEEE/CVF Int Conf Comput Vis, pp 7124–7133

  42. Wang H, Ho ESL, Shum HPH, Zhu Z (2021) Spatio-temporal manifold learning for human motions via long-horizon modeling. IEEE Trans Vis Comput Graph, 27(1):216–227. https://doi.org/10.1109/TVCG.2019.2936810

    Article  Google Scholar 

  43. Wang R, Shen M, Wang X, Cao W (2021) Rga-cnns: convolutional neural networks based on reduced geometric algebra. Sci China Inf Sci, 64. https://doi.org/10.1007/s11432-018-1513-5

  44. Wang W, Peng X, Su Y, Qiao Y, Cheng J (2021) Ttpp: Temporal transformer with progressive prediction for efficient action anticipation. Neurocomputing 438:270–279

  45. Xu K, Hu W, Leskovec J, et al (2019) How powerful are graph neural networks?[C]. The International Conference on Learning Representations. The accessed date is 22 Feb 2019

  46. Xu YT, Li Y, Meger D (2019) Human motion prediction via pattern completion in latent representation space. 16th conference on computer and robot vision (CRV), IEEE, 57–64

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China, No.61771322,61971290, the Shenzhen foundation for basic research JCYJ20220531100814033, and Shenzhen Stability Support General Project (Category A) 20200826104014001.

Author information

Authors and Affiliations

  1. State Key Laboratory of Radio Frequency Heterogeneous Integration, Shenzhen University, Shenzhen, China

    Jianqi Zhong & Wenming Cao

Authors
  1. Jianqi Zhong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wenming Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenming Cao.

Ethics declarations

Conflicts of interest

We have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

In this part, we give two proofs for the conclusions used in this paper.

  • Proof of (14). In Geometric Algebra \(\mathbb {G}^3\) space, a multivector consists of scalars, vectors, bivectors, and trivectors. Given two multivectors W and H:

    $$\begin{aligned} W= & {} \beta _{0}+\beta _{1} \textrm{e}_{1}+\beta _{2} \textrm{e}_{2}+ \beta _{3} \textrm{e}_{3}+\beta _{4} \textrm{e}_{12}+\beta _{5} \textrm{e}_{23}\nonumber \\{} & {} +\beta _{6} \textrm{e}_{31}+\beta _{7} \textrm{e}_{123} {\left[ \beta _{i} \in \mathbb {R}\right] } \nonumber \\ H= & {} \lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}+\lambda _{5} \textrm{e}_{23}\nonumber \\{} & {} +\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} {\left[ \lambda _{i} \in \mathbb {R}\right] } \end{aligned}$$
    (27)

    Therefore, the geometric product of the two multivectors W, H can be expressed as follows:

    $$\begin{aligned} W \odot H= & {} \beta _{0} (\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}\nonumber \\{} & {} +\lambda _{5} \textrm{e}_{23}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} ) \nonumber \\{} & {} + \beta _{1} (\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}\nonumber \\{} & {} +\lambda _{5} \textrm{e}_{23}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} ) \nonumber \\{} & {} + \beta _{2} (\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}\nonumber \\{} & {} +\lambda _{5} \textrm{e}_{23}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} ) \nonumber \\{} & {} +\beta _{3} (\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}\nonumber \\{} & {} +\lambda _{5} \textrm{e}_{23}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} ) \nonumber \\{} & {} +\beta _{4} (\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}\nonumber \\{} & {} +\lambda _{5} \textrm{e}_{23}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} ) \nonumber \\{} & {} +\beta _{5} (\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}\nonumber \\{} & {} +\lambda _{5} \textrm{e}_{23}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} ) \nonumber \\{} & {} +\beta _{6} (\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}\nonumber \\{} & {} +\lambda _{5} \textrm{e}_{23}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} ) \nonumber \\{} & {} +\beta _{7} (\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}\nonumber \\{} & {} +\lambda _{5} \textrm{e}_{23}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} ) \end{aligned}$$
    (28)

    according to (1) we expanding (28)

    $$\begin{aligned} W \odot H= & {} \lambda _{0} \beta _{0} +\lambda _{0} \beta _{1} \textrm{e}_{1} +\lambda _{0} \beta _{2} \textrm{e}_{2} +\lambda _{0} \beta _{3} \textrm{e}_{3} \nonumber \\{} & {} +\lambda _{0} \beta _{4} \textrm{e}_{12} +\lambda _{0} \beta _{5} \textrm{e}_{23} +\lambda _{0} \beta _{6} \textrm{e}_{31} +\lambda _{0} \beta _{7} \textrm{e}_{123} \nonumber \\{} & {} +\lambda _{1} \beta _{0} \textrm{e}_{1} +\lambda _{1} \beta _{1} +\lambda _{1} \beta _{2} \textrm{e}_{12} -\lambda _{1} \beta _{3} \textrm{e}_{31} \nonumber \\{} & {} +\lambda _{1} \beta _{4} \textrm{e}_{2} +\lambda _{1} \beta _{5} \textrm{e}_{123} -\lambda _{1} \beta _{6} \textrm{e}_{3} +\lambda _{1} \beta _{7} \textrm{e}_{23} \nonumber \\{} & {} +\lambda _{2} \beta _{0} \textrm{e}_{2} -\lambda _{2} \beta _{1} \textrm{e}_{12} +\lambda _{2} \beta _{2} +\lambda _{2} \beta _{3} \textrm{e}_{23} \nonumber \\{} & {} -\lambda _{2} \beta _{4} \textrm{e}_{1} +\lambda _{2} \beta _{5} \textrm{e}_{3} +\lambda _{2} \beta _{6} \textrm{e}_{123} +\lambda _{2} \beta _{7} \textrm{e}_{31} \nonumber \\{} & {} +\lambda _{3} \beta _{0} \textrm{e}_{3} +\lambda _{3} \beta _{1} \textrm{e}_{31} -\lambda _{3} \beta _{2} \textrm{e}_{23} +\lambda _{3} \beta _{3} \nonumber \\{} & {} +\lambda _{3} \beta _{4} \textrm{e}_{123} -\lambda _{3} \beta _{5} \textrm{e}_{2} +\lambda _{3} \beta _{6} \textrm{e}_{1} +\lambda _{3} \beta _{7} \textrm{e}_{12} \nonumber \\{} & {} +\lambda _{4} \beta _{0} \textrm{e}_{12} -\lambda _{4} \beta _{1} \textrm{e}_{2} +\lambda _{4} \beta _{2} \textrm{e}_{1} +\lambda _{4} \beta _{3} \textrm{e}_{123} \nonumber \\{} & {} -\lambda _{4} \beta _{4} -\lambda _{4} \beta _{5} \textrm{e}_{31} +\lambda _{4} \beta _{6} \textrm{e}_{23} -\lambda _{4} \beta _{7} \textrm{e}_{3} \nonumber \\{} & {} +\lambda _{5} \beta _{0} \textrm{e}_{23} +\lambda _{5} \beta _{1} \textrm{e}_{123} -\lambda _{5} \beta _{2} \textrm{e}_{3} +\lambda _{5} \beta _{3} \textrm{e}_{2} \nonumber \\{} & {} +\lambda _{5} \beta _{4} \textrm{e}_{31} -\lambda _{5} \beta _{5} -\lambda _{5} \beta _{6} \textrm{e}_{12} -\lambda _{5} \beta _{7} \textrm{e}_{1} \nonumber \\{} & {} +\lambda _{6} \beta _{0} \textrm{e}_{31} +\lambda _{6} \beta _{1} \textrm{e}_{3} +\lambda _{6} \beta _{2} \textrm{e}_{123} -\lambda _{6} \beta _{3} \textrm{e}_{1} \nonumber \\{} & {} -\lambda _{6} \beta _{4} \textrm{e}_{23} +\lambda _{6} \beta _{5} \textrm{e}_{12} -\lambda _{6} \beta _{6} -\lambda _{6} \beta _{7} \textrm{e}_{2} \nonumber \\{} & {} +\lambda _{7} \beta _{0} \textrm{e}_{123} +\lambda _{7} \beta _{1} \textrm{e}_{23} +\lambda _{7} \beta _{2} \textrm{e}_{31} +\lambda _{7} \beta _{3} \textrm{e}_{12} \nonumber \\{} & {} -\lambda _{7} \beta _{4} \textrm{e}_{3} -\lambda _{7} \beta _{5} \textrm{e}_{1} -\lambda _{7} \beta _{6} \textrm{e}_{2} -\lambda _{7} \beta _{7} \end{aligned}$$
    (29)

    simplifying and collecting up like terms

    $$\begin{aligned} W \odot H= & {} (\lambda _{0} \beta _{0}+ \lambda _{1} \beta _{1}+ \lambda _{2} \beta _{2}+ \lambda _{3} \beta _{3}- \lambda _{4} \beta _{4}\nonumber \\{} & {} -\lambda _{5} \beta _{5}- \lambda _{6} \beta _{6}- \lambda _{7} \beta _{7} ) \nonumber \\{} & {} +(\lambda _{0} \beta _{1}+ \lambda _{1} \beta _{0}- \lambda _{2} \beta _{4}+ \lambda _{3} \beta _{6}+ \lambda _{4} \beta _{2}\nonumber \\{} & {} -\lambda _{5} \beta _{7}- \lambda _{6} \beta _{3}- \lambda _{7} \beta _{5} )\textrm{e}_{1} \nonumber \\{} & {} +(\lambda _{0} \beta _{2}+ \lambda _{1} \beta _{4}+ \lambda _{2} \beta _{0}- \lambda _{3} \beta _{5}- \lambda _{4} \beta _{1}\nonumber \\{} & {} +\lambda _{5} \beta _{3}- \lambda _{6} \beta _{7}- \lambda _{7} \beta _{6} )\textrm{e}_{2} \nonumber \\{} & {} +(\lambda _{0} \beta _{3}- \lambda _{1} \beta _{6}+ \lambda _{2} \beta _{5}+ \lambda _{3} \beta _{0}- \lambda _{4} \beta _{7}\nonumber \\{} & {} -\lambda _{5} \beta _{2}+ \lambda _{6} \beta _{1}- \lambda _{7} \beta _{4} )\textrm{e}_{3} \nonumber \\{} & {} +(\lambda _{0} \beta _{4}+ \lambda _{1} \beta _{2}- \lambda _{2} \beta _{1}+ \lambda _{3} \beta _{7}+ \lambda _{4} \beta _{0}\nonumber \\{} & {} -\lambda _{5} \beta _{6}+ \lambda _{6} \beta _{5}+ \lambda _{7} \beta _{3} )\textrm{e}_{12} \nonumber \\{} & {} +(\lambda _{0} \beta _{5}+ \lambda _{1} \beta _{7}+ \lambda _{2} \beta _{3}- \lambda _{3} \beta _{2}+ \lambda _{4} \beta _{6}\nonumber \\{} & {} +\lambda _{5} \beta _{0}- \lambda _{6} \beta _{4}+ \lambda _{7} \beta _{1} )\textrm{e}_{23} \nonumber \\{} & {} +(\lambda _{0} \beta _{6}- \lambda _{1} \beta _{3}+ \lambda _{2} \beta _{7}+ \lambda _{3} \beta _{1}- \lambda _{4} \beta _{5}\nonumber \\{} & {} +\lambda _{5} \beta _{4}+ \lambda _{6} \beta _{0}+ \lambda _{7} \beta _{2} )\textrm{e}_{31} \nonumber \\{} & {} +(\lambda _{0} \beta _{7}+ \lambda _{1} \beta _{5}+ \lambda _{2} \beta _{6}+ \lambda _{3} \beta _{4}+ \lambda _{4} \beta _{3}\nonumber \\{} & {} + \lambda _{5} \beta _{1}+ \lambda _{6} \beta _{2}+ \lambda _{7} \beta _{0} )\textrm{e}_{123} \end{aligned}$$
    (30)

    which can be expressed as the real matrix form as follows:

    $$\begin{aligned}{} & {} \left[ \begin{array}{c} \textrm{e}_{0}\left( W\odot H\right) \\ \textrm{e}_{1}\left( W\odot H\right) \\ \textrm{e}_{2}\left( W\odot H\right) \\ \textrm{e}_{3}\left( W\odot H\right) \\ \textrm{e}_{12}\left( W\odot H\right) \\ \textrm{e}_{23}\left( W\odot H\right) \\ \textrm{e}_{31}\left( W\odot H\right) \\ \ \textrm{e}_{123}\left( W\odot H\right) \end{array}\right] \nonumber \\{} & {} =\left[ \begin{array}{cccccccc} \beta _{0} &{} \beta _{1} &{} \beta _{2} &{} \beta _{3} &{} -\beta _{4} &{} -\beta _{5} &{} -\beta _{6} &{} -\beta _{7} \\ \beta _{1} &{} \beta _{0} &{} -\beta _{4} &{} \beta _{6} &{} \beta _{2} &{} -\beta _{7} &{} -\beta _{3} &{} -\beta _{5} \\ \beta _{2} &{} \beta _{4} &{} \beta _{0} &{} \beta _{5} &{} -\beta _{1} &{} -\beta _{3} &{} -\beta _{7} &{} -\beta _{6} \\ \beta _{3} &{} -\beta _{6} &{} \beta _{5} &{} \beta _{0} &{} -\beta _{7} &{} -\beta _{2} &{} \beta _{1} &{} -\beta _{4} \\ \beta _{4} &{} \beta _{2} &{} -\beta _{1} &{} \beta _{7} &{} \beta _{0} &{} -\beta _{6} &{} \beta _{5} &{} \beta _{3} \\ \beta _{5} &{} \beta _{7} &{} \beta _{3} &{} -\beta _{2} &{} \beta _{6} &{} \beta _{0} &{} -\beta _{4} &{} \beta _{1} \\ \beta _{6} &{} -\beta _{3} &{} \beta _{7} &{} \beta _{1} &{} -\beta _{5} &{} \beta _{4} &{} \beta _{0} &{} \beta _{2} \\ \beta _{7} &{} \beta _{5} &{} \beta _{6} &{} \beta _{4} &{} \beta _{3} &{} \beta _{1} &{} \beta _{2} &{} \beta _{0} \end{array}\right] \!*\!\left[ \begin{array}{c} \lambda _{0} \\ \lambda _{1} \\ \lambda _{2} \\ \lambda _{3} \\ \lambda _{4} \\ \lambda _{5}\\ \lambda _{6} \\ \lambda _{7} \end{array}\right] \nonumber \\ \end{aligned}$$
    (31)

  • Proof of GA feature extractor as a differentiable function used in this paper.

    • Problem description: Let \({f} = {f(W)}: \mathbb {G}^{n}\) be a multivector-valued function, which has \({2}^{n}\) blade components:

      $$\begin{aligned} f(\varvec{H})=\sum _{i=1}^{n}f(\varvec{H})_{i} e_{i} \end{aligned}$$
      (32)

      where i \(\in \left( 0,1,2,...,23,...,123,123 (n-1)n\right) \) contains all possible \(2^n\) blades and \(f(\varvec{H})_{i}\) corresponds to sub-function accompanying each multivector base. In this paper, we would like to prove that \({f(\varvec{H})}\) is differentiable so that it can be applied as a GA feature extractor in the proposed GAMEDnet.

    • Proof: Throughout this proof, the following theorem and assumption are given. Theorem 1. If function \({z} = {f}(x,y,...,k)\) with n variables is differentiable with respect to point \(\left( x,y,...,k\right) \), its partial derivative with respect to the variable \(\left( x,y,...,k\right) \) must exit, and its total differential at point\(\left( x,y,...,k\right) \) can be obtained by:

      $$\begin{aligned} d {z}(x,y,...,k) = \frac{\partial {z}}{\partial x} \Delta x+\frac{\partial {z}}{\partial y} \Delta y\cdots +\frac{\partial {z}}{\partial k} \Delta k \end{aligned}$$
      (33)

      Theorem 2. If the partial derivative \(\frac{\partial {Z}}{\partial x} d x\),\(\frac{\partial {Z}}{\partial y} d y\) ,\(\cdots \) ,\(\frac{\partial {Z}}{\partial k} d k\) of function \({Z} = {f}(x,y,...,k)\) with respect to point \(\left( x,y,...,k\right) \) is continuous, the function \({Z} = {f}(x,y,...,k)\) is thus differentiable. Assumption. assuming multivector H=\(\lambda _{0}+\lambda _{1} \textrm{e}_{1}+\lambda _{2} \textrm{e}_{2}+\lambda _{3} \textrm{e}_{3}+\lambda _{4} \textrm{e}_{12}+\lambda _{5} \textrm{e}_{13}+\lambda _{6} \textrm{e}_{31}+\lambda _{7} \textrm{e}_{123} , {\left[ \lambda _{i} \!\in \! \mathbb {R}\right] }\), \(W=\beta _{0}+\beta _{1} \textrm{e}_{1}+\beta _{2} \textrm{e}_{2}+ \beta _{3} \textrm{e}_{3}+\beta _{4} \textrm{e}_{12}+\beta _{5} \textrm{e}_{23}+\beta _{6} \textrm{e}_{31}+\beta _{7} \textrm{e}_{123} , {\left[ \beta _{i} \in \mathbb {R}\right] }\). The variables \(\left( \lambda _{0},\lambda _{1},...,\lambda _{7}\right) \),\(\left( \beta _{0},\beta _{1},...,\beta _{7}\right) \) are independent, respectively. In this paper, we focus mainly on human motion prediction in \({\textbf {G}}^{3}\). According to Section 3.3.2, GA operation for feature extraction can thus be expressed by (32):

      $$\begin{aligned} {f}(\lambda _{0},\lambda _{1},...,\lambda _{7})= & {} W \odot H = \sum _{i=1}^{n} f(H)_{i} {e}_{i}\nonumber \\= & {} f(H)_{0}+ f(H)_{1}e_{1}+ f(H)_{2}e_{2} \nonumber \\{} & {} + f(H)_{3} e_{3}+f(H)_{12} e_{12}\nonumber \\{} & {} +f(H)_{23} e_{23}+f(H)_{31} e_{31}\nonumber \\{} & {} +f(H)_{123} e_{123} \end{aligned}$$
      (34)

      where \(\varvec{H}\) is the feature vector at the GA-based graph convolution layer, \(\varvec{W}\) denotes the trainable transformation parameters. According to (30), we expand (34) to obtain:

      $$\begin{aligned} \left\{ \begin{array}{l} f(\lambda _{0},\lambda _{1},...,\lambda _{7})_{0} = \lambda _{0} \beta _{0}+ \lambda _{1} \beta _{1}+ \lambda _{2} \beta _{2}+ \lambda _{3} \beta _{3}- \lambda _{4} \beta _{4}- \lambda _{5} \beta _{5}- \lambda _{6} \beta _{6}- \lambda _{7} \beta _{7} \\ f(\lambda _{0},\lambda _{1},...,\lambda _{7})_{1} = \lambda _{0} \beta _{1}+ \lambda _{1} \beta _{0}- \lambda _{2} \beta _{4}+ \lambda _{3} \beta _{6}+ \lambda _{4} \beta _{2}- \lambda _{5} \beta _{7}- \lambda _{6} \beta _{3}- \lambda _{7} \beta _{5} \\ f(\lambda _{0},\lambda _{1},...,\lambda _{7})_{2} = \lambda _{0} \beta _{2}+ \lambda _{1} \beta _{4}+ \lambda _{2} \beta _{0}- \lambda _{3} \beta _{5}- \lambda _{4} \beta _{1}+ \lambda _{5} \beta _{3}- \lambda _{6} \beta _{7}- \lambda _{7} \beta _{6} \\ f(\lambda _{0},\lambda _{1},...,\lambda _{7})_{3} = \lambda _{0} \beta _{3}- \lambda _{1} \beta _{6}+ \lambda _{2} \beta _{5}+ \lambda _{3} \beta _{0}- \lambda _{4} \beta _{7}- \lambda _{5} \beta _{2}+ \lambda _{6} \beta _{1}- \lambda _{7} \beta _{4} \\ f(\lambda _{0},\lambda _{1},...,\lambda _{7})_{12} = \lambda _{0} \beta _{4}+ \lambda _{1} \beta _{2}- \lambda _{2} \beta _{1}+ \lambda _{3} \beta _{7}+ \lambda _{4} \beta _{0}- \lambda _{5} \beta _{6}+ \lambda _{6} \beta _{5}+ \lambda _{7} \beta _{3} \\ f(\lambda _{0},\lambda _{1},...,\lambda _{7})_{23} = \lambda _{0} \beta _{5}+ \lambda _{1} \beta _{7}+ \lambda _{2} \beta _{3}- \lambda _{3} \beta _{2}+ \lambda _{4} \beta _{6}+ \lambda _{5} \beta _{0}- \lambda _{6} \beta _{4}+ \lambda _{7} \beta _{1} \\ f(\lambda _{0},\lambda _{1},...,\lambda _{7})_{31} = \lambda _{0} \beta _{6}- \lambda _{1} \beta _{3}+ \lambda _{2} \beta _{7}+ \lambda _{3} \beta _{1}- \lambda _{4} \beta _{5}+ \lambda _{5} \beta _{4}+ \lambda _{6} \beta _{0}+ \lambda _{7} \beta _{2} \\ f(\lambda _{0},\lambda _{1},...,\lambda _{7})_{123} \!=\! \lambda _{0} \beta _{7}+ \lambda _{1} \beta _{5}+ \lambda _{2} \beta _{6}+ \lambda _{3} \beta _{4}+ \lambda _{4} \beta _{3}+ \lambda _{5} \beta _{1}+ \lambda _{6} \beta _{2}+ \lambda _{7} \beta _{0}\\ \end{array} \right. \end{aligned}$$
      (35)

      The derivative of a multivector-value function \(f(\varvec{H})\) with respect to a multivector \(\varvec{H}\) is expressed using the Leibniz’s notation:

      $$\begin{aligned} \partial _{h} f(h)=\frac{\partial f(h)}{\partial h}=\lim _{\varDelta h \rightarrow 0} \frac{f(h+\varDelta h)-F(h)}{\varDelta h} \end{aligned}$$
      (36)

      In the study of fields in GA space, any elements can be represented as multivector spanned in GA with basis \({e_i}\). Remarkably, every component with basis \({e_i}\) inherit the derivative properties of a multivector, and thus we can investigate the partial derivative of part component(with basis \({e_i}\)) of a multivector-value function. We first take into account f \(({\lambda _{0},\lambda _{1},...,\lambda _{7})_{1}}\) with \({e_1}\). Given the definition of derivative36, the partial differential of \({f}(\lambda _{0},\lambda _{1},...,\lambda _{7})_{1}\) with respect to \(\lambda _{0},\lambda _{1},...,\lambda _{7}\) is as follows:

      $$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial {H}}{\partial \lambda _{0}} = \beta _{1}, \frac{\partial {H}}{\partial \lambda _{1}} = \beta _{0} \\ \frac{\partial {H}}{\partial \lambda _{2}} = -\beta _{4}, \frac{\partial {H}}{\partial \lambda _{3}} = \beta _{6} \\ \frac{\partial {H}}{\partial \lambda _{4}} = \beta _{2}, \frac{\partial {H}}{\partial \lambda _{5}} = -\beta _{7} \\ \frac{\partial {H}}{\partial \lambda _{6}} = -\beta _{3}, \frac{\partial {H}}{\partial \lambda _{7}} = -\beta _{5} \\ \end{array} \right. \end{aligned}$$
      (37)

      Therefore, we have the total differential of f \(({\lambda _{0},\lambda _{1},...,\lambda _{7})_{1}}\):

      $$\begin{aligned} d {f}({\lambda _{0},\lambda _{1},...,\lambda _{7})_{1}}= & {} \beta _{1} \varDelta \lambda _{0} +\beta _{0} \varDelta \lambda _{1} -\beta _{4} \varDelta \lambda _{2}\nonumber \\{} & {} +\beta _{6} \varDelta \lambda _{3} +\beta _{2} \varDelta \lambda _{4} -\beta _{7} \varDelta \lambda _{5}\nonumber \\{} & {} -\beta _{3} \varDelta \lambda _{6} -\beta _{5} \varDelta \lambda _{7} \end{aligned}$$
      (38)

      Therefore, f \(({\lambda _{0},\lambda _{1},...,\lambda _{7})_{1}}\) meets Theorem 1. In addition, the partial differential of \({f}(\lambda _{0},\lambda _{1},...,\lambda _{7})_{1}\) with respect to \(\lambda _{0},\lambda _{1},...,\lambda _{7}\) are a known constant, which show their continuity at \(({\lambda _{0},\lambda _{1},...,\lambda _{7})}\), and thus meet Theorem 2. Therefore, f \(({\lambda _{0},\lambda _{1},...,\lambda _{7})_{1}}\) is differentiable. The same principle applies to the proof of \({f}(\varvec{H})_{0}\),\({f}(\varvec{H})_{2}\),\({f}(\varvec{H})_{3}\),\({f}(\varvec{H})_{12}\),\({f}(\varvec{H})_{23}\),\({f}(\varvec{H})_{31}\), \({f}(\varvec{H})_{123}\). The proof for \({f(\varvec{H})}\) as a differentiable feature extraction is completed.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhong, J., Cao, W. Geometric algebra-based multiscale encoder-decoder networks for 3D motion prediction. Appl Intell 53, 26967–26987 (2023). https://doi.org/10.1007/s10489-023-04908-7

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-023-04908-7

Keywords

Search

Navigation