Abstract
Predicting students’ performance in distance courses is a very relevant task to help teachers identify students who need reinforcement or extension activities. Nevertheless, identifying the student’s progress is highly complicated due to the large number of students and the lack of direct interaction. Artificial intelligence algorithms contribute to overcoming this problem by automatically analyzing the features and interactions of each student with the e-learning platform. The main limitations of the previous proposals are that they do not consider a ranking between the different marks obtained by students and the most accurate models are usually black boxes without comprehensibility. This paper proposes to use an optimized ordinal classification algorithm, FlexNSLVOrd, that performs a prediction of student’s performance in four ranking classes (Withdrawn < Fail < Pass < Distinction) by generating highly understandable models. The experimental study uses the OULA dataset and compares 10 state-of-the-art methods on 7 different courses and 3 classical classification metrics. The results, validated with statistical analysis, show that FlexNSLVOrd has higher performance than the other models and achieves significant differences with the rest of the proposals. In addition, the interpretability of FlexNSLVOrd is compared with other rule-based models, and simpler and more representative rules are obtained.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Online education systems are becoming increasingly popular due to their flexibility and ability to reach a larger audience. The main advantages of this learning system for students are lower cost, flexible schedules, more in-depth information with directed tasks, and adaptation of the learning space [1, 2]. However, despite these benefits, teachers find it very complex to monitor their students. In contrast to traditional educational systems, it is very hard to keep track of each student, mainly due to the large number of students per course, and the lack of face-to-face interaction. Therefore, students must have discipline and be able to organize their time to pass the subject. For this reason, the completion rates of online learning are notoriously lower than face-to-face learning [3].
In addition, online systems make it possible to obtain a series of additional data on the students that can serve as an indication of their progress [4, 5]. However, the large volume of information stored on each student makes individual monitoring unfeasible. Therefore, it is necessary to use data mining techniques to establish rules and predictions about student performance. These techniques, together with the predictive models, make it possible to understand the critical factors that contribute to student success analysis [6], identify students in need of support on time [7], or store opinion data [8]. In addition, the initial learning period of a new course is crucial for students [9]. During this period, students can experience the novelty of the course, eliminate doubts and establish the foundation for the learning stages. In this scenario, a system capable of predicting the student’s performance is crucial in online learning where the number of students who fail or drop out of the course is very high. These systems could help us quickly detect students with learning difficulties, students who can be asked more complex concepts, and obtain valuable information about what activities have allowed students to pass the course. Therefore, there is a need for an effective framework to assess student performance in online education systems that predicts expected outcomes and early failures associated with students.
Although there is significant research addressing the problem of predicting the critical factors for student tracking [10], most of them simplify the problem to “student will or will not pass a course” or “student will drop out or will not drop out a course”. Nevertheless, this information alone is not always enough for early and effective action. Instead, it is necessary to know what characteristics allow us to predict the different students’ grades or marks from dropout to passing with excellence. In this way, it is useful to model students according to their potential performance to increase success rates and manage resources well.
In this context, the main contributions can be summarized as:
-
1.
Ordinal classification is a novelty in the problem of student’s performance prediction. This paper proposes an algorithm to predict student performance considering four ranking categories: Withdrawn < Fail < Pass < Distinction. The model is able to penalize the mistakes according to the ranking. Thus, the mistake of predicting withdrawal when it passed with distinguished is penalized more than the mistake of predicting withdrawal when it failed. Thus, the final classification will be more reliable.
-
2.
Understandable results that can be used easily by teachers. This paper proposes an algorithm that also includes interpretability. Thus, it uses fuzzy logic and a rule-based system to display comprehensive information. This information will identify the resources, activities, and materials available in a course that can affect the student’s performance and obtain as many behaviors that can benefit them to succeed in a subject as those that can harm them. In this way, the teacher will be able to redirect those students who have problems following the course and further encourage those who are doing excellent work.
-
3.
An exhaustive experimental study considering 10 state-of-the-art methods over 7 different courses and statistical analysis is carried out. Numerous studies in this area are carried out using non-availability datasets. Thus, it is very difficult to analyze the improvements of new proposals. We use the Open University Learning Analytics Dataset (OULAD) [11]. This dataset comprises a large sample size of students and courses and it is being used as a benchmark to draw any meaningful conclusions.
The rest of this paper is organized as follows. Section 2 reviews the previous studies to predict the student’s performance. Section 3 details preliminary concepts of fuzzy logic, machine learning performance metrics and the dataset used in this work. Section 4 describes the proposed framework for student’s performance prediction. Experimentation results and analysis are reported in Section 5, followed by the conclusions and future works in Section 6.
2 Related work
Predicting academic performance is one of the most studied tasks in Educational Data Mining (EDM) [10]. This section presents the latest advancements in this field with a special focus on the approaches using different classification categories. It should be taken into account that open-access datasets in the field of EDM are difficult to find [12], making comparisons of results difficult. For this reason, the OULA [11] dataset has become a benchmark in the field. Therefore, this section also reviews the different contributions that have used this dataset.
2.1 Student performance prediction
The prediction of academic success encompasses many attributes of students’ experience. Most studies focus on determining the student’s final grade in a course according to the grading system [12]. Specifically, most studies focus on predicting whether or not a student passes the course [13]. In this section, a review analyzing the most relevant and recent works on predicting student performance.
Recent surveys, as proposed by Namoun and Alshanqiti [10], show that the prediction of academic performance is addressed generally as a classification problem (47% of the works) instead of as a regression problem (28% of the works) [14]. Moreover, works consider different academic aspects like perceived competence, educational self-reports, attendance, etc. Focusing on classification works, 56% of them only consider two classes, while the rest adds different grades: 15% consider three classes, 9% consider four classes and 20% consider more than four. The number of classes to predict in the most studies is given by the final grades [10]; however, other measures can be the success at the program level or student satisfaction at the personal level. In the binary classification, commonly it is used two classes: ’pass’ and ’fail’ [15,16,17], while in multiple classification, classes usually take the next values: ’dropout’, ’fail’, ’satisfactory’, ’good’, or ’excellent’ [18].
Besides of type of problem (classification or regression) and the number of classes, interpretability is also vital in this problem. Thus, in Table 1, it is shown a summary of the most relevant analyzed studies attending to the aim of the prediction, the factors utilized for that prediction, the machine learning model implemented, and the number of classes that it predicts. The last column gives an idea of the possibilities of the prediction system implantation in a real scenario based on the interpretability of the output, i. e. whether the solutions are meaningful, and give instructors understandable explanations to include students in a specific category.
The analysis of the works detailed in Table 1 leads us to Fig. 1, which summarizes the relevant information related to the proposed work in this paper. This figure shows the number of classes and the type of machine learning algorithms applied. It can be seen that there are a large number of works based on binary classification (54%) and that in general, one of the most popular machine learning techniques are those based on decision trees and recurrent neural networks. Also, it is interesting to note that the analyzed works that predict more than two classes do not use ordinal classification to fix an order relation between classes. Indeed, to the best of the authors’ knowledge, only one previous work [31] makes the first approach to ordinal classification in the EDM domain. However, this work does not focus on predicting academic performance. It explores the feasibility of applying ordinal classification for data labeling in semi-supervised learning environments on three public EDM datasets.
2.2 Student performance prediction in OULAD
This subsection covers papers that use OULAD [11]. This dataset is one of the few open datasets available about learning analytics and educational data mining. It is collected from a real case of study at the Open UniversityFootnote 1, the largest institution of distance education in the United Kingdom. Section 3.1 describes the dataset in detail.
As OULAD is one of the few existing open EDM datasets, it is also one of the most used by the different authors to validate their proposals. Table 2 shows a summary of the analysis of the most relevant previous works that use OULAD to predict academic performance. For each one, it is analyzed the aim of the prediction, the factors utilized in the context of OULAD, the machine learning model, and the number of classes, among those contemplated in OULAD. Finally, the last column indicates if the model obtained by the proposal is comprehensive or is not. As in the previous analysis, a count by classification techniques has also been carried out, distinguishing the number of classes to be predicted. Figure 2 shows this analysis. In this case, it can be appreciated that most of the works focus on binary classification (86%), grouping similar classes like Pass and Distinction or ignoring the minority ones. Attending to the machine learning technique used, similar trends can be observed concerning the general analysis of the previous section: decisions tree models are widely used, probably due to a combination of accuracy and interpretability. On the other hand, contrary to previous analysis, it can be seen an increase in the use of deep learning methods, specifically recurrent networks because they are particularly good at capturing the temporal information available on OULAD.
Once the latest contributions in EDM have been reviewed, we propose the implementation of a fuzzy ordinal classification algorithm to model the order relationship existing between the groups in which a student can be classified. Thus, a student who drops out should be closer to failing than to being excellent. In our proposal, we seek to minimize the error of the prediction of the classes. A mistake with more than one order of difference is penalized more. In this way, the system will be more reliable, especially for minority classes. In addition, the system seeks to be as explainable as possible. Thus, the model provides a set of rules that give information on the most relevant factors associated with each category considered in the classification. In this line, an understandable algorithm based on fuzzy rules is proposed.
3 Preliminary
In this section, we present the preliminary background to understand the contribution of this work. Firstly, we explain in detail the OULA dataset, which is used to validate and compare our proposal. Secondly, we describe the problem and the main concepts of fuzzy systems and ordinal classification. Finally, we describe the main metrics which are used in section 5.
3.1 OULA dataset
The OULA dataset [11] is one of the few open-access EDM datasets (available for downloading inFootnote 2). The OULAD characteristics make it possible to use it in different EDM problems, such as predicting the students’ grades [44], measuring the engagement factors of the courses [34], or classifying the final outcome (see Table 2). This section explains which information contains the data source related to students and their academic activity in OULAD, and the following subsection details the preprocessing operations for adapting the data to a pattern mining scenario.
OULAD focuses on distance learning in higher education, i.e. fully online interaction through VLE systems. Thus, it contains anonymous information about seven independent courses presented at the Open University (The United Kingdom), with 10,655,280 entries of 32,593 students, their assessment results, and logs of their interactions with the VLE represented by daily summaries during 2013 and 2014.
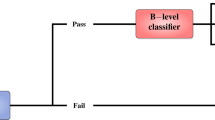
Although each course in OULAD has differences in terms of domain and difficulty levels, they share an equivalent structure that allows us to prove EDM proposals in different scenarios. Each course has several resources on the VLE used to present its contents, one or more assignments that mark the milestones of the course, and a final exam. An overview of the course structure can be seen in Fig. 3. The curriculum and contents of a course are usually available in VLE a couple of weeks before the official course starts, so that enrolled students can access it in an early way. Course content is classified into 20 types according to its nature (homepage, forum, glossary...). Thus, OULAD tracks the number of daily clicks that a student made on each type of resource. During the course presentation, students’ knowledge is evaluated through assignments that define milestones. Two types of assignments are considered: Tutor Marked Assessment (TMA) and Computer Marked Assessment (CMA). If a student decides to submit an assignment, the VLE collects information about the date of submission and the obtained mark. At the end of a course edition, enrolled students can take a final exam that provides them a final grade. Based on this grade, each student receives a final outcome that can take three different values: pass, distinction, or fail. Additionally, if a student does not take the exam, he/she does not finish the course and the final grade is set as withdrawn. In addition to the course activity, OULAD tracks demographic information of the students, such as their gender, region, or age band, and extra academic information, such as the number of previous enrollments in the course, if any, or the total credits currently enrolled.
Having commented on the similarities, we now analyze the differences between OULAD courses. Each of the seven courses belongs to a different domain and considers a difficulty level, i.e., they are independent of each other and have different patterns and enrolled students. Thus, starting for aaa course, is a level-3 course [11] belonging to the field of Social Sciences. As a specialized course, it usually has a few students (around 374 per edition), which makes it possible to have only TMA assignments. It has high rates of VLE interactions with a high success rate (students that pass the course or get distinction) are around 70%. Courses bbb, ccc, ddd, eee, and fff are 1-level courses, mostly belonging to the STEM field (except for bbb that is a Social Sciences course) [11]. All of them have more than 1000 students per edition and around 55% of them do not overcome the course, most of them due to withdrawal. These courses show a decrease in activity in the VLE as the course progresses. This lack of follow-up is also reflected in the assignments submitted. On average, these courses have six assignments of each type (TMA and CMA), but students submit around 3-4 of each type. The eee course deserves a special mention with a failure rate of 44% and with only TMA assignments. Finally, ggg is a Social Sciences preparatory course [11] with an average of 840 students. Its moderate follow-up in the VLE, together with most of the assignments of TMA type, contrasts with its relatively high success rate of 60%. It indicates that is an easy course, consequently to its introductory level.
3.1.1 OULA dataset preprocessing
The original OULAD format is composed of several CSV files which contain tables related to the different components: course, student, VLE, and assessments, as well as the interactions among them. These tables have to be processed in order to properly join all the factors considered in this study and match them with the ordered label to predict. Thus, these files have been loaded into a MySQL database and have been slightly restructured to ensure that it is maintained in Codd’s normal form [45] and avoid data duplication. Finally, the appropriate queries have been carried out with the aim of joining all the information available for each student in each course in a single pattern that can be used to extract the fuzzy rules in the proposed method. The attributes considered are the following:
-
Pattern identification: composed of the students’ identifications and the course edition.
-
Student demographics: student’s gender and age band, the highest level of studies reached by the student, its region and index of multiple deprivations, and if he/she has a disability condition.
-
Enrollment information: date of registration in the course, number of previous attempts to pass the course and the total credits enrolled by the student currently.
-
Assignments information: for each TMA/CMA assignment in the course, it is created an attribute to keep the score obtained by the student. It is used empty value if he/she does not submit the assignment.
-
Note that the number and identification of assignments depends of each course or module, so this attributes differ in the different dataset created.
-
-
VLE logs information: the total number of clicks given by each student in VLE resources during the whole curse. As it has been commented, there are twenty different types of resources, so twenty attributes are created under this category.
-
final grade: the student’s final grade achieved in each enrolled module. This is a categorical value with an implicit order so that the lowest category would be withdrawn, then fail, then pass, and finally distinction.
3.2 Fuzzy rule-based system
Two types of models are distinguished for solving classification problems. On the one hand, there are models which are called black-box models. Some examples of these models are neural networks, ensembles, and deep learning [46], among others. On the other hand, there are others called white-box models with decision trees [47] or rule-based systems [48] as examples. Both models solve the problem by giving an output from some inputs. The difference is that in black-box models, it is unknown how the input parameters are related to obtaining the outputs; while in white-box models, the steps and relationships between the input variables to provide the output are known [49].
Focusing on white-box models, in this work, the model knowledge is represented as a set of IF-THEN rules where if the antecedent is true, the consequent represents the output. To give more flexibility to the rule, the fuzzy logic concepts [50] are used. Fuzzy logic is an extension of boolean logic that uses concepts of membership to sets nearly to human beings thinking. If the classical sets (called crips set) take only two values: one, when an element belongs to the set, and zero, when it does not. In fuzzy set theory is not limited to these two extreme values, an element can belong to a fuzzy set with its membership degree ranging from zero to one. Thus, the variables in fuzzy logic are called “linguistic variables” and are defined by “linguistic terms” and each linguistic term is identified with a membership function to indicate the degree of belonging of an object to a particular label. Figure 4 shows the age variable with three linguistic terms child, young or old and the membership function that defines to each one of them.
Therefore, when fuzzy logic is used, the rules are transformed into more flexible rules, called fuzzy rules. So, the models which use a set of fuzzy rules are called fuzzy rule-based models, and the systems are called Fuzzy Rule-Base Systems (FRBS) which lead to eXplainable Artificial Intelligence (XAI) [51].
3.3 Ordinal classification
As was introduced previously, in the pattern classification field there are two kinds of methods or problems: classification and regression. However, between them, there is a special category of methods called ordinal classification [52].
Ordinal classification problems [53, 54] are defined as prediction problems of an unknown value of an attribute \(y=\{y_1, y_2, \dots , y_Q\}\), where Q is the number of classes. But unlike other types of prediction problems the labels have a predefined order among them \(y_1 \prec y_2 \prec \dots \prec y_Q\). For example, in an age classification problem with child, young, old classes, there is a logical order among them \(child \prec young \prec old\).
Hence, ordinal classification could seem like nominal classification because the target is the prediction of several nominal classes; however it is different because, as was commented before, the classes have a pre-established order among them. Moreover, ordinal classification methods share features with regression problems because there is an order in the output predicted values; however, in ordinal classification, the set of output values is finite in contrast with regression where the output values are undefined continuous values.
3.4 Evaluation metrics
As was previously described, classification models try to predict the labels of a class for new patterns. In this context, the confusion matrix allows us to know the model performance. Indeed, most of the paper of literature in EDM converts the problem into a binary classification considering only ’pass’ and ’fail’ classes or, equivalently, a positive class and a negative class. In binary classification, the confusion matrix is specified as follows:
where:
-
tp (true positive): represents the number of elements of the positive class correctly classified by the model.
-
fn (false negative): represents the number of elements of the positive class classified as negative class by the model.
-
fp (false positive): represents the number of elements of the negative class classified as positive class by the model.
-
tn (true negative): represents the number of elements of the negative class correctly classified by the model.
However, this confusion matrix is limited to a binary classification problem and cannot be used in ordinal classification problems. Hence, the confusion matrix is modified as follows to allow a general use of labels:
where:
-
\(n_{ij}\): represents the number of elements of i class which the classifier has classified as j class.
-
\(n_{i\bullet }\): is the number of elements of the i class.
-
\(n_{\bullet j}\): is the number of elements which the classifier has classified as j class.
Also, in this new matrix, the values of the diagonal represent the number of elements classified correctly by the model, and the other ones represent the classification errors. However, the confusion matrix is complex to handle when the number of classes grows or when comparisons with other proposals are intended. Thus, model performance metrics are extracted based on the information provided by the confusion matrix. The most usual metrics [53] within the field of classification are the following:
-
Accuracy or Correct Classification Rate (CCR): it is a ratio of correctly classified elements to the total of elements as the (1) shows:
$$\begin{aligned} CCR = \frac{1}{N}\sum _{i=1}^{Q} n_{ii} \; \end{aligned}$$(1) -
F1 Score: it is the weighted average of Precision and Recall, that is, this measure takes both false positives and false negatives into account. This metric is calculated following the (2):
$$\begin{aligned} F1 Score = 2 * \frac{Recall * Precision}{Recall + Precision} \; \end{aligned}$$(2)where \(Precision_{i} = \frac{n_{ii}}{n_{\bullet i}}\) and \(Recall_{i} = \frac{n_{ii}}{n_{i \bullet }}\).
-
The error measure for misclassification is even more relevant in ordinal classification problems than in nominal classification problems. In order to measure these errors the Ordinal Mean Absolute Error (OMAE) is obtained using the (3):
$$\begin{aligned} OMAE = \frac{1}{N} \sum _{i,j=1}^{Q} abs(i-j)n_{ij} \; \end{aligned}$$(3)where abs() indicates the function that computes the absolute value.
4 Proposed methodology
This section describes the methodology proposed to carry out the prediction of student performance by applying fuzzy ordinal classification algorithms. The first subsection describes the base algorithm chosen to carry out fuzzy rule learning. The second subsection specifies the main novelties introduced to the base algorithm to enhance the expected classification results.
As previously mentioned, many authors simplify the performance classification problem to a binary classification problem. However, the challenge is found when there are several classes and these have a logical order associated with them. Because of this, we are faced with an ordinal multi-class classification problem. Therefore, this paper proposes the use of the ordinal classification algorithm FlexNSLVOrd. This proposal is based on the NSLVOrd algorithm [54]. First, it is given the general features of the NSLVOrd algorithm. Then, the main improvements included in FlexNSLVOrd are detailed.
4.1 NSLVOrd algorithm
NSLVOrd is a machine learning algorithm that is categorized within fuzzy rule-based algorithms. This algorithm provides the advantage of generating rules whose antecedents are composed of fuzzy variables, allowing greater flexibility. Each rule is composed of a set of fuzzy input variables linked by a conjunctive operator. The values of the input variables can be a set of linguistic terms linked by disjunctive operators. In this way, the rules become fuzzy rules with the following general form for a specific rule \(R_B(A)\):
IF \(X_1~ \text {is } A_1 \text {and } \ldots \text {and } X_n \text {is } A_n~ \text {{\textbf {THEN }}} Y~ \text {is } B\) with weight w;
where:
-
\(X = \{X_1,X_2,\ldots , X_n\}\): are the set of antecedent variables.
-
\(A = \{A_1, A_2, \ldots , A_n\}\): are the subset of values of the fuzzy domain of variable \(X_i\).
-
Y: is the consequent.
-
B: is the value of the consequent (classes) with an specific weight (w) of the rule.
Regarding the antecedents of the rules, NSLVOrd employs fuzzy logic by converting numerical variables into fuzzy ones with a defined number of homogeneous labels. This transformation of variables can be defined by a determined number of linguistic terms (labels) using triangular, left linear, and right linear fuzzy membership functions on the domain boundaries. An example of the conversion of a numerical variable to a fuzzy variable is shown in Fig. 5 using the TMA input variable.
In addition, an antecedent variable of the rule may be composed of a subset of labels joined with a disjunctive operator such as OR. This feature makes it possible to generate more understandable rules. An example using the previous TMA variable is shown in Fig. 6 which represents the antecedent of the rule (“IF TMA = S2, S1 ...”) and its meaning where can be observed that TMA is less than or equal to the label S1.
Once the fuzzy input and output variables have been defined, we can explain the learning algorithm. NSLVOrd employs an iterative rule learning (IRL) [55] approach together with a Genetic Algorithm (GA) [56] in which each individual of the population represents one rule of the rule set. An individual is composed of a codification of antecedents of the rule and its corresponding consequent. More details about the codification are explained in [54].
This set of rules is created using a sequential covering strategy algorithm, which is detailed in Algorithm 1.
Algorithm 1 receives as input a set of instances or samples denoted as E. Firstly, the RemovedRules variable is initialized to true. This variable is the control variable in the first loop and indicates if, after the learning, some rule has been removed and the learning must continue. Next, the LearnedRules variable is initialized with the default rule. This variable contains the set of learned rules which will be the output of the algorithm. At the beginning of the first loop, a new rule is obtained using the \(Learn\_One\_Ord\_Rule\) function where the GA is used to obtain the best rule at the time which is added to the set of rules. The second loop controls if the new rule improves the performance of the system, and the learning can continue. For this, the \(PERFORMANCE\_ORD\) function together with the (4) are used. At the beginning of the second loop, if the performance is better, the new rule (Rule) is added to the set of rules (LearnedRules). Next, the PENALIZE function marks the examples covered by the set of rules. To end the second loop, a new rule is learned. When there is no improvement in the performance, the \(FILTER\_RULES\) function removes the superfluous rules. If there are no superfluous rules, the RemovedRules variable is set to false and finishes the algorithm. Once the algorithm has finished, the LearnedRules variable has stored the best rules which describe the behavior of E.
The \(Learn\_One\_Ord\_Rule\) function is the core of the algorithm where the rules are learned from the set E. This function uses a Steady State Genetic Algorithm (SSGA) over the individuals which represent the rules. These individuals are modified with mutation and crossover operations to get the best rule. The improvement of the rule is guided through a fitness function shown in (4).
This fitness function is a multi-criteria function where the selection of the best rule is guided by the next lexicographical order:
where:
-
\(\Phi (R_{B}(A))\) is the CCR-OMAE-Rate, that is, a measure proposed by us based on a modification of CCR (Correct Classification Rate) and OMAE (Ordinal Mean Absolute Error).
-
\(\Psi (R_{B}(A))\) is a modification of completeness and consistency proposed originally in [57].
-
\(svar(R_{B}(A))\) is the simplicity in variables and it indicates the simplicity in the variables of a rule \(R_B(A)\)
-
\(sval(R_{B}(A))\) is the comprehensibility also called the simplicity in values of a rule.
More details of these concepts can be found in [54].
4.2 Flexible NSLVOrd algorithm
This section describes the FlexNSLVOrd algorithm with the two relevant improvements carried out on the NSLVOrd algorithm. These adaptations allow the adaptation of the algorithm to solve this specific problem. They are comments in the following two subsections.
4.2.1 First improvement: cost matrix
To define the first two criteria in the fitness function, the concepts of coverage and the number of positive and negative examples, which can be found in [54], are considered for measuring the successes and errors in the classification. These errors are weighted with the same value for contiguous classes using the position of the class as it is shown in (5).
where:
-
Rank(B) is the ranking of the consequent.
-
Class(e) is the class of the example e.
Using this equation we can make a general matrix of cost of misclassification with Q classes as follows.
For the academic qualifications considered in this paper, the cost matrix composed of four classes would be:
However, the difference or importance of errors between contiguous classes may be different depending on the type of problem. For example, in the case of academic qualifications, the error that can occur when predicting that a student has dropped out when the student has actually failed is not the same. Considering this peculiarity, we would have to use a cost matrix in which we give more importance to certain errors. For this problem in question a possible cost matrix is the one presented below:
This cost matrix is used to consider the weighted error in (6) which substitutes to (5). Consequently, FlexNSLVOrd considers this modification in the concepts defined above and finally in the fitness function.
4.2.2 Second improvement: non-homogeneous linguistics terms
The original implementation of NSLVOrd converts numerical variables into fuzzy variables with a given number of linguistic terms. Moreover, the distribution of these linguistic terms is homogeneous throughout the variable domain. However, this feature is a disadvantage when working with numerical variables where the distribution of values is not homogeneous. A clear example of this problem can be found in the OULAD dataset with the variable “vle_homepage” among others. If the original implementation of NSLVOrd is used, as shown in Fig. 7, the distribution of the linguistic terms is homogeneous. However, as can be seen in the same figure represented by different colors, the percentages of the number of examples in the dataset that are covered by each linguistic term of the fuzzy variable, are not homogeneous. Indeed, a high percentage of the data is under the S2 label. Therefore, having non-homogeneous data distributions and homogeneous distributions of linguistic terms have a great influence on rule learning and can lead to errors in rule training.
To overcome this disadvantage, FlexNSLVOrd changes to the original implementation of NSLVOrd allowing a balance in the distribution of the training examples in the different fuzzy labels of the new fuzzy variables. This new definition of labels, for each fuzzy variable, is carried out using the algorithm 2.
The inputs of algorithm 2 are the set of samples E and the set of labels L. The first step of the algorithm consists in ordering the set of samples depending on its values, obtaining a new set denoted by Eo. Next, with the information provided by Eo, we calculate the number of samples N on each label. At this point, once the above variables have been calculated, a subset \(SetEo_{(i)}\) of N samples is obtained corresponding to label i. The rest of the calculations in for loop (\(a_i\), \(b_i\), and \(c_i\)) are used to obtain the values of the triangular membership function. The procedure of calculation of subset \(SetEo_{(i)}\) and the subsequent steps are repeated for all labels. Finally, when the loop is over the values of triangular membership for all labels are returned. It is important to note that this new label redefinition does not provide a precise fit to the sample distribution, thus obtaining a method to avoid overfitting.
Once explained how the algorithm works, Fig. 8 shows the new distribution of non-homogeneous fuzzy labels and shows that, unlike Fig. 7, now the label results are closer to the data distribution of the “vle_homepage” variable. For better understanding and visual perception, similar to Fig. 7, the percentages covered by each linguistic term of the fuzzy variable are represented with different colors. Moreover, the second sub-plot is a zoom of the linguistic terms S2, S1, CE, and part of B1.
5 Experimental study
This section compares the performance of our proposal. In order to carry out a detailed performance analysis, this section is divided into two parts. In section 5.1, it is compared our proposal with both shallow and deep machine learning. In section Section 5.2, it is shown a comparative study from an XAI point of view as well as an analysis of the obtained rules.
5.1 Comparison with other shallow and deep learning algorithms
This section compares our proposal with a wide selection of algorithms previously studied in the problem of predicting academic performance. The comparison is carried out in terms of performance using the metrics presented in Section 3.4. The analyzed algorithms include both shallow and deep learning algorithms widely used to solve these problems previously.
The traditional shallow machine learning algorithms used in the comparison belong to the state of the art in different approaches (Bayesian, decision trees, ensembles, etc.) and correspond to the most common approaches taken by the previous work to perform multi-class perform prediction in OULAD (see Table 2):
-
Naive Bayes: a numeric estimator precision value based on Bayes’s probabilities. These models are used by Pei et al. [36].
-
SimpleLogistic: a classifier for building linear logistic regression models. These models are used by Radovanovic et al. [32].
-
RBFNetwork: a normalized Gaussian radial basis function network that uses the k-means clustering algorithm to provide the basic functions. This model is used to build the approach of Quiao et al. [39].
-
Random Forest: an ensemble of random trees constructing a forest where each tree is trained using bagging without replacement. This model is used in [35, 37].
-
J48: an implementation of the C4.5 method that generates decision trees based on gain information. This model is used by Hussain et al. [34].
-
ZeroR: the simplest classification method that relies on the target and ignores all predictors, so it simply predicts the majority class.
-
OneR: a simple classification algorithm that generates one rule for each predictor in the data, then selects the rule with the smallest total error as its “one rule”.
-
PART: which uses separate-and-conquer and builds a partial C4.5 decision tree in each iteration and makes the “best” leaf into a rule. This model is used by Ruiz et al. [26].
The deep learning algorithms used in the comparison are based on the models previously analyzed in Table 2. Specifically, we have taken as reference the proposals that do not involve time series analysis, since our data does include that information. The deep learning algorithms used are the following:
-
DeepMLP: a deep multi-layer perceptron based on the proposal of Waheed et al. [38].
-
DeepCNN: a deep convolutional neural network based on the work of Song et al. [41]
Attending to implementation details, for the classical shallow machine learning algorithms we have used the versions available at Weka [58] with default configurations, and the deep learning models have been implemented using the Python library Tensorflow [59]. RÌegarding FlexNSLVOrd is the proposal presented in this work that includes the modifications presented in Section 4.2.1 and Section 4.2.2.
Tables 3, 4, and 5 present the results of CCR, F1-Score, and OMAE metrics respectively for each course. These results have been obtained using a cross-validation partitioning method of 5-folds (5x2CV): each course presented in OULAD (aaa, bbb, ..., ggg) is analyzed as a separate dataset, and each dataset is divided into two partitions of the same size (proportion of 50% / 50%) five different times following a stratification approach. In each partitioning, two experiments are performed: once using one partition for training and one for testing, and the other way around. Thus, for each course and algorithm, ten experiments are carried out.
Regarding the results of FlexNSLVOrd shown in the tables, it is important to remark that we used five non-homogeneous labels along with the cost matrix presented in Section 4.2.1. In general, we can see that FlexNSLVOrd outperforms the results of all the methods analyzed. Only for the “ggg” course, it is slightly below the CCR and OMAE average metrics. In this case, DeepMLP would be the best proposal. However, if we observe for the same course the value obtained by the F1-score average metric, FlexNSLVOrd is the clear winner. These results reinforce the use of an ordinal algorithm for this type of problem.
In order to confirm the superiority of the ordinal proposal, a statistical test is carried out with the results in the previous tables. Thus, Friedman test [60] is applied to determine whether there are significant differences between the performance of the different algorithms included in the comparative study. Then, Shaffer procedure [60] is applied as a post-hoc procedure to evaluate with more precision the differences between proposals. The results of Friedman’s test, including Friedman’s statistics and the p-values are shown in Table 6 as well as the ranking assigned for Friedman’s test in Table 7. These results show that FlexNSLVOrd obtains the lowest ranking for all measures. According to this test, the lower ranking values are achieved by algorithms that show better performance. Moreover, for all metrics, Friedman’s test rejects the null hypothesis (p-value lower than 0.01), and therefore, significant differences exist in the performance of the algorithms at 99% confidence. A Shaffer’s post-hoc test is applied to check what algorithms can be considered worse proposals. Significant differences among algorithms for these measures at 99% confidence level are shown in Fig. 9. These tests indicate that, for the problem studied, FlexNSLVOrd is significantly better than all other shallow and deep learning algorithms. Only, for the F1-score, the test determines that there are not significant differences between FlexNSLVOrd and RBFNetwork. However, FlexNSLVOrd has a lower ranking and includes higher interpretability, it will be studied in the following section.
Finally, attending to potential limitations of the proposed FlexNSLVOrd, it should mention its higher computational cost concerning most of the methods included in the comparative study. As an evolutive algorithm, the proposed method is slower than simpler algorithms like Naive Bayes, logistic regression, or tree-based algorithms. However, the building times of FlexNLSVOrd reach a few minutes for every studied course, which is acceptable in the context of outcome prediction in semestral courses, where data arrives daily or weekly. Nevertheless, there is a potential path for improvement in this aspect of the proposed method that can be addressed in future works.
5.2 Explainable knowledge obtained and analysis of the rules
As observed from the results in the previous section, FlexNSLVOrd obtains the most accurate results with significant differences compared to the other methods. However, these results only cover one of the objectives proposed in this work. The other objective was to obtain an understandable model. Therefore, in this section, we present the advantage of using a technique that permits us to obtain understandable knowledge according to the XAI trend [61]. XAI refers to methods and techniques of artificial intelligence whose operation can be understood by a human. So, XAI pretends to extract knowledge that can help a human expert to understand the behavior of a system or problem. Thus, this section presents the results, in terms of the number of rules, of the algorithms used in previous sections to compare with our proposal. However, as the majority of the previous algorithms do not represent the knowledge in an explainable way, only the algorithms that generate models providing output rules are considered in this section.
Table 8 shows the average number of rules for each course of each algorithm using again the 5x2-cv data partitioning scheme used in the previous section. ZeroR algorithm is not considered because it works for one class only and it classifies all examples as belonging to this class. Similarly, the OneR algorithm creates a rule for each attribute in the training data, then chooses the rule with the smallest error rate as its “one rule”. Finally, for the randomForest algorithm, we have run it with ten trees and we show the mean of the rules. We can observe that, in general, the number of rules is high for the randomForest algorithm. Without considering this algorithm, we can see that only for course “aaa” there is a similar number of rules in all considered algorithms. Nevertheless, the other courses present a notable difference in the number of rules which can indicate great difficulty in explaining the behavior in these cases. It provides a clearer idea of the benefits of using FlexNSLVord and ordinal classifications algorithms compared to other techniques in terms of interpretability.
Another interesting point to analyze, in addition to the number of rules generated, is the composition of the rules. By analyzing the rules in detail, it is possible to obtain relevant information on the number of attributes used and their importance to identify each class. As an example case, we have applied our FlexNSLVOrd proposal to the course “aaa” without considering partitioning schemes. In this case, a total of 23 rules explain the students’ behavior. Specifically, two rules for withdrawn, four rules for fail, five rules for pass, and twelve rules for distinction classes. The complete set of rules can be seen in Appendix.
Table 9 shows the used variables in the rules for the Withdrawn, Fail, Pass and Distinction classes. From this table, that comes from the rule analysis, we can determine that “code_module”, “AgeBand” and “studiedCredits” variables are irrelevant and are not used in the classification. Regarding to the Withdrawn class, it can be observed that “HigestEducation”, “DateUnregistration” and two assignments (“TMA1755”, and “TMA1756”) are the only used variables. These variables are of special interest because they are present not only in Withdrawn class but in most classes. Also, it can be observed that the most of variables used in inferior classes are used in upper classes too, except for “CodePresentation”, “ImdBand” and “VleHomepage” which are used in Fail and Distinction classes but they are not used in Pass class. This indicates that these variables are key to identifying for failing the course or passing it with a good grade. A similar effect can be seen in the assignments “TMA1754” and “TMA1752”, which are used only in Fail and Distinction classes, respectively. This behavior indicates that the marks assigned by the tutor in each variable are important to classify students into these two classes.
Finally, looking at the ratio of the number of variables used for all classes, it is relevant to remark that the number increases as the mark increases. This behavior can be considered normal because it is necessary to consider more aspects to get higher qualifications.
6 Conclusions
This paper has proposed a system for the classification of students’ academic performance in online and distance education courses. In total four classes have been identified: Withdrawn, Fail, Pass, Distinction. However, within the education environment, the order of the classes is not of equal importance. For example, in the case of an early classification, it is not the same to consider that a student is going to obtain a distinction when the student finally is going to drop out of the course. Therefore, and since the use of ordinal classification algorithms has not been widely explored in this context, this paper has proposed a fuzzy ordinal classification algorithm to perform the prediction task. Specifically, the FlexNSLVOrd algorithm has been presented in this work. The most relevant features of this algorithm are the inclusion of cost matrices, which weigh the distances between the four classes considered, in the fitness functions of the training phase of the algorithm and the generation of non-homogeneous labels based on the data distributions to adapt the fuzzy labels to the real data of the studied problem.
To analyze the performance of our proposal which combines ordinal classification and a rule-based system, an experimental study with the OULA datasets is carried out. In particular, comparisons have been made with ten shallow and deep learning algorithms. Experimental results show an excellent performance for FlexNSLVOrd which obtains the most accurate results in terms of classification using the CCR, F1-Score, and OMAE metrics. FlexNSLVOrd outperforms even deep learning methods.
Moreover, most of the models employed in related works are based on black-box models where the knowledge is not interpretable by humans. With respect to other models that obtain rules-based systems, FlexNSLVOrd achieves models with a lower number of rules using a fuzzy rules-based system. Hence, from the point of view of XAI, FlexNSLVOrd is the most interpretable.
Finally, given the good results obtained by applying ordinal classification using FlexNSLVOrd, it would be interesting to analyze and compare different ordinal classification algorithms in future research. Moreover, other interesting future work could be the performance analysis of ordinal classification and FlexNSLVOrd algorithms with other more flexible representations such as multi-instance and multi-label learning.
References
Rawashdeh AZA, Mohammed EY, Arab ARA, Alara M, Al-Rawashdeh B, Al-Rawashdeh B (2021) Advantages and disadvantages of using e-learning in university education: Analyzing students’ perspectives. Electron J e-Learn 19(3):107–117
Yang, C, Lin, JCW (2022) Design of distance assistance system for intelligent education by web-based applications. Mob Netw Appl, 1–12
Esteban A, Romero C, Zafra A (2021) Assignments as Influential Factor to Improve the Prediction of Student Performance in Online Courses. Appl Sci 11:1–26
Kőrösi, G, Farkas, R (2020) Mooc performance prediction by deep learning from raw clickstream data. In: International Conference on Advances in Computing and Data Sciences, Springer pp. 474–485
Lee C-A, Tzeng J-W, Huang N-F, Su Y-S (2021) Prediction of student performance in massive open online courses using deep learning system based on learning behaviors. Educ Technol & Soc 24(3):130–146
Saa AA, Al-Emran M, Shaalan K (2019) Factors affecting students’ performance in higher education: a systematic review of predictive data mining techniques. Technol Knowl Learn 24(4):567–598
Mohamed M, Waguih H (2017) Early prediction of student success using a data mining classification technique. Int J Sci Res 6(10):126–131
Li L-X, Huo Y, Lin JC-W (2021) Cross-dimension mining model of public opinion data in online education based on fuzzy association rules. Mob Netw Appl 26(5):2127–2140
Raga, R, Raga, J (2019) Early prediction of student performance in blended learning courses using deep neural networks. In: Proceedings - 2019 International Symposium on Educational Technology, ISET 2019, pp. 39–43
Namoun A, Alshanqiti A (2021) Predicting student performance using data mining and learning analytics techniques: A systematic literature review. Appl Sci 11(1):1–28
Kuzilek J, Hlosta M, Zdrahal Z (2017) Open university learning analytics dataset. Sci Data 4:170171
Alyahyan, E, Düstegör, D (2020) Predicting academic success in higher education: literature review and best practices. Int J Edu Technol Higher Edu 17(1)
Tsiakmaki M, Kostopoulos G, Kotsiantis S, Ragos O (2021) Fuzzy-based active learning for predicting student academic performance using automl: a step-wise approach. J Comput Higher Educ 33(3):635–667
Ulloa-Cazarez RL, García-Díaz N, Soriano-Equigua L (2021) Multi-layer adaptive fuzzy inference system for predicting student performance in online higher education. IEEE Latin Am Trans 19(01):98–106
Al-Shabandar R, Hussain A, Laws A, Keight R, Lunn J, Radi N (2017) Machine learning approaches to predict learning outcomes in Massive open online courses. Proceedings of the International Joint Conference on Neural Networks 05:713–720
Yu, CH, Wu, J, Liu, AC (2019) Predicting learning outcomes with MOOC clickstreams. Educ Sci 9(2)
Zabriskie, C, Yang, J, Devore, S, Stewart, J (2019) Using machine learning to predict physics course outcomes. Phys Rev Phys Educ Res 15(2)
Sokkhey P, Okazaki T (2020) Developing web-based support systems for predicting poor-performing students using educational data mining techniques. Int J Adv Comp Sci Appl 11(7):23–32
Shulruf B, Bagg W, Begun M, Hay M, Lichtwark I, Turnock A, Warnecke E, Wilkinson T, Poole P (2018) The efficacy of medical student selection tools in Australia and New Zealand. Med J Aust 208(5):214–218
Walsh, KR, Mahesh, S (2017) Exploratory study using machine learning to make early predictions of student outcomes. In: AMCIS 2017 - America’s Conference on Information Systems: A Tradition of Innovation, vol. 08, pp. 1–6
Nguyen, VA, Nguyen, QB, Nguyen, VT (2018) A model to forecast learning outcomes for students in blended learning courses based on learning analytics. In: ACM International Conference Proceeding Series, pp. 35–41
Akhtar S, Warburton S, Xu W (2017) The use of an online learning and teaching system for monitoring computer aided design student participation and predicting student success. Int J Technol Design Educ 27(2):251–270
Yu CH, Wu J, Liu AC (2019) Predicting learning outcomes with MOOC clickstreams. Educ Sci 9(2):1–15
Zaporozhko, VV, Parfenov, DI, Shardakov, VM (2020) Development Approach of Formation of Individual Educational Trajectories Based on Neural Network Prediction of Student Learning Outcomes. Adv Intell Sys Comput 1126 AISC, 305–314
Gray CC, Perkins D (2019) Utilizing early engagement and machine learning to predict student outcomes. Comput Educ 131:22–32
Ruiz S, Urretavizcaya M, Rodríguez C, Fernández-Castro I (2020) Predicting students’ outcomes from emotional response in the classroom and attendance. Interact Learn Environ 28(1):107–129
Pang Y, Judd N, O’Brien J, Ben-Avie M (2017) Predicting students’ graduation outcomes through support vector machines. Proceedings - Frontiers in Education Conference, FIE 10:1–8
Korosi, G, Esztelecki, P, Farkas, R, Toth, K (2018) Clickstream-based outcome prediction in short video MOOCs. In: CITS 2018 - 2018 International Conference on Computer, Information and Telecommunication Systems, pp. 1–5
Umer, R, Mathrani, A, Susnjak, T, Lim, S (2019) Mining activity log data to predict student’s outcome in a course. In: PervasiveHealth: Pervasive Computing Technologies for Healthcare, pp. 52–58
Tsiakmaki M, Kostopoulos G, Kotsiantis S, Ragos O (2020) Implementing autoML in educational data mining for prediction tasks. Appl Sci 10(1):1–27
Unal, F, Birant, D (2021) Educational Data Mining Using Semi-Supervised Ordinal Classification. In: HORA 2021 - 3rd International Congress on Human-Computer Interaction, Optimization and Robotic Applications, Proceedings, pp. 1–5
Radovanović S, Delibašić B, Suknović M (2021) Predicting dropout in online learning environments. Comp Sci Inform Syst 18(3):957–978
Rizvi S, Rienties B, Khoja SA (2019) The role of demographics in online learning; A decision tree based approach. Comp Educ 137(4):32–47
Hussain M, Zhu W, Zhang W, Abidi SMR (2018) Student Engagement Predictions in an e-Learning System and Their Impact on Student Course Assessment Scores. Comput Intell Neurosci 2018:1–21
Adnan M, Habib A, Ashraf J, Mussadiq S, Raza AA, Abid M, Bashir M, Khan SU (2021) Predicting at-Risk Students at Different Percentages of Course Length for Early Intervention Using Machine Learning Models. IEEE Access 9:7519–7539
Pei, B, Xing, W (2021) An Interpretable Pipeline for Identifying At-Risk Students. J Educ Comput Res 1–26
Hlioui F, Aloui N, Gargouri F (2021) A withdrawal prediction model of at-risk learners based on behavioural indicators. International J Web-Based Learn Teach Technol 16(2):32–53
Waheed H, Hassan SU, Aljohani NR, Hardman J, Alelyani S, Nawaz R (2020) Predicting academic performance of students from VLE big data using deep learning models. Comput Hum Behav 104(11):106189
Qiao C, Hu X (2019) A Joint Neural Network Model for Combining Heterogeneous User Data Sources: An Example of At-Risk Student Prediction. J Assoc Inform Sci Technol 71(10):1–13
He Y, Chen R, Li X, Hao C, Liu S, Zhang G, Jiang B (2020) Online at-risk student identification using RNN-GRU joint neural networks. Information 11(10):1–11
Song X, Li J, Sun S, Yin H, Dawson P, Doss RRM (2021) SEPN: A Sequential Engagement Based Academic Performance Prediction Model. IEEE Intell Syst 36(1):46–53
Hassan SU, Waheed H, Aljohani NR, Ali M, Ventura S, Herrera F (2019) Virtual learning environment to predict withdrawal by leveraging deep learning. Int J Intell Syst 34(8):1935–1952
Aljohani NR, Fayoumi A, Hassan SU (2019) Predicting at-risk students using clickstream data in the virtual learning environment. Sustainability 11(24):1–12
Tomasevic N, Gvozdenovic N, Vranes S (2020) An overview and comparison of supervised data mining techniques for student exam performance prediction. Comput Educ 143:103676
Roy-Hubara N, Sturm A (2020) Design methods for the new database era: a systematic literature review. Softw Syst Model 19(2):297–312
Alzubaidi L, Zhang J, Humaidi AJ, Al-Dujaili A, Duan Y, Al-Shamma O, Santamaría J, Fadhel MA, Al-Amidie M, Farhan L (2021) Review of deep learning: concepts, cnn architectures, challenges, applications, future directions. J Big Data 8:1–74
Mienye ID, Sun Y, Wang Z (2019) Prediction performance of improved decision tree-based algorithms: a review. Proced Manuf 35:698–703 (The 2nd International Conference on Sustainable Materials Processing and Manufacturing, SMPM 2019, 8-10 March 2019, Sun City, South Africa)
Liu H, Zhang L (2018) Fuzzy rule-based systems for recognition-intensive classification in granular computing context. Granular Computing 3:355–365
Linardatos, P, Papastefanopoulos, V, Kotsiantis, S (2021) Explainable ai: A review of machine learning interpretability methods. Entropy 23(1)
Zadeh LA (1983) Linguistic variables, approximate reasoning and dispositions. Med Inform 8(3):173–186
Došilović, FK, Brčić, M, Hlupić, N (2018) Explainable artificial intelligence: A survey. In: 2018 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), pp. 0210–0215
Tutz G (2022) Ordinal regression: A review and a taxonomy of models. WIREs Computational Statistics 14(2):1545
Gutiérrez PA, Pérez-Ortiz M, Sánchez-Monedero J, Fernández-Navarro F, Hervás-Martínez C (2016) Ordinal regression methods: Survey and experimental study. IEEE Trans Know Data Eng 28(1):127–146
Gámez JC, García D, González A, Pérez R (2016) Ordinal Classification based on the Sequential Covering Strategy. Int J Approx Reason 76:96–110
García D, Gámez JC, González A, Pérez R (2015) An interpretability improvement for fuzzy rule bases obtained by the iterative rule learning approach. Int J Approx Reason 67:37–58
Katoch S, Chauhan SS, Kumar V (2021) A review on genetic algorithm: past, present, and future. Multimed Tools Appl 80:8091–8126
Michalski RS (1983) A theory and methodology of inductive learning. Artif Intell 20:111–161
Frank E, Hall MA, Witten IH (2017) Appendix b - the weka workbench. In: Witten IH, Frank E, Hall MA, Pal CJ (eds) Data Mining, 4th edn. Morgan Kaufmann, Fourth edition edn, pp 553–571
Abadi, M, Agarwal, A, Barham, P, Brevdo, E, Chen, Z, Citro, C, Corrado, GS, Davis, A, Dean, J, Devin, M, Ghemawat, S, Goodfellow, I, Harp, A (2015) TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. Software available from tensorflow.org . https://www.tensorflow.org/
Dietterich TG (1998) Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput 10(7):1895–1923
Barredo Arrieta A, Díaz-Rodríguez N, Del Ser J, Bennetot A, Tabik S, Barbado A, Garcia S, Gil-Lopez S, Molina D, Benjamins R, Chatila R, Herrera F (2020) Explainable artificial intelligence (xai): Concepts, taxonomies, opportunities and challenges toward responsible ai. Information Fusion 58:82–115
Acknowledgements
This research was supported by the Spanish Ministry of Science and Innovation and the European Regional Development Fund, project PID2020-115832GB-I00.
Funding
Funding for open access publishing: Universidad de Córdoba/CBUA.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Rule base of course ’aaa’ obtained with 5 labels (NSLVOrd)

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gámez-Granados, J.C., Esteban, A., Rodriguez-Lozano, F. et al. An algorithm based on fuzzy ordinal classification to predict students’ academic performance. Appl Intell 53, 27537–27559 (2023). https://doi.org/10.1007/s10489-023-04810-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-023-04810-2