Abstract
This paper investigates a problem that lies at the intersection of three research areas, namely automated negotiation, vehicle routing, and multi-objective optimization. Specifically, it investigates the scenario that multiple competing logistics companies aim to cooperate by delivering truck loads for one another, in order to improve efficiency and reduce the distance they drive. In order to do so, these companies need to find ways to exchange their truck loads such that each of them individually benefits. We present a new heuristic algorithm that, given one set of orders for each company, tries to find the set of all truck load exchanges that are Pareto-optimal and individually rational. Unlike existing approaches, it does this without relying on any kind of trusted central server, so the companies do not need to disclose their private cost models to anyone. The idea is that the companies can then use automated negotiation techniques to negotiate which of these truck load exchanges will truly be carried out. Furthermore, this paper presents a new, multi-objective, variant of And/Or search that forms part of our approach, and it presents experiments based on real-world data, as well as on the commonly used Li & Lim data set. These experiments show that our algorithm is able to find hundreds of solutions within a matter of minutes. Finally, this paper presents an experiment with several state-of-the-art negotiation algorithms to show that the combination of our search algorithm with automated negotiation is viable.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Logistics companies have very small profit margins and are therefore always looking for ways to improve their efficiency. It is not uncommon for such companies to have their trucks only half full when they are on their way to make their deliveries. Moreover, after completing those deliveries they often head back home completely empty. This is a clear waste of resources, not only economically, but also environmentally, as it causes unnecessary emissions of CO2 [1].
For this reason, many logistics providers are looking for collaborative solutions that allow them to share trucks with other logistics companies. This is often referred to as horizontal collaboration (i.e. collaboration between companies that operate at the same level of the supply chain). In logistics, one typically distinguishes between two types of horizontal collaboration, namely co-loading (multiple companies loading their orders onto a shared vehicle) and backhauling (after making its deliveries, a truck picks up another load for a different company and delivers it on its way back home).
Finding the optimal co-loading and backhauling opportunities that minimize the costs of the companies is a difficult problem, because the number of possible solutions is exponential, and for each of these solutions calculating its cost savings amounts to solving a Vehicle Routing Problem (VRP). This collaborative variant of the VRP has been studied before, but mainly as a single-objective optimization problem. That is, one tries to find the solution that minimizes the total cost of all companies combined, under the assumption that the benefits will be fairly divided among them, according to some pre-defined scheme.
Unfortunately, however, such a single-objective approach is problematic in a real-world scenario, because it requires the companies to share highly sensitive data with each other about their respective cost functions (e.g. how much they pay their drivers, and how much they pay for fuel). The logistics companies that we have been working with have indicated that sharing such information is absolutely out of the question for them. In fact, they are not even willing to share such information with a trusted central server.
Therefore, in this paper, we are instead looking at collaborative vehicle routing from the point of view of automated negotiation. That is, we have developed an agent that only represents one of the companies involved, and only knows the exact cost function of that company, while it can only has an estimation of the other companies’ cost functions because they are kept secret. Our agent first tries to find the set of all solutions that are Pareto-optimal and individually rational (i.e. beneficial to each individual company), and then proposes these solutions to the other companies, according to a negotiation strategy that only aims to maximize the profits of the agent’s own company. These other companies (which are also each represented by their own negotiating agent) can then decide for themselves whether or not they accept the proposed solutions, and can make counter-proposals.
The work presented in this paper mainly focuses on the first task of this agent: to find the set of Pareto-optimal and individually rational solutions, which is a multi-objective optimization problem.
Of course, even if the other companies’ cost functions are not exactly known, one could still consider a single-objective approach, using a standard VRP-solver to find the solution that minimizes the total estimated costs of all companies combined. The problem with this approach, however, is that it only yields one single solution, and this solution may not be acceptable to the other companies, either because the estimations were not accurate enough, or because the returned solution is not individually rational, or because some of the other companies simply demand higher benefits, for strategic reasons. In contrast, our approach has the advantage that it can find a large set of potential proposals, which allows our agent to propose many alternatives in a negotiation process.
This research was carried out in cooperation with two major logistics providers in the UK, namely Nestlé and Pladis. Although both these companies’ primary activity is the production of fast-moving consumer goods (i.e. food, beverages and toiletries), they each have a large logistics department with large truck fleets that deliver several hundreds of loads throughout the UK every day. Their main operations consist in carrying products from their factories to their distributions centers (DC), and from their DCs to their customers, typically large supermarket chains.
It should be stressed that the goal of this work is to create a system that can truly be used in real life by our industrial partners. Therefore, we need to take into account as many constraints as possible that may appear in real life. For example, each delivery has to be picked up and delivered at specified locations and within a specified time-window, and each vehicle has volume- and weight- constraints. In other words, the problem we are dealing is known in the literature as a capacitated pickup and delivery problem with time windows (CPDPTW). Although in the rest of this paper we will just use the more general term VRP to refer to this problem.
Also, it should be remarked that, although we assume the companies involved do not disclose their cost models to each other, they do still have to disclose the locations of their customers. Otherwise, co-loading and backhauling would obviously not be possible. Fortunately, our partners have indicated that this is not a problem for them (their customers are mainly supermarkets, so their locations are not really secret anyway).
An earlier version of our algorithm was presented in [2], but several improvements have been made since, which are discussed later on.
In summary, this paper makes the following contributions:
-
A new heuristic search algorithm that allows a logistics company to find a large set of potential exchanges of orders between itself and some other company. These exchanges of orders should yield financial benefit for the company itself as well as for the other company.
-
A new multi-objective variant of And/Or search, which is used to combine the solutions found by our heuristic search into larger solutions.
-
Experiments that show that our approach is able to find hundreds of solutions in a matter of minutes (on real-world data, as well as on an artificial benchmark).
-
Experiments that show that existing negotiation algorithms can be employed by the companies to negotiate about which of the found solutions should be executed.
2 Related work
In this section we discuss existing work on the Vehicle Routing Problem, and how it has been combined with negotiation and other forms of multi-objective optimization.
2.1 Vehicle routing problems
The Vehicle Routing Problem (VRP) is a generalization of the well-known Traveling Salesman Problem, in which the goal is to find optimal routes for multiple vehicles visiting a set of locations. The VRP was introduced by Dantzig and Ramser in 1959 [3], and is one of the most extensively studied combinatorial optimization problems in the literature. They described a real-world application concerning the delivery of gasoline to service stations and proposed the first mathematical programming formulation and algorithmic approach. Since it is a generalization of the Traveling Salesman Problem, it is well-known that the VRP is NP-hard. In 1964, Clarke and Wright proposed an effective greedy heuristic that improved on the Dantzig–Ramser approach [4]. Following these two seminal papers, hundreds of models and algorithms were proposed to find optimal or approximate solutions to various versions of the VRP. A classification scheme was given in [5]. The VRP has been covered extensively in by Toth & Vigo [6] and a more recent survey of the state-of-the-art can be found in [7].
Many different versions and extensions of the VRP have been defined in the literature, such as the capacitated VRP [8] in which the vehicles are constrained by volume and/or maximum load weight, the VRP with pickups and deliveries [9], in which the loads have a specific pickup and delivery location, so if a vehicle passes a certain location to pick up a load it should also pass the delivery location of that load, and the VRP with time windows [10], in which the vehicles have to arrive at each location within a given time window. A recent survey of techniques applied to the VRP with time windows can be found in [11].
2.2 Collaborative vehicle routing problems
The collaborative VRP is a variant that involves multiple logistics operators. A recent survey of this topic was presented in [12]. This survey distinguishes between three methodologies: centralized collaborative planning, auction-based decentralized planning, and decentralized planning without auctions. For our purposes we are mainly concerned with the last type. They identify 14 papers of this type, but only four of them deal with VRPs that include time windows, and pickup-and-delivery. In [13, 14], and [15] the goal is to find a globally optimal solution that maximizes the total profit, and in [16] the central system calculates a price that fairly divides the benefits of collaboration among the two collaborating companies.
Although these approaches are labeled as ‘decentralized’, this really only means ‘not fully centralized’ because, although the final decisions are made by the individual logistics companies, in each of these cases there was still a central system that performed the search for potential solutions, based on the companies’ cost models. This means that the collaborative VRP is still mostly treated as a classical single-objective optimization problem. Therefore, none of the solutions suggested in these papers is feasible in our context, as our industrial partners have indicated that any form of sharing of information about their respective cost models is out of the question, even if it is only shared with a trusted central system.
2.3 Multi-objective vehicle routing problems
Since we are assuming each company has its own individual cost function, our work is also related to the Multi-Objective VRP. A large survey of VRPs with multiple objective functions has been conducted in [17], but all papers discussed in this survey assume there is just one logistics company which has multiple objective functions that are perfectly known by the algorithm. For example, a company may wish to minimize the distance traveled, as well as the number of vehicles used in the solution [18] so they try to find all Pareto-optimal solutions w.r.t. those objectives. None of the papers discussed in this survey covers the case that there are multiple companies, which are not willing to disclose their respective cost models.
2.4 Vehicle routing problems with negotiation
While many papers have been published that either involve multiple companies with a single shared objective function (the collaborative VRP) or a single company with multiple objective functions (the multi-objective VRP), much less has been published about VRPs with multiple companies where each company has its own individual objective function. We are aware of only a few papers that do treat somewhat similar problems.
In [19] a case study was presented that explores one-to-many negotiations between one 4PL provider and several 3PL providers (a 3PL provider is a logistics company with its own truck fleet, while a 4PL provider does not have a fleet, but receives large transport orders from shippers and then redistributes them among 3PL providers). A very similar scenario was treated in [20], except that they used auction mechanisms instead of negotiations. The two papers that are probably most closely related to our work, are [21] and [22]. In [21] the initial idea for a negotiation algorithm based on Branch & Bound was first put forward, which could be applied to negotiations among competing package delivery companies that could exchange their packages. A more detailed description of this algorithm was later presented in [22]. These papers, however, did not take into account time windows, or volume- and weight- constraints, and they only used artificial test cases, rather than real-world data.
3 Automated negotiation
The research field of automated negotiation deals with multi-agent systems in which each agent is purely self-interested, but in which the agents still need to cooperate to ensure beneficial outcomes. Each agent can propose potential solutions to the other agents, and each agent, upon receipt of such a proposal, may decide whether to accept it or to reject it [23].
Each agent associates a certain utility value with each potential solution, but that utility is only obtained if that solution is accepted by all agents involved in it. If the agents cannot come to any agreement before a given deadline, then none of the potential collaborative solutions can be executed. This situation is often referred to as the conflict outcome. The utility value an agent obtains in that case, is called its reservation value. A rational agent would only ever accept a proposal if the utility it obtains from it is greater than or equal to that agent’s reservation value. After all, the agent is already guaranteed to obtain its reservation value anyway without making any agreements. For this reason, in automated negotiation we are main interested in those solutions for which each agent receives a utility value that is greater than or equal to its reservation value. Such solutions are called individually rational.
One typically assumes the agents have to make their proposals according to some negotiation protocol, which defines when each agent is allowed to make or accept a proposal, and when such proposals become binding agreements. The most commonly used protocol is the alternating offers protocol [24], in which the agents take turns making proposals.
Although each agent is purely self-interested, the proposals it makes must also benefit the other agents, because otherwise they would never accept it. Therefore, a negotiating agent must strike a balance between maximizing its own utility, and providing enough utility to its opponents to make them accept the proposal. To do this, agents typically start by making very selfish proposals, but, as time passes, they slowly concede and make proposals that are less and less selfish. For the rest of this paper, it is important to understand that such a strategy requires the agent to have a large set of potential proposals available, with varying degree of selfishness.
Formally, a problem instance in the field of automated negotiations (a negotiation domain) is defined as follows.
Definition 1
A negotiation domain consists of:
-
A finite set of agents \(a_{1}, a_{2}, {\dots } a_{m}\).
-
A set Ω of potential proposals, called the agreement space.
-
A set of utility functions \(U_{1}, U_{2}, {\dots } U_{m}\), one for each agent. Each utility function maps the agreement space to the set of real numbers \(U_{i}: {\Omega } \rightarrow \mathbb {R}\).
-
A set of reservation values \(rv_{1}, rv_{2}, {\dots } rv_{m} \in \mathbb {R}\), one for each agent.
A typical example of a negotiation domain is the negotiation of a car sale between a customer and a salesperson. In that case, there are two agents (the customer and the salesperson), and the agreement space consists of all possible combinations (c,p) where c is a car and p is the price to pay for the car. The salesperson would start by making an offer with a high price, while the customer would start by making an offer with a low price. They alternate making offers, until they meet somewhere in the middle and one of them makes an offer that is acceptable to the other.
3.1 Applying automated negotiations to co-loading and backhauling
The aim of this work is to develop a negotiating agent that can be applied by a logistics company to negotiate co-loading opportunities with other logistics companies. However, this paper mainly focuses on one component of such an agent, namely the search algorithm to find the set of potential proposals. This set of potential proposals can then be fed as the input to some negotiation strategy.
The question how to implement such a negotiation strategy is beyond the scope of our work because many such algorithms have already been proposed, for example for the Automated Negotiating Agents Competition (ANAC), which has been organized annually since 2010. Throughout the years this competition has focused on many different aspects of automated negotiation. From simple bilateral negotiations with linear utility functions [25], to very large domains with non-linear utility functions [26], multilateral negotiations [27], negotiations with only partially known utility functions [28], negotiations between agents and humans [29], negotiations in the game of Diplomacy [30] or the game of Werewolves [28], to negotiations in a supply chain environment [28]. As we shall see in Section 7.5, some of the algorithms that were implemented for ANAC can indeed be applied to our scenario as well.
One important detail that should be pointed out, is that we are assuming the companies only negotiate about which company will deliver which orders, and not about any form of financial compensation for the delivery of another company’s orders. There are several reasons for this. Scientifically, price negotiations would make our scenario less interesting because the problem of finding a set of potential proposals would just be a single-objective optimization problem again, in which the goal is to find those solutions that minimize the sum of the costs of the companies. The companies would then only need to negotiate how to divide the joint financial gains. Such one-dimensional negotiations are not very interesting compared to the state-of-the-art in automated negotiations. A more practical reason, is that our partners have indicated that automated price negotiations would not be acceptable to them in a real-life working system, because automated day-to-day price negotiations could lead to a highly opaque pricing mechanism with strongly fluctuating prices. This would be a serious problem for their bookkeeping. Instead, our partners require prices to be fixed over a longer term, such as a whole year.
So, any form of financial compensation should be fixed in advance, and cannot be subject to automated negotiation. In this paper we simply assume the financial compensation is zero, meaning that any company would only accept to make a delivery for another company if that other company returns the favor by making a delivery for the first one in return.Footnote 1
The negotiation domain discussed in this paper is different from the more commonly studied domains in the automated negotiations literature, in the following two aspects:
-
1.
Although the agents do not have exact knowledge about their opponents’ utility functions, they can make reasonable estimations.
-
2.
Utility functions are expressed as a computationally complex problem (a VRP), so even with perfect knowledge an agent would still not be able to calculate utility values exactly. Instead, it has to resort to heuristic estimations.
Regarding the first point, most studies in automated negotiations assume the agents have absolutely no knowledge at all about their opponents’ utility functions [31]. Alternatively, in some work it is assumed that agents have perfect knowledge about each others’ utility [32]. In our domain, however, the truth lies somewhere in between. The agents do not know each others’ exact utility functions, but they are able to make reasonable estimations. After all, it is known that each company aims to minimize distance and time, and the distances between the locations are known. Furthermore, although each company may pay somewhat different prices for its fuel, the write-off of its vehicles, or the salaries of its drivers, those prices cannot be radically different among the companies.
One main example of a negotiation domain that has been studied extensively and that does also involve these two aspects, is the game of Diplomacy [33], but this is a purely artificial game, while in this paper we are studying a real-world scenario.
Search algorithms for automated negotiations have been studied, for example using simulated annealing [34], or genetic algorithms [35]. However, these papers only looked at problems in which the utility of a single deal could be computed quickly. They did not involve the complexity of the VRP. Also, as mentioned before a Branch & Bound approach has been proposed, but to a simpler and purely artificial scenario [22].
4 Definitions
Formally, the problem tackled in this paper is the following (the precise definitions of these concepts are given in the rest of this section). Let \(C_{1}, {\dots } C_{m}\) denote a number of logistics companies. Then, given a location graph (L,R,d), a distance cost \(dc \in \mathbb {R}\) a time cost \(tc \in \mathbb {R}\), and, for each company Ci a set of orders Oi, a vehicle fleet Vi and an initial fleet schedule \(\overline {\mathit {fs}}_{i}\), find the set of order assignments that are both individually rational and Pareto-optimal with respect to the cost model (dc,tc).
We use \(\mathbb {N}\) to denote the set of natural numbers and \(\mathbb {R}\) to denote the set of real numbers. We indicate time using natural numbers, which can be interpreted, for example, as Unix time stamps.
Definition 2
A location graph (L,R,d) is a weighted graph with vertices L, which we refer to as locations, edges R, which we refer to as roads, and a weight function \(d : R \rightarrow \mathbb {R}\), representing the length of a road (in kilometers).
A location graph represents a set of possible locations where a logistics provider could pick up or drop off loads (i.e. the factories and distribution centers of the logistics companies, as well as the locations of their customers), and the roads between those locations. It is assumed, without loss of generality, that the graph is complete and symmetric and that d satisfies the triangle inequality.
Customers place orders with the logistics companies. An order represents a certain number of pallets to be picked up and delivered within specified time windows and at specified locations.
Definition 3
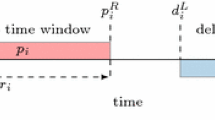
An order is a tuple (vol,w,lpu,t1,t2,tpu, ldo,t3,t4,tdo), where: \(vol \in \mathbb {N}\) is the volume of the load, measured as a number of pallets. \(w \in \mathbb {R}\) is the weight of the load, measured in kilograms. lpu ∈ L is the pick-up location. \(t_{1} \in \mathbb {N}\) and \(t_{2} \in \mathbb {N}\) represent the earliest and latest time respectively that a company can pick up the order (so they must satisfy t1 < t2), \(t_{pu}\in \mathbb {N}\) is the pick-up service time, i.e. time it takes to load the pallets onto a vehicle, ldo ∈ L is the drop-off location. \(t_{3} \in \mathbb {N}\) and \(t_{4} \in \mathbb {N}\) represent the earliest and latest time respectively that a company can drop off the order (so they must satisfy t3 < t4), and \(t_{do}\in \mathbb {N}\) is the drop-off service time, i.e. time it takes to offload the pallets from a vehicle.
To be precise, the interval [t1,t2] represents the time window within which a company can start loading the order onto the vehicle, so it must finish within the time window [t1 + tpu,t2 + tpu]. Similarly, [t3,t4] is the time window within which a company can start unloading the vehicle, so unloading should finish within the time window [t3 + tdo,t4 + tdo].
Definition 4
A vehicle is a tuple (volmax,wmax,s), where: \(vol_{max} \in \mathbb {N}\) is the volume of the vehicle, i.e. the maximum number of pallets it can carry. \(w_{max} \in \mathbb {R}\) is maximum load weight of the vehicle, measured in kilograms, and \(s \in \mathbb {R}\) is the average speed we can realistically assume the vehicle to drive.
4.1 Jobs and schedules
We define the solutions of a VRP in terms of what we call jobs. A job represents a number of orders scheduled to be picked up and/or a number of orders scheduled to be delivered, by a single vehicle, at a single location, starting at a specific time.
Definition 5
A job J is a tuple: (l,Opu,Odo,ts,te) with: l ∈ L some location, Opu a (possibly empty) set of orders to be picked up at l, Odo a (possibly empty) set of orders to be dropped off at l, \(t_{s} \in \mathbb {N}\) the scheduled start time of the job, and \(t_{e} \in \mathbb {N}\) the scheduled end time, satisfying the following constraints:
-
for each o ∈ Opu its pick-up location must be the location l of this job.
-
for each o ∈ Odo its drop-off location must be the location l of this job.
-
ts < te.
-
ts and and te must be consistent with the time windows of the orders (formalized in Section 4.4 by (6) and (7)).
A vehicle-schedule represents the itinerary of a single vehicle.
Definition 6
A vehicle schedule is an ordered list of jobs \((J_{0}, J_{1}, J_{2}, {\dots } , J_{n})\) where \(n \in \mathbb {N}\) can be any natural number. Any vehicle schedule must satisfy the following constraints (in the following, the sets of pick-up and drop-off orders of job Ji are denoted as Opu,i and Odo,i respectively).
-
The jobs are listed in chronological order: if i < j then te,i < ts,j (i.e. job Ji must be finished before we can start job Jj).
-
Each order appearing in any of the jobs of the vehicle schedule has to be picked up and dropped off exactly once (formalized in Section 4.4 by (8)).
-
Each order must first be picked up before it can be dropped off: if o ∈ Opu,i and o ∈ Odo,j then i < j.
-
The location of J0 is equal to the location of Jn, and is known as a depot (each company has one or more depots).
If o is an order, and vs is a vehicle schedule, we may write o ∈vs when we mean that o is picked-up and dropped off by vs. That is, o ∈vs is a shorthand for \(o \in \bigcup _{i \in 0,1{\dots } n}\) Opu,i ∪ Odo,i. The set of all possible vehicle schedules is denoted V S.
Definition 7
A fleet schedule fs for a set of vehicles V and a set of orders O is a map that assigns every vehicle in V to some vehicle schedule vs such that every order o ∈ O appears in exactly one of these vehicle schedules.
Furthermore, for each vehicle v ∈ V the corresponding vehicle schedule vs = fs(v) must satisfy:
-
After each job of vs, the volume and weight of the orders loaded onto the vehicle v cannot exceed the vehicle’s maximum load weight volmax and volume volmax (formalized in Section 4.4 by (9) and (10)).
-
The difference between the end time te,i and the start time ts,i+ 1 of any pair of consecutive jobs Ji,Ji+ 1 must be consistent with the distance between the locations of the two jobs and the speed s of the vehicle. That is, if li and li+ 1 are the respective locations of Ji and Ji+ 1, and d(li,li+ 1) the distance between them, then we must have:
$$ \begin{array}{@{}rcl@{}} &&\forall i\in{0,1,{\dots} n-1}: \quad s \cdot (t_{s,i+1} - t_{e,i}) \\&& \geq \quad d(l_{i},l_{i+1}) \end{array} $$(1)
4.2 Cost functions
For any vehicle schedule vs its cost \(c(\mathit {vs}) \in \mathbb {R}\) is calculated as follows:
where \(dc \in \mathbb {R}\) is the distance costFootnote 2 (in euros per kilometer), ri the road between the locations of Ji− 1 and Ji of vs, \(tc \in \mathbb {R}\) is the time cost (in euros per hour), \(t_{e,n} \in \mathbb {N}\) is the scheduled end time of the last job Jn of vs, and \(t_{s,0} \in \mathbb {N}\) is the scheduled start time of the first job J0 of vs.
The distance- and time costs dc and tc are together referred to as the cost model. In reality, each company would use a different cost model to calculate its own costs. However, since our algorithm represents only one company, and the cost models of the other companies are unknown, it always calculates the costs of any other company using the same cost model (of the company it represents). On the other hand, there is nothing that prevents our algorithm from using a different estimated cost model for every company, if there is reason to believe that that would yield more accurate results.
If fs is a fleet schedule for some set of vehicles V, then its cost \(c(\mathit {fs}) \in \mathbb {R}\) is defined as the sum of the costs of all its vehicle schedules:
4.3 Assignments
Suppose there are m logistics companies \(C_{1}, C_{2}, {\dots } C_{m}\). Each of these companies has a fleet of vehicles Vi and a set of orders Oi to fulfill. We say an order is owned by Ci if o ∈ Oi. However, any two companies Ci and Cj may agree together that some order o owned by Ci will be picked up and delivered by the other company Cj. In that case we say that an order is assigned to Cj.
Definition 8
An order assignment (or simply assignment) α for a set of orders O is a map that assigns each order in O to some company Ci.
We let Oα,i denote the set of orders assigned to Ci by α.
So, if O consists of all the orders owned by any of the companies and α is an assignment for O then we have \(O \ = \ \bigcup _{i=1}^{m} O_{i} \ = \ \bigcup _{i=1}^{m} O_{\alpha ,i}\). The initial assignment \(\overline {\alpha }\) is the assignment that simply assigns each order to the company that owns it, i.e. \(\overline {\alpha }(o) = C_{i}\) iff o ∈ Oi. Therefore, we have \(O_{\overline {\alpha }, i} = O_{i}\).
If Vi is the fleet of some company Ci and α some assignment, then FSα,i denotes the set of all possible fleet schedules for fleet Vi and orders Oα,i. Furthermore, \(\mathit {fs}_{\alpha ,i}^{*}\) denotes the optimal fleet schedule for company Ci under assignment α. That is:
and ci(α) denotes the cost of that fleet schedule:
In other words, if the companies have agreed to exchange orders between them according to assignment α, then \(\mathit {fs}_{\alpha ,i}^{*}\) is the most cost-effective way for company Ci to pick up and deliver all the orders assigned to it, and ci(α) is the cost of that solution. Furthermore, note that if the companies do not exchange any orders, then each company just delivers their own orders Oi, which corresponds to the initial assignment \(\overline {\alpha }\), so in that case the cost of each company Ci is \(c_{i}(\overline {\alpha })\).
An assignment α dominates another assignment \(\alpha ^{\prime }\) iff for all \(i\in \{1,{\dots } m\}\) \(c_{i}(\alpha ) \leq c_{i}(\alpha ^{\prime })\), and for at least one of these companies the inequality is strict. An assignment α is Pareto-optimal iff there is no \(\alpha ^{\prime }\) that dominates α, and we say that α is individually rational iff it dominates \(\overline {\alpha }\).
We are mainly interested in those assignments that are both Pareto-optimal and individually rational. After all, if an assignment α is not Pareto-optimal, it means that there is some assignment \(\alpha ^{\prime }\) that is better for everyone, so the companies would rather accept \(\alpha ^{\prime }\) than α. Furthermore, if an assignment α is not individually rational, it means that there is at least one company that prefers the initial assignment \(\overline {\alpha }\) over α, so it has no reason to ever accept α.
It should be remarked here that whenever we use terms like ‘Pareto-optimal’ or ‘individually rational’, we actually mean Pareto-optimal or individually rational with respect to the cost model(dc,tc). After all, our algorithm calculates all costs for all companies using that cost model, even though in reality each company would calculate its own costs using a different cost model.
In the language of the automated negotiation literature, our problem is a negotiation domain, where the agreement space consists of all possible assignments α for the orders of all companies. The utility functions are the (negations of) the cost functions ci(α) defined by (5), the conflict outcome, representing the case that no agreement is made, is the initial assignment \(\overline {\alpha }\), and the reservation values are given by \(c_{i}(\overline {\alpha })\).
Finally, note that to calculate ci(α) one needs to find the optimal fleet schedule \(\mathit {fs}_{\alpha ,i}^{*}\) which amounts to solving a Vehicle Routing Problem.
4.4 Time- and capacity- constraints
In the previous subsections it was mentioned that jobs, vehicle schedules and fleet schedules need to satisfy certain constraints. We here give a precise mathematical formalization of these constraints. Readers who are not interested in this can safely skip this section.
In Definition 5 it was mentioned that the start- and end-times ts and te of a job must be consistent with the time windows of the orders. This is formalized as follows. For any job J with orders Opu and Odo, the earliest time tes it can possibly start is given by:
where t1,o is the earliest time one can start picking up o and t3,o is the earliest time one can start dropping off order o. Similarly, the latest possible time the job can start is given by:
where t2,o is the latest time one can start picking up order o and t4,o is the latest time one start dropping off order o. So, the job has to start between the earliest and latest start times:
Furthermore, the amount of time required to pick up and drop off all the orders of the job (the service time) is given by:
so the job can only end after at least tserv has passed since the start time:
In Definition 6 it was mentioned that each order appearing in any of the jobs of the vehicle schedule has to be picked up and dropped off exactly once. This can be formalized as:
Recall here that o ∈vs is a shorthand for \(o \in \bigcup _{i \in 0,1{\dots } n}\) Opu,i ∪ Odo,i
In Definition 7 it was mentioned that for each vehicle v and vehicle schedule vs such that fs(v) = vs (meaning that the vehicle schedule vs is executed by vehicle v) one must have that after each job of vs, the volume and weight of the orders loaded onto the vehicle v cannot exceed the vehicle’s maximum load weight wmax and volume volmax. That is:
where volo and wo represent the volume and weight of order o, and where the total number of jobs in the vehicle schedule is n + 1.
To better understand these equations, note that \({\sum }_{o \in O_{pu,i}}\) volo represents the total volume of all orders that are being loaded onto the truck at job Ji. Therefore, \({\sum }_{i=0}^{k} {\sum }_{o \in O_{pu,i}}\) volo represents the total volume of all the orders that have been loaded onto the truck during the first k + 1 jobs. However, some of the orders that have been loaded onto the truck at some job Ji, may have already been offloaded at some other job that came after Ji, but before job Jk. Therefore, to get the total volume of all orders that are on the truck after job Jk, we have to subtract the volume of all those orders that have already been offloaded before Jk, so we get the expression \({\sum }_{i=0}^{k} {\sum }_{o \in O_{pu,i}} vol_{o} - {\sum }_{i=0}^{k}{\sum }_{o \in O_{do,i}} vol_{o}\). Clearly, this value has to be below wmax at any stage of the vehicle schedule, so the inequality has to hold for all values of \(k \in 0,1 {\dots } n-1\).
5 Order package heuristics
In this section we finally present our new search algorithm.
In order to know which deals to propose, the negotiating agents have to evaluate the possible ways to exchange orders between companies, and find the best ones. If there are m companies and each company has X orders, then there are mmX possible order assignments. For realistic cases this number is astronomical, because our industrial partners each typically have more than a hundred orders to deliver, every day. This means that our problem has two layers of complexity:
-
1.
There are many possible assignments: mmX.
-
2.
Given a single assignment α, it is hard to calculate its exact cost ci(α), because it involves solving a VRP (by (4)).
Typical (meta-)heuristic search algorithms like genetic algorithms and simulated annealing can deal with the first layer of complexity, because they are able to find good solutions while only evaluating a small fraction of the entire search space. However, such algorithms typically may still require thousands of evaluations, so if each of these evaluations requires solving a VRP, then the overall algorithm will still be prohibitively slow. For this reason we needed to invent a new heuristic algorithm that can deal with the complexity at both levels. We call it the Order Package Heuristics.
The idea is that we first only look at what we call one-to-one exchanges, which are exchanges of orders in which one company gives a number of orders to another company, which were originally scheduled to be delivered by the same vehicle, and that other company incorporates those orders into the schedule of one of its own vehicles. So, ‘one-to-one’ refers to the fact that the orders are moved from one vehicle to one other vehicle. After determining and evaluating the one-to-one exchanges they are then combined into more general solutions. Furthermore, the construction of one-to-one exchanges is restricted to the exchange of sets of orders that correspond to a sequence of consecutive locations to be visited. We call such sets of orders order packages.
Our algorithm represents company C1 and receives as input:
-
A location graph (L,R,d).
-
A set of orders Oi for each company Ci.
-
A set of vehicles Vi for each company Ci.
-
The cost model (dc,tc) of company C1.
-
For each company Ci, an initial fleet schedule \(\overline {\mathit {fs}}_{i} \!\in \! \mathit {FS}_{\overline {\alpha },i}\).
The output of the algorithm is:
-
A set of assignments \(\{\alpha _{1}, \alpha _{2}, \dots \}\), which, in the ideal case, would be exactly the set of all Pareto-optimal assignments.
The initial fleet schedules \(\overline {\mathit {fs}}_{i}\) are the schedules the companies would execute if there was no collaboration at all. These initial schedules can either be given to our agent by the other companies, or our agent can determine them by itself using a VRP-solving algorithm (although in that case they may be different from the ones actually used by the other companies). Ideally, the initial fleet schedules would be exactly the optimal initial fleet schedules \(\mathit {fs}_{\overline {\alpha },i}^{*}\), but these may be hard to calculate so in practice they may differ.
The rest of this section will give a detailed, step-by-step description of our algorithm.
5.1 Step 1: find compatible order-vehicle pairs
Given the orders Oi and the the initial fleet schedule \(\overline {\mathit {fs}}_{i}\) of each company, our approach starts by determining for each order o which vehicles of other companies could adjust their schedules to also pick up and drop off that order. If indeed it is possible for a vehicle v with schedule vs to make two detours to do this, then we say that o and vs are compatible, or that o and v are compatible.
Definition 9
Let o be an order of one company Ci, let \(\mathit {vs} = (J_{0}, J_{1}, {\dots } J_{n})\) be a vehicle schedule of another company Cj, and let v be the vehicle scheduled to execute vs (i.e. \({vs} = \overline {\mathit {fs}}_{j}(v)\)). We say that o and vs are compatible if it is possible to insert two jobs Jpu,Jdo anywhere into vs to obtain a new vehicle schedule
that satisfies all relevant time- and capacity-constraints (9), (10), and (1), where job Jpu is the pickup of order o, job Jdo is the drop-off of order o, and where every other job \(J_{i}^{\prime }\) is exactly the same as Ji, except that the scheduled start- and end times may have been adjusted. We then also say that o and v form a compatible order-vehicle pair.
Note that the operation of converting vs into \(\mathit {vs}^{\prime }\) is essentially the same as what Li and Lim call the PD-shift operator [36].
Knowing all compatible order-vehicle pairs will allow us to prune a large part of the search space in Step 3, because one can discard all solutions involving orders and vehicles that are incompatible.
Proposition 1
If there are m companies and each company has X orders, then the time complexity of Step 1 is O(m2X2).
Proof
If there are m companies and each company has X := |Oi| orders and for each company their initial fleet schedule involves Y vehicle schedules, then there are mX ⋅ (m − 1)Y possible order-vehicle pairs. For each of these order-vehicle pairs we need to check whether the order and the vehicle schedule are compatible or not. This means we need to check whether the pick-up and the drop-off of the order can be inserted into the vehicle schedule. If the vehicle schedule has n + 1 different jobs then the pick-up and the drop-off can both potentially be inserted in n different places, but since the drop off always needs to take place after the pickup, there are \(\frac {1}{2} n \cdot (n-1)\) options to check. Furthermore, the value n can be estimated as n ≈ 2X/Y (if a company has X orders and Y vehicle schedules, then each vehicle schedule has on average X/Y orders to pick up and drop off, so it may need to visit 2X/Y locations). So, for each possible order-vehicle pair we need to check whether it is compatible or not, which takes \(\frac {1}{2}\cdot 2X/Y \cdot ((2X/Y)-1) \) checks, so the overall time complexity is \((mX \cdot (m-1)Y) \cdot \frac {1}{2}\cdot 2X/Y \cdot ((2X/Y)-1) = O(m^{2} X^{3}/Y)\).
Finally, it is fair to say that the number of vehicle schedules of a company should grow linearly with the number of orders, since each vehicle has a limited capacity. Therefore, within the big-O notation one can set X equal to Y, which means that Step 1 has a time complexity of O(m2X2). □
5.2 Step 2: determine all order packages
The previous step checked for each individual order whether it can be delivered by some given other vehicle, but in general we want to know whether a set of orders can be exchanged from one vehicle (of one company) to another vehicle (of another company). However, since the number of such sets is exponential we only look at a particular type of order set, which we call an order package. An order package is a set of orders, originally scheduled in one vehicle schedule, such that if one removes them from the schedule, the vehicle can skip a set of consecutive locations.
The idea behind this, is that if a few of the locations to be visited by a vehicle are close to each other, then one is most likely to achieve a significant distance reduction if all of those locations are skipped, and such closely clustered locations are likely to be visited consecutively in the original schedule (as demonstrated in Fig. 1).
If \(\mathcal {J}\) is a set of jobs, then let \(Ord(\mathcal {J})\) denote the set of all orders that are either picked up or dropped off in any of the jobs in \(\mathcal {J}\).
Definition 10
Let \(\mathit {vs} = (J_{0}, J_{1}, {\dots } J_{n})\) be a vehicle schedule. An order package op from vs is a set of orders such that there exist two integers k,l with 0 < k < l < n for which
Step 2 consists in extracting all order packages from the vehicle schedules of the initial fleet schedules \(\overline {\mathit {fs}}_{i}\). For each of these order packages we then calculate the cost savingssav(op) associated with it. That is, the difference between the cost of the original vehicle schedule minus the cost of the new vehicle schedule \({vs}^{\prime }\) obtained by removing all pick-ups and drop-offs of the orders in op from vs.
In order to calculate \(c(\mathit {vs}^{\prime })\) one does not actually need to determine \(\mathit {vs}^{\prime }\) itself. Instead, one only needs to know its total time and distance (see (2)). To calculate the distance one can simply take vs and remove the locations that are skipped. Calculating the new time cost is more difficult, so we simplify it by simply assuming the start time ts,0 of the first job and then end time te,n of the last job stay the same. In reality, of course, this may be overly pessimistic, so in general the true cost savings will be even better than the calculated ones.
Note that Definition 10 indeed implies that removing an order package from a vehicle schedule will cause a number of consecutive locations to be skipped, corresponding to jobs Jk to Jl, but it may also imply that a number of other locations are skipped. For example, if some order o is picked up in Jl, but is dropped off in Jl+ 2, and no other order is picked up or dropped off in Jl+ 2, then Jl+ 2 will also be skipped. So, in practice an order package does not always correspond to a consecutive sequence of locations. This is not a problem, because it just means that sometimes even more locations can be skipped than the intended sequence, which is only an advantage.
Proposition 2
If there are m companies and each company has X orders, then the time complexity of Step 2 is O(mX).
Proof
Given a vehicle schedule vs, each order package from vs is uniquely defined by the integers k and l, which can be any number between 1 and n − 1. Therefore, for each vehicle schedule there are \(\frac {(n-1)\cdot (n-2)}{2} = O(n^{2})\) different order packages. As explained above, n can be estimated as 2X/Y, so the number of order packages obtained from vs is O(X2/Y2). Since the order packages are obtained from each vehicle schedule of each company one has to repeat this mY times, so there are O(mY ⋅ X2/Y2) = O(mX2/Y ) order packages in total. Furthermore, calculating the cost savings means summing the distances of all n roads between the visited locations, and again using n ≈ 2X/Y the total time complexity of Step 2 is O(mX2/Y ⋅ 2X/Y ) = O(mX3/Y2). Arguing as before that X can be set equal to Y, this can be simplified to O(mX). □
5.3 Step 3: generate one-to-one exchanges
Step 3 takes all order packages from Step 2, and all vehicle schedules from the initial fleet schedules \(\overline {\mathit {fs}}_{i}\) and combines them into one-to-one order exchanges.
Definition 11
A one-to-one order exchange or simply one-to-one exchange ξ is a pair ξ = (op,vs) where op is an order package of one company, and vs is a vehicle schedule of another company. A one-to-one exchange is feasible if it is possible to find a single vehicle schedule \({vs}^{\prime }\) that delivers all orders of op as well as all orders of vs while satisfying all relevant time- and capacity constraints (9), (10), and (1).
Definition 12
Let ξ = (op,vs) be some one-to-one exchange. Then the vehicle schedule vs of ξ is called the receiving vehicle schedule, which we may also denote as vsr(ξ). Furthermore, we define the receiving vehicle vr(ξ) to be the vehicle that was scheduled to execute vs (i.e. \(\overline {\mathit {fs}}_{i}(v_{r}(\xi )) = {vs}\)), and the receiving company Cr(ξ) to be the company that owns the receiving truck.
Similarly, we use the notation op(ξ) to denote the order package op of ξ, and we define the donating vehicle schedule vsd(ξ) to be the vehicle schedule that was originally supposed to pick-up and deliver the orders in op, the donating vehiclevd(ξ) to be the vehicle that was supposed to execute the donating vehicle schedule (i.e. \(\overline {fs}(v_{d}(\xi )) = {vs}_{d}(\xi ))\), and the donating company Cd(ξ) to be the company that owns the donating vehicle and the orders of the order package op.
These concepts are illustrated in Fig. 2.
These two images illustrate the concept of a one-to-one order exchange. Left: the two original vehicle schedules for Nestlé (red, the ‘receiving vehicle schedule’) and Pladis (blue, the ‘donating vehicle schedule’) respectively, before the exchange. Right: the two new vehicle schedules obtained by removing an order package from Pladis’ vehicle schedule, and adding it to Nestlé’s vehicle schedule. The exchanged order package involves the three consecutive locations A, B and C. Note that this exchange yields large savings for Pladis (the donating company), while yielding only a small distance increase (and hence financial loss) for Nestlé (the receiving company)
Determining whether a one-to-one exchange (op,vs) is feasible or not amounts to solving a VRP. For this, we use an existing VRP-solver from the OR-Tools library by Google [37]. Specifically, we take the set consisting of all orders from op and all orders from vs and then ask the VRP-solver to find a schedule for a single vehicle that delivers all those orders. If this is indeed possible, the solver will output a new vehicle schedule \({vs}^{\prime }\). We then calculate the loss loss(op,vs) for the receiving company, which is the difference between the cost \(c({vs}^{\prime })\) of this new schedule and the cost c(vs) of the original schedule (both calculated with (2)).
However, calling the VRP-solver is computationally expensive, so before doing this the results from Step 1 are used to directly discard many one-to-one exchanges without calling the solver. Specifically, a pair (op,vs) is only considered if every order o ∈ op is compatible (Def. 9) with vs. All other pairs (op,vs) are discarded.
It should be noted, however, that this procedure may discard many one-to-one exchanges that are actually feasible, because even if some orders of op are not compatible with vsr it may still be possible to find some vehicle schedule that does deliver all orders. This is because ‘compatible’ only means that the order can be incorporated in the vehicle schedule with a few minor adjustments. It does not take into account that an entirely re-arranged vehicle schedule could still be found that does succeed in delivering all orders.
After obtaining the set of feasible one-to-one exchanges, one can again discard many of them. Namely, those that do not yield any overall benefit because the loss for the receiving company is greater than the savings of the donating company, i.e. if loss(op,vs) > sav(op).
Proposition 3
If there are m companies and each company has X orders, then the time complexity of Step 3 is O(m2X2).
Proof
The number of one-to-one exchanges equals the number of order packages times the number of vehicle schedules. The first has been calculated to be O(mX2/Y ) and the second is mY, so the number of one-to-one exchanges is O(m2X2). In the worst case the VRP-solver needs to be called for each of these. Although calling the VRP-solver is expensive in practice, and solving a VRP in general takes exponential time, the formal computational complexity of this step is only O(1). This is because our approach only requires solving problem instances with a single vehicle, and the size of such instances is bounded by the capacity constraints of the vehicle. This means that the overall time complexity of Step 3 is O(m2X2). □
5.4 Step 4: combine one-to-one exchanges into full exchanges
After Step 3 one is left with a set of feasible one-to-one exchanges. Each of these already represents an order assignment, but many more order assignments can be found if they are combined, so that multiple order packages can be exchanged and loaded onto multiple other vehicles. Furthermore, if there is no form of payment between the companies, then a single one-to-one exchange would never be an acceptable deal, because the receiving company only loses money. But, if the overall benefit of each one-to-one exchange is positive (i.e. sav(op) > loss(op,vs)) then one can combine multiple one-to-one exchanges into bundles that are individually rational.
However, not every such bundle is feasible, because several one-to-one exchanges may contradict each other. For example, two different order packages, op1 and op2, may contain the same order o, and may appear in two different one-to-one exchanges (op1,vs1) and (op2,vs2) with different receiving schedules.
Definition 13
A full order exchange φ is a set of one-to-one exchanges, i.e. \(\varphi = \{(op_{1},\mathit {vs}_{1}), (op_{2}, \mathit {vs}_{2}), \dots (op_{k},\) vsk)}, such that all order packages are mutually disjoint: opi ∩ opj = ∅ for all \(i,j\in 1{\dots } k\).
Again, determining the exact set of all full order exchanges is costly, so we simplify this by only looking for those sets φ that satisfy the following constraint:
-
If a vehicle v is the receiving vehicle of any one-to-one exchange in φ, then it cannot appear in any other element of φ (neither as donating vehicle, nor as receiving vehicle).
This constraint not only reduces the size of the set of possible solutions, but also has one other great advantage: it means that for any company its total profit from the deal can be calculated simply as the sum of the profits (or losses) it makes from the individual elements of φ. On the other hand, if one vehicle acted as a receiver for more than one one-to-one exchange, then it is not guaranteed that the loss for that vehicle would be equal to the sum of the losses incurred from the two individual one-to-one exchanges. In fact, the combination of the two one-to-one exchanges might not even be feasible, because the receiving vehicle might not have the capacity to handle them both. Therefore, thanks to this constraint, we can define for any company Ci and any full order exchange φ a utility value as follows.
Definition 14
For any company Ci and any one-to-one exchange ξ = (op,vs) we define its utility ui(ξ) as:
and, for any company Ci and any full order exchange φ we define its utility as:
Note, in this definition, that sav and loss are both always non-negative, so a positive loss gives negative utility. Furthermore, note that each full order exchange φ corresponds to a unique assignment αφ and a fleet schedule \(\mathit {fs}_{\varphi ,i} \in FS_{\alpha _{\varphi }, i}\) for each company Ci, defined by (15) and (16).
where Cr(ξ) is the receiving company of ξ. That is, all orders that appear in the order package of any one-to-one exchange ξ in φ should be assigned to receiving company of that one-to-one exchange, while all other orders are assigned to their respective owners.
where \(vs_{r}^{\prime }\) is the vehicle schedule resulting from incorporating op(ξ) into vsr(ξ) and \(vs_{d}^{\prime }\) is the vehicle schedule resulting from removing op(ξ) from vsd(ξ).
Furthermore, note that by (3), (11) and (12), ui(φ) is equal to \(c(\overline {\mathit {fs}_{i}}) - c(\mathit {fs}_{\varphi ,i})\), which can be seen as an approximation for the true cost savings \(c_{i}(\overline {\alpha }) - c_{i}(\alpha _{\varphi })\).
The problem of finding the set of full order exchanges that are Pareto-optimal can now be modeled as a multi-objective optimization problem (MOOP), i.e. a constraint optimization problem with multiple objective functions (one for each of the m companies involved). That is, given the set Ξ of all one-to-one exchanges we found in Step 3, we aim to find those subsets \(\varphi \subseteq {\Xi }\) that are Pareto-optimal with respect to the objective functions ui(φ), under the given constraints. Formally:
In principle, this can be solved with any existing MOOP algorithm. However, for our specific case we have implemented our own algorithm which is a multi-objective variant of And/Or Search [38]. This algorithm is discussed in Section 6.
As a final step, every full exchange φ returned by the MOOP solver is converted to the corresponding assignment αφ, through (15). The set of these assignments in then returned by the algorithm.
Proposition 4
The time complexity of Step 4 is exponential in the number of one-to-one exchanges found by Step 3 (at least, if P≠NP), so it has a time-complexity of \(O(2^{m^{2}X^{2}})\).
Proof
(Sketch) Step 4 entails solving a (multi-objective) constraint optimization problem with hard constraints. The simpler problem of finding any solution φ that satisfies the hard constraints is already an NP-hard problem, because each one-to-one exchange ξ can be seen as a binary variable, so this is essentially a boolean satisfaction problem. As we already mentioned in the proof of Proposition 3, the number of one-to-one exchanges is O(m2X2), so any algorithm that solves this boolean satisfaction problem has a computational complexity of \(O(2^{m^{2}X^{2}})\). □
5.5 Discussion
The overall computational complexity of our algorithm is given simply by the combination of the four steps. We have seen that Steps 1 and 3 are quadratic (Propositions 1 and 3), Step 2 is linear (Proposition 2), and Step 4 is exponential (Proposition 4), so the overall time-complexity of our algorithm as a whole is also exponential.
Since it still takes exponential time, one may wonder what we have actually achieved with our heuristics. The point is that the problem to be solved in Step 4 is much simpler than the original problem. Firstly, because the preceding steps have greatly pruned the search space, and secondly because the new problem is an ordinary (multi-objective) constraint optimization problem with linear objective functions (by (14)). In other words, we have removed the second layer of complexity that we discussed at the beginning of this section. As we will see below in Section 7.4, our algorithm indeed turns out to have a very low run time in practice.
In summary, our approach is fast for the following reasons:
-
1.
The VRP-solver is only used to evaluate one-to-one exchanges rather than full exchanges, because one-to-one exchanges much smaller, and there are a lot less of them.
-
2.
The number of one-to-one exchanges is reduced by discarding those that involve non-compatible order-vehicle pairs.
-
3.
The number of one-to-one exchanges is further reduced by only considering those that exchange order packages rather than general sets of orders.
-
4.
The number of one-to-one exchanges is reduced even further, by discarding those for which the loss is greater than the savings.
-
5.
Our approach only considers full exchanges in which vehicles can act either as donating vehicle or receiving vehicle, but not both, and in which a vehicle can only receive at most one order package. This has the advantage that the number of full exchanges is reduced and that the cost saving of a full solution can be calculated with a linear formula.
On the other hand, our approach has the disadvantage that it may be pruning the search space too strongly, because the constraints that are imposed may also cause a number of good solutions to be discarded.
The algorithm presented here differs in three major points from the algorithm we presented earlier in [2]. Namely:
-
The current version takes into account service times (the time it takes to load or unload a vehicle).
-
The current version allows any vehicle that was not scheduled to also act as a receiving vehicle in a one-to-one exchange (so the receiving vehicle schedule can be the trivial schedule in which the vehicle never departs from the depot).
-
In the current version, the multi-objective optimization problem solved by the And/Or search is modeled a bit differently (see Section 6.3).
6 Multi-objective and/or search
In order to execute Step 4 of our algorithm, we need an algorithm to solve a discrete multi-objective optimization problem. Many algorithms for such problems exist [39], but most of them are only approximate and based on meta-heuristics. To the best of our knowledge, very few of them can solve the problem exactly, and are able to deal with domains in which the set of feasible solutions is very sparse.
For this reason we propose a new algorithm, which is a multi-objective variation of so-called And/Or Search [38]. And/Or Search is an exact search technique for constraint optimization problems that exploits the fact that not all variables depend on each other, which makes ordinary depth-first search unnecessarily inefficient. We propose a new variant of this technique, adapted to MOOPs, so, rather than just returning one solution or all solutions, it returns the set of Pareto-optimal solutions.
6.1 Ordinary and/or search
This subsection gives a brief overview of the existing And/Or Search algorithm for single-objective constraint optimization problems. For a more detailed discussion we refer to [38]. In the next subsection we will discuss our own multi-objective variant.
Definition 15
A (single objective) constraint optimization problem (COP) is a tuple \(\langle \mathcal {X},\mathcal {D},F\rangle \) where \(\mathcal {X} = \{x_{1},x_{2},{\dots } x_{N} \}\) is a set of variables, \(\mathcal {D} = \{D_{1}, D_{2}, {\dots } D_{N}\}\) a set of domains, that is, for each variable xi the corresponding domain Di is a set of possible values for that variable, and \(F = \{f_{1}, f_{2}, {\dots } f_{M}\}\) is a set of functions, called constraints. Each constraint is a map from the cartesian product of some subset of \(\mathcal {D}\), e.g. D2 × D3 × D7, to the set \(\mathbb {R} \cup \{-\infty \}\).
Definition 16
Let \(\langle \mathcal {X},\mathcal {D},F\rangle \) be a COP. A full solution, or simply a solution \(\vec {x}\) is an element of the Cartesian product of all domains, i.e. \(\vec {x} \in D_{1} \times D_{2} \times {\dots } D_{N}\). Furthermore, if \(\mathcal {X}^{\prime }\) is a subset of \(\mathcal {X}\), then a partial solution \(\vec {x}\) on \(\mathcal {X}^{\prime }\) is an element of the Cartesian product of all domains corresponding to the the variables in \(\mathcal {X}^{\prime }\). For example, if \(\mathcal {X}^{\prime } = \{x_{2}, x_{3}, x_{7}\}\) then a partial solution on \(\mathcal {X}^{\prime }\) would be an element from the set D2 × D3 × D7.
The goal of a COP is to find the full solution \(\vec {x}\) that maximizes the objective function \(f(\vec {x}) := {\sum }_{j=1}^{M} f_{j}(\pi _{j}(\vec {x}))\) (where πj is the projection operator that projects the full solution onto the domain of fj).
And/Or search iteratively expands a search tree, consisting of two kinds of nodes, called AND nodes and OR nodes. The root node is an AND node, the children of any AND node are OR nodes, and the children of any OR node are AND nodes. Every OR node is labeled with a variable xi of the COP and will have exactly |Di| children. Each of these children will be labeled with a different variable assignment xi↦di where di ∈ Di. The children of an AND node (which are OR nodes) are each labeled with a different variable xj.
For ordinary tree search algorithms such as depth-first search (DFS), each solution corresponds to a linear branch from the root to a leaf node. In And/Or search, on the other hand, each solution is represented by a sub-tree rather than a branch. Specifically, a solution treeτ is a sub-tree of the fully expanded And/Or search tree σ that satisfies the following conditions:
-
The root of τ is an AND node.
-
For each OR node ν in τ, τ also contains exactly one child of ν.
-
For each AND node ν in τ, τ also contains all children of ν.
If the root of τ is also the root of the full tree σ, then τ will contain exactly one AND node for each variable of the problem, so the labels of all the AND nodes in this solution tree together form a full solution to the COP. Otherwise, the solution tree just represents a partial solution.
The intuitive idea behind And/Or search is that each AND node ν corresponds to a partial solution xν consisting of all labels of all AND nodes in the path from the root to ν, and that given this partial solution, the rest of the problem can be simplified by dividing it into several sub-problems, involving different variables, that can be solved independently from each other.
The great advantage of And/Or search is that if not all variables depend on each other, then it is much faster than DFS because it exploits these independencies. In fact, in the extreme case that all variables can be optimized independently from each other, And/Or search can solve a COP in linear time. On the other hand, in the other extreme case that all variables depend on all other variables, then And/Or search cannot exploit any independencies, and it becomes equivalent to an ordinary depth-first search.
6.2 Our multi-objective variant of and/or search
This subsection describes our new variant of And/Or search, for multi-objective optimization problems.
Definition 17
A multi-objective constraint optimization problem (with m objectives) is a tuple \(\langle \mathcal {X},\mathcal {D},(F_{1}, F_{2}, \dots \) Fm)〉, where \(\mathcal {X}\) and \(\mathcal {D}\) are as before, but now the constraints are divided into m different sets \(F_{i} = \{f_{i,1}, f_{i,2}, {\dots } f_{i,M_{i}}\}\), which define m different objective functions \(f_{i}(\vec {x}) := {\sum }_{f_{i,j}\in F_{i}} f_{i,j}(\pi _{j}(\vec {x}))\).
First note that (just as in an ordinary And/Or search) one can associate with any AND node ν a set of partial solutions Xν, corresponding to exactly all solution trees with root ν. The idea of our multi-objective And/Or search, is that for each AND node ν, it stores a set of solutions pfν, consisting of exactly those partial solutions in Xν that are Pareto-optimal (within Xν). We call this set the local Pareto-set of ν, and it is generated as soon as the subtree under ν is fully expanded. If ν is a leaf node, then pfν is the singleton set consisting of the unique partial solution corresponding to ν, which is exactly the label of ν (i.e. pfν = Xν = {xi↦di}). Otherwise, pfν is generated by taking the union of the local Pareto-sets of all the grandchildren of ν (recall that the children of ν are OR nodes, so the grandchildren are AND nodes), then extending each of them with the label of ν, and then finally removing all dominated elements of this set, so that pfν is indeed a Pareto-set. Once the entire search tree has been expanded, the local Pareto-set for the root is generated. This Pareto-set will then be returned as the output of the algorithm. Note, however, that often it is not really necessary to expand the entire search tree, because pruning techniques such as brand-and-bound can be used.
6.3 Multi-objective and/or search applied to our case
We have applied our Multi-Objective And/Or Search to implement Step 4 of our algorithm. To do this, we modeled our problem as a MOOP \(\langle \mathcal {X}, \mathcal {D},(F_{1}, F_{2} {\dots } F_{m})\rangle \), where m is the number of companies. \(\mathcal {X}\) in this case is a set of binary variables, one for each one-to-one exchange found by Step 3 of our algorithm. That is, \(\mathcal {X} = \{x_{1}, x_{2}, {\dots } x_{N}\}\), where N is the number of one-to-one exchanges found, i.e. N = |Ξ|. These variables are binary, so for each xi its domain is Di = {0,1}.
Thus, a solution \(\vec {x}\) is an N-tuple consisting of zeroes and ones. Each solution represents a full order exchange φ by: ξj ∈ φ iff xj = 1. The constraints are given by Fi = {gi,1, \(g_{i, 2}, \ {\dots } \ g_{i,N},\ h_{1,2}, \ {\dots } \ h_{N-1,N}\}\), consisting of one soft constraint \(g_{i,j} : D_{j} \rightarrow \mathbb {R}\) for each variable xj, defined by:
with ui as in (13), and one hard constraint \(h_{j,k} : D_{j} \times D_{k} \rightarrow \{-\infty , 0\}\) for every pair of different one-to-one exchanges ξj,ξk, defined by:
Note that (17) says that the utility of one-to-one exchange ξj contributes to the utility of a solution for company Ci iff ξj is included in that solution (i.e. xj = 1), while the hard constraints defined by (18) are simply those mentioned earlier in Section 5.4. Also note that the hard constraints are the same for each company, so each Fi contains exactly the same hard constraints \(h_{1,2}, \ \dots , h_{N-1,N}\).
This MOOP is different from the MOOP that was presented in our previous paper [2], where each variable corresponded to a vehicle, rather than a one-to-one order exchange. However, they represent the same problem of combining one-to-one order exchanges into a full order exchange.
7 Experiments
We have tested our algorithm on two data sets. The first one is the Li & Lim benchmark data set [36], which is one of the most commonly used benchmarks for vehicle routing problems. The second data set consists of 10 new test cases that we generated from real-world data provided to us by our industrial partners. Furthermore, we performed an experiment in which we passed the solutions found by our search algorithm to a number of state-of-the-art automated negotiation algorithms to demonstrate the feasibility of automated negotiations applied to our scenario.
7.1 The Li & Lim data set
The Li & Lim data set [36] is a widely used benchmark for vehicle routing problems. This data set contains 6 types of test cases, labeled LR1, LC1, LRC1, LR2, LC2, and LRC2 respectively. The test cases of types LR1 and LR2 have locations that are randomly distributed, while for the types LC1 and LC2 the locations are clustered. Test cases of types LRC1 and LRC2 have a combination of random and clustered locations. The test cases of types LR1, LC1, and LRC1 have a short time horizon, while the test cases of types LR2, LC2, and LRC2 have a longer time horizon.
The Li & Lim data set was designed for non-collaborative vehicle routing, so we had to transform its instances to make them applicable to a collaborative setting. For this, we took a similar approach as Wang & Kopfer [13]. That is, we generated collaborative test cases for two companies, by combining pairs of instances from the original Li & Lim data set. In such a collaborative test case, each company owns a set of orders corresponding to one of the two original instances. To do this, all locations of one of the two instances have to be moved by a fixed amount of distance in one direction, to ensure the two companies do not have their depots at the same location. For our experiments we used the instances with 100 orders for each company (i.e. 100 pick-ups and 100 deliveries), and only those of types LC1, LR1, and LRC1, because Wang & Kopfer observed that the test cases with longer time horizon do not offer as much opportunity for collaboration.
We first determined which pairs of original test cases have the highest potential for improvement by collaboration. To do this, we considered all combinations of different test cases of the same type (e.g. there are 10 instances of type LRC1, so we can make (10 ⋅ 9)/2 = 45 combinations). Since we used 3 types of test case, we could potentially generate 3 × 45 = 135 different collaborative test cases.
Then, for each of these 135 possible test cases we had to find out the best way to move the locations of one of the two original instances. To do this, for each pair of original instances, we tried to combine them in 32 different ways, by shifting the second instance in 8 different directions (north, north-east, east, etc..), and over 4 different distances (30, 45, 60, and 75 ‘units’ of distance). Then, for each of these 32 shifts we used the VRP solver from OR-Tools to calculate the best collaboration-free solution and the best centralized collaborative solution, and picked the one for which the difference was greatest.
Finally, out of the 135 possible test cases, we picked the 5 best ones of each type (LC1, LR1, and LRC1), so in the end we used 15 instances for our experiments (by ‘best’ we again mean the instances that had the greatest difference between the optimal collaboration-free solution and the optimal centralized solution). They are listed in Tables 1 and 2.
We have given the collaborative test cases names of the form ‘A + B (x,y)’ where A and B are the names of the original test cases, and x and y are the number of units that instance B was shifted in the x-direction and y-direction respectively. For example, the test case LC1_2_10 + LC1_2_4 (30,0), was composed from original test cases LC1_2_10 and LC1_2_4, and the second of these was shifted 30 units in the x-direction, and 0 units in the y-direction.
7.2 Real-world test cases
As mentioned above, we also generated 10 test cases from real-world sample data provided to us by our industrial partners. In each of these test cases the two companies each had 100 orders to pick up and deliver on the same day. The total number of locations to be visited by either company varied among the test cases between 117 and 140. The average distance between any two locations varied between 189 km and 218 km and the diameter of each graph varied between 594 km and 680 km. The average volume of the orders was around 26 pallets. Each vehicle was assumed to have a maximum volume capacity of 56 pallets and a maximum weight capacity of 25,000 kg. The average speed of a vehicle was assumed to be 54 km/hr.
The most important differences between the real-world test cases and the Li & Lim test cases are the following:
-
1.
In the real-world test cases a company may have multiple depots (but each vehicle still needs to return to the same depot as were it started).
-
2.
The vehicles in the real-world test cases have two types of constraints: volume and weight, whereas the Li & Lim test cases only involve one type of constraint.
-
3.
In the real-world test cases most of the orders are picked up at one of the companies’ depots, while for the Li & Lim test cases the pick-up locations are typically entirely different from the depots.
-
4.
In the real-world test cases we assume each company has access to an unlimited supply of vehicles, while the Li & Lim test cases involve finite fleets.
The assumption that the companies in the real-world cases have an unlimited fleet is justified by the fact that in reality the companies can always rent vehicles from third parties whenever they do not have enough vehicles themselves (which indeed happens very often).
The 10 real-world test cases are exactly the same as the ones that were used for our experiments in [2], but since several improvements to our algorithm have been made since then, the results are different.
7.3 Performance measures
We have assessed the quality of our algorithm using five different performance measures. Let Φ denote the set of all full order-exchanges found by Step 4 of our algorithm. Then, our quality measures are the following:
-
1.
The total number of full order-exchanges found with positive social welfare: \(|\{\varphi \in {\varPhi } \mid {\sum }_{i} u_{i}(\varphi ) > 0 \}|\).
-
2.
The total number of full order-exchanges found that are individually rational: |{φ ∈Φ∣∀i ui(φ) ≥ 0}|.
-
3.
The diversity among the solutions (\(\hat {\gamma }_{1}\) and \(\hat {\gamma }_{2}\), explained below).
-
4.
The highest relative social welfare improvement among all full order exchanges found:
$$ \max_{\varphi \in {\varPhi}} \frac{{\sum}_{i} u_{i}(\varphi)}{{\sum}_{i} c(\overline{\mathit{fs}}_{i})} \cdot 100 \%$$Note that the numerator represents the total cost savings of all companies combined, while the denominator represents the total initial costs of all companies combined.
-
5.
The time it takes to execute the algorithm.
As explained in Section 3, a negotiation algorithm needs to have a large set of possible solutions available to propose to its opponent. Ideally, this set of possible proposals would be very diverse, with some proposals being very profitable to the agent itself, some being very profitable to the opponent, and others somewhere in between. The more diverse the set of solutions (in terms of utility), the easier it will be for the agent to follow a smooth, gradual, concession strategy. We therefore assess the diversity of the Pareto-frontier as follows. First, let \((\varphi _{1}, \varphi _{2}, {\dots } \varphi _{K})\) be a sorted list containing all full order exchanges found by Step 4 of our algorithm, plus the ‘empty solution’ ∅ representing the case that there is no exchange of orders. This list is sorted in order of increasing utility for company Ci, i.e. \(u_{i}(\varphi _{1}) \leq u_{i}(\varphi _{2}) \leq {\dots } u_{i}(\varphi _{K})\). We then define the max-gap γi as follows:
That is, the largest ‘gap’ between any two neighbors in the Pareto frontier. The lower this value, the more evenly the solutions are distributed along the frontier. We also calculate the largest possible gap between any two solutions: Γi := ui(φK) − ui(φ1) which we then use to calculate the relative max-gap:
The lower this value, the better the quality of the Pareto-frontier. See also Fig. 3 for a visualization of this quantity.
7.4 Results
The experiments were performed on a machine with a 12-core 3.70GHz CPU and 32GB RAM. Our algorithm was implemented in Java. The results are displayed in Tables 1 and 2.
In Table 1 the first column shows the identifier of each test case. The second, third, fourth, and fifth column show the quality measures 1-4 listed in Section 7.3 (the fifth quality measure is listed in Table 2). In order to compare our algorithm with the single-objective approach discussed in the introduction, the last column displays the relative social welfare improvement of the solution found by the single-objective approach (obtained with the same VRP-solver as we used for Step 3).
One main observation from Table 1, is that the results display high variance among the test cases. For some test cases we find many more solutions than for others. Furthermore, we note that for the artificial benchmark instances by Li & Lim better results are achieved than for the real-world test cases. For the Li & Lim instances solutions are found that reduce the combined costs by between 7% and 14%, while for the real-world test cases cost reductions are found between 2% and 7%. We also notice that in most cases the single-objective search is much better at finding a socially optimal solution, but of course such a search only returns one solution, while our approach yields hundreds of alternatives which can be proposed in the negotiations. Also, it can be seen that in most cases our approach yields a fairly uniform Pareto-frontier, with values of \(\hat {\gamma }_{i}\) between 1% and 10%, with only a few exceptions where this value is higher.
Table 2 displays the average time it took to execute Steps 3 and 4 of our algorithm, as well as the average time for the single-objective search, for comparison. The time it took to run Steps 1 and 2 was negligible (typically less than 100 ms.), so they are omitted. All values are averaged over 5 repetitions. The standard errors of these measurements are also displayed, but in many cases they were so small that they were rounded off to 0.
Again, one can see very high variance among the test cases, especially for Step 4. Step 3 took between 6 seconds and almost 4 minutes, while Step 4 took, in the far majority of cases, less than 5 seconds but with some exceptions taking between 1 and 3 minutes, and in one instance even more than 21 minutes. For the single-objective approach the VRP solver was given a time-budget of 5 minutes, but it can be seen that in all cases it converged to a near-optimal solution in much less time. Finally, one can observe that in most cases our heuristic approach finished faster than the single-objective approach, with a few exceptions.
7.5 Negotiations
As explained above, the idea of our heuristic search algorithm, is that its output can be used as the input to a negotiation algorithm. Since automated negotiations have been studied extensively in the literature there is no point in discussing how such algorithms can be implemented here. Instead, the goal of this section is to show empirically that such algorithms are indeed applicable to our scenario, and to determine which of them performs best in our scenario.
The experiments in this section were run on the Genius platform [40], which is arguably the most commonly used platform for experimentation in the field of automated negotiation. We used some of the best performing agents that were submitted to the Automated Negotiating Agents Competitions (ANAC) of 2017, 2018 and 2019 [28, 41], which are freely available with Genius. Specifically, the following agents were used:
-
PonPokoAgent Winner of the ‘individual utility’ category of 2017.
-
AgentHerb Winner of the ‘social welfare’ category of 2018.
-
AgreeableAgent2018 Winner of the ‘individual utility’ category of 2018.
-
KakeSoba Second place in the ‘individual utility’ category of 2019.
-
SAGA Third place in the ‘individual utility’ category of 2019.
-
FSEGA2019 Second place in the ‘social welfare’ category of 2019.
It should be remarked, however, that these agents were developed for negotiation domains that are slightly different from ours. Firstly, these agents were built under the assumption that each deal is represented as a tuple of values, and that the utility function is a linear additive function over these values. Specifically, they assume there is a set of ‘issues’ \(\mathcal {I} = \{I_{1}, I_{2}, {\dots } I_{n}\}\), where each issue Ij is itself a finite set and each deal ω is a tuple from the Cartesian product of the issues \(\omega = (w_{1}, w_{2}, {\dots } w_{n}) \in I_{1} \times I_{2} {\dots } \times I_{n}\). The utility function of each agent ai is then supposed to have the following form:
where each Ui,j is a function \(I_{j} \rightarrow \mathbb {R}\). Furthermore, the utility function is supposed to be normalized, so that Ui(ω) ∈ [0,1] for all possible deals ω.
In Section 4.3 it was explained that our scenario can be seen as a negotiation domain in which each deal ω is an assignment α, and in which the utility functions are the negations of the cost functions ci(α). However, this model does not have the normalized and linear additive structure required by the ANAC agents.
Nevertheless, with some modification we can still fit our domain into the required model, simply by modeling it as a single-issue domain. So, we set \(\mathcal {I} = \{I_{1}\}\), and \(I_{1} = \{\alpha _{1}, \alpha _{2}, {\dots } \alpha _{K}\}\), where each α is one of the individually rational assignments returned by our search algorithm. So, the utility function Ui(ω) of (20) then becomes:
and we can define Ui,1 as:
with ui as in (14), φ the full order exchange corresponding to α (through (15)), and φmax,i the full order exchange found by our algorithm with highest utility for Ci among those that are individually rational.
This means that the utility Ui(α) is always a value between 0 and 1, and the reservation value (i.e. the utility of the initial assignment) is 0 for each agent (note that we only use the individually rational assignments, so we ignore those assignments with utility smaller than zero).Footnote 3 Recall that ui(φ) is an approximation to \(c_{i}(\overline {\alpha }) - c_{i}(\alpha )\), so this model is still very close to the model discussed in Section 4.3.
A second major difference, is that the ANAC agents do not have any knowledge about their opponents’ utility functions. Therefore, it is not obvious for them whether a given deal is good or bad. For example, a deal ω that yields a utility of 0.6 may look good to agent a1, but if the opponent a2 receives a utility of 0.9 for that same deal, and they could have made another deal \(\omega ^{\prime }\) that yields 0.8 for both agents, then ω is actually quite unfair to a1. Typically, the agents are able to infer some information about their opponents’ utility functions from the offers they make combined with the knowledge that their utility functions have a linear-additive structure, but in our case there is no such linear-additive structure. However, as discussed in Section 3.1, in our scenario we can actually make estimation of the opponent’s utility function, so an agent developed specifically for our scenario might be be able to perform better than the ANAC agents, by using that knowledge.
To run our experiments, we generated 10 Genius domains, by taking the output of our algorithm from our 10 real-world test cases, and transforming these results into Genius’ xml-formatFootnote 4 (although we only used five of them in our experiments). Then, we used the Genius platform to run a tournament in which each agent negotiated 15 times against every other agent (including itself) in each of the first five test cases (labeled A-E), with a deadline of one minute. The results are displayed in Table 3. The first column shows the names of the agents, the second column shows in how many negotiation sessions the agents successfully came to an agreement, the third column shows the average utility obtained by the agents in those cases where an agreement was made, and the final column shows the average utility over all negotiation sessions (successful or unsuccessful), which is exactly the product of columns 2 and 3.
Note that a good negotiator does not necessarily always strike a deal. After all, in order to enforce a good deal, one should be able to make a credible threat to walk away from the negotiation table if the opponent is not willing to concede enough. Therefore, one should strike a balance between taking a hard stance demanding a good deal for oneself, and, on the other hand, being lenient enough to make a deal acceptable for the opponent. Indeed, Table 3 shows that the two most extreme negotiators are also the two worst performing ones. AgreeableAgent2018 takes a very harsh approach which allows it to obtain maximum utility in those cases that it strikes a deal, but this approach also leads a high rate of failure, striking a deal in only 30% of the cases, yielding low overall utility. SAGA, on the other hand, takes an overly lenient approach which does yield a success rate of 100%, but at the price that it only receives very low utility for those deals. We see that the algorithm that performs overall best is FSEGA2019, which takes a more balanced approach. We therefore conclude that FSEGA2019 would be the best negotiation strategy to employ in our setting.
In order to test whether the difference between FSEGA2019 and its opponents was statistically significant, we performed, for each of its opponents, a Welch t-test. Indeed, this test showed that FSEGA 2019 outperformed KakeSoba with p-value 0.01, that it outperformed PonPokoAgent with p-value 0.0075, that it outperformed AgentHerb with p-value 0.001, that it outperformed AgreeableAgent2018 with p-value 0.002, and that it outperformed SAGA with p-value 2 ⋅ 10− 48.
7.6 Analysis of results
This section discusses a number of observations that can be made from the experiments.
Observation 1
There is high variance in the number of solutions found by our algorithm. This fact is true for all types of test cases. For example, among the real-world domains there is one instance for which we find 128 solutions, and one instance for which we find 1302 solutions. Similarly, among the LC1 instances there is one instance with 60 solutions, and one with 449 solutions. Therefore, it is difficult to say what exactly causes this high variance. We will leave it as future work to answer this question.
Observation 2
Better results are obtained on the Li & Lim test cases than on the real-world test cases. This may be partially explained by the fact that in the real-world test cases most of the orders are picked up at one of the companies’ depots, while for the Li & Lim test cases the pick-up locations are typically entirely different from the depots. This greatly reduces the potential benefit of collaboration in the real-world test cases, because it means a company needs to drive much farther to pick up another company’s order than to pick up its own orders. Furthermore, this difference can also be seen when looking at the solutions found by the single-objective search. This suggests that it is indeed an artifact of the test cases themselves, rather than our algorithm.
Observation 3
The solutions found by our algorithm are fairly uniformly distributed. This is a very nice feature of our algorithm, because it allows a negotiation algorithm to follow a smooth negotiation strategy that makes very gradual concessions.
Observation 4
The solution found by the single-objective search is typically much better than the solutions found by our algorithm (in terms of social welfare). This is not surprising, given the fact that the single-objective search can dedicate all computational power towards finding one single optimal solution, whereas our algorithm aims to find many different solutions. However, it does show that apparently the socially optimal solution cannot be found simply by combining one-to-one order exchanges in the way our approach does. In other words, although our heuristics are efficient, they do tend to miss certain high-quality solutions.
Observation 5
In most cases our algorithm is faster than the single-objective search, but with a few exceptions. The comparison between the run time of the two algorithms should only be seen as a rough ‘ballpark’ estimation. Note that it does not even make sense to really compare them in detail, firstly because the two algorithms do different things (our algorithm aims to find the Pareto-frontier, while the single-objective search aims to find a single optimal solution), and secondly, because the variance among the problem instances is too large to draw any general conclusions. Nevertheless, it is important to note that their respective speeds are of the same order of magnitude, which allows us to conclude that our approach is a viable alternative to the single-objective approach.
Observation 6
The run time of Steps 1 and 2 are negligible compared to Steps 3 and 4. The fact that Step 4 takes much more time than Steps 1 and 2 makes sense, given that Steps 1 and 2 have quadratic and linear time complexity respectively, while Step 4 is exponential. What may seem more surprising, is the fact that Step 3 often takes more time than Step 4, even though Step 3 only has quadratic time complexity. However, recall from Section 5.3 that Step 3 involves solving a vehicle routing problem, and even though this formally only has constant time complexity (because the VRP instances have bounded size), in practice this is very costly. It is unlikely that this step can be made any faster, since it depends on the VRP solver from Google OR-Tools, which is already highly optimized.
Observation 7
The run time of our algorithm displays very high variance among the various test cases. For any given test case, the variance in the run times is generally low (with a few exceptions), but between different test cases we actually see very high variance, both in the run time of Step 3 and of Step 4. For Step 4 this can be easily explained, because the effectiveness of And/Or Search highly depends on the structure of the problem. If all variables in the instance depend on each other, then And/Or search is no more effective than DFS, while if all variables are completely independent from each other it can solve the problem in linear time. Therefore, small variations between instances can yield very large variations in run time.
Furthermore, the effectiveness of And/Or search also heavily depends on the order in which the variables appear in the tree. To find the optimal variable ordering our algorithm uses a non-deterministic heuristic, so this may sometimes yield less effective orderings.Footnote 5 This explains why there are a few test cases for which the variance is actually high. That is, because in those cases the And/Or search sometimes (but not always) fails to find the optimal variable ordering.
For Step 3 it is much more difficult for us to reason about the origin of the high variance of its run time, because this is mainly determined by the VRP solver of Google OR-Tools.
Observation 8
our results are different from (but similar to) the results published in our previous paper [2]. There are two reasons why the results are different. The first reason is that we are now taking into account that it takes time to load or unload a vehicle, which was not taken into account in our previous paper. This is an extra constraint that makes the problem more difficult, so we can expect this to have a negative impact on our results. Secondly, a number of improvements have been made to our algorithm (as mentioned in Section 5.5), which have had a positive effect on the results. Overall, it seems the positive and the negative effects roughly cancel out against each other, so the quality of the solutions is similar. Of course, the single-objective search is only affected by the increased difficulty of the problem, and indeed for the single-objective search the results are not as good as those in our previous paper.
Observation 9
The best negotiation algorithm is one that makes a trade-off between being very hard-headed, and being very conceding. This is actually well known in the literature on automated negotiation. However, most research in this area is based on artificial test cases, so it is interesting to see this fact confirmed on real-world test cases as well. Our experiments indicate that FSEGA 2019 would be the algorithm that is most applicable to this domain. Unfortunately, however, we are not aware of any publication that describes this algorithm, so it is unclear why exactly it outperforms the others.
Furthermore, it is striking to see how poorly the agent named SAGA performs compared to the others. Again, we are not aware of any publications that describe it, so we can only guess why. One reason may be that it is not able to handle single-issue domains. After all, many negotiation algorithms that were developed for ANAC exploit the fact that the utility functions are linear over the various ‘issues’ of the domain to make better estimations of the opponent’s utility values. This is not possible, however, in our single-issue test cases.
7.7 Limitations of our approach
One can identify three main limitations to our approach. The first, is that the number of solutions, the quality of the solutions, and the run time all display high variance among the various test cases. This means that it is difficult to predict how well the algorithm will perform on any unseen problem instances. A second limitation, is that the solutions found by our algorithm are of lower quality than the solution found by the single-objective search. This is because our heuristics sometimes prune the search space too strongly, and therefore discard good solutions. Finally, another main limitation is that there are a number of real-world constraints that our algorithm is not taking into account. For example, it currently does not take into account that truck drivers need to take a break once in a while. Also, it does not take into account that trucks may need to be loaded and unloaded in a last-in-first-out order, which may restrict the order in which customers can be visited. Solving these shortcomings is left as future work.
8 Conclusions and future work
We have presented a heuristic algorithm for a problem that, to the best of our knowledge, has never been studied before. Namely, a collaborative VRP without any form of trusted central system and in which the agents do not know each others’ cost functions, but are able to estimate them. The goal is, for one agent, to find a large set of potential exchanges of orders, which can then be used as the input for a negotiation algorithm. These solutions should ideally be Pareto-optimal and individually rational.
We have compared our approach with a single-objective approach and conclude that the two approaches are roughly equally fast. The single-objective approach returns a solution of higher quality, but has the disadvantage that it only yields one single solution. Our approach, on the other hand, yields hundreds of alternatives, which allows the two parties to negotiate about which one they will choose. We therefore argue that the best approach would actually be a combination of these two approaches. One could use the single-objective approach to find and propose a single high-quality solution, and then use our order package approach to find many alternative solutions that can be proposed in case the high-quality solution does not get accepted.
One important remark that should be made, is that it was argued in [42] that horizontal collaboration between logistics companies is typically more effective if those companies have complementary characteristics. In our test cases, however, this was not the case. Our two industrial partners are actually very similar, since they produce similar products, have similar size, and serve similar customers. This suggests that our algorithm could obtain even better results if it were applied to a more suitable combination of companies.
As explained above, there are still a number of real-world constraints that our algorithm does not take into account, such as the necessity for drivers to take breaks, and the order in which the pallets need to be loaded and unloaded. We leave it as future work to solve this. Furthermore, we would like to explore the possibility of applying our approach to ridesharing services such as Uber. After all, ridesharing can be seen as a kind of co-loading, but with the orders replaced by humans. Ridesharing has mainly been studied as a single-objective problem [43], but we think instead it might be useful to view each driver or customer as a separate agent that tries to optimize its own individual preferences.
As a final note, we would like to argue for what we call the BOASE model for automated negotiation. In the traditional literature it is argued that negotiation algorithms typically consist of three components: a Bidding strategy, an Opponent Modeling strategy, and an Acceptance strategy. This idea is known as the BOA model [44]. However, we argue that there are two more important components that are missing from this model, namely Search and Evaluation, which have received much less attention in the literature. The Evaluation component would be the algorithm that, given any potential deal ω, calculates its utility value ui(ω) for agent ai. In the traditional literature one mainly focused on domains with linear utility functions, so this calculation was trivial, but in our case it amounts to solving a VRP. The Search component would be the algorithm that determines which of the potential deals should be evaluated by the Evaluation component. This is important when the number of such potential proposals in the offer space is astronomical (as in our case), so one cannot possibly evaluate them all. Search algorithms have received some attention in the automated negotiations literature, for example in the ANAC 2014 competition [31], but they still remain relatively little explored.
Code Availability
Our code will not be made publicly available, because we may use it to build a commercial application.
Notes
More complex deals are also possible, as long as each company involved in the deal benefits.
Perhaps surprisingly, the distance cost does not depend on how much weight is loaded onto the vehicle. This may seem unrealistic, but this is how many real-world logistics companies do calculate their costs. Furthermore, to keep the discussion simple we here assume that dc does not depend on the vehicle. The implementation or our algorithm, however, does allow dc to be different for each vehicle.
Initially, we also performed some experiments in which we also included all deals that were not individually rational, but it turned out that some of the agents were not able to handle such domains well, as they made agreements below their own reservation values.
these will be made publicly available at https://www.iiia.csic.es/~davedejonge/homepage/downloads.
The outcome of the algorithm is still perfectly deterministic, though. It is just the run time that may differ as a consequence of this non-deterministic heuristic.
References
Ferrell W, Ellis K, Kaminsky P, Rainwater C (2020) Horizontal collaboration: opportunities for improved logistics planning. Int J Prod Res 58(14):4267–4284. https://doi.org/10.1080/00207543.2019.1651457https://doi.org/10.1080/00207543. https://doi.org/10.1080/00207543.2019.16514572019.1651457
de Jonge D, Bistaffa F, Levy J (2021) A heuristic algorithm for multi-agent vehicle routing with automated negotiation. In: Proceedings of the 20th international conference on autonomous agents and multiagent systems (AAMAS 2021). International Foundation for Autonomous Agents and Multiagent Systems
Dantzig GB, Ramser JH (1959) The truck dispatching problem. Manag Sci 6(1):80–91
Clarke G, Wright JW (1964) Scheduling of vehicles from a central depot to a number of delivery points. Oper Res 12(4):568–581
Desrochers M, Lenstra JK, Savelsbergh MWP (1990) A classification scheme for vehicle routing and scheduling problems. Eur J Oper Res 46(3):322–332
Toth P, Vigo D (2002) The vehicle routing problem, SIAM monographs on discrete mathematics and applications, vol 9. SIAM. https://doi.org/10.1137/1.9780898718515
Braekers K, Ramaekers K, Van Nieuwenhuyse I (2016) The vehicle routing problem: state of the art classification and review. Comput Ind Eng 99:300–313. https://doi.org/10.1016/j.cie.2015.12.007https://doi.org/10.1016/j.cie.2015. https://doi.org/10.1016/j.cie.2015.12.00712.007
Uchoa E, Pecin D, Pessoa A, Poggi M, Vidal T, Subramanian A (2017) New benchmark instances for the capacitated vehicle routing problem. Eur J Oper Res 257(3):845–858. https://doi.org/10.1016/j.ejor.2016.08.012https://doi.org/ https://doi.org/10.1016/j.ejor.2016.08.01210.1016/j.ejor.2016.08.012, https://www.sciencedirect.com/science/article/pii/S0377221716306270
Savelsbergh MWP, Sol M (1995) The general pickup and delivery problem. Transp Sci 29 (1):17–29
Dumas Y, Desrosiers J, Soumis F (1991) The pickup and delivery problem with time windows. Eur J Oper Res 54(1):7–22
Dixit A, Mishra A, Shukla A (2019) Vehicle routing problem with time windows using meta-heuristic algorithms: a survey. In: Yadav N, Yadav A, Bansal J C, Deep K, Kim J H (eds) harmony search and nature inspired optimization algorithms. Springer Singapore, Singapore, pp 539–546
Gansterer M, Hartl RF (2018) Collaborative vehicle routing: a survey. Eur J Oper Res 268 (1):1–12
Wang X, Kopfer H (2014) Collaborative transportation planning of less-than-truckload freight. OR Spectrum 36(2):357–380
Wang X, Kopfer H (2015) Rolling horizon planning for a dynamic collaborative routing problem with full-truckload pickup and delivery requests. Flex Serv Manuf J 27(4):509–533
Wang X, Kopfer H, Gendreau M (2014) Operational transportation planning of freight forwarding companies in horizontal coalitions. Eur J Oper Res 237(3):1133–1141
Dahl S, Derigs U (2011) Cooperative planning in express carrier networks - an empirical study on the effectiveness of a real-time decision support system. Decis Support Syst 51(3): 620–626. https://doi.org/10.1016/j.dss.2011.02.018, http://www.sciencedirect.com/science/article/pii/S0167923611000947http://www. http://www.sciencedirect.com/science/article/pii/S0167923611000947sciencedirect.com/science/article/pii/S0167923611000947
Jozefowiez N, Semet F, Talbi E-G (2008) Multi-objective vehicle routing problems. Eur J Oper Res 189(2):293–309
Ombuki BM, Ross B, Hanshar F (2006) Multi-objective genetic algorithms for vehicle routing problem with time windows. Appl Intell 24(1):17–30. https://doi.org/10.1007/s10489-006-6926-z
van der Putten S, Robu V, La Poutré H, Jorritsma A, Gal M (2006) Automating supply chain negotiations using autonomous agents: A case study in transportation logistics. In: Proceedings of the fifth international joint conference on autonomous agents and multiagent systems, AAMAS ’06. https://doi.org/10.1145/1160633.1160926. ACM, New York, pp 1506–1513
Robu V, Noot H, La Poutré H, van Schijndel W-J (April 2011) A multi-agent platform for auction-based allocation of loads in transportation logistics. Expert Syst Appl 38(4):3483–3491. https://doi.org/10.1016/j.eswa.2010.08.136
de Jonge D, Sierra C (2012) Automated negotiation for package delivery. In: Self-Adaptive and Self-Organizing Systems Workshops (SASOW), 2012 IEEE sixth international conference on, pp 83–88
de Jonge D, Sierra C (2015) NB3: a multilateral negotiation algorithm for large, non-linear agreement spaces with limited time. Auton Agent Multi-Agent Syst 29(5):896–942. https://doi.org/10.1007/s10458-014-9271-3
Faratin P, Sierra C, Jennings NR (1998) Negotiation decision functions for autonomous agents. Robot Auton Syst 24(3-4):159–182. https://doi.org/10.1016/S0921-8890(98)00029-3, http://www.sciencedirect.com/science/article/pii/S0921889098000293, Multi-Agent Rationality
Rosenschein JS, Zlotkin G (1994) Rules of encounter. The MIT Press, Cambridge
Baarslag T, Hindriks KV, Jonker CM, Kraus S, Lin R (2012) The first automated negotiating agents competition (ANAC 2010). In: new trends in agent-based complex automated negotiations, studies in computational intelligence. https://doi.org/10.1007/978-3-642-24696-8_7, vol 383. Springer, pp 113–135
Fujita K, Aydogan R, Baarslag T, Ito T, Jonker CM (2014) The fifth automated negotiating agents competition (ANAC 2014). In: Recent advances in agent-based complex automated negotiation [revised and extended papers from the 7th international workshop on Agent-based Complex Automated Negotiation, ACAN 2014, Paris, France, May 2014], studies in computational intelligence, vol 638. Springer, pp 211–224. https://doi.org/10.1007/978-3-319-30307-9_13
Fujita K, Aydoğan R, Baarslag T, Hindriks K, Ito T, Jonker C (2017) The sixth automated negotiating agents competition (anac 2015). In: Modern approaches to agent-based complex automated negotiation. Springer, pp 139–151
Aydoğan R, Baarslag T, Fujita K, Mell J, Gratch J, de Jonge D, Mohammad Y, Nakadai S, Morinaga S, Osawa H, Aranha C, Jonker CM (2020) Challenges and main results of the automated negotiating agents competition (anac) 2019. In: Bassiliades N, Chalkiadakis G, de Jonge D (eds) multi-agent systems and agreement technologies. Springer International Publishing, Cham, pp 366–381
Mell J, Gratch J, Baarslag T, Aydogan R, Jonker CM (2018) Results of the first annual human-agent league of the automated negotiating agents competition. In: Proceedings of the 18th international conference on Intelligent Virtual Agents, IVA 2018, Sydney, NSW, Australia, November 05-08, 2018. https://doi.org/10.1145/3267851.3267907. ACM, pp 23–28
de Jonge D, Baarslag T, Aydoğan R, Jonker C, Fujita K, Ito T (2019) The challenge of negotiation in the game of diplomacy. In: Lujak M (ed) agreement technologies, 6th international conference, AT 2018, Bergen, Norway, December 6-7, 2018, revised selected papers, lecture notes in computer science, vol 11327. Springer International Publishing, Cham, pp 100–114
Baarslag T, Aydoğan R, Hindriks KV, Fuijita K, Ito T, Jonker CM (2015) The automated negotiating agents competition, 2010-2015. AI Mag 36(4):115–118. http://www.aaai.org/ojs/index.php/aimagazine/article/view/2609
de Jonge D, Zhang D (2020) Strategic negotiations for extensive-form games. Auton Agent Multi-Agent Syst 34(1). https://doi.org/10.1007/s10458-019-09424-y
de Jonge D, Sierra C (2017) D-Brane: a diplomacy playing agent for automated negotiations research. Appl Intell 47(1):158–177. https://doi.org/10.1007/s10489-017-0919-y
Ito T, Klein M, Hattori H (2008) A multi-issue negotiation protocol among agents with nonlinear utility functions. Multiagent Grid Syst 4:67–83. http://dl.acm.org/citation.cfm?id=1378675.1378678
de Jonge D, Sierra C (2016) GANGSTER: an automated negotiator applying genetic algorithms. In: Fukuta N, Ito T, Zhang M, Fujita K, Robu V (eds) recent advances in agent-based complex automated negotiation, studies in computational intelligence. http://www.iiia.csic.es/davedejonge/homepage/files/articles/Gangster.pdf. Springer International Publishing, pp 225–234
Li H, Lim A (2003) A metaheuristic for the pickup and delivery problem with time windows. Int J Artif Intell Tools 12(02):173–186
Perron L, Furnon V (2019) Google or-tools v7.4. https://developers.google.com/optimization/
Marinescu R, Dechter R (2009) AND/OR branch-and-bound search for combinatorial optimization in graphical models. Artif Intell 173(16-17):1457–1491. https://doi.org/10.1016/j.artint.2009.07.003https://doi.org/10.1016/j. https://doi.org/10.1016/j.artint.2009.07.003artint.2009.07.003
Liu Q, Li X, Liu H, Guo Z (2020) Multi-objective metaheuristics for discrete optimization problems: a review of the state-of-the-art. Appl Soft Comput 93:106382. https://doi.org/10.1016/j.asoc.2020.106382https://doi.org/10. https://doi.org/10.1016/j.asoc.2020.1063821016/j.asoc.2020.106382, https://www.sciencedirect.com/science/article/pii/S1568494620303227
Lin R, Kraus S, Baarslag T, Tykhonov D, Hindriks K, Jonker CM (2014) Genius: An integrated environment for supporting the design of generic automated negotiators. Comput Intell 30(1):48–70. https://doi.org/10.1111/j.1467-8640.2012.00463.x
Aydogan R, Fujita K, Baarslag T, Jonker CM, Ito T (2019) ANAC 2018: Repeated multilateral negotiation league. In: Ohsawa Y, Yada K, Ito T, Takama Y, Sato-Shimokawara E, Abe A, Mori J, Matsumura N (eds) advances in artificial intelligence - selected papers from the annual conference of Japanese Society of Artificial Intelligence (JSAI 2019), Niigata, Japan, 4-7 June 2019, Advances in Intelligent Systems and Computing, vol 1128. Springer, pp 77–89. https://doi.org/10.1007/978-3-030-39878-1_8
Palhazi Cuervo D, Vanovermeire C, Sörensen K (2016) Determining collaborative profits in coalitions formed by two partners with varying characteristics. Transp Res Part C: Emerging Technol 70:171–184. https://doi.org/10.1016/j.trc.2015.12.011, https://www.sciencedirect.com/science/article/pii/S0968090X15004271
Farinelli A, Bicego M, Bistaffa F, Ramchurn SD (2017) A hierarchical clustering approach to large-scale near-optimal coalition formation with quality guarantees. Eng Appl Artif Intell 59:170–185. https://doi.org/10.1016/j.engappai.2016.12.018
Baarslag T, Hindriks K, Hendrikx M, Dirkzwager A, Jonker C (2014) Decoupling negotiating agents to explore the space of negotiation strategies. In: Marsa-Maestre I, Lopez-Carmona MA, Ito T, Zhang M, Bai Q, Fujita K (eds) Novel Insights in Agent-based Complex Automated Negotiation. Springer Japan, Tokyo, pp 61–83
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature. This work was supported by project LOGISTAR funded by the E.U. Horizon 2020 Research and Innovation Programme (Grant Agreement 769142), by project CI-SUSTAIN funded by the Spanish Ministry of Science and Innovation (PID2019-104156GB-I00), and by a Juan de la Cierva research grant from the Spanish Ministry of Science and Innovation (IJC2018-036443-I).
Author information
Authors and Affiliations
Contributions
– Dave de Jonge: Conceptualization, Methodology, Software, Formal analysis, Investigation, Writing - Original Draft, Visualization.
– Filippo Bistaffa: Conceptualization, Software, Formal analysis, Writing - Review & Editing.
– Jordi Levy: Conceptualization, Formal analysis, Writing - Review & Editing, Supervision.
Corresponding author
Ethics declarations
Competing Interests
Conflicts of Interests The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
de Jonge, D., Bistaffa, F. & Levy, J. Multi-objective vehicle routing with automated negotiation. Appl Intell 52, 16916–16939 (2022). https://doi.org/10.1007/s10489-022-03329-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-022-03329-2