A new approach to the design of acyclic chemical compounds using skeleton trees and integer linear programming

Abstract

Intelligent systems are applied in a wide range of areas, and computer-aided drug design is a highly important one. One major approach to drug design is the inverse QSAR/QSPR (quantitative structure-activity and structure-property relationship), for which a method that uses both artificial neural networks (ANN) and mixed integer linear programming (MILP) has been proposed recently. This method consists of two phases: a forward prediction phase, and an inverse, inference phase. In the prediction phase, a feature function f over chemical compounds is defined, whereby a chemical compound G is represented as a vector f(G) of descriptors. Following, for a given chemical property $\pi$, using a dataset of chemical compounds with known values for property $\pi$, a regressive prediction function $\psi$ is computed by an ANN. It is desired that $\psi (f(G))$ takes a value that is close to the true value of property $\pi$ for the compound G for many of the compounds in the dataset. In the inference phase, one starts with a target value $y^*$ of the chemical property $\pi$, and then a chemical structure $G^*$ such that $\psi (f(G^*))$ is within a certain tolerance level of $y^*$ is constructed from the solution to a specially formulated MILP. This method has been used for the case of inferring acyclic chemical compounds. With this paper, we propose a new concept on acyclic chemical graphs, called a skeleton tree, and based on it develop a new MILP formulation for inferring acyclic chemical compounds. Our computational experiments indicate that our newly proposed method significantly outperforms the existing method when the diameter of graphs is up to 8. In a particular example where we inferred acyclic chemical compounds with 38 non-hydrogen atoms from the set {C, O, S} times faster.

1 Introduction

Computer-aided drug design is one of the most significant areas for application of recently developed methods in artificial intelligence. One particular approach that has attracted extensive studies is the inverse QSAR/QSPR (quantitative structure-activity and structure-property relationship) [16, 23]. The task of QSAR/QSPR is to compute a regression function between the structure of chemical compounds and some chemical activity and/or property of interest. The structure of chemical compounds is commonly represented in the form of undirected graphs, and the regression function is computed by using statistical machine learning methods from a set of training data of pairs of known molecular compounds and their activities/properties. The inverse QSAR/QSPR then, given such a regression function, asks to infer the structure of a chemical compound that would exhibit certain activity or property, perhaps while obeying some additional constraints. A common method to the inverse QSAR/QSPR is to formulate an optimization problem that asks to find a chemical graph that maximizes or minimizes a particular objective function under various constraints.

Directly handling chemical graphs in statistical methods and machine learning methods poses a difficult challenge, and therefore it is common to represent chemical compounds by numerical vectors, called a set of descriptors, or a set of features. There have been several methods that have been developed for deriving graph structures that are optimal or close to optimal for a given objective function [10, 16, 20]. In addition to getting one solution that is optimal or close to optimal, it is often required to infer or enumerate graph structures that satisfy a given feature vector. There have been various methods developed for solving the task of enumerating graph structures [7, 11, 14, 18]. In addition, the computational complexity of the enumeration task has been studied [1, 17].

1.1 Related work

Undoubtedly Artificial Neural Networks (ANNs) and their application in deep learning have enjoyed unprecedentedly rapid progress recently. Applications of these technologies to the problem of the inverse QSAR/QSPR include variational autoencoders [8, 15], recurrent neural networks [22, 26], and grammar variational autoencoders [13]. These applications standardly involve training a neural network with a set of known compound/activity data. Then, the inverse QSAR/QSPR is solved by solving the problem of inverting a trained neural network, commonly done through statistical methods. However, one of the major drawbacks of statistical methods is that there is no guarantee that an obtained solution will be optimal or exact.

A recently proposed approach based on mixed integer linear programming (MILP) [3], comes with a mathematical guarantee for the optimality of the derived solution. Since the proposed method [3] relies on linear programming, the activation functions of the neurons in an ANN are represented as piece-wise linear functions, and therefore ReLU functions can be represented without any loss, whereas sigmoid functions must be approximated.

The MILP-based method for inverting trained ANNs [3] has recently been combined with methods for efficient enumeration of tree-like graphs, e.g., the algorithm proposed by Fujiwara et al. [7], into a two-phase framework for inverse QSAR/QSPR [4, 6].

The first phase in the framework solves (I) Prediction Problem, by constructing a prediction, or a regression, function by using an ANN $\mathcal {N}$. In this phase, given a set of chemical compounds, that is, chemical graphs G, and known values a(G) for a certain chemical property $\pi$, each chemical compound G in the set is represented by a feature vector f(G). These feature vectors are used as inputs for training the ANN $\mathcal {N}$, to obtain a prediction function $\psi _{\mathcal {N}}$ in such a way that a(G) is predicted as $\psi _{\mathcal {N}}(f(G))$.

The second phase solves (II) Inverse Problem. Starting with a given a target value $y^*$ for a chemical property $\pi$, in stage (II-a), a feature vector $x^*$ is computed based on the trained ANN $\mathcal {N}$ under the constraint that $\psi _{\mathcal {N}}(x^*)$ is within a certain tolerance range close to $y^*$. Following, (II-b) a set of chemical structures $G^*$ is generated under the condition that $f(G^*) = x^*$. Stage (II-a) in the methods of a combined framework [4, 6] is based on an MILP formulation, which incorporates the one due to Akutsu and Nagamochi [3]. In particular, the MILP formulation proposed by Azam et al.  [4] guarantees that for a given trained ANN $\mathcal {N}$ and a desired target value $y^*$, either:

• (i) every feature vector $x^*$ inferred from ANN $\mathcal {N}$ in (II-a) admits a corresponding chemical structure $G^*$, or

• (ii) no chemical structure exists for the given target value $y^*$ when no feature vector is inferred from the ANN $\mathcal {N}$.

Notable related works on the inverse QSAR/QSPR include the frameworks and results reported by Sumita et al. [24], as well as Takeda et al. [25]. However, there are certain drawbacks to these frameworks as compared to the combined framework described above [4, 6].

The work due to Sumita et al. [24] is noteworthy since it is reported that the finally obtained structures have been synthesized and their properties experimentally tested. A major drawback of this approach is that it relies on a Monte-Carlo based simulation, which is reported to take on the order of days of computation time.

On the other hand, Takeda et al. [25] propose a framework for constructing a regression function, solving the inverse problem on the regression function to obtain the descriptors of a desired chemical compound, and enumerating several chemical compounds with some desired properties. In this work, the descriptors used as arguments to construct a regression function are general sub-structure frequency vectors, which is a disadvantage, since such descriptors are dependent on the features of the training set. As opposed to general sub-structures, the framework on which we build [4, 6] uses graph-theoretical descriptors, which easily preserves explainability. Further, Takeda et al. [25] propose a custom-implemented gradient search method to solve the problem of inverting the regression function, which is not guaranteed to arrive at a globally optimal, and hence, exact solution. As opposed to that, using a solution to an MILP formulation offers an exact solution to the problem of inverting the regression function constructed by an ANN.

1.2 Our contribution

With this paper, we propose a new MILP formulation, which when included in the combined framework for the inverse QSAR/QSPR [4, 6], serves the purpose to infer acyclic chemical compounds with a bounded degree. To this purpose, we introduce the concept of skeleton trees, which are trees with the maximum number of vertices for a given diameter and degree. Then, an acyclic chemical graph to be inferred is constructed as an induced subgraph of a skeleton tree.

The aim for introducing a new MILP formulation is due to the fact that solving an MILP is known to be a computationally difficult problem. Even though modern-day commercial solvers such as CPLEX [9] are highly effective in practice, our intuition is that there is room for improvement, especially by taking into account the special structure of acyclic chemical compounds with a limited degree. Here we note that chemical graphs with diameter up to 11 and degree at most 3, and diameter at most 8 and maximum degree equal to 4 account for about 35% and 18%, respectively, out of all acyclic chemical graphs with 200 or fewer non-hydrogen atoms registered in the PubChem chemical database. Further, those figures are about 63% and 40% with respect to the acyclic chemical graphs with 200 or fewer non-hydrogen atoms with degree at most 3 and maximum degree 4, respectively.

We report computation experiments comparing the performance of our new approach with the method due to Azam et al. [4] over several chemical properties. The results of our experiments, presented in Section 6, indicate that the new method proposed with this paper consistently outperforms the previous method [4] in terms of running time for target compounds with a limited number of chemical elements and a small diameter.

2 Preliminaries

Let the sets of real and non-negative integer numbers be denoted by $\mathbb {R}$ and $\mathbb {Z}$, respectively. For two integers a and b, let [a, b] denote the closed interval between a and b, that is, the set of integers i with $a \le i \le b$.

Graphs Let $H=(V, E)$ be a graph with a set V of vertices and a set E of edges. For a vertex $v\in V$, let $N_H(v)$ denote the set of neighbors of v in H. Then, the degree $\mathrm{deg}_H(v)$ of v is defined to be the size $|N_H(v)|$ of $N_H(v)$. We define the length of a path to be the number of edges in the path. The distance $\mathrm{dist}_H(u,v)$ between two vertices $u, v\in V$ is defined to be the minimum length of a path in H whose endpoints are u and v. The diameter $\mathrm{dia}(H)$ of H is defined to be the maximum distance between two vertices in H. The sum-distance $\mathrm{smdt}(H)$ of H is defined to be the sum of distances over all vertex pairs.

Fig. 1

A chemical graph $G=(H,\alpha ,\beta )$ and its feature vector f(G)

Chemical graphs We represent the graph structure of a chemical compound in a hydrogen-suppressed model as a vertex-labeled multi-graph. Let $\Lambda$ be a set of labels, and each label represent a chemical element, such as C (carbon), O (oxygen), N (nitrogen), etc. Since we work with hydrogen-suppressed models, we assume that $\Lambda$ does not contain H (hydrogen). For a chemical element $\mathtt{a}\in \Lambda$, let $\mathrm{mass}(\mathtt{a})$ and $\mathrm{val}(\mathtt{a})$ denote its mass and valence, respectively. In our model, we round the ten-fold atomic mass value down to the nearest integer, i.e., we take $\mathrm{mass}^*(\mathtt{a})=\lfloor 10\cdot \mathrm{mass}(\mathtt{a})\rfloor$, $\mathtt{a}\in \Lambda$. Let the set $\Lambda$ of labels be totally-ordered based on the mass of the corresponding elements, and we write $\mathtt{a b}$ for chemical elements $\mathtt{a,b}\in \Lambda$ with $\mathrm{mass}(\mathtt{a}) \mathrm{mass}(\mathtt{b})$. For a tuple $\gamma =(\mathtt{a, b}, k)\in \Lambda \times \Lambda \times [1, 3]$, let $\overline{\gamma }$ denote the tuple $(\mathtt{b, a}, k)$. Let $\Gamma _{} \subseteq \Lambda \times \Lambda \times [1, 3]$ be a set of tuples $\gamma =(\mathtt{a, b}, k)$ such that $\mathtt{a b}$, and set $\Gamma _{>}=\{\overline{\gamma }\mid \gamma \in \Gamma _{ }\}$, $\Gamma _{=}=\{(\mathtt{a,a},k)\mid \mathtt{a}\in \Lambda , k\in [1,3]\}$ and $\Gamma = \Gamma _{}\cup \Gamma _{=}$. We denote by a tuple $\gamma =(\mathtt{a, b}, k)\in \Gamma$ a pair of atoms with labels $\mathtt{a}$ and $\mathtt{b}$ which are connected by a bond of multiplicity k.

We define a chemical graphs in a hydrogen-suppressed model to be a tuple $G=(H, \alpha , \beta )$ of a graph $H=(V,E)$, a mapping $\alpha : V\rightarrow \Lambda$ and a mapping $\beta : E\rightarrow [1, 3]$ such that the following conditions are satisfied:

(i):

H is connected; and

(ii):

for each vertex $u\in V$ it holds that $\sum _{e=uv\in E}\beta (e)\le \mathrm{val}(\alpha (u))$.

We note that nearly 55% of the acyclic chemical graphs with at most 200 non-hydrogen atoms that are registered in the chemical database PubChem¹ [12] have degree at most 3 in their hydrogen-suppressed model. Figure 1 illustrates an example of a chemical graph $G=(H, \alpha , \beta )$.

Descriptors To define feature vectors, we use only graph-theoretical descriptors. This choice serves our purpose to design an algorithm for constructing graphs. Henceforth, we define the feature vector f(G) of a chemical graph $G=(H=(V,E),\alpha ,\beta )$ to be a numerical vector that consists of the following eight kinds of descriptors:

n(H)::

the number of vertices in H;

$n_d(H)$ (d $\in [1, 4]$)::

the number of vertices of degree d in H;

$\overline{\mathrm{dia}}(H)$::

the diameter of H divided by |V|;

$\overline{\mathrm{smdt}}(H)$::

the sum of distances of H divided by $|V|^3$;

$n_\mathtt{a}(G)$ ($\mathtt{a}\in \Lambda$)::

the number of vertices with label $\mathtt{a}\in \Lambda$;

$\overline{\mathrm{ms}}(G)$::

the average of $\mathrm{mass}^*$ of atoms in G;

$b_i(G)$ ($i=2,3$)::

the number of double and triple bonds;

$n_{\gamma }(G)$ ($\gamma =(\mathtt{a,b},k)\in \Gamma$)::

the number of label pairs $\{\mathtt{a,b}\}$ with multiplicity k.

Figure 1 gives an example of a feature vector f(G) of a chemical graph $G=(H, \alpha , \beta )$.

3 A method for inferring chemical graphs

We review the framework for the inverse QSAR/QSPR [4] that employs both ANNs and MILPs. The framework is schematically illustrated in Fig. 2. Let G be a given chemical compound, represented by a chemical graph $G=(H, \alpha , \beta )$, and let $\pi$ denote a specified chemical property such as boiling point. We denote by a(G) the observed value of the property $\pi$ for chemical compound G. In the first phase of the two-phase framework, we solve (I) Prediction Problem for the inverse QSAR/QSPR through the following three steps, as schematically illustrated in Fig. 2.

• 1. Gather a dataset $D=\{(G_i, a(G_i)) \mid i=1, 2, \ldots ,m\}$ of pairs of a chemical graph $G_i$ and the value $a(G_i)$. We fix two values $\underline{a}, \overline{a} \in \mathbb {R}$ so that $\underline{a} \le a(G_i)\le \overline{a}$, $i=1, 2, \ldots , m$.

• 2. Choose a class of graphs $\mathcal {G}$ to be a set of chemical graphs such that $\mathcal {G} \supseteq \{ G_i \mid i=1, 2, \ldots , m\}$. Introduce a feature function $f: \mathcal {G} \rightarrow \mathbb {R}^{k}$ for a positive integer k. We call f(G) the feature vector of $G \in \mathcal {G}$, and call each entry of vector f(G) a descriptor of G.

• 3. Using the dataset D, train an ANN $\mathcal {N}$ to construct a regression prediction function $\psi _\mathcal {N}$ that given a vector in $x\in \mathbb {R}^{k}$, returns a real value $\psi _\mathcal {N}(x)$ with $\underline{a}\le \psi _\mathcal {N}(x)\le \overline{a}$ and such that $\psi _\mathcal {N}(f(G))$ takes a value nearly equal to a(G) for many of the chemical graphs in the dataset D.

In the second phase, we solve (II) Inverse Problem for the inverse QSAR/QSPR through the following two inference problems.

Fig. 2

An illustration of a property function a, a feature function f, a prediction function $\psi _{\mathcal {N}}$ and an MILP that either delivers a vector $(x^*,g^*)$ that forms a chemical graph $G^*\in {\mathcal {G}}$ such that $\psi _{\mathcal {N}}(f(G^*))=y^*$ (or $a(G^*)=y^*$) or detects that no such chemical graph $G^*$ exists in $\mathcal {G}$

• (II-a) Inference of Vectors

• Input: A real $y^*\in [\underline{a},\overline{a}]$.

• Output: Vectors $x^*\in \mathbb {R}^{k}$ and $g^*\in \mathbb {R}^{h}$ such that $\psi _\mathcal {N}(x^*)=y^*$ and $g^*$ forms a chemical graph $G^*\in \mathcal {G}$ with $f(G^*)=x^*$.

• (II-b) Inference of Graphs

• Input: A vector $x^*\in \mathbb {R}^{k}$.

• Output: All graphs $G^*\in \mathcal {G}$ such that $f(G^*)=x^*$.

In order to tackle Problem (II-a), we use the following result.

Theorem 1

[3] Let $\mathcal {N}$ be an ANN with a piecewise-linear activation function for an input vector $x\in \mathbb {R}^{k}$, $n_A$ denote the number of nodes in the architecture and $n_B$ denote the total number of break-points over all activation functions. Then there is an MILP $\mathcal {M}(x, y; \mathcal {C}_1)$ that consists of variable vectors $x\in \mathbb {R}^{k}$, $y\in \mathbb {R}$, and an auxiliary variable vector $z \in \mathbb {R}^p$ for some integer $p=O(n_A+n_B)$ and a set $\mathcal {C}_1$ of $O(n_A+n_B)$ constraints on these variables such that $\psi _{\mathcal {N}}(x^*)=y^*$ if and only if there is a vector $(x^*, y^*)$ feasible to $\mathcal {M}(x, y; \mathcal {C}_1)$.

In addition, we introduce a variable vector $g\in \mathbb {R}^{h}$, for some integer h, and a set $\mathcal {C}_2$ of constraints on x and g such that $(x^*, g^*)$ is feasible to the MILP $\mathcal {M}(x,g; \mathcal {C}_2)$ if and only if $g^*$ forms a chemical graph $G^* \in \mathcal {G}$ with $f(G^*)=x^*$ (see [4] for details). Finally, we note that by using MILPs, it is not difficult to introduce additional linear constraints or to fix some of the variables to specified constants.

To address Problem (II-b), we design a branch-and-bound algorithm, akin to the work of Fujiwara et al. [7] for enumerating acyclic chemical compounds.

The second phase comprises the following two steps.

• 4. Formulate Problem (II-a) as the above MILP $\mathcal {M}(x, y, g; \mathcal {C}_1, \mathcal {C}_2)$ taking into account the class $\mathcal {G}$ of graphs and the trained ANN $\mathcal {N}$. Reconstruct a set $F^*$ of vectors $x^*\in \mathbb {R}^{k}$ such that $(1-\varepsilon )y^* \le \psi _\mathcal {N}(x^*) \le (1+\varepsilon )y^*$ for a small positive tolerance $\varepsilon$.

• 5. To solve Problem (II-b), enumerate all graphs $G^* \in \mathcal {G}$ such that $f(G^*)=x^*$ for each vector $x^*\in F^*$.

Figure 2 illustrates Steps 4 and 5.

In the MILP formulation $\mathcal {M}(x, g; \mathcal {C}_2)$ proposed by Azam et al. [4] in order to construct an acyclic chemical graph $G^*$ with n vertices, we choose as edges a subset of $n-1$ vertex pairs from an $n\times n$ adjacency matrix, that is, a subset of $n-1$ edges from a complete graph $K_n$ on n vertices. In Section 4, we introduce an MILP formulation $\mathcal {M}(x,g; \mathcal {C}_2)$ in which a graph $G^*$ is constructed as an induced subgraph of a larger acyclic graph, which we call “a skeleton tree,” formally introduced in Section 4.

4 Skeleton trees

Before introducing our MILP formulation for inferring chemical graphs in Step 4 of the framework outlined in Section 3, we introduce the concept of skeleton trees. Based on this concept, we effectively reduce the number of variables and constraints, and thus the computational complexity and time needed to solve the formulation in practice.

For an integer D, let $\mathcal {T}_{[D, 3]}$ (resp., $\mathcal {T}_{[D, 4]}$) denote the set of trees H with $\mathrm{dia}(H)=D$ and whose maximum degree is at most 3 (resp., equal to 4). We define the skeleton tree $T_{[D, d]}^\dagger$, $d \in \{3, 4\}$, to be a tree in $\mathcal {T}_{[D, d]}$ with the maximum number of vertices. Let $n_{\max }(D, d)$ denote the number of vertices in $T_{[D, d]}^\dagger$.

Then, we assume that by convention the vertices and the edges in the skeleton tree $T_{[D, d]}^\dagger =(V^\dagger =\{v_1, v_2, \ldots ,$ $v_{n_{\max }(D,d)}\}, E^\dagger =\{e_1, e_2, \ldots , e_{n_{\max }(D, d)-1}\})$ are indexed in an ordering $\sigma$ as follows:

(i):

$T_{[D, d]}$ is rooted at vertex $v_1$, and for any vertex $v_i$ and a child $v_j$ of $v_i$ it holds that i < j;

(ii):

Each edge $e_j$ joins two vertices $v_{j+1}$ and $v_k$ with $k\le j$, and $\mathrm{tail}(j)$ denotes the index k of the parent $v_k$ of vertex $v_{j+1}$; and

(iii):

For each $i=1,2,\ldots ,D$, it holds that $v_iv_{i+1}\in E$, that is, $(e_1, e_2, \ldots , e_{D})$ is one of the longest paths in the tree $T_{[D,d]}^\dagger$.

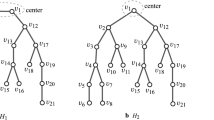
Figure 3 gives an illustration of an ordering $\sigma$ as described above for the skeleton trees $T_{[3,4]}^\dagger$ in Fig. 3(a) and $T_{[4, 4]}^\dagger$ in Fig. 3(b). For each $i=1, 2, \ldots , n_{\max }(D, d)$, let $N_{\sigma }(i)$ denote the set of indices j of edges $e_j$ incident to vertex $v_i$, and $\mathrm{dist}_{\sigma }(i, j)$ denote the distance $\mathrm{dist}_{T}(v_i, v_j)$ in the tree $T=T_{[D, d]}^\dagger$.

Fig. 3

(a) $T_{[3, 4]}^\dagger$, where $n_{\max }(3, 4)=8$; (b) $T_{[4, 4]}^\dagger$, where $n_{\max }(4, 4)=17$

For a subtree $H=(V,E)$ of $T_{[D, d]}^\dagger$ with $\{ e_1, e_2, \ldots , e_D \} \subseteq E$, and an integer $i = 2, 3, \ldots , D$, we denote by $H_{(i)}$ the subtree of H rooted at $v_i$ and induced by its descendants except the vertex $v_{i+1}$ and the descendants of $v_{i+1}$. An illustration is given in Fig. 4 (a).

For a rooted tree $T=(V, E)$ and a vertex $v \in V$, we denote by prt$_T(v)$ the parent of v, and by Cld$_T(v)$ the set of children of v in T.

Given integers $n^*\ge 3$, $\mathrm{dia}^*\ge 2$ and $d_{\max }\in \{3,4\}$, consider an acyclic chemical graph $G=(H=(V,E),\alpha ,\beta )$ such that $|V|=n^*$, $\mathrm{dia}(H)=\mathrm{dia}^*$ and the maximum degree in H is at most 3 for $d_{\max }=3$ (or equal to 4 for $d_{\max }=4$).

4.1 A proper form for subtrees

For integers $D \ge 2$ and $d \in \{3, 4\}$, let T denote $T_{[D, d]}^\dagger$ and B its base path. Let K be a rooted subtree of T with $E(B) \subseteq E(K)$. For a vertex $v \in V(T) \backslash V(B)$, we define the s-value s(v; K) of v with respect to K as follows:

• 1. $\mathrm{s}(v; K) = 0$ if $v \notin V(K)$;

• 2. $\mathrm{s}(v; K) = 1$ if “v is a leaf in K” or “v is a non-leaf vertex and $\vert \mathrm{Cld}(v; K) \vert \ {\text{<}} \ \vert \mathrm{Cld} (v; T) \vert$”; and

• 3. $\mathrm{s}(v; K) = \min _{u \in \mathrm{Cld}(v; K)} \mathrm{s}(u; K) + 1$ otherwise.

We give examples of the s-value of some vertices in the subtree H from Fig. 4 (a). For vertex $v_{14}$, we have s$(v_{14}; H) = 0$, since $v_{14} \notin V(H)$. The vertex $v_4$ is a non-leaf vertex in H, and we have Cld$(v_4; H) = \{ v_5, v_{10} \}$, whereas Cld$(v_4; T) = \{ v_5, v_{10}, v_{11} \}$, therefore it holds that $\vert \mathrm{Cld}(v_4; H) \vert \ {\text{<}} \ \vert \mathrm{Cld}(v_4; T) \vert$ and s$(v_4; H) = 1$. Similarly, the vertex $v_8$ is a non-leaf vertex in H and $\vert \mathrm{Cld}(v_8; H) \vert \kern1.5pt {\text{<}} \kern1.5pt \vert \mathrm{Cld} (v_8; T) \vert$, and therefore s$(v_8; H) = 1$. For vertex $v_9$, we have s$(v_9; H) = 1$, since $v_9$ is a leaf in H. For the non-leaf vertex $v_3$, we have $\mathrm{Cld}(v_3; H) = \mathrm{Cld}(v_3; T) = \{ v_4, v_8, v_9 \}$, and hence $\vert \mathrm{Cld}(v_3; H) \vert = \vert \mathrm{Cld} (v_3; T) \vert$. Thus s$s\left({v}_3;H\right)={\min}_{u\in \mathrm{Cld}\left({v}_3;H\right)}s\left(u;H\right)+1=2$, since IEQ259 $s\left({v}_4;H\right)=\mathrm{s}\left({v}_8;H\right)=s\left({v}_9;H\right)=1.$

We call K an s-left heavy tree if for each vertex $v \in V(K)$ with two positive integers i and m such that Cld$(v; T) = \{v_{i+j} \mid j \in [1, m]\}$ and each integer $j \in [1, m-1]$ it holds that $\mathrm{s}(v_{i +j}; K) \ge \mathrm{s}(v_{i+j+1}; K)$.

Let H be a subtree of T with $E(B) \subseteq E(H)$. We call H an s-proper tree, if for each integer $i \in [2, D]$, the subtree $H_{(i)}$ is an s-left heavy tree and one of the following conditions holds:

(a-1):

$d=3$ and $\vert V(H_{(2)}) \vert \ge \vert V(H_{(D)}) \vert$;

(a-2):

$d=4\ \mathrm{and}\ \left(s\left({v}_{D+2};{H}_{(2)}\right),s\left({v}_{D+3};{H}_{(2)}\right)\right)\succeq \left(s\left({v}_{3D-2};{H}_{(D)}\right),s\left({v}_{3D-1};{H}_{(D)}\right)\right).$

Fig. 4

Examples of s-proper tree and non-s-proper tree H. The vertices and edges in H are shown in black. (a) An example of $H_{(3)}$ for the tree $T_{[4, 4]}^\dagger$ shown in Fig. 3 (b). The vertices and edges in H are shown in black, while the remainder of $T_{[4, 4]}^\dagger$ not included in H is in gray. The subtree $H_{(3)}$ is enclosed by a dashed boundary. (b) $H_\mathrm{b}$ is an s-proper tree; (c) $H_\mathrm{c}$ is not an s-proper tree since $H_{\mathrm{c}(3)}$ is not an s-left heavy tree; and (d) $H_\mathrm{d}$ is not an s-proper tree since $(\mathrm{s}(v_{D+2}; H_{\mathrm{d}(2)}), \mathrm{s}(v_{D+3}; H_{\mathrm{d}(2)})) \prec (\mathrm{s}(v_{3D-2}; H_{\mathrm{d}(D)}), \mathrm{s}(v_{3D-1}; H_{\mathrm{d}(D)}))$

An illustration of an s-proper tree and non-s-proper trees is shown in Fig. 4. Recall that B denotes the base path in T. We define an s-proper form of H to be a subtree $H'$ such that (i) $E(B) \subseteq E(H')$; (ii) there is an isomorphism $\psi$ from $H'$ to H such that $\psi (u) \in V(B)$ for any vertex $u \in V(B)$; and (iii) $H'$ is an s-proper tree. Notice that an s-proper form of a subtree H is not necessarily unique.

Theorem 2

Every subtree H of $T_{[D, d]}^\dagger$ with $E(B) \subseteq E(H)$ has an s-proper form.

Proof

We set $G: = H$. If G is an s-proper tree then G is an s-proper form of H and we are done. Therefore, assume that G is not an s-proper tree. If G has a subtree $G_{(i)}$ for some $i\in [2, D]$ that is non-s-left heavy due to a vertex $v_j \in V(G_{(i)})$, then we can re-order the descendant subtrees of the children of $v_j$ so that the s-value of its children from left to right is non-increasing, since it will not change the s-value of $v_j$. Let $G^*$ denote the tree obtained by applying this re-ordering operation. Clearly there exists an isomorphism $\psi$ from $G^*$ to H such that $\psi (u) \in V(B)$ for any vertex $u \in V(B)$, since we only re-order the descendant subtrees of the children of a vertex in G. Then set $G:= G^*$ and repeat the same operation of re-ordering until all subtrees $G_{(i)} , i \in [2, D]$ of G are s-left heavy trees. Next, for the subtree G, if one of conditions (a-1) and (a-2) is satisfied, then G is an s-proper form of H. Otherwise, i.e., when none of conditions (a-1) and (a-2) is satisfied, we can get an s-proper form of H by switching $G_{(i)}$ and $G_{(D+2-i)}$, $i\in [ 2, \lfloor D/2 \rfloor +1]$, which completes the proof.

4.2 A proper set based on s-proper form

Let $P_{\mathrm{prc}}$ be a set of ordered index pairs (i, j) with $D +2 \le i \kern1.5pt {\text{<}} \kern1.5pt j \le n_{\max }$. We call $P_{\mathrm{prc}}$ proper if the next conditions hold:

(c-1):

For each subtree H of $T_{[D, d]}^\dagger$ with $E(B) \subseteq E(H)$, there is at least one subtree $H'$ with $E(B) \subseteq E(H')$ such that

1.:

there is an isomorphism $\psi$ from $H'$ to H such that $\psi (u) \in V(B)$ for any vertex $u \in V(B)$; and

2.:

for each pair $(i,j)\in P_{\mathrm{prc}}$, if $e_j \in E(H')$ then $e_i \in E(H')$; and

(c-2):

For each pair of edges $e_i$ and $e_j$ in $T_{[D, d]}^\dagger$ such that $e_i$ is the parent $e_j$, there exists a sequence $(i_1, i_2), (i_2, i_3), \ldots , (i_{k-1}, i_k)$ of index pairs in $P_{\mathrm{prc}}$ such that $i_1 = i$ and $i_k = j$.

Note that a given skeleton tree does not necessarily have a unique proper set $P_{\mathrm{prc}}$. In the remainder of this section, we give a construction method for a proper set $P_{\mathrm{prc}}$ based on s-proper form.

Let T denote $T_{[D, d]}^\dagger$. We define $P'_{\mathrm{prc}}$ of T to be the set of ordered index pairs (i, j) such that either

• (i) $v_{j+1}$ is the first child of $v_{i+1}$ or;

• (ii) $j = i + 1$ and $v_{i+1}$ and $v_{i+2}$ share the same parent in T.

In Fig. 5 (a) and (b), we illustrate an example of ordered index pairs (i, j) that satisfy conditions (i) and (ii), respectively, with $e_i$ at level $t - 1$ and $e_j$ at level t, $t \in [3, \lfloor D/2 \rfloor + 1]$.

Fig. 5

An illustration of elements (i, j) of $P'_{\mathrm{prc}}, P''^{(3)}_2, P''^{(3)}_4, P''^{(4)}_2$ and $P''^{(4)}_3$ presented by representing edges $e_i$ and $e_j$ with thick lines. The dashed lines show a level in $T_{[D, d]}^\dagger$. (a) An element of $P'_{\mathrm{prc}}$ such that $v_{j+1}$ is the first child of $v_{i+1}$ and edge $e_j$ is at level $t \ge 3$; (b) An element of $P'_{\mathrm{prc}}$ such that $j = i + 1$ and $v_{i+1}$ and $v_{i+2}$ share the same parent in $T_{[D, d]}^\dagger$ and edge $e_j$ is at level $t \ge 2$; (c) The element $(D+1, (d-2)(D-2)+D+1 = 2D-1)$ of $P''^{(3)}_2$ and edge $e_{D+1}$ and $e_{2D-1}$ are at level 2; (d) An element (i, j) of $P''^{(3)}_4$ such that $v_{i+1}, v_{j +1} \in V(T_{(p)})$ for some $p \in [2,D]$ and $v_{i+1}$ and $v_{j+1}$ are each the h-th child of their parents in $T_{[D, d]}^\dagger$ for some $h \in [1,d-1]$; (e) The elements $(D+1, (d-2)(D-2)+D+1 = 3D-3)$ and $(D+2, (d-2)(D-2)+D+2 = 3D-2)$ in $P''^{(4)}_2$; and (f) An element (i, j) of $P''^{(4)}_3$ such that $v_{i+1}, v_{j +1} \in V(T_{(p)})$ for some $p \in [2,D]$ and $v_{i+1}$ and $v_{j+1}$ are each the h-th child of their parents in $T_{[D, d]}^\dagger$ for some $h \in [1,d-1]$

For $d = 3$ and edges at level 2, we define $P''^{(3)}_{2}$ to be the set $\{ (D+1, (d-2)(D-2)+D+1 = 2D-1) \}$. For $d = 3$ and edges at level 4, we define $P''^{(3)}_{4}$ to be the set of ordered index pairs (i, j) such that

• (i) $v_{i+1}, v_{j +1} \in V(T_{(p)})$ for some $p \in [2,D]$; and

• (ii) $v_{i+1}$ and $v_{j+1}$ are each the h-th child of their parents in T for some $h \in [1,d-1]$.

For $d = 4$ and edges at level 2, we define $P''^{(4)}_{2}$ to be the set of ordered index pairs $\{ (D+1, (d-2)(D-2)+D+1 = 3D-3), (D+2, (d-2)(D-2)+D+2 = 3D-2) \}$. For $d = 4$ and edges at level 3, we define $P''^{(4)}_{3}$ to the set of ordered index pairs (i, j) such that

• (i) $v_{i+1}, v_{j +1} \in V(T_{(p)})$ for some $p \in [2,D]$ and;

• (ii) $v_{i+1}$ and $v_{j+1}$ are each the h-th child of their parents in T for some $h \in [1,d-1]$.

Finally we define $P''^{(3)}_{\mathrm{prc}} \triangleq P''^{(3)}_{2} \cup P''^{(3)}_{4}$ and $P''^{(4)}_{\mathrm{prc}} \triangleq P''^{(4)}_{2} \cup P''^{(4)}_{3}$.

Theorem 3

For two integers, $D \ge 2$ and $d \in \{3, 4\}$, the set $P'_{\mathrm{prc}} \cup P''^{(d)}_{\mathrm{prc}}$ is proper for the tree $T_{[D, d]}^\dagger$.

Proof

Let T denote the tree $T_{[D, d]}^\dagger$, and let $P = P'_{\mathrm{prc}} \cup P''^{(d)}_{\mathrm{prc}}$. To show that P is proper, we need to show that P satisfies conditions (c-1) and (c-2). Let H be a subtree of T with $\{ e_1, e_2, \ldots , e_D \} \subseteq E(H)$. By Theorem 2, we know that there exists an s-proper form of H. Let $H' = (V', E')$ be an s-proper form of H. Thus, $H'$ is isomorphic to H, by the definition of s-proper form. This implies that condition (c-1)(a) holds. Let $G := H'$. We next show that condition (c-1)(b) holds for $P'_{\mathrm{prc}}$ and $P''^{(d)}_{\mathrm{prc}}$ separately. Let $(i,j) \in P'_{\mathrm{prc}}$ such that $v_{j+1}$ is the first child of $v_{i+1}$. If $e_j \in E(G)$ but $e_i \notin E(G)$, then G would be disconnected, which is a contradiction. Let $(i,j) \in P'_{\mathrm{prc}}$ such that $j = i + 1$ and $v_{i+1}$ and $v_{i+2}$ share the same parent in T. This implies that there exists an integer $p \in [2,D]$ such that $v_{i+1}, v_{i+2} \in V(T_{(p)})$. Let K denote $G_{(p)}$. If $e_j \in E(G)$ but $e_i \notin E(G)$, then $\mathrm{s}(v_{i+1}; K) = 0$ and $\mathrm{s}(v_{i+2}; K) \ge 1$ holds. This implies that $\mathrm{s}(v_{i+1}; K) \kern1.5pt {\text{<}} \kern1.5pt \mathrm{s}(v_{i+2}; K)$, which contradicts the fact that K is an s-left heavy tree. Hence, $P'_{\mathrm{prc}}$ satisfies condition (c-1)(b). Let $d=3$ and $(i, j) \in P''^{(d)}_{\mathrm{prc}}$. This implies that $(i, j) \in P''^{(3)}_{2}$ or $(i, j) \in P''^{(3)}_{4}$. Let $(i, j) \in P''^{(3)}_{2}$, then $i = D+1$ and $j = (d-2)(D-2)+D+1$. Notice that $v_{i+1} \in V(T_{(2)})$ and $v_{j+1} \in V(T_{(D)})$. If $e_j \in E(G)$ but $e_i \notin E(G)$, then $\vert V(G_{(2)}) \vert \kern1.5pt {\text{<}} \kern1.5pt \vert V(G_{(D)}) \vert$ would hold, which contradicts the fact that G is an s-proper tree. Let $(i,j) \in P''^{(3)}_{4}$, then it holds that $\mathrm{level}(e_i) = \mathrm{level}(e_j) = 4$ and $v_{i+1}$ and $v_{j+1}$ are in the same rooted subtree $T_{(p)}$ for some integer $p \in [2,D]$. Let K denote $G_{(p)}$. Since $d=3$, there exists a positive integer u such that the four edges $e_{u}, e_{u+1}, e_{u+2}$ and $e_{u+3}$ are at level four. Note that $(u,u+1)$ and $(u+2,u+3)$ are the elements of $P'_{\mathrm{prc}}$ since the vertices in the pairs $(v_{u+1}, v_{u+2})$ and $(v_{u+3}, v_{u+4})$ have the same parents. This implies that the condition $v_{i+1}$ and $v_{j+1}$ are each the h-th child of their parents in T for some $h \in [1, d-1]$ can only be true for $(i,j) = (u,u+2)$ or $(u+1, u+3)$. Let $(i,j) = (u,u+2)$. If $e_{u+2} \in E(G)$ but $e_u \notin E(G)$, then it holds that $e_{u+1} \notin E(G)$ since $(u,u+1) \in P'_{\mathrm{prc}}$. Let $v_{x}$ and $v_{y}$ denote the parents of $v_{u+1}$ and $v_{u+3}$ in T, respectively. Then $\mathrm{s}(v_{x}; K) = 1$ and $\mathrm{s}(v_{y}; K) \ge 1$ would hold, which implies that $\mathrm{s}(v_{y}; K) \ge \mathrm{s}(v_{x}; K)$. Then we can get another s-proper form $H''=(V'',E'')$ by switching the two subtrees rooted at $v_{x}$ and $v_{y}$ in G. Clearly by the construction of $H''$, it holds that $e_u \in E''$ if $e_{u+2} \in E''$ and $E''$ satisfies all those conditions that are satisfied by E(G). In such a case, we set $G := H''$. Let $(i, j) = (u+1, u+3)$. If $e_{u+3} \in E(G)$ but $e_{u+1} \notin E(G)$, then it holds that $e_{u+2} \in E(G)$ since $(u+2, u+3) \in P'_{\mathrm{prc}}$ and $e_u \in E(G)$ since we have shown that $(u, u+2) \in P''^{(d)}_{\mathrm{prc}}$. Let $v_{x}$ and $v_y$ denote the parents of $v_{u+1}$ and $v_{u+3}$ in T, respectively. Then $\mathrm{s}(v_y; K) \ge 2$ and $\mathrm{s}(v_x; K) = 1$ would hold, which implies that $\mathrm{s}(v_x; K) \kern1.5pt {\text{<}} \kern1.5pt \mathrm{s}(v_y; K)$. Notice that $v_{x}$ and $v_{y}$ have the same parent in T by the choice of u. This and $\mathrm{s}(v_x; K) \kern1.5pt {\text{<}} \kern1.5pt \mathrm{s}(v_y; K)$ contradicts the fact that K is an s-left heavy tree. This implies that $e_{u+1} \in E(G)$ if $e_{u+3} \in E(G)$ holds.

Let $d=4$ and $(i, j) \in P''^{(d)}_{\mathrm{prc}}$. This implies that $(i, j) \in P''^{(4)}_{2}$ or $(i, j) \in P''^{(4)}_{3}$. Let $(i, j) \in P''^{(4)}_{2}$, then $(i, j) = (D+1, (d-2)(D-2)+D+1)$ or $(i,j) = (D+2, (d-2)(D-2)+D+2)$ by the definition of $P''^{(4)}_2$. In both cases, $v_{i+1} \in V(T_{(2)})$ and $v_{j+1} \in V(T_{(D)})$. If $e_j \in E(G)$ but $e_i \notin E(G)$, then it will result in a contradiction with the fact that G is an s-proper tree by the definition of an s-left heavy tree (a-2). Let $(i, j) \in P''^{(4)}_{3}$, then $\mathrm{level}(e_i) = \mathrm{level}(e_j) = 3$ and $v_{i+1}$ and $v_{j+1}$ are in the same rooted tree $T_{(p)}$ for some integer $p \in [2,D]$. Let K denote $G_{(p)}$. Since $d=4$, there exists a positive integer u such that the six edges $e_{u}, e_{u+1}, e_{u+2}, e_{u+3}, e_{u+4}$ and $e_{u+5}$ are at level three. Here $(u,u+1), (u+1,u+2)$, $(u+3,u+4)$ and $(u+4,u+5)$ are the elements of $P'_{\mathrm{prc}}$ since the vertices in the pairs $(v_{u+1}, v_{u+2}), (v_{u+2}, v_{u+3}), (v_{u+4}, v_{u+5})$ and $(v_{u+5}, v_{u+6})$ have the same parents. This implies that the condition $v_{i+1}$ and $v_{j+1}$ are each the h-th child of their parents in T for some $h \in [1, d-1]$ can only be true for $(i,j) = (u,u+3), (u+1,u+4)$ or $(u+2,u+5)$. Let $(i,j) = (u,u+3)$. If $e_{u+3} \in E(G)$ but $e_u \notin E(G)$, then it holds that $e_{u+1}, e_{u+2} \notin E(G)$ since $(u, u+1), (u+1,u+2) \in P'_{\mathrm{prc}}$. Let $v_{x}$ and $v_{y}$ denote the parents of $v_{u+1}$ and $v_{u+4}$ in T, respectively. Then $\mathrm{s}(v_{x}; K) = 1$ and $\mathrm{s}(v_{y}; K) \ge 1$ would hold, which implies that $\mathrm{s}(v_{y}; K) \ge \mathrm{s}(v_{x}; K)$. Then we can get another s-proper form $H''=(V'',E'')$ by switching the two subtrees rooted at $v_{x}$ and $v_{y}$ in G. Clearly by the construction of $H''$, it holds that $e_u \in E''$ if $e_{u+3} \in E''$ and $E''$ satisfies all those conditions that are satisfied by E(G). In such a case, we set $G := H''$. Let $(i,j) = (u+1,u+4)$. If $e_{u+4} \in E(G)$ but $e_{u+1} \notin E(G)$, then it holds that $e_{u+3} \in E(G)$ since $(u+3, u+4) \in P'_{\mathrm{prc}}$, $e_{u+2} \notin E(G)$ since $(u+1, u+2) \in P'_{\mathrm{prc}}$ and $e_{u} \in E(G)$ since we have shown that $(u,u+3) \in P''^{(d)}_{\mathrm{prc}}$. Let $v_x$ and $v_y$ denote the parents of $v_{u+1}$ and $v_{u+4}$ in T, respectively. Then $\mathrm{s}(v_x; K) = 1$ and $\mathrm{s}(v_y; K) \ge 1$ would hold, which implies that $\mathrm{s}(v_y; K) \ge \mathrm{s}(v_x; K)$. Then we can get another s-proper form $H''=(V'',E'')$ by switching the two subtrees rooted at $v_{x}$ and $v_{y}$ in G. Clearly by the construction of $H''$, it holds that $e_{u+1} \in E''$ if $e_{u+4} \in E''$ and $E''$ satisfies all those conditions that are satisfied by E(G). In such a case, we set $G := H''$. Let $(i,j) = (u+2,u+5)$. If $e_{u+5} \in E(G)$ but $e_{u+2} \notin E(G)$, then it holds that $e_{u+4}, e_{u+3} \in E(G)$ since $(u+4, u+5), (u+3, u+4) \in P'_{\mathrm{prc}}$ and $e_{u+1}, e_u \in E(G)$ since we have shown that $(u+1, u+4), (u, u+3) \in P''^{(d)}_{\mathrm{prc}}$. Let $v_x$ and $v_y$ denote the parents of $v_{u+1}$ and $v_{u+4}$ in T, respectively. Then $\mathrm{s}(v_y; K) \ge 2$ and $\mathrm{s}(v_x; K) = 1$ would hold, which implies that $\mathrm{s}(v_x; K) \kern1.5pt {\text{<}} \kern1.5pt \mathrm{s}(v_y; K)$. Notice that $v_{x}$ and $v_{y}$ have the same parent in T by the choice of u. This and $\mathrm{s}(v_x; K) \kern1.5pt {\text{<}} \kern1.5pt \mathrm{s}(v_y; K)$ contradicts the fact that K is an s-left heavy tree. This implies that $e_{u+2} \in E(G)$ if $e_{u+5} \in E(G)$ holds. Hence, in each of the cases $P''^{(d)}_{\mathrm{prc}}$ satisfies condition (c-1)(b).

Next we prove that P satisfies condition (c-2). Let $i_1 = i$, $i_2 + 1$ be the index of the first child of $v_{i+1}$ and $i_2, i_3, \ldots , i_k = j$ be consecutive integers. Then the sequence $(i_1, i_2), (i_2, i_3), \ldots , (i_{k-1}, i_k)$ are ordered index pairs in P such that $i_1 = i$ and $i_k = j$. Hence P is a proper set, which completes the proof.

4.3 An algorithm to calculate a proper set

In this section, we give an algorithm to compute a proper set based on Theorem 3. In Algorithm GenPprc(D , d), the variables $P_1, P_2, P_3, P_4$ and $P_5$ store the sets defined in Section 4.2, $P'_{\mathrm{prc}}$, $P''^{(3)}_2$, $P''^{(3)}_4$, $P''^{(4)}_2$, and $P''^{(4)}_3$, respectively. For an edge $e \in E(T_{[D, d]}^\dagger )$, the variable level[e] stores the level of e.

5 MILPs for representing acyclic chemical graphs

In this section, we propose a new MILP formulation $\mathcal {M}(x, g; \mathcal {C}_2)$ as used in Step 4 of the method introduced in Section 3. For our purpose, we consider acyclic chemical graphs where each vertex has degree at most 3 or the maximum degree is 4.

We formulate the MILP $\mathcal {M}(x, g; \mathcal {C}_2)$ so that the underlying graph H is an induced subgraph of the skeleton tree $T_{[\mathrm{dia}^*,d_{\max }]}^\dagger$ introduced in Section 4, and moreover, it holds that $\{v_1, v_2, \ldots , v_{\mathrm{dia}^*+1}\}\subseteq V$. We remark that in order to reduce the number of graph-isomorphic solutions to this MILP, for a skeleton tree, we make use of precedence constraints based on the proper set $P_{\mathrm{prc}}$ as formalized in Section 4.2.

For a technical reason, we introduce a dummy chemical element $\epsilon$, and denote by $\Gamma _0$ the set of dummy tuples $(\epsilon ,\epsilon ,k)$, $(\epsilon , \mathtt{a},k)$ and $(\mathtt{a}, \epsilon , k)$ ($\mathtt{a}\in \Lambda$, $k\in [0,3]$). To represent elements ${a} \in \Lambda \cup \left\{ \epsilon \right\} \cup\Gamma_< \cup \Gamma_{=} \cup\Gamma_{>}$ in an MILP, we encode these elements $\mathtt{a}$ into some integers denoted by $[\mathtt{a}]$, where we assume that $[\epsilon ]=0$. For simplicity, we also denote $n^*$ by n and $n_{\max }(\mathrm{dia}^*,d_{\max })$ by $n_{\max }$. Our new formulation is given as follows.

6 Experimental results

The main aim of our experiments is to compare implementations of the MILP formulations proposed in Section 5 and the one due to Azam et al. [4] in Step 4 of the method for the inverse QSAR/QSPR [4]. The results of this main experiment are presented in Section 6.2, after giving our findings on the construction of regression functions by training ANNs in Section 6.1.

We executed the experiments on a PC with Intel Core i5 CPU running at 1.6 GHz and 8 GB of RAM, under the Mac OS 10.14.4 operating system. For a study case, we selected three chemical properties: heat of atomization (Ha), octanol/water partition coefficient (Kow) and heat of combustion (Hc).

6.1 Experiments on Phase 1

In this section we present our experiments conducted on Phase 1, that is, the forward phase of the framework for the inverse QSAR/QSPR.

In Step 1, we collected a dataset D of acyclic chemical graphs for Ha made available by Roy and Saha [19]. For the properties Kow and Hc, we collected data available from the hazardous substances data bank (HSDB) from PubChem. We choose label set $\Lambda$ to be such that each element in $\Lambda$ appears as a chemical element in at least one of the chemical graphs in the dataset D; and similarly, we choose the set $\Gamma$ to be the set of all tuples $\gamma =(\mathtt{a, b}, k) \in \Lambda \times \Lambda \times [1, 3]$ appearing in at least one of the chemical graphs indataset D. In Step 2, we set a graph class $\mathcal {G}$ to be the set of all acyclic chemical graphs that are possible to be constructed with elements from the sets $\Lambda$ and $\Gamma$ chosen in Step 1. In Step 3, we used the MLPRegressor tool from the Python package scikit-learn² (version 0.24.2) to construct ANNs $\mathcal {N}$, and we set ReLU as the activation function of neurons. We tested several different architectures of ANNs for each chemical property. With simple preliminary experiments we identified promising ranges for hyperparameter values, and then performed a grid search over the following hyperparameter values:

• number of hidden layers in $\{1, 2, 3, 4, 5\}$,

• number of nodes per hidden layer in $\{7, 10, 15, 30, 50\}$,

• learning rate $\eta$ in $\{0.00025, 0.0005, 0.001, 0.002, 0.004\}$, and

• regularization term $\alpha$ in $\{10^{-5}, 2 \times 10^{-5}, 4 \times 10^{-5}, 8 \times 10^{-5}, 1.6 \times 10^{-4}\}$.

The maximum number of training epochs was set to $10^8$ due to the moderately small number of training data. Since our initial experiments derived satisfactory results, other model parameters were used with their default values provided by scikit-learn. We used 5-fold cross validation to evaluate the performance of the trained ANNs, where a given dataset D is randomly partitioned into five subsets $D_i$, $i\in [1, 5]$. The evaluation is given in terms of the coefficient of determination $\mathrm{R}^2$, which for a collection $(a_1, a_2, \ldots , a_p)$ of p real values with average $\widehat{a} = \frac{1}{p} \sum _{i = 1}^{p} a_i$ that are associated with a collection $(y_1, y_2, \ldots , y_p)$ of values predicted by a regression model, gives a model error as

$$\begin{array}{*{20}c} \mathrm{R}^2 = 1 - \frac{\sum _{i = 1}^{p}{(a_i - y_i)^2}}{\sum _{i = 1}^{p}{(a_i - \widehat{a})^2}}.\end{array}$$

Table 1 shows the size and range of values in the datasets that we used for each chemical property, as well as results on Phase 1. The notation and symbols used in Table 1 are as follows:

$\pi$::

the tested chemical property, one of Ha, Kow, and Hc;

|D|::

the number of data points in the collected dataset D for a chemical property $\pi$;

$\Lambda$::

the set of all chemical elements that appear in at least one of the chemical graphs in the dataset D;

$\underline{n}, \overline{n}$::

the minimum and maximum number of vertices in a chemical graph $G=(H,\alpha ,\beta )$ over the dataset D;

$\underline{a},\overline{a}$::

the minimum and maximum values of a(G) over the dataset D;

K::

the number of descriptors in f(G) for a chemical property $\pi$, where $K= |\Lambda |+|\Gamma |+12$ for our feature vector f(G);

Arch.::

the size of hidden layers of ANNs, where $\langle 10 \rangle \!\times \! 1$ (resp., $\langle 30 \rangle \!\times \! 2$) means an architecture (K, 10, 1) with an input layer with K nodes, one hidden layer with 10 nodes (resp., two hidden layers, each with 30 nodes), and an output layer with a singe node;

$\eta$::

the learning rate chosen for training the ANN;

$\alpha$::

the regularization term used for training the ANN;

L-time::

the average time, in seconds (s), to construct ANNs for each trial;

Test $\mathrm{R}^2$::

the coefficient of determination averaged over the five test sets for the corresponding combination of hyperparameter values.

Note that the parameters given in Table 1 for Step 3 are those that achieved the highest average coefficient of determination over the test set in the cross-validation trials. As can be observed in Table 1, we cannot draw a conclusion as to whether a certain hyperparameter of an ANN has a predictable influence on the performance of the ANN model. For different chemical properties, and in fact, for the case of property Hc, even for a single property observed over a different dataset of chemical compounds, noticeably different hyperparameter combinations achieve the best performance, i.e., the highest coefficient of determination over an unobserved test set.

Table 1 The results on Steps 1, 2 and 3

Table 2 The computation time of the AM and ST methods for Ha, $d_{\max } = 3$

Table 3 The computation time of the AM and ST methods for Ha, $d_{\max } = 4$

6.2 Experiments on Phase 2

In this section we delve into our main interest with this study, namely the inverse phase of the combined framework for the inverse QSAR/QSPR [4, 5], and in particular, Step 4, inverting a trained ANN by solving an MILP formulation.

We call the MILP formulation due to Azam et al. [4] based on an adjacency matrix the AM method, and the MILP formulation based on skeleton tree presented in Section 5 the ST method. We use the CPLEX (ILOG CPLEX version 12.9) [9] solver to solve MILP instances formulated in the framework. We performed experiments for each of the properties Ha, Kow, and Hc as follows. For several pairs $(d_{\max },\mathrm{dia}^*)$ of integers $d_{\max }\in \{3, 4\}$ and $\mathrm{dia}^* \in [6, 13]$, choose each integer $n^* \in [14, n_{\max }(\mathrm{dia}^*$, $d_{\max })]$ and six target values $y^*_{i}$, $i \in [1,6]$. We attempted to solve the six MILP instances by using the AM and ST methods. We started by setting $n^*=14$, and then gradually increased $n^*$ up to $n_{\max }(\mathrm{dia}^*, d_{\max })$. Whenever the running time while solving at least one of the six instances reached a time limit set to be 300 seconds, we stopped further attempts to solve the MILP instances with each of the two methods.

We present our findings in Tables 2 and 3, as well as Figure 4, where we summarize the results from our experiments, in particular, the computation time of the AM and ST methods in Step 4 for property Ha. The notation used is as follows:

AM::

the average time (s) to solve six MILP instances based on the AM method;

ST::

the average time (s) to solve six MILP instances based on the ST method;

T.O.::

indicates that the running time of one of the six instances exceeded 300 seconds.

For property Ha, additionally, we executed the AM method for instances with $n^*=36$, $n^*=38$, and $n^*=40$, $\mathrm{dia}^*=6$, and $d_{\max }=4$ without imposing a time limit. The respective computation times were 21,962 seconds for $n^*=36$, 124,903 seconds for $n^*=38$, and 148,672 seconds for $n^*=40$. Meanwhile, the computation time for the ST method was 2.133 seconds for the instances with $n^*= 38$, which means that for this range of instance size, the ST method was 58,557 times faster than the AM method.

Fig. 6

The average computation time of the AM and ST methods for Ha

We give a short comment summary on the results of the experiments with instances of Kow and Hc: The ST method outperformed the AM method for the cases of $(\pi \!=$ Kow$, |\Lambda |\!=3, d_{\max }\!=3, \mathrm{dia}^*\!\le 11)$, $(\pi \!=$ Kow$, |\Lambda |\!=3, d_{\max }\!=4, \mathrm{dia}^*\!\le 7)$, $(\pi \!=$ Kow$, |\Lambda |\!=7, d_{\max }\!=3, \mathrm{dia}^*\!\le 8)$, $(\pi \!=$ Kow$, |\Lambda |\!=7, d_{\max }\!=4, \mathrm{dia}^*\!\le 5)$, $(\pi \!=$ Hc$, |\Lambda |\!=3, d_{\max }\!=3, \mathrm{dia}^*\!\le 9)$, $(\pi \!=$ Hc$, |\Lambda |\!=3, d_{\max }\!=4, \mathrm{dia}^*\!\le 6)$, $(\pi \!=$ Hc$, |\Lambda |\!=6, d_{\max }\!=3, \mathrm{dia}^*\!\le 8)$, $(\pi \!=$ Hc$, |\Lambda |\!=6, d_{\max }\!=4, \mathrm{dia}^*\!\le 7)$, $(\pi \!=$ Hc$, |\Lambda |\!=10, d_{\max }\!=3, \mathrm{dia}^*\!\le 7)$ and $(\pi =$ Hc$, |\Lambda |=10, d_{\max }=4, \mathrm{dia}^*\le 5)$.

From the experimental results, we observe that the ST method completed Step 4 in shorter time than the AM method did when the diameter of graphs was up to around 11 for $d_{\max }=3$, and 8 for $d_{\max }=4$. In particular, it can be seen from Tables 2 and 3, as well as Fig. 6, that under such conditions, the ST method could handle chemical graphs with number $n^*$ of non-hydrogen vertices up to 48 in reasonable CPU time, whereas the AM method could only handle chemical graphs with $n^* \kern1.5pt {\text{<}} \kern1.5pt 30$. Therefore, the results of computational experiments suggest that the ST method can handle a much larger number of chemical graph than the AM method can. Finally, recall that chemical graphs with diameter up to 11 for $d_{\max }=3$ and 8 for $d_{\max }=4$ account for about 35 % and 18 %, respectively, out of all acyclic chemical graphs with 200 or fewer non-hydrogen atoms registered in the PubChem chemical database, and about 63 % and 40 % out of the acyclic chemical graphs with 200 or fewer non-hydrogen atoms with $d_{\max }=3$ and $d_{\max }=4$, respectively.

7 Concluding remarks

With this work, we presented a new MILP formulation for inferring acyclic chemical graphs. Our MILP formulation can be directly incorporated in the method for the inverse QSAR/QSPR proposed to Azam et al. [4]. One drawback of the formulation given by Azam et al. [4] is that in order to represent a tree on n vertices, subsets of vertex pairs over an $n\times n$ adjacency matrix are used, requiring the same number of variables in the MILP formulation. With the aim to reduce the number of variables in the MILP formulation, we introduced the concept of skeleton trees, which are trees with the maximum number of vertices for fixed diameter and maximum degree. Then, in our method, a target tree is chosen as an induced subgraph of a skeleton tree. In this way, whenever the target acyclic graphs have a limited diameter, we significantly reduce the number of variables used in our MILP formulation, and thereby also the time needed to solve it in practice when the number of chemical elements is relatively small. The results on some computational experiments confirm this, i.e., we observe that the proposed method is more efficient than the previously proposed method.

Even though the MILP formulation presented in this paper targets the class $\mathcal {G}$ of acyclic chemical graphs, we note that a similar formulation can be applied to the acyclic part of any chemical graph, regardless of the number of cycles it has. Based on the idea of prescribing a tree that serves as a supergraph of a target acyclic chemical graph, Azam et al. [5] and Akutsu and Nagamochi [2] have developed methods for inferring chemical acyclic graphs with a larger diameter and cyclic chemical graphs with any cycle index, respectively, where the proposed method/systems are available at GitHub https://github.com/ku-dml/mol-infer.

As future work it would be interesting to explore a way of defining the graph topology of a desired chemical graph, i.e., generate target chemical graphs with a fixed scaffold [21]. Another line of research would be to explore different methods for constructing a regressive prediction function, for example convolutional ANNs, different types of multiple linear regression, or decision trees.