1 Introduction

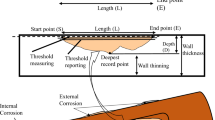
Internal corrosion in pipeline infrastructures used to transport gas and oil poses various threats to the environment and human beings in terms of both contamination and accidents, which may lead also to explosions in presence of gas leakages [1]. Therefore, the need to develop mechanisms able to predict the presence of such detrimental phenomenon is of utmost importance.

Unfortunately, this harmful phenomenon is very complex to be modeled or predicted. This is due to the incredible amount of factors it depends on. In carbon-steel pipelines, corrosion may be influenced by CO2, H2S, oil or water wetting, steel composition, and internal surface conditions [2]. Additionally, bacteria activity, fluid dynamics, transport conditions over the entire operating lifespan, as well as geometrical characteristics of the pipeline are certainly important influencing factors [3].

The complexity of the envisaged phenomenon is not the only critical issue for corrosion prediction. In fact, the difficulty in gathering information about all the influencing factors is an additional key concern. Indeed, only the geometrical characteristics of the pipeline and its fluid-dynamic information are available (the latter via simulation). On the other hand, information about all the other influencing factors is extremely difficult (or often impossible) to be gathered from the field. This is the reason why physical-based corrosion prediction models, e.g., [4], revealed to be not accurate in real-world corrosion scenarios.

Recently, Machine Learning (ML) techniques have proved to be able to model complex phenomena. Specifically, in our application scenario, there has been an increasing interest in leveraging these kinds of approaches in the context of internal corrosion modeling and prediction. For instance, in [3], a Neural Network (NN) is employed to build a predictive model of the corrosion phenomenon. Before training the NN, the most important features are selected with a Mutual Information-based approach. Similarly, a feature selection approach based on the sensitivity of the NN output w.r.t. infinitesimal variations of the input is applied in [5] before building a predictive model of internal corrosion, whereas in [6] the feature selection step is performed via a Grey Relational Analysis. One major critical point of these ML solutions is that, following a supervised approach, they require information about the presence of corrosion in a given pipeline. Such information is gathered directly from the field employing Pipeline Inspection Gauges (PIGs) that are robot inspection systems measuring the presence of corrosion within a pipeline. In other words, the main limitation of such supervised approaches for corrosion prediction is that a model is built only when information about the real presence of corrosion is already available (which is not usually the case for companies managing pipeline infrastructures).

Therefore, it is crucial to overcome such a limitation by designing corrosion prediction models able to operate even in the scenario where supervised information is not available for a given target pipeline. Achieving this goal would completely change the traditional way corrosion prediction is managed in oil and gas pipelines. Indeed, it would allow defining a predictive model of internal corrosion without sending a PIG through the target pipeline, hence avoiding such an expensive and time-consuming operation.

In this paper, to achieve this goal, we will leverage Transfer Learning (TL) to design an algorithmic solution for corrosion prediction when supervised information is not available for the target pipeline. TL allows overcoming the lack of supervised information on the target pipeline by exploiting a set of source pipelines where supervised information is available, which is a very common real-world scenario for oil and gas companies. In more detail, the proposed approach will rely on the joint use of a transductive TL technique and an Importance Weighted Cross-Validation (IWCV) technique; the former to build the predictive model onto the target pipeline and the latter to rank the sources w.r.t. their estimated performance over the pipeline of interest. Remarkably, the effectiveness of the proposed solution has been tested on a set of real-world gas pipelines.

The paper is structured as follows. In Section 2, an introduction to TL and the problem formulation are provided. In Section 3, our methodological approach is described in all its components, whereas, in Section 4 experimental results on a set of real-world pipelines are presented to thoroughly validate the proposed approach. Finally, in Sections 5 and 6, discussions and conclusions are drawn, respectively.

2 From supervised to transfer learning in corrosion prediction

From a machine learning perspective, predicting the presence of corrosion in an oil or gas pipeline requires effective modeling of the relationships between the corrosion-influencing factors and the presence of corrosion in a pipeline. More specifically, a pipeline is divided into bars, i.e., independent segments of the pipeline, and the machine learning task aims at modeling the relationship between the corrosion-description factors of each bar and its level of corrosion.

Let us define a learning task as the tuple (X,P(x),Y, P(y|x)), where Y is the label set, P(y|x) is the conditional distribution, X is the feature space and P(x) is the marginal distribution. Here x represents the feature vector associated with a bar and y its corrosion level. In the context of a learning task, the objective is to learn a function correctly predicting y when evaluated on x.

In this setting, two main problems arise. First, as commented in Section 1, not all the corrosion influencing factors are available. Hence the feature vector x comprises only geometrical and fluid dynamical information about a bar: the former is available given the pipeline on-the-field deployment, while the latter is provided by a fluid-dynamical simulator [7]. Second, as highlighted in Section 1, the supervised information, i.e., the presence or absence of corrosion in a bar, is provided through an inspection campaign where a PIG passes inside the pipeline collecting a set of corrosion level measurements together with their GPS coordinates along the pipeline profile. This poses a relevant compatibility issue since the geometrical characteristics, mainly represented by the inclination and curvature of the pipeline profile, are not directly compatible with the fluid dynamical descriptors creating a resolution mismatch between the information gathered through the PIG and the simulator [7]. More precisely, we can obtain fluid-dynamical data down to a certain granularity under which the simulator starts returning non-stationary solutions. This issue has been highlighted and addressed in [8] and we will follow this approach in the context of this work to build a given data set \(D=\{(x_{i},y_{i})\}_{i=1}^{n}\) with x representing the feature vector, made of fluid dynamical and geometrical components, and y representing the corrosion level.

From the machine learning perspective, supervised learning techniques, like the ones mentioned in Section 1, work under the assumption that the distribution of training and test data is the same. In real-world oil and gas pipeline infrastructures, it may happen that we would like to solve a certain target task (XT,PT(x),YT,PT(y|x)) for which some of the elements allowing a proper application of supervised learning techniques are missing (e.g., we do not have access to the labels since they are too costly to be retrieved), but we can access another related source task (XS,PS(x),YS,PS(y|x)) that may help us overcome the difficulties we would have in learning the target task by itself. This implies that we cannot directly build a predictive model onto a given pipeline (XS,PS(x),YS,PS(y|x)) for which the supervised information is available and then reuse it onto another pipeline (XT,PT(x), YT,PT(y|x)) for which the supervised information is missing. We emphasize that there is a potential distributional shift to take into account and our predictive models may suffer a performance hindering if this is not properly considered.

In this setting, TL allows us to leverage the source task in order to better approximate the conditional distribution of the target task. In the TL literature, several approaches are available differing in how source and target tasks relate to each other (see [9] for an extensive treatment). For instance, we can talk about inductive TL whenever (YS,PS(y|x))≠(YT,PT(y|x)) (notice that (XS,PS(x)) = (XT,PT(x)) or (XS, PS(x))≠(XT,PT(x))), whereas we have transductive TL whenever (YS,PS(y|x)) = (YT,PT(y|x)) and (XS,PS(x))≠(XT,PT(x)). The former requires access to at least a set of labeled data from the target context, whereas the latter only requires a set of unlabeled data coming from it. Furthermore, we can classify TL approaches w.r.t. the knowledge being transferred across the two tasks: parameters [10, 11], features [12,13,14,15], samples [16,17,18] or relational knowledge [19, 20]. Finally, TL techniques may be either homogeneous or heterogeneous as they are classified in [21, 22], where, in [22], we may find a review of recent works with the main focus on homogeneous approaches.

In the context of this work, we will focus on transductive TL techniques because companies managing pipelines usually have supervised information only for some of their pipeline infrastructures. In particular, this approach is justified by the assumption that, as commented by the domain experts, the corrosion phenomenon is the same in two different pipelines provided that the influencing factors are equal, which translates into PS(y|x) = PT(y|x) (trivially, the label set Y does not change w.r.t. the considered pipeline). This implies that, in the context of corrosion prediction for pipeline infrastructures, we can assume that (YS,PS(y|x)) = (YT,PT(y|x)) and (XS,PS(x))≠(XT,PT(x)), where the change is given by PS(x)≠PT(x) since the feature space is the same.

3 The proposed transfer-learning approach for corrosion prediction

An overview of the proposed approach based on TL for corrosion prediction in pipeline infrastructures is given in Fig. 1. More specifically, we have a set of source pipelines for which the supervised information is available and a target pipeline where only the influencing factors of the corrosion are accessible. Our goal is to create a predictive model for the target pipeline leveraging the source pipelines thanks to TL. This last step is done in two phases: at first, we rank the models built on a given source w.r.t. an estimate of their performance on the target (Algorithm 1 in Fig. 1); then the best B sources (being B a tunable parameter of the algorithm) are selected to build a predictive model for the target in a multi-task manner (Algorithm 2 in Fig. 1). Finally the predictive model \(\bar {\theta }\) is used onto the target pipeline to get the corrosion levels.

Fig. 1
figure 1

Comprehensive scheme of the approach (this image has been designed using resources from Flaticon.com)

Full size image

In the rest of this section, we will initially discuss how to build a model for the target pipeline when only one source is available, then we will review how to estimate the performance of a model onto the target pipeline, and finally, we will show how to leverage more than one source to build the target model in a multi-task manner.

3.1 Transfer Learning from a source to a target pipeline

Given \(D_{S}=\{({x^{s}_{i}},{y^{s}_{i}})\}_{i=1}^{n}\) and \(D_{T}=\{{x^{T}_{i}}\}_{i=1}^{n^{\prime }}\) representing the source and target pipelines data, the problem we want to tackle is:

$$ \theta^{*} \in \arg \min_{\theta \in {\varTheta}} ~\mathbb{E}_{(x,y)\sim P_{T}(\cdot,\cdot)}\left[l(x,y,f(x,\theta))\right], $$
(1)

where 𝜃 is the vector parametrazing our predictor f(x,𝜃) and l is a fixed loss function measuring the mismatch between predictions and ground truth. We emphasize that samples coming from PT(x,y) are not available, but we have samples coming from PT(x) and PS(x,y). Therefore, by exploiting Importance Sampling (IS) [23], we can rewrite the objective of (1) in the following way:

$$ \mathbb{E}_{(x,y)\sim P_{S}(\cdot,\cdot)}\left[\frac{P_{T}(x,y)}{P_{S}(x,y)}l(x,y,f(x,\theta))\right]. $$
(2)

Now, since we have finite samples, we reformulate our problem by optimizing the empirical version of the above objective function:

$$ \hat{\theta} \in \arg \min_{\theta \in {\varTheta}} \frac{1}{n}\sum\limits_{i=1}^{n}\frac{P_{T}({x^{S}_{i}},{y^{S}_{i}})}{P_{S}({x^{S}_{i}},{y^{S}_{i}})}l({x^{S}_{i}},{y^{S}_{i}},f({x^{S}_{i}},\theta)), $$
(3)

which gives us a consistent estimator of \(\hat {\theta }\) [24].

The problem of optimizing (3) can be tackled only if we can estimate the ratio \(\frac {P_{T}(x,y)}{P_{S}(x,y)}\). Since we do not have labels coming from the target pipeline, the aforementioned estimation, in a general case, cannot be achieved. In our scenario, we know that, by assumption of the domain experts, PS(y|x) = PT(y|x). Hence, by definition of conditional probability, \(\frac {P_{T}(x,y)}{P_{S}(x,y)}=\frac {P_{T}(x)}{P_{S}(x)}\), allowing an estimation of (3) on the available data.

In order to estimate the ratio \(\omega (x)=\frac {P_{T}(x)}{P_{S}(x)}\), we will resort to the approach proposed in [18], which consists in solving the following Kernel Mean Matching (KMM) optimization problem:

$$ \begin{array}{ll} &\min_{\omega}||\mu (P_{T}) - \mathbb{E}_{x\sim P_{S}(\cdot)}\left[\omega(x){\varPhi}(x)\right]||,\\ &subject~to:\\ &\quad\omega(x)\ge 0 ~and~ \mathbb{E}_{x\sim P_{S}(\cdot)}[\omega(x)]=1, \end{array} $$
(4)

where \(\mu (P_{T})=\mathbb {E}_{x\sim P_{T}(\cdot )}\left [{\varPhi }(x)\right ]\) and \({\varPhi }: X \rightarrow \mathfrak {F}\) (being \(\mathfrak {F}\) a feature space). Then, under the assumptions that PT is absolutely continuous w.r.t. PS and \(\mathfrak {F}\) is a Reproducing Kernel Hilbert Space (RKHS) with universal kernel \(k(x,u)=\left <{\varPhi }(x), {\varPhi }(u)\right >\), we have that a solution to (4) is such that PT(x) = ω(x)PS(x). Unfortunately, both μ(PT) and PS(x) are a priori unknown, but we have samples \(\{{x^{S}_{i}}\}_{i=1}^{n}\) and \(\{{x^{T}_{i}}\}_{i=1}^{n^{\prime }}\) to rely on. Considering the empirical version of the objective function in (4), under the assumptions that \(\omega : X \rightarrow [0, W]\) is a fixed function with finite mean and non-zero variance given \({x^{S}_{i}}\sim P_{S}\) (W is an upper bound on how much the two distributions can be different on a given x ∈ X), \(\{{x^{T}_{i}}\}_{i=1}^{n^{\prime }}\) is an iid (independent and identically distributed) set of samples drawn from PT(x) = ω(x)PS(x) and ||Φ(x)||≤ R for any x ∈ X then with probability at least 1 − δ:

$$ \begin{array}{@{}rcl@{}} &&\left|\left|\frac{1}{n}\sum\limits_{i=1}^{n}\omega({x^{S}_{i}}){\varPhi}({x^{S}_{i}}) - \frac{1}{n^{\prime}}\sum\limits_{i=1}^{n^{\prime}}{\varPhi}({x^{T}_{i}})\right|\right|\le \\ &&\qquad\qquad\qquad\left( 1+\sqrt{-\log\left( \frac{\delta}{2}\right)}\right)R\sqrt{\frac{W^{2}}{n}+\frac{1}{n^{\prime}}}, \end{array} $$
(5)

giving us an upper bound on the empirical optimization outcome (notice that the larger W, the larger the number of samples needed to obtain meaningful convergence guarantees). Now, letting \(K_{i,j}=k({x^{S}_{i}},{x^{S}_{j}})\), \(\kappa _{i}=\frac {n}{n^{\prime }}{\sum }_{j=1}^{n^{\prime }}k\) \(({x^{S}_{i}},{x^{T}_{j}})\) and \(\bar {\omega }_{i} = \omega ({x^{S}_{i}})\), the left hand side of (5) squared can be reformulated as follows:

$$ \frac{1}{n^{2}}\bar{\omega}^{T} K \bar{\omega} -\frac{2}{n^{2}}\kappa^{T}\bar{\omega} + const, $$
(6)

which yields the following optimization problem:

$$ \begin{array}{@{}rcl@{}} &&\min_{\bar{\omega}}\frac{1}{2}\bar{\omega}^{T} K \bar{\omega} -\kappa^{T}\bar{\omega}\\ &&subject~to:\\ & &\bar{\omega}_{i} \in [0,W] ~and~ \left|\sum\limits_{i=1}^{n}\bar{\omega}_{i} -n\right|\le n\varepsilon. \end{array} $$
(7)

The first constraint in (7) provides an upper bound to the degree up to which the two distributions may be different, whereas the second one forces ω(x)PS(x) to be close to a probability measure. For a more detailed discussion about KMM please refer to [18] and the references therein. Solving the optimization problem stated in (7) will return us the weight vector \(\bar {\omega }\) to correct the shift in distribution between the source and target pipelines.

3.2 Ranking the source pipelines

In a real-world scenarios, we may have multiple available source pipelines, \(\{D_{S_{m}}\}_{m=1}^{M}\). Hence, we would like to identify the most appropriate source within the given set. More precisely, we would like to select the source pipeline which allows us to minimize the generalization error defined as:

$$ \mathbb{E}_{\{({x^{T}_{i}},{y^{T}_{i}})\}_{i=1}^{n},u,v}\left[l(u,v,f(u,\hat{\theta}))\right], $$
(8)

where (u,v) is a test point coming from the target pipeline and not present in the training set. The generalization error is usually estimated through cross-validation (CV), which, in this context, is useless because we do not have access to the target pipeline labels. However, we can obtain this estimate through k-fold Importance Weighted Cross-Validation (kIWCV) [25] as follows:

$$ \frac{1}{k}\sum\limits_{j=1}^{k}\frac{1}{|D_{S_{m}}^{j}|}\sum\limits\limits_{(x,y)\in D_{S_{m}}^{j}}\omega(x)l\left( x,y, f\left( x, \hat{\theta}_{D_{S_{m}}^{j}}\right)\right), $$
(9)

where \(\hat {\theta }_{D_{S_{m}}^{j}}\) is the parametrization learned over the data set \(D_{S_{m}} \setminus D^{j}_{S_{m}}\) (∖ is the set difference operator) and the estimation of ω(x) can be performed by solving (7). The generalization error estimate provided by kIWCV with k = n is almost unbiased and a similar claim can be proved for k < n with a larger bias than that incurred with k = n (for a more thorough treatment see [25]). Therefore, choosing the source pipeline Sm maximizing the above equation will allow us to get the best performance for our models on the target pipeline. Moreover, from a more general standpoint, (9) allows us to optimize all the hyperparameters of our model to maximize performance on the target pipeline.

In Algorithm 1, we combine KMM, used to estimate ω(x), and kIWCV. More specifically, at line 4, we compute the importance weights to correct the distributional shift between the current source and the target pipeline. At line 5, we compute the optimal hyper-parameters and their performance through kIWCV. At line 6, the performance and hyperparameters of the current source pipeline are appended to their respective lists, (i.e., Perf and ρ). Finally, in line 8, we return the lists of performances and the corresponding hyper-parameters. This completes the TL framework we will use in the context of corrosion prediction for pipeline infrastructures.

We could extend this solution by considering more than one source pipeline for the corrosion prediction. This can be done through a multi-task learning approach which could use up to all the source pipelines together with their related importance weights to build a model for the target one [26, Chapter 9]. However, evaluating the performance of all the possible subsets of source pipelines does not scale well. To avoid this issue we could combine the B best sources according to the ranking we obtain by sorting the results of Algorithm 1 (the effect of B will be experimentally evaluated in Section 4). This procedure is reported in Algorithm 2, where, at lines 4 and 5, we concatenate the data sets and the weights. At line 7, we compute the optimal hyperparameters of the learning algorithm, and, finally, at line 8, the best parametrization for the predictor is computed and subsequently returned.

figure g
figure h

4 Experiments

This section aims to evaluate the effectiveness of the proposed TL approach in real-world scenarios of corrosion prediction within 4 different gas pipeline infrastructures, namely P1, P2, P3, and P4. The section is organized as follows: Section 4.1 describes the employed data sets, whereas the experimental results are given in Section 4.2.

4.1 Data sets description

In order to integrate the geometrical and fluid dynamical data, we rely on the approach proposed in [8]. Such an integration approach will return us a data set \(D=\{x_{i},y_{i}\}_{i=1}^{n}\) for each pipeline. Here the vector xi’s components represent the corrosion influencing factors (see Tables 1 and 2), whereas yi is the scalar value representing the corrosion level (in terms of bar thickness percentage being corroded). Such a value is transformed into a categorical variable with four possible classes according to the thresholds provided by the domain experts and reported in Table 3. After the integration, a data transformation and enrichment is performed as follows. The Lat, Long and Elev are transformed into their equivalent Cartesian coordinates x, y and z. Then their first and second-order derivatives are computed (and added to the feature set), which represent the pipeline profile’s rate of change along a fixed component. Additionally, some features have been removed from the data sets because, according to the domain experts, they showed unexpected behavior, whereas some others were removed due to redundancy. More specifically, GLWVT, QT, GT, QG, Bar length and GG have been removed under domain expert advice, together with Barinit because redundant. Finally, under the domain experts’ suggestion, the samples associated with the beginning or end of the pipeline were removed because they have completely different behavior in terms of corrosion. At the end of this enrichment step, the features are normalized. Some summary information on the different pipelines after the above-mentioned transformations is provided in Table 4, where we may notice a severe imbalance among the various classes. It is worth noting that the High class is very rare and the Absent class is dominating the others.

Table 1 Geometrical variables
Full size table
Table 2 Fluid-dynamical variables
Full size table
Table 3 Categories and Thresholds of the thickness percentage being corroded for a bar
Full size table
Table 4 Label (y) distribution across the different pipelines
Full size table

4.2 Results

For each available target pipeline, we will evaluate the performance of Algorithm 2 in three different configurations: B = 1, B = 2 and B = 3. We used a Support Vector Machine (SVM) [27] with Radial Basis Kernel as f(x,𝜃). In Table 5, we report the results returned by Algorithm 1 when the F1-Score is chosen to perform the 10-IWCV (the model hyper-parameters are not reported for the sake of brevity). We will review each one of the aforementioned configurations of Algorithm 2 one target pipeline at a time. We will first look at the multi-class confusion matrices, then at their binarized version (reported in Appendix A) to check also the corrosion detection capabilities of each solution, and, finally, at the performances in F1-Score and accuracy.

Table 5 Estimate of the performance (F1-Score) on the target pipeline through Algorithm 1
Full size table

4.2.1 P1

As we can see by comparing Fig. 2a and d, applying the TL technique gives us an improvement on the class low and the class absent recognition with a degradation effect on the class high and medium. For what concern the solution offered by using the first two sources (B = 2) according to IWCV (compare Fig. 2b and e), we have an improvement on both the absent and medium-class recognition with a degradation on the class low (the class high reduction is very slight). Using just the first ranked solution (B = 1) w.r.t. IWCV, we obtain a model that nearly always predicts absent (see Fig. 2f). If we take a look at the binarized version of the confusion matrices (see Fig. 6 in Appendix A), then only the solution proposed by leveraging the first two sources w.r.t. IWCV is useful in terms of corrosion detection (compare Fig. 6a, b, c with d, e, f respectively). Finally, by looking at Tables 6 and 7, we may notice that applying transfer almost always increases our performance w.r.t. these two figures of merit.

Fig. 2
figure 2

Multi-Class Confusion Matrices for P1

Full size image
Table 6 Accuracy on target
Full size table
Table 7 F1-Score on target
Full size table

4.2.2 P2

If we compare Fig. 3a and d (B = 3), we may notice an improvement on the absent class recognition at the expense of a degradation for the classes low and medium. For what concern Fig. 3b and e (B = 2), we can see an improvement on the recognition of the classes low and absent to which corresponds a slight reduction on the medium and high classes. By comparing Fig. 3c and f (B = 1), instead, we may see an improvement in the medium class recognition accompanied by a worsening on the absent class. Now, taking a look at the binarized versions of the confusion matrices (please compare Fig. 7a, b, c with d, e, f respectively in Appendix A) only the confusion matrix associated to the usage of the best source (B = 1) according to IWCV is meaningful. Finally, by looking at Tables 6 and 7, we see that applying transfer improves the accuracy and the F1-Score in all the cases except when we choose the best source (B = 1) w.r.t. IWCV. Furthermore, notice that, in some cases, the TL technique is able to get an improvement in F1-Score or accuracy w.r.t. to what was obtained by training a model onto a portion of the data set representing this target pipeline and then testing this model onto the held out part (i.e., the Supervised Oracle).

Fig. 3
figure 3

Multi-Class Confusion Matrices on P2

Full size image

4.2.3 P3

Comparing Fig. 4a with d (B = 3) and b with e (B = 2), we may see as the TL technique improves the absent and medium classes recognition at the cost of increasing misclassifications within the low class. Differently, when comparing Fig. 4c with f (B = 1), we have the same behavior as before with also an increment on the misclassification error for the class high. In the context of the binarized versions (please see Fig. 8a, b, c compared with d, e, f, respectively, in Appendix A), we have that both the confusion matrices represented in Fig. 8e and f are meaningful. Also in the case of this target pipeline, we have that applying transfer almost always improves accuracy and F1-Score (see Tables 6 and 7).

Fig. 4
figure 4

Multi-Class Confusion Matrices on P3

Full size image

4.2.4 P4

As we can see from Fig. 5a compared with 5d (B = 3) and Fig. 5b compared with 5e (B = 2), applying the TL technique allows us to improve the recognition performance both on the absent and medium classes with a degradation effect on the low class (in Fig. 5d a slight degradation on the high class is perceivable w.r.t. Figure 5a). In the context of Fig. 5c and f (B = 1), we have the same behavior described for Fig. 5a and d. Here, the only difference is that the absent class true positive rate remains the same. For what concern the binarized version (see Figure 9 in Appendix A), in the context of this target pipeline, choosing the best source (B = 1) w.r.t. IWCV does not produce a meaningful confusion matrix, whereas the other two approaches do (please compare Fig. 9a, b, c with d, e, f, respectively). Finally, as we may see from Tables 6 and 7, the TL technique always improves the two figures of merit surpassing or matching the performances obtained by training a model onto a portion of the target pipeline and then testing it onto the held out test set (i.e., the Supervised Oracle).

Fig. 5
figure 5

Multi-Class Confusion Matrices on P4

Full size image

5 Discussion

In the previous section, we have seen how the three configurations (B = 1,2,3) of the proposed solution behaved in terms of corrosion classification onto a target pipeline for which the labels are not available. The lack of labels was bridged with the aid of a TL technique described in Section 3.1. We have shown models’ performance along four distinct components: the multi-class confusion matrices, their binarized version (to assess the detection capabilities of the developed models), the accuracy, and the F1-Score. Among the three different configurations, the one built using the first two best sources (B = 2) according to IWCV seemed to be the most stable, especially concerning the binarized version of the confusion matrices. This is a reasonable solution to trade off the intrinsic uncertainty in identifying the best source pipeline with the need to limit the number of sources to be used.

In the context of corrosion classification for oil and gas pipelines (the tackled application scenario), it would be also useful to get access to the confidence with which the model is predicting a certain label. To achieve this, for what concerns SVMs, we can capture the probabilities for each class given a fixed sample. More precisely, multiclass probability estimates are computed by combining all pairwise probability estimates ri,j for class i and j. So, given all the ri,j, the estimate of p(y = i|x) is obtained by solving a linear system, see [28] for further details. The pairwise probability estimates are obtained by logistic regression on the score of the SVM [29]. It is noteworthy to point out that this technique to produce probabilities can be seamlessly integrated into the proposed TL approach.

6 Conclusion

In this paper, we tackled the problem of building a predictive model for the corrosion phenomenon in the context of a pipeline infrastructure for which the supervised information is not available. To achieve this goal we used a KMM-based TL technique to leverage labeled data coming from a source pipeline infrastructure. Moreover, in a context where different labeled source pipelines are available, we combined KMM, IWCV, and multi-task learning to produce a model for the target infrastructure by selecting the appropriate sources.

As possible future directions, we would like to mention the need to acquire time-varying data for a set of fixed pipelines to develop models accounting for time variations of the corrosion phenomenon both in the TL context and in the supervised learning one. Furthermore, taking into account the pipelines’ material and chemical composition of the blend flowing within the pipelines is another important future direction. As of right now, the material is homogeneous among our pipelines and we do not possess data describing the chemical composition of the blend flowing through them. However, it would be relevant to extend our methodology in this direction, maybe giving more importance to those source pipelines having similar material and chemical composition of the blend w.r.t. the target pipeline. Finally, we hope that this work may stimulate a renewed interest in this complex application, maybe attracting more investments in research from the oil and gas companies.