1 Introduction

The early research of the Vehicle Routing Problem (VRP) can be traced back to [1], shown as an essential issue with tremendous effect to the economy and society. In the classical Vehicle Routing Problem with Time Windows (VRPTW) [2], at the beginning of a planning horizon, a fleet of identical vehicles leave a center depot to visit/service a sequence of customers with certain demands, composing a number of so-called routes. Every customer is visited exactly once, satisfying the constraints (time window) specified by the customers. The sum of customer demands on each route cannot exceed the capacity of a vehicle, and all vehicles have to return the depot before the end of the planning horizon. The most common objectives in VRPTW are minimization of the number of vehicles used and minimization of the total travel distance.

1.1 Vehicle routing problem variants

Based on the VRPTW model, a large number of classic VRP variants have been proposed with diverse side constraints from practical scenarios. In this section, only the most relevant variants to our study are reviewed. In Vehicle Routing Problem with Pickups and Deliveries (VRPPD) [3], a service demand consists of picking up shipments from a customer and the associated delivery to another customer. Especially, if the depot is the only one pickup point and all the customers are delivery destinations, or in another case, all the customers are pickup points while only the depot is the delivery location, the problem is called a One-to-Many-to-One problem. If the customers are pickup points as well as delivery points, the problem is Many-to-Many. Last but not least, it is a One-to-One problem when the pickup demand of a customer is the delivery demand of another specific customer [4].

Furthermore, if the shipments can be consolidated, the problem would be classified as Less-than Truckload Transportation; otherwise, it is a Full Truckload Transportation (FTT) problem [5]. Container transportation problem is a specific variant of FTT, where one truck can carry only one demand item (container). Zhang et al. [6] model the container transportation problem with a node-based network, which is commonly used in VRPTW. The model integrates all activities of completing the transportation of a container into a so-called load node. This method has been widely used in the VRPPD with high loading and unloading time [7, 8].

In some cases of VRP, the scheduling horizon is very long, e.g. in soft drink industry, grocery distribution and waste collection. Their scheduling is usually performed over multiple periods/shifts, and the associated problems are categorized as Multi-Period Vehicle Routing Problem (MPVRP) [9]. Especially, when there is a specific service frequency to each customer over the scheduling horizon, the problem is called a Periodic Vehicle Routing Problem (PVRP) [10]. In this case, each customer may be visited more than once. The solution of PVRP is a combination of service shifts of customers, instead of the scheduled routes of one single period.

Apart from the two objectives in VRPTW mentioned above, there are various other objectives widely used in VRPs, e.g. minimizing the travel time, the waiting time, and other operational cost, maximizing the balance of workload, and so on [11]. With the increasing concern to the environment in recent years, the carbon emission and petrol consumption have also been considered in the VRP community, leading to the Pollution-Routing Problem and Green Vehicle Routing Problem [12]. From the cost perspective, labor cost (driver salary) usually is the dominated component in the overall cost [13]. This is one of the reasons why minimizing the number of vehicles used is a primary objective in VRPs, as fewer vehicles require fewer drivers being hired. In addition, making use of fewer vehicles generally implies a lower fuel consumption and a higher utilization rate of the vehicle capacity. When more than one objective are considered in a VRP, it is called a Multi-Objective Vehicle Routing Problem (MOVRP).

1.2 Existing methods

After decades of study in VRP, both exact and approximate methods have been extensively investigated. Exact methods explore the solution space of a problem exclusively to find the optimal solution. However, a critical issue of such methods is the unrealistic computational time needed searching the enormous size of the solution space in real-world problems. On the other hand, approximate methods (or heuristics) do not guarantee the optimality of solutions produced, but generate a good approximation of the optimal solution in an acceptable computation time [14]. Metaheuristics and Hyper-Heuristics methods guide the search with various strategies, showing powerful performance in solving diverse large scale and complex VRPs [15].

Population-based metaheuristics, such as Evolutionary Algorithms, Scatter Search, and Ant Colony Optimization Algorithms, evolve a population of solutions [14]. Using population improves the diversification of searches, these type of methods show powerful exploration ability while achieve high quality solutions in multi-objective and highly constrained problems. However, larger population is hard to operate and may greatly affect algorithm performance. For example, in Genetic Algorithm, which is a widely used population-based metaheuristic in VRPs, it is hard to use crossover to partition the periods and routes in the solution representation (e.g. genotype/chromosome) for MPVRP. Besides, in large size problems, the long chromosome and the associated large solution population is hard to manage as well. Population-based metaheuristics are not suitable to large scale problems with complex structures and constraints such as the MPVRP considered in this paper.

Differently, in each iteration of single solution-based metaheuristics, only one solution is updated by employing neighbourhood operators at each move during the search. In different algorithms, such as Tabu search [16], Simulated Annealing [17], and Variable Neighbourhood Search [18], different strategies are used in the Acceptance Criterion and Neighbourhood Operator Selection.

Metaheuristic algorithms are often designed to address specific problems by striking a balance between the diversity and intensity of the search for the specific problems. In the literature, a large number of problem specific and knowledge intensive metaheuristics have been developed for VRPs [19, 20]. Differently, Hyper-Heuristics is a type of high level algorithms which aim to develop generic approaches beyond the problem specific metaheuristics [21, 22]. Hyper-Heuristics work at a higher level to generate or select a set of Low-Level Heuristics (LLH) in a common framework, while the LLH execute the operations on problem solutions. Hyper-Heuristics focus on designing the high level framework, called High-Level Heuristic (HLH), instead of searching the specific solutions for the problem confronted. In a well-designed Hyper-Heuristics algorithm, its HLH would adaptively adjust the LLH used, creating proper algorithms for various searching scenarios for the given instances.

Hyper-heuristics approaches can be categorized to two classes: Heuristic Selection and Heuristic Generation [23]. Heuristic Selection methodologies choose existing heuristics from the LLH pool to tackle the problem given, while the methodologies of Heuristic Generation generate new heuristics using existing heuristics as the components. What’s more, each above class can be further divided into two subcategories, namely Construction Heuristic and Perturbation Heuristic, according to the constructive or perturbative low level heuristics used. Construction Heuristics construct solutions using the given LLH, while Perturbation Heuristics produce new solutions by perturbing existing solutions. More details can be found in [24, 25].

As a classic combinatorial optimization problem, VRP is an essential application of hyper-heuristics. Garrido and Riff [26] propose an evolutionary hyper-heuristic for Dynamic Vehicle Routing Problem (DVRP). Each genotype in this evolutionary algorithm consists of a constructive heuristic, an improvement heuristic and an ordering heuristic. This generative construction hyper-heuristic adapts well to the dynamic scenario in DVRP. Both hyper-heuristics of [27] and [28] obtain competitive results in Capacitated Vehicle Routing Problem (CVRP). The former generates LLH by searching the space of heuristic component (i.e. neighbourhood structure, neighbourhood combination, local search configuration and acceptance criterion), while the latter adjusts the order of LLH to perturb the current solution, incorporating an adaptive ordering scheme in an Iterated Local Search framework. In [29], besides the selection of LLH, a Gene Expression Programming framework is also proposed to automatically generate the acceptance criterion for different problem instances. The proposed method shows promising results in DVRP and CVRP.

Vidal et al. [30] propose an unified hybrid genetic search framework (UHGS), which replaces the mutation with a unified local search (ULS). In ULS, the route-evaluation operators vary according to the change of problem attributes, aiming to provide a general-purpose solver for diverse VRP variants. UHGS produces results better than or close to the state-of-the-art results on benchmarks. However, the experiment results show that its computation time increases significantly in MPVRPs again due to the period and route partition problem as explained above on genetic algorithms. The long computation time impedes its application to large scale MPVRP.

Benefiting from decades of intensive research in VRP, a large number of excellent heuristics have been developed, providing sufficient LLH for designing high performance hyper-heuristics. Potvin and Rousseau [31] and Taillard et al. [32] propose the 2-opt* and CROSS-exchange heuristics, respectively, which show excellent performance in routing problems with time windows. However, when facing large-scale problems with complex structure, they often converge prematurely due to their relatively small change (low perturbation) to a solution in each iteration, thus the search is often stuck to local optimum.

Shaw [33, 34] proposes the Large Neighbourhood Search (LNS) heuristic which removes a number of nodes (e.g. demands/customers) from the current solution and then reinserts them to generate an updated new solution (Destroy & Repair). This heuristic brings greater changes (higher perturbation) to escape from local optimum and avoid premature convergence. It obtains the best results in several VRP variants, although a larger computation time is required in each iteration [35]. A similar strategy called Ruin & Recreate is proposed in [36].

Nagata and Bräysy [37] propose the Guided Ejection Search (GES) heuristic combining the ideas of LNS and Ejection Pool methods [38]. In each iteration of GES, one route is removed and then the nodes of the removed route are reinserted into the destroyed solution. Any infeasible partial solutions are accepted with penalties. GES outperforms the existing heuristics on minimizing the number of routes, but longer computation time for each iteration is needed. For more details, see [39, 40].

Much research on MOVRP have been done as well. In some of them, a set of non-dominated solutions based on Pareto Dominance [41] are generated, providing the decision maker a pool of candidate solutions as a reference (Pareto Methods). In the literature, the Pareto Methods are mainly used in Evolutionary Algorithms [42,43,44,45]. Differently, in the other research, one single optimal solution is pursued. In this case, either the problem objectives are projected into one single objective and the problem is solved as a single-objective problem (Scalar Techniques), or different priorities are assigned to objectives which are considered separately (Non-Scalar and Non-Pareto Algorithms). More methodologies for MOVRP can be found in [46].

In real-life, the vehicle scheduling of different types of shifts are usually considered separately as independent problems. In this paper, a real-world Mixed-Shift Vehicle Routing Problem with Time windows (MS-VRPTW) is studied. A construction heuristic and a selection perturbation hyper-heuristic, which combine the scheduling work of two types of shifts, are proposed for the MS-VRPTW. The proposed algorithms integrate the independent resource for the two types of shifts, aiming to increase the utility of vehicles and reduce the scheduling stress for logistic companies. The algorithms are tested on a set of benchmark instances with different features.

The rest of this paper is organized as follows: Section 2 introduces the problem background and presents the mathematical problem model. Section 3 introduces the proposed solution methods. The benchmark instances and computation experiments are presented in Section 4. Section 5 shows the conclusions of this paper.

2 Problem definition & mathematical model

2.1 Problem description

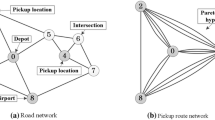
The problem studied is a container transportation problem faced by a logistic company at Ningbo Port, which is the second largest port in China. Every day, the company has to transship a number of commodities, each consists of a number of containers. Every commodity has a specific service time constraint. These commodities are transited among 19 container terminals including harbors and dry ports (see Fig. 1). There is a fleet of 250 trucks, whose depot locates at the Ningbo coast. Every day, the trucks leave the depot with a list of transport tasks and return to the depot after completing all the tasks.

Fig. 1
figure 1

The locations of 19 container terminals of the logistic company (screenshot taken from Google Maps [47]). The balloon icons represent dry ports and the ball stick icons represent harbors. The nine harbors are located along the coast of Ningbo City, while the 10 dry ports are either inland or far from the Ningbo coast

Full size image

The management of transportation involves three levels of planning, namely: strategic planning, tactical planning, and operational planning [5]. Strategic level management focuses on the decisions of the locations of facilities (e.g. the locations of depots and fleets), while the key tactical issues are terminal operation specification, service selection and other mixed decision making. Strategic planning and tactical planning are the preconditions to transportation problems, and they are long-term and medium-term planning. The operational planning focuses on the Vehicle Routing and Scheduling Problem, which is the major issue of the Ningbo Port problem.

As one truck in the Ningbo Port can carry only one container at a time, one container represents one transport task. Completing a transport task consists of loading the container to the truck at the source terminal, transporting the container from the source to the destination terminal and then unloading the container over there. The well-known Planning Domain Description Language (PDDL) is a complex descriptive system providing a standard and flexible formalism for various AI planning domains including the VRPs [48]. It is supported by state-of-the-art planning methodologies, producing high quality solutions in various planning problems. However, those methods have not shown to perform effectively or efficiently in solving large size real-life problems [49]. To simplify the problem model and make the prevailing neighbourhood search heuristics applicable, the node-based method of [7], instead of the PDDL, is employed for formulating the problem of this paper. A task node integrates the three activities to represent the service of a transport task. The service time of a task is the total time of the three activities.

From Fig. 1, we can find that the tasks associated with the dry ports are long-distance tasks (LDT), while those transportation between harbors are short-distance tasks (SDT). In the Ningbo Port, the service time of a SDT is less than seven hours, and all the harbors can be reached in less than 2 hours from the depot. On the other hand, because the service time of LDT and the travel time between the dry port and the depot is quite long, the average time of completing a LDT is longer than 13 hours. In some studies, the exact path between two points is also considered, i.e. the problem of Path Planning [50]. Since the paths among the terminals and the depot are fixed by the company in our problem, the drivers cannot change the fixed path when completing a task or going to the next task. Vehicle routing considering path planning presents an interesting and different integrated problem, thus is in the scope of our future research.

The Ningbo Port company sets up two types of working shifts: short shift and long shift. A short shift is 12 hours, meaning a day is divided into two short shifts (day shift and night shift). In the day shift, drivers drive trucks away from the depot, and drivers of the night shift return the trucks to the depot after completing their tasks. The two drivers using the same truck (called one-driver truck) have a shift-change in the middle of a day at a terminal. Shift-change cannot happen within a task node, so the shift-change terminal is either the last destination terminal of the day shift or the first source terminal of the night shift. Differently, a long shift is 24 hours. In this case, two drivers are assigned to one single truck (double-driver truck) at the same time. With this arrangement, the two drivers can drive the truck in turn, satisfying the associated regulations on continuous working hours in Labor Law.

The two types of shifts are associated with two different driver salary schemes, which lead to different overall operational cost to the company. In a working day, two drivers are required for one truck of either type. The difference between the two types of trucks is that the two drivers of a one-driver truck route work separately within their own short shifts, while both drivers of a double-driver truck route have to stay in the truck during the whole long shift. Correspondingly, the unit payment to the drivers of double-driver trucks is higher for their longer shift length. SDT can be completed in a short shift using one-driver trucks, while LDT must be completed with double-driver trucks in long shifts due to the long service time. When optimizing the assignment of LDT and SDT, considering both types of trucks simultaneously can reduce the overall number of trucks used, consequently minimizing the overall total operational cost of driver payment.

The truck scheduling for both types of shifts are combined in this study. Currently, the company handles LDT and SDT with two separate scheduling systems, resulting to inefficient use of trucks and lots of task lateness in busy seasons. This low efficiency schedule is mainly caused by the two separate scheduling systems which do not share the limited truck resource. In our study, the two scheduling systems are integrated to increase the efficiency of the scheduling and the utility of trucks. Artificial task which represents the driver shift-change between two short shifts is thus proposed. The routes of a truck in two consecutive short shifts are thus converted to one route in a long shift. To the best of our knowledge, this is the first time the Mixed-Shift Vehicle Routing Problem with Time Windows (MS-VRPTW) is proposed in the literature. In the Ningbo Port, the trucks in the fleet are identical and can be appointed to be either one-driver or double-driver according to the commodity situation.

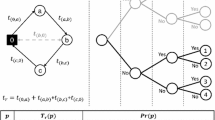
An example schedule of a working day (with one long shift or two short shifts) is presented in Fig. 2 to illustrate our proposed model. There are in total eight routes, three for one-driver trucks and five for double-driver trucks. We can see that, LDT (represented by rectangles) only appear in double-driver truck routes, while SDT (solid circles) exist in both one-driver truck routes and double-driver truck routes. The hollow circles in the top three routes are artificial tasks.

Fig. 2
figure 2

A schedule example of one long shift (two short shifts). Three one-driver trucks and five double-driver trucks are used in this schedule. The right subgraph presents the first and sixth routes in the schedule

Full size image

The fourth route in Fig. 2 explains why the LDT require double-driver trucks. Considering the travel time leaving and returning to the depot, completing a LDT takes more than 12 hours (maximum length of a short shift). In addition, if the distance between two LDT is small, more than one LDT might be serviced in one double-driver route. For instance, in the last route, as the destination of the first LDT is the source of the second LDT, the travel distance and time between the two tasks is zero. In this case, the two LDTs can be completed by one double-driver truck, leading to a more efficient use of vehicles.

Another special case of LDT is the rectangle in the seventh route. It represents a type of task which require short service time but can only be finished in double-driver routes. Because their time windows are narrow (i.e. 3 hours in this example) and across the middle of a working day, the shift-change between short shifts cannot be done when completing these type of tasks. Therefore, these type of tasks can only be assigned to double-driver trucks.

In different real-life scenarios, the shift lengths, the number of task types and the number of shift types might be different from that of the Ningbo Port problem. However, the method of using artificial tasks is still applicable, which integrates the scheduling and routing with different shift settings into one model. Therefore, the model of MS-VRPTW can cover various practical cases from real scenarios.

2.2 Mathematical model

To model the MS-VRPTW, a number of notations are defined, see Table 1.

Table 1 Definition of Notations
Full size table

The MS-OPVRPTW can be formally defined as follows.

Objective:

$$ Minimize\quad \qquad \quad DP= \sum\limits_{s\in S}\left( P_{o} \cdot {K_{O}^{s}}+P_{d}\cdot {K_{D}^{s}}\right) $$
(1)
$$ Minimize \quad \qquad \quad TD=\sum\limits_{p\in P}\sum\limits_{s\in S}\sum\limits_{i\in N\cup W}\sum\limits_{j\in N\cup W}c_{ij}\cdot x_{ij}^{sp} $$
(2)

Subject to:

$$ \sum\limits_{p\in P}\sum\limits_{s\in S}\sum\limits_{i\in W\cup N\texttt{\char92}\{0\}} x_{ij}^{sp}=1, \quad \qquad \qquad \forall j\in N\texttt{\char92}\{0\} $$
(3)
$$ \sum\limits_{p\in P}\sum\limits_{s\in S}\sum\limits_{j\in W\cup N\texttt{\char92}\{0\}} x_{ij}^{sp}=1, \qquad \qquad \quad \forall i\in N\texttt{\char92}\{0\} $$
(4)
$$\begin{array}{@{}rcl@{}} \sum\limits_{i\in W\cup N\texttt{\char92}\{0\}} x_{ij}^{sp}&=&\sum\limits_{f\in W\cup N\texttt{\char92}\{0\}} x_{jf}^{sp}, \qquad \forall j\in W\cup N\texttt{\char92}\{0\},\\&&\qquad\qquad\qquad\qquad s\in S, p\in P \end{array} $$
(5)
$$ {K_{O}^{s}} + {K_{D}^{s}} \leq K, \qquad \qquad \qquad \qquad \qquad \forall s\in S $$
(6)
$$ \sum\limits_{j\in N\cup W} x_{0j}^{sp}= \left\{\begin{array}{ll} {K_{O}^{s}} & \qquad \qquad \qquad \forall s\in S, p=O \\ {K_{D}^{s}} & \qquad \qquad \qquad \forall s\in S, p=D \end{array}\right. $$
(7)
$$ \sum\limits_{i\in N\cup W} x_{i0}^{sp}= \left\{\begin{array}{ll} {K_{O}^{s}} & \qquad \qquad \qquad \forall s\in S, p=O \\ {K_{D}^{s}} & \qquad \qquad \qquad \forall s\in S, p=D \end{array}\right. $$
(8)
$$ \sum\limits_{p\in P}\sum\limits_{j\in N} x_{wj}^{sp} = {K_{O}^{s}} \qquad \qquad \qquad \forall w\in W, s \in S $$
(9)
$$ \sum\limits_{p\in P}\sum\limits_{i\in N} x_{iw}^{sp} = {K_{O}^{s}} \qquad \qquad \qquad \forall w\in W, s \in S $$
(10)
$$ \sum\limits_{j\in N} x_{wj}^{sO} = {K_{O}^{s}} \qquad \qquad \qquad\qquad \forall w\in W, s \in S $$
(11)
$$ \sum\limits_{i\in N} x_{iw}^{sO} = {K_{O}^{s}} \qquad \qquad \qquad \qquad \forall w\in W, s \in S $$
(12)
$$ x_{wv}^{sp} = 0, \quad \qquad \qquad \qquad \qquad \forall w,v\in W, s \in S, p \in P $$
(13)
$$\begin{array}{@{}rcl@{}} T_{j} &=& \sum\limits_{p\in P}\sum\limits_{s\in S}((B_{i}+l_{i}+t_{ij})\cdot x_{ij}^{sp} + (Y_{s}+t_{0j})\cdot x_{0j}^{sp}), \\ &&\forall i\in N\texttt{\char92}\{0\} \end{array} $$
(14)
$$ B_{j} = T_{j} + max\{a_{j}-T_{j}, 0\}, \qquad \qquad \qquad\forall j\in N\texttt{\char92}\{0\} $$
(15)
$$\begin{array}{@{}rcl@{}} x_{ij}^{s0} \cdot (B_{i}+l_{i}+t_{i0})\leq x_{i0}^{sp}\cdot Z_{s},&& \quad \qquad \forall i\in N\cup W,\\&&\qquad\quad s\in\! S, p\in\! P \end{array} $$
(16)
$$ a_{i}\leq B_{i}\leq b_{i}-l_{i}, \qquad \qquad \qquad \qquad \forall i\in N\texttt{\char92}\{0\} $$
(17)
$$ x_{ij}^{sp} \in\{0,1\} \qquad \qquad \qquad \quad \forall i, j \in N \cup W, s\in S, p \in P $$
(18)
$$ {K_{O}^{s}}\in\{0,1,...,K\} \qquad \qquad \qquad \qquad \qquad\forall s \in S $$
(19)
$$ {K_{D}^{s}}\in\{0,1,...,K\} \qquad \qquad \qquad \qquad \qquad \forall s \in S $$
(20)

MS-VRPTW is a bi-objective problem. The first objective is minimizing the total driver payment (DP), see Eq. 1, which depends on the number and types of trucks used. It is notable that, the cost of a driver for double-driver truck is 1.5 times of a driver of one-driver truck in our study (i.e. Po = 1, Pd = 1.5). Minimizing the total travel distance (TD) (2) is the other objective. Actually, the target of TD is to minimize the empty-load travel distance as the total loaded travel distance in an instance is fixed. DP focuses on the operational cost, and TD concentrates on the utility of trucks which actually pursues a higher heavy-loaded travel distance rate in total travel distance.

Constraints (3) and (4) denote that every task node can be visited exactly once and all the tasks must be visited. Constraint (5) specifies that a task may only be serviced after the previous task is completed. Constraints (3)–(5) together make sure arcs over more than one shift are unacceptable. Constraint (6) guarantees the number of trucks used is not larger than the fleet size.

Constraints (7) and (8) place the limits on one-driver truck (p = O) and double-driver truck (p = D). Constraints (9)–(12) guarantee that there must be \({K_{O}^{s}}\) artificial tasks completed on the routes of one-driver trucks, while there is no artificial task on the routes of double-driver trucks. In addition, constraint (13) guarantees each route of one-driver truck has only one artificial task.

Equation (14) defines the arrival time at a task node. Equation (15) defines the beginning time of servicing a task node. This time is calculated by the arrival time plus the waiting time at the source of a task. Equations (14) and (15) enforce the correct successive relationship between consecutive nodes. Constraints (14)–(16) together define the time windows of shifts. Constraint (17) represents the time constraint on each task. The domains of the decision variables are presented in (18)–(20).

From this mixed integer programming (MIP) model, we can find that the MS-VRPTW is a large-scale and tightly constrained non-linear problem. In MS-VRPTW, the size of solution space is decided by the number of tasks (n), the number of shifts (|S|) and the size of the fleet (K). Since there are |S|⋅ K possible routes in a solution, which are either one-driver or double-driver, and each route has n! permutations of tasks, the size of the search space is 2|S|⋅K ⋅ n!. In real-life, a logistic company may face hundreds to thousands of containers to be transited, leading to a highly complex problem with huge solution space.

3 Solution methodologies for bi-objective mixed-shift vehicle routing problem with time windows

3.1 Exact search

In our study, exact search method is first implemented to address MS-VRPTW using a successful and widely used optimization solver, CPLEX. To address this bi-objective MIP problem with CPLEX, the objectives of the mathematical model has to be slightly modified since CPLEX is not a tool for multi-objective models. To this end, three different configurations are employed to linearly combine the two objectives into one (called decomposition in some research, see formula (21)). The configurations represent three scenarios in the modified objective: 1) DP has the same weight as TD, 2) DP dominates TD and 3) TD dominates DP. Considering the different ranges of DP and TD, the three configurations are {a = 200, b = 1}, {a = 10000, b = 1} and {a = 4, b = 1}, respectively.

$$ Minimize \qquad \qquad a\cdot D\!P+ b\cdot T\!D $$
(21)

The CPLEX script of exact search has been run on a high performance computer system. Considering the scale of this problem, a large number of computation resources have been assigned, which were 16 cores (2.6 GHz), 100 GB memory and 24 hours runtime limit for each experiment instance. However, the output of CPLEX shows that even with large amounts of computation resources, it is still very hard to obtain satisfying solutions for MS-VRPTW with exact search methods. CPLEX was out of memory within 10 minutes in all the three configurations. This observation indicates that exact search is not realistic for solving this large-scale tightly constrained nonlinear problem due to massive computation resources required for computation time and memory. It is no doubt that there may exist exact methods which can work better than CPLEX in this problem, however, the requirement of extensive computation resource still remains. Therefore our studies focus on developing efficient approximate approaches for MS-VRPTW.

3.2 Initial solution construction heuristic

Solomon [2] develops four classic construction heuristics for VRPTW, among which the Insertion Heuristic in general shows the best performance. Given a set of candidates to be assigned (e.g. customers, demands), in each iteration, a candidate is inserted to an insertion position in the existing routes using Insertion Selection Schemes. During the construction, if all existing routes are full, a new empty route will be created. The Insertion Selection Schemes used in existing routes and the newly created empty routes can be different. These steps are repeated until all candidates are assigned, obtaining a complete solution.

Insertion Heuristic is widely applied to diverse VRP variants using various Insertion Selection Schemes. Chen et al. [51] propose an emergency-based construction heuristic for the Open Periodic Vehicle Routing Problem with Time Windows. In that heuristic, tasks with higher emergency are dealt with a higher priority. Based on the emergency-based construction heuristic, we propose an Emergency Level-Based Insertion Construction Heuristic (EBIH) for MS-VRPTW.

In EBIH, all the tasks are classified into LDT or SDT following the definitions given in Section 2.1. Then they are further categorized according to their emergency levels. When a task i can be completed in shift s according to its time window, the task is either optional or mandatory. To be precise, if i can be completed in s and later shift(s), i is an optional task in shift s; otherwise, i is a mandatory task to s. So, to each shift, four sets of available tasks would be assigned, which are mandatory LDT, optional LDT, mandatory SDT, and optional SDT.

The four sets of tasks are considered in order in EBIH. It is easy to understand that we should assign mandatory tasks first. Because the delay of tasks may cause the containers missing the vessel appointed and greatly increase the operational cost of the company. Besides, SDT can be completed with both one-driver trucks and double-driver trucks while LDT can only use double-driver trucks, which means SDT have more insertion options than LDT when constructing a solution. Therefore, LDT is relatively harder to assign than SDT and should be assigned earlier.

In practice, logistic companies usually complete tasks as early as possible to avoid leaving many tasks to the following shifts and increasing later scheduling pressure. In real-life, extra commodities might be added in real time. Reducing the remainder tasks and leaving more available trucks for later shifts can also enhance the stability of the scheduling system. In EBIH, after arranging all mandatory tasks, if there still are available trucks in the fleet, optional tasks will be inserted to the current shift until all trucks are ran out. The order of task sets being assigned shift by shift is: mandatory LDT→ mandatory SDT → optional LDT → optional SDT.

Faced with a set of tasks to be inserted and a large number of potential insertion positions, the Insertion Selection Scheme used determines the performance of an Insertion Heuristic. The scheme of Greedy Strategy always executes the insertion bringing the least cost increase among all candidate insertions. The routes constructed with this scheme are relatively tighter. Less trucks would be employed with this strategy, but requiring more computation time to evaluate all possible candidates. Differently, First Feasible Strategy adopts the first feasible insertion to a task given. It takes less evaluation time but more trucks would be used in the solution generated.

When choosing the Insertion Selection Schemes, a trade-off between efficiency and effectiveness should be made. The key issue in the scheduling is that all tasks must be completed with the limited trucks. Thus, in EBIH, Greedy Strategy is adopted for mandatory tasks. This setting aims to guarantee the urgent tasks’ assignment first. On the other hand, to avoid long computation time, First Feasible Strategy is applied to the insertion of optional tasks. In addition, because the tasks with long service time are often too big to be inserted into the routes with existing tasks, the task with the longest service time will be selected as the first task in the newly created new route.

The performance of EBIH is tested on instances with diverse sizes and features. The test results are presented in Section 4.2.1.

3.3 A selective perturbation hyper-heuristic with two guidance indicators

To further reduce the operational cost of the company, based on the initial solution generated by EBIH, an improvement Hyper-Heuristic with Two Guidance Indicators (GIHH) is developed. GIHH is a Selection Perturbation Hyper-Heuristic, which selects perturbative low level heuristics (LLH) adaptively based on the changes of a problem scenario. Two guidance indicators are proposed to guide the selection of LLH. Considering the large scale and complex multi-level solution structure in MS-VRPTW, only one solution is updated in each algorithm iteration (single solution-based).

3.3.1 High-level heuristic

figure e
$$ Pr_{i}=\frac{weight_{i}}{\sum\limits_{j\in H}weight_{j}} \quad \qquad \qquad \qquad \qquad \forall i \in H $$
(22)

Algorithm 1 introduces the high level framework of GIHH. The input contains an initial feasible solution, a set of given LLH (H, introduced in Section 3.3.3) and the stopping criterion. To this bi-objective problem, GIHH is a Pareto Method whose output is a solution archive (ARCH) consisting of non-dominated solutions. The small range of DP reduces the diversity of DP, leading to a relatively small number of non-dominated solutions. Thus, no limit is set to the size of ARCH, which means all non-dominated solutions found will be stored. In addition, to increase the diversification of the search, different solutions with the same objective values are stored in ARCH.

In each iteration, one LLH is chosen and applied to a chosen solution (Sc), generating an updated solution. During the loop, to diversify the search, Sc is randomly selected from ARCH in Step 2.1. The stopping criterion is set as when ARCH is not being updated in a predefined number (N O N I M P) of iterations.

In GIHH, three scalars (W eight, S core A and S core B) are defined to guide the selection of LLH, generating better problem solutions. The LLH executed in an iteration is chosen with the Roulette Wheel Rule (Step 2.2). To avoid the probabilities of LLH converging to zero and the corresponding LLH never being called at all, a minimal probability limit of 5% is applied to every LLH. S core A and S core B are two guidance indicators, which record the performance of LLH in previous search history from two different aspects respectively. W eight is updated based on S core A and S core B. All these three scalars are adjusted adaptively during search (in Steps 2.3 and 2.4), details in Section 3.3.2.

Because the ranges of the two objectives in MS-VRPTW are significantly different, that is, the range of DP is remarkably smaller than that of TD, a small change on DP is usually accompanied by a great fluctuation on TD in a solution. To further investigate this issue, in addition to the Hill Climbing acceptance criteria, a Record-to-Record Travel (RRT) [52] acceptance criterion is also implemented in our study. RRT accepts the worst solutions (S′) of deteriorated quality from the current solution (Sc) in a predefined range. The comparison of experiment results are presented in Section 4.2.3.

3.3.2 Guidance indicators and weight adjustment scheme

ScoreAi stores the accumulated rewards to hi according to the change of objective values from Sc to S′, recording the performance of hi on improving solution quality. In each iteration, if S′ is acceptable, reward 1 is added to ScoreAi, otherwise no reward is added. Therefore, a larger ScoreAi represents a greater contribution of hi to generating new non-dominated solutions. This indicator emphasizes LLH’s contribution on solution quality improvement.

ScoreBi is a specially designed indicator for this bi-objective problem, which indicates which objective hi inclines to improve (improvement direction). In MS-VRPTW, a Pareto Solution Set with uniform distribution and good convergence on the Pareto Front is expected, instead of the solutions within local regions. During the search, the improvement on both of the two objectives is pursued. When updating ScoreBi, the objective values of Sc and S′ are compared. If S′ is better than Sc on DP, ScoreBi is increased by one; If S′ is better than Sc on TD, ScoreBi is decreased by one. A positive ScoreBi, thus, means the inclination of improving DP (generated more improved solutions on DP) to hi, while a negative one indicates that of improving TD.

Weighti is updated once in every SEG iterations (called a Segment) to avoid over-fitting. It is adjusted according to the feedback from the search history (Score Ai and Score Bi). The update is a two-phase procedure. The first phase is guided by Score Ai, see Eq. 23.

$$ weigh{t_{i}^{t}}=\alpha\cdot weight_{i}^{t-1}+\beta\cdot \frac{ScoreA_{i}}{Applied\ Times\ o\!f\ h_{i}} $$
(23)

In the second update phase, to find the improvement DEVIATION by Eq. (24) between the two objectives, the newly generated non-dominated solutions are compared with the first Sc in the last Segment, obtaining the number of the non-dominated solutions with improved DP (D P_I M P) and that of improved TD (T D_I M P). If DP was improved more times in the last Segment (D E V I A T I O N > 0), then the weighti of those LLH with TD inclination should be increased by using Eq. 25, obtaining a higher probability being selected in the current Segment. The similar operations are made when D E V I A T I O N < 0. This procedure aims to balance the improvement direction.

$$ DEVIATION = \frac{\mathit{DP\_IMP-TD\_IMP}}{\mathit{(DP\_IMP+TD\_IMP})\cdot0.5} $$
(24)
$$\begin{array}{@{}rcl@{}} weigh{t_{i}^{t}} \ += \gamma\cdot \frac{\mathit{ScoreB}_{i}}{\mathit{Applied}\ \mathit{Times}\ \mathit{of}\ h_{i}} \cdot \mathit{DEVIATION} \\ \mathit{when}\ (\mathit{DEVIATION} <0\ \mathit{And}\ \mathit{ScoreB}_{i}<0)\\ \ \mathit{Or}\ (\mathit{DEVIATION} >0\ \mathit{And}\ \mathit{ScoreB}_{i}>0) \end{array} $$
(25)

The three coefficients (α, β, γ) in Eqs. 23 and 25 determine the response speed to the search feedback and the influence of each guidance component on updating weighti, subject to α + β + γ = 1.

3.3.3 Low-level heuristics

Five LLH are adopted in GIHH. Each LLH changes the current solution to a certain extent, obtaining updated solutions. Heuristics with large changes perturb the operated solution dramatically. They increase the search diversity and avoid trapping to local optimum, but longer computation time is needed usually to produce a new feasible solution. Heuristics with small changes use relatively less computation time in each iteration, however, their common deficits are easily to stuck to local optimum and premature search. Previous research shows that properly combining heuristics can improve the performance of search [53].

  • Inter-Route 2-opt*. Lin [54] proposes the λ-opt route improvement heuristic which removes and reconnects λ edges in a route. This classic heuristic brings relatively small changes to a solution, obtaining good results in various VRPs. Potvin and Rousseau [31] develop an improved 2-opt heuristic (2-Opt*) which keeps the direction of each route segment during reconnection. This heuristic is devised for Traveling Salesman Problem at first, but shows excellent performance in various routing problems with time windows. In GIHH, Inter-Route 2-Opt* removes two edges from different routes and reconnects them while keeping the directions of associated route segments. Notice that the edges modified can be the starting or ending points of routes, which means two routes being connected into one route is possible.

  • Inter-Route CROSS-exchange. Taillard et al. [32] propose CROSS-exchange which swaps two route segments from two different routes while keeping their directions. This heuristic brings relatively small perturbation as well. The length of a route segment can be zero, e.g. when one of the two operated route segments is empty, the execution of Inter-Route CROSS-exchange actually relocates a route segment from one route to another route.

  • Intra-Route CROSS-exchange. In this heuristic, the swapping strategy of CROSS-exchange is applied to one single route.

  • Large Neighbourhood Search (LNS). In GIHH, Random Selection is used in the Destroy heuristic of LNS to remove q randomly chosen tasks. Then the removed tasks are reinserted into the destroyed solution using a greedy Repair heuristic. This heuristic always executes the insertion causing the least increase on the travel distance. Obviously, comparing all possible insertion positions for all the q tasks is time-consuming. To balance the solution quality and the computation time, the value of q is defined as min{5% ⋅ n, 10}, where n is the total number of tasks.

  • Guided Ejection Search (GES). To further reduce the number of trucks used and optimize DP, GES is employed in GIHH. The main ideas of GES have been summarized in Section 1.2. Using LNS and GES obtains larger change to solutions and greater perturbation in search, at the cost of longer execution time.

4 Experiments & analysis

4.1 Benchmark dateset

To evaluate the proposed algorithms in different scenarios, a benchmark of 24 instances with various features are generated (available at http://www.cs.nott.ac.uk/~pszrq/benchmarks.htm). The instances are extracted from the company’s historical dataset. In these instances, each item represents a commodity, which consists of its commodity ID, source terminal, destination terminal, available time to transport, deadline of completing the tasks, and the number of containers in this commodity. Notice that the number of containers in a commodity can be larger than one, meaning finishing one commodity transportation may need to complete multiple transport tasks.

A categorization scheme similar to [55] is adopted to define the features of the instances. Firstly, to a LDT, if its time window is smaller than 20 hours, it will be classified as an emergent task. The time window for SDT is smaller than 10 hours. These two values are suggested by the port company’s coordinator. In addition, index B (26) is used to measure the total throughput balance at terminals in each instance.

$$ B=\frac{1}{|V|}\sum\limits_{i\in V}|I_{i}-O_{i}| $$
(26)

Here, V is the set of terminals, is composed of the harbors and dry ports. Ii and Oi respectively represent the number of incoming and outgoing tasks at terminal i. A smaller B represents a more balanced throughput in the instance. Based on these, four types of features are used to create the benchmark instances.

  • Tight instance: 70%-80% tasks in the instance are emergent.

  • Loose instance: less than 30% tasks in the instance are emergent.

  • Balanced instance: the value of B in the instance is smaller than 30.

  • Unbalanced instance: the value of B in the instance is larger than or equal to 30.

According to the time of receiving transhipment requests before their deadlines in practice, two types of scheduling horizons (two and four days) are set for the instances. Based on this setting, we created in total eight combinations of features. They represent a comprehensive dataset of instances with various commodity emergencies and workload balance. For each combination, three instances are generated in sizes of small, medium and large, respectively. The details of instances are presented in Table 2. The last column provides the total loaded travel distances which are fixed in instances. These instances are generated based on the problem characteristics at Ningbo Port, e.g. the geographical distribution of the terminals and the lengths of shifts, and can be used as a set of benchmark instances with diverse features for testing the solution methods of other MS-VRPTWs.

Table 2 Features of the benchmark instances
Full size table

4.2 Comparison experiments

4.2.1 Initial solutions

Table 3 presents the initial solutions produced by EBIH, obtained on a PC with i7-3820 3.60GHz CPU and 16.0 GB memory. Feasible solutions can be obtained within an acceptable time for all instances. The computation time of generating a solution grows rapidly along with the number of tasks in the instance. The highest requirement of truck happens on instance TU2-3, where 71 one-driver trucks and 171 double-driver trucks are used.

Table 3 Initial solutions produced by EBIH
Full size table

4.2.2 Parameter setting and complexity discussion

GIHH adaptively employs LLH according to the search, with relatively few parameters to set. The parameters are tuned one by one, while the others are fixed.

In Eqs. 23 and 25, a large α means a low response speed to the change in the search space, often leading to slow convergence. However, high-quality solutions may be skipped over when the response speed is too high. On the other hand, high response speed usually leads to premature convergence. Our preliminary experiments show that, the setting of α = 0.5 makes a good trade-off between convergence speed and solution quality. The values of β and γ determine the influence of the two guidance indicators to update weighti. The setting of β = 0.4, γ = 0.1 is adopted based on preliminary experiments, indicating that ScoreA has a greater influence than ScoreB in GIHH.

When updating weighti, a smaller SEG would change weighti more frequently, when SEG is too large, the feedbacks cannot change in time. SEG is set to 80 in GIHH empirically. In addition, NONIMP = 150 is used as the stopping criterion to strike a balance between the computation time and the quality of results.

When assessing the computational complexity of metaheuristics and hyper-heuristics, time complexity cannot be determined since these approximate algorithms do not guarantee finding the global optimal solution within a given time limit. Whether or not the algorithm procedure would terminate depends on the applied problem and specific definition of its stopping criterion (e.g. the definition of NONIMP in GIHH). Therefore, the CPU time and objective function evaluations on benchmark are often used to compare the computational complexity of approximate methods in research. In this study, the algorithms with the above parameter setting are compared from the aspects of computational time and iterations at high level, and the results and associated analysis are presented in the next subsection. As only one solution is updated in each iteration, with the task node-based solution representation, the space complexity of GIHH is O(K ⋅|S|⋅ n), where K is the fleet size, |S| is the length of the planning horizon and n is the number of tasks to be assigned.

4.2.3 Comparison experiment results and analysis

Impacts of the guidance indicators

To evaluate the influence of the two proposed guidance indicators in GIHH, two variants (GIHH-A and RHH) of GIHH with different guidance indicator settings are developed for comparison. In GIHH-A, only ScoreA is adopted, while in RHH, LLH are randomly chosen without any guidance. Our preliminary experiments show that increasing the computation time does not improve the results significantly, so all the three algorithms use the same stopping criterion.

Table 4 presents the comparison of GIHH, GIHH-A and RHH. All the results are obtained in 20 runs. In the literature, to compare the performance of Pareto Methods, various quality indicators are proposed. Most of them focus on the comparison on the Pareto Set approximation [56]. One of the most widely used indicators is Hyper-Volume, which considers the convergence, uniformity and spread over the Pareto Front produced. Previous studies have shown that a Pareto Set with a larger hyper-volume is likely to have a better trade-off among multiple objectives [57]. To compare the three algorithm variants, the hyper-volumes of the ARCH s obtained are calculated and presented in Table 4. In our study, the reference points used in calculating hyper-volume are the initial feasible solutions generated by EBIH. It can be found that, comparing the three algorithms from multiple aspects, most of the best results are produced by GIHH.

Table 4 Results comparison among algorithms with different indicator configurations
Full size table

Among the three variants, RHH produced the worst hyper-volumes with the most iterations, while its standard deviation obtained is the largest. This shows that, when the High-Level Heuristic is random selection with no guidance, the algorithm would take more iterations to converge with a lower stability. However, it may have a higher probability of finding better solutions against objective (2), i.e. with the best DP.

It can be found that from Table 4, GIHH-A and GIHH obtained remarkably better solutions (higher HV) than RHH. Using ScoreA significantly improves the quality of the produced solution set. Generally, GIHH-A and GIHH used less iterations but longer computation time to obtain the output. This can be observed in Fig. 3. GIHH-A and GIHH may have less average iterations than RHH (blue columns), but their computation time (red crosses) are longer on all the eight sample instances. Because the unit computation time of LNS and GES are significantly longer than the other LLH, this observation indicates that, compared to RHH, GIHH-A and GIHH employed these two LLH with greater perturbation more frequently during the search.

Fig. 3
figure 3

The iteration times and computation time of the three algorithms on eight sample instances

Full size image

Between GIHH-A and GIHH, the latter obtained a higher average and the best hyper-volume on most instances with the guidance of ScoreB, while no obvious increase on iteration time and computation time is found. This can also be observed from Fig. 3. GIHH promotes the overall search performance and stability with the help of the two proposed guidance indicators.

With regard to the features of instances, Loose instances have broader time windows than Tight instances, which means more scheduling options and larger solution space. Thus, when the sizes of instances are similar, the Loose instances require more iterations and computation time to converge in all the three algorithms. In addition, comparing the iteration time, GIHH-A and GIHH work better on Loose instances, see Fig. 4. It can be found that, compared to RHH, the reduction of iterations is higher on Loose instances than on Tight instances, except GIHH on the LB4 instances. When the feature of throughput imbalance at terminals changes, no obvious difference is found.

Fig. 4
figure 4

Comparison of the iteration time reduction. The bars indicate the number of reduction of iterations. Longer bars represent greater reduction, while the negative values indicate more iterations than RHH

Full size image

Note that, in the ARCH generated by GIHH, each non-dominated point on the Pareto Front may have 20-40 different solutions on average. The number of different solutions with the same objectives stored does not affect the value of hyper-volume. Experiment results show that storing different solutions with the same objective values does not significantly increase the hyper-volume of a solution archive, but it boosts the diversification of the solution set. Those solutions provide the logistic company coordinator more reference solutions.

Impacts of solution selection and acceptance criterion

In each iteration of GIHH, the solution to be operated (Sc) is randomly selected from ARCH, aiming to increase the diversity in search. To justify the function of the random selection scheme, an algorithm with deterministic selection of Sc (named GIHH-D) is also implemented in our research. With this deterministic scheme, in ARCH, the solution farthest from the reference point will be selected as Sc. Because all solutions are derived from the initial solution (reference point), this deterministic scheme means that the solution with the highest improvement on both objectives will be selected. T-test is conducted on the output of GIHH and GIHH-D. The results are presented in Table 5.

In addition, as mentioned in Section 3.3.1, another variant adopting the Record-to-Record Travel acceptance criterion (GIHH-RRT) is also compared with GIHH. In GIHH-RRT, comparing to Sc, a worse solution would be accepted as long as the deterioration of objective value is less than 0.01 ⋅ TD(Sc) on TD and less than 1.5 on DP. Acceptance criterion in a perturbative algorithm should balance the diversification and intensification of search, while RRT can increase the diversification of search greatly. Its output is compared with that of Hill Climbing criterion presented in Table 5.

Table 5 T-test results with GIHH. Y means GIHH generates significantly better solutions, while N represents it does not
Full size table

From Table 5, it can be found that GIHH outperforms the other two algorithms. On the one hand, using the deterministic scheme to select the solution to be updated (GIHH-D) decreases the diversity of search, leading to significantly worse output than GIHH on most instances (19/24). On the other hand, accepting worse solutions (GIHH-RRT) does not improve the final search result on all instances. As the two objectives have remarkably different ranges, accepting worse solutions would bring great fluctuation and deterioration to Sc in the search. This observation indicates that, in MOVRP, when the difference in the ranges of objectives is big, accepting solutions of lower quality does not improve the search. Besides, our experiments also show that GIHH is more stable than the other two algorithms with smaller standard deviations.

Comparison with the state-of-the-art algorithms

MS-VRPTW is a newly introduced model in the literature, there is thus no existing algorithm applied to it yet. Three state-of-the-art algorithms (RVNS [58], FVNS [59] and ALNS [60, 61]) are adopted and applied to MS-VRPTW in our study. Both RVNS and FVNS use the Variable Neighbourhood Search framework and produce the best solutions in PVRP. Apart from the neighbourhood structures used, a main difference between them is that the order of shaking operators employed is fixed in FVNS, while they are randomly selected in RVNS. ALNS produces the best results for VRPPD with Adaptive Large Neighbourhood Search. The experiments show that GIHH outperforms the three algorithms on both solution quality and computation time in MS-VPRTW, especially on larger instances. Their result deterioration is presented in Table 6.

Table 6 Solution deterioration comparing with the results of GIHH
Full size table

Possible causes for these results include the following. Firstly, the neighbourhood structure employed in GIHH are highly effective. FVNS and RVNS only use the small perturbation neighbourhood operators (e.g. λ-opt, CROSS, relocation). With these smaller neighborhood structures, it is hard or needs a long time to escape from the local optimum in this nonlinear constrained problem. On average, 65% more computation time is required by FVNS and RVNS comparing to GIHH. Large perturbation operators are used in ALNS but are lacking of intensive exploitation. Secondly, without the guidance of specific indicators, e.g. ScoreB, the solutions generated are more likely to cluster, leading to a low hyper-volume. In addition, the three algorithms compared are problem specific metaheuristics. Different from hyper-heuristics, their performance may decline drastically for different instances even in the same problem. For example, both FVNS and ALNS obtain better results than GIHH on LU2 instances.

An observation from the results of FVNS and RVNS is that, they both produce many more solutions with the same objective values than GIHH. The small perturbation operators tend to generate a large number of solutions with small differences but of the same objective values in the solution archive. Comparing VNS and RVNS, the former performs better in MS-VRPTW with a fixed order of the neighbourhood operators of low perturbation to high perturbation. ALNS outperforms VNS and RVNS on the objective DP with the help of large perturbation, while has a higher stability than GIHH.

Results on VRPTW benchmarks

To evaluate its performance in other problems, GIHH is applied to classic VRPTW on the Solomon Benchmarks [2]. The VRPTW is the basis of many other complex VRPs, while the Solomon Benchmarks have been extended and adopted in the research of many other VRP variants as well. An equal priority is given to the two objectives, the number of vehicles used (NV) and the total travel distance (TD), in the VPRTW model of our study. The results obtained are compared with the best known solutions to date, see Table 7 in Appendix. It can be found that, GIHH obtains solutions the same as or close to the best known solutions (which are optimal actually) on the instances with clustered customers (C1 and C2). On the randomly and mixed distributed instances (R1, R2 and RC1, RC2), GIHH produces solutions close to the best known ones, and nine new non-dominated solutions are found. Considering that most of those best known solutions are generated by customized problem-specific algorithms with sufficient computation resources, the results of GIHH are satisfying.

5 Conclusions

This study defines a new bi-objective Mixed-Shift Vehicle Routing Problem with Time Windows (MS-VRPTW), which arises from a real-life container transportation problem between short-distance and long-distance terminals. Due to the big difference between the completion time of the transportation tasks, two types of shifts (long-shift and short-shift) with different operational costs are defined in this problem. The two objectives of this problem are minimizing the total driver payment and minimizing the total travel distance. A mathematical model of MS-VRPTW is proposed in this paper.

Using the proposed artificial node, the scheduling of two types of shifts is combined into one model. To the best of our knowledge, this is the first mixed-shift VRP model in the literature. Our investigation shows that it is unrealistic to tackle MS-VRPTW with exact search approaches even if a huge amount of computation resources is given. A hyper-heuristic is thus developed for MS-VRPTW. The proposed method showed to increase the utilization rate of trucks and reduce the operational cost of the logistic company.

In the proposed method, firstly, an initial feasible solution is generated using an Emergency Level-Based Insertion Construction Heuristic (EBIH). Then, a Hyper-Heuristic with two Guidance Indicators (GIHH) is proposed to improve the solutions. GIHH is a selection perturbation hyper-heuristic, adapting a set of Low-Level Heuristics (LLH) with different extents of perturbation to the problem solution. Two indicators are proposed to guide the LLH selection adaptively along with changes during the search, which evaluate LLH’s contribution to the solution quality improvement and the improvement direction, respectively.

To test the generality and performance of the proposed algorithms, a set of diverse benchmark problem instances is created based on a dataset derived from the real-world problem, considering the features of commodity emergency and workload balance. On all the benchmark instances, EBIH produced feasible solutions within an acceptable time. The experiment results show that, in different environments, the two proposed guidance indicators significantly improve the performance and stability of search for this bi-objective problem, producing solutions with higher hyper-volumes. In terms of the acceptance criterion and the selection scheme of solution, it is shown that, when the ranges of objectives are vastly different in the Multi-Objective Vehicle Routing Problem, the Hill Climbing acceptance criterion outperforms the acceptance criterion of accepting worse solutions (Record-to-Record Travel). Research also finds that randomly selecting the next current solution can increase the diversity of search, bringing better results than deterministic selection in MS-VRPTW. GIHH outperforms three state-of-the-art algorithms for PVRP and VRPPD on both the computation time and the quality of solutions generated. Comparing to the best known solutions to date, GIHH also produces promising results in the classic VRPTW.

In our future work, the MS-VRPTW model could be extended to other mixed-shift problems. The proposed algorithms can be applied to more practical complicated multi-objective optimization problems. Hybrid methodologies combining GIHH and exact methods can be another promising research direction.