Model and algorithm of quantum-inspired neural network with sequence input based on controlled rotation gates

Abstract

To enhance the approximation and generalization ability of classical artificial neural network (ANN) by employing the principles of quantum computation, a quantum-inspired neuron based on controlled-rotation gate is proposed. In the proposed model, the discrete sequence input is represented by the qubits, which, as the control qubits of the controlled-rotation gate after being rotated by the quantum rotation gates, control the target qubit for rotation. The model output is described by the probability amplitude of state |1〉 in the target qubit. Then a quantum-inspired neural network with sequence input (QNNSI) is designed by employing the quantum-inspired neurons to the hidden layer and the classical neurons to the output layer. An algorithm of QNNSI is derived by employing the Levenberg–Marquardt algorithm. Experimental results of some benchmark problems show that, under a certain condition, the QNNSI is obviously superior to the ANN.

1 Introduction

Over the last few decades, many researchers and publications have been dedicated to improve the performance of neural networks. Useful models to enhance the approximation and generalization abilities include: local linear radial basis function neural networks, which replaced the connection weights of conventional radial basis function neural networks by a local linear model [1]; selective neural networks ensemble with negative correlation, which employed the hierarchical pair competition-based parallel genetic algorithm to train the neural networks forming the ensemble [2]; polynomial based radial basis function neural networks [3]; hybrid wavelet neural networks, which employed rough set theory to help in decreasing the computational effort needed for building the networks structure [4]; simultaneous optimization of artificial neural networks, which employed GA to optimize multiple architectural factors and feature transformations of ANN to relieve the limitations of the conventional back propagation algorithm [5].

Many neurophysiological experiments indicate that the information processing character of the biological nerve system mainly includes the following eight aspects: the spatial aggregation, the multi-factor aggregation, the temporal cumulative effect, the activation threshold characteristic, self-adaptability, exciting and restraining characteristics, delay characteristics, conduction and output characteristics [6]. From the definition of the M–P neuron model, classical ANN preferably simulates voluminous biological neurons’ characteristics such as the spatial weight aggregation, self-adaptability, conduction and output, but it does not fully incorporate temporal cumulative effect because the outputs of ANN depend only on the inputs at the moment regardless of the prior moment. In the process of practical information processing, the memory and output of the biological neuron not only depend on the spatial aggregation of each input information, but also are related to the temporal cumulative effect. Although the ANNs in Refs. [7–10] can process temporal sequences and simulates delay characteristics of biological neurons; in these models, the temporal cumulative effect has not been fully reflected. Traditional ANN can only simulate point-to-point mapping between the input space and output space. A single sample can be described as a vector in the input space and output space. However, the temporal cumulative effect denotes that multiple points in the input space are mapped to a point in the output space. A single input sample can be described as a matrix in the input space, and a single output sample is still described as a vector in the output space. In this case, we claim that the network has a sequence input.

Since Kak [11] firstly proposed the concept of quantum-inspired neural computation in 1995, quantum neural network (QNN) has attracted a great attention by the international scholars during the past decade, and a large number of novel techniques have been studied for quantum computation and neural network. For example, Purushothaman et al. [12] proposed the model of quantum neural network with multilevel hidden neurons based on the superposition of quantum states in the quantum theory. In Ref. [13], an attempt was made to reconcile the linear reversible structure of quantum evolution with nonlinear irreversible dynamics of neural network. Michiharu et al. [14] presented a novel learning model with qubit neuron according to quantum circuit for XOR problem and describes the influence to learning by reducing the number of neurons. In Ref. [15], a new mathematical model of quantum neural network was defined, building on Deutsch’s model of quantum computational network, which provides an approach for building scalable parallel computers. Fariel Shafee [16] proposed the neural network with the quantum gated nodes, and indicates that such quantum network may contain more advantageous features from the biological systems than the regular electronic devices. In our previous work [17], we proposed a quantum BP neural network model with learning algorithm based on the single-qubit rotation gates and two-qubits controlled-rotation gates. In Ref. [18], we proposed a neural network model with quantum gated nodes and a smart algorithm for it, which shows superior performance in comparison with a standard error back propagation network. Adenilton et al. [19] proposed a weightless model based on quantum circuit. It is not only quantum-inspired but is actually a quantum NN. This model is based on Grover’s search algorithm, and it can perform both quantum learning and simulate the classical models. However, all the above QNN models, like M–P neurons, it also does not fully incorporate temporal cumulative effect because a single input sample is either irrelative to time or relative to a moment instead of a period of time.

In this paper, in order to fully simulate biological neuronal information processing mechanisms and to enhance the approximation and generalization ability of ANN, we proposed a qubit neural network model with sequence input based on controlled-rotation gates, called QNNSI. It’s worth pointing out that an important issue is how to define, configure and optimize artificial neural networks. Refs. [20, 21] make a deep research into this question. After repeated experiments, we opt to use a three-layer model with a hidden layer, which employs the Levenberg–Marquardt algorithm for learning. Under the premise of considering approximation ability and computational efficiency, this option is a relatively ideal. The proposed approach is utilized to predict the year mean of sunspot number, and the experimental results indicate that, under a certain condition, the QNNSI is obviously superior to the common ANN.

2 The qubit and quantum gate

2.1 Qubit

What is a qubit? Just as a classical bit has a state-either 0 or 1—a qubit also has a state. Two possible states for a qubit are the state |0〉 and |1〉, which as you might guess correspond to the states 0 and 1 for a classical bit. Notation like | 〉 is called the Dirac notation, and we will see it often in the following paragraphs, as it is the standard notation for states in quantum mechanics. The difference between bits and qubits is that a qubit can be in a state other than |0〉 or |1〉. It is also possible to form linear combinations of states, often called superposition

(1)

where 0≤θ≤π, 0≤ϕ≤2π.

Therefore, unlike the classical bit, which can only be set equal to 0 or 1, the qubit resides in a vector space parametrized by the continuous variables θ and ϕ. Thus, a continuum of states is allowed. The Bloch sphere representation is useful in thinking about qubits since it provides a geometric picture of the qubit and of the transformations that one can operate on the state of a qubit. Owing to the normalization condition, the qubit’s state can be represented by a point on a sphere of unit radius, called the Bloch Sphere. This sphere can be embedded in a three-dimensional space of Cartesian coordinates (x=cosϕsinθ, y=sinϕsinθ, z=cosθ). By definition, a Bloch vector is a vector whose components (x,y,z) single out a point on the Bloch sphere. We can say that the angles θ and ϕ define a Bloch vector, as shown in Fig. 1(a), where the points corresponding to the following states are shown: $|A\rangle=[1,0]^{\rm T}$, $|B\rangle=[0,1]^{\rm T}$, $|C\rangle=|E\rangle=[\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}]^{\rm T}$, $|D\rangle=[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^{\rm T}$, $|F\rangle=[\frac{1}{\sqrt{2}},-\frac{{\rm i}}{\sqrt{2}}]^{\rm T}$, $|G\rangle=[\frac{1}{\sqrt{2}},\frac{{\rm i}}{\sqrt{2}}]^{\rm T}$. For convenience, in this paper, we represent the qubit’s state by a point on a circle of unit radius as shown in Fig. 1(b). The corresponding relations between Figs. 1(a) and 1(b) can be written as

(2)

At this time, any state of the qubit may be written as

(3)

Fig. 1

A qubit description

A n qubits system has 2ⁿ computational basis states. For example, a 2 qubits system has basis |00〉, |01〉, |10〉, |11〉. Similar to the case of a single qubit, the n qubits system may form the superpositions of 2ⁿ basis states

$$ |\phi\rangle=\sum_{x\in \{0,1\}^n}a_x|x \rangle, $$

(4)

where a _x is called probability amplitude of the basis states |x〉, and {0,1}ⁿ means the set of strings of length two with each letter being either zero or one. The condition that these probabilities can sum to one is expressed by the normalization condition

$$ \sum_{x\in \{0,1\}^n}|a_x|^2=1. $$

(5)

2.2 Quantum rotation gate

In the quantum computation, the logic function can be realized by applying a series of unitary transform to the qubit states, which the effect of the unitary transform is equal to that of the logic gate. Therefore, the quantum services with the logic transformations in a certain interval are called the quantum gates, which are the basis of performing quantum computation.

The definition of a single qubit rotation gate is written as

$$ R(\theta)=\left [ \begin{array}{c@{\quad}c} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{array} \right ]. $$

(6)

Let the quantum state , then |ϕ〉 can be transformed by R(θ) as follows

$$ R(\theta)|\phi\rangle=\left [ \begin{array}{c} \cos(\theta_0+\theta)\\ \sin(\theta_0+\theta) \end{array} \right ]. $$

(7)

It is obvious that R(θ) shifts the phase of |ϕ〉.

2.3 Unitary operators and tensor products

A matrix U is said to be unitary if (U ^∗)^T U=I, where the ∗ indicates complex conjugation, and T indicates the transpose operation, I indicates the unit matrix. Similarly an operator U is unitary if (U ^∗)^T U=I. It is easily checked that an operator is unitary if and only if each of its matrix representations is unitary.

The tensor product is a way of putting vector spaces together to form larger vector spaces. This construction is crucial to understanding the quantum mechanics of multi-particle system. Suppose V and W are vector spaces of dimension m and n respectively. For convenience we also suppose the V and W are Hilbert spaces. Then V⊗W (read ‘V tensor W’) is an mn dimensional vector space. The elements of V⊗W are linear combinations of ‘tensor products’ |v〉⊗|w〉 of elements |v〉 of V and |w〉 of W. In particular, if |i〉 and |j〉 are orthonormal bases for the spaces V and W then |i〉⊗|j〉 is a basis for V⊗W. We often use the abbreviated notations |v〉|w〉, |v,w〉 or even |vw〉 for the tensor product |v〉⊗|w〉. For example, if V is a two-dimensional vector space with basis vectors |0〉 and |1〉 then |0〉⊗|0〉 and |1〉⊗|1〉 is an element of V⊗V.

2.4 Multi-qubits controlled-rotation gate

In a true quantum system, a single qubit state is often affected by a joint control of multi-qubits. A multi-qubits controlled-rotation gate C ⁿ(R) is a kind of control model. The multi-qubits system is also described by the wave function |x ₁ x ₂⋯x _n 〉. In a (n+1)-bits quantum system, when the target bit is simultaneously controlled by n input bits, the input/output relationship of the system can be described by multi-qubits controlled-rotation gate in Fig. 2.

Fig. 2

Multi-qubits controlled-rotation gate

In Fig. 2(a), suppose we have n+1 qubits, and then we define the controlled operation C ⁿ(R) as follows

(8)

where x ₁ x ₂⋯x _n in the exponent of R means the product of the bits x ₁,x ₂,…,x _n . That is, the operator R is applied to last a qubit if the first n qubits are all equal to one; otherwise, nothing is done.

Suppose that the |x _i 〉=cos(θ _i )|0〉+sin(θ _i )|1〉 are the control qubits, and the |ϕ〉=cos(φ)|0〉+sin(φ)|1〉 is the target qubit. From Eq. (8), the output of C ⁿ(R) is written by equation

(9)

We say that a state of a composite system having the property that it can’t be written as a product of states of its component systems is an entangled state. For reasons which nobody fully understands, entangled states play a crucial role in quantum computation and quantum information. It is observed from Eq. (9) that the output of C ⁿ(R) is in the entangled state of n+1 qubits, and the probability of the target qubit state |ϕ′〉, in which |1〉 is observed, equals to

$$ P=\prod_{i=1}^{n} \sin^{2}(\theta_i) \bigl(\sin^{2}(\varphi+ \overline{\varphi})-\sin^{2}(\varphi)\bigr)+\sin^{2}( \varphi). $$

(10)

In Fig. 2(b), the operator R is applied to last a qubit if the first n qubits are all equal to zero, and otherwise, nothing is done. The controlled operation C ⁿ(R) can be defined by the equation

$$ C^n(R)|x_1x_2\cdots x_n\rangle|\phi\rangle=|x_1x_2\cdots x_n\rangle R^{\overline{x_1+\cdots+x_n}}|\phi\rangle. $$

(11)

By a similar analysis with Fig. 2(a), the probability of the target qubit state |ϕ′〉, in which |1〉 is observed, equals to

$$ P=\prod_{i=1}^{n} \cos^{2}(\theta_i) \bigl(\sin^{2}(\varphi+ \overline{\varphi})-\sin^{2}(\varphi)\bigr)+\sin^{2}( \varphi). $$

(12)

At this time, after the joint control of the n input bits, the target bit |ϕ′〉 can be defined as follows

$$ |\phi'\rangle=\sqrt{1-P}|0\rangle+\sqrt{P}|1\rangle. $$

(13)

3 The QNNSI model

3.1 The quantum-inspired neuron based on controlled-rotation gate

In this section, we first propose a quantum-inspired neuron model based on controlled-rotation gate, as shown in Fig. 3. This model consists of quantum rotation gates and multi-qubits controlled-rotation gate. The {|x _i (t _r )〉} defined in time domain interval [0,T] denote the input sequences, where $t_{r}\in[0, {\rm T}]$. The |y〉 denotes the spatial and temporal aggregation results in [0,T]. The output is the probability amplitude of |1〉 after measuring |y〉. The control parameters are the rotation angles $\overline{\theta}_{i}(t_{r})$, $\overline{\varphi}(t_{r})$, i=1,2,…,n, r=1,2,…,q, n denotes the number of input space dimension, q denotes the length of input sequence.

Fig. 3

The model of quantum-inspired neuron based on controlled rotation gate

Unlike classical neuron, each input sample of quantum-inspired neuron is described as a matrix instead of a vector. For example, a single input sample can be written as

$$ \left [ \begin{array}{c} \{|x_1(t_r)\rangle\}\\ \{|x_2(t_r)\rangle\}\\ \cdots\\ \{|x_n(t_r)\rangle\} \end{array} \right ]= \left [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} |x_{1}(t_{1})\rangle & |x_{1}(t_{2})\rangle & \cdots &|x_{1}(t_{q})\rangle\\ |x_{2}(t_{1})\rangle & |x_{2}(t_{2})\rangle & \cdots &|x_{2}(t_{q})\rangle\\ \cdots & \cdots & \cdots & \cdots\\ |x_{n}(t_{1})\rangle & |x_{n}(t_{2})\rangle & \cdots & |x_{n}(t_{q})\rangle \end{array} \right ]. $$

(14)

Suppose |x _i (t _r )〉=cosθ _i (t _r )|0〉+sinθ _i (t _r )|1〉, |ϕ(t ₁)〉=|0〉. Let

$$ \overline{h}_{r}= \left \{ \begin{array}{l@{\quad}l} \prod_{i=1}^{n}\sin(\theta_i(t_r)+\overline{\theta}_{i}(t_r)),& \mbox{for Fig.~3(a)},\\[5pt] \prod_{i=1}^{n}\cos(\theta_i(t_r)+\overline{\theta}_{i}(t_r)),& \mbox{for Fig.~3(b)} . \end{array} \right . $$

(15)

According to the definition of quantum rotation gate and multi-qubits controlled-rotation gate, the |ϕ′(t ₁)〉 is given by

$$ \bigl|\phi'(t_1)\bigr\rangle=\sqrt{1-\bigl( \overline{h}_{1}\sin\overline{\varphi}(t_1) \bigr)^2}|0\rangle+\overline{h}_{1}\sin\overline{ \varphi}(t_1)|1\rangle. $$

(16)

Let t=t _r , r=2,3,…,q, from |ϕ(t _r )〉=|ϕ′(t _r−1)〉, the aggregate results of quantum neuron in [0,T] is finally written as

$$ |y\rangle=\bigl|\phi'(t_q)\bigr\rangle=\cos \varphi(t_q)|0\rangle+\sin\varphi(t_q)|1\rangle, $$

(17)

where $\varphi(t_{q})=\arcsin(\{(\overline{h}_{q})^{2}(\sin^{2}(\varphi(t_{q-1})+\overline{\varphi}(t_{q})) - \sin^{2}(\varphi(t_{q-1})))+\sin^{2}(\varphi(t_{q-1}))\}^{1/2})$.

In this paper, we define the output of the quantum neuron as the probability amplitude of the corresponding state, in which |1〉 is observed. Let h(t _r ) denote the probability amplitude of the state |1〉 in |ϕ′(t _r )〉. Using some trigonometry, the output of the quantum neuron is rewritten as

$$ y=h(t_q)=\sqrt{(\overline{h}_{q})^2U_{q}+ \bigl(h(t_{q-1})\bigr)^2}, $$

(18)

where $U_{q}=h(t_{q-1})\sqrt{1-(h(t_{q-1}))^{2}}\sin(2\overline{\varphi}(t_{q})) + (1-2(h(t_{q-1}))^{2})\sin^{2}(\overline{\varphi}(t_{q}))$, $h(t_{1})=\overline{h}_{1}\sin(\overline{\varphi}(t_{1}))$.

3.2 The QNNSI model

In this paper, the QNNSI model is shown in Fig. 4, where the hidden layer consists of p quantum-inspired neurons based on controlled-rotation gate (Type I is employed for odd serial number, and type II is employed for even serial number), {|x ₁(t _r )〉},{|x ₂(t _r )〉},…,{|x _n (t _r )〉} denote the input sequences, h ₁,h ₂,…,h _p denote the hidden output, the activation function in hidden layer employs the Eq. (18), the output layer consists of m classical neurons, w _jk denote the connection weights in output layer, y ₁,y ₂,…,y _m denote the network output, and the activation function in output layer employs the Sigmoid function.

Fig. 4

The model of quantum-inspired neural network with sequence input based on controlled-rotation gate

For the lth sample, suppose $|x_{i}^{l}(t_{r})\rangle=\cos\theta_{i}^{l}(t_{r})|0\rangle+\sin\theta_{i}^{l}(t_{r})|1\rangle$, $0=t_{1}<t_{2}<\cdots<t_{q}={\rm T}$ denote the discrete sampling time points, set $|\phi_{j}^{l}(t_{1})\rangle=|0\rangle$, j=1,2,…,p. Let

$$ \overline{h}_{jr}^l=\left \{ \begin{array}{l@{\quad}l} \prod_{i=1}^{n}\sin(\theta_i^l(t_r)+\theta_{ij}(t_r)),& j=1,3,5,\ldots,\\[5pt] \prod_{i=1}^{n}\cos(\theta_i^l(t_r)+\theta_{ij}(t_r)),& j=2,4,6,\ldots. \end{array} \right . $$

(19)

According to the input/output relationship of quantum neuron, the output of the jth quantum neuron in hidden layer can be written as

$$ h_j^l=h_j^l(t_q)= \sqrt{\bigl(\overline{h}_{jq}^l \bigr)^2U_{jq}^l+\bigl(h_j^l(t_{q-1}) \bigr)^2}, $$

(20)

where $U_{jq}^{l}=h_{j}^{l}(t_{q-1})\sqrt{1-(h_{j}^{l}(t_{q-1}))^{2}}\sin(2\overline{\varphi}_{j}(t_{q}))+ (1-2(h_{j}^{l}(t_{q-1}))^{2})\sin^{2}(\overline{\varphi}_{j}(t_{q}))$, $h_{j}^{l}(t_{1})=\overline{h}_{j1}^{l}\sin(\overline{\varphi}(t_{1}))$.

The kth output in output layer can be written as

$$ y_k^l=\frac{1}{1+e^{-\sum_{j=1}^{p}w_{jk}h_{j}^l}}, $$

(21)

where i=1,2,…,n, j=1,2,…,p, k=1,2,…,m, l=1,2,…,L, L denotes the total number of samples.

4 The learning algorithm of QNNSI

4.1 The pretreatment of the input and output samples

Set the sampling time points $0=t_{1}<t_{2}<\cdots<t_{q}={\rm T}$. Suppose the lth sample in n-dimensional input space $\{\overline{X}^{l}(t_{r})\}=[\{\overline{x}_{1}^{l}(t_{r})\},\ldots,\{\overline{x}_{n}^{l}(t_{r})\}]^{\rm T}$, where r=1,2,…,q, l=1,2,…,L. Let

(22)

$$ \theta_{i}^l(t_r)= \left \{\begin{array}{l@{\quad}l} \frac{\overline{x}_i^l(t_r)-\operatorname{Min}_{i,r}}{\operatorname{Max}_{i,r}-\operatorname{Min}_{i,r}}\frac{\pi}{2},& \mbox{if } \operatorname{Max}_{i,r}>\operatorname{Min}_{i,r},\\[5pt] \frac{\pi}{2},& \mbox{if } \operatorname{Max}_{i,r}=\operatorname{Min}_{i,r}\neq0,\\[5pt] 0,& \mbox{if } \operatorname{Max}_{i,r}=\operatorname{Min}_{i,r}=0. \end{array} \right . $$

(23)

These samples can be converted into the quantum states as follows

$$ \bigl\{\bigl|X^l(t_r)\bigr\rangle\bigr\}=\bigl[\bigl \{\bigl|x_1^l(t_r)\bigr\rangle\bigr\},\bigl \{\bigl|x_2^l(t_r)\bigr\rangle\bigr\},\ldots,\bigl \{\bigl|x_n^l(t_r)\bigr\rangle\bigr\} \bigr]^{\rm T}, $$

(24)

where $|x_{i}^{l}(t_{r})\rangle=\cos(\theta_{i}^{l}(t_{r}))|0\rangle+\sin(\theta_{i}^{l}(t_{r}))|1\rangle$.

It is worth pointing out that although a n-qubit system has 2ⁿ computational basis states, this n-qubit system may form the superpositions of 2ⁿ basis states. Although the number of these superpositions is infinite, in our approach, the superposition can be uniquely determined by the method of converting input samples into quantum states. Hence, the difference between our approach and a single input, zero-hidden layer, and one neuron ANN output, where input=n nodes, is embodied in the following two aspects. (1) For the former, the input sample is a specific quantum superposition state, and for the latter, the input sample is a specific real value vector. (2) For the former, the activation functions are designed through quantum computing principle, and for the latter, the classical Sigmoid functions are used as the activation functions.

Similarly, suppose the lth output sample $\{\overline{Y}^{l}\}=[\{\overline{y}_{1}^{l}\},\allowbreak\{\overline{y}_{2}^{l}\},\ldots,\{\overline{y}_{m}^{l}\}]^{\rm T}$, where l=1,2,…,L. Let

$$ \left \{\begin{array}{l} \operatorname{Max}_{k}=\max(\overline{y}_k^1,\overline{y}_k^2,\ldots,\overline{y}_k^L),\\[5pt] \operatorname{Min}_{k}=\min(\overline{y}_k^1,\overline{y}_k^2,\ldots,\overline{y}_k^L), \end{array} \right . $$

(25)

then, these output samples can be normalized by the following equation

$$ \overline{y}_k^l=\left \{ \begin{array}{l@{\quad}l} \frac{\overline{y}_k^l-\operatorname{Min}_{k}}{\operatorname{Max}_{k}-\operatorname{Min}_{k}},& \mbox{if }\operatorname{Max}_{k}>\operatorname{Min}_{k},\\[5pt] 1,& \mbox{if } \operatorname{Max}_{k}=\operatorname{Min}_{k}\neq0,\\[5pt] 0,& \mbox{if } \operatorname{Max}_{k}=\operatorname{Min}_{k}=0, \end{array} \right . $$

(26)

where k=1,2,…,m.

4.2 The adjustment of QNNSI parameters

The adjustable parameters of QNNSI include: (1) the rotation angles of quantum rotation gates in hidden layer: θ _ij (t _r ) and $\overline{\varphi}_{j}(t_{r})$; (2) the connection weights in output layer: w _jk .

Because the number of parameters is greater and gradient calculation is more complicated, the standard gradient descent algorithm is not easy to converge. Hence we employ the Levenberg–Marquardt algorithm in Ref. [22] to adjust the QNNSI parameters. Suppose $\overline{y}_{1}^{l}, \overline{y}_{2}^{l}, \ldots, \overline{y}_{m}^{l}$ denote the normalized desired outputs of the lth sample, and $y_{1}^{l}, y_{2}^{l}, \ldots, y_{m}^{l}$ denote the corresponding actual outputs. The evaluation function is defined as follows

$$ E=\max_{1\leq1\leq L}\max_{1\leq k\leq m}\bigl|e_k^l\bigr|= \max_{1\leq l\leq L}\max_{1\leq k\leq m}\bigl|\overline{y}_k^l-y_k^l\bigr|. $$

(27)

Let ${\bf p}$ denote the parameter vector, ${\bf e}$ denote the error vector, and ${\bf J}$ denote the Jacobian matrix. ${\bf p}$, ${\bf e}$ and ${\bf J}$ are respectively defined as follows

(28)

(29)

$$ {\bf J}({\bf p})= \left [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \frac{\partial e_1^1}{\partial\theta_{1,1}(t_1)}&\cdots&\frac{\partial e_1^1}{\partial\theta_{n,p}(t_q)}&\frac{\partial e_1^1}{\partial \overline{\varphi}_1(t_1)}&\cdots&\frac{\partial e_1^1}{\partial \overline{\varphi}_p(t_q)}&\frac{\partial e_1^1}{\partial w_{1,1}}&\cdots&\frac{\partial e_1^1}{\partial w_{p,m}} \\ \vdots&\cdots&\vdots&\vdots&\cdots&\vdots&\vdots&\cdots&\vdots\\ \frac{\partial e_m^1}{\partial\theta_{1,1}(t_1)}&\cdots&\frac{\partial e_m^1}{\partial\theta_{n,p}(t_q)}&\frac{\partial e_m^1}{\partial \overline{\varphi}_1(t_1)}&\cdots&\frac{\partial e_m^1}{\partial \overline{\varphi}_p(t_q)}&\frac{\partial e_m^1}{\partial w_{1,1}}&\cdots&\frac{\partial e_m^1}{\partial w_{p,m}}\\ \frac{\partial e_1^2}{\partial\theta_{1,1}(t_1)}&\cdots&\frac{\partial e_1^2}{\partial\theta_{n,p}(t_q)}&\frac{\partial e_1^2}{\partial \overline{\varphi}_1(t_1)}&\cdots&\frac{\partial e_1^2}{\partial \overline{\varphi}_p(t_q)}&\frac{\partial e_1^2}{\partial w_{1,1}}&\cdots&\frac{\partial e_1^2}{\partial w_{p,m}}\\ \vdots&\cdots&\vdots&\vdots&\cdots&\vdots&\vdots&\cdots&\vdots\\ \frac{\partial e_m^2}{\partial\theta_{1,1}(t_1)}&\cdots&\frac{\partial e_m^2}{\partial\theta_{n,p}(t_q)}&\frac{\partial e_m^2}{\partial \overline{\varphi}_1(t_1)}&\cdots&\frac{\partial e_m^2}{\partial \overline{\varphi}_p(t_q)}&\frac{\partial e_m^2}{\partial w_{1,1}}&\cdots&\frac{\partial e_m^2}{\partial w_{p,m}}\\ \vdots&\cdots&\vdots&\vdots&\cdots&\vdots&\vdots&\cdots&\vdots\\ \frac{\partial e_1^L}{\partial\theta_{1,1}(t_1)}&\cdots&\frac{\partial e_1^L}{\partial\theta_{n,p}(t_q)}&\frac{\partial e_1^L}{\partial \overline{\varphi}_1(t_1)}&\cdots&\frac{\partial e_1^L}{\partial \overline{\varphi}_p(t_q)}&\frac{\partial e_1^L}{\partial w_{1,1}}&\cdots&\frac{\partial e_1^L}{\partial w_{p,m}}\\ \vdots&\cdots&\vdots&\vdots&\cdots&\vdots&\vdots&\cdots&\vdots\\ \frac{\partial e_m^L}{\partial\theta_{1,1}(t_1)}&\cdots&\frac{\partial e_m^L}{\partial\theta_{n,p}(t_q)}&\frac{\partial e_m^L}{\partial \overline{\varphi}_1(t_1)}&\cdots&\frac{\partial e_m^L}{\partial \overline{\varphi}_p(t_q)}&\frac{\partial e_m^L}{\partial w_{1,1}}&\cdots&\frac{\partial e_m^L}{\partial w_{p,m}} \end{array} \right ], $$

(30)

where the gradient calculations in ${\bf J}({\bf p})$ see to the Appendix.

According to Levenberg–Marquardt algorithm, the iterative equation of adjusting QNNSI parameters is written as follows

$$ {\bf p}_{t+1}={\bf p}_{t}-\bigl({\bf J}^{\rm T}({\bf p}_t){\bf J}({\bf p}_t)+ \mu_t{\bf I}\bigr)^{-1}{\bf J}^{\rm T}({\bf p}_t){\bf e}({\bf p}_t), $$

(31)

where t denotes the iterative steps, ${\bf I}$ denotes the unit matrix, and μ _t is a small positive number to ensure the matrix ${\bf J}^{\rm T}({\bf p}_{t}){\bf J}({\bf p}_{t})+\mu_{t}{\bf I}$ is invertible.

4.3 The stopping criterion of QNNSI

If the value of the evaluation function E reaches the predefined precision within the preset maximum number of iterative steps, then the execution of the algorithm is stopped, else the algorithm is not stopped until it reaches the predefined maximum number of iterative steps.

4.4 Learning algorithm description

The structure of QNNSI is shown in the following.

Procedure QNNSI

Begin

t←0

• (1) The pretreatment of the input and output samples.

• (2) Initialization of QNNSI, including

  • (a) the predefined precision ε,

  • (b) the predefined maximum number of iterative steps N,

  • (c) the parameter of Levenberg–Marquardt algorithm μ _t ,

  • (d) the parameters of QNNSI $\{\theta_{ij}(t_{r}),\overline{\varphi}_{j}(t_{r})\}\in (-\frac{\pi}{2},\frac{\pi}{2})$, {w _jk }∈(−1,1).

• (3) While (not termination-condition)

  Begin

  • (a) computing the actual outputs of all samples by Eqs. (19)–(21),

  • (b) computing the value of the evaluation function E by Eq. (27),

  • (c) adjusting the parameters {θ _ij (t _r )}, $\{\overline{\varphi}_{j}(t_{r})\}$, {w _jk } by Eq. (31).

  • (d) t←t+1,

  End

End

4.5 Diagnostic explanatory capabilities

Finally, we briefly give the diagnostic explanatory capabilities of QNNSI, namely, given the complex model, how can one explain a given prediction, inference, or classification based on QNNSI. We believe that any given prediction, inference, or classification can be seen as an approximation problem from the input space to the output space. In this sense, the above problem is converted into the design problem of multi-dimension sequence samples. Our approach is below. For a n-dimension sample X of classical ANN, if n is a prime number, then extend the dimensions of this sample X to m=n+1 by setting X(m) equal X(n), and otherwise, nothing is done. We decompose m into the product of m ₁ and m ₂ and make these two numbers as close as possible. At this time, a n-dimension sample X of ANN is converted into a m ₁ dimension sequence sample of QNNSI where the sequence length equals m ₂, or a m ₂ dimension sequence sample of QNNSI where the sequence length equals m ₁.

5 Simulations

In order to experimentally illustrate the effectiveness of the proposed QNNSI, four examples are used to compare it with the ANN with a hidden layer in this section. In these experiments, we perform and evaluate the QNNSI in Matlab (Version 7.1.0.246) on a Windows PC with 2.19 GHz CPU and 1.00 GB RAM. Our QNNSI has the same structure and parameters as the ANN in these experiments, and the same Levenberg–Marquardt algorithm in Ref. [22] is applied in two models. Some relevant concepts are defined as follows.

Approximation error

Suppose $[\overline{y}_{1}^{l}, \overline{y}_{2}^{l}, \ldots, \overline{y}_{m}^{l}]$ and $[y_{1}^{l}, y_{2}^{l},\allowbreak \ldots ,y_{m}^{l}]$ denote the lth desired output and the corresponding actual output after training, respectively. The approximation error is defined as

$$ E=\max_{1\leq l\leq L}\max_{1\leq k\leq m}\bigl|\overline{y}_{k}^{l}-y_{k}^{l}\bigr|, $$

(32)

where L denotes the number of the training samples, and m denotes the dimension of the output space.

Average approximation error

Suppose E ₁,E ₂,…,E _N denote the approximation error over N training trials, respectively. The average approximation error is defined as

$$ E_{avg}=\frac{1}{N}\sum_{i=1}^{N}E_i. $$

(33)

Convergence ratio

Suppose E denotes the approximation error after training, and ε denotes the target error. If E<ε, the network training is considered to have converged. Suppose N denotes the total number of training trials, and C denotes the number of convergent training trials. The convergence ratio is defined as

$$ \lambda=\frac{C}{N}. $$

(34)

Iterative steps

In a training trial, the number of times of adjusting all network parameters is defined as iterative steps.

Average iterative steps

Suppose S ₁,S ₂,…,S _N denote the iterative steps over N training trials, respectively. The average iterative steps are defined as

$$ S_{avg}=\frac{1}{N}\sum_{i=1}^{N}S_i. $$

(35)

Average running time

Suppose T ₁,T ₂,…,T _N denote the running time over N training trials, respectively. The average running time is defined as

$$ T_{avg}=\frac{1}{N}\sum_{i=1}^{N}T_i. $$

(36)

5.1 Time series prediction for Mackey–Glass

Mackey–Glass time series can be generated by the following iterative equation

$$ x(t+1)-x(t)=a\frac{x(t-\tau)}{1+x^{10}(t-\tau)}-bx(t), $$

(37)

where t and τ are integers, a=0.2, b=0.1, τ=17, and x(0)∈(0,1).

From the above equation, we may obtain the time sequence $\{x(t)\}^{1000}_{t=1}$. We take the first 800, namely $\{x(t)\}^{800}_{t=1}$, as the training set, and the remaining 200, namely $\{x(t)\}^{1000}_{t=801}$, as the testing set. Our prediction schemes is to employ n data adjacent to each other to predict the next one data. Namely, in our model, the sequence length equals to n. Therefore, each sample consists of n input values and an output value. Hence, there is only one output node in QNNSI and ANN. In order to fully compare the approximation ability of two models, the number of hidden nodes are respectively set to 10,11,…,30. The predefined precision is set to 0.05, and the maximum of iterative steps is set to 100. The QNNSI rotation angles in hidden layer are initialized to random numbers in (−π/2,π/2), and the connection weights in output layer are initialized to random numbers in (−1,1). For ANN, all weights are initialized to random numbers in (−1,1), and the Sigmoid functions are used as activation functions in hidden layer and output layer.

Obviously, ANN has n input nodes, and an ANN’s input sample can be described as a n-dimensional vector. For the number of input nodes of QNNSI, we employ the following six kinds of settings shown in Table 1. For each of these settings in Table 1, a single QNNSI input sample can be described as a matrix.

Table 1 The input nodes and the sequence length setting of QNNSIs and ANN

It is worth noting that, in QNNSI, a n×q matrix can be used to describe a single sequence sample. In general, ANN cannot deal directly with a single n×q sequence sample. In ANN, a n×q matrix is usually regarded as q n-dimensional vector samples. For fair comparison, in ANN, we have expressed the n×q sequence samples into the nq-dimensional vector samples. Therefore, in Table 1, the sequence lengths for ANN are not changed. It is clear that, in fact, there is only one kind of ANN in Table 1, namely, ANN32.

Our experiment scheme is that, for each kind of combination of input nodes and hidden nodes, six QNNSIs and one ANN are respectively run 10 times. Then we use four indicators, such as the average approximation error, the average iterative steps, the average running time, and the convergence ratio, to compare QNNSI with ANN. Training results contrast are shown in Tables 2, 3, 4 and 5, where QNNSIn_q denotes QNNSI with n input nodes and q sequence length.

Table 2 Training results of average approximation error

Table 3 Training results of average iterative steps

Table 4 Training results of average running time (s)

Table 5 Training results of convergence ratio (%)

From Tables 2–5, we can see that when the input nodes take 4 and 8, the performance of QNNSIs are obviously superior to that of ANN, and the QNNSIs have better stability than ANN when the number of hidden nodes changes. The same results also are illustrated in Figs. 5, 6, 7 and 8.

Fig. 5

The average approximation error contrast

Fig. 6

The average iterative steps contrast

Fig. 7

The average running time contrast

Fig. 8

The convergence ratio contrast

Next, we investigate the generalization ability of QNNSI. Based on the above experimental results, we only investigate QNNSI4_8 and QNNSI8_4. Our experiment scheme is that two QNNSIs and one ANN train 10 times on the training set, and the generalization ability is immediately investigated on the testing set after each training. The average results of the 10 tests are regarded as the evaluation indexes. We first present the following definition of evaluation indexes.

Average prediction error

Suppose $[\overline{y}_{1}^{l}, \overline{y}_{2}^{l}, \ldots, \overline{y}_{m}^{l}]$ and $[\widehat{y}_{1}^{l}(t), \widehat{y}_{2}^{l}(t), \ldots, \widehat{y}_{m}^{l}(t)]$ denote the desired output of the lth sample and the corresponding prediction output after the tth testing respectively. The average prediction error over N testing is defined as

$$ \overline{E}_{avg}=\frac{1}{N}\sum _{t=1}^{N}\max_{1\leq l\leq L}\max _{1\leq k\leq m}\bigl|\overline{y}_{k}^{l}- \widehat{y}_{k}^{l}(t)\bigr|, $$

(38)

where m denotes the dimension of the output space, L denotes the number of the testing samples.

Average error mean

Suppose $\overline{y}^{l}=[\overline{y}_{1}^{l}, \overline{y}_{2}^{l}, \ldots, \overline{y}_{m}^{l}]$ and $\widehat{y}^{l}(t)=[\widehat{y}_{1}^{l}(t), \widehat{y}_{2}^{l}(t), \ldots, \widehat{y}_{m}^{l}(t)]$ denote the desired output of the lth sample and the corresponding prediction output after the tth testing respectively. The average error mean over N testing is defined as

$$ \overline{E}_{mean}=\frac{1}{N}\sum_{t=1}^{N} \frac{1}{L}\sum_{l=1}^{L}\bigl| \overline{y}^{l}-\widehat{y}^{l}(t)\bigr|, $$

(39)

Average prediction variance

Suppose $\overline{y}^{l}=[\overline{y}_{1}^{l}, \overline{y}_{2}^{l}, \ldots, \overline{y}_{m}^{l}]$ and $\widehat{y}^{l}(t)$= $[\widehat{y}_{1}^{l}(t), \widehat{y}_{2}^{l}(t), \ldots, \widehat{y}_{m}^{l}(t)]$ denote the desired output of the lth sample and the corresponding prediction output after the tth testing respectively. The average error variance over N testing is defined as

(40)

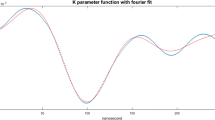
The evaluation indexes contrast of QNNSIs and ANN are shown in Table 6. Taking 24 hidden nodes for example, and the average prediction results contrast over 10 testing are illustrated in Fig. 9. The experimental results show that the generalization ability of the two QNNSIs is obviously superior to that of ANN.

Fig. 9

The average prediction results contrast of QNNSIs and ANN

Table 6 The average prediction error contrast of QNNSIs and ANN

These experimental results can be explain as follows. For processing of input information, QNNSI and ANN take two different approaches. QNNSI directly receives a discrete input sequence. In QNNSI, using quantum information processing mechanism, the input is circularly mapped to the output of quantum controlled-rotation gates in hidden layer. As the controlled-rotation gate’s output is in the entangled state of multi-qubits, therefore, this mapping is highly nonlinear, which makes QNNSI have the stronger approximation ability. In addition, QNNSI’s each input sample can be described as a matrix with n rows and q columns. It is clear from QNNSI’s algorithm that, for the different combination of n and q, the output of quantum-inspired neuron in hidden layer is also different. In fact, The number of discrete points q denotes the depth of pattern memory, and the number of input nodes n denotes the breadth of pattern memory. When the depth and the breadth are appropriately matched, the QNNSI shows excellent performance. For the ANN, because its input can only be described as a nq-dimensional vector, it does not directly deal with a discrete input sequence. Namely, it can only obtain the sample characteristics by way of breadth instead of depth. Hence, in the ANN information processing, there inevitably exists the loss of sample characteristics, which affects its approximation and generalization ability.

5.2 Annual average of sunspot prediction

In this section, we take the measured data of annual average of sunspot from 1749 to December 2007 as the experiment objects, and investigate the prediction ability of the proposed model. All samples data are shown in Fig. 10. In all samples, we use the first 200 years (1949–1948) data to train the network, and the remaining 59 years (1949–2007) data to test the generalization of the proposed model. For the input nodes and the sequence length, we employ the seven kinds of settings shown in Table 7. In this experiment, we set the number of hidden nodes to 20,21,…,40, respectively. The target error is set to 0.05, and the maximum number of iterative steps is set to 100. The other parameters of QNNSIs and ANNs are set by the same way as the previous experiment.

Fig. 10

The measured data of annual average of sunspot

Table 7 The input nodes and the sequence length setting of QNNSIs and ANNs

7 QNNSIs and 2 ANNs are run 10 times respectively for each setting of hidden nodes, and then we use the same evaluation indicators as the previous experiment to compare QNNSIs with ANNs. Training result contrasts are shown in Tables 8, 9, 10 and 11.

Table 8 Training results of average approximation error

Table 9 Training results of average iterative steps

Table 10 Training results of average running time (s)

Table 11 Training results of convergence ratio (%)

From Tables 8–11, we can see that the performance of QNNSI5_10, QNNSI7_7 and QNNSI10_5 are obviously superior to that of the two ANNs. The convergence ratio of these three QNNSIs reaches 100% under a variety of values of hidden nodes. Overall, the other three indicators of these three QNNSIs are better than that of two ANNs, and there is good stability when the number of hidden nodes changes. The same results also are illustrated in Figs. 11, 12, 13 and 14.

Fig. 11

The average approximation error contrast

Fig. 12

The average iterative steps contrast

Fig. 13

The average running time contrast

Fig. 14

The convergence ratio contrast

Next, we investigate the generalization ability of QNNSI. Based on the above experimental results, we only investigate QNNSI5_10, QNNSI7_7, and QNNSI10_5. Our experiment scheme is that three QNNSIs and two ANNs are respectively done 10 training by the first 200 years (1749–1948) data, and are immediately tested by the remaining 59 years (1949–2007) data after each training. The average prediction error of the 10 tests is regarded as the evaluation index. The average prediction error contrast of QNNSIs and ANNs are shown in Table 12. Taking 35 hidden nodes for example, the average prediction result contrast are illustrated in Fig. 15. The experimental results show that the generalization ability of three QNNSIs is obviously superior to that of corresponding ANNs.

Fig. 15

The average prediction results contrast of QNNSIs and ANNs

Table 12 The average prediction error contrast of QNNSIs and ANNs

5.3 Caravan insurance policy prediction

In this experiment, we predict who would be interested in buying a caravan insurance policy. This data set used in the CoIL 2000 Challenge contains information on customers of an insurance company and comes from the following url: http://kdd.ics.uci.edu/databases/tic/tic.html. The data was supplied by the Dutch data mining company Sentient Machine Research and is based on a real world business problem. The training set contains 5822 descriptions of customers. Each record consists of 86 attributes, containing sociodemographic data (attribute 1–43) and product ownership (attributes 44–86). The sociodemographic data is derived from zip codes. All customers living in areas with the same zip code have the same sociodemographic attributes. Attribute 86 is the target variable, which equals 0 or 1 and indicate information of whether or not they have a caravan insurance policy. The Dataset for predictions contains 4000 customer records of whom only the organisers know if they have a caravan insurance policy. It has the same format as the training set, only the target is missing. Participants are supposed to return the list of predicted targets only.

Considering the each customer consists of 85 feature attributes for the input nodes and the sequence length, we employ the four kinds of settings shown in Table 13. In this experiment, we set the number of hidden nodes to 10,11,…,20, respectively. The maximum number of iterative steps is set to 100. The other parameters of QNNSIs and ANN are set by the same way as the previous experiment. In this experiment, we do not set the value of target error. The algorithm is not stopped until it reaches the predefined maximum number of iterative steps.

Table 13 The input nodes and the sequence length setting of QNNSIs and ANN

QNNSIs and ANN train 10 times for each setting of hidden nodes by the training set data, and are immediately tested by the testing set data after each training. The evaluation indicators used in this experiment are defined as follows.

The number of correct prediction results

Suppose $\overline{y}^{1}, \overline{y}^{2},\allowbreak \ldots, \overline{y}^{M}$ denote the desired outputs of M samples, and y ¹,y ²,…,y ^M denote the corresponding actual outputs, where M denotes the number of samples in training set. The number of correct prediction results for training set is defined as

$$ N_{tr}=\sum_{n=1}^N\Biggl(M- \sum_{m=1}^{M}\bigl|\overline{y}^m- \bigl[y^m\bigr]\bigr|\Biggr)/N, $$

(41)

where N denotes the total number of training trials, if y ^m≥0.5, then [y ^m]=1, otherwise [y ^m]=0. Similarly, the number of correct prediction results for the testing set is defined as

$$ N_{te}=\sum_{n=1}^N\Biggl( \overline{M}-\sum_{m=1}^{\overline{M}}\bigl| \overline{y}^m-\bigl[y^m\bigr]\bigr|\Biggr)/N, $$

(42)

where $\overline{M}$ denotes the number of samples in testing set.

The ratio of correct prediction results

The ratio of correct prediction results for the training set is defined as

$$ R_{tr}=100N_{tr}/M. $$

(43)

Similarly, the ratio of correct prediction results for the testing set is defined as

$$ R_{te}=100N_{te}/\overline{M}. $$

(44)

Then, we use these four indicators and the average running time T _avg to compare QNNSIs with ANN. Experimental result contrasts are shown in Table 14.

Table 14 The performance contrast of QNNSIs and ANN for caravan insurance policy prediction

It can be seen from Table 14 that the average running time of QNNSI85_1 is the shortest, and so, it is the most efficient. The R _te of QNNSI17_5 is the greatest, and so, its generalization ability is the strongest. For ANN85, although the R _tr is the greatest of the five models, its generalization ability is inferior to QNNSI17_5 and QNNSI5_17. In addition, for the four QNNSIs, almost all of the R _te are greater than the corresponding R _tr , which suggests that QNNSI has stronger generalization ability than ANN.

5.4 Breast cancer prediction

In this experiment, we give an example of predicting breast cancer with QNNSI and ANN. Features are computed from a digitized image of a fine needle aspirate (FNA) of a breast mass. They describe characteristics of the cell nuclei present in the image. A few of the images can be found at the following url: http://www.cs.wisc.edu/~street/images/. The dataset is linearly separable using all 30 input features, and 2 prediction fields respectively are benign and malignant. The number of instances in the dataset equals to 569, where 357 instances are benign and 212 instances are malignant. The best predictive accuracy obtained using one separating plane in the 3-D space of Worst Area, Worst Smoothness and Mean Texture. Separating plane described above can be obtained using Multi-surface Method-Tree (MSM-T), a classification method which uses linear programming to construct a decision tree. The actual linear program used to obtain the separating plane in the 3-dimensional space is that described in Ref. [23]. The above-mentioned classifier has correctly diagnosed 176 consecutive new patients as of November 1995.

In all samples, we use the first 400 instances (where 227 are benign) to train the network, and the remaining 169 instances (where 130 are benign) to test the generalization of the proposed model. For the input nodes and the sequence length, we employ the eight kinds of settings shown in Table 15. In this experiment, we set the number of hidden nodes to 5,6,…,15, respectively. The maximum number of iterative steps is set to 100. The other parameters of QNNSIs and ANN are set in the same way as the previous experiment. In this experiment, we do not set the value of the target error. The algorithm is not stopped until it reaches the predefined maximum number of iterative steps.

Table 15 The input nodes and the sequence length setting of QNNSIs and ANN

Our experiment scheme is below. QNNSIs and ANN train 10 times for each setting of hidden nodes by the training set data, and are immediately tested by the testing set data after each training. Then, we use the same evaluation indicators as the previous experiment to compare QNNSIs with ANN. Experimental contrast results are shown in Table 16.

Table 16 The performance contrast of QNNSIs and ANN for breast cancer prediction

It can be seen from Table 16 that, as far as the approximation and generalization ability are concerned, QNNSI1_30 and QNNSI30_1 are obviously inferior to ANN30; QNNSI2_15 and QNNSI15_2 are roughly equal to ANN30; QNNSI3_10 and QNNSI10_3 are slightly superior to ANN30; QNNSI5_6 and QNNSI6_5 are obviously superior to ANN30. As far as the average running time are concerned, QNNSI1_30, QNNSI2_15, and QNNSI3_10 are obviously longer than ANN30; QNNSI5_6 and QNNSI6_5 are slightly longer than ANN30; QNNSI10_3, QNNSI15_2, and QNNSI30_1 are roughly equal to ANN30. Synthesizing the above-mentioned two aspects, QNNSI shows better performance than ANN when the number of input nodes is close to the sequence length.

Next, we theoretically explain the above experimental results. Assume that n denotes the number of input nodes, q denotes the sequence length, p denotes the number of hidden nodes, and m denotes the number of output nodes, and the product of nq is approximately a constant.

It is clear that the number of adjustable parameters in QNNSI and ANN is the same, i.e., equals npq+pm. The weights adjustment formula in the output layer of QNNSI and ANN is also the same. But, their parameters adjustment of hidden layer is completely different. The adjustment of hidden parameters in QNNSI is much more complex than that in ANN. In ANN, each hidden parameter adjustment only involves two derivative calculations. In QNNSI, each hidden layer parameter adjustment involves at least two and at most q+1 derivative calculations.

In QNNSI, when q=1, although the number of input nodes is the greatest possible, the calculation of the hidden layer output and hidden parameter adjustment are also the most simple, which directly lead to the reduction of the approximation ability. When n=1, the calculation of the hidden layer output is the most complex, which make the QNNSI have the strongest nonlinear mapping ability. However, at this time, the calculation of hidden parameter adjustment is also very complex. A large number of derivative calculations can lead to the adjustment of parameters which tend to zero or infinity. This can hinder the convergence of the training process and lead to the reduction of the approximation ability. Hence, when q=1 or n=1, the approximation ability of QNNSI is inferior to that of ANN. When n>1 or q>1, the approximation ability of QNNSI tends to improve, and under a certain condition, the approximation ability of QNNSI will certainly be superior to that of ANN. The above analysis is consistent with the experimental results.

In addition, what is the accurate relationship between n and q to make QNNSI approximation ability the strongest? This problem needs further study, and usually depends on the specific issues. Our conclusions based on experiments is as follows: when q/2≤n≤2q, QNNSIn_q is superior to the ANN with nq input nodes.

It is worth pointing out that QNNSI is potentially much more computationally efficient than all the models referenced above in the Introduction section. The efficiency of many quantum algorithms comes directly from quantum parallelism that is a fundamental feature of many quantum algorithms. Heuristically, and at the risk of over-simplifying, quantum parallelism allows quantum computers to evaluate a function f(x) for many different values of x simultaneously. Although quantum simulation requires many resources in general, quantum parallelism leads to very high computational efficiency by using the superposition of quantum states. In QNNSI, the input samples have been converted into corresponding quantum superposition states after preprocessing. Hence, as far as a lot of quantum rotation gates and controlled-not gates used in QNNSI are concerned, information processing can be performed simultaneously, which greatly improves the computational efficiency. Because the above four experiments are performed in classical computer, the quantum parallelism has not been explored. However, the efficient computational ability of QNNSI is bound to stand out in future quantum computer.

6 Conclusions

This paper proposes a quantum-inspired neural network model with sequence input based on the principle of quantum computing. The architecture of the proposed model includes three layers, where the hidden layer consists of quantum neurons and the output layer consists of classical neurons. An obvious difference from classical ANN is that each dimension of a single input sample consists of a discrete sequence rather that a single value. The activation function of hidden layer is redesigned according to the principle of quantum computing. The Levenberg–Marquardt algorithm is employed for learning. With the application of the information processing mechanism of quantum controlled-rotation gates, the proposed model can effectively obtain the sample characteristics by way of breadth and depth. The experimental results reveal that a greater difference between input nodes and sequence length leads to a lower performance of the proposed model than that of the classical ANN, on the contrary, it obviously enhances the approximation and generalization ability of the proposed model when input nodes are closer to the sequence length. The following issues to the proposed model, such as continuity, computational complexity, and improvement of the learning algorithm, are subject of further research.

Appendix: The gradient calculation in Levenberg–Marquardt algorithm

According to the gradient descent algorithm in Ref. [22], the gradient of the rotation angles of the quantum rotation gates in hidden layer and the connection weights in output layer can be calculated as follows

$$ \left\{ \begin{array}{l} \frac{\partial e_k^l}{\partial h_j^l(t_q)}=-y_k^l(1-y_k^l)w_{jk},\\[10pt] \frac{\partial h_j^l(t_r)}{\partial h_j^l(t_{r-1})}=(V_{jr}^l+\overline{V}_{jr}^l)/(2h_j^l(t_r)\sqrt{1-(h_j^l(t_{r-1}))^2}),\\[10pt] \frac{\partial h_j^l(t_r)}{\partial \theta_{ij}(t_{r})}= \left\{ \begin{array}{l} \frac{(\overline{h}_{jr}^l)^2(U_{jr}^l+\overline{U}_{jr}^l)\cot(\theta_i^l(t_r)+\theta_{ij}(t_r))}{h_j^l(t_r)},\\[6pt] \quad j=1,3,5,\ldots,\\[6pt] -\frac{(\overline{h}_{jr}^l)^2(U_{jr}^l+\overline{U}_{jr}^l)\tan(\theta_i^l(t_r)+\theta_{ij}(t_r))}{h_j^l(t_r)},\\[6pt] \quad j=2,4,6,\ldots, \end{array}\right. \\[40pt] \frac{\partial h_j^l(t_r)}{\partial \overline{\varphi}_{j}(t_{r})}=\frac{(\overline{h}_{jr}^l)^2(W_{jr}^l+\overline{W}_{jr}^l)}{h_j^l(t_r)}, \end{array}\right. $$

(45)

where

$$ \left \{ \begin{array}{l} \overline{h}_{jr}^l= \left\{ \begin{array}{l} \prod_{i=1}^{n}\sin(\theta_i^l(t_r)+\theta_{ij}(t_r))\quad j=1,3,5,\ldots,\\[6pt] \prod_{i=1}^{n}\cos(\theta_i^l(t_r)+\theta_{ij}(t_r))\quad j=2,4,6,\ldots, \end{array}\right. \\[6pt] U_{jr}^l=h_j^l(t_{r-1}) \sqrt{1-\bigl(h_j^l(t_{r-1}) \bigr)^2}\sin\bigl(2\overline{\varphi}_j(t_r) \bigr), \\[6pt] \overline{U}_{jr}^l=\bigl(1-2\bigl(h_j^l(t_{r-1}) \bigr)^2\bigr)\sin^2\bigl(\overline{\varphi}_j(t_r) \bigr), \\[6pt] V_{jr}^l=\bigl(1-2\bigl(h_j^l(t_{r-1}) \bigr)^2\bigr) \bigl(\overline{h}_{jr}^l \bigr)^2\sin\bigl(2\overline{\varphi}_j(t_r) \bigr), \\[6pt] \overline{V}_{jr}^l=2h_j^l(t_{r-1}) \bigl(1-2\bigl(\overline{h}_{jr}^l\bigr)^2 \sin^2\bigl(\overline{\varphi}_j(t_r)\bigr) \bigr) \\[6pt] \phantom{\overline{V}_{jr}^l=\,}\times\sqrt{1- \bigl(h_j^l(t_{r-1})\bigr)^2}, \\[6pt] W_{jr}^l=h_j^l(t_{r-1}) \sqrt{1-\bigl(h_j^l(t_{r-1}) \bigr)^2}\cos\bigl(2\overline{\varphi}_j(t_r) \bigr), \\[6pt] \overline{W}_{jr}^l=0.5\bigl(1-2\bigl(h_j^l(t_{r-1}) \bigr)^2\bigr)\sin\bigl(2\overline{\varphi}_j(t_r) \bigr). \end{array} \right . $$

(46)

Based on the above Eq. (45), we obtain

(47)

(48)

where j=1,2,…,p, k=1,2,…,m, r=1,2,…,q, l=1,2,…,L.

The gradient of the connection weights in the outer layer can be calculated as follows

$$ \frac{\partial e_k^l}{\partial w_{jk}}=-y_k^l\bigl(1-y_k^l \bigr)h_j^l(t_q). $$

(49)