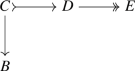Locally Coherent Exact Categories

Abstract

A locally coherent exact category is a finitely accessible additive category endowed with an exact structure in which the admissible short exact sequences are the directed colimits of admissible short exact sequences of finitely presentable objects. We show that any exact structure on a small idempotent-complete additive category extends uniquely to a locally coherent exact structure on the category of ind-objects; in particular, any finitely accessible category has the unique maximal and the unique minimal locally coherent exact category structures. All locally coherent exact categories are of Grothendieck type in the sense of Št’ovíček. We also discuss the canonical embedding of a small exact category into the abelian category of additive sheaves in connection with the locally coherent exact structure on the ind-objects, and deduce two periodicity theorems as applications.

1 Introduction

Noetherian rings and modules over them play an important role in commutative algebra and representation theory. Over a Noetherian ring R, the category of finitely generated modules ${{\textsf{mod}\text {--}}}R$ is abelian, and the abelian category of arbitrary modules ${{\textsf{Mod}\text {--}}}R$ is locally Noetherian. Coherent rings are a natural generalization of Noetherian ones: over a coherent ring, the category of finitely presentable modules ${{\textsf{mod}\text {--}}}R$ is abelian, and the abelian category of arbitrary modules ${{\textsf{Mod}\text {--}}}R$ is locally coherent. Still, there are many rings that are not coherent.

The aim of this paper is to suggest a point of view allowing to consider the category of modules over an arbitrary ring as “locally coherent” in some sense. This comes at the cost of passing from abelian to exact categories (in Quillen’s sense).

We explain that, for any ring R, the abelian category ${{\textsf{Mod}\text {--}}}R$ (as, more generally, any finitely accessible additive category) has a complete lattice of locally coherent exact structures. The minimal locally coherent exact structure is the pure exact structure. The maximal locally coherent exact structure is the closest locally coherent approximation to the abelian exact structure on ${{\textsf{Mod}\text {--}}}R$.

The maximal locally coherent exact structure keeps track of the short exact sequences of finitely presentable R-modules, but disregards the short exact sequences in which the middle term and the cokernel are finitely presentable while the kernel is not. All information about short exact sequences of the latter type is destroyed by considering ${{\textsf{Mod}\text {--}}}R$ as an exact category with the maximal (or any other) locally coherent exact structure. That is the price one has to pay for viewing the category of modules over an arbitrary ring through coherent lens.

More generally, for any regular cardinal $\kappa$ and any $\kappa$-accessible additive category ${\textsf{A}}$, an exact structure on ${\textsf{A}}$ is said to be locally $\kappa$-coherent if the admissible short exact sequences in ${\textsf{A}}$ are precisely the $\kappa$-directed colimits of admissible short exact sequences of $\kappa$-presentable objects. We show that locally $\kappa$-coherent exact structures on ${\textsf{A}}$ correspond bijectively to arbitrary exact structures on the full subcategory ${\textsf{A}}_{<\kappa }$ of $\kappa$-presentable objects in ${\textsf{A}}$. (Notice that an abelian category ${\textsf{A}}$ is locally coherent if and only if it is locally finitely presentable and its full subcategory of finitely presentable objects is abelian; in other words, this means that ${\textsf{A}}$ is the category of ind-objects of a small abelian category.)

Beyond the abelian category ${\textsf{A}}={{\textsf{Mod}\text {--}}}R$ of arbitrary R-modules, the additive category ${\textsf{A}}={{\mathsf {Mod_{fl}}\text {--}}}R$ of flat R-modules provides an important example for our theory. There is a phenomenon of flat coherence: for any regular cardinal $\kappa$, the kernel of any surjective morphism of $\kappa$-presentable flat R-modules is again a $\kappa$-presentable flat R-module [24, Lemma 4.1], [25, Corollary 10.12]. In the language of the present paper, this observation appears as a corollary of the fact that the category ${{\mathsf {Mod_{fl}}\text {--}}}R$ with its natural exact structure is locally $\kappa$-coherent for any ring R. The exact structure on ${{\mathsf {Mod_{fl}}\text {--}}}R$ is pure, but it is not $\kappa$-pure, of course.

So, for any small exact category ${\textsf{E}}$, the accessible category ${{\,\mathrm{\textsf{Ind}}\,}}{\textsf{E}}$ of ind-objects of ${\textsf{E}}$ acquires the induced locally coherent exact category structure. As a digression, we discuss the classical construction of the canonical embedding of ${\textsf{E}}$ into the abelian category ${\textsf{K}}$ of left exact functors ${\textsf{E}}^\textsf{op}\longrightarrow \textsf{Ab}$ in Sect. 6. We observe that the category ${\textsf{K}}$ is locally finitely presentable (and in fact, locally type $\textrm{FP}_\infty$), and the locally coherent exact category structure on ${{\,\mathrm{\textsf{Ind}}\,}}{\textsf{E}}$ is inherited from the abelian exact structure on ${\textsf{K}}$ via a natural fully faithful embedding ${{\,\mathrm{\textsf{Ind}}\,}}{\textsf{E}}\longrightarrow {\textsf{K}}$.

The main results of this paper are two periodicity theorems. Theorem 7.1 generalizes the flat/projective periodicity theorem of Benson–Goodearl and Neeman [6, 20] and the fp-projective periodicity theorem of Šaroch–Št’ovíček [32], while Theorem 7.6 generalizes the cotorsion periodicity theorem of Bazzoni, Cortés-Izurdiaga, and Estrada [4]. The idea of these generalizations is to replace the split exact category of finitely generated projective R-modules (or the abelian category of finitely presentable modules over a coherent ring R) by an arbitrary small exact category.

As a particular case of Theorem 7.1, we deduce in Theorem 8.3 a new version of fp-projective periodicity theorem applicable to an arbitrary (and not necessarily coherent) ring R. Another such version of fp-projective periodicity was previously obtained in the paper [5].

Beyond periodicity theorems, what can one do with locally coherent exact categories? Let us explain the idea which motivated the present research. The results of [23, Theorem 9.39 and Corollary 9.42], and particularly [27, Theorem 8.19 and Corollary 8.20], describe compact generators of the coderived categories of locally coherent abelian DG-categories, such as the category of curved DG-modules over a curved DG-ring with a coherent underlying graded ring. The coherence condition involved is somewhat restrictive, as mentioned in the beginning of this introduction.

The definition of an exact DG-category was given and studied in the paper [23]; the abelian DG-categories [23, 27] are a particular case. The definition of a locally coherent abelian DG-category can be found in [23, Section 9.5] and [27, Section 8.3]. We hope that a suitable definition of a locally coherent exact (rather than abelian) DG-category can be worked out so that the results concerning compact generators of coderived categories mentioned above would be generalizable to locally coherent exact DG-categories, such as the maximal locally coherent exact DG-category structure on the category of CDG-modules over an arbitrary CDG-ring.

2 Basic Properties of Locally $\kappa$-Coherent Exact Categories

Let $\kappa$ be a regular cardinal. We refer to the beginning paragraphs of the Appendix for the definitions, notation, and references concerning $\kappa$-presentable objects and $\kappa$-accessible categories.

Given an (additive) category ${\textsf{A}}$, consider the category ${\textbf{M}}^3({\textsf{A}})$ of composable pairs of morphisms in ${\textsf{A}}$, and its full subcategory ${\textbf{C}}^3({\textsf{A}})\subset {\textbf{M}}^3({\textsf{A}})$ of three-term complexes in ${\textsf{A}}$ (that is, composable pairs of morphisms with zero composition). We also consider the category ${\textbf{C}}^2({\textsf{A}})={\textbf{M}}^2({\textsf{A}})$ of morphisms in ${\textsf{A}}$.

Proposition 1.1

Let ${\textsf{A}}$ be a $\kappa$-accessible category. In this context:

(a):

The category of morphisms ${\textbf{M}}^2({\textsf{A}})$ is $\kappa$-accessible. A morphism $A^1\longrightarrow A^2$ in ${\textsf{A}}$ is $\kappa$-presentable as an object of ${\textbf{M}}^2({\textsf{A}})$ if and only if both the objects $A^1$ and $A^2$ are $\kappa$-presentable in ${\textsf{A}}$.

(b):

The category of composable pairs of morphisms ${\textbf{M}}^3({\textsf{A}})$ is $\kappa$-accessible. A pair of morphisms $A^1\longrightarrow A^2\longrightarrow A^3$ in ${\textsf{A}}$ is $\kappa$-presentable as an object of ${\textbf{M}}^3({\textsf{A}})$ if and only if all the three objects $A^1$, $A^2$, and $A^3$ are $\kappa$-presentable in ${\textsf{A}}$.

(c):

Assume that the category ${\textsf{A}}$ is additive. Then the category of three-term complexes ${\textbf{C}}^3({\textsf{A}})$ is $\kappa$-accessible. A three-term complex $A^1\longrightarrow A^2\longrightarrow A^3$ in ${\textsf{A}}$ is $\kappa$-presentable as an object of ${\textbf{C}}^3({\textsf{A}})$ if and only if all the three objects $A^1$, $A^2$, and $A^3$ are $\kappa$-presentable in ${\textsf{A}}$.

Proof

Part (a) is an easy particular case of Proposition A.5, or alternatively, a special case of Proposition A.3. Part (b) is also an easy particular case of Proposition A.5; it can be also obtained by an iterated application of Proposition A.3. Part (c) is an easy particular case of Proposition A.6 (for $k={\mathbb {Z}}$).

Alternatively, here is a simple direct proof of the “if and only if” assertion in part (c), not depending on the assumption that ${\textsf{A}}$ is $\kappa$-accessible, but only that $\kappa$-directed colimits exist in ${\textsf{A}}$. Denoting by ${\textsf{A}}^3$ the Cartesian product of three copies of ${\textsf{A}}$, we have to show that the forgetful functor $F^3:{\textbf{C}}^3({\textsf{A}})\longrightarrow {\textsf{A}}^3$ preserves and reflects $\kappa$-presentability of objects (cf. Lemma A.2). Indeed, the functor $F^3$ preserves $\kappa$-presentability, since its right adjoint functor $G^{3-}:{\textsf{A}}^3\longrightarrow {\textbf{C}}^3({\textsf{A}})$, which is easily constructed explicitly in terms of finite direct sums of objects in ${\textsf{A}}$, preserves $\kappa$-directed colimits (the assumption that ${\textsf{A}}$ is additive is used here). The converse assertion follows from the fact that directed colimits commute with finite limits in the category of sets, and holds in any finite diagram category [14, Proposition 2.1]. $\square$

We refer to the survey paper [9] for the background material on exact categories (in the sense of Quillen). The expositions in [15, Appendix A] and [21, Appendix A] can be used as supplements. Notice that any $\kappa$-accessible additive category ${\textsf{A}}$ and its full subcategory of $\kappa$-presentable objects ${\textsf{A}}_{<\kappa }$ are idempotent-complete by [1, Observation 2.4 and Proposition 1.16]. Hence both ${\textsf{A}}$ and ${\textsf{A}}_{<\kappa }$ are weakly idempotent-complete in the sense of [9, Section 7].

Let ${\textsf{A}}$ be a $\kappa$-accessible additive category. We will say that an exact category structure on ${\textsf{A}}$ is locally $\kappa$-coherent if the admissible short exact sequences in ${\textsf{A}}$ are precisely the $\kappa$-directed colimits of admissible short exact sequences in ${\textsf{A}}$ with the terms belonging to ${\textsf{A}}_{<\kappa }$. The $\kappa$-directed colimits here are taken in the category of three-term complexes ${\textbf{C}}^3({\textsf{A}})$.

Lemma 1.2

In any locally $\kappa$-coherent exact category, the class of all (admissible) short exact sequences is preserved by $\kappa$-directed colimits.

Proof

Follows from Proposition 1.1(c) together with Proposition A.1 (applied to the $\kappa$-accessible category ${\textbf{C}}^3({\textsf{A}})$ and the class ${\textsf{T}}$ of all short exact sequences in ${\textsf{A}}$ with the terms belonging to ${\textsf{A}}_{<\kappa }$).

Notice that we have shown more than the lemma claims. Applied to the situation at hand, Proposition A.1 tells us that the category of short exact sequences in ${\textsf{A}}$ is $\kappa$-accessible, and its full subcategory of $\kappa$-presentable objects consists of all the short exact sequences of $\kappa$-presentable objects in ${\textsf{A}}$. $\square$

Remark 1.3

Let ${\textsf{A}}$ be a locally $\kappa$-coherent exact category. Then it follows from Lemma 1.2 that the classes of admissible monomorphisms and admissible epimorphisms in ${\textsf{A}}$ are also preserved by $\kappa$-directed colimits. Therefore, the admissible monomorphisms in ${\textsf{A}}$ are precisely all the $\kappa$-directed colimits of admissible monomorphisms with $\kappa$-presentable domain and codomain. Similarly, the admissible epimorphisms in ${\textsf{A}}$ are precisely all the $\kappa$-directed colimits of admissible epimorphisms with $\kappa$-presentable domain and codomain.

Proposition 1.4

In any locally $\kappa$-coherent exact structure on a $\kappa$-accessible additive category ${\textsf{A}}$, the full subcategory of $\kappa$-presentable objects ${\textsf{A}}_{<\kappa }$ is closed under extensions in ${\textsf{A}}$. So ${\textsf{A}}_{<\kappa }$ inherits an exact category structure from ${\textsf{A}}$.

Proof

Let $0\longrightarrow A^1\longrightarrow A^2\longrightarrow A^3\longrightarrow 0$ be a short exact sequence in ${\textsf{A}}$. Then there exists a $\kappa$-directed poset $\Xi$ and a $\Xi$-indexed diagram of short exact sequences $0\longrightarrow S^1_\xi \longrightarrow S^2_\xi \longrightarrow S^3_\xi \longrightarrow 0$ with $S^i_\xi \in {\textsf{A}}_{<\kappa }$ whose $\kappa$-directed colimit over $\xi \in \Xi$ is the short exact sequence $0\longrightarrow A^1\longrightarrow A^2 \longrightarrow A^3\longrightarrow 0$.

Now assume that $A^1\in {\textsf{A}}_{<\kappa }$ and $A^3\in {\textsf{A}}_{<\kappa }$. Then, for $i=1$ and 3, the isomorphism $A^i\longrightarrow \varinjlim _{\xi \in \Xi }S^i_\xi$ factorizes through some objects in the diagram. So there exists an index $\eta \in \Xi$ for which both the morphisms $S^1_\eta \longrightarrow A^1$ and $S^3_\eta \longrightarrow A^3$ are split epimorphisms in ${\textsf{A}}_{<\kappa }$. As all split epimorphisms are admissible (since ${\textsf{A}}$ is weakly idempotent-complete), and an extension of two admissible epimorphisms in an exact category is an admissible epimorphism [9, Corollary 3.6], it follows that the morphism $S^2_\eta \longrightarrow A^2$ is also an admissible epimorphism in ${\textsf{A}}$.

For every $i=1$, 2, 3, denote by $B^i$ the kernel of the admissible epimorphism $S^i_\eta \longrightarrow A^i$. As the kernel of a termwise admissible epimorphism of short exact sequences in an exact category is a short exact sequence [9, Corollary 3.6], we get a short exact sequence $0\longrightarrow B^1\longrightarrow B^2\longrightarrow B^3\longrightarrow 0$ in ${\textsf{A}}$. Now a direct summand of a $\kappa$-presentable object is $\kappa$-presentable, so $B^1$ and $B^3$ belong to ${\textsf{A}}_{<\kappa }$.

Applying the same argument to the short exact sequence $0\longrightarrow B^1 \longrightarrow B^2\longrightarrow B^3\longrightarrow 0$, we obtain a termwise admissible epimorphism from a short exact sequence $0\longrightarrow T^1\longrightarrow T^2 \longrightarrow T^3\longrightarrow 0$ with $T^i\in {\textsf{A}}_{<\kappa }$ to the short exact sequence $0\longrightarrow B^1\longrightarrow B^2\longrightarrow B^3\longrightarrow 0$. Finally, we can conclude that the object $A^2$ belongs to ${\textsf{A}}_{<\kappa }$, because $A^2$ is the cokernel of the composition $T^2\longrightarrow B^2\longrightarrow S^2_\eta$ and finite colimits of $\kappa$-presentable objects are $\kappa$-presentable [1, Proposition 1.16]. $\square$

Lemma 1.5

Let ${\textsf{A}}$ be a locally $\kappa$-coherent exact category and $D\longrightarrow E$ be a morphism in ${\textsf{A}}$. Then the following conditions are equivalent:

• (1) $D\longrightarrow E$ is an admissible epimorphism in ${\textsf{A}}$;

• (2) for any object $S\in {\textsf{A}}_{<\kappa }$, any morphism $S\longrightarrow E$ in ${\textsf{A}}$ can be included into a commutative square diagram

  

with an object $T\in {\textsf{A}}_{<\kappa }$ and an admissible epimorphism $T\longrightarrow S$ in ${\textsf{A}}$.

Proof

(1) $\Longrightarrow$ (2) By the definition, there exists a $\kappa$-directed poset $\Xi$ and a $\Xi$-indexed diagram of short exact sequences $0\longrightarrow U_\xi \longrightarrow T_\xi \longrightarrow S_\xi \longrightarrow 0$ in ${\textsf{A}}$ with the terms $U_\xi$, $T_\xi$, $S_\xi$ belonging to ${\textsf{A}}_{<\kappa }$ such that the morphism $D\longrightarrow E$ is the colimit of the morphisms $T_\xi \longrightarrow S_\xi$ over $\xi \in \Xi$. Now the morphism $S\longrightarrow E$ factorizes as $S\longrightarrow S_\xi \longrightarrow E$ for some $\xi \in \Xi$. It remains to consider the pullback diagram

where the pullback object T exists in ${\textsf{A}}$, since all pullbacks of admissible epimorphisms exist by the definition of an exact category. By Proposition 1.4, we have $T\in {\textsf{A}}_{<\kappa }$, since $U_\xi \in {\textsf{A}}_{<\kappa }$ and $S\in {\textsf{A}}_{<\kappa }$.

(2) $\Longrightarrow$ (1) The following observation plays the key role. Let $T'\longrightarrow S'$ be a morphism in ${\textsf{A}}_{<\kappa }$, and let $(T'\rightarrow S')\longrightarrow (D\rightarrow E)$ be a morphism of morphisms in ${\textsf{A}}$. By (2), there exist an object $T''\in {\textsf{A}}_{<\kappa }$, an admissible epimorphism $T''\twoheadrightarrow S'$ in ${\textsf{A}}$, and a morphism of morphisms $(T''\twoheadrightarrow S')\longrightarrow (D\rightarrow E)$ in ${\textsf{A}}$. Then the morphism $T'\oplus T''\longrightarrow S'$ with the components $T'\longrightarrow S'$ and $T''\longrightarrow S'$ is an admissible epimorphism in ${\textsf{A}}$ by the dual version of [9, Exercise 3.11(i)]. There is a commutative triangular diagram of morphisms of morphisms $(T'\rightarrow S')\longrightarrow (T'\oplus T''\twoheadrightarrow S')\longrightarrow (D\rightarrow E)$; so the morphism $(T'\rightarrow S')\longrightarrow (D\rightarrow E)$ factorizes through the object $(T'\oplus T'' \twoheadrightarrow S')$ in the category of morphisms in ${\textsf{A}}$.

Now, for the given fixed morphism $D\longrightarrow E$, denote by $\Xi$ the small category formed by all the commutative squares as in (2) with T, $S\in {\textsf{A}}_{<\kappa }$ and admissible epimorphisms $T\longrightarrow S$. Then $\Xi$ is a $\kappa$-filtered category and the colimit of the morphisms $T_\xi \longrightarrow S_\xi$ over all $\xi \in \Xi$ is the morphism $D\longrightarrow E$. These assertions follow from Proposition 1.1(a) and (the proof of) Proposition A.1 applied to the $\kappa$-accessible category ${\textbf{M}}^2({\textsf{A}})$ of morphisms in ${\textsf{A}}$ and the class ${\textsf{T}}$ of all admissible epimorphisms in ${\textsf{A}}$ between objects from ${\textsf{A}}_{<\kappa }$.

Finally, the class of all admissible epimorphisms in ${\textsf{A}}$ is preserved by $\kappa$-directed colimits in view of Lemma 1.2. $\square$

Proposition 1.6

In any locally $\kappa$-coherent exact structure on a $\kappa$-accessible additive category ${\textsf{A}}$, the full subcategory of $\kappa$-presentable objects ${\textsf{A}}_{<\kappa }\subset {\textsf{A}}$ is closed under the kernels of admissible epimorphisms and the cokernels of admissible monomorphisms in ${\textsf{A}}$.

Proof

The full subcategory of $\kappa$-presentable objects is closed under the cokernels of all morphisms (more generally, under all $\kappa$-small colimits) that exist in ${\textsf{A}}$, for any category ${\textsf{A}}$ with $\kappa$-directed colimits [1, Proposition 1.16]. The assertion concerning the kernels of admissible epimorphisms is nontrivial (and needs the epimorphism to be admissible).

Let $0\longrightarrow C\longrightarrow D\longrightarrow E\longrightarrow 0$ be an (admissible) short exact sequence in ${\textsf{A}}$ with $\kappa$-presentable objects D and E. Put $S=E$, and consider the identity morphism $S\longrightarrow E$. By Lemma 1.5 (1) $\Rightarrow$ (2) there exists a commutative diagram of a morphism of short exact sequences

with $T\in {\textsf{A}}_{<\kappa }$. Moreover, following the proof of Lemma 1.5 (1) $\Rightarrow$ (2), the diagram can be constructed in such a way that the object U is $\kappa$-presentable. By [9, Proposition 2.12 (iv) $\Rightarrow$ (ii)], we have a short exact sequence $0\longrightarrow U\longrightarrow C\oplus T\longrightarrow D \longrightarrow 0$ in ${\textsf{A}}$. Now $C\oplus T\in {\textsf{A}}_{<\kappa }$ by Proposition 1.4, hence $C\in {\textsf{A}}_{<\kappa }$. $\square$

Remark 1.7

(1) Proposition 1.1(c) together with Proposition A.1 (applied to the $\kappa$-accessible category ${\textbf{C}}^3({\textsf{A}})$ and the class ${\textsf{T}}$ of all short exact sequences in ${\textsf{A}}_{<\kappa }$) provide the following description of the class of all short exact sequences in ${\textsf{A}}$. A three-term complex in a locally $\kappa$-coherent exact category ${\textsf{A}}$ is a short exact sequence if and only if any morphism into it from a three-term complex in ${\textsf{A}}_{<\kappa }$ factorizes through a short exact sequence in ${\textsf{A}}_{<\kappa }$.

(2) Moreover, Proposition 1.1(b) together with Proposition A.1 (applied to the $\kappa$-accessible category ${\textbf{M}}^3({\textsf{A}})$ and the class ${\textsf{T}}$ of all short exact sequences in ${\textsf{A}}_{<\kappa }$, viewed as objects of ${\textbf{M}}^3({\textsf{A}})$) provide the following description. A pair of composable morphisms in ${\textsf{A}}$ is a short exact sequence if and only if any morphism into it from a pair of composable morphisms in ${\textsf{A}}_{<\kappa }$ factorizes through a short exact sequence in ${\textsf{A}}_{<\kappa }$.

(3) Remark 1.3 together with Proposition 1.4 (see also Proposition 1.6) imply that the admissible epimorphisms in ${\textsf{A}}$ are precisely the $\kappa$-directed colimits of admissible epimorphisms in (or between the objects of) ${\textsf{A}}_{<\kappa }$, and the admissible monomorphisms in ${\textsf{A}}$ are precisely the $\kappa$-directed colimits of admissible monomorphisms in (or between the objects of) ${\textsf{A}}_{<\kappa }$. Hence one can similarly characterize the admissible epimorphisms and the admissible monomorphisms in ${\textsf{A}}$ by factorization properties. In particular, we obtain the following lemma.

Lemma 1.8

Let ${\textsf{A}}$ be a locally $\kappa$-coherent exact category and $C\longrightarrow D$ be a morphism in ${\textsf{A}}$. Then the following conditions are equivalent:

• (1) $C\longrightarrow D$ is an admissible monomorphism in ${\textsf{A}}$;

• (2) any morphism into $C\longrightarrow D$ from a morphism in ${\textsf{A}}_{<\kappa }$ factorizes through an admissible monomorphism in (the inherited exact category structure on) ${\textsf{A}}_{<\kappa }$.

Proof

(1) $\Longrightarrow$ (2) By definition, $C\longrightarrow D$ is a $\kappa$-directed colimit of admissible monomorphisms in ${\textsf{A}}_{<\kappa }$. It remains to use Proposition 1.1(a) to the effect that all morphisms between objects from ${\textsf{A}}_{<\kappa }$ are $\kappa$-presentable in ${\textbf{M}}^2({\textsf{A}})$.

(2) $\Longrightarrow$ (1) Applying Proposition A.1 to the $\kappa$-accessible category of morphisms in ${\textsf{A}}$, we conclude that $C\longrightarrow D$ is a $\kappa$-directed colimit of admissible monomorphisms in ${\textsf{A}}_{<\kappa }$. It follows immediately by the definition of a locally $\kappa$-coherent exact category structure that $C\longrightarrow D$ is an admissible monomorphism in ${\textsf{A}}$. $\square$

Lemma 1.9

Let $\lambda$ and $\mu$ be a pair of regular cardinals such that $\lambda \triangleleft \mu$ in the sense of [1, Definition 2.12]. Then any locally $\lambda$-coherent exact category is locally $\mu$-coherent.

Proof

Any $\lambda$-accessible category is $\mu$-accessible by [1, Theorem 2.11]. The class of all admissible short exact sequences in a locally $\lambda$-coherent exact category ${\textsf{A}}$ is closed under $\lambda$-directed colimits by Lemma 1.2; hence it is also closed under $\mu$-directed colimits. It remains to obtain any short exact sequence $0\longrightarrow C\longrightarrow D \longrightarrow E\longrightarrow 0$ in ${\textsf{A}}$ as a $\mu$-directed colimit of short exact sequences of $\mu$-presentable objects. The construction from [1, proof of Theorem 2.11 (iv) $\Rightarrow$ (i)] fulfills the task, producing the desired representation from a given representation of $0\longrightarrow C\longrightarrow D\longrightarrow E\longrightarrow 0$ as a $\lambda$-directed colimit of short exact sequences of $\lambda$-presentable objects. $\square$

3 The Induced Exact Category Structure on the Ind-Objects

In this section, as in the previous one, $\kappa$ denotes a regular cardinal. Let ${\textsf{S}}$ be a small additive category. Consider the category ${\textsf{A}}={{\,\mathrm{\textsf{Ind}}\,}}_{(\kappa )}{\textsf{S}}$ of ind-objects representable by $\kappa$-directed diagrams of objects of ${\textsf{S}}$. Then the additive category ${\textsf{A}}$ is $\kappa$-accessible, and the full subcategory of $\kappa$-presentable objects in ${\textsf{A}}$ is naturally equivalent to the idempotent completion $\overline{{\textsf{S}}}$ of the category ${\textsf{S}}$. Conversely, for any $\kappa$-accessible additive category ${\textsf{A}}$, and any full additive subcategory ${\textsf{S}}\subset {\textsf{A}}_{<\kappa }$ such that all the objects of ${\textsf{A}}_{<\kappa }$ are direct summands of objects from ${\textsf{S}}$, one has a natural equivalence of categories ${\textsf{A}}\simeq {{\,\mathrm{\textsf{Ind}}\,}}_{(\kappa )}{\textsf{S}}$. In the case of the countable cardinal $\kappa =\aleph _0$, we will use the notation ${{\,\mathrm{\textsf{Ind}}\,}}{\textsf{S}}$ instead of ${{\,\mathrm{\textsf{Ind}}\,}}_{(\aleph _0)}{\textsf{S}}$.

The aim of this section is to show that any exact structure on ${\textsf{S}}$ extends uniquely to a locally $\kappa$-coherent exact structure on ${\textsf{A}}$ with the property that the full subcategory ${\textsf{S}}$ is closed under extensions in ${\textsf{A}}$. By Proposition 1.4, the latter condition holds automatically when the category ${\textsf{S}}$ is idempotent-complete. In particular, for any $\kappa$-accessible additive category ${\textsf{A}}$, locally $\kappa$-coherent exact structures on ${\textsf{A}}$ correspond bijectively to exact structures on the (essentially small) additive category ${\textsf{A}}_{<\kappa }$.

We proceed in two steps: first, extend a given exact category structure on ${\textsf{S}}$ to an exact category structure on the idempotent completion $\overline{{\textsf{S}}}={\textsf{A}}_{<\kappa }$ of ${\textsf{S}}$, and then extend it further to a locally $\kappa$-coherent exact structure on ${\textsf{A}}={{\,\mathrm{\textsf{Ind}}\,}}_{(\kappa )}{\textsf{S}}$. But first of all we present a counterexample demonstrating a pitfall involved with the question of uniqueness of extension of exact structures from ${\textsf{S}}$ to $\overline{{\textsf{S}}}$.

Example 2.1

Let ${\textsf{B}}$ denote the abelian category of morphisms of finite-dimensional vector spaces $f:V_0\longrightarrow V_1$ over a field k. Let ${\textsf{S}}\subset {\textsf{B}}$ be the full additive subcategory whose objects are all the morphisms f satisfying the equation $\dim _k V_0-\dim _k V_1= {{\,\textrm{rk}\,}}f$ (where ${{\,\textrm{rk}\,}}f=\dim _k{{\,\textrm{im}\,}}f$ is the rank of f). Then ${\textsf{S}}$ is a weakly idempotent-complete additive category and all objects of ${\textsf{B}}$ are direct summands of objects from ${\textsf{S}}$. Still all short exact sequences in ${\textsf{B}}$ with all the three terms belonging to ${\textsf{S}}$ are split (as the equation ${{\,\textrm{rk}\,}}g={{\,\textrm{rk}\,}}f+{{\,\textrm{rk}\,}}h$ implies splitness of a short exact sequence $0\longrightarrow f\longrightarrow g \longrightarrow h\longrightarrow 0$ in ${\textsf{B}}$). So both the abelian exact structure and the split exact structure on ${\textsf{B}}$ restrict to the split exact structure on ${\textsf{S}}$. Notice that ${\textsf{S}}$ is not closed under extensions in the abelian exact structure on ${\textsf{B}}$, however.

Lemma 2.2

Let ${\textsf{E}}$ be an exact category and $\overline{{\textsf{E}}}$ be the idempotent completion of the additive category ${\textsf{E}}$. Then there is a unique exact category structure on $\overline{{\textsf{E}}}$ such that ${\textsf{E}}$ is closed under extensions in $\overline{{\textsf{E}}}$ and the inherited exact category structure on ${\textsf{E}}$ is the originally given exact category structure. Specifically, the exact category structure on $\overline{{\textsf{E}}}$ is defined by the condition that the short exact sequences in $\overline{{\textsf{E}}}$ are the direct summands of short exact sequences in ${\textsf{E}}$.

Proof

Uniqueness: let $0\longrightarrow {\overline{A}}\longrightarrow {\overline{B}}\longrightarrow {\overline{C}}\longrightarrow 0$ be a short exact sequence in $\overline{{\textsf{E}}}$. Then there exist objects ${\overline{A}}'$ and ${\overline{C}}'\in \overline{{\textsf{E}}}$ such that $A={\overline{A}}\oplus {\overline{A}}'\in {\textsf{E}}$ and $C={\overline{C}}\oplus {\overline{C}}'\in {\textsf{E}}$. Now we have a short exact sequence $0\longrightarrow A\longrightarrow {\overline{A}}'\oplus \overline{B}\oplus {\overline{C}}'\longrightarrow C\longrightarrow 0$ in $\overline{{\textsf{E}}}$. Since the full subcategory ${\textsf{E}}$ is closed under extensions in $\overline{{\textsf{E}}}$ by assumption, it follows that all the three terms of the new short exact sequence belong to ${\textsf{E}}$. So any short exact sequence in $\overline{{\textsf{E}}}$ is a direct summand of a short exact sequence in ${\textsf{E}}$. Conversely, in any exact category, any direct summand of a short exact sequence is a short exact sequence, as one can easily show using the pullback and pushout axioms.

Existence: define the short exact sequences in $\overline{{\textsf{E}}}$ to be the direct summands of short exact sequences in ${\textsf{E}}$. This endows $\overline{{\textsf{E}}}$ with an exact category structure satisfying all the conditions [9, Proposition 6.13]. In particular, the fact that ${\textsf{E}}$ is closed under extensions in $\overline{{\textsf{E}}}$ is provable using the pullback and pushout axioms in the exact category ${\textsf{E}}$. $\square$

Lemma 2.3

Let ${\textsf{A}}$ be a $\kappa$-accessible additive category. Suppose given an exact category structure on ${\textsf{A}}_{<\kappa }$. Let $D\longrightarrow E$ be a morphism in ${\textsf{A}}$. Then the following conditions are equivalent:

• (1) $D\longrightarrow E$ is a $\kappa$-directed colimit in ${\textsf{A}}$ of admissible epimorphisms in ${\textsf{A}}_{<\kappa }$;

• (2) for any object $S\in {\textsf{A}}_{<\kappa }$, any morphism $S\longrightarrow E$ in ${\textsf{A}}$ can be included into a commutative square diagram

  

with an object $T\in {\textsf{A}}_{<\kappa }$ and an admissible epimorphism $T\longrightarrow S$ in ${\textsf{A}}_{<\kappa }$.

Proof

The proof is similar to that of Lemma 1.5. The only differences are that, in the proof of (1) $\Longrightarrow$ (2), the pullback should be taked in the exact category ${\textsf{A}}_{<\kappa }$; and in the proof of (2) $\Longrightarrow$ (1), the result of [9, Exercise 3.11(i)] should be applied in the exact category ${\textsf{A}}_{<\kappa }$. $\square$

Lemma 2.4

Let ${\textsf{A}}$ be a $\kappa$-accessible additive category. Suppose given an exact category structure on ${\textsf{A}}_{<\kappa }$. Then

(a):

any diagram

in the category ${\textsf{A}}$ whose upper line is a $\kappa$-directed colimit in ${\textsf{A}}$ of short exact sequences in ${\textsf{A}}_{<\kappa }$ can be obtained as a $\kappa$-directed colimit in ${\textsf{A}}$ of similar diagrams in ${\textsf{A}}_{<\kappa }$ with short exact sequences in the upper line;

(b):

any diagram

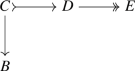
in the category ${\textsf{A}}$ whose upper line is a $\kappa$-directed colimit in ${\textsf{A}}$ of short exact sequences in ${\textsf{A}}_{<\kappa }$ can be obtained as a $\kappa$-directed colimit in ${\textsf{A}}$ of similar diagrams in ${\textsf{A}}_{<\kappa }$ with short exact sequences in the upper line.

Proof

Denote by ${\textsf{E}}$ the full subcategory in ${\textbf{C}}^3({\textsf{A}})$ consising of all the $\kappa$-directed colimits of short exact sequences in ${\textsf{A}}_{<\kappa }$. By Propositions 1.1(c) and A.1,  ${\textsf{E}}$ is a $\kappa$-accessible category, and its $\kappa$-presentable objects are the short exact sequences in ${\textsf{A}}_{<\kappa }$ (since the class of all short exact sequences in ${\textsf{A}}_{<\kappa }$ is closed under direct summands in ${\textbf{C}}^3({\textsf{A}})$). Now both the parts (a) and (b) are provable by applying Proposition A.3 to a suitable pair of functors. For part (a), take ${\textsf{K}}={\textsf{M}}={\textsf{A}}$,  ${\textsf{L}}={\textsf{E}}$, the identity functor $F:{\textsf{K}}\longrightarrow {\textsf{M}}$, and the functor $G:{\textsf{L}}\longrightarrow {\textsf{M}}$ assigning the object E to a three-term complex $C\longrightarrow D\longrightarrow E$. For part (b), take ${\textsf{K}}={\textsf{E}}$,  ${\textsf{L}}={\textsf{M}}={\textsf{A}}$, the identity functor $G:{\textsf{L}}\longrightarrow {\textsf{M}}$, and the functor $F:{\textsf{K}}\longrightarrow {\textsf{M}}$ assigning the object C to a three-term complex $C\longrightarrow D\longrightarrow E$. $\square$

Proposition 2.5

Let ${\textsf{A}}$ be a $\kappa$-accessible additive category. Suppose given an exact category structure on ${\textsf{A}}_{<\kappa }$. Then the class of all $\kappa$-directed colimits in ${\textsf{A}}$ of short exact sequences in ${\textsf{A}}_{<\kappa }$ is an exact category structure on ${\textsf{A}}$. Any short exact sequence in this exact category structure on ${\textsf{A}}$ whose terms belong to ${\textsf{A}}_{<\kappa }$ is a short exact sequence in the original exact category structure on ${\textsf{A}}_{<\kappa }$. Consequently, the resulting exact structure on ${\textsf{A}}$ is locally $\kappa$-coherent.

Proof

It is clear from Lemma 2.3 that the class of all admissible epimorphisms in the would-be exact structure on ${\textsf{A}}$ is closed under compositions. The pullback and pushforward axioms for short exact sequences in ${\textsf{A}}$ are provable using Lemma 2.4.

Here, in the case of the pullbacks, one also needs to use the fact that the $\kappa$-directed colimits of objects from ${\textsf{A}}_{<\kappa }$ in ${\textsf{A}}$ take pullbacks in ${\textsf{A}}_{<\kappa }$ to pullbacks in ${\textsf{A}}$ (more generally, this holds for all $\kappa$-small limits that happen to exist in ${\textsf{A}}_{<\kappa }$). In the case of the pushouts, the fact that the inclusion ${\textsf{A}}_{<\kappa }\longrightarrow {\textsf{A}}$ preserves those pushouts (and more generally, $\kappa$-small colimits) that happen to exist in ${\textsf{A}}_{<\kappa }$ needs to be used. Alternatively, it is convenient to check the axioms Ex2(a–b) from [21, Section A.3] and use [21, Corollary A.3].

The second assertion of the proposition follows from Proposition 1.1(c) and Proposition A.1 (applied to the $\kappa$-accessible category ${\textbf{C}}^3({\textsf{A}})$ and the class ${\textsf{T}}$ of all short exact sequences in ${\textsf{A}}_{<\kappa }$). Here one needs to use the observation that the class of all short exact sequences in ${\textsf{A}}_{<\kappa }$ (as in any exact category) is closed under direct summands, as mentioned in the proofs of Lemmas 2.2 and 2.4. The third and last assertion of the proposition follows from the previous ones. $\square$

Corollary 2.6

For any small exact category ${\textsf{S}}$, there exists a unique locally $\kappa$-coherent exact structure on the additive category of ind-objects ${{\,\mathrm{\textsf{Ind}}\,}}_{(\kappa )}{\textsf{S}}$ such that ${\textsf{S}}$ is closed under extensions in this exact category structure on ${{\,\mathrm{\textsf{Ind}}\,}}_{(\kappa )}{\textsf{S}}$ and the inherited exact structure on ${\textsf{S}}$ is the given one.

Proof

Notice that ${\textsf{A}}={{\,\mathrm{\textsf{Ind}}\,}}_{(\kappa )}{\textsf{S}}$ is a $\kappa$-accessible additive category with the full subcategory of $\kappa$-presentable objects ${\textsf{A}}_{<\kappa }$ naturally equivalent to the idempotent completion $\overline{{\textsf{S}}}$. Then use Lemma 2.2, and Propositions 2.5 and 1.4. $\square$

Theorem 2.7

For any $\kappa$-accessible additive category ${\textsf{A}}$, there is a natural bijective correspondence between exact structures on the small additive category ${\textsf{A}}_{<\kappa }$ and locally $\kappa$-coherent exact structures on the additive category ${\textsf{A}}$. To any exact structure on ${\textsf{A}}_{<\kappa }$, the exact structure on ${\textsf{A}}$ given by the class of all $\kappa$-directed colimits in ${\textsf{A}}$ of short exact sequence in ${\textsf{A}}_{<\kappa }$ is assigned. To any locally $\kappa$-coherent exact structure on ${\textsf{A}}$, the inherited exact structure on the full subcategory ${\textsf{A}}_{<\kappa }\subset {\textsf{A}}$ is assigned.

Proof

Follows from Propositions 2.5 and 1.4. $\square$

4 Example: Maximal Locally Coherent Exact Structure

Notice that there is a natural partial order on the class of all exact structures on any given additive category (given by inclusion of classes of admissible short exact sequences). Moreover, the intersection of any nonempty set/class of classes of short exact sequences defining exact structures is again a class of short exact sequences defining an exact structure. Furthermore, any additive category has a unique maximal exact category structure [11, 30, 31]. Hence the set of all exact structures on a small additive category is a complete lattice.

Let $\kappa$ be a regular cardinal and ${\textsf{A}}$ be a $\kappa$-accessible additive category. Then Theorem 2.7 provides an order-preserving bijection between the poset of locally $\kappa$-coherent exact structures on ${\textsf{A}}$ and the poset of all exact structures on the essentially small additive category ${\textsf{A}}_{<\kappa }$ of all $\kappa$-presentable objects in ${\textsf{A}}$. Thus the poset of all locally $\kappa$-coherent exact structures on ${\textsf{A}}$ is also a complete lattice. In this section, we are interested in the maximal locally $\kappa$-coherent exact structure on ${\textsf{A}}$.

Recall that a category ${\textsf{A}}$ is said to be locally $\kappa$-presentable [1, Definition 1.17 and Theorem 1.20] if ${\textsf{A}}$ is $\kappa$-accessible and all colimits exist in ${\textsf{A}}$. Locally $\aleph _0$-presentable categories are called locally finitely presentable [1, Definition 1.9 and Theorem 1.11].

The following lemma describes the maximal exact structure on the category of $\kappa$-presentable objects ${\textsf{A}}_{<\kappa }$ of a locally $\kappa$-presentable abelian category ${\textsf{A}}$. Given an additive category ${\textsf{E}}$ and two morphisms f, g in ${\textsf{E}}$, we denote by $\ker _{\textsf{E}}(g)$ and ${{\,\textrm{coker}\,}}_{\textsf{E}}(f)$ the kernel and cokernel of g and f computed in the category ${\textsf{E}}$.

Lemma 3.1

Let ${\textsf{A}}$ be a locally $\kappa$-presentable abelian category and $S\overset{f}{\longrightarrow }T\overset{g}{\longrightarrow }U$ be a composable pair of morphisms in the full subcategory ${\textsf{A}}_{<\kappa }\subset {\textsf{A}}$. In this context:

(a) if $g={{\,\textrm{coker}\,}}_{{\textsf{A}}_{<\kappa }}(f)$, then one also has $g={{\,\textrm{coker}\,}}_{\textsf{A}}(f)$;

(b) if $f=\ker _{{\textsf{A}}_{<\kappa }}(g)$, then one also has $f=\ker _{\textsf{A}}(g)$.

Consequently, the exact category structure on ${\textsf{A}}_{<\kappa }$ inherited from the abelian exact structure on ${\textsf{A}}$ is the maximal exact structure on ${\textsf{A}}_{<\kappa }$.

Proof

Notice first of all that the full subcategory ${\textsf{A}}_{<\kappa }$ is closed under extensions in ${\textsf{A}}$ by [33, Lemma A.4] (the running assumption in [33] that the category is Grothendieck is not needed for this lemma, as it suffices to know that the $\kappa$-directed colimit functors are exact in any locally $\kappa$-presentable abelian category [1, Proposition 1.59]). So ${\textsf{A}}_{<\kappa }$ inherits an exact category structure from the abelian exact structure of ${\textsf{A}}$, and the last assertion of the lemma makes sense.

Part (a): notice that the full subcategory ${\textsf{A}}_{<\kappa }$ is closed under all $\kappa$-small colimits, and in particular, under cokernels in ${\textsf{A}}$   [1, Proposition 1.16]. Consequently, one has ${{\,\textrm{coker}\,}}_{{\textsf{A}}_{<\kappa }}(f)={{\,\textrm{coker}\,}}_{\textsf{A}}(f)$ for any morphism f in ${\textsf{A}}_{<\kappa }$.

Part (b): denote by $S'=\ker _{\textsf{A}}(g)$ the kernel of the morphism g computed in the category ${\textsf{A}}$. Then the morphism f factorizes as $S\overset{h}{\longrightarrow }S'\longrightarrow T$. Now $S'$ is the sum of the images of the morphisms into $S'$ from $\kappa$-presentable objects $V\in {\textsf{A}}_{<\kappa }$. Any such morphism $V\longrightarrow S'$ factorizes through h, since the composition $V\longrightarrow S'\longrightarrow T$ factorizes through $S\longrightarrow T$, and $S'\longrightarrow T$ is a monomorphism in ${\textsf{A}}$. Hence the morphism h is an epimorphism in ${\textsf{A}}$.

Finally, the kernel K of the morphism $S\longrightarrow S'$ in ${\textsf{A}}$ is the sum of the images of the morphisms into K from $\kappa$-presentable objects $W\in {\textsf{A}}_{<\kappa }$. Any such morphism $W\longrightarrow K$ has to vanish, since the composition $W\longrightarrow K\longrightarrow S\longrightarrow S'\longrightarrow T$ vanishes, while the morphism $S\longrightarrow T$ is a monomorphism in ${\textsf{A}}_{<\kappa }$ and the morphism $K\longrightarrow S$ is a monomorphism in ${\textsf{A}}$. Thus $K=0$ and h is an isomorphism. $\square$

The following two corollaries describe the admissible epimorphisms and the admissible monomorphisms in the maximal locally $\kappa$-coherent exact structure on ${\textsf{A}}$.

Corollary 3.2

Let ${\textsf{A}}$ be a locally $\kappa$-presentable abelian category and $D\longrightarrow E$ be a morphism in ${\textsf{A}}$. Then the following conditions are equivalent:

• (1) $D\longrightarrow E$ is an admissible epimorphism in the maximal locally $\kappa$-coherent exact structure on ${\textsf{A}}$;

• (2) for any object $S\in {\textsf{A}}_{<\kappa }$, any morphism $S\longrightarrow E$ in ${\textsf{A}}$ can be included into a commutative square diagram

  

such that $T\in {\textsf{A}}_{<\kappa }$ and $T\longrightarrow S$ is an epimorphism in ${\textsf{A}}$ with the kernel $\ker (T\twoheadrightarrow S)$ belonging to ${\textsf{A}}_{<\kappa }$.

Proof

Follows from Lemmas 2.3 and 3.1. $\square$

Corollary 3.3

Let ${\textsf{A}}$ be a locally $\kappa$-presentable abelian category and $C\longrightarrow D$ be a morphism in ${\textsf{A}}$. Then the following conditions are equivalent:

• (1) $C\longrightarrow D$ is an admissible monomorphism in the maximal locally $\kappa$-coherent exact structure on ${\textsf{A}}$;

• (2) any morphism into $C\longrightarrow D$ from a morphism in ${\textsf{A}}_{<\kappa }$ factorizes through a morphism in ${\textsf{A}}_{<\kappa }$ that is a monomorphism in ${\textsf{A}}$.

Proof

It is worth noticing that a morphism g in ${\textsf{A}}_{<\kappa }$ is a monomorphism in ${\textsf{A}}$ if and only if g is a monomorphism in ${\textsf{A}}_{<\kappa }$ (by Lemma 3.1(b)). Furthermore, any monomorphism is admissible in the maximal exact structure on ${\textsf{A}}_{<\kappa }$, as the full subcategory ${\textsf{A}}_{<\kappa }$ is closed under cokernels in ${\textsf{A}}$ (by [1, Proposition 1.16]). In view of these remarks, the assertion of the corollary follows from Lemma 1.8. $\square$

A locally $\kappa$-presentable abelian category ${\textsf{A}}$ is said to be locally $\kappa$-coherent (as an abelian category) if the kernel of any epimorphism between two $\kappa$-presentable objects is again $\kappa$-presentable in ${\textsf{A}}$. Equivalently, ${\textsf{A}}$ is locally $\kappa$-coherent if and only if the full subcategory ${\textsf{A}}_{<\kappa }$ is closed under kernels (of arbitrary morphisms) in ${\textsf{A}}$. In the case of the cardinal $\kappa =\aleph _0$, this definition agrees with the definition of a locally coherent abelian category introduced in the paper [29, Section 2] and discussed in [23, Section 9.5], [27, Section 8.2].

Corollary 3.4

Let ${\textsf{A}}$ be a locally $\kappa$-presentable abelian category. Then the maximal locally $\kappa$-coherent exact structure on ${\textsf{A}}$ coincides with the abelian exact structure on ${\textsf{A}}$ if and only if ${\textsf{A}}$ is locally $\kappa$-coherent as an abelian category.

Proof

“Only if”: by Proposition 1.6, the full subcategory ${\textsf{A}}_{<\kappa }$ is closed under kernels of admissible epimorphisms in any locally $\kappa$-coherent exact structure on ${\textsf{A}}$.

“If”: when ${\textsf{A}}$ is a locally $\kappa$-coherent abelian category, the full subcategory ${\textsf{A}}_{<\kappa }$ is closed under kernels and cokernels in ${\textsf{A}}$; so ${\textsf{A}}_{<\kappa }$ is an abelian category. We have to show that the locally $\kappa$-coherent exact structure on ${\textsf{A}}$ corresponding to the abelian exact structure on ${\textsf{A}}_{<\kappa }$ is the abelian exact structure on ${\textsf{A}}$.

For this purpose, in view of Corollary 3.2, it suffices to check that any epimorphism $D\longrightarrow E$ in ${\textsf{A}}$ and any morphism $S\longrightarrow E$ in ${\textsf{A}}$ with $S\in {\textsf{A}}_{<\kappa }$ can be included into a commutative square diagram

with an object $T\in {\textsf{A}}_{<\kappa }$ and an epimorphism $T\longrightarrow S$ in ${\textsf{A}}$. The latter assertion holds in any locally $\kappa$-presentable abelian category ${\textsf{A}}$, as explained in [25, proof of Lemma 10.7]. $\square$

Example 3.5

To give another example of a locally $\kappa$-coherent exact category structure, consider a locally $\kappa$-presentable abelian category ${\textsf{A}}$, and suppose given a class of $\kappa$-presentable objects ${\textsf{T}}\subset {\textsf{A}}_{<\kappa }$ such that ${\textsf{T}}$ is closed under extensions in ${\textsf{A}}_{<\kappa }$, or equivalently, in ${\textsf{A}}$ (cf. the proof of Lemma 3.1).

Then, by Proposition A.1, the full subcategory ${\textsf{B}}=\varinjlim _{(\kappa )}{\textsf{T}}\subset {\textsf{A}}$ is $\kappa$-accessible, and the full subcategory of all $\kappa$-presentable objects in ${\textsf{B}}$ coincides with the idempotent completion of ${\textsf{T}}$, that is ${\textsf{B}}_{<\kappa }=\overline{{\textsf{T}}}$. Following the discussion in the beginnning of Sect. 2, we have an equivalence of additive categories ${\textsf{B}}\simeq {{\,\mathrm{\textsf{Ind}}\,}}_{(\kappa )}{\textsf{T}}$.

Endow the additive category ${\textsf{T}}$ with the exact category structure inherited from the abelian category ${\textsf{A}}$. Then the additive category ${\textsf{B}}\simeq {{\,\mathrm{\textsf{Ind}}\,}}_{(\kappa )}{\textsf{T}}$ acquires the induced locally $\kappa$-coherent exact structure, as per Corollary 2.6. We will call this exact structure the standard locally $\kappa$-coherent exact structure on ${\textsf{B}}=\varinjlim _{(\kappa )}{\textsf{T}}$.

Notice that, even when ${\textsf{T}}={\textsf{A}}_{<\kappa }$, and consequently, ${\textsf{B}}={\textsf{A}}$, the standard locally $\kappa$-coherent exact structure on ${\textsf{A}}$ differs from the abelian exact structure (generally speaking). In fact, the standard locally $\kappa$-coherent exact structure on ${\textsf{B}}={\textsf{A}}$ is the maximal locally $\kappa$-coherent exact structure (by Lemma 3.1). For example, when $\kappa =\aleph _0$ and ${\textsf{A}}={{\textsf{Mod}\text {--}}}R$ is the category of right modules over a ring R, the maximal locally coherent exact structure on ${{\textsf{Mod}\text {--}}}R$ coincides with the abelian exact structure if and only if the ring R is right coherent (by Corollary 3.4).

5 Example: Pure Exact Structure and Flat Coherence

Let $\kappa$ be a regular cardinal and ${\textsf{A}}$ be a $\kappa$-accessible additive category. The minimal element in the complete lattice of all locally $\kappa$-coherent exact structures on ${\textsf{A}}$ (as per the discussion in Sect. 3) is the locally $\kappa$-coherent exact structure corresponding to the split exact structure on ${\textsf{A}}_{<\kappa }$. This exact structure on a $\kappa$-accessible additive category ${\textsf{A}}$ is called the $\kappa$-pure exact structure, or in the case of $\kappa =\aleph _0$, simply the pure exact structure [10, Section 3], [35, Section 4].

The admissible short exact sequences in the $\kappa$-pure exact structure on ${\textsf{A}}$ are the $\kappa$-directed colimits of split short exact sequences in ${\textsf{A}}_{<\kappa }$, or equivalently (by Lemma 1.2), the $\kappa$-directed colimits of split short exact sequences in ${\textsf{A}}$. So the $\kappa$-pure exact structure is locally $\kappa$-coherent by definition, and in particular, the pure exact structure is locally coherent.

The following lemmas and propositions provide a description of admissible epimorphisms and admissible monomorphisms in the $\kappa$-pure exact structure. These descriptions are fairly standard and usually taken as the definitions of pure epimorphisms and pure monomorphisms (cf. [1, Definition 2.27], [2, Definition 1], [10, 35]); nevertheless, our results provide a generalization of [2, Proposition 5] from abelian to additive categories.

Lemma 4.1

Let ${\textsf{A}}$ be a category and $p:D\longrightarrow E$, $e:S\longrightarrow E$ be a pair of morphisms in ${\textsf{A}}$ with the same codomain. Then there exists a commutative square

with a split epimorphism $s:T\longrightarrow S$ in ${\textsf{A}}$ if and only if the morphism $e:S\longrightarrow E$ factorizes through the morphism $p:D\longrightarrow E$,

If this is the case, one can choose $T=S$ and $s=\textrm{id}_S$.

Proof

Given a splitting $i:S\longrightarrow T$ (such that $si=\textrm{id}_S$), it suffices to put $l=di$. The remaining assertions are even more obvious. $\square$

Proposition 4.2

Let ${\textsf{A}}$ be a $\kappa$-accessible additive category and $p:D\longrightarrow E$ be a morphism in ${\textsf{A}}$. Then p is an admissible epimorphism in the $\kappa$-pure exact structure on ${\textsf{A}}$ if and only if, for every object $S\in {\textsf{A}}_{<\kappa }$, any morphism $e:S\longrightarrow E$ can be lifted over the morphism p,

Proof

Compare Lemma 2.3 with Lemma 4.1. $\square$

Lemma 4.3

Let ${\textsf{A}}$ be a $\kappa$-accessible additive category. Suppose given a commutative square diagram

in ${\textsf{A}}$ with objects S, $T\in {\textsf{A}}_{<\kappa }$. Then the following two conditions are equivalent:

• (1) the morphism of morphisms $(c,d):(S\overset{t}{\rightarrow }T)\longrightarrow (C\overset{i}{\rightarrow }D)$ factorizes through a split monomorphism $(U\overset{j}{\rightarrow }V)$ in ${\textsf{A}}$ with U, $V\in {\textsf{A}}_{<\kappa }$;

• (2) the morphism $c:S\longrightarrow C$ factorizes through the morphism $t:S\longrightarrow T$,

  

Proof

(1) $\Longrightarrow$ (2) Suppose given a factorization

with $au=c$ and $bv=d$ as in (1), and let $q:V\longrightarrow U$ be a splitting (such that $qj=\textrm{id}_U$). Then one has $aqvt=aqju=au=c$, so it remains to put $e=aqv: T\longrightarrow C$ in order to satisfy (2).

(2) $\Longrightarrow$ (1) Consider the morphism $f=d-ie:T\longrightarrow D$. One has $ft=dt-iet=ic-ic=0$, so the composition $S\overset{t}{\longrightarrow }T\overset{f}{\longrightarrow }D$ vanishes.

Let $D=\varinjlim _{\xi \in \Xi }V_\xi$ be a representation of D as a $\kappa$-directed colimit of $\kappa$-presentable objects $V_\xi$. Let $b_\xi :V_\xi \longrightarrow D$ be the morphisms in the colimit cocone. Since the object T is $\kappa$-presentable, there exists an index $\xi _0\in \Xi$ such that the morphism $f:T\longrightarrow D$ factorizes as $T\longrightarrow V_{\xi _0}\overset{b_{\xi _0}}{\longrightarrow }D$. Then the composition $S\overset{t}{\longrightarrow }T\longrightarrow V_{\xi _0} \overset{b_{\xi _0}}{\longrightarrow }D$ vanishes. Since the object S is $\kappa$-presentable, there exists an index $\xi _1\in \Xi$,  $\xi _1>\xi _0$, such that the composition $S\overset{t}{\longrightarrow }T\longrightarrow V_{\xi _0}\longrightarrow V_{\xi _1}$ vanishes. Denote the composition $T\longrightarrow V_{\xi _0}\longrightarrow V_{\xi _1}$ by $v':T\longrightarrow V_{\xi _1}$; so we have $v't=0$ and $b_{\xi _1}v'=f$. Now the commutative diagram

provides the desired factorization with $T\oplus V_{\xi _1}\in {\textsf{A}}_{<\kappa }$ and a split monomorphism $j=(\textrm{id}_T,0)$. $\square$

Proposition 4.4

Let ${\textsf{A}}$ be a $\kappa$-accessible additive category and $i:C\longrightarrow D$ be a morphism in ${\textsf{A}}$. Then i is an admissible monomorphism in the $\kappa$-pure exact structure on ${\textsf{A}}$ if and only if, for every commutative square diagram

in ${\textsf{A}}$ with objects S, $T\in {\textsf{A}}_{<\kappa }$, the morphism $c:S\longrightarrow C$ factorizes through the morphism $t:S\longrightarrow T$,

Proof

Compare Lemma 1.8 with Lemma 4.3. $\square$

Example 4.5

Let R be a ring and ${\textsf{A}}={{\mathsf {Mod_{fl}}\text {--}}}R$ be the category of flat right R-modules. Then ${\textsf{A}}$ is a finitely accessible additive category, and its finitely presentable objects are precisely all the finitely generated projective R-modules (since the flat R-modules are the directed colimits of finitely generated projective ones, by the classical Govorov–Lazard theorem [13, 17]).

Furthermore, the exact category structure on ${\textsf{A}}$ inherited from the abelian exact structure of the ambient abelian category of arbitrary R-modules ${{\textsf{Mod}\text {--}}}R\supset {{\mathsf {Mod_{fl}}\text {--}}}R$ coincides with the pure exact structure on ${\textsf{A}}$. Indeed, the functors of directed colimit are exact in ${{\textsf{Mod}\text {--}}}R$, so the directed colimits of split short exact sequences of finitely generated projective modules are short exact sequences of flat modules. Conversely, any surjective morphism of flat R-modules is an epimorphism in the pure exact structure on ${\textsf{A}}={{\mathsf {Mod_{fl}}\text {--}}}R$, as one can see from Proposition 4.2.

The assertion that the pure exact structure on ${{\mathsf {Mod_{fl}}\text {--}}}R$ is inherited from the abelian exact structure on ${{\textsf{Mod}\text {--}}}R$ is also a special case of Theorem 6.3 below. See the first paragraph of Example 7.7.

Proposition 4.6

For any ring R and regular cardinal $\kappa$, the exact category of flat R-modules ${\textsf{A}}={{\mathsf {Mod_{fl}}\text {--}}}R$ (with the exact structure inherited from the abelian exact structure on ${{\textsf{Mod}\text {--}}}R$) is locally $\kappa$-coherent. The $\kappa$-presentable objects of ${{\mathsf {Mod_{fl}}\text {--}}}R$ are the flat R-modules that are $\kappa$-presentable in ${{\textsf{Mod}\text {--}}}R$.

Proof

For any uncountable regular cardinal $\kappa$ one has $\aleph _0 \triangleleft \kappa$   [1, Example 2.13(1)]. So the first assertion of the proposition follows from Example 4.5 and Lemma 1.9. The second assertion can be easily obtained from [1, proof of Theorem 2.11(iv) $\Rightarrow$ (i)]; see [24, Lemma 1.2]. $\square$

The following corollary, which can be also found in [24, Lemma 4.1] for $\kappa =\aleph _1$ and in [25, Corollary 10.12] in the general case, describes the “flat coherence” phenomenon.

Corollary 4.7

Let R be a ring and $\kappa$ be a regular cardinal. Then the kernel of any surjective morphism of $\kappa$-presentable flat R-modules is a $\kappa$-presentable flat R-module.

Proof

Compare Proposition 4.6 with Proposition 1.6. $\square$

6 Locally Coherent Exact Categories are of Grothendieck Type

Starting from this section, we gradually specialize our discussion in this paper from the case of an arbitrary regular cardinal $\kappa$ to that of $\kappa =\aleph _0$. In this context, we will call the locally $\aleph _0$-coherent exact categories in the sense of the definition in Sect. 1 simply locally coherent exact categories.

The aim of this section is to show that all locally coherent exact categories are of Grothendieck type in the sense of Št’ovíček [34, Definitions 3.4 and 3.11]. Consequently, the small object argument can be used to prove completeness of cotorsion pairs in such exact categories [34, Theorem 5.16]; and in particular, any such exact category has enough injective objects [34, Corollary 5.9].

Let ${\textsf{A}}$ be a category and $\alpha$ be an ordinal. An $\alpha$-indexed chain (of objects and morphisms) $(A_\beta )_{0\le \beta <\alpha }$ in ${\textsf{A}}$ is a diagram in ${\textsf{A}}$ indexed by the ordered set $\alpha$. So $A_\beta$ is an object of ${\textsf{A}}$ for every $0\le \beta <\alpha$, and a commutative diagram of morphisms $A_\beta \longrightarrow A_\gamma$ in ${\textsf{A}}$ is given, indexed by all pairs of ordinals $0\le \beta< \gamma <\alpha$. An $\alpha$-indexed chain $(A_\beta )_{0\le \beta <\alpha }$ in ${\textsf{A}}$ is said to be smooth if $A_\gamma =\varinjlim _{\beta <\gamma }A_\beta$ in ${\textsf{A}}$ for every limit ordinal $\gamma <\alpha$. If the colimit $A_\alpha =\varinjlim _{\beta <\alpha }A_\beta$ of a smooth chain $(A_\beta )_{0\le \beta <\alpha }$ of objects and morphisms in ${\textsf{A}}$ exists, then the morphism $A_0\longrightarrow A_\alpha$ is said to be the transfinite composition of the morphisms $A_\beta \longrightarrow A_{\beta +1}$, $0\le \beta<\beta +1<\alpha$.

Let ${\textsf{M}}$ be a class of morphisms in ${\textsf{A}}$. We will say that transfinite compositions of morphisms from ${\textsf{M}}$ exist in ${\textsf{A}}$ if, for every smooth chain $(A_\beta )_{0\le \beta <\alpha }$ of objects and morphisms in ${\textsf{A}}$ such that the morphism $A_\beta \longrightarrow A_{\beta +1}$ belongs to ${\textsf{M}}$ for all $0\le \beta<\beta +1<\alpha$, the colimit $A_\alpha = \varinjlim _{\beta <\alpha }A_\beta$ exists in ${\textsf{A}}$. If this is the case, and moreover, the transfinite composition $A_0\longrightarrow A_\alpha$ then also belongs to ${\textsf{M}}$, we will say that transfinite compositions of morphisms from ${\textsf{M}}$ exists in ${\textsf{A}}$ and are themselves morphisms from ${\textsf{M}}$.

Let ${\textsf{A}}$ be a category and ${\textsf{M}}$ be a class of morphisms in ${\textsf{A}}$. Then an object $B\in {\textsf{A}}$ is said to be small relative to ${\textsf{M}}$ if there exists a cardinal $\lambda$ satisfying the following condition. For every smooth chain of objects and morphisms $(A_\beta )_{0\le \beta <\alpha }$ in ${\textsf{A}}$ such that the morphisms $A_\beta \longrightarrow A_{\beta +1}$ belong to ${\textsf{M}}$ for all $0\le \beta<\beta +1<\alpha$ and the cofinality of the ordinal $\alpha$ is not smaller than $\lambda$, the natural map of sets $\varinjlim _{\beta <\alpha }{{\,\textrm{Hom}\,}}_{\textsf{A}}(B,A_\beta )\longrightarrow {{\,\textrm{Hom}\,}}_{\textsf{A}}(B,A_\alpha )$ must be bijective. It is presumed here that the colimit $A_\alpha = \varinjlim _{\beta <\alpha }A_\beta$ exists in ${\textsf{A}}$.

Let ${\textsf{A}}$ be an exact category. An $\alpha$-indexed filtration $(F_\beta )_{0\le \beta \le \alpha }$ in ${\textsf{A}}$ is a smooth $(\alpha +1)$-indexed chain of objects and morphisms such that $F_0=0$ and the morphism $F_\beta \longrightarrow F_{\beta +1}$ is an admissible monomorphism for all $0\le \beta <\alpha$. Given an $\alpha$-indexed filtration $(F_\beta )_{0\le \beta \le \alpha }$, the object $F=F_\alpha$ is said to be filtered by the cokernels $U_\beta ={{\,\textrm{coker}\,}}(F_\beta \rightarrow F_{\beta +1})$ of the morphisms $F_\beta \longrightarrow F_{\beta +1}$, $0\le \beta <\alpha$.

Given a class of objects ${\textsf{U}}\subset {\textsf{A}}$, one says that an object $F\in {\textsf{A}}$ is filtered by (objects from) ${\textsf{U}}$ if there is an ordinal $\alpha$ and an $\alpha$-indexed filtration $(F_\beta )_{0\le \beta \le \alpha }$ on $F=F_\alpha$ such that ${{\,\textrm{coker}\,}}(F_\beta \rightarrow F_{\beta +1})\in {\textsf{U}}$ for all $0\le \beta <\alpha$. The class of all objects in ${\textsf{A}}$ filtered by objects from ${\textsf{U}}$ is denoted by ${{\,\mathrm{\textsf{Fil}}\,}}({\textsf{U}})\subset {\textsf{A}}$.

A class of objects ${\textsf{F}}\subset {\textsf{A}}$ is said to be deconstructible if there exists a set of objects ${\textsf{U}}\subset {\textsf{F}}$ such that ${\textsf{F}}={{\,\mathrm{\textsf{Fil}}\,}}({\textsf{U}})$. In particular, the exact category ${\textsf{A}}$ is said to be deconstructible in itself if there exists a set of objects ${\textsf{U}}\subset {\textsf{A}}$ such that ${\textsf{A}}={{\,\mathrm{\textsf{Fil}}\,}}({\textsf{U}})$.

Given an exact category ${\textsf{A}}$, we say that ${\textsf{A}}$ admits a generator if there is an object $G\in {\textsf{A}}$ such that for every object $B\in {\textsf{A}}$ there exists a set $\Lambda$ and an admissible epimorphism $G^{(\Lambda )}\longrightarrow B$. Here $G^{(\Lambda )}$ denotes the coproduct of $\Lambda$ copies of G in ${\textsf{A}}$.

An exact category ${\textsf{A}}$ is called efficient [34, Definition 3.4] if it satisfies the following conditions:

(Ef0) or (GT0):

The additive category ${\textsf{A}}$ is weakly idempotent-complete.

(Ef1) or (GT1):

All transfinite compositions of admissible monomorphisms exist in ${\textsf{A}}$, and are themselves admissible monomorphisms.

(Ef2) or (GT2):

Every object of ${\textsf{A}}$ is small relative to the class of all admissible monomorphisms.

(Ef3) or (GT3):

The exact category ${\textsf{A}}$ admits a generator.

An exact category ${\textsf{A}}$ is said to be of Grothendieck type [34, Definition 3.11] if ${\textsf{A}}$ is efficient (i. e., it satisfies conditions (GT0)–(GT3)), and the following additional condition holds:

• (GT4) The exact category ${\textsf{A}}$ is deconstructible in itself.

Given a finitely accessible category ${\textsf{A}}$, we will use the notation ${\textsf{A}}_\textsf{fp}={\textsf{A}}_{<\aleph _0}$ for the full subcategory of finitely presentable objects in ${\textsf{A}}$. The following well-known lemma is a generalization of [5, Lemma 2.2] and [22, Proposition 5.2].

Lemma 5.1

Let ${\textsf{A}}$ be a finitely accessible additive category and ${\mathcal {S}}$ be a small category equivalent to ${\textsf{A}}_\textsf{fp}$, viewed as a ring with many objects. Then the additive category ${\textsf{A}}$ is naturally equivalent to the additive category ${{\mathsf {Mod_{fl}}\text {--}}}{\mathcal {S}}$ of flat right ${\mathcal {S}}$-modules. The pure exact structure on ${\textsf{A}}$ corresponds to the exact structure on ${{\mathsf {Mod_{fl}}\text {--}}}{\mathcal {S}}$ inherited from the abelian category ${{\textsf{Mod}\text {--}}}{\mathcal {S}}$ of all right ${\mathcal {S}}$-modules.

Proof

This is [10, Section 1.4] or [35, Proposition 4.2], and a particular case of [1, Theorem 2.26]. The point is that the category ${\textsf{A}}_\textsf{fp}$ is naturally equivalent to the category of finitely generated projective right ${\mathcal {S}}$-modules (since ${\textsf{A}}_\textsf{fp}$ is additive and idempotent-complete), and the flat right ${\mathcal {S}}$-modules are the directed colimits of the finitely generated projective ones. For the second assertion, cf. Example 4.5. $\square$

Let ${\textsf{A}}$ be an exact category. We will say that ${\textsf{A}}$ has exact functors of directed colimit if all directed colimits exist in the additive category ${\textsf{A}}$ and the directed colimits of admissible short exact sequences are admissible short exact sequences. A locally $\kappa$-coherent exact category need not have exact functors of directed colimit, but it always has exact functors of $\kappa$-directed colimit (in the obvious sense), by Lemma 1.2.

Proposition 5.2

Let ${\textsf{A}}$ be a $\kappa$-accessible additive category with directed colimits, endowed with an exact structure with exact functors of directed colimit. Then ${\textsf{A}}$ is an efficient exact category.

Proof

We check the axioms one by one.

(Ef0) or (GT0) Any additive category with $\kappa$-directed colimits is idempotent-complete.

(Ef1) or (GT1) All transfinite compositions of chains of morphisms exist in any category with directed colimits. All transfinite compositions of admissible monomorphisms are admissible monomorphisms in any exact category with exact functors of directed colimit (since finite compositions of admissible monomorphisms are admissible monomorphisms in any exact category, and directed colimits of admissible monomorphisms are admissible monomorphisms in an exact category with exact functors of directed colimit).

(Ef2) or (GT2) All objects in any accessible category have presentability ranks, so they are small with respect to the class of all morphisms. In fact, if $B=\varinjlim _{\xi \in \Xi }S_\xi$ in a category ${\textsf{A}}$ with $\kappa$-directed colimits, where $\Xi$ is a small $\kappa$-filtered category and $S_\xi \in {\textsf{A}}_{<\kappa }$ for all $\xi \in \Xi$, and if $\lambda \ge \kappa$ is a regular cardinal greater than the cardinality of (the set of all objects and morphisms in) $\Xi$, then the object B is $\lambda$-presentable in ${\textsf{A}}$ (see [1, Proposition 1.16]).

(Ef3) or (GT3) The point is that any admissible epimorphism in the $\kappa$-pure exact structure on ${\textsf{A}}$ is also an admissible epimorphism in any exact structure on ${\textsf{A}}$ with exact functors of $\kappa$-directed colimit. So it suffices to consider the case of the $\kappa$-pure exact structure on ${\textsf{A}}$.

Now the coproduct of all representatives of isomorphism classes of $\kappa$-presentable objects is a generator in the $\kappa$-pure exact structure on any $\kappa$-accessible additive category ${\textsf{A}}$. In fact, if $B=\varinjlim _{\xi \in \Xi }S_\xi$ in ${\textsf{A}}$, where $\Xi$ is a small $\kappa$-filtered category and $S_\xi \in {\textsf{A}}_{<\kappa }$ for all $\xi \in \Xi$, then the natural morphism $\coprod _{\xi \in \Xi }S_\xi \longrightarrow \varinjlim _{\xi \in \Xi }S_\xi$ is a $\kappa$-pure epimorphism in (i. e., an admissible epimorphism in the $\kappa$-pure exact structure on) ${\textsf{A}}$, as one can see from Proposition 4.2. $\square$

Theorem 5.3

Let ${\textsf{A}}$ be a finitely accessible category endowed with an exact structure with exact functors of directed colimit. Then ${\textsf{A}}$ is an exact category of Grothendieck type.

Proof

In view of Proposition 5.2, it remains to check the last axiom (GT4). Indeed, for any ring with many objects ${\mathcal {S}}$, the exact category of flat ${\mathcal {S}}$-modules ${{\mathsf {Mod_{fl}}\text {--}}}{\mathcal {S}}$ is deconstructible in itself, essentially by [8, Lemma 1 and Proposition 2]. In view of Lemma 5.1, it follows that any finitely accessible additive category ${\textsf{A}}$ endowed with the pure exact structure is deconstructible in itself. As, under the assumptions of the theorem, any filtration in the pure exact structure on ${\textsf{A}}$ is also a filtration in the given exact structure on ${\textsf{A}}$, we can conclude that any exact category ${\textsf{A}}$ satisfying the assumptions of the theorem is deconstructible in itself. $\square$

Corollary 5.4

All locally coherent exact categories are of Grothendieck type. In particular, in any locally coherent exact category, there are enough injective objects.

Proof

Follows from Theorem 5.3 and [34, Corollary 5.9]. Alternatively, one can refer to Propositions 6.1(a,c) and 6.2 below, [22, Proposition A(i–ii) in Section 0.2], and [34, Theorem 3.16] (for the first assertion of the corollary). $\square$

7 Canonical Embedding into Abelian Category

The aim of this section is to represent an arbitrary locally coherent exact category ${\textsf{C}}$ as a full subcategory in a locally finitely presentable (in fact, locally type $\textrm{FP}_\infty )$ Grothendieck abelian category ${\textsf{K}}$, and show that ${\textsf{C}}$ enjoys nice closure properties as a full subcategory in ${\textsf{K}}$. It is important that the locally coherent exact structure on ${\textsf{C}}$ turns out to be inherited from the abelian exact structure on ${\textsf{K}}$.

For any small exact category ${\textsf{E}}$, there is a classical construction of the canonical embedding of ${\textsf{E}}$ into the abelian category ${\textsf{K}}$ of additive sheaves on ${\textsf{E}}$. Let us recall some details [15, Proposition A.2], [36, Section A.7], [9, Appendix A].

The category ${\textsf{K}}$ is defined as the category of all left exact contravariant functors ${\textsf{E}}^\textsf{op}\longrightarrow \textsf{Ab}$. Here $\textsf{Ab}$ denotes the category of abelian groups; and a contravariant functor $K:{\textsf{E}}^\textsf{op}\longrightarrow \textsf{Ab}$ is said to be left exact if, for any admissible short exact sequence $0\longrightarrow E'\longrightarrow E\longrightarrow E''\longrightarrow 0$ in ${\textsf{E}}$, the sequence of abelian groups $0\longrightarrow K(E'') \longrightarrow K(E)\longrightarrow K(E')$ is left exact. The functor $\rho :{\textsf{E}}\longrightarrow {\textsf{K}}$ assigns to every object $E\in {\textsf{E}}$ the representable functor $\rho (E)={{\,\textrm{Hom}\,}}_{\textsf{E}}({-},E)$. The following proposition summarizes the classical theory.

Proposition 6.1

(a) The functor $\rho$ is fully faithful. The category ${\textsf{K}}$ is abelian.

(b) A short sequence $0\longrightarrow E'\longrightarrow E\longrightarrow E'' \longrightarrow 0$ in ${\textsf{E}}$ is admissible exact if and only if its image $0\longrightarrow \rho (E')\longrightarrow \rho (E)\longrightarrow \rho (E'')\longrightarrow 0$ is exact in ${\textsf{K}}$.

(c) The essential image of the functor $\rho$ is closed under extensions in ${\textsf{K}}$.

(d) For any objects $K\in {\textsf{K}}$ and $E\in {\textsf{E}}$, and any epimorphism $K\longrightarrow \rho (E)$ in ${\textsf{K}}$, there exists an admissible epimorphism $F\longrightarrow E$ in ${\textsf{E}}$ and a morphism $\rho (F)\longrightarrow K$ in ${\textsf{K}}$ making the triangular diagram $\rho (F)\longrightarrow K\longrightarrow \rho (E)$ commutative in ${\textsf{K}}$.

(e) If the category ${\textsf{E}}$ is weakly idempotent-complete, then the essential image of the functor $\rho$ is closed under kernels of epimorphisms in ${\textsf{K}}$.

Proof

The first assertion of part (a) holds by Yoneda’s lemma. The second assertion of part (a) is [36, Proposition A.7.13] or [9, Lemma A.20]. Part (b) is [36, Propositions A.7.14 and A.7.16(a)] or [9, Lemmas A.21 and A.23]. Part (c) is [36, Lemma A.7.18] or [9, Lemma A.24]. Part (d) is [36, second paragraph of Lemma A.7.15] or [9, Lemma A.22]. Part (e) is [36, Proposition A.7.16(b)]. $\square$

Following [12, Section 3] and [7, Section 3 of the published version or Section 2 of the arXiv version], an object S in a Grothendieck category ${\textsf{K}}$ is said to be of type $\textrm{FP}_\infty$ if, for every $n\ge 0$, the functor ${{\,\textrm{Ext}\,}}^n_{\textsf{K}}(S,{-}): {\textsf{K}}\longrightarrow \textsf{Ab}$ preserves directed colimits. Obviously, objects of type $\textrm{FP}_\infty$ are finitely presentable. A Grothendieck category ${\textsf{K}}$ is said to be locally type $\textrm{FP}_\infty$ if it has a set of generators consisting of objects of type $\textrm{FP}_\infty$.

Proposition 6.2

The category ${\textsf{K}}$ is a locally finitely presentable Grothendieck category, and in fact, it is locally type $\textrm{FP}_\infty$. The objects in the image of the functor $\rho :{\textsf{E}}\longrightarrow {\textsf{K}}$ are of type $\textrm{FP}_\infty$, and they form a set of generators of ${\textsf{K}}$.

Proof

By construction, ${\textsf{K}}$ is a full subcategory in the category ${{\,\mathrm{\textsf{Fun}}\,}}_{\mathbb {Z}}({\textsf{E}}^\textsf{op},\textsf{Ab})$ of all contravariant additive functors ${\textsf{E}}^\textsf{op}\longrightarrow \textsf{Ab}$. Specifically, the full subcategory ${\textsf{K}}\subset {{\,\mathrm{\textsf{Fun}}\,}}_{\mathbb {Z}}({\textsf{E}}^\textsf{op},\textsf{Ab})$ consists of all the left exact functors. Since directed colimits of left exact sequences of abelian groups are left exact, the full subcategory ${\textsf{K}}$ is closed under directed colimits in ${{\,\mathrm{\textsf{Fun}}\,}}_{\mathbb {Z}}({\textsf{E}}^\textsf{op},\textsf{Ab})$. The objects $\rho (E)$,  $E\in {\textsf{E}}$ are finitely presentable (in fact, finitely generated projective) in ${{\,\mathrm{\textsf{Fun}}\,}}_{\mathbb {Z}}({\textsf{E}}^\textsf{op},\textsf{Ab})$, and it follows that these objects are also finitely presentable in ${\textsf{K}}$.

The objects $\rho (E)$ form a set of generators of ${{\,\mathrm{\textsf{Fun}}\,}}_{\mathbb {Z}}({\textsf{E}}^\textsf{op},\textsf{Ab})$, hence they also form a set of generators of ${\textsf{K}}$. By [1, Theorem 1.11], the category ${\textsf{K}}$ is locally finitely presentable. The assertion that the category ${\textsf{K}}$ is Grothendieck can be found in [36, Proposition A.7.13]; but in fact any locally finitely presentable abelian category is Grothendieck [1, Proposition 1.59].

It remains to show that the objects $\rho (E)$ are of type $\textrm{FP}_\infty$ in ${\textsf{K}}$. Replacing the category ${\textsf{E}}$ with its (weak) idempotent completion does not change the category ${\textsf{K}}$, so without loss of generality we can assume ${\textsf{E}}$ to be weakly idempotent-complete. Then Proposition 6.1(e) is applicable, and it remains to refer to [22, Lemma 3.5]. $\square$

Theorem 6.3

Let ${\textsf{C}}$ be a locally coherent exact category and ${\textsf{C}}_\textsf{fp}\subset {\textsf{C}}$ be its exact subcategory of finitely presentable objects. Put ${\textsf{E}}={\textsf{C}}_\textsf{fp}$, and consider the canonical embedding $\rho :{\textsf{E}}\longrightarrow {\textsf{K}}$ of the exact category ${\textsf{E}}$ into the abelian category ${\textsf{K}}$ of left exact functors ${\textsf{E}}^\textsf{op}\longrightarrow \textsf{Ab}$. Then the full subcategory $\varinjlim \rho ({\textsf{E}})\subset {\textsf{K}}$ is closed under coproducts, directed colimits, extensions, and kernels of epimorphisms in the abelian category ${\textsf{K}}$. Endowed with the exact category structure inherited from the abelian category ${\textsf{K}}$, the category $\varinjlim \rho ({\textsf{E}})$ is naturally equivalent to the exact category ${\textsf{C}}$.

Proof

To establish the closure properties of the full subcategory $\varinjlim \rho ({\textsf{E}})\subset {\textsf{K}}$, it suffices to refer to Proposition 6.1(c,e), Proposition 6.2, and [22, Proposition 3.6]. By Proposition A.1, the category $\varinjlim \rho ({\textsf{E}})$ is finitely accessible and $\rho ({\textsf{E}})$ is its full subcategory of finitely presentable objects; so $\varinjlim \rho ({\textsf{E}})\simeq {{\,\mathrm{\textsf{Ind}}\,}}\rho ({\textsf{E}}))$. Similarly we have ${\textsf{C}}\simeq {{\,\mathrm{\textsf{Ind}}\,}}({\textsf{E}})$, so the category equivalence $\rho :{\textsf{E}}\simeq \rho ({\textsf{E}})$ induces a category equivalence ${\textsf{C}}\simeq \varinjlim \rho ({\textsf{E}})$. It remains to show that the inherited exact structure on $\varinjlim \rho ({\textsf{E}})\subset {\textsf{K}}$ agrees with the original locally coherent exact structure on ${\textsf{C}}$.

The (admissible) short exact sequences in ${\textsf{C}}$ are the directed colimits of short exact sequences in ${\textsf{E}}$. Since the functor $\rho$ is exact by Proposition 6.1(b) and the directed colimits are exact functors in ${\textsf{K}}$, it follows that any short exact sequence in ${\textsf{C}}$ is also a short exact sequence in $\varinjlim \rho ({\textsf{E}})$. To prove the converse implication, we will use the characterization of admissible epimorphisms in ${\textsf{C}}$ provided by Lemma 1.5.

Let $0\longrightarrow L\longrightarrow M\longrightarrow N\longrightarrow 0$ be a short exact sequence in ${\textsf{K}}$ with the terms L, M, $N\in \varinjlim \rho ({\textsf{E}})$. Given an object $E\in \rho ({\textsf{E}})$ and a morphism $E\longrightarrow N$ in ${\textsf{K}}$, we need to construct a commutative square

with an object $F\in \rho ({\textsf{E}})$ and an admissible epimorphism $F\longrightarrow E$ in $\rho ({\textsf{E}})$. Indeed, let K be the pullback of the pair of morphisms $M\longrightarrow N$ and $E\longrightarrow N$ in the abelian category ${\textsf{K}}$. Then the morphism $K\longrightarrow E$ is an epimorphism in ${\textsf{K}}$, since the morphism $M\longrightarrow N$ is. It remains to refer to Proposition 6.1(d).

Now that we have shown that the morphism $M\longrightarrow N$ comes from an admissible epimorphism in ${\textsf{C}}$, it follows that the whole short exact sequence $0\longrightarrow L\longrightarrow M\longrightarrow N\longrightarrow 0$ comes from a short exact sequence in ${\textsf{C}}$ (since we already know that the functor ${\textsf{C}}\longrightarrow \varinjlim \rho ({\textsf{E}})\subset {\textsf{K}}$ is exact). $\square$

8 Two Periodicity Theorems

Let ${\textsf{C}}$ be an idempotent-complete additive category and ${\textsf{F}}\subset {\textsf{C}}$ be a class of objects. Following the notation of Sect. 2, we denote by $\overline{{\textsf{F}}}\subset {\textsf{C}}$ the class of all direct summands of objects from ${\textsf{F}}$ in ${\textsf{C}}$.

The aim of this section is to formulate and prove two periodicity theorems for a locally coherent exact category. We state the first one right away, postponing the formulation of the second one towards the end of the section.

Theorem 7.1

Let ${\textsf{C}}$ be a locally coherent exact category and ${\textsf{P}}=\overline{{{\,\mathrm{\textsf{Fil}}\,}}({\textsf{C}}_\textsf{fp})}$ be the class of all direct summands of objects filtered by finitely presentable objects in ${\textsf{C}}$ (in the sense of the definition in Sect. 5). Let $0\longrightarrow C\longrightarrow P\longrightarrow C\longrightarrow 0$ be an admissible short exact sequence in ${\textsf{C}}$ with $P\in {\textsf{P}}$. Then one has $C\in {\textsf{P}}$.

Examples 7.2

(1) Let R be a ring and ${\textsf{C}}={{\mathsf {Mod_{fl}}\text {--}}}R$ be the category of flat right R-modules. Then ${\textsf{C}}$ is a finitely accessible category, and the finitely presentable objects of ${\textsf{C}}$ are the finitely generated projective right R-modules. Endowed with the exact structure inherited from the ambient abelian category of modules ${{\textsf{Mod}\text {--}}}R$, the category ${\textsf{C}}$ becomes a locally coherent exact category with the pure exact structure (see Example 4.5).

In this context, the class ${\textsf{P}}=\overline{{{\,\mathrm{\textsf{Fil}}\,}}({\textsf{C}}_\textsf{fp})}\subset {\textsf{C}}$ is the class of all projective R-modules. Theorem 7.1 claims that, for any short exact sequence of R-modules $0\longrightarrow C\longrightarrow P\longrightarrow C\longrightarrow 0$ with a flat R-module C and a projective R-module P, the R-module C is also projective. This result is due to Benson and Goodearl [6, Theorem 2.5], see also Neeman [20, Remark 2.15 and Theorem 8.6].

(2) Let R be a ring and ${\textsf{C}}={{\textsf{Mod}\text {--}}}R$ be the abelian category of right R-modules. Then ${\textsf{C}}$ is a locally finitely presentable category, and the finitely presentable objects of ${\textsf{C}}$ are the cokernels of morphisms of finitely generated free R-modules. Endowed with the maximal locally coherent exact structure as per Sect. 3,  ${\textsf{C}}$ becomes a locally coherent exact category. Assume additionally that the ring R is right coherent; then ${\textsf{C}}$ is a locally coherent abelian category, so the maximal locally coherent exact structure on ${\textsf{C}}$ coincides with the abelian exact structure by Corollary 3.4.

In this context, the class ${\textsf{P}}=\overline{{{\,\mathrm{\textsf{Fil}}\,}}({\textsf{C}}_\textsf{fp})}\subset {\textsf{C}}$ is known as the class of all fp-projective R-modules. Theorem 7.1 claims that, for any short exact sequence of R-modules $0\longrightarrow C\longrightarrow P\longrightarrow C\longrightarrow 0$ with an fp-projective R-module P, the R-module C is also fp-projective. This result is due to Šaroch and Št’ovíček [32, Example 4.3], see also [5, Theorem 0.7 or Corollary 4.9].

For an extension of example (2) to arbitrary rings R, see Example 8.4 below.

Let ${\textsf{K}}$ be an exact category, and let ${\textsf{A}}$, ${\textsf{B}}\subset {\textsf{K}}$ be two classes of objects. Then ${\textsf{A}}^{\perp _1}\subset {\textsf{K}}$ denotes the class of all objects $X\in {\textsf{K}}$ such that ${{\,\textrm{Ext}\,}}_{\textsf{K}}^1(A,X)=0$ for all $A\in {\textsf{A}}$. Similarly, ${\textsf{A}}^{\perp _{\ge 1}}\subset {\textsf{K}}$ is the class of all objects $X\in {\textsf{K}}$ such that ${{\,\textrm{Ext}\,}}_{\textsf{K}}^n(A,X)=0$ for all $A\in {\textsf{A}}$ and $n\ge 1$. Dually, ${}^{\perp _1}{\textsf{B}}\subset {\textsf{K}}$ is the class of all objects $Y\in {\textsf{K}}$ such that ${{\,\textrm{Ext}\,}}_{\textsf{K}}^1(Y,B)=0$ for all $B\in {\textsf{B}}$, while ${}^{\perp _{\ge 1}}{\textsf{B}}\subset {\textsf{K}}$ is the class of all objects $Y\in {\textsf{K}}$ such that ${{\,\textrm{Ext}\,}}_{\textsf{K}}^n(Y,B)=0$ for all $B\in {\textsf{B}}$ and $n\ge 1$.

The following classical result is known as the Eklof lemma.

Lemma 7.3

For any exact category ${\textsf{K}}$ and any class of objects ${\textsf{B}}\subset {\textsf{K}}$, all objects filtered by objects from ${}^{\perp _1}{\textsf{B}}\subset {\textsf{K}}$ belong to ${}^{\perp _1}{\textsf{B}}$, that is ${{\,\mathrm{\textsf{Fil}}\,}}({}^{\perp _1}{\textsf{B}})={}^{\perp _1}{\textsf{B}}$.

Proof

The argument from [26, Lemma 4.5] applies; see also [34, Proposition 5.7] for an earlier approach and [5, Lemma 1.1] for further references. $\square$

A pair of classes of objects $({\textsf{A}},{\textsf{B}})$ in an exact category ${\textsf{K}}$ is said to be a cotorsion pair if ${\textsf{B}}={\textsf{A}}^{\perp _1}$ and ${\textsf{A}}={}^{\perp _1}{\textsf{B}}$. A cotorsion pair $({\textsf{A}},{\textsf{B}})$ in ${\textsf{K}}$ is said to be complete if, for every object $K\in {\textsf{K}}$ there exist (admissible) short exact sequences

in ${\textsf{K}}$ with A, $A'\in {\textsf{A}}$ and B, $B'\in {\textsf{B}}$.

A class of objects ${\textsf{A}}\subset {\textsf{K}}$ is said to be generating if every object $K\in {\textsf{K}}$ is the codomain of an admissible epimorphism $A\longrightarrow K$ with $A\in {\textsf{A}}$. Dually, a class of objects ${\textsf{B}}\subset {\textsf{K}}$ is said to be cogenerating if every object $K\in {\textsf{K}}$ is the domain of an admissible monomorphism $K\longrightarrow B$ with $B\in {\textsf{B}}$. Notice that in any complete cotorsion pair $({\textsf{A}},{\textsf{B}})$ the class ${\textsf{A}}$ is generating and the class ${\textsf{B}}$ is cogenerating. The following lemma is standard.

Lemma 7.4

Let $({\textsf{A}},{\textsf{B}})\subset {\textsf{K}}$ be a cotorsion pair such that the class ${\textsf{A}}$ is generating and the class ${\textsf{B}}$ is cogenerating. Then the following conditions are equivalent:

• (1) the class ${\textsf{A}}$ is closed under kernels of admissible epimorphisms in ${\textsf{K}}$;

• (2) the class ${\textsf{B}}$ is closed under cokernels of admissible monomorphisms in ${\textsf{K}}$;

• (3) ${{\,\textrm{Ext}\,}}^2_{\textsf{K}}(A,B)=0$ for all $A\in {\textsf{A}}$ and $B\in {\textsf{B}}$;

• (4) ${{\,\textrm{Ext}\,}}^n_{\textsf{K}}(A,B)=0$ for all $A\in {\textsf{A}}$,  $B\in {\textsf{B}}$, and $n\ge 1$.

Proof

See, e. g., [34, Lemma 6.17]. $\square$

A cotorsion pair $({\textsf{A}},{\textsf{B}})$ satisfying the equivalent conditions of Lemma 7.4 is said to be hereditary.

Proof of Theorem 7.1

Consider the exact category ${\textsf{E}}={\textsf{C}}_\textsf{fp}$, and let $\rho :{\textsf{E}}\longrightarrow {\textsf{K}}$ be its canonical embedding into an abelian category ${\textsf{K}}$. According to Proposition 6.2,  ${\textsf{K}}$ is a locally finitely presentable Grothendieck category, and the full subcategory $\rho ({\textsf{E}})\subset {\textsf{K}}$ consists of finitely presentable objects. Following Theorem 6.3,  ${\textsf{C}}\simeq \varinjlim \rho ({\textsf{E}})$ is naturally a full subcategory in ${\textsf{K}}$, and the locally coherent exact structure on ${\textsf{C}}$ is inherited from the abelian exact structure on ${\textsf{K}}$.

We will obtain the assertion of Theorem 7.1 as a (rather special) particular case of [22, Theorem A in Section 0.2 or Corollary 7.3] for ${\textsf{S}}={\textsf{E}}={\textsf{C}}_\textsf{fp}\subset {\textsf{K}}$ and $\kappa =\aleph _0$. We have ${\textsf{C}}=\varinjlim {\textsf{S}}\subset {\textsf{K}}$, and the class ${\textsf{C}}$ is deconstructible in ${\textsf{K}}$ by [22, Proposition A(i–ii)] together with Proposition 6.2 above, or alternatively, because ${\textsf{C}}$ is deconstructible in itself by Corollary 5.4 and closed under directed colimits and extensions in ${\textsf{K}}$ by Theorem 6.3. Comparing the notation in Theorem 7.1 with the one in [22, Corollary 7.3], we have ${\textsf{A}}={\textsf{P}}$.

Following [34, Theorem 5.16] or [22, Theorem 4.3], we have a complete cotorsion pair $({\textsf{A}},{\textsf{B}})$ in ${\textsf{C}}$. By [28, Lemma 6.1] and Proposition 6.1(d,e), the cotorsion pair $({\textsf{A}},{\textsf{B}})$ is hereditary in ${\textsf{C}}$. Alternatively, one can construct a complete cotorsion pair $({\textsf{A}},{\textsf{A}}^{\perp _1})$ in ${\textsf{K}}$, observe that it is hereditary by [5, Lemma 1.3] with Proposition 6.1(d,e), and restrict it to a hereditary complete cotorsion pair $({\textsf{A}},\>{\textsf{B}}= {\textsf{A}}^{\perp _1}\cap {\textsf{C}})$ in ${\textsf{C}}$ using [22, Lemma 2.2]. Notice that ${\textsf{A}}^{\perp _1}={\textsf{S}}^{\perp _1}$ by Lemma 7.3, and that the class ${\textsf{C}}$ is closed under the kernels of epimorphisms in ${\textsf{K}}$ by Theorem 6.3.

The assertion that $({\textsf{A}},{\textsf{B}})$ is a hereditary cotorsion pair in ${\textsf{C}}$ implies ${\textsf{A}}'={\textsf{A}}$ and ${\textsf{B}}'={\textsf{B}}$ in the notation of [22, Corollary 7.3]. Applying [22, Corollary 7.3], we obtain the desired assertion of Theorem 7.1.

Remark 7.5

One can observe that the main argument in the proof of [22, proof of Theorem A or Theorem 7.1] happens within the exact category ${\textsf{C}}$, so it may appear that the construction of the embedding into a locally finitely presentable abelian category ${\textsf{K}}$ is unnecessary for the proof above. The problem is, however, that the Hill lemma [33, Theorem 2.1] for the countable cardinal $\kappa =\aleph _0$ is only known for locally finitely presentable Grothendieck categories, and not for exact categories of Grothendieck type. The Hill lemma, restated as [22, Proposition 2.6 or 6.7], plays a key role in the proof of [22, Theorem 2.9(b) or 7.1(b)]. For this reason, the results of Sect. 6 are important for our proof of Theorem 7.1.

Here is our second periodicity theorem.

Theorem 7.6

Let ${\textsf{C}}$ be a locally coherent exact category and ${\textsf{C}}\longrightarrow {\textsf{K}}$ be its natural embedding into a locally finitely presentable abelian category described in Theorem 6.3. Put ${\textsf{B}}=({\textsf{C}}_\textsf{fp})^{\perp _1}\subset {\textsf{K}}$ and ${\textsf{D}}={\textsf{C}}^{\perp _1} \subset {\textsf{K}}$. Let $0\longrightarrow B\longrightarrow D\longrightarrow B\longrightarrow 0$ be a short exact sequence in ${\textsf{K}}$ with $B\in {\textsf{B}}$ and $D\in {\textsf{D}}$. Then one has $B\in {\textsf{D}}$.

Proof

This is a (rather special) particular case of [22, Theorem B in Section 0.3 or Theorem 1.2] for ${\textsf{S}}={\textsf{C}}_\textsf{fp}\subset {\textsf{K}}$ and ${\textsf{T}}=\varnothing$. Notice that the class ${\textsf{S}}={\textsf{E}}={\textsf{C}}_\textsf{fp}$ is closed under extensions and kernels of epimorphisms in ${\textsf{K}}$ by Proposition 6.1(c,e), so [22, Proposition B] is applicable. $\square$

Example 7.7

Let R be a ring and ${\textsf{C}}={{\mathsf {Mod_{fl}}\text {--}}}R$ be the category of flat right R-modules endowed with the pure exact structure, as in Example 7.2(1). Then ${\textsf{K}}={{\textsf{Mod}\text {--}}}R$ is the abelian category of right R-modules, and the embedding ${\textsf{C}}\longrightarrow {\textsf{K}}$ from Theorem 6.3 agrees with the identity inclusion ${{\mathsf {Mod_{fl}}\text {--}}}R\longrightarrow {{\textsf{Mod}\text {--}}}R$. The full subcategory ${\textsf{B}}=({\textsf{C}}_\textsf{fp})^{\perp _1}\subset {\textsf{K}}$ coincides with the whole abelian module category, ${\textsf{B}}={\textsf{K}}={{\textsf{Mod}\text {--}}}R$, while the full subcategory ${\textsf{D}}={\textsf{C}}^{\perp _1}\subset {\textsf{K}}$ is the class of all cotorsion right R-modules, ${\textsf{D}}={{\mathsf {Mod^{cot}}\text {--}}}R$.

Theorem 7.6 claims that, for any short exact sequence of R-modules $0\longrightarrow B\longrightarrow D\longrightarrow B \longrightarrow 0$ with a cotorsion R-module D, the R-module B is also cotorsion. This result is due to Bazzoni, Cortés-Izurdiaga, and Estrada [4, Theorem 1.2(2) or Proposition 4.8(2)].

9 Maximal Locally Coherent Exact Structure II

In Example 7.2(2) we spelled out what Theorem 7.1 says in the context of the abelian category ${\textsf{C}}={{\textsf{Mod}\text {--}}}R$ of right modules over a right coherent ring R (and the abelian exact structure on ${\textsf{C}}$). The aim of this section is to extend this discussion to arbitrary rings R and the maximal locally coherent exact structure on ${\textsf{C}}={{\textsf{Mod}\text {--}}}R$. This will lead us to a new version of fp-projective periodicity theorem for modules over an arbitary ring, and more generally, for objects of an arbitrary locally finitely presentable abelian category.

Let ${\textsf{C}}$ be a locally $\kappa$-presentable Grothendieck category (where $\kappa$ is a regular cardinal). Following [5, Remark 4.11], we will say that an object $P\in {\textsf{C}}$ is $\kappa$-p-projective if P is a direct summand of an object filtered by $\kappa$-presentable objects in ${\textsf{C}}$. In the case of the cardinal $\kappa =\aleph _0$, the term fp-projective objects is used [5, Section 2].

Lemma 8.1

Let ${\textsf{C}}$ be a locally $\kappa$-presentable Grothendieck category and $0\longrightarrow P\longrightarrow D\longrightarrow E\longrightarrow 0$ be a short exact sequence in ${\textsf{C}}$ with a $\kappa$-p-projective object P. Then $0\longrightarrow P\longrightarrow D\longrightarrow E\longrightarrow 0$ is an admissible short exact sequence in the maximal locally $\kappa$-coherent exact structure on ${\textsf{C}}$.

Proof

Let $Q\in {\textsf{C}}$ be an object that the object $P\oplus Q$ is filtered by $\kappa$-presentable ones. Consider the short sequence $0\longrightarrow P\oplus Q\longrightarrow D\oplus Q \longrightarrow E\longrightarrow 0$ constructed as the direct sum of the short sequences $0\longrightarrow P\longrightarrow D\longrightarrow E\longrightarrow 0$ and $0\longrightarrow Q \longrightarrow Q\longrightarrow 0\longrightarrow 0$. If the sequence $0\longrightarrow P\oplus Q\longrightarrow D\oplus Q\longrightarrow E\longrightarrow 0$ is admissible exact, then so is the sequence $0\longrightarrow P\longrightarrow D \longrightarrow E\longrightarrow 0$ (by the pushout axiom). Hence we can assume without loss of generality that the object P is filtered by $\kappa$-presentable objects.

It suffices to show that the morphism $D\longrightarrow E$ is an admissible epimorphism in the maximal locally $\kappa$-coherent exact structure on ${\textsf{C}}$. For this purpose, we will apply the criterion provided by Corollary 3.2. Given a $\kappa$-presentable object S and a morphism $S\longrightarrow E$ in ${\textsf{C}}$, we need to construct a commutative square diagram

with an epimorphism $T\longrightarrow S$ such that both T and $\ker (T\twoheadrightarrow S)$ are $\kappa$-presentable objects in ${\textsf{C}}$.

Denote by H the pullback of the pair of morphisms $D\longrightarrow E$ and $S\longrightarrow E$ in ${\textsf{C}}$. Then we have a short exact sequence $0\longrightarrow P\longrightarrow H \longrightarrow S\longrightarrow 0$ in ${\textsf{C}}$. A given filtration of the object P by $\kappa$-presentable objects then can be extended to such a filtration of the object H by adding a single top quotient object S (since the object S is $\kappa$-presentable). Applying the Hill lemma [33, Theorem 2.1], the desired $\kappa$-presentable object T can be now found as a suitable subobject in H. $\square$

Corollary 8.2

Let ${\textsf{C}}$ be a locally $\kappa$-presentable Grothendieck category. Then the class of all objects of ${\textsf{C}}$ filtered by $\kappa$-presentable objects in the abelian exact structure on ${\textsf{C}}$ coincides with the class of all objects of ${\textsf{C}}$ filtered by $\kappa$-presentable objects in the maximal locally $\kappa$-coherent exact structure on ${\textsf{C}}$.

Proof

It follows from Lemma 8.1 that any filtration by $\kappa$-presentable objects in the abelian exact structure on ${\textsf{C}}$ is also a filtration in the maximal locally $\kappa$-coherent exact structure on ${\textsf{C}}$. $\square$

Theorem 8.3

Let ${\textsf{C}}$ be a locally finitely presentable abelian category, and let $0\longrightarrow C\longrightarrow P\longrightarrow C\longrightarrow 0$ be an admissible short exact sequence in the maximal locally coherent exact structure on ${\textsf{C}}$. Assume that the object P is fp-projective. Then the object C is fp-projective as well.

Proof

Apply Theorem 7.1 to the maximal locally coherent exact structure on ${\textsf{C}}$, and take Corollary 8.2 (for $\kappa =\aleph _0$) into account. $\square$

Example 8.4

In particular, let R be an arbitrary ring and $0\longrightarrow C\longrightarrow P \longrightarrow C\longrightarrow 0$ be an admissible short exact sequence in the maximal locally coherent exact structure on the category ${\textsf{C}}={{\textsf{Mod}\text {--}}}R$. Theorem 8.3 tells us that if the R-module P is fp-projective, then so is the R-module C.

Notice that the assertions of Theorem 8.3 and Example 8.4 are certainly not true with the assumption of admissible exactness in the maximal locally coherent exact structure replaced by exactness in the abelian category ${\textsf{C}}$ (unless one assumes local coherence, which makes the two exact structures coincide). This is explained in [5, Corollary 4.6(2) $\Rightarrow$ (4)].

Remark 8.5

The proof of Theorem 8.3 via the proof of Theorem 7.1, applied in the context of Example 8.4, may appear to be confusing, so let us provide some explanation. Given the module category ${\textsf{C}}={{\textsf{Mod}\text {--}}}R$ with its maximal locally coherent exact structure, we consider the full subcategory ${\textsf{E}}={{\mathsf {Mod_{fp}}\text {--}}}R\subset {{\textsf{Mod}\text {--}}}R$ of finitely presentable R-modules, endowed with the maximal exact structure, which coincides with the exact structure inherited from the abelian exact structure of ${{\textsf{Mod}\text {--}}}R$ (as per Lemma 3.1). Then we consider the abelian category ${\textsf{K}}$ of all left exact functors ${\textsf{E}}^\textsf{op}\longrightarrow \textsf{Ab}$. What category is that?

The category of contravariant functors $({{\mathsf {Mod_{fp}}\text {--}}}R)^\textsf{op}\longrightarrow \textsf{Ab}$ taking cokernels to kernels is naturally equivalent to ${\textsf{C}}={{\textsf{Mod}\text {--}}}R$, as one can easily see. Any functor $({{\mathsf {Mod_{fp}}\text {--}}}R)^\textsf{op}\longrightarrow \textsf{Ab}$ taking cokernels to kernels has the form $S\longmapsto {{\,\textrm{Hom}\,}}_R(S,M)$, where $M\in {{\textsf{Mod}\text {--}}}R$. So what is the difference between the categories ${\textsf{C}}$ and ${\textsf{K}}$ ? The difference is that a functor $K:({{\mathsf {Mod_{fp}}\text {--}}}R)^\textsf{op}\longrightarrow \textsf{Ab}$ belonging to the category ${\textsf{K}}$ need not take cokernels to kernels. The left exactness condition imposed on objects of the category ${\textsf{K}}$ is weaker, and only requires the functor K to take cokernels of injective morphisms of finitely presentable R-modules to kernels in $\textsf{Ab}$. The difference manifests itself when the ring R is not right coherent.

Appendix: Generalities on Accessible Categories

Throughout this appendix, $\kappa$ is a regular cardinal. We use the book [1] as the background reference source on accessible categories. In particular, we refer to [1, Definition 1.4, Theorem 1.5, Corollary 1.5, Definition 1.13(1), and Remark 1.21] for an important discussion of $\kappa$-directed posets vs. $\kappa$-filtered small categories, and accordingly, $\kappa$-directed vs. $\kappa$-filtered colimits (for a regular cardinal $\kappa$).

Let ${\textsf{A}}$ be a category with $\kappa$-directed (equivalently, $\kappa$-filtered) colimits. An object $S\in {\textsf{A}}$ is said to be $\kappa$-presentable if the functor ${{\,\textrm{Hom}\,}}_{\textsf{A}}(S,{-}):{\textsf{A}}\longrightarrow \textsf{Sets}$ preserves $\kappa$-directed colimits. We will use the notation ${\textsf{A}}_{<\kappa }\subset {\textsf{A}}$ for the full subcategory of all $\kappa$-presentable objects of ${\textsf{A}}$. Given a class of objects ${\textsf{S}}\subset {\textsf{A}}$, we denote by $\varinjlim _{(\kappa )}{\textsf{S}}\subset {\textsf{A}}$ the class of all $\kappa$-directed colimits of objects from ${\textsf{S}}$ in ${\textsf{A}}$. In the case of the cardinal $\kappa =\aleph _0$, we will use the notation $\varinjlim {\textsf{S}}$ instead of $\varinjlim _{(\aleph _0)}{\textsf{S}}$.

The category ${\textsf{A}}$ is said to be $\kappa$-accessible [1, Definition 2.1] if there is a set of $\kappa$-presentable objects ${\textsf{S}}\subset {\textsf{A}}$ such that every object of ${\textsf{A}}$ is a $\kappa$-directed colimit of objects from ${\textsf{S}}$, i. e., ${\textsf{A}}=\varinjlim _{(\kappa )}{\textsf{S}}$. If this is the case, then the $\kappa$-presentable objects of ${\textsf{A}}$ are precisely all the retracts of the objects from ${\textsf{S}}$.

In particular, $\aleph _0$-presentable objects are known as finitely presentable [1, Definition 1.1], and $\aleph _0$-accessible categories are called finitely accessible [1, Remark 2.2(1)].

The following proposition is well-known.

Proposition A.1

Let ${\textsf{A}}$ be a $\kappa$-accessible category and ${\textsf{T}}\subset {\textsf{A}}_{<\kappa }$ be a set of $\kappa$-presentable objects. Then the class of objects $\varinjlim _{(\kappa )}{\textsf{T}}\subset {\textsf{A}}$ is closed under $\kappa$-directed colimits in ${\textsf{A}}$. An object $B\in {\textsf{A}}$ belongs to $\varinjlim _{(\kappa )}{\textsf{T}}$ if and only if, for every object $S\in {\textsf{A}}_{<\kappa }$, any morphism $S\longrightarrow B$ in ${\textsf{A}}$ factorizes through an object from ${\textsf{T}}$.

The full subcategory $\varinjlim _{(\kappa )}{\textsf{T}}\subset {\textsf{A}}$ is $\kappa$-accessible, and its $\kappa$-presentable objects are precisely those objects of $\varinjlim _{(\kappa )}{\textsf{T}}$ that are $\kappa$-presentable in ${\textsf{A}}$. The intersection ${\textsf{A}}_{<\kappa }\cap \varinjlim {\textsf{T}}$ consists precisely of all the retracts of objects from ${\textsf{T}}$ in ${\textsf{A}}$.

Assume that the category ${\textsf{A}}$ is additive and the set of objects ${\textsf{T}}$ is closed under finite direct sums in ${\textsf{A}}$. Then so is the class of objects $\varinjlim _{(\kappa )}{\textsf{T}}$. When $\kappa =\aleph _0$, the class of objects $\varinjlim _{(\kappa )}{\textsf{T}}$ is closed under all coproducts in ${\textsf{A}}$.

Proof

In the context of additive categories and $\kappa =\aleph _0$, this result, going back to [18, Proposition 2.1], can be found in [10, Section 4.1] and [16, Proposition 5.11]. (The terminology “locally finitely presented categories” was used in [10, 16] for what we call finitely accessible categories.)

The nontrivial part is to prove the “if” implication in the second assertion: if any morphism $S\longrightarrow B$ factorizes through an object from ${\textsf{T}}$, then $B\in \varinjlim _{(\kappa )}{\textsf{T}}$. Here one has to use the assumption that B is a $\kappa$-directed colimit of objects from ${\textsf{A}}_{<\kappa }$ in ${\textsf{A}}$, and show that the canonical diagram of morphisms into B from objects of ${\textsf{T}}$ is $\kappa$-filtered and has B as the colimit. We refer to [25, Proposition 1.2] for further details. $\square$

1.1 A.1 Comma-Categories with Equations

We start with the following simple lemma, which will be used in Section A.2.

Lemma A.2

Let $\kappa$ be a regular cardinal, I be a set of the cardinality smaller than $\kappa$, and $({\textsf{K}}_i)_{i\in I}$ be an I-indexed family of $\kappa$-accessible categories. Then the Cartesian product ${\textsf{K}}=\prod _{i\in I}{\textsf{K}}_i$ is a $\kappa$-accessible category again. The $\kappa$-presentable objects of ${\textsf{K}}$ are precisely all the collections of objects $(S_i\in {\textsf{K}}_i)_{i\in I}$, where the object $S_i$ is $\kappa$-presentable in ${\textsf{K}}_i$ for every $i\in I$.

Proof

This assertion can be found [1, proof of Proposition 2.67], with the difference that the assumption that the cardinality of I is smaller than $\kappa$ is erroneously missing in [1]. We refer to [25, Proposition 2.1] for the details. $\square$

Let ${\textsf{K}}$, ${\textsf{L}}$, and ${\textsf{M}}$ be three categories, and let $F:{\textsf{K}}\longrightarrow {\textsf{M}}$ and $G:{\textsf{L}}\longrightarrow {\textsf{M}}$ be two functors. In this context, the comma-category ${\textsf{C}}=F\downarrow G$ is the category of triples $(K,L,\theta )$, where $K\in {\textsf{K}}$ and $L\in {\textsf{L}}$ are objects, while $\theta :F(K)\longrightarrow G(L)$ is a morphism in ${\textsf{M}}$.

It is easy to see that if $\kappa$-directed colimits exist in ${\textsf{K}}$, ${\textsf{L}}$, and ${\textsf{M}}$, and are preserved by the functor F, then $\kappa$-directed colimits also exist in ${\textsf{C}}$, and are preserved by the natural forgetful functors ${\textsf{C}}\longrightarrow {\textsf{K}}$ and ${\textsf{C}}\longrightarrow {\textsf{L}}$.

Proposition A.3

Assume that the categories ${\textsf{K}}$, ${\textsf{L}}$, and ${\textsf{M}}$ are $\kappa$-accessible, and the functors F and G preserve $\kappa$-directed colimits. Assume further that the functor F takes $\kappa$-presentable objects to $\kappa$-presentable objects. Then the category ${\textsf{C}}$ is also $\kappa$-accessible, and the $\kappa$-presentable objects of ${\textsf{C}}$ are precisely all the triples $(S,T,\sigma )\in {\textsf{C}}$ where the object S is $\kappa$-presentable in ${\textsf{K}}$ and the object T is $\kappa$-presentable in ${\textsf{L}}$.

Proof

This is [1, proof of Theorem 2.43]. Notice that [25, Theorem 4.1] is not applicable here, as the latter theorem requires two cardinals $\lambda <\kappa$, which we do not have (and do not need) in the context of this proposition. $\square$

Consider the comma-category ${\textsf{C}}=F\downarrow G$ as above, and denote by $\Pi _{\textsf{K}}:{\textsf{C}}\longrightarrow {\textsf{K}}$ and $\Pi _{\textsf{L}}:{\textsf{C}}\longrightarrow {\textsf{L}}$ the two natural forgetful functors. Assume further that we are given a category ${\textsf{N}}$ and two functors $P:{\textsf{K}}\longrightarrow {\textsf{N}}$ and $Q:{\textsf{L}}\longrightarrow {\textsf{N}}$. Consider the two compositions of functors $P\Pi _{\textsf{K}}:{\textsf{C}}\longrightarrow {\textsf{N}}$ and $Q\Pi _{\textsf{L}}:{\textsf{C}}\longrightarrow {\textsf{N}}$, and suppose given a pair of parallel natural transformations $\phi$, $\psi :P\Pi _{\textsf{K}}\rightrightarrows Q\Pi _{\textsf{L}}$.

Denote by ${\textsf{E}}\subset {\textsf{C}}$ the full subcategory consisting of all the objects $C\in {\textsf{C}}$ such that $\phi _C=\psi _C$. We will call the category ${\textsf{E}}$ the comma-category with equations.

Clearly, if $\kappa$-directed colimits exist in the four categories ${\textsf{K}}$, ${\textsf{L}}$, ${\textsf{M}}$, and ${\textsf{N}}$, and are preserved by the two functors F and P, then the full subcategory ${\textsf{E}}$ is closed under $\kappa$-directed colimits in ${\textsf{C}}$.

Theorem A.4

Assume that the four categories ${\textsf{K}}$, ${\textsf{L}}$, ${\textsf{M}}$, and ${\textsf{N}}$ are $\kappa$-accessible, and the four functors F, G, P, Q preserve $\kappa$-directed colimits. Assume further that the functors F and P take $\kappa$-presentable objects to $\kappa$-presentable objects. Then the category ${\textsf{E}}$ is also $\kappa$-accessible, and the $\kappa$-presentable objects of ${\textsf{E}}$ are precisely all the triples $(U,V,\upsilon )\in {\textsf{E}}\subset {\textsf{C}}$ where the object U is $\kappa$-presentable in ${\textsf{K}}$ and the object V is $\kappa$-presentable in ${\textsf{L}}$.

Proof

In view of Propositions A.1 and A.3, it suffices to check that, for every pair of objects $(K,L,\theta )\in {\textsf{E}}$ and $(S,T,\sigma )\in {\textsf{C}}_{<\kappa }$, and any morphism $(f,g):(S,T,\sigma )\longrightarrow (K,L,\theta )$ in ${\textsf{C}}$, there exists an object $(U,V,\upsilon )\in {\textsf{C}}_{<\kappa }\cap {\textsf{E}}$ such that the morphism (f, g) factorizes through the object $(U,V,\upsilon )$ in the category ${\textsf{C}}$.

Indeed, let $L=\varinjlim _{\xi \in \Xi }V_\xi$ be a representation of the object $L\in {\textsf{L}}$ as a $\kappa$-directed colimit of $\kappa$-presentable objects $V_\xi$, indexed by some $\kappa$-directed poset $\Xi$. Then, since the object $T\in {\textsf{L}}$ is $\kappa$-presentable, there exists an index $\xi _0\in \Xi$ such that the morphism $g:T\longrightarrow L$ factorizes through the morphism $V_\xi \longrightarrow L$.

Since $(K,L,\theta )\in {\textsf{E}}$ and (f, g) is a morphism in ${\textsf{C}}$, the two compositions

are equal to each other in the category ${\textsf{N}}$. As $Q(L)=\varinjlim _{\xi \in \Xi }Q(V_\xi )$ in ${\textsf{N}}$ and P(S) is a $\kappa$-presentable object in ${\textsf{N}}$, it follows that there exists an index $\xi _1\in \Xi$,  $\xi _1\ge \xi _0$, such that the two compositions

are equal to each other in ${\textsf{N}}$.

It remains to put $U=S$ and $V=V_{\xi _1}$, and let $\upsilon :F(U) \longrightarrow G(V)$ be the composition $F(S)\overset{\sigma }{\longrightarrow }G(T) \longrightarrow G(V_{\xi _1})$ in the category ${\textsf{M}}$. $\square$

1.2 A.2 Finitely Presented Rigid Diagram Categories

We start with restating a result going back to [3, Exposé I]. Given a small category ${\textsf{D}}$ and a category ${\textsf{A}}$, we denote by ${{\,\mathrm{\textsf{Fun}}\,}}({\textsf{D}},{\textsf{A}})$ the category of functors ${\textsf{D}}\longrightarrow {\textsf{A}}$.

Proposition A.5

Let ${\textsf{A}}$ be a $\kappa$-accessible category and ${\textsf{D}}$ be a finite category with no nonidentity endomorphisms of objects. Then the category ${{\,\mathrm{\textsf{Fun}}\,}}({\textsf{D}},{\textsf{A}})$ is $\kappa$-accessible. The $\kappa$-presentable objects of ${{\,\mathrm{\textsf{Fun}}\,}}({\textsf{D}},{\textsf{A}})$ are the functors ${\textsf{D}}\longrightarrow {\textsf{A}}_{<\kappa }$.

Proof

In the case of $\kappa =\aleph _0$, this is the result of [3, Exposé I, Proposition 8.8.5] or [19, p. 55]. For an arbitrary regular cardinal $\kappa$, the assertion of the proposition is a particular case of [14, Theorem 1.3]. $\square$

The aim of this section is to extend the result of Proposition A.5 from arbitrary nonadditive to k-linear functors, where k is a commutative ring. The related assertion is stated as Proposition A.6 below. Both Propositions A.5 and A.6 are provable by induction on the number of objects in the category ${\textsf{D}}$ using Theorem A.4 for the induction step. We will spell out the proof of Proposition A.6, as this is the result we use in the main body of this paper.

A k-linear category ${\textsf{A}}$ is a category enriched in k-modules. So, for any two objects A and $B\in {\textsf{A}}$, the set ${{\,\textrm{Hom}\,}}_{\textsf{A}}(A,B)$ has a k-module structure, and the composition maps are k-bilinear. Let us describe the class of small k-linear categories ${\textsf{D}}$ to which our result applies.

Suppose given a totally ordered, finite set of objects $\{a\}$. For every pair of objects $a<b$, suppose given a generating set of morphisms ${{\,\textrm{Gen}\,}}(a,b)$. For $a\ge b$, put ${{\,\textrm{Gen}\,}}(a,b)=\varnothing$. Then, just as in [25, Section 6], one can construct the k-linear category ${\textsf{B}}$ on the given set of objects freely generated by the given sets of morphisms. For every pair of objects a, b, the free k-module ${{\,\textrm{Hom}\,}}_{\textsf{B}}(a,b)$ is spanned by the set of all formal compositions $g_n\cdots g_1$,  $n\ge 0$, where $g_i\in {{\,\textrm{Gen}\,}}(c_i,c_{i+1})$, $c_1=a$,  $c_{n+1}=b$. Notice that one has ${{\,\textrm{Hom}\,}}_{\textsf{B}}(a,a)=k$ for all objects a, and ${{\,\textrm{Hom}\,}}_{\textsf{B}}(a,b)=0$ if $a>b$.

Furthermore, suppose given a set of defining relations ${{\,\textrm{Rel}\,}}(a,b)\subset {{\,\textrm{Hom}\,}}_{\textsf{B}}(a,b)$ for every pair of objects $a<b$. Let ${\textsf{J}}$ be the two-sided ideal of morphisms in ${\textsf{B}}$ generated by all the sets ${{\,\textrm{Rel}\,}}(a,b)$. Consider the k-linear quotient category ${\textsf{D}}={\textsf{B}}/{\textsf{J}}$ of the k-linear category ${\textsf{A}}$ by the ideal of morphisms ${\textsf{J}}$.

We will say that a k-linear category ${\textsf{D}}$ is a finitely presented rigid category if it has the form ${\textsf{D}}={\textsf{B}}/{\textsf{J}}$ as per the construction above, where the set of all objects a, the set of all generators $\coprod _{a,b}{{\,\textrm{Gen}\,}}(a,b)$, and the set of all relations $\coprod _{a,b}{{\,\textrm{Rel}\,}}(a,b)$ are all finite. The word “rigid” here refers to the assumption that all the generating morphisms go in one direction with respect to a given total order on the set of objects.

Given a small k-linear category ${\textsf{D}}$ and a k-linear category ${\textsf{A}}$, we denote by ${{\,\mathrm{\textsf{Fun}}\,}}_k({\textsf{D}},{\textsf{A}})$ the k-linear category of k-linear functors ${\textsf{D}}\longrightarrow {\textsf{A}}$. The following proposition is a k-linear version of Proposition A.5.

Proposition A.6

Let ${\textsf{A}}$ be a $\kappa$-accessible k-linear category and ${\textsf{D}}$ be a finitely presented rigid k-linear category. Then the category ${{\,\mathrm{\textsf{Fun}}\,}}_k({\textsf{D}},{\textsf{A}})$ is $\kappa$-accessible. The $\kappa$-presentable objects of ${{\,\mathrm{\textsf{Fun}}\,}}_k({\textsf{D}},{\textsf{A}})$ are the k-linear functors ${\textsf{D}}\longrightarrow {\textsf{A}}_{<\kappa }$.

Proof

The argument proceeds by induction on the number of objects in ${\textsf{D}}$. If the set of objects of ${\textsf{D}}$ is a singleton, then one has ${{\,\mathrm{\textsf{Fun}}\,}}_k({\textsf{D}},{\textsf{A}})\simeq {\textsf{A}}$, and there is nothing to prove. Otherwise, we separate all the objects of ${\textsf{D}}$ into two nonempty groups, the upper and the lower one, so that one has $a'<a''$ for any object $a'$ from the lower group and any object $a''$ from the upper one. Let ${\textsf{D}}'$ and ${\textsf{D}}''\subset {\textsf{D}}$ be the full subcategories on the lower and the upper groups of objects in ${\textsf{D}}$, respectively. Then both ${\textsf{D}}'$ and ${\textsf{D}}''$ are also finitely presented rigid categories; indeed, the sets of generators and relations of ${\textsf{D}}'$ are just the sets of all generators and relations of ${\textsf{D}}$ on objects from ${\textsf{D}}'$, and similarly for ${\textsf{D}}''$.

The claim is that the category ${\textsf{E}}={{\,\mathrm{\textsf{Fun}}\,}}({\textsf{D}},{\textsf{A}})$ can be produced from the categories ${\textsf{K}}={{\,\mathrm{\textsf{Fun}}\,}}({\textsf{D}}',{\textsf{A}})$ and ${\textsf{L}}={{\,\mathrm{\textsf{Fun}}\,}}({\textsf{D}}'',{\textsf{A}})$ by the construction of the comma-category with equations from Section A.1. Specifically, let ${\textsf{M}}$ be the product of copies of the category ${\textsf{A}}$ indexed by the finite set $\coprod _{a'\in {\textsf{D}}',a''\in {\textsf{D}}''}{{\,\textrm{Gen}\,}}(a',a'')$. Let $F:{\textsf{K}}\longrightarrow {\textsf{M}}$ be the functor assigning to a functor $A':{\textsf{D}}'\longrightarrow {\textsf{A}}$ the collection of objects whose component indexed by a generator $g\in {{\,\textrm{Gen}\,}}(a',a'')$ is the object $A'(a')\in {\textsf{A}}$. Similarly, let $G:{\textsf{L}}\longrightarrow {\textsf{M}}$ be the functor assigning to a functor $A'':{\textsf{D}}''\longrightarrow {\textsf{A}}$ the collection of objects whose component indexed by a generator $g\in {{\,\textrm{Gen}\,}}(a',a'')$ is the object $A''(a'')\in {\textsf{A}}$. Then the comma-category ${\textsf{C}}=F\downarrow G$ is naturally equivalent to the category of functors ${{\,\mathrm{\textsf{Fun}}\,}}_k(\widetilde{\textsf{B}},{\textsf{A}})$, where $\widetilde{\textsf{B}}$ is the finitely presented rigid category whose objects are all the objects of ${\textsf{D}}$, generating morphisms are all the generating morphisms of ${\textsf{D}}$, and the set of defining relations is $\coprod _{a',b'\in {\textsf{D}}'}{{\,\textrm{Rel}\,}}(a',b')\sqcup \coprod _{a'',b''\in {\textsf{D}}''} {{\,\textrm{Rel}\,}}(a'',b'')$.

Finally, let ${\textsf{N}}$ be the product of copies of the category ${\textsf{A}}$ indexed by the finite set $\coprod _{a'\in {\textsf{D}}',a''\in {\textsf{D}}''}{{\,\textrm{Rel}\,}}(a',a'')$. Let $P:{\textsf{K}}\longrightarrow {\textsf{N}}$ be the functor assigning to a functor $A':{\textsf{D}}'\longrightarrow {\textsf{A}}$ the collection of objects whose component indexed by a relation $r\in {{\,\textrm{Rel}\,}}(a',a'')$ is the object $A'(a')\in {\textsf{A}}$. Similarly, let $Q:{\textsf{L}}\longrightarrow {\textsf{N}}$ be the functor assigning to a functor $A'':{\textsf{D}}''\longrightarrow {\textsf{A}}$ the collection of objects whose component indexed by a relation $r\in {{\,\textrm{Rel}\,}}(a',a'')$ is the object $A''(a'')\in {\textsf{A}}$. Let $\phi :P\Pi _{\textsf{K}}\longrightarrow Q\Pi _{\textsf{L}}$ be the natural transformation assigning to a functor $A\in {\textsf{C}}={{\,\mathrm{\textsf{Fun}}\,}}_k(\widetilde{\textsf{B}},{\textsf{A}})$ the morphism in the category ${\textsf{N}}$ whose component indexed by a relation $r\in {{\,\textrm{Rel}\,}}(a',a'')$ is the morphism $A(r):A(a')\longrightarrow A(a'')$ for all $a'\in {\textsf{D}}'$,  $a''\in {\textsf{D}}''$. Let $\psi :P\Pi _{\textsf{K}}\longrightarrow Q\Pi _{\textsf{L}}$ be the zero natural transformation. Then the comma-category with relations ${\textsf{E}}$ is naturally equivalent to the category of functors ${{\,\mathrm{\textsf{Fun}}\,}}_k({\textsf{D}},{\textsf{A}})$.

The induction assumption tells us that the categories ${\textsf{K}}$ and ${\textsf{L}}$ are $\kappa$-accessible, and provides descriptions of their full subcategories of $\kappa$-presentable objects. Lemma A.2 tells us that the categories ${\textsf{M}}$ and ${\textsf{N}}$ are $\kappa$-accessible, and provides descriptions of their full subcategories of $\kappa$-presentable objects. So Theorem A.4 is applicable, proving that the category ${\textsf{E}}={{\,\mathrm{\textsf{Fun}}\,}}_k({\textsf{D}},{\textsf{A}})$ is $\kappa$-accessible, and providing the desired description of its full subcategory of $\kappa$-presentable objects. $\square$