Abstract
We treat the problem of lifting bicategories into double categories through categories of vertical morphisms. We consider structures on decorated 2-categories allowing us to formally implement arguments of sliding certain squares along vertical subdivisions in double categories. We call these structures \(\pi _2\)-indexings. We present a construction associating, to every \(\pi _2\)-indexing on a decorated 2-category, a length 1 double internalization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Symmetric monoidal structures on bicategories are, in some cases, more naturally expressed as horizontalizations of symmetric monoidal structures of double categories. In order to define a symmetric monoidal structure on a bicategory B, in the general sense of [2], it is sometimes convenient to ’lift’ B to a symmetric monoidal double category C, where the coherence equations for the symmetric monoidal structure are expressed in terms of vertical arrows of C. In the case in which the double category C is a framed bicategory, the image of the symmetric monoidal structure on C, under the horizontal bicategory functor H, defines a symmetric monoidal bicategory structure on B [8, 9]. Whether this technique can be applied to a given bicategory B depends on the specifics of B. We are interested in the problem of establishing general criteria for when this procedure can be applied.
We consider the following problem: Given a bicategory B, and a category \(B^*\), such that the collections of objects of B and \(B^*\) are equal, we wish to construct interesting double categories C having B as horizontal bicategory, and having \(B^*\) as category of objects. Succintly \(H^*C=(B^*,B)\). We say that the pair \((B^*,B)\) is a decorated bicategory and C is an internalization of \((B^*,B)\). The problem of finding interesting internalizations to a given decorated bicategory \((B^*,B)\) models the case in which one wishes to define a symmetric monoidal structure on the bicategory B, where coherence data would be more naturally expressed in terms of a collection of vertical arrows, \(B^*\). We then wish to have knowledge of the possible extensions of B to double categories C having \(B^*\) as category of objects, i.e. \(H^*C=(B^*,B)\). With this knowledge we would, in principle, be able to decide whether we can choose, among the internalizations of \((B^*,B)\), a framed bicategory where the symmetric monoidal structure we are trying to define on B is naturally defined.
The problem of understanding internalizations of decorated bicategories has been considered in the series of papers [3,4,5], where the 2-category of double categories is fibered over a coreflective subcategory minimizing the internalization problem. This allows the definition of a numerical invariant, called the vertical length \(\ell C\), associated to every double category C. Roughly, the number \(\ell C\) measures the amount of work one would be expected to do to construct a generic square in C, from squares in \(H^*C\). 1 is the minimum possible length of a double category, and the condition \(\ell C=1\) roughly means that we can express squares of C in terms of squares of \(H^*C\) in a relatively straightforward way. Most framed bicategories in the literature, e.g. \({\mathbb {M}}{{{\textbf {od}}}},{\mathbb {P}}{{{\textbf {rof}}}},{\mathbb {B}}{{{\textbf {ord}}}},{\mathbb {A}}{{{\textbf {dj}}}}\) are of length 1. It is thus natural to conjecture that every framed bicategory is of length 1. This conjecture will be treated in a subsequent paper.
In this paper we consider the problem of deciding whether a decorated bicategory \((B^*,B)\) admits internalizations of length 1. The condition of a double category C being of length 1 depends on certain 2-dimensional compatibility conditions satisfied by squares in \(H^*C\), see Sect. 2.4. We study a type of structure allowing for the construction of internalizations satisfying this compatibility condition. We call the structure we study \(\pi _2\)-indexings. \(\pi _2\)-indexings are a type of indexing associated to a decorated bicategory \((B^*,B)\), relating the arrows of \(B^*\) with 2-cells of a specific type in B. The definition of \(\pi _2\)-indexing appears in Definition 3.1, where related structures, which we call \(\pi _2\)-opindexings also appear. The main goal of the paper is to prove the following result
Theorem 1.1
Let \((B^*,B)\) be a decorated 2-category. For every \(\pi _2\)-indexing, or \(\pi _2\)-opindexing \(\Phi \) on \((B^*,B)\), there exists an internalization \(B\rtimes _\Phi B^*\) of \((B^*,B)\) such that \(B\rtimes _\Phi B^*\) is of length 1.
We present examples and conjectures related to the construction in Theorem 1.1.
We now present the contents of this paper. In Sect. 2 we briefly review the notions of internalization, globularly generated double category, and length. In Sect. 3 we present our definition of \(\pi _2\)-indexing, and state our main theorem. We review some of the intuitive ideas behind the definition of \(\pi _2\)-indexings. In Sect. 4 we present the proof of our main theorem. In Sect. 5 we present examples relevant to our construction. Finally, in Sect. 6 we present open problems and possible directions related to the results presented in this paper.
2 Preliminaries
2.1 Double Categories
We will write \(C_0,C_1\) for the category of objects and the category of morphisms of a double category C, we will write L, R for the left and right frame functors of C, and we will write U for the unit functor of C. Following [9] we will write  for the vertical and horizontal composition operations of C respectively. We will write dCat for the 2-category of ’weak double categories’, pseudo-double functors, and horizontal natural transformations [7, Section 1.4]. We will represent squares in double categories as diagrams of the form:
for the vertical and horizontal composition operations of C respectively. We will write dCat for the 2-category of ’weak double categories’, pseudo-double functors, and horizontal natural transformations [7, Section 1.4]. We will represent squares in double categories as diagrams of the form:

where squares are read from left to right and from top to bottom, i.e. the edges f, g are the left and right frame of the square \(\varphi \), while the edges \(\alpha ,\beta \) are the vertical domain and codomain of \(\varphi \) respectively. We will adopt the following convention: Vertical and horizontal identity arrows will always be colored red, e.g. in the following squares

the left frame of the square on the left is an identity, the right frame of the square in the middle is an identity and the domain and codomain of the rightmost square are both identities. We identify unit squares as being marked with the letter U:

An important class of squares is the collection squares of the form

We will write \(\pi _2(C,a)\) for the set of all such squares with vertex a. Observe that by the Eckmann-Hilton argument, the horizontal composition and the vertical composition of such squares coincide and are commutative. The set \(\pi _2(C,a)\) is thus a commutative monoid, with the following square as identity element:

Squares of the form:

are called globular. The collection of globular squares of a double category C forms a bicategory HC, the horizontal bicategory of C. The horizontal bicategory construction assembles into a 2-functor \(H:{{\textbf {dCat}}}\rightarrow {{\textbf {bCat}}}\), the horizontalization 2-functor. Thus defined H admits a left adjoint \({\mathbb {H}}:{{\textbf {bCat}}}\rightarrow {{\textbf {dCat}}}\) associating to every bicategory B the vertically trivial double category of B. Thus defined \({\mathbb {H}}\) is an embedding, and we identify every bicategory B with its image \({\mathbb {H}}B\) under \({\mathbb {H}}\). Under this identification, bicategories are precisely the double categories whose squares are all globular.
2.2 Internalization
A decoration of a bicategory B is a category \(B^*\) having the same collection of objects as B. If \(B^*\) is a decoration of B we say that \((B^*,B)\) is a decorated bicategory. The pair \((C_0,HC)\) is a decorated bicategory for every double category C. We write \(H^*C\) for this decorated bicategory, and we call it the decorated horizontalization of C. We will write bCat\(^*\) for the category of decorated bicategories and decorated 2-functors, see [3]. We are interested in the following problem:
Problem 2.1
Let \((B^*,B)\) be a decorated bicategory. Find double categories C satisfying the equation \(H^*C=(B^*,B)\).
We understand Problem 2.1 as the problem of lifting a bicategory B to a double category through an orthogonal direction, provided by \(B^*\). A solution to Problem 2.1 for a decorated bicategory \((B^*,B)\) will be called an internalization of B. Problem 2.1 can be interpreted as follows: Suppose we are given a collection of globular squares:

forming a bicategory, together with a collection of vertical arrows of the form:

forming a category, satisfying the condition that the collection of vertices of both sets of diagrams coincide. With this data we can form hollow squares of the form:

formed by the edges of the diagrams we are provided with. Problem 2.1 asks about ways to fill these hollow squares equivariantly with respect to the globular diagrams in our set of initial conditions. That is, Problem 2.1 asks for the existence of systems of solid squares of the form:

forming a double category such that the only solid squares of the form:

are the globular diagrams provided as set of initial conditions. We regard the decorated horizontalization condition of Problem 2.1 as a formalization of the equivariance condition on the above squares.
Constructions of this sort appear in different parts of the theory of double categories. Notably the Ehresmann double category of quintets [1], the double category of adjoint pairs [6], and the double categories of spans and cospans constructions all follow the pattern described above. The double category of quintets has a given 2-category and the corresponding category of 1-cells as set of initial data, the double category of adjoints has a given 2-category together with adjoint pairs of 1-cells as set of initial data, and the double category of spans/cospans has the bicategory of spans/cospans of a category with pushouts/pullbacks and the arrows of this category as globular and vertical sets of initial data. In all cases solid squares are carefully chosen so as to encode different aspects of the globular theory.
2.3 Globularly Generated Double Categories
Globularly generated double categories were introduced in [3] as minimal solutions to Problem 2.1. A double category C is globularly generated if C is generated, as a double category, by its collection of globular squares. Pictorially a double category C is globularly generated if every square of C can be written as vertical and horizontal compositions of squares of the form:

Given a double category C we write \(\gamma C\) for the sub-double category of C generated by squares of the above form. We call \(\gamma C\) the globularly generated piece of C. \(\gamma C\) is globularly generated, satisfies the equation
and is contained in every sub-double category D of C satisfying the equation \(H^*C=H^*D\). Moreover, a double category C is globularly generated if and only if C does not contain proper sub-double categories satisfying the above equation. Globularly generated double categories are thus minimal with respect to \(H^*\).
Let gCat denote the full sub-category of dCat generated by globularly generated double categories. Decorated horizontalization extends to a functor \(H^*:{{{\textbf {dCat}}}}\rightarrow {{{\textbf {bCat}}}}^*\) and the globularly generated piece construction extends to a functor \(\gamma :{{{\textbf {dCat}}}}\rightarrow {{{\textbf {gCat}}}}\). In [3, Proposition 3.6] it is proven that \(\gamma \) is a coreflector of gCat in dCat. It is easily seen that this implies that \(\gamma \) is a Grothendieck fibration. Moreover, \(H^*\) is constant on \(\gamma \)-fibers. We present this through the following diagram:

where i denotes the inclusion of gCat in dCat. The above diagram breaks Problem 2.1 into the problem of studying bases of \(\gamma \) and then understanding the double categories in each fiber. We follow this strategy and thus study globularly generated double categories, i.e. bases with respect to \(\gamma \). In [4] it is proven that the above diagram can be completed to a diagram of the form:

2.4 Length
Globularly generated double categories admit a helpful combinatorial description provided in the form of a filtration of their categories of squares. Given a globularly generated double category C we write \(V^1_C\) for the category formed by vertical compositions of squares of the form:

and we denote by \(H^1_C\) the (possibly weak) category formed by horizontal compositions of squares in \(V^1_C\). Assuming we have defined \(V^k_C\) and \(H^k_C\) we make \(V^{k+1}_C\) to be the category generated by morphisms in \(H^k_C\) under vertical composition, and \(H^{k+1}_C\) the (possibly weak) category generated by squares in \(V^{k+1}_C\), under horizontal composition. The category of squares \(C_1\) of C satisfies the equation \(C_1=\varinjlim V^k_C\). Then, we define the length \(\ell C\in {\mathbb {N}}\cup \left\{ \infty \right\} \) of any double category C as the minimal k such that the equation \(\gamma C_1=V^k_{\gamma C}\) holds. Intuitively the vertical length of a double category C measures the complexity of expressions of globularly generated squares in C.
We further explain the vertical filtration construction pictorially: We regard the globular squares and horizontal identities of a double category C as the simplest possible squares of C. We thus represent globular and horizontal identity squares diagrammatically as squares marked by 0, i.e. as:

Below we write \({\mathbb {G}}\) for the collection of 0-marked squares. Observe that the collection of 0-marked squares is closed under horizontal composition. Squares in \(V^1_C\) are those squares in C admitting a subdivision as vertical composition of 0-marked squares. Diagramatically:

where we draw internal 0-marked squares as rectangles for convenience. If a square \(\varphi \) as above is not a globular square or a horizontal identity, i.e. is not marked with 0, we mark \(\varphi \) with 1. We represent 1-marked squares pictorially as:

Squares in \(H^1_C\) are thus those squares in C that admit a subdivision as horizontal composition of squares marked with \(i\le 1\). Given two horizontally composable squares \(\varphi ,\psi \) in \(V^1_C\) we might be able to find compatible vertical subdivisions of \(\varphi \) and \(\psi \) in 0-marked squares, i.e. we might be able to represent the horizontal composition of \(\varphi \) and \(\psi \) as:

where the internal 0-marked squares of the left and right outer squares match. In that case we can use the exchange identity to re-arrange the above composition into a vertical subdivision of 0-marked squares. Example [5, Example 4.1] shows that this is not always the case and that there might exist horizontally composable squares \(\varphi ,\psi \) such that any two vertical subdivisions into 0-squares look like:

i.e. where the internal 0-squares cannot be arranged to match horizontally. Such horizontal compositions are not 1-marked. We represent squares in \(H^1_C\) as above, i.e. squares in \(H^1_C\setminus V^1_C\) as squares marked with 1+1/2, i.e. as:

\(V^2_C\) is thus the category of squares admitting a vertical subdivision into squares marked with \(\le 1+1/2\). Inductively, given \(k\ge 1\), \(V^k_C\) is the category of squares admitting vertical subdivisions as:

where the \(i_j\)’s are all \(\le k-1/2\). Squares marked with k are squares in \(V^k_C\) not marked with \(i<k\). \(H^{k+1}_C\) is the (possibly weak) category of squares admitting a horizontal subdivision as:

where the \(i_j\)’s are all \(\le k\). Squares marked with \(k+1/2\) are those squares in \(H^k_C\) such that no subdivision as above can be reduced as a vertical subdivision as i-squares with \(i\le k-1/2\). In [5] it is shown that there exist globularly generated double categories such that squares marked with \(k+1/2\) exist for every \(k\ge 0\). The formula \(C_1=\varinjlim V^k_C\) thus means that in a globularly generated double category C every square admits a \({\mathbb {N}}+1/2{\mathbb {N}}\)-marking as above. The length of a square \(\varphi \) marked by \(x\in {\mathbb {N}}+1/2{\mathbb {N}}\) is \(\lceil x\rceil \) and the length \(\ell C\) is the maximum of lengths of squares in C. The above pictorial representation is only meant to serve as intuition for the vertical filtration construction and we will not use it for the reminder of the paper.
2.5 Assumptions
We will assume, for the rest of the paper, that all double categories are strict, i.e. we will assume that horizontal composition is associative on the nose, and that unit squares act as units with respect to horizontal composition strictly. We will thus only consider decorated 2-categories and not general decorated bicategories, with some exceptions in Sect. 3.1. We will denote by \({{\textbf {2Cat}}}^*\) the subcategory of \({{\textbf {bCat}}}^*\) generated by decorated 2-categories. It is not difficult to see how the results of this paper could be extended to the general setting of decorated bicategories. This will be pursued in subsequent work.
3 \(\pi _2\)-Indexings and Canonical Decompositions
Theorem 1.1 associates, to a certain type of structure defined on a decorated 2-category, an internalization of length 1. In this section we spell out what this structure is. We provide examples, and we then explain the main ideas behind how the proof of Theorem 1.1 works. The main argument for the proof of Theorem 1.1 is delayed until Sect. 4.
3.1 \(\pi _2\)-Indexings
Definition 3.1
Let \((B^*,B)\in {{\textbf {2Cat}}}^*\). A \(\pi _2\)-indexing on \((B^*,B)\) is a functor
such that for every object a in \(B^*\), the monoid \(\Phi (a)\) is the commutative monoid \(\pi _2(B,a)\) of a, in B. A \(\pi _2\)-opindexing on \((B^*,B)\) is an indexing on \((B^{*op},B)\). We write \(\pi _2{{\textbf {Ind}}}_{(B^*,B)}\) and \(\pi _2{{\textbf {opInd}}}_{(B^*,B)}\) for the collection of \(\pi _2\)-indexings on \((B^*,B)\) and the collection of \(\pi _2\)-opindexings on \((B^*,B)\) respectively.
\(\pi _2\)-indexings and \(\pi _2\)-opindexings are the types of structure we associate to decorated 2-categories in order to construct internalizations of length 1. We explain the ideas behind Definition 3.1 in 3.2. We now present our main examples of \(\pi _2\)-indexings.
Example 3.2
Let A be an abelian group and let G be a group. Consider the decorated 2-category \((\Omega G,2\Omega A)\), where \(\Omega G\) denotes the delooping groupoid generated by G, i.e. \(\Omega G\) is the groupoid with a single object \(\bullet \), whose automorphism group is G, and where \(2\Omega A\) is the 2-category with a single object \(\bullet \), whose monoidal category of automorphisms is \(\Omega A\). A \(\pi _2\)-indexing on the decorated bicategory \((\Omega G,2\Omega A)\) is a functor
such that \(\Phi (\bullet )=A\). Given a morphism \(g\in \Omega G\), i.e. given an element \(g\in G\), the image \(\Phi (g)\) of g, is an automorphism of A. \(\Phi \) is thus precisely the data of a morphism \(G\rightarrow Aut(A)\), i.e. \(\Phi \) is an action by automorphisms \(G\curvearrowright A\). Analogously, a \(\pi _2\)-opindexing on \((\Omega G, 2\Omega A)\) is the data of a morphism \(G^{op}\rightarrow Aut(A)\).
Example 3.3
Let \({\mathcal {C}}\) be a tensor category over a field \({\mathbb {K}}\) and let G be a group. Consider the decorated bicategory \((\Omega G, \Omega C)\), where \(\Omega C\) is the bicategory with a single object \(\bullet \), whose category of endomorphisms is C. A \(\pi _2\)-indexing on the pair \((\Omega G, \Omega C)\) is a functor \(\Phi : \Omega G \rightarrow {{\textbf {commMon}}}\) such that \(\Phi (\bullet )= \text {End(1)} \cong {\mathbb {K}}\). Given an element \(g\in G\), the image \(\Phi (g)\) of g, is an automorphism of \({\mathbb {K}}\). Thus, \(\Phi \) is precisely the data of a morphism \(G\rightarrow {\mathbb {K}}^\times \), i.e. \(\Phi \) is a character of G on \({\mathbb {K}}\). Analogously, a \(\pi _2\)-opindexing on \((\Omega G, \Omega {\mathcal {C}})\) is a character of \(G^{op}\) on \({\mathbb {K}}\).
Example 3.4
Let \({{\textbf {Ring}}}^{{{\textbf {surj}}}}\) be the category of unital rings and surjective ring morphisms. Let \({{\textbf {Mod}}}\) be the bicategory of bimodules over unital rings. Consider the decorated bicategory \(({{\textbf {Ring}}}^{{{\textbf {surj}}}}, {{\textbf {Mod}}})\). Let A be a ring. The monoid \(\pi _2({{\textbf {Mod}}}, A)\) is isomorphic to Z(A). Now, if \(f:A\rightarrow B\) is a surjective morphism, then \(f(Z(A))\subset Z(B).\) The assignments \(A\mapsto Z(A)\) and \(f\mapsto f|_{Z(A)}\) assemble into a \(\pi _2\)-indexing on \(({{\textbf {Ring}}}^{{\textbf {surj}}}, {{\textbf {Mod}}})\):
More generally, let \({{\textbf {Ring}}}^{{{{\textbf {Z}}}}}\) be the category of unital rings and ring morphisms that preserve centers. There is an \(\pi _2\)-indexing on \(({{\textbf {Ring}}}^{{{{\textbf {Z}}}}}, {{\textbf {Mod}}})\):
The following are examples of decorated bicategories with a single \(\pi _2\)-indexing.
Example 3.5
Let C be a category with enough pullbacks and let \({{\textbf {Span}}}(C)\) be the bicategory of spans over C. If c is an object on C there is only one endomorphism over the span

i.e. \(\pi _2(C,c)\) is trivial for every c on C. Thus, there is only one \(\pi _2\)-indexing and only one \(\pi _2\)-opindexing on \((C,{{\textbf {Span}}}(C))\). Analogously, if D is a category with enough pushouts and \({{\textbf {coSpan}}}(D)\) is the bicategory of cospans over D, then there is only one \(\pi _2\)-indexing and only one \(\pi _2\)-opindexing on \((D, {{\textbf {coSpan}}}(D)).\)
Example 3.6
Let \(n{{\textbf {Man}}}\) denote the category of closed oriented n-manifolds and diffeomorphisms, and let \(n{{\textbf {Cob}}}\) denote the bicategory of \((n+1)\)-cobordisms with 2-cells being diffeomorphisms that fix tubular neighborhoods. If X is a closed oriented n-manifold, then the identity of the cylinder \(X\times [0,1]\) is the only element in \(\pi _2(n{{\textbf {Cob}}},X)\). The decorated bicategory \((n{{\textbf {Man}}},n{{\textbf {Cob}}})\) thus admits only one indexing and one opindexing.
The following is an example of a decorated 2-category not admitting \(\pi _2\)-indexings.
Example 3.7
Let \(B^*\) be the groupoid generated by the free standing arrow

i.e. let \(B^*\) be the free living isomorphism, and let B be the 2-category with two objects \(\bullet ,\bullet '\), no non-trivial 1-cells, and where \(\pi _2(B,\bullet )\) and \(\pi _2(B,\bullet ')\) are not isomorphic commutative monoids. If there existed a \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\) or \(\Phi \in \pi _2{{\textbf {opInd}}}_{(B^*,B)}\), then \(\Phi (\alpha )\) would be an isomorphism between \(\pi _2(\bullet ,B)\) and \(\pi _2(\bullet ',B)\).
3.2 Canonical Decompositions
The proof of Theorem 1.1 is presented in Sect. 4. In the reminder of this section we explain the main ideas behind considering \(\pi _2\)-indexings as the type of structure that would yield internalizations of length 1.
All squares of length 1 in a globularly generated double category C admit an expression as vertical composition of globular and unit squares. Moreover, in [3, Lemma 4.6] it is proven that every square

of length 1 in a double category C can be written as a vertical composition of the form

where the top and bottom squares \(\varphi _{\uparrow }\) and \(\varphi _{\downarrow }\) of the above decomposition are globular squares of the form

and where \(U_1,....,U_{n+1}\) and \(\psi _1,\ldots ,\psi _n\) are squares of the form

i.e. where the \(U_i\)’s in the middle of the decomposition are unit squares, and the \(\psi _i\)’s are squares in \(\pi _2(C,a_i)\) for some \(a_i\). The above decomposition can be summarized as

where the middle square is a vertical composition of squares of the form \(U_i\) and \(\psi _i\) as above. The simplest possible form of such decompositions is a decomposition of the form

Not every square of length 1 in a globularly generated double category admits a simple expression as above. If a square \(\varphi \) in a double category C admits an expression as above, we will say that \(\varphi \) admits a canonical decomposition, and we will call any decomposition as above a canonical decomposition for \(\varphi \). We prove the following lemma.
Lemma 3.8
Let C be a double category. If every non globular square \(\varphi \) in C, of length 1, admits a canonical decomposition, then \(\ell C=1\).
Proof
We prove that the collection of globularly generated non globular squares of length 1 of C is closed under the operation of horizontal composition. Let \(\varphi ,\varphi '\) be horizontally composable globularly generated non globular squares of length 1 in C. Represent \(\varphi \) and \(\varphi '\) in canonical form

The condition that \(\varphi ,\varphi '\) are horizontally composable means that the black edges of \(\varphi \) and \(\varphi '\) are equal. The horizontal composition  is the composition
is the composition

The horiozntal composition of two horizontal identity squares is a horizontal identity square. The above composite square is thus equal to

The horizontal composites  and
and  are globular squares, and thus the above square is of length 1. We conclude that the double category C is of length 1. \(\square \)
are globular squares, and thus the above square is of length 1. We conclude that the double category C is of length 1. \(\square \)
3.3 Obtaining Canonical Decomposition
Lemma 3.8 provides us with a strategy for proving that a double category C is of length 1: To prove that all the globularly generated squares of C admit a canonical decomposition. The proof of Theorem 1.1 describes the construction of a double category \(B\rtimes _\Phi B^*\) associated to \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\) for a decorated 2-category \(B^*\), such that every globular square in \(B\rtimes _\Phi B^*\) has a canonical decomposition, and thus is of length 1. We describe the idea behind the fact that \(\pi _2\)-indexings and \(\pi _2\)-opindexing make our construction work. In order to provide every length 1 non-globular, globularly generated square \(\varphi \) of C with a canonical decomposition, we would like to be able to turn every vertical composition of the form (1) into a canonical decomposition. The mid-part of a decomposition of the form (1) is a vertical composition of squares of the form:

If we can turn squares as above into squares of the form

for some other square \(\psi \), i.e. if we can slide red boundary squares down along unit squares, then we can, in decomposition (1), inductively slide all red boundary squares down all the unit squares of the vertical composition and obtain a composite square of the form

where \(\Theta \) is the vertical composition of all the squares resulting of sliding all red-boundary squares in decomposition (1) down unit squares. The vertical composition of the two squares at the bottom of the above decomposition is a square of the form

and thus the above decomposition is canonical. \(\pi _2\)-indexings are precisely the type of structure that allows us to apply the above procedure and thus obtain canonical decomposition for globularly generated squares of length 1. Another way of obtaining canonial decompositions for squares as above is by sliding red-boundary squares up unit squares, as opposed to sliding down. \(\pi _2\)-opindexings are the structure implementing the operation of sliding squares up.
3.4 Vertical Composition and Canonical Decompositions
Another problem we consider with respect to canonical decompositions is how to express the vertical composition of two non-globular, globularly generated squares, admitting canonical decompositions, as a canonical decomposition. Given two vertically compatible squares

Assume both \(\varphi \) and \(\psi \) admit canonical decompositions

The vertical composition  is the square
is the square

The red-boundary square  is ’trapped’ in between unit squares and the square \(\varphi _\uparrow \) and \(\psi _\downarrow \), and thus the above decomposition is not canonical. Under the action of a \(\pi _2\)-indexing, as explained in Sect. 3.2, we could slide the composite red-boundary squre
is ’trapped’ in between unit squares and the square \(\varphi _\uparrow \) and \(\psi _\downarrow \), and thus the above decomposition is not canonical. Under the action of a \(\pi _2\)-indexing, as explained in Sect. 3.2, we could slide the composite red-boundary squre  down and obtain a square of the form
down and obtain a square of the form

which again, is canonical. The operation of sliding red-boundary squares up units, i.e. the action of a \(\pi _2\)-opindexing would yield a similar result. Warning: The ideas presented in this and the previous subsection are the intuitive foundation of our definition of \(\pi _2\)-indexing and \(\pi _2\)-opindexing appearing in Sect. 3, but they do not appear in an essential way in the proof of Theorem 1.1. In the proof of Theorem 1.1, the operation of sliding squares up and down only makes a short appearance in proving that the double category we construct indeed provides an internalization.
4 Proof of Theorem 1.1
In this section we present the proof of Theorem 1.1. This is done in several steps. We begin with the following observation.
Observation 4.1
Let \((B^*,B)\) be a decorated 2-category. Let \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\). The delooping embedding \(\Omega :{{\textbf {commMon}}}\rightarrow {{\,\mathrm{\textbf{Cat}}\,}}\) associating to every commutative monoid A the delooping category \(\Omega A\) of A, allows us to see \(\Phi \) as a functor from \(B^*\rightarrow {{\,\mathrm{\textbf{Cat}}\,}}\), where the evaluation on any object b in \(B^*\) is \(\Omega \pi _2(B,b)\). To simplify notation, we will refer to \(\Omega \pi _2(B,b)\) as \(\pi _2(B,b)\). We consider the Grothendieck construction \(\int _{B^*}\Phi \) of \(\Phi \). The objects of \(\int _{B^*}\Phi \) are pairs \((b, \bullet )\) where b is an object in \(B^*\), morphisms in \(\int _{B^*}\Phi \) are pairs of the form \((f, \varphi )\) where \(f:b\rightarrow c\) is a morphism in \(B^*\) and \(\varphi \) is a morphism in \(\pi _2(B,c)\). We will use the symbol  for the composition of composable pairs \((g,\phi ),(f,\varphi )\) in \(\int _{B^*}\Phi \), i.e.
for the composition of composable pairs \((g,\phi ),(f,\varphi )\) in \(\int _{B^*}\Phi \), i.e.  . We will represent every \((f,\varphi )\) in \(\int _{B^*}\Phi \) pictorially as:
. We will represent every \((f,\varphi )\) in \(\int _{B^*}\Phi \) pictorially as:

Composition in \(\int _{B^*}\Phi \) is thus represented as:

Observation 4.2
Let \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\):
-
1.
The projection functor \(P:\int _{B^*}\Phi \rightarrow B^*\) associating b to every object \((b,\bullet )\) in \(\int _{B^*}\Phi \) and f to every morphism \((f,\varphi )\), is a fiber functor. The functor \(U:B^*\rightarrow \int _{B^*}\Phi \) associating to every object b in \(B^*\), \((b,\bullet )\), to every morphism f in \(B^*\), \((f, id_c)\) is faithful, and satisfies \(PU=id_{B^*}\).
-
2.
For every object b in \(B^*\) there is a faithful functor \(\pi _2(B,b)\rightarrow \int _{B^*}\Phi \) that sends the single object to \((b,\bullet )\) and sends every \(\varphi \in \pi _2(B,b)\) to \((id_b,\varphi )\). These functors extend into a functor \(\bigsqcup \pi _2(B,b)\rightarrow \int _{B^*}\Phi \).
Definition 4.3
Let \((B^*,B)\in {{\textbf {2Cat}}}^*\), \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\). Let \(B_1\) denote the category whose objects and morphisms are 1- and 2-cells of B respectively, under vertical composition. The coproduct \(\bigsqcup \pi _2(B,b)\) over all objects b in \(B^*_0\) is the full subcategory of \(B_1\) generated by horizontal identities of objects in \(B^*\). We denote by \(\int _{B^*}\Phi \sqcup _\pi B_1\) the pushout of categories:

The objects of \(\int _{B^*}\Phi \sqcup _\pi B_1\) are the objects of \(B_1\) and the objects of \(\int _{B^*}\Phi \) identifying \((b,\bullet )\) with the horizontal identity of b for all \(b\in B^*_0\). Morphisms in \(\int _{B^*}\Phi \sqcup _\pi B_1\) are composites of the morphisms of \(B_1\) and the morphisms of \(\int _{B^*}\Phi \), identifying \(\varphi \) with \((id_b, \varphi )\) for all \(b\in B^*_0\) and all \(\varphi \in \pi _2(B,b)\). Pictorially, morphisms in \(\int _{B^*}\Phi \sqcup _\pi B_1\) are thus composites of squares of either of the following two forms:

where squares on the left are as in Observation 4.1, squares on the right represent 2-cells in B, and where the two possible interpretations as above of a square

are identified. Observe that the composition, in \(\int _{B^*}\Phi \sqcup _\pi B_1\), of 2-cells in B that are not elements of \(\pi _2(B,a)\) for some object a, and morphisms in \(\int _{B^*}\Phi \), is a formal concatenation.
Observation 4.4
Let \((B^*,B)\in {{\textbf {2Cat}}}^*\). Let \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\). Consider two composable morphisms of the form \((id,\varphi )\) and (f, id) in \(\int _{B^*}\Phi \). We have the identity

which diagramatically looks like:

Now, observe that for every \((f,\phi )\) in \(\int _{B^*}\Phi \) we have

Diagramatically, the above equation is the composition:

Combining the last two diagrammatic equations, we have the relation  . Diagramatically:
. Diagramatically:

The above equation says that the \(\pi _2\)-indexing \(\Phi \) gives us a way to slide squares down along squares parametrized by an f. See the comments in Sect. 3.3.
In the following observation we analyze the composition of morphisms in \(\int _{B^*}\Phi \sqcup _\pi B_1\).
Observation 4.5
In order to spell out the composition operation in \(\int _{B^*}\Phi \sqcup _\pi B_1\) we consider several cases. Case 1: The two morphisms are in \(B_1\). In that case the composition is the composition in \(B_1\). Case 2: The two morphisms are in \(\int _{B^*}\Phi \). In that case the composition is the composition in Observation 4.1. Case 3: The first morphism is a morphism \(\varphi \) in \(B_1\) but not in \(\int _{B^*}\Phi \) and the second morphism is a morphism \((f,\psi )\) in \(\int _{B^*}\Phi \) but not in \(B_1\). Then the composition  is the formal concatenation of \((f,\psi )\) and \(\varphi \). Case 4: The first morphism is a morphism \((f,\varphi )\) in \(\int _{B^*}\Phi \) but not in \(B_1\) and the second morphism is a morphism \(\psi \) in \(B_1\) but not in \(\int _{B^*}\Phi \). Then, we have the next equation for the composition of \(\psi \) with \((f,\varphi )\):
is the formal concatenation of \((f,\psi )\) and \(\varphi \). Case 4: The first morphism is a morphism \((f,\varphi )\) in \(\int _{B^*}\Phi \) but not in \(B_1\) and the second morphism is a morphism \(\psi \) in \(B_1\) but not in \(\int _{B^*}\Phi \). Then, we have the next equation for the composition of \(\psi \) with \((f,\varphi )\):

Thus, geometrically, the composition of \(\psi \) and \((f,\varphi )\) is the concatenation:

We now proceed to the proof of Theorem 1.1. We begin with the construction of the double category \(B\rtimes _\Phi B^*\).
Construction of \(B\rtimes _\Phi B^*\): Let \((B^*,B)\in {{\textbf {2Cat}}}^*\) and \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\). The construction of \(B\rtimes _\Phi B^*\) will be performed in a series of steps:
-
1.
Underlying categories: We make the category of objects \(B\rtimes _\Phi B^*_0\) of \(B\rtimes _\Phi B^*\) be \(B^*\). We make the category of morphisms \(B\rtimes _\Phi B^*_1\) of \(B\rtimes _\Phi B^*\) be the category \(\int _{B^*}\Phi \sqcup _\pi B_1\) of Definition 4.3.
-
2.
Unit functor: The unit functor \(U:B\rtimes _\Phi B^*_0\rightarrow B\rtimes _\Phi B^*_1\) of \(B\rtimes _\Phi B^*\) will be the functor:

Given a morphism \(f\in (B^*,B)\), the square U(f) is thus defined by the pictorial equation:
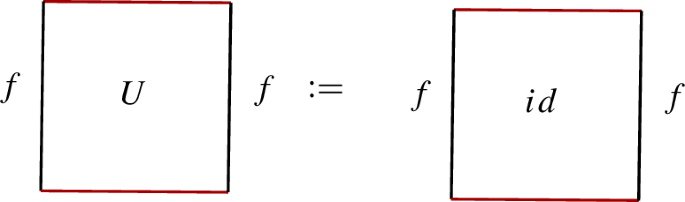
-
3.
Frame functors: Observe that there is a functor \(\int _{B^*}\Phi \sqcup B_1\rightarrow B^*\) given by the universal property of the coproduct applied to the fibred functor \(P:\int _{B^*}\Phi \rightarrow B^*\) and the domain function \(dom: B_1\rightarrow B^*\). Clearly we have that \(P((id,\varphi ))=dom(\varphi )=id\), then we obtain a left frame functor \(L: \int _{B^*}\Phi \sqcup _\pi B \rightarrow B^*\). The right frame functor \(R:\int _{B^*}\Phi \sqcup _\pi B_1\rightarrow B^*\) for \(B\rtimes _\Phi B^*\) is obtained analogously. These two functors match with the convention for the pictorial representation of \((f,\varphi )\) in Observation 4.1.
-
4.
Horizontal composition: We define the horizontal composition functor for \(B\rtimes _\Phi B^*\) in parts. First consider the functor
 defined as
defined as  . Pictorially:
. Pictorially: 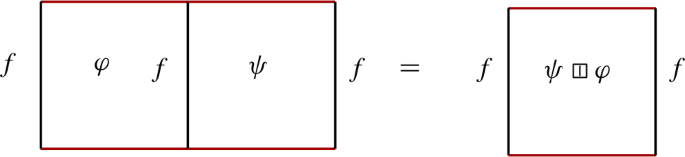
Horizontal composition of B defines a functor
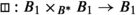 . Observe that
. Observe that  . The two composition operations defined above thus coincide in \(\bigsqcup \pi _2(B,b)\). We obtain a horizontal composition functor
. The two composition operations defined above thus coincide in \(\bigsqcup \pi _2(B,b)\). We obtain a horizontal composition functor 
making the following diagram commute:

-
5.
Relations: We check that the relations between the structure functors defined above, making \(B\rtimes _\Phi B^*\) into a double category are satisfied. Let f be a morphism in \(B^*\), by definition of L and U we have that \(LU(f) = L((f,id))= f\), so \(LU = id_{B^*}\). In the same way, we have the equation \(RU=id_{B^*}\). Now, let \(\varphi , \psi \) two morphisms in \(\int _{B^*}\Phi \sqcup _\pi B_1\) such that \(R(\varphi )\)=\(L(\psi )\). If \(\varphi ,\psi \) are both in \(B_1\), then
 and
and  . Similarly, if \(\varphi ,\psi \) are in \(\int _{B^*} \Phi \) by definition of
. Similarly, if \(\varphi ,\psi \) are in \(\int _{B^*} \Phi \) by definition of  we have that that
we have that that  and
and 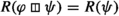 . We conclude that
. We conclude that  and
and  where \(\pi _l\) is and \(\pi _r\) are the projections of the fibered product. We conclude that with the structure defined above \(B\rtimes _\Phi B^*\) is a double category. \(B\rtimes _\Phi B^*\) is a globularly generated internalization of length 1: We finalize the proof of Theorem 1.1 by proving that the double category \(B\rtimes _\Phi B^*\) indeed is a globularly generated internalization of \((B^*,B)\) of length 1. We first prove that \(B\rtimes _\Phi B^*\) is globularly generated and that \(\ell (B\rtimes _\Phi B^*)=1\). By Observaton 4.4, every square appearing in Definition 4.3 admits a decomposition in canonical form. By Lemma 3.8, the double category \(B\rtimes _\Phi B^*\) is globularly generated and of length 1. We now prove the equation \(H^*(B\rtimes _\Phi B^*)=(B^*,B)\). Squares in \(B\rtimes _\Phi B^*\) are either squares of the form
where \(\pi _l\) is and \(\pi _r\) are the projections of the fibered product. We conclude that with the structure defined above \(B\rtimes _\Phi B^*\) is a double category. \(B\rtimes _\Phi B^*\) is a globularly generated internalization of length 1: We finalize the proof of Theorem 1.1 by proving that the double category \(B\rtimes _\Phi B^*\) indeed is a globularly generated internalization of \((B^*,B)\) of length 1. We first prove that \(B\rtimes _\Phi B^*\) is globularly generated and that \(\ell (B\rtimes _\Phi B^*)=1\). By Observaton 4.4, every square appearing in Definition 4.3 admits a decomposition in canonical form. By Lemma 3.8, the double category \(B\rtimes _\Phi B^*\) is globularly generated and of length 1. We now prove the equation \(H^*(B\rtimes _\Phi B^*)=(B^*,B)\). Squares in \(B\rtimes _\Phi B^*\) are either squares of the form 
representing 2-cells in B, or admit decompositions of the form

A square as above is globular if and only if f is an identity, in which case it would be a vertical composition of 2-cells in B and thus would itself be a 2-cell in B. This proves the equation \(H^*B\rtimes _\Phi B^*=(B^*,B)\). This concludes the proof of the Theorem. \(\square \)
-
5.
Note 4.6
A construction analogous to that appearing in Observation 4.5 can be associated to an opindexing. The construction and the arguments appearing in the proof of Theorem 1.1 for the case of opindexings is completely analogous as to those presented above.
5 Examples
Example 5.1
Let G be a group. Let A be an abelian group. Let \(\Phi \in \pi _2{{\textbf {Ind}}}_{(\Omega G,2\Omega A)}\). Example 3.2 says that \(\Phi \) can be identified with an action \(\Phi :G\curvearrowright A\) of G on A by automorphisms. The 2-category \(2\Omega A\) has a single 0- and 1-cell. Every square in \(2\Omega A\rtimes _\Phi \Omega G\) is thus of the form

for some \(g\in G\) and \(a\in A\). By Observation 4.4 every such square can be subdivided as

The horizontal composition of two such squares

is the square

Now, the vertical composition of two squares:

is the square

Which is equal to the square:

The category of morphisms \(2\Omega A\rtimes _\Phi \Omega G_1\) of \(2\Omega A\rtimes _\Phi \Omega G\) can thus be identified with the delooping groupoid \(\Omega (A\rtimes _\Phi G)\) of the semidirect product \(A\rtimes _\Phi G\). An analogous argument identifies the category of mosphisms of internalizations of \((\Omega G,2\Omega A)\) of the form \(2\Omega A\rtimes _\Phi \Omega G\) with the delooping groupoid of \(A\rtimes _\Phi G^{op}\) for a \(\pi _2\)-opindexing \(\Phi \in \pi _2{{\textbf {opInd}}}_{(\Omega G,2\Omega A)}\).
Example 5.2
Let G be a group. Let \({\mathbb {K}}\) be a field, and let C be a strict tensor category over \({\mathbb {K}}\). Let \(\Phi \in \pi _2{{\textbf {Ind}}}_{(\Omega G,\Omega C)}\). Example 3.3 says that we can identify \(\Phi \) with a character of G on \({\mathbb {K}}\). Squares in \(\Omega G\rtimes _\Phi \Omega C\) are of the form:

where a, b are objects in C, \(\varphi :a\rightarrow {\mathbb {K}}\) and \(\psi :{\mathbb {K}}\rightarrow b\) are a costate on a and a state in b respectively, and where \(g\in G\). The composition of two such squares is:

which is equal to

where the above notation represents multiplication by the scalar  .
.
Observation 5.3
Example 5.2 suggests the following notational device: Given a decorated 2-category \((B^*,B)\) and \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\), we denote the square

in \(B\rtimes _\Phi B^*\) as \(|\varphi _\downarrow \rangle f\langle \varphi _\uparrow |\), in analogy with the Bra-ket notation. In that case the horizontal composition of two horizontally compatible squares \(|\varphi _\downarrow \rangle f\langle \varphi _\uparrow |\) and \(|\psi _\downarrow \rangle f\langle \psi _\uparrow |\) is equal to  . We write the vertical composite of two vertically compatible squares \(|\varphi _\downarrow \rangle f\langle \varphi _\uparrow |\) and \(|\psi _\downarrow \rangle g\langle \psi _\uparrow |\) as the square \(\langle \psi _\uparrow |\varphi _\downarrow \rangle |\psi _\downarrow \rangle gf\langle \varphi _\uparrow |\).
. We write the vertical composite of two vertically compatible squares \(|\varphi _\downarrow \rangle f\langle \varphi _\uparrow |\) and \(|\psi _\downarrow \rangle g\langle \psi _\uparrow |\) as the square \(\langle \psi _\uparrow |\varphi _\downarrow \rangle |\psi _\downarrow \rangle gf\langle \varphi _\uparrow |\).
Example 5.4
Let C be a category with enough pullbacks. Assume a choice of pullback for every span in C has been made, so as to make SpanC into a 2-category. The pair (C, SpanC) is a decorated 2-category. Let \(\Phi \in \pi _2{{\textbf {Ind}}}_{(C,SpanC)}\) be the unique \(\pi _2\)-indexing of (C, SpanC). Every square in SpanC of the form

is a span of the form

for a morphism f in C. A square in SpanC of the form

is a span of the form

for some morphisms h, s in C. We suggestively represent the unit square \(U_g\) of a morphism g in C as

With this notation, squares in \(SpanC\rtimes _\Phi C\) are all of the form

The following is an example of a globularly generated double category C of length 1, such that not every square in C admits a canonical decomposition and thus is not of the form \(B\rtimes _\Phi B^*\) for a \(\pi _2\)-indexing or a \(\pi _2\)-opindexing \(\Phi \).
Example 5.5
Let \(B^*\) be the category 2 freely generated by arrows:

Let B be the 2-category with 0-cells 0,1,2, with only horizontal identity cells, and such that \(\pi _2(0)={{\,\mathrm{{\mathbb {Z}}}\,}}/2{{\,\mathrm{{\mathbb {Z}}}\,}},\pi _2(1)={{\,\mathrm{{\mathbb {Z}}}\,}}/2{{\,\mathrm{{\mathbb {Z}}}\,}}\), and \(\pi _2(2)=1\). The pair \((B^*,B)\) is a decorated 2-category. Let \(Q_{(B^*,B)}\) be the free globularly generated double category generated by \((B^*,B)\), see [5]. \(Q_{(B^*,B)}\) is a globularly generated internalization of \((B^*,B)\), see [5, Proposition 3.2]. Moreover, it is easily seen that the horizontal composition of any two squares of length 1 in \(Q_{(B^*,B)}\) is again of length 1, and thus \(\ell Q_{(B^*,B)}=1\). The square:

in \(Q_{(B^*,B)}\) cannot be written as the vertical composition of less than four globular and horizontal identity squares of \(Q_{(B^*,B)}\) and thus does not admit canonical decompositions. We conclude that \(Q_{(B^*,B)}\) is not of the form \(B\rtimes _\Phi B^*\) for a \(\Phi \in \pi _2{{\textbf {Ind}}}_{(B^*,B)}\) nor \(\Phi \in \pi _2{{\textbf {opInd}}}_{(B^*,B)}\).
6 Outlook
In this last section we present open problems and lines of study related to the material presented in this paper.
-
1.
Coherence: One of the obvious shortcomings of the construction presented in Theorem 1.1 is that it only considers decorated 2-categories. A version of this construction for decorated bicategories would, in principle, be analogous to its 2-categorical counterpart, but unit isomorphisms, and associators must come into play. We consider that in the context of this paper, this extra structure would obscure the arguments in the proof of Theorem 1.1 and were thus omitted. A version of our results for decorated bicategories will appear in future work. Another point where the strictness of our construction might be weakened is in the fact that \(\pi _2\)-indexings were taken to be strict functors. One can think of a version of the construction \(B\rtimes _\Phi B^*\) for pseudofunctors, or lax/oplax functors \(\Phi :B^*\rightarrow {{\,\mathrm{\textbf{Cat}}\,}}\). These conditions will again be considered in future work.
-
2.
Functoriality: We have not addressed any questions of functoriality of the construction appearing in the proof of Theorem 1.1. There are different ways of providing collections of \(\pi _2\)-indexings with the structure of a category. The problem of choosing the best possible such structure on \(\pi _2{{\textbf {Ind}}}_{(B^*,B)}\) making the construction \(B\rtimes _\Phi B^*\) functorial, in the appropriate sense, will be addressed in future work. Functoriality is related to the problem of comparison, i.e. the problem of deciding when two double categories of the form \(B\rtimes _\Phi B^*\) and \(B\rtimes _\Psi B^*\) are double equivalent, in terms of the \(\pi _2\)-indexings \(\Phi \) and \(\Psi \). We conjecture that a categorical structure on \(\pi _2{{\textbf {Ind}}}_{(B^*,B)}\) can be chosen so as to make the construction \(B\rtimes _\Phi B^*\) into an embedding of \(\pi _2{{\textbf {Ind}}}_{(B^*,B)}\) into \({{\textbf {gCat}}}\), and thus the two double categories \(B\rtimes _\Phi B^*\) and \(B\rtimes _\Psi B^*\) would be double equivalent if and only if \(\Phi \) and \(\Psi \) are equivalent in the appropriate sense.
-
3.
Frameability: One of the main questions we are interested in is when a decorated bicategory \((B^*,B)\) admits an internalization that is a framed bicategory. In the particular context of this paper we are interested in the question of when a double category of the form \(B\rtimes _\Phi B^*\) is the globularly generated piece \(\gamma C\) of a framed bicategory. This question will be addressed in future work.
Data Availability
We declare that there is no Availability of Data and Materials for this manuscript.
References
Ehresmann, C.: Categories structurées. III. Quintettes et applications covariantes. Topol. Geom. Differ. (Sem. C. Ehresmann) 5, 21 (1963)
Gordon, R., Power, A.J., Street, R.: Coherence for tricategories. Mem. Am. Math. Soc. 117, 558 (1999)
Orendain, J.: Lifting bicategories into double categories: the globularily generated condition. Theory Appl. Categ. 34, 80–108 (2019)
Orendain, J.: Free globularly generated double categories ii: the canonical double projection. Theory Appl. Categ. 34(42), 1343–1385 (2019)
Orendain, J.: Free globularly generated double categories. Cah. Topol. Géom. Différ. Catég., LXII Issue 3, 243–302 (2021)
Palmquist, P.H.: The double category of adjoint squares. PhD Thesis, University of Chicago (1969)
Paré, R., Grandis, M.: Limits in double categories. Cah. Topol. Geom. Differ. Categ. 40(3), 162–220 (1990)
Shulman, M.A.: Framed bicategories and monoidal fibrations. Theory Appl. Categ. 18, 650–738 (2008)
Shulman, M.A.: Comparing composites of left and right derived functors. N. Y. J. Math. 17, 75–125 (2011)
Acknowledgements
The authors would like to thank the anonymous referee, whose valuable comments greatly improved the quality of the paper.
Author information
Authors and Affiliations
Contributions
Juan Orendain and José Rubén Maldonado-Herrera contributed to the manuscript equally. Juan Orendain did not receive financial support. Jose Ruben Maldonado-Herrera was financially supported by CONAHCYT program 001458.
Corresponding author
Ethics declarations
Conflict of interest
We declare that there is no Conflict of interest for this manuscript.
Additional information
Communicated by Nicola Gambino.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Orendain, J., Maldonado-Herrera, J.R. Internalizations of Decorated Bicategories via \(\pi _2\)-Indexings. Appl Categor Struct 32, 16 (2024). https://doi.org/10.1007/s10485-024-09774-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10485-024-09774-z




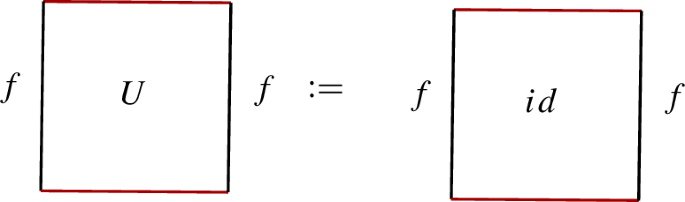
 defined as
defined as  . Pictorially:
. Pictorially: 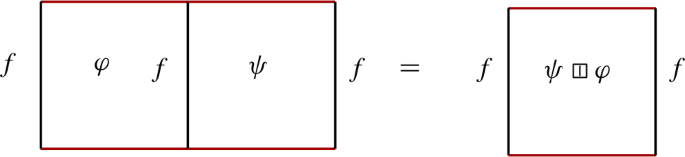
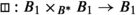 . Observe that
. Observe that  . The two composition operations defined above thus coincide in
. The two composition operations defined above thus coincide in 

 and
and  . Similarly, if
. Similarly, if  we have that that
we have that that  and
and 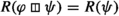 . We conclude that
. We conclude that  and
and  where
where 
