Abstract
Suppose \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is an n-exangulated category. We show that the idempotent completion and the weak idempotent completion of \(\mathcal {C}\) are again n-exangulated categories. Furthermore, we also show that the canonical inclusion functor of \(\mathcal {C}\) into its (resp. weak) idempotent completion is n-exangulated and 2-universal among n-exangulated functors from \((\mathcal {C},\mathbb {E},\mathfrak {s})\) to (resp. weakly) idempotent complete n-exangulated categories. Furthermore, we prove that if \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is n-exact, then so too is its (resp. weak) idempotent completion. We note that our methods of proof differ substantially from the extriangulated and \((n+2)\)-angulated cases. However, our constructions recover the known structures in the established cases up to n-exangulated isomorphism of n-exangulated categories.
Similar content being viewed by others
1 Introduction
Idempotent completion began with Karoubi’s work [20] on additive categories. It was shown that an additive category embeds into an associated one which is idempotent complete, that is, in which all idempotent morphisms admit a kernel. Particularly nice examples of idempotent complete categories include Krull-Schmidt categories, which can be characterised as idempotent complete additive categories in which each object has a semi-perfect endomorphism ring (see Chen–Ye–Zhang [12, Thm. A.1], Krause [24, Cor. 4.4]). Other examples include the vast class of pre-abelian categories (see e.g. [33, Rem. 2.2]); e.g. a module category, or the category of Banach spaces (over the reals, say).
Suppose \(\mathcal {C}\) is an additive category. The objects of the idempotent completion \(\widetilde{\mathcal {C}}\) of \(\mathcal {C}\) are pairs (X, e), where X is an object of \(\mathcal {C}\) and \(e:X \rightarrow X\) is an idempotent morphism in \(\mathcal {C}\), i.e. \(e^2 = e\). What is particularly nice is that if \(\mathcal {C}\) has a certain kind of structure, then in several cases this induces the same structure on \(\widetilde{\mathcal {C}}\). For example, Karoubi had already shown that the idempotent completion of an additive category is again additive (see [20, (1.2.2)]). Furthermore, it has been shown for the following, amongst other, extrinsic structures that if \(\mathcal {C}\) has such a structure, then so too does \(\widetilde{\mathcal {C}}\):
-
(i)
triangulated (see Balmer–Schlichting [7, Thm. 1.5]);
-
(ii)
exact (see Bühler [11, Prop. 6.13]);
-
(iii)
extriangulated (see [27, Thm. 3.1]); and
-
(iv)
\((n+2)\)-angulated, where \(n\geqslant 1\) is an integer (see Lin [25, Thm. 3.1]).
See also Liu–Sun [26] and Zhou [35].
Idempotent complete exact and triangulated categories are verifiably important in algebra and algebraic geometry. As a classical example, in Neeman [28] an idempotent complete exact category \(\mathcal {E}\) is needed to give a clean description of the kernel of the localisation functor from the homotopy category of \(\mathcal {E}\) to its derived category. And, more generally, many equivalences only hold up to direct summands, i.e. up to idempotents (see, for example, Orlov [31, Thm. 2.11], or Kalck–Iyama–Wemyss–Yang [21, Thm. 1.1]). Therefore, it is usually helpful to view an algebraic structure as sitting inside its idempotent completion.
The idempotent completion \(\widetilde{\mathcal {C}}\) comes equipped with an inclusion functor  given by
given by  on objects. Moreover, in several of the cases above it has been shown that this functor is 2-universal in an appropriate sense; see e.g. Proposition 2.8 for a precise formulation. For example, without any assumptions other than additivity, the functor
on objects. Moreover, in several of the cases above it has been shown that this functor is 2-universal in an appropriate sense; see e.g. Proposition 2.8 for a precise formulation. For example, without any assumptions other than additivity, the functor  is additive and 2-universal amongst additive functors from \(\mathcal {C}\) to idempotent complete additive categories. On the other hand, if e.g. \(\mathcal {C}\) has an exact structure, then
is additive and 2-universal amongst additive functors from \(\mathcal {C}\) to idempotent complete additive categories. On the other hand, if e.g. \(\mathcal {C}\) has an exact structure, then  is exact and 2-universal amongst exact functors from \(\mathcal {C}\) to idempotent complete exact categories.
is exact and 2-universal amongst exact functors from \(\mathcal {C}\) to idempotent complete exact categories.
In homological algebra two parallel generalisations have been made from the classical settings of exact and triangulated categories. One of these has been the introduction of extriangulated categories as defined by Nakaoka–Palu [30]. An extriangulated category is a triplet \((\mathcal {C},\mathbb {E},\mathfrak {s})\), where \(\mathcal {C}\) is an additive category,  is a biadditive functor to the category of abelian groups, and \(\mathfrak {s}\) is a so-called additive realisation of \(\mathbb {E}\). The realisation \(\mathfrak {s}\) associates to each \(\delta \in \mathbb {E}(Z,X)\) a certain equivalence class
is a biadditive functor to the category of abelian groups, and \(\mathfrak {s}\) is a so-called additive realisation of \(\mathbb {E}\). The realisation \(\mathfrak {s}\) associates to each \(\delta \in \mathbb {E}(Z,X)\) a certain equivalence class  of a 3-term complex. As an example, each triangulated category \((\mathcal {C},\Sigma ,{{\triangle }})\), where \(\Sigma \) is a suspension functor and \({{\triangle }}\) is a triangulation, is an extriangulated category. Indeed, one defines the corresponding bifunctor by
of a 3-term complex. As an example, each triangulated category \((\mathcal {C},\Sigma ,{{\triangle }})\), where \(\Sigma \) is a suspension functor and \({{\triangle }}\) is a triangulation, is an extriangulated category. Indeed, one defines the corresponding bifunctor by  . See [30, Prop. 3.22] for more details. In addition, each suitable exact category is extriangulated; see [30, Exam. 2.13]. A particular advantage of this theory is that the collection of extriangulated categories is closed under taking extension-closed subcategories. Although an extension-closed subcategory of an exact category is again exact, the same does not hold in general for triangulated categories.
. See [30, Prop. 3.22] for more details. In addition, each suitable exact category is extriangulated; see [30, Exam. 2.13]. A particular advantage of this theory is that the collection of extriangulated categories is closed under taking extension-closed subcategories. Although an extension-closed subcategory of an exact category is again exact, the same does not hold in general for triangulated categories.
We note here that, importantly, it was shown in [27, Sec. 3.1] that the extriangulated structure on \(\widetilde{\mathcal {C}}\) produced from case (iii) above is compatible with the more classical constructions of (i) and (ii). For instance, given a triangulated category \(\mathcal {C}\), one can equip its idempotent completion \(\widetilde{\mathcal {C}}\) with a triangulation by (i) or with an extriangulation by (iii), but these structures are the same in the sense of [30, Prop. 3.22]. Analogously, (iii) also recovers (ii) if one starts with an extriangulated category that is exact.
Let \(n\geqslant 1\) be an integer. The other aforementioned generalisation in homological algebra has been the development of higher homological algebra. This includes the introduction of n-exact and n-abelian categories by Jasso [19], and \((n+2)\)-angulated categories by Geiss–Keller–Oppermann [14]. Respectively, these generalise exact, abelian and triangulated categories, in that one recovers the classical notions by setting \(n=1\). For instance, an \((n+2)\)-angulated category is a triplet  satisfying some axioms, where \(\Sigma \) is still an automorphism of \(\mathcal {C}\), but now
satisfying some axioms, where \(\Sigma \) is still an automorphism of \(\mathcal {C}\), but now  consists of a collection of \((n+2)\)-angles each of which has \(n+3\) terms.
consists of a collection of \((n+2)\)-angles each of which has \(n+3\) terms.
The focal point of this paper is on the idempotent completion of an n-exangulated category. These categories were axiomatised by Herschend–Liu–Nakaoka [16], and simultaneously generalise extriangulated, \((n+2)\)-angulated, and suitable n-exact categories (see [16, Sec. 4]). Like an extriangulated category, an n-exangulated category \((\mathcal {C},\mathbb {E},\mathfrak {s})\) consists of an additive category \(\mathcal {C}\), a biadditive functor  , and a so-called exact realisation \(\mathfrak {s}\) of \(\mathbb {E}\), which satisfy some axioms (see Sect. 3.1). The realisation \(\mathfrak {s}\) now associates to each
, and a so-called exact realisation \(\mathfrak {s}\) of \(\mathbb {E}\), which satisfy some axioms (see Sect. 3.1). The realisation \(\mathfrak {s}\) now associates to each  a certain equivalence class (see Sect. 3.1)
a certain equivalence class (see Sect. 3.1)

of an \((n+2)\)-term complex. In this case, the pair  is called an \(\mathfrak {s}\)-distinguished n-exangle. We recall that structure-preserving functors between n-exangulated categories were defined in [10, Def. 2.32]. They are known as n-exangulated functors and they send distinguished n-exangles to distinguished n-exangles.
is called an \(\mathfrak {s}\)-distinguished n-exangle. We recall that structure-preserving functors between n-exangulated categories were defined in [10, Def. 2.32]. They are known as n-exangulated functors and they send distinguished n-exangles to distinguished n-exangles.
Suppose that \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is an n-exangulated category. Let \(\widetilde{\mathcal {C}}\) denote the idempotent completion of \(\mathcal {C}\) as an additive category. We define a biadditive functor  as follows. For any pair of objects \((X,e),(Z,e')\in \widetilde{\mathcal {C}}\), we let \(\mathbb {F}((Z,e'),(X,e))\) consist of triplets \((e,\delta ,e')\) where \(\delta \in \mathbb {E}(Z,X)\) such that \(\mathbb {E}(Z,e)(\delta ) = \delta = \mathbb {E}(e',X)(\delta )\). On morphisms \(\mathbb {F}\) is essentially a restriction of \(\mathbb {E}\); see Definition 4.4 for details. Now we define a realisation \(\mathfrak {t}\) of \(\mathbb {F}\). For \((e,\delta ,e') \in \mathbb {F}((Z,e'),(X,e))\), we have that
as follows. For any pair of objects \((X,e),(Z,e')\in \widetilde{\mathcal {C}}\), we let \(\mathbb {F}((Z,e'),(X,e))\) consist of triplets \((e,\delta ,e')\) where \(\delta \in \mathbb {E}(Z,X)\) such that \(\mathbb {E}(Z,e)(\delta ) = \delta = \mathbb {E}(e',X)(\delta )\). On morphisms \(\mathbb {F}\) is essentially a restriction of \(\mathbb {E}\); see Definition 4.4 for details. Now we define a realisation \(\mathfrak {t}\) of \(\mathbb {F}\). For \((e,\delta ,e') \in \mathbb {F}((Z,e'),(X,e))\), we have that  for some \((n+2)\)-term complex
for some \((n+2)\)-term complex  with
with  and
and  since \(\mathfrak {s}\) is a realisation of \(\mathbb {E}\). We choose an idempotent morphism
since \(\mathfrak {s}\) is a realisation of \(\mathbb {E}\). We choose an idempotent morphism  of complexes, such that
of complexes, such that  and
and  ; see Corollary 4.13. Lastly, we set \(\mathfrak {t}((e,\delta ,e'))\) to be the equivalence class of the complex
; see Corollary 4.13. Lastly, we set \(\mathfrak {t}((e,\delta ,e'))\) to be the equivalence class of the complex

in \(\widetilde{\mathcal {C}}\). We say that an n-exangulated category is idempotent complete if its underlying additive category is (see Definition 4.31).
Theorem A
(Theorem 4.32, Theorem 4.39) The triplet \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) is an idempotent complete n-exangulated category. Furthermore, the inclusion functor  extends to an n-exangulated functor
extends to an n-exangulated functor  , which is 2-universal among n-exangulated functors from \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) to idempotent complete n-exangulated categories.
, which is 2-universal among n-exangulated functors from \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) to idempotent complete n-exangulated categories.
An n-exact category \((\mathcal {C}, \mathcal {X})\) (see [19, Def. 4.2]) induces an n-exangulated category \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) if, for each pair of objects \(A,C\in \mathcal {C}\), the collection  of n-extensions of C by A forms a set; see [16, Prop. 4.34]. As in [23, Def. 4.6], we say that an n-exangulated category \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is n-exact if its n-exangulated structure arises in this way. Combining Theorem A with [23, Cor. 4.12], we deduce the following.
of n-extensions of C by A forms a set; see [16, Prop. 4.34]. As in [23, Def. 4.6], we say that an n-exangulated category \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is n-exact if its n-exangulated structure arises in this way. Combining Theorem A with [23, Cor. 4.12], we deduce the following.
Corollary B
(Corollary 4.34) If \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is an n-exangulated category that is n-exact, then the idempotent completion \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) is n-exact.
We explain in Remark 4.40 how Theorem A unifies the constructions in cases (i)–(iv) above. Furthermore, we comment on some obstacles faced in proving the n-exangulated case in Remark 4.41.
From Theorem A we deduce the following corollary, giving a way to produce Krull-Schmidt n-exangulated categories.
Corollary C
(Corollary 4.33) If each object in \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) has a semi-perfect endomorphism ring, then the idempotent completion \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) is a Krull-Schmidt n-exangulated category.
Finally, we note that analogues of Theorem A and Corollary B are shown for the weak idempotent completion in Sect. 5. The importance of being weakly idempotent complete for extriangulated categories was very recently demonstrated in [23, Prop. 2.7]. It turns out that for an extriangulated category, the underlying category being weakly idempotent complete is equivalent to the condition (WIC) defined in [30, Cond. 5.8]. Moreover, (WIC) is a key assumption in many results on extriangulated categories, e.g. [30, §§5–7], [17, §3], Zhao–Zhu–Zhuang [36]. We remark that the analogue of (WIC) for n-exangulated categories is automatic if \(n\geqslant 2\), but it is not equivalent to the weak idempotent completeness of the underlying category; see [23, Thm. B] for more details.
2 On the Splitting of Idempotents
In this section we recall some key definitions regarding idempotents and idempotent completions of categories. We focus on the idempotent completion of an additive category in Sect. 2.1 and on the weak idempotent completion in Sect. 2.2. Throughout this section, we let \(\mathcal {A}\) denote an additive category. For a more in-depth treatment, we refer the reader to [11, Secs. 6–7].
2.1 Idempotent Completion
Recall that by an idempotent (in \(\mathcal {A}\)) we mean a morphism \(e:X\rightarrow X\) satisfying \(e^2 = e\) for some object \(X\in \mathcal {A}\).
The following definition is from Borceux [6].
Definition 2.1
[6, Defs. 6.5.1, 6.5.3] An idempotent \(e :X \rightarrow X\) in \(\mathcal {A}\) is said to split if there exist morphisms \(r :X \rightarrow Y\) and \(s :Y \rightarrow X\), such that \(sr=e\) and  . The category \(\mathcal {A}\) is idempotent complete, or has split idempotents, if every idempotent in \(\mathcal {A}\) splits.
. The category \(\mathcal {A}\) is idempotent complete, or has split idempotents, if every idempotent in \(\mathcal {A}\) splits.
If \(\mathcal {A}\) has split idempotents and \(e:X \rightarrow X\) is an idempotent in \(\mathcal {A}\), then the object X admits a direct sum decomposition  (see e.g. Auslander [3, p. 188]). In particular, the idempotent e and its counterpart
(see e.g. Auslander [3, p. 188]). In particular, the idempotent e and its counterpart  each admit a kernel. Idempotent complete additive categories can be characterised by such a criterion and its dual.
each admit a kernel. Idempotent complete additive categories can be characterised by such a criterion and its dual.
Proposition 2.2
[6, Prop. 6.5.4] An additive category is idempotent complete if and only if every idempotent admits a kernel, if and only if every idempotent admits a cokernel.
From this point of view, idempotent complete categories sit between additive categories and pre-abelian categories, the latter being additive categories in which every morphism admits a kernel and a cokernel; see for example Bucur–Deleanu [4, §5.4].
Every additive category can be viewed as a full subcategory of an idempotent complete one. This goes back to Karoubi [20, Sec. 1.2], so the idempotent completion of \(\mathcal {A}\) is also often referred to as the Karoubi envelope of \(\mathcal {A}\).
Definition 2.3
The idempotent completion \(\widetilde{\mathcal {A}}\) of \(\mathcal {A}\) is the category defined as follows. Objects of \(\widetilde{\mathcal {A}}\) are pairs (X, e), where X is an object of \(\mathcal {A}\) and  is idempotent. For objects \((X,e), (Y,e') \in \hbox {obj}\widetilde{\mathcal {A}}\), a morphism from (X, e) to \((Y,e')\) is a triplet \((e',r,e)\), where \(r \in \mathcal {A}(X,Y)\) satisfies
is idempotent. For objects \((X,e), (Y,e') \in \hbox {obj}\widetilde{\mathcal {A}}\), a morphism from (X, e) to \((Y,e')\) is a triplet \((e',r,e)\), where \(r \in \mathcal {A}(X,Y)\) satisfies
in \(\mathcal {A}\). Composition of morphisms is defined by
whenever \((e',r,e)\in \widetilde{\mathcal {A}}((X,e), (Y, e'))\) and \((e'',s,e')\in \widetilde{\mathcal {A}}((Y,e'), (Z, e''))\). The identity of an object \((X,e)\in \hbox {obj}\widetilde{\mathcal {A}}\) will be denoted  and is the morphism (e, e, e).
and is the morphism (e, e, e).
A morphism \((e',r,e) :(X,e) \rightarrow (Y,e')\) in the idempotent completion \(\widetilde{\mathcal {A}}\) of \(\mathcal {A}\) is usually denoted more simply as r; see e.g. [7, Def. 1.2] and [11, Rem. 6.3]. However, for precision in Sects. 4–5, we use triplets for morphisms in \(\widetilde{\mathcal {A}}\) so that we can easily distinguish morphisms in \(\mathcal {A}\) from morphisms in its idempotent completion. Our choice of notation also has the added benefit of keeping track of the (co)domain of a morphism in \(\widetilde{\mathcal {A}}\). This becomes important later when different morphisms in \(\widetilde{\mathcal {A}}\) have the same underlying morphism; see Notation 4.37.
By a functor we always mean a covariant functor. The inclusion functor  is defined as follows. An object \(X \in \hbox {obj}\mathcal {A}\) is sent to
is defined as follows. An object \(X \in \hbox {obj}\mathcal {A}\) is sent to  and a morphism \(r \in \mathcal {A}(X,Y)\) is mapped to
and a morphism \(r \in \mathcal {A}(X,Y)\) is mapped to  .
.
Lemma 2.4
If  is a split idempotent, with a splitting \(e=sr\) where \(r :X \rightarrow Y\) and \(s :Y \rightarrow X\), then
is a split idempotent, with a splitting \(e=sr\) where \(r :X \rightarrow Y\) and \(s :Y \rightarrow X\), then  .
.
Proof
We have  and
and  . Hence, there are morphisms
. Hence, there are morphisms  and
and  in \(\widetilde{\mathcal {A}}\) with
in \(\widetilde{\mathcal {A}}\) with  and
and  . Hence, \(\tilde{r}\) and \(\tilde{s}\) are mutually inverse isomorphisms in \(\widetilde{\mathcal {A}}\). \(\square \)
. Hence, \(\tilde{r}\) and \(\tilde{s}\) are mutually inverse isomorphisms in \(\widetilde{\mathcal {A}}\). \(\square \)
If \(\mathcal {A}\) is an idempotent complete category, then the functor  is an equivalence of categories; see e.g. [11, Rem. 6.5]. But more generally we have the following.
is an equivalence of categories; see e.g. [11, Rem. 6.5]. But more generally we have the following.
Proposition 2.5
[11, Rem. 6.3] The idempotent completion \(\widetilde{\mathcal {A}}\) is an idempotent complete additive category with biproduct given by \((X, e) \oplus (Y, e') = (X \oplus Y, e \oplus e')\). The inclusion functor  is fully faithful and additive.
is fully faithful and additive.
Remark 2.6
Let (X, e) be an arbitrary object of \(\widetilde{\mathcal {A}}\). Then (X, e) is a direct summand of  . Indeed, there is an isomorphism
. Indeed, there is an isomorphism  . The canonical inclusion of (X, e) into
. The canonical inclusion of (X, e) into  is given by the morphism
is given by the morphism  , and the projection of
, and the projection of  onto (X, e) by
onto (X, e) by  . Similarly for
. Similarly for  .
.
The functor  is 2-universal in some sense; see Proposition 2.8. For this we recall the notion of whiskering a natural transformation by a functor. We will use Hebrew letters (e.g.
is 2-universal in some sense; see Proposition 2.8. For this we recall the notion of whiskering a natural transformation by a functor. We will use Hebrew letters (e.g.  (beth),
(beth),  (tsadi),
(tsadi),  (daleth),
(daleth),  (mem)) for natural transformations. Suppose \(\mathcal {B},\mathcal {C},\mathcal {D}\) are categories and that we have a diagram
(mem)) for natural transformations. Suppose \(\mathcal {B},\mathcal {C},\mathcal {D}\) are categories and that we have a diagram

where \(\mathscr {F},\mathscr {G},\mathscr {H}\) are functors and  is a natural transformation.
is a natural transformation.
Definition 2.7
The whiskering of \(\mathscr {F}\) and  is the natural transformation
is the natural transformation  defined by
defined by  for each \(X\in \mathcal {B}\).
for each \(X\in \mathcal {B}\).
The next proposition explains the 2-universal property satisfied by  .
.
Proposition 2.8
[11, Prop. 6.10] For any additive functor \(\mathscr {F}:\mathcal {A}\rightarrow \mathcal {B}\) with \(\mathcal {B}\) idempotent complete:
-
(i)
there is an additive functor \(\mathscr {E}:\widetilde{\mathcal {A}} \rightarrow \mathcal {B}\) and a natural isomorphism
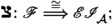 and, in addition,
and, in addition, -
(ii)
for any functor \(\mathscr {G}:\widetilde{\mathcal {A}} \rightarrow \mathcal {B}\) and any natural transformation
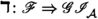 , there exists a unique natural transformation
, there exists a unique natural transformation 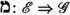 with
with  .
.
2.2 Weak Idempotent Completion
A weaker notion than being idempotent complete is that of being weakly idempotent complete. This was introduced in the context of exact categories by Thomason–Trobaugh [34, Axiom A.5.1]. It is, however, a property of the underlying additive category and gives rise to the following definition.
Definition 2.9
[11, Def. 7.2] An additive category is weakly idempotent complete if every retraction has a kernel.
Definition 2.9 is actually self-dual. Indeed, in an additive category, every retraction has a kernel if and only if every section has a cokernel; see e.g. [11, Lem. 7.1].
If \(r :X \rightarrow Y\) is a retraction in \(\mathcal {A}\), with corresponding section \(s :Y \rightarrow X\), and r admits a kernel k, then the split idempotent  also has kernel k. Conversely, if \(e:X\rightarrow X\) is a split idempotent, with splitting given by \(e=sr\) where \(r :X \rightarrow Y\), then a kernel of e is also a kernel of r. Therefore, weakly idempotent complete categories are those additive categories in which split idempotents admit kernels, in contrast to idempotent complete categories in which all idempotents admit kernels (see Proposition 2.2).
also has kernel k. Conversely, if \(e:X\rightarrow X\) is a split idempotent, with splitting given by \(e=sr\) where \(r :X \rightarrow Y\), then a kernel of e is also a kernel of r. Therefore, weakly idempotent complete categories are those additive categories in which split idempotents admit kernels, in contrast to idempotent complete categories in which all idempotents admit kernels (see Proposition 2.2).
Definition 2.10
The weak idempotent completion \(\widehat{\mathcal {A}}\) of \(\mathcal {A}\) is the full subcategory of \(\widetilde{\mathcal {A}}\) consisting of all objects \((X, e)\in \widetilde{\mathcal {A}}\) such that  is a split idempotent in \(\mathcal {A}\).
is a split idempotent in \(\mathcal {A}\).
Remark 2.11
We note that Definition 2.10 above differs slightly from the definition of the weak idempotent completion of \(\mathcal {A}\) suggested in [11, Rem. 7.8]. If, as in [11], we ask that objects of \(\widehat{\mathcal {A}}\) are pairs (X, e) where \(e:X\rightarrow X\) splits, then \(\widehat{\mathcal {A}}\) is equivalent to \(\mathcal {A}\). Indeed, if \(sr=e\) and  , where \(r:X\rightarrow Y\) and \(s:Y\rightarrow X\), then
, where \(r:X\rightarrow Y\) and \(s:Y\rightarrow X\), then  in \(\widetilde{\mathcal {A}}\) by Lemma 2.4. That is, we have not added any objects that are not already isomorphic to some object of
in \(\widetilde{\mathcal {A}}\) by Lemma 2.4. That is, we have not added any objects that are not already isomorphic to some object of  . On the other hand, if we take objects in \(\widehat{\mathcal {A}}\) to be pairs (X, e) where
. On the other hand, if we take objects in \(\widehat{\mathcal {A}}\) to be pairs (X, e) where  splits (as in Definition 2.10), then we have
splits (as in Definition 2.10), then we have  in \(\widehat{\mathcal {A}}\), where
in \(\widehat{\mathcal {A}}\), where  and
and  , where \(r':X\rightarrow Y'\) and \(s':Y'\rightarrow X\). In this case, since
, where \(r':X\rightarrow Y'\) and \(s':Y'\rightarrow X\). In this case, since  in \(\widetilde{\mathcal {A}}\), we see that a “complementary” summand of
in \(\widetilde{\mathcal {A}}\), we see that a “complementary” summand of  in
in  has been added. This discrepancy has been noticed previously; see e.g. Henrard–van Roosmalen [18, Prop. A.11].
has been added. This discrepancy has been noticed previously; see e.g. Henrard–van Roosmalen [18, Prop. A.11].
It follows that \(\widehat{\mathcal {A}}\) is an additive subcategory of \(\widetilde{\mathcal {A}}\) and that it is weakly idempotent complete; see e.g. [11, Rem. 7.8] or [18, Sec. A.2]. From this observation, we immediately have the next lemma.
Lemma 2.12
Suppose \(\widetilde{X}, \widetilde{Y}, \widetilde{Z} \in \widetilde{\mathcal {A}}\) with \(\widetilde{X} \oplus \widetilde{Y} \cong \widetilde{Z}\). Then any two of \(\widetilde{X}, \widetilde{Y}, \widetilde{Z}\) being isomorphic to objects in \(\widehat{\mathcal {A}}\) implies that the third object is also isomorphic to an object in \(\widehat{\mathcal {A}}\).
Analogously to the construction in Sect. 2.1, there is an inclusion functor  , given by
, given by  on objects, which is 2-universal among additive functors from \(\mathcal {A}\) to weakly idempotent complete categories; see e.g. [28, Rem. 1.12] or [11, Rem. 7.8].
on objects, which is 2-universal among additive functors from \(\mathcal {A}\) to weakly idempotent complete categories; see e.g. [28, Rem. 1.12] or [11, Rem. 7.8].
Proposition 2.13
For any additive functor \(\mathscr {F}:\mathcal {A}\rightarrow \mathcal {B}\) with \(\mathcal {B}\) weakly idempotent complete:
-
(i)
there is an additive functor \(\mathscr {E}:\widehat{\mathcal {A}} \rightarrow \mathcal {B}\) and a natural isomorphism
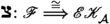 ; and, in addition,
; and, in addition, -
(ii)
for any additive functor \(\mathscr {G}:\widehat{\mathcal {A}} \rightarrow \mathcal {B}\) and any natural transformation
 , there exists a unique natural transformation
, there exists a unique natural transformation 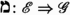 with
with 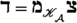 .
.
Let  denote the inclusion functor of the subcategory \(\widehat{\mathcal {A}}\) into \(\widetilde{\mathcal {A}}\). The functor
denote the inclusion functor of the subcategory \(\widehat{\mathcal {A}}\) into \(\widetilde{\mathcal {A}}\). The functor  factors through
factors through  as
as  . An additive functor \(\mathscr {F}:\widehat{\mathcal {A}} \rightarrow \mathcal {B}\) to a weakly idempotent complete category \(\mathcal {B}\) is determined up to unique natural isomorphism by its behaviour on the image
. An additive functor \(\mathscr {F}:\widehat{\mathcal {A}} \rightarrow \mathcal {B}\) to a weakly idempotent complete category \(\mathcal {B}\) is determined up to unique natural isomorphism by its behaviour on the image  of \(\mathcal {A}\) in \(\widehat{\mathcal {A}}\); similarly, a natural transformation
of \(\mathcal {A}\) in \(\widehat{\mathcal {A}}\); similarly, a natural transformation  of additive functors \(\widehat{\mathcal {A}}\rightarrow \mathcal {B}\) is also completely determined by its action on
of additive functors \(\widehat{\mathcal {A}}\rightarrow \mathcal {B}\) is also completely determined by its action on  ; see [11, Rems. 6.7, 6.9].
; see [11, Rems. 6.7, 6.9].
Remark 2.14
In [11, Rem. 7.9], it is remarked that there is a subtle set-theoretic issue regarding the existence of the weak idempotent completion of an additive category. Let NBG denote von Neumann-Bernays-Gödel class theory (see Fraenkel–Bar-Hillel–Levy [13, p. 128]), and let (AGC) denote the Axiom of Global Choice [13, p. 133]. The combination NBG + (AGC) is a conservative extension of ZFC [13, p. 131–132, 134]. If one chooses an appropriate class theory to work with, such as NBG + (AGC), then the weak idempotent completion always exists as a category. This would follow from the Axiom of Predicative Comprehension for Classes (see [13, p. 123]); this is also known as the Axiom of Separation (e.g. Smullyan–Fitting [32, p. 15]). Furthermore, a priori it is not clear to the authors if Proposition 2.8 and 2.13 follow in an arbitrary setting without (AGC). This is because in showing that, for example, an additive functor \(\mathscr {F}:\widetilde{\mathcal {A}} \rightarrow \mathcal {B}\), where \(\mathcal {B}\) is idempotent complete, is determined by its values on  , one must choose a kernel and an image of the idempotent \(\mathscr {F}(e)\) for each idempotent e in \(\mathcal {A}\).
, one must choose a kernel and an image of the idempotent \(\mathscr {F}(e)\) for each idempotent e in \(\mathcal {A}\).
3 n-Exangulated Categories, Functors and Natural Transformations
Let \(n\geqslant 1\) be an integer. In this section we recall the theory of n-exangulated categories established in [16], n-exangulated functors as defined in [10], and n-exangulated natural transformations as recently introduced in [9]. We also use this opportunity to set up some notation.
3.1 n-Exangulated Categories
The definitions in this subsection and more details can be found in [16, Sec. 2]. For this subsection, suppose that \(\mathcal {C}\) is an additive category and that  is a biadditive functor.
is a biadditive functor.
Let A, C be objects in \(\mathcal {C}\). We denote by  the identity element of the abelian group \(\mathbb {E}(C,A)\). Suppose \(\delta \in \mathbb {E}(C,A)\) and that \(a:A\rightarrow B\) and \(d:D\rightarrow C\) are morphisms in \(\mathcal {C}\). We put
the identity element of the abelian group \(\mathbb {E}(C,A)\). Suppose \(\delta \in \mathbb {E}(C,A)\) and that \(a:A\rightarrow B\) and \(d:D\rightarrow C\) are morphisms in \(\mathcal {C}\). We put  and
and  . Since \(\mathbb {E}\) is a bifunctor, we have that
. Since \(\mathbb {E}\) is a bifunctor, we have that  .
.
An \(\mathbb {E}\)-extension is an element \(\delta \in \mathbb {E}(C,A)\) for some \(A,C\in \mathcal {C}\). A morphism of \(\mathbb {E}\)-extensions from \(\delta \in \mathbb {E}(C,A)\) to \(\rho \in \mathbb {E}(D,B)\) is given by a pair (a, c) of morphisms \(a:A\rightarrow B\) and \(c:C\rightarrow D\) in \(\mathcal {C}\) such that  .
.
Let  be a product and
be a product and  be a coproduct in \(\mathcal {C}\), and let \({\delta \in \mathbb {E}(C,A)}\) and \(\rho \in \mathbb {E}(D,B)\) be \(\mathbb {E}\)-extensions. The direct sum of \(\delta \) and \(\rho \) is the unique \(\mathbb {E}\)-extension \(\delta \oplus \rho \in \mathbb {E}(C\oplus D,A\oplus B)\) such that the following equations hold.
be a coproduct in \(\mathcal {C}\), and let \({\delta \in \mathbb {E}(C,A)}\) and \(\rho \in \mathbb {E}(D,B)\) be \(\mathbb {E}\)-extensions. The direct sum of \(\delta \) and \(\rho \) is the unique \(\mathbb {E}\)-extension \(\delta \oplus \rho \in \mathbb {E}(C\oplus D,A\oplus B)\) such that the following equations hold.

From the Yoneda Lemma, each \(\mathbb {E}\)-extension \(\delta \in \mathbb {E}(C,A)\) induces two natural transformations. The first is  given by
given by  for all objects \(B\in \mathcal {C}\) and all morphisms \(a:A\rightarrow B\). The second is
for all objects \(B\in \mathcal {C}\) and all morphisms \(a:A\rightarrow B\). The second is  and defined by
and defined by  for all objects \(D\in \mathcal {C}\) and all morphisms \(d:D\rightarrow C\).
for all objects \(D\in \mathcal {C}\) and all morphisms \(d:D\rightarrow C\).
Let \(\textsf {\textrm{Ch}}({\mathcal {C}})\) be the category of complexes in \(\mathcal {C}\). Its full subcategory consisting of complexes concentrated in degrees \(0,1,\ldots , n,n+1\) is denoted  . If
. If  , we depict
, we depict  as
as

omitting the trails of zeroes at each end.
Definition 3.1
Let  be complexes, and suppose that
be complexes, and suppose that  and
and  are \(\mathbb {E}\)-extensions.
are \(\mathbb {E}\)-extensions.
-
(i)
The pair
 is known as an \(\mathbb {E}\)-attached complex if
is known as an \(\mathbb {E}\)-attached complex if 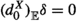 and
and 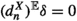 . An \(\mathbb {E}\)-attached complex
. An \(\mathbb {E}\)-attached complex  is called an n-exangle (for \((\mathcal {C},\mathbb {E})\)) if, further, the sequences
is called an n-exangle (for \((\mathcal {C},\mathbb {E})\)) if, further, the sequences 
of functors are exact.
-
(ii)
A morphism
 of \(\mathbb {E}\)-attached complexes is given by a morphism
of \(\mathbb {E}\)-attached complexes is given by a morphism 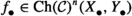 such that
such that  . Such an
. Such an  is called a morphism of n-exangles if
is called a morphism of n-exangles if  and
and 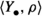 are both n-exangles.
are both n-exangles. -
(iii)
The direct sum of the \(\mathbb {E}\)-attached complexes (or the n-exangles)
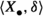 and
and  is the pair
is the pair 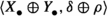 .
.
From the definition above, one can form the additive category of \(\mathbb {E}\)-attached complexes, and its additive full subcategory of n-exangles.
Given a pair of objects \(A,C\in \mathcal {C}\), we define a subcategory  of
of  in the following way. An object
in the following way. An object  is an object of
is an object of  that satisfies
that satisfies  and
and  . For
. For  , a morphism
, a morphism  is a morphism
is a morphism  with
with  and
and  . Note that this implies
. Note that this implies  is not necessarily a full subcategory of
is not necessarily a full subcategory of  , nor necessarily additive.
, nor necessarily additive.
Let  be complexes. Two morphisms in
be complexes. Two morphisms in  are said to be homotopic if they are homotopic in the standard sense viewed as morphisms in
are said to be homotopic if they are homotopic in the standard sense viewed as morphisms in  . This induces an equivalence relation \(\sim \) on
. This induces an equivalence relation \(\sim \) on  . We define
. We define  as the category with the same objects as
as the category with the same objects as  and with
and with  .
.
A morphism  is called a homotopy equivalence if its image in the category
is called a homotopy equivalence if its image in the category  is an isomorphism. In this case,
is an isomorphism. In this case,  and
and  are said to be homotopy equivalent. The isomorphism class of
are said to be homotopy equivalent. The isomorphism class of  in
in  (equivalently, its homotopy class in
(equivalently, its homotopy class in  ) is denoted
) is denoted  . Since the (usual) homotopy class of
. Since the (usual) homotopy class of  in \(\textsf {\textrm{Ch}}({\mathcal {C}})\) may differ from its homotopy class in
in \(\textsf {\textrm{Ch}}({\mathcal {C}})\) may differ from its homotopy class in  , we reserve the notation
, we reserve the notation  specifically for its isomorphism class in
specifically for its isomorphism class in  .
.
Notation 3.2
For \(X \in \mathcal {C}\) and \(i \in \{ 0, \dots , n\}\), we denote by  the object in
the object in  given by
given by  for \(j = i, i+1\) and
for \(j = i, i+1\) and  for \(0 \leqslant j \leqslant i-1\) and \(i+2 \leqslant j \leqslant n+1\), as well as
for \(0 \leqslant j \leqslant i-1\) and \(i+2 \leqslant j \leqslant n+1\), as well as  .
.
Definition 3.3
Let \(\mathfrak {s}\) be an assignment that, for each pair of objects \(A,C\in \mathcal {C}\) and each \(\mathbb {E}\)-extension \({\delta \in \mathbb {E}(C,A)}\), associates to \(\delta \) an isomorphism class  in
in  . The correspondence \(\mathfrak {s}\) is called an exact realisation of \(\mathbb {E}\) if it satisfies the following conditions.
. The correspondence \(\mathfrak {s}\) is called an exact realisation of \(\mathbb {E}\) if it satisfies the following conditions.
-
(R0)
For any morphism \((a,c):\delta \rightarrow \rho \) of \(\mathbb {E}\)-extensions with \(\delta \in \mathbb {E}(C,A)\), \(\rho \in \mathbb {E}(D,B)\),
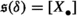 and
and  , there exists
, there exists 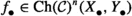 such that \(f_{0}=a\) and
such that \(f_{0}=a\) and  . In this setting, we say that
. In this setting, we say that 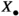 realises \(\delta \) and
realises \(\delta \) and  is a lift of (a, c).
is a lift of (a, c). -
(R1)
If
 , then
, then 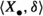 is an n-exangle.
is an n-exangle. -
(R2)
For each object \(A\in \mathcal {C}\), we have
 and
and  .
.
In case \(\mathfrak {s}\) is an exact realisation of \(\mathbb {E}\) and  the following terminology is used. The morphism
the following terminology is used. The morphism  is said to be an \(\mathfrak {s}\)-inflation and the morphism
is said to be an \(\mathfrak {s}\)-inflation and the morphism  an \(\mathfrak {s}\)-deflation. The pair
an \(\mathfrak {s}\)-deflation. The pair  is known as an \(\mathfrak {s}\)-distinguished n-exangle.
is known as an \(\mathfrak {s}\)-distinguished n-exangle.
Suppose \(\mathfrak {s}\) is an exact realisation of \(\mathbb {E}\) and  . We will often use the diagram
. We will often use the diagram

to express that  is an \(\mathfrak {s}\)-distinguished n-exangle. If we also have that
is an \(\mathfrak {s}\)-distinguished n-exangle. If we also have that  and
and  is a morphism of n-exangles, then we call
is a morphism of n-exangles, then we call  a morphism of \(\mathfrak {s}\)-distinguished n-exangles and we depict this by the following commutative diagram.
a morphism of \(\mathfrak {s}\)-distinguished n-exangles and we depict this by the following commutative diagram.

We need one last definition before being able to define an n-exangulated category.
Definition 3.4
Suppose  is a morphism in
is a morphism in  , such that
, such that  for some
for some  . The mapping cone
. The mapping cone  of
of  is the complex
is the complex

with  ,
,  , and
, and  for \(i\in \{1,\ldots ,n-1\}\).
for \(i\in \{1,\ldots ,n-1\}\).
We are in position to state the main definition of this subsection.
Definition 3.5
An n-exangulated category is a triplet \((\mathcal {C},\mathbb {E},\mathfrak {s})\), consisting of an additive category \(\mathcal {C}\), a biadditive functor  and an exact realisation \(\mathfrak {s}\) of \(\mathbb {E}\), such that the following conditions are met.
and an exact realisation \(\mathfrak {s}\) of \(\mathbb {E}\), such that the following conditions are met.
- (\(\hbox {EA1}\)):
-
The collection of \(\mathfrak {s}\)-inflations is closed under composition. Dually, the collection of \(\mathfrak {s}\)-deflations is closed under composition.
- (\(\hbox {EA2}\)):
-
Suppose \(\delta \in \mathbb {E}(D,A)\) and \(c\in \mathcal {C}(C,D)\). If
 and
and 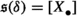 , then there exists a morphism
, then there exists a morphism 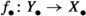 lifting
lifting  , such that
, such that  . In this case, the morphism
. In this case, the morphism  is called a good lift of
is called a good lift of 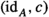 .
. 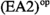 :
:-
The dual of (EA2).
Notice that the definition of an n-exangulated category is self-dual. In particular, the dual statements of several results in Sects. 4–5 are used without proof.
3.2 n-Exangulated Functors and Natural Transformations
In order to show that the canonical functor from an n-exangulated category \((\mathcal {C},\mathbb {E},\mathfrak {s})\) to its idempotent completion is 2-universal among structure-preserving functors from \((\mathcal {C},\mathbb {E},\mathfrak {s})\) to idempotent complete n-exangulated categories, we will need the notion of a morphism of n-exangulated categories and that of a morphism between such morphisms.
For this subsection, suppose \((\mathcal {C},\mathbb {E},\mathfrak {s})\), \((\mathcal {C}',\mathbb {E}',\mathfrak {s}')\) and \((\mathcal {C}'',\mathbb {E}'',\mathfrak {s}'')\) are n-exangulated categories. If \(\mathscr {F}:\mathcal {C}\rightarrow \mathcal {C}'\) is an additive functor, then it induces several other additive functors, e.g.  and obvious restrictions thereof. These are all defined in the usual way. However, by abuse of notation, we simply write \(\mathscr {F}\) for each of these.
and obvious restrictions thereof. These are all defined in the usual way. However, by abuse of notation, we simply write \(\mathscr {F}\) for each of these.
Definition 3.6
[10, Def. 2.32] Suppose that \(\mathscr {F}:\mathcal {C}\rightarrow \mathcal {C}'\) is an additive functor and that \( \Gamma :\mathbb {E}(-,-) \Rightarrow \mathbb {E}'(\mathscr {F}-, \mathscr {F}-) \) is a natural transformation of functors  . The pair \((\mathscr {F},\Gamma ) :(\mathcal {C},\mathbb {E},\mathfrak {s}) \rightarrow (\mathcal {C}',\mathbb {E}',\mathfrak {s}')\) is called an n-exangulated functor if, for all \(A,C\in \mathcal {C}\) and each \(\delta \in \mathbb {E}(A,C)\), we have that
. The pair \((\mathscr {F},\Gamma ) :(\mathcal {C},\mathbb {E},\mathfrak {s}) \rightarrow (\mathcal {C}',\mathbb {E}',\mathfrak {s}')\) is called an n-exangulated functor if, for all \(A,C\in \mathcal {C}\) and each \(\delta \in \mathbb {E}(A,C)\), we have that  whenever
whenever  .
.
If we have a sequence of n-exangulated functors, then the composite of \((\mathscr {F},\Gamma )\) and \((\mathscr {L},\Phi )\) is defined to be

This is an n-exangulated functor \((\mathcal {C},\mathbb {E},\mathfrak {s})\rightarrow (\mathcal {C}'',\mathbb {E}'',\mathfrak {s}'')\); see [9, Lem. 3.19(ii)].
The next result implies that n-exangulated functors preserve finite direct sum decompositions of distinguished n-exangles. It will be used in the main result of Sect. 4.5.
Proposition 3.7
Let \(\mathscr {F}:\mathcal {C}\rightarrow \mathcal {C}'\) be an additive functor and \({\Gamma :\mathbb {E}(-,-) \Rightarrow \mathbb {E}'(\mathscr {F}-,\mathscr {F}-)}\) a natural transformation. Suppose \(\delta \in \mathbb {E}(C,A)\) and \(\rho \in \mathbb {E}(D,B)\) are \(\mathbb {E}\)-extensions, and  and
and  are \(\mathfrak {s}\)-distinguished.
are \(\mathfrak {s}\)-distinguished.
-
(i)
If
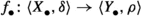 is a morphism of \(\mathbb {E}\)-attached complexes, then the induced morphism
is a morphism of \(\mathbb {E}\)-attached complexes, then the induced morphism  is a morphism of \(\mathbb {E}'\)-attached complexes.
is a morphism of \(\mathbb {E}'\)-attached complexes. -
(ii)
We have
 as \(\mathbb {E}'\)-attached complexes.
as \(\mathbb {E}'\)-attached complexes.
Proof
(i) Note that  since \(\Gamma \) is natural and
since \(\Gamma \) is natural and  is an \(\mathbb {E}\)-attached complex. Similar computations show that both
is an \(\mathbb {E}\)-attached complex. Similar computations show that both  and
and  are \(\mathbb {E}'\)-attached complexes. As
are \(\mathbb {E}'\)-attached complexes. As  is a morphism
is a morphism  of complexes, it suffices to prove
of complexes, it suffices to prove

This follows immediately from  and the naturality of \(\Gamma \).
and the naturality of \(\Gamma \).
(ii) This follows from applying (i) to the morphisms in the appropriate biproduct diagram of \(\mathbb {E}\)-attached complexes. \(\square \)
Lastly, we recall the notion of a morphism of n-exangulated functors. The extriangulated version was defined in Nakaoka–Ogawa–Sakai [29, Def. 2.11(3)].
Definition 3.8
[9, Def. 4.1] Suppose \((\mathscr {F},\Gamma ), (\mathscr {G},\Lambda ):(\mathcal {C},\mathbb {E},\mathfrak {s})\rightarrow (\mathcal {C}',\mathbb {E}',\mathfrak {s}')\) are n-exangulated functors. A natural transformation  of functors is said to be n-exangulated if, for all \(A,C\in \mathcal {C}\) and each \(\delta \in \mathbb {E}(C,A)\), we have
of functors is said to be n-exangulated if, for all \(A,C\in \mathcal {C}\) and each \(\delta \in \mathbb {E}(C,A)\), we have

We denote this by  . In addition, if
. In addition, if  has an n-exangulated inverse, then it is called an n-exangulated natural isomorphism. It is straightforward to check that
has an n-exangulated inverse, then it is called an n-exangulated natural isomorphism. It is straightforward to check that  has an n-exangulated inverse if and only if
has an n-exangulated inverse if and only if  is an isomorphism for each \(X\in \mathcal {C}\).
is an isomorphism for each \(X\in \mathcal {C}\).
4 The Idempotent Completion of an n-Exangulated Category
Throughout this section we work with the following setup.
Setup 4.1
Let \(n\geqslant 1\) be an integer. Let \((\mathcal {C},\mathbb {E},\mathfrak {s})\) be an n-exangulated category. We denote by  the inclusion of the category \(\mathcal {C}\) into its idempotent completion \(\widetilde{\mathcal {C}}\); see Sect. 2.
the inclusion of the category \(\mathcal {C}\) into its idempotent completion \(\widetilde{\mathcal {C}}\); see Sect. 2.
In this section, we will construct a biadditive functor  (see Sect. 4.1) and an exact realisation \(\mathfrak {t}\) of \(\mathbb {F}\) (see Sect. 4.2), and then show that \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) is an n-exangulated category (see Sects. 4.3–4.5). For \(n=1\), we recover the main results of [27]. First, we establish some notation to help our exposition.
(see Sect. 4.1) and an exact realisation \(\mathfrak {t}\) of \(\mathbb {F}\) (see Sect. 4.2), and then show that \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) is an n-exangulated category (see Sects. 4.3–4.5). For \(n=1\), we recover the main results of [27]. First, we establish some notation to help our exposition.
Notation 4.2
We reserve notation with a tilde for objects and morphisms in \(\widetilde{\mathcal {C}}\).
-
(i)
If \(\widetilde{X}\in \widetilde{\mathcal {A}}\) is some object, then we will denote the identity morphism of \(\widetilde{X}\) by
 . Recall from Definition 2.3 that the identity of an object \((X,e)\in \widetilde{\mathcal {A}}\) is
. Recall from Definition 2.3 that the identity of an object \((X,e)\in \widetilde{\mathcal {A}}\) is  .
. -
(ii)
Given a morphism \((e',r,e)\in \widetilde{\mathcal {C}}((X,e),(Y,e'))\), we call \(r:X\rightarrow Y\) the underlying morphism of \((e',r,e)\).
-
(iii)
Suppose \((X,e), (Y,e') \in \widetilde{\mathcal {C}}\) and \(r \in \mathcal {C}(X, Y)\) with \(e' r = r = r e\). Then there is a unique morphism \(\tilde{r} \in \widetilde{\mathcal {C}}((X,e), (Y,e'))\) with underlying morphism r. This morphism \(\tilde{r}\) is the triplet \((e', r, e)\). Moreover, we will use this notation specifically for this correspondence. That is, we write \(\tilde{s}:(X,e) \rightarrow (Y,e')\) is a morphism in \(\widetilde{\mathcal {C}}\) if and only if we implicitly mean that the underlying morphism of \(\tilde{s}\) is denoted s, i.e. we have \(\tilde{s} = (e',s,e)\).
Remark 4.3
By Notation 4.2(iii), two morphisms \(\tilde{r}, \tilde{s} \in \widetilde{\mathcal {C}} ((X,e), (Y,e'))\) are equal if and only if their underlying morphisms r and s, respectively, are equal in \(\mathcal {C}\). Thus, for all objects \(\widetilde{X},\widetilde{Y}\in \widetilde{\mathcal {C}}\), removing the tilde from morphisms in \(\widetilde{\mathcal {C}}(\widetilde{X},\widetilde{Y})\) defines an injective abelian group homomorphism \(\widetilde{\mathcal {C}}(\widetilde{X},\widetilde{Y}) \rightarrow \mathcal {C}(X,Y)\). In particular, a diagram in \(\widetilde{\mathcal {C}}\) commutes if and only if its diagram of underlying morphisms commutes.
4.1 Defining the Biadditive Functor \(\mathbb {F}\)
The following construction is the higher version of the one given in [27, Sec. 3.1] for extriangulated categories.
Definition 4.4
We define a functor  as follows. For objects
as follows. For objects  and
and  in \(\widetilde{\mathcal {C}}\), we put
in \(\widetilde{\mathcal {C}}\), we put

For morphisms  in \(\widetilde{\mathcal {C}}\), we define
in \(\widetilde{\mathcal {C}}\), we define

Remark 4.5
We make some comments on Definition 4.4.
-
(i)
The assignment \(\mathbb {F}\) on morphisms takes values where claimed due to the following. For morphisms
 and
and 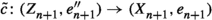 , and an \(\mathbb {F}\)-extension
, and an \(\mathbb {F}\)-extension  , we have $$\begin{aligned} \mathbb {E}(e''_{n+1}, e'_{0})\mathbb {E}(c,a)(\delta )&= \mathbb {E}(ce''_{n+1},e'_{0}a)(\delta ) \\&= \mathbb {E}(c,a)(\delta ). \end{aligned}$$
, we have $$\begin{aligned} \mathbb {E}(e''_{n+1}, e'_{0})\mathbb {E}(c,a)(\delta )&= \mathbb {E}(ce''_{n+1},e'_{0}a)(\delta ) \\&= \mathbb {E}(c,a)(\delta ). \end{aligned}$$Therefore,
 lies in
lies in 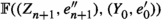 . It is then straightforward to verify that \(\mathbb {F}\) is indeed a functor.
. It is then straightforward to verify that \(\mathbb {F}\) is indeed a functor. -
(ii)
The set
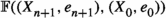 is an abelian group by defining
is an abelian group by defining 
for
 . The additive identity element of
. The additive identity element of  is
is 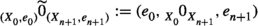 . The inverse of
. The inverse of 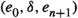 is
is 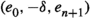 . Notice that we get an abelian group monomorphism:
. Notice that we get an abelian group monomorphism: 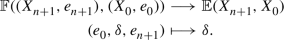
This homomorphism plays a role later in the proof of Theorem 4.39.
-
(iii)
It follows from the definition of \(\mathbb {F}\) that it is biadditive since \(\mathbb {E}\) is.
-
(iv)
Given
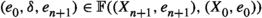 , the pair
, the pair 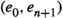 is a morphism of \(\mathbb {E}\)-extensions \(\delta \rightarrow \delta \). Indeed, we have that
is a morphism of \(\mathbb {E}\)-extensions \(\delta \rightarrow \delta \). Indeed, we have that 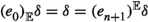 from Definition 4.4.
from Definition 4.4.
Notation 4.6
As for objects and morphisms in \(\widetilde{\mathcal {C}}\), we use tilde notation for \(\mathbb {F}\)-extensions, which gives us a way to pass back to \(\mathbb {E}\)-extensions.
-
(i)
We will denote an \(\mathbb {F}\)-extension of the form
 by \({\tilde{\delta }}\). We call
by \({\tilde{\delta }}\). We call 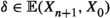 the underlying \(\mathbb {E}\)-extension of \({\tilde{\delta }}\).
the underlying \(\mathbb {E}\)-extension of \({\tilde{\delta }}\). -
(ii)
For
 and
and  with
with  , there is a unique \(\mathbb {F}\)-extension
, there is a unique \(\mathbb {F}\)-extension  with underlying \(\mathbb {E}\)-extension \(\delta \). This \(\mathbb {F}\)-extension is
with underlying \(\mathbb {E}\)-extension \(\delta \). This \(\mathbb {F}\)-extension is 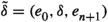 . Again, we use this instance of the tilde notation for this correspondence: we write
. Again, we use this instance of the tilde notation for this correspondence: we write 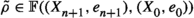 if and only if the underlying \(\mathbb {E}\)-extension of \({\tilde{\rho }}\) is \(\rho \), i.e.
if and only if the underlying \(\mathbb {E}\)-extension of \({\tilde{\rho }}\) is \(\rho \), i.e.  .
.
Remark 4.7
Analogously to our observations in Remark 4.3, we note that by Notation 4.6(ii) any two \(\mathbb {F}\)-extensions  are equal if and only if their underlying \(\mathbb {E}\)-extensions are equal. Hence, removing the tilde from \(\mathbb {F}\)-extensions defines an injective abelian group homomorphism \(\mathbb {F}((Y,e'), (X,e)) \rightarrow \mathbb {E}(Y,X)\) for \((X,e), (Y,e') \in \widetilde{\mathcal {C}}\).
are equal if and only if their underlying \(\mathbb {E}\)-extensions are equal. Hence, removing the tilde from \(\mathbb {F}\)-extensions defines an injective abelian group homomorphism \(\mathbb {F}((Y,e'), (X,e)) \rightarrow \mathbb {E}(Y,X)\) for \((X,e), (Y,e') \in \widetilde{\mathcal {C}}\).
4.2 Defining the Realisation \(\mathfrak {t}\)
To define an exact realisation \(\mathfrak {t}\) of the functor \(\mathbb {F}\) defined in Sect. 4.1, given a morphism of extensions consisting of two idempotents, we will need to lift this morphism to an \((n+2)\)-tuple of idempotents. That is, we require a higher version of the idempotent lifting trick (see [27, Lem. 3.5] and [7, Lem. 1.13]). This turns out to be quite non-trivial and requires an abstraction of the case when \(n=1\) in order to understand the mechanics of why this trick is successful.
We start with two lemmas related to the polynomial ring \(\mathbb {Z}[x]\). Recall that \(\mathbb {Z}[x]\) has the universal property that for any (unital, associative) ring R and any element \(r \in R\) there is a unique (identity preserving) ring homomorphism \(\varphi _r :\mathbb {Z}[x] \rightarrow R\) with \(\varphi _r(x) = r\). For \(p=p(x) \in \mathbb {Z}[x]\), we denote \(\varphi _r(p)\) by p(r) as is usual.
Lemma 4.8
For each \(m \in \mathbb {N}\), the ideals \((x^m) = {(x)}^m\) and \(((x-1)^m) = {(x-1)}^m\) of \(\mathbb {Z}[x]\) are coprime.
Proof
The ideals \(\sqrt{{(x)}^m} = (x)\) and \(\sqrt{{(x-1)}^m} = (x-1)\) are coprime in \(\mathbb {Z}[x]\). Hence, \((x^m)\) and \(( (x-1)^m )\) are also coprime by Atiyah–MacDonald [2, Prop. 1.16]. \(\square \)
Lemma 4.9
For each \(m \in \mathbb {N}_{\geqslant 1}\), there is a polynomial \(p_m \in (x^m) \unlhd \mathbb {Z}[x]\), such that for every (unital, associative) ring R we have:
-
(i)
\(p_m(e) = e\) for each idempotent \(e \in R\); and
-
(ii)
the element \(p_m(r) \in R\) is an idempotent for each \(r \in R\) satisfying \((r^2-r)^m = 0\).
Proof
Fix an integer \(m \geqslant 1\). By Lemma 4.8, we can write \(1 = x^m p_m' + (x-1)^m q_m'\) for some polynomials \(p_m'\) and \(q_m'\) in \(\mathbb {Z}[x]\). We set \(p_m :=x^m p_m'\).
Let R be a ring. For any idempotent \(e \in R\), evaluating \(x = x^{m+1} p_m' + x(x-1)^m q_m'\) at e and using \(e(e-1) = 0\) yields \(e = e^{m+1} p_m'(e) = e^m p_m'(e) = p_m(e)\), proving (i).
Now suppose \(r \in R\) is an element with \((r^2-r)^m = 0\). Evaluation of
at r shows \(p_m(r)^2 = p_m(r)\) since \((r^2-r)^m = 0\), which finishes the proof. \(\square \)
The following is an abstract formulation of [27, Lem. 3.5] and [7, Lem. 1.13].
Lemma 4.10
Let  be a complex in an additive category \(\mathcal {A}\) and suppose
be a complex in an additive category \(\mathcal {A}\) and suppose  is a weak cokernel of
is a weak cokernel of  . Suppose
. Suppose  is a morphism of complexes with
is a morphism of complexes with  and
and  both idempotent. Then there exists a morphism
both idempotent. Then there exists a morphism  , such that the following hold.
, such that the following hold.
-
(i)
The triplet
 is a morphism of complexes.
is a morphism of complexes. -
(ii)
The element
 is idempotent and satisfies
is idempotent and satisfies 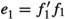 .
. -
(iii)
The triplet
 is an idempotent morphism of complexes.
is an idempotent morphism of complexes. -
(iv)
If
 is a homotopy of morphisms
is a homotopy of morphisms  , then the pair
, then the pair 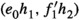 yields a homotopy
yields a homotopy 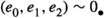 .
.
Proof
Choose a polynomial  as obtained in Lemma 4.9. Define \(q :=xp'_{2}\) and set
as obtained in Lemma 4.9. Define \(q :=xp'_{2}\) and set  . We show this morphism satisfies the claims in the statement. For this, we will make use of the following. Let \(p=p(x)\in \mathbb {Z}[x]\) be any polynomial. Since
. We show this morphism satisfies the claims in the statement. For this, we will make use of the following. Let \(p=p(x)\in \mathbb {Z}[x]\) be any polynomial. Since  is a morphism of complexes, we have that
is a morphism of complexes, we have that  is also a morphism of complexes, i.e. the diagram
is also a morphism of complexes, i.e. the diagram

commutes.
(i) Note that  , where the last equality follows from Lemma 4.9(i). Similarly,
, where the last equality follows from Lemma 4.9(i). Similarly,  . Thus, using \(p=q\) in the commutative diagram (4.1) shows that
. Thus, using \(p=q\) in the commutative diagram (4.1) shows that  is a morphism of complexes.
is a morphism of complexes.
(ii) Since \(f_1' = q(f_1)\) is a polynomial in \(f_1\), we immediately have that  . Furthermore, we see that
. Furthermore, we see that  . Thus, to show that
. Thus, to show that  is idempotent, it is enough to show that \((f_1^2 - f_1)^2 = 0\) by Lemma 4.9(ii). Let \(r(x) = x^2 -x\). We see that
is idempotent, it is enough to show that \((f_1^2 - f_1)^2 = 0\) by Lemma 4.9(ii). Let \(r(x) = x^2 -x\). We see that  and
and  vanish as
vanish as  and
and  are idempotents. Therefore, by choosing \(p = r\) in (4.1) we have
are idempotents. Therefore, by choosing \(p = r\) in (4.1) we have  and so there is
and so there is  with
with  , because
, because  is a weak cokernel of
is a weak cokernel of  . This implies
. This implies  as
as  , and hence
, and hence  is idempotent.
is idempotent.
(iii) Note that  is a morphism of complexes using
is a morphism of complexes using  in (4.1).
in (4.1).
(iv) Suppose  is a homotopy. Then we see that
is a homotopy. Then we see that

Hence,  is a null homotopy as desired. \(\square \)
is a null homotopy as desired. \(\square \)
Remark 4.11
Let \(p'_2 = -2x + 3\) and \(q'_2 = 2x + 1\). Then indeed \(1 = x^2p'_2 + (x-1)^2q'_2\). Hence,  is a possible choice for \(m=2\) in Lemma 4.9. Letting \(h = x^2 - x\) and \(i = x\), we see that
is a possible choice for \(m=2\) in Lemma 4.9. Letting \(h = x^2 - x\) and \(i = x\), we see that  . Then the idempotent
. Then the idempotent  obtained in Lemma 4.10 is the idempotent obtained through the idempotent lifting trick in [27, Lem. 3.5].
obtained in Lemma 4.10 is the idempotent obtained through the idempotent lifting trick in [27, Lem. 3.5].
Lemma 4.12
Suppose  is an \(\mathfrak {s}\)-distinguished n-exangle and
is an \(\mathfrak {s}\)-distinguished n-exangle and  is an idempotent with
is an idempotent with  . Then
. Then  can be extended to a null homotopic, idempotent morphism
can be extended to a null homotopic, idempotent morphism  with
with  for \(2 \leqslant i \leqslant n+1\). Further, the null homotopy of \(e_{\bullet }\) can be chosen to be of the shape
for \(2 \leqslant i \leqslant n+1\). Further, the null homotopy of \(e_{\bullet }\) can be chosen to be of the shape  .
.
Proof
We have  so
so  is a morphism of \(\mathbb {E}\)-extensions. The solid morphisms of the diagram
is a morphism of \(\mathbb {E}\)-extensions. The solid morphisms of the diagram

clearly commute, so we need to find a morphism  making the two leftmost squares commute. Since
making the two leftmost squares commute. Since  is an \(\mathfrak {s}\)-distinguished n-exangle, there is an exact sequence
is an \(\mathfrak {s}\)-distinguished n-exangle, there is an exact sequence

The morphism  is in the kernel of
is in the kernel of  as
as  . Therefore, there exists
. Therefore, there exists  with
with  . If we put
. If we put  , then
, then  is morphism of \(\mathfrak {s}\)-distinguished n-exangles and
is morphism of \(\mathfrak {s}\)-distinguished n-exangles and  is a homotopy. By Lemma 4.10, using that
is a homotopy. By Lemma 4.10, using that  and 0 are idempotents, there is an idempotent
and 0 are idempotents, there is an idempotent  , such that
, such that  is an idempotent morphism of complexes and that
is an idempotent morphism of complexes and that  is a homotopy. Finally,
is a homotopy. Finally,  is a morphism of \(\mathfrak {s}\)-distinguished n-exangles since
is a morphism of \(\mathfrak {s}\)-distinguished n-exangles since  . \(\square \)
. \(\square \)
Corollary 4.13
Suppose  and that
and that  is an \(\mathfrak {s}\)-distinguished n-exangle. The morphism
is an \(\mathfrak {s}\)-distinguished n-exangle. The morphism  of \(\mathbb {E}\)-extensions has a lift
of \(\mathbb {E}\)-extensions has a lift  that is idempotent and satisfies
that is idempotent and satisfies  for all \(2 \leqslant i \leqslant n -1\), such that there is a homotopy
for all \(2 \leqslant i \leqslant n -1\), such that there is a homotopy  .
.
Proof
Define  and
and  , we have
, we have  and so
and so  . Therefore, by Lemma 4.12 we can extend
. Therefore, by Lemma 4.12 we can extend  of \(\mathfrak {s}\)-distinguished n-exangles with \(e'_{i} = 0\) for \(i\in \{ 2,\ldots ,n+1 \}\), having a homotopy
of \(\mathfrak {s}\)-distinguished n-exangles with \(e'_{i} = 0\) for \(i\in \{ 2,\ldots ,n+1 \}\), having a homotopy  . Similarly, by the dual of Lemma 4.12, we can extend \(e''_{n+1}\) to an idempotent morphism
. Similarly, by the dual of Lemma 4.12, we can extend \(e''_{n+1}\) to an idempotent morphism  with \(e''_{i} = 0\) for \(i\in \{ 0,\ldots ,n-1 \}\), such that there is a homotopy
with \(e''_{i} = 0\) for \(i\in \{ 0,\ldots ,n-1 \}\), such that there is a homotopy  . Consider the morphism
. Consider the morphism  and hence
and hence  is a homotopy.
is a homotopy.
If \(n = 1\), then  and
and  is a homotopy. Lemma 4.10 yields an idempotent morphism
is a homotopy. Lemma 4.10 yields an idempotent morphism  and a homotopy
and a homotopy  . Then
. Then  and
and  are the desired idempotent morphism and homotopy, respectively.
are the desired idempotent morphism and homotopy, respectively.
If \(n \geqslant 2\), then the compositions \(e'_{\bullet }e''_{\bullet } \) and \(e''_{\bullet } e'_{\bullet }\) are zero. This implies that  is idempotent. Hence,
is idempotent. Hence,  and
and  are the desired idempotent morphism and homotopy, respectively. \(\square \)
are the desired idempotent morphism and homotopy, respectively. \(\square \)
The following simple lemma will be used several times.
Lemma 4.14
Suppose that \((X,e), (Y,e')\) are objects in \(\widetilde{\mathcal {C}}\) and \(r:X\rightarrow Y\) is a morphism in \(\mathcal {C}\). Setting \(s :=e're\) yields a morphism \(\tilde{s} = (e',s,e) :(X,e)\rightarrow (Y,e')\) in \(\widetilde{\mathcal {C}}\).
The previous result allows us to view a complex in \(\mathcal {C}\) that is equipped with an idempotent endomorphism as a complex in the idempotent completion \(\widetilde{\mathcal {C}}\), as follows.
Definition 4.15
Suppose  is a complex in \(\mathcal {C}\) and
is a complex in \(\mathcal {C}\) and  is an idempotent morphism of complexes. We denote by
is an idempotent morphism of complexes. We denote by  the complex in \(\widetilde{\mathcal {C}}\) with object
the complex in \(\widetilde{\mathcal {C}}\) with object  in degree i and differential
in degree i and differential  .
.
In the notation of Definition 4.15, the underlying morphism of the differential  satisfies
satisfies

since  is a morphism of complexes and consists of idempotents. Furthermore, whenever we write
is a morphism of complexes and consists of idempotents. Furthermore, whenever we write  to denote a complex in \(\widetilde{\mathcal {C}}\), we always mean that
to denote a complex in \(\widetilde{\mathcal {C}}\), we always mean that  is an idempotent morphism in \(\textsf {\textrm{Ch}}({\mathcal {C}})\) and that
is an idempotent morphism in \(\textsf {\textrm{Ch}}({\mathcal {C}})\) and that  is the induced object in \(\textsf {\textrm{Ch}}({\widetilde{\mathcal {C}}})\) as described in Definition 4.15.
is the induced object in \(\textsf {\textrm{Ch}}({\widetilde{\mathcal {C}}})\) as described in Definition 4.15.
We make a further remark on the notation  . Because of the need to tweak the differentials in
. Because of the need to tweak the differentials in  according to (4.2), one cannot recover the original complex
according to (4.2), one cannot recover the original complex  with differentials
with differentials  from the pair
from the pair  defined in Definition 4.15. This is in contrast to the description of an object in \(\widetilde{\mathcal {C}}\) as a pair (X, e) where one can recover \(X\in \mathcal {C}\) uniquely. Thus,
defined in Definition 4.15. This is in contrast to the description of an object in \(\widetilde{\mathcal {C}}\) as a pair (X, e) where one can recover \(X\in \mathcal {C}\) uniquely. Thus,  is an abuse of notation but should hopefully cause no confusion.
is an abuse of notation but should hopefully cause no confusion.
Lemma 4.14 allows us to induce morphisms of complexes in \(\widetilde{\mathcal {C}}\) given a morphism between complexes in \(\mathcal {C}\) if the complexes involved come with idempotent endomorphisms. The proof is also straightforward.
Lemma 4.16
Suppose that  are objects in \(\textsf {\textrm{Ch}}({\widetilde{\mathcal {C}}})\) and that
are objects in \(\textsf {\textrm{Ch}}({\widetilde{\mathcal {C}}})\) and that  is a morphism in
is a morphism in  . Then defining
. Then defining  for each \(i\in \mathbb {Z}\) gives rise to a morphism
for each \(i\in \mathbb {Z}\) gives rise to a morphism  in \(\textsf {\textrm{Ch}}({\widetilde{\mathcal {C}}})\) with
in \(\textsf {\textrm{Ch}}({\widetilde{\mathcal {C}}})\) with  .
.
Notation 4.17
In the setup of Lemma 4.16, the composite  is a morphism of complexes
is a morphism of complexes  . In this case, we call
. In this case, we call  the underlying morphism of
the underlying morphism of  .
.
We need two more lemmas before we can define a realisation of the functor \(\mathbb {F}\).
Lemma 4.18
Assume  . Further, suppose that
. Further, suppose that  is an \(\mathfrak {s}\)-distinguished n-exangle and
is an \(\mathfrak {s}\)-distinguished n-exangle and  is an idempotent lift of
is an idempotent lift of  . Then
. Then  is an n-exangle for \((\widetilde{\mathcal {C}}, \mathbb {F})\).
is an n-exangle for \((\widetilde{\mathcal {C}}, \mathbb {F})\).
Proof
Let \((Y,e')\in \widetilde{\mathcal {C}}\) be arbitrary. We will show that the induced sequence

where \((\tilde{d}_i^{(X,e)})_{*} = \widetilde{\mathcal {C}}((Y,e'), \tilde{d}_i^{(X,e)})\), is exact. The exactness of the dual sequence can be verified similarly. Checking the above sequence is a complex is straightforward using that  and that
and that  .
.
To check exactness at  for some \(1\leqslant i \leqslant n\), suppose we have a morphism
for some \(1\leqslant i \leqslant n\), suppose we have a morphism  with \(\tilde{d}_i^{(X,e)} \tilde{r} = 0\), that is,
with \(\tilde{d}_i^{(X,e)} \tilde{r} = 0\), that is,  . As
. As  , we see that \(d_i^Xr=0\), whence there exists
, we see that \(d_i^Xr=0\), whence there exists  such that \(d_{i-1}^Xs = r\) because
such that \(d_{i-1}^Xs = r\) because  is an \(\mathfrak {s}\)-distinguished n-exangle. By Lemma 4.14, there is a morphism
is an \(\mathfrak {s}\)-distinguished n-exangle. By Lemma 4.14, there is a morphism  with \(t = e_{i-1} s e'\). Then we observe that
with \(t = e_{i-1} s e'\). Then we observe that  , whence \(\tilde{d}_{i-1}^{(X,e)} \tilde{t} = \tilde{r}\).
, whence \(\tilde{d}_{i-1}^{(X,e)} \tilde{t} = \tilde{r}\).
Lastly, suppose  is a morphism with
is a morphism with  . Then we have
. Then we have  . Hence, there is a morphism
. Hence, there is a morphism  such that
such that  as
as  is an \(\mathfrak {s}\)-distinguished n-exangle. Then the morphism
is an \(\mathfrak {s}\)-distinguished n-exangle. Then the morphism  with
with  satisfies \(\tilde{d}^{(X,e)}_n \tilde{w} = \tilde{u}\), as required. \(\square \)
satisfies \(\tilde{d}^{(X,e)}_n \tilde{w} = \tilde{u}\), as required. \(\square \)
Lemma 4.19
Suppose  and that
and that  in \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\). If
in \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\). If  and
and  are idempotent lifts of
are idempotent lifts of  , then
, then  are isomorphic in
are isomorphic in  , i.e.
, i.e.  .
.
Proof
We will use [16, Prop. 2.21]. To this end, note that  and
and  are both n-exangles in \((\widetilde{\mathcal {C}}, \mathbb {F})\) by Lemma 4.18. Hence, we only have to show that
are both n-exangles in \((\widetilde{\mathcal {C}}, \mathbb {F})\) by Lemma 4.18. Hence, we only have to show that

are both non-empty. Since we have  , there are morphisms
, there are morphisms  and
and  in
in  (with
(with  and
and  ). We then obtain morphisms
). We then obtain morphisms  and
and  in
in  with
with  and
and  by Lemma 4.16. Note that
by Lemma 4.16. Note that  and
and  . So, since
. So, since  , we have that
, we have that  and \(\tilde{k}_{\bullet }\) are morphisms in
and \(\tilde{k}_{\bullet }\) are morphisms in  and we are done. \(\square \)
and we are done. \(\square \)
Hence, the following is well-defined.
Definition 4.20
For  , pick
, pick  so that
so that  and, by Corollary 4.13, an idempotent morphism
and, by Corollary 4.13, an idempotent morphism  lifting
lifting  . We put
. We put  .
.
Remark 4.21
For  , the definition of
, the definition of  depends on neither the choice of
depends on neither the choice of  with
with  , nor on the choice of
, nor on the choice of  lifting
lifting  by Lemma 4.19. By Corollary 4.13, for each
by Lemma 4.19. By Corollary 4.13, for each  , we can find an \(\mathfrak {s}\)-distinguished n-exangle
, we can find an \(\mathfrak {s}\)-distinguished n-exangle  and an idempotent morphism
and an idempotent morphism  , such that
, such that  and
and  is null homotopic in
is null homotopic in  .
.
Proposition 4.22
The assignment \(\mathfrak {t}\) is an exact realisation of \(\mathbb {F}\).
Proof
(R0) Suppose  and
and  , and let \((\tilde{a},\tilde{c}):{\tilde{\delta }} \rightarrow {\tilde{\rho }}\) be a morphism of \(\mathbb {F}\)-extensions. Suppose
, and let \((\tilde{a},\tilde{c}):{\tilde{\delta }} \rightarrow {\tilde{\rho }}\) be a morphism of \(\mathbb {F}\)-extensions. Suppose  and
and  . Since (a, c) is a morphism of \(\mathbb {E}\)-extensions, there is a lift
. Since (a, c) is a morphism of \(\mathbb {E}\)-extensions, there is a lift  of it using that \(\mathfrak {s}\) is an exact realisation of \(\mathbb {E}\). As
of it using that \(\mathfrak {s}\) is an exact realisation of \(\mathbb {E}\). As  and
and  are morphisms in \(\widetilde{\mathcal {C}}\), we have that
are morphisms in \(\widetilde{\mathcal {C}}\), we have that  and
and  . Hence, by Lemma 4.16, it follows that
. Hence, by Lemma 4.16, it follows that  with
with  lifts \((\tilde{a},\tilde{c})\).
lifts \((\tilde{a},\tilde{c})\).
(R1) This is Lemma 4.18.
(R2) Let \((X,e)\in \widetilde{\mathcal {C}}\) be arbitrary. By Remark 4.5(ii), we have that the zero element of \(\mathbb {F}((0,0),(X,e))\) has the zero element \(_{X}0_{0}\) of \(\mathbb {E}(0,X)\) as its underlying \(\mathbb {E}\)-extension. Since \(\mathfrak {s}\) is an exact realisation of \(\mathbb {E}\), we know

The tuple  is an idempotent morphism lifting
is an idempotent morphism lifting  . Thus, by Definition 4.20 and using
. Thus, by Definition 4.20 and using  , we see that
, we see that

Dually,  . \(\square \)
. \(\square \)
4.3 The Axiom (EA1) for \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\)
Now that we have a biadditive functor  and an exact realisation \(\mathfrak {t}\) of \(\mathbb {F}\), we can begin to verify axioms (EA1), (EA2) and (EA2)
and an exact realisation \(\mathfrak {t}\) of \(\mathbb {F}\), we can begin to verify axioms (EA1), (EA2) and (EA2) . In this subsection, we will check that the collection of \(\mathfrak {t}\)-inflations is closed under composition. One can dualise the results here to see that \(\mathfrak {t}\)-deflations compose to \(\mathfrak {t}\)-deflations.
. In this subsection, we will check that the collection of \(\mathfrak {t}\)-inflations is closed under composition. One can dualise the results here to see that \(\mathfrak {t}\)-deflations compose to \(\mathfrak {t}\)-deflations.
The following result only needs that \(\mathfrak {s}\) is an exact realisation of  . It is an analogue of [22, Lem. 2.1] for n-exangulated categories, allowing us to complete a “partial” lift of a morphism of extensions.
. It is an analogue of [22, Lem. 2.1] for n-exangulated categories, allowing us to complete a “partial” lift of a morphism of extensions.
Lemma 4.23
(Completion Lemma) Let  and
and  be \(\mathfrak {s}\)-distinguished n-exangles. Let l, r be integers with \(0 \leqslant l \leqslant r-2 \leqslant n-1\). Suppose there are morphisms
be \(\mathfrak {s}\)-distinguished n-exangles. Let l, r be integers with \(0 \leqslant l \leqslant r-2 \leqslant n-1\). Suppose there are morphisms  and
and  , where
, where  , such that
, such that  is a morphism of \(\mathbb {E}\)-extensions and the solid part of the diagram
is a morphism of \(\mathbb {E}\)-extensions and the solid part of the diagram

commutes. Then there exist morphisms  such that (4.3) commutes.
such that (4.3) commutes.
Proof
We proceed by induction on \(l \geqslant 0\). Suppose \(l=0\). We induct downwards on \(r \leqslant n+1\). If \(r = n+1\), then the result follows from axiom (R0) for \(\mathfrak {s}\) since  is a morphism of \(\mathbb {E}\)-extensions. Now assume that the result holds for \(l=0\) and some \(3 \leqslant r\leqslant n+1\). Suppose we are given morphisms
is a morphism of \(\mathbb {E}\)-extensions. Now assume that the result holds for \(l=0\) and some \(3 \leqslant r\leqslant n+1\). Suppose we are given morphisms  and
and  such that
such that  for \(i\in \{ r-1,\ldots , n \}\). By the induction hypothesis, we obtain a morphism
for \(i\in \{ r-1,\ldots , n \}\). By the induction hypothesis, we obtain a morphism

of \(\mathfrak {s}\)-distinguished n-exangles. We will denote this morphism by  . Next, note that we have
. Next, note that we have  . Since
. Since  is a weak kernel of
is a weak kernel of  , there exists
, there exists  so that
so that  . Set
. Set  for
for  . Notice that we have
. Notice that we have  for \(i \notin \{r-1, r-2\}\). We claim that (4.3) commutes. By construction, we only need to check commutativity of the two squares involving
for \(i \notin \{r-1, r-2\}\). We claim that (4.3) commutes. By construction, we only need to check commutativity of the two squares involving  . These indeed commute since
. These indeed commute since

and

using the commutativity of (4.4). This concludes the base case \(l=0\).
The inductive step for \(l\geqslant 0\) is carried out in a similar way to the inductive step above on r, using that  is a weak cokernel of
is a weak cokernel of  . \(\square \)
. \(\square \)
From the Completion Lemma 4.23 and some earlier results from this section we derive the following, which is used in the main result of this subsection.
Lemma 4.24
Suppose  is an \(\mathfrak {s}\)-distinguished n-exangle. Assume
is an \(\mathfrak {s}\)-distinguished n-exangle. Assume  and
and  are idempotents, such that
are idempotents, such that  and
and

commutes. Then  and
and  can be extended to an idempotent morphism
can be extended to an idempotent morphism  with
with  for
for  .
.
Proof
First, suppose \(n = 1\). Then the solid morphisms of the diagram

form a commutative diagram, and by [16, Prop. 3.6(1)] there is a morphism  such that
such that  is a morphism of \(\mathfrak {s}\)-distinguished 1-exangles. Recall the polynomial
is a morphism of \(\mathfrak {s}\)-distinguished 1-exangles. Recall the polynomial  from Lemma 4.9. We will show that
from Lemma 4.9. We will show that  , where
, where  , is the desired idempotent morphism of \(\mathfrak {s}\)-distinguished n-exangles.
, is the desired idempotent morphism of \(\mathfrak {s}\)-distinguished n-exangles.
Since  is an \(\mathfrak {s}\)-distinguished 1-exangle, there is an exact sequence
is an \(\mathfrak {s}\)-distinguished 1-exangle, there is an exact sequence

As  , there exists a morphism
, there exists a morphism  with
with  . This shows that
. This shows that  because
because  is idempotent. Hence,
is idempotent. Hence,  is an idempotent morphism of complexes by Lemma 4.9(ii). Furthermore,
is an idempotent morphism of complexes by Lemma 4.9(ii). Furthermore,  using Lemma 4.9(i), so that
using Lemma 4.9(i), so that  is a morphism of \(\mathbb {E}\)-extensions. This computation also shows the existence of
is a morphism of \(\mathbb {E}\)-extensions. This computation also shows the existence of  with underlying \(\mathbb {E}\)-extension \(\delta \).
with underlying \(\mathbb {E}\)-extension \(\delta \).
Now suppose \(n \geqslant 2\). We have  . Therefore,
. Therefore,  is an element of
is an element of  with underlying \(\mathbb {E}\)-extension \(\delta \). The solid morphisms of the diagram
with underlying \(\mathbb {E}\)-extension \(\delta \). The solid morphisms of the diagram

form a commutative diagram, and  is a morphism of \(\mathbb {E}\)-extensions as
is a morphism of \(\mathbb {E}\)-extensions as  . Since the rows are the \(\mathfrak {s}\)-distinguished n-exangle
. Since the rows are the \(\mathfrak {s}\)-distinguished n-exangle  , by Lemma 4.23 we can find a morphism
, by Lemma 4.23 we can find a morphism  , so that the diagram above is a morphism
, so that the diagram above is a morphism  . Furthermore, as
. Furthermore, as  and
and  are idempotent, we may assume that
are idempotent, we may assume that  is an idempotent by Lemma 4.10. \(\square \)
is an idempotent by Lemma 4.10. \(\square \)
Given a \(\mathfrak {t}\)-inflation \(\tilde{f}\) that fits into a \(\mathfrak {t}\)-distinguished n-exangle  , we cannot a priori say too much about how
, we cannot a priori say too much about how  might look. This is one of the main issues in trying to prove (EA1) for \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\). The next lemma gives us a way to deal with this and is the last preparatory result we need before the main result of this subsection.
might look. This is one of the main issues in trying to prove (EA1) for \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\). The next lemma gives us a way to deal with this and is the last preparatory result we need before the main result of this subsection.
Lemma 4.25
Let  be a \(\mathfrak {t}\)-inflation. Then there is an \(\mathfrak {s}\)-distinguished n-exangle \(\langle X'_{\bullet }, \delta \rangle \) with
be a \(\mathfrak {t}\)-inflation. Then there is an \(\mathfrak {s}\)-distinguished n-exangle \(\langle X'_{\bullet }, \delta \rangle \) with  and
and  for some \(C \in \mathcal {C}\), such that
for some \(C \in \mathcal {C}\), such that  and
and  for some
for some  .
.
Proof
Since  is an \(\mathfrak {t}\)-inflation, there is a \(\mathfrak {t}\)-distinguished n-exangle
is an \(\mathfrak {t}\)-inflation, there is a \(\mathfrak {t}\)-distinguished n-exangle  with
with  ,
,  and \(\tilde{d}_0^{\widetilde{Y}} = \tilde{f}\). By definition of \(\mathfrak {t}\), this means there is an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Y'_{\bullet }, \delta ' \rangle \) with an idempotent morphism \(e'_{\bullet } :\langle Y'_{\bullet }, \delta ' \rangle \rightarrow \langle Y'_{\bullet }, \delta ' \rangle \), such that
and \(\tilde{d}_0^{\widetilde{Y}} = \tilde{f}\). By definition of \(\mathfrak {t}\), this means there is an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Y'_{\bullet }, \delta ' \rangle \) with an idempotent morphism \(e'_{\bullet } :\langle Y'_{\bullet }, \delta ' \rangle \rightarrow \langle Y'_{\bullet }, \delta ' \rangle \), such that  and
and  , and there are mutually inverse homotopy equivalences
, and there are mutually inverse homotopy equivalences  which satisfy
which satisfy  and
and  . Note that we, thus, have
. Note that we, thus, have  and
and  . In particular, we have a commutative diagram
. In particular, we have a commutative diagram

in \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\), where  .
.
Consider the complex  and the \(\mathbb {E}\)-extension
and the \(\mathbb {E}\)-extension  . Note that if \(n=1\), then
. Note that if \(n=1\), then  ; otherwise we have \({{Y''_{n+1}}} =0\). In either case, we have an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Y''_{\bullet }, \delta '' \rangle \) using the axiom (R2) for \(\mathfrak {s}\), and hence also an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Y''_{\bullet } \oplus Y'_{\bullet }, \delta '' \oplus \delta ' \rangle \) by [16, Prop. 3.3]. Using the canonical isomorphism
; otherwise we have \({{Y''_{n+1}}} =0\). In either case, we have an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Y''_{\bullet }, \delta '' \rangle \) using the axiom (R2) for \(\mathfrak {s}\), and hence also an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Y''_{\bullet } \oplus Y'_{\bullet }, \delta '' \oplus \delta ' \rangle \) by [16, Prop. 3.3]. Using the canonical isomorphism  we see that the complex
we see that the complex

realises  in \((\mathcal {C},\mathbb {E},\mathfrak {s})\) by [16, Cor. 2.26(2)]. Consider the diagram
in \((\mathcal {C},\mathbb {E},\mathfrak {s})\) by [16, Cor. 2.26(2)]. Consider the diagram

in \(\mathcal {C}\), where  and
and  . This diagram commutes since
. This diagram commutes since

and

Notice that the composition ba is an automorphism of  , and so the complex
, and so the complex

forms part of an \(\mathfrak {s}\)-distinguished n-exangle \(\langle X'_{\bullet }, \delta \rangle \) by [16, Cor. 2.26(2)]. We have

as  ,
,  and
and  . Setting
. Setting  and \(C :=Y'_{1}\) finishes the proof. \(\square \)
and \(C :=Y'_{1}\) finishes the proof. \(\square \)
We close this subsection with the following result, which together with its dual demonstrates that axiom (EA1) holds for \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\).
Proposition 4.26
Suppose  and
and  are \(\mathfrak {t}\)-inflations with
are \(\mathfrak {t}\)-inflations with  . Then
. Then  is a \(\mathfrak {t}\)-inflation.
is a \(\mathfrak {t}\)-inflation.
Proof
By Lemma 4.25, there exists an \(\mathfrak {s}\)-distinguished n-exangle \(\langle X'_{\bullet }, \delta \rangle \) with  and
and  for some \(C \in \mathcal {C}\), so that
for some \(C \in \mathcal {C}\), so that  for some
for some  and
and  . Similarly, there is also an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Y'_{\bullet }, \delta ' \rangle \) with
. Similarly, there is also an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Y'_{\bullet }, \delta ' \rangle \) with  and
and  for some \(C' \in \mathcal {C}\), so that
for some \(C' \in \mathcal {C}\), so that  for some
for some  and
and  . Setting
. Setting  , we also have the n-exangle
, we also have the n-exangle  by axiom (R2) for \(\mathfrak {s}\). Then
by axiom (R2) for \(\mathfrak {s}\). Then  is \(\mathfrak {s}\)-distinguished by [16, Prop. 3.3]. We have
is \(\mathfrak {s}\)-distinguished by [16, Prop. 3.3]. We have  and
and  , and
, and

is the \(\mathfrak {s}\)-inflation of  with respect to the given decompositions. Since
with respect to the given decompositions. Since  and \(d^{Y'\oplus Y''}_0\) are \(\mathfrak {s}\)-inflations, by (EA1) for \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\), we have that the morphism
and \(d^{Y'\oplus Y''}_0\) are \(\mathfrak {s}\)-inflations, by (EA1) for \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\), we have that the morphism

is an \(\mathfrak {s}\)-inflation, where we used that  . Therefore, there is an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Z''_{\bullet }, \delta '' \rangle \) with
. Therefore, there is an \(\mathfrak {s}\)-distinguished n-exangle \(\langle Z''_{\bullet }, \delta '' \rangle \) with  ,
,  and
and  .
.
Our next aim is to apply Lemma 4.24 to \(\langle Z''_{\bullet }, \delta '' \rangle \). Thus, we claim that  . Since
. Since  , we can apply [16, Prop. 3.6(1)] to obtain a morphism
, we can apply [16, Prop. 3.6(1)] to obtain a morphism

of \(\mathfrak {s}\)-distinguished n-exangles. In particular, we have that

As  and
and  is idempotent, we see that
is idempotent, we see that

This implies that

Since \(\langle X'_{\bullet }, \delta \rangle \) is an \(\mathfrak {s}\)-distinguished n-exangle, by [16, Lem. 3.5] there is an exact sequence

As seen above,  vanishes under
vanishes under  , so there is a morphism
, so there is a morphism  with
with  . Since
. Since  , this implies
, this implies

showing that  .
.
Now consider the idempotent  . A quick computation yields the equality
. A quick computation yields the equality  . Therefore, by Lemma 4.24, there is an idempotent morphism \(e''_{\bullet } :\langle Z''_{\bullet }, \delta '' \rangle \rightarrow \langle Z''_{\bullet }, \delta '' \rangle \) with
. Therefore, by Lemma 4.24, there is an idempotent morphism \(e''_{\bullet } :\langle Z''_{\bullet }, \delta '' \rangle \rightarrow \langle Z''_{\bullet }, \delta '' \rangle \) with  , \(e''_{1} = e'_{1} \oplus 0 \oplus 0\) as well as an \(\mathbb {F}\)-extension
, \(e''_{1} = e'_{1} \oplus 0 \oplus 0\) as well as an \(\mathbb {F}\)-extension  with underlying \(\mathbb {E}\)-extension \(\rho = \delta ''\). We obtain a \(\mathfrak {t}\)-distinguished n-exangle \(\langle (Z''_{\bullet }, e''_{\bullet }), {\tilde{\rho }} \rangle \). Then the \(\mathfrak {t}\)-inflation of this n-exangle is given by the morphism
with underlying \(\mathbb {E}\)-extension \(\rho = \delta ''\). We obtain a \(\mathfrak {t}\)-distinguished n-exangle \(\langle (Z''_{\bullet }, e''_{\bullet }), {\tilde{\rho }} \rangle \). Then the \(\mathfrak {t}\)-inflation of this n-exangle is given by the morphism  satisfying
satisfying

As  is an isomorphism in \(\widetilde{\mathcal {C}}\), the complex
is an isomorphism in \(\widetilde{\mathcal {C}}\), the complex

with \(\mathfrak {t}\)-inflation  and
and  forms part of the \(\mathfrak {t}\)-distinguished n-exangle \(\langle \widetilde{X}''_{\bullet }, {\tilde{\rho }} \rangle \) by [16, Cor. 2.26(2)]. \(\square \)
forms part of the \(\mathfrak {t}\)-distinguished n-exangle \(\langle \widetilde{X}''_{\bullet }, {\tilde{\rho }} \rangle \) by [16, Cor. 2.26(2)]. \(\square \)
4.4 The Axiom (EA2) for \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\)
The goal of this subsection is to show that axiom (EA2) holds for the triplet \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\). Again, by dualising one can deduce that axiom (EA2) also holds. We need two key technical lemmas first.
also holds. We need two key technical lemmas first.
Lemma 4.27
Suppose that:
-
(i)
 is an \(\mathbb {F}\)-extension;
is an \(\mathbb {F}\)-extension; -
(ii)
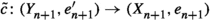 is a morphism in \(\widetilde{\mathcal {C}}\) for some
is a morphism in \(\widetilde{\mathcal {C}}\) for some 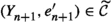 ;
; -
(iii)
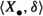 and
and  are \(\mathfrak {s}\)-distinguished n-exangles with
are \(\mathfrak {s}\)-distinguished n-exangles with 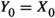 ;
; -
(iv)
 is an idempotent morphism lifting
is an idempotent morphism lifting  , such that
, such that  is null homotopic; and
is null homotopic; and -
(v)
 is an idempotent morphism lifting
is an idempotent morphism lifting  , such that
, such that 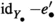 is null homotopic.
is null homotopic.
Then a good lift  of the morphism
of the morphism  of \(\mathbb {E}\)-extensions exists, so that
of \(\mathbb {E}\)-extensions exists, so that

is commutative in \(\mathcal {C}\). In particular, we have  as morphisms
as morphisms  .
.
Remark 4.28
Notice that  and \( c e'_{n+1}= c\) imply
and \( c e'_{n+1}= c\) imply

Therefore,  is indeed a morphism of \(\mathbb {E}\)-extensions and condition (v) makes sense. Condition (iv) makes sense due to Remark 4.5(iv).
is indeed a morphism of \(\mathbb {E}\)-extensions and condition (v) makes sense. Condition (iv) makes sense due to Remark 4.5(iv).
Proof of Lemma 4.27
Since  is a morphism of \(\mathbb {E}\)-extensions, it admits a good lift
is a morphism of \(\mathbb {E}\)-extensions, it admits a good lift  using axiom (EA2) for the n-exangulated category \((\mathcal {C},\mathbb {E},\mathfrak {s})\). Define
using axiom (EA2) for the n-exangulated category \((\mathcal {C},\mathbb {E},\mathfrak {s})\). Define  for \(0\leqslant i \leqslant n+1\). Note that
for \(0\leqslant i \leqslant n+1\). Note that  and
and  by assumption. For \(i=0\), we have
by assumption. For \(i=0\), we have  . On the other hand, for \(i=n+1\) we have
. On the other hand, for \(i=n+1\) we have  . Therefore, the morphism
. Therefore, the morphism  is of the form
is of the form  .
.
The squares on the top and bottom faces in (4.7) commute as  and
and  , respectively, are morphisms of complexes. The squares on the front and back faces in (4.7) commute because
, respectively, are morphisms of complexes. The squares on the front and back faces in (4.7) commute because  is the sum of morphisms of complexes from
is the sum of morphisms of complexes from  to
to  . This also implies
. This also implies  is a lift of
is a lift of  . Of the remaining squares, the leftmost clearly commutes and the rightmost commutes as
. Of the remaining squares, the leftmost clearly commutes and the rightmost commutes as  is a morphism in \(\widetilde{\mathcal {C}}\). For \(1\leqslant i \leqslant n\), we have
is a morphism in \(\widetilde{\mathcal {C}}\). For \(1\leqslant i \leqslant n\), we have

Therefore, diagram (4.7) commutes and, further, the last assertion follows.
It remains to show that  is a good lift of
is a good lift of  . Recall that
. Recall that  and
and  are both null homotopic by assumption, and so
are both null homotopic by assumption, and so  is also null homotopic. Then it follows from [16, Rem. 2.33(1)] that
is also null homotopic. Then it follows from [16, Rem. 2.33(1)] that  is a good lift of
is a good lift of  since \(g'_{\bullet }\) is. \(\square \)
since \(g'_{\bullet }\) is. \(\square \)
The next result allows us to define a good lift in \(\widetilde{\mathcal {C}}\) from the one we created in Lemma 4.27.
Lemma 4.29
In the setup of Lemma 4.27, the morphism  with under-lying morphism
with under-lying morphism  is a good lift of the morphism
is a good lift of the morphism  of \(\mathbb {F}\)-extensions.
of \(\mathbb {F}\)-extensions.
Proof
From (4.8), we see that  is indeed an \(\mathbb {F}\)-extension and
is indeed an \(\mathbb {F}\)-extension and  a morphism of \(\mathbb {F}\)-extensions. Using
a morphism of \(\mathbb {F}\)-extensions. Using  and
and  , as well as the commutativity of (4.7), we see that
, as well as the commutativity of (4.7), we see that  is a morphism
is a morphism  of \(\mathfrak {t}\)-distinguished n-exangles, lifting
of \(\mathfrak {t}\)-distinguished n-exangles, lifting  .
.
Recall from Definition 3.4 that  denotes the mapping cone of
denotes the mapping cone of  in \(\mathcal {C}\), and that
in \(\mathcal {C}\), and that  is \(\mathfrak {s}\)-distinguished as
is \(\mathfrak {s}\)-distinguished as  is a good lift of
is a good lift of  . Using the commutativity of (4.7), that
. Using the commutativity of (4.7), that  and
and  are morphisms of complexes, and that
are morphisms of complexes, and that  , one can verify that the diagram
, one can verify that the diagram

commutes. Thus, the vertical morphisms form an idempotent morphism \({e''_{\bullet } :{M_{g}^\mathcal {C}}_{\bullet } \rightarrow {M_{g}^\mathcal {C}}_{\bullet }}\) of complexes. Furthermore, (4.9) is a morphism of \(\mathfrak {s}\)-distinguished n-exangles as

This calculation also shows that  . Thus, by definition of \(\mathfrak {t}\), we have that \(\mathfrak {t}({\tilde{\rho }}) = [ ({M^{\mathcal {C}}_g}_{\bullet }, e''_{\bullet }) ]\), i.e. \(\langle ({M^{\mathcal {C}}_g}_{\bullet }, e''_{\bullet }), {\tilde{\rho }} \rangle \) is \(\mathfrak {t}\)-distinguished.
. Thus, by definition of \(\mathfrak {t}\), we have that \(\mathfrak {t}({\tilde{\rho }}) = [ ({M^{\mathcal {C}}_g}_{\bullet }, e''_{\bullet }) ]\), i.e. \(\langle ({M^{\mathcal {C}}_g}_{\bullet }, e''_{\bullet }), {\tilde{\rho }} \rangle \) is \(\mathfrak {t}\)-distinguished.
It is straightforward to verify that the object \(({M^{\mathcal {C}}_g}_{\bullet }, e''_{\bullet })\) is equal to the mapping cone \({M^{\widetilde{\mathcal {C}}}_{\tilde{h}}}_{\bullet }\) of  in
in  , so \(\langle {M^{\widetilde{\mathcal {C}}}_{\tilde{h}}}_{\bullet }, {\tilde{\rho }} \rangle \) is \(\mathfrak {t}\)-distinguished. Lastly, we note that
, so \(\langle {M^{\widetilde{\mathcal {C}}}_{\tilde{h}}}_{\bullet }, {\tilde{\rho }} \rangle \) is \(\mathfrak {t}\)-distinguished. Lastly, we note that  because
because

Hence,  is a \(\mathfrak {t}\)-distinguished n-exangle. \(\square \)
is a \(\mathfrak {t}\)-distinguished n-exangle. \(\square \)
We are in position to prove axiom (EA2) for \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\). Axiom (EA2) can be shown dually.
can be shown dually.
Proposition 4.30
(Axiom (EA2) for \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\)) Let  -extension and suppose
-extension and suppose  is a morphism in \(\widetilde{\mathcal {C}}\). Suppose
is a morphism in \(\widetilde{\mathcal {C}}\). Suppose  are \(\mathfrak {t}\)-distinguished n-exangles. Then
are \(\mathfrak {t}\)-distinguished n-exangles. Then  has a good lift
has a good lift  .
.
Proof
Notice that the underlying \(\mathbb {E}\)-extension of  is
is  . By definition of \(\mathfrak {t}\) and Remark 4.21, there are \(\mathfrak {s}\)-distinguished n-exangles \(\langle X'_{\bullet }, \delta \rangle \) and
. By definition of \(\mathfrak {t}\) and Remark 4.21, there are \(\mathfrak {s}\)-distinguished n-exangles \(\langle X'_{\bullet }, \delta \rangle \) and  and idempotent morphisms
and idempotent morphisms  and
and  , such that
, such that  and \(\mathfrak {t}(\tilde{c}^\mathbb {F}{\tilde{\delta }}) = [(Y'_{\bullet }, e'_{\bullet })]\), and so that
and \(\mathfrak {t}(\tilde{c}^\mathbb {F}{\tilde{\delta }}) = [(Y'_{\bullet }, e'_{\bullet })]\), and so that  and
and  are null homotopic in
are null homotopic in  . We note that since
. We note that since  and
and  , we have that
, we have that  and, in particular, that
and, in particular, that  . Moreover, it follows that all the hypotheses of Lemma 4.27 are satisfied.
. Moreover, it follows that all the hypotheses of Lemma 4.27 are satisfied.
Therefore, by Lemma 4.29, the morphism  of \(\mathbb {F}\)-extensions has a good lift
of \(\mathbb {F}\)-extensions has a good lift  . Since
. Since  and
and  , there is a homotopy equivalence
, there is a homotopy equivalence  in
in  and a homotopy equivalence
and a homotopy equivalence  in
in  . By [16, Cor. 2.31], the composite
. By [16, Cor. 2.31], the composite  is then also a good lift of
is then also a good lift of  . \(\square \)
. \(\square \)
4.5 Main Results
In this subsection we present our main results regarding the idempotent completion and an n-exangulated structure we can impose on it.
Definition 4.31
We call an n-exangulated category \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) (resp. weakly) idempotent complete if the underlying additive category \(\mathcal {C}\) is (resp. weakly) idempotent complete.
In [5, Prop. 2.5] a characterisation of weakly idempotent complete extriangulated categories is given. Next we note that the first part of Theorem A from Sect. 1 summarises our work from Sects. 4.1–4.4.
Theorem 4.32
Let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an n-exangulated category. Then the triplet \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) is an idempotent complete n-exangulated category.
Proof
This follows from Propositions 2.5, 4.22, 4.26 and 4.30, and the duals of the latter two. \(\square \)
And Corollary C from Sect. 1 is a nice consequence of this.
Corollary 4.33
Let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an n-exangulated category, such that each object in \(\mathcal {C}\) has a semi-perfect endomorphism ring. Then the idempotent completion \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) is a Krull-Schmidt n-exangulated category.
Proof
By Theorem 4.32, the idempotent completion \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) is an idempotent complete n-exangulated category. By [12, Thm. A.1] (or [24, Cor. 4.4]), it is enough to show that endomorphism rings of objects in \(\widetilde{\mathcal {C}}\) are semi-perfect rings. Let (X, e) be an object in \(\widetilde{\mathcal {C}}\). We have that  is semi-perfect since
is semi-perfect since  is fully faithful (see Proposition 2.5). By Remark 2.6, we have that
is fully faithful (see Proposition 2.5). By Remark 2.6, we have that  . In particular, we see that
. In particular, we see that  is an idempotent subring of the semi-perfect ring
is an idempotent subring of the semi-perfect ring  . Hence, by Anderson–Fuller [1, Cor. 27.7], we have that the endomorphism ring of each object in \(\widetilde{\mathcal {C}}\) is semi-perfect. \(\square \)
. Hence, by Anderson–Fuller [1, Cor. 27.7], we have that the endomorphism ring of each object in \(\widetilde{\mathcal {C}}\) is semi-perfect. \(\square \)
We recall that, by [23, Cor. 4.12], an n-exangulated category is n-exact if and only if its inflations are monomorphisms and its deflations are epimorphisms.
Corollary 4.34
Suppose \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is n-exact. Then \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) is n-exact.
Proof
We use [23, Cor. 4.12] and only show that \(\mathfrak {t}\)-inflations are monomorphisms; showing \(\mathfrak {t}\)-deflations are epimorphisms is dual. Let  be a \(\mathfrak {t}\)-inflation and suppose there is a morphism
be a \(\mathfrak {t}\)-inflation and suppose there is a morphism  in \(\widetilde{\mathcal {C}}\) with \(\tilde{f} \tilde{g} = \widetilde{0}\). By Lemma 4.25, there is an \(\mathfrak {s}\)-inflation
in \(\widetilde{\mathcal {C}}\) with \(\tilde{f} \tilde{g} = \widetilde{0}\). By Lemma 4.25, there is an \(\mathfrak {s}\)-inflation  , which is monic as \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is n-exact. We have \(fg = 0\) as \(\tilde{f} \tilde{g} = \widetilde{0}\), and we also have
, which is monic as \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is n-exact. We have \(fg = 0\) as \(\tilde{f} \tilde{g} = \widetilde{0}\), and we also have  because the underlying morphism g of \(\tilde{g}\) satisfies
because the underlying morphism g of \(\tilde{g}\) satisfies  . Thus, we see that
. Thus, we see that  and this implies \(g = 0\) as
and this implies \(g = 0\) as  is monic. Hence, \(\tilde{g} = 0\) and we are done. \(\square \)
is monic. Hence, \(\tilde{g} = 0\) and we are done. \(\square \)
The main aim of this subsection is to establish the relevant 2-universal property of the inclusion functor  . We will show that
. We will show that  forms part of an n-exangulated functor
forms part of an n-exangulated functor  , and that this is 2-universal in an appropriate sense. The next lemma is straightforward to check.
, and that this is 2-universal in an appropriate sense. The next lemma is straightforward to check.
Lemma 4.35
The family of abelian group homomorphisms

for  , defines a natural isomorphism
, defines a natural isomorphism  .
.
Proposition 4.36
The pair  is an n-exangulated functor from \((\mathcal {C},\mathbb {E},\mathfrak {s})\) to \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\).
is an n-exangulated functor from \((\mathcal {C},\mathbb {E},\mathfrak {s})\) to \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\).
Proof
We verify that if  is an \(\mathfrak {s}\)-distinguished n-exangle, then
is an \(\mathfrak {s}\)-distinguished n-exangle, then  is \(\mathfrak {t}\)-distinguished, where
is \(\mathfrak {t}\)-distinguished, where  . We have the idempotent morphism
. We have the idempotent morphism  , so from Definition 4.20 we see that
, so from Definition 4.20 we see that  . \(\square \)
. \(\square \)
We lay out some notation that will be used in the remainder of this section and also in Sect. 5.
Notation 4.37
Let (X, e) be an object in the idempotent completion \(\widetilde{\mathcal {C}}\) of \(\mathcal {C}\). Then (X, e) is a direct summand of  by Remark 2.6. By
by Remark 2.6. By  and
and  , we denote the canonical inclusion and projection morphisms, respectively.
, we denote the canonical inclusion and projection morphisms, respectively.
Recall that, for an additive category \(\mathcal {C}'\) and a biadditive functor  , the \(\mathbb {E}'\)-attached complexes and morphisms between them were defined in Definition 3.1, and together they form an additive category.
, the \(\mathbb {E}'\)-attached complexes and morphisms between them were defined in Definition 3.1, and together they form an additive category.
Lemma 4.38
Let  be an \(\mathbb {F}\)-extension. Suppose
be an \(\mathbb {F}\)-extension. Suppose  and
and  is an idempotent morphism. With
is an idempotent morphism. With  , we have that
, we have that

as \(\mathfrak {t}\)-distinguished n-exangles.
Proof
Let  . First, note that
. First, note that  and
and  are \(\mathbb {F}\)-attached complexes, and
are \(\mathbb {F}\)-attached complexes, and  is a \(\mathfrak {t}\)-distinguished n-exangle since \((\mathscr {F},\Gamma )\) is an n-exangulated functor.
is a \(\mathfrak {t}\)-distinguished n-exangle since \((\mathscr {F},\Gamma )\) is an n-exangulated functor.
Consider the morphisms  and
and  of complexes induced by
of complexes induced by  , as well as the corresponding ones \(\tilde{i}_{e'_{\bullet }}\) and \(\tilde{p}_{e'_{\bullet }}\) for \(e'_{\bullet }\). We claim that there is a biproduct diagram
, as well as the corresponding ones \(\tilde{i}_{e'_{\bullet }}\) and \(\tilde{p}_{e'_{\bullet }}\) for \(e'_{\bullet }\). We claim that there is a biproduct diagram

in the category of \(\mathbb {F}\)-attached complexes. To see that  is a morphism of \(\mathbb {F}\)-attached complexes, we just need to check that
is a morphism of \(\mathbb {F}\)-attached complexes, we just need to check that  . By Remark 4.7, it is enough to see that
. By Remark 4.7, it is enough to see that  holds, and this is indeed true because
holds, and this is indeed true because  is a morphism of \(\mathbb {F}\)-attached complexes. To see that \(\tilde{i}_{e'_{\bullet }}\) and \(\tilde{p}_{e'_{\bullet }}\) are morphisms of \(\mathbb {F}\)-attached complexes, one uses that
is a morphism of \(\mathbb {F}\)-attached complexes. To see that \(\tilde{i}_{e'_{\bullet }}\) and \(\tilde{p}_{e'_{\bullet }}\) are morphisms of \(\mathbb {F}\)-attached complexes, one uses that  . Furthermore, we have the identities
. Furthermore, we have the identities  ,
,  and
and  , so (4.11) is a biproduct diagram in the additive category of \(\mathbb {F}\)-attached complexes. Therefore, we have that (4.10) is an isomorphism as \(\mathbb {F}\)-attached complexes.
, so (4.11) is a biproduct diagram in the additive category of \(\mathbb {F}\)-attached complexes. Therefore, we have that (4.10) is an isomorphism as \(\mathbb {F}\)-attached complexes.
Lastly, since  is \(\mathfrak {t}\)-distinguished, it follows from [16, Prop. 3.3] that (4.10) is an isomorphism of \(\mathfrak {t}\)-distinguished n-exangles. \(\square \)
is \(\mathfrak {t}\)-distinguished, it follows from [16, Prop. 3.3] that (4.10) is an isomorphism of \(\mathfrak {t}\)-distinguished n-exangles. \(\square \)
Thus, we can now present and prove the main result of this section, which shows that the n-exangulated inclusion functor  is 2-universal amongst n-exangulated functors from \((\mathcal {C},\mathbb {E},\mathfrak {s})\) to idempotent complete n-exangulated categories.
is 2-universal amongst n-exangulated functors from \((\mathcal {C},\mathbb {E},\mathfrak {s})\) to idempotent complete n-exangulated categories.
Theorem 4.39
Suppose \((\mathscr {F},\Lambda ) :(\mathcal {C}, \mathbb {E}, \mathfrak {s}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) is an n-exangulated functor to an idempotent complete n-exangulated category \((\mathcal {C}', \mathbb {E}', \mathfrak {s}')\). Then the following statements hold.
-
(i)
There is an n-exangulated functor \((\mathscr {E}, \Psi ) :(\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) and an n-exangulated natural isomorphism
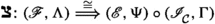 .
. -
(ii)
In addition, for any n-exangulated functor \((\mathscr {G}, \Theta ) :(\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) and any n-exangulated natural transformation
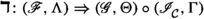 , there is a unique n-exangulated natural transformation
, there is a unique n-exangulated natural transformation  with
with 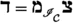 .
.
Proof
(i) By Proposition 2.8(i), there exists an additive functor \(\mathscr {E}:\widetilde{\mathcal {C}} \rightarrow \mathcal {C}'\) and a natural isomorphism  . It remains to show that \(\mathscr {E}\) forms part of an n-exangulated functor \((\mathscr {E},\Psi )\) and that
. It remains to show that \(\mathscr {E}\) forms part of an n-exangulated functor \((\mathscr {E},\Psi )\) and that  is n-exangulated.
is n-exangulated.
First, we define a natural transformation \(\Psi :\mathbb {F}(-,-) \Rightarrow \mathbb {E}'(\mathscr {E}-, \mathscr {E}-)\) as the composition of several abelian group homomorphisms. For  , we set
, we set

For  and
and  in \(\widetilde{\mathcal {C}}\), we define an abelian group homomorphism
in \(\widetilde{\mathcal {C}}\), we define an abelian group homomorphism

and put

For morphisms  and
and  in \(\mathcal {C}\), we have
in \(\mathcal {C}\), we have

as  is natural. For morphisms
is natural. For morphisms  , we have
, we have

using how \(\mathbb {F}\) is defined on morphisms (see Definition 4.4). We claim that the family of abelian group homomorphisms

for  defines a natural transformation \(\Psi :\mathbb {F}(-,-) \Rightarrow \mathbb {E}'(\mathscr {E}-, \mathscr {E}-)\). To this end, fix objects
defines a natural transformation \(\Psi :\mathbb {F}(-,-) \Rightarrow \mathbb {E}'(\mathscr {E}-, \mathscr {E}-)\). To this end, fix objects  and
and  , and morphisms
, and morphisms  and
and  in \(\widetilde{\mathcal {C}}\). First, note that we have
in \(\widetilde{\mathcal {C}}\). First, note that we have

and, similarly,

Therefore, we see that

Next, we must show that \((\mathscr {E},\Psi )\) sends \(\mathfrak {t}\)-distinguished n-exangles to \(\mathfrak {s}'\)-distinguished n-exangles. Thus, let  and
and  , and suppose
, and suppose  . We need that
. We need that  , which will follow from seeing that
, which will follow from seeing that  is a direct summand of an \(\mathfrak {s}'\)-distinguished n-exangle.
is a direct summand of an \(\mathfrak {s}'\)-distinguished n-exangle.
By Remark 4.21, we may take a complex  in
in  with
with  and an idempotent morphism
and an idempotent morphism  lifting
lifting  , such that
, such that  . Note for later that we thus have
. Note for later that we thus have  , and hence
, and hence  . Let
. Let  . Since \((\mathscr {F}, \Lambda ) :(\mathcal {C}, \mathbb {E}, \mathfrak {s}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) is an n-exangulated functor, the n-exangle
. Since \((\mathscr {F}, \Lambda ) :(\mathcal {C}, \mathbb {E}, \mathfrak {s}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) is an n-exangulated functor, the n-exangle  is \(\mathfrak {s}'\)-distinguished. As we have an isomorphism of complexes
is \(\mathfrak {s}'\)-distinguished. As we have an isomorphism of complexes  , the \(\mathbb {E}'\)-attached complex
, the \(\mathbb {E}'\)-attached complex  is \(\mathfrak {s}'\)-distinguished by [16, Cor. 2.26(2)]. Since is just the identity homomorphism, a quick computation yields
is \(\mathfrak {s}'\)-distinguished by [16, Cor. 2.26(2)]. Since is just the identity homomorphism, a quick computation yields

In particular, this implies that  is \(\mathfrak {s}'\)-distinguished.
is \(\mathfrak {s}'\)-distinguished.
Note that  as \(\mathbb {F}\)-attached complexes by Lemma 4.38, where
as \(\mathbb {F}\)-attached complexes by Lemma 4.38, where  . We see that
. We see that  is a direct summand of the \(\mathfrak {s}'\)-distinguished n-exangle
is a direct summand of the \(\mathfrak {s}'\)-distinguished n-exangle  by Proposition 3.7(ii). Hence,
by Proposition 3.7(ii). Hence,  by [16, Prop. 3.3], and so \((\mathscr {E},\Psi )\) is an n-exangulated functor.
by [16, Prop. 3.3], and so \((\mathscr {E},\Psi )\) is an n-exangulated functor.
Lastly, it follows immediately from (4.16) that  is an n-exangulated natural transformation
is an n-exangulated natural transformation  .
.
(ii) By Proposition 2.8(ii), there exists a unique natural transformation  with
with  , so it remains to show that
, so it remains to show that  induces an n-exangulated natural transformation \((\mathscr {E}, \Psi ) \Rightarrow (\mathscr {G}, \Theta )\). For this, let
induces an n-exangulated natural transformation \((\mathscr {E}, \Psi ) \Rightarrow (\mathscr {G}, \Theta )\). For this, let  and
and  be arbitrary. Note that we have
be arbitrary. Note that we have

Hence, we obtain

and the proof is complete. \(\square \)
We close this section with some remarks on our main results and constructions.
Remark 4.40
Before commenting on how our results unify the constructions in cases in the literature and on how our proof methods compare, we set up and recall a little terminology. Suppose \((\mathcal {C},\mathbb {E},\mathfrak {s})\) and \((\mathcal {C}',\mathbb {E}',\mathfrak {s}')\) are n-exangulated categories. We call an n-exangulated functor \((\mathscr {F},\Gamma ) :(\mathcal {C},\mathbb {E},\mathfrak {s}) \rightarrow (\mathcal {C}',\mathbb {E}',\mathfrak {s}')\) an n-exangulated isomorphism if \(\mathscr {F}\) is an isomorphism of categories and \(\Gamma \) is a natural isomorphism. This terminology is justified by [9, Prop. 4.11]. Lastly, we recall that n-exangulated functors between \((n+2)\)-angulated categories are \((n+2)\)-angulated in the sense of [10, Def. 2.7] (or exact as in Bergh–Thaule [8, Sec. 4]), and that n-exangulated functors between n-exact categories are n-exact in the sense of [10, Def. 2.18]; see [10, Thms. 2.33, 2.34].
It has been shown that a triplet \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is a 1-exangulated category if and only if it is extriangulated (see [16, Prop. 4.3]). Suppose that \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is an extriangulated category and consider the idempotent completion \(\widetilde{\mathcal {C}}\) of \(\mathcal {C}\). By [27, Thm. 3.1], there is an extriangulated structure \((\mathbb {F}',\mathfrak {t}')\) on \(\widetilde{\mathcal {C}}\). By our Theorem 4.32, there is a 1-exangulated (or extriangulated) category \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\). By direct comparison of the constructions, one can check that \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) and \((\widetilde{\mathcal {C}},\mathbb {F}',\mathfrak {t}')\) are n-exangulated isomorphic. Indeed, the bifunctors \(\mathbb {F}\) and \(\mathbb {F}'\) differ only by a labelling of the elements due to our convention in Definition 4.4; and, ignoring this re-labelling, the realisations \(\mathfrak {s}\) and \(\mathfrak {s}'\) are the same by Lemma 4.19. Furthermore, since \((\widetilde{\mathcal {C}},\mathbb {F}',\mathfrak {t}')\) recovers the triangulated and exact category cases, we see that our construction agrees with the classical (i.e. \(n=1\)) cases up to n-exangulated isomorphism.
For larger n, we just need to compare \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) with the construction in [25]. Thus, suppose \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is the n-exangulated category coming from an \((n+2)\)-angulated category  . Recall that in this case \(\mathbb {E}(Z,X) = \mathcal {C}(Z,\Sigma X)\) for \(X,Z\in \mathcal {C}\). Using [25, Thm. 3.1], one obtains an \((n+2)\)-angulated category
. Recall that in this case \(\mathbb {E}(Z,X) = \mathcal {C}(Z,\Sigma X)\) for \(X,Z\in \mathcal {C}\). Using [25, Thm. 3.1], one obtains an \((n+2)\)-angulated category  , where \(\widetilde{\Sigma }\) is induced by \(\Sigma \). From this \((n+2)\)-angulated category, just like above, we obtain an induced n-exangulated category \((\widetilde{\mathcal {C}},\mathbb {F}',\mathfrak {t}')\). Notice that \(\mathbb {F}'(-,-) = \widetilde{\mathcal {C}}(-,\widetilde{\Sigma }-)\). Comparing \((\widetilde{\mathcal {C}},\mathbb {F}',\mathfrak {t}')\) to the n-exangulated category \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) found from Theorem 4.32, again we see that \(\mathbb {F}\) and \(\mathbb {F}'\) differ by the labelling convention we chose in Definition 4.4. By [16, Prop. 4.8] we have that \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) induces an \((n+2)\)-angulated category
, where \(\widetilde{\Sigma }\) is induced by \(\Sigma \). From this \((n+2)\)-angulated category, just like above, we obtain an induced n-exangulated category \((\widetilde{\mathcal {C}},\mathbb {F}',\mathfrak {t}')\). Notice that \(\mathbb {F}'(-,-) = \widetilde{\mathcal {C}}(-,\widetilde{\Sigma }-)\). Comparing \((\widetilde{\mathcal {C}},\mathbb {F}',\mathfrak {t}')\) to the n-exangulated category \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) found from Theorem 4.32, again we see that \(\mathbb {F}\) and \(\mathbb {F}'\) differ by the labelling convention we chose in Definition 4.4. By [16, Prop. 4.8] we have that \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) induces an \((n+2)\)-angulated category  , and therefore the n-exangulated inclusion functor
, and therefore the n-exangulated inclusion functor  is, moreover, \((n+2)\)-angulated. It follows from [25, Thm. 3.1(2)] that
is, moreover, \((n+2)\)-angulated. It follows from [25, Thm. 3.1(2)] that  and
and  must be equal, and hence \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) and \((\widetilde{\mathcal {C}},\mathbb {F}',\mathfrak {t}')\) are n-exangulated isomorphic.
must be equal, and hence \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) and \((\widetilde{\mathcal {C}},\mathbb {F}',\mathfrak {t}')\) are n-exangulated isomorphic.
Remark 4.41
Our proofs in this article differ from the proofs in both the extriangulated and the \((n+2)\)-angulated cases. First, the axioms for an n-exangulated category look very different from the axioms for an extriangulated category. Therefore, the proofs from [27] cannot be directly generalised to the \(n>1\) case. Even of the results that seem like they might generalise nicely, one comes across immediate obstacles. Indeed, Lin [25, p. 1064] already points out that lifting idempotent morphisms of extensions to idempotent morphisms of n-exangles is non-trivial. Despite this, we are able to overcome this here. This, amongst other problems, forces Lin to use another approach, and hence demonstrates why our methods are distinct.
Remark 4.42
He–He–Zhou [15] have considered idempotent completions of n-exangulated categories in a specific setup. In their setup, there is an ambient Krull-Schmidt \((n+2)\)-angulated category \(\mathcal {C}\) and an additive subcategory \(\mathcal {A}\) that is n-extension-closed (see Definition 5.2) and closed under direct summands in \(\mathcal {C}\). The main aim of [15] is to show that the idempotent completion \(\widetilde{\mathcal {A}}\) of \(\mathcal {A}\) is an n-exangulated subcategory of \(\widetilde{\mathcal {C}}\).
Since \(\mathcal {A}\) is an additive subcategory of and closed under direct summands in a Krull-Schmidt category, it is Krull-Schmidt itself. In particular, \(\mathcal {A}\simeq \widetilde{\mathcal {A}}\) is already idempotent complete by [24, Cor. 4.4]. Moreover, in the setup of [15], it already follows that \(\mathcal {A}\) inherits an n-exangulated structure from \(\mathcal {C}\simeq \widetilde{\mathcal {C}}\). Indeed, (EA1) is proven in [22, Lem. 3.8], and (EA2) and (EA2) are straightforward to check directly. It is then clear that \(\mathcal {A}\) inherits an n-exangulated structure from \(\mathcal {C}\).
are straightforward to check directly. It is then clear that \(\mathcal {A}\) inherits an n-exangulated structure from \(\mathcal {C}\).
5 The Weak Idempotent Completion of an n-Exangulated Category
Just as in Sect. 4, we assume \(n\geqslant 1\) is an integer and that \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is an n-exangulated category. By Theorems 4.32 and 4.39, the idempotent completion of \((\mathcal {C},\mathbb {E},\mathfrak {s})\) is an n-exangulated category \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) and the inclusion functor  of \(\mathcal {C}\) into \(\widetilde{\mathcal {C}}\) is part of an n-exangulated functor
of \(\mathcal {C}\) into \(\widetilde{\mathcal {C}}\) is part of an n-exangulated functor  , which satisfies the 2-universal property from Theorem 4.39. In this section, we turn our attention to the weak idempotent completion \(\widehat{\mathcal {C}}\) of \(\mathcal {C}\) and we show that it forms part of a triplet \((\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r})\) that is n-extension-closed (see Definition 5.2) in \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\). It will then follow that \((\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r})\) is itself n-exangulated, and, moreover, there is an analogue of Theorem 4.39 for \((\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r})\); see Theorem 5.5.
, which satisfies the 2-universal property from Theorem 4.39. In this section, we turn our attention to the weak idempotent completion \(\widehat{\mathcal {C}}\) of \(\mathcal {C}\) and we show that it forms part of a triplet \((\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r})\) that is n-extension-closed (see Definition 5.2) in \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\). It will then follow that \((\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r})\) is itself n-exangulated, and, moreover, there is an analogue of Theorem 4.39 for \((\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r})\); see Theorem 5.5.
We begin with the following proposition, which is an analogue of Lemma 4.38 for the weak idempotent completion.
Proposition 5.1
Suppose  are objects,
are objects,  is an \(\mathbb {F}\)-extension and
is an \(\mathbb {F}\)-extension and  . Then there is a \(\mathfrak {t}\)-distinguished n-exangle
. Then there is a \(\mathfrak {t}\)-distinguished n-exangle  with
with  and an \(\mathfrak {s}\)-distinguished n-exangle
and an \(\mathfrak {s}\)-distinguished n-exangle  , such that
, such that

as \(\mathfrak {t}\)-distinguished n-exangles.
Proof
By Corollary 4.13, there exists an idempotent morphism  with
with  for \(2 \leqslant i \leqslant n-1\), as well as a homotopy
for \(2 \leqslant i \leqslant n-1\), as well as a homotopy  , where
, where  . Notice
. Notice  for \(i = 0, n+1\) by assumption. Furthermore,
for \(i = 0, n+1\) by assumption. Furthermore,  for
for  . By Lemma 4.38 we have
. By Lemma 4.38 we have  -distinguished n-exangles. We will show that there is an isomorphism
-distinguished n-exangles. We will show that there is an isomorphism  in
in  for some
for some  , as well as an isomorphism
, as well as an isomorphism  in
in  for some object
for some object  .
.
If \(i = 0,n+1\), then  is split by assumption, so by Lemma 2.4 there are objects \(Y'_i \in \mathcal {C}\) and isomorphisms
is split by assumption, so by Lemma 2.4 there are objects \(Y'_i \in \mathcal {C}\) and isomorphisms  . For \(2\leqslant i \leqslant n-1\), we see that
. For \(2\leqslant i \leqslant n-1\), we see that  , so by Lemma 2.4 again we have isomorphisms
, so by Lemma 2.4 again we have isomorphisms  , but now where \( Y'_{i} = 0 \in \mathcal {C}\). Since
, but now where \( Y'_{i} = 0 \in \mathcal {C}\). Since  by assumption and because
by assumption and because  for \(2 \leqslant i \leqslant n-1\), we put
for \(2 \leqslant i \leqslant n-1\), we put  and
and  for \(i \in \{ 0,n+1\} \cup \{2,\ldots , n-1\}\). It remains to find appropriate isomorphisms
for \(i \in \{ 0,n+1\} \cup \{2,\ldots , n-1\}\). It remains to find appropriate isomorphisms  and \(\tilde{s}'_i\) for \(i=1,n\).
and \(\tilde{s}'_i\) for \(i=1,n\).
We have a morphism  with underlying morphism
with underlying morphism  and another
and another  with underlying morphism
with underlying morphism  by Lemma 4.14. Since
by Lemma 4.14. Since  is a homotopy, we see that
is a homotopy, we see that  . This implies
. This implies

and so  . Similarly, we also have
. Similarly, we also have  .
.
-
1.
If \(n=1\), then (5.1) shows that
 is a section in the complex
is a section in the complex  , and hence this complex is a split short exact sequence by [16, Claim 2.15]. In particular, we have that
, and hence this complex is a split short exact sequence by [16, Claim 2.15]. In particular, we have that  . So we put \(Y'_{1} :=Y'_{0}\oplus Y'_{2}\) and define
. So we put \(Y'_{1} :=Y'_{0}\oplus Y'_{2}\) and define 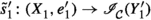 to be this composition of isomorphisms. As
to be this composition of isomorphisms. As 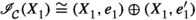 , and
, and 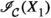 and
and  are isomorphic to objects in \(\widehat{\mathcal {C}}\), by Lemma 2.12 there is an isomorphism
are isomorphic to objects in \(\widehat{\mathcal {C}}\), by Lemma 2.12 there is an isomorphism  for some
for some 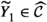 .
. -
2.
If \(n \geqslant 2\), then the form of the homotopy
 implies that the identities
implies that the identities  and
and  hold. Therefore, we see that
hold. Therefore, we see that 
which shows that
 and
and 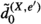 are mutually inverse isomorphisms. We now define \(Y'_{1} :=Y'_{0}\) and
are mutually inverse isomorphisms. We now define \(Y'_{1} :=Y'_{0}\) and  . Because there are isomorphisms
. Because there are isomorphisms  , and
, and 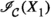 and
and  are isomorphic to objects in \(\widehat{\mathcal {C}}\), by Lemma 2.12 there is an isomorphism
are isomorphic to objects in \(\widehat{\mathcal {C}}\), by Lemma 2.12 there is an isomorphism  for some
for some  . In a similar way, one can show that
. In a similar way, one can show that 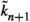 and
and 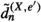 are mutually inverse isomorphisms. We set \(Y'_{\textit{n}} :=Y'_{n+1}\) and
are mutually inverse isomorphisms. We set \(Y'_{\textit{n}} :=Y'_{n+1}\) and  . In addition, there is an isomorphism
. In addition, there is an isomorphism  for some
for some 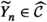 .
.
The complex  with object
with object  in degree \(0\leqslant i \leqslant n+1\) and differential
in degree \(0\leqslant i \leqslant n+1\) and differential  in degree \(0\leqslant i\leqslant n\) is isomorphic to
in degree \(0\leqslant i\leqslant n\) is isomorphic to  via
via  . Furthermore, as
. Furthermore, as  and
and  are identity morphisms, we have that
are identity morphisms, we have that  is \(\mathfrak {t}\)-distinguished by [16, Cor. 2.26(2)]. The complex \(\widetilde{Y}'_{\bullet }\) with object
is \(\mathfrak {t}\)-distinguished by [16, Cor. 2.26(2)]. The complex \(\widetilde{Y}'_{\bullet }\) with object  in degree \(0\leqslant i \leqslant n+1\) and differential
in degree \(0\leqslant i \leqslant n+1\) and differential  in degree \(0\leqslant i \leqslant n\) is isomorphic to
in degree \(0\leqslant i \leqslant n\) is isomorphic to  via \(\tilde{s}'_{\bullet }\). Moreover, this induces an isomorphism
via \(\tilde{s}'_{\bullet }\). Moreover, this induces an isomorphism  of \(\mathbb {F}\)-attached complexes, and hence of \(\mathfrak {t}\)-distinguished n-exangles. It is clear that
of \(\mathbb {F}\)-attached complexes, and hence of \(\mathfrak {t}\)-distinguished n-exangles. It is clear that

by the construction of \(\widetilde{Y}'_\bullet \). Lastly,  is \(\mathfrak {s}\)-distinguished using [16, Prop. 3.3] and that \(\mathfrak {s}\) is an exact realisation of \(\mathbb {E}\). \(\square \)
is \(\mathfrak {s}\)-distinguished using [16, Prop. 3.3] and that \(\mathfrak {s}\) is an exact realisation of \(\mathbb {E}\). \(\square \)
From Proposition 5.1 we see that \(\widehat{\mathcal {C}}\) is n-extension-closed in \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) in the following sense.
Definition 5.2
[17, Def. 4.1] Let \((\mathcal {C}',\mathbb {E}',\mathfrak {s}')\) be an n-exangulated category. A full subcategory \(\mathcal {D}\subseteq \mathcal {C}'\) is said to be n-extension-closed if, for all \(A,C\in \mathcal {D}\) and each \(\mathbb {E}'\)-extension \(\delta \in \mathbb {E}'(C,A)\), there is an object  such that
such that  for all \(1\leqslant i \leqslant n\) and
for all \(1\leqslant i \leqslant n\) and  .
.
Let us now define the biadditive functor and realisation with which we wish to equip \(\widehat{\mathcal {C}}\).
Definition 5.3
-
(i)
Let
 be the restriction of
be the restriction of  .
. -
(ii)
For a \(\mathbb {G}\)-extension
 , there is a \(\mathfrak {t}\)-distinguished n-exangle
, there is a \(\mathfrak {t}\)-distinguished n-exangle 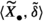 with
with 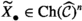 by Proposition 5.1. We put
by Proposition 5.1. We put  , the isomorphism class of
, the isomorphism class of  in
in 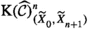 .
. -
(iii)
Recall from Sect. 2.2 that
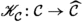 is the inclusion functor defined by
is the inclusion functor defined by 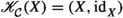 on objects \(X \in \mathcal {C}\). Let
on objects \(X \in \mathcal {C}\). Let 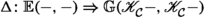 be the restriction of the natural transformation
be the restriction of the natural transformation  defined in Lemma 4.35. This means
defined in Lemma 4.35. This means  for
for  .
.
Since \(\widehat{\mathcal {C}}\) is an n-extension closed subcategory of \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) by Proposition 5.1, one can use [17, Prop. 4.2(1)] to deduce axioms (EA2) and (EA2) hold for the triplet \((\widehat{\mathcal {C}}, \mathbb {G}, \mathfrak {r})\). The difficult part is then to show that (EA1) is satisfied; this follows from Lemma 5.4 below. We note here, however, it has been shown in [23, Thm. A] that any n-extension-closed subcategory of an n-exangulated category that is also closed under isomorphisms inherits an n-exangulated structure in the expected way. Although the isomorphism-closure in [23] is assumed only for convenience, we highlight that the weak idempotent completion is not necessarily closed under isomorphisms in the idempotent completion using the constructions in Sect. 2. Indeed, one can show that \(\widehat{\mathcal {C}}\) is isomorphism-closed in \(\widetilde{\mathcal {C}}\) if and only if \(\mathcal {C}\) is already weakly idempotent complete.
hold for the triplet \((\widehat{\mathcal {C}}, \mathbb {G}, \mathfrak {r})\). The difficult part is then to show that (EA1) is satisfied; this follows from Lemma 5.4 below. We note here, however, it has been shown in [23, Thm. A] that any n-extension-closed subcategory of an n-exangulated category that is also closed under isomorphisms inherits an n-exangulated structure in the expected way. Although the isomorphism-closure in [23] is assumed only for convenience, we highlight that the weak idempotent completion is not necessarily closed under isomorphisms in the idempotent completion using the constructions in Sect. 2. Indeed, one can show that \(\widehat{\mathcal {C}}\) is isomorphism-closed in \(\widetilde{\mathcal {C}}\) if and only if \(\mathcal {C}\) is already weakly idempotent complete.
Lemma 5.4
Let  be a \(\mathfrak {t}\)-inflation with
be a \(\mathfrak {t}\)-inflation with  . Then there is a \(\mathfrak {t}\)-distinguished n-exangle
. Then there is a \(\mathfrak {t}\)-distinguished n-exangle  with
with  and
and  .
.
Proof
By Lemma 4.25 there is an object \(C \in \mathcal {C}\), a morphism  and an \(\mathfrak {s}\)-distinguished n-exangle
and an \(\mathfrak {s}\)-distinguished n-exangle  and
and  . The solid morphisms of the diagram
. The solid morphisms of the diagram

form a commutative diagram. By Lemma 4.24 there exists an idempotent morphism of n-exangles  ,
,  and
and  for \(3 \leqslant i \leqslant n+1\), which makes the diagram above commute. Let
for \(3 \leqslant i \leqslant n+1\), which makes the diagram above commute. Let  and
and  . Notice that the underlying \(\mathbb {E}\)-extension of \({\tilde{\rho }}'\) is \(\rho \). Set
. Notice that the underlying \(\mathbb {E}\)-extension of \({\tilde{\rho }}'\) is \(\rho \). Set  . Then
. Then  as \(\mathfrak {t}\)-distinguished n-exangles by Lemma 4.38.
as \(\mathfrak {t}\)-distinguished n-exangles by Lemma 4.38.
We claim that there is a split short exact sequence

Since  realises the trivial \(\mathbb {F}\)-extension
realises the trivial \(\mathbb {F}\)-extension  , we have that
, we have that  is a section by [16, Claim 2.15]. If \(n=1\), then this is enough to see that (5.2) is split short exact. For \(n\geqslant 2\) we notice that there is an isomorphism
is a section by [16, Claim 2.15]. If \(n=1\), then this is enough to see that (5.2) is split short exact. For \(n\geqslant 2\) we notice that there is an isomorphism  in \(\widetilde{\mathcal {C}}\), so
in \(\widetilde{\mathcal {C}}\), so  . Thus, since
. Thus, since  is a weak kernel of
is a weak kernel of  , we see that
, we see that  factors through
factors through  . In particular, this implies
. In particular, this implies  is a cokernel of
is a cokernel of  . Again, (5.2) is split short exact.
. Again, (5.2) is split short exact.
In particular, we have an isomorphism  . We know that the objects
. We know that the objects  and
and  are isomorphic to objects in
are isomorphic to objects in  by Lemma 2.4, as
by Lemma 2.4, as  and
and  are split idempotents. This implies that
are split idempotents. This implies that  is isomorphic to an object in \(\widehat{\mathcal {C}}\) by Lemma 2.12. Again Lemma 2.12 and the isomorphism
is isomorphic to an object in \(\widehat{\mathcal {C}}\) by Lemma 2.12. Again Lemma 2.12 and the isomorphism  imply that there is an isomorphism
imply that there is an isomorphism  for some
for some  .
.
The morphism  with underlying morphism
with underlying morphism  is an isomorphism. Finally, put
is an isomorphism. Finally, put  for \(i = 0\) and \(3 \leqslant i \leqslant n+1\). Then the complex
for \(i = 0\) and \(3 \leqslant i \leqslant n+1\). Then the complex

is isomorphic to  via
via  in
in  . With
. With  , we see that
, we see that  is \(\mathfrak {t}\)-distinguished by [16, Cor. 2.26(2)], as desired. \(\square \)
is \(\mathfrak {t}\)-distinguished by [16, Cor. 2.26(2)], as desired. \(\square \)
We may state and prove our main result of this section.
Theorem 5.5
Suppose that \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is an n-exangulated category. Then \((\widehat{\mathcal {C}}, \mathbb {G}, \mathfrak {r})\) is a weakly idempotent complete n-exangulated category, and  is an n-exangulated functor, such that the following 2-universal property is satisfied. Suppose \((\mathscr {F},\Lambda ) :(\mathcal {C}, \mathbb {E}, \mathfrak {s}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) is an n-exangulated functor to a weakly idempotent complete n-exangulated category \((\mathcal {C}', \mathbb {E}', \mathfrak {s}')\). Then the following statements hold.
is an n-exangulated functor, such that the following 2-universal property is satisfied. Suppose \((\mathscr {F},\Lambda ) :(\mathcal {C}, \mathbb {E}, \mathfrak {s}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) is an n-exangulated functor to a weakly idempotent complete n-exangulated category \((\mathcal {C}', \mathbb {E}', \mathfrak {s}')\). Then the following statements hold.
-
(i)
There is an n-exangulated functor \((\mathscr {E}, \Psi ) :(\widehat{\mathcal {C}}, \mathbb {G}, \mathfrak {r}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) and an n-exangulated natural isomorphism
 .
. -
(ii)
In addition, for any n-exangulated functor \((\mathscr {G}, \Theta ) :(\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r}) \rightarrow (\mathcal {C}', \mathbb {E}', \mathfrak {s}')\) and any n-exangulated natural transformation
 , there is a unique n-exangulated natural transformation
, there is a unique n-exangulated natural transformation  with
with  .
.
Proof
Since \(\widehat{\mathcal {C}}\) is a full subcategory of \(\widetilde{\mathcal {C}}\) and because \((\widetilde{\mathcal {C}}, \mathbb {F}, \mathfrak {t})\) is n-exangulated, we can apply [17, Prop. 4.2] and Definition 5.2. We showed above that \(\widehat{\mathcal {C}}\) is n-extension-closed in \(\widetilde{\mathcal {C}}\); see Proposition 5.1. Moreover, it follows immediately from Lemma 5.4 and its dual that \((\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r})\) satisfies (EA1). Therefore, we deduce that \((\widehat{\mathcal {C}}, \mathbb {G}, \mathfrak {r})\) is an n-exangulated category.
One may argue that  is an n-exangulated functor as in Proposition 4.36, by using the definition of \(\mathfrak {r}\) and noting that
is an n-exangulated functor as in Proposition 4.36, by using the definition of \(\mathfrak {r}\) and noting that  lies in \(\widehat{\mathcal {C}}\) for all \(X\in \mathcal {C}\).
lies in \(\widehat{\mathcal {C}}\) for all \(X\in \mathcal {C}\).
(i) One argues like in the proof of Theorem 4.39(i), but using Proposition 2.13 instead of Proposition 2.8, and Proposition 5.1 instead of Lemma 4.38. In particular, we note that the isomorphism  of \(\mathfrak {t}\)-distinguished n-exangles from the statement of Proposition 5.1 induces an isomorphism
of \(\mathfrak {t}\)-distinguished n-exangles from the statement of Proposition 5.1 induces an isomorphism

of \(\mathfrak {r}\)-distinguished n-exangles.
(ii) Similarly, one adapts the proof of Theorem 4.39(ii), using Proposition 2.13 instead of Proposition 2.8. \(\square \)
Finally, we have an analogue of Corollary 4.34 as a consequence.
Corollary 5.6
Suppose \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is n-exact. Then \((\widehat{\mathcal {C}}, \mathbb {G}, \mathfrak {r})\) is n-exact.
Proof
The n-exangulated category \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\) is n-exact by Corollary 4.34. As \((\widehat{\mathcal {C}},\mathbb {G},\mathfrak {r})\) inherits its structure as an n-extension closed subcategory of \((\widetilde{\mathcal {C}},\mathbb {F},\mathfrak {t})\), the result follows from the proof of [23, Cor. 4.15]. \(\square \)
Data availability
Not applicable.
References
Anderson, F. W., Fuller, K. R.: Rings and categories of modules, volume 13 of Graduate Texts in Mathematics, 2nd ed. Springer, New York (1992)
Atiyah, M. F., MacDonald, I. G.: Introduction to commutative algebra. Addison-Wesley Publishing Co., Reading, Mass.-London-Don Mills, Ont. (1969)
Auslander, M.: Representation theory of Artin algebras. I. Commun. Algebra 1, 177–268 (1974)
Bucur, I., Deleanu, A.: Introduction to the theory of categories and functors. A Wiley-Interscience Publication. John Wiley & Sons, Ltd., London-New York-Sydney (1968)
Brüstle, T., Hassoun, S., Shah, A., Tattar, A.: Stratifying systems and Jordan–Hölder extriangulated categories. Preprint arXiv:2208.07808v3 (2022)
Borceux, F.: Handbook of categorical algebra. 1. Basic category theory, volume 50 of Encyclopedia of Mathematics and its Applications. Cambridge Univ. Press, Cambridge (1994)
Balmer, P., Schlichting, M.: Idempotent completion of triangulated categories. J. Algebra 236(2), 819–834 (2001)
Bergh, P.A., Thaule, M.: The Grothendieck group of an \(n\)-angulated category. J. Pure Appl. Algebra 218(2), 354–366 (2014)
Bennett-Tennenhaus, R., Haugland, J., Sandøy, M.H., Shah, A.: The category of extensions and a characterisation of \(n\)-exangulated functors. Math. Z. 305(3), 44 (2023)
Bennett-Tennenhaus, R., Shah, A.: Transport of structure in higher homological algebra. J. Algebra 574, 514–549 (2021)
Bühler, T.: Exact categories. Expo. Math. 28(1), 1–69 (2010)
Chen, X.-W., Ye, Y., Zhang, P.: Algebras of derived dimension zero. Commun. Algebra 36(1), 1–10 (2008)
Fraenkel, A. A., Bar-Hillel, Y., Levy, A.: Foundations of set theory, volume 67 of Studies in Logic and the Foundations of Mathematics. North-Holland Publishing Co., Amsterdam-London, revised edition (1973)
Geiss, C., Keller, B., Oppermann, S.: \(n\)-angulated categories. J. Reine Angew. Math. 675, 101–120 (2013)
He, J., He, J., Zhou, P.: Idempotent completion of certain \(n\)-exangulated categories. Preprint. arXiv:2207.01232v1 (2022)
Herschend, M., Liu, Y., Nakaoka, H.: \(n\)-exangulated categories (I): definitions and fundamental properties. J. Algebra 570, 531–586 (2021)
Herschend, M., Liu, Y., Nakaoka, H.: \(n\)-exangulated categories (II): constructions from \(n\)-cluster tilting subcategories. J. Algebra 594, 636–684 (2022)
Henrard, R., van Roosmalen, A.-C.: Derived categories of (one-sided) exact categories and their localizations. Preprint. arXiv:1903.12647v3 (2019)
Jasso, G.: \(n\)-abelian and \(n\)-exact categories. Math. Z. 283(3–4), 703–759 (2016)
Karoubi, M.: Algèbres de Clifford et \(K\)-théorie. Ann. Sci. École Norm. Sup. 4(1), 161–270 (1968)
Kalck, M., Iyama, O., Wemyss, M., Yang, D.: Frobenius categories, Gorenstein algebras and rational surface singularities. Compos. Math. 151(3), 502–534 (2015)
Klapproth, C.: \(n\)-exact categories arising from \((n+2)\)-angulated categories. Preprint. arXiv:2108.04596v2 (2021)
Klapproth, C.: \(n\)-extension closed subcategories of \(n\)-exangulated categories. Preprint. arXiv:2209.01128v3 (2023)
Krause, H.: Krull–Schmidt categories and projective covers. Expo. Math. 33(4), 535–549 (2015)
Lin, Z.: Idempotent completion of \(n\)-angulated categories. Appl. Categ. Struct. 29(6), 1063–1071 (2021)
Liu, J., Sun, L.: Idempotent completion of pretriangulated categories. Czechoslovak Math. J. 64(139)(2), 477–494 (2014)
Msapato, D.: The Karoubi envelope and weak idempotent completion of an extriangulated category. Appl. Categ. Struct. 30(3), 499–535 (2022)
Neeman, A.: The derived category of an exact category. J. Algebra 135(2), 388–394 (1990)
Nakaoka, H., Ogawa, Y., Sakai, A.: Localization of extriangulated categories. J. Algebra 611, 341–398 (2022)
Nakaoka, H., Palu, Y.: Extriangulated categories, Hovey twin cotorsion pairs and model structures. Cah. Topol. Géom. Différ. Catég. 60(2), 117–193 (2019)
Orlov, D.: Formal completions and idempotent completions of triangulated categories of singularities. Adv. Math. 226(1), 206–217 (2011)
Smullyan, R. M., Fitting, M.: Set theory and the continuum problem, volume 34 of Oxford Logic Guides. The Clarendon Press, Oxford University Press, New York (1996)
Shah, A.: Auslander-Reiten theory in quasi-abelian and Krull–Schmidt categories. J. Pure Appl. Algebra 224(1), 98–124 (2020)
Thomason, R.W., Trobaugh, T.: Higher algebraic \(K\)-theory of schemes and of derived categories. In: The Grothendieck Festschrift, Vol. III, volume 88 of Progr. Math., pp. 247–435. Birkhäuser Boston, Boston (1990)
Zhou, Y.: Idempotent completion of right suspended categories. AIMS Math. 7(7), 13442–13453 (2022)
Zhao, T., Zhu, B., Zhuang, X.: Tilting pairs in extriangulated categories. Proc. Edinb. Math. Soc. (2), 64(4):947–981 (2021)
Acknowledgements
The authors would like to thank Theo Bühler, Ruben Henrard and Adam-Christiaan van Roosmalen for useful email communications, and Andrew Brooke-Taylor and Peter Jørgensen for helpful discussions. The authors are very grateful to the referees for their comments and suggestions. In particular, these comments led to Corollaries 4.34 and 5.6, and improvements to the exposition.
Funding
The second author was supported by an EPSRC Doctoral Training Partnership (Grant EP/R513258/1) through the University of Leeds. The first and last authors are supported by: the Danish National Research Foundation (Grant DNRF156); the Independent Research Fund Denmark (Grant 1026-00050B); and the Aarhus University Research Foundation (Grant AUFF-F-2020-7-16). The last author also gratefully acknowledges funding from the London Mathematical Society with support from Heilbronn Institute for Mathematical Research (Grant ECF-1920-57).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by all authors. The first draft of the manuscript was written by all authors. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflicts of interest
Not applicable.
Additional information
Communicated by Alice Rizzardo.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klapproth, C., Msapato, D. & Shah, A. Idempotent Completions of n-Exangulated Categories. Appl Categor Struct 32, 7 (2024). https://doi.org/10.1007/s10485-023-09758-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10485-023-09758-5
Keywords
- Additive category
- Idempotent completion
- Karoubi envelope
- n-exangulated category
- n-exangulated functor
- n-exangulated natural transformation
- Split idempotents
- Weak idempotent completion




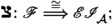 and, in addition,
and, in addition,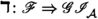 , there exists a unique natural transformation
, there exists a unique natural transformation 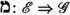 with
with  .
.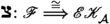 ; and, in addition,
; and, in addition, , there exists a unique natural transformation
, there exists a unique natural transformation 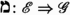 with
with 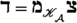 .
. is known as an
is known as an 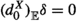 and
and 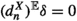 . An
. An  is called an n-exangle (for
is called an n-exangle (for 
 of
of 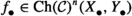 such that
such that  . Such an
. Such an  is called a morphism of n-exangles if
is called a morphism of n-exangles if  and
and 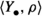 are both n-exangles.
are both n-exangles.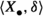 and
and  is the pair
is the pair 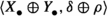 .
.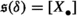 and
and  , there exists
, there exists 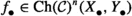 such that
such that  . In this setting, we say that
. In this setting, we say that 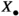 realises
realises  is a lift of (a, c).
is a lift of (a, c). , then
, then 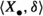 is an n-exangle.
is an n-exangle. and
and  .
. and
and 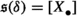 , then there exists a morphism
, then there exists a morphism 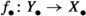 lifting
lifting  , such that
, such that  . In this case, the morphism
. In this case, the morphism  is called a good lift of
is called a good lift of 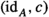 .
.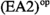 :
: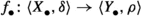 is a morphism of
is a morphism of  is a morphism of
is a morphism of  as
as  . Recall from Definition
. Recall from Definition  .
. and
and 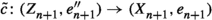 , and an
, and an  , we have
, we have  lies in
lies in 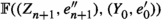 . It is then straightforward to verify that
. It is then straightforward to verify that 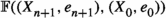 is an abelian group by defining
is an abelian group by defining 
 . The additive identity element of
. The additive identity element of  is
is 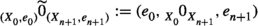 . The inverse of
. The inverse of  is
is  . Notice that we get an abelian group monomorphism:
. Notice that we get an abelian group monomorphism: 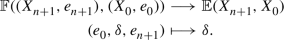
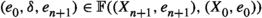 , the pair
, the pair  is a morphism of
is a morphism of 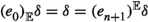 from Definition
from Definition  by
by 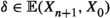 the underlying
the underlying  and
and  with
with  , there is a unique
, there is a unique  with underlying
with underlying 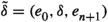 . Again, we use this instance of the tilde notation for this correspondence: we write
. Again, we use this instance of the tilde notation for this correspondence: we write 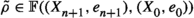 if and only if the underlying
if and only if the underlying  .
. is a morphism of complexes.
is a morphism of complexes. is idempotent and satisfies
is idempotent and satisfies 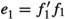 .
. is an idempotent morphism of complexes.
is an idempotent morphism of complexes. is a homotopy of morphisms
is a homotopy of morphisms  , then the pair
, then the pair 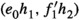 yields a homotopy
yields a homotopy 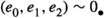 .
. is an
is an 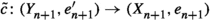 is a morphism in
is a morphism in 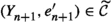 ;
;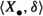 and
and  are
are  ;
; is an idempotent morphism lifting
is an idempotent morphism lifting  , such that
, such that  is null homotopic; and
is null homotopic; and is an idempotent morphism lifting
is an idempotent morphism lifting  , such that
, such that  is null homotopic.
is null homotopic.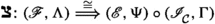 .
.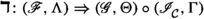 , there is a unique n-exangulated natural transformation
, there is a unique n-exangulated natural transformation  with
with 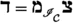 .
. is a section in the complex
is a section in the complex  , and hence this complex is a split short exact sequence by [
, and hence this complex is a split short exact sequence by [ . So we put
. So we put 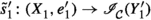 to be this composition of isomorphisms. As
to be this composition of isomorphisms. As 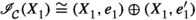 , and
, and 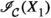 and
and  are isomorphic to objects in
are isomorphic to objects in  for some
for some 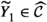 .
. implies that the identities
implies that the identities  and
and  hold. Therefore, we see that
hold. Therefore, we see that 
 and
and 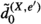 are mutually inverse isomorphisms. We now define
are mutually inverse isomorphisms. We now define  . Because there are isomorphisms
. Because there are isomorphisms  , and
, and 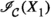 and
and  are isomorphic to objects in
are isomorphic to objects in  for some
for some  . In a similar way, one can show that
. In a similar way, one can show that 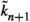 and
and 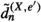 are mutually inverse isomorphisms. We set
are mutually inverse isomorphisms. We set  . In addition, there is an isomorphism
. In addition, there is an isomorphism  for some
for some 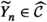 .
. be the restriction of
be the restriction of  .
. , there is a
, there is a 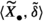 with
with 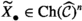 by Proposition
by Proposition  , the isomorphism class of
, the isomorphism class of  in
in 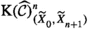 .
.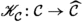 is the inclusion functor defined by
is the inclusion functor defined by 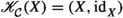 on objects
on objects 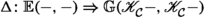 be the restriction of the natural transformation
be the restriction of the natural transformation  defined in Lemma
defined in Lemma  for
for  .
. .
. , there is a unique n-exangulated natural transformation
, there is a unique n-exangulated natural transformation  with
with  .
.