Abstract
Right triangulated categories can be thought of as triangulated categories whose shift functor is not an equivalence. We give intrinsic characterisations of when such categories are appearing as the (co-)aisle of a (co-)t-structure in an associated triangulated category. Along the way, we also give an interpretation of these structures in the language of extriangulated categories.
We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.
Avoid common mistakes on your manuscript.
1 Introduction
The notion of a t-structure in a triangulated category was introduced by [9] in the study of perverse sheaves. They are central to the study of stability conditions, in the sense of Bridgeland [16] and tilting theory [27] and are an area of interest in their own right [4, 25, 54]. Co-t-structures, introduced by Paukzstello [56] and Bondarko [15] (under the name of ‘weight structures’) are a more recent development and arise from dualising one of the axioms of a t-structure. They are, however, not quite a dual notion, for example, the heart of a t-structure is an abelian subcategory, whereas the co-heart of a co-t-structure is rarely so. Co-t-structures have been studied in the context of Auslander-Buchweitz approximation theory [30] and in (co-)silting theory [37, 42, 50], where t-structures also play a key role.
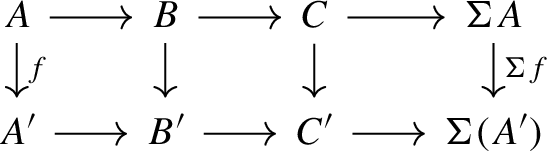
In more detail, a (co-)t-structure on a triangulated category \(\mathcal {T}\) consists of a pair of additive subcategories \((\mathcal {U}, \mathcal {V})\) called the ‘aisle’ and ‘co-aisle’ respectively satisfying three axioms. The first two of these axioms ask for \((\mathcal {U}, \mathcal {V})\) to be a torsion pair on \(\mathcal {T}\) and the third axiom requires that \(\mathcal {U}\) be closed under the (inverse) shift functor of \(\mathcal {T}\) (see Definition 4.1). We remark that there is not a consistent terminology in the literature here, for instance in some works, the term ‘torsion pair’ refers to a t-structure. There are some pleasant articles concerning the general torsion pairs on triangulated categories [19, 35, 69] though they have seemed attracted somewhat less interest than (co-)t-structures.
The corresponding notion for abelian categories is that of torsion pairs, which are extremely important objects [2, 17, 18]. Rump [59] and Bondal & Van den Bergh [3] discovered that every torsion and torsionfree class (the aisles and co-aisles of the abelian world) is a quasi-abelian category. Moreover, each quasi-abelian category appears as a tilting torsion(free) class in an associated abelian category. In this article, we give the triangulated analogues of these results for (co-)t-structures. Namely, we answer the question: What are precisely the categorical structures that appear as aisles and co-aisles of (co-)t-structures in triangulated categories?
We answer this question in detail for aisles of t-structures and co-aisles of co-t-structures, whence other co-aisles and aisles have a dual structure. As we mentioned above, the structures that we are interested in are closed under the shift of the ambient triangulated category, it is not hard to see that these subcategories have the structure of a right triangulated category (with right semi-equivalence) which we discuss next.
The data of a right triangulated category (or suspended category), first introduced in [41] consists of an additive category \(\mathcal {R}\), an endofunctor \(\Sigma :\mathcal {R}\rightarrow \mathcal {R}\) called ‘the shift of \(\mathcal {R}\)’ and a class of right triangles of the form \(A \rightarrow B \rightarrow C \rightarrow \Sigma A\) subject to essentially the same axioms as the triangles of a triangulated category (see Definition 2.16). Informally, a right triangulated category is a triangulated category whose shift functor is not necessarily an equivalence. Such categories (or their left-handed analogues) have been the subject of study in many articles [7, 10, 40, 43, 45, 47]. In [6], the class of ‘right triangulated categories with right semi-equivalence’ were introduced, these are the right triangulated categories whose shift functor is fully faithful and with image that is closed under extensions.
To every right triangulated category \(\mathcal {R}\) there is an associated triangulated category: the stabilisation \(\mathcal {S}(\mathcal {R})\) (see Sect. 2.3.1 for details and construction). In the case where \(\mathcal {R}\) has a right semi-equivalence, \(\mathcal {S}(\mathcal {R})\) can be thought of as the smallest triangulated category containing \(\mathcal {R}\) as a subcategory. Furthermore, we show in Lemma 4.4 that if \(\mathcal {R}\) is a (co-)aisle in a triangulated category then it is also a (co-)aisle in \(\mathcal {S}(\mathcal {R})\). Thus we look to characterise when \(\mathcal {R}\) is a (co-)aisle in \(\mathcal {S}(\mathcal {R})\).
We give an intrinsic characterisations of when a right triangulated category with right semi-equivalence, \(\mathcal {R}\), appears as the aisle of a t-structure in terms of internal torsion pairs of \(\mathcal {R}\) and homological properties.
Theorem A
(Theorem 4.11.) Let \(\mathcal {R}\) be a right triangulated category with right semi-equivalence. Then the following are equivalent
-
(a)
\(\mathcal {R}\) is the aisle of a t-structure \((\mathcal {R}, \mathcal {V})\) in \(\mathcal {S}(\mathcal {R})\);
-
(b)
There is a torsion pair \((\Sigma \mathcal {R}, \mathcal {F})\) in \(\mathcal {R}\);
-
(c)
\(\mathcal {S}(\mathcal {R})\) is equivalent to the co-stabilisation of \(\mathcal {R}\). That is, \(\mathcal {S}(\mathcal {R})\) has the following universal property: Every right triangle functor \(G:\mathcal {T}\rightarrow \mathcal {R}\) with \(\mathcal {T}\) being a triangulated category factors uniquely through \(\mathcal {S}(\mathcal {R})\) (see Sect. 2.3.1).
We note that there are related works [39, 44, 64] that give various characterisations of aisles and that our approach differs in the sense that we look to give characterisations intrinsic to the right triangulated category, that is, the aisle, rather than properties of the aisle related to the ambient triangulated category. We also present our characterisations of co-aisles of co-t-structures.
Theorem B
(Theorem 4.6.) Let \(\mathcal {R}\) be a right triangulated category with right semi-equivalence. Then the following are equivalent
-
(a)
\(\mathcal {R}\) is the co-aisle of a co-t-structure \((\mathcal {U}, \mathcal {R})\) in \(\mathcal {S}(\mathcal {R})\);
-
(b)
\(\mathcal {R}\) has enough projectives;
-
(c)
There is a torsion pair \((\textsf{Proj} \mathcal {R}, \Sigma \mathcal {R})\) in \(\mathcal {R}\).
Moreover, suppose that for all \(A, B \in \mathcal {R}\) we have that \(\mathcal {R}(A, \Sigma ^i B ) =0 \) for \(i>>0\), that is, \(\mathcal {R}\) is bounded. Then the above conditions are also equivalent to
-
(d)
\(\textsf{Proj}\mathcal {R}\) is a silting subcategory of \(\mathcal {S}(\mathcal {R})\).
Part (d) of the above result adds to the interpretations of silting subcategories in a triangulated category, which are surveyed in [46]. We also note that this result can be thought of as a generalisation of [7, Theorem 4.2] and that the work of [30] is useful in the proof. We also obtain the following as a direct consequence.
Corollary A
(Corollary 4.7.) There is a correspondence between silting subcategories of triangulated categories and bounded right triangulated categories with right semi-equivalence that have enough projectives.
An immediate application is that the torsion pairs in Theorems A and B allow us to describe intermediate (co-)t-structures (Proposition 4.12).
In order to formally discuss the projective objects, like in Theorem B, and other homological properties of a right triangulated category, we use the language of extriangulated categories. These categories were introduced by Nakaoka and Palu in [52] as a simultaneous generalisation of exact categories and triangulated categories. The framework of extriangulated categories allows one to axiomatise properties of categories that have structural similarities to exact and/or triangulated categories but fall into neither class, for example extension closed subcategories of triangulated categories. The formalism of extriangulated categories then allows homological algebra to be applied to such categories which has been done successfully by many authors, for example [21, 53, 68]. For us, we are interested in the fact that right triangulated categories with right semi-equivalence enjoy homological properties close to those of triangulated categories. We formalise this similarity by showing the following.
Theorem C
(Corollary 3.13.) A right triangulated category has the natural structure of an extriangulated category if and only if the shift functor is a right semi-equivalence.
Moreover, we are able to characterise which extriangulated categories have a natural right triangulated structure.
Theorem D
(Theorem 3.12.) The extriangles of an extriangulated category \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) induce a right triangulated structure with right semi-equivalence on \(\mathcal {C}\) if and only if the morphism \(X \rightarrow 0\) is an \(\mathbb {E}\)-inflation for all objects \(X \in \mathcal {C}\). In other words, the zero object of \(\mathcal {C}\) is the only \(\mathbb {E}\)-injective object and there are enough \(\mathbb {E}\)-injectives.
To prove this, we use an extriangulated generalisation of the constructions of a right triangulated quotient category from a contravariantly finite subcategory (of an additive category) due to [14] and [6] (see Proposition 3.6). We also use ideas from relative homological algebra to characterise which extriangulated structures give rise to right triangulated quotient categories (with right semi-equivalence) (see Proposition 3.7).
The construction of these right triangulated structures can be thought of as a ‘one-sided’ analogue of the triangulated structure of the stable category of a Frobenius exact (or even extriangulated) category [26, 28]. See [13, 36] for similar constructions. Unsurprisingly, given the terminology, this one-sidedness also appears in Theorem D as triangulated categories are precisely the extriangulated categories satisfying both this condition and its dual [52, Proposition 3.22].
We also show that in the case of Frobenius extriangulated categories, aisles of t-structures in the triangulated stable category may be constructed as (shifts of) right triangulated quotients.
Theorem E
(Theorem 5.1.) Let \(\mathcal {C}= (\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be a Frobenius extriangulated category and \((\mathcal {U},\mathcal {V})\) be a t-structure in the triangulated stable category \(\underline{\mathcal {C}}\) and set \(\mathcal {D}:= \Sigma ^{-1}\mathcal {V}\). Then there is an equivalence of right triangulated categories \(\mathcal {U}\cong \Sigma _\mathcal {D}\underline{\mathcal {C}}_\mathcal {D}\), where \(\underline{\mathcal {C}}_\mathcal {D}\) denotes the stable category of \(\mathcal {C}\) by the ideal of morphisms factoring through objects of \(\mathcal {D}\) and \(\Sigma _\mathcal {D}\) is its shift functor.
In [61, Proposition 3.9], it was shown that t-structures in an algebraic triangulated category correspond bijectively to certain complete cotorsion pairs in the associated Frobenius exact category. Additionally, it was observed in [51, Proposition 2.6] that t-structures in a triangulated category are precisely cotorsion pairs satisfying a shift closure property. Thus these results and Theorem E complement each other since, via these bijections, a t-structure \((\mathcal {U}, \mathcal {V})\) corresponds to a cotorsion pair \((\mathcal {U}, \Sigma ^{-1} \mathcal {V})\) (Remark 5.2).
The article is organised as follows. In Sect. 2 we recall the necessary background material on relative homological algebra, extriangulated categories and right triangulated categories. In Sect. 3 we show how one may use relative homological algebra to construct new extriangulated structures and characterise the projectives and injectives of these new structures. We then investigate how such extriangulated structures induce a right triangulated structure on a quotient category and use this to prove Theorems C and D. We begin Sect. 4 with a discussion of torsion pairs in a right triangulated category with right semi-equivalence. We then go on to prove the characterisations of right triangulated categories as (co-)aisles of (co-)t-structures of Theorems A and B and use these to describe related classes of (co-)t-structures. We end in Sect. 5 by proving Theorem E using the right triangulated quotient categories from Sect. 3.
Although the theory of extriangulated categories and relative homological algebra is not necessary for Theorem A and Theorem B(a,c), we have chosen this order as it allows us to discuss the role of extriangulated categories throughout.
We note that dual results for left triangulated categories (with left semi-equivalence) hold but remain unstated. Categories are assumed to be additive and idempotent complete. When we say an additive subcategory, we mean a subcategory that is closed under isomorphisms, direct sums and direct summands.
2 Background
2.1 Relative Homological Algebra
We briefly recall some basic definitions from relative homological algebra introduced in [32] and state some useful properties. Let \(\mathcal {C}\) be an additive category and let \(\textsf{Mor}_\mathcal {C}\) denote the category of morphisms in \(\mathcal {C}\).
Definition 2.1
Let \(\mathcal {D} \subset \textsf{Ob}(\mathcal {C})\) be a class of objects. A morphism \(f: A \rightarrow B\) in \(\mathcal {C}\) is \(\mathcal {D}\)-monic if all morphisms \(A \rightarrow D\) with \(D \in \mathcal {D}\) factor through f

or, equivalently, \(\mathcal {C}(f, -)|_\mathcal {D}: \mathcal {C}(B,-)|_\mathcal {D}\rightarrow \mathcal {C}(A,-)|_\mathcal {D}\) is an epimorphism. By \(\textsf{Mon}(\mathcal {D})\) we denote the class of all \(\mathcal {D}\)-monic morphisms in \(\mathcal {C}\). We define the notion of a \(\mathcal {D}\)-epic morphism and the class \(\textsf{Epi}(\mathcal {D})\) dually.
Similarly, for a class of morphisms \(\omega \subset \textsf{Ob}(\textsf{Mor}_\mathcal {C})\), an object \(J \in \mathcal {C}\) is \(\omega \)-injective if for every morphism \(f: A \rightarrow B\) in \(\omega \), all morphisms \(A \rightarrow J\) factor through f

or, equivalently, \(\mathcal {C}(f, J)\) is an epimorphism for all \(f \in \omega \). By \(\textsf{Inj}(\omega )\) we denote the class of all \(\omega \)-injective objects in \(\mathcal {C}\). We define the notion of an \(\omega \)-projective object and the class \(\textsf{Proj}(\omega )\) dually.
Example 2.2
-
(a)
\(\mathcal {C}\)-monics are precisely sections.
-
(b)
The injective objects of \(\mathcal {C}\), \(\textsf{Inj}{\mathcal {C}}\), are defined to be those objects that are injective relative to the class of monomorphisms of \(\mathcal {C}\), \(\mathfrak {M}\). That is \(\textsf{Inj}{\mathcal {C}} = \textsf{Inj}(\mathfrak {M}) \). \(\mathcal {C}\) is said to have enough injective objects if every object A in \(\mathcal {C}\) admits a monomorphism \(g:A \hookrightarrow I\) where \(I \in \textsf{Inj}{\mathcal {C}}\) called the injective hull of A. Suppose that \(\mathcal {C}\) has enough injective objects, then the class of \(\textsf{Inj}{\mathcal {C}}\)-monic morphisms coincides with \(\mathfrak {M}\), the class of monomorphisms in \(\mathcal {C}\). Indeed, clearly \(\mathfrak {M} \subseteq \textsf{Mon}(\textsf{Inj}\mathcal {C})\). For the converse, let \(f:A \rightarrow B\) be \(\textsf{Inj}{\mathcal {C}}\)-monic. Then the injective hull \(g: A \hookrightarrow I\) of A factors as \(g'f\) for some \(g': B \rightarrow I\). It follows that f is also a monomorphism.
-
(c)
A left \(\mathcal {D}\)-approximation [8] of an object A is just a \(\mathcal {D}\)-monic morphism \(A \rightarrow B\) such that \(B \in \mathcal {D}\).
-
(d)
In an extriangulated category (defined in the next section) \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) the \(\mathbb {E}\)-injectives are precisely \(\textsf{Inj}(\{\mathbb {E}\text {-inflations}\})\).
Definition 2.3
A commutative square

in \(\mathcal {C}\) is a weak pushout if for all pairs of morphisms \(g:A' \rightarrow C\), \(y:B \rightarrow C\) such that \(gf=yx\), there exists a (not necessarily unique) morphism \(h:B' \rightarrow C\) such that \(hf' = y\) and \(hx'=g\):

We collect some useful properties.
Lemma 2.4
Let \(\mathcal {D}\) be a class of objects in \(\mathcal {C}\). Then the following hold.
-
(a)
\(\textsf{Mon}(\mathcal {D})\) is closed under composition and retracts;
-
(b)
\(\textsf{Mon}(\mathcal {D})\) is left divisive, that is, \(gf \in \textsf{Mon}(\mathcal {D})\) implies that \(f \in \textsf{Mon}(\mathcal {D})\);
-
(c)
\(\textsf{Mon}(\mathcal {D})\) is closed under weak pushouts.
Proof
(a) and (b) are easily verified. Let us show (c). Let

be a weak pushout square in \(\mathcal {C}\) with \(x \in \textsf{Mon}\mathcal {D}\). We must show that \(x' \in \textsf{Mon}\mathcal {D}\). To this end, let \(g: A' \rightarrow D\) be a morphism with \(D \in \mathcal {D}\). Then, as x is \(\mathcal {D}\)-monic, there exists a morphism \(y: B \rightarrow D\) such that \(yx = gf\). Now, by the weak pushout property there exists a morphism \(h:B'\rightarrow D\) such that \(hx'=g\) as required. \(\square \)
The interested reader may look at [49] and [60] for more properties of \(\mathcal {D}\)-monics and \(\omega \)-injectives. For other applications of these notions, look, for instance in [11, 20, 33].
2.2 Extriangulated Categories
In this section we put the background on extriangulated categories following [52, Section 2] where such categories were introduced. Let \(\mathcal {C}\) be an additive category and \(\mathbb {E}: \mathcal {C}^{op} \times \mathcal {C}\rightarrow \textsf{Ab}\) be an additive bifunctor.
Definition 2.5
For any \(A,C \in \mathcal {C}\), two pairs of composable morphisms in \(\mathcal {C}\)
are equivalent if there exists an isomorphism \(b: B \rightarrow B'\) such that

commutes. We denote the equivalence class of \(A\overset{x}{\longrightarrow }B\overset{y}{\longrightarrow }C\) by \([A\overset{x}{\longrightarrow }B\overset{y}{\longrightarrow }C]\), and by \(\mathcal {S}(C,A)\) we denote the class of all such equivalence classes.
Notation 2.6
For \(a:A \rightarrow A'\) write \(a_{*} = \mathbb {E}(-,a):\mathbb {E}(-,A) \rightarrow \mathbb {E}(-,A')\). Similarly, we write \(c^{*} = \mathbb {E}(c,-): \mathbb {E}(C',-) \rightarrow \mathbb {E}(C,-)\) for \(c:C \rightarrow C'\).
Definition 2.7
[52, Definitions 2.9, 2.10] An assignment \(\mathfrak {s}_{C, A}: \mathbb {E}(C, A) \rightarrow \mathcal {S}(C, A)\) for all \(C, A \in \mathcal {C}\) is an additive realisation of \(\mathbb {E}\) if it satisfies the following axioms.
-
(S1)
\(\mathfrak {s}(0) = [A \rightarrow A \oplus C \rightarrow C]\).
-
(S2)
\(\mathfrak {s}(\delta )\oplus \mathfrak {s}(\delta ') = \mathfrak {s}(\delta \oplus \delta ') \in \mathcal {S}(C \oplus C', A \oplus A')\) for \(\delta \in \mathbb {E}(C, A)\), \(\delta ' \in \mathbb {E}(C', A')\).
-
(S3)
For all \(\mathfrak {s}(\delta ) = [A\overset{x}{\longrightarrow }B\overset{y}{\longrightarrow }C] \) and \(\mathfrak {s}(\delta ) = [A'\overset{x'}{\longrightarrow }B'\overset{y'}{\longrightarrow }C'] \) such that \(a_{*}\delta = c^{*}\delta '\) for \(a: A \rightarrow A'\) and \(c: C \rightarrow C'\) (that is, \((a,c): \delta \rightarrow \delta '\) is a morphism of \(\mathbb {E}\)-extensions), there is a commutative diagram in \(\mathcal {C}\)
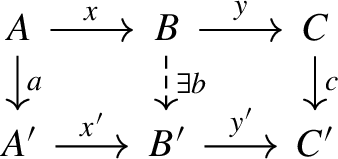
and in this case we say that the triple (a, b, c) realises the morphism of \(\mathbb {E}\)-extensions \((a,c): \delta \rightarrow \delta '\).
Notation 2.8
If \(\mathfrak {s}(\delta ) = [A\overset{x}{\longrightarrow }B\overset{y}{\longrightarrow }C]\) we may also write

and call this an extriangle. In this situation we also call x an \(\mathbb {E}\)-inflation and y an \(\mathbb {E}\)-deflation. We may also say that \(y:B \rightarrow C\) is the cone of x and \(x:A \rightarrow B\) is the co-cone of y.
Definition 2.9
[52, Definition 2.12] A triple \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is an extriangulated category if it satisfies the following conditions. In this case we call the pair \((\mathbb {E}, \mathfrak {s})\) an external triangulation of \(\mathcal {C}\) and \(\mathfrak {s}\) an \(\mathbb {E}\)-triangulation of \(\mathcal {C}\).
-
(ET1) \(\mathbb {E}: \mathcal {C}^{op} \times \mathcal {C}\rightarrow \textsf{Ab}\) is an additive bifunctor.
-
(ET2) \(\mathfrak {s}\) is an additive realisation of \(\mathbb {E}\).
-
(ET3) For all commutative diagrams with extriangles as rows
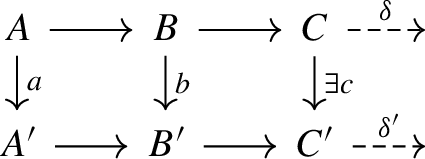
there exists \(c:C \rightarrow C'\) making the diagram commute and such that \((a,c): \delta \rightarrow \delta '\) is a morphism of extriangles.
-
(ET3)\(^{op}\) Dual to (ET3).
-
(ET4) For any pair of extriangles of the form
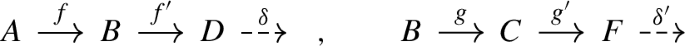
there exists a commutative diagram
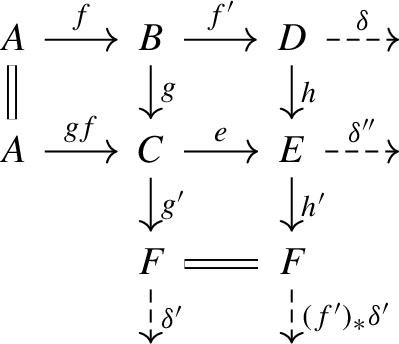
with columns and rows being extriangles such that \(h^{*}\delta ''= \delta \) and \(f_{*}\delta '' = (h')^{*} \delta '\) (that is, \((f,h'): \delta '' \rightarrow \delta '\) is a morphism of extriangles).
-
(ET4)\(^{op}\) Dual to (ET4).
For the rest of this section, let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category.
Remark 2.10
[52, Remark 2.18] Let \(\mathcal {X} \subseteq \mathcal {C}\) be a subcategory of \(\mathcal {C}\) that is closed under \(\mathbb {E}\)-extensions, that is, for all extriangles

the implication \(A, C \in \mathcal {X} \Rightarrow B \in \mathcal {X}\) holds. Then \((\mathcal {X}, \mathbb {E}|_{\mathcal {X}}, \mathfrak {s}|_{\mathcal {X}})\) is an extriangulated category.
Lemma 2.11
[52, Corollary 3.12] Let 
be an extriangle. Then there are long exact sequences

of functors and natural transformation in the functor categories \([\mathcal {C}^{\text {op}}, \textsf{Ab}]\) and \([\mathcal {C}, \textsf{Ab}]\) respectively. The maps \(\delta _\#\) and \(\delta ^\#\) are given at \(X \in \mathcal {C}\) by
Lemma 2.12
[48, Proposition 1.20] Let \(\delta \in \mathbb {E}(C, A)\) be an extriangle and \(a \in \mathcal {C}(A, A')\) a morphism. Then there exists a morphism b such that (a, b, 1) realises the morphism of extriangles \((a,1): \delta \rightarrow a_{*}\delta \)

and such that the sequence  is an extriangle.
is an extriangle.
Corollary 2.13
The left hand square in Diagram (1) is a weak pushout and weak pullback.
Proof
By Lemma 2.11, every \(\mathbb {E}\)-deflation of an extriangle is a weak cokernel of the \(\mathbb {E}\)-inflation and dually every \(\mathbb {E}\)-inflation is a weak kernel. The claim now follows from Lemma 2.12, since the weak pushout property is equivalent to \(\left[ \begin{array}{l} y \, b \end{array} \right] : A' \oplus B \rightarrow C\) being a weak cokernel of \(\left[ \begin{array}{l} -a \\ x \end{array} \right] : A \rightarrow A' \oplus B\). \(\square \)
Lemma 2.14
[52, Corollary 3.5] Let

be a morphism of extriangles. Then the following are equivalent
-
(a)
a factors through x;
-
(b)
\(a_*\delta = c^*\delta ' = 0\);
-
(c)
c factors through \(y'\).
Definition 2.15
Let \(\mathcal {C}=(\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category. An object \(P \in \mathcal {C}\) is \(\mathbb {E}\)-projective if \(\mathbb {E}(P, C) =0\) for all \(C \in C\). By \(\textsf{Proj}_{\mathbb {E}}\mathcal {C}\) we denote the subcategory of \(\mathbb {E}\)-projective objects. We say that \(\mathcal {C}\) has enough \(\mathbb {E}\)-projectives if for all \(C \in \mathcal {C}\) there exists an extriangle

with \(P \in \textsf{Proj}_{\mathbb {E}}\mathcal {C}\). The notions of \(\mathbb {E}\)-injectives and having enough \(\mathbb {E}\)-injectives are defined dually. The subcategory of \(\mathbb {E}\)-injective objects is denoted by \(\textsf{Inj}_{\mathbb {E}}\mathcal {C}\).
2.3 Right Triangulated Categories
We begin by recalling in full the definition of a right triangulated (or suspended) category first introduced in [41].
Definition 2.16
Let \(\mathcal {R}\) be an additive category and \(\Sigma : \mathcal {R} \rightarrow \mathcal {R}\) an endofunctor. A right triangulation of the pair \((\mathcal {R}, \Sigma )\) is a collection \(\Delta \) of sequences of the form

in \(\mathcal {R}\) that satisfy the following axioms.
-
(R1)
-
(i)
\(\Delta \) is closed under isomorphisms. That is, for every commutative diagram
in \(\mathcal {R}\) whose vertical arrows are isomorphisms, one row belongs to \(\Delta \) if and only if the other row also belongs to \(\Delta \).
-
(ii)
For every \(A \in \mathcal {R}\), the sequence
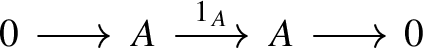
belongs to \(\Delta \).
-
(iii)
Every morphism \(x: A \rightarrow B \) in \(\mathcal {R}\) can be embedded into a sequence
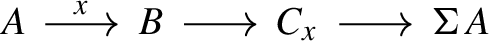
in \(\Delta \).
-
(i)
-
(R2)
If the sequence
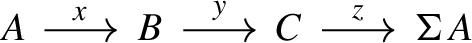
is in \(\Delta \) then so is the sequence
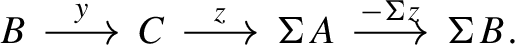
-
(R3)
Every commutative diagram
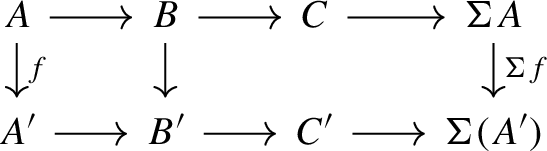
in \(\mathcal {R}\) whose rows belong to \(\Delta \) can be extended to a commutative diagram
-
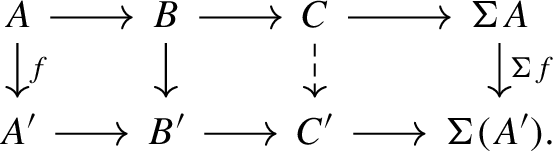
(R4)
Let

and
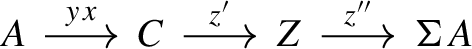
be sequences in \(\Delta \). Then there is a commutative diagram
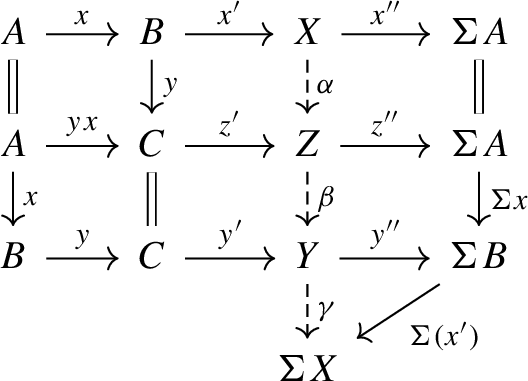
in \(\mathcal {R}\) such that the dotted column belongs to \(\Delta \).
If \(\Delta \) is a right triangulation of \((\mathcal {R}, \Sigma )\), then the triple \((\mathcal {R}, \Sigma , \Delta )\) is called a right triangulated category and the sequences in \(\Delta \) are called right triangles. Following [6], if the functor \(\Sigma \) is fully faithful and its image, \(\Sigma \mathcal {R}\), is closed under extensions we call \(\Sigma \) a right semi-equivalence and \(\mathcal {R}\) a right triangulated category with right semi-equivalence.
Definition 2.17
Let \((\mathcal {R}, \Sigma , \Delta )\) and \((\mathcal {R}', \Sigma ', \Delta ')\) be right triangulated categories. An additive functor \(F: \mathcal {R}\rightarrow \mathcal {R}'\) is a right triangle functor if
-
(a)
There is a natural isomorphism
 ;
; -
(b)
For all right triangles
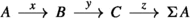 in \(\Delta \), the sequence
in \(\Delta \), the sequence 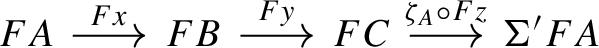
is in \(\Delta '\).
Remark 2.18
Let \(\mathcal {R}= (\mathcal {R}, \Sigma , \Delta )\) be a right triangulated category such that \(\Sigma \mathcal {R}\) is closed under extensions. Then the subcategory \(\Sigma \mathcal {R}\) naturally inherits the structure of a right triangulated category. Clearly, if \(\Sigma \) is a right semi-equivalence then \(\Sigma \mathcal {R}\) is also a right triangulated category with right semi-equivalence. We will see in Sect. 5 examples where \(\Sigma \mathcal {R}\) is a right triangulated category with right semi-equivalence but \(\mathcal {R}\) is not.
For homological properties of right triangulated categories we point the reader to [6].
We finish this subsection by noting that there are no finite right triangulated categories with right semi-equivalence that are not triangulated. This is one of the many ways to see that any additively finite (that is, the set of isomorphism classes of indecomposables in \(\mathcal {R}\) is finite) idempotent complete hom finite triangulated category admits no non-trivial (co-)t-structures. We refer to [5] for a discussion of such categories in the k-linear setting.
Lemma 2.19
Let \(\mathcal {R}= (\mathcal {R}, \Sigma , \Delta )\) be a hom finite right triangulated category with right semi-equivalence. Suppose that \(\mathcal {R}\) is additively finite, then \(\Sigma \) is an autoequivalence. In particular, \(\mathcal {R}= (\mathcal {R}, \Sigma , \Delta )\) is a triangulated category.
Proof
Let \(S=\{X_1, \dots , X_n\}\) be a set of isomorphism classes of indecomposable objects in \(\mathcal {R}\). Since \(\Sigma \) is additive, fully faithful and \(\mathcal {R}\) is idempotent complete, \(\Sigma \) acts as a permutation on the set S and we deduce that \(\Sigma ^m = 1_\mathcal {R}\) for some \(m \in \mathbb {N}\). \(\square \)
2.3.1 (Co-)stabilisation of a Right Triangulated Category
We recall the definitions of two triangulated categories associated to a right triangulated category: the stabilisation and costabilisation.
The stabilisation of a right triangulated category, \(\mathcal {R}=(\mathcal {R}, \Sigma , \Delta )\), consists of a pair \((\mathcal {S}(\mathcal {R}), s)\) where \(\mathcal {S}(\mathcal {R})\) is a triangulated category and \(s: \mathcal {R}\rightarrow \mathcal {S}(\mathcal {R})\) is a right triangle functor satisfying a universal property: For all right triangle functors \(F: \mathcal {R}\rightarrow \mathcal {T}\) with \(\mathcal {T}\) being a triangulated category, there exists a unique triangle functor \(F': \mathcal {S}(\mathcal {R})\rightarrow \mathcal {T}\) such that \(F's=F\)

Dually, the co-stabilisation of \(\mathcal {R}\) consists of a pair \((\mathcal {C}(\mathcal {R}), c)\) where \(\mathcal {C}(\mathcal {R})\) is a triangulated category and \(c:C(\mathcal {R}) \rightarrow \mathcal {R}\) is a right triangle functor satisfying a universal property: For all right triangle functors \(G:\mathcal {T}\rightarrow \mathcal {R}\) with \(\mathcal {T}\) being a triangulated category, there exists a unique triangle functor \(G':\mathcal {T}\rightarrow \mathcal {C}(\mathcal {R})\) such that \(G=cG'\).
The stabilisation and co-stablisation of a right triangulated category always exist. Since we will use it explicitly, we recall the construction of the stablisation from [12, Section 3.1] and [29]; see also [22]. For more information on the co-stabilisation, which may be constructed as the category of spectra, we refer to [24, Section 4.5-4.7]; see also [12, 38].
Let \(\mathcal {R}=(\mathcal {R}, \Sigma , \Delta )\) be a right triangulated category.
Definition 2.20
We define the additive category \(\mathcal {S}(\mathcal {R})\) as follows. The objects of \(\mathcal {S}(\mathcal {R})\) are pairs (A, n) with \(A \in \mathcal {R}\) and \(n \in \mathbb {Z}\). The spaces of morphisms are given by
There is an autoequivalence of \(\mathcal {S}(\mathcal {R})\) which is given on objects by \(\Sigma (A,n) = (A, n+1)\) and induced on morphisms by the natural map
for all \(k \le \textsf{min}\{m, n\}\). By abuse of notation, we denote this autoequivalence also by \(\Sigma \).
The functor \(s: \mathcal {R}\rightarrow \mathcal {S}(\mathcal {R})\) is given on objects by \(s(A) = (A, 0)\) and for a morphism \(f:A \rightarrow B\), \(s(f:A \rightarrow B)\) is the zero-representative of \(\mathcal {S}(\mathcal {R})((A,0), (B,0))\).
Triangles in \(\mathcal {S}(\mathcal {R})\) are given by sequences isomorphic to sequences of the form

such that there exists \(k \le \textsf{min}\{n, m, l\}\) such that

is a right triangle in \(\mathcal {R}\).
One may verify that \(s\Sigma \cong \Sigma s\) and that s is a right triangle functor.
Remark 2.21
We make some observations.
-
(a)
If the endofunctor \(\Sigma : \mathcal {R}\rightarrow \mathcal {R}\) is fully faithful, then the morphism spaces in \(\mathcal {S}(\mathcal {R})\) are neater
$$\begin{aligned} \mathcal {S}(\mathcal {R})\left[ (A, n), (B,m)\right] \cong \mathcal {R}(\Sigma ^{n-k}A, \Sigma ^{m-k} B), \; \forall k \le \textsf{min}\{n, m\}. \end{aligned}$$Further, in this case, \(s:\mathcal {R}\rightarrow \mathcal {S}(\mathcal {R})\) is fully faithful and \(\mathcal {S}(\mathcal {R})\) is the smallest triangulated category that contains \(\mathcal {R}\) as a full right triangulated subcategory.
-
(b)
If \(\Sigma :\mathcal {R}\rightarrow \mathcal {R}\) is a right semi-equivalence then the ‘there exists’ preceding Equation (2) can be replaced by ‘for all’.
-
(c)
If \(\Sigma \) is not dense, then every non-zero indecomposable object in \(\mathcal {S}(\mathcal {R})\setminus \mathcal {R}\) is isomorphic to an object of the form (A, n) with \(A \in (\mathcal {R}\setminus \Sigma \mathcal {R})\) and \(n <0\). Indeed, let \(X \in \mathcal {S}(\mathcal {R})\) be indecomposable, then by definition, \(X \cong (B,m)\) for some indecomposable \(B \in \mathcal {R}\) and \(m \in \mathbb {Z}\). If \(m \ge 0\) then \((B, m) \cong (\Sigma ^m B, 0)\) and \(X \in \mathcal {R}\), thus we may assume that \(m \le 0\). Now, if \(B \in \mathcal {R}\setminus \Sigma \mathcal {R}\) then we are done. Else, \(B = \Sigma B'\) for some \(B' \in \mathcal {R}\) and \(X \cong (B', m+1)\). The statement now follows by an inductive argument since this process must terminate in fewer than m steps by the above. We note that given a presentation \(X \cong (A,n)\) with \(A \in (\mathcal {R}\setminus \Sigma \mathcal {R})\) indecomposable and \(n <0\), then n is maximal, that is, there exists no \(B \in \mathcal {R}\) and \(m > n\) such that \(X \cong (B, m)\). Indeed, if this were the case, then we would have that \(A \cong \Sigma ^{m-n} B\), which is a contradiction.
Many categorical properties of \(\mathcal {S}(\mathcal {R})\) are inherited from \(\mathcal {R}\), for instance if \(\mathcal {R}\) has (co-)products then so does \(\mathcal {S}(\mathcal {R})\). The following properties will be useful for our work.
Lemma 2.22
Suppose that the endofunctor \(\Sigma : \mathcal {R}\rightarrow \mathcal {R}\) is fully faithful and that for all \(A, B \in \mathcal {R}\) we have that \(\mathcal {R}(A, \Sigma ^i B ) =0 \) for \(i>>0\). Then, for all \(X, Y \in \mathcal {S}(\mathcal {R})\) we have that \(\mathcal {S}(\mathcal {R})(X, \Sigma ^i Y) =0\) for all \(i>>0\).
Proof
Let \(X, Y \in \mathcal {S}(\mathcal {R})\) then there exists \(A, B \in \mathcal {R}\) and \(k >0\) such that \(\Sigma ^k X \cong A\) and \(\Sigma ^k Y \cong B\). Therefore, for \(i>>0\), we have that
\(\square \)
We call a right triangulated category satisfying the condition of the above Lemma 2.22bounded.
Lemma 2.23
Let \(\mathcal {R}=(\mathcal {R}, \Sigma , \Delta )\) be a right triangulated category with right semi-equivalence. Then \(\mathcal {R}\) is extension closed as a subcategory of \(\mathcal {S}(\mathcal {R})\).
Proof
Let

be a triangle in \(\mathcal {S}(\mathcal {R})\) with (A, n), (C, l) in \(\mathcal {R}\). We must show that \((B,m) \in \mathcal {R}\). We may assume that \(n = l = 0\) and it suffices to show that \((B, m) \cong (B', m')\) for some \(B' \in \mathcal {R}\) and \(m' \ge 0\).
For that purpose, suppose \(m<0\), then \(\textsf{min}\{m,n,l\} = m\) and, by definition, there is a right triangle in \(\mathcal {R}\)

As \(\Sigma : \mathcal {R}\rightarrow \mathcal {R}\) is a right semi-equivalence, we deduce that \(B \in \Sigma \mathcal {R}\) so that \(B = \Sigma B_1\) for some \(B_1 \in \mathcal {R}\). Then \((B, m) = (\Sigma B_1, m) \cong (B_1, m+1)\). By repeating this argument m times, we find a \(B'\) so that \((B, m) \cong (B', 0) \in \mathcal {R}\) as required. \(\square \)
Example 2.24
Let \(\mathcal {T}\) be a triangulated category and \(\mathcal {R}\subset \mathcal {T}\) a subcategory that is closed under positive shifts and extensions. Then \(\mathcal {R}\) is a right triangulated category with right semi-equivalence and \(\mathcal {S}(\mathcal {R})\cong \textsf{cosusp}_{\mathcal {T}}(\mathcal {R})\), the smallest subcategory of \(\mathcal {T}\) containing \(\mathcal {R}\) that is closed under negative shifts and extensions.
For more examples of the stabilisation of right triangulated categories, see [12, Section 3.1] and [41].
3 Right Triangulated Categories as Extriangulated Categories
The aim of this section is show that right triangulated categories have a natural extriangulated structure precisely when the shift functor is a right semi-equivalence. We also describe which extriangulated categories have a right triangulated structure. To do this, we begin by using relative homological algebra to define new extriangulated structures from existing ones (Sect. 3.1). We then show when these new extriangulations induce right triangulated structures on a quotient category (Sect. 3.2). With these tools in hand we complete the above aims in Sect. 3.3.
3.1 Extriangulated Structures Using Relative Homological Algebra
In this section we show how one can use relative homological algebra to construct new extriangulated structures and characterise when these exact structures have enough injectives/ projectives. The existence of these extriangulated structures also follows from [31, Proposition 3.17] for \(n=1\) but we give an alternative proof using relative notions. We begin with an easy lemma.
Lemma 3.1
Let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category, \(\mathcal {D}\) be a class of objects in \(\mathcal {C}\) and \(\delta \) be an extriangle. Then the following are equivalent
-
(a)
There exists representative of \(\mathfrak {s}(\delta )\), \(A\overset{x}{\longrightarrow }B\overset{y}{\longrightarrow }C\), such that x is \(\mathcal {D}\)-monic;
-
(b)
The \(\mathbb {E}\)-inflation of every representative of \(\mathfrak {s}(\delta )\) is \(\mathcal {D}\)-monic.
Proof
(a)\(\Rightarrow \)(b) follows from Lemma 2.4(c). (b)\(\Rightarrow \)(a) is obvious. \(\square \)
Proposition 3.2
Let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category and \(\mathcal {D}\) a class of objects in \(\mathcal {C}\). Consider the classes of extriangles for \(A, C \in \mathcal {C}\)

Then \((\mathbb {I}_\mathcal {D}, \mathfrak {s}|_{\mathbb {I}_\mathcal {D}}), (\mathbb {P}_\mathcal {D}, \mathfrak {s}|_{\mathbb {P}_\mathcal {D}})\) and \((\mathbb {D}_{\mathcal {D}}, \mathfrak {s}|_{\mathbb {D}_\mathcal {D}})\) all define external triangulations of \(\mathcal {C}\). Moreover,
Additionally, suppose that \(\mathcal {D}= \textsf{Add}(\mathcal {D})\) then the following hold.
-
(a)
If \(\mathcal {D}\) is covariantly finite and left \(\mathcal {D}\)-approximations are \(\mathbb {E}\)-inflations then \(\mathcal {D} = \textsf{Inj}_{\mathbb {I}_\mathcal {D}} \mathcal {C}\) and \(\mathcal {C}\) has enough \(\mathbb {I}_\mathcal {D}\)-injectives.
-
(b)
If \(\mathcal {D}\) is contravariantly finite and right \(\mathcal {D}\)-approximations are \(\mathbb {E}\)-deflations then \(\mathcal {D} = \textsf{Proj}_{\mathbb {P}_\mathcal {D}} \mathcal {C}\) and \(\mathcal {C}\) has enough \(\mathbb {P}_\mathcal {D}\)-projectives.
-
(c)
If \(\mathcal {D}\) is functorially finite, left (resp. right) \(\mathcal {D}\)-approximations are \(\mathbb {E}\)-inflations (resp. \(\mathbb {E}\)-deflations) and cones (resp. co-cones) of left (resp. right) \(\mathcal {D}\)-approximations are \(\mathcal {D}\)-epic (resp. \(\mathcal {D}\)-monic) then \(\mathcal {D} = \textsf{Inj}_{\mathbb {D}_\mathcal {D}}\mathcal {C}=\textsf{Proj}_{\mathbb {D}_\mathcal {D}}\mathcal {C}\) and \(\mathcal {C}\) has enough \(\mathbb {D}_\mathcal {D}\)-injectives and \(\mathbb {D}_\mathcal {D}\)-projectives.
Proof
We prove the statements for \(\mathbb {I}_\mathcal {D}\) whence the remaining claims follow from dual and combined arguments. Let \(\delta \in \mathbb {I}_\mathcal {D}(C', A)\), \(a \in \mathcal {C}( A, A')\) and \(c \in \mathcal {C}(C, C')\). By [31, Proposition 3.14] it is enough to show that \(a_{*} \delta \in \mathbb {I}_\mathcal {D}(C', A'), c^{*}\delta \in \mathbb {I}_\mathcal {D}(C, A)\) and \(\mathbb {I}_\mathcal {D}\)-inflations are closed under composition. The first follows from Corollary 2.13 and Lemma 2.4(c) and the third from Lemma 2.4(a). To show the second claim consider the morphism of extriangles \((1, c): c^{*}\delta \rightarrow \delta \)

We see that \(x' = bx \in \textsf{Mon}(\mathcal {D})\) and hence x is \(\mathcal {D}\)-monic by Lemma 2.4(b).
We verify the additional claims. By construction we have that the class of \(\mathbb {I}_\mathcal {D}\)-inflations, \(\omega \), is contained in the class of \(\mathcal {D}\)-monic morphisms. Thus
Now additionally suppose that \(\mathcal {D}= \textsf{Add}(\mathcal {D})\), \(\mathcal {D}\) is covariantly finite and left \(\mathcal {D}\)-approximations are \(\mathbb {E}\)-inflations. Then for every object \(I \in \textsf{Inj}_{\mathbb {I}_\mathcal {D}}\mathcal {C}\) there is an \(\mathbb {I}_\mathcal {D}\)-inflation \(i:I \rightarrow D\) with \(D \in \mathcal {D}\). We deduce that I is a direct summand of \(\mathcal {D}\) and we are done. \(\square \)
Notation 3.3
Let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category. For brevity, in the sequel we will say a subcategory \(\mathcal {D}\) of \(\mathcal {C}\) has property \((*)\) if \(\mathcal {D}= \textsf{Add}(\mathcal {D})\), \(\mathcal {D}\) is covariantly finite and all left \(\mathcal {D}\)-approximations are \(\mathbb {E}\)-inflations.
We note that one may view the Frobenius property [26, 28] of external triangulations of an idempotent complete category through the lens of relative homological algebra.
Corollary 3.4
An extriangulated category \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) is Frobenius if and only if there exists a functorially finite additive subcategory \(\mathcal {P}\) such that
-
(a)
All left \(\mathcal {P}\)-approximations are \(\mathbb {E}\)-inflations and all \(\mathbb {E}\)-inflations are \(\mathcal {P}\)-monic;
-
(b)
All right \(\mathcal {P}\)-approximations are \(\mathbb {E}\)-deflations and all \(\mathbb {E}\)-deflations are \(\mathcal {P}\)-epic.
In other words, \(\mathcal {P}= \textsf{Proj}_{\mathbb {D}_\mathcal {P}}\mathcal {C}= \textsf{Inj}_{\mathbb {D}_\mathcal {P}}\mathcal {C}\) and \(\mathbb {D}_\mathcal {P}= \mathbb {E}\).
3.2 Right Triangulated Stable Categories
We show how extriangulations can induce right triangulated structures on a quotient category. The construction is reminiscent of the triangulated structure of the stable category of a Frobenius exact category [26, 28].
Set-up: For the rest of this section, let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category and \(\mathcal {D}\subseteq \mathcal {C}\) be a subcategory satisfying property \((*)\). For each \(A \in \mathcal {C}\) we make a choice of extriangle

where \(i_A\) is a left \(\mathcal {D}\)-approximation of A. We also define \(\Sigma _D\) on morphisms: Let \(f: A \rightarrow B\). Then, as \(i_A\) is \(\mathcal {D}\)-monic, there exists \(\mathcal {D}(f): \mathcal {D}(A) \rightarrow \mathcal {D}(B)\) such that \(\mathcal {D}(f)i_A = i_B f\) and thus, by (ET3) there exists a morphism \(\Sigma _\mathcal {D}f: \Sigma _\mathcal {D}A \rightarrow \Sigma _\mathcal {D}B\) such that \((f, \Sigma _\mathcal {D}f ): \delta _A \rightarrow \delta _B\) is a morphism of extriangles

By \(\underline{\mathcal {C}}_\mathcal {D}\) we denote the stable category of \(\mathcal {C}\) by the ideal of morphisms factoring through objects of \(\mathcal {D}\).
The following lemma is similar to [52, Claim6.1].
Lemma 3.5
The construction above of \(\Sigma _\mathcal {D}\) defines an additive endofunctor \(\underline{\mathcal {C}}_\mathcal {D}\rightarrow \underline{\mathcal {C}}_\mathcal {D}\). Further, any other choice of extriangles \(\delta _A\) yields a naturally isomorphic endofunctor.
Proof
We keep the notation of the above paragraph. First we show that \(\Sigma _\mathcal {D}\) is well-defined on morphisms in \(\underline{\mathcal {C}}_\mathcal {D}\), that is, the construction of \(\Sigma _\mathcal {D}f\) is independent of the choices made of \(\mathcal {D}(f)\) and in (ET3). Indeed, let \(g: \Sigma _\mathcal {D}A \rightarrow \Sigma _\mathcal {D}B\) be any morphism such that \((f,g): \delta _A \rightarrow \delta _B\) is a morphism of extriangles. Then \(g^{*}\delta _B = f_{*}\delta _A = (\Sigma _\mathcal {D}f)^*\delta _B\) and therefore \((g-\Sigma _\mathcal {D}f)^*\delta _B =0\). By Lemma 2.14, \(g-\Sigma _\mathcal {D}f\) factors through \(p_B\) and hence \(\underline{g-\Sigma _\mathcal {D}f} =0\) in \(\underline{\mathcal {C}}_\mathcal {D}\).
Now suppose for all \(A \in \mathcal {C}\) we have another choice of extriangle

which then results in another endofunctor \(\Sigma _\mathcal {D}' : \underline{\mathcal {C}}_\mathcal {D}\rightarrow \underline{\mathcal {C}}_\mathcal {D}\). Then, since \(i_A\) is \(\mathcal {D}\)-monic, there exists \(s:\mathcal {D}(A) \rightarrow \mathcal {D}'(A)\) such that \(si_A = i'_A\). Then, by (ET3) there exists \(t_A =t:\Sigma _\mathcal {D}A \rightarrow \Sigma _\mathcal {D}' A\) such that \((1, t): \delta _A \rightarrow \delta '_A\) is a morphism of extriangles. Similarly, we obtain a morphism \(t'_A=t': \Sigma _\mathcal {D}' A \rightarrow \Sigma _\mathcal {D}A \) such that \((1, t'): \delta '_A \rightarrow \delta _A\) is a morphism of extriangles

We claim that \(\{t_A\}_{A \in \underline{\mathcal {C}}_\mathcal {D}}\) is an isomorphism of functors \(\Sigma _\mathcal {D}\rightarrow \Sigma _\mathcal {D}'\) with inverse given by \(\{t'_A\}_{A \in \underline{\mathcal {C}}_\mathcal {D}}\). The fact that the \(t_A\) are isomorphisms in \(\underline{\mathcal {C}}_\mathcal {D}\) follows from the observation that \((1, t't): \delta _A \rightarrow \delta _A\) is a morphism of extriangles and hence, by using a similar argument to the above, we see that \(\underline{t't} = \underline{1_{\Sigma _\mathcal {D}A}}\) in \(\underline{\mathcal {C}}_\mathcal {D}\). Dually, \(\underline{tt'} = \underline{1_{\Sigma _\mathcal {D}'A}}\).
It remains to verify that \(\{t_A\}_{A \in \underline{\mathcal {C}}_\mathcal {D}}\) is a natural transformation. Let \(f:A \rightarrow B\) we must show that \(\underline{t_B \Sigma _\mathcal {D}f} = \underline{\Sigma _\mathcal {D}'f t_A}\). This follows from the observation that the pairs \((f, ( t_B \Sigma _\mathcal {D}f))\) and \((f, (\Sigma _\mathcal {D}'f t_A))\) both define morphisms of extriangles \(\delta _A \rightarrow \delta '_B\). \(\square \)
Proposition 3.6
The stable category \(\underline{\mathcal {C}}_\mathcal {D}\) with the endofunctor \(\Sigma _\mathcal {D}\) admits a right triangulation given by the collection of all sequences isomorphic to sequences of the form

that fit into a commutative diagram in \(\mathcal {C}\)

Furthermore, \(\Sigma _\mathcal {D}\underline{\mathcal {C}}_\mathcal {D}\) is always closed under extensions and \(\Sigma _\mathcal {D}\) is fully faithful if and only if \(\mathcal {D} \subset \textsf{Proj}_{\mathbb {I}_\mathcal {D}} \mathcal {C}\).
Proof
The arguments of [6, Theorem 3.3] and [14, Theorem 3.1] may be recycled to the extriangulated setting. \(\square \)
We can precisely describe when \(\Sigma _\mathcal {D}\) is a right semi-equivalence.
Proposition 3.7
Suppose additionally that cones of left \(\mathcal {D}\)-approximations are \(\mathcal {D}\)-epic. Then the following hold.
-
(a)
\(\mathbb {I}_\mathcal {D}= \mathbb {D}_\mathcal {D}\).
-
(b)
\(\underline{\mathcal {C}}_\mathcal {D}\) is a right triangulated category with right semi-equivalence.
-
(c)
For all \(A, C \in \mathcal {C}\) there is a functorial isomorphism of abelian groups
$$\begin{aligned} F = F_{C,A}: \underline{\mathcal {C}}_\mathcal {D}(C, \Sigma _\mathcal {D}A )&\overset{\cong }{\longrightarrow }\ \mathbb {D}_\mathcal {D}(C, A) \\ \underline{f}&\longmapsto f^{*}\delta _A. \end{aligned}$$
Proof
Claims (a) and (b) follow directly from Propositions 3.2 and 3.6. It remains to show (c):
F is well-defined: We must check that if \(\underline{f} = \underline{g} \in \underline{\mathcal {C}}_\mathcal {D}(C, \Sigma _\mathcal {D}A)\) then \(f^*\delta _A = g^*\delta _A\). Indeed, in this case, \(\underline{f-g} =0\) and, since \(p_A\) is \(\mathcal {D}\)-epic by part (a), \(f-g\) factors through \(p_A\). Now, by Lemma 2.14, \((f-g)^*\delta _A =0\) and we are done. Note that this also shows the injectivity of F, since \(f^* \delta _A = 0\) implies that f factors through \(p_A\) and thus \(\underline{f} =0\).
F is bijective: It remains to show that F is surjective. Let \(\gamma \in \mathbb {D}_\mathcal {D}(C, A)\) be realised by  . Then, since x is \(\mathcal {D}\)-monic there exists \(g:B \rightarrow \mathcal {D}(A)\) such that \(gx = i_A\). By (ET3), there then exists \(f: C \rightarrow \Sigma _\mathcal {D}A\) such that \((1, f): \gamma \rightarrow \delta _A\) is a morphism of extriangles. In other words, \(\gamma = f^{*}\delta _A =:F(\underline{f})\).
. Then, since x is \(\mathcal {D}\)-monic there exists \(g:B \rightarrow \mathcal {D}(A)\) such that \(gx = i_A\). By (ET3), there then exists \(f: C \rightarrow \Sigma _\mathcal {D}A\) such that \((1, f): \gamma \rightarrow \delta _A\) is a morphism of extriangles. In other words, \(\gamma = f^{*}\delta _A =:F(\underline{f})\).

F is a homomorphism of abelian groups: This is straightforward:
Functorality in the first argument: Let \(\underline{c} \in \mathcal {C}(C,C')\). Then for all \(\underline{f} \in \underline{\mathcal {C}}_\mathcal {D}(C', \Sigma _A)\)
which proves the claim.
Functorality in the second argument: Let \(\underline{\alpha } \in \underline{\mathcal {C}}_\mathcal {D}( A, A')\) and set \(\Sigma _\mathcal {D}\underline{\alpha } = \underline{a} \in \underline{\mathcal {C}}_\mathcal {D}(\Sigma _\mathcal {D}A, \Sigma _\mathcal {D}A')\). Then for all \(\underline{f} \in \underline{\mathcal {C}}_\mathcal {D}(C, \Sigma _\mathcal {D}A)\)
where the last equality in the second line follows from the definition of \(\Sigma _\mathcal {D}\). \(\square \)
In light of Corollary 3.4, extriangulated categories \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) such that the injective stable category \(\underline{C}_{\textsf{Inj} \mathbb {E}}\) is a right triangulated category with right semi-equivalence have a ‘one-sided Frobenius’ property: There are enough injectives and each injective object is projective. This imbalance of projectives and injectives and also Lemma 2.19 indicate that we must look in extriangulated categories with infinitely many objects for examples of quotients that are right triangulated with right semi-equivalence.
Example 3.8
-
(a)
Let Q be the infinite quiver
$$\begin{aligned} 1 \leftarrow 2 \leftarrow 3 \leftarrow \dots \end{aligned}$$and consider the category \(\mathcal {A}= \text {mod}KQ / \textsf{rad}^m\) for some \(m>1\). \(\mathcal {A}\) is an abelian category and with its maximal exact structure it is an extriangulated category. Observe that \(\mathcal {A}\) has enough injectives and that each injective object is projective. Indeed, \(I_r = P_{r+m-1}\). But not every projective object is injective, for instance \(P_1 = S_1\) is not injective. Thus, by Theorem 3.6, the quotient category \(\underline{\mathcal {A}}_{\textsf{Inj}\mathcal {A}}\) is a right triangulated category with semi-equivalence with the shift given by the co-syzygy functor.
-
(b)
Let \(\mathcal {C}= (\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category and let \((\mathcal {U}, \mathcal {V})\) be a cotorsion pair in \(\mathcal {C}\) [52, Definition4.1]. It is easily verified that \(\mathcal {V}\) satisfies property \((*)\). Thus \(\underline{\mathcal {C}}_\mathcal {V}\) is a right triangulated category. We will investigate examples of this flavour for the case of Frobenius extriangulated categories further in Sect. 5. Let us note that the class of subcategories satisfying property \((*)\) is more general than the class of cotorsion pairs, since the subcategories giving cotorsion pairs must be closed under extensions.
-
(c)
Let \(\mathcal {T}\) be a compactly generated triangulated category. Recall that a subcategory \(\mathcal {X}\) of \(\mathcal {T}\) is definable if there is a class of morphisms \(\omega \) between compact objects in \(\mathcal {T}\) such that \(\mathcal {X}= \textsf{Inj}(\omega )\) [34, Section 4.1]; where it was also shown that every definable category admits left approximations. Thus, since in a triangulated category every morphism is an \(\mathbb {E}\)-inflation, it follows that \(\underline{\mathcal {T}}_\mathcal {X}\) is a right triangulated category.
The author would be interested to know if is possible to classify when the examples in (b) and (c) that result in right triangulated categories with right semi-equivalence.
3.3 Right Triangulated Extriangulated Categories
We characterise right triangulated categories as extriangulated categories. We begin with some terminology and a useful lemma.
Definition 3.9
Let \((\mathcal {R}, \Sigma , \Delta )\) be a right triangulated category. We say that the right triangulation \(\Delta \) induces an extriangulated structure on \(\mathcal {R}\) if there exists an external triangluation \((\mathbb {E}, \mathfrak {s})\) of \(\mathcal {R}\) such that for all right triangles \(A\overset{x}{\longrightarrow }B\overset{y}{\longrightarrow }C \overset{z}{\longrightarrow }\ \Sigma A\), there is an extriangle \(A\overset{x}{\longrightarrow }B\overset{y}{\longrightarrow }C \overset{\delta }{\dashrightarrow }\).
Lemma 3.10
[52, Proposition 3.30] Let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category and \(\mathcal {D}\subseteq \textsf{Proj}_\mathbb {E}(\mathcal {C}) \cap \textsf{Inj}_\mathbb {E}(\mathcal {C})\) be a full, additive, replete subcategory. Then the stable category \(\underline{\mathcal {C}}_\mathcal {D}\) inherits an external triangulation, \((\underline{\mathbb {E}}, \underline{\mathfrak {s}})\), given by
-
(a)
\(\underline{\mathbb {E}}(C,A) = \mathbb {E}(C, A)\) for all \(A, C \in \mathcal {C}\);
-
(b)
\(\underline{\mathbb {E}}(\underline{c}, \underline{a}) = \mathbb {E}(c, a)\) for all \(a \in \mathcal {C}(A, A')\), \(c \in \mathcal {C}(C', C)\);
-
(c)
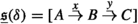 where
where  for all extriangles \(\delta \).
for all extriangles \(\delta \).
Example 3.11
We give two important classes of examples.
-
(a)
Let \(\mathcal {T}\) be a triangulated category. Then the triangulation of \(\mathcal {T}\) is a right triangulation which induces an extriangulated structure on \(\mathcal {T}\). See [52, Section 3.3]. This was a motivating example for the introduction of extriangulated categories.
-
(b)
Let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category and \(\mathcal {D}\subset \mathcal {C}\) be a subcategory satisfying property \((*)\) and such that all cones of left \(\mathcal {D}\)-approximations are \(\mathcal {D}\)-epic. By Proposition 3.2 we have that \(\mathcal {D}\subseteq \textsf{Proj}_{\mathbb {D}_\mathcal {D}} (\mathcal {C}) \cap \textsf{Inj}_{\mathbb {D}_\mathcal {D}} (\mathcal {C})\) and it follows from Proposition 3.7(c) that the right triangulated structure on \(\underline{\mathcal {C}}_\mathcal {D}\) of Proposition 3.6 coincides with the extriangulated structure of Lemma 3.10 induced by the external triangulation \((\mathbb {D}_\mathcal {D}, \mathfrak {s}|_{\mathbb {D}_\mathcal {D}})\). In other words, the right triangulation of \(\underline{\mathcal {C}}_\mathcal {D}\) (with right semi-equivalence) induces an extriangulation on \(\underline{\mathcal {C}}_\mathcal {D}\). Let us note that this could also be deduced from a combination of Lemma 2.23, Remark 2.10 and the above Example.
We may now state and prove the main result of this section.
Theorem 3.12
Let \((\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category. Then the following are equivalent
-
(a)
There exists a fully faithful additive endofunctor \(\Sigma : \mathcal {C}\rightarrow \mathcal {C}\) such that \(\mathbb {E}(-, ?) \cong \mathcal {C}(-, \Sigma ?)\) and that the image \(\Sigma \mathcal {C}\) is closed under \(\mathbb {E}\)-extensions;
-
(b)
\(\textsf{Inj}_\mathbb {E}(\mathcal {C}) = \{0 \}\) and there are enough \(\mathbb {E}\)-injectives;
-
(c)
There is a right triangulation of \(\mathcal {C}\) that induces the extriangulated structure \((\mathbb {E}, \mathfrak {s})\).
Proof
(a)\(\Rightarrow \)(b): We claim that, for each \(A \in \mathcal {C}\), the morphism \(1_{\Sigma A} \in \mathcal {C}(\Sigma A, \Sigma A) \cong \mathbb {E}(A, \Sigma A)\) is realised by the sequence \([A \rightarrow 0 \rightarrow \Sigma A]\). Indeed, we may use a similar argument to that of [52, Lemma3.21]: Let  , then by Lemma 2.11 there is a long exact sequence in \([\mathcal {C}^{\text {op}}, \textsf{Ab}]\)
, then by Lemma 2.11 there is a long exact sequence in \([\mathcal {C}^{\text {op}}, \textsf{Ab}]\)

It follows that \( y=0\) and \(\Sigma x=0\). Thus \(x=0\) since \(\Sigma \) is faithful. Now the exactness of \(0 \rightarrow \mathcal {C}(-,E) \rightarrow 0\) implies that \(E \cong 0\). Thus, if I is an \(\mathbb {E}\)-injective object then it is a direct summand of 0 and so \(I=0\).
(b)\(\Rightarrow \)(a),(c): In this case, the subcategory \(\{0\}\) satisfies \(\mathbb {E}= \mathbb {I}_{\{0\}}=\mathbb {D}_{\{0\}}\). Thus the stable category \(\underline{\mathcal {C}}_{\{0\}} \cong \mathcal {C}\) has a right triangulated structure with right semi-equivalence by Propositions 3.6 and 3.7 with shift functor given by \(\Sigma X= \Sigma _{\{0\}} X := \textsf{cone}(X \rightarrow 0)\). The claims follow from Example 3.11(b). In particular, by Proposition 3.7(c) there is a functorial isomorphism
(c)\(\Rightarrow \)(b): By the axiom (R3)(iii), for all \(A \in \mathcal {C}\), the morphism \(A \rightarrow 0\) is the first morphism in a right triangle. Thus, by assumption, \(A \rightarrow 0\) is an \(\mathbb {E}\)-inflation and the claim follows. \(\square \)
As a direct consequence, we see that, in general, right triangulated categories do not have a natural extriangulated structure.
Corollary 3.13
Let \((\mathcal {R}, \Sigma , \Delta )\) be a right triangulated category. Then \(\Delta \) induces an extriangulated structure on \(\mathcal {R}\) if and only if \(\Sigma \) is a right semi-equivalence.
Remark 3.14
The concept of negative (first) extensions of an extriangulated category has been recently introduced and studied [1, 23]. For a triangulated category \(\mathcal {T}\) one may take \(\mathbb {E}^{-1}(-,?) = \mathcal {T}(-, \Sigma ^{-1} ?)\) as a negative first extension. Since by Lemma 2.23 a right triangulated category with right semi-equivalence \(\mathcal {R}\) is an extension closed subcategory of the triangulated category \(\mathcal {S}(\mathcal {R})\) there is a natural first negative extension structure on \(\mathcal {R}\) given by \(\mathbb {E}^{-1}(C,A) := \mathcal {S}(\mathcal {R})(C, \Sigma ^{-1}A) \cong \mathcal {R}(\Sigma C, A)\) for all \(A, C \in \mathcal {R}\).
4 Aisles and Co-aisles
In this section, we show that the language of extriangulated categories allows us, under some assumptions, to give an intrinsic characterisation of which right triangulated categories with right semi-equivalence occur as (co)-aisles of (co-)t-structures in its stabilisation. Let \(\mathcal {R}= (\mathcal {R}, \Sigma , \Delta )\) be a right triangulated category with right semi-equivalence that is not triangulated (i.e. \(\Sigma \) is not dense). We add this final assumption as many statements are trivial when \(\mathcal {R}\) is triangulated and this allows us to freely use Remark 2.21(c).
4.1 Torsion Pairs
We begin by recalling some important definitions.
Definition 4.1
Let \(\mathcal {C}= (\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be an extriangulated category. A pair of additive subcategories, \((\mathcal {U}, \mathcal {V})\), of \(\mathcal {C}\) is a torsion pair in \(\mathcal {C}\) if
-
(a)
\(\mathcal {C}(\mathcal {U}, \mathcal {V}) = 0\);
-
(b)
For all \(C \in \mathcal {C}\) there exists an extriangle

with \(U \in \mathcal {U}\) and \(V \in \mathcal {V}\).
If \(\mathcal {C}\) is a triangulated category (viewed naturally as an extriangulated category) with shift functor \(\Sigma \), a torsion pair in \(\mathcal {C}\), \((\mathcal {U}, \mathcal {V})\), is a t-structure [9] (resp. co-t-structure [15, 56]) if \(\Sigma \mathcal {U} \subseteq \mathcal {U}\) (resp. \(\Sigma ^{-1} \mathcal {U} \subseteq \mathcal {U}\)) with heart \(\mathcal {H} = \mathcal {U} \cap \Sigma \mathcal {V}\) (resp. co-heart \(\mathcal {M} = \mathcal {U} \cap \Sigma ^{-1} \mathcal {V}\)). We call the subcategory \(\mathcal {U}\) the aisle of the (co-)t-structure and \(\mathcal {V}\) the co-aisle. A (co-)t-structure is bounded if the equalities \(\mathcal {C}= \bigcup _{n \in \mathbb {Z}} \Sigma ^n \mathcal {U}= \bigcup _{m \in \mathbb {Z}} \Sigma ^m \mathcal {V}\) hold.
The reader should be aware that the terminology and notation of torsion pairs and (co-)t-structures in a triangulated category varies, often by a shift, throughout the literature and that co-t-structures were introduced under the name ‘weight structures’ in [15].
Remark 4.2
Let \((\mathcal {U}, \mathcal {V})\) be a torsion pair in \(\mathcal {C}= (\mathcal {C}, \mathbb {E}, \mathfrak {s})\). Then it follows quickly from the definition that the following properties hold.
-
(a)
\(\mathcal {U}\), \(\mathcal {V}\) are closed under extensions.
-
(b)
\(\mathcal {U}= \{ A \in \mathcal {C}\mid \mathcal {C}(A, \mathcal {V}) =0\}\) and \(\mathcal {V}= \{A \in \mathcal {C}\mid \mathcal {C}(\mathcal {U}, A ) =0\}\).
-
(c)
The morphism u (resp. v) in the extriangle (5) is a right \(\mathcal {U}\) (resp. left \(\mathcal {V}\)) approximation of C.
Before we proceed, let us compare the above definition of a torsion pair in \(\mathcal {R}\) with other notions appearing in the literature:
-
(a)
A torsion pair \((\mathcal {U}, \mathcal {V})\) in \(\mathcal {R}\) is a right torsion pair [47] if \(\Sigma \) preserves \(\mathcal {V}\)-monics.
-
(b)
When \(\mathcal {R}\) is equipped with a negative first extension structure, \(\mathbb {E}^{-1}\), (see Remark 3.14) a torsion pair \((\mathcal {U}, \mathcal {V})\) in \(\mathcal {R}\) is an \(\mathfrak {s}\)-torsion pair [1] if \(\mathbb {E}^{-1}(\mathcal {U}, \mathcal {V}) =0\). In this case the extriangle (5) is essentially unique and assigments \(C \mapsto U\) and \(C \mapsto V\) are functorial [1, Proposition 3.7].
The next lemma shows that right torsion pairs and \(\mathfrak {s}\)-torsion pairs in \(\mathcal {R}\) coincide (when we equip \(\mathcal {R}\) with the natural first negative extension structure \(\mathbb {E}^{-1}(-,?) = \mathcal {S}(\mathcal {R})( -, \Sigma ^{-1} ?)\)) and that such torsion pairs remind us of t-structures; which are precisely the \(\mathfrak {s}\)-torsion pairs in a triangulated category. For a class of objects \(\mathcal {X}\) in \(\mathcal {R}\), by \(\Sigma ^{-1}\mathcal {X}\) we denote the class of objects \(\{ X \in \mathcal {R}\mid \Sigma X \in \mathcal {X}\}\).
Lemma 4.3
Let \((\mathcal {U}, \mathcal {V})\) be a torsion pair in \(\mathcal {R}\). Then the following are equivalent
-
(a)
\(\Sigma \mathcal {U}\subseteq \mathcal {U}\);
-
(b)
\(\Sigma ^{-1}\mathcal {V}\subseteq \mathcal {V}\);
-
(c)
\(\mathcal {R}( \Sigma \mathcal {U}, \mathcal {V})=0\);
-
(d)
\(\Sigma \) preserves \(\mathcal {V}\)-monics.
Proof
(a)\(\Rightarrow \)(b): Suppose that \(\Sigma \mathcal {U}\subseteq \mathcal {U}\) and let \(Y \in \Sigma ^{-1}\mathcal {V}\). Then there is a right triangle

with \(U \in \mathcal {U}\) and \(V \in \mathcal {V}\). Consider the morphism \(\Sigma u : \Sigma U \rightarrow \Sigma Y\). By assumption, \(\Sigma U \in \mathcal {U}\) and \(\Sigma Y \in \mathcal {V}\); thus, \(\Sigma u =0\). Since \(\Sigma \) is faithful, \(u =0\) and we deduce that Y is a direct summand of \(V \in \mathcal {V}\).
(b)\(\Rightarrow \)(a): Let \(X \in \mathcal {U}\), then there is a right triangle

with \(U \in \mathcal {U}\) and \(V \in \mathcal {V}\). Then, as \(\Sigma \mathcal {R}\) is closed under extensions, we have that \(V \in \Sigma \mathcal {R}\). Thus there exists \(V' \in \Sigma ^{-1} \mathcal {V}\subseteq \mathcal {V}\) such that \(\Sigma V' = V\). Moreover, there is a right triangle of the form

where \(\Sigma v' = - v\). Since \(\mathcal {U}\) is closed under extensions, we deduce that \(V' \in \mathcal {U}\). Together, we have that \(V' \in \mathcal {U}\cap \mathcal {V}= \{0\}\). Thus, \(V = 0\), \(v=0\) and \(\Sigma X\) is a direct summand of \(U \in \mathcal {U}\).
(a)\(\Rightarrow \)(c): Follows from the fact that \(\mathcal {R}(\mathcal {U}, \mathcal {V})=0\).
(c)\(\Rightarrow \)(d): Let \(f:A \rightarrow B\) be a \(\mathcal {V}\)-monic morphism. There are right triangles

and

with \(U, U' \in \mathcal {U}\) and \(V, V' \in V\). Then, as f is \(\mathcal {V}\)-monic, there exists \(g:B \rightarrow V\) such that \(gf=v\). Since \(\mathcal {R}(\Sigma \mathcal {U}, \mathcal {V}) =0\) there exists \(a: \Sigma U \rightarrow U'\) such that \(\Sigma u = u' a\). Thus, by the axiom (R3) = (ET3) there exists \(c: \Sigma V \rightarrow V'\) such that \(c (\Sigma v )= v'\)

Thus
This finishes the proof since \(v'\) is a left \(\mathcal {V}\)-approximation of \(\Sigma A\) and so all morphisms from \(\Sigma A\) to \(\mathcal {V}\) factor through \(v'\).
(d)\(\Rightarrow \)(a). Let \(U \in \mathcal {U}\). Then, since \(\mathcal {R}(U, \mathcal {V})=0\) we have that \(U \rightarrow 0\) is \(\mathcal {V}\)-monic. Thus, by assumption \(\Sigma U \rightarrow 0\) is also \(\mathcal {V}\)-monic from which we deduce that \(\Sigma U \in \mathcal {U}\).
\(\square \)
4.2 Co-asiles of Co-t-Structures
The next lemma justifies why we will look to describe \(\mathcal {R}\) as a (co-)aisle in \(\mathcal {S}(\mathcal {R})\).
Lemma 4.4
Let \(\mathcal {T}\) be a triangulated category, \((\mathcal {V}, \mathcal {W})\) (resp. \((\mathcal {U}, \mathcal {V})\)) be a t-structure (resp. co-t-structure) in \(\mathcal {T}\) and \(\mathcal {S}:= \textsf{cosusp}_\mathcal {T}\mathcal {V} \cong \mathcal {S}(\mathcal {V})\). Then \((\mathcal {V}, \mathcal {W} \cap \mathcal {S})\) (resp. \((\mathcal {U} \cap \mathcal {S}, \mathcal {V})\)) is a t-structure (resp. co-t-structure) in \(\mathcal {S}\).
Proof
We prove the t-structure case, whence statement for co-t-structures will follow dually. Let \((\mathcal {V}, \mathcal {W})\) be a t-structure in \(\mathcal {T}\) and set \(\mathcal {S}:= \textsf{cosusp}_\mathcal {T}\mathcal {V} \cong \mathcal {S}(\mathcal {V})\). Clearly, \(\mathcal {S}(\mathcal {V}, \mathcal {W} \cap \mathcal {S})=0\) and \(\Sigma \mathcal {V} \subset \mathcal {V}\). Thus it remains to show that \(\mathcal {S} = \mathcal {V} *(\mathcal {W} \cap \mathcal {S})\). Since \(\mathcal {V}, (\mathcal {W} \cap \mathcal {S}) \subset \mathcal {S}\) and \(\mathcal {S}\) is closed under extensions, \( \mathcal {V} *(\mathcal {W} \cap \mathcal {S}) \subset \mathcal {S}\). To show the converse, let \(A \in \mathcal {S}\) then there exists a triangle in \(\mathcal {T}\)

with \(V \in \mathcal {V}\) and \(W \in \mathcal {W}\). Thus \(W \in \mathcal {S} *\Sigma \mathcal {V} \subset \mathcal {S} *\mathcal {S} \subset \mathcal {S}\). \(\square \)
We also note that the boundedness of right triangulated categories (Lemma 2.22) relates to the boundedness of (co-)t-structures.
Lemma 4.5
Suppose that \(\mathcal {R}\) is the co-aisle of a co-t-structure, \((\mathcal {U}, \mathcal {R})\) in \(\mathcal {S}(\mathcal {R})\). If \(\mathcal {R}\) is bounded then the co-t-structure \((\mathcal {U}, \mathcal {R})\) is bounded. A dual statement holds for a t-structure \((\mathcal {R}, \mathcal {V})\) in \(\mathcal {S}(\mathcal {R})\).
Proof
Let \((\mathcal {U}, \mathcal {R})\) be a co-t-structure in \(\mathcal {S}(\mathcal {R})\). By construction of \(\mathcal {S}(\mathcal {R})\), the equality \(\mathcal {S}(\mathcal {R}) = \bigcup _{n \in \mathbb {Z}} \Sigma ^n \mathcal {R}\) holds. It remains to verify that \(\mathcal {S}(\mathcal {R}) = \bigcup _{m \in \mathbb {Z}} \Sigma ^m \mathcal {U}\). Observe that since \(\mathcal {R}\) is bounded, in light of Lemma 2.22, for all \(X \in \mathcal {S}(\mathcal {R})\) we have that \(\mathcal {S}(\mathcal {R})(\mathcal {R}, \Sigma ^i X) =0\) for \(i>>0\). Thus, by Remark 4.2, \(\Sigma ^iX \in \mathcal {V}\) for \(i>>0\); whence the claim follows. \(\square \)
Before we give our characterisations of \(\mathcal {R}\) as the co-aisle of a co-t-structure, we make some comments. Note, by Proposition 3.7, the \(\mathbb {E}\)-projectives of \(\mathcal {R}\) are precisely the objects \(P \in \mathcal {R}\) satisfying \(\mathcal {R}(P, \Sigma -) = 0\). Recall from [63] that a subcategory \(\mathcal {X} = \textsf{add}\mathcal {X}\) of a triangulated category \(\mathcal {T}\) is silting if \(\mathcal {T}(\mathcal {X}, \Sigma ^{>0} \mathcal {X}) = 0\) and \(\mathcal {T} = \textsf{thick}\mathcal {X}\), the smallest triangulated subcategory of \(\mathcal {T}\) containing \(\mathcal {X}\) that is closed under direct summands. We are now ready to give characterisations of \(\mathcal {R}\) as the co-aisle of a co-t-structure in \(\mathcal {S}(\mathcal {R})\) in terms of torsion pairs, \(\mathbb {E}\)-projectives of \(\mathcal {R}\) and silting subcategories.
Theorem 4.6
The following are equivalent
-
(a)
\(\mathcal {R}\) is the co-aisle of a co-t-structure \((\mathcal {U}, \mathcal {R})\) in \(\mathcal {S}(\mathcal {R})\);
-
(b)
\(\mathcal {R}\) has enough \(\mathbb {E}\)-projectives;
-
(c)
There is a torsion pair \((\textsf{Proj}_{\mathbb {E}} \mathcal {R}, \Sigma \mathcal {R})\) in \(\mathcal {R}\).
Moreover, if \(\mathcal {R}\) is bounded then the above conditions are also equivalent to
-
(d)
\(\textsf{Proj}_{\mathbb {E}}\mathcal {R}\) is a silting subcategory of \(\mathcal {S}(\mathcal {R})\).
Proof
(a)\(\Rightarrow \)(b): Suppose there is a co-t-structure \((\mathcal {U}, \mathcal {R})\) in \(\mathcal {S}(\mathcal {R})\). We must show that for all \(X \in \mathcal {R}\) there is a right triangle
in \(\mathcal {R}\) with \(P \in \textsf{Proj}\mathcal {R}\). Since \((\mathcal {U}, \mathcal {R})\) is a co-t-structure in \(\mathcal {S}(\mathcal {R})\) there is a triangle in \(\mathcal {S}(\mathcal {R})\)
with \(U \in \mathcal {U}\), \(R \in \mathcal {R}\). By rotating we obtain the triangle
We claim that \(\Sigma U \in \textsf{Proj}_{\mathbb {E}}\mathcal {R}\). The fact that \(\Sigma U \in \mathcal {R}\) follows from this triangle since \(\mathcal {R}\) is closed under extensions in \(\mathcal {S}(\mathcal {R})\) by Lemma 2.23. It remains to verify that \(\Sigma U\) is \(\mathbb {E}\)-projective in \(\mathcal {R}\), that is \(\mathcal {R}(\Sigma U, \Sigma \mathcal {R})=0\):
where we have the first equality from the properties of co-t-structures.
(b)\(\Rightarrow \)(c): Let \(X \in \mathcal {R}\). By assumption there is a right triangle \(R \rightarrow P \rightarrow X \rightarrow \Sigma R\) in \(\mathcal {R}\) with \(P \in \textsf{Proj}_{\mathbb {E}}\mathcal {R}\). We rotate this to the right triangle
whence the claim follows as \(\mathcal {R}(P, \Sigma \mathcal {R})=0\).
(c)\(\Rightarrow \)(a): We use a similar argument to [30, Theorem 3.11]. Suppose that there is a torsion pair \((\textsf{Proj}_{\mathbb {E}}\mathcal {R}, \Sigma \mathcal {R})\) in \(\mathcal {R}\) and set \(\mathcal {P}:= \textsf{Proj}_{\mathbb {E}}\mathcal {R}\) and \(\mathcal {U}:= \{Y \in \mathcal {S}(\mathcal {R})\mid \mathcal {S}(\mathcal {R})(Y, \mathcal {R}) =0\}\). Let \(0\ne X \in \mathcal {S}(\mathcal {R})\), we must show that there is a triangle
in \(\mathcal {S}(\mathcal {R})\) with \(U \in \mathcal {U}\) and \(R \in \mathcal {R}\). It is enough to verify this for X being indecomposable. If \(X \in \mathcal {R}\) then we may simply take the triangle \(0 \rightarrow X \rightarrow X \rightarrow 0\). If \(X \in \mathcal {S}(\mathcal {R})\setminus \mathcal {R}\) then by Remark 2.21(c), there exists \(A \in \mathcal {R}\setminus \Sigma R\) and \(n<0\) such that \(X \cong (A, n) \cong \Sigma ^n A \).
We proceed by an inductive argument on n. By assumption, there is a right triangle in \(\mathcal {R}\)
with \(P \in \mathcal {P}\) and \(R \in \mathcal {R}\). This rotates to a triangle
in \(\mathcal {S}(\mathcal {R})\). Let us show that \(\Sigma ^n P \in \mathcal {U}\):
since \(\mathcal {R}(P, \Sigma \mathcal {R}) =0\) and \(n < 0\). For \(n=-1\), the base case, we have that \(\Sigma ^{n+1}R = R \in \mathcal {R}\) the triangle (6) suffices as \(\Sigma ^{-1} P \in \mathcal {U}\). For \(n<-1\), by the induction hypothesis, there is a triangle in \(\mathcal {S}(\mathcal {R})\)
with \(U \in \mathcal {U}\) and \(V \in \mathcal {R}\). We apply (ET4)\(^{\text {op}}\) to this triangle and triangle (6) to obtain

and claim that the triangle \(E \rightarrow \Sigma ^n A \rightarrow V \rightarrow \Sigma E\) satisfies the required conditions. Since \(V \in \mathcal {R}\) by construction, we only have to show that \(E \in \mathcal {U}\). We have already seen above that \(\Sigma ^n P \in \mathcal {U}\), thus the top row of the Diagram (7) shows that \(E \in \mathcal {U}\) since \(\mathcal {U}\) is closed under extensions.
(d)\(\Leftrightarrow \)(a): Since \(\mathcal {R}\) is bounded, by Lemma 2.22 the co-t-structure \((\mathcal {U}, \mathcal {R})\) is bounded in \(\mathcal {S}(\mathcal {R})\). Observe that \(\textsf{Proj}_{\mathbb {E}}\mathcal {R}\) is the co-heart of this co-t-structure. The claim then follows from [30, Corollary 5.9] where it was shown that a subcategory of a triangulated category is silting precisely when it is the co-heart of a bounded co-t-structure. \(\square \)
As a consequence, we obtain the following.
Corollary 4.7
There is a correspondence between silting subcategories of triangulated categories and bounded right triangulated categories with right semi-equivalence that have enough projectives.
The above result is a triangulated analogue of a result due to Bondal & van den Bergh ([3, Proposition B.3]) and Rump ([59, Theorem 2] and [58, Theorem 1]), which states that there is a correspondence between tiltings in abelian categories and quasi-abelian categories. For more information on quasi-abelian categories and the construction of the right associated category, see the above references and [62, 65, 66]. When working with derived categories/ module categories of nice finite dimensional algebras these correspondences have a natural connection which we explain in the next paragraph.
4.3 Tilting and Silting Connection
Let us first describe the tilting–quasi-abelian correspondence in the abelian setting in more detail: Let \(\mathcal {Q}\) be a quasi-abelian category, then \(\mathcal {Q}\) appears as a tilting torsion class in the right associated abelian category \(\mathcal {A}\). In particular, \(\textsf{Proj}\mathcal {Q}\) is a tilting subcategory of \(\mathcal {A}\), that is, every object is a subobject of an object in \(\textsf{Proj}\mathcal {Q}\).
There is a natural way to associate a right triangulated category (with right semi-equivalence) to a quasi-abelian category. For a quasi-abelian category \(\mathcal {Q}\) as above, we define the right triangulated category \(\mathcal {R}_\mathcal {Q}:= \text{ susp}_{\textsf{D}^b(\mathcal {A})}\mathcal {Q}\), that is, the smallest subcategory of \(\textsf{D}^b(\mathcal {A})\) that is closed under positive shifts and extensions that contains \(\mathcal {Q}\).
Lemma 4.8
In the notation as above, the following hold.
-
(a)
\(\mathcal {R}_\mathcal {Q}= \{ X^\bullet \in \textsf{D}^b(\mathcal {A}) \mid \textsf{H}^0 (X^\bullet ) \in \mathcal {Q}, \, \textsf{H}^i (X^\bullet ) = 0 \, \forall \, i <0 \} \);
-
(b)
\(\mathcal {S}(\mathcal {R}_\mathcal {Q})= \textsf{D}^b(\mathcal {A})\);
-
(c)
If \(\mathcal {A}\) has finite global dimension, \(\mathcal {R}_\mathcal {Q}\) is bounded;
-
(d)
If \(\mathcal {Q}\) has a projective generator then \(\textsf{Proj}\mathcal {R}_\mathcal {Q}= \textsf{Proj}\mathcal {Q}\) and \(\mathcal {R}_\mathcal {Q}\) has enough projectives.
Proof
The left-to-right inclusion of part (a) is obvious. For the converse, note that it is enough to show that \(\Sigma \mathcal {A}= \{ \Sigma X \mid X \in \mathcal {A}\} \subseteq \mathcal {R}_\mathcal {Q}\). To this end, let \(X \in \mathcal {A}\), then, as \(\textsf{Proj}\mathcal {Q}\) is a tilting subcategory of \(\mathcal {A}\), there is a short exact sequence
in \(\mathcal {A}\) with \(Q \in \mathcal {Q}\). Since \(\mathcal {Q}\) is a torsion class in \(\mathcal {A}\), it is closed under quotients in \(\mathcal {A}\) and thus \(Q' \in \mathcal {Q}\). This short exact sequence gives rise to a triangle in \(\textsf{D}^b(\mathcal {A})\)
which we rotate to obtain the triangle
The claim now follows since \(Q', \Sigma Q \in \mathcal {R}_\mathcal {Q}\) and \(\mathcal {R}_\mathcal {Q}\) is closed under extensions. (b) and (c) follow from (a). For (d), let P be a projective generator of \(\mathcal {Q}\). We will show that every object A in \(\mathcal {R}_\mathcal {Q}\) admits a right triangle
in \(\mathcal {R}_\mathcal {Q}\) for a set J. Note that it suffices to show this for indecomposable objects. Since for \(X \in \Sigma \mathcal {R}_\mathcal {Q}\) we may make take the triangle
we only have to show the claim for objects in \(\mathcal {R}_\mathcal {Q}\setminus \Sigma \mathcal {R}_\mathcal {Q}\subset \mathcal {Q}\sqcup \Sigma \mathcal {A}\). For every object \(Q' \in Q\) there is a short exact sequence in \(\mathcal {Q}\) (and hence also in \(\mathcal {A}\)) \( 0 \rightarrow K \rightarrow P^J \rightarrow Q' \rightarrow 0 \) which induces a triangle in \(\textsf{D}^b(\mathcal {A})\)
which is a right triangle in \(\mathcal {R}_\mathcal {Q}\) since all terms are in \(\mathcal {R}_\mathcal {Q}\). For \(X \in \mathcal {A}\) we apply (ET4)op to the above triangle and a rotation of the triangle (8) to obtain the following commutative diagram of triangles in \(\textsf{D}^b(\mathcal {A})\)

Since \(K, Q \in \mathcal {R}_\mathcal {Q}\) we have that \(E \in \mathcal {R}_\mathcal {Q}\). Thus, the middle column of the above diagram, \(E \rightarrow P^J \rightarrow \Sigma X \rightarrow \Sigma E\), gives us the desired right triangle in \(\mathcal {R}_\mathcal {Q}\). \(\square \)
Corollary 4.9
Let \(\mathcal {Q}\) be a quasi-abelian category with an injective cogenerator I and a projective generator P and let \(\mathcal {A}\) be the right associated abelian category of \(\mathcal {Q}\). Suppose that, \(\mathcal {Q}\) is artinian with respect to subobjects and \(\textsf{End}_\mathcal {Q}(I)\) is an artin algebra of finite global dimension. Then P is a tilting module in \(\mathcal {A}\) and \(\textsf{add} P\) is a silting subcategory of \(\textsf{D}^b(\mathcal {A})\).
Proof
The first claim is a combination of (the duals of) [65, Theorem III.4.9 and Corollary III.4.11]. The second claim follows from Theorem 4.6 and Lemma 4.8. \(\square \)
Remark 4.10
Let \(\Lambda \) be a finite dimensional algebra over a field k and set \(\mathcal {A}= \textsf{mod}\Lambda \). By [2, Theorems 2.7 & 3.2] and [37, Theorem 2.2] (see also [42]) there are bijections between the following
-
(a)
Functorially finite torsion classes in \(\mathcal {A}\);
-
(b)
Isomorphism classes of \(\tau \)-tilting modules in \(\mathcal {A}\);
-
(c)
Two-term silting complexes in \(\textsf{K}^b(\textsf{proj} \mathcal {A})\);
-
(d)
Intermediate co-t-structures of \(\textsf{K}^b(\textsf{proj} \mathcal {A})\).
and that the first bijection restricts to a bijection between tilting torsion classes in \(\mathcal {A}\) and isomorphism classes of tilting modules in \(\mathcal {A}\). Along these bijections, a functorially finite torsion class \(\mathcal {T}\) corresponds to the \(\tau \)-tilting module M, where M is a projective generator of \(\mathcal {T}\). M, in turn, corresponds to the 2-term silting complex \((P^1 \rightarrow P^0) \in \textsf{K}^b({\textsf{proj}\mathcal {A}})\), where \(P^1 \rightarrow P^0 \rightarrow M \rightarrow 0\) is a projective presentation of M in \(\mathcal {A}\). The co-t-structure corresponding to \((P^1 \rightarrow P^0)\) has co-aisle \(\textsf{susp}_{\textsf{K}^b(\textsf{proj}\mathcal {A})}(P^1 \rightarrow P^0)\).
When \(\Lambda \) is of finite global dimension we have that \(\textsf{K}^b(\textsf{proj}\mathcal {A}) \cong \textsf{D}^b(\mathcal {A})\). Thus, by Lemma 4.8, following the correspondences above from (a) to (d), a tilting torsion class \(\mathcal {T}\) is associated to (the co-t-structure with co-aisle) \(\mathcal {R}_\mathcal {T}\) as we defined at the start of this subsection. Of course, without the finite global dimension assumption on \(\Lambda \), one could define \(\mathcal {R}_\mathcal {T}\) as \(\textsf{susp}_{\textsf{K}^b(\textsf{proj}\mathcal {A})}(P^1 \rightarrow P^0)\) but this is somewhat less natural.
4.4 Aisles of t-Structures
We now present our characterisations of aisles of t-structures.
Theorem 4.11
The following are equivalent
-
(a)
\(\mathcal {R}\) is the aisle of a t-structure \((\mathcal {R}, \mathcal {V})\) in \(\mathcal {S}(\mathcal {R})\);
-
(b)
There is a torsion pair \((\Sigma \mathcal {R}, \mathcal {F})\) in \(\mathcal {R}\);
-
(c)
There is an equivalence of triangulated categories \(\phi : \mathcal {S}(\mathcal {R})\rightarrow \mathcal {C}(\mathcal {R})\)
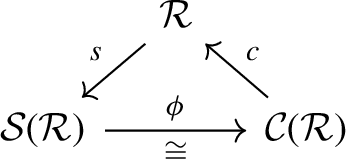
such that \(c\phi s = 1_\mathcal {R}\).
Proof
The equivalence of (a) and (b) follows from dualising the arguments used in the proof of Theorem 4.6.
(a)\(\Rightarrow \)(c): We show that in this case, \(\mathcal {S}(\mathcal {R})\) satisfies the universal property of the co-stabilisation of \(\mathcal {R}\). Let \(r: \mathcal {S}(\mathcal {R})\rightarrow \mathcal {R}\) denote the functor induced by the t-structure \((\mathcal {R}, \mathcal {V})\). Let \(\mathcal {T}\) be a triangulated category and \(F: \mathcal {T}\rightarrow \mathcal {R}\) be a right triangle functor. Define the functor \(F': \mathcal {T}\rightarrow \mathcal {S}(\mathcal {R})\) by \(F'X = (FX, 0)\). Clearly \(rF' = F\) and \(F'\) is a triangle functor.
We quickly verify that \(F'\) is unique with this property. Suppose that \(F'': \mathcal {T}\rightarrow \mathcal {S}(\mathcal {R})\) is another triangle functor such that \(rF''=F\). Then for all \(X \in \mathcal {T}\) there are triangles in \(\mathcal {S}(\mathcal {R})\)
with \(\mathcal {S}(\mathcal {R})(\mathcal {R}, V') = 0 = \mathcal {S}(\mathcal {R})(\mathcal {R}, V'')\). Observe that, for \(n>>0\), \(\Sigma ^n F'X, \Sigma ^n F''X \in \mathcal {R}\). Thus, \(\Sigma ^n F'X \cong \Sigma ^n FX \cong \Sigma ^n F''X\). So, since \(F'\) and \(F''\) are triangle functors, \(F''\Sigma ^n X \cong F' \Sigma ^n X\) and we are done.
(c)\(\Rightarrow \)(a): We will show that that \(c\phi \) is right adjoint to the inclusion s whence we will be done by [39, Proposition 1.2]. It is enough to show that for all \(X, Y \in \mathcal {R}\) and \(m \in \mathbb {Z}\) that there is a natural isomorphism
If \(m \ge 0\) then \((Y,m) = s(\Sigma ^m Y)\) and thus, by assumption \(c\phi (Y,m) = c\phi s (\Sigma ^m Y) \cong \Sigma ^m Y\). On the other hand
and we are done.
If \(m <0\), then \(\mathcal {S}(\mathcal {R})( sX, (Y,m) ) \cong \mathcal {R}(\Sigma ^{-m}X, Y)\). On the other hand, \( \mathcal {R}(X, c \phi (Y,m)) \cong \mathcal {R}( \Sigma ^{-m}X, \Sigma ^{-m}c\phi (Y,m)) \) and
and we are done since all isomorphisms used are natural. \(\square \)
We end this section by noting that the language of the torsion pairs in \(\mathcal {R}\) also allows us to describe related classes of (co-)t-structures.
Proposition 4.12
\(\mathcal {R}= (\mathcal {R}, \Sigma , \Delta )\) be a right triangulated category with right semi-equivalence.
-
(a)
Suppose that there is a co-t-structure \((\mathcal {U}, \mathcal {R})\) in \(\mathcal {S}(\mathcal {R})\). Then there is a bijection

which preserves the inclusion of aisles and restricts to a bijection
$$\begin{aligned} \{ (\mathcal {X}, \mathcal {Y}) \text { co-t-structure in } \mathcal {S}(\mathcal {R})&\mid \Sigma \mathcal {R}\subseteq \mathcal {Y} \subseteq \mathcal {R}\} \\ \longleftrightarrow&\{ (\mathcal {A}, \mathcal {B}) \text { torsion pair in } \mathcal {R}\mid \Sigma ^2 \mathcal {R} \subseteq \mathcal {B} \subseteq \Sigma \mathcal {R}\}. \end{aligned}$$ -
(b)
Suppose that there is a t-structure \((\mathcal {R}, \mathcal {V})\) in \(\mathcal {S}(\mathcal {R})\). Then there is a bijection

which preserves the inclusion of aisles and restricts toa bijection
$$\begin{aligned} \{ (\mathcal {X}, \mathcal {Y}) \text { t-structure in } \mathcal {S}(\mathcal {R})&\mid \Sigma \mathcal {R}\subseteq \mathcal {X} \subseteq \mathcal {R}\} \\ \longleftrightarrow&\{ (\mathcal {A}, \mathcal {B}) \text { torsion pair in } \mathcal {R}\mid \Sigma ^2 \mathcal {R} \subseteq \mathcal {A} \subseteq \Sigma \mathcal {R}\}. \end{aligned}$$
Proof
We do not write the proof of (a) since it is a straightforward generalisation of the proof of [66, Theorem 4.4]. Part (b) can be proved in a similar way. Alternatively, since all torsion pairs in (b) are \(\mathfrak {s}\)-torsion pairs, the bijections of (b) are, after shifting, special cases of [1, Theorem 3.9]. \(\square \)
The (co-)t-structures in the second correspondences in parts (a) and (b) are called intermediate with respect to the (co-)t-structure of \(\mathcal {R}\). Let us mention related work on this property. Intermediate t-structures also correspond to torsion pairs in the heart [11, 27] and have applications in, for example, stability conditions [67] and algebraic geometry [57]. In the case of co-t-structures, it has been shown that intermediate co-t-structures correspond to certain two term silting subcategories [37] and to cotorsion pairs in the ‘extended coheart’ [55].
5 Aisles Through Quotients
We fix some conventions. Let \(\mathcal {C}= (\mathcal {C}, \mathbb {E}, \mathfrak {s})\) be a Frobenius extriangulated category, with projectives-injectives \(\mathcal {I}\) and \(\underline{\mathcal {C}} = \underline{\mathcal {C}}_{\mathcal {I}}\) be the stable category, which has the natural structure of triangulated category [52, Corollary 7.4] with shift functor \(\Sigma \). By \(\mathcal {I}(X)\) we denote the object such that \(X \rightarrow \mathcal {I}(X)\) is a minimal left \(\mathcal {I}\)-approximation.
In this section, we show the following.
Theorem 5.1
Let \((\mathcal {U}, \mathcal {V})\) be a t-structure in \(\underline{\mathcal {C}}\) and set \(\mathcal {D}= \Sigma ^{-1} \mathcal {V}\). Then there is an equivalence of right triangulated categories \(\Sigma _\mathcal {D}\underline{\mathcal {C}}_\mathcal {D}\cong \mathcal {U}\).
Remark 5.2
In [61, Proposition 3.9], it was shown that t-structures in an algebraic triangulated category correspond bijectively to certain complete cotorsion pairs in the associated Frobenius exact category. Along that bijection a t-structure \((\mathcal {U}, \mathcal {V})\) in \(\underline{\mathcal {C}}\) corresponds to the cotorsion pair \(( \mathcal {U}, \Sigma ^{-1} \mathcal {V})\) in \(\mathcal {C}\). This bijection generalises immediately to the extriangulated setting. Further, when applied to the case of a triangulated category \(\mathcal {T}\) (which is Frobenius extriangulated category [52, Proposition 3.22]), this specialises to the observation of [51, Proposition 2.6] that t-structures in \(\mathcal {T}\) are in bijection with cotorsion pairs \((\mathcal {U}, \mathcal {V})\) in \(\mathcal {T}\) such that \(\Sigma \mathcal {U}\subseteq \mathcal {U}\). Thus, these results and Theorem 5.1 complement each other.
We note that a class of objects \(\mathcal {V}\subset \textsf{Obj}(\mathcal {C}) = \textsf{Obj}(\underline{\mathcal {C}})\) defines subcategories of both \(\mathcal {C}\) and \(\underline{\mathcal {C}}\).
Lemma 5.3
Let \(\mathcal {D}= \textsf{Add}\mathcal {D}\) be a covariantly finite additive subcategory of \(\underline{\mathcal {C}}\). Then \(\mathcal {D}\) is also a covariantly finite additive subcategory of \(\mathcal {C}\). Moreover, left \(\mathcal {D}\)-approximations are \(\mathbb {E}\)-inflations in \(\mathcal {C}\).
Proof
For any \(X \in \mathcal {C}\), let \(\underline{\alpha }: X \rightarrow D\) and \(\beta : X \rightarrow \mathcal {I}(X) = I\) be a left \(\mathcal {D}\)-approximation of X in \(\underline{\mathcal {C}}\) and a left \(\mathcal {I}\)-approximation of X in \(\mathcal {C}\) respectively. We claim that \(\left[ {\begin{matrix} \alpha \\ \beta \end{matrix}} \right] : X \rightarrow D \oplus I\) is a left \(\mathcal {D}\)-approximation of X in \(\mathcal {C}\).
Indeed, since \(\mathcal {D}\) is additive, \(0 \cong \mathcal {I}\subset \mathcal {D}\), so \(D \oplus I \in \mathcal {D}\). Let \(f: X \rightarrow W\) be a morphism in \(\mathcal {C}\) with \(W \in \mathcal {D}\). Then there exists \((\underline{g}:D \rightarrow W) \in \underline{\mathcal {C}}(D,W)\) such that \(\underline{f}=\underline{g \alpha }\). Now, \(\underline{f - g \alpha } =0\) so \(f - g \alpha \) factors through \(\mathcal {I}\) and so must factor through the left \(\mathcal {I}\)-approximation of X. Thus there exists \(g':I \rightarrow W\) such that \(f - g \alpha = g' \beta \). Rearranging we have

The remaining claim follows from Lemma 2.12. \(\square \)
Let \((\mathcal {U}, \mathcal {V})\) be a t-structure on \(\underline{\mathcal {C}}\), so that for all objects X there exists a unique (up to isomorphism) triangle in \(\underline{\mathcal {C}}\)

therefore there is a unique (up to isomorphism) triangle in \(\underline{\mathcal {C}}\)

Note that this triangle is also the canonical triangle of X with respect to the t-structure \((\Sigma ^{-1} \mathcal {U}, \Sigma ^{-1} \mathcal {V})\). Set \(\mathcal {D}:= \Sigma ^{-1}\mathcal {V}\subset \mathcal {C}\), which by Lemma 5.3 satisfies property \((*)\) and thus the category \(\underline{\mathcal {C}}_\mathcal {D}\) is a right triangulated category by Proposition 3.6. We also set \(\mathcal {V}'(X) := \Sigma ^{-1} \mathcal {V}(\Sigma X)\) and \(J(X):= \mathcal {V}' (X)\oplus \mathcal {I}(X)\).
Lemma 5.4
For all \(X \in \mathcal {C}\), \(\Sigma _\mathcal {D} X \cong \mathcal {U}(\Sigma X)\) in \(\underline{\mathcal {C}}\).
Proof
By the definition of the functor \(\Sigma _\mathcal {D}\) and Lemmas 2.12 and 5.3, \(\Sigma _\mathcal {D}X\) fits into a commutative diagram of extriangles in \(\mathcal {C}\)

where \(\underline{v}'_X:X \rightarrow \mathcal {V}'(X)\) fits into the triangle (9). Thus \(\Sigma _\mathcal {D}X = \textsf{cone}_{\underline{\mathcal {C}}}(\underline{v}'_X) \cong \mathcal {U}(\Sigma X)\) in \(\underline{\mathcal {C}}\). \(\square \)
Consider the diagram

where G is the unique additive functor rendering the diagram commutative which exists since \(\mathcal {I}\subseteq \mathcal {D}\). The next result finishes the proof of Theorem 5.1.
Proposition 5.5
The composition \(\psi := Gi: \mathcal {U}\rightarrow \underline{\mathcal {C}}_\mathcal {D}\) is a full and faithful right triangle functor and induces an equivalence of right triangulated catgeories \(\mathcal {U}\cong \Sigma _\mathcal {D}\underline{\mathcal {C}}_\mathcal {D}\).
Proof
\(\psi \) is a right triangulated functor: Note that for all \(U \in \mathcal {U}\), \(\mathcal {U}(U) \cong U\) and \(\mathcal {V}'(U) \cong 0\) in \(\underline{\mathcal {C}}\). Thus, by Lemma 5.4, there is a natural isomorphism of functors \(\Sigma |_{\mathcal {U}} \cong \Sigma _\mathcal {D}|_{\mathcal {U}}\) and \(\mathcal {I}(U) \cong J(U)\) so that (right) triangles in \(\mathcal {U}\) are also right triangles in \(\underline{\mathcal {C}}_\mathcal {D}\).
\(\psi \) is full: Follows from the fact that i and G are both full.
\(\psi \) is faithful: Let \(\underline{f} :X \rightarrow Y\) be a morphism in \(\mathcal {U}\). Suppose that \(\psi (\underline{f}) = 0\). Then \(\underline{f}\) must factor through \(\mathcal {D}= \Sigma ^{-1} \mathcal {V}\) in \(\underline{\mathcal {C}}\). But since \(\underline{\mathcal {C}}(\mathcal {U}, \mathcal {V})=0\) and \(\Sigma ^{-1} \mathcal {V}\subset \mathcal {V}\) this is only possible if \(\underline{f}=0\).
\(\textsf{Im}\psi \cong \Sigma _\mathcal {D}\underline{\mathcal {C}}_\mathcal {D}\): Let \(\Sigma _\mathcal {D}X \in \Sigma _\mathcal {D}\underline{\mathcal {C}}_\mathcal {D}\), by Lemma 5.4, \(\Sigma _\mathcal {D}X \cong \mathcal {U}(\Sigma X)\) in \(\underline{\mathcal {C}}\) and hence also in \(\underline{\mathcal {C}}_\mathcal {D}\). Thus \(\psi (\mathcal {U}(\Sigma X)) \cong \Sigma _\mathcal {D}X\). Conversely, let \(Y \in \mathcal {U}\). Then \(Y \cong \Sigma _\mathcal {D}(\Sigma ^{-1} Y) \in \underline{\mathcal {C}}_\mathcal {D}\) by Lemma 5.4. \(\square \)
Corollary 5.6
\(\Sigma _\mathcal {D}G \Sigma ^{-1}: \underline{\mathcal {C}} \rightarrow \Sigma _\mathcal {D}\underline{\mathcal {C}}_\mathcal {D}\cong \mathcal {U}\) is right adjoint to the inclusion \(\mathcal {U}\hookrightarrow \underline{\mathcal {C}}\). In particular, \(\Sigma _\mathcal {D}G \Sigma ^{-1} \cong \mathcal {U}(-)\).
Remark 5.7
Theorem 5.1 cannot be directly dualised to give co-aisles of co-t-structures since the aisle of a co-t-structure is contravariantly finite. The author would be interested to know if there is a way to work around this problem.
Data Availibility Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Adachi, T., Enomoto, H., Tsukamoto, M.: Intervals of s-torsion pairs in extriangulated categories with negative first extensions. In Mathematical Proceedings of the Cambridge Philosophical Society, pp. 1–19. Cambridge University Press, Cambridge (2022)
Adachi, T., Iyama, O., Reiten, I.: \(\tau \)-tilting theory. Compos. Math. 150(3), 415–452 (2014)
Aleksei Igorevich Bondal and Michel Van den Bergh: Generators and representability of functors in commutative and noncommutative geometry. Mosc. Math. J. 3(1), 1–36 (2003)
Al-Nofayee, S.: Simple objects in the heart of a t-structure. J. Pure Appl. Algebra 213(1), 54–59 (2009)
Amiot, C.: On the structure of triangulated categories with finitely many indecomposables. Bull. Soc. Math. France 135(3), 435–474 (2007)
Assem, I., Beligiannis, A., Marmaridis, N.: Right triangulated categories with right semi-equivalences. In CMS Conference Proceedings, vol. 24, pp. 17–37 (1998)
Assem, I., Salorio, M.J.S., Trepode, S.: Ext-projectives in suspended subcategories. J. Pure Appl. Algebra 212(2), 423–434 (2008)
Auslander, M., Reiten, I.: Applications of contravariantly finite subcategories. Adv. Math. 86(1), 111–152 (1991)
Beĭlinson, A., Bernstein, J., Deligne, P.: Faisceaux pervers. In: Analysis and topology on singular spaces. I (Luminy, 1981), volume 100 of Astérisque, pp. 5–171. Soc. Math. France, Paris (1982)
Beligiannis, A., Marmaridis, N.: On left derived categories of a stable category. In Proceedings of the Sixth International Conference on Representations of Algebras (Ottawa, ON, 1992), volume 14 of Carleton-Ottawa Math. Lecture Note Ser., p. 31. Carleton Univ., Ottawa, ON, (1992)
Beligiannis, A., Reiten, I.: Homological and Homotopical Aspects of Torsion Theories. American Mathematical Soc., (2007)
Beligiannis, A.: The homological theory of contravariantly finite subcategories: Auslander-Buchweitz contexts, Gorenstein categories and (co-)stabilization. Comm. Algebra 28(10), 4547–4596 (2000)
Beligiannis, A.: Relative homological algebra and purity in triangulated categories. J. Algebra 227(1), 268–361 (2000)
Beligiannis, A., Marmaridis, N.: Left triangulated categories arising from contravariantly finite subcategories. Comm. Algebra 22(12), 5021–5036 (1994)
Bondarko, M.V.: Weight structures versus t-structures; weight filtrations, spectral sequences, and complexes (for motives and in general). J. K-Theory 6(3), 387–504 (2010)
Bridgeland, T.: Stability conditions on triangulated categories. Ann. Math. 166(2), 317–345 (2007)
Brüstle, T., Smith, D., Treffinger, H.: Stability conditions and maximal green sequences in abelian categories. Rev. Un. Mat. Argent. 63(1), 203–221 (2022)
Dickson, S.E.: A torsion theory for abelian categories. Trans. Am. Math. Soc. 121(1), 223–235 (1966)
Dugas, A.: Torsion pairs and simple-minded systems in triangulated categories. Appl. Categ. Struct. 23(3), 507–526 (2015)
Enochs, E.E., Jenda, O.M.G.: Relative homological algebra, volume 30 of De Gruyter Expositions in Mathematics. Walter de Gruyter & Co., Berlin (2000)
Enomoto, H.: Classifying substructures of extriangulated categories via serre subcategories. Appl. Categ. Struct. 1–14 (2021)
Freyd, P.: Stable homotopy. In Proceedings of the Conference Categorical Algebra (La Jolla, Calif, 1965), pp. 121–172. Springer, New York (1966)
Gorsky, M., Nakaoka, H., Palu, Y.: Positive and negative extensions in extriangulated categories (2021) arXiv preprint arXiv:2103.12482
Grandis, M.: Homotopical algebra and triangulated categories. Math. Proc. Camb. Philos. Soc. 118(2), 259–285 (1995)
Gratz, S., Zvonareva, A.: Lattices of t-structures and thick subcategories for discrete cluster categories. J. Lond. Math. Soc. 107(3), 973–1001 (2021)
Happel, D.: Triangulated Categories in the Representation of Finite Dimensional Algebras, vol. 119. Cambridge University Press, Cambridge (1988)
Happel, D., Reiten, I., Smalø, S.O.: Tilting in abelian categories and quasitilted algebras. Mem. Am. Math. Soc. 120(575), viii+88 (1996)
Heller, A.: The loop-space functor in homological algebra. Trans. Am. Math. Soc. 96, 382–394 (1960)
Heller, A.: Stable homotopy categories. Bull. Am. Math. Soc. 74, 28–63 (1968)
Hernández, O.M., Valadez, E.C.S., Vargas, V.S., Salorio, M.J.S.: Auslander–Buchweitz context and co-\(t\)-structures. Appl. Categ. Struct. 21(5), 417–440 (2013)
Herschend, M., Liu, Y., Nakaoka, H.: n-exangulated categories (i): definitions and fundamental properties. J. Algebra 570, 531–586 (2021)
Hochschild, G.P.: Relative homological algebra. Trans. Am. Math. Soc. 82, 246–269 (1956)
Hügel, L.A., Marks, F., Vitória, J.: Silting modules. Int. Math. Res. Not. 2016(4), 1251–1284 (2015)
Hügel, L.A., Marks, F., Vitória, J.: Torsion pairs in silting theory. Pacific J. Math. 291(2), 257–278 (2017)
Iyama, O., Yoshino, Y.: Mutation in triangulated categories and rigid Cohen-Macaulay modules. Invent. Math. 172(1), 117–168 (2008)
Iyama, O., Yoshino, Y.: Mutation in triangulated categories and rigid Cohen-Macaulay modules. Invent. Math. 172(1), 117–168 (2008)
Iyama, O., Jørgensen, P., Yang, D.: Intermediate co-\(t\)-structures, two-term silting objects, \(\tau \)-tilting modules, and torsion classes. Algebra Number Theory 8(10), 2413–2431 (2014)
Jørgensen, P.: Spectra of modules. J. Algebra 244(2), 744–784 (2001)
Keller, B., Vossieck, D.: Aisles in derived categories. In Deuxième Contact Franco-Belge en Algèbre, vol. 40, pp. 239–253. Société Mathématique de Belgique, Brussels (1988)
Keller, B.: Chain complexes and stable categories. Manuscripta Math. 67(4), 379–417 (1990)
Keller, B., Vossieck, D.: Sous les catégories dérivées. C. R. Acad. Sci. Paris Sér. I Math. 305(6), 225–228 (1987)
Koenig, S., Yang, D.: Silting objects, simple-minded collections, \(t\)-structures and co-\(t\)-structures for finite-dimensional algebras. Doc. Math. 19, 403–438 (2014)
Kvamme, S.: \(d\mathbb{Z} \)-cluster tilting subcategories of singularity categories. Math. Z. 297(1–2), 803–825 (2021)
Laking, R., Vitória, J.: Definability and approximations in triangulated categories. Pac. J. Math. 306(2), 557–586 (2020)
Li, Z.-W.: The triangulation of the subfactor categories of additive categories with suspensions (2015) arXiv preprint arXiv:1510.02258
Lidia Angeleri Hügel: Silting objects. Bull. Lond. Math. Soc. 51(4), 658–690 (2019)
Lin, Y., Xin, L.: On one-sided torsion pair. Sci. China Ser. A 50(1), 13–26 (2007)
Liu, Yu., Nakaoka, H.: Hearts of twin cotorsion pairs on extriangulated categories. J. Algebra 528, 96–149 (2019)
Maranda, J.-M.: Injective structures. Trans. Am. Math. Soc. 110(1), 98–135 (1964)
Marks, F., Vitória, J.: Silting and cosilting classes in derived categories. J. Algebra 501, 526–544 (2018)
Nakaoka, H.: General heart construction on a triangulated category (I): unifying \(t\)-structures and cluster tilting subcategories. Appl. Categ. Struct. 19(6), 879–899 (2011)
Nakaoka, H., Palu, Y.: Extriangulated categories, Hovey twin cotorsion pairs and model structures. Cah. Topol. Géom. Différ. Catég 60(2), 117–193 (2019)
Padrol, A., Palu, Y., Pilaud, V., Plamondon, P.-G.: Associahedra for finite type cluster algebras and minimal relations between g-vectors (2019) arXiv preprint arXiv:1906.06861
Parra, C.E., Saorín, M.: Direct limits in the heart of a t-structure: the case of a torsion pair. J. Pure Appl. Algebra 219(9), 4117–4143 (2015)
Pauksztello, D., Zvonareva, A.: Co-t-structures, cotilting and cotorsion pairs. In Mathematical Proceedings of the Cambridge Philosophical Society, pp. 1–18. Cambridge University Press (2022)
Pauksztello, D.: Compact corigid objects in triangulated categories and co-\(t\)-structures. Cent. Eur. J. Math. 6(1), 25–42 (2008)
Polishchuk, A.: Constant families of \(t\)-structures on derived categories of coherent sheaves. Mosc. Math. J. 7(1), 109–134 (2007)
Rump, W.: *-modules, tilting, and almost abelian categories. Comm. Algebra 29(8), 3293–3325 (2001)
Rump, W.: Almost abelian categories. Cahiers Topologie Géom. Différentielle Catég. 42(3), 163–225 (2001)
Rump, W.: Triadic categories without localization. J. Algebra 322(4), 995–1012 (2009)
Saorín, M., Šťovíček, J.: On exact categories and applications to triangulated adjoints and model structures. Adv. Math. 228(2), 968–1007 (2011)
Schneiders, J.-P.: Quasi-abelian categories and sheaves. Mém. Soc. Math. Fr. (N.S.) 76, vi+134 (1999)
Takuma, A., Osamu, I.: Silting mutation in triangulated categories. J. Lond. Math. Soc. 85(3), 633–668 (2012)
Tarrío, L.A., López, A.J., Salorio, M.J.S.: Localization in categories of complexes and unbounded resolutions. Can. J. Math. 52(2), 225–247 (2000)
Tattar, A.: Torsion structures, subobjects and unique filtrations in non-abelian categories. PhD thesis, Universität zu Köln, (2021)
Tattar, A.: Torsion pairs and quasi-abelian categories. Algebr. Represent. Theory 24(6), 1557–1581 (2021)
Woolf, J.: Stability conditions, torsion theories and tilting. J. Lond. Math. Soc. 82(3), 663–682 (2010)
Zhou, P., Zhu, B.: Triangulated quotient categories revisited. J. Algebra 502, 196–232 (2018)
Zhou, Yu., Zhu, B.: Mutation of torsion pairs in triangulated categories and its geometric realization. Algebr. Represent. Theory 21(4), 817–832 (2018)
Acknowledgements
This work was part of the author’s PhD studies and the content overlaps with Chapters II and V of their thesis [65]. When required, other parts of the thesis, that fall outside of the area of this article, have been cited. The author would like to thank their PhD supervisor Sibylle Schroll for many helpful discussions and the EPSRC for financial support. The author also thanks the anonymous referee for their comments and suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author has no financial or proprietary interests in any material discussed in this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Communicated by Henning Krause.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tattar, A. The Structure of Aisles and Co-aisles of t-Structures and Co-t-structures. Appl Categor Struct 32, 5 (2024). https://doi.org/10.1007/s10485-023-09755-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10485-023-09755-8


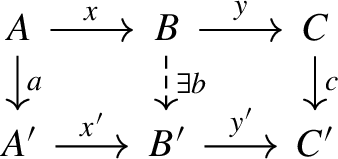

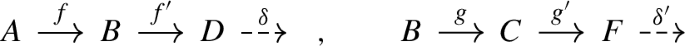
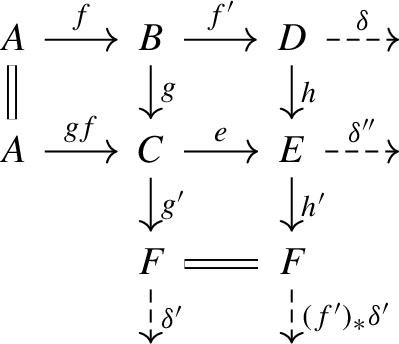

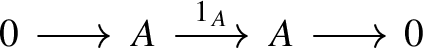
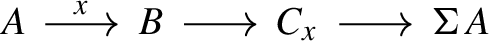
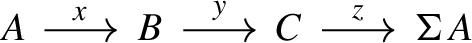
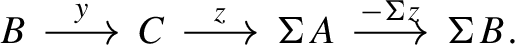
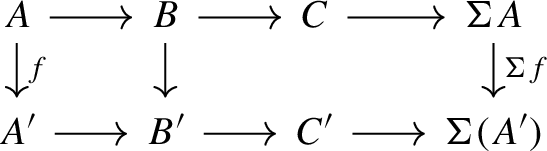


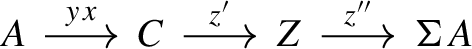
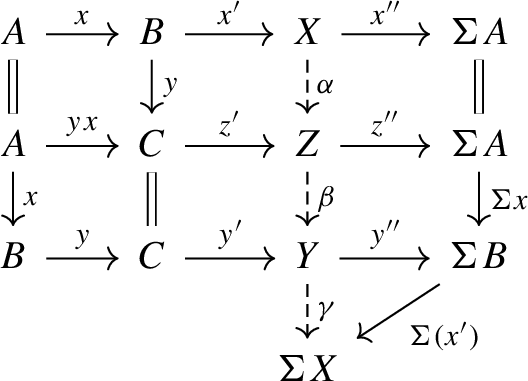
 ;
;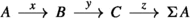 in
in 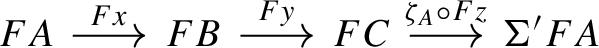
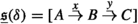 where
where  for all extriangles
for all extriangles 


