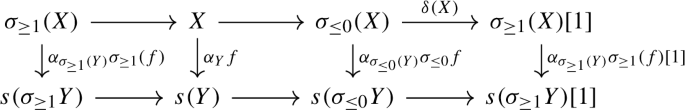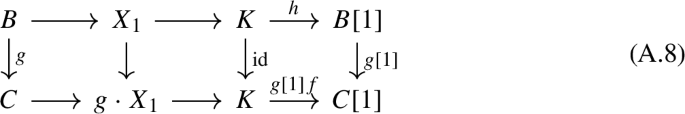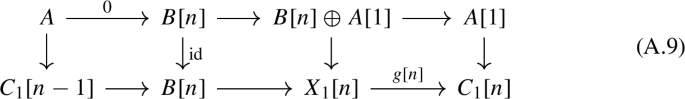Abstract
We describe how to obtain a global t-structure from a semiorthogonal decomposition with compatible t-structures on every component. This result is used to generalize a well-known theorem of Bondal on full strong exceptional sequences.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The notion of algebraic triangulated categories has raised great attention in the last decades. These particular triangulated categories are described in several equivalent ways: they admit an enhancement by dg categories or \(A_{\infty }\)-categories; alternatively, they are obtained as the stable category of a Frobenius category. The most important examples are derived categories (assuming they are categories).Footnote 1 Interestingly, many results can be extended from derived categories to algebraic triangulated categories. We focus on the following.
Theorem—Bondal. [3, Theorem 6.2] Assume that the bounded derived category \({{\text {D}}^{{\text {b}}}}(X)\) of coherent sheaves on a smooth manifold X is generated by a strong exceptional sequence \(\langle E_1 , \ldots , E_n \rangle \). Then \({{\text {D}}^{{\text {b}}}}(X)\) is equivalent to the bounded derived category \({{\text {D}}^{{\text {b}}}}({\text {mod-}}A)\) of right finite-dimensional modules over the algebra \(A={\text {End}} (\bigoplus _{i=1}^n E_i)\).
Bondal’s result has been generalized to algebraic triangulated categories by Keller [15, Theorem 8.7]. In particular, the statement below is a consequence of Keller’s work.
Theorem—Keller-Orlov. [20, Corollary 1.9] Let \(\mathscr {T}\) be an algebraic triangulated category. Assume that \(\mathscr {T}\) has a full strong exceptional sequence \(\langle E_1 , \ldots , E_n \rangle \). Then the category \(\mathscr {T}\) is equivalent to the derived category \({{\text {D}}^{{\text {b}}}}({\text {mod-}}A)\), where \(A={\text {End}} (\bigoplus _{i=1}^n E_i )\) is the algebra of endomorphisms of the collection \(\langle E_1 , \ldots , E_n \rangle \).
A question may arise: is it possible to drop the algebraic requirement? At the moment, no answer has been found. As a matter of fact, it is incredibly hard to study the general case of triangulated categories; indeed, the definition of an exceptional object requires the category to be \(\mathbb {K}\)-linear, with \(\mathbb {K}\) a field, and the only known example of non-algebraic \(\mathbb {K}\)-linear triangulated category is studied in [23].
Our aim is to generalize Bondal’s result. For this reason, we deal with the construction of a global t-structure, starting with compatible t-structures on semiorthogonal components. Surprisingly, the result is not hard to prove and it follows from basic theory. As a corollary, a full strong exceptional sequence of length 2 gives a heart of dimension at most 1, so that Hubery’s result [11, Theorem 3.2] can be applied without any additional requirement on the triangulated category. We obtain the following.
Corollary 3.13. Let \(\mathbb {K}\) be a field. Any \(\mathbb {K}\)-linear triangulated category \(\mathscr {T}\) with a full strong exceptional sequence \(\langle E_1 , E_2 \rangle \) such that \(\dim _{\mathbb {K}}{\text {Hom}}(E_1 , E_2) < \infty \) is algebraic. In particular, \(\mathscr {T}\cong {{\text {D}}^{{\text {b}}}}({\text {mod-}}A)\), where \(A={\text {End}}(\bigoplus _{i=1}^2 E_i)\).
For a strong exceptional sequence with length greater than 2 we deal with realized triangulated categories, i.e. triangulated categories \(\mathscr {T}\) admitting an exact functor \(\mathsf {real}:{{\text {D}}^{{\text {b}}}}(\mathscr {A}) \rightarrow \mathscr {S}\) for every heart \(\mathscr {A}\) of a bounded t-structure on a full subcategory \(\mathscr {S}\) of \(\mathscr {T}\). In particular, it has been proven that all algebraic triangulated categories are realized (see Example 6.2 for a discussion on examples of realized triangulated categories). By induction on the length of the exceptional sequence, we can prove the main result.
Theorem 6.6. Let \(\mathbb {K}\) be a field and let \(\mathscr {T}\) be a realized \(\mathbb {K}\)-linear triangulated category with a full strong exceptional sequence \(\langle E_1 , \ldots , E_n \rangle \) such that \(\bigoplus _i {\text {Hom}}(X,Y[i])\) is a finite-dimensional vector space for any \(X,Y \in \mathscr {T}\). Then \(\mathscr {T}\cong {{\text {D}}^{{\text {b}}}}({\text {mod-}}A)\), where \(A= {\text {End}}(\bigoplus _{i=1}^n E_i)\).
In Sect. 2, we recall some basic results on t-structures. Section 3 is devoted to the notion of compatible t-structures with respect to a semiorthogonal decomposition. Section 4 covers the needed knowledge on quivers, while Sect. 5 deals with filtered triangulated categories, introduced by Beilinson in [1, Appendix A]. In Sect. 6, we introduce the concept of realized triangulated category and state the main theorem. “Appendix A” generalizes a result on Yoneda extensions of exact categories.
2 Some Basic Results on Bounded t-Structures
In this section, we define t-structures and hearts, and state some classical results.
Definition 2.1
A t-structure on a triangulated category \(\mathscr {T}\) is a full subcategory \(\mathscr {T}^{\le 0}\) closed by left shifts, i.e. \(\mathscr {T}^{\le 0}[1] \subset \mathscr {T}^{\le 0}\), and such that for any object \(E \in \mathscr {T}\) there is a distinguished triangle \(A \rightarrow E \rightarrow B \rightarrow A[1]\), where \(A \in \mathscr {T}^{\le 0}\) and \(B \in \mathscr {T}^{\ge 1}:= (\mathscr {T}^{\le 0})^\bot \).
We remember that for any full subcategory \(\mathscr {C} \subset \mathscr {T}\), we write \(\mathscr {C}^\bot \) to mean the full subcategory whose objects are Y such that \({\text {Hom}}(X,Y)=0\) for any \(X \in \mathscr {C}\).
We will write \(\mathscr {T}^{\le i}:=\mathscr {T}^{\le 0}[-i]\) and \(\mathscr {T}^{\ge j} := \mathscr {T}^{\ge 1}[-j+1]\) for any i, j integers. A t-structure is said to be bounded if
Moreover, the t-structure is non-degenerate if \(\bigcap _i \mathscr {T}^{\le i}=\bigcap _j \mathscr {T}^{\ge j}=0\).
The heart (of the bounded t-structure \(\mathscr {T}^{\le 0}\)) is the additive category \(\mathscr {A}:= \mathscr {T}^{\ge 0} \cap \mathscr {T}^{\le 0}\), and it is proven to be abelian. We define the homological dimension of \(\mathscr {A}\) in \(\mathscr {T}\), denoted by \(\dim _{\mathscr {T}}\mathscr {A}\), as the greatest integer n such that \({\text {Hom}}(A,B[n])\ne 0\) for some \(A,B \in \mathscr {A}\).
Notation 2.2
Given a map \(f:A\rightarrow B\) in a triangulated category, its cone will be denoted by \({\text {C}}(f)\). When there is no need to make f explicit, we will write \({\text {C}}(A\rightarrow B)\).
Definition/Proposition. 2.3
[4, Lemma 3.2]. Let \(\mathscr {T}\) be a triangulated category. A heart (of bounded t-structure) on \(\mathscr {T}\) is an additive category \(\mathscr {A}\) satisfying the following properties:
-
1.
For any two objects \(A,B \in \mathscr {A}\), \({\text {Hom}}(A,B[n])=0\) for every \(n<0\).
-
2.
Given an object \(E \in \mathscr {T}\), we can find integers \(k_1> \cdots >k_m\) and a filtration
$$\begin{aligned} 0=E_0 \rightarrow E_1 \rightarrow \cdots \rightarrow E_{m-1}\rightarrow E_m=E \end{aligned}$$such that \({\text {C}}(E_{i-1} \rightarrow E_{i})=A_i[k_i]\) for some \(A_i \in \mathscr {A}\). The cohomology objects (with respect to \(\mathscr {A}\)) are defined as \(H^{-k_i}(E):=A_i\).
Lemma 2.4
Every bounded t-structure \(\mathscr {T}^{\le 0}\) is non-degenerate. In particular, the collection of functors \(H^i\) is conservative and \(H^i(E)=0\) for all \(i>0\) (respectively \(i<0\)) if and only if \(E \in \mathscr {T}^{\le 0}\) (respectively \(\mathscr {T}^{\ge 0}\)); this is [2, Proposition 1.3.7].
Proof
Let E be in the intersection of all \(\mathscr {T}^{\le i}\). Since \(\mathscr {T}^{\le 0}\) is bounded, E must be in \(\mathscr {T}^{\le j} \cap \mathscr {T}^{\ge h}\) for some j, h. Then E is in \(\mathscr {T}^{\ge h}\), but also in \(\mathscr {T}^{\le h-1}\). By definition,
So \({\text {Hom}}(E,E)=0\), therefore E is a zero object. In the same way one proves that also \(\bigcap _i \mathscr {T}^{\ge i} =0\).\(\square \)
Lemma 2.5
Let \(\mathscr {A} \subset \mathscr {T}\) be a heart. Then \(0\rightarrow A \overset{\alpha }{\rightarrow } B \overset{\beta }{\rightarrow } C \rightarrow 0\) is a short exact sequence in \(\mathscr {A}\) if and only if there exists a map \(\gamma :C \rightarrow A[1]\) such that

is a distinguished triangle (cf. proof of [2, Theorem 1.3.6]).
Proof
Notice that \(H^i(A)=0\) for \(i\ne 0\) and \(H^0(A) =A \) for any \(A \in \mathscr {A}\). We recall that, given a distinguished triangle \(E \rightarrow F \rightarrow G \rightarrow E[1]\), we have an induced exact sequence
in \(\mathscr {A}\).
Let \(0\rightarrow A \overset{\alpha }{\rightarrow } B \overset{\beta }{\rightarrow } C \rightarrow 0\) be a short exact sequence in \(\mathscr {A}\) and set \(C':={\text {C}}(A\rightarrow B)\). The cohomology functors give rise to an exact sequence
in \(\mathscr {A}\). Since \(\alpha \) is a monomorphism in \(\mathscr {A}\), \(H^{-1}(C')\) must be zero; on the other side, \(H^0(C')\cong {\text {coker}}(A\rightarrow B)= C\). The filtration in the definition proves that \(C' \cong H^0(C')\cong C\), so we can choose \(C'\) to be C with the same map appearing in the distinguished triangle.
Conversely, let \(A\overset{\alpha }{\rightarrow } B \overset{\beta }{\rightarrow } C \overset{\gamma }{\rightarrow } A[1]\) be a distinguished triangle with \(A,B,C \in \mathscr {A}\). Then the cohomology functors show that there is an exact sequence
concluding that \(0\rightarrow A \overset{\alpha }{\rightarrow } B \overset{\beta }{\rightarrow } C \rightarrow 0\) is a short exact sequence. \(\square \)
3 Semiorthogonal Decompositions and t-Structures
After recalling the notion of semiorthogonal decomposition, we define compatibility between t-structures with respect to such decomposition. In Theorem 3.7 we show how this situation gives rise to a global t-structure. As an application of the result, we study exceptional sequences and state Corollary 3.13, which generalizes Bondal’s theorem [3, Theorem 6.2] for exceptional sequences of length 2.
Definition 3.1
Let \(\mathscr {T}\) be a triangulated category. A semiorthogonal decomposition is a sequence of full triangulated subcategories \(\mathscr {T}_1 , \mathscr {T}_2 , \ldots , \mathscr {T}_n\) such that
-
1.
\({\text {Hom}}(\mathscr {T}_i,\mathscr {T}_j)=0\) with \(i>j\);
-
2.
For any \(E \in \mathscr {T}\), there is a filtration
$$\begin{aligned} 0 = E_{n} \rightarrow E_{n-1} \rightarrow \cdots \rightarrow E_1 \rightarrow E_0= E \end{aligned}$$such that \({\text {C}}(E_{i} \rightarrow E_{i-1}) \in \mathscr {T}_i\) for any \(i \in \lbrace 1, \ldots , n \rbrace \).
In this situation, we will write \(\mathscr {T}=\langle \mathscr {T}_1 , \mathscr {T}_2, \ldots , \mathscr {T}_n\rangle \).
Remark 3.2
Item 1 entails that both the filtration and its cones are unique up to isomorphism and functorial, as observed in [18, Remark 2.2].
Definition 3.3
Let \(\mathscr {T}\) be a triangulated category. Given two full subcategories \(\mathscr {X}\) and \(\mathscr {Y}\) of \(\mathscr {T}\), we define \(\mathscr {X}* \mathscr {Y}\) to be the full subcategory of \(\mathscr {T}\) whose objects are
This construction gives rise to an operation \(*\) between full subcategories of \(\mathscr {T}\).
Proposition 3.4
[2, Lemma 1.3.10]. The operation \(*\) is associative.
Example 3.5
Let \(\mathscr {T}\) be a triangulated category. Given a semiorthogonal decomposition \(\mathscr {T}= \langle \mathscr {T}_1 , \ldots , \mathscr {T}_n \rangle \), we can write \(\mathscr {T}= \mathscr {T}_n*\ldots *\mathscr {T}_2*\mathscr {T}_1\). If we consider a t-structure \(\mathscr {T}^{\le 0}\) on \(\mathscr {T}\), we have \(\mathscr {T}= \mathscr {T}^{\le 0}*\mathscr {T}^{\ge 1} \).
Definition 3.6
Let \(\mathscr {T}=\langle \mathscr {T}_1 , \mathscr {T}_2 \rangle \) be a semiorthogonal decomposition, \(\mathscr {T}\) any triangulated category. Assume that \(\mathscr {T}_i\) has a t-structure \(\mathscr {T}_i^{\le 0}\) for \(i=1,2\). Then \(\mathscr {T}_1^{\le 0}\) and \(\mathscr {T}_2^{\le 0}\) are compatible in \(\mathscr {T}\) if \({\text {Hom}}(\mathscr {T}_1^{\le 0} , \mathscr {T}_2^{\ge 1}) = 0\).
Denoted by \(\mathscr {A}_1\) and \(\mathscr {A}_2\) the hearts of \(\mathscr {T}_1^{\le 0} \) and \(\mathscr {T}^{\le 0}_2\) respectively, the relative dimension of \(\mathscr {A}_1\) and \(\mathscr {A}_2\) in \(\mathscr {T}\) is the number
Notice that, whenever the set above is nonempty, \({\text {rdim}}_{\mathscr {T}}(\mathscr {A}_1, \mathscr {A}_2) \ge 0\) by compatibility. The reason why we have chosen the value \(-1\) in case the set is empty will become clear reading the statement of Theorem 3.7.
Theorem 3.7
Let \(\mathscr {T}\) be a triangulated category with a semiorthogonal decomposition \(\mathscr {T}= \langle \mathscr {T}_1 , \mathscr {T}_2 \rangle \). Given two compatible t-structures \(\mathscr {T}_1^{\le 0}\) and \(\mathscr {T}_2^{\le 0}\) on \(\mathscr {T}_1\) and \(\mathscr {T}_2\) respectively, the full subcategory defined by
is a t-structure. Furthermore,
-
1.
If \(\mathscr {T}_1^{\le 0}\) and \(\mathscr {T}_2^{\le 0}\) are bounded (respectively non-degenerate), then \(\mathscr {T}^{\le 0}\) is bounded (respectively non-degenerate).
-
2.
Let \(\mathscr {A}_1\), \(\mathscr {A}_2\) and \(\mathscr {A}\) be the hearts associated to \(\mathscr {T}_1^{\le 0}\), \(\mathscr {T}_2^{\le 0}\) and \(\mathscr {T}^{\le 0}\) respectively. Then
$$\begin{aligned} \mathscr {A}=\mathscr {A}_2 * (\mathscr {A}_1[1]). \end{aligned}$$ -
3.
The following equality holds true whenever at least one of the two hearts \(\mathscr {A}_1, \mathscr {A}_2\) is nonzero:
$$\begin{aligned} \dim _{\mathscr {T}} \mathscr {A} = \max \lbrace \dim _{\mathscr {T}_1} \mathscr {A}_1 , \dim _{\mathscr {T}_2} \mathscr {A}_2 , {\text {rdim}}_{\mathscr {T}} (\mathscr {A}_1 , \mathscr {A}_2)+1\rbrace . \end{aligned}$$
Proof
Since \(\mathscr {T}_i^{\le 0}[1] \subset \mathscr {T}_i^{\le 0}\) for \(i=1,2\), it is clear that also \(\mathscr {T}^{\le 0}\) is closed by left shifts. We aim to show that \(\mathscr {T}= \mathscr {T}^{\le 0}* \mathscr {T}^{\ge 1}\), where \(\mathscr {T}^{\ge 1}:= (\mathscr {T}^{\le 0})^{\bot }\). Notice that
Since \(\langle \mathscr {T}_1 , \mathscr {T}_2 \rangle \) is a semiorthogonal decomposition and compatibility holds, we have
Therefore, \(\mathscr {T}=\mathscr {T}_2^{\le 0} *(\mathscr {T}_1^{\le 0} [1])* \mathscr {T}_2^{\ge 1} * (\mathscr {T}_1^{\ge 1} [1])\). We claim that \(\mathscr {T}_2^{\ge 1} * (\mathscr {T}_1^{\ge 1} [1])= \mathscr {T}^{\ge 1}\).
Let \(A \in \mathscr {T}_2^{\ge 1} * (\mathscr {T}_1^{\ge 1} [1])\). There exists a distinguished triangle \(A_2^{\ge 1}\rightarrow A \rightarrow A_1^{\ge 1}[1] \rightarrow A_2^{\ge 1}[1]\) with \(A_2^{\ge 1} \in \mathscr {T}_2^{\ge 1}\) and \(A_1^{\ge 1}[1] \in \mathscr {T}_1^{\ge 1}[1]\). Now let \(B\in \mathscr {T}^{\le 0}\) and consider the distinguished triangle \(B_2^{\le 0} \rightarrow B \rightarrow B_1^{\le 0}[1] \rightarrow B_2^{\le 0}[1]\), where \(B_2^{\le 0} \in \mathscr {T}_2^{\le 0}\) and \(B_1^{\le 0}[1] \in \mathscr {T}_1^{\le 0}[1]\). The two distinguished triangles introduced give rise to the following hom-exact sequences:

Since \(\langle \mathscr {T}_1 ,\mathscr {T}_2\rangle \) is a semiorthogonal decomposition, \({\text {Hom}}(B_2^{\le 0} , A_1^{\ge 1}[1])=0\), and the properties of t-structures tell us that \({\text {Hom}}(B_1^{\le 0}[1] , A_1^{\ge 1}[1]) =0= {\text {Hom}}(B_2^{\le 0} , A_2^{\ge 1})\). By compatibility, we also have \({\text {Hom}}(B_1^{\le 0}[1] , A_2^{\ge 1})=0\). Then the last two exact sequences prove that \({\text {Hom}}(B,A_1^{\ge 1}[1])={\text {Hom}}(B,A_2^{\ge 1})=0\). The first exact sequence concludes that \({\text {Hom}}(B,A)=0\). Finally, \(A \in \mathscr {T}^{\ge 1}\).
Conversely, if \(A \in \mathscr {T}^{\ge 1}\), then there exists a distinguished triangle
with \(A^{\le 0} \in \mathscr {T}^{\le 0}\) and \(A^{\ge 1} \in \mathscr {T}_2^{\ge 1} * (\mathscr {T}_1^{\ge 1} [1])\). Notice \(A^{\le 0} \rightarrow A\) must be zero because \(A \in \mathscr {T}^{\ge 1}\). Since \(A^{\ge 1}\) cannot have a direct summand in \(\mathscr {T}^{\le 0}\), we get that \(A^{\le 0}=0\). In particular, \(A=A^{\ge 1}\); as wanted, \(\mathscr {T}_2^{\ge 1} * (\mathscr {T}_1^{\ge 1} [1])= \mathscr {T}^{\ge 1}\).
-
1.
First, we deal with boundedness. Let \(A \in \mathscr {T}\). From the semiorthogonal decomposition, we get a distinguished triangle \(A_2 \rightarrow A \rightarrow A_1[1]\rightarrow A_2[1]\) where \(A_i \in \mathscr {T}_i\) for \(i=1,2\).Footnote 2 Since \(\mathscr {T}_i^{\le 0}\) is bounded, \(A_i \in \mathscr {T}_i^{\le k_i} \cap \mathscr {T}_i^{\ge h_i}\) for some integers \(k_i,h_i\). Let \(k:= \max \lbrace k_1 , k_2\rbrace \) and \(h:= \min \lbrace h_1, h_2\rbrace \).
By assumption, \(A_i \in \mathscr {T}_i^{\le 0}[-k_i]\), so \(A_i[k] \in \mathscr {T}_i^{\le 0}[k-k_i] \subseteq \mathscr {T}_i^{\le 0}\) being t-structures closed by left shifts. Therefore, \(A[k] \in \mathscr {T}^{\le 0}\); in other words \(A\in \mathscr {T}^{\le 0}[-k]=\mathscr {T}^{\le k}\).
Similarly, \(A_i \in \mathscr {T}_i^{\ge 1}[1-h_i]\) implies \(A_i[h-1] \in \mathscr {T}_i^{\ge 1}[1 -h_i+h-1] \subseteq \mathscr {T}_i^{\ge 1}\) (here we use the closure by right shifts). We conclude that \(A[h-1] \in \mathscr {T}^{\ge 1}\), which means that \(A\in \mathscr {T}^{\ge 1}[1-h] = \mathscr {T}^{\ge h}\). We have showed that \(A \in \mathscr {T}^{\le k} \cap \mathscr {T}^{\ge h}\).
To prove non-degeneracy when \(\mathscr {T}_1^{\le 0}\) and \(\mathscr {T}_2^{\le 0}\) are non-degenerate, let \(C \in \bigcap _j \mathscr {T}^{\le j}\). By Remark 3.2, we have \(C= {\text {C}}(E \rightarrow F)\) for \(E \in \bigcap _j \mathscr {T}_1^{\le j}\) and \(F \in \bigcap _j \mathscr {T}_2^{\le j}\). By hypothesis, both intersections are zero, so \(C \cong 0\) as wanted. The proof of \(\bigcap _j \mathscr {T}^{\ge j}=0\) is analogous since \(\mathscr {T}^{\ge 1} =\mathscr {T}_2^{\ge 1} * (\mathscr {T}_1^{\ge 1} [1])\).
-
2.
For any \(A \in \mathscr {A}\) we can find two distinguished triangles, according to the fact that \(A \in \mathscr {T}^{\le 0}\) and \(A[-1] \in \mathscr {T}^{\ge 1}=\mathscr {T}_2^{\ge 1} * (\mathscr {T}_1^{\ge 1} [1])\). Then Remark 3.2 proves that \(\mathscr {A}\) is exactly as described in the statement.
-
3.
Let \(A= {\text {C}}(A_1 \rightarrow A_2)\) and \(B= {\text {C}}(B_1 \rightarrow B_2)\) be two objects of \(\mathscr {A}\), with \(A_i,B_i \in \mathscr {A}_i\), \(i=1,2\). For any m, we consider the long exact sequence
$$\begin{aligned} \cdots \rightarrow {\text {Hom}}(A_1[1] , B[m]) \rightarrow {\text {Hom}}(A, B[m]) \rightarrow {\text {Hom}}(A_2,B[m]) \rightarrow \cdots \end{aligned}$$associated to the distinguished triangle \(A_1 \rightarrow A_2 \rightarrow A \rightarrow A_1[1]\). By considering the first and the last term, we can create two exact sequences associated to \(B_1 \rightarrow B_2\rightarrow B \rightarrow B_1[1]\):
$$\begin{aligned} \cdots \rightarrow {\text {Hom}}(A_1[1] , B_2[m]) \rightarrow {\text {Hom}}(A_1[1],B[m]) \rightarrow {\text {Hom}}(A_1[1], B_1[m+1]) \rightarrow \cdots \\ \cdots \rightarrow {\text {Hom}}(A_2, B_2[m]) \rightarrow {\text {Hom}}(A_2,B[m]) \rightarrow {\text {Hom}}(A_2,B_1[m+1]) \rightarrow \cdots \end{aligned}$$Notice that \({\text {Hom}}(A_2,B_1[m+1])=0\) since \(A_2 \in \mathscr {T}_2\) and \(B_1 \in \mathscr {T}_1\). Taking
$$\begin{aligned} \ell :=\max \lbrace \dim _{\mathscr {T}_1} \mathscr {A}_1 , \dim _{\mathscr {T}_2} \mathscr {A}_2 , {\text {rdim}}_{\mathscr {T}} (\mathscr {A}_1 , \mathscr {A}_2)+1\rbrace , \end{aligned}$$the exact sequences above prove that \({\text {Hom}}(A,B[m])=0\) for any \(m>\ell \), so \(\dim _{\mathscr {T}}\mathscr {A} \le \ell \). To conclude, it suffices to show that \(\dim _{\mathscr {T}}\mathscr {A}\ge \ell \).
We have two cases. If \(\ell \) is realized by the homological dimension of \(\mathscr {A}_1\) or \(\mathscr {A}_2\), we notice that \(\mathscr {A}_1[1], \mathscr {A}_2 \subset \mathscr {A}\) by item 2, so \(\dim _{\mathscr {T}}\mathscr {A}\ge \ell \).
Assume \(\ell ={\text {rdim}}_{\mathscr {T}}(\mathscr {A}_1 , \mathscr {A}_2)+1\). If \(0< \ell <+\infty \), for some choices of \(A_1[1]\) and \(B_2\) in \(\mathscr {A}\) we have \({\text {Hom}}(A_1[1],B_2[\ell ])\ne 0\). Similarly, if \(\ell =+ \infty \), there is a sequence \((a_n) \subset \mathbb {Z}\) such that \(a_n \rightarrow +\infty \) and \({\text {Hom}}(A_1^{n}[1],B_2^{n}[a_n])\ne 0\) for any \(a_n\) and some \(A_1^{n}[1], B_2^{n} \in \mathscr {A}\). Since item 2 tells us that \(A_1[1], A_1^n[1] ,B_2 , B_2^n \in \mathscr {A}\), in both cases \(\dim _{\mathscr {T}}\mathscr {A}\) cannot be less than \(\ell \). If \(\ell =0\), then \(\ell \) is also equal to the homological dimensions of \(\mathscr {A}_1\) or \(\mathscr {A}_2\), and this possibility has already been addressed.
\(\square \)
Remark 3.8
As already used in the last part of the proof, the constructed t-structure may not behave as wanted. For instance, using the notation of the statement, \(\mathscr {A}_1\) is not contained in \(\mathscr {A}\): we need to consider its shift \(\mathscr {A}_1[1]\).
One may think this shifting could be easily adjusted, but the requirement needed is incredibly strong. The first idea it comes to mind is to consider the t-structure \(\mathscr {T}_1^{\le 1}= \mathscr {T}_1^{\le 0}[-1]\) instead of \(\mathscr {T}_1^{\le 0}\). Indeed, if we ask \(\mathscr {T}_1^{\le 1}\) and \(\mathscr {T}_2^{\le 0}\) to be compatible, no shift will be involved, and in particular \(\mathscr {A}_1, \mathscr {A}_2 \subset \mathscr {A}\). However, requiring \(\mathscr {T}_1^{\le 1}\) and \(\mathscr {T}_2^{\le 0}\) to be compatible implies that \({\text {Hom}}(\mathscr {A}_1, \mathscr {A}_2)=0\), which is generally too restrictive.
Remark 3.9
Theorem 3.7 is incredibly linked to torsion pairs (for an introduction of the concept, we refer to [10, Section I.2]). Let \(\mathscr {T}\) be a triangulated category with a semiorthogonal decomposition \(\langle \mathscr {T}_1 , \mathscr {T}_2 \rangle \) and a t-structure \(\mathscr {T}^{\le 0}\) such that \(\mathscr {T}_i^{\le 0} = \mathscr {T}^{\le 0}\cap \mathscr {T}_i\) is a t-structure on \(\mathscr {T}_i\) for \(i=1,2\). If these t-structures are compatible in \(\mathscr {T}\), Theorem 3.7 gives rise to a t-structure \(\mathscr {T}_{\#}^{\le 0}\), which is different from \(\mathscr {T}^{\le 0}\). Indeed, \(E \in \mathscr {T}_1^{\le 0}\cap \mathscr {T}_1^{\ge 0}\) is an object in \((\mathscr {T}_{\#}^{\le 0}\cap \mathscr {T}_{\#}^{\ge 0})[-1]\).
As a matter of fact, \(\mathscr {T}_{\#}^{\le 0}\) gives rise to a heart which is a tilted version of the heart \(\mathscr {A}\) of \(\mathscr {T}^{\le 0}\). This is simply true by picking the couple \(\mathscr {F}= \mathscr {A} \cap \mathscr {T}_1\) and \(\mathscr {T}= \mathscr {A}\cap \mathscr {T}_2\), which is a torsion pair by [17, Exercise 6.5].
Remark 3.10
Theorem 3.7 is very similar to [2, Theorem 1.4.10], which constructs global t-structures via recollements instead of semiorthogonal decompositions. Let us explain this relation in detail.
First of all, we recall that any recollement gives rise to a semiorthogonal decomposition. We consider \(\mathscr {T}=\langle \mathscr {T}_1 ,\mathscr {T}_2 \rangle \) a semiorthogonal decomposition and let \(\mathscr {T}_i^{\le 0}\) a t-structure on \(\mathscr {T}_i\) for \(i=1,2\). Then, under their respective assumptions, from Theorem 3.7 we get the global t-structure \(\mathscr {T}_2^{\le 0} * (\mathscr {T}_1^{\le 0}[1])\), while [2, Theorem 1.4.10] gives the t-structure \(\mathscr {T}_2^{\le 0} * \mathscr {T}_1^{\le 0}\). In other words, the new result gives a tilted version of the old statement (see Remark 3.9).
Moreover, the two theorems deal with different situations. Indeed, although it is possible to construct a left adjoint \(i^*\) to the inclusion \(i_*:\mathscr {T}_1 \rightarrow \mathscr {T}\) (i.e. \(\mathscr {T}_1\) is left admissible) and a right adjoint \(j^*\) to the inclusion \(j_!:\mathscr {T}_2 \rightarrow \mathscr {T}\) (i.e. \(\mathscr {T}_2\) is right admissible) by [3, Lemma 3.1], in general a left (respectively right) admissible subcategory does not need to be right (respectively left) admissible. Conversely, a recollement does not ensure that the compatibility requirement is satisfied, since \(\mathscr {T}_2^{\ge 1}\) is not necessarily equal to \(\mathscr {T}^{\ge 1}\cap \mathscr {T}_2\).
Concerning our studies, Theorem 3.7 is to be preferred because it computes the homological dimension of the obtained heart; this is crucial, especially for Corollary 3.13.
The definition of compatible t-structures so that Theorem 3.7 holds can be generalized to semiorthogonal decompositions of any length, but the requirement may result unnatural since we need to consider some shifting.
Definition 3.11
Let \(\mathscr {T}= \langle \mathscr {T}_1, \ldots , \mathscr {T}_m\rangle \) and assume \(\mathscr {T}_i\) has a t-structure \(\mathscr {T}_i ^{\le 0}\) for \(i=1, \ldots , m\). Then all the t-structures are compatible if \({\text {Hom}}(\mathscr {T}_i^{\le 0}[k-i-1],\mathscr {T}_k^{\ge 1})=0\) for any \(k>i\).
With this notion of compatibility, an analogous of Theorem 3.7 can be obtained by recursion. With the same notation of the definition above, if \(\mathscr {A}_i\) is the heart of \(\mathscr {T}_i^{\le 0}\), the heart \(\mathscr {A}\subset \mathscr {T}\) built via Theorem 3.7 is described as
Example 3.12
—Exceptional sequence Let \(\mathbb {K}\) be a field and consider a \(\mathbb {K}\)-linear triangulated category \(\mathscr {T}\). We recall that an exceptional object is an object \(E \in \mathscr {T}\) such that
A sequence of exceptional objects \(E_1, \ldots , E_m \in \mathscr {T}\), such that \({\text {Hom}}(E_i , E_j[n])=0\) for any \(i>j\) and all n, is called exceptional sequence. It is full if \(\mathscr {T}\) is generated by \(E_1 , \ldots , E_m\), i.e. if \(\mathscr {T}\) is exact equivalent to the smallest full triangulated subcategory of \(\mathscr {T}\) containing \(E_1, \ldots , E_m\).
Consider a \(\mathbb {K}\)-linear triangulated category with a full exceptional sequence \(E_1, \ldots , E_m\) such that \(\bigoplus _i {\text {Hom}}(A,B[i])\) is a finite-dimensional vector space for any \(A,B \in \mathscr {T}\).Footnote 3 By [12, §1.4], it is known that such a full exceptional sequence gives rise to a semiorthogonal decomposition given by \(\mathscr {T}_i = \lbrace \bigoplus _\ell E_i^{\oplus b_\ell } [\ell ] : b_\ell \in \mathbb {N} \rbrace \). We will use the notation \(\langle E_1, \ldots , E_m \rangle \) to indicate exceptional sequences. Notice that on each \(\mathscr {T}_i\) we can consider a bounded t-structure with heart \(\mathscr {A}_i= \lbrace E_i^{\oplus b}: b \in \mathbb {N} \rbrace \).
If the full exceptional sequence is also strong,Footnote 4 i.e. \({\text {Hom}}(E_i , E_j[n])=0\) for any i, j and \(n\ne 0\), the above t-structures are compatible: indeed, taking \(k>i\),
Moreover, the t-structure induced on \(\mathscr {T}\) is bounded.
Corollary 3.13
Let \(\mathbb {K}\) be a field. Any \(\mathbb {K}\)-linear triangulated category \(\mathscr {T}\) with a full strong exceptional sequence \(\langle E_1 , E_2 \rangle \) such that \(\dim _{\mathbb {K}}{\text {Hom}}(E_1 , E_2) < \infty \) is algebraic. In particular, \(\mathscr {T}\cong {{\text {D}}^{{\text {b}}}}({\text {mod-}}A)\), where \(A={\text {End}}(\bigoplus _{i=1}^2 E_i)\).
Proof
Theorem 3.7 and Example 3.12 prove that \(\mathscr {T}\) has a heart of dimension at most 1. By [11, Theorem 3.2], \(\mathscr {T}\) is algebraic. We conclude by [20, Corollary 1.9].\(\square \)
Example 3.14
By the previous corollary, \({{\text {D}}^{{\text {b}}}}(\mathbb {P}_{\mathbb {K}}^1)\) is the unique \(\mathbb {K}\)-linear triangulated category with a full strong exceptional sequence \(\langle E_1 , E_2 \rangle \) such that \(\dim _{\mathbb {K}}{\text {Hom}}(E_1 , E_2)=2\).
4 Quivers
In order to study exceptional sequences of length greater than 2, we will need some basic knowledge on quivers. Here we will give a brief introduction, mostly following [3, Section 5].
Definition 4.1
A quiver is a quadruple \(Q=(Q_0 , Q_1, s,t)\), where \(Q_0\) is a set of vertices, \(Q_1\) a set of arrows between vertices and \(s,t:Q_1 \rightarrow Q_0\) are the maps indicating source and target respectively. A quiver is finite if \(Q_0\) and \(Q_1\) are finite. It is ordered if the vertices are ordered and for every arrow a, \(s(a)\le t(a)\).
A path p of length n is a sequence of arrows \(a_1 , \ldots ,a_n \in Q_1\) such that \(t(a_i)=s(a_{i+1})\). Moreover, with the same notation, \(t(p):=t(a_n)\) and \(s(p):=s(a_1)\). We also allow paths of length 0: such paths are in correspondence with the vertices. Let p, q be two paths. Then the composition of paths \(q\circ p\) is defined to be the concatenated path whenever \(s(q)=t(p)\).
Let \(\mathbb {K}\) be a field. The path algebra \(\mathbb {K}Q\) is the \(\mathbb {K}\)-vector space with basis the paths. The product is described as follows:
where \(\lambda , \mu \in \mathbb {K}\) and p, q are paths. In particular, paths of length 0 are idempotents in \(\mathbb {K}Q\).
If \(S\subset \mathbb {K}Q\) is any subset, (Q, S) is called quiver with relations and its associated path algebra is given by \(\mathbb {K}Q/\langle S \rangle \), where \(\langle S \rangle \) is the ideal generated by S.
Now, let us consider \(A= \mathbb {K}Q /\langle S \rangle \) the path algebra associated to the quiver with relations (Q, S). A left A-module is a vector space V over \(\mathbb {K}\) with the left action of the algebra A. This is also called representation of a quiver. Using the paths of length 0, which are associated to the vertices of Q, then V, as a vector space, decomposes into a direct sum \(\bigoplus _{i \in Q_0} V_i\), where \(V_i\) is the vector space associated to the vertex i. Moreover, for every path \(p \in A\), we get a linear operator \(V_{s(p)} \rightarrow V_{t(p)}\).
When dealing with right A-modules, one can consider the opposite quiver \(Q^{{\text {op}}}\) where s, t are swapped with respect to Q. In other words, arrows go in the other direction, analogously to what happens with the notion of opposite category. As one expects, left modules associated to \((Q^{{\text {op}}},S^{{\text {op}}})\) are right modules of A.
In case the quiver Q is finite and ordered, let \(X_1, \ldots , X_n\) be the vertices and \(p_i\) the idempotent in A associated to \(X_i\). Every right A-module V has a decomposition \(V=\bigoplus _{i \in Q_0} G_i V = \bigoplus _{i \in Q_0} Vp_i\).
Let us denote with \(S_i\) the representation for which \(G_j S_i = \delta _{ij} \mathbb {K}\), where \(\delta _{ij}\) is the Kronecker delta, and all arrows are represented by the zero morphisms. Notice that for each right A-module V we can create a filtration
such that each quotient \(F^i V / F^{i-1} V\) is a direct sum of copies of \(S_i\). Projective modules are \(P_i=p_i A\) and the decomposition \(A= \bigoplus _{i=1}^n P_i\) holds. As a matter of fact,
These isomorphisms allow to interpret the arrows of a quiver as morphisms between projective modules. In particular, being A the path algebra of an ordered quiver, \({\text {Hom}}(P_i , P_j)=0\) for \(i>j\). Furthermore, it is possible to consider the exact sequence
for every \(i =1, \ldots , n\). Notice that \(P_1 =S_1\).
Let \(\mathscr {T}\) be a \(\mathbb {K}\)-linear algebraic triangulated category with a full strong exceptional sequence \(\langle E_1 , \ldots , E_n\rangle \). Then \(A={\text {End}}(\bigoplus _{i=1}^n E_i)\) is the path algebra of an ordered and finite quiver with relations. In particular, the equivalence \(F:\mathscr {T}\rightarrow {{\text {D}}^{{\text {b}}}}({\text {mod-}}A)\) obtained in [20, Corollary 1.9] is such that \(F(E_i)=P_i\), the projective modules of the path algebra A.
5 Filtered Enhancements
In this section, we explore the definition of filtered triangulated categories and give a fairly simple result that has not been found in the literature, namely if a triangulated category admits a filtered enhancement, then every full triangulated subcategory admits a filtered enhancement in a natural way (see Proposition 5.4). Main reference is [1, Appendix A]. In Remark 5.6, we discuss the relation of filtered enhancements with realization functors.
Definition 5.1
Let us consider a quintuple \((\mathscr {F}, \mathscr {F}(\le 0) , \mathscr {F}(\ge 0) , s, \alpha )\), where \(\mathscr {F}\) is a triangulated category, \(\mathscr {F}(\le 0 )\) and \(\mathscr {F}(\ge 0)\) are strict full triangulated subcategories, \(s: \mathscr {F} \rightarrow \mathscr {F}\) is an exact equivalence and \(\alpha : {\text {id}}_{\mathscr {F}} \rightarrow s\) is a natural transformation. We set \(\mathscr {F}(\le n)=s^n \mathscr {F}(\le 0)\) and \(\mathscr {F}(\ge n)=s^n \mathscr {F}(\ge 0)\). In this picture, \(\mathscr {F}\) is called filtered triangulated category if it satisfies the following axioms:
- fcat 1:
-
\(\mathscr {F}(\le 0) \subset \mathscr {F}(\le 1)\) and \(\mathscr {F}(\ge 1) \subset \mathscr {F}(\ge 0)\).
- fcat 2:
-
\(\mathscr {F}= \bigcup _n \mathscr {F}(\le n)=\bigcup _n \mathscr {F}(\ge n)\).
- fcat 3:
-
\({\text {Hom}}(\mathscr {F}(\ge 1 ), \mathscr {F}(\le 0))=0\).
- fcat 4:
-
For any \(X \in \mathscr {F}\) there exists a distinguished triangle \(A \rightarrow X \rightarrow B \rightarrow A[1]\) where \(A \in \mathscr {F}(\ge 1)\) and \(B \in \mathscr {F}(\le 0)\); in other words, \(\mathscr {F}=\mathscr {F}(\ge 1) * \mathscr {F}(\le 0)\).
- fcat 5:
-
For any \(X \in \mathscr {F}\), it holds that \(\alpha _{s(X)}=s(\alpha _X)\).
- fcat 6:
-
For any \(X \in \mathscr {F}(\ge 1)\) and \(Y \in \mathscr {F}(\le 0)\), \(\alpha \) induces isomorphisms
$$\begin{aligned} {\text {Hom}}(Y,X) \cong {\text {Hom}}(Y,s^{-1}X) \cong {\text {Hom}}(sY,X). \end{aligned}$$
A triangulated category \(\mathscr {T}\) admits a filtered enhancement if there exists a filtered triangulated category \(\mathscr {F}\) such that \(\mathscr {T}\cong \mathscr {F}(\le 0) \cap \mathscr {F}(\ge 0)\) in the sense of triangulated categories. With an abuse of notation, we will always assume that \(\mathscr {T}=\mathscr {F}(\le 0) \cap \mathscr {F}(\ge 0)\).
Proposition 5.2
[1, Proposition A.3]. Let \(\mathscr {F}\) be a filtered triangulated category. Then the following assertions hold true:
-
1.
The inclusion \(i_{\le n}:\mathscr {F}(\le n) \rightarrow \mathscr {F}\) has a left adjoint \(\sigma _{\le n}\), and the inclusion \(i_{\ge n}:\mathscr {F}(\ge n) \rightarrow \mathscr {F}\) has a right adjoint \(\sigma _{\ge n}\). In particular, these adjoints are exact (see, for instance, [12, Proposition 1.41]).
-
2.
There is a unique natural transformation \(\delta : \sigma _{\le n} \rightarrow \sigma _{\ge n+1}[1]\) such that, for any \(X \in \mathscr {F}\),
$$\begin{aligned} \sigma _{\ge n+1} (X) \rightarrow X \rightarrow \sigma _{\le n}(X) \overset{\delta (X)}{\rightarrow } \sigma _{\ge n+1}(X)[1] \end{aligned}$$is a distinguished triangle. Up to unique isomorphism, this is the only distinguished triangle \(A \rightarrow X \rightarrow B \rightarrow A[1]\) with \(A \in \mathscr {F}(\ge n+1)\) and \(B \in \mathscr {F}(\le n)\).
-
3.
For any two integers m, n, we have the following natural isomorphisms:
$$\begin{aligned} \sigma _{\le m} \sigma _{\le n}\cong \sigma _{\le \min \lbrace m,n\rbrace } , \qquad \sigma _{\ge m}\sigma _{\ge n} \cong \sigma _{\le \max \lbrace m,n \rbrace }, \qquad \sigma _{\ge m} \sigma _{\le n} \cong \sigma _{\le n} \sigma _{\ge m}. \end{aligned}$$
Part of the proof. We want to prove the first two isomorphisms of item 3, since it is the only part of the statement not considered in [1]. Being the reasoning analogous, let us focus just on the first isomorphism. Let \(X \in \mathscr {F}\). If \(m\ge n\), then \(\mathscr {F}(\le m) \supset \mathscr {F}(\le n)\). We recall that \(\sigma _{\le m} i_{\le m} \cong {\text {id}}\) because the inclusion \(i_{\le m}\) is fully faithful. Since \(\sigma _{\le n}(X) \in \mathscr {F}(\le m)\), we simply have that \(\sigma _{\le m}\sigma _{\le n} (X) \cong \sigma _{\le n} (X)\) by the natural isomorphism mentioned before. We conclude that \(\sigma _{\le m} \sigma _{\le n}\cong \sigma _{\le n}\).
Let \(m\le n\), so that \(\mathscr {F}(\le m)\subset \mathscr {F}(\le n)\). Then, by adjunction, we have the following isomorphisms for any \(X \in \mathscr {F}\) and \(Y \in \mathscr {F}(\le m)\):
In particular, \(\sigma _{\le m} \sigma _{\le n}\) is left adjoint to \(i_{\le m}\). Since adjoints are determined up to a natural isomorphism, \(\sigma _{\le m}\sigma _{\le n} \cong \sigma _{\le m}\) as wanted.
Remark 5.3
By item 2 of Proposition 5.2, we also have the following isomorphisms:
Let us set \({\text {gr}}^n:= \sigma _{\le n}\sigma _{\ge n}\). This is not the definition used in [1], but it will come in handy in the proof of the following statement.
Proposition 5.4
Let \(\mathscr {T}\) be a triangulated category admitting a filtered enhancement \(\mathscr {F}\). Then any full triangulated subcategory \(\mathscr {S}\) of \(\mathscr {T}\) has a filtered enhancement given by the full subcategory \(\mathscr {G}\) of \(\mathscr {F}\) with objects
Proof
First of all, we would like to show that \(\mathscr {G}\) is a triangulated subcategory of \(\mathscr {F}\). Notice that the shift functor of \(\mathscr {F}\) obviously restricts to \(\mathscr {G}\) since \(s^{-n}{\text {gr}}^n\) is exact, being composition of exact functors. Let us consider \(X \rightarrow Y\) with \(X,Y \in \mathscr {G}\). This gives a distinguished triangle \(X \rightarrow Y \rightarrow Z \rightarrow X[1]\) in \(\mathscr {F}\). We get that
is a distinguished triangle in \(\mathscr {T}\), with \(s^{-n} {\text {gr}}^n (X)\) and \(s^{-n} {\text {gr}}^n (Y)\) objects of \(\mathscr {S}\). This suffices to conclude that \(s^{-n} {\text {gr}}^n (Z) \in \mathscr {S}\), so that \(Z \in \mathscr {G}\). Next, we set \(\mathscr {G}(\le 0):= \mathscr {G}\cap \mathscr {F}(\le 0)\) and \(\mathscr {G}(\ge 0):= \mathscr {G}\cap \mathscr {F}(\ge 0)\). We would like to prove that the autoequivalence \(s: \mathscr {F} \rightarrow \mathscr {F}\) can be restricted to \(\mathscr {G}\). Let \(X \in \mathscr {G}\). Then, by Remark 5.3, we have
So we can restrict s and create an exact autoequivalence \(s:\mathscr {G}\rightarrow \mathscr {G}\), called s as well by an abuse of notation. Of course, the restriction of \(\alpha : {\text {id}}_{\mathscr {F}} \rightarrow s\) gives us the required natural transformation and fcat 5 is ensured. We set \(\mathscr {G}(\le n)\) and \(\mathscr {G}(\ge n)\) via s as described in Definition 5.1. Being s an equivalence, we have the following
and analogously \(\mathscr {G}(\le n) = \mathscr {G}\cap \mathscr {F}(\le n)\). This immediately shows that fcat 1, 2, 3, 6 hold. As fcat 5 has already been dealt with, it remains to show fcat 4. In order to do that, we recall the distinguished triangle in item 2 of Proposition 5.2. Therefore, the statement is reduced to establish that the images of \(\sigma _{\le n}\) and \(\sigma _{\ge n}\) are in \(\mathscr {G}(\le n)\) and \(\mathscr {G}(\ge n)\) respectively, so that these functors are adjoints to the inclusions as in \(\mathscr {F}\). Let \(X \in \mathscr {G}\) and consider \(\sigma _{\le m}\). By item 3 of Proposition 5.2 and Remark 5.3 the following isomorphisms hold:
In particular, \(s^{-n}{\text {gr}}^n(\sigma _{\le m}X)\cong \sigma _{\le m-n} (A)\), where \(A \in \mathscr {S}\). If \(m-n\ge 0\), we have the following inclusions:
so \(\sigma _{\le m-n}(A)=A\). If \(m-n<0\), being \(A \in \mathscr {F}(\ge 0)\) it holds that \({\text {Hom}}(A,\sigma _{\le m-n}(A))=0\) by fcat 3. In particular, item 2 of Proposition 5.2 entails that \(\sigma _{\le m-n}(A)=0\). As wanted, \(s^{-n}{\text {gr}}^n(\sigma _{\le m}X)\in \mathscr {S}\), so that \(\sigma _{\le m}X \in \mathscr {G}\). With a similar reasoning, one can prove that \(\sigma _{\ge m} X \in \mathscr {G}\). \(\square \)
The reason why filtered enhancements become of great interest is their relation with realization functors.
Definition 5.5
Let \(\mathscr {T}\) be a triangulated category. Given a heart (of a bounded t-structure) \(\mathscr {A}\subset \mathscr {T}\), we call realization functor (of \(\mathscr {A}\) in \(\mathscr {T}\)) an exact functor \(\mathsf {real}:{{\text {D}}^{{\text {b}}}}(\mathscr {A}) \rightarrow \mathscr {T}\) such that \(\mathsf {real}_{\mid \mathscr {A}}={\text {id}}_{\mathscr {A}}\).
Remark 5.6
In [1, Appendix], it is proven that every triangulated category with a filtered enhancement admits a realization functor for any heart. However, some authors point out that an additional requirement, called fcat 7, may be necessary to provide the result (see [21, Appendix A] for further details).
For the sake of completeness, let us state this new axiom using the same notation of Definition 5.1.
- fcat 7:
-
Given any morphism \(f: X \rightarrow Y\) in \(\mathscr {F}\), the diagram
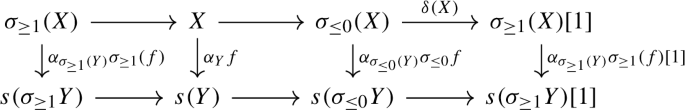
can be extended to a \(3 \times 3\)-diagram whose rows and columns are distinguished triangles.
Once ensured that \(\mathscr {F}\) satisfies fcat 7, it is easy to prove that also \(\mathscr {G}\) as defined in Proposition 5.4 fulfills fcat 7. This will be key in what follows.
6 Realized Triangulated Categories
This section revolves around the unconventional notion of realized triangulated categories. After the definition, we will give some large classes of examples studied in the literature and prove a crucial result, Proposition 6.3. As an application, the generalization of Bondal’s theorem [3, Theorem 6.2] is ensured for realized triangulated categories.
Definition 6.1
A triangulated category \(\mathscr {T}\) is called realized if for every heart \(\mathscr {A}\) of every full triangulated subcategory \(\mathscr {S} \subset \mathscr {T}\) there exists a realization functor \(\mathsf {real}:{{\text {D}}^{{\text {b}}}}(\mathscr {A}) \rightarrow \mathscr {S}\subset \mathscr {T}\).
Example 6.2
-
1.
Triangulated categories with a filtered enhancement are realized, as discussed in Proposition 5.4 and Remark 5.6.
-
2.
Algebraic triangulated categories are realized by [16, Theorem 3.2], where the first item is proved in detail in [14, Section 4]. In fact, every algebraic triangulated category has a filtered enhancement, as proved in [5, Proposition 3.8], but fcat 7 has not been investigated.
-
3.
Every triangulated category which is the underlying category of a stable derivator admits a filtered enhancement; this is the content of [19].
Furthermore, topological triangulated categories obtained by stable combinatorial model categories are filtered by [9, Example 4.2]. In particular, there are examples of triangulated categories with a filtered enhancement which are not algebraic.
Proposition 6.3
[6, Corollary 2.8]. Let \(\mathscr {T}\) be a realized triangulated category and let \(\mathscr {A}\) be a heart on \(\mathscr {T}\). The following assertions are equivalent:
-
1.
\(\mathscr {T}\) has all the Ext groups of \(\mathscr {A}\) according to Definition A.12.
-
2.
The realization functor \(\mathsf {real}:{{\text {D}}^{{\text {b}}}}(\mathscr {A}) \rightarrow \mathscr {T}\) is fully faithful.
-
3.
The realization functor is full.
Moreover, under such circumstances, \(\mathsf {real}\) is an exact equivalence.
Proof
We start with \(1. \Rightarrow 2\). Let \(E,F \in {{\text {D}}^{{\text {b}}}}(\mathscr {A})\) and consider \(\tilde{E}=\mathsf {real}(E)\) and \(\tilde{F}=\mathsf {real}(F)\). Then, by Proposition 2.3, there exist integers \(k_1> \cdots > k_m\), \(j_1 > \cdots j_n\) and filtrations
with \({\text {C}}(E_{i-1} \rightarrow E_i)=E^i\in \mathscr {A}[k_i]\) and \({\text {C}}(F_{h-1} \rightarrow F_h)=F^h \in \mathscr {A}[j_h]\). Since \(\mathsf {real}\) is an exact functor, their images \(\tilde{E}_i, \tilde{E}^i, \tilde{F}_h\) and \(\tilde{F}^h\) give the same filtrations. We consider the exact hom-sequences

From these sequences, an induction on i and h proves that \({\text {Hom}}(E_{i},F_h)\cong {\text {Hom}}(\tilde{E}_{i} , \tilde{F}_h)\), so finally \({\text {Hom}}(E,F)\cong {\text {Hom}}(\tilde{E}, \tilde{F})\) as wanted. Notice the base case is ensured since \(\mathscr {T}\) has all the Ext groups of \(\mathscr {A}\).
The implication \(2. \Rightarrow 3.\) is trivial. We deal with \(3. \Rightarrow 1\). In order to do that, we use item 3 and 4 of Proposition A.7, remembering Proposition A.15. Let \(A,B \in \mathscr {A}\). Since \(f_{1,A,B}: {\text {Ext}}^1(A,B) \rightarrow {\text {Hom}}_{\mathscr {T}} (A,B[1])\) is an isomorphism by Dyer’s Theorem A.2, we know that \(f_{2,A,B}\) is injective. Moreover, since \(\mathsf {real}\) is full, \(f_{2,A,B}\) is surjective, thus an isomorphism. The same reasoning proves that \(f_{n,A,B}\) is an isomorphism for every n, concluding that \(\mathscr {T}\) has all the Ext groups of \(\mathscr {A}\).
We now assume that \(\mathsf {real}\) is fully faithful and prove that it is also an equivalence. Let \(E \in \mathscr {T}\). By Proposition 2.3, there are a sequence of integers \(k_1> \cdots > k_m\) and a filtration
such that \({\text {C}}(E_{i-1} \rightarrow E_i)=E^i \in \mathscr {A}[k_i]\). We prove by induction on m that E is in the essential image of \(\mathsf {real}\). If \(m=0\), there is nothing to prove. If \(m>0\), then by induction hypothesis \(E_{m-1}= \mathsf {real}(\hat{E}_{m-1})\). Obviously, \(E^m= \mathsf {real}(\hat{E}^m)\) because all shifts of the heart \(\mathscr {A}\) are in the essential image of \(\mathsf {real}\). By the filtration, \(E={\text {C}}(E^m[-1] \rightarrow E_{m-1})\). The map associated to this cone is the image of a unique map \(f:\hat{E}^m[-1] \rightarrow \hat{E}_{m-1}\) in \({{\text {D}}^{{\text {b}}}}(\mathscr {A})\) because \(\mathsf {real}\) is fully faithful. We consider its cone \({\text {C}}(f)\). Since \(\mathsf {real}\) is exact, we obtain an isomorphism \(\mathsf {real}({\text {C}}(f)) \cong E\). \(\square \)
Remark 6.4
As a corollary, it is immediately proven that not all hearts in a derived category have all the Ext groups. Indeed, in \({{\text {D}}^{{\text {b}}}}(\mathbb {P}^1)\) one can show that \(\mathscr {A}=\lbrace \mathscr {O}_{\mathbb {P}^1}^{\oplus a_0}[2] \oplus \mathscr {O}_{\mathbb {P}^1}(1)^{\oplus a_1} \mid a_0 , a_1\ge 0 \rbrace \) gives a heart (this can be done by applying Theorem 3.7). As highlighted in [17, Exercise 5.3], \({{\text {D}}^{{\text {b}}}}(\mathscr {A})\cong {{\text {D}}^{{\text {b}}}}({\text {pt}})^{\oplus 2}\) is not equivalent to \({{\text {D}}^{{\text {b}}}}(\mathbb {P}^1)\), so \({{\text {D}}^{{\text {b}}}}(\mathbb {P}^1)\) cannot have all the Ext groups of \(\mathscr {A}\).
With a different approach, notice that \(\mathscr {A}\ni \mathscr {O}_{\mathbb {P}^1}[2] \rightarrow \mathscr {O}_{\mathbb {P}^1}(1)[2]\in \mathscr {A}[2]\) does not factor through an object in \(\mathscr {A}[1]\), and therefore Corollary A.13 proves that \({{\text {D}}^{{\text {b}}}}(\mathbb {P}^1)\) does not have all the Ext groups of \(\mathscr {A}\).
Remark 6.5
Let \(\mathbb {K}\) be a field and consider a realized \(\mathbb {K}\)-linear triangulated category \(\mathscr {T}\) with a full strong exceptional sequence \(\langle E_1 , \ldots , E_n\rangle \). Then we can consider the heart \(\mathscr {A}\) on \(\mathscr {T}\) obtained according to Theorem 3.7 and Example 3.12, giving rise to a realization functor \({{\text {D}}^{{\text {b}}}}(\mathscr {A}) \rightarrow \mathscr {T}\). One would like to prove that such functor is in fact an equivalence, so that [20, Corollary 1.9] can be applied to ensure the generalization of Bondal’s result [3, Theorem 6.2]. However, when \(n>2\), it is not said that \(\mathscr {T}\) has all the Ext groups of \(\mathscr {A}\); for instance, if \(n=3\),
does not necessarily factor through \(\mathscr {A}[1]\). In general, we would have \(f \notin {\text {Ext}}^2_{\mathscr {A}}(E_1[2],E_3)\) by Proposition A.7, item 1. For example, consider the quiver obtained by the following vertices and arrows:

In order to resolve this issue, we recall what already discussed in Remark 3.9. If the length of the exceptional sequence is 2, the heart obtained by Theorem 3.7 is a tilt of \({\text {mod-}}A\), where \(A={\text {End}}(\bigoplus _{i=1}^2 E_i)\). As we will see, the same idea can be used to prove the general case.
Theorem 6.6
Let \(\mathbb {K}\) be a field and let \(\mathscr {T}\) be a realized \(\mathbb {K}\)-linear triangulated category with a full strong exceptional sequence \(\langle E_1 , \ldots , E_n \rangle \) such that \(\bigoplus _i {\text {Hom}}(X,Y[i])\) is a finite-dimensional vector space for any \(X,Y \in \mathscr {T}\). Then \(\mathscr {T}\cong {{\text {D}}^{{\text {b}}}}({\text {mod-}}A)\), where \(A= {\text {End}}(\bigoplus _{i=1}^n E_i)\).
Proof
We will prove the statement by induction on n, the length of the exceptional sequence. The base case \(n=2\) is already taken care of by Corollary 3.13.
If \(n>2\), we write \(\mathscr {T}= \langle \tilde{\mathscr {T}} , E_n \rangle \). By induction hypothesis, there exists an exact equivalence \(\varphi : {{\text {D}}^{{\text {b}}}}({\text {mod-}}\tilde{A})\rightarrow \tilde{\mathscr {T}}\) with \(\tilde{A}={\text {End}}(\bigoplus _{i=1}^{n-1} E_i)\). We divide the proof in two parts:
-
1.
The t-structures associated to \(\varphi ({\text {mod-}}\tilde{A})\) and \(E_n\) are compatible. By Theorem 3.7, we obtain a heart \(\mathscr {A}\) on \(\mathscr {T}\).
-
2.
\(\mathscr {T}\) has all the Ext groups of \(\mathscr {A}\).
Once both items are ensured, Proposition 6.3 can be applied, proving that \(\mathscr {T}\cong {{\text {D}}^{{\text {b}}}}(\mathscr {A})\), and an application of [20, Corollary 1.9] will complete the proof.
From (3.2), every object \(X \in {\text {mod-}}\tilde{A}\) has an associated filtration
where \(F^{k}X/F^{k-1}X\) is a direct sum of copies of \(S_k\). Moreover, for each \(P_k\) there is a short exact sequence \(0 \rightarrow F^{k-1} P_k \rightarrow P_k \rightarrow S_k \rightarrow 0\) by (3.3). In particular, \(S_1 =P_1\).
Let us deal with 1. In order to prove it, it suffices to show that \({\text {Hom}}(\varphi (X),E_n[m])=0\) for every \(m\le -1\) and \(X \in {\text {mod-}}\tilde{A}\). This can be done by induction on k, requiring \(F^k X=X\). If \(k=1\), \(F^1 X \) is in fact a direct sum of copies of \(P_1=\varphi ^{-1}(E_1)\), so the claim holds.
If \(k>1\), notice that the short exact sequence \(0\rightarrow F^{k-1} P_k \rightarrow P_k \rightarrow S_k\rightarrow 0\) is associated to a distinguished triangle in \(\mathscr {T}\), so it gives rise to the hom-sequence
By induction, \({\text {Hom}}(\varphi (F^{k-1} P_k) [1] , E_n [m])=0\), while \({\text {Hom}}(E_k , E_n[m])=0\) by hypothesis. Therefore, \({\text {Hom}}(\varphi (S_k) , E_n[m])=0\). We now consider \(X=F^k X\) and the distinguished triangle
obtained by the filtration. From the associated hom-sequence, \({\text {Hom}}(\varphi (X), E_n[m])=0\) since the same holds for \(F^{k-1} X\) and \(X/F^{k-1} X\), the last one being a direct sum of copies of \(S_k\).
It remains to prove item 2. According to Corollary A.14, we will prove by induction on m that \({\text {Hom}}(\varphi (X),E_n[m])\cong {\text {Ext}}_{\mathscr {A}}^m(\varphi (X),E_n)\) with \(\varphi (X) \in \varphi ({\text {mod-}}\tilde{A})[1] \subset \mathscr {A}\). The cases \(m=0,1\) are true since \(\mathscr {A}\) is a heart. Let \(m>1\). By Proposition A.7, it holds that \({\text {Ext}}^m(E_k[1] , E_n)\subset {\text {Hom}}(E_k[1],E_n[m])=0\), and therefore \({\text {Ext}}^m(E_k[1] , E_n)=0\). Let us consider the distinguished triangle \(F^{k-1} P_k \rightarrow P_k \rightarrow S_k \rightarrow F^{k-1} P_k [1]\). Applying \({\text {Hom}}(\varphi ( -) , E_n[m])\), we get the following commutative diagram

proving that \({\text {Ext}}^m (\varphi (S_k)[1] , E_n) \cong {\text {Hom}}(\varphi (S_k)[1] , E_n[m])\) for every k (use, for instance, the five lemma).
Now, we proceed by induction on the length of the filtration. If \(X=F^1 X\), there is nothing to prove since \(F^1 X\) is a sum of copies of \(S_1 =E_1\), and therefore \({\text {Hom}}(\varphi (F^1 X)[1] , E_n[m])=0\) since \(m>1\). If \(X=F^k X\), we consider the short exact sequence \(0 \rightarrow F^{k-1} X \rightarrow X \rightarrow X/F^{k-1} X \rightarrow 0\). Then we get the following diagram:

To show that \(f_k\) is an isomorphism, it suffices to apply the five lemma whenever \(g_k\) is a monomorphism. More strongly, we claim that \(g_k\) is an isomorphism. The idea is exactly the one seen above with the diagram (5.7). In order to prove that
we will check that \({\text {Ext}}^{m} (E_k[1] , Y) \cong {\text {Hom}}(E_k[1], Y[m])\) for any \(Y \in \mathscr {A}\), and conclude by item 3 of Proposition A.7. This is in fact true. Indeed, notice that
for any \(X \in {\text {mod-}}\tilde{A}\) because \(E_k\) is projective in \(\varphi ({\text {mod-}}\tilde{A})\). Furthermore, as remarked before (5.7), \({\text {Ext}}^m(E_k[1] , E_n)={\text {Hom}}(E_k[1],E_n[m])=0\). We conclude that
since any \(Y\in \mathscr {A}\) is the extension of a direct sum of copies of \(E_n\) and an object \(\varphi (X)[1] \in \varphi ({\text {mod-}}\tilde{A})\). \(\square \)
Notes
Here, and in the following, category is used to mean locally small category.
The choice of \(A_1[1]\) in the distinguished triangle is motivated by the fact that \(\mathscr {T}^{\le 0} = \mathscr {T}_2^{\le 0} *(\mathscr {T}_1^{\le 0}[1])\).
In fact, it suffices to require this property for \(A,B \in \lbrace E_1 , \ldots , E_m \rbrace \).
This condition can be weakened.
References
Beĭlinson, A.A.: On the derived category of perverse sheaves. In: Manin, Y.I. (ed.) K-Theory, Arithmetic and Geometry: Seminar, Moscow University, 1984–1986, pp. 27–41. Springer, Berlin (1987)
Beĭlinson, A.A., Bernstein, J., Deligne, P.: Faisceaux pervers. In: Analysis and Topology on Singular Spaces, I (Luminy, 1981), vol. 100, pp. 5–171. Asterisque. Soc. Math. France, Paris (1982)
Bondal, A.I.: Representations of associative algebras and coherent sheaves. Izv. Akad. Nauk SSSR Ser. Mat. 53(1), 25–44 (1989)
Bridgeland, T.: Stability conditions on triangulated categories. Ann. Math. (2) 166(2), 317–345 (2007)
Chen, X.W., Ringel, C.M.: Hereditary triangulated categories. J. Noncommut. Geom. 12, 1425–1444 (2018)
Chen, X.W., Han, Z., Zhou, Y.: Derived equivalences via HRS-tilting. Adv. Math. 354, 106749 (2019)
Dyer, M.J.: Exact subcategories of triangulated categories. https://www3.nd.edu/~dyer/papers/extri.pdf (2005)
Gelfand, S.I., Manin, Y.I.: Methods of Homological Algebra. Springer Monographs in Mathematics, 2nd edn. Springer, Berlin (2003)
Groth, M.: Derivators, pointed derivators and stable derivators. Algebra Geom. Topol. 13(1), 313–374 (2013)
Happel, D., Reiten, I., Smalø, S.O.: Tilting in abelian categories and quasitilted algebras. Mem. Am. Math. Soc. 120, 575 (1996)
Hubery, A.: Characterising the bounded derived category of an hereditary abelian category. https://arxiv.org/abs/1612.06674 (2016)
Huybrechts, D.: Fourier-Mukai Transforms in Algebraic Geometry. Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, Oxford (2006)
Iversen, B.: Cohomology of Sheaves. Universitext, Springer, Berlin (1986)
Keller, B.: Chain complexes and stable categories. Manuscr. Math. 67(4), 379–417 (1990)
Keller, B.: Derived categories and tilting. In: Handbook of Tilting Theory, pp. 49–104 (2010)
Keller, B., Vossieck, D.: Sous les catégories dérivées. C. R. Acad. Sci. Paris Sér. I Math. 305(6), 225–228 (1987)
Macrì, E., Schmidt, B.: Lectures on Bridgeland stability. In: Moduli of Curves, vol. 21. Lecture Notes of the Unione Matematica Italiana, pp. 139–211. Springer, Cham (2017)
Macrì, E., Stellari, P.: Lectures on Non-commutative K3 Surfaces, Bridgeland Stability, and Moduli Spaces. https://arxiv.org/abs/1807.06169 (2018)
Modoi, G.C.: Reasonable triangulated categories have filtered enhancements. Proc. Am. Math. Soc. 147(7), 2761–2773 (2019)
Orlov, D. O.: Geometric realizations of quiver algebras. Proc. Steklov Inst. Math. 290(1), 70–83 (2015). Published in Russian in Tr. Mat. Inst. Steklova 290(1), 80–94 (2015)
Psaroudakis, C., Vitória, J.: Realisation functors in tilting theory. Math. Z. 288(3–4), 965–1028 (2018)
Quillen, D.: Higher algebraic K-theory: I. In: Algebraic K-Theory, I: Higher K-Theories (Proceedings of the Conference Held at the Seattle Research Center of Battelle Memorial Institute, 1972). Lecture Notes in Mathematics, vol. 341, pp. 85–147 (1973)
Rizzardo, A., Van den Bergh, M.: A k-linear triangulated category without a model. Ann. Math. (2) 191(2), 393–437 (2020)
Acknowledgements
I am very thankful to my supervisor Alberto Canonaco for his suggestions and corrections. I would also like to thank Irakli Patchkoria and Xiao-Wu Chen, who pointed out the existence of Hubery’s result [11, Theorem 3.2] after the first preliminary version of this article. I am grateful to the referee who provided insightful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Bernhard Keller.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Yoneda Extensions in a Triangulated Category
Yoneda Extensions in a Triangulated Category
A necessary remark to prove Hubery’s main result is that, for a heart \(\mathscr {A}\) in a triangulated category \(\mathscr {T}\), if \(\dim _{\mathscr {T}}(\mathscr {A})\le 1\), then \(\dim _{{{\text {D}}^{{\text {b}}}}(\mathscr {A})}(\mathscr {A})\le 1\) (see [11, Section 3]). This appendix aims to generalize this observation, providing results on Yoneda extensions in any triangulated category.
First of all, we want to recall a theorem by Dyer, as it will give the desired generality for Proposition A.7. For this reason, let us give the definition of exact category according to Quillen [22].
Definition A.1
An exact category \(\mathscr {A}\) is a full extension closed additive subcategory of an abelian category \(\mathscr {B}\). A conflation (or short exact sequence) is given by a short exact sequence in \(\mathscr {B}\) contained in \(\mathscr {A}\).
Theorem A.2
(Dyer) [7]. Let \(\mathscr {A}\) be a full extension closed additive subcategory of a triangulated category \(\mathscr {T}\) such that \({\text {Hom}}(A,B[-1])=0\) for any \(A,B \in \mathscr {A}\).
Then \(\mathscr {A}\) has a natural exact structure, given by defining \(0 \rightarrow A \rightarrow B \rightarrow C\rightarrow 0\) a conflation if \(A \rightarrow B \rightarrow C \rightarrow A[1]\) is a distinguished triangle in \(\mathscr {T}\) for some \(C \rightarrow A[1]\). This association gives rise to a natural isomorphism \({\text {Ext}}^1_\mathscr {A}(A,B) \cong {\text {Hom}}_{\mathscr {T}}(A,B[1])\) for all \(A,B \in \mathscr {A}\).
Remark A.3
A heart \(\mathscr {A}\) in a triangulated category \(\mathscr {T}\) satisfies the requirements of Theorem A.2 thanks to Lemma 2.5.
Definition A.4
(Yoneda extensions) Let \(\mathscr {A}\) be an abelian category. The elements of the group \({\text {Ext}}^n(A,B)\cong {\text {Hom}}_{{{\text {D}}^{{\text {b}}}}(\mathscr {A})}(A,B[n])\) are n-extensions for \(n>0\), i.e. exact sequences
under the equivalence relation generated by identifying two exact sequences \(\mathbf {X}\), \(\mathbf {Y}\) if there is a family of morphisms \(\psi = \lbrace \psi _1 , \ldots , \psi _n \rbrace \) satisfying the following commutative diagram

(cf. [8, Theorem III.5.5]). For \(n=0\), \({\text {Ext}}^0(A,B)\cong {\text {Hom}}_{{{\text {D}}^{{\text {b}}}}(\mathscr {A})}(A,B)\cong {\text {Hom}}_{\mathscr {A}}(A,B)\).
The Yoneda product is given by maps \(Y^{n,m}_{A,B,C}:{\text {Ext}}^n (A,B) \times {\text {Ext}}^m(B,C) \rightarrow {\text {Ext}}^{n+m}(A,C)\) for any \(n,m\ge 0\) and any \(A,B,C \in \mathscr {A}\). For \(n,m \ge 1\), the Yoneda product is the map

If \(n=m=0\), the product is simply the composition of maps. The case \(n> 0\) and \(m=0\) requires a more sophisticated definition. Let \(X_1 \in {\text {Ext}}^1(K,B)\) and \(g:B \rightarrow C\). Then \(g \cdot X_1\) is described by the following commutative diagram

where \(g\cdot X_1\) is the pushout of g and \(B \rightarrow X_1\). Now, considering an n-extension
and \(g:B \rightarrow C\), the Yoneda product is given by substituting \(0 \rightarrow B \rightarrow X_1\) with \(0 \rightarrow C \rightarrow g \cdot X_1\):
Dually, one can describe the case \(n=0\) and \(m>0\). The Yoneda product so defined behaves according to the composition of maps (up to shift)
The structure of abelian group of \({\text {Hom}}_{{{\text {D}}^{{\text {b}}}}(\mathscr {A})}(A,B[n])\) can be considered on \({\text {Ext}}^n(A,B)\) via the Baer sum, described as follows. Let \(\mathbf {X},\mathbf {Y}\in {\text {Ext}}^n(A,B)\). Consider the direct sum of the long exact sequences
the diagonal map \(\Delta _A=\left( {\begin{matrix} {\text {id}}\\ {\text {id}}\end{matrix}}\right) : A \rightarrow A \oplus A\) and the codiagonal map \(\nabla _B = ({\text {id}}\ {\text {id}}) : B\oplus B \rightarrow B\). Then the Baer sum is given by \(\mathbf {X} + \mathbf {Y}:=\nabla _B \cdot (\mathbf {X}\oplus \mathbf {Y})\cdot \Delta _A\).
The (absolute) homological dimension of \(\mathscr {A}\), denoted by \(\dim \mathscr {A}\), is the greatest integer n such that \({\text {Ext}}^n(A,B) \ne 0\) for some \(A,B \in \mathscr {A}\).
Remark A.6. Last definition can be generalized to any exact category \(\mathscr {A}\), where an n-extension is a sequence

such that, for \(i=1, \ldots , n-1\), \(\xi _i\) factor through an object \(C_i \in \mathscr {A}\) and
are conflations. In particular, \(C_i = {\text {im}}\xi _i=\ker \xi _{i+1}\).
Proposition A.7. [6, Lemma 2.1]. Let \(\mathscr {A}\) be a heart of a triangulated category \(\mathscr {T}\). More generally, let \(\mathscr {A}\) be an exact subcategory of \(\mathscr {T}\) as in Dyer’s Theorem A.2. Then there is a well-defined map \(f_{n,A,B}:{\text {Ext}}^n(A,B) \rightarrow {\text {Hom}}_{\mathscr {T}}(A,B[n])\) for any \(A,B \in \mathscr {A}\) and \(n\ge 0\). The following facts are true.
-
1.
The image of \(f_{n,A,B}\) is given by all the maps \(A \rightarrow B[n]\) factoring as
$$\begin{aligned} A \rightarrow C_{n-1} [1] \rightarrow \cdots \rightarrow C_1[n-1]\rightarrow B[n] \end{aligned}$$for some \(C_i \in \mathscr {A}\), \(i\in \lbrace 1, \ldots , n-1 \rbrace \).
-
2.
The Yoneda product is sent to composition as expected: therefore, \(f_{n,-,-}\) is a natural transformation and \(f_{n,A,B}\) is a group homomorphism with respect to the Baer sum on \({\text {Ext}}^n(A,B)\).
-
3.
If \(f_{n-1,A,B}\) is an isomorphism for any \(B\in \mathscr {A}\), then \(f_{n,A,B}\) is injective.
-
4.
Let \(g_{n,A,B}: {\text {Ext}}^n(A,B) \rightarrow {\text {Hom}}_{\mathscr {T}}(A,B[n])\) be a map for any \(n\ge 0\) and \(A,B \in \mathscr {A}\). If \(g_{1,A,B}\) is the natural isomorphism of Theorem A.2 and the Yoneda product is sent to composition, then \(g_{n,A,B}=f_{n,A,B}\).
Proof
For \(n=0\), \(f_{0,A,B}: {\text {Hom}}_{\mathscr {A}} (A,B) \rightarrow {\text {Hom}}_{\mathscr {T}}(A,B)\) is an isomorphism since \(\mathscr {A}\) is a full subcategory of \(\mathscr {T}\). Let \(n>0\) and consider \(\mathbf {X}\) an exact sequence

To \(\mathbf {X}\) we can associate short exact sequences

which are associated to distinguished triangles; therefore, we can consider a map
We need to show that if \((\mathbf {X}, \xi )\) and \((\mathbf {Y},\eta )\) give the same n-extension, then the associated map \(A\rightarrow B[n]\) obtained is the same. Without loss of generality, assume there is a family of morphisms \(\psi \) as in Definition A.4. Then for each \(i\in \lbrace 0, \ldots , n-1\rbrace \) we have

where \(\varphi _i\) is obtained by the universal property of the kernel. In order to prove that the middle square is commutative, we notice that
so \(X_{i+1} \rightarrow {\text {im}}\xi _{i+1} \rightarrow {\text {im}}\eta _{i+1}=X_{i+1} \rightarrow Y_{i+1} \rightarrow {\text {im}}\eta _{i+1}\). Since \(\varphi _{i+1}\) is the only one making the middle square commutative by the universal property of the cokernel, TR3 entails that also the right-hand square is commutative.
We obtain a commutative diagram

where \(\varphi _n={\text {id}}\) and \(\varphi _0={\text {id}}\), so that the rows are in fact the same map. This gives the well-definition of every \(f_{n,A,B}\).
-
1.
Let us consider a map \(\alpha :A \rightarrow B[n]\) factoring through \(A=C_n \rightarrow C_{n-1}[1] \rightarrow \cdots \rightarrow C_1[n-1]\rightarrow C_0[n]=B[n]\). To any \(C_{i}[-1] \rightarrow C_{i-1}\), we can associate a cone, which is in \(\mathscr {A}\) by Theorem A.2. Let us call such cone \(X_i\). We have the following short exact sequences: \(0 \rightarrow C_{i-1} \rightarrow X_i \rightarrow C_i\rightarrow 0\). Since \(C_{i}\) is also the kernel of \(X_{i+1} \rightarrow C_{i+1}\), we manage to create an exact sequence
$$\begin{aligned} 0\rightarrow B \rightarrow X_1 \rightarrow X_2 \rightarrow \cdots \rightarrow X_n \rightarrow A \rightarrow 0. \end{aligned}$$It is easy to notice that such exact sequence is associated to the map \(\alpha : A\rightarrow B[n]\) via \(f_{n,A,B}\).
-
2.
In the case of \({\text {Ext}}^n\) and \({\text {Ext}}^m\) with \(n,m>0\), the Yoneda product is sent to composition with a reasoning similar to item 1. Therefore, it suffices to show it is true when either m or n is zero.
First, we recall that \(f_{1,A,B}\) is exactly the map considered in Theorem A.2, which is a natural transformation for both entries. So (A.5) can be translated to
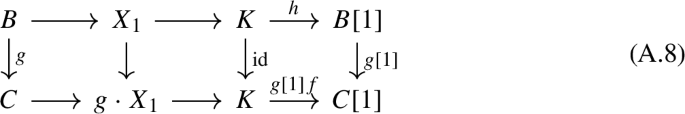
in \(\mathscr {T}\). Let us prove that \(f_{n,A,-}\) is a natural transformation, the proof of \(f_{n,-,B}\) being dual. For a general n-extension
$$\begin{aligned} \mathbf {X}:0 \rightarrow B \rightarrow X_1 \rightarrow X_2 \rightarrow \cdots \rightarrow X_n \rightarrow A \rightarrow 0 \end{aligned}$$and \(g:B \rightarrow C\), the map \(A \rightarrow C[n]\) associated to \(g \cdot \mathbf {X}\) factors through \(K[n-1]\rightarrow C[n]\), where \(K= {\text {im}}(g\cdot X_1 \rightarrow X_2)= {\text {im}}(X_1\rightarrow X_2)\), according to (A.8). Furthermore, the same diagram shows that \(K \rightarrow C[1]\) is obtained as a composition \(K \rightarrow B[1] \rightarrow C[1]\), where the latter morphism is g[1]. Therefore, \(A \rightarrow C[n]\) can be written as the composition of \(A \rightarrow B[n]\), obtained by \(\mathbf {X}\), and \(g[n]: B[n] \rightarrow C[n]\), as wanted.
Finally, \(f_{n,-,-}\) is a natural transformation for both entries A and B. Moreover, \(f_{n,A,B}\) is a group homomorphism since the Baer sum of two extensions is given by Yoneda products as explained in Definition A.4.
-
3.
We want to show that the zero map \(A \rightarrow B[n]\) is associated to only one equivalence class of extensions, the trivial one, whenever \(f_{n-1,A,X}\) is an isomorphism for any \(X \in \mathscr {A}\).
Let us consider
$$\begin{aligned} \mathbf {X}:0 \rightarrow B \rightarrow X_1 \rightarrow X_2 \rightarrow \cdots \rightarrow X_n \rightarrow A \rightarrow 0 \end{aligned}$$such that \(f_{n,A,B}(\mathbf {X})=0\) and the associated factorization
$$\begin{aligned} A \rightarrow C_{n-1}[1] \rightarrow \cdots \rightarrow C_2[n-2] \rightarrow C_1[n-1] \rightarrow B[n]. \end{aligned}$$We have the following diagram, where the rows are distinguished triangles:
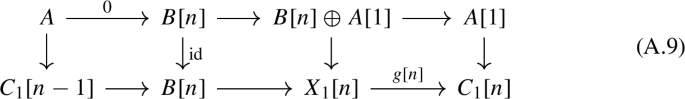
Now we pick the map \(A[1] \rightarrow B[n] \oplus A[1] \rightarrow X_1[n]\). Since \(f_{n-1,A,X_1}\) is a surjective, we get that \(A\rightarrow X_1[n-1]\) is associated to an exact sequence
$$\begin{aligned} \mathbf {Y}: 0 \rightarrow X_1 \rightarrow Y_1 \rightarrow \cdots \rightarrow Y_{n-1} \rightarrow A \rightarrow 0. \end{aligned}$$Composing \(\mathbf {Y}\) with \(0 \rightarrow B \rightarrow X_1 \oplus B \rightarrow X_1 \rightarrow 0\), we have the following:

We want to prove there are maps \(Y_i \rightarrow X_{i+1}\) making every square of the diagram above commutative. It suffices to consider the sequences starting at \(X_1\) and \(C_1\) respectively (remember that \(C_1\) is the image of \(X_1 \rightarrow X_2\)). The Yoneda product of \(\mathbf {Y}\) and \(g:X_1 \rightarrow C_1\) gives us \(g \cdot \mathbf {Y}\), whose associated map \(A\rightarrow X_1[n-1] \rightarrow C_1[n-1]\) factors as \(A \rightarrow C_{n-1}[1] \rightarrow \cdots \rightarrow C_1[n-1]\) because of the right-hand commutative square in (A.9). Since \(f_{n-1,A,C_1}\) is injective by assumption, we know that \(g \cdot \mathbf {Y}\) is in the same equivalence class of
$$\begin{aligned} 0 \rightarrow C_1 \rightarrow X_2 \rightarrow \cdots \rightarrow X_n \rightarrow A \rightarrow 0 . \end{aligned}$$Therefore, we can assume, up to equivalence, that \(\mathbf {X}\) is in fact
$$\begin{aligned} 0 \rightarrow B \rightarrow X_1 \rightarrow g \cdot Y_1 \rightarrow Y_2 \rightarrow \cdots \rightarrow Y_{n-1}\rightarrow A \rightarrow 0. \end{aligned}$$With this assumption, (A.10) can be completed with maps \(Y_i \rightarrow X_{i+1}\) as wanted: the first morphism is given according to (A.5), while all the others are the identity. It remains to show that the equivalence class of
$$\begin{aligned} 0 \rightarrow B \rightarrow X_1 \oplus B \rightarrow Y_1 \rightarrow \cdots \rightarrow Y_{n-1} \rightarrow A\rightarrow 0 \end{aligned}$$is the one associated to 0, which is obvious because the diagram

commutes.
-
4.
Let \(g_{n,A,B}\) as in the statement and assume by induction that \(g_{m,C,D}=f_{m,C,D}\) for any \(m<n\) and \(C,D \in \mathscr {A}\). We consider \(\mathbf {X} \in {\text {Ext}}^n(A,B)\) given by
$$\begin{aligned} 0 \rightarrow B \rightarrow X_1 \overset{\xi _1}{\rightarrow } X_2 \rightarrow \cdots \rightarrow X_n \rightarrow A \rightarrow 0. \end{aligned}$$Such an extension can be split into two shorter extensions:
$$\begin{aligned} \begin{aligned} \mathbf {X}_1:&\quad 0 \rightarrow B \rightarrow X_1 \rightarrow {\text {coker}}(\xi _1) \rightarrow 0\\ \mathbf {X}_2:&\quad 0 \rightarrow {\text {coker}}(\xi _1) \rightarrow X_2 \rightarrow \cdots \rightarrow X_n \rightarrow A \rightarrow 0. \end{aligned} \end{aligned}$$Moreover, \(\mathbf {X}_1 \cdot \mathbf {X}_2=\mathbf {X}\). As \(g_{n,A,B}\) sends Yoneda product to composition, we have
$$\begin{aligned} \begin{aligned} g_{n,A,B}(\mathbf {X})&= g_{n,A,B}(\mathbf {X}_1 \cdot \mathbf {X}_2) \\&= g_{1,{\text {coker}}(\xi _1),B}(\mathbf {X}_1) \circ g_{n-1,A,{\text {coker}}(\xi _1)}(\mathbf {X}_2)\\&= f_{1,{\text {coker}}(\xi _1),B}(\mathbf {X}_1) \circ f_{n-1,A,{\text {coker}}(\xi _1)}(\mathbf {X}_2)\\&= f_{n,A,B}(\mathbf {X}_1 \cdot \mathbf {X}_2)= f_{n,A,B}(\mathbf {X}). \end{aligned} \end{aligned}$$
\(\square \)
Remark A.11. By Proposition A.7, for any exact subcategory \(\mathscr {A} \subset \mathscr {T}\) as in Dyer’s Theorem A.2, it holds that \({\text {Ext}}^2(A,B) \subset {\text {Hom}}(A,B[2])\) for any \(A,B \in \mathscr {A}\). In case \(\mathscr {A}\) is a heart, \(\dim _{\mathscr {T}}(\mathscr {A})\le 1\) implies that \(\dim \mathscr {A}\le 1\).
Definition A.12. Let \(\mathscr {T}\) be a triangulated category and \(\mathscr {A}\) an exact subcategory as in Dyer’s Theorem A.2. We say that \(\mathscr {T}\) has all the Ext groups of \(\mathscr {A}\) if the morphism \(f_{n,A,B}\) defined in Proposition A.7 is an isomorphism for any \(A,B \in \mathscr {A}\) and all \(n \in \mathbb {N}\).
Corollary A.13. A triangulated category \(\mathscr {T}\) has all the Ext groups of an exact subcategory \(\mathscr {A}\) as in Dyer’s Theorem A.2 if and only if for every map \(A \rightarrow B[n]\) there exists a factorization
with \(C_i \in \mathscr {A}\) for \(i \in \lbrace 1, \ldots , n-1\rbrace \). In particular, if \(\mathscr {A}\) is a heart and \(\dim _{\mathscr {T}}\mathscr {A}\le 1\), then \(\mathscr {T}\) has all the Ext groups of \(\mathscr {A}\) and \(\dim \mathscr {A}=\dim _{\mathscr {T}}\mathscr {A}\).
Proof
The only if part is obvious: if \(f_{n,A,B}\) is an isomorphism, then the image of such map contains all morphisms \(A \rightarrow B[n]\): item 1 of Proposition A.7 concludes.
Conversely, item 1 of Proposition A.7 shows that \(f_{n,A,B}\) is surjective. By Theorem A.2, \(f_{1,A,B}\) is an isomorphism: we obtain that \(f_{2,A,B}\) is injective according to item 3 of Proposition A.7. An induction proves that this holds for every n.
Using Remark A.11 and Theorem A.2, we prove the last part of the statement. \(\square \)
Corollary A.14. Let \(\mathscr {T}\) be a triangulated category with a semiorthogonal decomposition \(\mathscr {T}=\langle \mathscr {T}_1 , \mathscr {T}_2 \rangle \) and two compatible t-structures \(\mathscr {T}_1^{\le 0}\) and \(\mathscr {T}_2^{\le 0}\) on \(\mathscr {T}_1\) and \(\mathscr {T}_2\) respectively. We denote with \(\mathscr {A}_i\) the heart associated to \(\mathscr {T}_i^{\le 0}\). By Theorem 3.7, we obtain the heart
We consider the following hypotheses:
-
1.
\(\mathscr {T}_i\) has all the Ext groups of \(\mathscr {A}_i\);
-
2.
\({\text {Hom}}_{\mathscr {T}}(A,B[m])\cong {\text {Ext}}_{\mathscr {A}}^m(A,B)\) for every \(A \in \mathscr {A}_1[1]\) and \(B \in \mathscr {A}_2\).
Then \(\mathscr {T}\) has all the Ext groups of the heart \(\mathscr {A}\).
Proof
Before starting the actual proof, let us remark that \({\text {Ext}}^m_{\mathscr {A}}(A,B) = {\text {Ext}}^m_{\mathscr {A}_2} (A,B)\) whenever \(A,B \in \mathscr {A}_2\). Indeed, let
be an extension in \(\mathscr {A}\) with \(A,B \in \mathscr {A}_2\) and let \(\sigma _2 : \mathscr {T}\rightarrow \mathscr {T}_2\) be the right adjoint of the inclusion functor \(\iota : \mathscr {T}_2 \rightarrow \mathscr {T}\). Then we get

which shows that \(\iota \sigma _2 \mathbf {X} \cong \mathbf {X}\) in \({\text {Ext}}^m_{\mathscr {A}}(A,B)\) (recall the equivalence relation used to describe the Yoneda extensions in Definition A.4). Since \(\sigma _2\mathbf {X} \in {\text {Ext}}^m_{\mathscr {A}_2}(A,B)\), we conclude that \(\iota \) gives an isomorphism between \({\text {Ext}}^m_{\mathscr {A}_2}(A,B)\) and \({\text {Ext}}^m_{\mathscr {A}}(A,B) \) whenever \(A,B \in \mathscr {A}_2\). In a similar way, considering the left adjoint of the inclusion \(\mathscr {T}_1 \rightarrow \mathscr {T}\), one can prove that \({\text {Ext}}^m_{\mathscr {A}}(A,B)= {\text {Ext}}^m_{\mathscr {A}_1[1]}(A,B)\) if \(A,B \in \mathscr {A}_1[1]\).
Given \(A,B \in \mathscr {A}\), we consider two distinguished triangle \(A_2 \rightarrow A \rightarrow A_1 \rightarrow A_2[1]\) and \(B_2 \rightarrow B \rightarrow B_1 \rightarrow B_2[1]\) with \(A_2,B_2 \in \mathscr {A}_2\) and \(A_1 , B_1 \in \mathscr {A}_1[1]\). We obtain the following hom-exact sequences

By Proposition A.7, these exact sequences have maps from the Ext groups. We proceed by induction on m. From the induction hypothesis and item 3 of Proposition A.7 we deduce that
Therefore, hypothesis 1 and five lemma entails that \({\text {Hom}}(A_2,B[m])\cong {\text {Ext}}_{\mathscr {A}}^m(A_2,B)\). The second row proves that \({\text {Hom}}(A_1,B[m])\cong {\text {Ext}}_{\mathscr {A}}^m(A_1,B)\) using both hypotheses and five lemma. From the first row, we conclude that \({\text {Hom}}(A,B[m])\cong {\text {Ext}}_{\mathscr {A}}^m(A,B)\). \(\square \)
Proposition A.15. [13, Propositions XI.4.7 and 4.8]. In the case of \({{\text {D}}^{{\text {b}}}}(\mathscr {A})\), the map \(f_{n,A,B}:{\text {Ext}}^n(A,B) \rightarrow {\text {Hom}}(A,B[n])\) above is exactly the classical one, that associates to each \(\mathbf {X} \in {\text {Ext}}^n(A,B)\) the map given by the composition of the inverse of the quasi-isomorphism
(the left-hand complex is such that \(X_n\) is at level 0) and the morphism
In particular, in the case of \({{\text {D}}^{{\text {b}}}}(\mathscr {A})\) every \(f_{n,A,B}\) is an isomorphism.
Proof
This is a direct consequence of item 4 of Proposition A.7 . The last sentence is a classical result; see, for instance, [13, Proposition XI.4.8]. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lorenzin, A. Compatibility of t-Structures in a Semiorthogonal Decomposition. Appl Categor Struct 30, 755–778 (2022). https://doi.org/10.1007/s10485-022-09672-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10485-022-09672-2