Skip to main content
SpringerLink
Log in

Dynamics and response reshaping of nonlinear predator-prey system undergoing random abrupt disturbances

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

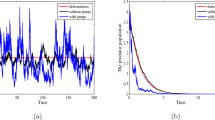
An actual ecological predator-prey system often undergoes random environmental mutations owing to the impact of natural disasters and man-made destruction, which may destroy the balance between the species. In this paper, the stochastic dynamics of the nonlinear predator-prey system considering random environmental mutations is investigated, and a feedback control strategy is proposed to reshape the response of the predator-prey system against random abrupt environmental mutations. A delayed Markov jump system (MJS) is established to model such a predator-prey system. A novel first integral is constructed which leads to better approximation solutions of the ecosystem. Then, by applying the stochastic averaging method based on this novel first integral, the stochastic response of the predator-prey system is investigated, and an analytical feedback control is designed to reshape the response of the ecosystem from the disturbed state back to the undisturbed one. Numerical simulations finally illustrate the accuracy and effectiveness of the proposed procedure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. LI, W., XU, W., ZHAO, J. F., and JIN, Y. F. Stochastic stability and bifurcation in a macroeconomic model. Chaos Solitons & Fractals, 31(3), 702–711 (2007)

    Article  MathSciNet  Google Scholar 

  2. QIAN, J. M. and CHEN, L. C. Random vibration of SDOF vibro-impact oscillators with restitution factor related to velocity under wide-band noise excitations. Mechanical Systems and Signal Processing, 147, 107082 (2021)

    Article  Google Scholar 

  3. WANG, X. F., WEI, X. Y., PU, D., and HUAN, R. H. Single-electron detection utilizing coupled nonlinear microresonators. Microsystems & Nanoengineering, 6(1), 78 (2020)

    Article  Google Scholar 

  4. XU, Y., LI, H., WANG, H. Y., JIA, W. T., YUE, X. L., and KURTHS, J. The estimates of the mean first exit time of a bistable system excited by Poisson white noise. Journal of Applied Mechanics—Transactions of the ASME, 84(9), 091004 (2017)

    Article  Google Scholar 

  5. YAN, B., WANG, Z. H., MA, H. Y., BAO, H. H., WANG, K., and WU, C. Y. A novel lever-type vibration isolator with eddy current damping. Journal of Sound and Vibration, 494, 115862 (2021)

    Article  Google Scholar 

  6. CAI, G. Q. and LIN, Y. K. Stochastic analysis of the Lotka-Volterra model for ecosystems. Physical Review E, 70(4), 041910 (2004)

    Article  Google Scholar 

  7. HU, H. X., TENG, Z. D., and GAO, S. J. Extinction in nonautonomous Lotka-Volterra competitive system with pure-delays and feedback controls. Nonlinear Analysis: Real World Applications, 10(4), 2508–2520 (2009)

    Article  MathSciNet  Google Scholar 

  8. MAY, R. M. Stability and Complexity in Model Ecosystems, Princeton University Press, Princeton, NJ (1973)

    Google Scholar 

  9. JIA, W. T., XU, Y., and LI, D. Stochastic dynamics of a time-delayed ecosystem driven by Poisson white noise excitation. Entropy, 20(2), 143 (2018)

    Article  Google Scholar 

  10. PEI, B., XU, Y., and WU, J. L. Two-time-scales hyperbolic-parabolic equations driven by Poisson random measures: existence, uniqueness and averaging principles. Journal of Mathematical Analysis and Applications, 447(1), 243–268 (2017)

    Article  MathSciNet  Google Scholar 

  11. PEI, B., XU, Y., and YIN, G. Averaging principles for SPDEs driven by fractional Brownian motions with random delays modulated by two-time-scale Markov switching processes. Stochastics and Dynamics, 18(4), 1850023 (2018)

    Article  MathSciNet  Google Scholar 

  12. ZHU, C. and YIN, G. On hybrid competitive Lotka-Volterra ecosystems. Nonlinear Analysis: Theory Methods & Applications, 71(12), e1370–e1379 (2009)

    Article  MathSciNet  Google Scholar 

  13. TSARKOV, Y. Asymptotic methods for stability analysis of Markov impulse dynamical systems. Nonlinear Dynamics and Systems Theory, 2(1), 103–115 (2002)

    MathSciNet  MATH  Google Scholar 

  14. TURCHIN, P. Complex Population Dynamics: a Theoretical/Empirical Synthesis, Princeton University Press, Princeton, NJ (2003)

    MATH  Google Scholar 

  15. BAZYKIN, A. D. Nonlinear Dynamics of Interacting Populations, World Scientific, Singapore (1998)

    Book  Google Scholar 

  16. ROSENZWEIG, M. L. and MACARTHUR, R. H. Graphical representation and stability conditions of predator-prey interactions. American Naturalist, 97(895), 209–223 (1963)

    Article  Google Scholar 

  17. CAI, G. Q. and LIN, Y. K. Stochastic analysis of time-delayed ecosystems. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 76, 041913 (2007)

    Article  Google Scholar 

  18. SHASTRI, Y. and DIWEKAR, U. Sustainable ecosystem management using optimal control theory, part 1: deterministic systems. Journal of Theoretical Biology, 241(3), 506–521 (2006)

    Article  MathSciNet  Google Scholar 

  19. LIU, J. L. and ZHAO, W. C. Dynamic analysis of stochastic Lotka-Volterra predator-prey model with discrete delays and feedback control. Complexity, 2019, 1–15 (2019)

    MATH  Google Scholar 

  20. GU, X. D. and ZHU, W. Q. Stochastic optimal control of predator-prey ecosystem by using stochastic maximum principle. Nonlinear Dynamics, 85(2), 1177–1184 (2016)

    Article  MathSciNet  Google Scholar 

  21. WONHAM, W. Random differential equations in control theory. Matematika, 17, 129–167 (1973)

    Google Scholar 

  22. HUAN, R. H., ZHU, W. Q., HU, R. C., and YING, Z. G. Asymptotic stability with probability one of random-time-delay-controlled quasi-integrable Hamiltonian systems. Journal of Applied Mechanics—Transactions of the ASME, 83(9), 091009 (2016)

    Article  Google Scholar 

  23. HUAN, R. H., ZHU, W. Q., MA, F., and YING, Z. G. Stationary response of a class of nonlinear stochastic systems undergoing Markovian jumps. Journal of Applied Mechanics—Transactions of the ASME, 82(5), 051008 (2015)

    Article  Google Scholar 

  24. HUAN, R. H., ZHU, W. Q., MA, F., and YING, Z. G. Asymptotic stability of a class of nonlinear stochastic systems undergoing Markovian jumps. Probabilistic Engineering Mechanics, 45, 13–21 (2016)

    Article  Google Scholar 

  25. HUO, H. F. and LI, W. T. Positive periodic solutions of a class of delay differential system with feedback control. Applied Mathematics and Computation, 148(1), 35–46 (2004)

    Article  MathSciNet  Google Scholar 

  26. LV, W. S., WANG, F., and LI, Y. Adaptive finite-time tracking control for nonlinear systems with unmodeled dynamics using neural networks. Advances in Difference Equations, 2018, 159 (2018)

    Article  MathSciNet  Google Scholar 

  27. XIA, L., HUAN, R. H., ZHU, W. Q., and ZHU, C. X. Reshaping of the probability density function of nonlinear stochastic systems against abrupt changes. Journal of Vibration and Control, 26, 532–539 (2020)

    Article  MathSciNet  Google Scholar 

  28. HAS’MINSKIĬ, R. Z. Certain limit theorems for solutions of differential equations with a random right side. Transmission Problems, 1966, 755–758 (1966)

    MathSciNet  Google Scholar 

  29. ZHU, W. Q. Nonlinear stochastic dynamics and control in Hamiltonian formulation. Applied Mechanics Reviews, 59, 230–248 (2006)

    Article  Google Scholar 

  30. ZHU, C. X. and ZHU, W. Q. Control of quasi non-integrable Hamiltonian systems for targeting a specified stationary probability density. International Journal of Control, 92, 1117–1122 (2019)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanics, Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, Zhejiang University, Hangzhou, 310027, China

    Lei Xia, Jiaojiao Sun, Zuguang Ying, Ronghua Huan & Weiqiu Zhu

Authors
  1. Lei Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiaojiao Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zuguang Ying
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ronghua Huan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Weiqiu Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ronghua Huan.

Additional information

Citation: XIA, L., SUN, J. J., YING, Z. G., HUAN, R. H., and ZHU, W. Q. Dynamics and response reshaping of nonlinear predator-prey system undergoing random abrupt disturbances. Applied Mathematics and Mechanics (English Edition), 42(8), 1135–1154 (2021) https://doi.org/10.1007/s10483-021-2755-8

Project supported by the National Natural Science Foundation of China (Nos. 11772293 and 12072312) and Zhejiang Science and Technology Project (No. 2019C03129)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xia, L., Sun, J., Ying, Z. et al. Dynamics and response reshaping of nonlinear predator-prey system undergoing random abrupt disturbances. Appl. Math. Mech.-Engl. Ed. 42, 1123–1134 (2021). https://doi.org/10.1007/s10483-021-2755-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-021-2755-8

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation