Skip to main content
SpringerLink
Log in

Vibration of axially moving beam supported by viscoelastic foundation

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

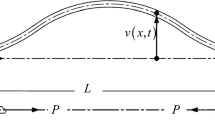
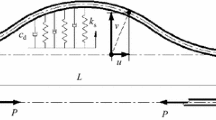
In this paper, transverse vibration of an axially moving beam supported by a viscoelastic foundation is analyzed by a complex modal analysis method. The equation of motion is developed based on the generalized Hamilton’s principle. Eigenvalues and eigenfunctions are semi-analytically obtained. The governing equation is represented in a canonical state space form, which is defined by two matrix differential operators. The orthogonality of the eigenfunctions and the adjoint eigenfunctions is used to decouple the system in the state space. The responses of the system to arbitrary external excitation and initial conditions are expressed in the modal expansion. Numerical examples are presented to illustrate the proposed approach. The effects of the foundation parameters on free and forced vibration are examined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bhat, R. B., Xistris, G. D., and Sanker, T. S. Dynamic behavior of a moving belt supported on elastic foundation. Journal of Mechanics Design, 104, 143–147 (1982)

    Article  Google Scholar 

  2. Perkins, N. C. Linear dynamics of a translating string on an elastic foundation. Journal of Vibration and Acoustics, 112, 2–7 (1990)

    Article  Google Scholar 

  3. Wickert, J. A. Response solutions for the vibration of a traveling string on an elastic foundation. Journal of Vibration and Acoustics, 116, 137–139 (1994)

    Article  Google Scholar 

  4. Xiong, Y. and Hutton, S. G. Vibration and stability analysis of a multi-guided rotating string. Journal of Sound and Vibration, 169, 669–683 (1994)

    Article  MATH  Google Scholar 

  5. Tan, C. A. and Zhang, L. Dynamic characteristics of a constrained string translating across an elastic foundation. Journal of Vibration and Acoustics, 116, 318–325 (1994)

    Article  Google Scholar 

  6. Riedel, C. H. and Tan, C. A. Dynamic characteristics and mode localization of elastically constrained axially moving strings and beams. Journal of Sound and Vibration, 215, 455–473 (1998)

    Article  MATH  Google Scholar 

  7. Saeed, H. M. and Festroni, F. Simulation of combined system by periodic structures: the wave transfer matrix approach. Journal of Sound and Vibration, 213, 53–73 (1998)

    Article  Google Scholar 

  8. Parker, R. G. Supercritical speed stability of the trivial equilibrium of an axially-moving string on an elastic foundation. Journal of Sound and Vibration, 221, 205–219 (1999)

    Article  MATH  Google Scholar 

  9. Jha, R. K. and Parker, R. G. Spatial discretization of axially moving media vibration problems. Journal of Vibration and Acoustics, 122, 290–294 (2000)

    Article  Google Scholar 

  10. Kartik, V. and Wickert, J. A. Vibration and guiding of moving media with edge weave imperfections. Journal of Sound and Vibration, 291, 419–436 (2006)

    Article  Google Scholar 

  11. Yurddaş. A., Özkaya, E., and Boyacı, H. Nonlinear vibrations of axially moving multi-supported strings having non-ideal support condition. Nonlinear Dynamics, 73, 1223–1244 (2012)

    Article  MathSciNet  Google Scholar 

  12. Yang, X. D., Lim, C. W., and Liew, K. M. Vibration and stability of an axially moving beam on elastic foundation. Advances in Structural Engineering, 13, 241–248 (2010)

    Article  Google Scholar 

  13. Baǧatli, S. M., Özkaya, E., and Öz, H. R. Dynamics of axially accelerating beams with an intermediate support. Journal of Vibration and Acoustics, 133, 470–476 (2011)

    Google Scholar 

  14. Baǧatli, S. M., Özkaya, E., and Öz, H. R. Dynamics of axially accelerating beams with multiple supports. Nonlinear Dynamics, 74, 237–255 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. Kural, S. and Özkaya, E. Vibrations of an axially accelerating, multiple supported flexible beam. Structural Engineering and Mechanics, 44, 521–538 (2012)

    Article  Google Scholar 

  16. Ghayesh, M. H. Stability and bifurcations of an axially moving beam with an intermediate spring support. Nonlinear Dynamics, 69, 193–210 (2012)

    Article  MathSciNet  Google Scholar 

  17. Yang, Y., Ding, H., and Chen, L. Q. Dynamic response to a moving load of a Timoshenko beam resting on a nonlinear viscoelastic foundation. Acta Mechanica Sinica, 29, 718–727 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  18. Sun, L. A closed-form solution of a Bernoulli-Euler beam on a viscoelastic foundation under harmonic line loads. Journal of Sound and Vibration, 242, 619–627 (2001)

    Article  Google Scholar 

  19. Ghayesh, M. H. Nonlinear transversal vibration and stability of an axially moving viscoelastic string supported by a partial viscoelastic guide. Journal of Sound and Vibration, 314, 757–774 (2008)

    Article  Google Scholar 

  20. Ahmadian, M. T., Nasrabadi, V. Y., and Mohammadi, H. Nonlinear transversal vibration of an axially moving viscoelastic string on a viscoelastic guide subjected to mono-frequency excitation. Acta Mechanica, 214, 357–373 (2010)

    Article  MATH  Google Scholar 

  21. Li, X. J. and Chen, L. Q. Modal analysis of coupled vibration of belt drive systems. Applied Mathematics and Mechanics (English Edition), 9(1), 9–13 (2008) DOI 10.1007/s10483-008-0102-x

    Article  MATH  Google Scholar 

  22. Huang, L. H. and Liu, X. T. Eigenvalue and stability analysis for transverse vibrations of axially moving strings based on Hamiltonian dynamics. Acta Mechanica Sinica, 21, 485–494 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  23. Chung, C. H. and Kao, I. Modeling of axially moving wire with damping: eigenfunctions, orthogonality and applications in slurry wiresaws. Journal of Sound and Vibration, 330, 2947–2963 (2011)

    Article  Google Scholar 

  24. Ding, H. and Jean, W. Z. Steady-state responses of pulley-belt systems with a one-way clutch and belt bending stiffness. Journal of Vibration and Acoustics, 136, 041006 (2014)

    Article  Google Scholar 

  25. Ding, H., Zhang, G. C., Chen, L. Q., and Yang, S. P. Forced vibrations of supercritically transporting viscoelastic beams. Journal of Vibration and Acoustics, 134, 051007 (2012)

    Article  Google Scholar 

  26. Zhang, H. J. and Chen, L. Q. Vibration of an axially moving string supported by a viscoelastic foundation. Acta Mechanica Solida Sinica, 26(3), 221–231 (2016)

    Article  Google Scholar 

  27. Yan, Q. Y., Ding, H., and Chen, L. Q. Nonlinear dynamics of an axially moving viscoelastic Timoshenko beam under parametric and external excitations. Applied Mathematics and Mechanics (English Edition), 36(8), 971–984 (2015) DOI 10.1007/s10483-015-1966-7

    Article  MathSciNet  MATH  Google Scholar 

  28. Ding, H. Steady-state responses of a belt-drive dynamical system under dual excitations. Acta Mechanics Sinica, 32, 156–169 (2016)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai, 200072, China

    Haijuan Zhang, Hu Ding & Liqun Chen

  2. School of Mechanical Engineering, Anhui University of Technology, Maanshan 243032, Anhui Province, China

    Haijuan Zhang & Jian Ma

  3. Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai, 200072, China

    Hu Ding & Liqun Chen

  4. Department of Mechanics, College of Sciences, Shanghai University, Shanghai, 200444, China

    Liqun Chen

Authors
  1. Haijuan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hu Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Liqun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Liqun Chen.

Additional information

Project supported by the State Key Program of the National Natural Science Foundation of China (No. 11232009) and the National Natural Science Foundation of China (Nos. 11372171 and 11422214)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, H., Ma, J., Ding, H. et al. Vibration of axially moving beam supported by viscoelastic foundation. Appl. Math. Mech.-Engl. Ed. 38, 161–172 (2017). https://doi.org/10.1007/s10483-017-2170-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-017-2170-9

Keywords

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation