Skip to main content
SpringerLink
Log in

Dynamic behavior of thin rectangular plate attached to moving rigid

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

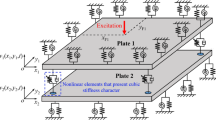
A nonlinear dynamic model of a thin rectangular plate attached to a moving rigid was established by employing the general Hamilton’s variational principle. Based on the new model, it is proved theoretically that both phenomena of dynamic stiffening and dynamic softening can occur in the plate when the rigid undergoes different large overall motions including overall translational and rotary motions. It was also proved that dynamic softening effect even can make the trivial equilibrium of the plate lose its stability through bifurcation. Assumed modes method was employed to validate the theoretical result and analyze the approximately critical bifurcation value and the postbuckling equilibria.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Kane T R, Ryan R R, Banerjee A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance, Control and Dynamics, 1987, 10(2):139–151.

    Google Scholar 

  2. Bloch A M. Stability analysis of a rotating flexible system[J]. Acta Applicandae Mathematicae, 1989, 15:211–234.

    Article  MATH  MathSciNet  Google Scholar 

  3. Wallrapp O. Linearized flexible multibody dynamics including geometric stiffening effects[J]. Mech Strut and Mach, 1991, 19:385–409.

    MathSciNet  Google Scholar 

  4. Haering W J, Ryan R R. New formulation for flexible beams undergoing large overall motions[J]. Journal of Guidance, Control and Dynamics, 1994, 17(1):76–83.

    Google Scholar 

  5. Ryu J, Kim S S, Kim S S. A general approach to stress stiffening effects on flexible multibody dynamic systems[J]. Mech Strut and Mach, 1994, 22(2):157–180.

    Google Scholar 

  6. Zhang D J, Liu C O, Huston R L. On dynamics stiffening of an arbitary flexible body with large overall motion an integrated approach[J]. Mech Strut and Mach, 1995, 23:419–438.

    Google Scholar 

  7. Zhang D J, Huston R L. On dynamic stiffening of flexible bodies having high angular velocity[J]. Mech Strut and Mach, 1996, 24:313–329.

    Google Scholar 

  8. Banerjee A K, Dickens J M. Dynamics of an arbitrary flexible body in large rotation and translation[J]. Journal of Guidance, Control and Dynamics, 1996, 19:221–227.

    Google Scholar 

  9. Xiao Shifu, Chen Bin. Dynamic characteristic and stability analysis of a beam mounted on a moving rigid body[J]. Archive of Applied Mechanics, 2005, 74(5/6):415–426.

    Google Scholar 

  10. Xiao Shifu, Chen Bin. Modelling and bifurcation analysis of internal cantilever beam system on a steadily rotating ring[J]. Science in China, Series A, 1998, 41(5):527–533.

    Google Scholar 

  11. Xiao Shifu, Chen Bin. Modeling and bifurcation analysis of the centre rigid-body mounted on an external Timoshenko beam[J]. Applied Mathematics and Mechanics (English Edition), 1999, 20(12):1389–1393.

    Google Scholar 

  12. Xiao Shifu, Du Qiang, Chen Bin, et al. Modal test and analysis of cantilever beam with tip mass[J]. Acta Mechanica Sinica, English Series, 2002, 18:407–413.

    Google Scholar 

  13. Xiao Shifu, Chen Bin, Du Qiang. On dynamic behavior of a cantilever beam with tip mass in a centrifugal field[J]. Mechanics Based Design of Structures and Machines, 2005, 33(1):79–98.

    Article  Google Scholar 

  14. Xiao Shifu, Chen Bin. On characteristics of modal analysis for flexible appendages of a typical rigid-flexible coupling system[J]. Chinese Space Science and Technology, 1998, 18(4):8–13 (in Chinese).

    MathSciNet  Google Scholar 

  15. Banerjee A K, Kane T R. Dynamics of a plate in large overall motion[J]. J of Applied Mechanics, 1989, 56:887–892.

    Google Scholar 

  16. Chang Bilin, Shabana A A. Nonlinear finite element formulation for the large displacement analysis of plates[J]. J of Applied Mechanics, 1990, 57:707–718.

    Google Scholar 

  17. Boutaghou Z E, Erdman A G, Stolarski H K. Dynamics of flexible beams and plates in large overall motions[J]. J of Applied Mechanics, 1992, 59:991–999.

    Google Scholar 

  18. Yoo H H, Pierre C. Modal characteristic of a rotating rectangular cantilever plate[J]. J of Sound and Vibration, 2003, 259(1):81–96.

    Google Scholar 

  19. Musat S D, Epureanu B I. Dynamics and stability of a multi-body system with respect to a rotating reference system[J]. Transactions of the Canadian Society for Mechanical Engineering, 2002, 26(1):57–73.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Southwest Institute of Structural Mechanics, P. O. Box 919-401, Mianyang, 621900, Sichuan Province, P. R. China

    Xiao Shi-fu Doctor  (肖世富)

  2. Department of Mechanics and Engineering Science, Peking University, Beijing, 100871, P. R. China

    Chen Bin  (陈滨)

Authors
  1. Xiao Shi-fu Doctor  (肖世富)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chen Bin  (陈滨)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiao Shi-fu Doctor  (肖世富).

Additional information

Communicated by YE Qing-kai

Project supported by the National Natural Science Foundation of China (No.10272002) and the Doctoral Foundation of Ministry of Education of China (No.20020001032)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xiao, Sf., Chen, B. Dynamic behavior of thin rectangular plate attached to moving rigid. Appl Math Mech 27, 555–566 (2006). https://doi.org/10.1007/s10483-006-0416-1

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-006-0416-1

Key words

Chinese Library Classification

2000 Mathematics Subject Classification

Search

Navigation