Modelling sustainable investing in the CAPM

Abstract

Empirical studies investigate various causes and effects of sustainable investments. While some attempts have been made to describe the results found by theoretical models, these are relatively complex and heterogeneous. We relate to existing studies and use a parsimonious Capital Asset Pricing Model (CAPM) in which we model different aspects of sustainable investing. The basic reasoning of the CAPM, that investors need to be compensated for the bad aspects of assets applies so that investors demand higher returns for investments that are harmful from an environmental, social, or governance (ESG) perspective. Moreover, if investors have heterogeneous views on the ESG–characteristics of a company, the market requires higher returns for that company, provided richer investors care more about ESG than poorer investors, which is known as the Environmental Kuznets Curve. Besides the effect on asset prices, we find that sustainable investing has an impact on a firm’s production decision through two channels—the growth and the reform channel. Sustainable investment reduces the size of dirty firms through the growth channel and makes firms cleaner through the reform channel. We illustrate the magnitude of these effects with numerical examples calibrated to real-world data, providing a clear indication of the high economic relevance of the effects.

1 Introduction

The share of sustainable investments has increased tremendously in recent years and appears to be growing even further (GSIA, 2020; SIF US., 2018, 2020, 2022). Meanwhile, several studies address the question of the inclusion of environmental, social, and governance (ESG) aspects within an investor’s portfolio decision (Geczy & Guerard Jr, 2023; SIF US., 2018). However, the empirical results found so far are very mixed and do not provide a clear conclusion. Different reasons why investors demand sustainable investing are analyzed. Some examine whether investors care about the sustainability aspect of sustainable investing or whether this is more of a secondary concern (Hartzmark & Sussman, 2019; Heeb, Kölbel, Paetzold, & Zeisberger, 2023; Riedl & Smeets, 2017). Others investigate the performance of such sustainable investments. Likewise, the empirical results found are mixed. For example, Hong and Kacperczyk (2009) identify a so-called “sin premium” for non–sustainable investments, whereas Friede et al. (2015) cannot solely confirm this when examining more than 2000 academic papers. However, the bottom line of their meta-study is that sustainable investing obtains higher returns. Whether companies reform and make their production more sustainable due to sustainable investments forms a further strand in the literature. Various channels such as the cost of capital or the engagement channel are discussed through which investors can influence the firm’s production decision (Berk & van Binsbergen, 2021; Heinkel et al., 2001; Kölbel et al., 2020). The question that immediately arises from the empirical observations is: How can we explain these findings with a relatively simple model? For this purpose, we make use of parsimonious adjustments in the Capital Asset Pricing Model (CAPM) and analyze the impact of ESG preferences on asset returns. Considering sustainable investing using the CAPM provides a suitable way to describe the impact of sustainable investing on financial markets.

With this paper, we contribute, among others, to the existing literature of Berk and van Binsbergen (2021); Heinkel et al. (2001); Pástor, Stambaugh, and Taylor (2021); Pedersen, Fitzgibbons, and Pomorski (2021); Zerbib (2022) who address the empirical findings from a theoretical perspective and analyze the impact of sustainable investors on asset prices. Using a much simpler model, we include ESG preferences in the CAPM and examine whether ESG is rewarded or if ESG investments cost returns. In line with the existing literature, we find a clear direct effect that asset holding with bad ESG is rewarded. Obviously, this result is in line with the basic idea of the CAPM, which compensates for bad. We further find that a heterogeneity in ESG valuations is rewarded (Avramov, Cheng, Lioui, & Tarelli, 2022). ESG heterogeneity increases required returns if richer investors care more about ESG. This relates to the Environmental Kuznets Curve (EKC), where the desire for a clean environment increases with rising prosperity (Grossman & Krueger, 1991, 1995; Kuznets, 1955). In addition to the impact on asset prices, we examine the impact of sustainable investment on firms’ production decisions and answer whether firms produce cleaner. In order to analyze the effect on the company’s behavior in more detail, we distinguish between the growth and the reform channel.¹ By introducing endogenous ESG preferences for the mean–variance investor, we reach the following conclusions: sustainable investing reduces the size of dirty companies through the growth channel and makes companies cleaner via the reform channel. Using a much more parsimonious model, we can support and extend existing results in the literature. Moreover, we discover new and simpler conditions under which the previously shown results hold.

Our paper is organized as follows: in Sect. 2, we provide a brief overview of the existing literature, followed by an introduction to the notation used. In Sect. 4, we analyze the impact of ESG in the CAPM with homogeneous and heterogeneous expectations, while in Sect. 5 we examine the effect on firms’ decisions. As the analytical results already provide several insights, in Sect. 6 we provide a numerical example to get some idea of the size of the effects so that we can judge their economic relevance. Finally, the paper is concluded in Sect. 7.

2 Literature

Due to the urgency of climate change, research in sustainability is growing enormously (cf. SIF US., 2018, 2020 and 2022). The financial literature in the area of sustainable investing is huge and conclusions are diverse. The importance of social screening and investing beyond conventional investment criteria has long been debated in the literature, as exemplified by Kinder and Domini (1997); Moskowitz (1972, 1997).² Empirical studies investigate various aspects of sustainable investing. The literature distinguishes between different motivations for sustainable investments: investors are truly interested in sustainable investments, investors achieve excess returns, and companies improve their production through sustainable investments.

Empirical literature: Exploiting an experiment to study investors’ motivation to hold so-called social responsible funds Riedl and Smeets (2017) provide evidence that financial reasons are minor, while social preferences and social signaling proved to be major determinants. In particular, the signaling effect is an important factor for investors with weaker social preferences. While Riedl and Smeets (2017) find a positive willingness to pay (WTP), Heeb et al. (2023) conclude that investors’ WTP does not increase significantly to achieve a higher impact. They find that investors show substantial WTP for sustainable investments. However, they stress that investors do not show a significant propensity to pay a higher price for investments that promise greater impact.³ Hong and Kacperczyk (2009) study the effect of investors refusing to hold so-called”sin–stocks”, where sin-stocks are referred to stocks such as tobacco, gaming, and alcohol. They present empirical evidence of a”sin premium” as an incentive for investors to hold these companies in their portfolios. Consequently, they conclude that there is an inverse relationship between ESG and expected returns. Likewise, Bolton and Kacperczyk (2021) provide evidence for a carbon premium. Investors require compensation in the form of higher returns for their exposure to increased emissions. This is in line with Chava (2014), who finds that investors demand a higher return on the shares of companies with a higher score in the climate concern category. At the same time, however, they find no support for a meaningful relationship between expected returns and a firm’s environmental strength score. Investors may be willing to sacrifice returns in order to invest in non–financial characteristics. Barber, Morse, and Yasuda (2021) compare the impact and traditional venture capital and find that impact funds have lower ex–post internal rates of return than traditional venture capital. However, they pointed out that the WTP varies depending on specific circumstances such as time or the legal/ regulatory environment. This is further supported by Renneboog, Ter Horst, and Zhang (2008), who conduct a literature review and conclude that socially responsible investors are willing to accept slightly lower returns in order to pursue social or ethical objectives.⁴ Similarly, Friede et al. (2015) investigate the excess return for sustainable investing by studying more than 2000 recent empirical studies that study the relationship between ESG criteria and financial performance. Overall, they find mixed results from academic studies on the relationship between sustainable investing and corporate financial performance. On the other hand, Geczy et al. (2020) examine the integration of ESG criteria and conclude that responsible investing may not consistently lead to lower financial performance under certain circumstances. This highlights the potential benefits of integrating ESG considerations into financial decisions. From 1986 to 1994, Guerard Jr (1997) investigates the difference between the socially screened and unscreened equity universes and does not find any statistically significant difference in the average monthly mean return. Likewise, Statman and Glushkov (2009) find that the social responsibility aspect of stocks has no impact on returns. However, a significant amount of literature examines the relation between a company’s social performance (CSP) and its financial performance (CFP), and finds a positive correlation between these two. Evans and Peiris (2010) support the positive relationship between CSP and CFP: firms with strong CSP are likely to be better managed and outperform. Kim and Starks (2016) investigate the relationship between gender diversity on a company’s board and the value of the firm. The study examines the manner in which gender diversity enhances firm value. Female directors contribute a distinctive expertise, diversify the board, and bring unique skills to the board. Flammer (2015) supports the notion that corporate social responsibility (CSR) is a valuable resource. Additionally, she notes the diminishing marginal returns of CSR and the concave relationship between CSR and CFP. The relevance of CSR is further supported by Moskowitz (1972, 1997). Moskowitz provides empirical evidence that funds investing in companies that meet traditional investment criteria and contribute to enhancing the quality of life perform better. Similar positive effects between the CSP, the past or future financial performance, the benefits of including ESG criteria in portfolio analysis, and the implications for pensions funds are supported by Edmans (2011); El Ghoul et al. (2011); Ferrell, Liang, and Renneboog (2016); Fulton, Kahn, and Sharples (2012); Geczy and Guerard (2021); Geczy and Guerard Jr (2023); Orlitzky, Schmidt, and Rynes (2003); Pástor, Stambaugh, and Taylor (2022); Sautner and Starks (2023); Statman and Glushkov (2009); Waddock and Graves (1997).

Theoretical literature: So far, several theoretical studies try to explain the empirical results. In particular, the ones that deal with the ESG investment component in the CAPM. However, what they all have in common is that the models they use are rather complex. By taking a relatively simple twist, that is, incorporating ESG preferences into the CAPM, we arrive at comparable results.

Using a general equilibrium model Heinkel et al. (2001) analyze the impact of ethical investing. In particular, they differentiate between three types of firms (acceptable, unacceptable, reformed) and two types of investors (green, neutral). Acceptable firms use clean technology to produce, while unacceptable firms use dirty technology. A reformed company incurs costs to move from an unacceptable to an acceptable firm. In their model, managers maximize the value of the business. They are not faced with the financing costs of producing, the only costs incurred are the costs of changing technology. Heinkel et al. (2001) find that the stock price of an unacceptable firm is lower than that of an acceptable firm.⁵ In their empirical investigation they provide evidence that more than 20% green investors are needed to reform unacceptable firms. By using a much simpler model, we relate our paper to their findings and analyze the fraction of 20% of green investors in Sect. 6. Associated with the effect on firm’s production decision Berk and van Binsbergen (2021) use a CAPM to study the cost of capital channel. According to their findings preferences for ESG do not have a significant impact on a firm’s cost of capital. How can we make sense of these observations in a parsimonious model? To achieve this, we do some simple adjustments to the CAPM in our paper. Furthermore, Pástor et al. (2021) use an equilibrium model to provide evidence that investors’ ESG preferences move asset prices. Sustainable investors are willing to pay a higher price for environmentally friendly investments and thus forgo potential returns. They earn a lower expected return but are compensated by receiving a benefit from simply holding the assets and hedging against climate risk. Within the framework of their model, they come to the following important conclusions: sustainable investment creates incentives for companies to become more environmentally friendly. And sustainable investors cause green companies to invest more and brown companies to invest less. Rojo-Suárez and Alonso-Conde (2024) extend their model and find that brown assets generally exhibit negative ESG betas in the US equity market data. Additionally, they discover that the price associated with ESG risk decreases over time, approaching zero. Similar attempts to model ESG with the CAPM are made by Pedersen et al. (2021). They develop an ESG efficient frontier and validate their results within an empirical part. Pedersen et al. (2021) indicate that investors tend to select portfolios that lie on the ESG efficiency frontier. This frontier is defined as a combination of the risk–free rate, the tangent portfolio, the minimum variance portfolio, and the ESG tangent portfolio.⁶ Likewise, Zerbib (2022) examines the effects of sustainable investing on asset returns. Zerbib (2022) extends the CAPM and develops what he refers to as the”Sustainable Capital Asset Pricing Model”. The two different channels through which sustainable investments can affect asset returns, according to Zerbib (2022), are exclusion screening and ESG integration. He concludes that both the taste and exclusion premia have a significant impact on asset returns. Moreover, he emphasizes that sustainable investing can raise the cost of capital for companies with low ethical standards and high environmental risk. By accounting for additional uncertainty in ESG ratings, Avramov et al. (2022) examine the equilibrium implications and the implication for portfolio decisions and asset prices. High uncertainty in ESG ratings leads to reduced demand for them. They reveal a positive relationship between ESG uncertainty and both the CAPM alpha and the effective beta. Moreover, under ESG uncertainty, the negative relationship between ESG alpha and investment performance weakens. We use their results and study how heterogeneous preferences for environmental performance affect asset prices. In doing so, we conclude that ESG heterogeneity is compensated and that higher returns are required. Similar to Avramov et al. (2022); Berk and van Binsbergen (2021); Heinkel et al. (2001); Pástor et al. (2021); Pedersen et al. (2021); Zerbib (2022), we study the impact of ESG investments on asset prices and on firm’s production decision. We rely on their approach, as our goal is to simplify their models. We use a parsimonious CAPM to model ESG preferences and receive comparable results. Furthermore, while our analytical results already provide several insights, we provide a numerical example to get some idea of the size of the effects so that we can judge their economic relevance.

3 Model

In this paper, sustainable investing is modeled using the Capital Asset Pricing Model (CAPM) (Lintner, 1965; Mossin, 1966; Sharpe, 1964). A short section introducing the notation used is followed by a simple solution of how ESG preferences can be modeled in the CAPM. We examine whether ESG is rewarded or whether it costs returns. Furthermore, we investigate the impact of sustainable investment on firm’s production decisions.

3.1 Set–up

In the following, the notation used is introduced and fundamental concepts are outlined.⁷ For simplicity, we assume a standard two-period world, $t = \text{0,1}$. In period $t = 0$ the investor invests in an asset whereas in period $t = 1$ the asset pays off. At time t = 1 several possible states of the world $s = 1,\dots ,S$ can occur.⁸ Different states can be considered, such as different scenarios of how many degrees the world will heat up, e.g. 1,2,3 degrees Celsius or the amount of CO2 emissions by the economy. The probability measure is defined by $p\in\Delta =\left\{x\in {R}_{+}^{S},{\sum }_{s=1}^{S} {x}_{s}=1\right\}$, and thus $\upmu \left(x\right)={E}_{p}\left(x\right)=px$ denotes the expected value of asset x. Similarly, for the covariance of two assets, x and y, we have $COV\left(x,y\right)=\upmu \left(xy\right)-\upmu \left(x\right)\upmu \left(y\right)$. There are $k = \text{0,1},2,\dots ,K$ assets with payoffs expressed by ${D}_{s}^{k}$. The first asset, k = 0, is the risk–free asset delivering the certain payoff of 1 in all second–period states. We capture the structure of payoffs for all assets in the state–asset payoff matrix $D \in {R}^{SxK}$. ${q}^{k}$ represents the time 0 price of asset k. The price of the risk-free asset is ${q}^{0}=\frac{1}{{R}_{f}}$ with R_f being the gross risk-free rate.⁹ We consider a finite set of investors, each investor $i = 1,\dots ,I$ is described by an exogenously given initial wealth level in period t = 0, wⁱ. By providing the investor with wealth and given the asset prices $q={\left({q}^{0},\dots ,{q}^{K}\right)}^{\prime},$ the investor can finance its consumption ${c}^{i}={\left({c}_{1}^{i},\dots ,{c}_{S}^{i}\right)}^{\prime}$ by trading the assets. We define the demand of assets of investor i by (θ^i,0,θⁱ)^′ where θ^i,0 denotes the demand for the risk–free asset and ${\theta }^{i}=\left({\theta }^{i,1},\dots ,{\theta }^{i,K}\right)$ characterizes the demand for the asset of firm k.¹⁰ Thus, the value of investor's portfolio is ${\sum }_{k=0}^{K}{q}^{k}{\uptheta }^{i,k}.$ By ${\lambda }^{i}={\left({\lambda }^{i,1},\dots ,{\lambda }^{i,K }\right)}^{\prime}$ we represent the demand vector in terms of asset allocation i.e. ${\uplambda }^{i,k}=\frac{{q}^{k}{\uptheta }^{i,k}}{{w}^{i}}$. Further, λ^i,0 denotes the share of investor i^′s wealth invested in the risk–free rate.¹¹ The household's budget constraint is given by $\uptheta ^{i,0} + q^{\prime}\uptheta ^{i} = w^{i}$ or ${\sum }_{k=0}^{K}{\lambda }^{i,k}=1$ indicating how the investor's wealth is allocated to the assets. Further, we denote the supply of assets by firms $\overline{{\theta }^{k}}={\theta }^{M,k},$ for $k= 1, \dots , K$. In the market equilibrium, all shares ${\theta }^{i,k}$ held by the investors correspond to the supply of the asset $k:{\sum }_{i}{\theta }^{i,k}={\theta }^{M,k}$ or ${\sum }_{i}\frac{{\lambda }^{i,k}}{1-{\lambda }^{i,0}}{r}^{i}={\lambda }^{M,k},$ where ${r}^{i}=\frac{\left(1-{\lambda }^{i,0}\right){w}^{i}}{{\sum }_{i}\left(1-{\lambda }^{i,0}\right){w}^{i}}$ refers to the relative wealth of investor $i$. ${\lambda }^{M,k}$ is the relative market capitalization of asset $k$ i.e. $\frac{{q}^{k}{\theta }^{M,k}}{{\sum }_{k}{q}^{k}{\theta }^{M,k}}$.¹²

Consequently, ${\uplambda }^{M}$ denotes the vector of market capitalization and ${R}^{M}={\sum }_{k=1}^{K}{R}_{s}^{k}{\uplambda }^{M,k}$ defines the market return, where the return of asset $k$ is defined by ${R}_{s}^{k}=\frac{{D}_{s}^{k}}{{q}^{k}}$.¹³

4 Asset pricing

We use a parsimonious CAPM to study the effect of investors’ ESG preferences on asset returns (Lintner, 1965; Mossin, 1966; Sharpe, 1964). Our paper mainly refers to the papers of Heinkel et al. (2001); Pástor et al. (2021); Pedersen et al. (2021); Zerbib (2022) and provides a much simpler model, which allows us to draw similar conclusions.

We assume that investors have mean–variance preferences, there exists a risk–free asset and investors have homogeneous expectations. Additionally, we, later on, expand our analysis and provide a generalization with investors having heterogeneous expectations regarding environmental performance. To model ESG preferences in the CAPM we introduce a ''badness'' of the firm's ESG rating, $b\in {R}^{K}$. Where b can be either negative (acceptable/ clean firm) or positive (unacceptable/ dirty firm). Hence, a dirty company gets a bad ESG rating, whereas a clean company gets a good ESG rating. The dirtier a firm is, the more it reduces investor i’s utility. Note that we start to assume that b is uniform across all individuals. Using the budget restriction ${\uplambda }^{i,0} =1 - {\sum }_{k=1}^{K}{\lambda }^{i,k}$, the investor faces the following maximization problem

$$\underset{{\uplambda }^{i}}{\text{max}}\left(\upmu -b-{R}_{f}1\right)^{\prime}{\uplambda }^{i}-\frac{{\Psi }^{i}}{2}{\uplambda }^{i{\prime}}COV{\uplambda }^{i}$$

where ${\uplambda }^{i}\in {R}^{K}$ denotes the vector of risky asset weights, ${\Psi }^{i}$ defines the investor's risk aversion, $\upmu$ is the vector of risky assets' mean returns, $COV$ is their covariance matrix, and $1$ is the unit vector, which is omitted in the following for presentation reasons. We apply a change of variables and define $\widehat{\mu }=\upmu -b$. Thus, the adjusted optimization can be rewritten as in the standard CAPM

$$\underset{{\uplambda }^{i}}{\text{max}}\left(\widehat{\mu }-{R}_{f}\right)^{\prime}{\uplambda }^{i}-\frac{{\Psi }^{i}}{2}{\uplambda }^{i{\prime}}COV{\uplambda }^{i}$$

Consequently, we obtain the security market line (SML) (cf. Lintner (1965); Mossin (1966); Sharpe (1964) or in a simpler form Appendix B).

$$\widehat{{\mu }^{k}}-{R}_{f}={\upbeta }^{k}\left(\widehat{{\mu }^{k,M}}-{R}_{f}\right),\forall k\in K$$

with ${\upbeta }^{k}=COV\left({R}^{k},{R}^{M}\right)/VAR\left({R}^{M}\right)$ and where ${R}^{M}$ denotes the market return. $\widehat{{\mu }^{k}}$ represents the expected return on asset k, taking into account the badness of the firm, and hence $\left(\widehat{{\mu }^{k,M}}-{R}_{f}\right)$ defines the market risk premium. Resubstitution leads to

$${\upmu }^{k}-{b}^{k}-{R}_{f}={\upbeta }^{k}\left({\upmu }^{M}-{b}^{M}-{R}_{f}\right)$$

where ${b}^{M}={\sum }_{k=1}^{K}{b}^{k}{\uplambda }^{M,k}$ and ${\upmu }^{M}={\sum }_{k=1}^{K}{\mu }^{k}{\lambda }^{M,k}.$ Using the relatively simple trick of variable substitution we obtain

$${\upmu }^{k}={b}^{k}+{R}_{f}+{\upbeta }^{k}\left({\upmu }^{M}-{b}^{M}-{R}_{f}\right)$$

Hence, we provide evidence that holding assets with bad ESG scores will be rewarded. The finding that bad is being compensated is clearly in line with the CAPM logic. Obviously, as the SML does not include ${\Psi }^{i}$ i.e. the cross-section of expected returns are independent of the investor's risk aversion. However, investor's risk aversion determines the market risk premium ${\upmu }^{M}-{R}_{f}={b}^{M}+VAR\left({R}^{M}\right)/{\sum }_{i}\frac{{r}^{i}}{\left(1-{\uplambda }^{i,0}\right){\Psi }^{i}}$. Furthermore, it should be noted that the ESG harmfulness of the market does not have any impact on the SML. But the composition of the market portfolio changes with the degree of ESG investing. Suppose that bad ESG stocks have similar returns, then investing less in them reduces their beta and thus the required return. Note that the systematic risk of any asset $k,\hspace{0.25em}{\upbeta }^{k}$, depends on the composition of the market portfolio, ${\uplambda }^{M}.$ If the bad assets are high market capitalization assets, ${\uplambda }^{M,k}$ is high and ${\upbeta }^{k}$ is larger for them than for low market capitalization assets.¹⁴ We use a vector of ESG scores b to model ESG preferences in the CAPM. Consistent with the CAPM, where bad things are rewarded, bad ESG scores generate higher returns than good ESG scores. Our result aligns with findings of Pástor et al. (2021); Pedersen et al. (2021); Zerbib (2022). From a neutral investor ‘s perspective, the b^k is the alpha of asset k. Referring to the study of Heeb et al. (2023) this alpha is in the range of 4.5%—which is sizable compared to other well-known alphas like size and value. Moreover, our results are consistent with the empirical observation of the existence of a sin-premium found by Bolton and Kacperczyk (2021); Hong and Kacperczyk (2009). For holding unsustainable assets investors must be financially compensated.

So far we have assumed that all investors have homogeneous expectations regarding the assets’ expected returns. This is obviously inaccurate since in reality there are many different opinions about the future and, for example, the importance of sustainability. While we have just shown a simple way to incorporate ESG preferences for a given investor, we extend the model to heterogeneous investors and try to answer how heterogeneity in ESG scores impacts asset return (Hens & Gerber, 2017; Lintner, 1969).¹⁵ We refer to Avramov et al. (2022) who incorporate uncertainty in ESG ratings to examine the equilibrium implications and the resulting consequences on portfolio decisions and asset prices. Further, Gibson Brandon, Krueger, and Schmidt (2021) provide evidence that high uncertainty in ESG ratings leads investors to demand higher compensation. The optimization problem with heterogeneous expectations can be written as follows

$$\underset{{\uplambda }^{i}}{\text{max}}\left({\upmu }^{i}-{b}^{i}-{R}_{f}1\right)^{\prime}{\uplambda }^{i}-\frac{{\Psi }^{i}}{2}{\uplambda }^{i{\prime}}COV{\uplambda }^{i}$$

where ${b}^{i}\in {R}^{K}$ denotes the investor i's view on the firm's ESG score, ${\Psi }^{i}$ stands for the individual risk aversion of investor i, ${\mu }^{i}$ is the vector of assets' mean returns and ${\lambda }^{i}$ represents a vector with the weights of the respective risky assets.¹⁶ Using the same technique as before and using a change of variables $\left(\widehat{{\mu }^{i}}={\upmu }^{i}-{b}^{i}\right)$, we get

$${\underset{{\uplambda }^{i}}{\text{max}}\left(\widehat{{\mu }^{i}}-{R}_{f}\right)}^{\prime}{\uplambda }^{i}-\frac{{\Psi }^{i}}{2}{\uplambda }^{{i}{\prime}}COV{\uplambda }^{i}$$

In Appendix B we derive the SML with heterogeneous expectations. After resubstitution, we have

$${\overline{\upmu }}^{k}-{\overline{b}}^{k}-{R}_{f}={\upbeta }^{k}\left({\overline{\upmu }}^{M}-{\overline{b}}^{M}-{R}_{f}\right)$$

This is the SML with average expectations where

${\overline{\upmu }}^{k}-{\overline{b}}^{k}-{R}_{f}={\sum }_{i}{a}^{i}\left({\upmu }^{i,k}-{b}^{i,k}-{R}_{f}\right)$ and ${\overline{\upmu }}^{M}-{\overline{b}}^{M}-{R}_{f}=\sum_{i}{a}^{i} \left({\upmu }^{i,M}-{b}^{i,M} -{R}_{f}\right)$. With $\begin{aligned} & {a}^{i}=\frac{{r}^{i}}{\left(1-{\uplambda }^{i,0}\right){\uppsi }^{i}}/{\sum }_{i}\frac{{r}^{i}}{\left(1-{\uplambda }^{i,0}\right){\Psi }^{i}},{\overline{b}}^{k}={\sum }_{i}{a}^{i}{b}^{i,k},{b}^{i,M}={\sum }_{k=1}^{K}{\uplambda }^{M,k}{b}^{i,k},{\overline{b}}^{M}\\ & ={\sum }_{k=1}^{K}{\uplambda }^{M,k}{\overline{b}}^{k},{\overline{\upmu }}^{k}={\sum }_{i}{a}^{i}{\upmu }^{i,k},{\upmu }^{i,M}={\sum }_{k=1}^{K}{\uplambda }^{M,k}{\upmu }^{i,k},\end{aligned}$ and ${\overline{\upmu }}^{M}={\sum }_{i}{a}^{i}{\upmu }^{i,M}$. In the CAPM with varying expectations, the SML is determined by the average expected return and the collective ESG viewpoint of all investors. Note that the averaging takes into account both the risk aversion and the relative wealth of the investors. Consequently, investors with greater wealth and lower risk aversion have a stronger influence on determining this average. Note that as all investors have the same covariance expectations, the beta factors are as in the model with homogeneous beliefs. The average ESG view is rewarded, and if the investor i does not invest in risky assets i.e. ${\uplambda }^{i,0}=1$, his view will not be taken into account. Note that the heterogeneity of ESG ratings increases the required returns as ${\sum }_{i}{a}^{i}{b}^{i,k}={E}_\frac{1}{I}\left(a{b}^{k}\right)={E}_\frac{1}{I}\left(a\right){E}_\frac{1}{I}\left({b}^{k}\right)+CO{V}_\frac{1}{I}\left(a,{b}^{k}\right)$.¹⁷ Using the correlation ${\uprho }^{k}$ between a and ${b}^{k}$ we obtain $CO{V}_\frac{1}{I}\left(a,{b}^{k}\right)={\uprho }^{k}\upsigma \left(a\right)\upsigma \left({b}^{k}\right).$ It can therefore be concluded that ESG heterogeneity $\upsigma \left({b}^{k}\right)$ increases returns whenever ${\uprho }^{k}>0$.

Our finding holds when richer investors put more weight on ESG investments, which is in line with the Environmental Kuznets Curve (EKC) (Grossman & Krueger, 1991, 1995; Kuznets, 1955). The EKC hypothesis states that there is an inverted U–shaped relationship between environmental degradation and income. Above a certain economic standard, after basic needs are met, a stronger appreciation is placed on a cleaner environment. Investors are more interested in investments that are ESG compliant. As in the case of homogeneous expectations on returns and ratings, for a neutral investor, the compensation for environmental concerns is an alpha. And with heterogeneous expectations, this alpha will exceed the 4.5% (Heeb et al., 2023). Moreover, it can be expected that investors get richer over time so that based on the EKC the alpha might even increase.

All in all, our conclusions so far are as follows: the CAPM can be adapted to include ESG preferences. In line with Pástor et al. (2021); Pedersen et al. (2021); Zerbib (2022) bad ESG will be rewarded. Investing in dirty firms requires higher compensation. Furthermore, in line with Avramov et al. (2022), ESG heterogeneity will be rewarded. The investor requires higher compensation. Besides the effect that ESG investing has on asset prices, we will look at the effect on the behavior of the firm within Sect. 5. The environment remains indifferent to whether an investor benefits more or less from sustainable investing. The crucial focus lies in the extent to which production practices undergo substantial transformations. This particular aspect will be the central focus of our next section.

5 Corporate finance

Now we examine the effects of sustainable investing in the view of corporate finance. In doing so, this paper answers the following questions: What impact does sustainable investment have on a company’s production decisions? Does it make companies cleaner? And if so, through which channel? We refer to existing literature and describe two different channels: the growth and the reform channel.

5.1 Investors

Each investor $i= 1, \dots , I$ is endowed with an initial wealth level. The investor's budget constraint is given by $\uptheta ^{i,0} + q^{\prime}\uptheta ^{i} = w^{i}$, where ${\uptheta }^{i,0}$ represents the amount of wealth invested in the risk-free bond that yields ${R}_{f}$, while ${\uptheta }^{i}$ is the portfolio of equities bought. The price to be paid for firm k is ${q}^{k}$ and the firm might raise capital ${D}_{0}^{k}$ from the bond market. Investors choose their portfolios according to mean–variance preferences on consumption and sustainable investing.

$${U}^{i}\left({c}^{i},{\uptheta }^{i}\right)=\upmu \left({c}^{i}\right)-{b}^{{i}^{{\prime}}}{\uptheta }^{i}-\frac{{\Psi }^{i}}{2}{\upsigma }^{2}\left({c}^{i}\right)$$

where, ${\Psi }^{i}>0$ denotes a measure of investor's risk aversion and consumption is given by ${c}^{i}=D{\uptheta }^{i}+{R}_{f}{\uptheta }^{i,0}$. Thus, ${\upmu }\left( {c^{i} } \right) = p^{\prime}D{\uptheta }^{i} + R_{f} {\uptheta }^{i,0}$. Besides enjoying consumption the investor derives utility from investing in clean firms and disutility from investing in dirty firms, represented by the ''bad'' ESG score${b}^{i}\in {R}^{K}$.

Investors differ in their tolerance for environmental damage. Each investor i has a known preference for the environment. Now, ${b}^{i}$ is endogenous, $b^{i^{\prime}} = {\upgamma }^{i^{\prime}} D,$ where ${\upgamma }^{i}$ denotes a vector that describes the environmental performance or can be viewed as an ESG rating and D is the state-asset payoff matrix. The higher ${b}^{i},$ the more the investor suffers from the firm polluting/ having a high ''bad'' score. The dirtier the firm the higher the investor's utility reduction. Thus, a firm is not bad as such but this depends on what it does within its production activity. We rewrite the investor's optimization as follows

$${\underset{{\uptheta }^{i}}{\text{max}}p}^{{\prime}}D{\uptheta }^{i}+{R}_{f}{\uptheta }^{i,0}-{\upgamma }^{{i}^{{\prime}}}D{\uptheta }^{i}-\frac{{\Psi }^{i}}{2}{\uptheta }^{{i}^{{\prime}}}COV\left(D\right){\uptheta }^{i}$$

and using the budget constraint, its corresponding maximization problem is

$$\underset{{\uptheta }^{i}}{\text{max}}{R}_{f}\left[{w}^{i}-{q}^{{\prime}}{\uptheta }^{i}\right]+\left[{p}^{{\prime}}D-{\upgamma }^{{i}^{{\prime}}}D\right]{\uptheta }^{i}-\frac{{\Psi }^{i}}{2}{\uptheta }^{{i}^{{\prime}}}COV\left(D\right){\uptheta }^{i}$$

Note that we have the first-order condition

$${\uptheta }^{i}={COV\left(D\right)}^{-1}\frac{1}{{\Psi }^{i}}\left[{D}^{{\prime}}p-{D}^{{\prime}}{\upgamma }^{i}-q{R}_{f}\right]$$

and therefore we can already conclude that the ratio of the risky assets (k,l) of two different individuals (i,j) is not identical. Obviously, as we have heterogeneous expectations, the result is not consistent with the Two-Fund Separation Theorem. The reason is that the first-order condition is now a system of linear equations that differs not only by the scalar ${\Psi }^{i}$ but also by the environmental valuation ${b}^{i}$ of the firm k.

As shown in Appendix C the investor's maximization problem leads us to the following asset price ${q}^{k}$

$${q}^{k}={\left[{\sum }_{i}\frac{1}{{\Psi }^{i}}{R}_{f}\right]}^{-1}\left[{\sum }_{i}\frac{1}{{\Psi }^{i}}{D}^{k{\prime}}p-{\sum }_{i}\frac{1}{{\Psi }^{i}}{D}^{k{\prime}}{\upgamma }^{i}-COV\left({D}^{k},{D}^{M}\right)\right]$$

(1)

After the derivation of the asset price formula, we conclude that there exists a negative relationship between the asset price and the ''dirtiness'' of a firm. The higher the ''bad'' value of the firm is, the lower the price of an asset. Therefore, with our parsimonious model, we can state that ESG preferences and environmental valuations are important for a firm's production decision.

5.2 Firms

There are $k= 1, \dots , K$ firms that produce payoffs ${D}_{s}^{k}$ from capital ${D}_{0}^{k}$. The firm uses a production function given by ${G}^{k}$ and ${f}^{k}$. Given a fixed supply of the firm's assets, $\overline{{\uptheta }^{k}},$ managers maximize the value of the firm, and therefore the optimization problem is

$$\underset{{D}_{0}^{k}}{\text{max}}{q}^{k}\left({D}^{k}\right)\overline{{\uptheta }^{k}}-{D}_{0}^{k}\overline{{\uptheta }^{k}}$$

$$s.t.{D}_{s}^{k}={g}_{s}^{k}{f}^{k}\left({D}_{0}^{k}\right)$$

with the production function being separated in a directional and a size term, ${g}^{k}\in {G}^{k}\subset {R}_{+}^{S}$ and ${f}^{k}:{R}_{+}\to {R}_{+}.$ Thus, with Eq. (1) we have

$$\underset{{D}_{0}^{k}}{\text{max}}\left[{\sum }_{s}{\sum }_{i}\frac{{p}_{s}-{\upgamma }_{s}^{i}}{{\Psi }^{i}}{g}_{s}^{k}{f}^{k}\left({D}_{0}^{k}\right)-COV\left({D}^{k},{D}^{M}\right)\right]\overline{{\uptheta }^{k}}-\left[{\sum }_{i}\frac{1}{{\Psi }^{i}}{R}_{f}\right]{D}_{0}^{k}\overline{{\uptheta }^{k}}$$

Using ${D}_{s}^{k}={g}_{s}^{k}{f}^{k}\left({D}_{0}^{k}\right)$ the solution is obtained from

$$\underset{{D}_{0}^{k}}{\text{max}}\left[{\sum }_{s}{\sum }_{i}\frac{{p}_{s}-{\upgamma }_{s}^{i}}{{\Psi }^{i}}{g}_{s}^{k}-{\sum }_{s}{p}_{s}{g}_{s}^{k}{D}_{s}^{M}-{\sum }_{s}{p}_{s}{g}_{s}^{k}{\sum }_{s}{p}_{s}{D}_{s}^{M}\right]{f}^{k}\left({D}_{0}^{k}\right)-\left[{\sum }_{i}\frac{1}{{\Psi }^{i}}{R}_{f}\right]{D}_{0}^{k}$$

We define ${A}^{k}$ to be

$${A}^{k}=\left[{\sum }_{s}{\sum }_{i}\frac{{p}_{s}-{\upgamma }_{s}^{i}}{{\Psi }^{i}}{g}_{s}^{k}-{\sum }_{s}{p}_{s}{g}_{s}^{k}{D}_{s}^{M}-{\sum }_{s}{p}_{s}{g}_{s}^{k}{\sum }_{s}{p}_{s}{D}_{s}^{M}\right]$$

Now we can easily examine the two partial derivatives w.r.t. ${D}_{0}^{k}$ and ${g}_{s}^{k}$. We investigate the following two sub-problems. First

$$\underset{{D}_{0}^{k}}{\text{max}}{A}^{k}{f}^{k}\left({D}_{0}^{k}\right)-\left[{\sum }_{i}\frac{1}{{\Psi }^{i}}{R}_{f}\right]{D}_{0}^{k}$$

and second

$$\underset{{{g}_{s}}^{k}\in {G}^{k}}{\text{max}}{\sum }_{s}{\nabla }_{s}{g}_{s}^{k}$$

(2)

where

$${\nabla }_{s}={\sum }_{i}\left(\frac{{p}_{s}-{\upgamma }_{s}^{i}}{{\Psi }^{i}}\right)- {p}_{s}{D}_{s}^{M}-{p}_{s}{\sum }_{s}{p}_{s}{D}_{s}^{M}$$

(3)

We assume that firm k is small relative to the market so that ${D}_{s}^{k}$ is a negligible part of ${D}_{s}^{M}$. For reasons of illustrations, we use the specification of an ln-function, ${f}^{k}=ln$. Thus, one part of the firm's optimization problem is

$$\underset{{D}_{0}^{k}}{\text{max}}{A}^{k}ln\left({D}_{0}^{k}\right)-\left[{\sum }_{i}\frac{1}{{\Psi }^{i}}{R}_{f}\right]{D}_{0}^{k}$$

It is easily seen that the solution is

$${D}_{0}^{k}={\left[{\sum }_{i}\frac{1}{{\Psi }^{i}}{R}_{f}\right]}^{-1}{A}^{k}.$$

We are interested in the comparative statics of ${D}_{0}^{k}$ w.r.t. ${\upgamma }_{s}^{i}$, i.e. how the size of the firm changes with its rating. As shown in Appendix D, we get

$${\partial }_{{\upgamma }_{s}^{i}}{D}_{0}^{k}={\left[{\sum }_{i}\frac{1}{{\Psi }^{i}}{R}_{f}\right]}^{-1}{\partial }_{{\upgamma }_{s}^{i}}{A}^{k}<0$$

and refer to this effect as the growth or market channel. Thus, when the environmental concerns increase the firms will downsize.¹⁸

To illustrate the second part we assume ${G}^{k} = \{ x \in {R}_{+}^{S}| {\sum }_{s}{\upsilon }_{s}^{k} exp({x}_{s})=c\}$ and thus consider Eq. (4) for some positive weights ${\upupsilon }_{s}^{k}>0$. If ${\upupsilon }_{c}^{k}>{\upupsilon }_{d}^{k}$, we refer this firm to be dirty, whereas if ${\upupsilon }_{c}^{k}<{\upupsilon }_{d}^{k}$ we refer this firm to be clean. This definition is based on the firm's resource utilization, depending on the relation of ${\upupsilon }_{s}^{k}$ in the green and brown state. The dirty firm has a higher resource utilization in the green state and will thus tend to produce more in the dirty state.

$$\underset{{g}_{s}^{k}}{\text{max}}{\sum }_{s}{\nabla }_{s}{g}_{s}^{k}\text{ s.t. }{\sum }_{s}{\upupsilon }_{s}^{k}exp\left({g}_{s}^{k}\right)=c$$

(4)

c denotes a positive constant. Since exp(.) is convex the transformation curve is concave and the production possibility set is convex so that we are optimizing a linear function on a convex set. The solution derived from the first-order condition gives

$${g}_{s}^{k}=ln\left(c{\nabla }_{s}\right)-ln\left({\sum }_{s}{\nabla }_{s}\right)-ln\left({\upupsilon }_{s}^{k}\right)$$

(5)

Consequently, we get that ${\partial }_{{\upgamma }_{s}^{i}}{g}_{s}^{k}<0$ (see Appendix D). Thus an increased concern for a specific state will redirect production away from it. Related to Heeb (2022) we refer to this effect as the”reform” channel. Pástor et al. (2021) have claimed that the effect of environmental concerns on production decreases when risk aversion increases. In our model, this is not generally true, for the numerical example that we calibrate in Sect. 6 it does not hold, as we show in Appendix E.

In summary, we observe the following results when modeling sustainable investing in the CAPM: sustainable investing reduces the size of dirty firms through the growth channel. Moreover, sustainable investing makes firms cleaner through the reform channel. Interestingly, the higher the risk aversion, the smaller the impact. A possible reason to explain this effect might be that when an investor is more risk–averse he holds fewer shares so that his opinion does not count as much in the general assembly of the firm. Our paper provides a valuable contribution to the existing literature by examining the impact of sustainable investing on asset prices and asset returns. We further analyze the effect of heterogeneous ratings and establish a link between the heterogeneity of ESG ratings and the EKC. Presenting a more general model as Heinkel et al. (2001); Pástor et al. (2021); Pedersen et al. (2021) and Zerbib (2022), we additionally investigate the important direct and indirect effects of sustainable investments on a firm’s payoff and its production decision. To conclude our paper, in the next section, we check whether these qualitative comparative statics results are economically relevant.

6 Economic Relevance

While our analytical results outlined above provide important insights into the direction of the impact of sustainable investing, in this section we use numerical examples calibrated to real–world data to provide a clear indication of the high economic relevance of the effects we identify. The existing literature does not provide a clear consensus on the relevance of such effects. In fact, some findings appear to be contradictory. Therefore, the following analyses aim to contribute to the clarification of this discussion. While Berk and van Binsbergen (2021) claim that ESG investing has a marginal impact (increase in the cost of capital by 0.35 basis points), Heinkel et al. (2001) claim that 20% of green investors are sufficient to reform brown firms becoming green.

We use two different datasets: annual CO2 emissions and stock market data for the United States (US). The CO2 emissions data are from the World Bank Open Data and the stock market data are from the data Shiller published on his website to illustrate his book “Irrational Exuberance” (Shiller, 2015, 2024; The World Bank, 2024). Using the Shiller data, we focus on the aggregate yearly earnings growth of the stock market, D^M. Our data is annual and ranges from 1990 to 2020.

The CO2 emissions data is used to differentiate between two states: dirty vs. clean, based on whether percentage changes in CO2 emissions are above or below the median.¹⁹ The conditional expected value of earnings in the dirty state is approximately ${D}_{d}^{M}=1.33$, while in the clean state, it is around ${D}_{c}^{M}=0.91$.²⁰ Thus, in dirty (clean) states CO2 emissions increase (decrease) on average by 33% (9%). With ${D}_{c}^{M}$ and ${D}_{d}^{M}$ we calculate the different state prices, ∇_s, according to Eq. (3). In our analysis, we consider one unit of agents I = 1. As in Heinkel et al. (2001), this does not mean that investors are homogeneous. In particular, we divide investors into a green and neutral type, where the fraction of green investors is denoted by $\updelta \in \left[\text{0,1}\right].$ We compare an economy with 0% and 100% green investors to an economy with only 20% green investors. According to Heinkel et al. (2001), it takes a minimum of 20% green investors to reform brown companies. We assume that both investors have the same degree of risk aversion and based on the market equity risk premium we calibrate the investor's risk aversion parameter to be about $\Psi = 0.15$.²¹ As we use the median to classify the world into two different states, we have ${p}_{s}=0.5,s=\text{1,2}$.We assume that the ESG concerns of the neutral investors are zero and further on, γ_s denotes the environmental awareness of the green investors in state s. We allow γ_s to range between 0 and 0.1. Riedl and Smeets (2017) find that the annual total expense ratio is 70 basis points higher for green funds than for brown funds. Whereas Heeb et al. (2023) report that the average willingness to pay for green investments is 4.567% of the total investment amount. In our model, this means that a realistic γ_s is below 10%.

We also differentiate between two types of firms: a green and a brown firm and define ${\upupsilon }_{s}^{k}$ based on the firm's resource utilization. The brown firm has a higher resource utilization in the clean state than the green firm. Thus it tends to produce more in the dirty state. In particular, we use the specification of ${\upupsilon }_{c}^{g}=0.2,{\upupsilon }_{d}^{g}=0.8$ for the green firm and ${\upupsilon }_{c}^{b}=0.8,{\upupsilon }_{d}^{b}=0.2$ for the brown firm, respectively.²²

Moreover, we analyze two different industries in more detail to study the impact of how a shift in investor environmental awareness affects a firm's cost of capital. Therefore, we utilize Center for Research in Security Prices (CRSP) and S&P Compustat data to compare the net income of two distinct sectors. In particular, we compare the energy and health care sector in the US using the Global Industry Classification Standard (GICS).²³ The comparison between these two sectors is intuitive. Compared to the energy sector, the health care sector emits significantly less greenhouse gases (Polizu, Khan, Kernan, Ellis, & Georges, 2023). The conditional means of net income growth rate for energy are ${D}_{d}^{energy}=1.31$ and ${D}_{c}^{energy}=0.35$, while for health care we have ${D}_{d}^{health}=1.09$ and ${D}_{c}^{health}=1.03$. The unconditional means are ${D}^{energy} =0.84$ and ${D}^{health}=1.06$, respectively. Due to its relatively higher output in the dirty state compared to the health care sector, the energy sector is referred to as the ''brown firm'', while the health care sector is referred to as the ''green firm''. According to our model, the ${g}^{energy}\left({g}^{health}\right)$ vector is more likely to point in the direction of a dirty (clean) state.

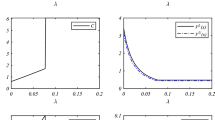
To study the growth channel, we assume ${\upgamma }_{c}={\upgamma }_{d}=\gamma$ and examine the effect of $\upgamma$ on ${D}_{0}^{k}$. Increasing the investor's environmental preference is associated with a decrease in ${D}_{0}^{k}.$ We observe a drastic decrease in production if environmental concerns increase in an economy with only green investors. The proportion of green investors impacts significantly on how much production is reduced. As Fig. 1 shows, if as in Heinkel et al. (2001), 20% of the investors are environmentally concerned up to the degree of $\upgamma = 5\%$ then we find that compared to no environmental concerns both firms shrink by almost 3% while both shrink by 15% if all investors are environmentally concerned, i.e. if $\updelta =1$. Thus, the fraction of people being concerned and the degree by which they are concerned matters a lot—for both firms, irrespective of whether they are green or brown.

Fig. 1

$\Psi =0.15.{D}_{0}^{k}$ as a function of $\upgamma$. The dotted lines refer to the brown firm, whereas the continuous lines refer to the green firm. Green lines refer to 100% green investors within the economy, while red lines refer to the 20% of green investors within the economy

Figure 2 shows how ${D}_{0}^{k}$ changes with $\upepsilon$. As $\epsilon$ increases (i.e., the environmental damage becomes disproportionately worse), the green firms grow while the brown firms shrink. On the other hand, if the environmental damage becomes disproportionately better, the opposite is true (cf. Hartzmark & Shue, 2022). Only this latter case would support the claim of Hartzmark and Shue (2022) that it is better to invest in the brown firms than in the green firms.

Fig. 2

$\Psi =0.15.{D}_{0}^{k}$ as a function of $\gamma$. The dotted lines refer to the brown firm, whereas the continuous lines refer to the green firm. Green lines refer to 100% green investors within the economy, while red lines refer to the 20% of green investors within the economy

In addition to the growth channel, we investigate the reform channel. To separate this reform channel from the growth channel, we adjust ${\upgamma }_{c}$ and ${\upgamma }_{d}$ so that the total change is 0, thus we set ${\upgamma }_{c}=0.05-\epsilon$ and ${\upgamma }_{d}=0.05+\epsilon$. Motivated by Heeb et al. (2023) the changes in γ are centered around 0.05. While an increase in ϵ goes along with a decrease of investor’s environmental awareness in the clean state, it increases investor’s awareness in the dirty state. This implies that an increase in CO2 in a dirty state is perceived as worse than the same increase in a clean state, e.g. because the damage caused by CO2 is more than proportional—an example of this are so–called. “tipping points”, because once they are reached, the damage is potentially catastrophic. Figure 3 illustrates the impact of an increase in environmental preference on state prices. As investor’s environmental awareness increases, the state price decreases. With a proportion of green investors, δ, Eq. (3) adjusts accordingly

$${\nabla }_{s}={\sum }_{i}\left(\frac{{p}_{s}-\updelta {\upgamma }_{s}^{i}}{{\Psi }^{i}}\right)- {p}_{s}{D}_{s}^{M}-{p}_{s}{\sum }_{s}{p}_{s}{D}_{s}^{ M}$$

(6)

Fig. 3

Relationship between ${\nabla }_{d}$ and ${\upgamma }_{d}.$ $\Psi = 0.15$

It is evident that state prices become less sensitive to environmental awareness as the fraction of green investors within the economy decreases. As Eq. (6) shows, the impact of environmental concerns on state prices increases with a higher fraction of green investors.

It is obvious from Eq. (5) that the reform channel, i.e. the direction of production,

$\frac{{g}_{d}^{k}}{{g}_{c}^{k}},$ only depends on the relative state prices, $\frac{{\nabla }_{d}}{{\nabla }_{c}}$. Thus, we now investigate how $\frac{{g}_{d}^{k}}{{g}_{c}^{k}}$ depends on the relative ESG concerns, which is determined by our parameter ϵ.

As Fig. 4 points out, with an increase in ϵ we observe a reduction in $\frac{{g}_{d}^{k}}{{g}_{c}^{k}}$ relative to the green state. An increase in investor’s environmental awareness in the dirty state leads to an increasing punishment of firm’s production in the dirty state. Furthermore, this punishment is more sensitive for brown firms.

Fig. 4

Ratio of $\frac{{g}_{d}^{k}}{{g}_{c}^{k}}$. The dotted lines refer to the brown firm, whereas the continuous lines refer to the green firm. Green lines refer to 100% green investors within the economy, while red lines refer to the 20% of green investors within the economy. Note that all lines were horizontal for 0% green investors

Heinkel et al. (2001) distinguishes between a clean, so-called. “acceptable” production, A, and a dirty, so-called”unacceptable” production, U. Therefore G^k is identical for all companies and has only the two elements g^A and g^U, i.e. G^k = {g^A,g^U}. The asset prices depend on the preferences of the green and the neutral investors. Heinkel et al. (2001) provide evidence that more than 20% green investors are needed for an unacceptable firm to reform. Figure 4 shows that in our model the impact of the reform channel is smaller than that of the growth channel.

For both industries, we find that an increase in investor’s environmental awareness decreases asset prices q^k. Using $CO{C}^{k}\left(\upgamma \right)=\frac{E\left({D}^{k}\right)}{{q}^{k}\left(\upgamma \right)}-1$, we refer to the effect of γ and ϵ on firm’s cost of capital. Figures 5 and 6 reveal that an increase in environmental awareness increases firm’s cost of capital. It is important to emphasize the sensitivity of the cost of capital to the investor’s environmental preference. As Fig. 5 shows, with only 20% of green investors, when the environmental concerns were to double from its current size, the cost of capital changes by 28% for the green firm and by 51% for the brown firm, which in percentage points is an increase of 0.7 and 1.28, respectively. But with only green investors, the cost of capital increases so much that it becomes prohibitive. The cost of capital for green (brown) firms rises from 13.6% (18.0%) to 27.8% (33.1%). Finally, note that from a neutral investor’s perspective, the cost of capital are the returns he should consider when making his investment decision. Thus, our paper might also be used to guide neutral investors seeking outperformance. On the other hand, a change in the relative concern for environmental damage (an increase in ϵ) leads to smaller effects and the cost of capital of the green firm decreases, as Fig. 6 shows.

Fig. 5

COC^k as a function of γ. The dotted lines refer to the energy GICS sector, whereas the continuous lines refer to the health care GICS sector. Green lines refer to 100% green investors within the economy, while red lines refer to the 20% of green investors within the economy

Fig. 6

COC^k as a function of ϵ. The dotted lines refer to the energy GICS sector, whereas the continuous lines refer to the health care GICS sector. Green lines refer to 100% green investors within the economy, while red lines refer to the 20% of green investors within the economy

In this section, we have provided a numerical example calibrated to real–world data, which shows that the magnitude of the effects is of high economic relevance. Overall, our model contributes to a recent debate in the literature (summarized e.g. by Kölbel et al. (2020)). In particular, it shows that sustainable investing is much more relevant than Berk and van Binsbergen (2021) thought.

7 Conclusion

Many aspects of sustainable investing can be modeled in the CAPM. Using a parsimonious model, we find the following results: bad ESG investments must earn higher returns, and ESG rating heterogeneity increases returns. Sustainable investing affects a firm’s production through two channels: namely, the growth channel and the reform channel. Furthermore, we provide a numerical example to get some idea of the size of the effects so that we can judge their economic relevance. There remains room for further research as there are still missing aspects such as inflows into ESG funds (disequilibrium) can temporarily lead to higher returns (cf. van der Beck, 2021).

Appendices

Appendix A: Derivation market identity

$$ \begin{aligned} & \forall k = 1, \ldots ,K{\text{ we have }} \\ & \sum_{i} \theta^{i,k} = \theta^{M,k} {\text{, where }}\left. {\theta^{i,k} = \frac{{\lambda^{i,k} w^{i} }}{{q^{k} }}} \right|{ } \cdot q^{k} \\ & \sum_{i} \lambda^{i,k} w^{i} = q^{k} \theta^{M,k} \left| { \cdot \left( {1 - \lambda_{0}^{i} } \right)} \right|:\left( {1 - \lambda^{i,0} } \right) \\ & \left. {\sum_{i} \frac{{\lambda^{i,k} }}{{\left( {1 - \lambda^{i,0} } \right)}}\left( {1 - \lambda^{i,0} } \right)w^{i} = q^{k} \theta^{M,k} } \right|{ }:\sum_{i} \left( {1 - \lambda^{i,0} } \right)w^{i} = \sum_{i} \sum_{k = 1}^{K} q^{k} \theta^{i,k} = \sum_{k = 1}^{K} q^{k} \theta^{M,k} \\ & \sum_{i} \frac{{\lambda^{i,k} }}{{\left( {1 - \lambda^{i,0} } \right)}}r^{i} = \frac{{q^{k} \theta^{M,k} }}{{\sum_{k = 1}^{K} q^{k} \theta^{M,k} }} = \lambda^{M,k} ,{\text{ where }}r^{i} = \frac{{\left( {1 - \lambda^{i,0} } \right)w^{i} }}{{\sum_{i} \left( {1 - \lambda^{i,0} } \right)w^{i} }} \\ \end{aligned} $$

Appendix B: Derivation SML with heterogeneous expectations

$$ \begin{aligned} & \mathop{max}\limits_{{\lambda^{i} }} \left( {\mu^{i} - R_{f} } \right)\lambda^{i} - \frac{{{\Psi }^{i} }}{2}\lambda^{{i{\prime}}} {\text{COV}}\lambda^{i} \\ & {\text{FOC: }} \Psi ^{i} {\text{COV}}\lambda^{i} = \mu^{i} - R_{f} \\ & {\text{COV}}\mathop \sum \limits_{i} \frac{{\lambda^{i} }}{{1 - \lambda^{i,0} }}r^{i} \left. { = \mathop \sum \limits_{i} \frac{{r^{i} }}{{\left( {1 - \lambda^{i,0} } \right){\Psi }^{i} }}\left( {\mu^{i} - R_{f} } \right)} \right|\cdot\mathop \sum \limits_{i} \frac{{\lambda^{i} }}{{1 - \lambda^{i,0} }}r^{i} = \lambda^{M} \\ & {\text{COV}}\lambda^{M} = \mathop \sum \limits_{i} \frac{{r^{i} }}{{\left( {1 - \lambda^{i,0} } \right){\Psi }^{i} }}\left( {\mu^{i} - R_{f} } \right) \\ & {\text{VAR}}\left( {R^{M} } \right) = \mathop \sum \limits_{i} \frac{{r^{i} }}{{\left( {1 - \lambda^{i,0} } \right){\Psi }^{i} }}\left( {\mu^{i,M} - R_{f} } \right) \\ & {\text{with }}a^{i} = \frac{{r^{i} }}{{\left( {1 - \lambda^{i,0} } \right){\Psi }^{i} }}/\mathop \sum \limits_{i} \frac{{r^{i} }}{{\left( {1 - \lambda^{i,0} } \right){\Psi }^{i} }} \\ & {(1) }\frac{{{\text{COV}}\lambda^{M} }}{{\mathop \sum \nolimits_{i} \frac{{r^{i} }}{{\left( {1 - \lambda^{i,0} } \right){\Psi }^{i} }}}} = \mathop \sum \limits_{i} a^{i} \left( {\mu^{i,k} - R_{f} } \right) \\ & {(2) }\frac{{{\text{VAR}}\left( {R^{M} } \right)}}{{\mathop \sum \nolimits_{i} \frac{{r^{i} }}{{\left( {1 - \lambda^{i,0} } \right){\Psi }^{i} }}}} = \mathop \sum \limits_{i} a^{i} \left( {\mu^{i,M} - R_{f} } \right) \\ & \Rightarrow \frac{\left( 1 \right)}{{\left( 2 \right)}} = \frac{{{\text{COV}}\left( {R^{k} ,R^{M} } \right)}}{{{\text{VAR}}\left( {R^{M} } \right)}} = \frac{{\mathop \sum \nolimits_{i} a^{i} \left( {\mu^{i,k} - R_{f} } \right)}}{{\mathop \sum \nolimits_{i} a^{i} \left( {\mu^{i,M} - R_{f} } \right)}} \\ \end{aligned} $$

SML:

$$ \begin{aligned} & \overline{\mu }^{k} - R_{f} = \beta^{k} \left( {\overline{\mu }^{M} - R_{f} } \right) \\ & {\text{where }}\overline{\mu }^{k} = \mathop \sum \limits_{i} a^{i} \mu^{i,k} ,\overline{\mu }^{M} = \mathop \sum \limits_{i} a^{i} \mu^{i,M} = \mathop \sum \limits_{k = 1}^{K} \overline{\mu }^{k} \lambda^{M,k} ,\mu^{i,M} = \mathop \sum \limits_{k = 1}^{K} \mu^{i,k} \lambda^{M,k} \\ \end{aligned} $$

Note that for homogeneous expectations we get the usual SML as a special case since: ${\sum }_{i} {a}^{i}=1$ and ${\sum }_{k= 1}^{K} {\lambda }^{M,k}=1$.

Appendix C: Derivation asset prices

$$ \mathop {{\text{max}}}\limits_{{\theta^{i} }} R_{f} \left[ {w^{i} - q^{\prime}\theta^{i} } \right] + \left[ {p^{\prime}D - b^{{i}^{\prime }} } \right]\theta^{i} - \frac{{{\Psi }^{i} }}{2}\theta^{{i^{\prime}}} {\text{COV}}\left( D \right)\theta^{i} $$

$$ \begin{aligned} {\text{ FOC: }}qR_{f} & = D^{\prime}p - b^{i} - {\Psi }^{i} {\text{COV}}\left( D \right)\theta^{i} \\ {\Psi }^{i} {\text{COV}}\left( D \right)\theta^{i} & = D^{\prime}p - b^{i} - qR_{f} \\ {\text{COV}}\left( D \right)\theta^{i} & = \frac{1}{{{\Psi }^{i} }}\left[ {D^{\prime}p - b^{i} - qR_{f} } \right] \\ \end{aligned} $$

Summing over i using $\sum_{i} \theta^{i} = \overline{\theta }$ we get

$$ \begin{aligned} {\text{COV}}\left( D \right)\overline{\theta } & = \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}\left[ {D^{\prime}p - b^{i} - qR_{f} } \right] \\ {\text{COV}}\left( D \right)\overline{\theta } & = \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}D^{\prime}p - \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}b^{i} - \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}qR_{f} \\ \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}qR_{f} & = \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}D^{\prime}p - \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}b^{i} - {\text{COV}}\left( D \right)\overline{\theta } \\ q & = \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}D^{\prime}p - \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}b^{i} - {\text{COV}}\left( D \right)\overline{\theta }} \right] \\ \end{aligned} $$

Thus, asset price for asset $\text{k}$:

$${q}^{k}={\left[\sum_{i} \frac{1}{{\Psi }^{i}}{R}_{f}\right]}^{-1}\left[\sum_{i} \frac{1}{{\Psi }^{i}}{D}^{k{\prime}}p-\sum_{i} \frac{1}{{\Psi }^{i}}{b}^{i,k}-\text{COV}\left({D}^{k},{D}^{M}\right)\right]$$

Consequently, as $b^{i,k} = D^{k^{\prime}} \gamma^{i}$ we have

$${q}^{k}={\left[\sum_{i} \frac{1}{{\Psi }^{i}}{R}_{f}\right]}^{-1}\left[\sum_{i} \frac{1}{{\Psi }^{i}}{D}^{k{\prime}}p-\sum_{i} \frac{1}{{\Psi }^{i}}{D}^{k{\prime}}{\gamma }^{i}-\text{COV}\left({D}^{k},{D}^{M}\right)\right]$$

Appendix D: Firm’s maximization problem

Given that the supply of assets, $\overline{{\theta }^{k}}$, is assumed to be fixed the firm faces the following maximization problem

$$ \begin{aligned} & \mathop {{\text{max}}}\limits_{{D_{0}^{k} }} \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}D^{{k{^{\prime}}}} p - \mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}b^{i,k} - {\text{COV}}\left( {D^{k} ,D^{M} } \right)} \right]\overline{{\theta^{k} }} - D_{0}^{k} \overline{{\theta^{k} }} \\ & {\text{s}}{\text{.t}}{. }D_{s}^{k} = g_{s}^{k} f^{k} \left( {D_{0}^{k} } \right) \\ & \mathop {{\text{max}}}\limits_{{D^{k} }} \left[ {\mathop \sum \limits_{s} \mathop \sum \limits_{i} \frac{{p_{s} - \gamma_{s}^{i} }}{{{\Psi }^{i} }}g_{s}^{k} f^{k} \left( {D_{0}^{k} } \right) - {\text{COV}}\left( {D^{k} ,D^{M} } \right)} \right]\overline{{\theta^{k} }} - \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]D_{0}^{k} \overline{{\theta^{k} }} \\ \end{aligned} $$

We use the definition of the covariance to obtain

$$ \begin{aligned} {\text{COV}}\left( {D^{k} ,D^{M} } \right) & = {\mathbb{E}}\left[ {D^{k} D^{M} } \right] - {\mathbb{E}}\left[ {D^{k} } \right]{\mathbb{E}}\left[ {D^{M} } \right] \\ & = {\mathbb{E}}\left[ {g_{s}^{k} f^{k} \left( {D_{0}^{k} } \right)D_{s}^{M} } \right] - {\mathbb{E}}\left[ {g_{s}^{k} f^{k} \left( {D_{0}^{k} } \right)} \right]{\mathbb{E}}\left[ {D_{s}^{M} } \right] \\ & = \mathop \sum \limits_{s} p_{s} g_{s}^{k} f^{k} \left( {D_{0}^{k} } \right)D_{s}^{M} - \mathop \sum \limits_{s} p_{s} g_{s}^{k} f^{k} \left( {D_{0}^{k} } \right)\mathop \sum \limits_{s} p_{s} D_{s}^{M} \\ & = \left[ {\mathop \sum \limits_{s} p_{s} g_{s}^{k} D_{s}^{M} - \mathop \sum \limits_{s} p_{s} g_{s}^{k} \mathop \sum \limits_{s} p_{s} D_{s}^{M} } \right]f^{k} \left( {D_{0}^{k} } \right) \\ \end{aligned} $$

This yields

$$ \begin{aligned} & \mathop {{\text{max}}}\limits_{{D_0^k }} \left[ {\mathop \sum \limits_{s} \mathop \sum \limits_{i} \frac{{p_{s} - \gamma_{s}^{i} }}{{{\Psi }^{i} }}g_{s}^{k} f^{k} \left( {D_{0}^{k} } \right) - \left[ {\mathop \sum \limits_{s} p_{s} g_{s}^{k} D_{s}^{M} - \mathop \sum \limits_{s} p_{s} g_{s}^{k} \mathop \sum \limits_{s} p_{s} D_{s}^{M} } \right]f^{k} \left( {D_{0}^{k} } \right)} \right] - \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]D_{0}^{k} \\ & \mathop {{\text{max}}}\limits_{{D_0^k }} \left[ {\mathop \sum \limits_{s} \mathop \sum \limits_{i} \frac{{p_{s} - \gamma_{s}^{i} }}{{{\Psi }^{i} }}g_{s}^{k} - \mathop \sum \limits_{s} p_{s} g_{s}^{k} D_{s}^{M} - \mathop \sum \limits_{s} p_{s} g_{s}^{k} \mathop \sum \limits_{s} p_{s} D_{s}^{M} } \right]f^{k} \left( {D_{0}^{k} } \right) - \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]D_{0}^{k} \\ \end{aligned} $$

We define ${A}^{k}$ as follows

$${A}^{k}=\left[\sum_{s} \sum_{i} \frac{{p}_{s}-{\gamma }_{s}^{i}}{{\Psi }^{i}}{g}_{s}^{k}-\sum_{s} {p}_{s}{g}_{s}^{k}{D}_{s}^{M}-\sum_{s} {p}_{s}{g}_{s}^{k}\sum_{s} {p}_{s}{D}_{s}^{M}\right]$$

We investigate the two partial derivatives with respect to ${D}_{0}^{k}$ and ${g}_{s}^{k}$. Therefore, we separate the decision problem in

$$\underset{{D}_{0}^{k}}{\text{max}} {A}^{k}{f}^{k}\left({D}_{0}^{k}\right)-\left[\sum_{i} \frac{1}{{\Psi }^{i}}{R}_{f}\right]{D}_{0}^{k}$$

and

$$ \begin{aligned} & \mathop {{\text{max}}}\limits_{{g^{k} \in G^{k} }} \mathop \sum \limits_{s = 1}^{S} \nabla_{s} g_{s}^{k} \\ & {\text{where }}\nabla_{s} = \mathop \sum \limits_{i} \frac{{p_{s} - \gamma_{s}^{i} }}{{{\Psi }^{i} }} - p_{s} D_{s}^{M} - p_{s} \mathop \sum \limits_{s} p_{s} D_{s}^{M} \\ \end{aligned} $$

Part I:

We assume that ${D}_{0}^{k}$ is a negligible part of ${D}_{s}^{M}$ and use ${f}^{k}=\text{ln}$.

$$ \begin{aligned} & \mathop {{\text{max}}}\limits_{{D_{0}^{k} }} A^{k} {\text{ln}}\left( {D_{0}^{k} } \right) - \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]D_{0}^{k} \\ & {\text{FOC: }}D_{0}^{k} = \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} A^{k} \\ \end{aligned} $$

Part II:

We assume ${G}^{k}=\left\{x\in {R}_{+}^{S}\mid {\sum }_{s} {v}_{s}^{k}\text{exp}\left({x}_{s}\right)=c\right\}$ and thus consider for some positive weights ${v}_{s}^{k}>0$

$$\underset{{g}_{s}^{k}}{\text{max}} \sum_{s} {\nabla }_{s}{g}_{s}^{k}\text{ s.t. }\sum_{s} {v}_{s}^{k}\text{exp}\left({g}_{s}^{k}\right)=c$$

where $\text{c}$ denotes a constant. We use a change of variable

$${y}_{s}^{k}=\text{exp}\left({g}_{s}^{k}\right)\leftrightarrow {g}_{s}^{k}=\text{ln}\left({y}_{s}^{k}\right)$$

and hence have

$$\underset{{y}_{s}^{k}}{\text{max}} \sum_{s} {\nabla }_{s}\text{ln}\left({y}_{s}^{k}\right)\text{ s.t. }\sum_{s} {v}_{s}^{k}{y}_{s}^{k}=c$$

Lagrange & FOC:

$$ \begin{aligned} & L\left( {y_{s}^{k} ,\lambda } \right) = \sum\limits_{s} {\nabla_{s} } {\text{ln}}\left( {y_{s}^{k} } \right) + \lambda \left( {\sum\limits_{s} {v_{s}^{k} } y_{s}^{k} - c} \right) \\ & \partial_{{y_{s}^{k} }} L = \frac{{\nabla_{s} }}{{y_{s}^{k} }} + \lambda v_{s}^{k} = 0 \leftrightarrow y_{s}^{k} = - \frac{{\nabla_{s} }}{{\lambda v_{s}^{k} }} \\ & {\text{we}}\,{\text{have}} \sum\limits_{s} {v_{s}^{k} } y_{s}^{k} = c \\ & - \sum\limits_{s} {v_{s}^{k} } \frac{{\nabla_{s} }}{{\lambda v_{s}^{k} }} = c \leftrightarrow - \frac{1}{\lambda }\sum\limits_{s} {\nabla_{s} } = c \leftrightarrow \lambda = - \frac{1}{c}\sum\limits_{s} {\nabla_{s} } \\ \end{aligned} $$

hence, we have

$${y}_{s}^{k}=\frac{{\nabla }_{s}c}{\sum_{s} {\nabla }_{s}{v}_{s}^{k}}$$

Resubstitution gives

$${g}_{s}^{k}=\text{ln}\left({\nabla }_{s}c\right)-\text{ln}\left(\sum_{s} {\nabla }_{s}\right)-\text{ln}\left({v}_{s}^{k}\right)$$

Now we analyze how the optimal production, ${g}_{s}^{k}$, and financing decisions, ${D}_{0}^{k}$, of the firm change when the environmental concerns, ${\gamma }_{s}^{i}$, increase.

$$\underset{\_}{\text{Derivative: }{\partial }_{{\gamma }_{s}^{i}}{g}_{s}^{k}}$$

$$ \begin{aligned} g_{s}^{k} & = {\text{ln}}\left( {c\nabla_{s} } \right) - {\text{ln}}\left( {\mathop \sum \limits_{s} \nabla_{s} } \right) - {\text{ln}}\left( {v_{s}^{k} } \right) \\ \partial_{{\gamma_{s}^{i} }} g_{s}^{k} & = \frac{1}{{\nabla_{s} }}\partial_{{\gamma_{s}^{i} }} \nabla_{s} - \frac{1}{{\mathop \sum \nolimits_{s} \nabla_{s} }}\partial_{{\gamma_{s}^{i} }} \nabla_{s} \\ \partial_{{\gamma_{s}^{i} }} g_{s}^{k} & = \underbrace {{\partial_{{\gamma_{s}^{{\text{i}}} }} \nabla_{s} }}_{ < 0}\left( {\underbrace {{\underbrace {{\frac{1}{{\nabla_{s} }}}}_{ > 0} - \underbrace {{\frac{1}{{\mathop \sum \nolimits_{s} \nabla_{s} }}}}_{ > 0}}}_{{{\text{as }}\frac{1}{{\nabla_{s} }} > \frac{1}{{{\Sigma }_{s} \nabla_{s} }}{\text{ we have } >\; 0 \;{\text{as}}\;1/ \nabla_s > 1/ \sum_s \nabla_s}}}} \right) > 0 \\ \end{aligned} $$

Finally, we analyze ${\partial }_{{\gamma }_{s}^{i}}{D}_{0}^{k}$.

$$\underset{\_}{\text{Derivative: }{\partial }_{{\gamma }_{s}^{\text{i}}}{D}_{0}^{k}}$$

$$ \begin{aligned} D_{0}^{k} & = \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} A^{k} \\ & = \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} \mathop \sum \limits_{s} g_{s}^{k} \left( {\nabla_{s} } \right)\nabla_{s} \\ {\text{with }}\nabla_{s} & = \mathop \sum \limits_{i} \left( {\frac{{p_{s} - \gamma_{s}^{i} }}{{{\Psi }^{i} }}} \right) - p_{s} D_{s}^{M} - p_{s} \mathop \sum \limits_{s} p_{s} D_{s}^{M} {\text{ we have }}\partial_{{\gamma_{s}^{i} }} \nabla_{s} = - \frac{1}{{{\Psi }^{i} }} < 0 \\ {\text{and with }}g_{s}^{k} & = \ln \left( {c\nabla_{s} } \right) - \ln \left( {\mathop \sum \limits_{s} \nabla_{s} } \right) - {\text{ ln}}\left( {v_{s}^{k} } \right){\text{ we have }}\partial_{{\gamma_{s}^{i} }} g_{s}^{k} = - \frac{1}{{{\Psi }^{i} }}\frac{1}{{\nabla_{s} }} + \frac{1}{{{\Psi }^{i} }}\frac{1}{{\mathop \sum \nolimits_{s} \nabla_{s} }} < 0 \\ \partial_{{\gamma_{s}^{i} }} D_{0}^{k} & = \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} \partial_{{\gamma_{s}^{i} }} \nabla_{s} g_{s}^{k} \left( {\nabla_{s} } \right) + \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} \nabla_{s} \partial_{{\gamma_{s}^{i} }} g_{s}^{k} \left( {\nabla_{s} } \right) \\ & = \left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} \left[ {\partial_{{\gamma_{s}^{i} }} \nabla_{s} g_{s}^{k} \left( {\nabla_{s} } \right) + \nabla_{s} \partial_{{\gamma_{s}^{i} }} g_{s}^{k} \left( {\nabla_{s} } \right)} \right] \\ & = - \frac{1}{{{\Psi }^{i} }}\left[ {\mathop \sum \limits_{i} \frac{1}{{{\Psi }^{i} }}R_{f} } \right]^{ - 1} \left[ {\underbrace {{g_{s}^{k} \left( {\nabla_{s} } \right)}}_{ > 0} + \underbrace {{\nabla_{s} \left( {\frac{1}{{\nabla_{s} }} - \frac{1}{{\mathop \sum \nolimits_{s} \nabla_{s} }}} \right)}}_{{ > 0{\text{ as }}\frac{1}{{\nabla_{s} }} > \frac{1}{{\mathop \sum \nolimits_{s} \nabla_{s} }}}}} \right] < 0 \\ \end{aligned} $$

Appendix E: Economic relevance

Calibration Ψ

$$ \begin{aligned} COC + 1 & = \frac{{E\left( {D^{M} } \right)}}{{q^{M} }} \\ {\text{where}}\; q^{M} & = \left( {\frac{1}{\Psi }R_{f} } \right)^{ - 1} \left( {\frac{1}{\Psi }E\left( {D^{M} } \right) - {\text{Var}}\left( {D^{M} } \right)} \right) \\ \end{aligned} $$

We use $COC=0.07,{R}_{f}=1.02$ and $I=1$. Hence, we have $\Psi =\frac{E\left({D}^{M}\right)-\frac{1.02E\left({D}^{M}\right)}{1.07}}{\text{Var}\left({D}^{M}\right)}$.

Fig. 7

Definition median to classify two states: clean vs. dirty year. The median is about 0.995

Fig. 8

Relationship between CO2 and earnings growth rate

Fig. 9

Differentiation between green and brown firm

Fig. 10

Effect of $\upepsilon$ on ${g}_{s}^{k}$. 100% of green investors within the economy. The dotted lines refer to brown firm, whereas the continuous lines refer to the green firm. Green lines refer to clean states, while red lines refer to dirty states of the world

Fig. 11

Effect of ϵ on ${g}_{s}^{k}.$ 20% of green investors within the economy. The dotted lines refer to the brown firm, whereas the continuous lines refer to the green firm. Green lines refer to clean states, while red lines refer to dirty states of the world

Fig. 12

q^k as a function of γ. The dotted lines refer to the energy GICS sector, whereas the continuous lines refer to the health care GICS sector. Green lines refer to 100% green investors within the economy, while red lines refer to the 20% of green investors within the economy

Fig. 13

q^k as a function of ϵ. The dotted lines refer to the energy GICS sector, whereas the continuous lines refer to the health care GICS sector. Green lines refer to 100% green investors within the economy, while red lines refer to the 20% of green investors within the economy

Fig. 14

δ = 0.2. Ψ = 0.2. D₀^k as a function of γ. The dotted lines refer to the brown firm, whereas the continuous lines refer to the green firm. Green lines refer to a risk aversion of Ψ = 0.3, while red lines refer to a risk aversion of Ψ = 0.15

Fig. 15

δ = 0.2. Relationship between ∇_d and γ_d. Green lines refer to a risk aversion of Ψ = 0.3, while red lines refer to a risk aversion of Ψ = 0.15

Fig. 16

δ = 0.2. Ratio of $\frac{{g}_{d}^{k}}{{g}_{c}^{k}}$. The dotted lines refer to the brown firm, whereas the continuous lines refer to the green firm. Green lines refer to a risk aversion of Ψ = 0.3, while red lines refer to a risk aversion of Ψ = 0.15