1 Introduction

1.1 Commute times

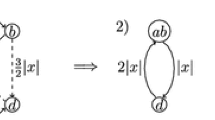
The commute time, or round-trip time, C(x, y), between two points, x and y is defined for (reversible) random walks on graphs with weighted edges in Barlow (2017)—it is the expected time taken to travel from x to y and then return to x. The original commute time identity, giving a simple formula for the expected commute time between two nodes in the graph, was only announced in 1989 Chandra et al. (1989), with details appearing only in 1997 in Chandra et al. (1997).

The standard equivalence between reversible random walks and electrical networks (see Lovasz (1996) or Barlow (2017)), for a network \(\mathcal {X}\), with edge weights/conductances \(\mu (x,y)\), sets \(\mu _x=\sum _{y\in \mathcal {X}}\mu _{x,y}\) and \(\mu (\mathcal {X})=\sum _{u,v\in \mathcal {X}}\mu (u,v)\), then fixes one-step transition probabilities \(P_{x,y}= \frac{\mu _{x,y}}{\mu _x}\). The commute-time identity is then

$$\begin{aligned} C(x,y)=R_{\text {eff}}(x,y)\mu (\mathcal {X}), \end{aligned}$$

where \(R_{\text {eff}}(x,y)\) is the effective resistance between x and y. We give a version more suited to our purposes later in (3.1).

The commute time has attracted substantial interest as a tool for the analysis of random networks. In Shang (2012), Shang... remarks that “...the commute time has received increasing attention, since it can be used as a robust measure of network search efficiency”. von Luxburg et al. note that “Since vertices in the same cluster of the graph have a small commute distance, whereas vertices in different clusters of the graph have a large commute distance to each other...the commute distance is considered a convenient tool to encode the cluster structure of the graph” (von Luxburg et al., 2014), while Khoa and Chawla state that the “Commute time has been used as a robust metric for different learning tasks such as clustering and anomaly detection. It has also found widespread applications in personalized search, collaborative filtering and image segmentation. The fact that the commute time is averaged over all paths (and not just the shortest path) makes it more robust to data perturbations” (Khoa & Chawla, 2016), and “[Commute time] between two nodes can capture both the distance between them and their local neighbourhood densities so that we can capture both global and local outliers using distance based methods” (Khoa & Chawla, 2010).

Qiu and Hancock’s “...paper exploits the properties of the commute time between nodes of a graph for the purposes of clustering and embedding and explores its applications to image segmentation and multibody motion tracking.” Qiu and Hancock (2007) See Lovasz (1996) for a survey. See also Qiu and Hancock (2006), Konsowaa et al. (2013), Xia et al. (2020), Helali and Löwe (2019) and Wenhang et al. (2023) and references therein.

1.2 The problem

Now suppose that \(X^\mu \) is a diffusion on [0, 1], started at x and given by

$$\begin{aligned} X^\mu _t=x+\int _0^t \sigma (X^\mu _u) \mathop {}\!\textrm{d}B_u+\int _0^t \mu (X^\mu _u) \mathop {}\!\textrm{d}u\,\,\,\text { on } \, (0,1) \end{aligned}$$
(1.1)

with instantaneous reflection at 0 and 1 (see Williams (1979) or Ito and McKean (1974) for details).

Define \(T_x\) to be the first time that the diffusion reaches x, then define \({\mathcal {S}}={\mathcal {S}}(X^\mu )\), the commute time (between 0 and 1), by

$$\begin{aligned} {\mathcal {S}}(X^\mu ):=\inf \left\{ t>T_1(X^\mu ):\, X^\mu _t=0 \right\} . \end{aligned}$$

In Jacka and Hernández-Hernández (2022), motivated by a question arising in simulated tempering (see Atchade et al. (2011)), we considered the following problem (and several variants and generalisations):

Problem 1.1

Minimise the expected commute time \(\mathbb {E}[\, {\mathcal {S}}\,]\); i.e. find the infimum (over a control constraint):

$$\begin{aligned} \inf _\mu \mathbb {E}_x [{\mathcal {S}}(X^\mu )], \end{aligned}$$

or, more generally, find, for suitable positive functions f, the value function \(\Phi \), given by

$$\begin{aligned} \Phi (x):=\inf _\mu [\Phi (\mu ,x)]\text { where } \Phi (\mu ,x):=\mathbb {E}_x\left[ \int _0^{\mathcal {S}}f(X^\mu _t) \mathop {}\!\textrm{d}t\right] . \end{aligned}$$
(1.2)

The control constraint is that the drift, \(\mu (x)\), at each level x, must be chosen at or before \(X^\mu \)’s first visit to that level and thereafter remains fixed.

1.3 Problem motivation

The problem models one arising in simulated tempering -a form of Markov Chain Monte Carlo (MCMC). Simulated tempering is designed to address the issue that arises in MCMC when simulating a draw from a highly multimodal distribution – the algorithm reaches a local minimum and cannot exit its basin of attraction to attain the global minimum. To address this, simulated tempering uses a reversible Markov Process (essentially the level corresponds to the temperature in a “heat bath”) to move from a low to a high temperature state (in which modes are smeared out) so that the Markov chain can then move around the statespace; then, returning to a low temperature, we sample from the true distribution (see Atchade et al. (2011)). Our problem addresses how to design the “temperature chain’ to minimise the expected time to perform the tempering.

1.4 Hypothesised form of the optimal control

Under the assumption that \(\mu \) was already fixed on some interval [0, y), the drift is otherwise unconstrained and the starting state is in [0, y), we gave the optimal drift to minimise the quantity in (1.2) in Theorem 4.6 of Jacka and Hernández-Hernández (2022),. We left open the question of the optimal control when \(\mu \) is, initially, fixed on some other interval. The key observation enabling the identification of the solution in Jacka and Hernández-Hernández (2022) was that we can follow the same solution as for the static case – where we choose the drift function at time 0 – because ‘there can be no surprises’ (in the path of X). This statement is no longer valid when the set on which the drift is constrained is not of the form [0, y) and we gave, as an example in Remark 4.1 of Jacka and Hernández-Hernández (2022), a heuristic argument for why a different solution would be optimal in the case where the constraint set was of the form (i, 1]. To quote from Jacka and Hernández-Hernández (2022): “...If the controlled diffusion starts at \(x>0\) then there is a positive probability that it will not reach zero before hitting 1, in which case the drift will not have been chosen at levels below \(I_{T_1}\), the infimum on \([0, T_1]\). Consequently, on the way down we can set the drift to be very large and negative below \(I_{T_1}\). Thus the optimal dynamic control will achieve a strictly lower payoff than the optimal static one in this case.”

Our aim, in the current paper, is to present the solution (in Theorem 4.2) to the dynamic problem in this case, where the ‘surprises’ are how far down the controlled process gets before time \(T_1\). Indeed, we shall show that the optimal policy implements a pre-determined drift at all levels below i which are reached before \(I_{T_1}\) and then, essentially, imposes infinite downward drift at all lower levels. We shall make this statement more precise in the subsequent section.

The structure of the paper is as follows: in Sect. 2 we give a formal definition of the model and a version of the main theorem; Section 3 is devoted to calculating the candidate value function; Section 4 gives the proof that this is correct and we then give some concluding remarks.

2 The model and some notation

2.1 The model

Let \(X_{t}^{\mu ,x}\) be a regular diffusion on [0, 1] with instantaneous reflection at 0 and 1, starting at \(x\in [0,1]\), and given by (1.1).

We need to define the set of admissible controls quite carefully. Two approaches are possible: the first is to restrict controls to choosing the drift \(\mu \) whilst the second is to control the corresponding random scale function. We adopt the second approach, although we should warn that the identified optimal policy will not, in general, be in this class (or, equivalently, the relevant infimum will not be attained by any policy in this class).

We assume the usual Markovian setup, so that each stochastic process lives on a suitable filtered space \((\Omega ,\mathcal {F},(\mathcal {F}_t)_{t\ge 0})\), with the usual family of probability measures \((\mathbb {P}_x)_{x\in [0,1]}\) corresponding to the possible initial values.

Let \(X^{\mu }\) be the diffusion with instantaneous reflection as given in (1.1). Denote by \(s^\mu \) the standardised scale measure of \(X^\mu \) and by \(m^\mu \) the corresponding speed measure.

Remark 2.1

Since \(X^\mu \) is regular and reflection is instantaneous we have (up to an arbitrary multiplicative constant):

$$\begin{aligned} s^\mu (x):=s^\mu [0,x]= & {} \int _0^x\exp \biggl ( {-2\int _0^u\frac{\mu (t)}{\sigma ^2(t)} \mathop {}\!\textrm{d}t}\biggr ) \mathop {}\!\textrm{d}u, \\ m^\mu ([0,x]):=m^\mu (x)= & {} 2\int _0^x\frac{ \mathop {}\!\textrm{d}u}{\sigma ^2(u)s^{\prime }{}(u)}=2\int _0^x\frac{\exp \bigl ({2\int _0^u\frac{\mu (t)}{\sigma ^2(t)} \mathop {}\!\textrm{d}t}\bigr )}{\sigma ^2(u)} \mathop {}\!\textrm{d}u, \end{aligned}$$

(see Revuz and Yor (2004)).

From now on, we consider the more general case where we only know that s and m are absolutely continuous with respect to Lebesgue measure (denoted by \(\lambda \)) so that, denoting the respective Radon-Nikodym derivatives by \(s^{\prime }{}\) and \(m^{\prime }{}\) we have

$$\begin{aligned} s^{\prime }{}m^{\prime }{}= \frac{2}{\sigma ^2}\,\,\lambda \text {-a.e.} \end{aligned}$$

For such a pair we shall, for now, denote the corresponding diffusion, when it exists, by \(X^s\). We emphasize that we are only considering regular diffusions with Brownian “martingale part” \(\int \sigma \mathop {}\!\textrm{d}B\) or, more precisely, diffusions X with scale functions s such that, away from 0 and 1,

$$\begin{aligned} \mathop {}\!\textrm{d}s(X_t)=s'(X_t)\sigma (X_t) \mathop {}\!\textrm{d}B_t, \end{aligned}$$
(2.1)

for some Brownian Motion B, so that, for example, sticky points are excluded, as are singular scale measures (see Englebert and Schmidt (1985) for a description of driftless sticky Brownian Motion and its construction, see also Englebert (2000) for other problems arising in solving stochastic differential equations).

Remark 2.2

Note that our assumptions do allow generalised drift: if s is the difference between two convex functions then

$$\begin{aligned} X^s_t=x+\int _0^t\sigma (X^s_u) \mathop {}\!\textrm{d}B_u-\frac{1}{2}\int _{\mathbb {R}}L^a_t(X)\frac{s^{\prime }{}^{\prime }{}( \mathop {}\!\textrm{d}a)}{s^{\prime }{}_-(a)}, \end{aligned}$$
(2.2)

where \(s^{\prime }{}_-\) denotes the left-hand derivative of s, \(s^{\prime }{}^{\prime }{}\) denotes the signed measure induced by \(s^{\prime }{}_-\) and \(L^a_t(X)\) denotes the local time at a developed by X by time t (see Revuz and Yor (2004) Chapter VI for details).

Remark 2.3

Essentially, we treat (2.1) as the canonical dynamics for our problem, but note that we shall consider random scale measures for which, for example, s(0) is not known at time 0 so that it is more helpful to model our problem as one of progressively choosing the restriction of the measure s to a suitable, dynamically updated, subset of [0, 1].

2.2 The control setting

From now on, we will adopt the weak approach to the control problem so that we work on canonical pathspace \(\Omega =D_{[0,\infty )}[0,1]\), the space of paths in [0, 1], indexed by \([0,\infty )\), which are right-continuous with left limits, and equip it with the Borel \(\sigma \)-algebra on \(\Omega \) with respect to the Skorokhod metric with natural filtration \((\mathcal {F}_t)_{t\ge 0}\), and simply take

$$\begin{aligned} X:\omega \mapsto \omega \end{aligned}$$

(see Ethie and Kurtz (1986) for details).

Let \(\mathcal {M}\) be the set of scale functions/measures on [0, 1] that are absolutely continuous with respect to Lebesgue measure. Given a fixed scale function \({s_0} \in \mathcal {M}\) and a Borel subset F of [0, 1], define the set \(\mathcal {M}_{F}^{{s_0}}\) as follows

$$\begin{aligned} \mathcal {M}_{F}^{s_{0}} :=\left\{ s \in \mathcal {M}\; a.s.: \,\,\mathop {}\!\textrm{d}s \Big |_F = \mathop {}\!\textrm{d}{s_0} \Big |_F\; \right\} . \end{aligned}$$

Then define the set of available controls

$$\begin{aligned} \mathcal {C}_{F}^{s_{0}} :=\left\{ \text {random measures } s \in \mathcal {M}\; a.s.: \,\,\mathop {}\!\textrm{d}s \Big |_F = \mathop {}\!\textrm{d}{s_0} \Big |_F,\; s'(X_{\cdot })\text { is predictable}\right\} . \end{aligned}$$
(2.3)

Now define the admissible control policies \(\mathcal {A}_{F}^{x,s_{0}}\) to be the set of \(s\in \mathcal {C}_{F}^{s_{0}}\) such that the corresponding controlled process, starting at \(x \in [0,1]\), with random scale function s, exists; in other words,

$$\begin{aligned} \mathcal {A}_{F}^{x,s_{0}}= & {} \{s\in \mathcal {C}_{F}^{s_{0}}\text { s.t. there exists a p.m. }\mathbb {P}_{s,x}, \text { with }X_0=x,\;\mathbb {P}_{s,x}-a.s.\text { and }\nonumber \\ ds(X_t,\omega )= & {} s'(X_t,\omega )\sigma (X_t)dB_t, \text { for some }\mathbb {P}_{s,x}-\text {Brownian Motion},\; B\}. \end{aligned}$$
(2.4)

We denote the expectation corresponding to such a p.m. \(\mathbb {P}_{s,x}\) by \(\mathbb {E}_{s,x}\).

Recall that \(T_y\) is the first hitting time at level y of the process X, that is

$$\begin{aligned} T_y:= \inf \{ t > 0:\, X= y\}, \end{aligned}$$

and \({\mathcal {S}}\) denotes the first time the controlled process reaches 0 after having hit level 1, that is

$$\begin{aligned} {\mathcal {S}}: = \inf \{ t > T_1 :\, X_{t} = 0\}. \end{aligned}$$
(2.5)

We are able to choose \(s'\) (the derivative of the scale function s) dynamically, but only once for each level, and we seek to minimise.

$$\begin{aligned} \mathbb {E}_{s,x} \left[ \int _{0}^{{\mathcal {S}}} f (X_{t}) \mathop {}\!\textrm{d}t\right] \end{aligned}$$

(See (Jacka & Hernández-Hernández 2022, Remark 4.1)).

More precisely, we will assume the following:

Assumption 2.1

For a given level \(\ell \) and a starting point x, with \(\ell \le i_0\le x\), suppose that \(s'\) has been fixed to be \({s_0}'\) at every level on \(F:=[0,\ell ] \cup [i_0,1]\).

Then, for a given positive cost function f, the control problem consists in finding

$$\begin{aligned} \Phi ({s_0},F,x,i):=\inf _{s\in \mathcal {A}_{F}^{i,{s_0}}} \mathbb {E}_{s,x} \bigl [\int _0^{{\mathcal {S}}} f(X_{t})\mathop {}\!\textrm{d}t\bigr ]. \end{aligned}$$
(2.6)

Define the running minimum and maximum of X by setting

$$\begin{aligned} I_{t} \,\,:=\,\,\inf _{0\le u \le t} X_{u},\text { and } S_t\,\,:=\,\,\sup _{0\le u \le t} X_{u}, \end{aligned}$$

and then set

$$\begin{aligned} \mathcal {I}_t:=\min (i_0,I_t). \end{aligned}$$

Remark 2.2

The reason we denote the left-hand endpoint of the second interval in F as \(i_0\) is that, setting \(F_0=F\), the set on which the scale measure is constrained at time t is

$$\begin{aligned} F_t=[0,\ell ]\cup [\mathcal {I}_t,1], \end{aligned}$$

since the range of \(X\big |_{[0,t]}\) is \([I_t,S_t]\). It follows that, if we treat \(\ell \) as fixed, we may reconstruct \(F_t\) from the knowledge of \(\mathcal {I}_t\).

2.3 Heuristic for the optimal strategy

We suppose that the strategy s has been fixed as \({s_0}\) on \(F_0\), and we need to determine how to proceed on \(F_0^c=(\ell ,i_0)\). Since we are only allowed to choose \(s'\) once for each level, we need choose a strategy value at \(y\in (\ell , i_0)\) before time \(T_1\) only if such a level is reached from above before X hits 1. Conversely, if \(\mathcal {I}_{T_1}>y>\ell \), then we need only choose the drift at level y after the process has hit level 1. Consequently we are not constrained to enable the process to hit level 1 (again) so may choose an arbitrarily large downward drift at any such level.

Our optimal control should respect this and we proceed to calculate the optimal control (essentially) in this class. As we shall see, in Theorem 4.2, the optimal policy is of this form.

Example 2.3

In the case where \(\sigma ^2=f=s_0'\equiv 1\) and \(F_0=[\frac{1}{2},1]\), the optimal payoff, starting at \(x=i_0=\frac{1}{2}\), is \(\Psi _0^*(\frac{1}{2})\) where \(\Psi _0^*\) is the convex conjugate of the function

$$\begin{aligned} \Psi _0:(1,\infty )\rightarrow \mathbb {R}_+;\;\; \Psi _0:z\mapsto \frac{e^{-z}}{\int _1^z\frac{du}{ue^u}}, \end{aligned}$$

and the optimal control is of the form we hypothesised above.

3 The candidate optimal payoff and policy

3.1 Initial calculations

The commute time identity:

$$\begin{aligned} \mathbb {E}_{s,0}[{\mathcal {S}}]=s[0,1]m[0,1] \end{aligned}$$
(3.1)

is generalised as follows. For any pair \(x,y \in [0,1]\), and any \(s\in \mathcal {M}\), define the function

$$\begin{aligned} \phi ^s(x,y):= \mathbb {E}_{s,x} \left[ \int _{0}^{T_{y}} f(X_{t}) \mathop {}\!\textrm{d}t\right] \end{aligned}$$

It follows (by (Jacka & Hernández-Hernández Jacka and Hernández-Hernández (2022), Theorem 2.4)) that, defining the measure \(m_f\) by

$$\begin{aligned} {m_f}'= & {} fm',\nonumber \\ \phi ^s(x,y)= & {} \left\{ \begin{array}{cc} \int _{x}^{y} \mathop {}\!\textrm{d}v s'(v) \int _{0}^{v} \frac{2f(u)}{\sigma ^{2}(u) s'(u)} \mathop {}\!\textrm{d}u=\int _{x}^{y} \mathop {}\!\textrm{d}v s'(v) m_f(v), &{} x \le y \\ &{}\\ \int _{y}^{x} \mathop {}\!\textrm{d}v s'(v) \int _{v}^{1} \frac{2f(u)}{\sigma ^{2}(u) s'(u)} \mathop {}\!\textrm{d}u=\int _{y}^{x} \mathop {}\!\textrm{d}v s'(v){{\tilde{m}}_f}(v), &{} x \ge y, \end{array} \right. \end{aligned}$$
(3.2)

and

$$\begin{aligned} \mathbb {E}_{s,0}\biggl [\int _0^{\mathcal {S}}f(X_t)dt\biggr ]=\phi ^s(0,1)+\phi ^s(1,0)=s[0,1]m_f[0,1]. \end{aligned}$$

Definition 3.1

We suppose that s is an arbitrary (deterministic) scale measure which is assumed to equal \({s_0}\) on the intervals \([0,\ell ]\) and [i, 1] (for some \(\ell \in [0,1]\) fixed in advance) and which will be dynamically reset to give infinite downward drift on the interval \([\ell ,\mathcal {I}_{T_1}\vee \ell )\) at time \(T_1\). We denote the corresponding (random) scale measure by \(s^*\).

Remark 3.2

Of course, such a scale measure does not belong to our admissible class \(\mathcal {A}_{F}^{x,s_{0}}\) but, as we will see, there are admissible \(\epsilon \)-optimal strategies of this form.

Definition 3.3

As is standard, we will call

$$\begin{aligned} \Phi ^s({s_0},F,x,i_0):=\mathbb {E}_{s,x}\left[ \int ^{\mathcal {S}}_0 f(X_t)dt\right] \end{aligned}$$

the payoff of policy \(s\in \mathcal {A}^{x,{s_0}}_F\) and call the optimum payoff \(\Phi ({s_0},F,x,i_0)\), given by

$$\begin{aligned} \Phi ({s_0},F,x,i_0)=\inf _{s\in \mathcal {A}^{x,{s_0}}_F}\Phi ^s({s_0},F,x,i_0), \end{aligned}$$

the value function. For the reason enunciated in Remark 2.2, we shall henceforth suppress the dependence of \(\Phi \) and \(\Phi ^s\) on F.

Define

$$\begin{aligned} \rho :z\mapsto \frac{2f(z)}{\sigma ^2(z)}. \end{aligned}$$

We make the following standing assumption whose relevance follows:

Assumption 3.4

$$\begin{aligned} \sqrt{\rho }\in L^1[0,1]. \end{aligned}$$

Remark 3.5

Suppose that s is a scale measure, then the Cauchy-Schwarz inequality tells us that

$$\begin{aligned} \int _0^1\sqrt{\rho (z)}dz= & {} \int _0^1\sqrt{\frac{2f(z)}{\sigma ^2(z)}}dz\le \biggl (\int _0^1 s'(z)dz\biggr )^\frac{1}{2}\biggl (\int _0^1 \frac{2f(z)}{\sigma ^2(z)s'(z)}dz\biggr )^\frac{1}{2}\\= & {} \sqrt{\mathbb {E}_{s,0}\bigl [\int ^{{\mathcal {S}}}_0f(X_t)dt\bigr ]}, \end{aligned}$$

so that Assumption 3.4 is a necessary condition for the existence of a scale function with finite payoff.

To complete the (infinite-dimensional) state of the problem, we recall that

$$\begin{aligned} F_t:=[0,\ell ]\cup [\mathcal {I}_{t\wedge T_1},1], \end{aligned}$$

and let \(F=F(i):=[0,\ell ]\cup [i,1]\) denote a generic constraint set.

We compute the corresponding payoff of the controlled process \((X_{t})_{t\ge 0}\), when i is the starting point.

Set \(s:x\mapsto s[0,x]\), \(m_f:x\mapsto m_f[0,x]\), \(\tilde{s}:x\mapsto s[x,1]\), and \({{\tilde{m}}_f}:x\mapsto m_f[x,1]\)

Definition 3.6

Fix \(s\in \mathcal {M}_{F}^{{s_0}}\) and define

$$\begin{aligned} \kappa= & {} \int _0^\ell s'(v)m_f [v,\ell ]\mathop {}\!\textrm{d}v=\int _0^l s'(v){{\tilde{m}}_f}(v)\mathop {}\!\textrm{d}v-s(\ell ){{\tilde{m}}_f}(\ell )\nonumber \\ a= & {} a(i):= \tilde{m}_f (i) \nonumber \\ b= & {} b(i):= \tilde{s} (i) \nonumber \\ c:= & {} m_f(\ell )\nonumber \\ n:= & {} \tilde{s} (\ell ) \nonumber \\ k:= & {} s (\ell ), \end{aligned}$$
(3.3)

and note that, since \(s'\) is fixed on \(F=[0,\ell ]\cup [i,1]\), \(n\) is the only one of the parameters in (3.3) which is not determined by the restriction of \(s'\) to F.

Lemma 3.7

Let \(s\in \mathcal {M}_{F}^{{s_0}}\), then the payoff of the policy \(s^*\), given by Definition 3.1, is given by

$$\begin{aligned} \Phi ^{s^*}({s_0},i,i)= \left\{ \kappa + bc + ab H(i) + \frac{1}{e^{H(i)}} \int _l^i\frac{\rho H e^H }{H'} \mathop {}\!\textrm{d}z \right\} \end{aligned}$$
(3.4)

where H is defined by

$$\begin{aligned} H:z\mapsto 1 + \frac{n}{c} + \ln \frac{c}{\tilde{s}(z)}\text { and, as stated earlier, } \rho :z\mapsto \frac{2f(z)}{\sigma ^2(z)}. \end{aligned}$$

Proof

First note that \(s^*=s\) on the event \((\mathcal {I}_{T_1}\le \ell )\), whereas, on \((\mathcal {I}_{T_1}>\ell )\), \(s^{*'}=s'\) on \((\mathcal {I}_{T_1},1]\) and when \(X^{s^*}\) reaches \(\mathcal {I}_{T_1}\) for the first time after time \(T_1\), the effect of infinite downwards drift is that X is instantaneously translated to level \(\ell \), and thereafter a reflecting (downwards) barrier is imposed at level \(\ell \).

It follows that

$$\begin{aligned} \Phi ^{s^*}({s_0},i,i)=\phi ^s(i,1)+\mathbb {E}_{s,i}\biggl [\phi ^s(1,0)1_{(\mathcal {I}_{T_1}\le \ell )}+\bigl (\phi ^s(1,\mathcal {I}_{T_1})+\phi ^s_{\ell }(\ell ,0)\bigr )1_{(\mathcal {I}_{T_1}> \ell )}\biggr ],\nonumber \\ \end{aligned}$$
(3.5)

where

$$\begin{aligned} \phi ^s_{\ell }(x,y):=\mathbb {E}_{s,x} \left[ \int _{0}^{T_{y}} f(X_{t}) 1_{(X_{t}\in [0,\ell ])}\mathop {}\!\textrm{d}t\right] =\mathbb {E}^{(\ell )}_{s,x} \left[ \int _{0}^{T_{y}} f(X_{t})\mathop {}\!\textrm{d}t\right] \end{aligned}$$
(3.6)

and \(\mathbb {E}^{(\ell )}_{s,x}\) is the expectation operator corresponding to the probability law \(\mathbb {P}^{(\ell )}_{s,x}\), under which the scale measure is s and the controlled process starts at x and has a reflecting barrier at level \(\ell \).

It is easy to see that

$$\begin{aligned} \phi ^s_{\ell }(x,y) = \int _{y}^{x} \mathop {}\!\textrm{d}v s'(v) \int _{v}^{\ell } \frac{2f(u)}{\sigma ^{2}(u) s'(u)} \mathop {}\!\textrm{d}u=\int _{x}^{y} \mathop {}\!\textrm{d}v s'(v) m_f(v,\ell ), \text { for } y \le x \le \ell ,\nonumber \\ \end{aligned}$$
(3.7)

so that \(\phi ^s_{\ell }(\ell ,0)=\kappa \), while, under the control s, with X starting at i, the distribution function of \(\mathcal {I}_{T_1}\) is

$$\begin{aligned} G:x\mapsto {\left\{ \begin{array}{ll} 1&{}\text {for }x>i\\ \frac{\tilde{s}(i)}{\tilde{s}(x)}&{}\text {for }i\ge x\ge 0\\ 0&{}\text {for }x<0. \end{array}\right. } \end{aligned}$$
(3.8)

Now equation (3.5) implies that

$$\begin{aligned} \Phi ^{s^*}({s_0},i,i)=\phi ^s(i,1)+\phi ^s(1,0)G(\ell )+[1-G(\ell )]\kappa +\int _{\ell }^i\phi ^s(1,x)dG(x), \end{aligned}$$

which becomes (on integrating by parts and recalling (3.2 and (3.8))

$$\begin{aligned} \Phi ^{s^*}({s_0},F_0,i,i)= & {} \int _i^1 s'(v)m_f(v)\mathop {}\!\textrm{d}v+\frac{\tilde{s}(i)}{\tilde{s}(\ell )}\int _0^1 s'(v){{\tilde{m}}_f}(v)\mathop {}\!\textrm{d}v+\kappa \biggl (1-\frac{\tilde{s}(i)}{\tilde{s}(\ell )}\biggr )\\{} & {} +\int _{\ell }^i \frac{\tilde{s}(i)}{\tilde{s}(x)}s'(x){{\tilde{m}}_f}(x)dx+G(i)\phi ^s(1,i)-G(\ell )\phi ^s(1,\ell )\\= & {} \int _i^1 s'(v)m_f(v)\mathop {}\!\textrm{d}v+\kappa + \int _{\ell }^i \frac{\tilde{s}(i)}{\tilde{s}(x)}s'(x){{\tilde{m}}_f}(x)dx\\{} & {} +\int _i^1 s'(v){{\tilde{m}}_f}(v)\mathop {}\!\textrm{d}v-\frac{\tilde{s}(i)}{\tilde{s}(\ell )}\left( \int _{\ell }^1 s'(v){{\tilde{m}}_f}(v)\mathop {}\!\textrm{d}v+\kappa \right. \\{} & {} \left. -\int _0^1 s'(v){{\tilde{m}}_f}(v)\mathop {}\!\textrm{d}v\right) \\= & {} \int _i^1 s'(v)m_f(v)\mathop {}\!\textrm{d}v+\kappa + \int _{\ell }^i \frac{\tilde{s}(i)}{\tilde{s}(x)}s'(x){{\tilde{m}}_f}(x)dx\\{} & {} +\int _i^1 s'(v){{\tilde{m}}_f}(v)\mathop {}\!\textrm{d}v+\frac{\tilde{s}(i)}{\tilde{s}(\ell )}s(\ell ){{\tilde{m}}_f}(\ell )\\= & {} \tilde{s}(i)m_f([0,1])+\kappa +\int _i^1 s'(v){{\tilde{m}}_f}(v)\mathop {}\!\textrm{d}v+\frac{\tilde{s}(i)}{\tilde{s}(\ell )}s(\ell ){{\tilde{m}}_f}(\ell )\\= & {} \tilde{s}(i)m_f(\ell )+\kappa +\tilde{s}(i)\biggl [(1+\frac{s(\ell )}{\tilde{s}(\ell )}){{\tilde{m}}_f}(\ell )+\int _\ell ^i\frac{{{\tilde{m}}_f}(y)}{\tilde{s}(y)}s'(y)\mathop {}\!\textrm{d}y \biggr ]\\= & {} \tilde{s}(i)m_f(\ell )+\kappa +\tilde{s}(i)\biggl [(1+\frac{s(\ell )}{\tilde{s}(\ell )}){{\tilde{m}}_f}(\ell )+\int _\ell ^i {{\tilde{m}}_f}(y)H'(y)\mathop {}\!\textrm{d}y \biggr ]\\= & {} \tilde{s}(i)m_f(\ell )+\kappa +\tilde{s}(i)\biggl [H(i){{\tilde{m}}_f}(i)+\int _\ell ^i {m_f}'(y)H(y)\mathop {}\!\textrm{d}y\biggr ]\\= & {} \kappa +bc+abH(i)+b\int _\ell ^i {m_f}'(y)H(y)\mathop {}\!\textrm{d}y.\\ \end{aligned}$$

Now \({m_f}'=\frac{\rho }{s'}\) so, using the equalities

$$\begin{aligned} H'(z) = \frac{s'(z)}{\tilde{s}(z)}, \text { and } e^H = \frac{c}{\tilde{s}(z)} e^{1+ n/c}, \end{aligned}$$

we obtain

$$\begin{aligned} \Phi ^{s^*}({s_0},i,i)=\kappa +bc+abH(i)+ \frac{1}{e^{H(i)}} \int _l^i\frac{\rho H e^H }{H'} \mathop {}\!\textrm{d}z, \end{aligned}$$

as required. \(\square \)

3.2 A calculus of variations approach

We wish to find

$$\begin{aligned} v({s_0},i,i):=\inf _{s\in \mathcal {M}_{F_0}^{{s_0}}}\Phi ^{s^*}({s_0},i,i). \end{aligned}$$
(3.9)

since our candidate optimal control lies in this class. To do this, we first treat \(H(\ell )\) and H(i) as fixed parameters and then optimise over suitable values for these parameters.

Lemma 3.8

$$\begin{aligned} v({s_0},i,i)&:= \kappa + bc + \inf _{n\ge b} \left\{ ab \left( 1+ \frac{k}{n} + \ln \frac{n}{b}\right) \right. \\&\quad \left. + \frac{\beta ^2(i)}{e^{1+ \frac{k}{n} + \ln \frac{n}{b}} \bigl (\theta (1+\frac{k}{n})-\theta (1+ \frac{k}{n} + \ln \frac{n}{b})\bigr )}\right\} \end{aligned}$$

where

$$\begin{aligned} \theta :x\mapsto \int _{x}^{\infty } \frac{\mathop {}\!\textrm{d}u}{ue^u},\quad \quad \beta (i) = \int _{\ell }^i \sqrt{\rho (v)}\mathop {}\!\textrm{d}v. \end{aligned}$$
(3.10)

Proof

Fixing \(H(\ell )\) and H(i), the Euler-Lagrange equation for the minimisation of \(\int _{\ell }^i\frac{\rho H e^H }{H'} \mathop {}\!\textrm{d}z \) yields

$$\begin{aligned} (2\rho H'(1+H)+\rho ' H)H'-2H''\rho H=0. \end{aligned}$$

Dividing by \(2\rho HH'\) gives

$$\begin{aligned} H'(1+\frac{1}{H})=\frac{H''}{H'}-\frac{1}{2}\frac{\rho '}{\rho }. \end{aligned}$$
(3.11)

Integrating (3.11) yields

$$\begin{aligned} H+\ln H=\ln H'-\frac{1}{2}\ln \rho -\ln D, \end{aligned}$$

or

$$\begin{aligned} \frac{H'}{He^H}={D\sqrt{\rho }}, \end{aligned}$$
(3.12)

for some constant of integration D. Integrating (3.12) from \(\ell \) to y yields

$$\begin{aligned} D\beta (y)=\int _{H(\ell )}^{H(y)}\frac{du}{ue^u}=\theta (H(\ell ))-\theta (H(y)), \end{aligned}$$
(3.13)

and applying the boundary condition at i yields

$$\begin{aligned} D=\frac{\theta (H(\ell ))-\theta (H(i))}{\beta (i)}. \end{aligned}$$
(3.14)

Substituting (3.12) into (3.4) gives

$$\begin{aligned} v({s_0},i,i)= & {} \kappa + bc + \inf _{H(i)}\biggl (ab H(i) + \frac{\beta (i) }{De^{H(i)}}\biggr )\\= & {} \kappa +bc+\inf _{H(i)}\biggl (abH(i)+\frac{\beta ^2(i) }{[\theta (H(\ell ))-\theta (H(i))]e^{H(i)}}\biggr )\\= & {} \kappa + bc + \inf _{n\ge b}\left( ab \left( 1+ \frac{k}{n} + \ln \frac{n}{b}\right) \right. \\{} & {} \left. + \frac{\beta ^2(i)}{e^{1+ \frac{k}{n} + \ln \frac{n}{b}} \bigl [\theta (1+\frac{k}{n})-\theta (1+ \frac{k}{n} + \ln \frac{n}{b})\bigr ]}\right) \end{aligned}$$

as required. \(\square \)

3.3 Further characterisation of the candidate optimal payoff

Define

$$\begin{aligned} \delta =\delta (i)=\frac{k}{b}=\frac{s(\ell )}{\tilde{s}(i)} \end{aligned}$$

and

$$\begin{aligned} p_{\delta }:y\mapsto 1+\frac{{\delta }}{y}+\ln y, \end{aligned}$$

Note that \({{\,\mathrm{arg\,min}\,}}(p_{\delta })={\delta }\) and, so, defining \(\Gamma _{\delta }=\max ({\delta },1)\), \(p_{\delta }\) is decreasing on \([1,\Gamma _{\delta }]\) and increasing on \([\Gamma _{\delta },\infty )\), with infimum

$$\begin{aligned} \gamma _{\delta }={\left\{ \begin{array}{ll} 1+{\delta }&{}{\delta }\le 1\\ 2+\ln {\delta }&{}d>1. \end{array}\right. } \end{aligned}$$

Define \(p_{\delta }^{-1}:[\gamma _{\delta },\infty )\rightarrow [\Gamma _{\delta },\infty )\) then the change of variable \( z = p_{\delta }(\frac{n}{b}):= 1+\frac{k}{n} + \ln (\frac{n}{b})\) yields

$$\begin{aligned} v({s_0},i,i):= \kappa + \tilde{s}(i) m_f(l) + ab + \inf _{z\ge \gamma _{\delta }} \left\{ ab z + \frac{\beta ^2 (l,i)e^{-z}}{\theta (z-\ln p_{\delta }^{-1}(z))-\theta (z)}\right\} . \end{aligned}$$

We define the function

$$\begin{aligned} \Psi _{\delta }:(\gamma _{\delta },\infty )\rightarrow \mathbb {R}_+;\;\; \Psi _{\delta }:z\mapsto \frac{e^{-z}}{\theta (z-\ln p_{\delta }^{-1}(z))-\theta (z)}. \end{aligned}$$
(3.15)

For now, we shall omit the dependence of \(\Psi _{\delta }\) on \({\delta }\).

Lemma 3.9

\(\Psi \) is a positive, decreasing convex function on \((\gamma _{\delta },\infty )\).

Proof

Since \(\theta \) is strictly decreasing, \(\Psi \) is finite and positive on \((\gamma _{\delta },\infty )\).

Define

$$\begin{aligned} g:x\mapsto \frac{1}{x}+\frac{{\delta }p_{\delta }^{-1}(x)^2}{p_{\delta }^{-1}(x)^2-{\delta }^2}. \end{aligned}$$

Differentiating \(\Psi \), we obtain

$$\begin{aligned} \Psi '(x)= & {} -\biggl (\Psi (x)+e^x\Psi ^2(x)\bigl [\theta '(x-\ln p_{\delta }^{-1}(x))\bigl (1-\frac{(p_{\delta }^{-1})'(x)}{p_{\delta }^{-1}(x)}\bigr )-\theta '(x)\bigr ]\biggr )\nonumber \\= & {} -\biggl (\Psi (x)+e^x\Psi ^2(x)\biggl [\frac{1}{xe^x}+\frac{{\delta }}{(p_{\delta }^{-1}(x)-{\delta })}\frac{e^{\ln p_{\delta }^{-1}(x)-x}}{(x-\ln p_{\delta }^{-1}(x))}\biggr ]\biggr )\nonumber \\= & {} -\biggl (\Psi (x)+\Psi ^2(x)\biggl [\frac{1}{x}+\frac{{\delta }}{(p_{\delta }^{-1}(x)-{\delta })}\frac{p_{\delta }^{-1}(x)}{(x-\ln p_{\delta }^{-1}(x))}\biggr ]\biggr )\nonumber \\= & {} -\biggl (\Psi (x)+\Psi ^2(x)g(x)\biggr )\text { (since }x-\ln p_{\delta }^{-1}(x)=1+\frac{{\delta }}{p_{\delta }^{-1}(x)})\nonumber \\< & {} 0\text { (since } \Psi >0 \text { and } p_{\delta }^{-1}\ge \Gamma _{\delta }\ge {\delta }\text {)}. \end{aligned}$$
(3.16)

Observe that the function g, appearing in (3.16), is positive and decreasing on \([\gamma _{\delta },\infty )\), since \(p_{\delta }^{-1}\) is increasing and greater than \({\delta }\) on \([\gamma _{\delta },\infty )\).

Finally, from (3.16),

$$\begin{aligned} \Psi '(x)=-\Psi (x)-\Psi ^2(x)g(x) \end{aligned}$$
(3.17)

and so

$$\begin{aligned} \Psi ''(x)=-\Psi '(x)(1+2\Psi (x)g(x))-\Psi ^2(x)g'(x)>0,\text { since } \Psi ,g>0, \Psi '<0 \text { and } g'\le 0, \end{aligned}$$

establishing that \(\Psi \) is strictly convex on \((\gamma _{\delta },\infty )\). \(\square \)

We denote the convex conjugate of \(\Psi \) by \(\Psi ^*_{\delta }\),or just \(\Psi ^*\), so that

$$\begin{aligned} \Psi ^*:x\mapsto \inf _{z\ge \gamma _{\delta }}\biggl (zx+\Psi (z)\biggr ). \end{aligned}$$

Observe that we have established the following:

Lemma 3.10

For any \(s\in \mathcal {M}^{{s_0}}_F\), define

$$\begin{aligned} r=r(s,i):= \frac{ab}{\beta ^2 (i)} =\frac{{{\tilde{m}}_f}(i)\tilde{s}(i)}{\beta ^2 (i)}. \end{aligned}$$
(3.18)

Then, \(v(s,i,i)\) is given by

$$\begin{aligned} v(s,i,i):= \kappa + bc+\beta ^2(i)\Psi ^*( r)=\kappa +\tilde{s}(i)m_f(i)+\beta ^2(i)\Psi ^*(r(s,i)). \end{aligned}$$
(3.19)

4 The dynamic solution

Adopting the usual dynamic approach, we want to give the (conditional) future payoff from our candidate for the optimal control when \(\mathcal {I}_t=i\) and \(X_t=x\) (with \(x\ge i\)) (both in the case where the process has not yet reached level 1 and the case where it has).

Consider first the case where the process has already reached level 1: Since we cannot control the process until it reaches \(\mathcal {I}_t\) again, the payoff is given by

$$\begin{aligned} \tilde{v}(s,x,i)=\textbf{E}_{s,x} \left[ \int _0^{T_i} f(X_u)\mathop {}\!\textrm{d}u\right] +\phi ^s_{\ell }(\ell ,0), \end{aligned}$$
(4.1)

where \(\phi ^s_{\ell }\) is given in (3.6).

In the case where the process has not yet reached level 1, since we cannot control the process until it reaches \(\mathcal {I}_t\) again, the payoff is given by

$$\begin{aligned} v(s,x,i)= & {} \textbf{E}_{s,x} \int _0^{T_1 \wedge T_i} f(X_u)\mathop {}\!\textrm{d}u\nonumber \\{} & {} +\mathbb {P}_{s,x}(X \text { hits level } i \text { before 1 })v(s,i,i) + \mathbb {P}_{s,x}(X \text { hits level 1 before } i) \tilde{v}(s,1,i)\nonumber \\= & {} \textbf{E}_{s,x}\biggl [ \int _0^{T_1 \wedge T_i} f(X_u)\mathop {}\!\textrm{d}u\biggr ] + \frac{\tilde{s} (x)}{\tilde{s} (i)} v(s,i,i) + \left( 1 - \frac{\tilde{s} (x)}{\tilde{s} (i)} \right) \tilde{v}(s,1,i), \end{aligned}$$
(4.2)

and we calculate

$$\begin{aligned} \textbf{E}_{s,x} \biggl [\int _0^{T_1 \wedge T_i} f(X_u)\mathop {}\!\textrm{d}u\biggr ]= & {} -\int _x^1 \mathop {}\!\textrm{d}u s'(u) \tilde{m}_f (u) + \frac{\tilde{s} (x)}{\tilde{s} (i)} \int _i^1\mathop {}\!\textrm{d}u s'(u)\tilde{m}_f (u)\\{} & {} \text {and }\\ \tilde{v}(s,1,i)= & {} \mathbb {E}_{s,1}\left[ \int _0^{T_i} f(X_u) \mathop {}\!\textrm{d}u\right] + \mathbb {E}_{s,x}^{(\ell )} \int _0^{T_0} f(X_u)\mathop {}\!\textrm{d}u, \end{aligned}$$

and observe that \(\mathbb {E}_{s,\ell }^{(\ell )} \int _0^{T_0} f(X_u)\mathop {}\!\textrm{d}u=\kappa \), where \(\kappa \) is given in Definition 3.6.

It follows that we can rewrite (4.2) as

$$\begin{aligned} v(s,x,i)&= \textbf{E}_{s,x} \left[ \int _0^{T_i } f(X_u)\mathop {}\!\textrm{d}u\right] + \frac{\tilde{s} (x)}{\tilde{s} (i)} v(s,i,i) + \left( 1 - \frac{\tilde{s} (x)}{\tilde{s} (i)} \right) \kappa \\&= \int _i^x \mathop {}\!\textrm{d}u s'(u) \tilde{m}_f (u)+ \frac{\tilde{s} (x)}{\tilde{s} (i)} v(s,i,i) + \left( 1 - \frac{\tilde{s} (x)}{\tilde{s} (i)} \right) \kappa \\&= \int _i^x \mathop {}\!\textrm{d}u s'(u) \tilde{m}_f (u)+ \frac{\tilde{s} (x)}{\tilde{s} (i)} \bigl (v(s,i,i) - \kappa \bigr ) + \kappa \end{aligned}$$

As is usual, to show that \(v\) really is the optimal payoff, we consider the processes \(S^s\) corresponding to using the policy s until time t and then behaving optimally. What is non-standard here is the ‘phase change’ at time \(T_1\) — after \(T_1\), \({\mathcal {S}}\) just looks like \(T_0\).

Consequently, we enlarge the state by including a flag process \({{\mathbb {F}}}\):

$$\begin{aligned} {{\mathbb {F}}}_t=0\text { on }[0,T_1)\text { and }{{\mathbb {F}}}_t=1 \text{ on } [T_1,{\mathcal {S}}], \end{aligned}$$

so that the generic state becomes \((s,x,i,{ j })\), and define

$$\begin{aligned} S^s_t=\int _0^{{\mathcal {S}}\wedge t} f(X_u)du +v(s,X_{{\mathcal {S}}\wedge t},\mathcal {I}_t)1_{{{\mathbb {F}}}_t=0}+\tilde{v}(s,X_{{\mathcal {S}}\wedge t},\mathcal {I}_{t})1_{{{\mathbb {F}}}_t=1}, \end{aligned}$$
(4.3)

where \(\tilde{v}\) is our proposed ‘post-\(T_1\)’ payoff given by

$$\begin{aligned} \tilde{v}(s,x,i):= & {} {\left\{ \begin{array}{ll}\mathbb {E}_{s,x}\left[ \int _0^{T_i} f(X_u) \mathop {}\!\textrm{d}u\right] + \mathbb {E}_{s,l}^{(\ell )} \int _0^{T_0} f(X_u)\mathop {}\!\textrm{d}u&{}x\ge i\\ \mathbb {E}_{s,l}^{(\ell )} \int _0^{T_0} f(X_u)\mathop {}\!\textrm{d}u&{}x\in (\ell ,i)\\ \mathbb {E}_{s,x}^{(\ell )} \int _0^{T_0} f(X_u)\mathop {}\!\textrm{d}u&{}x\le \ell \end{array}\right. }\nonumber \\= & {} {\left\{ \begin{array}{ll} \int _i^x s'(v){{\tilde{m}}_f}(v)dv+\kappa &{}\text { for }x\ge \max (i,\ell )\\ \kappa &{}\text { for }x\in (\ell ,\max (i,\ell ))\\ \int _0^x s'(v)m_f(v,\ell )dv&{}\text { for }x\in [0,\ell ]. \end{array}\right. } \end{aligned}$$
(4.4)

Theorem 4.1

Suppose that \((S^s_{t\wedge {\mathcal {S}}})_{t\ge 0}\) is a \(\mathbb {P}_{s,x}\)-submartingale for any x, and any admissible policy \(s\in \mathcal {A}^{x,{s_0}}_F\), and

  1. Property 1

    For each x, \({s_0}\), \(\mathbb {E}_{{\hat{s}},x,i,0} [S^{{\hat{s}}}_{T_1}]=v({s_0},x,i)\) for some admissible policy \({\hat{s}}\) with \({\hat{s}}\in \mathcal {A}^{x,{s_0}}_{F}\);

  2. Property 2

    For each x, \({s_0}\), \(\liminf \mathbb {E}_{{\hat{s}}^n_x,x,i,1} [S^{{\hat{s}}^n_x}_{{\mathcal {S}}}]=\tilde{v}({s_0},x,i)\), for some sequence of admissible policies \(({\hat{s}}^n_x)_{n\ge 1}\) with \({\hat{s}}^n_x\in \mathcal {A}^{x,{s_0}}_{F}\)

then

$$\begin{aligned} \Phi (s,x,i,{ j })={\left\{ \begin{array}{ll} v(s,x,i):&{}{ j }=0\\ \tilde{v}(s,x,i):&{}{ j }=1, \end{array}\right. } \end{aligned}$$

\({\hat{s}}\) is an optimal policy on \([0,T_1]\), and if \({{\bar{s}}}^n_x\) is defined by

$$\begin{aligned} ({{\bar{s}}}^n_x)'(y)={\left\{ \begin{array}{ll} {\hat{s}}'(y)&{}\text { if }y\le \ell \\ ({\hat{s}}^n_x)'(y)&{}\text { if }y\in (\ell ,\mathcal {I}_t)\\ {{\hat{s}}'(y)}&{}\text { if }y\ge \mathcal {I}_t, \end{array}\right. } \end{aligned}$$

then \({{\bar{s}}}^n_x\) is an \(\epsilon \)-optimal sequence, in other words

$$\begin{aligned} \Phi (s,x,i)=\liminf \Phi ^{{{\bar{s}}}^n_x}(s,x,i). \end{aligned}$$

Proof

Suppose that s is admissible and \((S^s_{t\wedge {\mathcal {S}}})_{t\ge 0}\) is a submartingale and \({{\mathbb {F}}}_0=1\) then

$$\begin{aligned} \tilde{v}({s_0},x,i)=S^{s_0}\le \mathbb {E}_{s,x,i,1}[S^s_{t\wedge {\mathcal {S}}}]=\mathbb {E}_{s,x}\left[ \int _0^{T_0\wedge t} f(X_u)du +\tilde{v}(s,F,X^s_{T_{0}\wedge t})\right] . \end{aligned}$$

Letting \(t\uparrow \infty \) we see, by dominated convergence, that

$$\begin{aligned} \tilde{v}({s_0},x,i)\le \mathbb {E}_{s,x}\biggl [\int _0^{T_0} f(X_t)dt\biggr ]. \end{aligned}$$

Minimising over admissible s yields

$$\begin{aligned} \Phi ({s_0},x,i,1)\ge \tilde{v}({s_0},x,i). \end{aligned}$$

Conversely, Property 2 implies that \(\Phi ({s_0},x,1)\le \tilde{v}({s_0},x,i)\), establishing equality.

Now suppose that s is admissible and \((S^s_{t\wedge {\mathcal {S}}})_{t\ge 0}\) is a submartingale and \(F_0=0\) then

$$\begin{aligned} v({s_0},x,i)=S^{s_0}\le \mathbb {E}_{s,x,i,0}[S^s_{t\wedge T_1}]=\mathbb {E}_{s,x,i,0}\bigg [\int _0^{T_1\wedge t} f(X_u)du +v(s,X_{T_1\wedge t},\mathcal {I}_{T_1\wedge t})\biggr ]. \end{aligned}$$

Letting \(t\uparrow \infty \) we see that

$$\begin{aligned} v({s_0},x,i)\le \mathbb {E}_{s,x,i,0}\left[ \int _0^{\mathcal {S}}f(X_t)dt\right] . \end{aligned}$$

Since s is arbitrary, we deduce \(v({s_0},x,i)\le \Phi ({s_0},x,i,0).\) Conversely, Property 1 implies that \(\Phi ({s_0},x,i,0)\le v({s_0},x,i)\), establishing equality. \(\square \)

Now we establish our main result.

Theorem 4.2

The value function \(\Phi (s_0,F,x,i)\equiv \inf _{s\in \mathcal {A}^{i,s_0}_F}\mathbb {E}_{s,x}\biggl [\int _0^{\mathcal {S}}f(X_t)dt\biggr ]\), when \(F=[0,\ell ]\cup [i,1]\) is given by

$$\begin{aligned} \Phi ({s_0},x,i,{ j })={\left\{ \begin{array}{ll} v({s_0},x,i):&{}{ j }=0\\ \tilde{v}({s_0},x,i):&{}{ j }=1, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} v(s,x,i)= & {} \int _i^x \mathop {}\!\textrm{d}u s'(u) \tilde{m}_f (u)+ \frac{\tilde{s} (x)}{\tilde{s} (i)} \bigl (v(s,i,i) - \kappa \bigr ) + \kappa \end{aligned}$$
(4.5)
$$\begin{aligned} \tilde{v}(s,x,i)= & {} {\left\{ \begin{array}{ll} \int _i^x s'(v){{\tilde{m}}_f}(v)dv+\kappa &{}\text { for }x\ge \max (i,\ell )\\ \kappa &{}\text { for }x\in (\ell ,\max (i,\ell ))\\ \int _0^x s'(v)m_f(v,\ell )dv&{}\text { for }x\in [0,\ell ], \end{array}\right. } \end{aligned}$$
(4.6)

with

$$\begin{aligned} v(s,i,i)= \kappa + bc+\beta ^2(i)\Psi ^*( \frac{ab}{\beta ^2 (i)}) \end{aligned}$$

or, collecting the definitions throughout the text,

$$\begin{aligned} v(s,i,i)=\int _0^l s'(v){{\tilde{m}}_f}(v)\mathop {}\!\textrm{d}v-s(\ell ){{\tilde{m}}_f}(\ell )+{m_f}(\ell )\tilde{s}(i) + \Psi ^*\biggl ( \frac{{{\tilde{m}}_f}(i)\tilde{s}(i)}{\beta ^2(i)}\biggr ), \end{aligned}$$

where \(\beta :z\mapsto \int _\ell ^z\sqrt{ \frac{2f(t)}{\sigma ^2(t)}}dt\), and \(\Psi ^*\) is the convex conjugate of \(\Psi _{\delta }\) given in equation (3.15).

In addition, a sequence of \(\epsilon \)-optimal controls is given by \(({\hat{s}}^n)_{n\ge 1}\),

$$\begin{aligned} ({\hat{s}}^n)'(x):={\left\{ \begin{array}{ll} {\hat{s}}'(x)&{}\text { if }x\le \ell \\ {\hat{s}}'(i)\exp \bigl (-\int _x^i\frac{2n}{\sigma ^2(t)}dt\bigr )&{}\text { if }x\in (\ell ,i)\\ {{\hat{s}}'(x)}&{}\text { if }x\ge i, \end{array}\right. } \end{aligned}$$
(4.7)

where, setting \({\hat{r}}:=r({\hat{s}},i)\) and \({\hat{R}}:=R({\hat{s}},i)={\Psi ^*}'({\hat{r}})\), \({\hat{r}}\) satisfies the ODE

$$\begin{aligned} \frac{{\hat{r}}'}{{\hat{r}}}=-(\ln \beta )'\bigl [2+\frac{{\hat{R}}}{\Psi ({\hat{R}})}+\frac{\Psi ({\hat{R}})}{{\hat{r}}{\hat{R}}}\bigr ]. \end{aligned}$$
(4.8)

Proof

We prove that \(v\) and \(\tilde{v}\) satisfy the conditions of Theorem 4.1.

  1. Property 1

    Consider \(S^s_t\). Using the fact that

    $$\begin{aligned} N_t:=\int _0^{t\wedge T_1}f(X_u)\mathop {}\!\textrm{d}u+\phi ^s(X_{t\wedge T_1},1)=\mathbb {E}_{s,x,i}\left[ \int _0^{T_1}f(X_u)\mathop {}\!\textrm{d}u|\mathcal {F}_{t\wedge T_1}\right] \end{aligned}$$
    (4.9)

    is a \(\mathbb {P}_{s,x}\)-martingale, we see that \(S^s_{\cdot }\) is a \(\mathbb {P}_{s,x}\)-martingale, M say, on the stochastic interval \([[t,T_{\mathcal {I}_t}]]\) if \({{\mathbb {F}}}_t=0\), and hence

    $$\begin{aligned} dS^s_t=dM_t+v_i(s,X_t,\mathcal {I}_t)d\mathcal {I}_t, \end{aligned}$$

    where N is a local martingale.

    So, to establish that S is a submartingale on \([0,T_1]\), since \(\mathcal {I}\) is a decreasing process which only decreases when \(\mathcal {I}_t=X_t\), it is sufficient to show that

    $$\begin{aligned} \Delta (s,i):=\frac{\partial }{\partial i}v(s,x,i)\Big |_{x=i}\le 0\text { and that there exists } {\hat{s}} \text { such that }\Delta ({\hat{s}},i)= 0. \end{aligned}$$

    Differentiating with respect to i yields

    $$\begin{aligned} \frac{\partial }{\partial i}v(s,x,i)&= - s'(i) \tilde{m}_f (i)+ \frac{\tilde{s} (x)}{\tilde{s} (i)} \frac{\partial }{\partial i}v(s,i,i) + (v(s,i,i)-\kappa ) \tilde{s} (x) \frac{s'(i)}{(\tilde{s} (i) )^2} \end{aligned}$$

    Setting \(x=i\) implies

    $$\begin{aligned} \Delta (s,i) = - s'(i) \tilde{m}_f (i)+ \frac{\partial }{\partial i}v(s,i,i) + (v(s,i,i)-\kappa ) \frac{s'(i)}{\tilde{s} (i) } \end{aligned}$$
    (4.10)

    Now \(v(s,i,i)= \kappa + bc+\beta ^2(i)\Psi ^*( r)=\kappa +{m_f}(\ell )\tilde{s}(i)+\beta ^2(i)\Psi ^*_{\delta }(r)\) with \({\delta }={\delta }(i)=\frac{s(\ell )}{\tilde{s}(i)}\) and \(r=\frac{{{\tilde{m}}_f}(i)\tilde{s}(i)}{\beta ^2(i)}\). Consequently

    $$\begin{aligned} \frac{\partial }{\partial i}v(s,i,i)=-{m_f}(\ell )s'(i)+{\beta ^2}'\Psi ^*_{\delta }(r)+\beta ^2[{\Psi ^*_{\delta }}'(r)r'(i)+{\delta }'(i)\frac{\partial }{\partial {\delta }}\Psi ^*_{\delta }(r)]\nonumber \\ \end{aligned}$$
    (4.11)

    Observe that \({\delta }'(i)=\frac{s(\ell )s'(i)}{\tilde{s}^2(i)}={\delta }\frac{s'(i)}{\tilde{s}(i)}\) while \(r'(i)=-\frac{{\beta ^2}'}{\beta ^2}r-\frac{\tilde{s}(i){m_f}'(i)+{{\tilde{m}}_f}(i)s'(i)}{\beta ^2}\).

    As is standard for convex conjugate functions, \({\Psi ^*}'(x)={\Psi }'^{-1}(-x)\) and \(\Psi ^*(x)=x{\Psi }'^{-1}(-x)+\Psi ({\Psi }'^{-1}(-x))\) so,

    $$\begin{aligned} \frac{\partial }{\partial {\delta }}\Psi ^*_{\delta }(r)= & {} \frac{\partial }{\partial {\delta }}[r{\Psi _{\delta }}'^{-1}(-r)+\Psi _{\delta }({\Psi _{\delta }}'^{-1}(-r))]\\= & {} r\frac{\partial }{\partial {\delta }}{\Psi _{\delta }}'^{-1}(-r)+\left( \frac{\partial }{\partial {\delta }}\Psi _{\delta }\right) (({\Psi _{\delta }}'^{-1}(-r)))+{\Psi _{\delta }}'({\Psi _{\delta }}'^{-1}(-r))\frac{\partial }{\partial {\delta }}{\Psi _{\delta }}'^{-1}\\= & {} \left( \frac{\partial }{\partial {\delta }}\Psi _{\delta }\right) (({\Psi _{\delta }}'^{-1}(-r))). \end{aligned}$$

    Setting \(R_{\delta }=R={\Psi ^*}'(r)\), we see that

    $$\begin{aligned} \frac{\partial }{\partial {\delta }}\Psi ^*_{\delta }(r)=\left( \frac{\partial }{\partial {\delta }}\Psi _{\delta }\right) (R)=\frac{\Psi ^2(R)p_{\delta }^{-1}(R)^2}{p_{\delta }^{-1}(R)^2-{\delta }^2}=\Psi ^2(R)(g(R)-\frac{1}{R}). \end{aligned}$$

    Substituting in (4.10) and applying (4.11) yields

    $$\begin{aligned} \Delta (s,i)= & {} {\beta ^2}'[\Psi ^*_{\delta }(r)-rR]+\beta ^2{\delta }'(i)\frac{\partial }{\partial {\delta }}\Psi ^*_{\delta }(r)]\nonumber \\{} & {} -\frac{s'(i)}{\tilde{s}(i)}[{{\tilde{m}}_f}(i)\tilde{s}(i)-\beta ^2(i)\Psi ^*(r)+{{\tilde{m}}_f}(i)\tilde{s}(i)R]-{m_f}'(i)\tilde{s}(i)R\nonumber \\= & {} {\beta ^2}'[\Psi ^*_{\delta }(r)-rR]+\beta ^2{\delta }'(i)\frac{\partial }{\partial {\delta }}\Psi ^*_{\delta }(r)]-\frac{s'(i)}{\tilde{s}(i)}\beta ^2(i)[r(R+1)-\Psi ^*(r)]\nonumber \\{} & {} -{m_f}'(i)\tilde{s}(i)R\nonumber \\= & {} {\beta ^2}'[\Psi ^*_{\delta }(r)-rR]-\frac{s'(i)}{\tilde{s}(i)}\beta ^2(i)[r(R+1)-\Psi ^*(r)-\Psi ^2(R)(g(R)-\frac{1}{R})]\nonumber \\{} & {} -\rho R\frac{\tilde{s}(i)}{s'(i)}. \end{aligned}$$
    (4.12)

    Now

    $$\begin{aligned} \Psi ^*(r)= & {} rR+\Psi (R)\Rightarrow r(R+1)-\Psi ^*(r)=r-\Psi (R)\\= & {} -\Psi '(R)-\Psi (R) =\Psi ^2(R)g(R), \end{aligned}$$

    and thus

    $$\begin{aligned} \Delta (s,i)={\beta ^2}'\Psi (R)-\frac{s'(i)}{\tilde{s}(i)}\beta ^2(i)\frac{\Psi ^2(R)}{R}-\rho R\frac{\tilde{s}(i)}{s'(i)}. \end{aligned}$$
    (4.13)

    If we now use the fact, noted in Jacka and Hernández-Hernández (2022), that for \(a,b\ge 0\),

    $$\begin{aligned} \inf _{x>0}(ax+\frac{b}{x})=2\sqrt{ab}\,\,\text { and if }\,\,a,b>0\,\,\text { this is attained at }x=\sqrt{\frac{b}{a}}, \end{aligned}$$
    (4.14)

    we see that

    $$\begin{aligned} \Delta (s,i)\le {\beta ^2}'\Psi (R)-2\sqrt{\beta ^2(i)\rho \Psi ^2(R)}=2\beta \Psi (R)(\beta '(i)-\sqrt{\rho })=0, \end{aligned}$$

    as required, with equality attained at \(s={\hat{s}}\) satisfying

    $$\begin{aligned} \frac{{\hat{s}}'(i)}{{\hat{R}}\tilde{{\hat{s}}}(i)}=\sqrt{\frac{\rho }{\beta ^2(i)\Psi ^2({\hat{R}})}}\Rightarrow \frac{{\hat{s}}'(i)}{\tilde{{\hat{s}}}(i)} =\frac{{\hat{R}}(\ln \beta )'(i)}{\Psi ({\hat{R}})}\text { for }i\in (\ell ,i_0)\Leftrightarrow {\hat{r}}\text { satisfies }(4.8).\nonumber \\ \end{aligned}$$
    (4.15)

    The fact that a solution exists to (4.8) follows easily from rewriting it as the autonomous ODE:

    $$\begin{aligned} \frac{{\hat{r}}'}{w({\hat{r}})}=(\ln \beta )', \end{aligned}$$

    with

    $$\begin{aligned} w:y\rightarrow 2+\frac{{\Psi ^*}'(y)}{\Psi \bigl ({\Psi ^*}'(y)\bigr )}+\frac{\Psi \bigl ({\Psi ^*}'(y)\bigr )}{y{\Psi ^*}'(y)}. \end{aligned}$$
  2. Property 2

    Note that (4.4) implies that \(S^s_t\) is a \(\mathbb {P}_{s,x}\)-martingale, N say, on the stochastic interval \([[t\vee T_1,\inf \{u\ge t:\;X\in [\ell , \mathcal {I}_{T_1}]\}]]\), and \(S^s_t\) is constant on the stochastic interval \([[t\vee T_1,\inf \{u\ge t:\;X\not \in [\ell , \mathcal {I}_{T_1}]\}]]\). It follows from the Ito-Tanaka-Meyer formula that, denoting \(\frac{\partial }{\partial x}\tilde{v}(s,x,i)|_{y+}-\frac{\partial }{\partial x}\tilde{v}(s,x,i)|_{y}\) by \(D(y)\),

    $$\begin{aligned} dS^s_t=dN_t+D(i)dL^i_t+D(\ell )dL^\ell _t, \end{aligned}$$

    (recall that \(L^a_t\) denotes the local time of X at the level a by time t).

    Now it follows from (4.4) that \(D(\ell )=-s'(i){m_f}(\ell ,\ell )=0\) and \(D(i)=s'(i){{\tilde{m}}_f}(i)>0\), so we conclude that, since \(L^i\) is an increasing process, \(S^s\) is a \(\mathbb {P}_{s,x}\)-submartingale on \([[T_1,{\mathcal {S}}]]\).

    Now, defining \({\hat{s}}^n\) as in (4.7), it is easy to check that

    $$\begin{aligned} \liminf \mathbb {E}_{{\hat{s}}^n,x,i,1} [S^{{\hat{s}}^n}_{{\mathcal {S}}}]=\tilde{v}(s,x,i), \end{aligned}$$

    as required.

All that remains is to show that \({{\bar{s}}}^n\), given by

$$\begin{aligned} ({{\bar{s}}}^n)'={\hat{s}}'\big |_{F_{T_1}}+({\hat{s}}^n)'\big |_{[0,1]\setminus F_{T_1}} \end{aligned}$$

is admissible.

Set \(Y={\hat{s}}(X)\). The existence up to time \(T_{i_0}\wedge T_{\ell }\) of a weak solution to

$$\begin{aligned} dY=-s'\circ \tilde{s}^{-1}(Y_t)dB_t \end{aligned}$$

follows easily from Englebert and Schmidt (1985) on observing that \(\beta \) and \(\beta '\) are strictly positive on \((\ell ,i_0]\), \(\Psi \) is strictly positive on \((\gamma _{\delta },\infty )\), and, for \(\ell<i<i_0\),

$$\begin{aligned} {\tilde{{\hat{s}}}}(i)=\tilde{s}(i_0)\exp \left( \int _\ell ^i\frac{\beta '(y)}{\beta (y)\Psi (R(y))}dy\right) . \end{aligned}$$

We may then extend this to a solution for all t using standard techniques since \({s_0}\) is, by assumption, admissible. This implies that \(\mathbb {P}_{s,x}\) (as in (2.4)) exists establishing that s is admissible. \(\square \)

5 Concluding remarks and further problems

We remark first that the optimally controlled process is not a diffusion nor even strong Markov. To make it into one we have to adopt an infinite dimensional statespace recording the choice of \(s'\) at each level so far visited.

Although we have solved the minimisation problem when \(F_0\) is of the form \([0,\ell ]\cup [i,1]\) the problem remains open for other forms of constraint sets. It is tempting to speculate that a similar approach to the one adopted here would, with much further work, yield a result when \(F_0\) is of the form

$$\begin{aligned} {[}0,\ell _1]\cup [i_2,\ell _2]\cup \cdots \cup [i_n,1] \end{aligned}$$

and \(X_0\ge i_n\) but we have no suggestions as to the form of optimal controls for any other forms of the constraint set. A complete solution would be fascinating.

The corresponding network problem, where X is a reversible Markov chain on a specified graph is equally interesting and merits further exploration.