Cleaning the carbon market! Market transparency and market efficiency in the EU ETS

Abstract

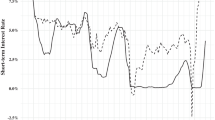
This paper revisits the informational efficiency of the EU ETS at a micro level, by introducing a novel time variant structural decomposition of variance. The new modelling introduces GARCH-like effects into a structural price modelling. With this, all variance components, including public information and price discreteness, can be estimated, for the first time, in a continuously updated setup that is free of sampling bias. The empirical findings report that although all variance components decrease in magnitude, this is primarily due to higher overall market liquidity that results in less price discovery per trade. On a proportional basis, though, the EU ETS appears to be increasingly inefficient prior to the introduction of MiFID II rules, with the situation reversing after their implementation. This is evidence that transparency is vital in rendering emission allowances a policy rather than a speculative instrument.

Appendix

The specification of the pricing model used in this study (for the extended MRR (1997)) is:

$$ \Delta p_{i} = \theta_{i} \left( {q_{i} - \rho q_{i - 1} } \right) + \Delta \varphi_{i} q_{i} + \underbrace {{\varepsilon_{i} + \Delta \xi_{i} }}_{{u_{i} }} $$

(14)

where

$$ \begin{gathered} \theta_{i} = \theta_{1} \zeta_{i} = \theta_{1} \left( {E\left( {ti_{i} {|}F_{i - 1} } \right)} \right)^{ - 1} \hfill \\ \varphi_{i} = \varphi_{0} + \varphi_{1} \zeta_{i} = \varphi_{0} + \varphi_{1} \left( {E\left( {ti_{i} {|}F_{i - 1} } \right)} \right)^{ - 1} \hfill \\ \end{gathered} $$

(15)

This study follows Kalaitzoglou and Ibrahim (2015) who model volume weighted durations, ${ti}_{i}={d}_{i}*K\left({v}_{i}\right)$, $v={\text{exp}}(-\left({volume}_{i}-\overline{volume }\right)/2{\sigma }_{volume}$, where $d$ is the diurnally adjusted durations and $volume\sim \left(\overline{volume },{\sigma }_{volume}\right)$ is the volume of transaction $i$. The expected trading intensity ${\zeta }_{i}={\left(E\left({ti}_{i}|{F}_{i-1}\right)\right)}^{-1}$ is computed using a Weibull-ACWD (1,1) model (Kalaitzoglou & Ibrahim, 2015) of the form ${ti}_{i}=E\left({ti}_{i}|{ti}_{i-1},\omega ,\alpha ,\beta \right){w}_{i}$ where $w\sim W\left(1,{\sigma }_{w},\gamma \right)$ and $\gamma$ is a scalce parameter that is estimated along with $\omega ,\alpha ,\beta$, using a Maximum Likelihood estimation with the BFGS optimization algorithm. The conditional mean and conditional density specifications are:

$$ \begin{gathered} E\left( {ti_{i} {|}ti_{i - 1} } \right) = \omega + ati_{i - 1} + \beta E\left( {ti_{i - 1} {|}ti_{i - 2} } \right) \hfill \\ f\left( {\left. {ti_{i} } \right|F_{i} ;\gamma } \right) = {\raise0.7ex\hbox{$\gamma $} \!\mathord{\left/ {\vphantom {\gamma {ti_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${ti_{i} }$}}\left[ {\frac{{ti_{i} \Gamma \left( {1 + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \gamma }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\gamma $}}} \right)}}{{E\left( {ti_{i} |ti_{i - 1} } \right)}}} \right]^{\gamma } \exp \left( { - \left[ {\frac{{ti_{i} \Gamma \left( {1 + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \gamma }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\gamma $}}} \right)}}{{E\left( {ti_{i} |ti_{i - 1} } \right)}}} \right]^{\gamma } } \right) \hfill \\ \end{gathered} $$

(16)

In addition, in order to estimate a time variant contribution of the public information and price discreteness to price change variance, the variance of the error term ${u}_{i}$ is assumed to be time variant with autoregressive properties:

$${\sigma }_{\varepsilon ,i}^{2}=\left({\sigma }_{u,i}^{2}-2{\sigma }_{\xi ,i}^{2}\right):={c}_{\varepsilon ,0}+{c}_{\varepsilon ,1}\left({u}_{i-1}^{2}-2{\sigma }_{\xi ,i-1}^{2}\right)$$

(17)

The same applies to ${\sigma }_{\xi ,\iota }^{2}$, which is estimated from the auto-covariance of ${u}_{i}$ (e.g., Madhavan et al., 1997), but in this specification is also time variant with autoregressive properties

$${\sigma }_{\xi ,i}^{2}=-{u}_{i}{u}_{i-1}={c}_{\xi ,0}+{c}_{\xi ,1}{u}_{i-1}{u}_{i-2}$$

(18)

Consequently, the part of price change variance attributed to public information can be derived from Eq. (17).

Equation (14) is estimated using the iterative generalized method of moments (iGMM). First, let ${\varvec{\beta}}={\left({{\varvec{\theta}}}_{n},{\boldsymbol{\varphi }}_{n},\rho ,{c}_{\varepsilon ,n},{c}_{\xi ,n}\right)}{\prime},$ where $n=\mathrm{1,2}$, be the vector of parameters; ${{\varvec{\upsilon}}}_{i}$ be a vector of all available variables at transaction time i;${\zeta }_{\iota }={E\left[{ti}_{i}|{F}_{i-1}\right]}^{-1}$; and ${{\varvec{z}}}_{i}=\left({q}_{i},{q}_{i-1}\right){\prime}$ be a vector that contains the direction of the current and preceding trades. In addition, let ${e}_{i}=\left({u}_{i}-a\right)$, with ${u}_{i}={r}_{i}-E\left[{r}_{i}|{F}_{i}\right]$ be the forecast error of the return Eq. (14) with a constant drift $a$, where ${r}_{i}=\Delta {p}_{i}$. In consistence with Ibrahim and Kalaitzoglou (2016), the following moment conditions exactly identify ${\varvec{\beta}}$ and the constant (drift) a.

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {q_{i} q_{{i - 1}} - \rho } \\ {e_{i} } \\ {e_{i} \zeta _{i} \left( {q_{i} - \rho q_{{i - 1}} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {e_{i} \Delta q_{i} } \\ {e_{i} \Delta \left( {\zeta _{i} q_{i} } \right)} \\ {e_{i} e_{{i - 1}} + \left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {e_{i} e_{{i - 1}} + \left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \right)e_{{i - 1}} e_{{i - 2}} } \\ {\left[ {\underbrace {{\left( {e_{i}^{2} - 2\left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \right)}}_{{A_{i} }} - \left( {c_{{\varepsilon ,0}} + c_{{\varepsilon ,1}} A_{{i - 1}} } \right)} \right]} \\ {\left[ {A_{i} - \left( {c_{{\varepsilon ,0}} + c_{{\varepsilon ,1}} A_{{i - 1}} } \right)} \right]A_{{i - 1}} } \\ \end{array} } \\ \end{array} } \right\} = 0 $$

(19)

The first condition defines the first–order autocorrelation ($\rho$) of the order flow variable. The second condition tests the constant drift (a) as the average pricing error. The third line defines ${\theta }_{1}$. Lines four and five define the parameters ${\varphi }_{0}$ and ${\varphi }_{1}$. Lines six and seven define the variance of price discreteness $\left({\sigma }_{\xi ,i}^{2}={c}_{\xi ,0}+{c}_{\xi ,1}{e}_{i-1}{e}_{i-2}\right)$, while lines eight and nine define the variance of public information $\left({\sigma }_{\varepsilon ,i}^{2}={c}_{\varepsilon ,0}+{c}_{\varepsilon ,1}{A}_{i-1}={c}_{\varepsilon ,0}+{c}_{\varepsilon ,1}\left({e}_{i-1}^{2}-2\left({c}_{\xi ,0}+{c}_{\xi ,1}{e}_{i-2}{e}_{i-3}\right)\right)\right)$. The iGMM is estimated with Newey–West heteroskedasticity–consistent errors.

The moment conditions for the other (less sophisticated) models are derived in a similar manner.

1.1 Roll (1984)

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {e_{i} } \\ {e_{i} \Delta q_{i} } \\ {e_{i} \zeta _{i} q_{i} } \\ \end{array} } \\ {\begin{array}{*{20}c} {e_{i} e_{{i - 1}} + \left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \\ {\left( {e_{i} e_{{i - 1}} + \left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \right)e_{{i - 1}} e_{{i - 2}} } \\ {\left[ {\underbrace {{\left( {e_{i}^{2} - 2\left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \right)}}_{{A_{i} }} - \left( {c_{{\varepsilon ,0}} + c_{{\varepsilon ,1}} A_{{i - 1}} } \right)} \right]} \\ \end{array} } \\ {\left[ {A_{i} - \left( {c_{{\varepsilon ,0}} + c_{{\varepsilon ,1}} A_{{i - 1}} } \right)} \right]A_{{i - 1}} } \\ \end{array} } \right\} = 0 $$

(20)

1.2 Glosten and Harris (1988)—G&H

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {e_{i} } \\ {e_{i} q_{i} } \\ {e_{i} \Delta q_{i} } \\ \end{array} } \\ {\begin{array}{*{20}c} {e_{i} \Delta \left( {\zeta _{i} q_{i} } \right)} \\ {e_{i} e_{{i - 1}} + \left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \\ {\left( {e_{i} e_{{i - 1}} + \left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \right)e_{{i - 1}} e_{{i - 2}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\left[ {\underbrace {{\left( {e_{i}^{2} - 2\left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \right)}}_{{A_{i} }} - \left( {c_{{\varepsilon ,0}} + c_{{\varepsilon ,1}} A_{{i - 1}} } \right)} \right]} \\ {\left[ {A_{i} - \left( {c_{{\varepsilon ,0}} + c_{{\varepsilon ,1}} A_{{i - 1}} } \right)} \right]A_{{i - 1}} } \\ \end{array} } \\ \end{array} } \right\} = 0 $$

(21)

1.3 Huang and Stoll (1997) with autocorrelation—H&S(ρ)

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {q_{i} q_{{i - 1}} - \rho } \\ {e_{i} } \\ {e_{i} \zeta _{i} \left( {q_{{i - 1}} - \rho q_{{i - 2}} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {e_{i} \Delta q_{i} } \\ {e_{i} \Delta \left( {\zeta _{i} q_{i} } \right)} \\ {e_{i} e_{{i - 1}} + \left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {e_{i} e_{{i - 1}} + \left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \right)e_{{i - 1}} e_{{i - 2}} } \\ {\left[ {\underbrace {{\left( {e_{i}^{2} - 2\left( {c_{{\xi ,0}} + c_{{\xi ,1}} e_{{i - 1}} e_{{i - 2}} } \right)} \right)}}_{{A_{i} }} - \left( {c_{{\varepsilon ,0}} + c_{{\varepsilon ,1}} A_{{i - 1}} } \right)} \right]} \\ {\left[ {A_{i} - \left( {c_{{\varepsilon ,0}} + c_{{\varepsilon ,1}} A_{{i - 1}} } \right)} \right]A_{{i - 1}} } \\ \end{array} } \\ \end{array} } \right\} $$

(22)