Discrete half-logistic distributions with applications in reliability and risk analysis

Abstract

In the statistical literature, several discrete distributions have been developed so far for modeling non-negative integer-valued phenomena, yet there is still room for new counting models that adequately capture the diversity of real data sets. Here, we first discuss a count distribution derived as a discrete analogue of the continuous half-logistic distribution, which is obtained by preserving the expression of its survival function at each non-negative integer support point. The proposed discrete distribution has a mode at zero and allows for over-dispersion; these two features make it suitable for modeling purposes in many fields (e.g., insurance and ecology), when these conditions are satisfied by the data. In order to widen its spectrum of applications, a discrete analogue is also presented of the type I generalized half-logistic distribution (obtained by adding a shape parameter to the simple one-parameter half-logistic), which allows us to model count data whose mode is not necessarily zero. For these new count distributions, the main statistical properties are outlined, and parameter estimation along with related issues is discussed. Their feasibility is proved on two real data sets taken from the literature, which have already been fitted by other well-established count distributions. Finally, a possible application is illustrated in the insurance field, related to the exact/approximate determination of the distribution of the total claims amount through the well-known Panjer’s recursive formula, within the framework of collective risk models.

1 Introduction

When modeling lifetimes, such as the survival time of cancer patients or the lifetime of a mechanical component, continuous random distributions are usually employed. However, one often comes across situations where lifetimes are actually measured on a discrete scale; for example, the survival time is recorded in months, weeks, etc. Here, using a discrete random variable (rv) rather than a continuous one would be much more appropriate.

Moreover, in many practical problems related to engineering and other applied sciences, an intrinsic count phenomenon is often of interest, such as the number of occurrences of earthquakes in a calendar year, the number of accidents at a certain location, the number of times an individual visits a doctor, the number of claims an insurance company has to face, and so on.

Therefore, we can easily infer that although several consolidated discrete models are available, there is still a need for more flexible discrete distributions that can adequately capture the diverse features of real data sets, such as their degree of asymmetry, their under- or over-dispersion, the different shapes of their failure rate function, etc.

Developing a discrete version of continuous distributions, in particular, has drawn the attention of researchers in recent decades; different methods can be followed to pursue this objective (Chakraborty, 2015). The method that has encountered by far the greatest appreciation by researchers is the one based on matching the survival function (sf) of the continuous distribution at integer values. Relying on it, the discrete Weibull distribution was proposed as a discrete counterpart of the two-parameter continuous Weibull distribution (Nakagawa and Osaki, 1975), a discrete normal distribution was proposed by Roy (2003), a discrete Laplace by Inusah and Kozubowski (2006), a discrete Pareto and Burr by Krishna and Pundir (2009), and a discrete Lindley by Gómez-Déniz and Calderín-Ojeda (2011), just to name a few. Moreover, from a broader perspective, discretization and discrete approximation schemes are often applied in operations research for scenario modeling to solve one-stage and multistage distributionally robust optimization problems (Liu et al., 2019). In this work, we provide our original contribution to the existing literature by discussing discrete counterparts of the half-logistic distribution and a generalization thereof, which can serve as alternative random distributions to the existing discrete models for describing count or discrete data in various fields, including engineering, insurance, economics, etc.

The layout of the paper is as follows. In the next section, we briefly review the continuous half-logistic distribution. In Sect. 3, we discuss a possible discrete analogue of the continuous half-logistic distribution, which preserves the expression of the original sf at the integer values of its support. We illustrate its main properties, also related to reliability concepts, and present different methods for parameter estimation. Section 4 introduces a two-parameter generalization of the proposed discrete distribution and updates the estimation methods previously presented. Section 5 describes a Monte Carlo study comparing different statistical estimators of the parameter(s) of the discrete half-logistic distributions. In Sect. 6, two real data sets are fitted by the two proposed discrete distributions. Section 7 suggests two other possible discrete analogues for the continuous half-logistic rv based on minimization of a discrepancy measure between cumulative distribution functions. Section 8 applies the discrete half-logistic distribution to the solution of a well-known problem in the insurance field, i.e., the determination of the distribution of the total claims amount in a collective risk model by means of Panjer’s recursive formula. Final remarks and research perspectives are provided in the last section.

2 The univariate half-logistic distribution

The half-logistic distribution is a random distribution over the positive real line obtained by folding the logistic distribution, which is defined over the whole real line, about the origin (Balakrishnan, 1985). Thus, if Y is an rv that follows the logistic distribution with parameter $\theta >0$, with the cumulative distribution function (cdf)

$$\begin{aligned} F_Y(y)=P(Y\le y)=\frac{1}{1+e^{-\theta y}} \end{aligned}$$

and the probability density function (pdf)

$$\begin{aligned} f_Y(y)=\frac{\theta e^{-\theta y}}{(1+e^{-\theta y})^2}, \end{aligned}$$

the rv $X=|Y|$ follows the half-logistic distribution with the same parameter $\theta$; its pdf is

$$\begin{aligned} f_X(x)=\frac{2\theta e^{-\theta x}}{(1+e^{-\theta x})^2},\quad x\in {\mathbb {R}}^+,\theta \in {\mathbb {R}}^+ \end{aligned}$$

(1)

(note that this expression is wrongly reported in Ebrahimi et al. (2015), where the multiplicative factor 2 is missing); its cdf is

$$\begin{aligned} F_X(x)=\frac{2}{1+e^{-\theta x}}-1=\frac{2e^{\theta x}}{1+e^{\theta x}}-1 =\frac{e^{\theta x}-1}{e^{\theta x}+1},\quad x\in {\mathbb {R}}^+, \end{aligned}$$

(2)

and its sf is

$$\begin{aligned} S(x)=P(X\ge x)=\frac{2}{1+e^{\theta x}},\quad x\in {\mathbb {R}}^+. \end{aligned}$$

(3)

The expressions of the expected value and variance are

$$\begin{aligned} \left\{ \begin{aligned}&{\mathbb {E}}(X)=\log 4/\theta \\&\sigma _X^2=(\pi ^2/3 - (\log 4)^2)/\theta ^2. \end{aligned}\right. \end{aligned}$$

The half logistic distribution is overdispersed if $\theta <\theta _0=\frac{\pi ^2/3-(\log 4)^2}{\log 4}\approx 0.9868439$; it is underdispersed if $\theta >\theta _0$. It is positively skewed and leptokurtic; Pearson’s kurtosis is approximately equal to 6.584 for any value of $\theta$ (see Olapade, 2014).

The naïve hazard rate function, which is defined as $r(x)=f(x)/S(x)$, has the following expression:

$$\begin{aligned} r(x)=\frac{\theta }{1+e^{-\theta x}}=\frac{\theta e^{\theta x}}{1+e^{\theta x}}, \end{aligned}$$

which is a strictly increasing function in x with minimum value $\theta /2$, attained at zero, and supremum value $\theta$, attained asymptotically for $x\rightarrow +\infty$. This means that the half-logistic distribution belongs to the increasing failure rate (IFR) class (Barlow and Proschan, 1981), a property shared by relatively few distributions that have support on the positive real half-line, and represents one of the main attractions of this distribution in the context of reliability theory.

A “standard” version of the half-logistic distribution, obtained by setting $\theta$ equal to 1 in (1), was investigated by Balakrishnan (1985), who established some recurrence relations for the moments and product moments of order statistics, as well as modes and quantiles.

The maximum likelihood estimate of the parameter $\theta$ of the half-logistic distribution, based on an iid sample $\pmb {x}=(x_1,x_2,\ldots ,x_n)$, is obtained as the value ${\hat{\theta }}_{ML}$ maximizing the log-likelihood function

$$\begin{aligned} \ell (\theta ;\pmb {x})=\sum _{i=1}^n \log \frac{2\theta e^{-\theta x_i}}{(1+e^{-\theta x_i})^2}= n\log (2\theta )-\theta \sum _{i=1}^n x_i -2\sum _{i=1}^n \log (1+e^{-\theta x_i}), \end{aligned}$$

or alternatively as the value satisfying the first-order condition $\ell '(\theta ;\pmb {x})=0$:

$$\begin{aligned} n/\theta - \sum _{i=1}^n x_i + 2\sum _{i=1}^n \frac{x_ie^{-\theta x_i}}{1+e^{-\theta x_i}}=0, \end{aligned}$$

which does not in general provide an explicit expression for ${\hat{\theta }}_{ML}$ (see, e.g., Balakrishnan and Wong, 1991), but can be solved only numerically.

As occurs with the exponential distribution, an alternative parametrization of the half-logistic distribution, instead of considering the rate parameter $\theta$, uses the scale parameter $\sigma$: the pdf, in this case, becomes

$$\begin{aligned} f(x)=\frac{2 e^{-x/\sigma }}{\sigma (1+e^{-x/\sigma })^2},\quad x\in {\mathbb {R}}^+,\sigma \in {\mathbb {R}}^+. \end{aligned}$$

(4)

The half-logistic distribution with this latter parametrization is implemented in the R package bayesmeta (Röver, 2020), where the functions implementing the pmf, cdf, quantile function, and pseudo-random generation are provided.

3 A discrete half-logistic distribution based on the preservation of the expression of the survival function

A discrete analogue of a continuous random distribution defined on the positive half-line can be obtained by setting its pmf equal to the difference $S(x)-S(x+1)$, for $x=0,1,2,\ldots$, where S(x) is the sf of the parent continuous model (Chakraborty, 2015). Applying this discretization to the half-logistic distribution in (3), we obtain the following expression for the pmf:

$$\begin{aligned} p(x)&= 2\left[ 1+e^{\theta x}\right] ^{-1} - 2\left[ 1+e^{\theta (x+1)}\right] ^{-1} \\&= 2e^{-\theta x}/[1+e^{-\theta x}] - 2e^{-\theta (x+1)}/[1+e^{-\theta (x+1)}],\quad x=0,1,2,\ldots \nonumber . \end{aligned}$$

(5)

For this discrete half-logistic distribution, the expression of the sf at each non-negative integer value is thus displayed in (3).

This discrete counterpart was first introduced in Nadarajah (2015), using the alternative parametrization for the parent model (4), with a pmf equal to

$$\begin{aligned} p(x)=2/(1+e^{-(x+1)/\sigma }) - 2/(1+e^{-x/\sigma }),\quad x=0,1,2,\ldots , \end{aligned}$$

and was then presented in Barbiero and Hitaj (2020), where some basic properties were outlined. By setting $\omega =e^{-\theta }$, the pmf (5) can be rewritten as $p(x)=\frac{2\omega ^x}{1+\omega ^x}-\frac{2\omega ^{x+1}}{1+\omega ^{x+1}}$.

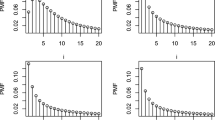
By construction, since the probability p(x) of a non-negative integer value x corresponds to the integral of the pdf f(x) of the continuous distribution between x and $x+1$, and since f(x) is a strictly decreasing function for $x>0$, it descends that p(x) is strictly decreasing too and has a unique mode at 0. Figure 1 displays the pmf (5) for four different values of $\theta$.

Fig. 1

Pmf for the discrete half-logistic distribution for four different values of the parameter $\theta$, computed according to Eq. (5)

The cdf, for any non-negative integer value x, is given by

$$\begin{aligned} F(x)=1-P(X>x)=1-S(x+1)=1-\frac{2}{1+e^{\theta (x+1)}} =\frac{e^{\theta (x+1)}-1}{e^{\theta (x+1)}+1}. \end{aligned}$$

(6)

From (6), one can easily derive the expression of the quantile of order $0<u<1$, which is

$$\begin{aligned} x_u = \Big \lceil {\frac{1}{\theta } \log \frac{1+u}{1-u} - 1}\Big \rceil , \end{aligned}$$

(7)

where $\lceil \cdot \rceil$ denotes the ceiling function. A random number can be sampled from the proposed model through the usual inverse transformation method. Letting u be a random number drawn from a uniform distribution on the unit interval, a random number following the discrete half-logistic distribution with parameter $\theta$ can be obtained by computing the right-hand side of Eq. (7).

The expectation of the discrete half-logistic distribution is given by

$$\begin{aligned} {\mathbb {E}}(X) = \sum _{x=1}^{\infty } S(x) = \sum _{x=1}^{\infty } \frac{2}{1+e^{\theta x}}, \end{aligned}$$

which can be expressed in terms of the q digamma (special case of the q-polygamma) function. The following relationship also holds:

$$\begin{aligned} \sum _{x=1}^{\infty } \frac{2}{1+e^{\theta x}}< \int _0^{\infty } \frac{2}{1+e^{\theta x}}\text {d}x < \sum _{x=0}^{\infty } \frac{2}{1+e^{\theta x}}. \end{aligned}$$

In other terms, the mean $\mu _d$ of the discrete half-logistic rv is such that

$$\begin{aligned} \mu _d< \mu _c < \mu _d +1, \end{aligned}$$

where $\mu _c=\log (4)/\theta$ is the mean of the continuous logistic distribution, or

$$\begin{aligned} \mu _c- 1< \mu _d < \mu _c. \end{aligned}$$

For small values of $\theta$ ($\theta \ll 1$), the expected value of this discrete distribution can then be roughly approximated by $\mu _c$.

Note that given

$$\begin{aligned} \frac{\text {d}}{\text {d}\theta } \frac{1}{(1+e^{\theta x})^2} = -\frac{xe^{\theta x}}{1+e^{\theta x}}<0\quad x=1,2,\ldots ,\forall \theta >0, \end{aligned}$$

we have that ${\mathbb {E}}(X)$ is a strictly decreasing function of $\theta$, as happens to the continuous half-logistic distribution. The graph of the expected value as a function of $\theta$ is displayed in Fig. 2.

Fig. 2

Expected value and dispersion index as functions of the parameter $\theta$ for the discrete half-logistic distribution

The variance of the distribution can be written as an infinite sum and can then be evaluated only numerically (see Chakraborti et al. 2019 for the first equality):

$$\begin{aligned} \sigma _X^2 = \sum _{x=1}^\infty (2x-1)S(x)=2\sum _{x=1}^\infty \frac{(2x-1)}{1+e^{\theta x}}=4\sum _{x=1}^{\infty } \frac{x}{1+e^{\theta x}}-{\mathbb {E}}(X). \end{aligned}$$

By numerical inspection, we can state that the discrete half-logistic distribution is over-dispersed for any value of $\theta$; in particular, the coefficient of overdispersion, given by the ratio $\sigma ^2_X/{\mathbb {E}}(X)$, is a decreasing function of $\theta$, tending asymptotically to 1 (see again Fig. 2). This is in contrast with what we observed with the continuous parent distribution, which is underdispersed or overdispersed according to whether the $\theta$ parameter is greater or smaller than a certain threshold (the coefficient of overdispersion is a decreasing function of $\theta$, but tends asymptotically to 0 as $\theta$ goes to $+\infty$).

3.1 Relationships with other distributions

Proposition 1

If X is a half-logistic distribution with parameter $\theta$, then $Y=\lfloor \beta X\rfloor$ is a discrete half-logistic with parameter $\theta /\beta$.

Proof

For any $y=0,1,2,\ldots$

$$\begin{aligned} P(Y\ge y)&=P(\lfloor \beta X\rfloor \ge y)=P(\beta X\ge y)=P(X\ge y/\beta )=\frac{2}{1+e^{\theta y/\beta }}. \end{aligned}$$

(8)

Then, Y follows the discrete half-logistic distribution with parameter $\theta /\beta$. $\square$

Proposition 2

If X is an exponential distribution with parameter $\lambda =1$, then $Y=\lfloor |\log (e^X-1)|\rfloor$ is a discrete half-logistic distribution with parameter $\theta =1$.

Proof

For $y=0,1,2,\ldots$.

$$\begin{aligned} P(Y\ge y)&=P(\lfloor |\log (e^X-1)|\rfloor \ge y)=P(|\log (e^X-1)|\ge y)\\&=P(\log (e^X-1)\ge y)+P(\log (e^X-1)\le -y)\\&=P(e^X-1\ge e^y)+P(e^X-1\le e^{-y})\\&=P(X\ge \log (e^y+1))+P(X\le \log (1+e^{-y}))\\&=e^{-\log (e^y+1)}+1-e^{-\log (1+e^{-y})}\\&=1/(1+e^y)+1-1/(1+e^{-y})=2/(1+e^y). \end{aligned}$$

Thus Y is a discrete half-logistic rv with parameter $\theta =1$. $\square$

Proposition 3

If X is a discrete half-logistic distribution with parameter $\theta$ and if B is a dichotomous rv independent from X taking the values $-1$ and $+1$ with equal probabilities, then the transformation $Y=BX+B/2-1/2$ is the discrete logistic distribution in Chakraborty and Chakravarty (2016) with parameters $\mu =0$ and $p=e^{-\theta }$.

Proof

By construction, Y is equal to either X with probability 1/2 (when $B=1$) or $-X-1$ with probability 1/2 (when $B=-1$). Then, the support of X being equal to $\lbrace 0,1,2,\ldots \rbrace$, the support of Y is the whole set ${\mathbb {Z}}$. The probability of Y taking an integer value y is thus given by $0.5 P(X=y)$ if $y\ge 0$ and by $0.5 P(X=-y-1)$ if $y<0$. Thus, recalling the expression (5) for the pmf of a discrete half-logistic distribution, the pmf of Y is $P(Y=y)=\frac{e^{-\theta y}(1-e^{-\theta })}{(1+e^{-\theta y})(1+e^{-\theta (y+1)})}$ if $y\ge 0$ and $P(Y=y)=\frac{e^{\theta (y+1)}(1-e^{-\theta })}{(1+e^{\theta (y+1)})(1+e^{\theta y})}=\frac{e^{-\theta y}(1-e^{-\theta })}{(1+e^{-\theta y})(1+e^{-\theta (y+1)})}$ if $y<0$. Since these last two expressions coincide, we can write that

$$\begin{aligned} P(Y=y)=\frac{e^{-\theta y}(1-e^{-\theta })}{(1+e^{-\theta y})(1+e^{-\theta (y+1)})}, \end{aligned}$$

for any $y\in {\mathbb {Z}}$, which corresponds to the pmf of the discrete logistic distribution introduced by Chakraborty and Chakravarty (2016), Equation (2), with parameters $p=e^{-\theta }$ and $\mu =0$. $\square$

3.2 Reliability properties

Some properties of the discrete half-logistic distribution related to reliability concepts are now reviewed, in a similar manner to what has been done in Chakraborty and Chakravarty (2016).

3.2.1 Recurrence relation for probabilities and long-tailedness

The ratio of successive probabilities $p(x+1)/p(x)$, for $x=0,1,2,\ldots$, is given by

$$\begin{aligned} p(x+1)/p(x)=\frac{e^{\theta (x+2)}-e^{\theta (x+1)}}{e^{\theta (x+1)}-e^{\theta x}}\cdot \frac{1+e^{\theta x}}{1+e^{\theta (x+2)}}=e^{\theta }\cdot \frac{1+e^{\theta x}}{1+e^{\theta (x+2)}}, \end{aligned}$$

which is a decreasing function in x and tends to $e^{-\theta }$ as x tends to $+\infty$. Since we know that for a discrete distribution, the value of the limit $L=\lim _{x\rightarrow \infty } p(x+1)/p(x)$ in comparison with the Poisson distribution, which has $L = 0$, gives the relative long-tailedness of the distribution, we easily conclude that the discrete half-logistic distribution has longer tails than the Poisson.

3.2.2 Log-concavity

The discrete half-logistic distribution is log-concave. In fact, since the ratio between successive probabilities is a strictly decreasing function of $x\ge 0$, we have that

$$\begin{aligned} p(x;\theta )^2 > p(x-1;\theta )\cdot p(x+1;\theta ) \end{aligned}$$

for any $x=1,2,\ldots$, and this is a sufficient condition for the log-concavity of a pmf. We recall that a log-concave distribution satisfies the following properties: i. it has an increasing failure (hazard) rate distribution; ii. it is strongly unimodal; iii. it has all its moments; iv. it remains log-concave if truncated; v. its convolution with any other discrete distribution is also unimodal and log-concave (Chakraborty and Chakravarty, 2016).

3.2.3 Some relavant reliability quantities

The naïve failure rate or hazard rate for a count distribution can be defined as (Gupta, 2015)

$$\begin{aligned} r(x)=p(x)/P(X\ge x); \end{aligned}$$

it can be interpreted as the conditional probability of a subject failure at time x given that it did not fail by $x-1$; thus, by construction, it is bounded between 0 and 1. For the model under study,

$$\begin{aligned} r(x)=[2(1+e^{\theta x})^{-1} - 2(1+e^{\theta (x+1)})^{-1}]/[2/(1+e^{\theta x})]=1-\frac{1+e^{\theta x}}{1+e^{\theta (x+1)}}. \end{aligned}$$

We note that the naïve rate function is strictly increasing in x for any value of $\theta$, it takes value $r(0)=(e^{\theta }-1)/(e^{\theta }+1)$ at zero, and it tends to $1-e^{-\theta }$ for x tending to $\infty$.

The second hazard rate function $r^*(x)$, defined as $\log S(x)-\log S(x+1)$ (Roy and Gupta, 1992), becomes

$$\begin{aligned} r^*(x) = \log (1+e^{\theta (x+1)}) - \log (1+e^{\theta x}). \end{aligned}$$

By computing its first derivative with respect to x,

$$\begin{aligned} \frac{\partial r^*(x)}{\partial x} = \frac{\theta e^{\theta (x+1)}}{1+e^{\theta (x+1)}} - \frac{\theta e^{\theta x}}{1+e^{\theta x}} = \frac{\theta [e^{\theta (x+1)}-e^{\theta x}]}{[1+e^{\theta x}][1+e^{\theta (x+1)}]}, \end{aligned}$$

which is always strictly greater than zero for any $x=0,1,2,\ldots$, we can conclude that $r^*(x)$ is a strictly increasing function taking the value $\log (1+e^{\theta })-\log 2$ when $x=0$ and tending asymptotically to $\theta$, which thus assumes the meaning of the asymptotic bound of the second hazard rate function.

The mean residual life function (MRLF) $\mu _F(k)$, defined as

$$\begin{aligned} \mu _F(k) = {\mathbb {E}}(X-k|X\ge k)=\frac{\sum _{x=k}^\infty (1-F(x))}{1-F(k-1)}, \end{aligned}$$

is equal to

$$\begin{aligned} \mu _F(k) = \frac{\sum _{x=k}^{\infty } 1/(1+e^{\theta (x+1)})}{1/(1+e^{\theta k})} = (1+e^{\theta k})\sum _{x=k}^{\infty } \frac{1}{1+e^{\theta (x+1)}}. \end{aligned}$$

From Theorem 2.1 in Gupta (2015), we deduce that $\mu _F(k)$ is a decreasing function in k.

The reversed hazard rate function, which is defined as $r^\star =p(x)/F(x)$ and can be interpreted as the conditional probability of a subject failure at time x given that it failed by x, is clearly decreasing with x (the numerator is decreasing with x; the denominator is increasing with x) and is equal to

$$\begin{aligned} r^\star (x)&=p(x)/F(x) = \frac{2e^{-\theta x}/(1+e^{-\theta x}) - 2e^{-\theta (x+1)}/(1+e^{-\theta (x+1)})}{(1-e^{-\theta (x+1)})/(1+e^{-\theta (x+1)})}\\&=\frac{2e^{-\theta x}(1-e^{-\theta })}{(1+e^{-\theta x})(1-e^{-\theta (x+1)})}. \end{aligned}$$

3.2.4 Stress-strength model

Let us consider two independent discrete half-logistic rvs X and Y with parameters $\theta _1$ and $\theta _2$, respectively. Then, one can be interested in determining the value of the reliability parameter $R=P(X<Y)$ or $R^*=P(X<Y)+0.5 P(X=Y)$.

The former can be computed as

$$\begin{aligned} R&=\sum _{x=0}^{\infty } \sum _{y=x+1}^{\infty } p(x;\theta _1)p(y;\theta _2) = \sum _{x=0}^{\infty } p(x;\theta _1) S(x+1;\theta _2)\\&=\sum _{x=0}^{\infty } \frac{2e^{\theta _1x}(e^{\theta _1}-1)}{(1+e^{\theta _1x })(1+e^{\theta _1(x+1)})}\cdot \frac{2}{(1+e^{\theta _2(x+1)})}\\&=4(e^{\theta _1}-1)\sum _{x=0}^{\infty }\frac{e^{\theta _1x}}{(1 +e^{\theta _1x})(1+e^{\theta _1(x+1)})(1+e^{\theta _2(x+1)})}; \end{aligned}$$

the second as

$$\begin{aligned} R^*&= R+\frac{1}{2}\sum _{x=0}^{\infty } p(x;\theta _1)p(x;\theta _2)\\&=R+2(e^{\theta _1}-1)(e^{\theta _2}-1)\sum _{x=0}^{\infty } \frac{e^{(\theta _1+\theta _2)x}}{(1+e^{\theta _1x})(1+e^{\theta _1(x+1)})(1+e^{\theta _2x})(1+e^{\theta _2(x+1)})}. \end{aligned}$$

3.3 Estimation

Parameter estimation of the proposed distribution, based on an iid sample $\pmb {x}=(x_1,x_2,\ldots ,x_n)$, can be carried out resorting to different methods, which we will discuss in the following.

3.3.1 The method of proportions

Since from (5), the probability of X being 0 is

$$\begin{aligned} p(0) = 1 - 2/(1+e^{\theta }) =\frac{e^{\theta }-1}{e^{\theta }+1}, \end{aligned}$$

after defining ${\hat{p}}_0$ as the relative frequency of zeros in the sample, then we can find an estimate for $\theta$ by equating p(0) to ${\hat{p}}_0$ (assumed to be non-null) and solving with respect to the unknown parameter $\theta$:

$$\begin{aligned} {\hat{\theta }}_P = \log \left( \frac{1+{\hat{p}}_0}{1-{\hat{p}}_0} \right) . \end{aligned}$$

(9)

This method, particularly suited for discrete rvs, though very intuitive and simple to apply, is yet intrinsically less efficient than other methods, such as the method of moments or the maximum likelihood method, since it does not exploit the whole information contained in the sample. An approximate standard error for ${\hat{\theta }}_P$ can be computed by applying the delta method:

$$\begin{aligned} \text {SE}({\hat{\theta }}_P) = \text {SE}({\hat{p}}_0)\cdot \bigg |\frac{\text {d}{\hat{\theta }}_P}{\text {d}{\hat{p}}_0}\bigg |=\sqrt{{\hat{p}}_0(1-{\hat{p}}_0)/n} \cdot \frac{2}{(1+{\hat{p}}_0)(1-{\hat{p}}_0)}, \end{aligned}$$

given

$$\begin{aligned} \frac{\text {d}}{\text {d}x}\log [(1+x)/(1-x)]=\frac{2}{(1-x)(1+x)}. \end{aligned}$$

Obviously, one can consider other integer value than 0 and the corresponding probability, and equate it to its sample relative frequency; however, the resulting equation fails to provide $\theta$ in a closed form. For example, by considering $x=1$, Eq. (5) yields

$$\begin{aligned} p(1)= 2/(1+e^{\theta }) - 2/(1+e^{2\theta }) = \frac{2e^{\theta }(e^{\theta }-1)}{(1+e^{\theta })(1+e^{2\theta })}; \end{aligned}$$

then, by equating the expression above for p(1) to the relative frequency of ones, ${\hat{p}}_1$ (assumed to be non-null), we obtain a third-degree equation in the unknown $t=e^{\theta }$:

$$\begin{aligned} (1+t)(1+t^2){\hat{p}}_1-2t(t-1)=0, \end{aligned}$$

which can be solved numerically; however, depending on the value of ${\hat{p}}_1$, the solution may not exist, exist and be unique, or exist and not be unique. Using the value of 0 also has the advantage that since it represents the most probable value of the distribution, on average, 0 is also the most frequent value in the sample, and thus a larger part of the information contained in the sample is retained.

3.3.2 Least-square estimation

From the expression of S(x) in (3), one can derive

$$\begin{aligned} \log \left( \frac{2-S(x)}{S(x)}\right) = \theta x \end{aligned}$$

or

$$\begin{aligned} z=\theta x, \end{aligned}$$

(10)

with $z=\log \left( \frac{2-S(x)}{S(x)}\right)$. The linear equation in (10) serves as an important tool for checking model adequacy. By computing the empirical sf as ${\hat{S}}(x)=\sum _{i=1}^n \mathbbm {1}_{x_i\ge x}/n$ from the data and plotting z against x, one can prescribe the discrete half-logistic distribution as an adequate model for the given data, provided that the plot is nearly a straight line passing through the origin. The unknown parameter $\theta$ in (10) can be recovered by least-squares regression as ${\hat{\theta }}_{LS}=\sum _{i=1}^n x_iz_i/\sum _{i=1}^n x_i^2$. This estimation method has the clear advantage of providing a closed-form solution; it is hopefully more efficient than the method of proportions, since it exploits the whole sample information.

3.3.3 Maximum likelihood estimation

Recalling (5), the log-likelihood function for the discrete half-logistic distribution can be written as

$$\begin{aligned} \ell (\theta ;\pmb {x}) = n\log 2 + \sum _{i=1}^n \log [e^{\theta (x_i+1)} - e^{\theta x_i}] - \sum _{i=1}^n \log [1+e^{\theta x_i}] - \sum _{i=1}^n \log [1+e^{\theta (x_i+1)}]. \end{aligned}$$

Maximizing it with respect to $\theta$ over the natural parameter space $\Theta =(0,\infty )$, one obtains the MLE ${\hat{\theta }}_{ML}= \arg \max _{\theta \in \Theta } \ell (\theta ;\pmb {x})$. The first-order derivative of $\ell (\theta ;\pmb {x})$ is equal to

$$\begin{aligned} \ell '(\theta ;\pmb {x})= \sum \frac{(x_i+1)e^{\theta (x_i+1)}-x_ie^{\theta x_i}}{e^{\theta (x_i+1)}-e^{\theta x_i}} -\sum \frac{x_i e^{\theta x_i}}{1+e^{\theta x_i}} -\sum \frac{(x_i+1)e^{\theta (x_i+1)}}{1+e^{\theta (x_i+1)}}, \end{aligned}$$

and setting it equal to zero and solving the resulting equation numerically for the unknown $\theta$ would provide the value of the MLE. The second derivative of $\ell (\theta ;\pmb {x})$ is given by

$$\begin{aligned} \ell ''(\theta ;\pmb {x}) = -\sum \frac{e^{\theta (2x_i+1)}}{[e^{\theta (x_i+1)}-e^{\theta x_i}]^2} -\sum \frac{x_i^2 e^{\theta x_i}}{(1+e^{\theta x_i})^2} -\sum \frac{(x_i+1)^2 e^{\theta (x_i+1)}}{[1+e^{\theta (x_i+1)}]^2}; \end{aligned}$$

$\ell ''(\theta )$ is equal to $-n$ times the observed Fisher information. The expected value of $\ell ''(\theta )$, with the minus sign, is equal to n times the Fisher information. An approximate estimate of the variance of the MLE is thus given by $-1/\ell ''({\hat{\theta }}_{ML})$, so an approximate and symmetric $(1-\alpha )100\%$ confidence interval for $\theta$ can be built as

$$\begin{aligned} {\hat{\theta }}_{ML}\pm z_{1-\alpha /2}\sqrt{-\frac{1}{\ell ''({\hat{\theta }}_{ML};\pmb {x})}}. \end{aligned}$$

Table 1 reports the MLEs of $\theta$ for a single observation x ($x=1,2,\ldots ,10$). Note that for this discrete analogue of the half-logistic distribution, the MLE does not exist if $n=1$ and $x_1=0$ (actually, the log-likelihood would tend to its supremum as $\theta \rightarrow \infty$).

Table 1 Maximum likelihood and method of moment’s estimates of $\theta$ for the discrete half-logistic distribution for different sample values x

3.3.4 Method of moments

In order to estimate $\theta$, one can alternatively resort to the method of moments; although there is no closed-form expression for the first moment of the distribution, thanks to the one-to-one monotonic decreasing relationship linking it to the unique parameter $\theta$ (see Fig. 2), and given the value of the sample mean ${\bar{x}}=\sum _{i=1}^n x_i/n$, finding a moment estimate of $\theta$ reduces to find the unique root ${\hat{\theta }}_{M}$ of the equation

$$\begin{aligned} {\bar{x}} = {\mathbb {E}}(X;\theta ) =\sum _{i=1}^{\infty } \frac{2}{1+e^{\theta x}}, \end{aligned}$$

where the infinite sum can be conveniently truncated to some appropriate upper bound; the latter can be set equal to some high-order quantile, which can be obtained by (7). As an initial trial value for ${\hat{\theta }}_{M}$, one can consider the one that is obtained by setting the sample mean equal to the expectation of the “parent” continuous half-logistic distribution, i.e., $\theta _0=\log 4/{\bar{x}}$. Table 1, in its last column, reports the estimates of $\theta$ derived according to the method of moments for a single observation x ($x=1,2,\ldots ,10$).

4 A discrete type I generalization of the half-logistic

4.1 Definition

As we have seen in the previous section, the proposed discrete half-logistic distribution has mode 0 for any eligible value of its parameter $\theta$ and, secondarily, it allows for overdispersion only. These features can limit the applicability of the model and hints that one should look for a generalization that can introduce more flexibility. We will present such a generalization as the discrete analogue of a generalized (continuous) half-logistic distribution. The cdf of the so-called type I generalized half-logistic distribution can be defined by taking the cdf of the half-logistic distribution (2) and exponentiating it through the additional parameter $\alpha >0$ (Kantam et al., 2013):

$$\begin{aligned} F(x;\theta ,\alpha )= \left( \frac{e^{\theta x}-1}{e^{\theta x}+1}\right) ^\alpha . \end{aligned}$$

Exponentiating the cdf of a given one-parameter distribution probably represents the easiest way to generate a two-parameter generalization (see, for example, El-Morshedy et al., 2020). The corresponding sf is

$$\begin{aligned} S(x;\theta ,\alpha )= 1-\left( \frac{e^{\theta x}-1}{e^{\theta x}+1}\right) ^\alpha , \end{aligned}$$

and the pmf of the discrete analogue of the generalized half-logistic distribution, which we will call “type I generalized discrete half-logistic,” can be defined as

$$\begin{aligned} p(x;\theta ,\alpha )=S(x)-S(x+1)=\left( \frac{e^{\theta (x+1)}-1}{e^{\theta (x+1)}+1}\right) ^\alpha -\left( \frac{e^{\theta x}-1}{e^{\theta x}+1}\right) ^\alpha . \end{aligned}$$

(11)

For this discrete model, the cdf results in

$$\begin{aligned} F(x;\theta ,\alpha )=\left( \frac{e^{\theta (x+1)}-1}{e^{\theta (x+1)}+1}\right) ^\alpha ; \end{aligned}$$

(12)

the quantile of level u, $0<u<1$, is

$$\begin{aligned} x_u = \Big \lceil \frac{1}{\theta }\log \frac{1+u^{1/\alpha }}{1-u^{1/\alpha }}-1 \Big \rceil . \end{aligned}$$

For a given $\theta$, increasing the value of $\alpha$ results in moving the probability mass toward higher values, as can be seen in the panels of Fig. 3. In this way, the mode can be different from zero, and there can even be two modes. For example, if one sets the parameters $\theta =1$ and $\alpha =\log (2)/(2\log (e+1)-\log (e^2+1)) =1.3874$, the resulting distribution has two modes at 0 and 1, with common probability $p_0=p_1\approx 0.3427$, as can be easily verified by recalling Eq. (11).

Fig. 3

Pmf of the generalized discrete half-logistic distribution for some values of its two parameters

As for the moments, expressions for the expectation and the variance are not available in a closed form, but can be numerically evaluated using analogous formulas to those used for the one-parameter discrete model in Sect. 3. In Table 2, for several parameters’ combinations, the values of expectation, variance, skewness, and kurtosis (all obtained numerically under the R statistical environment) are reported. It is easy to notice that the suggested model, as expected, being a discrete analogue of a generalized half-logistic distribution, is always positively skewed and leptokurtic; both skewness and kurtosis decrease by increasing $\alpha$ for a given $\theta$. The expectation and variance increase by increasing $\alpha$ for a given $\theta$ and by decreasing $\theta$ for a given $\alpha$. It can be easily noted that this statistical distribution, differently from the one-parameter case, is able to model even under-dispersed data, although the parameter combinations leading to this condition may be not so meaningful from a modeling perspective (e.g., $\theta =2$, $\alpha =1.5$ or 2; the corresponding values of expectation and variance are both typically smaller than 1).

Table 2 Moments of the discrete type I generalized half-logistic distribution

The log-concavity property, which was proved for the one-parameter discrete half-logistic distribution in Sect. 3.2, no longer holds for the discrete type I generalized half-logistic distribution. As a counterexample, one can consider the combination $\theta =1,\alpha =1/2$, for which, according to (11), $p(1)^2= 0.03721104< p(0)p(2)=0.05349907$.

We note that starting from the expression of the cdf (12), it can be easily derived that

$$\begin{aligned} \log \frac{1+F(x;\theta ,\alpha )^{1/\alpha }}{1-F(x;\theta ,\alpha )^{1/\alpha }}=\log \frac{\frac{2e^{\theta (x+1)}}{e^{\theta (x+1)}+1}}{\frac{2}{e^{\theta (x+1)}+1}} =\theta (x+1), \end{aligned}$$

a relationship that can be used for model diagnosis: after having estimated $\alpha$ and $\theta$ (according to one of the methods that will be illustrated in the next section), for each $x=0,1,2,\ldots$, one can compute $\log \frac{1+{\hat{F}}(x)^{1/{\hat{\alpha }}}}{1-{\hat{F}}(x)^{1/{\hat{\alpha }}}}$, where ${\hat{F}}(x)$ stands for the empirical cdf ${\hat{F}}(x)=\frac{1}{n+1}\sum _{i=1}^n \mathbbm {1}_{x_i\le x}$, and compare it with the corresponding ${\hat{\theta }}(x+1)$: close values of the two quantities for each x indicate a good fit of the discrete type I generalized half-logistic distribution.

We just want to mention that other generalizations of the continuous half-logistic distribution have been proposed in the literature: for example, a three-parameter generalized half-logistic distribution (Olapade, 2014), a two-parameter Poisson half-logistic distribution (Muhammad, 2017), and a three-parameter Poisson generalized half-logistic distribution (Muhammad and Liu 2019), which is itself an extension of the generalized half-logistic proposed by Kantam et al. (2013). Obviously, discrete counterparts can be obtained from these distributions following the usual criterion of matching the survival function at integer values.

4.2 Estimation

Estimation of the two parameters of the type I generalized half-logistic distribution has been studied in Seo and Kang (2015) and Gui (2017); the latter work provided a necessary and sufficient condition for the existence and uniqueness of the MLE and suggested inverse moment estimation, a modification thereof, and two different confidence regions for the joint estimation of $(\theta ,\alpha )$.

Estimation of the two parameters $\theta$ and $\alpha$ based on an iid sample of size n, $\pmb {x}=(x_1,\ldots ,x_n)$, drawn from the type I generalized discrete half-logistic distribution, can be performed by resorting to different methods. We can consider the methods already discussed in Sect. 3.3, although some of them need to be appropriately adapted and others may become infeasible. We will assume, if not stated otherwise, that both parameters are unknown and need to be estimated.

4.2.1 Method of maximum likelihood

The expression of the log-likelihood function for the discrete type I generalized half-logistic distribution is:

$$\begin{aligned} \ell (\theta ,\alpha ;\pmb {x}) = \sum _{i=1}^n \ln \left[ \left( \frac{e^{\theta (x_i+1)}-1}{e^{\theta (x_i+1)}+1}\right) ^\alpha -\left( \frac{e^{\theta x_i}-1}{e^{\theta x_i}+1}\right) ^\alpha \right] . \end{aligned}$$

In order to find the MLEs of $\theta$ and $\alpha$, the function above has to be maximized numerically, since the two equations obtained by setting the partial first-order derivatives (with respect to $\theta$ and $\alpha$) equal to zero are not manageable algebraically. Such a task, under the R programming environment, can be carried out by using, for example, the mle2 function within the bbmle package.

4.2.2 Method of proportions

Since from the expression of the pmf (11), we have that

$$\begin{aligned} p_0=p(0)=\left( \frac{e^{\theta }-1}{e^{\theta }+1}\right) ^\alpha , \end{aligned}$$

one derives

$$\begin{aligned} \log p_0 =\alpha \log \frac{e^\theta -1}{e^\theta +1} \end{aligned}$$

and then

$$\begin{aligned} \alpha =\frac{\log p_0}{\log \frac{e^\theta -1}{e^\theta +1}}, \end{aligned}$$

(13)

which provides an interpretation of the additional parameter $\alpha$, which is the ratio between the logarithmic probability of zero of the discrete type I generalized half-logistic distribution with parameters $\theta$ and $\alpha$ and the logarithmic probability of zero of the one-parameter discrete half-logistic distribution with parameter $\theta$. Evaluating the cdf (12) at $x=1$ and substituting the expression for $\alpha$ in (13), one derives

$$\begin{aligned} F(1)= \left( \frac{e^{2\theta }-1}{e^{2\theta }+1}\right) ^{\log p_0/\log \frac{e^\theta -1}{e^\theta +1}} \end{aligned}$$

or

$$\begin{aligned} \frac{\log (p_1+p_0)}{\log p_0}=\log \frac{1-\omega ^2}{1+\omega ^2}\bigg /\log \frac{1-\omega }{1+\omega }, \end{aligned}$$

(14)

with $\omega =e^{-\theta }$. The above equation can be rewritten, by letting $c=\log (p_0+p_1)/\log p_0$, as

$$\begin{aligned} \frac{1-\omega ^2}{1+\omega ^2}=\left( \frac{1-\omega }{1+\omega }\right) ^c \end{aligned}$$

and then

$$\begin{aligned} (1+\omega )^c(1-\omega ^2)=(1+\omega ^2)(1-\omega )^c \end{aligned}$$

or

$$\begin{aligned} (1+\omega )^{c+1} = (1+\omega ^2)(1-\omega )^{c-1}. \end{aligned}$$

Now, replacing $p_0$ and $p_1$ with the corresponding sample frequencies, say ${\hat{p}}_0$ and ${\hat{p}}_1$, in the expression of c, we obtain a non-linear equation in the only unknown $\omega$, which can be solved numerically, providing the root ${\hat{\omega }}_P$ and then ${\hat{\theta }}_P=-\log {\hat{\omega }}_P$. An estimate for $\alpha$ can then be obtained as

$$\begin{aligned} {\hat{\alpha }}_P =\frac{\log {\hat{p}}_0}{\log \dfrac{e^{{\hat{\theta }}_P}-1}{e^{{\hat{\theta }}_P}+1}}. \end{aligned}$$

If we assume that ${\hat{p}}_0$ and ${\hat{p}}_1$ are both non-zero, and that ${\hat{p}}_0+{\hat{p}}_1<1$, i.e., the sample does not consist of only zeros and ones, $\log ({\hat{p}}_1+{\hat{p}}_0)/\log {\hat{p}}_0$ is a value between 0 and 1, and the function $w(\omega )=\log \frac{1-\omega ^2}{1+\omega ^2}/\log \frac{1-\omega }{1+\omega }$ on the right side of Eq. (14) ranges continuously between 0 and 1, so the method of proportions can always find a feasible estimate for $\theta$ and then for $\alpha$.

$\theta$ known, $\alpha$ unknown: If the value of the parameter $\theta$ is known, in order to find an estimate for $\alpha$, one can equate the probability of 0 to the sample fraction of zeros and then solve for the unknown $\alpha$. From $p_0=\left( \frac{e^\theta -1}{e^\theta +1}\right) ^\alpha$, one obtains $\alpha =\log p_0/\log \frac{e^\theta -1}{e^\theta +1}$ and then ${\hat{\alpha }}_P = \log {\hat{p}}_0/\log \frac{e^\theta -1}{e^\theta +1}$. Alternatively, one can use any other probability p(x), $x= 1,2,\ldots$, and equate it to the corresponding relative frequency of x in the sample; in this case, however, it is no longer possible to derive a closed-form expression for the estimate of $\alpha$, but only to recover it numerically.

$\alpha$ known, $\theta$ unknown: If the value of the parameter $\alpha$ is known, by equating the probability of 0 to the sample fraction of zeros, one obtains an estimate for $\theta$ as ${\hat{\theta }}_P = \log \frac{1+{\hat{p}}_0^{\alpha }}{1-{\hat{p}}_0^{\alpha }}$.

4.2.3 Minimum chi-square estimation

Another technique that can be used for estimating $\theta$ and $\alpha$ is based on the minimization of the chi-square statistic (for a review of minimum chi-square and related methods together with some historical background, see Harris and Kanji, 1983). Letting $n_i$ be the absolute frequency of the value i ($i=0,1,\ldots ,x_{(n)}$, where $x_{(n)}=\max \lbrace x_j,j=1,\ldots ,n\rbrace$ is the largest observed value in the sample), the customary chi-square statistic is defined as

$$\begin{aligned} \chi ^2=\sum _{i=0}^{\infty } \frac{(n_i-np_i)^2}{np_i} = \sum _{i=0}^{x_{(n)}} \frac{(n_i-np_i)^2}{np_i} + n(1-F_{x_{(n)}}), \end{aligned}$$

(15)

where $p_i=p(i)$ and $F_{x_{(n)}}=F(x_{(n)})$ depend on the (unknown) parameters $\theta$ and $\alpha$, which can be estimated by minimizing $\chi ^2$. The minimum chi-square estimates of $\theta$ and $\alpha$ for the model at hand cannot be derived explicitly but can be obtained numerically quite easily using some optimization routine (see, e.g., Barbiero, 2017, where the method is applied to the type I discrete Weibull distribution and implemented in the R environment).

When the sample contains only one or two distinct values, then the minimum chi-square method fails to find a valid pair of estimates; in fact, the lower bound of the chi-square distance (15) is obtained by letting both parameters go to $+\infty$ while satisfying one constraint only. As an example, let us assume that the sample consists of only zeros and ones, with proportions ${\hat{p}}_0$ and $1-{\hat{p}}_0$, respectively. Then, it is easy to see that the chi-square distance tends to its infimum value (zero) by letting both $\theta$ and $\alpha$ go to $\infty$ under the constraint $\alpha =\log {\hat{p}}_0/\log \frac{e^\theta -1}{e^\theta +1}$. In this case, the first term of the sum in (15) is exactly zero, whereas the second term of the sum and the term outside the sum both tend to zero (see again Barbiero, 2017).

4.2.4 Method of moments

The method of moments can be theoretically applied by considering the first two raw moments of the discrete type I generalized distribution, ${\mathbb {E}}(X)$ and ${\mathbb {E}}(X^2)$, to be both regarded as functions of the unknown $\theta$ and $\alpha$, and equating them to the corresponding sample quantities ${\bar{x}}$ and ${\hat{\mu }}_2$. A direct numerical solution of this system of two non-linear equations in two unknowns can be hard to find; as an alternative (Khan et al., 1989), one can consider the quadratic loss function,

$$\begin{aligned} Q(\theta ,\alpha ;\pmb {x})= ({\mathbb {E}}(X;\theta ,\alpha )-{\bar{x}})^2 + ({\mathbb {E}}(X^2;\theta ,\alpha )-{\hat{\mu }}_2)^2, \end{aligned}$$

which is zero if and only if the two theoretical moments are equal to the corresponding sample moments; if minimized numerically with respect to $\theta$ and $\alpha$, the resulting minimizer $({\hat{\theta }}_M,{\hat{\alpha }}_M)$ represents the method of moments’ estimate.

5 Monte Carlo simulation study

The long-run performances of the estimation methods presented in Sect. 4.2 have been compared through an extensive simulation study.

We have calculated, by Monte Carlo simulation, the average value (AV), the bias (B), the standard deviation (SD), and the root mean squared error (RMSE) of the four couples of estimators of $\theta$ and $\alpha$ of the discrete (type I generalized) half-logistic distribution derived by the maximum likelihood (ML) method, the method of moments (M), the method of proportions (P), and the minimum chi-square (MCS) method. Additionally, for the ML estimators, we have computed the average lengths (AL) of the asymptotic confidence intervals (CIs) and their coverage probabilities (CP). The quantities of interest were estimated by the following expressions (here below, we refer to $\theta$ and to the generic estimator ${\hat{\theta }}$, but the same quantities have been calculated for $\alpha$ and ${\hat{\alpha }}$ as well):

• $\text {AV}({\hat{\theta }})= (1/N)\sum _{i=1}^N {\hat{\theta }}_i= \hat{{\bar{\theta }}}$, which approximates ${\mathbb {E}}({\hat{\theta }})$.

• $\text {B}({\hat{\theta }}) = \hat{{\bar{\theta }}}-\theta$, which approximates ${\mathbb {E}}({\hat{\theta }})-\theta$.

• $\text {SD}({\hat{\theta }}) = \sqrt{(1/N)\sum _{i=1}^N ({\hat{\theta }}_i-\hat{{\bar{\theta }}})^2}$, which approximates $\sigma _{{\hat{\theta }}}=\sqrt{{\mathbb {E}}({\hat{\theta }}-{\mathbb {E}}({\hat{\theta }}))^2}$.

• $\text {RMSE}({\hat{\theta }})=\sqrt{(1/N)\sum _{i=1}^N ({\hat{\theta }}_i-\theta )^2}$, which approximates $\sqrt{{\mathbb {E}}({\hat{\theta }}-\theta )^2}$.

• ${\text {AL}({\hat{\theta }})}=(1/N)\sum _{i=1}^N UB_i-LB_i$, where $UB_i$ and $LB_i$ are the upper and lower bounds of the $95\%$ log-likelihood-based CI constructed on the i-th sample, by default, based on inverting a spline fit to the profile log-likelihood (Bolker, 2022).

• $\text {CP}{({\hat{\theta }}})=(1/N)\sum _{i=1}^N \mathbbm {1}_{\left\{ LB_i \le \theta \le UB_i \right\} }$, which is simply the proportion of the $95\%$ log-likelihood-based CIs containing the true value of $\theta$.

We have considered $\theta \in \left\{ 1/8, 1/4, 1/2, 1, 2\right\}$ and $\alpha \in \left\{ 1,2,3\right\}$, with sample sizes $n = 25$, 50, and 100. $N=50,000$ samples of the discrete type I generalized half-logistic distribution were drawn for each artificial scenario using the R statistical environment (R Core Team, 2023).

Table 3 reports the values of AV, B, SD, and RMSE for the pair of estimators derived according to the four different methods, for all the examined combinations of parameters, when $n=100$. For better comparability among methods, for each artificial scenario, we highlight in boldface the smallest value of RMSE for both $\theta$ and $\alpha$ estimators. As expected, the numerical simulation experiments suggest that the ML method overall outperforms the other methods, even if for some combination values of the distribution parameters and sample size, the MCS method and, occasionally, the M method can be preferable (implicitly, we consider a pair of estimators to be preferable to another if it provides smaller values of both RMSEs, although other more elaborated criteria can be considered). MLE performs better for the combinations of parameters $(\theta ,\alpha )$ which are more meaningful (smaller values of $\theta$, higher values of $\alpha$) in the sense that they make the random distribution range over a wider set of integers with non-negligible probability. The method of proportion, despite being the only method that can provide an analytic expression for the estimate of at least one parameter, pays the price for not exploiting all the information contained in the sample, which translates into larger values of RMSE for both estimators of $\theta$ and $\alpha$. If compared to the estimators of $\theta$, the estimators of $\alpha$, even taking into account the different magnitudes of the two parameter values, turn out to be much more variable, in terms of either SD or RMSE. Also for the omitted scenarios, related to $n=50$ and $n=25$, the MLEs overall perform better than the competitors, with some exceptions, where the M and MCS methods are slightly better.

Table 4 displays the 95% CI values of AL and CP for the same parameter combinations considered in Table 3, with $n\in \lbrace 25,50,100\rbrace$. One can easily note that when $n=100$, the CP is always very close to the nominal level (95%); a discrepancy is observed when $\theta =2$ (in this case, the actual CP is larger than the nominal level). By decreasing the sample size n, we notice that the CP falls below the nominal value, even if keeping quite close to it (values in any case larger than 93.79%), except for the scenarios with $\theta =2$, where the CP increases to values around 97%. As for the average length of the CIs, as one could guess, it increases by decreasing the sample size, for each fixed parameter combination; it increases with $\theta$, for an assigned value of $\alpha$; it decreases with $\alpha$, for an assigned value of $\theta$. If compared to the CIs for $\theta$, the CIs for $\alpha$, even taking into account the different magnitudes of the two parameter values, turn out to be much less precise.

Table 3 Monte Carlo simulation for the discrete type I generalized half-logistic distribution: summary statistics for the estimators of $\theta$ and $\alpha$ derived according to the maximum likelihood method (ML), the method of proportions (P), the minimum chi-square method (MCS), and the method of moments (M), for $n=100$

Figure 4 displays the Monte Carlo distributions of the estimators of $\theta$ and $\alpha$ for the discrete type I generalized half-logistic distribution with $\theta =0.5$ and $\alpha =2$, based on samples of size $n=100$. The larger variability of the pair of estimators derived according to the method of proportion, if compared to the other methods, is apparent. Moreover, one can notice that the distributions of all the estimators of $\alpha$ are characterized by a larger variability and a more relevant presence of outliers than the corresponding estimators of $\theta$.

Fig. 4

Boxplots of the Monte Carlo distributions of the estimators of $\theta$ (left panel) and $\alpha$ (right panel) for the discrete type I generalized half-logistic distribution with $\theta =0.5$ and $\alpha =2$, for $n=100$. Dashed lines are drawn at ordinate values of $\theta =0.5$ (left panel) and $\alpha =2$ (right panel). Be aware of the different scales at the ordinate axis

We also note that especially when reducing the sample size, the method of proportion, under some scenarios, typically involving small values of $\theta$, can become unusable: it may happen, in fact, that the sample does not contain 0 s or 1 s and therefore cannot provide feasible estimates for either $\theta$ or $\alpha$. This also results in a negative and large—in absolute value—bias for the estimator of $\alpha$. Similarly, some other scenarios (typically, for large $\theta$ and small $\alpha$) may produce samples that make the MP, ML, and MCS methods infeasible: in fact, if a sample contains only 0 s and 1 s, it can be easily shown that for all these methods, the estimate of $\theta$ diverges to infinity.

Table 4 Coverage probability (CP) and average length (AL) of log-likelihood-based confidence intervals for the parameters $\theta$ and $\alpha$ of the discrete type I generalized half-logistic distribution, for several artificial scenarios and sample sizes

6 Application to real data

In this section, we provide some empirical evidence of the usefulness of the proposed discrete distributions by fitting them to two real data sets and comparing them to some traditional models.

The first data set, shown in Table 5, deals with the number of claims of automobile liability policies (Gómez-Déniz et al., 2008; Klugman et al., 1998). Observations are displayed in the first and second columns. These data have a mode at 0 and are overdispersed ($s_x^2=3.669>{\bar{x}}=1.708$) and right-skewed (the standardized third central moment is 1.716).

By maximizing the log-likelihood function, we estimate the unique parameter of the discrete half-logistic distribution proposed in this paper, ${\hat{\theta }}_{ML}=0.6327834$. The corresponding maximum value of the log-likelihood function is $-528.7358$; the AIC is 1059.472. By using the least-squares method, one obtains ${\hat{\theta }}_{LS}=0.6096149$; by using the method of moments, the estimate is ${\hat{\theta }}_M=0.6354825$; given ${\hat{p}}_0=99/298=0.3322$, one can compute ${\hat{\theta }}_P=0.6931472$ by using (9). In order to evaluate the goodness-of-fit, the $\chi ^2$ statistic was calculated according to the formula $\chi ^2 = \sum _ {i=1}^h (O_i - E_i)^2/E_i$, where $O_i$ and $E_i$ denote the observed and expected frequencies under the model fitted through the MLE, respectively, of the i-th value, and h is the number of classes into which the sample data were classified. After pooling the last seven categories into a unique category (in order to have all the $E_i$ greater than 5), we compute $\chi ^2=2.624072$, with a corresponding p-value 0.7577 (the number of degrees of freedom is $7-1-1=5$).

By comparing these results with the fits obtained in Gómez-Déniz et al. (2011), we observe that the discrete half-logistic distribution provides significant improvement over the negative binomial (NB), the Poisson-inverse Gaussian distributions (PIG), and the new discrete distribution introduced in Gómez-Déniz et al. (2011) (ND), as judged by its higher p-value; the value of the AIC is smaller than the corresponding value of ND only (1060.790), but larger than NB, 1056.992, and PIG, 1054.674.

Table 5 Distribution of the number of claims of automobile liability policies (Gómez-Déniz et al., 2008; Klugman et al., 1998), fitted by the one-parameter discrete half-logistic distribution

The diagnostic plot of Fig. 5 (see Sect. 3.3.2), graphing a transformation of the sf versus the observed values x, confirms a more than satisfactory goodness-of-fit of the discrete half-logistic distribution for the data.

Fig. 5

Diagnostic plot: scatter plot of $z=\log [(2-{\hat{S}}(x))/{\hat{S}}(x)]$ vs. x for the insurance policies data set fitted by the discrete half-logistic distribution

Moving to the two-parameter generalization, introduced and discussed in Sect. 4, we consider the maximum likelihood method and obtain for the two parameters the estimates ${\hat{\theta }}_{ML}=0.6018332$ and ${\hat{\alpha }}_{ML}=0.9064219$; the maximized log-likelihood function is $\ell _{\max }=-528.27$, but the AIC value (1060.54) is greater than that of the one-parameter discrete half-logistic (and those of the competing models in Gómez-Déniz et al. (2011), except for the ND model). Therefore, adding the $\alpha$ parameter hasn’t produced a significant relative increase in the fit of the model. The method of proportions provides ${\hat{\theta }}_P=0.5146831$ and ${\hat{\alpha }}_P=0.7990579$, which are a bit different from the corresponding MLEs.

Now, we consider a second data set, see Table 6, which is taken from Ridout and Besbeas (2004) and is about the number of outbreaks of strikes in UK coal mining industries in four successive weeks in the years 1948–59; it has been considered and fitted by different discrete distributions in Chakraborty and Chakravarty (2012). This data set is interesting since the empirical distribution has a unique mode at 1, and not at 0, like the previous one, so the discrete generalized half-logistic should be much more suitable than the one-parameter discrete half-logistic, which has a unique mode at 0.

If we fit the one-parameter discrete half-logistic distribution, the maximum likelihood method provides ${\hat{\theta }}_{ML}=0.9907381$, and the maximized log-likelihood function is $\ell _{\max }=-202.9996$, with an AIC value of 407.9992. If we compare the observed frequencies with the theoretical ones under this model, we notice how the latter is unsuitable, as expected.

The discrete type I generalized half-logistic model provides ${\hat{\theta }}_{ML}=1.557542$ and ${\hat{\alpha }}_{ML}=2.847660$. One can easily note that the value of $\alpha$ is much larger than 1, and this allows the data to be fitted with a mode different from 0. The maximum value of the log-likelihood function is $\ell _{\max }=-187.54$, and the AIC value is 379.08. The value of the chi-square goodness-of-fit statistic (computed over all five categories, although the last theoretical frequency is smaller than 5) is 1.722681, with a corresponding p-value of 0.4226. Such values are very close to those of the two-parameter discrete gamma distribution, which has been introduced and considered in Chakraborty and Chakravarty (2012).

Table 6 Distribution of the number of outbreaks of strikes (Ridout and Besbeas, 2004), fitted by the discrete type I generalized half-logistic distribution

As a tool for model checking, we can consider the values of ${\hat{\theta }}_{ML}\cdot x$, $x=0,1,2,3,4$ and those of $\log \frac{1+{\hat{F}}(x)^{1/{\hat{\alpha }}_{ML}}}{1-{\hat{F}}(x)^{1/{\hat{\alpha }}_{ML}}}$, with ${\hat{F}}(x)$ being the empirical cdf computed at x with $n+1$ as the denominator (see Table 7). The values of the two quantities are quite close to each other for all values of x, except for the last one, and this confirms that the proposed distribution provides a good fit.

Table 7 Model checking for the second data set

7 Other possible discrete analogues

It is possible to generate discrete analogues of a continuous random distribution by using other techniques than imposing the preservation of the sf at integer support values, as done in this work. One can, for example, define the (optimal) discrete analogue of a continuous distribution as the discrete rv supported over all the (non-negative) integer values minimizing an assigned statistical distance or discrepancy measure between the two cdfs (Barbiero and Hitaj, 2021). Letting $Q_i$ be the optimal value of the cdf of the discrete analogue at i, $i=0,1,\ldots ,\infty$, we have the following results for the half-logistic distribution (we limit the discussion to this distribution, although one can easily extend the results to the type I generalized half-logistic). By minimizing the Cramér–von Mises distance, one obtains for $i=0,1,\ldots$

$$\begin{aligned} Q_i= & {} \frac{1}{2}[F_X(i)+F_X(i+1)]= 1 -\frac{1}{2}\left[ \frac{2}{1+e^{\theta i}} + \frac{2}{1+e^{\theta (i+1)}}\right] \\= & {} 1-\frac{2+e^{\theta i}+e^{\theta (i+1)}}{(1+e^{\theta i})(1+e^{\theta (i+1)})}, \end{aligned}$$

with $F_X(x)$ from (2); therefore, one can easily construct the probabilities as follows:

$$\begin{aligned} p(0)=Q_0=1-\frac{3+e^\theta }{2(1+e^\theta )}=\frac{e^\theta -1}{2(1+e^\theta )} \end{aligned}$$

and

$$\begin{aligned} p(i)&=Q_i-Q_{i-1}=-\frac{2+e^{\theta i}+e^{\theta (i+1)}}{(1+e^{\theta i})(1+e^{\theta (i+1)})}+\frac{2+e^{\theta (i-1)}+e^{\theta i}}{(1+e^{\theta (i-1)})(1+e^{\theta i})}\\&=\frac{e^{\theta (i-1)}(e^{2\theta }-1)}{(1+e^{\theta (i-1)})(1+e^{\theta (i+1)})},i=1,2,\ldots \end{aligned}$$

By minimizing the Cramér distance, the optimal discrete analogue of the half-logistic distribution has cumulative probabilities given by

$$\begin{aligned} Q_i&=\int _i^{i+1} F_X(x)\text {d}x=\int _i^{i+1} 1-\frac{2}{1+e^{\theta x}}\text {d}x = 1-2\int _i^{i+1} \frac{1+e^{\theta x}-e^{\theta x}}{1+e^{\theta x}}\\&=1-2\int _i^{i+1} 1-\frac{e^{\theta x}}{1+e^{\theta x}}\text {d}x=1-2+2\left[ \frac{\log (1+e^{\theta x})}{\theta }\right] _i^{i+1}\\&=-1+\left[ \frac{2\log (1+e^{\theta x})}{\theta }\right] _i^{i+1}=\frac{2}{\theta } \log \frac{1+e^{\theta (i+1)}}{1+e^{\theta i}}-1,i=1,2,\ldots , \end{aligned}$$

and therefore

$$\begin{aligned} p(0)=Q_0=\frac{2}{\theta } \log \frac{1+e^\theta }{2}-1 \end{aligned}$$

and

$$\begin{aligned} p(i)=Q_i-Q_{i-1}=\frac{2}{\theta }\log \frac{(1+e^{\theta (i+1)})(1+e^{\theta (i-1)})}{(1+e^{\theta i})^2}, i=1,2,\ldots \end{aligned}$$

In order to preliminarily compare the three different discrete analogues suggested here, when the parameter $\theta$ of the parent continuous distribution takes the value of 1, Table 8 displays the probabilities of the values $\lbrace 0,1,\ldots ,10\rbrace$.

Table 8 Probabilities of three discrete analogues of the half-logistic distribution for $\theta =1$

Note how the homologous probabilities for the two discrete analogues obtained by the minimization of a statistical distance between cdfs are very close to each other, but are rather different from those of the discrete analogue proposed in this work and obtained through the preservation of the sf. For the former two, in fact, we have that $F_X(i)<Q_i<F_X(i+1)$ for any integer i, whereas for the first one, $Q_i=F_X(i+1)>F(i)$ (remember that being $p(i)=F_X(i+1)-F_X(i)$, then $Q_i=\sum _{j=0}^i p(j)=F_X(i+1)$). Moreover, one can notice that the two alternative discrete analogues, for the chosen value of $\theta$, have a unique mode at 1, whereas for the distribution proposed in Sect. 3, the mode is 0.

Studying the properties and potential applications of these two further discrete analogues of the half-logistic distribution can be the object of future study.

8 Application to an actuarial problem

Let $S=\sum _{i=1}^N X_i$ be the sum of N iid rvs $X_i\sim F$, with N being a discrete rv, independent from $X_i$, supported over the set of non-negative integers (if $N=0$, $S=0$). S can represent the aggregate loss of an insurance company related to the number N of claims occurring over a specified time period, with claim size $X_i$, typically modeled by a continuous positive rv. S is therefore a compound random distribution, whose cdf is in general not easy to determine, at least analytically, since it requires the computation of convolutions. Alternatively, one can find an approximation of the cdf of S by resorting to the application of Panjer’s recursion formula, which can be used as long as the random distribution of X is discrete, with pmf p, and the random distribution of N belongs to a specific class of discrete distributions, the (a, b, 0) class, which comprises the binomial, the negative binomial, and the Poisson (see, for example, Dickson, 2016, p. 64). These three discrete distributions are characterized by the following recursive relationship for the pmf f:

$$\begin{aligned} f(n)=\left( a+\frac{b}{n}\right) f(n-1); \end{aligned}$$

for the Poisson distribution, in particular, $a=0$ and $b=\lambda$. Panjer’s formula allows us to determine the distribution of S, $g(x)=P(S\le x)$, recursively, by using the following formula:

$$\begin{aligned} g(x) = \frac{1}{1-ap(0)}\sum _{i=1}^x \left( a+\frac{bi}{x}\right) p(i)g(x-i),x=1,2,\ldots , \end{aligned}$$

(16)

starting from the value g(0). Since X is typically continuous and not discrete, as required for applying Panjer’s formula exactly, in order to use it, we will first need to proceed to a proper discretization of X.

Table 9 Approximate values of the cdf of the random sum S of N iid half-logistic rvs with parameter $\theta =1/10$ (N following a Poisson distribution with parameter $\lambda =5$): Monte Carlo simulation vs. approximation via discretization and normal approximation; values of x from 5 to 200 in steps of 5

Let us illustrate the following example, where N follows a Poisson distribution with parameter $\lambda =5$ and $X_i$ are iid half-logistic rvs with parameter $\theta =1/10$. The use of the half-logistic distribution is motivated by the fact that it is a right-skewed, leptokurtic distribution supported on ${\mathbb {R}}^+$, and therefore it can be effective in modeling claim sizes. If we need to find the distribution of $S=\sum _{i=1}^N X_i$, first we have to construct a discrete version of $X_i$, with pmf p(i), for example using the discrete half-logistic distribution proposed in this work. Then we can recursively determine an approximate distribution g(x) of S by employing (16), starting from $g(0)=e^{-\lambda }+\sum _{j=1}^\infty \frac{\lambda ^j e^{-\lambda }}{j!}p(0)^j$. Table 9 displays the values of g(x) for several integers x. Along with these approximated values based on the discretization of the continuous distribution of X, we report also the values derived from the normal approximation, i.e., by approximating the random sum S through a normal distribution with parameters $\mu ={\mathbb {E}}(S)$ and $\sigma ^2=\text {Var}(S)$, and as a proxy for the exact value of the cdf of S at x, we report the values obtained from Monte Carlo simulation, based on $NSim=1,000,000$ pseudo values $s_j$ of S, i.e., $\frac{1}{NSim}\sum _{j=1}^{NSim} \mathbbm {1}_{s_j\le x}$. We note that the approximation-by-discretization is able to supply estimates of the cdf that are very close to the ones provided by Monte Carlo simulation (they are almost always identical up to the third decimal digit); the normal approximation is not as satisfactory, since it provides absolute errors even as large as 0.07 near the center of the distribution of S. We note that for the exact distribution of S (which is a compound Poisson distribution), one can calculate the first moment as ${\mathbb {E}}(S)={\mathbb {E}}(N){\mathbb {E}}(X)=\frac{\lambda \log 4}{\theta }\approx 69.31$ and the exact variance as $\text {Var}(S)=\lambda {\mathbb {E}}(X^2)=\frac{\lambda \pi ^2}{3\theta ^2}\approx 1644.93$.

Looking at the last rows of Table 9, we note that the values of the normal approximation tend to 1 more quickly than those obtained by the approximation-by-discretization procedure; in other terms, the distribution of the normal approximation has, as expected, a thinner right tail than that of the cdf obtained by applying Panjer’s recursion formula to the discretized half-logistic distribution. The latter approximation is thus more capable of capturing the leptokurtosis of S, which is theoretically established by a known result about compound Poisson distributions (see, for example, Dickson, 2016, p. 58).

Ad-hoc code has been developed in the R environment to implement the two discrete distributions of Sects. 3 and 4, to carry out the Monte Carlo simulation study of Sect. 5, to fit them to the data sets analysed in Sect. 6, and to accomplish the application to a real problem in Sect. 8. Researchers and practitioners interested in using the code for their research or replicating the computations can find it available here: https://tinyurl.com/ANOR-D-23-00161.

9 Conclusion

We discussed a discrete analogue to the one-parameter half-logistic distribution and a discrete analogue to a two-parameter generalization of the half-logistic distribution, obtained by the exponentiation of its continuous cdf. Both discrete analogues are based on the matching of the sf of the corresponding parent distribution at every integer support value.

Supported by their theoretical properties and fitting results on real data, we believe that the proposed models can profitably join the class of discrete random distributions and can serve a wide spectrum of applications, including reliability and survival analysis, especially in modeling long-tailed count data. However, we observe that other generalizations of the continuous half-logistic distribution would yield different discrete analogues, which might be worth studying. Moreover, although the two-parameter model discussed here shows a reasonable level of flexibility, we remark that adding a location parameter to the half-logistic distribution would ensure additional versatility.

Future research will investigate the possible application of the proposed distributions in a count regression model, as opposed to Poisson and negative binomial regression, and the construction of a bivariate discrete family that can be used for modeling correlated counts.