Robustness of priority deriving methods for pairwise comparison matrices against rank reversal: a probabilistic approach

Abstract

This work aims to answer the natural question of how probable it is that a given method produces rank reversal in a priority vector (PV) if a decision maker (DM) introduces perturbations to the pairwise comparison matrix (PCM) under concern. We focus primarily on the concept of robustness against rank reversal, independent of specific methods, and provide an in-depth statistical insight into the application of the Monte Carlo (MC) approach in this context. This concept is applied to three selected methods, with a special emphasis on scenarios where a method may not provide outputs for all possible PCMs. All results presented in this work are replicable using our open-source implementation.

1 Introduction

One of the primary challenges in decision theory involves determining the appropriate weights for a given set of criteria, such as activities, alternatives, or objects, based on their respective levels of importance. Typically, importance is evaluated by using a variety of criteria that may be applicable to some or all of the activities. For instance, the criteria may relate to specific objectives that the activities are intended to achieve. This process, which is referred to as multiple criteria decision making, follows a hierarchical structure that includes the goal, criteria, and alternatives, and can be viewed as a theory of measurement.

In order to address these challenges, the Analytic Hierarchy Process (AHP) (Satty, 1977) is often utilized. The primary subproblem within AHP involves the calculation of priority vectors, which are weights assigned to the various objects within the hierarchy. This includes both criteria (or subcriteria) and alternatives (or variants), which must be weighted properly in order to make effective decisions.

Assume that there are n objects of interest, where n is an integer number, i.e., $n \in \mathbb {N} = \{1, 2, \dots \}$, which have to be assessed/evaluated by a decision maker (DM) so that the objects could be rank ordered. Formally, the DM is interested in finding a positive priority vector (PV) $v = (v_1, \dots , v_n) \in \mathbb {R}^n$, where $v_i$ expresses the priority rank/importance/quality/etc. of object i among the considered objects. In practice, the DM is trying to derive the PV by using different methods. Here, it is assumed that there exists a true PV for the objects of interest, however, the DM does not know it and tries to find it via a pairwise comparison method. There, it is assumed that the DM is able to provide her/his priorities for each pair of objects separately. Formally, the DM is able to provide a priority $a_{ij} \in \mathbb {R}$ expressing how much the object i is preferred over the object j for each $i, j \in \breve{n}$, where $\breve{n}= \{1,\dots , n\}$. Gathering these pairwise priorities together, one forms a pairwise comparison matrix (PCM) $\varvec{A} = (a_{ij}) \in \mathbb {R}^{n\times n}$.

Given $\varvec{A}$, there exists a plethora of methods for calculating the priority vector v from $\varvec{A}$, such as the Geometric Mean Method (GMM) (Crawford & Williams, 1985) or Saaty’s Eigenvector Method (EVM) (Saaty, 1987, 1990) among the most popular ones; see Choo and Wedley (2004) and Ramík (2020) for an overview. In order to get a reliable PV from a PCM, several desirable properties of the PCM can be requested, such as reciprocity or consistency, which are detailed below. Given a PCM consistent with a PV v, denoted $\varvec{A}_v$, the pairwise comparison methods mentioned above are able to recover v from $\varvec{A}_v$ exactly. However, due to emotions, health conditions, etc. of the DM or due to using a predetermined discrete scale (e.g. Saaty’s 1–9 scale (Satty, 1977)) during the construction of the PCM, the DM might, instead of $\varvec{A}_v$, provide a PCM that is not consistent in general. In other words, the DM might involve perturbations to the possibly consistent pairwise comparisons, which could lead to rank reversal, a phenomenon where a slight adjustment in pairwise comparisons can unexpectedly alter the order of priorities among the alternatives. Given a method for calculating a PV from a PCM, the following natural question may arise: how robust is the method against the rank reversal caused by the perturbations?

One can observe a growing body of research on the issue of robustness against rank reversal in the context of PCMs, and a variety of approaches have been proposed to address this issue. In Mazurek et al. (2021), One-Factor-At-a-Time sensitivity analysis via Monte Carlo simulations is applied to the GMM, EVM and Best-Worst Method (BMW), the latter being introduced in Rezaei (2015). The authors’ findings suggest that the BWM is, on average, significantly more sensitive statistically (and thus less robust) and more susceptible to rank reversal than the GMM and EVM for every examined matrix (vector) size, even after adjustment for the different numbers of pairwise comparisons required by each method. On the other hand, differences in sensitivity and rank reversal between the GMM and EMM were found to be mostly statistically insignificant. In Faramondi et al. (2023), the authors propose an approach complementary to measuring inconsistency. This approach is able to integrate and evaluate the concept of uncertainty in PCMs in order to verify the credibility of the final outcome. The approach characterizes how DM’s uncertainty reflects into rank reversal, which is done via an optimization problem aiming to identify the smallest perturbations of the pairwise comparison values which result in an altered ranking of alternatives. Already in Saaty and Vargas (1987), the effect of uncertainty in judgment on the stability of the rank order of alternatives is studied for EVM, with a finding that interval estimate approach can be implemented more easily by means of simulation assuming that all points of the interval are equiprobable. In Crawford and Williams (1985), a Monte Carlo (MC) simulation study comparing robustness against rank reversal of GMM and EVM is presented, showing slightly larger robustness for GMM.

In contrast to all these studies, which focus on evaluation of the robustness for some selected method(s), we rather focus on the concept of the robustness independently of particular methods, and provide an in-depth statistical look at the development of the related MC approach. That is, we rigorously define the robustness of a method against rank reversal by using probability theory (Sect. 2.2) and then advocate the necessity of the MC approach (Sect. 2.3). We also we emphasize the fact that there exists an important relationship among the expected value of perturbations, reciprocity of the PCM, and the scale of the priorities, which should be respected during the design of an MC study in order to avoid confusing results (Sect. 2.4). Moreover, as we purely focus on the rank ordering of the involved priorities (note that other measures of robustness based on the Euclidean or Chebyshev distance, or Maximal ratio are also commonly used (Csató, 2023)), our probabilistic concept of the robustness is scale invariant, which we address in Sect. 2.1 via alo-groups (Bartl & Ramík, 2022; Cavallo & D’Apuzzo, 2009). Further, we provide two theorems which allow us to limit the computational burden during the MC experiments by reducing the dimension of the problem by utilizing a relationship between the distribution of the perturbations and that of the randomized PV under concern (Sect. 2.6).

With all this at hand, we apply our MC design to three particular methods for calculating PVs from PCMs: We compare the robustness of two standard methods (GMM and EVM) with the robustness of a method based on coherent weights for PCMs (Cavallo, 2019). For the latter, we develop a fast algorithm that computes the ranks of the priorities for a given PCM directly (Sect. 3.3). As not all PCMs are coherent, which can be easily recognized by using our proposed theorem (Theorem 4), the algorithm does not return the rank ordering of the priorities implying that the robustness of this method has to be computed in a special way. We show that our framework is able to deal also with such methods, which supports its general applicability (Sect. 5). For the latter method, we also show that its robustness can be accessed analytically (Sect. 4.1), which allowed us to further tune our MC experiments presented in Sect. 5. Importantly, all the results shared in this study can conveniently be replicated as the Python source code for our implementation is openly accessible on GitHub. For further details, please visit: https://github.com/gorecki/robustness.

The paper is organized as follows. Section 2 presents the development of our probabilistic concept of the robustness and the related MC approach. Section 3 recalls the three aforementioned methods. In Sect. 4, an analytical approach to the robustness is considered, and Sect. 5 presents an MC study based on our design. Section 7 concludes.

2 Methodology

2.1 The question

Given a PCM $\varvec{A}$, one can choose an appropriate method for calculating the priority vector v from $\varvec{A}$ from a wide range of methods including, e.g., GMM or EVM. However, to get a reliable PV from a PCM, several desirable properties of the PCM can be requested, such as reciprocity or consistency. As their definition depends on the framework we are operating on, let us first recall a unifying approach involving Abelian linearly ordered groups, alo-groups for short, introduced in Cavallo and D’Apuzzo (2009).

The triplet $(H, \odot , \le )$, where H is a set endowed with an operation $\odot$, and $\le$ is a linear order on H, is said to be an Abelian linearly ordered group denoted $\mathcal {R}_\odot$, if $(H, \odot )$ is an Abelian group, and for all $a, b, c \in H$

$$\begin{aligned} a \le b \text { implies } a \odot c \le b \odot c. \end{aligned}$$

We denote the identity element of $(H, \odot )$ by e (for all $a \in H$, $a \odot e = e \odot a = a$), and we define a binary operation $\div$ such that $a \div b = a \odot b^{(-1)}$ for all $a, b \in H$, where $b^{(-1)}$ denotes the inverse element of b on $(H, \odot )$. The two well-known examples of alo-groups are the Multiplicative alo-group $\mathcal {R}_* = ((0,\infty ), *, \le )$, and the Additive alo-group $\mathcal {R}_+ = (\mathbb {R}, +, \le )$ (Cavallo & D’Apuzzo, 2009).

A PCM $\varvec{A}$ is said to be reciprocal on $\mathcal {R}_\odot$, if

$$\begin{aligned} a_{ij} = a_{ji}^{(-1)} \text { for all } i,j \in \breve{n}. \end{aligned}$$

A PCM $\varvec{A}$ is consistent on $\mathcal {R}_\odot$, if there exists a PV $v \in H^n$, such that

$$\begin{aligned} a_{ij} = v_i \div v_i \text { for all } i,j \in \breve{n}. \end{aligned}$$

A PCM consistent with a PV v is further denoted by $\varvec{A}_v$. Also, note that the consistency implies the reciprocity, but not vice-versa.

Given $\varvec{A}_v$, the pairwise comparison methods mentioned above are able to recover v from $\varvec{A}_v$ exactly. However, due to emotions, health conditions, etc. of the DM or due to using a predetermined discrete scale (e.g. Saaty’s 1–9 scale) during the construction of the PCM, the DM might, instead of $\varvec{A}_v$, provide a perturbed reciprocal PCM $\varvec{A}_{v,\varvec{X}} = (\hat{a}_{ij})$ with $\hat{a}_{ij} = v_i \div v_j \odot x_{ij}$, where $\varvec{X} = (x_{ij}) \in H^{n \times n}$ is a reciprocal matrix of perturbations.

Clearly, this PCM is in general not consistent and the following natural question may arise: Given a method for calculating a PV from a PCM, how robust is the method against the rank reversal caused by the perturbations?

2.2 Robustness against rank reversal

Before we precisely introduce our approach to robustness against rank reversal, some clarifications on the phenomenon of rank reversal are necessary. This is because rank reversal has different meanings in the literature, as the following results demonstrate. For example, rank reversal can be caused by the difference between the left and right eigenvectors (Bozóki & Rapcsák, 2008; Csató, 2023; Ishizaka & Lusti, 2006; Johnson et al., 1979). This might lead to strong rank reversal in group decision making, that is, the alternative with the highest priority according to all individual vectors may lose its position when evaluations are derived from the aggregated group comparison matrix (Csató, 2017a; Pérez & Mokotoff, 2016). Furthermore, if the eigenvector method is used to derive the weights, increasing a pairwise comparison can result in a counter-intuitive rank reversal since the weights are not always monotonic (Csató & Petróczy, 2021). Finally, changing the scale of ordinal pairwise comparisons can also imply rank reversal (Genest et al., 1993; Petróczy & Csató, 2021).

In this work, we define rank reversal as any instance when the original ordering, provided by a consistent PCM, is permuted in any way due to perturbations introduced into the PCM. For instance, consider we have alternatives A, B, and C. Initially, our pairwise comparisons suggest that $A \succ B \succ C$. However, a slight perturbation in these comparisons, possibly due to minor changes in stakeholder opinions or measurement error, could unexpectedly change the ranking order to $B \succ A \succ C$ or $A \succ C \succ B$. In this case, we consider that a rank reversal has happened.

Having this clear, we can address robustness against rank reversal by answering the last question from Sect. 2.1 in the probabilistic sense. This involves the following three notions:

• 1. The rank mapping $r:H^n \rightarrow \mathbb {N}^n$ defined by $r(v) = (r_1, \dots , r_n)$, where $v =(v_1,\dots ,v_n) \in H^n$ such that $v_i \ne v_j$ for $i \ne j$, and the rank $r_i$ of $v_i$ is the position of $v_i$ in v sorted in the ascending order for $i \in \breve{n}$, e.g., if $H = \mathbb {R}$, $r(0, -1, 1) = (2, 1, 3)$.

• 2. A pairwise comparison method, shortly a method, M for calculating a PV from a PCM is a mapping $M:H^{n\times n} \rightarrow H^{n}$ given for any $\varvec{A} \in H^{n\times n}$ by

  $$\begin{aligned} M(\varvec{A}) = v, \end{aligned}$$

  (1)

  where v is the PV calculated by the method M for the PCM $\varvec{A}$.

• 3. A random perturbed reciprocal PCM $\varvec{A}_{v,F} = (\hat{\hat{a}}_{ij})$, where $\hat{\hat{a}}_{ij} = v_i \div v_j \odot X_{ij}$, where $X_{ij}, ~i < j$, are independent copies of a random variable (RV) X distributed according to a cumulative distribution function (CDF) $F :H \rightarrow [0,1]$, denoted $X \sim F$, where $X_{ii} = e$ and $X_{ji} = (X_{ji})^{(-1)}$ for all $i < j$. Note that X is a measurable function from $(\Omega , \mathcal {A}, \mathbb {P})$ to $(H, \mathcal {B})$, where $(\Omega , \mathcal {A}, \mathbb {P})$ is a probability space and $\mathcal {B}$ is the Borel $\sigma$-algebra on H generated by the open intervals of the alo-group $(H,\odot ,\le )$.

Given a PV v, a CDF F and a method M, we define the v-robustness against rank reversal of the method M under perturbations distributed according to F, shortly v-robustness, denoted R(v, F, M), as the probability of the binary event that $r(M(\varvec{A}_{v,F}))$ matches r(v), i.e.,

$$\begin{aligned} R(v, F, M) = \mathbb {P}\big (r(M(\varvec{A}_{v,F})) = r(v)\big ). \end{aligned}$$

(2)

Hence, given a method M such that $r(M(\varvec{A}_v)) = r(v)$ for all $v \in H^n$, which is satisfied for all standardly used methods, the v-robustness quantifies how likely it is that the rank ordering calculated by M for $\varvec{A}_v$ remains the same after perturbations distributed according to F are introduced into $\varvec{A}_v$. Given a PV v and two methods $M_1$ and $M_2$, the DM requiring high robustness then could choose between the methods based on the values of $R(v, F, M_{m}),$ $m \in \{1,2\}$.

However, it is important to note that this approach to robustness against rank reversal does not distinguish the methods if they fail to reproduce the correct order, that is, it does not consider whether the true ranking is missed by exchanging the two bottom alternatives, or by completely reversing the ranking. A way to address this issue is discussed later in Sect. 6.

Also consider that as v is assumed to be unknown, which is a realistic scenario, there remains the question how to assess the robustness of a method without knowing v. In order to tackle this problem, we suggest to substitute the unknown v by a random vector $V = (V_1, \dots , V_n)$ distributed according to a n-variate CDF $G :H^n \rightarrow [0,1]$. That is, substituting v-robustness R(v, F, M) by the robustness R(G, F, M) given by

$$\begin{aligned} R(G, F, M) = \mathbb {P}\big (r(M(\varvec{A}_{V,F})) = r(V)\big ), \end{aligned}$$

(3)

where $V \sim G$. Then, the CDF G represents the knowledge of the DM about the priority vector v.

According to Sklar (1959), G can be decomposed to its univariate marginal functions $G_1, \dots , G_n$, and the copula $C :[0,1]^n \rightarrow [0,1]$ given implicitly by $G(x_1,\dots , x_d)=C(G_1(x_1),\dots , G_d(x_d))$ for $x_1,\dots , x_d\in H$. Using this decomposition, the following two approaches reflecting the level of the knowledge about the unknown v can be distinguished.

• 1. If the DM has some knowledge of the distribution of the variables $V_1, \dots ,$ $V_n$, this knowledge can be used to assume some model for the CDFs $G_1,\dots , G_n$. Otherwise, we suggest to use, given some reasonable $a,b \in H$, the uniform distribution $\mathcal {U}[a,b]$, which reaches the maximum Shannon entropy for a continuous variable (Thomas & Joy, 2006).

• 2. If the DM has some knowledge of the copula of G, some convenient model for C can be assumed. Otherwise, we suggest to use the independence copula $C_\Pi (u_1,\dots , u_n) = \prod _{i=1}^{n} u_i, ~u_1,\dots , u_n \in [0,1]$, representing the independence among the variables $V_1, \dots , V_n$.

2.3 A Monte Carlo approach

The probability R(v, F, M) and particularly R(G, F, M) is typically hard to access in an analytical way, which is detailed in Sect. 4. Due to that, one can utilize the Monte Carlo (MC) approach as a feasible alternative. In order to do so for the v-robustness, consider that

$$\begin{aligned} R(v, F, M) = \mathbb {P}\big (r(M(\varvec{A}_{v,F})) = r(v)\big ) = \mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v,F})) = r(v)}]. \end{aligned}$$

(4)

where $\mathbb {E}[Z]$ denotes the expected value of a RV Z, and $\textbf{1}$ denotes the indicator function that returns 1 if the condition in its index is satisfied, and 0 otherwise. Let

$$\begin{aligned} Y = \textbf{1}_{r(M(\varvec{A}_{v,F})) = r(v)}, \end{aligned}$$

(5)

then $\mathbb {E}[Y] = \mathbb {P}\big (r(M(\varvec{A}_{v,F})) = r(v)\big )$ is the value we are interested in. Hence, to compute its estimate, we draw N independent samples of Y denoted $Y_1, \dots , Y_N$, and compute its average

$$\begin{aligned} \bar{Y}_N = \frac{1}{N}\sum _{k=1}^{N} Y_k. \end{aligned}$$

(6)

The strong law of large numbers implies that $\mathbb {P}(\lim \nolimits _{N \rightarrow \infty } \bar{Y}_N = \mathbb {E}[Y]) = 1$, i.e., $\bar{Y}_N$ converges almost surely to $\mathbb {P}\big (r(M(\varvec{A}_{v,F})) = r(v)\big )$ with respect to probability $\mathbb {P}$.

If $H = \mathbb {R}$, F is a CDF defined on H, and $X \sim F$, then $\mathbb {E}[X] = \int _{x \in H} x dF(x)$, where $\int \nolimits _{-\infty }^{\infty } h(x) dF(x)$ generally denotes the Lebesgue-Stieltjes integral of h with respect to F, a real-valued, right-continuous, non-decreasing function $F :\mathbb {R}\rightarrow \mathbb {R}$ (which defines a Borel measure), and a measurable function $h :\mathbb {R}\rightarrow \mathbb {R}$ with respect to this measure. By using the law of total expectation, we can rewrite (4) to

$$\begin{aligned}&\mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v,F})) = r(v)}] \\&\quad =~\mathbb {E}[\mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v,F})) = r(v)} \mid X_{12}, X_{13}, \dots , X_{n-1,n}]] \\&\quad =~\int \limits _{x_{12} \in H}\dots \int \limits _{x_{n-1,n} \in H} \mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v,\varvec{X}})) = r(v)} \mid X_{12} = x_{12}, X_{13} = x_{13}, \\&\qquad \dots , X_{n-1,n} = x_{n-1,n}] dF(x_{12})dF(x_{13})\dots dF(x_{n-1,n}) \\&\quad =\int \limits _{x_{12} \in H}\dots \int \limits _{x_{n-1,n} \in H} \textbf{1}_{r(M(\varvec{A}_{v,\varvec{X}})) = r(v)} dF(x_{12})dF(x_{13})\dots dF(x_{n-1,n}), \end{aligned}$$

using that $\mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v,\varvec{X}})) = r(v)}] = \textbf{1}_{r(M(\varvec{A}_{v,\varvec{X}})) = r(v)}$ in the last equation, which follows from that $\textbf{1}_{r(M(\varvec{A}_{v,\varvec{X}}))}$ is not a random variable (recall that $\varvec{X} = (x_{ij})$ is a matrix of reals). Apart from showing that, e.g., numerical integration would be at least a challenging task even for low dimensions n, and thus advocating the MC approach, this expression directly leads to an MC algorithm for computing estimates of v-robustness:

• 1. Generate a realization $x_{ij}$ of $X_{ij} \sim F$ for all $i < j$;

• 2. Compute $\varvec{A}_{v,\varvec{X}}$;

• 3. Return $y = \textbf{1}_{r(M(\varvec{A}_{v,\varvec{X}})) = r(v)}$,

which returns a realization y of Y.

2.4 Expected value of perturbations, reciprocity, and the additive alo-group

When it comes to the choice of the expected value of perturbations, there are two distinct assumptions used in the literature. Both of them are formulated on the Multiplicative alo-group, which means that if $v_i/v_j$ is the priority of object i over object j, then $(v_i/v_j)X_{ij}$ is the perturbed priority of i over j. The first assumption, which takes the form $\mathbb {E}[X_{ij}] = 1$ (and thus $\log (\mathbb {E}[X_{ij}]) = 0$), is suggested in Saaty (1990, p. 158) where perturbation $X_{ij}$ is denoted by $\epsilon _{ij}$. The other one, suggested in Crawford and Williams (1985), takes the form $\mathbb {E}[\log (X_{ij})] = 0$. To advocate our choice out of these two, let us present the following ideas.

Consider a DM who perturbs the consistent priority $v_i/v_j$ by 2. For example, in 50% in favor of i over j (the DM provides the value $2v_i/v_j$), and in 50% in favor of j over i (the DM provides the value $2v_j/v_i$, meaning, due to reciprocity, priority of $1/2v_i/v_j$ of i over j). This implies the distribution of $X_{ij}$: $\mathbb {P}(X_{ij} = 2) = 1/2$ following from the former case, and, $\mathbb {P}(X_{ij} = 1/2) = 1/2$ following from the latter case. In our opinion, this kind of perturbations is semantically correct, and this is the way we understand them in the rest of this work.

However, note that $\mathbb {E}[X_{ij}] = 2 * 1/2 + 1/2 * 1/2 = 5/4 \ne 1$, which contradicts the assumption on perturbations suggested in Saaty (1990, p. 158). Under such an assumption, and assuming only two values of $X_{ij}$ with non-zero probability, the DM described above either reaches a value outside of $(0, \infty )$ (if $\mathbb {P}(X_{ij} = 2) = 1/2$ then it must be $\mathbb {P}(X_{ij} = 0) = 1/2$ or if $\mathbb {P}(X_{ij} = 1/2) = 1/2$ then it must $\mathbb {P}(X_{ij} = 3/2) = 1/2$, which violates the reciprocity of the perturbation.

In the light of these facts, we rather follow the assumption $\mathbb {E}[\log (X_{ij})] = 0$, which allows us to model the DM described above (observe that $\mathbb {E}[\log (X_{ij})] = \log (2) * 1/2 + \log (1/2) * 1/2 = \log (2) * 1/2 - \log (2) * 1/2 = 0$).

Using the isomorphism between the Multiplicative and Additive alo-groups, $\log (x)$, translating from the Multiplicative to the Additive one allows the latter assumption to take the most standard form, $\mathbb {E}[X_{ij}] = 0$. In order to follow this standard, from now on, all the reasoning is made in the Additive alo-group $\mathcal {R}_+$.

Under this choice, we mostly model F by the Normal distribution, which is defined on the support of $\mathcal {R}_+$. Of course, if one prefers the Multiplicative alo-group, the corresponding distribution would be the log-Normal distribution, defined on $(0, \infty )$, which is the support of $\mathcal {R}_*$. The latter is the way how perturbations are modelled in Crawford and Williams (1985).

Finally, as the condition $r(M(\varvec{A}_{v,F})) = r(v)$ is based purely on the ranks of $M(\varvec{A}_{v,F})$ and of v, it is important to note that the v-robustness R(v, F, M) is independent of the choice of the alo-group from the two aforementioned ones. The similar holds also for the robustness R(G, F, M).

2.5 Alternatives to robustness based on ranks

Of course, instead of R(v, F, M) or R(V, F, M), one could also choose another criterion for robustness, e.g., based on the Euclidean distance of $M(\varvec{A}_{v,F})$ and v. However, this distance is not invariant to the choice of the alo-group, so we base the robustness on the ranks as they provide more universal results. Moreover, in Sect. 3, we propose an efficient algorithm for one of the considered methods that is able to return just the ranks of $M(\varvec{A}_{v,F})$ in substantially lower run-time as compared to the case when we require directly the PV $M(\varvec{A}_{v,F})$. Consequently, by solely relying on rank-based evaluation, we have gained the ability to conduct a greater number of simulations within a specific timeframe. This leads to increased stability in our simulations.

2.6 Invariance of robustness

2.6.1 The v-robustness

Given a method M and a perturbations distribution F, a full picture about the v-robustness of M under F would be obtained after evaluating R(v, F, M) for all $v \in \mathbb {R}^n$. Clearly, this is neither feasible nor necessary, as is explained in the following.

First, assuming the Additive alo-group, let e be the vector $(1, 1,\dots ,1)$ consisting of n ones. Denote by $v+\delta e$ the PV $(v_1+\delta , \dots ,, v_n+\delta )$ for all $\delta \in \mathbb {R}$. Then, as $(v_i + \delta - (v_j + \delta )) = v_i - v_j$, and thus $\varvec{A}_{v+\delta e} = \varvec{A}_{v}$, if follows that $R(v+\delta e,F,M) = R(v,F,M)$. That is, the v-robustness is invariant to a “shift” of v. One can thus restrict the evaluation of v-robustness to an $n-1$ dimensional subspace of $\mathbb {R}^n$, e.g., containing only $v - v_n e$, thus PVs of size n with the n-th element fixed to 0.

Similarly, given $\sigma \in (0,\infty )$, under rescaling of both priorities and perturbations, i.e., $\sigma v$ and $\sigma \varvec{X}$ instead of v and $\varvec{X}$ are provided, one might expect the ranks produced by a method M to remain the same, formally

$$\begin{aligned} r(M(\varvec{A}_{\sigma v, \sigma \varvec{X}})) = r(M(\varvec{A}_{v,\varvec{X}})) \text {~~for all~~} \sigma \in (0, \infty ) \text {~~and~~} \varvec{A} \in \mathbb {R}^{n \times n}. \end{aligned}$$

(7)

Note that $\varvec{A}_{\sigma v, \sigma \varvec{X}} = \sigma \varvec{A}_{v,\varvec{X}}$ as $\sigma (v_i - v_j) + \sigma x_{ij} = \sigma (v_i - v_j + x_{ij})$. Also note that the condition (7) is a rank version of so-called scale invariance, see Petróczy and Csató (2021, Axiom 1) which already appeared in Genest et al. (1993).

When $x_{ij}$ is replaced by a RV $X_{ij}$, the concept of rescaling can be formalized by the following definition.

Definition 1

Let $F_\sigma$ be a CDF of a RV $X_\sigma$ parametrized by $\sigma \in (0, \infty )$ such that

$$\begin{aligned} F_\sigma (\sigma x) = F_1(x) \text {~~for all~~} \sigma \in (0, \infty ) \text {~~and~~} x \in \mathbb {R}. \end{aligned}$$

(8)

Then $F_\sigma$ is called $\sigma$-rescalable.

Note that if $F_\sigma$ is absolutely continuous with its probability density function (PDF) denoted $f_\sigma$, condition (8) can equivalently be stated as

$$\begin{aligned} f_\sigma (\sigma x) = \frac{1}{\sigma }f_1(x) \text {~~for all~~} \sigma \in (0, \infty ) \text {~~and~~} x \in \mathbb {R}. \end{aligned}$$

The meaning of the $\sigma$-rescalability is explained by the following lemma.

Lemma 1

Given $X_\sigma \sim F_\sigma$, where $F_\sigma$ is $\sigma$-rescalable, then $X_\sigma$ and $\sigma X_1$ are identical in the distribution, i.e., $\mathbb {P}(X_\sigma \le x) = \mathbb {P}(\sigma X_1 \le x)$ for all $x \in \mathbb {R}$.

Proof

Observe that $\mathbb {P}(X_\sigma \le x) = F_\sigma (x) = F_1(x/\sigma ) = \mathbb {P}(X_1 \le x/\sigma ) = \mathbb {P}(\sigma X_1 \le x)$. $\square$

Hence, having $X_{ij} \sim F_\sigma$, where $F_\sigma$ is $\sigma$-rescalable, the distribution of the RV $\sigma v_i - \sigma v_j + X_{ij}^\sigma$ is identical to the distribution of the RV $\sigma v_i - \sigma v_j + \sigma X_{ij}^1 = \sigma (v_i - v_j + X_{ij}^1$). This implies that the corresponding elements of $\varvec{A}_{\sigma v, F_\sigma }$ and of $\sigma \varvec{A}_{v, F_1}$ are identical in the distribution. Such an observation leads to the following theorem.

Theorem 2

Let M be a method in the sense of (1) satisfying (7), and let $F_\sigma$ be $\sigma$-rescalable. Then

$$\begin{aligned} R(\sigma v,F_\sigma ,M) = R(v,F_1,M). \end{aligned}$$

(9)

Proof

Let the i, j-th perturbation distributed according to $F_\sigma$ be denoted $X_{ij}^\sigma$, and the i, j-th perturbation distributed according to $F_1$, i.e., if $\sigma = 1$, be denoted $X_{ij}$. Hence, $\sigma (v_i - v_j) + X_{ij}^\sigma$ is the i, j-th element of $\varvec{A}_{\sigma v,F_\sigma }$. Then

$$\begin{aligned}&R(\sigma v,F_\sigma ,M) = \mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{\sigma v,F_\sigma })) = r(\sigma v)}] = \mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{\sigma v,F_\sigma })) = r(v)}] \\&\quad =~\mathbb {E}[\mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{\sigma v,F_\sigma })) = r(v)} \mid X_{12}^\sigma , \dots , X_{n-1,n}^\sigma ]] \\&\quad =~\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \textbf{1}_{r(M(\varvec{A}_{\sigma ,\varvec{X}_\sigma })) = r(v)} dF_\sigma (x_{12}^\sigma )\dots dF_\sigma (x_{n-1,n}^\sigma ), \end{aligned}$$

where $\varvec{X}_\sigma = (x_{ij}^\sigma ) \in \mathbb {R}^{n \times n}$. Substituting $x_{ij}^\sigma$ by $\sigma x_{ij}$ and using (8), we obtain

$$\begin{aligned}&\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \textbf{1}_{r(M(\varvec{A}_{\sigma v,\varvec{X}_\sigma })) = r(v)} dF_\sigma (x_{12}^\sigma )\dots dF_\sigma (x_{n-1,n}^\sigma ) \\&\quad =~ \int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \textbf{1}_{r(M(\varvec{A}_{\sigma v,\sigma \varvec{X}})) = r(v)} dF_\sigma (\sigma x_{12})\dots dF_\sigma (\sigma x_{n-1,n}) \\&\quad =~ \int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \textbf{1}_{r(M(\varvec{A}_{\sigma v,\sigma \varvec{X}})) = r(v)} dF_1(x_{12}) \dots dF_1(x_{n-1,n}). \end{aligned}$$

Finally, by using (7), it follows that

$$\begin{aligned}&\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \textbf{1}_{r(M(\varvec{A}_{\sigma v,\sigma \varvec{X}})) = r(v)} dF_1(x_{12}) \dots dF_1(x_{n-1,n}) \\&\quad =~ \int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \textbf{1}_{r(M(\varvec{A}_{v,\varvec{X}})) = r(v)} dF_1(x_{12}) \dots dF_1(x_{n-1,n}) \\&\quad =~\mathbb {E}[\mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v,F_1})) = r(v)} \mid X_{12}, \dots , X_{n-1,n}]] = \mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v,F_1})) = r(v)}] \\&\quad =~ R(v,F_1,M). \end{aligned}$$

$\square$

An example a $\sigma$-rescalable CDF is the zero mean Normal distribution denoted by $\mathcal {N}(0,\sigma ^2)$, as, denoting its PDF by $f_\sigma$, one has

$$\begin{aligned} f_\sigma (\sigma x) = \frac{1}{\sqrt{2\pi \sigma ^2}}\exp \biggl (-\frac{(\sigma x)^2}{2\sigma ^2}\biggr ) = \frac{1}{\sigma }f_1(x). \end{aligned}$$

(10)

Also, if $f_\sigma$ is the PDF of the uniform distribution with the parameters $a =0$ and $b = \sigma$, denoted by $\mathcal {U}[0,\sigma ]$, then

$$\begin{aligned} f_\sigma (\sigma x) = \frac{1}{\sigma } = \frac{1}{\sigma }f_1(x) \end{aligned}$$

(11)

for all $x \in (0, 1)$ and $f_\sigma (\sigma x) = 0 = \frac{1}{\sigma }f_1(x)$ for all $x \in \mathbb {R}{\setminus } (0, 1)$.

Theorem 2 can reduce the evaluation of the v-robustness by another dimension. Clearly, as $R(\sigma v,F_\sigma ,M) = R(v,F_1,M)$, it does not have sense to compute both quantities. Rather, one can fix, e.g., another dimension of v, say $v_1$ to 1, and then evaluates $R((v-v_n)/v_1,F_\sigma ,M)$. Note that in the case that $v_1$ is zero, one can fix $v_2$ to 1 (or $v_3$, if $v_2$ is also zero, etc.). If $v_1 = \dots = v_n = 0$, then we are facing a rare scenario where all priorities are equal, which we do not further consider.

For example, if $n = 3$, a full picture of v-robustness under $F_\sigma$ is obtained after evaluation of $(1, v_2, 0)$-robustness for $v_2 \in (0, 1)$. This design is used in the MC study presented in Sect. 5.1.

2.6.2 The robustness

In order to obtain an analogue of Theorem 2 also for the robustness $R(G, F_\sigma , M)$, we assume the random variables $V_1, \dots , V_n$ to be independent and distributed according to some $\sigma$-rescalable CDF $G_\sigma$. This implies that $G(x_1, \dots , x_n) = G_\sigma (x_1)G_\sigma (x_2) \dots G_\sigma (x_n)$ for all $x_1, \dots , x_n \in \mathbb {R}$, i.e., the copula of G is the independence copula. As G is thus fully determined by $G_\sigma$, we denote the robustness R(G, F, M) by $R(G_\sigma , F, M)$, where $G_\sigma$ is thus an univariate CDF.

Theorem 3

Let $V_\sigma = (V_1^\sigma , \dots , V_n^\sigma )$ with independent and identically distributed random variables $V_i^\sigma \sim G_\sigma ,~ i \in \breve{n}$, where $G_\sigma$ is a $\sigma$-rescalable CDF defined on $\mathbb {R}$. If $F_\sigma$ is $\sigma$-rescalable, then

$$\begin{aligned} R(G_\sigma , F_\sigma , M) = R(G_1, F_1, M). \end{aligned}$$

(12)

Proof

$$\begin{aligned}&R(G_\sigma ,F_\sigma ,M) = \mathbb {P}(r(M(\varvec{A}_{V_\sigma ,F_\sigma })) = r(V_\sigma )) = \mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{V_\sigma ,F_\sigma })) = r(V_\sigma )}] \\&\quad =~\mathbb {E}[\mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{V_\sigma ,F_\sigma })) = r(V_\sigma )} \mid V_1^\sigma , \dots , V_n^\sigma ]] \\&\quad =~\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v_\sigma ,F_\sigma })) = r(v_\sigma )} \mid V_1^\sigma = v_1^\sigma , \dots , V_n^\sigma = v_n^\sigma ] dG_\sigma (v_1^\sigma )\dots dG_\sigma (v_n^\sigma ) \\&\quad =~\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \mathbb {E}[R(v_\sigma , F_\sigma , M)] dG_\sigma (v_1^\sigma )\dots dG_\sigma (v_n^\sigma ). \end{aligned}$$

Using similar arguments as in the proof of Theorem 2, one has

$$\begin{aligned}&\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \mathbb {E}[R(v_\sigma , F_\sigma , M)] dG_\sigma (v_1^\sigma )\dots dG_\sigma (v_n^\sigma ) \\&\quad =~\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \mathbb {E}[R(\sigma v, F_\sigma , M) ] dG_1(v_1) \dots dG_1(v_n)\\&\quad =~\int \limits _{-\infty }^{\infty }\dots \int \limits _{-\infty }^{\infty } \mathbb {E}[R(v, F_1, M)] dG_1(v_1) \dots dG_1(v_n) \\&\quad =~\mathbb {E}[\mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{V_1,F_1})) = r(V_1)} \mid V_1, \dots , V_n]] = R(G_1,F_1,M). \end{aligned}$$

$\square$

Theorem 3 explicitly shows how the distributions $G_\sigma$ and $F_\sigma$ underlying the unknown v and the perturbations, respectively, are interconnected when the robustness is evaluated. Hence, once we compute $R(G_1,F_1,M)$, e.g., by using the MC approach, it is no longer necessary to compute $R(G_\sigma ,F_\sigma ,M)$ for other values of $\sigma \in (0, \infty )$. Rather, to compute some further reasonable values of the robustness, we can fix the scale of either $G_\sigma$ or $F_\sigma$, and then compute the robustness with the scale varying in just one of these two distributions. For example, we can fix $G_\sigma$ to $G_1$, and then evaluate $R(G_1,F_\sigma ,M)$ for $\sigma \in (0, \infty )$. This is the way we design the MC experiments in Sect. 5.2.

3 Methods

This section recalls two frequently used methods for calculating a PV from a PCM, namely the Geometric Mean Method (GMM) (Rabinowitz, 1976; Crawford & Williams, 1985), and the Eigenvalue Method (EVM) (Saaty, 1977, 1987, 1990), as well as one method recently introduced in Bartl and Ramík (2022) based on the coherence of PCMs, a concept introduced in Cavallo et al. (2014). The latter method is denoted COH.

As the first two methods are introduced in the Multiplicative alo-group, given a PCM in $\varvec{A} \in \mathbb {R}^{n \times n}$ in the Additive alo-group, we first use the isomorphism between the alo-groups, and define $\varvec{A}^* = (a_{ij}^*)$, where $a_{ij}^* = \exp (a_{ij})$. Then, the method is presented as usual on the Multiplicative alo-group, and finally the output is transformed back to the the Additive alo-group, i.e., $M(\varvec{A}) = \log (M(\varvec{A}^*)) = \log (M(\exp (\varvec{A})))$, where $\log$ and $\exp$ are applied element-wise.

3.1 Geometric mean method

Given $\varvec{A} \in \mathbb {R}^{n \times n}$, the mapping $M_{\mathrm{{GMM}}}$ representing the GMM method in the sense of (1) is given by $M_{\mathrm{{GMM}}}(\varvec{A}) = \bar{v}$, where $\bar{v}= (\bar{v}_1,\dots ,\bar{v}_n)$ and

$$\begin{aligned} \bar{v}_i = \log \biggl (\prod _{j=1}^{n} (a_{ij}^*)^{\frac{1}{n}}\biggr ) = \log \biggl (\prod _{j=1}^{n} \exp (a_{ij})^{\frac{1}{n}}\biggr ) = \frac{1}{n}\sum _{j=1}^{n} a_{ij} \end{aligned}$$

(13)

for all $i \in \breve{n}$. Clearly, $M_{\mathrm{{GMM}}}(\varvec{A}_v) = \frac{1}{n}\sum _{j=1}^{n} v_i - v_j = v_i - \frac{1}{n}\sum _{j=1}^{n} v_j$. If v is normalized, i.e, $\sum _{i=1}^{n} v_i = 0$, then $\bar{v}_i = v_i$, and thus

$$\begin{aligned} M_{\mathrm{{GMM}}}(\varvec{A}_v) = v. \end{aligned}$$

(14)

for any normalized v.

3.2 Eigenvalue method

In Saaty (1987), the Eigenvalue Method (EVM) is introduced as a solution to the eigenvalue problem $\varvec{A}^*v^* = \lambda _{\max } v^*$ given by

$$\begin{aligned} v = \log (v^*) = \log \biggl (\lim \limits _{k \rightarrow \infty } \frac{(\varvec{A}^*)^k e^\text {T}}{e (\varvec{A}^*)^k e^\text {T}}\biggr ) = \log \biggl (\lim \limits _{k \rightarrow \infty } \frac{(\exp (\varvec{A}))^k e^\text {T}}{e (\exp (\varvec{A}))^k e^\text {T}}\biggr ), \end{aligned}$$

(15)

where $e = (1, 1, \dots , 1)$. Note that for $n = 3$, the solution of EVM coincides with the solution of GMM (Crawford & Williams, 1985).

3.3 Coherence method

The COH method is based on the idea that a PV v calculated from a PCM $\varvec{A}$ is reliable only if v is a coherent PV of $\varvec{A}$, i.e., if $a_{ij} > 0$ implies $v_i > v_j$ for all $i,j \in \breve{n}$. In Bartl and Ramík (2022), an algorithm for calculating such PVs is presented for the so-called fuzzy PCMs, which are PCMs with elements $a_{ij}$ being fuzzy numbers. Here, we restrict ourselves to the crisp case, where $a_{ij} \in \mathbb {R}$, i.e., $\varvec{A} \in \mathbb {R}^{n \times n}$. It is important to note that the algorithm proposed in Bartl and Ramík (2022) outputs a PV only in the cases when the PCM is coherent. Hence, to reflect this fact, we below compare the robustness of the considered methods only for coherent PCMs.

Bartl and Ramík (2022) present the COH method in the form of an optimization problem, see Problem 5 and 6 therein. However, if one is interested only in the ranks of v, as we do in this work, there exists a simpler and faster algorithm that computes these ranks directly, thus avoiding the time demanding computation of v. This algorithm is based on the following theorem.

Theorem 4

Let $\varvec{A} = (a_{ij}) \in \mathbb {R}^{n \times n}$ be an additively reciprocal PCM (i.e., $a_{ij} = -a_{ji}$) and such that $a_{ij} \ne 0$ if $i \ne j$ for $i,j \in \breve{n}$. Then $\varvec{A}$ is coherent, if and only if $\{\tilde{r}_1, \dots , \tilde{r}_n\} = \breve{n}$, where

$$\begin{aligned} \tilde{r}_i = 1 + \sum _{j=1}^{n} \textbf{1}_{a_{ij} > 0}. \end{aligned}$$

(16)

Moreover, if $\varvec{A}$ is coherent, any priority vector $\tilde{v}= (\tilde{v}_1, \dots , \tilde{v}_n)$ with $r(\tilde{v}) = (\tilde{r}_1, \dots , \tilde{r}_n)$ is a PV coherent with $\varvec{A}$.

To have consistent notation in the sense of (1) also for COH, $M_{\mathrm{{COH}}}$ is implicitly defined via $r(M_{\mathrm{{COH}}}(\varvec{A})) = \tilde{r}$, avoiding exact specification of $M_{\mathrm{{COH}}}$, which is not necessary here.

Proof of Theorem 4

(the “only if” part): Let $\varvec{A}$ be coherent and w.l.o.g. let $v_1> v_2> \dots > v_n$ be the elements of v that is a PV coherent with $\varvec{A}$. This implies that $a_{ij} > 0$ for $i<j,~i,j\in \breve{n}$, and $a_{ij} \le 0$ otherwise. Thus the first row of $\varvec{A}$ contains $n-1$ positive values, meaning that $\tilde{r}_1 = 1 + n - 1$. Similarly, there are $n-2$ positive values in the second row, implying $\tilde{r}_2 = 1 + n - 2$, etc., until the last row, where $\tilde{r}_n = 1 + n - n = 1$. Hence, $\tilde{r}_i = n - i + 1$ for $i \in \breve{n}$, which establishes this part of the proof.

(the “if” part): Let $\varvec{A}$ be a reciprocal PCM and let $\{\tilde{r}_1, \dots , \tilde{r}_n\} = \breve{n}$. Without loss of generality, we can assume that

$$\begin{aligned} \tilde{r}_i = n - i + 1 \end{aligned}$$

(17)

for $i \in \breve{n}$. Now, let $\tilde{v}= (\tilde{v}_1, \dots , \tilde{v}_n)$ be a PV such that $r(\tilde{v}) = (\tilde{r}_1, \dots , \tilde{r}_n)$, e.g., let $\tilde{v}_i = \tilde{r}_i$ for $i \in \breve{n}$. For $i = 1$, (17) implies that $a_{12}> 0,~a_{13}> 0, \dots , a_{1n} > 0$, as well as $a_{21}< 0,~a_{31}< 0, \dots , a_{n1} < 0$. Observe that $n = \tilde{v}_1 > \tilde{v}_j = n - j + 1$ for $j \in \{2,\dots ,n\}$. Hence, the condition for $\tilde{v}$ to be a PV coherent with $\varvec{A}$, i.e., $a_{ij} > 0$ implies $\tilde{v}_i > \tilde{v}_j$, is satisfied for $i = 1$.

For $i=2$, as we know that $a_{21} < 0$, (17) implies that $a_{23}> 0,~a_{24}> 0, \dots , a_{2n} > 0$, as well as $a_{32}< 0,~a_{42}< 0, \dots , a_{n2} < 0$. We thus observe that $n-1 = \tilde{v}_2 > \tilde{v}_j = n - j + 1$ for $j \in \{3,\dots ,n\}$, which, similarly to the previous step, implies that the condition for $\tilde{v}$ to be a PV coherent with $\varvec{A}$ is satisfied for $i = 2$. Analogously, we continue until $i = n - 1$, where (17) implies that $a_{n-1,n} > 0$, and this part of the proof is established by observing that $2 = \tilde{v}_{n-1} > \tilde{v}_n = 1$. $\square$

In Bartl and Ramík (2022), the authors consider three desirable properties of PVs (PCMs), see Equations (6), (7) and (8) therein for consistency, intensity and coherence, respectively. The authors show that the sets of PVs with these properties can be ordered as follows: Consistent PVs are included among intensity PVs which are then included among coherent PVs. Here, we consider only the crisp case, which is a special case of their fuzzy approach. As we add perturbations to a consistent PCM $\varvec{A}_v$, the probability of the event that $\varvec{A}_{v,F}$ is a consistent PCM is equal to 0 for any continuous CDF F. We thus do not measure robustness for consistent $\varvec{A}_{v,F}$. Further, given an intensity PCM, the authors show that any PV that is an intensity PV of this PCM is also a PV that is coherent with this PCM. As follows from Theorem 4, the coherence induces a particular rank ordering, so, as the intensity is a special case of the coherence, this holds also for intensity PVs. In other words, an intensity PV, if it exists, has the same rank ordering as any PV that is coherent with the same PCM. Hence, as we here consider only the ranks of PVs, we consider only coherence, for which we have an efficient algorithm represented by (16).

3.4 Example

As an example illustrating all these three aforementioned methods, let us consider the following PCM:

$$\begin{aligned} \varvec{A} =\left( \begin{array}{cccc} 0 &{} 1/10 &{} 2 &{} 1/10 \\ -1/10 &{} 0 &{} 1 &{} 2 \\ -2 &{} - 1 &{} 0 &{} 4 \\ -1/10 &{} - 2 &{} - 4 &{} 0 \\ \end{array}\right) \end{aligned}$$

Then,

$$\begin{aligned} M_{\mathrm{{GMM}}}(\varvec{A}) = (&0.0 + 0.1 + 2.0 + 0.1, -0.1 + 0.0 + 1.0 + 2.0, \\ -&2.0-1.0 + 0.0 + 4.0, -0.1-2.0-4.0+0.0) / 4 \\ = (&2.2, 2.9, 1.0 , -6.1) / 4 = (0.550, 0.725, 0.250, -1.525) \end{aligned}$$

and thus

$$\begin{aligned} r(M_{\mathrm{{GMM}}}(\varvec{A})) = r(0.550, 0.725, 0.250, -1.525) = (3, 4, 2, 1). \end{aligned}$$

Further, $\lambda _{\max }$ for $\exp (\varvec{A})$ is 8.773 and the corresponding eigenvector is (0.67, 0.38, 0.63, 0.08), so

$$\begin{aligned} r(M_{\mathrm{{EVM}}}(\varvec{A})) = r(\log (0.67, 0.38, 0.63, 0.08)) = (4, 2, 3, 1). \end{aligned}$$

Finally, by using Theorem 4,

$$\begin{aligned} r(M_{\mathrm{{COH}}}(\varvec{A})) = (4, 3, 2, 1). \end{aligned}$$

Hence, we obtained three distinct rank orderings for the same PCM.

4 Analytical approach

In this section, we first provide an analytical form of the v-robustness for COH. Then, we explain reasons why a numerical approach to evaluation of the v-robustness of GMM is necessary. As EVM involves solving an eigenvalue problem, an analytical approach to the v-robustness is at least challenging and remains an open problem here.

4.1 The v-robustness of COH

Let $\hat{\tilde{r}} = (\hat{\tilde{r}}_1, \dots , \hat{\tilde{r}}_n) = r(M_{\mathrm{{COH}}}(\varvec{A}_{v,F}))$ be the output of the COH method for a coherent $\varvec{A}_{v,F}$. Then

$$\begin{aligned} \hat{\tilde{r}}_i - 1 = \sum _{j=1}^{n} \textbf{1}_{v_i - v_j + X_{ij} > 0} \end{aligned}$$

(18)

for $i \in \breve{n}$. Now, we shall calculate the value of $R(v, F, M_{\mathrm{{COH}}})$.

Without loss of generality, assume that $\hat{\tilde{r}}_1> \dots > \hat{\tilde{r}}_n$. For simplicity, start with $n=3$, i.e., let $v = (v_1, v_2, v_3)$ and $r(v) = (3, 2, 1)$ and hence $v_1 - v_2> 0, v_1 - v_3 > 0$ and $v_2 - v_3 > 0$. Thus

$$\begin{aligned} R(v, F, M_{\mathrm{{COH}}}) = \mathbb {P}(\hat{\tilde{r}}_1 = 3, \hat{\tilde{r}}_2 = 2, \hat{\tilde{r}}_3 = 1) = \\ \mathbb {P}(v_1 - v_2 + X_{12}> 0, v_1 - v_3 + X_{13}> 0, v_2 - v_3 + X_{23} > 0). \end{aligned}$$

Importantly, the RVs $X_{12}, X_{13}$ and $X_{23}$ are independent, implying that

$$\begin{aligned}&\mathbb {P}(v_1 - v_2 + X_{12}> 0, v_1 - v_3 + X_{13}> 0, v_2 - v_3 + X_{23}> 0) = \\&\mathbb {P}(v_1 - v_2 + X_{12}> 0) \mathbb {P}(v_1 - v_3 + X_{13}> 0) \mathbb {P}(v_2 - v_3 + X_{23}> 0) = \\&\mathbb {P}(X_{12}> v_2 - v_1) \mathbb {P}(X_{13}> v_3 - v_1) \mathbb {P}(X_{23} > v_3 - v_2) = \\&(1 - F(v_2 - v_1)) (1 - F(v_3 - v_1)) (1 - F(v_3 - v_2)). \end{aligned}$$

It follows that the value of $R(v, F, M_{\mathrm{{COH}}})$ is directly accessible for anyone who is able to evaluate F. Also note that generalization to $n > 3$ is straightforward. If $v_1> v_2> \dots > v_n$, then

$$\begin{aligned} R(v, F, M_{\mathrm{{COH}}}) = \prod _{{\mathop {i < j}\limits ^{i, j \in \breve{n}}}} (1 - F(v_j - v_i)). \end{aligned}$$

(19)

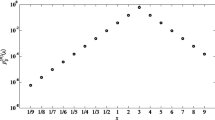
For illustration, the $R(v, \mathcal {N}(0, (1/2)^2), M_{\mathrm{{COH}}})$ for all v such that $v = (1, v_2, 0)$ and $v_2 \in (0, 1)$ is shown as the black solid line in Fig. 1.

Fig. 1

The black line shows the robustness $R(v, \mathcal {N}(0, 1/2^2), M_{\mathrm{{COH}}})$ computed using (19) at $v = (1, v_2, 0)$, where $v_2 \in (0, 1)$. The circles are MC estimates for $N \in \{100, 1000, 10{,}000\}$ evaluated at 21 points

As expected, the largest value of the $(1, v_2, 0)$-robustness is at $v_2 = 0.5$, where the probability that the perturbations cause rank reversal is the lowest.

The same figure also shows estimates of $R(v, \mathcal {N}(0, 1/2^2), M_{\mathrm{{COH}}})$ computed via the MC approach for $N \in \{100, 1000, 10{,}000\}$, see (6). It can be observed that for $N = 10{,}000$, the estimated values are relatively close to the true values.

4.2 The v-robustness of GMM

Let v be a normalized PV, that is, $\sum _{i=1}^{n}v_i = 0$. Also, let $\hat{\bar{v}} = (\hat{\bar{v}}_1, \dots , \hat{\bar{v}}_n) = M_{\mathrm{{GMM}}}(\varvec{A}_{v,F})$ be the output of GMM for $\varvec{A}_{v,F}$. Then the elements of $\hat{\bar{v}}$ can be written as

$$\begin{aligned} \hat{\bar{v}}_i =&\frac{1}{n}\sum _{j=1}^{n} (v_i - v_j + X_{ij}) = \frac{1}{n}(nv_i) - \frac{1}{n}\sum _{j=1}^{n}v_j + \frac{1}{n}\sum _{j=1}^{n} X_{ij} \\ =&v_i + \frac{1}{n}\sum _{j=1}^{n} X_{ij} = v_i + \frac{X_i}{n}, \end{aligned}$$

where $X_i = \sum _{j=1}^{n} X_{ij}$. The definition of $\varvec{A}_{v,F}$ implies that $X_i = \sum _{j=1}^{i-1} -X_{ji}$ + 0 + $\sum _{j=i+1}^{n} X_{ij}$.

Now, assume that $X_{ij}$ is distributed according to a Normal distribution with a zero mean and a standard deviation equal to $\sigma$, i.e., $X_{ij} \sim \mathcal {N}(0, \sigma ^2)$. Considering that if $Y \sim \mathcal {N}(0, \sigma ^2)$, then $-Y \sim \mathcal {N}(0, \sigma ^2)$, $X_i$ can be expressed as a sum of $n-1$ independent RVs, each distributed according to $\mathcal {N}(0, \sigma ^2)$. Hence, $X_i \sim \mathcal {N}(0, (n-1)\sigma ^2)$. Without loss of generality, assume that $v_1> v_2> \dots > v_n$. The v-robustness, $R(v,\mathcal {N}(0, \sigma ^2),M_{\mathrm{{GMM}}})$, is then the probability of the event that $v_{i-1} + X_{i-1}/n > v_i + X_i/n$ and $v_i + X_i/n > v_{i+1} + X_{i+1}/n$ for all $i \in \{2, \dots , n-1\}$. These inequalities can be written using the reciprocity of $\varvec{A}_{v,F}$ as

$$\begin{aligned}&~nv_1 + 0 + X_{12} + X_{13} + \dots + X_{1n}> \\>&~nv_2 - X_{12} + 0 + X_{23} + X_{24} + \dots + X_{2n}> \\>&~nv_3 - X_{13} - X_{23} + 0 + X_{34} + X_{35} + \dots + X_{3n}> \\>&~\dots>\\ >&~nv_n - X_{1n} - X_{2n} - X_{3n} - \dots - X_{n-1,n} + 0. \end{aligned}$$

These can be further rewritten as

$$\begin{aligned}&-2X_{12} + (X_{23} - X_{13}) + (X_{24} - X_{14}) + \dots + (X_{2n} - X_{1n})&< n(v_1 - v_2)\\&-2X_{23} - (X_{13} - X_{12}) + (X_{34} - X_{24}) + \dots + (X_{3n} - X_{2n})&< n(v_2 - v_3)\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \vdots \\&-2X_{n-1, n} - (X_{1n} - X_{1,n-1}) - \dots - (X_{n-2,n} - X_{n-2,n-1})&< n(v_{n-1} - v_n).\\ \end{aligned}$$

This results in a system of $n-1$ inequalities with $n(n-1)/2$ RVs, $X_{ij},~ i < j$. As $X_{ij}$s are independent and identically distributed according to $\mathcal {N}(0,\sigma ^2)$, the random vector containing all these RVs is distributed according to the multivariate Normal distribution, $\mathcal {N}(\varvec{0}, \sigma ^2\varvec{I})$, where $\varvec{0}$ is the zero vector of length n and $\varvec{I}$ denotes the identity matrix of order n. Hence, to obtain the probability that this random vector satisfies the system of the derived inequalities – i.e., to obtain the v-robustness of GMM – we need to integrate the density of $\mathcal {N}(\varvec{0}, \sigma ^2\varvec{I})$ over the set of the solutions to that system of inequalities. For larger dimensions, this task can be challenging, so we approach it via MC simulations.

5 Numerical approach

This section presents an MC simulation study, in which the (v-)robustness of GMM, EVM, and COH is evaluated. First, the v-robustness is assessed for $n=3$ to gain insights for particular values of $v \in \mathbb {R}^3$ (Sect. 5.1). Then, an aggregated perspective, represented by the robustness R(G, F, M), is presented for $n \ge 3$ (Sects. 5.2 and 5.3). Finally, to gain further insights into the impact of perturbations on robustness, we provide an additional simulation study exploring their connection to the inconsistency of the corresponding randomly perturbed reciprocal PCM (Sect. 5.4).

According to Bartl and Ramík (2022), when a PCM is not coherent, COH does not generate any output. Hence, to get an objective comparison of GMM and EVM with COH, we restrict to cases when all methods generate an output. Denoting the set of all reciprocal coherent matrices on $\mathbb {R}^{n \times n}$ by $\mathcal {A}_c$, we thus, instead of R(v, F, M) and R(G, F, M), evaluate the conditional probabilities

$$\begin{aligned} R_c(v, F, M) = \mathbb {P}\big (r(M(\varvec{A}_{v,F})) = r(v) \mid \varvec{A}_{v,F} \in \mathcal {A}_c\big ) \end{aligned}$$

and

$$\begin{aligned} R_c(G, F, M) = \mathbb {P}\big (r(M(\varvec{A}_{V,F})) = r(V) \mid \varvec{A}_{V,F} \in \mathcal {A}_c\big ). \end{aligned}$$

5.1 The v-robustness

The simulation is conducted as follows. Given a PV $v \in \mathbb {R}^n$, for each $k \in \{1, \dots , N\}$, where $N = 10{,}000$, perform the following algorithm:

• 1. Generate a realization $x_{ij}$ of $X_{ij} \sim F$ for all $i < j$;

• 2. Compute $\varvec{A}_{v,\varvec{X}}$. If $\varvec{A}_{v,\varvec{X}} \notin \mathcal {A}_c$, return to Step 1;

• 3. Compute $y_{k,m} = \textbf{1}_{r(M_m(\varvec{A}_{v,\varvec{X}})) = r(v)}$ for $m \in \{\textrm{GMM}, \textrm{EVM}, \textrm{COH}\}$.

Let $Y_c = \mathbb {E}[\textbf{1}_{r(M(\varvec{A}_{v,F})) = r(v)} \mid \varvec{A}_{v,F} \in \mathcal {A}_c]$, $Y^c_{1}, \dots , Y^c_{N}$ be independent copies of $Y_c$ and $\hat{R}_c(v, F, M_m) = \frac{1}{N}\sum _{i=1}^{N}Y^c_i$. Then, $\frac{1}{N}\sum _{k=1}^{N}y_{k,m}$ is a realization of the robustness estimator $\hat{R}_c(v, F, M_m)$ of $R_c(v, F, M_m)$. Note that $N = 10{,}000$ was set according to the results presented in Fig. 1.

5.1.1 Zero mean perturbations

This section presents results computed under the assumption of $\mathbb {E}[X_{ij}] = 0$. First, F is modeled using the Normal distribution $\mathcal {N}(0, \sigma ^2)$ with $\sigma \in \{1/2, 1, 2\}$. To get also insights into the v-robustness under some level of skewness of F, we also model F with the Skewed Normal distribution $\mathcal{S}\mathcal{N}(a, \mu , \sigma ^2)$ (Azzalini & Capitanio, 1999), with the skewness parameter $a \in \{-5, 0, 5\}$, the deviation parameter $\sigma \in \{1/2, 1, 2\}$ and the location parameter $\mu$ adjusted in the way that F has zero mean. Note that if $a = 0$, this implies that $\mathcal{S}\mathcal{N}(a, \mu , \sigma ^2) = \mathcal {N}(0, \sigma ^2)$. We thus consider different parametrizations of $\mathcal{S}\mathcal{N}(a, \mu , \sigma ^2)$.

Using the shift and rescaling invariance of the v-robustness described in Sect. 2.6, it is enough, for $n = 3$, to evaluate the $(v_1, v_2, v_3)$-robustness for $v_1 = 1$, $v_3 = 0$ and $v_2 \in (v_3, v_1)$. This also allows one to represent it as a real function on [0, 1]. Realizations of $\hat{R}_c((1, v_2, 0), \mathcal{S}\mathcal{N}(a, \mu , \sigma ^2), M_m)$ for $v_2 \in$¹(0, 1) and the method $m \in \{\textrm{GMM}, \textrm{EVM}, \textrm{COH}\}$ are depicted in the first row of panels in Fig. 2. Note that as GMM and EVM coincide for $n = 3$, their results are denoted by “GMM (EVM)”.

Fig. 2

The first row of the panels shows realizations of $\hat{R}_c((1, v_2, 0), \mathcal{S}\mathcal{N}(a, \mu , \sigma ^2), M_m)$ for $m \in \{\textrm{GMM}, \textrm{EVM}, \textrm{COH}\}$ and $n = 3$. The second row of the panels shows realizations of an estimator $\mathbb {P}(\varvec{A}_{v,F} \in \mathcal {A}_c)$. The third row of the panels shows PDFs of $\mathcal{S}\mathcal{N}(a, \mu , \sigma ^2)$

We can observe that the values for GMM and EVM, which are by definition identical for $n = 3$, are larger than for COH in almost all cases. Exceptions are for $a = -5$, $\sigma = 1$ and roughly for $v_2 \in (0, 0.1) \cup (0.9, 1)$. So, for skewed perturbations, COH can reach the v-robustness larger than GMM (EVM). However, in average, GMM (EVM) dominate COH in v-robustness. As expected, the v-robustness decreases as $\sigma$ increases, as larger perturbations are more likely to cause rank reversal. Also note that v-robustness is sensitive to the “side” of the skewness of F, i.e., $a = -5$ vs $a = 5$, which can be observed particularly for $\sigma = 1/2$ and COH.

The second row of panels in Fig. 2 depicts realizations of an MC estimator of $\mathbb {P}(\varvec{A}_{v,F} \in \mathcal {A}_c)$ based on $Y = \textbf{1}_{\varvec{A_{v,F}} \in \mathcal {A}_c}$ in the sense of the previous estimators. Interestingly, a coherent matrix is least probable when $v_2$ is around 0.5, i.e., where the v-robustness reaches the maximum for all the methods.

5.1.2 Non-zero mean perturbations

Seeing the dominance of GMM (EVM) over COH in the previous section, one might be interested if there exist settings, where this dominance is violated. This section gives a positive answer, however, under a rather unrealistic assumption of non-zero mean perturbations.

Realizations of $\hat{R}_c((1, v_2, 0), \mathcal {N}(\mu , \sigma ^2), M_m)$ for $v_2 \in (0, 1)$, $\mu \in \{-1, -1/2,$ $1/2, 1\}$, $\sigma \in \{1/2, 1, 2\}$, and the method $m \in \{\textrm{GMM}, \textrm{EVM}, \textrm{COH}\}$ are depicted in the first row of the panels in Fig. 3.

Fig. 3

The first row of the panels shows realizations of $\hat{R}_c((1, v_2, 0), \mathcal {N}(\mu , \sigma ^2), M_m)$ for $m \in \{\textrm{GMM}, \textrm{EVM}, \textrm{COH}\}$ and $n = 3$. The second row of the panels shows realizations of estimates $\mathbb {P}(\varvec{A}_{v,F} \in \mathcal {A}_c)$. The third row of the panels shows PDFs of $\mathcal {N}(\mu , \sigma ^2)$

In the panels corresponding to the positive values of $\mu$, one can observe the dominance of COH over GMM (EVM). For the remaining panels, the opposite is observed.

The increased v-robustness for the positive values of $\mu$ clearly follows from its analytical expression presented in Sect. 4.1. If $v_i - v_j > 0$, then, the larger $\mathbb {E}[X_{ij}]$, the less likely it is that $v_i - v_j + X_{ij} < 0$, i.e., the less likely the rank reversal is to happen.

To sum up, the results obtained here for $n=3$ shed some light on the compared method and substantially help to understand and explain the results presented in the next section.

5.2 The robustness

The robustness R(G, F, M) allows one to conveniently aggregate the results from the previous section, and it also allows us to compute new ones for dimensions larger than $n = 3$. This section presents results for an MC simulation conducted as follows. For each $k \in \{1, \dots , N\}$, where $N = 100{,}000$, perform the following algorithm:

• 0. Generate a realization v of the random vector $V \sim G$.

• 1–3. Use the sampling algorithm for the v-robustness.

Then, $\frac{1}{N}\sum _{k=1}^{N}y_{k,m}$ is a realization of the estimator $\hat{R}_c(G, F, M_m)$ of $R_c(G, F, M_m)$, where $\hat{R}_c(G, F, M_m)$ is defined analogously to $\hat{R}_c(v, F, M_m)$.

In order to exploit the experimental design developed in Sect. 2.6 represented by Theorem 3, we assume that the copula of G is the independence copula. Also, as we do not have any information about the the univariate margins of G, we assume for each one the $\mathcal {U}[0, 1]$ distribution. Hence, we evaluate $R_c(G,$ $F_\sigma , M)$, where $F_\sigma$ is the Normal distribution $\mathcal {N}(0, \sigma ^2)$ and $\sigma \in \{0.05, 0.1, 0.2, 0.5, 1\}$. The realizations of $\hat{R}_c(G,$ $\mathcal {N}(0, \sigma ^2), M)$ for $n \in \{3,\dots ,6\}$ are shown in Fig. 4.

Fig. 4

Realizations of $\hat{R}_c(G, \mathcal {N}(0, \sigma ^2), M_m)$ for $\sigma \in \{0.05, 0.1, 0.2, 0.5, 1\}$, $n \in \{3,\dots ,6\}$ and $m \in \{\textrm{EVM}, \textrm{GMM}, \textrm{COH}\}$

In all cases, the robustness of COH is lower than that of EVM and that of GMM, which was already indicated by the results computed for the v-robustness for $n=3$. For $n \ge 4$, GMM and EVM are no longer equivalent, however, we can observe rather slight differences. In most of the cases, GMM has larger robustness than EVM, which is in agreement with Crawford and Williams (1985), where these two methods were also compared via an MC simulation.

As expected, the robustness decreases as $\sigma$ or n increases, which is caused by larger impact of the perturbations to cause the rank reversal. Note that for $n \ge 4$, condition (7) holds only for GMM and COH, whereas not for EVM. For example, given

$$\begin{aligned} \varvec{A}_{v,\varvec{X}} = \begin{pmatrix} 0 &{} 0 &{} 2 &{} 0 \\ 0 &{} 0 &{} 1 &{} 2 \\ -2 &{} -1 &{} 0 &{} 4 \\ 0 &{} -2 &{} -4 &{} 0 \end{pmatrix}, \end{aligned}$$

$r(M_{\mathrm{{EVM}}}(\varvec{A}_{v,\varvec{X}})) = (4, 2, 3, 1)$, but $r(M_{\mathrm{{EVM}}}(\varvec{A}_{\sigma v, \sigma \varvec{X}})) = r(M_{\mathrm{{EVM}}}(\sigma \varvec{A}_{v, \varvec{X}})) = (3, 2, 4, 1)$ for $\sigma = 14$. Another example can be found, e.g., in Genest et al. (1993, Example 2.1). Note that we evaluated (7) for the example above and $\sigma \in \{1, \dots , 100\}$ and $M = M_{\mathrm{{EVM}}}$, and found out that it has been satisfied in 49 cases (out of 100). Hence, one might still expect that $R(G_\sigma , F_\sigma , M)$, introduced in Sect. 2.6.2, will not differ much from $R(G_1, F_1, M)$ for $M = M_{\mathrm{{EVM}}}$. To check this, we also tried $G_\sigma$ set to $\mathcal {U}[0, \sigma ]$ with $\sigma \in \{1/10, 10\}$, and found out that the differences between $R(\mathcal {U}[0, \sigma ], \mathcal {N}(0,\sigma ^2), M_{\mathrm{{EVM}}})$ and $R(\mathcal {U}[0, 1], \mathcal {N}(0,1), M_{\mathrm{{EVM}}})$ are negligible.

5.3 A version of the robustness not limited to coherent PCMs

Given that GMM and EVM are predominantly the preferred methods for calculating PVs from PCMs, and considering that PCMs are usually not coherent, particularly as their dimension increases, it becomes interesting to numerically compare the robustness of GMM and EVM across this much broader set of matrices. We can do this by modifying the original algorithm for estimating of the robustness from Sect. 5.2, specifically replacing Step 2 with “Compute $\varvec{A}_{v,\varvec{X}}$”, thereby eliminating the coherence condition on $\varvec{A}_{v,\varvec{X}}$. We denote the thus computed estimate as $\hat{R}$. Unsurprisingly, this implies that the COH method, which relies on coherence, is incapable of returning ranks for potentially non-coherent $\varvec{A}_{v,\varvec{X}}$ matrices, and so is excluded from the forthcoming comparison, which is presented in Fig. 5. In this figure, the filled bars, labeled as “(all PCMs)”, represent realizations of $\hat{R}(G, \mathcal {N}(0, \sigma ^2), M_m)$ for $\sigma \in \{0.05, 0.1, 0.2, 0.5, 1\}$, $n \in \{3,\dots ,6\}$ and $m \in \{\textrm{EVM}, \textrm{GMM}\}$.

Fig. 5

The filled bars show the realizations of $\hat{R}(G, \mathcal {N}(0, \sigma ^2), M_m)$ for $\sigma \in \{0.05, 0.1, 0.2, 0.5, 1\}$, $n \in \{3,\dots ,6\}$ and $m \in \{\textrm{EVM}, \textrm{GMM}\}$. The bars without filling are the values $\hat{R}_c(G, \mathcal {N}(0, \sigma ^2), M_m)$ from Fig. 4

We note that the negligible difference in robustness between GMM and EVM is not limited to coherent PCMs. The remaining observations from Sect. 5.2 are also applicable here. An interesting point arises when comparing, for a given method m, the estimate $\hat{R}(G, \mathcal {N}(0, \sigma ^2), M_m)$ with $\hat{R}_c(G, \mathcal {N}(0, \sigma ^2), M_m)$, where the latter (represented by bars without filling) corresponds to results from Fig. 4. It is evident that the robustness of GMM and EVM is greater when the method is applied solely to perturbed PCMs that are coherent. Given that perturbed PCMs are typically what we obtain from a DM for the reasons outlined in Sect. 1, these results hint at the possibility of achieving higher robustness if only coherent PCMs are considered.

5.4 Connection of perturbation parameters to inconsistency

This section aims to clarify the interpretation and practical implications of the perturbation parameters in our methodology. One way to assess the significance of these parameters in practice is to link them to the level of inconsistency in the corresponding randomly perturbed reciprocal PCM, where the latter is introduced in Sect. 2.2. To illustrate this, we propose an additional simulation study wherein the perturbations follow the Normal distribution $\mathcal {N}(0, \sigma ^2)$, and the perturbation parameter $\sigma$ varies across the set $\{0.1, 0.2, 0.5, 1\}$. For each value of $\sigma$, we generate a total of one million PCMs of orders $n \in \{3,\dots ,6\}$. Each PCM is sampled from $\varvec{A}_{V, F}$, where $V = (V_1, \dots , V_n)$, $V_i \sim \mathcal {U}[0,1]$, for $i \in \breve{n}$, and F denotes the Normal distribution $\mathcal {N}(0, \sigma ^2)$. This method of sampling is identical to the one employed in Sects. 5.2 and 5.3.

To evaluate the level of inconsistency, we employ Saaty’s consistency ratio (CR), a measure widely accepted within AHP (Saaty, 1980). This ratio compares the consistency index of our PCM, calculated as $(\lambda _{\max } - n) / (n - 1)$, with a random index derived from a randomly generated PCM of the same order. Here, $\lambda _{\max }$ is defined in Sect. 3.2. A lower CR indicates a less inconsistent PCM, with a CR below 0.1 often considered acceptable.

The results are presented in Fig. 6.

Fig. 6

The four smaller panels show histograms (20 bins on [0, 0.5]) of the distribution of the CR of one million randomly sampled perturbed PCMs with the perturbations distributed according to $\mathcal {N}(0, \sigma ^2)$, and the larger panel at right shows the corresponding mean CR. All plots are evaluated for $\sigma \in \{0.1, 0.2, 0.5, 1\}$ and $n \in \{3,\dots ,6\}$

The four smaller panels depict histograms of the distribution of CR values across the sampled PCMs for each $\sigma$ and n. These plots offer an empirical perspective on the level of inconsistency introduced by the perturbations. For all considered dimensions, we observe a clear shift of the distribution’s body to the right as $\sigma$ increases. This shift is corroborated by the larger plot on the right side of the figure, which presents the mean of each distribution. Specifically, the mean CR increases as $\sigma$ escalates. It is also important to note that these means are generally not, or only slightly, affected by the dimension of the PCM.

These results augment our analysis by elucidating the relationship between perturbation parameters and the observed levels of inconsistency in the PCMs. They offer insights into how these parameters, when manipulated, can alter the distribution of CR, hence affecting the overall inconsistency of the PCMs. Furthermore, we can now discern how the robustness of a chosen method for calculating PVs from PCMs might vary with the level of inconsistency.

6 Discussion

As mentioned in Sect. 2.2, our approach to robustness against rank reversal has several limitations. Here, we discuss the issue that if a method fails to reproduce the correct order, it is not considered whether the true ranking is missed by exchanging the two bottom alternatives, or by completely reversing the ranking. A possible solution might be the following enhancement. Rather than yielding binary outcomes that simply indicate success or failure in reproducing the true ranking, one can try to calculate a certain distance between the true ranking and the ranking generated by the method. This distance serves as a more granular and informative measure of robustness, since it reflects the extent of divergence from the true ranking, rather than merely indicating the presence or absence of divergence. Note that distances of rankings are extensively considered in the literature. For example, Csató (2017b) considers a weighted distance where a disagreement at the top of the ranking is more significant than a disagreement at the bottom, which is the usual case in decision-making. Its theoretical foundation is provided by Can (2014).

Consider an illustrative example involving four alternatives – denoted as A, B, C, and D – and a known metric such as the Chebyshev distance. Suppose the true ranking is $A \succ B \succ C \succ D$. Now, we introduce two scenarios. In the first, we observe a simple permutation such that the ranking produced by the method is $A \succ B \succ D \succ C$. The Chebyshev distance in this case is 1, as the rank of D has changed by one position. In the second scenario, the ranking is completely reversed to $D \succ C \succ B \succ A$. Here, the Chebyshev distance is 3, the greatest difference in rank positions (for example, for A from position 1 to 4).

Another approach consists in that we express the change of the ranking by an $n \times n$ permutation matrix P. To illustrate, consider the example given above: the true ranking is $A\succ B\succ C\succ D$ and for a ranking produced by the method, such as $A\succ B\succ D\succ C$, we define the $4 \times 4$ permutation matrix P as follows: we let $p_{AA} = p_{BB} = p_{CD} = p_{DC} = 1$, and we let the other elements of the matrix be 0. In general, given a PV $v = (v_1,\ldots ,v_n) \in \mathbb {R}^n$, let $\rho = r(v)$ be the true ranking and let $\hat{{\hat{\rho }}} = r(M(\varvec{A}_{v,F}))$ be the ranking returned by the method M applied to the perturbed PCM, and define the $n \times n$ permutation matrix P by letting $p_{\smash {\rho _k\hat{\hat{\rho }}_k}} = 1$ and $p_{\rho _kj} = 0$ for all $j \in \{1,\ldots ,n\} {\setminus } \{\hat{\hat{\rho }}_k\}$ for $k = 1$, ..., n. The distance between the rankings is defined as the deviation of the matrix P from the identity matrix, such as $\delta (\rho , \hat{\hat{\rho }}) = \sum _{i=1}^n \sum _{j=1}^n \sum _{k=1,p_{ik}=1}^n \mathopen \mid j-k\mathclose \mid$, cf. Bartl and Ramík (2023). We would like to pursue these directions in future research.

Additionally, we should highlight that our proposed approach, initially designed for complete PCMs, might also be applicable to incomplete PCMs. Suppose the method of calculating PVs from PCMs is sufficiently robust to handle incomplete matrices. For example, GMM and EVM have such an extension, see Bozóki et al. (2010). In that case, we can hypothesize that our approach for estimating robustness would still function effectively. Let us assume a PCM, $\varvec{A}$, with some missing entries. A method that calculates PVs from $\varvec{A}$, even with its incomplete nature, should hypothetically work with our robustness estimation approach. This is under the assumption that the method fills in missing entries in a way that maintains consistency in the rank of the alternatives in the decision-making process. In future work, we plan to explore this potential extension, examining its feasibility and the conditions under which it holds true. This could provide further avenues for the use of our robustness estimation method, increasing its versatility and utility in real-world decision-making contexts where complete data are not always be available.

7 Conclusions

A probabilistic concept for evaluation of methods calculating priority vectors from pairwise comparison matrices (PCMs) was introduced. The concept gives an answer to the natural question of how probable it is that perturbations introduced to a consistent PCM cause rank reversal. To this end, the notion of the v-robustness and its aggregated complement, the robustness, was introduced via alo-groups. Three example methods were considered for the evaluation, and for one of them, COH, an efficient evaluation algorithm was derived, as well as an analytical expression of its v-robustness. For the remaining methods, the necessity of the Monte Carlo (MC) approach was advocated. To partially limit the size of the related MC experiments, two kinds of invariance of the (v-)robustness were analyzed, leading to a particular design of the MC experiments. Then, the mentioned methods were compared in terms of the v-robustness using different models for the distribution of the perturbations. The results shown substantial dominance of GMM and EMV over COH. Note that cases where COH dominated GMM and EVM were also presented, however, under rather unrealistic assumptions. Then, the methods were compared in terms of the robustness, and a slight dominance of GMM over EVM was observed, as well as a strong dominance of these two methods over COH. For the latter method, we shown that its robustness can be accessed analytically, which allowed us to further tune our MC experiments. As not all PCMs are coherent and the COH method does not return a rank ordering of the priorities in that case, the robustness of this method had to be computed in a special way. We shown that our framework is able to deal also with such methods, which supports its general applicability. Further, to gain insights into the impact of perturbations on robustness, we provided an additional simulation study exploring their connection to the inconsistency of the corresponding randomly perturbed reciprocal PCM. Finally note that the reader can immediately verify all the presented results using a Python implementation of our methodology, which is freely available at https://github.com/gorecki/robustness.