Product life cycles, product innovation and firm growth

Abstract

This paper studies research and development (R &D) for product innovation of firms faced with “product life cycles.” We represent the concept of product life cycles with bounded revenue and profit functions and describe R &D for product innovation as an activity to control the “birth rate of a new product” (i.e., the probability of product innovation). We then derive the optimal level of R &D, corresponding to the optimal birth rate of a new product, and show that the growth rate of the firm’s expected total revenue converges to the optimal birth rate of a new product in the long run.

1 Introduction

Economic growth is usually taken as a supply-side phenomenon; the endogenous growth theory (cf. Romer, 1990; Grossman &Helpman, 1991; Jones, 1995; Aghion &Howitt, 1998) explains economic growth as a consequence of technical progress driven by profit-seeking firms’ research and development (R &D) (including human capital accumulation). Certainly, there is no doubt that technical progress, through the improvement of the supply side, has made a great contribution to economic growth (cf. Solow, 1957), but the role of the demand side in economic growth should not be ignored; for stable economic growth, the growth of the demand side should keep pace with that of the supply side.¹

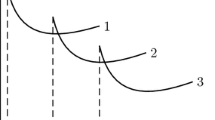
The Schumpeterian growth theory (cf. Seggerstorm et al., 1990; Grossman & Helpman 1991, chap. 12), on the other hand, emphasizes the role of product innovation in economic growth based on the fact that newly invented products, providing a higher utility for consumers, replace existing ones; it examines the implications of “product life cycles” on R &D and economic growth. It contributes to the development of the growth theory shedding a light on the important demand-side phenomena of product life cycles, but it ignores some of their notable features: products have different phases in their life cycles.² The concept of product life cycles, established as a stylized fact in management sciences (cf. Day, 1981), argues that each innovative product (good or service) has its life cycle composed of the four typical phases: Introduction, Growth, Maturity and Decline (Fig. 1). In the Schumpeterian growth theory, however, the distinctions between the four phases are not taken seriously.

Fig. 1

Product life cycles

This paper aims to take seriously the concept of product life cycles in a framework of the endogenous growth theory; it examines the R &D and growth processes of firms faced with product life cycles. By so doing, it attempts to provide a demand-side model for economic growth. To focus on the impact of product life cycles on the demand side through product innovation, “process innovation” is ignored; it is a supply-side phenomenon which is mainly concerned with the improvement of productivity.

The remaining part of this paper is organized as follows. Section 2 presents our model; we describe the life cycle of each product with bounded revenue and profit functions and treat the firm’s R &D for product innovation as an activity to control the “birth rate of a new product” (i.e., the probability of product innovation). Section 3 derives the optimal level of R &D corresponding to the optimal birth rate of a new product. We also show that the growth rate of the firm’s expected total revenue converges to the optimal birth rate of a new product; the long-run determinant of firm growth is the intensity of product innovation.³ Sect. 4 concludes this paper. Appendices provide the proofs for the propositions in the main text.

2 The model

This section presents a model of product life cycles and product innovation. The model is similar to those of Aoki and Yoshikawa (2007, chap. 8) and Murakami (2017), but it is more general than them because it allows for the Decline phase of product life cycles.

2.1 Product life cycles

To formalize the concept of product life cycles, it is assumed that the revenue (measured in value added) and profit of each kind of product depend on the “age” of this product or the time elapsing from its birth; we assume that, at time t,  the revenue and profit of a product which appears in the market as a consequence of product innovation at time $s\le t,$ denoted by $y_s^t$ and $\pi _s^t,$ respectively, are represented in the following forms⁴

$$\begin{aligned} y_s^t=y(t-s), \end{aligned}$$

(1)

$$\begin{aligned} \pi _s^t=\pi (t-s). \end{aligned}$$

(2)

The following fairly weak assumption is made on the revenue and profit functions.⁵

Assumption 1

$y:{\mathbb {R}}_{+}\rightarrow {\mathbb {R}}_{+}$ is bounded with $y(0)>0$ and differentiable with a bounded (first) derivative, and $\pi :{\mathbb {R}}_{+}\rightarrow {\mathbb {R}}$ is bounded and continuous.

The boundedness of the revenue and profit functions (and the derivative of the former) is consistent with the concept of product life cycles as illustrated in Fig. 1; due to the boundedness, firm growth can only be sustained by creations of new products through product innovation. Also, $y(0)>0$ and $y(t)\ge 0$ are based on the fact that a product is produced at its birth ($y(0)>0$) but its production may eventually be stopped ($y(t)=0$) due to its obsolescence; some aspects of production life cycles (the Introduction and Decline phases) are reflected.

2.2 Product innovation

Product innovation (inventions of a new product) is a successful outcome of R &D. We may then describe R &D (for product innovation) as an activity to control the probability of product innovation. Intensive R &D increases the probability of product innovation, but it does not always result in success. To describe this, we represent a product innovation as a random event. Also, a new product is usually invented by a “new combination” of knowledge on the existing products (cf. schumpeter,1934, chap. 2). Then, the number of the firm’s existing products (outcomes of past successful product innovations) is assumed to have a positive influence on the probability of future product innovation; the number of existing products is assumed to be proportional to the stock of knowledge on product innovation, accumulated through learning by doing (cf. Arrow, 1962). Thus, we assume that, when the firm produces N kinds of products at time t (i.e., when it invented N kinds of products up to time t), it succeeds in inventing a new product in the period between t and $t+\Delta t$ with the probability $\lambda (t)N\Delta t,$ where $\Delta t$ is an infinitesimal time and $\lambda (t)\ge 0$ is the intensity of product innovation; $\lambda$ is called the “birth rate of a new product” in what follows.⁶

Let P(N, t) be the probability that the firm has N (distinct) types of products at time t. Then, since a new product is invented between time t and $t+\Delta t$ with the probability $\lambda (t)N\Delta t,$ the change in P(N, t) in the time interval $(t,\ t+\Delta t)$ can be given by

$$\begin{aligned} P(N,t+\Delta t)-P(N,t)=\lambda (t)(N-1)P(N-1,t)\Delta t-\lambda (t)NP(N,t)\Delta t +o(\Delta t). \end{aligned}$$

Dividing both sides by $\Delta t$ and letting $\Delta t\rightarrow 0,$ we obtain

$$\begin{aligned} {\dot{P}}(N,t)\Bigl (=\frac{\partial P}{\partial t}(N,t)\Bigr )=\lambda (t)(N-1)P(N-1,t)-\lambda (t)NP(N,t). \end{aligned}$$

(3)

The solution of this equation is given as follows.

Lemma 1

If $P(N_0,0)=1$ (i.e., if the number of product types at time 0 is $N_0$), then

$$\begin{aligned} P(N,t)=\frac{(N-1)!}{(N_0-1)!(N-N_0)!}\Bigl [\exp \left( -\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N_0}\Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\right) \Bigr ]^{N-N_0}, \end{aligned}$$

for $N\ge N_0.$

Proof

See Appendix A. $\square$

2.3 Expected total profit

It is seen from Lemma 1 that the expected total profit at time t,  denoted by $\Pi (t),$ is given by

$$\begin{aligned} \begin{aligned} \Pi (t)&=\sum _{i=1}^{N_0}\pi (t-s_i)+\sum _{N=N_0}^{\infty }\int _0^t \lambda (s)NP(N,s)\pi (t-s)ds\\&=\sum _{i=1}^{N_0}\pi (t-s_i)+\int _0^t \lambda (s)\sum _{N=N_0}^{\infty }NP(N,s)\pi (t-s)ds, \end{aligned} \end{aligned}$$

(4)

where $s_i\le 0,\ i=1,...,\ N_0,$ are the times when products existing at time 0 were invented.

Let L(t) be the expected number of product types that the firm produces at time t. The following lemma provides a useful expression for L(t).

Lemma 2

$$\begin{aligned} L(t)=\sum _{N=N_0}^\infty NP(N,t)=N_0\exp \Bigl (\int _0^t \lambda (s)ds\Bigr ). \end{aligned}$$

Proof

See Appendix B. $\square$

Lemma 2 implies that the expected number of product types L changes at the rate of $\lambda$; this is the reason why $\lambda$ is called the birth rate of a new product. Since the stock of knowledge on product innovation is proportional to the number of product types as argued above, the expected number of product types L can be labeled as the “expected stock of knowledge (on product innovation).”⁷

It then follows from (4) and Lemma 2 that

$$\begin{aligned} \begin{aligned} \Pi (t)&=\sum _{i=1}^{N_0}\pi (t-s_i)+\int _0^t \lambda (s)L(s)\pi (t-s)ds\\&=\sum _{i=1}^{N_0}\pi (t-s_i)+N_0\int _0^t \lambda (s)\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )\pi (t-s)ds. \end{aligned} \end{aligned}$$

(5)

This implies that the expected total profit $\Pi$ is raised by an increase in the expected stock of knowledge L.

2.4 Expected R &D expenditure

Since the objective of R &D is to raise the probability of product innovation, R &D may be defined as the activity to control the birth rate of a new product $\lambda .$ Thus, we define an R &D plan as a time path of the birth rate of a new product $[\lambda (t)]_{t=0}^\infty .$

Regarding R &D plans, it is costlier to increase the birth rate of a new product $\lambda .$ We may then assume that, for each existing product type, the expenditure on R &D associated with the (target) birth rate of a new product $\lambda$ is $\varphi (\lambda ),$ which is the cost for setting the birth rate of a new product to $\lambda$ at each moment of time; $\varphi$ is called the R &D expenditure function in what follows.

Following Murakami (2017), the following assumption is made on the R &D expenditure function.

Assumption 2

$\varphi : {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+$ is twice continuously differentiable with

$$\begin{aligned} \varphi (0)=0,\ \varphi '(\lambda )>0,\ \varphi ''(\lambda )>0, \end{aligned}$$

for all $\lambda \ge 0.$

Given that a new product is invented from the existing products, the expected total expenditure at time t along an R &D plan $[\lambda (t)]_{t=0}^\infty$ is equal to the product of the expenditure associated with the birth rate of a new product $\lambda$ or $\varphi (\lambda )$ and the expected number of product types L. It then follows from (2) that the expected total expenditure at time t can be given by

$$\begin{aligned} \Phi (t)=\sum _{N=N_0}^\infty \varphi (\lambda (t)) NP(N,t)=\varphi (\lambda (t))L(t)=N_0\varphi (\lambda (t))\exp \left( \int _0^t \lambda (\tau )d\tau \right) , \end{aligned}$$

(6)

where $\Phi$ denotes the expected total expenditure (on R &D).

The relationship between the expected stock of knowledge L and the birth rate of a new product $\lambda$ is similar to that between the stock of capital K and the rate of capital accumulation z. Thus, the expected total expenditure $\Phi$ may be seen as the counterpart of the effective cost (including adjustment cost) of investment; the R &D expenditure function $\varphi$ has the same properties as those of the effective (adjustment) cost function (cf. Uzawa, 1969).

2.5 The R &D planning problem

The expected net profit maximization problem can be formulated as follows:

$$\begin{aligned} \max _{[\lambda (t)]_{t=0}^\infty }&\int _0^\infty [\Pi (t)-\Phi (t)]e^{-\rho t}dt, \end{aligned}$$

which, by using (5) and (6), becomes

$$\begin{aligned}&\max _{[\lambda (t)]_{t=0}^\infty } \int _0^\infty \left[ \sum _{i=1}^{N_0}\pi (t-s_i)+N_0\int _0^t\lambda (s)\exp \left( \int _0^s \lambda (\tau )d\tau \right) \pi (t-s)ds\right. \nonumber \\&\quad \left. -N_0\varphi (\lambda (t))\exp \left( \int _0^t \lambda (\tau )d\tau \right) \right] e^{-\rho t}dt, \end{aligned}$$

(7)

where $\rho$ is a positive constant that represents the interest rate. The optimal R &D plan can be derived as a solution of (7).

The times when products existing at the planning time 0 were invented, $s_i,\ i=1,...,N_0,$ have no influence in (7); we may assume that $s_i=0$ for all $i=1,...,N_0.$ It is then seen that the maximand of (7) is proportional to the original number of product types $N_0$; we may further assume that the original number of product types $N_0$ is unity. Thus, Problrem (7) can be simplified as

$$\begin{aligned} \max _{[\lambda (t)]_{t=0}^\infty }&\int _0^\infty \Bigl [\pi (t)+\int _0^t\lambda (s)\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )\pi (t-s)ds\nonumber \\&\quad -\varphi (\lambda (t))\exp \Bigl (\int _0^t \lambda (\tau )d\tau \Bigr )\Bigr ]e^{-\rho t}dt. \end{aligned}$$

(8)

3 Analysis

This section analyzes Problem (8) to derive the optimal birth rate of a new product and show that the growth rate of the firm’s expected revenue converges to it.

3.1 The optimal R &D plan

Let

$$\begin{aligned} V= & {} \int _0^\infty \Bigl [\pi (t)+\int _0^t \lambda (s)\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )\pi (t-s)ds\nonumber \\{} & {} -\varphi (\lambda (t))\exp \Bigl (\int _0^t \lambda (\tau )d\tau \Bigr )\Bigr ]e^{-\rho t}dt. \end{aligned}$$

(9)

Suppose that the firm changes the original R &D plan so that the birth rate of a new product $\lambda$ is increased by the amount of $\Delta \lambda$ in the time interval $(t,\ t+\Delta t),$ where $\Delta \lambda$ and $\Delta t$ are both infinitesimal values. Let $\Delta V$ be the resultant change in V due to the change in the R &D plan:

$$\begin{aligned} \begin{aligned} \Delta V&=\int _t^{t+\Delta t} e^{-\rho u}\int _t^u \Bigl [(\lambda (s)+\Delta \lambda )\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )e^{\Delta \lambda (s-t)}-\lambda (s)\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )\Bigr ]\\&\quad \pi (u-s)dsdu\\&{+}\int _{t+\Delta t}^{\infty } e^{{-}\rho u}\int _t^{t{+}\Delta t} \Bigl [(\lambda (s){+}\Delta \lambda )\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )e^{\Delta \lambda (s-t)}{-}\lambda (s)\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )\Bigr ]\\&\quad \pi (u-s)dsdu\\&+\int _{t+\Delta t}^{\infty } e^{-\rho u}\int _{t+\Delta t}^u \lambda (s)\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )(e^{\Delta \lambda \Delta t}-1)\pi (u-s)dsdu\\&-\int _t^{t+\Delta t} e^{-\rho u}\Bigl [\varphi (\lambda (u)+\Delta \lambda )\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )e^{\Delta \lambda (u-s)}\\&-\varphi (\lambda (u))\exp \Bigl (\int _0^u \lambda (\tau )d\tau \Bigr )\Bigr ]dsdu-\int _{t+\Delta t}^\infty e^{-\rho u}\varphi (\lambda (u))\\&\exp \Bigl (\int _0^u \lambda (\tau )d\tau \Bigr )(e^{\Delta \lambda \Delta t}-1)dsdu. \end{aligned} \end{aligned}$$

(10)

Economic reasoning implies that along an optimal R &D plan $[\lambda ^*(t)]_{t=0}^\infty$ (if it is an inner solution), $\Delta V$ must converge to 0 as $\Delta \lambda \Delta t\rightarrow 0$; along an optimal R &D plan, the marginal gain by a change in the R &D plan or the first three terms of the right-hand side of (10), must be equal to the marginal loss or the last two terms.

The following proposition presents a necessary condition for an optimal R &D plan.

Proposition 1

Let Assumptions 1 and 2 hold. Assume that the following condition is satisfied for all $t\ge 0$⁸:

$$\begin{aligned} \lambda (t)<\rho . \end{aligned}$$

(11)

If there exists a solution of (8), $[\lambda ^*(t)]_{t=0}^\infty ,$ with $\lambda ^*(t)>0$ for all $t\ge 0,$ then

$$\begin{aligned} {\dot{\lambda }}^*(t)=\frac{1}{\varphi ''(\lambda ^*(t))}[\varphi '(\lambda ^*(t))(\rho -\lambda ^*(t))-(r-\varphi (\lambda ^*(t)))], \end{aligned}$$

(12)

where⁹

$$\begin{aligned} r= \rho \int _0^\infty \pi (t)e^{-\rho t}dt. \end{aligned}$$

(13)

Proof

See Appendix C. $\square$

We can rewrite (13) as follows:

$$\begin{aligned} r=\rho \int _t^\infty \pi (\tau -t)e^{-\rho (\tau -t)}d\tau . \end{aligned}$$

Given that $\pi (\tau -t)$ is the instantaneous profit obtained at time $\tau$ from a product which is invented by (expected) product innovation at time t,  the right-hand side is equal to the product of the interest rate $\rho$ and the (expected) discounted present value of profit (evaluated at time t). Then, r is the (expected) average profit through the product life cycle, which is common among products regardless of when they are invented (due to Assumption 1); it is also the (expected) profit obtained from a new product innovation. The expected stock of knowledge L is, on the other hand, increased by one through a new product innovation. Thus, r can be regarded as the “profit rate” on expected stock of knowledge (cf. Murakami, 2017).

The conclusion of Proposition 1 can be sharpened as follows.

Theorem 1

Under the hypotheses of Proposition 1, the solution of (8), if it exists, is equal to the constant $\lambda ^*$ for all $t\ge 0$ such that

$$\begin{aligned} \left\{ \begin{array}{l} [r-\varphi (\lambda ^*)]/(\rho -\lambda ^*)=\varphi '(\lambda ^*)\ \ \textrm{if}\ r/\rho >\varphi '(0)\\ \lambda ^*=0\ \ \textrm{if}\ r/\rho \le \varphi '(0). \end{array} \right. \end{aligned}$$

Proof

See Appendix C. $\square$

It is seen from Theorem 1 that the birth rate of a new product corresponding to the optimal R &D plan, $\lambda ^*,$ can be illustrated as in Fig. 2. It also shows that $\lambda ^*$ is positive (only) if

$$\begin{aligned} \frac{r}{\rho }=\int _0^\infty \pi (t)e^{-\rho t}dt>\varphi '(0). \end{aligned}$$

(14)

The left-hand side is the discounted present value of the profit from a new product or the “marginal benefit” of R &D, while the right-hand side is the marginal expenditure on R &D evaluated at $\lambda =0$. Thus, Theorem 1 implies that the firm does not invest on R &D unless its marginal benefit is larger than its marginal cost.

Fig. 2

Optimal R &D plan

Theorem 1 can also be interpreted from a viewpoint of Tobin’s (1969) q theory. Given that r is the profit rate on expected stock of knowledge, $[r-\varphi (\lambda ^*)]/(\rho -\lambda ^*)$ is the counterpart of Tobin’s q in our R &D investment model; the R &D expenditure function $\varphi$ corresponds to the effective cost function for investment (cf. Uzawa, 1969) and Tobin’s q theory can be explained by the adjustment cost theory of investment (cf. Yoshikawa, 1980; Murakami 2016). Indeed, as the last paragraph indicates, the firm does not engage in R &D unless the ratio $r/\rho$ exceeds the threshold value $\varphi '(0)$; this is similar to Tobin’s q theory, which argues that capital investment is not carried out unless the q ratio, the ratio between the profit rate on capital and the interest rate, exceeds the threshold value 1.

3.2 Firm growth

It is seen from (7) that the expected total revenue along the optimal R &D plan at time t,  denoted by Y(t),  can be calculated as

$$\begin{aligned}&Y(t)=\sum _{i=1}^{N_0}y(t-s_i)+\int _0^t \lambda ^*\sum _{N=N_0}^{\infty }NP(N,s)y(t-s)ds\nonumber \\&\quad =\sum _{i=1}^{N_0}y(t-s_i)+N_0 \lambda ^* e^{\lambda ^* t}\int _0^t y(\tau )e^{-\lambda ^* \tau }d\tau . \end{aligned}$$

(15)

If $Y(t)>0$,¹⁰ the growth rate of the expected total revenue, denote by g,  is given by

$$\begin{aligned} g(t)=\frac{{\dot{Y}}(t)}{Y(t)}=\lambda ^*+\frac{\lambda ^*[N_0y(t)-\sum _{i=1}^{N_0}y(t-s_i)]+\sum _{i=1}^{N_0} {\dot{y}}(t-s_i)}{Y(t)}. \end{aligned}$$

(16)

In what follows, we refer to g as the growth rate.

If the optimal birth rate of a new product $\lambda ^*$ (exists and) is positive, it can be proved that the asymptotic value of the growth rate g is equal to $\lambda ^*.$

Theorem 2

Let Assumption 1 hold. If there exists a positive solution of (8), $\lambda ^*(t)=\lambda ^*>0$ for all $t\ge 0$, then g(t) converges to $\lambda ^*$ as $t \rightarrow \infty .$

Proof

See Appendix E. $\square$

Theorem 2 implies that the long-run growth rate is equal to the (optimal) birth rate of a new product $\lambda ^*$; firm growth is ultimately determined by the intensity of product innovation. This is a natural consequence because the revenue of each product is bounded (and population growth is absent); the firm must continue R &D activities for sustainable growth in the presence of product life cycles.

Our model has explained some demand-side growth processes: the growth of corporate revenue is constrained by product life cycles but can be driven by product innovation. It can provide a demand-side growth theory with microeconomic foundations; it is also consistent with the Keynesian growth theory (cf. Pasinetti, 1981).

3.3 A numerical example

This subsection gives a numerical example to illustrate the main idea of our analysis.

It is assumed, following Aoki and Yoshikawa (2007) and Murakami (2017), that the diffusion (ownership) rate of a product which is invented at time $s\le t,$ denoted by d,  depends on the age $t-s$ and is described as follows¹¹:

$$\begin{aligned} d(t-s)=\frac{\alpha e^{v(t-s)}}{1-\alpha +\alpha e^{v(t-s)}}, \end{aligned}$$

(17)

where $\alpha <1$ and v are positive constants which stand for the initial diffusion rate and the diffusion speed of each product, respectively; it is the solution of the following differential equation with $d(0)=\alpha$:

$$\begin{aligned} {\dot{d}}(t-s)=vd(t-s)[1-d(t-s)]. \end{aligned}$$

Suppose that the size of population and the price of each product are constant over time; they are both normalized as unity. Given that the diffusion rate d is the share or number of people who have already purchased a product, the instantaneous demand for each product, which can be identified with the instantaneous revenue y,  is equal to the number of people who newly purchase the product at time t or the time derivative of d:

$$\begin{aligned} y(t-s)={\dot{d}}(t-s). \end{aligned}$$

It then follows from (17) that

$$\begin{aligned} y(t-s)=\frac{\alpha (1-\alpha )v e^{v(t-s)}}{[1-\alpha +\alpha e^{v(t-s)}]^2}. \end{aligned}$$

(18)

We assume that the capital (profit) share (i.e., the ratio between profit and revenue (value added)) is constant. It then follows from (18) that the profit function is given by

$$\begin{aligned} \pi (t-s)=\beta y(t-s)=\frac{\alpha (1-\alpha )\beta v e^{v(t-s)}}{[1-\alpha +\alpha e^{v(t-s)}]^2}, \end{aligned}$$

(19)

where $\beta$ is a positive constant less than unity which represents the capital share.

The parameters in (19) are set as follows. The capital share is, based on empirical data in the U.S. (cf. Jones, 2016), set to $\beta =0.35;$ it is tentatively assumed that the initial diffusion rate is $\alpha =0.01;$ the diffusion speed is, under the assumption that it takes about thirty years for each product to get a 50% diffusion rate since its birth, set to $v=0.15.$¹² It then follows from (18) and (19) that the revenue and profit functions are given by

$$\begin{aligned}{} & {} y(t-s)=\frac{14.85 e^{0.15(t-s)}}{[99+e^{0.15(t-s)}]^2}, \end{aligned}$$

(20)

$$\begin{aligned}{} & {} \pi (t-s)=\frac{5.1975 e^{0.15(t-s)}}{[99+e^{0.15(t-s)}]^2}. \end{aligned}$$

(21)

The following figure illustrates these functions; it looks like Fig. 1, which describes product life cycles.

Fig. 3

Revenue and profit

Based on the estimate of the average natural real interest rate for the U.S. (cf. Laubach & Williams 2003), the interest rate is set to

$$\begin{aligned} \rho =0.03. \end{aligned}$$

(22)

Suppose tentatively that the R &D expenditure function is given by

$$\begin{aligned} \varphi (\lambda )=0.1\lambda +2.5\lambda ^2. \end{aligned}$$

(23)

It follows from (13), (21) and (22) that the profit rate of expected stock of knowledge can be calculated as

$$\begin{aligned} r=0.004346. \end{aligned}$$

Thus, it is seen from Theorem 1 that the optimal birth rate of a new product, with (23), is given by

$$\begin{aligned} \lambda ^*=0.01098. \end{aligned}$$

(24)

For simplicity, assume that the firm has invented its first product at time 0: $N_0=1$ and $s_1=0.$ It then follows from (15) and (16) that the expected total revenue and its growth rate are given by

$$\begin{aligned} Y(t)= & {} y(t)+ \lambda ^* e^{\lambda ^* t}\int _0^t y(\tau )e^{-\lambda ^* \tau }d\tau ,\\ g(t)= & {} \lambda ^*+\frac{{\dot{y}}(t)}{Y(t)}. \end{aligned}$$

The following figure illustrates the time series of the growth rate with (20) and (24); this shows that the growth rate converges to the optimal birth rate of a new product $\lambda ^*=0.01098$.

Fig. 4

Growth rate

4 Conclusion

This paper has examined a general model of firm growth through product innovation in the existence of product life cycles; we have derived the optimal R &D plan for product innovation and showed that the growth rate of the firm converges to the optimal birth rate of a new product. It is no wonder that the firm, faced with product life cycles, must keep inventing new products to enjoy sustained growth, but the preceding studies have not thoroughly explored the implications of product life cycles on product innovation; this paper has shed a new light on the mechanism of product innovation with product life cycles.

Throughout this paper, we have stressed that the long-run growth of economies faced with product life cycles is determined by the intensity of demand creation through product innovation. Our approach is consistent with the Keynesian growth theory, which emphasizes the role of effective demand in the long run.

Appendices

Appendices

A Proof of Lemma 1

Proof

This lemma is proved by mathematical induction with respect to $N\ge N_0.$

For $N=N_0,$ it is seen from (3) that since $P(N_0-1,t)=0$ for all $t\ge 0,$

$$\begin{aligned} {\dot{P}}(N_0,t)=-\lambda (t)N_0P(N_0,t). \end{aligned}$$

With $P(N_0,0)=1,$ this equation can be solved as

$$\begin{aligned} P(N_0,t)=\exp \Bigl (-N_0\int _0^t\lambda (s)ds\Bigr )=\Bigl [\exp \Bigl (-\int _0^t\lambda (s)ds\Bigr )\Bigr ]^{N_0}. \end{aligned}$$

Assume that the assertion of this lemma holds for N. It then follows from (3) that

$$\begin{aligned} {\dot{P}}(N+1,t)=\lambda (t)NP(N,t)-\lambda (t)(N+1)P(N+1,t), \end{aligned}$$

or

$$\begin{aligned} {\dot{P}}(N+1,t)+(N+1)\lambda (t)P(N+1,t)=\lambda (t)NP(N,t). \end{aligned}$$

Multiplying both sides by $\exp ((N+1)\int _0^t \lambda (s)ds)(=[\exp (\int _0^t \lambda (s)ds)]^{N+1})$ gives

$$\begin{aligned}{} & {} [{\dot{P}}(N+1,t)+(N+1)\lambda (t)P(N+1,t)]\exp \Bigl ((N+1)\int _0^t \lambda (s)ds\Bigr )\nonumber \\{} & {} \quad =\lambda (t)NP(N,t)\exp \Bigl ((N+1)\int _0^t \lambda (s)ds\Bigr ), \end{aligned}$$

or

$$\begin{aligned}&\Bigr [{\dot{P}}(N+1,t)+(N+1)\lambda (t)P(N+1,t)\Bigr ]\exp \Bigl ((N+1)\int _0^t \lambda (s)ds\Bigr )\\&=\frac{N!}{(N_0-1)!(N-N_0)!}\lambda (t)\exp \Bigl (\int _0^t \lambda (s)ds\Bigr )\Bigl [\exp \Bigl (\int _0^t \lambda (s)ds\Bigr )-1\Bigr ]^{N-N_0}, \end{aligned}$$

With $P(N+1,0)=0,$ integrating both sides with respect to time from 0 to t yields

$$\begin{aligned}{} & {} P(N+1,t)\exp \Bigl ((N+1)\int _0^t \lambda (s)ds\Bigr )=\frac{N!}{(N_0-1)!(N+1-N_0)!}\\{} & {} \Bigl [\exp \Bigl (\int _0^t \lambda (s)ds\Bigr )-1\Bigr ]^{N+1-N_0}, \end{aligned}$$

because

$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\Bigl (P(N+1,t)\exp \Bigl ((N+1)\int _0^t \lambda (s)ds\Bigr )\Bigr )=\\{} & {} \quad [{\dot{P}}(N+1,t)+(N+1)\lambda (t)P(N+1,t)]\exp \Bigl ((N+1)\int _0^t \lambda (s)ds\Bigr ),\\{} & {} \frac{\partial }{\partial t} \Bigl [\exp \Bigl (\int _0^t \lambda (s)ds\Bigr )-1\Bigr ]^{N+1-N_0}\\{} & {} \quad =(N+1-N_0)\lambda (t)\exp \Bigl (\int _0^t \lambda (s)ds\Bigr )\Bigl [\exp \Bigl (\int _0^t \lambda (s)ds\Bigr )-1\Bigr ]^{N-N_0}. \end{aligned}$$

Hence

$$\begin{aligned} P(N+1,t){} & {} =\frac{N!}{(N_0-1)!(N+1-N_0)!}\Bigl [\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N_0}\\{} & {} \quad \Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N+1}, \end{aligned}$$

which implies that the assertion of this lemma holds for $N+1.$ $\square$

B Proof of Lemma 2

Proof

Let

$$\begin{aligned} S_{N_0}=\sum _{N=N_0}^{\infty }\frac{N!}{N_0!(N-N_0)!} \Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N-N_0}. \end{aligned}$$

It then follows that

$$\begin{aligned} S_{N_0}=\sum _{N=0}^{\infty }\frac{(N_0+N)!}{N_0!N!} \Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N}. \end{aligned}$$

Also, we have

$$\begin{aligned} \Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]S_{N_0}&=\sum _{N=0}^{\infty }\frac{(N+N_0)!}{N_0!N!} \Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N+1}\\&=1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )+\sum _{N=1}^{\infty }\frac{(N_0+N-1)!}{N_0!(N-1)!}\\&\quad \Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^N. \end{aligned}$$

The last two equations imply that

$$\begin{aligned} \exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )S_{N_0}=&1+N_0\Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]\\&+\sum _{N=2}^\infty \Bigl [\frac{(N_0+N)!}{N_0!N!}-\frac{(N_0+N-1)!}{N_0!(N-1)!}\Bigr ]\Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^N\\=&\sum _{N=0}^\infty \frac{[(N_0-1)+N]!}{(N_0-1)!N!}\Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^N=S_{N_0-1} \end{aligned}$$

or

$$\begin{aligned} S_{N_0}=\exp \Bigl (\int _0^t \lambda (s)ds\Bigr ) S_{N_0-1}. \end{aligned}$$

Hence

$$\begin{aligned} S_{N_0}=\Bigl [\exp \Bigl (\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N_0} S_{0}=\Bigl [\exp \Bigl (\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N_0+1}, \end{aligned}$$

because

$$\begin{aligned} S_0=\sum _{N=0}^{\infty }\Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N}=\exp \Bigl (\int _0^t \lambda (s)ds\Bigr ). \end{aligned}$$

Thus, it is seen from Lemma 1 that

$$\begin{aligned} L(t)&=\sum _{N=N_0}^\infty NP(N,t)\\&{=}\sum _{N{=}N_0}^\infty N\frac{(N{-}1)!}{(N_0{-}1)!(N-N_0)!}\Bigl [\exp \Bigl ({-}\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N_0}\Bigl [1{-}\exp \Bigl ({-}\int _0^t \lambda (s)ds\Bigl )\Bigr ]^{N-N_0}\\&=N_0\Bigl [\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N_0} \sum _{N=N_0}^\infty \frac{N!}{N_0!(N-N_0)!}\Bigl [1-\exp \Bigl (-\int _0^t \lambda (s)ds\Bigl )\Bigr ]^{N-N_0}\\&=N_0\Bigl [\exp \Bigl (-\int _0^t \lambda (s)ds\Bigr )\Bigr ]^{N_0} S_{N_0}=N_0\exp \Bigl (\int _0^t \lambda (s)ds\Bigr ). \end{aligned}$$

$\square$

C Proof of Proposition 1

Proof

By the mean value theorem, it is seen from (10) that for some $\theta _i,\theta '_i,\theta ''_i \in (0,1), i=1,2,3,4,5,$

$$\begin{aligned} \Delta V=&e^{-\rho (t+\theta '_1 \Delta t)} \\&\quad \Bigl [\lambda (t+\theta _1 \theta '_1 \Delta t) \exp \Bigl (\int _0^{t+\theta _1 \theta '_1} \Delta t \lambda (\tau )d\tau \Bigr )(e^{\theta _1 \theta '_1 \theta ''_1 \Delta \lambda \Delta t}\Delta t)\\&\times + \exp \Bigl (\int _0^{t+\theta _1 \theta '_1 \Delta t} \lambda (\tau )d\tau \Bigr )e^{\theta _1 \theta '_1 \Delta \lambda \Delta t}\Bigr ]\pi (t+(1-\theta _1)\theta '_1 \Delta t)\Delta \lambda (\Delta t)^2\\ +&\Delta \lambda \Delta t \int _{t+\Delta t}^{\infty } e^{-\rho u}\\&\quad \Bigl [(\lambda (t+\theta _2 \Delta t)\exp \Bigl (\int _0^{t+\theta _2 \Delta t} \lambda (\tau )d\tau \Bigr )e^{\theta _2 \theta '_2 \Delta \lambda \Delta t}\Delta t\\&+\Bigl (\int _0^{t+\theta _2 \Delta t} \lambda (\tau )d\tau \Bigr )\Bigr ]\pi (u-t-\theta \Delta t)du\\ +&e^{\theta _3 \Delta \lambda \Delta t} \Delta \lambda \Delta t \int _{t+\Delta t}^{\infty } e^{-\rho u}\int _{t+\Delta t}^u \lambda (s)\exp \Bigl (\int _0^s \lambda (\tau )d\tau \Bigr )\pi (u-s)dsdu\\ -&e^{-\rho (t+ \theta _4 \Delta t)} \\&\quad \Bigl (\int _0^{t+ \theta _4 \Delta t} \lambda (\tau )d\tau \Bigr ) [\varphi ( \lambda (t+\theta _4 \Delta t)) e^{\theta '_4 \Delta \lambda \Delta t} \Delta t+ \varphi '(\lambda (t+\theta _4 \Delta t)+\theta ''_4 \Delta \lambda )\\&+\varphi '(\lambda (t+\theta _4 \Delta t)+\theta '_4 \Delta \lambda )]\Delta \lambda \Delta t\\ -&e^{\theta _5 \Delta \lambda \Delta t} \Delta \lambda \Delta t \int _{t+\Delta t}^\infty e^{-\rho u}\varphi (\lambda (u))\Bigl (\int _0^u \lambda (\tau )d\tau \Bigr ) du. \end{aligned}$$

Along an optimal R &D plan $[\lambda ^*(t)]_{t=0}^\infty$, the following condition must be satisfied for all $t\ge 0$:

$$\begin{aligned} \lim _{\Delta \lambda \rightarrow 0, \Delta t \rightarrow 0} \frac{\Delta V}{\Delta \lambda \Delta t}=0, \end{aligned}$$

or

$$\begin{aligned} \begin{aligned}&\int _t^\infty \Bigl [\pi (u-t)+\int _{t}^u \lambda ^*(s)\exp \Bigl (\int _t^u \lambda ^*(\tau )d\tau \Bigr )\pi (u-s)ds\\&\quad -\varphi (\lambda ^*(u))\exp \Bigl (\int _t^u \lambda ^*(\tau )d\tau \Bigr )\Bigr ]e^{-\rho (u-t)}du=\varphi '(\lambda ^*(t)). \end{aligned} \end{aligned}$$

(25)

This is the condition for optimality in (8) in the case of an inner solution with $\lambda ^*>0$. By differentiating both sides with respect to t, we can obtain (12). $\square$

D Proof of Theorem 1

Proof

Define

$$\begin{aligned} V_0^*(t)=&\,\max _{[\lambda (u)]_{u=t}^\infty } \int _t^\infty \Bigl [\pi (u-t)+\int _{t}^u \lambda (s)\exp \Bigl (\int _t^u \lambda (\tau )d\tau \Bigr )\pi (u-s)ds\\&-\varphi (\lambda (u))\exp \Bigl (\int _t^u \lambda (\tau )d\tau \Bigr )\Bigr ]e^{-\rho (u-t)}du. \end{aligned}$$

Since the planning time t is irrelevant to the value of the right-hand side, the value (if it exsists) is equal to a constant, denoted by $V_0^*,$ for all $t\ge 0$:

$$\begin{aligned} V_0^*=&\,\max _{[\lambda (u)]_{u=t}^\infty } \int _t^\infty \Bigl [\pi (u-t)+\int _{t}^u \lambda (s)\exp \Bigl (\int _t^u \lambda (\tau )d\tau \Bigr )\pi (u-s)ds\nonumber \\&-\varphi (\lambda (u))\exp \Bigl (\int _t^u \lambda (\tau )d\tau \Bigr )\Bigr ]e^{-\rho (u-t)}du. \end{aligned}$$

(26)

Let $[\lambda ^*(t)]_{t=0}^\infty$ be an inner solution of (8) with $\lambda (t)>0.$ Due to its optimality, we have

$$\begin{aligned}&\max _{[\lambda (u)]_{u=t}^\infty } \int _t^\infty \Bigl [\pi (u-t)+\int _{t}^u \lambda (s)\exp \Bigl (\int _t^u \lambda (\tau )d\tau \Bigr )\pi (u-s)ds\\&\qquad -\varphi (\lambda (u)) \exp \Bigl (\int _t^u \lambda (\tau )d\tau \Bigr )\Bigr ]e^{-\rho (u-t)}du&\\&\quad =\int _t^\infty \Bigl [\pi (u-t)+\int _{t}^u \lambda ^*(s)\exp \Bigl (\int _t^u \lambda ^*(\tau )d\tau \Bigr )\pi (u-s)ds\\&\qquad -\varphi (\lambda ^*(u))\exp \Bigl (\int _t^u \lambda ^*(\tau )d\tau \Bigr )\Bigr ]e^{-\rho (u-t)}du.&\end{aligned}$$

It then follows from (25) and (26) that for all $t\ge 0$

$$\begin{aligned} V^*_0=\varphi '(\lambda ^*(t)). \end{aligned}$$

Since $V^*_0$ is constant, it is seen from Assumption 2 that $\lambda ^*(t)>0$ is a constant, denoted by $\lambda ^*>0,$ for all $t\ge 0$. Hence, if $\lambda ^*>0,$ it is given by letting ${\dot{\lambda }}^*=0$ in (12):

$$\begin{aligned} \frac{r-\varphi (\lambda ^*)}{\rho -\lambda ^*}=\varphi '(\lambda ^*). \end{aligned}$$

(27)

Let

$$\begin{aligned} f(\lambda )=[r-\varphi (\lambda )]-\varphi '(\lambda )(\rho -\lambda ). \end{aligned}$$

It then follows from Assumption 2 that if $0\le \lambda <\rho ,$

$$\begin{aligned} f'(\lambda )=-\varphi ''(\lambda )(\rho -\lambda )<0. \end{aligned}$$

Thus, for some positive $\lambda ^*<\rho$ to satisfy $f(\lambda ^*)=0$ or (27), it is necessary (but not sufficient) that

$$\begin{aligned} f(0)=r-\rho \varphi '(0)>0. \end{aligned}$$

Otherwise, there is no positive $\lambda ^*$ that satisfies (27). $\square$

D Proof of Theorem 2

Proof

Due to the continuity of y and $y(0)>0$ (cf. Assumption 1), there exists a $t_0>0$ such that $y(t)>0$ for all $t\in [0,t_0].$ Given that $\lambda ^*>0,$ it is then seen from (15) that, for $t\ge t_0$

$$\begin{aligned} Y(t)\ge N_0 \lambda ^* e^{\lambda ^* t}\int _0^t y(\tau )e^{-\lambda ^* \tau }d\tau \ge N_0 \lambda ^* e^{\lambda ^* t}\int _0^{t_0} y(\tau )e^{-\lambda ^* \tau }d\tau >0, \end{aligned}$$

where the inequalities follow from $y(t)\ge 0$ for all $t\ge 0$ (cf. Assumption 1) and $y(t)>0$ for all $t\in [0,t_0].$ Hence

$$\begin{aligned} Y(t)\ge N_0 \lambda ^* e^{\lambda ^* t}\int _0^{t_0} y(\tau )e^{-\lambda ^* \tau }d\tau \rightarrow \infty , \end{aligned}$$

as $t\rightarrow \infty$. Because of the boundedness of y and ${\dot{y}}$ (cf. Assumption 1), it follows from (16) that

$$\begin{aligned} |g(t)-\lambda ^*|\le \frac{\lambda ^*[N_0|y(t)|+\sum _{i=1}^{N_0}|y(t-s_i)|]+ \sum _{i=1}^{N_0}|{\dot{y}}(t-s_i)|}{Y(t)}\rightarrow 0, \end{aligned}$$

as $t\rightarrow \infty$. $\square$