On optimal lockdown policies while facing socioeconomic costs

Abstract

The paper analyzes the optimal lockdown policy using the SQAIRD model over a network with three population groups (young, adult, and old). We show that different lockdown policies may be justified by different socioeconomic structures (objective cost functions that are either convex or concave). We also show that a lockdown policy is always better than a laissez-faire policy, and a targeted policy specific to each group outperforms a uniform policy. In our benchmark example, we consider the case of Italy. Our simulations show that: (a) a lockdown policy is always better than the laissez-faire policy because it limits the costs generated by the pandemic in an uncontrolled situation; (b) a group-specific targeted lockout policy is more effective than a uniform policy to the extent that the groups differ. The latter is a less expensive targeted policy (as it optimally minimizes direct, indirect, and vaccination costs), and it is equally effective in controlling the pandemic. One finding of particular interest is that the optimal lockdown rate should be higher for the young and elderly than for adults. This is motivated by the fact that younger individuals are more likely to spread the virus in question asymptomatically.

1 Introduction

Since the emergence of the novel SARS-CoV-2 that causes the Coronavirus disease (COVID-19), which turned out to be highly infectious and potentially lethal, the scientific community, including epidemiologists, physicians, and social scientists, has devoted its efforts to mitigating the pandemic’s negative effects.¹ The scientific community was largely united in the need for strong action, but there was a wide variety of policies implemented by the government, including extreme options (Calcagnini et al., 2023; Powell, 2022). During the first wave of the pandemic, some governments, such as Sweden, preferred not to take any direct action to limit the spread of the virus (Walker et al., 2020), while others elected to impose a full lockdown even before having a first case recorded, for example, Finland (Moisio, 2020).

Social scientists, such as economists, tried to measure the empirical effects of these confinement policies on several health and socioeconomic indicators, helping to define optimal measures with minimal economic and social costs. Many empirical studies concerning the outbreak of the COVID-19 pandemic have tried to evaluate the various policies implemented by governments to stem the infection rate. For instance, Zhixiam and Meissner (2020) found that the policies most strongly and significantly associated with slowing the growth in cases were public transport closures, enforced workplace closures, limited domestic travel, and restrictions on international travel. School closures and limits on public events were not found to have a statistically significant effect. For example, from a cross-country perspective, the effectiveness of non-pharmaceutical policies was negatively correlated with per capita GDP, population density, and surface area and positively correlated with health expenditure (Bargain & Aminjonov, 2020; Castex et al., 2020).

There are abundant studies in the literature on the optimization and efficacy of non-pharmaceutical measures against COVID-19. Several authors have used the SIR model pioneered by Kermack and McKendrick (1927) in an optimal control framework with governments seeking to minimize the economic losses resulting from the pandemic (see, for instance, (Alvarez et al., 2021; Atkeson, 2020; Gallic et al., 2021; Gori et al., 2022, 2023; Hritonenko et al., 2021; Caulkins et al., 2021)). Almost all contributions to the literature fail to take into account the epidemiological evidence according to which the adverse effects of COVID-19 vary greatly among different demographic groups, being more severe in the elderly. Gallic et al. (2021) used a SIR-based model to compare two different policies with respect to their economic costs, one aimed at reaching natural herd immunity as Sweden and the Netherlands did during the pandemic’s first wave, and another opposing strategy aimed at flattening the epidemic curve and avoiding congestion in intensive care units; their hypothesis was that infection rates and the probability of needing intensive care did not differ between age groups. Hritonenko et al. (2021) added a delay in the COVID-19 infection process in a modified SIR model to improve the prediction of the waves of the pandemic and more accurately assess the corresponding mitigation policies. Caulkins et al. (2021) used a baseline SIR model to investigate the optimal lockdown intensity (the authors use the term “optimal degree of lockdown”) as the infection rate evolved. Here again, an underlying hypothesis is that the adverse effects of infection did not differ among demographic groups. Aspri et al. (2021) engaged in a similar exercise by introducing restrictions to the functions accessible to the social planner and, in particular, imposing the requirement that they remain constant over some fixed period. Again, one of the limitations of the study was the assumption that the effects of the virus are constant across the population.

To the best of our knowledge, there are very few studies that take into account this epidemiological evidence when trying to determine the optimal lockdown policy. One is certainly that of Gori et al. (2023), which extends the papers by Alvarez et al. (2021) and Acemoglu et al. (2021), by considering one additional control (namely, the tax rate to finance vaccine production), thus obtaining two optimal trajectories of social distancing (lockdown) and cost of vaccination in different scenarios, which basically depend on the weight the social planner gives to the direct epidemic costs compared to the indirect (economical) costs and the characteristics of the vaccines. In their paper, they develop a two-stage optimal control problem, where in the first stage, the social planner uses the only available control (i.e. social distancing), while in the second stage, vaccines become available and this control is added to the model. A combination of the two policies, i.e. social distancing and vaccination, outperforms the single social distancing policy, and the longer the vaccine-free period, the worse the effectiveness of the cost-minimization policy. Another study aimed at determining the optimal containment policies is that of Gori et al. (2022). The authors compared two non-pharmaceutical policies, specifically, a generalized lockdown measure and a test and trace isolation policy for limiting the adverse effect of COVID-19 with particular attention to capital accumulation, using as a baseline a SIR model in which all individuals were assumed to be identical in their health characteristics. Unlike these papers, we assume that the social planner can implement specific policies based on the age of the population, thus exploiting the different epidemiological impact that the COVID-19 pandemic has on various demographic groups. This is the main advantage and innovation of our paper, which basically combines lockdown and vaccination policies aimed at different demographic groups of the population. We assume that vaccination is available from the first period, which makes our model better fit a second wave of pandemic, while Gori et al. (2023), instead, assume that vaccines are available after a certain time, so they fit the entire period of the pandemic.

Few scholars have supported the idea that specific age-based confinement policies could be beneficial in saving lives and minimizing losses.² Two contributions on this topic are the following. Gollier (2020) assessed two different policies (referred to as “suppression” and “flatten the curve” strategies that traded loss of life and GDP, respectively) on a uniform basis with a heterogeneous population, finding that in France confining the elderly throughout the pandemic would halve economic costs by a factor of two. In a similar exercise, Acemoglu et al. (2021) came to similar conclusions. These contributions, like our own, support the idea that age-targeted lockdown policies work better both in terms of loss of life and loss of GDP using a SIR model as the underlying epidemiological transmission scheme. It is worth emphasizing that the contribution by Acemoglu et al. (2021) integrates a SIR model in an optimal control problem that minimizes a loss function and assumes that the population is divided into three groups (young, middle-aged, and old) with different levels and rates of infection, hospitalization, and mortality. Their main result is that a policy with differentiated lockdown intensities for different demographics outperforms a uniform lockdown policy, allowing more effective minimization of the economic losses resulting from the containment policy. In their model, Acemoglu et al. (2021) assume that the detection and isolation of an infected individual are imperfect and that once an individual recovers, they become immune for the remainder of the period. An individual can only assume four different states: susceptible, infected, recovered, or dead.

In the studies cited above, lockdown measures are studied until the vaccines were released. After such a release, the authors assumed that the lockdowns were no longer needed. This is a first point that distinguishes our research and represents an added value that our paper offers. However, we must point out that our model is similar to that of Acemoglu et al. (2021); Buratto et al. (2022), and Gori et al. (2023). The similarities with those papers are that we consider a SIR-based epidemic model under the effect of socioeconomic costs and and we build an optimal protection strategy using optimal control. However, our paper differs from those contributions since it is a bit more sophisticated: first of all, we introduce different demographic groups (young, adult, and old) and, secondly, we extend the classical SIR model by adding Asymptomatic, Quarantined, and Dead subgroups.³ We also consider two types of controls, that is, quarantine and vaccination, and compare their effectiveness in order to minimize the social cost function. That is, we allow differentiation in the types of costs that an economy faces, and in the vaccination strategy that is offered. We also work with a structured but not randomly distributed population and as a result we use the SQAIRD model under the network formulations. Therefore, the control strategies are different, as well as the technical differences in the method to solve the optimal control problem. Hence, our dynamics of the infection path are slightly different from those of Acemoglu et al. (2021) and Gori et al. (2023). Crucially, in our model, vaccines are available and are used as an additional control to minimize the social losses of the pandemic. Our model does not admit individual behavior: both lockdown and vaccination, if prescribed by the government, are fully accepted by the population.⁴ In other words, while the models assumed by Acemoglu et al. (2021), Gori et al. (2023) and others apply to the pandemic’s first wave, our model is a better fit for the longer term and accounts for subsequent waves in which vaccines are potentially available, with their cost included as a positive component of total pandemic costs. The reason why we use vaccination⁵ as an additional control for the social planner is that since vaccines are costly, and since some strata of the population may experience slight effects or very dramatic consequences from the virus: total vaccination or no vaccination may not be optimal since it does not minimize social costs, so a graduation of this policy may be preferable. In the rest of this paper, we assume that vaccine production is private and that the social planner assumes a fixed cost for each injected dose.

Our paper has two aims. First, it aims to explain the great variety of policies implemented by similar countries in Europe and globally. One may wonder if there are reasons for these differences in response that are not explained by culture or lifestyle differences; for example, these differences are evident among rich and developed countries with similar cultural backgrounds and geological and climate characteristics. As discussed below, extreme policies of full lockdown or the total absence of any confinement measure can be justified by the concavity of the social cost function of the country, which in turn implies non-decreasing returns to scale. By contrast, when the social cost functions are convex, “intermediate” or “moderate” policies become optimal and the optimal intensity of lockdown can be defined (or can specify the appropriate groups for confinement), and the optimal level of vaccination s determined to minimize economic losses.⁶ It is widely documented that China’s policy for limiting the diffusion of the pandemic was a very strict lockdown in the cities and regions implicated, even after the initial wave. This is consistent with the claim by Ren and Jie (2019) that China’s strategy for economic growth from 1993 to 2015 was to implement structural reforms on the supply-side of the economy to decrease the share of sectors characterized by constant and/or decreasing returns to scale and fostering and subsidizing sectors characterized by increasing returns to scale. In Finland, Mukkala (2004) documented that regional concentration of economic activities was prevalent in almost every industry for which the choice of location does not depend on natural resources, thus showing the existence of agglomeration economies that exploit the positive externalities due to specialization; similar conclusions can be drawn for Sweden (Andersson et al., 2019). Assuming concavity of a country’s cost functions justifies extreme confinement or vaccination policies, many scholars have studied the dynamics of infection and its impacts on economies assuming convexity of costs.⁷

Our numerical simulations corroborate the results in terms of optimizing the lockdown time policy and the socioeconomic costs while considering the heterogeneity of the economic agents (elderly, adults, and young people). We also simulate the dynamic of the pandemic with no policy implemented. Simulations highlighted the fact that: a) a policy of lockdown is always better than the laissez faire policy, because it limits the costs that the pandemic generates in an uncontrolled situation; b) a targeted policy by age of the individuals is better than a uniform policy in terms of costs that it generates, being a targeted policy less costly and equally effective in the control of the pandemic. In the numerical exercises, the parameters of the model were calibrated according to the empirical evidence taken from data of the websites: https://www.worldometers.info/coronavirus/ and https://ourworldindata.org/coronavirus. Our model can be applied to any country, but we decided to consider the case of the spread of the virus in Italy during the second wave of Covid-19 (Bontempi, 2021),⁸ so we select data on the recovered, infected and dead people by age group.

The reminder of the paper is organized as follows: Sect. 2 illustrates the epidemic process; Sect. 3 presents the theoretical optimal control problem, and derives the conditions under which extreme lockdown policies or moderate policies are optimal; Section 4 calibrates the model under the hypothesis of a convex cost function, defines the functional form of the objective and state equations and sets out the numerical results. It is important to point out that calibration of the costs and parameters used in the model are based on data available for Italy. Section 5 concludes.

2 The epidemic process

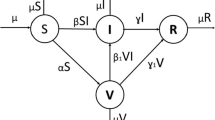
We model virus spread in a population by extending a classical Susceptible-Infected-Recovered-Dead (SIRD) model by Allan (2008), Altman et al. (2011); Gubar and Zhu (2013), and Gubar et al. (2017). Within this model, we first divide the population into three demographic groups, denoted by $p=1,2,3$, representing youth (1), adults (2), and older persons (3), respectively. Within each demographic group, the population is divided into six subgroups: Susceptible (S), Quarantined or Isolated (Q), Asymptomatic (A), Infected (I), Recovered (R), or Dead (D). This division of the population, as previously mentioned, extends the classical SIRD model by introducing two additional groups comprising individuals who are quarantined and asymptomatic. The SIRD model thus becomes a “SQAIRD” model, specifically:

• The Susceptible group, S, comprises those who are exposed to the virus and are, at the beginning of the pandemic, the majority of the population.

• The Quarantined group, Q, includes individuals isolated at home, by law or voluntarily. People are quarantined before contracting the disease, which makes sense when viewing quarantine as a preventive measure (but also in this case where there could have been a contact with an asymptomatic person) in line with the COVID experience (asymptomatic patients are generally quarantined while infected patients are hospitalized).⁹

• The Asymptomatic group, A, comprises individuals who have the virus but did not exhibit symptoms. These people can behave as if susceptible but they can also infect other people. Once infected, a person in this group will either recover (then shift into the group of recovered individuals, R) or develop symptoms, then shifting in the group I of the infected with symptoms with probability $\alpha _p \in (0,1)$, for each demographic group $p=1,2,3$.

• Those belonging to the infected I group, on the other hand, can recover and go to the R group or die going to the D group.¹⁰

At each time t and for each demographic group p,a fraction of the groups of susceptible, quarantined, infected, recovered and dead individuals exist, and are denoted by $S_p(t)$, $Q_p(t)$, $A_p(t)$, $I_p(t)$, $R_p(t)$ and $D_p(t)$, respectively. By normalization:

$$\begin{aligned} \sum _{p=1}^3 S_p(t)+ \sum _{p=1}^3 Q_p(t) +\sum _{p=1}^3 A_p(t) +\sum _{p=1}^3 I_p(t)+\sum _{p=1}^3 R_p(t)+\sum _{p=1}^3 D_p(t)=1, \end{aligned}$$

(1)

The sum of the group shares is equal to one. The entire population is assumed to be constant and equal to $N = 1$ throughout the period of analysis.¹¹

At the beginning of the pandemic ($t=0$), most people were members of the Susceptible group, and a small fraction of people were infected (see, for example, Sahneh et al. (2013); Mieghem et al. (2009)Taynitskiy et al., 2018). Hence, for each demographic group p, the initial states are:

$$\begin{aligned}{} & {} S_p(0) =S_p^0>0, \\{} & {} Q_p(0) =Q_p^0\ge 0, \\{} & {} A_p(0) =A_p^0\ge 0, \\{} & {} I_p(0) =I_p^0>0, \\{} & {} R_p(0) =R_p^0\ge 0, \\{} & {} D_p(0) =D_p^0=N_p-S_p^0- Q_p^0-A_p^0-I_p^0-R_p^0. \end{aligned}$$

where $\sum _{p=1}^3 N_p = 1$ and $S_p(t)+Q_p(t)+A_p(t)+I_p(t)+R_p(t)+D_p(t)=N_p$. The following Fig. 1 illustrates the pandemic process in this SQAIRD model. In such a scheme, the arrows indicate the infection process among the groups, ending at the node of agents that are either recovered or dead.

Fig. 1

The scheme of epidemic process, index is $p=1,2,3$. Nodes corresponds to the fraction of infected people in the entire population

Figure 1 clearly depicts the pandemic process. Specifically, we provide as follows:

• A Susceptible individual would be infected and shift into the category of Asymptomatic with probability $\beta _p=\beta , \; \forall p=1, 2, 3$. We assume that $\beta$ is constant for all categories of individuals (youth, adults and old people). A susceptible person can also shift into the Quarantined group by their own free will - they decide to isolate (that is, stay at home) with probability $\gamma _p$ to isolate himself (i.e. stay at home). Another reason why a susceptible person can shift into the quarantined group is by law (the government implement a lockdown policy) with probability up. These measures (irrespective of whether they are defined by people’s will or by law) have the effect of reducing the number of susceptible people that can be infected, so these measures are also able to reduce the speed of circulation of the virus.¹²

• The $\delta _p$ parameter defines the probability of breaking the quarantine rules. So people can recover naturally with probability $(1-\alpha _p)\sigma _p$ (where $\alpha _p$ represents the probability of developing symptoms once infected and $\sigma _p$ is the natural rate of recovery) or develop symptoms with probability $\alpha _p$.

• The parameter $k_p$ represents the “speed" at which an asymptomatic individual shifts into the Infected group.¹³ Once infected, she/he can recover with a rate $\sigma _p$ or die with a rate $\mu _p$.¹⁴ Notice that the probability to recover or to die differs between demographic groups, contrary to the probability of catching the virus (i.e., transitioning to the asymptomatic group).

• The parameter $v_p$ measures the intensity of vaccination in each group $p= 1, 2, 3$. That is, the intensity of vaccination is different for each demographic group, but for example at the end of the pandemic process it could be the same intensity of vaccine application in each group.

Therefore, according to the virus propagation process that we have just described, we formalize all this through the following differential equations:

$$\begin{aligned} \frac{dS_p(t)}{dt}= & {} -\beta S_p(t)A(t)-(u_{p}(t)+\gamma _p)S_p(t)-v_pS_p(t), \end{aligned}$$

(2)

$$\begin{aligned} \frac{dQ_p(t)}{dt}= & {} (u_{p}(t)+\gamma _p)S_p(t)-\delta _p\beta Q_p(t)A(t), \end{aligned}$$

(3)

$$\begin{aligned} \frac{dA_p(t)}{dt}= & {} \beta S_p(t)A(t)+ \delta _p\beta Q_p(t)A(t) - \alpha _pk_pA_p(t)-(1-\alpha _p)\sigma _pA_p(t), \end{aligned}$$

(4)

$$\begin{aligned} \frac{dI_p(t)}{dt}= & {} \alpha _pk_pA_p(t)-( \sigma _p+\mu _p)I_p(t), \end{aligned}$$

(5)

$$\begin{aligned} \frac{dR_p(t)}{dt}= & {} \sigma _p I_p(t)+(1-\alpha _p)\sigma _p A_p(t)+v_pS_p(t), \end{aligned}$$

(6)

$$\begin{aligned} \frac{dD_p(t)}{dt}= & {} \mu _p I_p(t). \end{aligned}$$

(7)

Where in Eqs. (2)–(7) the term $A(t)=\sum _{p=1}^{3} A_p(t)$ indicates the number of asymptomatic individuals in the society at time t. That is, specifically:

• Equation (2) describes the dynamics of the Susceptible group, $S_p$. During the pandemic it is intended that this group will decrease as time passes. In fact, a fraction of those in the Susceptible group are infected with probability $\beta$ each time contact with an infected or asymptomatic person occurs. In fact, the probability of becoming infected is proportional to the stock of freely circulating infected people (essentially, the virus spreads by causing infected people to become infected but only exhibit symptoms 1 to 5 days later) and is equal to $\beta A( t)$. Another reason why this group decreases is that people transfer to the quarantine group because they self-isolate or because the government forces them to stay home. This probability is given by by $(u_{p}(t)+\gamma _p)$. Then, the fraction of those in the Susceptible group that to others (in particular, to the Asymptomatic or Quarantined groups) is described by Eq. 2.

• The group of quarantined – as we already mentioned – represents the share of susceptible individuals subject to compulsory isolation ($u_{p}$) or self-isolation ($\gamma _p$). The dynamics denoting the behavior of group $Q_p$ is denoted by Equation (3).

• Equation (4) describes the dynamics of the Asymptomatic group ($A_p$). With the probability $\alpha _p$, an asymptomatic person can develop symptoms and become infected. This happens at the rate $k_p$, reflecting the fact that an asymptomatic person usually takes 5 days to develop symptoms. The asymptomatic person will recover from the virus without developing any symptom with the probability $(1-\alpha _p)\sigma _p$.

• Equation (5) describes the dynamics of the Infected group ($I_p$). There is a positive contribution to this group from asymptomatic individuals who become infected (that is, develop symptoms) at a rate of $\alpha _p k_p$. This group decreases because some of the infected recover and others die. These counterbalancing forces will produce an inverse U-shaped curve describing the number of infected during the pandemic to be, with an increasing trend in the early periods of the pandemic and a negative trend thereafter. As previously mentioned, an infected individual would recover with probability $\sigma _p$ and we assume that an infected person is detected after 5 days of the first appearance of symptoms.¹⁵ Recovery happens, on average, after 30 to 40 days from infection (we assume 30 days for the young, 40 days for adults and 60 days for the elderly). Infected individuals who do not recover are assumed to die with probability $\mu _p$. Therefore, while the Infected group increases because those in the Susceptible group get sick with probability $\beta A(t)$, this group decreases because the infected can either recover or die with probability $(\sigma _p +\mu _p)$.

• Equation (6) describes the dynamics of the Recovered group ($R_p$), which increases over time because some of those infected defeat the virus (this may be due to effective treatment or without intervention), and this happens with probability $\sigma _p$. This probability determines the positive flow of individual coming from the Infected and Asymptomatic groups. Equation 6 formalises this dynamics.

• Equation (7) describes the dynamic of the Deaths group ($D_p$). During the pandemic, it increases over time according to the proportion of those infected who are unable to recover. Then, in each period, this group increases by a proportion of $I_p(t)$ equal to $\mu _p$.

We now proceed to develop the behavioral dynamics for the system of Eqs. (2)–(7) applying network theory to understand the pandemic process described above and schematically represented in Fig. 1 above. An optimal control problem is then applied to minimize the structure of cost functions that are generated in a pandemic as a result of lockdown measures.

2.1 The network epidemic model

Following Shane and Scoglio (2011); Sahneh et al. (2013) and Taynitskiy et al. (2017) we proceed from the ordinary SQAIRD model (the system of equations (2) - (7)) to a Generalized Epidemic Mean-Field (GEMF) model that represents a systematic procedure to design different spreading mean-field models. This extension of the epidemic models allows us to describe any propagation process, formulated in a population and taking into account a contact network. The GEMF model requires the network structure, which defines social contacts in human populations, the agents’ states in a population (susceptible, infected, etc.), and the rules of transition between them. For any specific scenario, the Compartment set, and corresponding influencer compartments should be identified, and transition rate graphs determined.

Definition 1

Complex network is defined by graphs G(N, Y), where N is the set of nodes and Y is the set of edges, that represent the connections between nodes.

In our case the network consists of $N=N_1+N_2+N_3$ interacting agents in the entire population, each of whom can be in one of the states (compartments). In the general case we assume that each agent can be in one of the states or compartments $M_p=\{S_p,Q_p,A_p,I_p,R_p,D_p\}$. Such a network makes it possible to take into account various patterns of contacts between the agents of the population. Interaction between agents is defined by an adjacency matrix $C=\{c_{ij}\}$. If an agent i contacts an agent j, then $c_{ij}=c_{ji}=1$, otherwise $c_{ij}=0$. A general rule for the revision of the population states can be represented as follows.

• 1. First, let agent i, which remains in state $w_{ia}=a$, move to state $w_{ib}=b$ with probability $r_{ab}$. This transition $a\rightarrow b$ occurs independently of the neighbors of agent i. For example, the transition $I_p\rightarrow R_p$ in the SQAIRD network gives probability $r_{I_pR_p}=\sigma _p$.

• 2. Second, the stochastic transitions of an agent may depend not only on its own state, but also on the states of other agents $j\in \{1,\ldots , M_p\}\setminus \{ i\}$, where $c_{ij}=c_{ji}=1$. For example, the transition $S_p\rightarrow A_p$ in such a network, where $r_{S_pA_p}=\beta _p.$

We now present several definitions to define the transition between subpopulations in the network formulation of the SQAIRD model

Definition 2

A nodal transition is a process that occurs independently of the states of other agents (see Fig. 2. From the definition of 2 we can say that the agents of the infected subgroup recover only according to the recovery factor $\sigma$ and not by agents of other groups).

Fig. 2

Nodal transition

Definition 3

An edge-based transition is a process that occurs as the result of interaction between a pair of agents an edge-based transition. Edge-based transitions are different from nodal transitions because they depend on the states of other agents (see Fig. 3).

Fig. 3

Edge-based transition

Definition 4

An influencer compartment q is any state in the network which impacts the Edge-Based Transition.

Remark 1

A state q is defined as an influencer compartment if it causes the transition of a given node i to the state j. For example, in the basic SIR model the state of Infected is the influencer compartment for the contact network. In our extended model state, $A_p$ is an influencer compartment in a susceptible state in each demographic group. This causes the transition from the susceptible to the asymptomatic state under the impact of the asymptomatic agent.

Therefore, to consider the SQAIRD model mapped as a GEMF model, transitions from infected to recovered subpopulations occur regardless of the status of neighbors, while transition from the susceptible subpopulation depends on asymptomatic individuals and can be described by a different mechanism, that is, a graph $\mathbf {\mathcal {{\hat{G}}}}(\mathbf {{\mathcal {N}}},\mathbf {{\mathcal {Y}}})$ describing nodal transitions.

• That is, we have an influencer compartment $q_p\in \{1,\ldots ,M_p\}$ and a graph $\mathbf {\mathcal {{\hat{G}}}}(\mathbf {{\mathcal {M}}},\mathbf {{\mathcal {Y}}})$, which corresponds to the network G. Here $\mathbf {{\mathcal {M}}}$ is a set of nodes. For the influencer compartment state, we define a population state $q_p$ that influences the edge-based transition. The set $\mathbf {{\mathcal {Y}}}$ is the set of edges that corresponds to connections between agents.

• It is supposed that if a transition $i\rightarrow j$ is the edge-base or nodal transition then it occurs with a probability $r_{ij}$.

• A graph $\mathbf {\mathcal {{\hat{G}}}}(\mathbf {\mathcal {M_p}},\mathbf {{\mathcal {Y}}})$ can be represented by adjacency matrices of edge-based transition rates X or a matrix of Kirchhoff K. Let $i,j\in \{1,\ldots ,M\}$ then the components of the matrix X are determined by the rule: if the edge-base transition $i\rightarrow j$ exists and its probability $r_{ij}$ is defined, then $a_{{ij}}=r_{ij}$, and 0 otherwise.

Definition 5

The adjacency matrix of edge-based transition rates corresponding to graph G(N, Y) is denoted by $X=[a_{{ij}}]$. Its elements are defined by the rule

$$\begin{aligned} \begin{array}{l} x_{ij}=\left\{ \begin{array}{l} r_{ij},\text{ for } \text{ the } \text{ edge-base } \text{ transition }\ i\rightarrow j,\ {i, j}\in \{1, M\}\\ 0, \text{ otherwise }. \end{array}\right. \end{array}\end{aligned}$$

(8)

Definition 6

Elements of the Kirchhoff’s matrix $K=[q_{ij}]$ are defined in the following way:

$$\begin{aligned} \begin{array}{l} k_{ij} = {\left\{ \begin{array}{ll} \displaystyle \sum _{\begin{array}{c} 0 <j\leqslant {\mathcal {M}}\\ (i, j)\in {\mathcal {Y}} \end{array}} \omega _{i j}, &{} \hbox { if}\ i=j;\\ - \omega _{i j}, &{} \text {if }(i, j)\in {\mathcal {Y}};\\ 0, &{} \text {otherwise.}\\ \end{array}\right. } \end{array}\end{aligned}$$

(9)

Matrix $K^{\xi }$, that corresponds to graph of nodal transitions, is defined analogously to K. A graph $\mathbf {\mathcal {{\hat{G}}^{\xi }}}(\mathbf {{\mathcal {M}}},\mathbf {{\mathcal {Y}}})$ describes nodal transitions.

2.1.1 Stochastic (Markov) network model

Next, we represent the extended SQAIRD model for different infected subpopulations, belonging to precise demographic groups, as the N-interwined model (see Mieghem et al. (2009)). As discussed above, each agent in each demographic subpopulation (elderly, adult, and young) may be in the susceptible, asymptomatic, infected, recovered, or dead (compartment) subgroups. Therefore, the number of compartments in this case is $M_p=6$, while the influencer compartments in this case are $q_p=A_p$, $p=\overline{1,3}$.

Definition 7

The vector $W_i(t)=[w_{i,1}(t),w_{i,2}(t),\ldots w_{i,M}(t)]$ shows the states of a node i, where $w_{ i,k} (t)$ is the probability that node i at time t is in state k, where the condition that must be met is $w_{i,1}+w_{i,2}+\ldots +w_{i,M}=1.$

Therefore the variables $S_p(t)$, $Q_p(t)$, $A_p(t)$, $I_p(t)$, $R_p(t)$, $D_p(t)$, $p= 1,2,3$ that correspond to the fractions of the relevant nodes (susceptible, quarantined, asymptomatic, infected, recovered and dead), can be rewritten in terms of the vector $W_i(t)$:

$\displaystyle S_p(t)=\frac{\sum \limits _{i=1}^N w_{i,S_p}(t)}{N},$ $\displaystyle Q_p(t)=\frac{\sum \limits _{i=1}^N w_{i,{Q_p}}(t)}{N},$ $\displaystyle A_p(t)=\frac{\sum \limits _{i=1}^N w_{i,{A_p}}(t)}{N},$

$$\begin{aligned} \displaystyle I_p(t)=\frac{\sum \limits _{i=1}^N w_{i,{I_p}}(t)}{N}, \displaystyle R_p(t)=\frac{\sum \limits _{i=1}^N w_{i,R_p}(t)}{N},\displaystyle D_p(t)=\frac{\sum \limits _{i=1}^N w_{i,{D_p}}(t)}{N}. \end{aligned}$$

Based on the theory of Markovian processes, the vector state evolutions $W_i$ for a node $i \in \{1, \ldots , N\}$ of the generalized GEMF model (Sahneh et al., 2013) are defined as:

$$\begin{aligned} \frac{d W_i(t)}{dt}= -(K^{\xi })^\textrm{T}W_i - \sum \limits _{j=1}^N c_{ij} w_{j,A_p} K^\textrm{T}W_i; \end{aligned}$$

(10)

for $i \in \{1, \ldots , N\}$. Here K is the Kirchhoff’s matrix. Each equation in the system (10) contains two terms, the first describes the evolution of the vector of states under the influence of edge-based transitions. The second term defines the nodal transitions, corresponding to matrix $K^\xi$. Where the probabilities of being susceptible, infected, and recovered are denoted by $W_{i,S_p}$, $W_{i,{I_p}}$, and $W_{i,R_p}$ and the state vector is

$$\begin{aligned} W_i(t)=\left( w_{i,S_p}(t),w_{i,{Q_p}}(t), w_{i,{A_p}}(t), w_{i,{I_p}}(t),w_{i,R_p}(t), w_{i,{D_p}}(t) \right) ,\; i=1,\ldots ,N, \end{aligned}$$

N, is the set of nodes and $p=1,2,3$ is the number of subgroups. The sum $\sum \nolimits _{j=1}^N c_{ij} w_{j,A_p}$ is the value of the effect of influencer compartment j on the node i, where $j\in \{1,\ldots ,N\}\setminus \{i\}$, for each $c_{ij}=c_{ji}=1$.

In this case the adjacency matrix of the edge-based transition rates on the subgroup p is:

$$\begin{aligned} Adj_{p}= \left[ \begin{array}{llllll} 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right] ; \end{aligned}$$

The corresponding Kirchhoff’s matrix of the group p can be calculated as:

$$\begin{aligned} K_p= \left[ \begin{array}{llllll} \beta &{} 0 &{} -\beta &{} 0 &{} 0 &{} 0 \\ \beta &{} 0 &{} -\beta &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array}\right] . \end{aligned}$$

Figure 4 represents the transition probabilities of the contact network, and Fig. 5 shows the nodal transitions for the extended SQAIRD model.

Fig. 4

Graph of transition probabilities of SQAIRD model

Fig. 5

Graph of the nodal probabilities

Nodal transition In the current SQAIRD model, the nodal transition describes the processes that appear in the system independently of the other states. It includes the application of quarantine and vaccination measures to prevent the spread of the virus and transitions (from the infected to the recovered or dead state). The adjacency matrix of nodal transition rates is defined as follows:

$$\begin{aligned} Adj^{\xi }_p= \left[ \begin{array}{llllll} 0 &{} \gamma _p+u_p(t) &{} 0 &{} 0 &{} v_p(t) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \alpha _p k_p &{} (1-\alpha _p)\sigma _p &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \sigma _p &{} \mu _p \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right] ; \end{aligned}$$

where Kirchhoff’s matrix is:

$$\begin{aligned} K^{\xi }= \begin{bmatrix} \gamma _p+u_p(t)+v_p(t) &{} -\gamma _p-u_p(t) &{} 0 &{} 0 &{} -v_p(t) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \alpha _p k_p+(1-\alpha _p)\sigma _p &{} -\alpha _p k_p &{} -(1-\alpha _p)\sigma _p &{} 0 \\ 0 &{} 0 &{} 0 &{} \sigma _p+\mu _p &{} -\sigma _p &{} -\mu _p \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{bmatrix} \end{aligned}$$

System (11) describes the states (10) in terms of fractions $S_p$, $Q_p$, $A_p$, $I_p$, $R_p$, and $D_p$ for each node i in the network.

$$\begin{aligned} \begin{array}{l} \left[ \begin{array}{ccc} \dot{S_p} \\ \dot{Q_p} \\ \dot{A_p} \\ \dot{I_p} \\ \dot{R_p} \\ \dot{D_p} \\ \end{array} \right] _i =-K_p^{\xi } \left[ \begin{array}{ccc} S_p \\ Q_p \\ A_p \\ I_p \\ R_p \\ D_p \\ \end{array} \right] _i- \sum ^N_{j=1}c_{ij} A_p K^T \left[ \begin{array}{ccc} S_p \\ Q_p \\ A_p \\ I_p \\ R_p \\ D_p \\ \end{array} \right] _i \end{array}\end{aligned}$$

(11)

Thus, we rewrite system (2)–(7) using the Kirchhoff’s and adjacency matrices and obtain System (11). We use such notations to make the transition from a randomly distributed population to a population on a network. As a result, it will be possible to use our model to analyze the propagation of the virus on the specific networks with different connectivity parameters. Next, we formulate the optimal control problem for System (11) and analyze the situation where the government implements a mandatory lockdown policy for each demographic group (young, adult, and old). Depending on the cost structures in the economy, various scenarios may emerge that justify different policy approaches implemented by similar countries (both in terms of infection level and other characteristics). In addition, it is possible to show, with numerical simulations, that policies focused on the different demographic groups allow reducing the economic losses of the confinement.

3 The optimal control problem

Estimates of the economic losses caused by the COVID-19 pandemic are highly relevant: Harary and Keep (2021) estimated a loss in the UK’s annual GDP of approximately 9.7% during 2020, with respect to the previous year and a loss of 25% in April 2020 with respect to two months earlier. In the first quarter of 2020, Eurostat estimated that Italy’s GDP dropped by 5.2% with respect to the GDP of the previous quarter. The picture for many other European countries is no less dramatic. The reasons for this are that illness and lost lives have a huge impact on the labor market due to the temporary and permanent loss of human capital. A negative shock in the labor force negatively affects production, potentially resulting in an impoverished population and a decrease in economic growth. The pandemic has also had a strong negative effect on the health system, which has to bear the treatment costs of a great number of infected, often without the necessary technical and human resources. Politically, a pandemic that is not well managed may affect the political choices of the citizens and jeopardize the government’s re-election. The correct management of a pandemic emergency is of vital importance for any government. Therefore, there is a need to find an effective way to control the impacts of pandemics, such as COVID-19, with minimal economic and social disruptions.

Optimal control theory, in this special case, may explain how to apply one or more time-varying control policies to a nonlinear dynamic system to optimize a given objective function, which, in this case, could be a cost and profit function (Kissler et al., 2020; Perkins & España, 2020). Here, we apply optimal control theory to determine optimal strategies for the implementation of lockdown policies to control a pandemic. As discussed below, an optimal strategy (that is, a strategy that minimizes the costs of a lockdown) may depend on the socioeconomic cost structure of the economy, in particular, on the concavity or convexity of these functions.

We introduce the objective function to be optimized by the government, using as controls the lockdown measures $u_p(t)$, $p=1,2,3$ and vaccination $v_p(t)$, $p=1,2,3$. This objective function is determined by the sum of direct and indirect costs related to the management of the pandemic, eventually summed to a “profit function” for those who re-enter the job market after recovery. In other words, the government has to optimize the balance between profits and costs through the application of a policy that requires a fraction of those who are susceptible to stay isolated and avoid contact with other individuals. This policy is differentiated between demographic groups; that is, the obligation for the young and susceptible individuals could be different from that for adults or for old and susceptible individuals. We define the following:

• $f_p(I_p(t))$ is a function measuring the direct costs of infection, with a non-decreasing, twice differentiable function, such that $f_p(0)=0$, $f_p(I_p(t))>0$ for $I_p(t)>0$. These costs can be interpreted as the price the government pays for the health system to treat the infected and increase the probability of recovery for the treated individuals. Infected individuals who are not detected because they are asymptomatic are not treated, and therefore there are no direct costs for them.

• It is also costly to impose quarantine on those who are susceptible or for individuals to self-isolate to avoid contact with infected people. While there are no direct costs of medical treatment because they are not sick, these individuals stay away from the job market, meaning that they stop producing for the whole period of isolation. Similarly, for the infected, the interruption of production implies a loss (and this may require corrective action in support of the necessary consumption of those heavily affected by the lockdown) and a decrease in government revenue. We model such socioeconomic costs by using functions $h^S_1(u_1(t))$, $h^S_2(u_2(t))$ and $h^S_3(u_3(t))$,that depend on the fraction of isolated susceptible individuals belonging to the three groups: (1) young, (2) adults, and (3) old. These functions $h^S_{p}(u_{p}(t))$ are assumed to be increasing in the arguments $u_{p}(t)$, and twice differentiable, such that $h^S_{p}(0)=0$, $h^S_{p}(u_{p}(t))>0$ when $u_{p}(t)>0$ for each $p=1,2,3$.

• Vaccination $v_p(t)$ generates costs for the health system and society; however, its socioeconomic cost is lower than the costs of having high levels of infections since the latter requires the entire health system for the treatment of those infected. Let us denote by $h^{vac}_p(v_p(t))$ the vaccination cost function.

• The treatment or medical cure of those infected produces direct costs for society, while both isolation and hospitalization and death produce indirect costs because people are prevented from working, or the market suffers a loss of human capital. The function $h^I_p(I_p(t))$ represents the indirect costs of treating the infected (by isolation and hospitalization) to keep them out of the labor market until recovery. The function $h^I_p(I_p(t))$ is increasing on the argument $I_p(t)$, is twice differentiable, and is such that $h^I_p(I_p(0))=0$.

• Furthermore, each life lost (death) produces a cost for society, that is, a loss of human capital. This cost is assumed to be constant for each individual in a given demographic group (but varies between groups). We define these costs by means of the function $h^D_p(D_p(t))$.

Hence, the problem that a government must face is maximizing the difference between benefits and costs, using as controls the lockdown measures, $u_p(t)$, and vaccination $v_p(t)$ for each demographic group $p=1,2,3$ and taking into account the dynamics of the pandemic as represented by System (11) or the system of Equations (2)-(7). The cost-profit function is mathematically represented by the following equation:

$$\begin{aligned} J(u_1,u_2,u_3,v_1,v_2,v_3)=J_1(u_1,v_1)+J_2(u_2,v_2)+J_3(u_3,v_3) \end{aligned}$$

(12)

where

$$\begin{aligned} J_p(u_p,v_p)= & {} \displaystyle \int _{0}^{T} \Big [ f_p(I_p(t))+h^I_p(I_p(t))+h^S_{p}(u_{p}(t))+h^{vac}_{p}(v_{p}(t))+h^D_p(D_p(t))\Big ]dt,\nonumber \\{} & {} \quad p=1,2,3. \end{aligned}$$

(13)

Therefore, the problem that the Government faces is optimizing the objective function (13), subject to the SQAIRD dynamics represented by Equations (2)-(7).

Recall that we define the costs $h^S_p(u_p(t))$ and $h^{vac}_p(v_p(t))$  $p=1,2,3$ as twice differentiable and increasing in their arguments, but we did not specify the sign of the second derivative, which may imply convex or concave cost functions. This behavior dramatically changes the optimal duration of a lockdown. Proposition 1 states our main theoretical result.

Proposition 1

If the cost functions $h^S_p(\cdot )$ or $h^{vac}_p(\cdot )$, $i=1,2,3$ are concave, that is, the second derivative with respect to their arguments are negative or equal to zero, then there exists an optimal $t_0 \in [0,T]$ such that for any $p=1,2,3$,

$$\begin{aligned} u^*_p(t)=\left\{ \begin{array}{l} u_{max},\ \text{ for }\ 0\le t\le t_0;\\ 0,\text{ for }\ t_0<t\le T.\end{array}\right. \end{aligned}$$

This means that the solution is a corner solution, implying that there exists a threshold period $t_0$ such that below such a threshold, the optimal policy is to impose total lockdown ($u_{max}=1-\gamma _p$), for the whole population and, above this threshold, the optimal policy is to not impose any lockdown. The reason for this result is quite intuitive. As long as the period of lockdown is short enough, the economic losses in terms of production are smaller relative to the benefits due to infections avoided, the treatment for which is costly. If the period of lockdown increases above the threshold, then it is preferable to bear the costs of infection rather than the losses due to missed production.

If, instead, the costs $h^S_p(\cdot )$ or $h^{vac}_p(\cdot )$, $p=1,2,3$ are convex, that is to say, the second derivative with respect to their arguments are greater or equal to zero, there exists two time moments, which we denote by $(t_0, t_1)\in [0,T]$ such that, for any $p=1,2,3$ and $\zeta (t) \in (0,u_{max})$,

$$\begin{aligned} u^*_p(t)= \left\{ \begin{array}{l}u_{max}, 0\le t\le t_0;\\ \zeta (t),t_0<t\le t_1;\\ 0,t_1<t\le T.\\ \end{array}\right. \end{aligned}$$

Note that if the costs of quarantine are convex, then, in addition to the corner solutions identified previously, there exists an interior solution identified by the fraction $\zeta (t)$ of the isolated population if the period of lockdown lies between these two thresholds $t_0$ and $t_1$.

This optimal lockdown model can explain the dramatically different policies implemented by several countries in Europe and elsewhere. For example, it is not surprising that countries like Sweden decided not to force citizens into strict confinement, limiting themselves to suggesting the well-known measures of social distancing, the use of masks, and attention to personal hygiene. The opposite case could be Finland, which imposed a strict lockdown for all productive activities (with very few exceptions) and a strict curfew for citizens even before recording a single death from the virus. This difference can be attributed to the concavity of the social cost function, which, in turn, depends on the structure of the economy. It is documented in the economic literature that both Finland and Sweden’s economic and productive organizations benefit from increasing returns to scale due to the agglomeration of industries that can benefit from the positive externalities due to specialization (Mukkala, 2004; Andersson et al., 2019). China, which also implemented a very extreme confinement policy for its citizens, had, during the years immediately before the beginning of the pandemic, implemented important structural reforms aimed at promoting sectors exhibiting increasing returns to scale (Ren & Jie, 2019).

Claim 1

Economies exhibiting increasing returns to scale have a concave cost structure with respect to the duration of the confinement policy. The government will optimally decide either to apply a full lockdown or no lockdown at all.

Claim 2

Economies that, on the contrary, exhibit non-increasing returns to scale, and are characterized by convex cost structures, will choose an “intermediate” policy of lockdown by selecting the optimal intensity during the duration of the pandemic.

In addition, we can state that an obvious consequence of the above analysis is that at $t_0\in (0, T)$, an optimal strategy is for the government to introduce a policy of selective confinement. This strategy has the objective of protecting the population from the spread of the virus by selectively choosing the most vulnerable and/or least productive individuals for confinement while allowing others to maintain their economic activity.

Remark 2

Our analysis indicates that from the initial moment $t_0\in (0, T)$, the fight against COVID-19 requires flexibility in economic activities, but only if each of the following conditions is strictly respected: there are rules to contain the virus combined with more selective containment and lockdown measures and these are determined based on age groups.

Next, we provide the formal proof for the optimization of the Hamiltonian obtained from Equation (13) considering the concave and convex cost function. The reasoning offered is formally robust and intuitive, providing an understanding of how the optimization works in the two different cases.

3.1 Hamiltonian and the adjoint system

Let us define the Hamiltonian and the adjoint system for the initial system (2)–(7) of differential equations that describes the propagation of the virus (see Altman et al. (2011); Gubar and Zhu (2013)). By using Pontryagin’s maximum principle (see Pontryagin et al. (1962)), we construct the optimal controls $u(t)=(u_1(t), u_2(t), u_3(t))$ and $v(t)=(v_1(t), v_2(t), v_3(t))$ to the problem described above in Sect. 2. To simplify the presentation, we use short-hand notations $S,I_1,u_1,$ etc. in place of $S(t),I_1(t),u_1(t),$ etc. Define the associated Hamiltonian H and adjoint functions $\lambda _{S_p}(t)$, $\lambda _{Q_p}(t)$, $\lambda _{A_p}(t)$, $\lambda _{I_p}(t)$, $\lambda _{R_p}(t)$, and $\lambda _{D_p}(t)$, $p=1,2,3$ as follows:

$$\begin{aligned} \begin{array}{l} H=H_1+H_2+H_3, \end{array} \end{aligned}$$

(14)

where

$$\begin{aligned} \begin{array}{l} H_p=f_p(I_p)+h^I_p(I_p)+h^S_p(u_p)+h^{vac}_p(v_p)+h^D(D_p)+(\lambda _{A_p}-\lambda _{S_p})\beta S_p\sum _{p=1}^{3} A_p+\\ (\lambda _{Q_p}-\lambda _{S_p})(u_p+\gamma _p)S_p+(\lambda _{I_p}-\lambda _{A_p})\alpha _p k_p A_p+(\lambda _{R_p}-\lambda _{A_p})(1-\alpha _p)\sigma _pA_p+\\ (\lambda _{R_p}-\lambda _{I_p})\sigma _pI_p+(\lambda _{D_p}-\lambda _{I_p})\mu _pI_p+(\lambda _{R_p}-\lambda _{S_p})v_pS_p+(\lambda _{Q_p}-\lambda _{A_p})\delta _p\beta Q_p\sum _{p=1}^{3} A_p. \end{array}\nonumber \\ \end{aligned}$$

(15)

The adjoint system is defined as follows:

$$\begin{aligned} \begin{array}{l} {\dot{\lambda }}_{S_p}(t) = (\lambda _{S_p}-\lambda _{A_p})\beta \sum _{p=1}^{3} A_p+(\lambda _{S_p}-\lambda _{Q_p})(u_p+\gamma _p)+(\lambda _{S_p}-\lambda _{R_p})v_p;\\ {\dot{\lambda }}_{Q_p}(t) = (\lambda _{Q_p}-\lambda _{A_p})\delta _p\beta \sum _{p=1}^{3} A_p;\\ {\dot{\lambda }}_{A_p}(t) = (\lambda _{S_p}-\lambda _{A_p})\beta S_p+(\lambda _{A_p}-\lambda _{I_p})\alpha _p k_p+(\lambda _{A_p}-\lambda _{R_p})(1-\alpha _p)\sigma _p+(\lambda _{Q_p}-\lambda _{A_p})\delta _p\beta Q_p;\\ {\dot{\lambda }}_{I_p}(t) = -f_{p'}(I_p)-h^I_{p'}(I_p)+(\lambda _{S_p}-\lambda _{A_p})\beta S_p+(\lambda _{I_p}-\lambda _{R_p})\sigma _p+(\lambda _{I_p}-\lambda _{D_p})\mu _p;\\ {\dot{\lambda }}_{R_p}(t)=0;\\ {\dot{\lambda }}_{D_p}(t) = -h^D_{p'}(D_p),\\ \end{array}\nonumber \\ \end{aligned}$$

(16)

with the transversality conditions given by

$$\begin{aligned} \lambda _{S_p}(T)=\lambda _{Q_p}(T)=\lambda _{A_p}(T)=\lambda _{I_p}(T)=\lambda _{R_p}(T)=\lambda _{D_p}(T)=0. \end{aligned}$$

(17)

According to Pontryagin’s maximum principle, there exist continuous and piece-wise continuously differentiable co-state functions $\lambda _r(t),\ r\in \{S_p,Q_p,A_p,I_p,R_p,D_p\}$, $p=1,2,3$ that satisfy (16) and (17) for $t\in [0, T]$ together with continuous functions $u^*_p(t)$ and $v^*_p(t)$:

$$\begin{aligned} \begin{array}{l} (u^*_1, u^*_2, u^*_3,v^*_1, v^*_2, v^*_3)\in \text {arg} \min \limits _{{u}_p\in [0,u_{max}],{v}_p\in [0,v_{max}]} H(\lambda _r,S_p,Q_p,A_p,I_p,R_p,D_p,{u}_p,{v}_p).\end{array}\nonumber \\ \end{aligned}$$

(18)

Let us define the functions $\varphi _p(t)$ and $\psi _p(t)$ as follows:

$$\begin{aligned} \begin{array}{l} \varphi _1(t)=(\lambda _{S_1}(t)-\lambda _{Q_1}(t))S_1(t), \psi _1(t)=(\lambda _{S_1}(t)-\lambda _{R_1}(t))R_1(t),\\ \varphi _2(t)=(\lambda _{S_2}(t)-\lambda _{Q_2}(t))S_2(t), \psi _2(t)=(\lambda _{S_2}(t)-\lambda _{R_2}(t))R_2(t), \\ \varphi _3(t)=(\lambda _{S_3}(t)-\lambda _{Q_3}(t))S_3(t), \psi _3(t)=(\lambda _{S_3}(t)-\lambda _{R_3}(t))R_3(t). \end{array} \end{aligned}$$

(19)

3.2 Functions $h^S_p(\cdot )$ or $h^{vac}_p(\cdot )$ are concave

Let $h^S_p(\cdot )$ or $h^{vac}_p(\cdot )$ be concave functions (the second derivative is strictly less than zero), then by (14), the Hamiltonian is a concave function of $u_p$ and $v_p,\ p=\overline{1,3}$. There are two different options for $u_p\in [0,1]$ and $v_p\in [0,1]$ that minimize the Hamiltonian, that is if at time t

$$\begin{aligned} h^S_p(0)-\varphi _p(t)\cdot 0<h^S_p(u_{max})-\varphi _p(t)u_{max}, \\ h^{vac}_p(0)-\psi _p(t)\cdot 0<h^{vac}_p(v_{max})-\psi _p(t)v_{max}, \end{aligned}$$

or

$$\begin{aligned} h^S_p(u_{max})>\varphi _p(t)u_{max}, \\ h^{vac}_p(v_{max})>\psi _p(t)v_{max}, \end{aligned}$$

then optimal control is $u_p=0$ and $v_p=0$ (see Fig. 6 (left)); otherwise $u_p=u_{max}$ and $v_p=v_{max}$ (see Fig. 6 (right)).

Fig. 6

Hamiltonian if functions $h^S_i(\cdot )$ are concave

For $p=\overline{1,3}$, the optimal control parameters $u_p(t)$ and $v_p(t)$ are defined as follows:

$$\begin{aligned} u^*_p(t)=\left\{ \begin{array}{l} 0,\text{ for }\ \ \varphi _p(t)u_{max}<h^S_p(u_{max}),\\ u_{max}, \text{ for }\ \ \varphi _p(t)u_{max}\ge h^S_p(u_{max}).\\ \end{array}\right. \end{aligned}$$

(20)

$$\begin{aligned} v^*_p(t)=\left\{ \begin{array}{l} 0,\text{ for }\ \ \psi _p(t)v_{max}<h^{vac}_p(v_{max}),\\ v_{max}, \text{ for }\ \ \psi _p(t)v_{max}\ge h^{vac}_p(v_{max}).\\ \end{array}\right. \end{aligned}$$

(21)

Concave cost functions indeed imply a concave Hamiltonian. The first order conditions for minimization (i.e. the derivatives of the Hamiltonian with respect to the controls equal to zero) are only a necessary - but not sufficient - condition for minimization, being the second requirement a negative second derivative (concavity). If the second derivative is positive, like in this case, it means that the point obtained is a maximum, not a minimum, therefore the solutions offered by this problem is a "corner" solution, which in this case it means total lockdown or no lockdown at all.

3.3 Functions $h^S_p(\cdot )$ or $h^{vac}_p(\cdot )$ are strictly convex

Let $h^S_p(\cdot )$ or $h^{vac}_p(\cdot )$ be strictly convex functions (second derivative is greater than zero), then Hamiltonian is a convex function. Consider the following derivatives:

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\partial }{\partial x}(h^S_p(x)-\varphi _p x)\mid _{x=x_p}=0, \end{array}\end{aligned}$$

(22)

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\partial }{\partial y}(h^{vac}_p(y)-\psi _p y)\mid _{y=y_p}=0, \end{array}\end{aligned}$$

(23)

where $x_p\in [0,u_{max}]$, $u^*_p(t)=x_p$ ($y_p\in [0,v_{max}]$, $v^*_p(t)=y_p$). There are three different types of points at which the Hamiltonian reaches its minimum (Fig. 7). To find them, we need to consider the derivatives of the Hamiltonian at $u_p=0$ and $u_p=u_{max}$ ($v_p=0$ and $v_p=v_{max}$). If the derivatives (22) at $u_p=0$ are increasing ($h^{S'}_p(0)-\varphi _p\ge 0$), then the value of the control that minimizes the Hamiltonian is less than 0, and according to our restrictions ($u_p\in [0,u_{max}]$) optimal control will be equal to 0 (Fig. 7a). If the derivatives at $u_p=u_{max}$ are non-increasing ($h'_p(u_{max})-\varphi _p<0$), it means that the value of the control that minimizes the Hamiltonian is greater than $u_{max}$. Hence the optimal control will be $u_{max}$ (Fig. 7c); otherwise, we can find such value $u^*_p\in (0,u_{max})$ (see Fig. 7b). The same argument applies to the costs corresponding to the vaccination measures $v_p(t)$.

Fig. 7

Hamiltonian when functions $h_p(\cdot )$ are convex

For $p=\overline{1,3}$, the optimal control parameters $u_p(t)$ and $v_p(t)$ are defined as follows:

$$\begin{aligned} u^{*}_p(t)=\left\{ \begin{array}{l} 0, \text{ for }\ \varphi _p(t)\le h_p^{S'}(0);\\ h_{p}^{{S'}^{-1}}(\varphi _p), \text{ for }\ h_{p}^{S'}(0)<\varphi _p(t)\le h_{p}^{S'}(u_{max});\\ u_{max}, \text{ for }\ h_{p}^{S'}(u_{max})<\varphi _p(t). \end{array}\right. \end{aligned}$$

(24)

$$\begin{aligned} v^{*}_p(t)=\left\{ \begin{array}{l} 0, \text{ for }\ \psi _p(t)\le h_{p}^{{vac}'}(0);\\ h_{p}^{{{vac}'}^{-1}}(\psi _{p}), \text{ for }\ h_{p}^{{vac}'}(0)<\psi _p(t)\le h_{p}^{{vac}'}(v_{max});\\ v_{max}, \text{ for }\ h_{p}^{{vac}'}(v_{max})<\psi _p(t). \end{array}\right. \end{aligned}$$

(25)

This means that if the economy’s socioeconomic costs curve is convex, that is strictly increasing in its production levels and very damaging due to the duration of the lockdown, then there are three possibilities for optimal lockdown time ($t_0$ and $t_1$, where $0< t_0<t_1<T$): a nullity or a unit level and the case in which the lockdown implies that the socioeconomic costs have a value between 0 and umax, that is, depending on the different lockdown durations.

4 Numerical simulations

We corroborate our results by performing several numerical simulations. We used Matlab software to program our model and conduct the experiments.¹⁶ In this section, we first simulate the economic impact of the pandemic without any policy aimed at limiting this effect. We first simulate the economic impact of the pandemic without any policy aimed at mitigating this effect. We then simulate the same impact but assume the existence of a lockdown policy targeted to each demographic subpopulation (elderly, adult, and young). Finally, we simulate the economic impact of the pandemic, assuming that there is no differentiation (untargeted) between demographic groups; that is, the same policy is applied to the whole population irrespective of the differentiated effects of the virus among individuals of different ages. With respect to the theoretical model introduced in Sect. 3, to simplify and without loss of generality, we simulate only the case of convex cost functions,¹⁷ and assume that the profits from recovery are zero; people obtain no benefit beyond the social standard they enjoyed prior to contracting the virus (Acemoglu, 2021).

As a benchmark, we examine the case of Italy, which has a population of 49,581,000 over the age of 20; the population is denoted as Z for the remainder of the study. The distribution of the population is assumed to be as follows: 44.68% of the people are aged 20-49 (we label this group the young), 27.22% of the population is aged between 50 and 64 (adults), and the remaining 28,10% of the population are those aged over 65 (the old). As in Acemoglu et al., we consider a fatality rate by age group, as given by (Table 1).

Table 1 COVID-19 fatality rate by age cohort

Those in the susceptible group become infected according to infection rate $\beta =0.256$ (Caccavo, 2020; Loli Piccolomini & Zama, 2020). Not all individuals in the infected group develop symptoms: as in Verity et al. (2020), we assume that, on average, only two-thirds of cases are sufficiently symptomatic to self-isolate, with a probability of developing symptoms equal to $\alpha _1=1/2$ for the young, $\alpha _2=2/3$ for adults and, for the elderly, equal to $\alpha _3=5/6$. In the following subsections, we introduce the methods for calibrating the costs and benefits functions of our model.

4.1 Direct costs of infection.

The direct socioeconomic costs of the infection,¹⁸ as introduced in section 3, are represented by the functions:

$$\begin{aligned} Z \cdot f_p(I_p(t)) = Z \cdot E_p^f I_p(t), \end{aligned}$$

where $E_p^f$ denotes the daily cost of treatment for one infected person belonging to the demographic group p. Let $I_p(t)$ be the fraction of infected people in group p over the total population, denoted by N. The total cost borne by the government for the infected individuals in group p is, therefore, equal to 49,581,000 $\cdot$ $E_p^f I_p(t)$. When computing the cost of treatment of the infected $E_p^f$, we must take into account that some, but not all, individuals who are hospitalized need intensive care. As in Ferguson et al. (2020), we assume a probability of hospitalization of 2.8% for the young, 10% for adults, and 26% for the elderly; the proportion of those hospitalized who require critical care is 5% for the young, 20% for the adult group and 50% for older persons.

According to the most recent medical literature (Gaythorpe et al., 2020), the average hospital stay is approximately 15 days: 5 days for the young ($\sigma _1=0.2$), 15 days for adults ($\sigma _2=0.066$) and 25 days for the elderly ($\sigma _3=0.04$), with a daily cost per patient of €1,500.00 in critical care, and a cost of approximately €300.00 in ordinary care.¹⁹ After discharge, we will assume that the patient is recovered.

We ensure our model is calibrated correctly by estimating the cost of treatment for each age group by multiplying the probability of hospitalization by its cost. Since not all patients hospitalized need critical care, we consider the cost of treatment with respect to the probability of needing intensive care, which is five times more costly than ordinary care. This is expressed as follows

$E_p^f$ = Prob. of hospitalization $\cdot$ (€1500 $\cdot$ prob. of critical care + €300 $\cdot$ (1 - prob. of critical care)).

Therefore, for each age group, the daily cost of treatment is equal to:

• $E_1^f$= 0.028 $\cdot$(1500.00 $\cdot$ 0.005 + 300.00 $\cdot$ 0.995) = 8.57,

• $E_2^f$= 0.1 $\cdot$ (1,500.00 $\cdot$ 0.2 + 300.00 $\cdot$ 0.8) = 54.00,

• $E_3^f$= 0.26 $\cdot$ (1,500.00 $\cdot$ 0.5 + 300.00 $\cdot$0.5) = 234.00.

Obviously, the direct costs of infection are related only to individuals in the Infected group, since those in the other groups are assumed not to have symptoms and, therefore, do not need to be assisted or cured.

4.2 Indirect Costs of Infection

Indirect socioeconomic costs of infection here refer to the job opportunities (and thus GDP) lost due to isolation, irrespective of whether this was a consequence of an infection, a lockdown, or a death. These effects are group-specific, in the sense that they vary according to age and whether the individual is infected, quarantined, asymptomatic (or has died).

We begin by illustrating the indirect socioeconomic costs for those in the Infected group. An infected person must be isolated or treated during the course of illness and cannot work. According to the Italian Bureau of Statistics (ISTAT) the average yearly nominal GDP per worker in 2019 was €70,105.30, which leads to a daily income per worker (considering 365 working days in a year) of €192.07. Following Acemoglu et al. (2021), we assume that the loss of productivity of young and adult individuals is the same in this model, while that for the elderly is 26% of the young (or adults), reflecting the fact that those over 65 who still work constitute only 20% of the total. The indirect socioeconomic costs for individuals quarantined by law (that is, the fraction up of the susceptible) can be defined as:

$$\begin{aligned} Z \cdot h^I_p(I_p(t)) = Z \cdot E^I_pI_p(t), \end{aligned}$$

(26)

where $E^I_p$ is equal to:

• $E_1^I$=192.07,

• $E_2^I$= 192.07,

• $E_3^I= 192.07\cdot 0.26= 49.94$.

The indirect socioeconomic costs for the individuals quarantined by law (that is to say, the fraction $u_p$ of the susceptible) can be defined as:

$$\begin{aligned} Z \cdot h^S_p(u_p(t)) = Z \cdot E^S_p(u_p(t)+\gamma _p)^2. \end{aligned}$$

(27)

As previously noted, the government treats all infected individuals they are able to detect. Treatment may consist of hospitalization, if the symptoms are severe, or isolation, if the individual suffers only mild symptoms. The policy of lockdown is therefore directed to the susceptible only, who, not being sick, may decide to act as freely as they did before the pandemic. We assume that these costs grow exponentially with the number of infected individuals because we assume diminishing returns to scale for labor (as the number of infected individuals increases, the productivity of the non-isolated individuals decreases, up to the point where additional increases in output are impossible).

Every individual that goes into isolation experiences a productivity loss. We previously assumed that an infected individual, for each day they remain isolated or hospitalized, experiences a productivity loss of 100% of their daily income. By comparison, a susceptible individual that is auto-isolated or quarantined by law may maintain their ordinary activity (whenever possible) from home, resulting in a lower productivity loss. Following Acemoglu et al. (2021), the susceptible that are auto-isolated or quarantined have a productivity loss of 70%; $E^S_p$ is represented by the following values:

• $E_1^S$=192.07 $\cdot$ 0.7 = 134.45,

• $E_2^S$= 192.07 $\cdot$ 0.7 = 134.45,

• $E_3^S$= 49.94 $\cdot$ 0.7 = 34.96.

Finally, each death as a consequence of infection results in a loss for society that is difficult to estimate. The function of indirect costs of death is expressed as follows:

$$\begin{aligned} Z \cdot h^D_p(D_p) = Z \cdot E^D_pD_p(t). \end{aligned}$$

(28)

We assume that the cost of a life is, for each of the three groups:

• $E_1^D$= 2,800,000.00,

• $E_2^D$= 2,000,000.00,

• $E_3^D$= 273,000.00.

A vaccination campaign can be limited by the maximum number of vaccine doses available at time t, which we account for in the simulation model by the value $v^{max}(t)$.²⁰ The function $h^{vac}_p(v_p(t))$ represents the cost of implementing the vaccination system at time t. Then,

$$\begin{aligned} Z \cdot h^{vac}_p(v_p(t)) = Z \cdot E^{vac}_p v^2_p(t). \end{aligned}$$

(29)

That is, for each demographic group, vaccination costs are:

• $E_1^{vac}$= 10.00,

• $E_2^{vac}$= 10.00,

• $E_3^{vac}$= 10.00.

That is, once the vaccination campaign begins, the cost of implementation does not differ between demographic groups; we have illustrated how we calibrated the model for numerical simulations.²¹ As already noted, our numerical simulations refer to the case where the cost functions $h_p(\cdot )$ are strictly convex, and there are no profits from recovery.

4.3 Numerical results

We use Euler’s method to describe the evolution of our model. We rewrite the derivatives of the differential system (2)-(7) by step-wise iteration from t to $t + \Delta t$, with $\Delta t$ of one day. At each step, we calculate the switching functions’ $\phi$ and use these to construct the optimal control according to Pontryagin’s maximum principle. Using this data, we construct the necessary graphs. Matlab was chosen as the calculation software.

We perform two experiments. In the first, a policy determined by optimal control is compared with having no policy. An estimation of the dynamics of all groups is performed through time. We also computed the costs associated with the two policies (an optimal rather than a laissez-faire policy). The second experiment simulates an optimal uniform policy without distinguishing between demographic groups. This experiment is important to estimate the costs associated with the optimal policy and compare it with the optimal targeted policy in Experiment 1. In numerical simulations, data from open-access web-sites are collected (see: Website of Johns Hopkins University and “Our World In Data”).

Experiment 1 Using data of column 1 in table A.1 (see Appendix), we estimated the behavior over time of those in the Susceptible, Quarantined, Asymptomatic, Infected, Recovered, and Dead groups for the three age demographics. Figures 8 and 9 describe the behavior of these groups without any policy aimed at limiting the spread of the virus, while Figs. 10 - 12 describe the same variables when this policy is introduced. For this and the next experiment, we considered a population of 49,581,000 people, with the following demographic strata: 22,150,000 aged 20-49 (44.68%), 13,498,000 aged 50-64 (27.22%), and 13,933,000 aged over 65 (28.10%). Notably, in the absence of a policy, the total number of infected increases up to the peak of day 62 (about) and decreases thereafter. The maximum number of infected (and asymptomatic) persons may reach about 12 million (24% of the whole population) if no policy is implemented. Conversely, when a targeted policy (based on demographic groups) is implemented to reduce the contagion, a different scenario results. In fact, the maximum number of infected is reduced by more than half, from approximately 12 million to approximately 5.7 million at the peak of the pandemic, while almost half of the population is in quarantine (see Fig. 10); the peak of the pandemic occurs 58 to 62 days from the start, compared to 62 to 64 days in an uncontrolled case.

Fig. 8

Experiment 1. Subpopulation behavior in uncontrolled case. Note: young (left), adult (center), and old (right) subpopulations in the uncontrolled case

Fig. 9

Experiment 1, number of asymptomatic, infected, and dead in the uncontrolled case

It is obvious that the most affected group in terms of number of deaths is the elderly. Without any control, this group loses more than 5 million people (about 10%), against 2.7 million in the adult group (5.4%) and a negligible number among the young. Without control, those who are quarantined are only a fraction of the group of older people that arbitrarily decide to self-quarantine (about 14%).

Fig. 10

Experiment 1. Sum of share of all groups in the controlled case

When a control policy is implemented globally, about half the population is quarantined. Figure 10 shows a total of 25 million people isolated (which amounts to roughly half, given the experiment’s total population of 49.5 million).

Fig. 11

Experiment 1, the behavior of the system in young (left), adult (center), and old (right) subpopulations in the controlled case

Figure 11 displays the behavior of those in the Susceptible, Quarantined, Asymptomatic, Infected, Recovered and Dead groups for the three age demographics. Intuitively, our simulations show that about 7.5 million young people (corresponding to about 33% of the group) are quarantined at the end of the pandemic, compared to 9 million adults (67% of the group) and 11.3 million older people (81% of the group). Quarantined people include those who are quarantined by law and those who voluntarily quarantined. The reason for this effect is that a young person has a higher probability of being asymptomatic and infecting other people belonging to the other two groups. Figure 12 highlights this phenomenon.

Fig. 12

Experiment 1, number of asymptomatic, infected, and dead in the controlled case

Since the virus transmission rate is the same among the three groups, it is clear that the group at higher risk of being asymptomatic (and undetectable) has to be quarantined to avoid deaths in the other two groups, despite the cost of a life lost being unbalanced or skewed toward the young and adults.

An optimal control policy here assumes that at the beginning of the pandemics (at $t=0$), there was immediate isolation of 110000 young, 140000 adults, and 210000 old people. The subsequent number of isolated people remains at this level for a period and then decreases day by day. The left panel of  13 shows, for each day of the pandemic, the number of isolated people in each demographic. The center panel of Figure  13 shows the recommended number of people to be vaccinated daily to minimize the added costs in each subgroup. As can be seen, after 200 days of intense vaccination for the elderly group, the socioeconomic costs began to decrease, while for adults, the vaccination campaign has to last at least 250 days, and for young people, the vaccination campaign should extend almost 300 days, after which the socioeconomic costs decrease and are optimally minimized.

Fig. 13

Experiment 1, structure of the optimal controls. Note: Optimal controls for medical treatment (left) and for vaccination (middle). Aggregated system costs are $J=115.63\times 10^{6}$ m.u. in the controlled case and $J=227.58\times 10^{6}$ m.u. in the uncontrolled case (right)

The right-hand panel of Fig. 13 shows that the aggregated costs of the no-intervention policy amount to €227.58$\cdot 10^{6}$, against a control policy which generates costs for €115.63$\times 10^{6}$.

Experiment 2 In this second experiment, we run the simulation using data from the first experiment (and averaging when necessary) and considering the entire population as a single group. This experiment was performed to compare the aggregated costs arising when the policy implemented to limit the spread of the virus does not exploit demographic differences and, therefore, does not account for differences in the health outcomes produced by the virus.

Fig. 14

Experiment 2, system behavior. Note: System behavior when population is a single group in controlled case (left). Number of asymptomatic, infected, and dead in the controlled case (right)

What is immediately noticeable is that, by the end of the pandemic, 33 million people had been quarantined; 66.5% of the population compared to the 20% of an optimal targeted policy. This has consequences for aggregated costs. The untargeted policy generates a cost of $123.75\times 10^{6}$ against a cost of $115.63\cdot 10^{6}$ of a targeted policy (Figs. 13 and 15).

Fig. 15

Experiment 2, structure of the optimal control. Note: For medical treatment (left) and for vaccination (middle). Aggregated system costs are $J=123.75\times 10^{6}$ m.u. in the controlled case and $J=322.8\times 10^{6}$ m.u. in the uncontrolled case (right)

It is fairly evident that a selective, targeted policy outperforms a uniform policy in terms of costs; a uniform policy generates at least 7% more costs than a targeted one. It is important, then, to calibrate the controls for the different demographic groups to exploit the differential impact of the pandemic on those populations. Even though this does not allow for shortening the lockdown, it allows the more productive and young people (therefore, those who suffer less the consequences of the virus) to remain in the job market, thus limiting the costs associated with the policy of lockdown.

5 Concluding remarks

In this paper, we modified a classic SIR model to develop an optimal control policy of lockdown aimed at minimizing a cost-profit social function. This paper presents a model that studies lockdown as an optimal policy to face the spread of COVID-19. It consists of a generalization of the well-known SIRD model in which new groups of individuals, those that are quarantined and asymptomatic, are introduced. Each group is further divided according to age (young, adult, and old), with each subgroup having different risks of death and health complications. With the objective of minimizing social cost, an optimal control problem is formalized and solved; the government must decide how many people belonging to the susceptible group should be isolated. We tackle the dynamic system of the SQAIRD model as a Markovian process and show that different socioeconomic structures, such as convex or concave cost functions, justify different lockdown policies.

Our main results are that different lockdown policies (total lockdown, laissez-faire, and a mixed policy, that is to say, partial lockdown) may be explained by countries’ different cost structures. If the two corner solutions, that is to say, total lockdown and no lockdown, may arise in the presence of concave cost functions, under the hypothesis of convex cost functions, an internal solution is optimal.

Under the hypothesis of a convex cost function, that is, when it is optimal to apply a mixed strategy (a partial lockdown), we also showed that a targeted lockdown policy based on age outperforms a uniform policy; according to our simulations, it allows a saving of about 56% of the costs. From a political perspective, it is important for policymakers to handle an emergency such as the recent COVID-19 pandemic in the best way. This requires implementing an effective policy of lockdown (in the absence of any medical treatment like a vaccine to develop immunity for the whole population) that produces minor social costs.

A lockdown has a profound impact on the economies of families (especially of those whose income is linked to activities that present a greater risk of contagion). However, catching the virus may also be tragic because the long-run consequences may be serious and result in income losses. Responsible management of such health emergencies is of crucial importance for the well-being of society and limits subsequent hard economic policies aimed at restoring the basic subsistence levels of the population.

Finally, we must point out that our optimal policy does not consider additional prescriptions like social distancing, mask-wearing, and the like. Our results may be extended by including such additional policies (for those who are not impacted by any lockdown) that, according to the medical literature, reduce the propagation rate of the virus. Moreover, we only consider age as a policy discriminant. COVID-19 has proven to also have differentiated impacts on the health of the individuals depending on existing comorbidities. Our results could be improved, and better policies implemented if, instead of considering just three age-based groups, we distinguished groups on the basis of regressed comorbidities and age. We decided, however, to leave these experiments to future research.

No less important is to let the reader know that, despite our efforts to calibrate the model in the most realistic way, there is considerable uncertainty about the parameters that govern the dynamics of the infection. As a result, there is a potential bias in the determination of the costs associated with the policies implemented, irrespective of the content of the policy.

We want to make our apologies to those who, on reading this paper, have been offended by the aseptic presentation of the argument, which has been focused on the mere computation of economic costs and profits of a policy intervention without regard for the psychological impact on relatives and society of lost lives. We are aware that the pandemic has caused such loss, and an argument focused exclusively on costs and profits could be hurtful. As economists, we are trained to think in such terms; we have a “mental deviation” of sorts that induces us to analyze strategic situations like this one in an impersonal, aseptic, and distant way, on the basis of economic indicators only. In spite of everything, we believe that this kind of presentation could be useful for policymakers who want to manage health emergencies in an effective (and hopefully efficient) way.

Appendix

Table 2 Parameters used for simulations in the experiments

Table 3 Maximum values