1 Introduction

For more than 20 years data envelopment analysis (DEA) has been accepted as the method to fit frontiers and estimate efficiencies of various financial assets (see, for example, Liu et al. (2015)). We know of only two attempts to use stochastic frontier analysis (SFA), its close relative, to fit frontier to a set of assets (Santos et al., 2005; Ferreira & Oliveira, 2016) (though it is used more broadly in finance (Daraio et al., 2020)). This is surprising. DEA and SFA (Bogetoft & Otto, 2011) are the two most important of a number of methods (Wu et al., 2011) for frontier fitting and efficiency estimation. We should choose a method because it is appropriate, not merely because it is convenient.

DEA and SFA were not developed for financial assets but for production economics. There the problem is to estimate how much of various outputs is possible with various inputs. We apply them to financial assets using an analogy: return behaves like an output and risk measures behave like inputs. The analogy is imperfect. Some assumptions from production economics, such as free-disposability and convexity (Bogetoft & Otto, 2011), remain reasonable. Others do not. Typically production inputs are measured in comparable units and are not reduced by diversification, but this is not always true of risks (Lamb & Tee, 2012b). And there is invariably uncertainty in the estimates of risk and return measures (Xiao et al., 2021; Lamb & Tee, 2012a).

There are three reasons to think SFA might be a better choice for financial assets than DEA. First, DEA assumes inputs and outputs are fixed and known. But measures of financial assets such as mean and standard deviation are never more than realisations of random variables (from sampling distributions). Thus, a stochastic (involving random variables) model such as SFA is more appropriate than a deterministic model such as DEA. Second, while financial-asset frontier models can have several inputs (risk measures), they nearly always use exactly one output (mean return), the easiest case to fit with SFA. Third, the assumption of nonincreasing returns to scale and a smooth frontier that passes through the origin (Lamb & Tee, 2012a) is precisely what SFA fits.

The objective of this article, then, is to develop methods to allow us to apply SFA in modelling investment fund performance and so help close the gap between the extensive literature on DEA and the surprisingly limited literature on SFA for investment funds. The relevance of SFA is that it is better suited than DEA to situations where there is uncertainty in the input and output measures. So the motivation of this article is to answer the question, given that it is better suited, how can we apply SFA to model investment funds?

In practice it is difficult to fit standard SFA models to financial asset data. When we consider the nature of the data it becomes clear that there are several challenges to overcome and we are unlikely to be able to use the multiplicative translog models (Bogetoft & Otto, 2011) most commonly used in production economics.

The first challenge is estimation risk (Jorion, 1986), which causes sample estimators to overestimate the largest and underestimate the smallest observed statistics. As far as we know it has not been considered before in any SFA, or even DEA, model. We will see that the effect on the estimate of the frontier can be dramatic.

Randomness occurs not just in the position, relative to the efficient frontier, of individual assets, but in the measurement of their inputs and outputs (Xiao et al., 2021). This second challenge is called measurement error (Carroll et al., 1998) and can potentially affect the fit of a model.

The final challenge is to find a suitable model and develop a method to fit it. Multiplicative SFA models are common in production economics. But we cannot use multiplicative assumptions about the distributions of noise and inefficiency terms when we use risk as an input and return as an output. The assumptions of an additive model are more plausible. But if we use an additive model we need to develop new models to deal with heteroscedasticity in the regression residuals. We also develop methods to test the quality of fit.

Our contribution is this. We overcome the three challenges that have limited the use of SFA by developing several new SFA models for financial assets, show how to fit them and how to deal with measurement error. To make it practical for others to fit these models we provide an R (R Core, 2020) package, including a method, similar to residual plots in linear regression analysis, to visualise the residuals of our SFA models and check the model assumptions. This method should be useful for any SFA model, including those with multiple inputs. We test our methods on real data taken from various asset returns.

2 Background

SFA was developed by Meeusen & van den Broeck (1977) and by Aigner et al. (1977). Bogetoft & Otto (2011) provide a good introduction. We fit a frontier

$$\begin{aligned} y=f(x;\beta )+v-u, \end{aligned}$$
(1)

where \(f\) is a production function, \(v\) is a noise and \(u>0\) an inefficiency term. This is an additive SFA model. We choose it rather than the multiplicative model \(y=f(x;\beta )\exp (v)\exp (-u)\) (Bogetoft & Otto, 2011) [Table 7], because it allows us to make more plausible assumptions about the distributions of \(u\) and \(v\) and deal with heteroscedasticity separately.

SFA was developed for production economics, not financial assets; so we should explore what risk and return measures and what form of \(f\) make sense in the context of financial assets. We first note that it is very rare to use a return other than the mean return. So, a single-output model makes sense. It is also convenient, because SFA, like regression, is well-developed for multiple inputs, but so far allows only one output. There are many possible risk measures and it is tempting, for example, to use variance or excess kurtosis. When estimating efficiency it is preferable (Lamb & Tee, 2012a) to use risk measures in the same units as the return measure. This excludes excess kurtosis and variance, but not standard deviation. Coherent measures of risk (Artzner & Delbaen, 1999) such as conditional value-at-risk have become more and more common because they have properties that are desirable when comparing risks of different assets. In particular coherent measures of risk, in common with standard deviation, are convex functions: if the risk of an asset represented by random variable \(A\) is given by \(x(A)\) then, for \(t\in [0,1]\),

$$\begin{aligned} x(tA+(1-t)B)\le tx(X)+(1-t)x(B). \end{aligned}$$

All the coherent measures of risk we know of are measured in the same units as mean return.

If we allow only mean return as the return measure and coherent measures of risk or standard deviation as the risk measure, what does this tell us about the form of \(f\)? First, we can assume \(f({\textbf{0}})=0\), because we can always obtain zero mean return with zero risk. Plausibly we may also obtain a positive return with zero risk. But we can handle this by subtracting a risk-free rate of return. Second, we assume the efficient frontier is non-decreasing, \(\mathbf {\nabla }f>{\textbf{0}}\) by assuming free disposability of risks: that is, if we can obtain a higher return with lower risk, we assume that we can more efficiently obtain the same higher return by freely taking on extra risk with no return through some financial investment. In practice, we do not know of such an investment, though gambling allows a good approximation. Third, the choice of return and risk measures satisfy

$$\begin{aligned} y(tA+(1-t)B)&=ty(A)+(1-t)y(B) \end{aligned}$$
(2)
$$\begin{aligned} {\textbf{x}}(tA+(1-t)B)&\le t{\textbf{x}}(A)+(1-t){\textbf{x}}(B) \end{aligned}$$
(3)

for \(t\in [0,1]\) and random variables \(A\) and \(B\) representing assets. From \(\mathbf {\nabla }f>{\textbf{0}}\) and Eq. (3) we have

$$\begin{aligned} f(t{\textbf{x}}(A)+(1-t){\textbf{x}}(B))&\ge f({\textbf{x}}(tA+(1-t)B))\\&=tf({\textbf{x}})+(1-t)f({\textbf{x}}(B)) \end{aligned}$$

by Eq. (2). It follows that \(f\) is concave or, equivalently, \(\nabla ^2f\) is negative semidefinite.

The properties we have found for \(f\), \(f({\textbf{0}})=0\), \(\mathbf {\nabla }f>{\textbf{0}}\) and \(f\) concave, are satisfied by

$$\begin{aligned} f(x_1,\ldots ,x_p)=\beta _0x_1^{\beta _1}\cdots x_p^{\beta _p} \end{aligned}$$

with \(\beta _0>0\), \(\beta _1,\ldots ,\beta _p\in (0,1)\) and \(\beta _1+\cdots +\beta _p\le 1\), which is a Cobb–Douglas production function.

Although the methods we develop can be applied with multiple risk measures, we focus on mean–standard-deviation frontiers. That is, we consider the case where \(y\) is the mean return and \(x\) is the standard deviation in the return because standard deviation is the only risk measure for which we currently have methods to handle estimation risk (Sect. 3.2). In this case the Cobb–Douglas production function is

$$\begin{aligned} f(x)=\beta _0x^{\,\beta _1} \end{aligned}$$
(4)

with \(\beta _0>0\) and \(\beta _1\in (0,1)\). The noise term \(v\) and smooth frontier also make SFA a natural choice for fitting a frontier, because we expect substantial random variation and not just inefficiency in the performance of an individual asset.

By contrast, DEA (Bogetoft & Otto, 2011) has been applied much more widely to fitting frontiers and estimating inefficiency of assets or portfolios (see, for example, Gregoriou et al. (2005)). DEA fits a piecewise continuous frontier rather than a smooth one. More plausible frontiers, using diversification-consistent models with nonincreasing returns to scale (Lamb & Tee, 2012a; Liu et al., 2015; Branda, 2015), have recently been developed. The form of these is closer to that more naturally produced by SFA. And recently (see, for example, Lamb & Tee (2012b)) there have been attempts to deal with the stochastic nature of the data.

Although there are stochastic versions of DEA (Olesen & Petersen, 2016), SFA remains the more natural choice when we posit both an inefficiency and a noise in fitting the frontier. But to use it well, we need to consider three issues: the choice of \(v\) and \(u\), estimation risk and measurement error. In fact, all but the choice of \(u\) should ideally be considered for DEA models too, though we restrict our discussion to SFA.

Typically, \(v\) is assumed normal with mean zero and variance \(\sigma _v\) and \(u\) half-normal. Normal noise is plausible because it is the error arising from estimating \(y\) of Eq. (1) from a sample mean. The half-normal distribution gives positive inefficiency. While its shape has been questioned and others suggested (see Papadopoulos (2021)), the mean–standard-deviation frontier presents a different issue: we expect \(\sigma _v\) to be proportional to \(x\) and \(\sigma _u\) to increase, perhaps proportionally, with \(x\) or \(y\).

We ought to consider estimation risk when fitting a mean–standard-deviation frontier. When we have \(n\) assets or portfolios with similar means and large variances and estimate the means with a multivariate sample mean, the smaller sample means will tend to underestimate and the larger, overestimate the population mean so that we should expect to overestimate the slope of the frontier. Formally, estimation risk is the expectation of a risk function (usually mean-squared difference between population and sample), and is something we wish to minimise (Jorion, 1986). It gets worse as \(n\) increases (Frost & Savarino, 1986) and affects statistics other than the mean. There are methods to reduce, though not eliminate, estimation risk for both the mean (Jorion, 1986) and covariance matrix (Ledoit & Wolf, 2004, 2017) and these are commonly used in related research areas (Herold & Maurer, 2006; Michaud & Michaud, 2007; Alexander et al., 2009; Antoine, 2012; Davarnia & Cornuéjols, 2017; DeMiguel et al., 2013).

Usually we can assume \(x\) and \(y\) are measured without error in SFA . But when \(x\) and \(y\) are the standard deviation and mean of assets, we observe

$$\begin{aligned} w=x+{\psi }\quad \text {and}\quad d=y+\kappa \end{aligned}$$

where \({\psi }\) and \(\kappa \) are random variables with mean \(0\). These are called measurement errors (Carroll et al., 1998; Buonaccorsi, 2010) and can influence the coefficients of a regression model such as those we use to fit Eq. (4). As far as we know measurement error has not been considered in any SFA model. One way to deal with it is simulation extrapolation (simex) (Cook & Stefanski, 1994). We can assume that \({\psi }\) and \(\kappa \) are uncorrelated, but not that they are normal or have constant variance, as required for the original, parametric, simex. But we can generate repeated measurements for \(w\) and \(y\), and so adapt the empirical simex method of Devanarayan & Stefanski (2002) to extrapolate model parameters without measurement error.

3 A methodology for mean–standard-deviation SFA 

We wish to fit an SFA frontier of the form of Eq. (1) where \(x\) is standard deviation and \(y\) is mean and so estimate the efficiency of individual assets. To do this we must solve three problems. First, we find a way to deal with heteroscedasticity in both \(u\) and \(v\). Section 3.1 does this and then develops a method to test the SFA fit. Second, Sect. 3.2 shows it is straightforward to deal with estimation risk. Third, Sect. 3.3 deals with measurement error.

While estimation risk and measurement error are issues for assets or portfolios, note that the methods of Sect. 3.1 can be applied to any SFA.

3.1 Fitting SFA with heteroscedasticity in u and v

The frontier we fit should pass through the origin and have nonincreasing returns to scale (Lamb & Tee, 2012a), and while we do not here deal directly with diversification-consistency (Lamb & Tee, 2012a; Liu et al., 2015; Branda, 2015), we expect the SFA frontier shape to be close to that of a diversification-consistent frontier where there are few data points near the frontier.

We assume that \(f\) of Eq. (1) has the form of Eq. (4), \(v\sim N\left( 0,(r_v(x))^2\right) \), \(u\) is half-normal with density

$$\begin{aligned} h_{u\mid x}(z)=\sqrt{\frac{2}{\pi }}\,\frac{1}{r_u(x)}\,\exp \left( -\frac{1}{2}\left( \frac{z}{r_u(x)} \right) ^2 \right) \qquad (z\ge 0) \end{aligned}$$

for some functions \(r_v\) and \(r_u\), and \(u\) and \(v\) are conditionally independent: that is,

$$\begin{aligned} f_{v,u\mid x}(w,z\mid x) =f_{v \mid x}(w\mid x)h_{u\mid x}(z\mid x). \end{aligned}$$

We consider three possibilities:

$$\begin{aligned} r_t(x)=\sigma _t,\qquad r_t(x)=x\sigma _t,\qquad r_t(x)=\beta _0x^{\,\beta _1}\sigma _t,\qquad (t\in \{u,v\}). \end{aligned}$$
(5)

That is, we allow the error in \(v\) or \(u\) to be constant, proportional to \(x\) or (cf. Eq. (4)) proportional to \(y\). To fit an SFA frontier we choose \(r_v\) and \(r_u\), estimate \(\sigma _v\) and \(\sigma _u\), and check how well the model fits the assumptions made by the choices of \(r_v\) and \(r_u\).

As is usual in SFA, we fit \(\sigma _v\) and \(\sigma _u\) using maximum likelihood estimation. Write \(\sigma ^2=(r_v(x))^2+(r_u(x))^2\), \(\lambda =r_u(x)/r_v(x)\) and \(\Phi \) for the standard normal distribution function. Then we can write \(\varepsilon _x=v-u=y-\beta _0x^{\,\beta _1}\), and substitute \(r_v(x)\) and \(r_u(x)\) for \(\sigma _v\) and \(\sigma _u\) in Eq. (7.10) of Bogetoft & Otto (2011) to get the density of \(\varepsilon _x\):

$$\begin{aligned} \phi _{\varepsilon }(\varepsilon _x)=2\Phi \left( -\frac{\lambda \varepsilon _x}{\sigma } \right) \, \frac{1}{\sqrt{2\pi \sigma ^2}} \exp \left( -\frac{1}{2}\left( \frac{\varepsilon _x}{\sigma }\right) ^2 \right) {,} \end{aligned}$$
(6)

which is a skew-normal distribution (Azzalini & Capitanio, 2013). Here we just modify the usual definition of the density to allow for different forms of heteroscedasticity in \(v\) and \(u\). When we have observations \((x_1,y_1),\ldots ,(x_n,y_n)\) we define \(\varepsilon _i=y_i-\beta _0x^{\,\beta _1}\), \(\sigma _i^2=(r_v(x_i))^2+(r_u(x_i))^2\) and \(\lambda _i=r_u(x_i)/r_v(x_i)\), and compute the log-likelihood function by summing the logarithm of Eq. (6) over all \(n\) observations:

$$\begin{aligned} l(\sigma _v,\sigma _u,\beta _0,\beta _1) =-\frac{n}{2}\log \left( \frac{\pi }{2}\right) +\sum _{i=1}^n\left( -\log \sigma _i+\log \Phi \left( -\frac{\lambda _i}{\sigma _i}\varepsilon _i \right) -\frac{1}{2}\left( \frac{\varepsilon _i}{\sigma _i} \right) ^2 \right) . \end{aligned}$$
(7)

We then obtain estimates of \(\sigma _v\), \(\sigma _u\), \(\beta _0\) and \(\beta _1\) by maximising the log-likelihood function.

Equation (5) allow us to fit up to nine different SFA models. So we want some way both to compare models and to check that the residuals \(\varepsilon _i\) of an individual model fit the assumptions we make. In a linear regression model we would plot the standardised regression residuals against the regression predicted values to test these assumptions. We develop a similar method that can be used for SFA.

If the model assumptions are correct then, see Eq. (6), the residual \(\varepsilon _i\) is a random variate from a distribution with density

$$\begin{aligned} \phi _{\varepsilon }(x_i;\lambda _i,\sigma _i)=g(x_i/\sigma _i;\lambda _i)/\sigma _i \quad \text {where }g(x,\lambda )=2\Phi (-\lambda x)\phi (x). \end{aligned}$$

Since \(g\) is a skew-normal distribution we can use efficient numerical methods (Azzalini & Capitanio, 2013)[Section 2.1.5] to evaluate its distribution function \(G(x;\lambda )\) and thus the distribution function for \(\varepsilon _i\),

$$\begin{aligned} \Phi _{\varepsilon }(x_i;\lambda _i,\sigma _i)=G \left( {x_i}/{\sigma _i},\lambda _i\right) /\sigma _i. \end{aligned}$$

Then, if the model assumptions are correct,

$$\begin{aligned} z_i=\Phi ^{-1}(\Phi _{\varepsilon }(x_i;\lambda _i,\sigma _i))\sim N(0,1). \end{aligned}$$
(8)

So we can check the model assumptions by plotting \(z_i\) against \(\beta _0x_i^{\,\beta _1}\) (\(i=1,\ldots ,n\)) as we do, for example, in Fig. 2.

We use SFA to estimate the technical efficiency of individual asset \(k\) in an additive SFA model,

$$\begin{aligned} \rho _k=1-{\mathbb {E}}[u_k\mid \varepsilon _k]/\beta _0x_k^{\,\beta _1} \end{aligned}$$

(Bogetoft & Otto, 2011)[Eq. (7.1’)]. Since \({\mathbb {E}}[u_k\mid \varepsilon _k]\) depends only on the distributions of \(u\) and \(v\) at \(x_k\), we can adopt Eq. (7.17) of Bogetoft & Otto (2011) to estimate

$$\begin{aligned} {\mathbb {E}}[u_k\mid \varepsilon _k] = \sigma _{k,*}\left( \frac{\phi (\varepsilon _{k,*})}{1-\Phi (\varepsilon _{k,*})}-\varepsilon _{k,*} \right) \quad \text {where }\varepsilon _{k,*}=\varepsilon _k\frac{\lambda _k}{\sigma _k}, \ \sigma _{k,*}=\frac{r_v(x_k)r_u(x_k)}{\sigma _k}. \end{aligned}$$

3.2 Estimation risk

For fitting an SFA model, we assume we have returns for \(n\) assets over \(T\) time periods, from which we can estimate sample mean and sample standard deviation vectors \({\textbf{y}}=(y_1,\ldots ,y_n)^\top \) and \({\textbf{x}}=(x_1,\ldots ,x_n)^\top \). Although these are unbiased, setting \(\theta ={\mathbb {E}}[{\textbf{y}}]\) does not minimise the risk function

$$\begin{aligned} (\theta -\mu )^\top \Sigma ^{-1}(\theta -\mu ) \end{aligned}$$
(9)

where \(\mu \) is the vector of true mean returns of the assets and \(\Sigma \) is the covariance matrix (Stein, 1955). The lower means tend to be underestimated and the higher ones overestimated so that a James–Stein estimator (James & Stein, 1961),

$$\begin{aligned} \hat{{\textbf{y}}}=(1-\alpha ){\textbf{y}}+\alpha {\overline{y}}{\textbf{1}}, \end{aligned}$$
(10)

where \({\overline{y}}\) is the mean of \(y_1,\ldots ,y_n\) and \({\textbf{1}}\) is a vector of ones of length \(n\), has lower risk for some \(\alpha \in [0,1)\). We set, for some estimator \(S\) of the covariance matrix,

$$\begin{aligned} \alpha =\frac{n+2}{n+2+T({\textbf{y}}-{\overline{y}}{\textbf{1}})^\top S^{-1}({\textbf{y}}-{\overline{y}}{\textbf{1}})} \end{aligned}$$
(11)

(Jorion, 1986)[Eq. (17)]. This does not necessarily minimise risk function (9) but gives a shrinkage estimator, which gives a better estimate than the sample mean for fitting SFA. We use this shrinkage estimator because it is well-established in the finance literature and shrinks towards the mean of all the estimates of means rather than the less plausible target of \(0\) of many earlier shrinkage estimators.

We can also reduce estimation risk in the sample covariance matrix using recently-developed shrinkage estimators (Ledoit & Wolf, 2004, 2017). We use the nonlinear shrinkage estimator of Ledoit & Wolf (2017) to estimate both \(S\) in Eq. (11) and the standard deviations of the asset returns. It has no explicit formula but is implemented in an R-package (Ramprasad, 2016). Like Eq. (9), there is good evidence that this shrinkage estimator works well in practice.

We show the sample and shrinkage estimators for the mean and standard deviation as hollow and filled circles for each of a set of stocks, together with grey lines joining each pair of circles in Figs. 1, 4, 5 and 6. We write \(x_i\) and \(y_i\) for both the sample and shrinkage estimators of asset \(i\), because the context will indicate which is meant.

3.3 Measurement error

The estimators of the coefficients \(\sigma _v\), \(\sigma _u\), \(\beta _0\) and \(\beta _1\) of the model of Sect. 3.1 are called naive estimators because the model does not account for the measurement errors in the estimates of \(x\) and \(y\) that arise from sample data. We do not observe \(x_i\) and \(y_i\) (\(i=1,\ldots ,n\)) but rather

$$\begin{aligned} w_i=x_i+{\psi }_i\quad \text {and}\quad d_i=y_i+\kappa _i, \end{aligned}$$

where \({\psi }_i\) and \(\kappa _i\) are measurement errors satisfying \({\mathbb {E}}[{\psi }_i]={\mathbb {E}}[\kappa _i]=0\), \({{\,\textrm{var}\,}}({\psi })=\tau _{{\psi },i}^2\) and \({{\,\textrm{var}\,}}(\kappa _i)=\tau _{\kappa ,i}^2\). We can reasonably assume \({\psi }_i\) and \(\kappa _i\) are independent. Here \(x_i\) and \(y_i\) are the mean and standard deviation of a distribution. If we assume that the distribution is approximately normal and the samples are independent, then \(w_i\) and \(d_i\) are observations from the sampling distributions of the sample mean and sample standard deviation, which are independent. Hence \({\psi }_i\) and \(\kappa _i\) are independent. In practice, we can assume the distribution is approximately normal and the sample values obtained as if from independent samples so that the assumption of independence is reasonable.

We wish to take account of these measurement errors because they may lead us to misestimate the coefficients of the SFA model. One way to do this is to use simulation extrapolation (simex) (Cook & Stefanski, 1994) , which give consistent and unbiased estimators Suppose we wish to estimate a coefficient \(\beta \). Define \(\beta (\lambda )\) to be the expected value of the SFA naive estimator of \(\beta \) if \({{\,\textrm{var}\,}}({\psi }_i)=(1+\lambda )\tau _{{\psi },i}\) and \({{\,\textrm{var}\,}}(\kappa _i)=(1+\lambda )\tau _{\kappa ,i}\). Then we can always estimate \(\beta (0)\). And if we can simulate data to estimate \(\beta (\lambda )\) for several values of \(\lambda >0\) we can extrapolate a value for \(\beta (-1)\), the coefficient without measurement error.

We estimate standard deviation and mean from \(T\) time periods, which means that we can use bootstrap replications of the data to estimate the distributions of \({\psi }_i\) and \(\kappa _i\). This means we can adapt the empirical simex method of Devanarayan & Stefanski (2002). If the asset returns are \(r_{ti}\) (\(t=1,\ldots ,T\), \(i=1,\ldots ,n\)) then we generate \(M\) bootstrap replications by choosing \(u(m,t)\) uniformly with replacement from \(1,\ldots ,T\) and setting

$$\begin{aligned} r_{mti}=r_{u(m,t),i}\qquad (m=1,\ldots ,M). \end{aligned}$$

(In practice we choose \(M=2000\), which is typical for the bootstrap.) Write \(d_i\) and \(w_i\) for the mean and standard deviation of \(r_{1i},\ldots ,r_{Ti}\), and \(d_{mi}\) and \(w_{mi}\) for those of \(r_{m1i},\ldots ,r_{mTi}\). Then \(d_{mi}\) and \(w_{mi}\) are resampled estimates for \(d_i\) and \(w_i\). But, we wish to resample shrinkage estimators. If \(d^*_i\) and \(w^*_i\) are the shrinkage estimators for the means and standard deviations of the asset returns then it is straightforward to check that

$$\begin{aligned} d^*_{mi}=\left( d_{mi}-d_i\right) \frac{w_i^*}{w_i}+d^*_i\quad \text {and}\quad w^*_{mi}=w_{mi}\frac{w_i^*}{w_i} \end{aligned}$$

are resampled estimates for the shrinkage estimators.

We can use these estimates in empirical simex. We give the details of the calculations, because we modify the method of Devanarayan & Stefanski (2002) to include an error in \(y\) and not just \(x\). First, we choose \(B\) (in practice we use \(B=2000\)) and let

$$\begin{aligned} z_{b,i,m}\qquad (i=1,\ldots ,n,\;m=1,\ldots ,M,\;b=1,\ldots ,B) \end{aligned}$$

be standard normal variates. Then we calculate

$$\begin{aligned} {\overline{z}}_{b,i}=\frac{1}{M}\sum _{m=1}^Mz_{b,i,m}\quad \text {and}\quad c_{b,i,m}=\frac{z_{b,i,m}-{\overline{z}}_{b,i}}{\sqrt{\sum _{m=1}^M\left( z_{b,i,m}-{\overline{z}}_{b,i}\right) ^2}}. \end{aligned}$$

Then we define

$$\begin{aligned} {\overline{w}}^*_{i}=\frac{1}{M}\sum _{m=1}^Mw^*_{i,m},\quad {\overline{d}}^*_{i}=\frac{1}{M}\sum _{m=1}^Md^*_{i,m}\qquad (i=1,\ldots ,n). \end{aligned}$$

using the resampled estimates for the shrinkage estimators.

For each value of \(\lambda \) for which we wish to estimate \(\beta (\lambda )\) for some coefficient \(\beta \) we compute, for \(b=1,\ldots ,B\),

$$\begin{aligned} w^*_{b,i,\lambda }={\overline{w}}^*_{i}+\sqrt{\frac{\lambda }{M}}\sum _{m=1}^Mc_{b,i,m}w^*_{i,m}\quad \text {and}\quad d^*_{b,i,\lambda }={\overline{d}}^*_{i}+\sqrt{\frac{\lambda }{M}}\sum _{m=1}^Mc_{b,i,m}d^*_{i,m} \end{aligned}$$

and estimate the coefficients of

$$\begin{aligned} d^*_{b,i,\lambda }=\beta _{0;b,\lambda }w_{b,i,\lambda }^{*\,\,\beta _{1;b,\lambda }} +v^*_{i;b,\lambda }-u^*_{i;b,\lambda } \end{aligned}$$

by the maximum likelihood method of Sect. 3.1. We then estimate \(\beta _{0;\lambda }\), \(\beta _{1;\lambda }\) and (usually) \(\sigma _{v;\lambda }\) and \(\sigma _{u;\lambda }\) as the averages of the \(B\) estimates of these coefficients. And we estimate \(\beta _0\), \(\beta _1\), \(\sigma _v\) and \(\sigma _u\) using one of the standard extrapolation methods (Cook & Stefanski, 1994; Carroll et al., 1998). These first fit the estimates \(\beta (\lambda )\) to a model \(\beta (\lambda )=g(\lambda )\), then extrapolate to get \(\beta (-1)\) as an estimate of \(\beta \). There is no one right function \(g\). Typically either the rational or quadratic extrapolant,

$$\begin{aligned} g(\lambda )=c_1+\frac{c_2}{c_3+\lambda }\quad \text {or} \quad g(\lambda )=c_1+c_2\lambda +c_3\lambda ^2, \end{aligned}$$
(12)

are used. The first has better theoretical justification. The second is more stable. Typically we test both, together with a linear extrapolant, and plot the best fits (see Fig. 3) before choosing a value for \(\beta \).

3.4 Implementation

We implement our methods in an R (R Core, 2020) package, using C++ (Eddelbuetel, 2013) when R code would be too slow.

We use the nlshrink R-package (Ramprasad, 2016) for covariance and compute mean shrinkage using Eqs. (10)–(11) with the shrinkage covariance estimate. We implement SFA fitting as described in Sect. 3.1, using the C++ with the GNU scientific library (Galassi et al., 2009) to compute the log-likelihood function (7) and also to maximise it (we use the Nelder–Mead simplex method because it is convenient and easy to implement). We also use the GNU scientific library to compute \(G(x;\lambda )\) numerically and so compute \(z_i\) in Eq. (8) to produce residual plots to test model fit. We implement simex in R as described in Sect. 3.3.

4 Fitting SFA to historic asset returns

We now test the methods of Sect. 3 on some real data. The data we use are stocks in each of the FTSE 100 (61 stocks), Standard and Poor (S &P, 326 stocks) and Nikkei (183 stocks) indices together with DAX and hedge-fund data described below. For each of these stocks we obtain 300 consecutive monthly returns to the beginning of June 2019 from Datastream (2019). As usual in efficiency modelling for asset returns, we ignore time-series effects when estimating mean and standard deviation, though our methods could be adapted to consider them. Since we fit historic asset returns rather than prices, we expect the data to exhibit stationarity. Nonetheless, we use augmented Dickey-Fuller (ADF) tests to test for unit roots. The p-values were negligible except for two hedge funds with p-values of (0.0591) and (0.57). For purpose of verification, we re-test for unit roots using the Philips–Perron (PP) method,Footnote 1

Table 1 Summary statistics for data
Full size table

Table 1  shows summary statistics for the monthly percentage stock returns. The values of skewness and kurtosis immediately suggest many of the returns are not plausibly normally or lognormally distributed. However, we are not fitting the returns, but rather estimates of their means and standard deviations, which, by the central limit theorem, are much more likely to be approximately normally distributed. So a translog function and multiplicative model, which would assume lognormally distributed mean returns, are not appropriate, even if we could find a way to deal with the negative mean returns in the Nikkei data. On the other hand, an additive model assumes approximately normal mean returns, which are plausible here.

Fig. 1
figure 1

SFA fit for FTSE 100 stocks

Full size image

Figure 1 shows the means and standard deviations of the ftse stocks. For each stock, we show the sample mean and standard deviation by an unfilled circle and the shrinkage mean and standard deviation by a filled one. We join the circles by a grey line to show the effect of using shrinkage estimators. We fit an SFA model

$$\begin{aligned} y=\beta _0x^{\,\beta _1}+v-u \end{aligned}$$

using the shrinkage estimators and \(r_v(x)=x\sigma _v\) and \(r_u(x)=\sigma _u\); see Eq. (5). That is, we assume the standard deviation in the noise is proportional to \(x\) while that of the inefficiency is constant and find estimates of the coefficients

$$\begin{aligned} \beta _0=0.387,\quad \beta _1=0.366,\quad \sigma _v=0.018\quad \text {and} \quad \sigma _u=0.003. \end{aligned}$$
(13)

The solid black line shows the SFA efficient frontier. The dotted line shows the SFA frontier for the sample means and standard deviations with the same model assumptions. It also shows that how much estimation risk can distort our estimate of the frontier. The technical efficiencies of the stocks range from \(0.9969\) to \(0.9979\), reflecting the small \(\sigma _u\). The model assigns nearly all the variation in stock performance (relative to the frontier) to noise.

The dashed grey line in Fig. 1 shows, for comparison, an estimated diversification-consistent DEA frontier (Lamb & Tee, 2012a; Liu et al., 2015). Like the SFA frontiers it passes through the origin, has nonegative gradient and is concave. However, since we do not know of a way to estimate a DEA frontier that takes account of uncertainty in risk and return measures, no point can be above the DEA frontier.

It is interesting to note the much more plausible frontier shape close to the origin, where we expect nonnegligible return for negligible risk, because there is typically a risk-free rate of return (DeMiguel et al., 2009). We have also fitted SFA models with a risk-free rate of return, which we get by subtracting US treasury bill returns from each period. The results are negligibly different. For example, for the FTSE stocks we get \(\beta _0=0.394\) and \(\beta _1=0.361\). So we do not report these results further.

Fig. 2
figure 2

Standard normalised residuals for four SFA models for FTSE 100 stocks

Full size image

We wish to check both the quality of fit of the SFA model and whether different assumptions of the form of \(r_v\) and \(r_v\) work better. We do both by plotting charts of the standard normalised model residuals calculated using Eq. (8) against the predicted frontier values calculated using Eq. (4). Panel A of Fig. 2 shows the residual plot for the model of Fig. 1: the fit is good and the model plausible.

The most plausible alternative model uses \(r_v=\beta _0x^{\,\beta _1}\sigma _v\) instead of \(r_v=\sigma _v\) and Fig. 2, Panel B shows its residual plot. The fit is good and the model coefficients hardly different, which are less surprising because the frontier is close to constant for standard deviations in the range we observe. Panel C shows SFA with \(r_v=\beta _0x^{\,\beta _1}\sigma _v\) and \(r_u=\sigma _u\), and panel D shows the standard SFA model, with \(r_v=\sigma _v\) and \(r_u=\sigma _u\). These fit less well and the standard SFA model has the least good fit.

Fig. 3
figure 3

Simex extrapolation plots for FTSE 100 stocks

Full size image

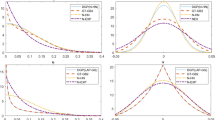
We consider also measurement error as described in Sect. 3.3, because it can improve model coefficients. Figure 3 shows plots of the model coefficients with various levels \(\lambda \) of noise added. The coefficients of Eq. (13) are approximately the simex ones at \(\lambda =0\), and we extrapolate values without measurement error at \(\lambda =-1\). We use three standard extrapolants: the rational linear (when available, dotted lines) and quadratic (dot-dash lines) extrapolants of Eq. (12), and a linear (dashed lines) extrapolant. The changes in \(\beta _0\), \(\beta _1\) and \(\sigma _v\) are too small to noticeably affect model fit. The quadratic extrapolant, which we would choose for \(\sigma _u\), gives greater relative change but not enough to reduce the efficiencies noticeably. While it is important to check the effects of measurement error, they are not guaranteed to impact the model coefficients substantially (van Smeden et al., 2020).

Fig. 4
figure 4

SFA fit and standard normalised residuals for Standard and Poor stocks

Full size image

Figure 4 shows the SFA frontiers for the s &p stocks in the same format as Fig. 1 with \(r_v(x)=x\sigma _v\) and \(r_u(x)=\sigma _u\) as before, together with a standard normalised residual plot for the shrinkage frontier. The coefficients of the SFA fit with shrinkage estimators,

$$\begin{aligned} \beta _0=0.395,\quad \beta _1=0.503,\quad \sigma _v=0.017\quad \text {and} \quad \sigma _u=0.002 \end{aligned}$$

are similar to those of the ftse stocks in Eq. (13). The residual plot suggests very good model fit. Efficiencies are, again, all close to \(1\). And simex shows even more negligible effects from measurement errors.

Fig. 5
figure 5

SFA fit and standard normalised residuals for Nikkei stocks

Full size image

Figure 5  shows the SFA frontiers for the Nikkei stocks, together with a standard normalised residual plot for the SFA frontier using shrinkage estimators. This time the best fit comes from the standard (\(r_v(x)=\sigma _v\), \(r_u(x)=\sigma _u\)) SFA model: the residual plot suggests mild heteroscedasticity, but changing the \(r_v\) and \(r_u\) always produces a much worse residual plot even when the SFA frontier appears reasonable. The shrinkage SFA coefficients are

$$\begin{aligned} \beta _0=0.270,\quad \beta _1=0.325,\quad \sigma _v=0.1\quad \text {and} \quad \sigma _u=0.012. \end{aligned}$$

And the efficiencies in the range \(0.980\)–\(0.987\), slightly lower than those of the ftse and s &p stocks, as we expect with a larger value of \(\sigma _v\). As before, simex hardly changes the coefficient estimates.

Fig. 6
figure 6

SFA fits for DAX stocks and hedge funds

Full size image

We conclude with two cases where our methodology works less well. Figure 6 left shows SFA fits for 280 monthly percentage returns for 20 DAX stocks to end of May 2019 (Datastream, 2019). And Fig. 6 right shows fits for 168 monthly percentage returns for hedge funds to the end of December 2019 (Refinitiv, 2019). The DAX fit and residual plot are good but the sample size limits our confidence in the model. By contrast the large sample of hedge funds do not fit any variant of our model assumptions well. It may be that the mix of hedge fund strategies makes a single fit less sensible. Or it may be that we really need a different form for \(f(x;\beta )\) in Eq. (1). In any case, even if is not clear from Figure 6 right, the residual plots show none of our models are plausible in these two cases.

5 Conclusions

SFA can be seen as an alternative to DEA for fitting frontiers and finding efficiencies for asset returns. However, asset return and risk measures do not behave entirely like the inputs and outputs of production economics for which SFA was developed. So we have had to develop new theory and methods. Specifically, we show why a Cobb–Douglas frontier is plausible and how to deal with estimation risk. Then we note that, probably in contrast to production economics, we may expect heteroscedasticy in the SFA regression residuals and measurement error in the risk measures. So we have developed methods to handle these and to test for model fit. In doing so we have had to resolve several issues and have some findings that may be surprising.

One intriguing empirical finding is that there was very little evidence of technical inefficiency in our SFA models. This finding is similar to that of Ferreira & Oliveira (2016) and may be an indication that, for our data, the market is good at estimating both the mean return and the volatility of assets. It may also be a limitation of modelling with one input or a feature of stocks drawn from market indices.

The first issue we resolve is the choice of SFA model. We consider several that allow heteroscedasticity in the noise \(v\) or inefficiency \(u\) and develop log-likelihood functions to fit them. We find errors of the form \(x\sigma _v\) for \(v\) and \(\sigma _u\) for \(u\) fit best, though the form \(\beta _0x^{\,\beta _1}\sigma _u\) also fits reasonably for \(u\). This leads us to the second issue: how to test model fit.

We resolve this issue by developing a new method for creating residual plots, like those used in linear regression modelling. These are much better for checking model assumptions and model fit than plotting the data and frontier, and we recommend using them for any SFA model. We anticipate that they will be especially useful in models with more than one input variable.

A third issue we had to investigate was the effect of measurement error, which arises because of uncertainty in the measured values of mean and variance. We resolved this by adapting an empirical simex method to work with SFA. The surprising finding was that the measurement errors had very little influence on the model parameters. This, however, is not a general result and we recommend using simex to check any SFA model that may be influenced by measurement error in the same way as one would routinely check for heteroscedasticity or non-normality. Such checks show the accuracy of the findings even if they hardly improve them.

Finally, we address the issue of estimation risk. Estimation risk is the tendency of statistics like the sample mean and standard deviation to underestimate small values and overestimate large ones when we have several values. As far as we know, no previous frontier-fitting method has dealt with estimation risk, and SFA studies for assets (Santos et al., 2005; Ferreira & Oliveira, 2016) do not show the frontier to let us check plausibility of fit. We resolve the issue by introducing shrinkage estimators instead of the sample ones. The impact is too striking to be ignored. Without shrinkage estimators, our results suggest a frontier whose curvature substantially underestimates that of the true one. With shrinkage estimators, the frontier becomes plausible.

5.1 Limitations and future recommendations

The methods of this article currently have several limitations. They do not work well when there are few assets, as we saw for the DAX stocks. This may be a difficult issue to overcome without adding more assets, because asset returns typically have high volatility relative to return.

The methods can also fail for some assets such as the hedge funds. We can think of three plausible explanations that might be addressed in future studies. First, the hedge funds vary in their choice of investment strategy. So it may be possible to fit separate strategies separately. Second, not all smooth, nondecreasing, concave functions that pass through the origin are well represented by a Cobb–Douglas frontier. So it may be helpful to test other frontier forms both for assets and in production economics. Third, and perhaps most challenging, the assumptions about the distribution of errors and, (since the error in a mean is more plausibly normal) especially, the inefficiencies may be inappropriate in the hedge fund case.

The most obvious limitation is that we only consider one input and one output. The one-output limitation is a well-known issue in SFA . It is less important in fitting assets, where mean return is nearly always the only output wanted. But, future studies could address the issue of multiple inputs. In fact, the theory we have developed can readily be used in the multiple-input case with suitable risk measures. Such, coherent (Artzner & Delbaen, 1999), risk measures are already widely used. The real limitation is that we do not yet have methods to reduce estimation risk for them. So, besides investigating the shape and distribution of inefficiencies, a major challenge for future research is finding estimators of coherent risk measures that substantially reduce estimation risk. This challenge is important both for SFA and DEA, where, to the best of our knowledge, estimation risk has not been considered at all.