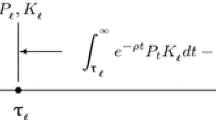Time-to-build and capacity expansion

Abstract

In this study, we investigate a firm’s optimal investment timing and capacity decisions in the presence of uncertain time-to-build. The firm raises revenue from the investment after an uncertain amount of time elapses, while the time-to-build of the follow-up investment is expectedly shorter than that of the initial investment due to learning by doing. We derive the optimal investment strategies and examine the impact of time-to-build on the investment dynamics. We show that both the initial and follow-up investment can be made earlier in the presence of time-to-build than they would in the absence of the lags, especially in a volatile market. This is in contrast to the case of a single investment, whose timing is always delayed by the time-to-build. Furthermore, the capacity of the follow-up project dominates that of the initial project in the presence of time-to-build, whereas the latter dominates the former in the absence of lags. The capacity choice of each project, however, is nonmonotone with respect to the size of the lags. We also show that uncertainty delays investment even when the investment involves lags but the negative impact softens in the presence of time-to-build and learning effects.

1 Introduction

Ramping up production usually takes longer than initial expectations. During the COVID-19 pandemic and the accompanying global supply chain disruption, this was more true than ever before. The Global COVID-19 Vaccine Supply Chain and Manufacturing Summit¹ reported that 837 million doses of vaccines were projected to be produced in 2020 but only 31 million were produced, which is less than 4% of the original projection. The production speed increased throughout 2021 as vaccine makers expanded their capacities, but there have been occasional hiccups in the manufacturing process due to the shutdown of factories and the shortage of raw materials. Furthermore, developing and manufacturing vaccines for a new variant still make their time-to-build highly uncertain.

Time-to-build and its inherent uncertainty are not limited to manufacturing new vaccines. As global demand for semiconductors surged, chipmakers strove to expand their capacities. The Taiwan Semiconductor Manufacturing Company (TSMC), the chip-making industry leader, is investing more than $100 billion over the next three years, and Samsung plans to invest $150 billion by the end of the decade. However, the chipmakers cannot expand their capacities instantly despite their desire to do so.² In an interview with the Financial Times, the chief executive of Intel, which is planning to invest up to €80 billion and $40 billion in Europe and the U.S., respectively, acknowledged that the shortage of chip-making equipment will delay their capacity-expansion plans. He noted that it would take two years to build the shell of the chip factory and start to fill it with equipment in year three or four. The chief executive of ASML, the largest supplier of lithography machines for manufacturing semiconductors,³ warned that the shortage of chip-making equipment could last for the next two years (Hollinger and Waters 2022). The delay of capacity expansion in the semiconductor industry has caused production lags in other industries as well.⁴

Recent trends show that time-to-build is a universal phenomenon, especially in mass production based on state-of-the-art technology, and many studies have investigated the impact of time-to-build on a firm’s optimal investment strategy. In most studies, however, the modeling was not comprehensive enough to reflect the features of real-world investment projects and the dimensions of investment decisions. For instance, many of them considered the impact of time-to-build only on investment timing, leaving the impact on its size unanswered [e.g., Majd and Pindyck (1987), Bar-Ilan and Strange (1996, 1998), Jeon (2021a)]. Some studies have not considered the inherent uncertainty in time-to-build [e.g., Majd and Pindyck (1987), Bar-Ilan and Strange (1996, 1998), Boonman and Siddiqui (2017)]; others have not allowed a follow-up investment [e.g., Majd and Pindyck (1987), Bar-Ilan and Strange (1996), Boonman and Siddiqui (2017), Jeon (2021a)]. Even when the follow-up investment is considered, learning by doing, which is a distinct feature in a sequential investment, has often been overlooked [e.g., Bar-Ilan and Strange (1998), Pacheco-de-Almeida and Zemsky (2003)].

A conventional result from these studies is that time-to-build delays investment unless there is an abandonment option that truncates the downside risk of investment. Another conventional result from the real options literature is that uncertainty delays investment yet increases its size. In this study, we investigate if these results still hold when investment projects involve uncertain time-to-build and there is a learning effect between the initial and follow-up investment. In particular, we take both investment timing and its size into account in the discussion regarding investment strategy. To be more specific, we suppose it takes an uncertain amount of time until a firm begins raising revenue from its initial investment. After the capacity is in operation, the firm can expand its capacity further, and the time-to-build of the subsequent project is expected to be shorter than that of the initial one because of learning by doing. With this setup, we derive the optimal investment timing and capacity choice for each investment project and discuss how investment lags—combined with learning by doing—affect the firm’s investment dynamics and how they change the impact of volatility on investment decisions. To the best of our knowledge, this is the first study to examine the impacts of uncertain time-to-build and learning by doing on investment dynamics from the perspective of timing and size.

First, we show that the follow-up investment can be made earlier in the presence of uncertain time-to-build than it would in the absence of the lags. Due to time-to-build, the firm does not make any instant profits after the initial investment. As demand grows further without generating any revenue, the opportunity for the follow-up investment becomes more valuable than the case in which the initial project yields revenue instantly. That is, time-to-build makes the firm favor the capacity expansion option more. This is in contrast to the case of a firm holding a single investment opportunity with uncertain lags. Jeon (2021a) showed that the one-shot investment is always delayed in the presence of uncertain time-to-build because the lags reduce the expected profits of the project and thereby increase the value of waiting. Given the expansion option, however, the initial project’s time-to-build undermines the value of waiting to invest in the follow-up project, and this effect can dominate the decrease in the expected profits by the lags, advancing the timing of the capacity expansion.

Given substantial learning effects, not only the follow-up investment but also the initial investment is made earlier in the presence of time-to-build than it would in the absence of lags. This implies that the earlier investment in the initial project is not because the firm wants to make revenue from it sooner but because the firm wants to learn from it earlier, expecting shorter lags in the follow-up investment. In other words, the initial project becomes more of a source of learning than that of revenue. Bar-Ilan and Strange (1996) showed that the presence of time-to-build can hasten investment. They analyzed the optimal timing decision regarding a single investment with fixed lags, but they assumed that the firm could abandon the project later on. The lags increase uncertainty, and thus, the value of waiting, but the abandonment option truncates the downside risks. For this reason, longer lags increase the expected value of investment, inducing earlier investment. In our model, the firm faces uncertain time-to-build without the option to truncate the downside risks. Nevertheless, time-to-build induces earlier follow-up investment while learning effects result in earlier initial investment.

We also find that the capacity of the follow-up investment can be greater than that of the initial investment in the presence of time-to-build. This is in sharp contrast to the case of no lags in which the initial capacity exceeds the subsequent capacity. The follow-up project, which can benefit from learning by doing, becomes more valuable when the initial lags are longer and the firm places more weight on the follow-up investment than on the initial one. Combined with the timing decision, this implies that the firm invests earlier in more capacity in the follow-up project in the presence of time-to-build than it would without the lags. The capacity size, however, is not monotone with respect to the lags; after the lags exceed a certain level, the capacity of the initial and follow-up investment increases and decreases with the lags, respectively. This is because the initial time-to-build becomes so lengthy that the revenue from the expansion is expected to be generated in the distant future, even after taking learning effects into account. Boonman and Siddiqui (2017) investigated the effects of operational flexibility with fixed lags and showed that longer lags lead to a greater capacity. In their model, a suspension option that does not involve lags truncates the downside risk of the investment, while revenues are expected to increase during the resumption’s lags. For this reason, the optimal capacity size increases with the lags. In contrast, our model shows that the capacity of the follow-up investment can increase with time-to-build even when the lags are uncertain and the downside risk cannot be truncated, mainly because of learning effects from the initial investment.

Lastly, we show that uncertainty delays investment as many studies have shown [e.g., McDonald and Siegel (1986), Pindyck (1988, 1993)], but the negative impact of uncertainty softens in the presence of time-to-build and learning by doing. That is, the investment thresholds increase with volatility but at a slower rate in the presence of the lags. This is in sharp contrast with the case of a single investment in which time-to-build amplifies the negative impact of uncertainty on investment timing. We also observe that uncertainty increases the capacity size, which is also in line with the conventional finding [e.g., Dangl (1999), Bar-Ilan and Strange (1999), Seta et al. (2012)], but the size of impact on the initial and follow-up capacities is altered. Without the lags, the initial capacity increases with volatility at a much faster rate than the subsequent capacity, and thus, the former dominates the latter. In the presence of time-to-build, however, both capacities increase at a similar rate, and the latter is dominant over the former. Bar-Ilan and Strange (1996) found that uncertainty can hasten investment in the prsence of time-to-build, but this is mainly because of the abandonment option that truncates the downside risk of the investment. Bar-Ilan et al. (2002) found that when lags are significant, uncertainty accelerates investment but reduces its size. This is because they assumed that excess capacity incurs costs, which naturally induces earlier investment with a smaller capacity. Unlike these studies, our model supports the conventional result regarding the effects of uncertainty on investment, but the size of the impact is altered due to time-to-build and learning effects.

The remainder of this paper is organized as follows. Section 2 presents a literature review. Section 3.1 introduces the setup of the model, and in Sect. 3.2 the case without time-to-build is examined as the benchmark model. In Sect. 3.3, we investigate the main model, which incorporates uncertain time-to-build into investment decisions. Section 4 presents the comparative statics results and related discussion; Sect. 4.1 discusses the impact of the size of time-to-build on the optimal investment strategies, and in Sect. 4.2, we investigate how time-to-build affects the impact of the volatility on the investment strategies. Section 5 summarizes the main results and discusses future work. All the proofs are provided in Appendix A, and the results of the benchmark case with a single investment opportunity are given in Appendix B. Appendix C presents the decomposition of option values into their intrinsic values and time values. In the Online Appendix, we extend the model by incorporating the case in which the firm can make the follow-up investment even before the completion of the initial project and discuss the results from comparative statics. It also provides a table that summarizes important notations that appear throughout the manuscript.

2 Literature review

The seminal work of Majd and Pindyck (1987) pioneered the research of time-to-build in a firm’s investment decision, demonstrating that the investment is delayed as the maximum rate at which it can be made decreases. Bar-Ilan and Strange (1996) directly modeled the lags by assuming that a certain amount of time has to elapse until the project yields revenue and showed that the presence of time-to-build can hasten the investment. Bar-Ilan and Strange (1998) extended their previous research to a project requiring a two-stage investment to make profits and showed that the investment can be made sequentially if the firm has the option to suspend the second investment. However, a series of their works only considered a timing decision of the investment without uncertainty in the lags. By contrast, the current study examines both the timing and size decisions of capacity expansion and clarifies the impact of uncertain time-to-build on the investment dynamics. Pacheco-de-Almeida and Zemsky (2003) studied the effect of time-to-build in a duopoly market based on a three-period discrete model and showed that when time-to-build is significant, both firms can make an incremental investment, whereas insignificant lags lead to lumpy investments. Jeon (2021b) also studied the impact of time-to-build on duopoly competition, but the study incorporated asymmetry in firms’ time-to-build and showed that the disadvantaged firm with longer time-to-build can become a leader in the market. Boonman and Siddiqui (2017) studied a firm’s investment decision in the presence of operational flexibility and lags, and found that longer time lags result in a larger capacity but that the impact of the lags on the timing decision depends on the volatility.

Most studies of time-to-build implicitly assume that after the investment is made, nothing happens until the project’s completion; however, there are a few exceptions. Gauthier and Morellec (2000) incorporated the option of abandonment into the discussion of implementation delay. They investigated the European abandonment option, which requires the price to be above a certain level after the delay has passed, and the Parisian abandonment option, which requires the price to remain above a certain level throughout the period of delay. Costeniuc et al. (2008) extended the discussion of the latter and derived an analytic solution to the problem. Agliardi and Koussis (2013) incorporated debt financing into two-stage investment decisions and considered the firm’s default between the two investments, but the investment timing was exogenously given in their model. By contrast, Jeon (2021a) also considered the default decision during time-to-build but the investment, financing, and default decisions were endogenously derived. The study showed that the default probability in the presence of time-to-build can be lower than that in the absence of the lags. Our study does not address the option of abandonment or default after the investment. Instead, we focus on what can occur between the initial and the follow-up investments and how it affects the firm’s optimal investment strategies.

Time-to-build has been extensively studied in the literature on real business cycles (RBC). The seminal article of Kydland and Prescott (1982) showed that time-to-build contributes to the persistence of the business cycle, paving the way for numerous RBC-based models. For instance, Asea and Zak (1999) and Bambi (2008) suggested exogenous and endogenous growth models with time-to-build, respectively. Zhou (2000) showed that the introduction of time-to-build leads to the positive autocorrelation of investment, which has been empirically observed in several studies. Gomme et al. (2001) focused on the household sector, and showed that time-to-build can yield a positive correlation between business and household investment and household investment’s leading business investment over the business cycle, which has been considered anomalous in the literature. Edge (2007) considered not only time-to-build but also time-to-plan, and showed that the investment lags and habit-persistence in consumption allow the sticky-price monetary business cycle model to generate liquidity effects. Although our study is based on a partial equilibrium approach, notably, time-to-build, the key component in our model, also plays a pivotal role in general equilibrium models.

Numerous studies have been devoted to a firm’s capacity decision. Manne (1961) pioneered the decision of the capacity expansion with stochastic growth and showed that the optimal size of investment increases with the volatility. Bean et al. (1992) extended this study to allow more general demand processes and cost structures. Bar-Ilan and Strange (1999) studied the decisions of both investment timing and capacity, and found that an increase in volatility delays the investment but increases its size. Dangl (1999) examined a firm’s investment timing and capacity decisions with flexible capacity adjustment and also showed that higher uncertainty leads to an increase in capacity. Hagspiel et al. (2016) found that a firm’s flexibility in output choice leads to greater capacity. Our study does not consider the firm’s flexibility in the output choice after capacity installation. That is, we implicitly assume that the firm produces up to its capacity after the capacity is in place. Bar-Ilan et al. (2002) incorporated capacity decisions into the discussion on the interaction of time-to-build and volatility based on the impulse control approach. They showed that when the lags are short, an increase in volatility delays investment and increases its size, whereas, given significant lags, volatility speeds up investment and reduces its size. Goyal and Netessine (2007) studied duopoly firms’ technology, capacity, and production decisions and showed that flexibility in the choice of technology is not always the optimal response to competition. Kort et al. (2010) studied a firm’s choice between a lumpy investment with cost efficiency and a stepwise investment with timing flexibility, and found that the former is preferred when demand is more uncertain. However, the size of capacity is exogenously given in their model. Bensoussan and Chevalier-Roignant (2019) presented a mathematical framework for studies on capacity expansion based on the impulse control approach, adopting an affine structure of investment costs.

The seminal study of Arrow (1962) embraced a learning curve as a novel factor in macroeconomic growth models. Spence (1981) studied the impact of the learning curve on market competition and found that the learning curve creates entry barriers in the market, protecting incumbents from competition, but the entry timing was exogenously given. Lieberman (1984) empirically analyzed the determinants of the learning curve and showed that learning is a function of cumulative output and investment rather than calendar time. Cohen and Levinthal (1989) claimed that R &D investments not only generate new information but also enhance the firm’s ability to exploit existing information, referred to as learning or absorptive capacity. Rob (1991) investigated a competitive market with firms learning about the market size in a Bayesian manner and found that the equilibrium rate of entry monotonically decreases over time. Majd and Pindyck (1989) studied the impact of the learning curve on a firm’s production decision, assuming that marginal production costs decrease with cumulative output. They found that the learning curve becomes a less important factor for the production decision when uncertainty in market demand is significant, but their study assumed no adjustment costs and did not consider the capacity choice. Seta et al. (2012) extended this study by incorporating the capacity decision. They showed that greater learning makes the investment earlier yet at a smaller scale, but the possibility of capacity expansion was not considered in their study. Our study incorporates a learning curve via the channel of time-to-build, which is in contrast with previous studies that describe the learning effect through the reduction of investment costs in subsequent projects. Using this novel setup, we examine the impact of learning by doing on a monopolistic firm’s investment dynamics. Martzoukos (2000) adopted a controlled diffusion process to describe a firm’s costly action of learning. The study found that the impact of learning is more significant for a less profitable project, but the investment timing was pre-specified. Chang et al. (2002) incorporated learning by doing into the RBC model. They showed that learning by doing provides a significant propagation mechanism and that it generates a positive correlation in output growth even when the exogenous technology follows a random walk. Koussis et al. (2007) extended this study to incorporate timing flexibility and path dependency, and Martzoukos and Zacharias (2013) followed a similar setup and further considered learning spillovers between firms.

3 Models and solutions

3.1 Setup

Suppose a risk-neutral firm with the option to invest. The firm makes the investment decision in terms of its timing and capacity. The price of the product at time t is given by

$$\begin{aligned} P(t)=X(t)(1-\eta Q(t)), \end{aligned}$$

(1)

where Q(t) is a total market output, $\eta >0$ is a constant, and X(t) is a demand shock. The demand shock follows a geometric Brownian motion:

$$\begin{aligned} \textrm{d}X(t)=\mu X(t)\textrm{d}t+\sigma X(t)\textrm{d}W(t), \end{aligned}$$

(2)

where $\mu$ and $\sigma$ are positive constants and $(W_t)_{t\ge 0}$ is a standard Brownian motion on a filtered probability space $(\Omega ,\mathcal {F},\mathbb {F}:=(\mathcal {F}_t)_{t\ge 0},\mathbb {P})$ satisfying the usual conditions. The production incurs marginal costs c per unit, and the discount rate is given by a constant $r(>\mu )$ to ensure the finiteness of value functions. The firm chooses the investment timing and capacity size to maximize its value. The investment timing is a stopping time with respect to the Brownian filtration, and the firm’s choice of capacity is measurable with respect to the $\sigma$-algebra at the time of investment.

The exercise of the option to invest, however, does not imply that the firm generates revenue instantly. That is, the investment involves an uncertain amount of time-to-build. We assume that it takes an exponential time with an intensity parameter $\lambda$ to succeed in manufacturing products and generate revenue from the investment. The lags are assumed to be independent of the demand shock.

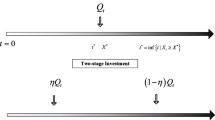
Having the option exercised, the firm has another option to invest: the option to expand its capacity further. In other words, the firm’s option to invest can be read as a compound option, and each investment incurs lump-sum costs $\delta$ per unit. We assume that the option of capacity expansion can only be exercised after the initial capacity starts to operate, which is relaxed in Online Appendix.

It is reasonable to assume that there is learning by doing in mass production. That is, we suppose that the expected time-to-build for the follow-up investment can be shorter than that of the initial investment, which will be discussed in detail in Sect. 3.3. Salomon and Martin (2008) conducted a comprehensive analysis to investigate the determinants of time-to-build in the global semiconductor industry. They found empirical evidence to strongly support the hypothesis that time-to-build decreases as learning from experience increases. Specifically, they gathered 265 time-to-build data sets from 571 semiconductor plants between 1982 and 2001, finding that an experienced chip manufacturer completes work more than one month earlier, on average, than an inexperienced firm building the same plant.

The modeling of time-to-build by exponential distribution is not only tractable but also appropriate for describing the inherent uncertainty, especially the lags from mass production based on state-of-the-art technologies. For instance, the first flight of the C919, a narrow-body airliner developed by the Commercial Aircraft Corporation of China (COMAC), was initially scheduled in 2014; however, it was repeatedly delayed until May 2017.⁵ The delivery of LNG-powered vessels built by the China State Shipbuilding Corporation (CSSC) was delayed twice.⁶

3.2 Benchmark model: without time-to-build

For comparative purposes, we examine a benchmark model that does not incorporate the investment lags. By backward induction, we first investigate the firm’s optimal investment strategy for the follow-up investment.

In the absence of time-to-build, the firm generates revenue instantly after the initial investment in $Q_1$. With $Q_1$ in place, the firm holds the option to expand the capacity further: the option to invest in $Q_2$. Thus, the firm value after the investment in $Q_1$ can be described as follows:

$$\begin{aligned} \bar{V}_2(X,Q_1)&=\max _{T_2\ge 0,Q_2\ge 0}\mathbb {E}\bigg [\int _0^{T_2}e^{-rt}Q_1\{X(t)(1-\eta Q_1)-c\}\textrm{d}t\nonumber \\ {}&\qquad +\int _{T_2}^\infty e^{-rt}(Q_1+Q_2)\{X(t)(1-\eta (Q_1+Q_2))-c\}\textrm{d}t-e^{-rT_2}\delta Q_2\bigg |X(0)=X\bigg ]. \end{aligned}$$

(3)

The bar on top of each value indicates that it is from the benchmark model. The investment timing can be characterized by the level of demand shock at which the firm invests. That is, it can be described as $T_2:=\inf \{t\ge T_1|X(t)\ge X_2\}$, where $T_1$ denotes the initial investment timing, which will be described shortly. Following the standard arguments from real options literature, we can easily derive the optimal timing and capacity for the follow-up investment as follows:

Proposition 1

(Optimal capacity expansion without time-to-build) Given the demand shock X, the value function after the investment in the initial capacity $Q_1$ in the absence of time-to-build is

$$\begin{aligned} \bar{V}_2(X,Q_1)= {\left\{ \begin{array}{ll} \bar{\Pi }_1(X,Q_1)-\bar{\Gamma }(Q_1)+\bar{A}_2(Q_1)\big (\frac{X}{\bar{X}_2^*(Q_1)}\big )^\beta &{}\text {if }X<\bar{X}_2^*(Q_1),\\ \bar{\Pi }_1(X,Q_1)-\bar{\Gamma }(Q_1)+\bar{A}_2(X,Q_1)&{}\text {if }X\ge \bar{X}_2^*(Q_1), \end{array}\right. } \end{aligned}$$

(4)

where $\bar{A}_2(Q_1):=\bar{A}_2(\bar{X}_2^*(Q_1),Q_1)$ and

$$\begin{aligned} \bar{A}_2(X,Q_1)=\bar{\Pi }_2(X,Q_1,\bar{Q}_2^*(Q_1))-\bar{\Gamma }(Q_2)-\delta \bar{Q}_2^*(Q_1), \end{aligned}$$

(5)

with

$$\begin{aligned}&\bar{\Pi }_1(X,Q_1)=\frac{Q_1(1-\eta Q_1)X}{r-\mu }, \end{aligned}$$

(6)

$$\begin{aligned}&\bar{\Pi }_2(X,Q_1,Q_2)=\frac{Q_2(1-\eta Q_2-2\eta Q_1)X}{r-\mu }, \end{aligned}$$

(7)

$$\begin{aligned}&\bar{\Gamma }(Q)=\frac{cQ}{r}\quad \text {for }Q\in \{Q_1,Q_2\}, \end{aligned}$$

(8)

and

$$\begin{aligned} \beta =\frac{1}{2}-\frac{\mu }{\sigma ^2}+\sqrt{\Big (\frac{1}{2}-\frac{\mu }{\sigma ^2}\Big )^2 +\frac{2r}{\sigma ^2}}(>1). \end{aligned}$$

(9)

The optimal investment threshold and capacity are

$$\begin{aligned}&\bar{X}_2^*(Q_1)=\frac{(\beta +1)(c/r+\delta )(r-\mu )}{(\beta -1)(1-2\eta Q_1)}, \end{aligned}$$

(10)

$$\begin{aligned}&\bar{Q}_2^*(Q_1)=\frac{1-2\eta Q_1}{\eta (\beta +1)}. \end{aligned}$$

(11)

Proof

See Appendix A.1. $\square$

$\bar{\Pi }_1(X,Q_1)-\bar{\Gamma }(Q_1)$ in (4) denotes the expected profits from the initial capacity $Q_1$, while $\bar{\Pi }_2(X,Q_1,Q_2)-\bar{\Gamma }(Q_2)$ in (5) refers to those from the additional capacity $Q_2$, given the initial capacity $Q_1$.⁷

Now, suppose that the firm has not yet made the initial investment. The firm value with the initial option, which yields another option described in (4), can be expressed as follows:

$$\begin{aligned} \bar{V}_1(X)=\max _{T_1\ge 0,Q_1\ge 0} \mathbb {E}\Big [e^{-rT_1}\big \{\bar{V}_2(X(T_1),Q_1)-\delta Q_1\big \}\Big |X(0)=X\Big ]. \end{aligned}$$

(12)

The initial investment timing can be illustrated as $T_1:=\inf \{t>0|X(t)\ge X_1\}$, and the same arguments lead to the following optimal investment strategy:

Proposition 2

(Optimal initial investment without time-to-build) Given the demand shock X, the initial value function in the absence of time-to-build is

$$\begin{aligned} \bar{V}_1(X)= {\left\{ \begin{array}{ll} \bar{A}_1(\bar{X}_1^*)\big (\frac{X}{\bar{X}_1^*}\big )^\beta &{}\text {if }X<\bar{X}_1^*,\\ \bar{A}_1(X)&{}\text {if }X\ge \bar{X}_1^*, \end{array}\right. } \end{aligned}$$

(13)

where

$$\begin{aligned} \bar{A}_1(X)=\bar{\Pi }_1(X,\bar{Q}_1^*)-\bar{\Gamma }(\bar{Q}_1^*) +\bar{A}_2(\bar{Q}_1^*)\Big (\frac{X}{\bar{X}_2^*(\bar{Q}_1^*)}\Big )^\beta -\delta \bar{Q}_1^*. \end{aligned}$$

(14)

The optimal investment threshold is $\bar{X}_1^*:=\bar{X}_1^*(\bar{Q}_1^*)$ with

$$\begin{aligned} \bar{X}_1^*(Q_1)=\frac{\beta (c/r+\delta )(r-\mu )}{(\beta -1)(1-\eta Q_1)}, \end{aligned}$$

(15)

and the optimal capacity $\bar{Q}_1^*$ is implicitly derived from

$$\begin{aligned} \frac{(1-2\eta Q_1)\bar{X}_1^*(Q_1)}{r-\mu }-\frac{c}{r}-\delta =\frac{2(c/r+\delta )}{\beta -1}\Big (\frac{(\beta -1)(1-2\eta Q_1)\bar{X}_1^*(Q_1)}{(\beta +1)(c/r+\delta )(r-\mu )}\Big )^\beta . \end{aligned}$$

(16)

Proof

See Appendix A.2. $\square$

Note that $\bar{A}_1(X)$ in (14) can be rewritten as $\bar{A}_1(X)=\bar{V}_2(X,\bar{Q}_1^*)-\delta \bar{Q}_1^*$ with $\bar{V}_2(X,Q_1)$ corresponding to the first row of (4), and this is in line with the description as a compound option in (12).

3.3 Main model: with time-to-build

Now, we proceed to the main model that incorporates time-to-build with uncertainty. Unlike the benchmark model, there are two phases after the initial investment: before and after the initial capacity commences operations. For evaluating the value functions of each phase, we denote their associated values using 20 and 21 as subscripts, respectively. Even though we assume in this section that the firm can only make after the initial capacity is in operation, we will use the subscript 21 for the values associated with capacity expansion instead of just 2 to ensure the notations’ consistency when we extend the model in Online Appendix to the case in which a firm can make the follow-up investment either before or after the initial project is finished.

3.3.1 After initial project is finished

By backward induction, we analyze the firm’s capacity expansion decision first. Suppose that the initial investment project in the capacity $Q_1$ is finished, and the firm is generating revenue from it. Given the initial capacity $Q_1$ in operation, the firm value with the option to make the follow-up investment can be expressed as follows:

$$\begin{aligned} V_{21}(X,Q_1)&=\max _{T_{21}\ge 0,Q_{21}\ge 0}\mathbb {E}\bigg [\int _0^{\hat{T}_{21}}e^{-rt}Q_1\{X(t)(1-\eta Q_1)-c\}\textrm{d}t\nonumber \\&\qquad +\int _{\hat{T}_{21}}^\infty (Q_1+Q_{21})\{X(t)(1-\eta (Q_1+Q_{21}))-c\}\textrm{d}t-e^{-rT_{21}}\delta Q_{21}\bigg |X(0)=X\bigg ] \end{aligned}$$

(17)

where $\hat{T}_{21}:=T_{21}+\tau _{21}$ denotes the manufacturing timing of the capacity $Q_{21}$ and $\tau _{21}$ follows an exponential distribution with an intensity parameter $\lambda _{21}$. The investment timing can be described as $T_{21}:=\inf \{t\ge \hat{T}_1|X(t)\ge X_{21}\}$, where $\hat{T}_1:=T_1+\tau _1$ denotes the manufacturing timing of the capacity $Q_1$ and $\tau _1$ follows an exponential distribution with an intensity parameter $\lambda _1$. Given learning by doing, we suppose that the expected time-to-build of the follow-up investment can be shorter than that of the initial investment project (i.e., $\lambda _{21}\ge \lambda _1$).

Following the standard arguments from real options literature, we can derive the optimal investment strategy for the capacity expansion with the initial capacity in operation in the presence of time-to-build as follows:

Proposition 3

(Optimal capacity expansion) Given the demand shock X and the capacity $Q_1$ in operation, the value function in the presence of time-to-build is

$$\begin{aligned} V_{21}(X,Q_1)= {\left\{ \begin{array}{ll} \bar{\Pi }_1(X,Q_1)-\bar{\Gamma }(Q_1)+A_{21}(Q_1)\big (\frac{X}{X_{21}^*(Q_1)}\big )^\beta &{}\text {if }X<X_{21}^*(Q_1),\\ \bar{\Pi }_1(X,Q_1)-\bar{\Gamma }(Q_1)+A_{21}(X,Q_1)&{}\text {if }X\ge X_{21}^*(Q_1), \end{array}\right. } \end{aligned}$$

(18)

where $A_{21}(Q_1):=A_{21}(X_{21}^*(Q_1),Q_1)$ and

$$\begin{aligned} A_{21}(X,Q_1)=\Pi _{21}(X,Q_1,Q_{21}^*(Q_1))-\Gamma _{21}(Q_{21}^*(Q_1))-\delta Q_{21}^*(Q_1), \end{aligned}$$

(19)

with

$$\begin{aligned}&\Pi _{21}(X,Q_1,Q_{21})=\frac{\lambda _{21}Q_{21}(1-\eta Q_{21}-2\eta Q_1)X}{(r-\mu )(r+\lambda _{21}-\mu )}, \end{aligned}$$

(20)

$$\begin{aligned}&\Gamma _{21}(Q_{21})=\frac{\lambda _{21}cQ_{21}}{r(r+\lambda _{21})}. \end{aligned}$$

(21)

The optimal investment threshold and capacity are

$$\begin{aligned}&X_{21}^*(Q_1)=\frac{(\beta +1)(\frac{\lambda _{21}c}{r(r+\lambda _{21})} +\delta )(r-\mu )(r+\lambda _{21}-\mu )}{(\beta -1)\lambda _{21}(1-2\eta Q_1)}, \end{aligned}$$

(22)

$$\begin{aligned}&Q_{21}^*(Q_1)=\frac{1-2\eta Q_1}{\eta (\beta +1)}. \end{aligned}$$

(23)

Proof

See Appendix A.3. $\square$

$\bar{\Pi }_1(X,Q_1)$ and $\bar{\Gamma }(Q_1)$ in (18) follow (6) and (8), respectively, and $\Pi _{21}(X,Q_1,Q_{21})-\Gamma _{21}(Q_{21})$ in (19) denotes the expected profits from the follow-up capacity $Q_{21}$, taking time-to-build into account, given the initial capacity $Q_1$ in operation. Note that (23) is independent of $\lambda _2$, This, however, does not imply that the capacity choice is irrelevant to time-to-build; it comes into play via the channel of $Q_1$, the choice of which we will discuss later.

3.3.2 Possible scenarios of capital expansion

Recall that we assumed the follow-up investment can only be made after the initial capacity is in operation. Thus, the capacity expansion can be triggered not only by the demand shock hitting the threshold (i.e., $\hat{T}_1<T_{21}$) but also by the completion of the initial project (i.e., $\hat{T}_1=T_{21}$). To be more specific, for $X\ge X_{21}$, the follow-up investment in $Q_{21}$ will be made as soon as $Q_1$ starts operation.

Fig. 1

Timeline of capacity expansion

Fig. 2

Possible scenarios of capacity expansion

Figures 1 and 2 illustrate the timeline of capacity expansion and their possible scenarios, respectively. If the initial project is completed when $X<X_{21}$, the investment in $Q_{21}$ is triggered by hitting the threshold $X_{21}$ (i.e., $\hat{T}_1<T_{21}$), which corresponds to Case 1 in Fig. 1. More specifically, it can be either the very first time the demand shock hits the threshold (Fig. 2a) or not the first time ever but the first time since the initial project’s completion (Fig. 2b). The former and latter can be characterized by $\bar{T}_{21}=T_{21}$ and $\bar{T}_{21}<T_{21}$, respectively, where $\bar{T}_{21}:=\inf \{t>0|X(t)\ge X_{21}\}$ denotes the very first time the demand shock hits the threshold $X_{21}$, which does not necessarily coincide with $T_{21}=\inf \{t\ge \hat{T}_1|X(t)\ge X_{21}\}$.

If the initial project is completed when $X\ge X_{21}$, the follow-up investment in $Q_{21}$ is triggered instantly (i.e., $\hat{T}_1=T_{21}$), which corresponds to Case 2 in Fig. 1. Similarly, it can be either the very first time the demand shock remains in the region $[X_{21},\infty )$ (Fig. 2c) or not the first time ever but after repeatedly going in and out of the region (Fig. 2d). The former and latter can be characterized by $T_{21}<\underline{T}_{21}$ and $\underline{T}_{21}\le T_{21}$, respectively, where $\underline{T}_{21}:=\inf \{t\ge \bar{T}_{21}|X(t)<X_{21}\}$ denotes the very first time the demand shock exits the region of $[X_{21},\infty )$ because of the decrease in the demand shock. The value function before the completion of the initial project must consider these possible scenarios.

3.3.3 Before initial project is finished

The firm value after the initial investment but before the initial capacity starts operating can be expressed as follows:

$$\begin{aligned} V_{20}(X,Q_1)\!=\!\mathbb {E}\Big [1_{\{\hat{T}_1<T_{21}\}}e^{-rT_{21}}V_{21}(X_{21}^*(Q_1),Q_1) \!+\!1_{\{\hat{T}_1=T_{21}\}}e^{-r\hat{T}_1}V_{21}(X(\hat{T}_1),Q_1)\Big |X(0)\!=\!X\Big ]. \end{aligned}$$

(24)

Following similar arguments, we can evaluate the firm value before the initial capacity is in operation as follows:

Proposition 4

(Value function before capacity expansion) Given the demand shock X and the capacity $Q_1$ not in operation, the value function in the presence of time-to-build is

$$\begin{aligned}&V_{20}(X,Q_1)\nonumber \\ {}&= {\left\{ \begin{array}{ll} \Pi _1(X,Q_1)-\Gamma _1(Q_1)+A_{21}(Q_1)\big (\frac{X}{X_{21}^*(Q_1)}\big )^\beta \\ \quad -\Big [A_{21}(Q_1)-\hat{A}_{21}(X_{21}^*(Q_1),Q_1)-\{B_{21}(Q_1)-\hat{B}_{21}(Q_1)\} \Big ]\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^{\beta _1}&{}\text {if }X<X_{21}^*(Q_1),\\ \Pi _1(X,Q_1)-\Gamma _1(Q_1)+\hat{A}_{21}(X,Q_1)+\{B_{21}(Q_1) -\hat{B}_{21}(Q_1)\}\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^{\gamma _1}&{}\text {if }X\ge X_{21}^*(Q_1), \end{array}\right. } \end{aligned}$$

(25)

where

$$\begin{aligned}&\hat{A}_{21}(X,Q_1)\!\!=\!\!\hat{\Pi }_{21}(X,Q_1,Q_{21}^*(X,Q_1)) \!-\!\hat{\Gamma }_{21}(Q_{21}^*(X,Q_1))\!-\!\frac{\lambda _1}{r\!+\!\lambda _1}\delta Q_{21}^*(X,Q_1), \end{aligned}$$

(26)

$$\begin{aligned}&B_{21}(Q_1)=\frac{\beta _1-\beta }{\beta _1-\gamma _1}\Big \{\Pi _{21}(X_{21}^*(Q_1),Q_1,Q_{21}^*(Q_1)) -\Gamma _{21}(Q_{21}^*(Q_1))-\delta Q_{21}^*(Q_1)\Big \}, \end{aligned}$$

(27)

$$\begin{aligned}&\hat{B}_{21}(Q_1)=\frac{\beta _1-1}{\beta _1-\gamma _1}\hat{\Pi }_{21}(X_{21}^*(Q_1),Q_1,Q_{21}^*(Q_1))-\frac{\beta _1}{\beta _1-\gamma _1}\hat{\Gamma }_{21}(Q_{21}^*(Q_1))\nonumber \\ {}&\qquad \qquad \quad -\frac{\beta _1\lambda _1}{(\beta _1-\gamma _1)(r+\lambda _1)}\delta Q_{21}^*(Q_1), \end{aligned}$$

(28)

with

$$\begin{aligned}&\Pi _1(X,Q_1)=\frac{\lambda _1Q_1(1-\eta Q_1)X}{(r-\mu )(r+\lambda _1-\mu )}, \end{aligned}$$

(29)

$$\begin{aligned}&\Gamma _1(Q_1)=\frac{\lambda _1cQ_1}{r(r+\lambda _1)}, \end{aligned}$$

(30)

$$\begin{aligned}&\hat{\Pi }_{21}(X,Q_1,Q_{21})=\frac{\lambda _1\lambda _{21}Q_{21}(1-\eta Q_{21}-2\eta Q_1)X}{(r-\mu )(r+\lambda _1-\mu )(r+\lambda _{21}-\mu )}, \end{aligned}$$

(31)

$$\begin{aligned}&\hat{\Gamma }_{21}(Q_{21})=\frac{\lambda _1 \lambda _{21}cQ_{21}}{r(r+\lambda _1)(r+\lambda _{21})}, \end{aligned}$$

(32)

and

$$\begin{aligned}&\beta _1=\frac{1}{2}-\frac{\mu }{\sigma ^2}+\sqrt{\Big (\frac{1}{2} -\frac{\mu }{\sigma ^2}\Big )^2+\frac{2(r+\lambda _1)}{\sigma ^2}}(>1), \end{aligned}$$

(33)

$$\begin{aligned}&\gamma _1=\frac{1}{2}-\frac{\mu }{\sigma ^2}-\sqrt{\Big (\frac{1}{2} -\frac{\mu }{\sigma ^2}\Big )^2+\frac{2(r+\lambda _1)}{\sigma ^2}}(<0). \end{aligned}$$

(34)

The optimal capacity choice of $Q_{21}^*(X,Q_1)$ in (26) is given by (A.18).

Proof

See Appendix A.4. $\square$

$\Pi _1(X,Q_1)-\Gamma _1(Q_1)$ in (25) denotes the expected profits from the capacity $Q_1$, which has not yet operated. By comparing the first rows of (18) and (25), we can see that they have the same term associated with $A_{21}$, which implies that the firm has the option to invest in $Q_{21}$ by hitting the threshold $X_{21}$ after the initial project’s completion. Before the initial capacity starts operating, however, the follow-up investment can be triggered instantly by the initial project’s completion (Fig. 2c and 2d), and thus, the option value needs to be adjusted, which is represented by the terms in the bracket in the second row of (25). Note that $\hat{\Pi }_{21}(X,Q_1,Q_{21})-\hat{\Gamma }_{21}(Q_{21})$ in (26) represents the expected profits from the follow-up investment in $Q_{21}$ triggered by the initial project’s completion (i.e., $\hat{T}_1=T_{21}$), whereas $\Pi _{21}(X,Q_1,Q_{21})-\Gamma _{21}(Q_{21})$ in (19) represents those from $Q_{21}$ invested at the hitting timing of the threshold $X_{21}$ (i.e., $\hat{T}_1<T_{21}$). Note also that $(X/X_{21})^\beta$ represents the probability of hitting the threshold $X_{21}$, while $(X/X_{21})^{\beta _1}$ represents the probability of hitting $X_{21}$ before the initial project is finished.

To comprehend the economic implications of the option values described in Proposition 4, we rewrite the first case of (25) (i.e., $X<X_{21}$) as follows:

$$\begin{aligned}&\Pi _1(X,Q_1)-\Gamma _1(Q_1)+A_{21}(Q_1)\Big \{\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^\beta -\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^{\beta _1}\Big \} +B_{21}(Q_1)\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^{\beta _1}\nonumber \\&\qquad +\{\hat{A}_{21}(X_{21}^*(Q_1),Q_1)-\hat{B}_{21}(Q_1)\}\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^{\beta _1}. \end{aligned}$$

(35)

The first row of (35) represents the option value of capacity expansion triggered by hitting the threshold $X_{21}$ (i.e., $\hat{T}_1<T_{21}$). It might be the very first time the demand shock hits $X_{21}$ (i.e., $\bar{T}_{21}=T_{21}$), and in this case the initial project should be finished before reaching the threshold. In other words, we must exclude the probability of hitting $X_{21}$ before $Q_1$ is in operation, and this is reflected in the term $A_{21}\{(X/X_{21})^\beta -(X/X_{21})^{\beta _1}\}$. Meanwhile, it might be not the first time ever to reach the threshold but the first time since the initial project’s completion (i.e., $\bar{T}_{21}<T_{21}$). Specifically, the demand shock can exceed the level of $X_{21}$ but it must decline to below $X_{21}$ before $Q_1$ starts operation. This is reflected in the term $B_{21}(X/X_{21})^{\beta _1}$.

The second row of (35) is the option value of the investment in $Q_{21}$ triggered by the completion of the initial project (i.e., $\hat{T}_1=T_{21}$). It might be the very first time the demand shock remains in the region of $[X_{21},\infty )$ (i.e., $T_{21}<\underline{T}_{21}$) or not the first time ever but after repeatedly going in and out of the region (i.e., $\underline{T}_{21}\le T_{21}$). In either case, the demand shock must exceed $X_{21}$ before $Q_1$ starts operation, but we need to exclude the case of going out of the region and not making it back before the initial project’s completion. This is reflected in the term $(\hat{A}_{21}-\hat{B}_{21})(X/X_{21})^{\beta _1}$.

3.3.4 Before initial investment

Lastly, we proceed to the firm’s initial investment decision. For $t<T_1$, the firm value with the compound option can be described as follows:

$$\begin{aligned} V_1(X)=\max _{T_1\ge 0,Q_1\ge 0}\mathbb {E}\Big [e^{-rT_1}\big \{V_{20}(X(T_1),Q_1)-\delta Q_1\big \}\Big |X(0)=X\Big ] \end{aligned}$$

(36)

The investment timing can be described as $T_1:=\inf \{t>0|X(t)\ge X_1\}$, and similar arguments yield the following results:

Proposition 5

(Optimal initial investment) Given the demand shock X, the initial value in the presence of time-to-build is

$$\begin{aligned} V_1(X)= {\left\{ \begin{array}{ll} A_1(X_1^*,Q_1^*)\big (\frac{X}{X_1^*}\big )^\beta &{}\text {if }X<X_1^*,\\ A_1(X,Q_1^*)&{}\text {if }X\ge X_1^*, \end{array}\right. } \end{aligned}$$

(37)

where

$$\begin{aligned} A_1(X,Q_1)&=\Pi _1(X,Q_1)-\Gamma _1(Q_1)+A_{21}(Q_1)\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^\beta \nonumber \\&\quad -\Big [A_{21}(Q_1)-\hat{A}_{21}(X_{21}^*(Q_1),Q_1)-\{B_{21}(Q_1)-\hat{B}_{21}(Q_1)\}\Big ] \Big (\frac{X}{X_{21}^*(Q_1)}\Big )^{\beta _1}-\delta Q_1. \end{aligned}$$

(38)

The optimal investment capacity is $Q_1^*:=Q_1^*(X_1^*)$ with

$$\begin{aligned} Q_1^*(X):=\underset{Q_1\ge 0}{\arg \max }A_1(X,Q_1), \end{aligned}$$

(39)

and the optimal investment threshold is $X_1^*:=X_1^*(Q_1^*)$ where $X_1^*(Q_1)$ is derived from

$$\begin{aligned}&(\beta -1)\Pi _1(X_1,Q_1)-\beta \Gamma _1(Q_1)-(\beta -\beta _1)\big [A_{21}(Q_1)-\hat{A}_{21}(X_{21}^*(Q_1),Q_1)\nonumber \\ {}&\quad -\{B_{21}(Q_1) -\hat{B}_{21}(Q_1)\}\big ]\Big (\frac{X_1}{X_{21}^*(Q_1)}\Big )^{\beta _1}-\beta \delta Q_1=0. \end{aligned}$$

(40)

Proof

See Appendix A.5. $\square$

We can see from (38) that the exercise of the initial investment option yields the option of the follow-up investment without generating any revenue instantly.

In summary, the firm chooses the investment thresholds and capacity size for the initial and follow-up investments described in Proposition 3 and 5 (i.e., $X_1^*$, $Q_1^*$, $X_{21}^*:=X_{21}^*(Q_1^*)$, $Q_{21}^*:=Q_{21}^*(Q_1^*)$). If the initial project is finished while the demand shock is below the expansion threshold (i.e., $X(\hat{T}_1)<X_{21}^*$), capacity expansion is triggered by hitting the threshold, which corresponds to Case 1 in Fig. 1. If the initial project is finished while the demand shock is above the expansion threshold (i.e., $X({\hat{T}_1})\ge X_{21}^*$), it immediately triggers capacity expansion, which corresponds to Case 2 in Fig. 1.

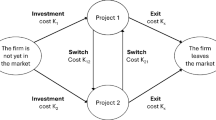
The progress of investment can be illustrated by a tuple (i, j, k), where $i,j,k\in \{0,1,2\}$ denotes the state of investment in $Q_1$, $Q_{21}$ at $t>\hat{T}_1$, and $Q_{21}$ at $t=\hat{T}_1$. Stages 0, 1, and 2 correspond to the state in which the investment has not been made, the investment has been made but not in operation yet, and the capacity is in operation, respectively. Figure 3 presents the state diagram (i, j, k); the solid and dashed lines represent the progression of the state by the investment and operation, respectively.

Fig. 3

A state diagram of investment dynamics

Given the optimal investment strategies, we can evaluate the state prices of capacity expansion in each scenario as follows:

Corollary 1

(State prices of capacity expansion) Given the optimal investment strategy, the state prices of the follow-up investment triggered by hitting the threshold (i.e., $\hat{T}_1<T_{21}$) and the completion of the initial project (i.e., $\hat{T}_1=T_{21}$) are

$$\begin{aligned} \psi _{21}:=\mathbb {E}\Big [1_{\{\hat{T}_1<T_{21}\}}e^{-rT_{21}}\Big |X(0)=X_1^*\Big ] =\Big (\frac{X_1^*}{X_{21}^*}\Big )^\beta -\frac{\beta -\gamma _1}{\beta _1-\gamma _1}\Big (\frac{X_1^*}{X_{21}^*}\Big )^{\beta _1}, \end{aligned}$$

(41)

and

$$\begin{aligned} \hat{\psi }_{21}:=\mathbb {E}\Big [1_{\{\hat{T}_1=T_{21}\}}e^{-rT_{21}} \Big |X(0)=X_1^*\Big ]=-\frac{\lambda _1\gamma _1}{(r+\lambda _1)(\beta _1-\gamma _1)}\Big (\frac{X_1^*}{X_{21}^*}\Big )^{\beta _1}, \end{aligned}$$

(42)

respectively.

Note that the last term on the right-hand side of (41) is negative while the right-hand side of (42) is positive due to $\gamma _1<0$. The state prices in Corollary 1 can be used to analyze which scenario is more likely to occur between Cases 1 and 2 from Fig. 1, and we will discuss this in the following section.

Meanwhile, we can decompose the firm’s option values of the investment based on the capacity from which the revenue is generated. For the benchmark model, the decomposition is straightforward because at each investment timing, the additional expected profits only come from the newly invested capacity. That is, $\bar{\Lambda }_1(X):=\{\bar{\Pi }_1(\bar{X}_1^*,\bar{Q}_1^*)-\bar{\Gamma }(\bar{Q}_1^*)-\delta \bar{Q}_1^*\}(X/\bar{X}_1^*)^\beta$ and $\bar{\Lambda }_2(X):=\bar{A}_2(\bar{Q}_1^*)\big (X/\bar{X}_2^*\big )^\beta$ denote the values of the initial and follow-up investment, respectively, given the demand shock $X(<\bar{X}_1^*)$. Note that $\bar{V}_1(X)$ in the first row of (13) can be expressed as $\bar{\Lambda }_1(X)+\bar{\Lambda }_2(X)$.

In the main model, the capacity expansion can be triggered by either hitting the threshold or the the initial project’s completion, and the option value can be decomposed as follows:

Corollary 2

(Decomposition of option values) Given the initial demand shock of X and the optimal investment strategy, the value of the initial investment is

$$\begin{aligned} \Lambda _1(X):=\Big [\Pi _1(X_1^*,Q_1^*)-\Gamma _1(Q_1^*)-\delta Q_1^*\Big ]\Big (\frac{X}{X_1^*}\Big )^{\beta }. \end{aligned}$$

(43)

Likewise, the option values of the follow-up investment made at $T_{21}>\hat{T}_1$ and $T_{21}=\hat{T}_1$ are

$$\begin{aligned} \Lambda _{21}(X):=\Big [A_{21}(Q_1^*)\Big \{\Big (\frac{X_1^*}{X_{21}^*}\Big )^\beta -\Big (\frac{X_1^*}{X_{21}^*}\Big )^{\beta _1}\Big \}+B_{21}(Q_1^*) \Big (\frac{X_1^*}{X_{21}^*}\Big )^{\beta _1}\Big ]\Big (\frac{X}{X_1^*}\Big )^{\beta }, \end{aligned}$$

(44)

and

$$\begin{aligned} \hat{\Lambda }_{21}(X):=\Big [\hat{A}_{21}(X_{21}^*,Q_1^*)-\hat{B}_{21}(Q_1^*) \Big ]\Big (\frac{X_1^*}{X_{21}^*} \Big )^{\beta _1}\Big (\frac{X}{X_1^*}\Big )^{\beta }, \end{aligned}$$

(45)

respectively. $V_1(X)$ in the first row of (37) can be expressed as $\Lambda _1(X)+\Lambda _2(X)$ where $\Lambda _2(X):=\Lambda _{21}(X)+\hat{\Lambda }_{21}(X)$ represents the value of capacity expansion.

4 Comparative statics and discussion

In this section, we present the comparative statics results and discuss their economic implications. The comparative statics for the size of time-to-build and the volatility of demand shocks are given in Sects. 4.1 and 4.2, respectively. To describe the relationship between the time-to-build of the initial and follow-up investment, we introduce the following equation:

$$\begin{aligned} \frac{1}{\lambda _{21}}=\phi \frac{1}{\lambda _1}, \end{aligned}$$

(46)

where $\phi \in [0,1]$ denotes the degree of learning by doing in the manufacturing process with $\phi =1$ corresponding to no learning by doing.

Table 1 Benchmark parameters for numerical calculation

For the numerical calculation, we adopt the parameters in Table 1 as a benchmark case. The seminal work of Kydland and Prescott (1982) noted that an average construction period is nearly two years for plants, while consumer durables have much shorter average construction periods. Having one type of capital in the model, they assumed that one year is required for the construction of new productive capital, and Zhou (2000) and Gomme et al. (2001) also adopted the same parameter for their estimation. Thus, we presume that the expected time-to-build of the initial investment is one year (i.e., $1/\lambda _1=1$ as a baseline case). Other parameters such as the expected growth rate and volatility of demand shock are chosen from a modest range that can be easily found from standard real options literature [e.g., Leland (1994), Hackbarth and Mauer (2012), Sundaresan et al. (2015)]. Note that we need to have a sufficiently low $\eta$ to ensure that the price of the product given by (1) is positive.

4.1 The size of time-to-build

To emphasize the effects of time-to-build on investment dynamics, we first present the results for the case in which a firm only has a single investment opportunity. This is discussed as the benchmark model in Jeon (2021b), which studied the effects of time-to-build in a duopoly market. It is straightforward to derive the optimal investment strategy, which is provided in Appendix B. We denote the optimal investment threshold and capacity in the presence of time-to-build by $X_0^*$ and $Q_0^*$, respectively, and those without time-to-build are denoted by $\bar{X}_0^*$ and $\bar{Q}_0^*$, respectively.

Fig. 4

Comparative statics regarding the expected time-to-build for a single investment

Figure 4a shows that when a firm holds a single investment option, the investment is delayed as the investment lags lengthen (i.e., $\bar{X}_0^*<X_0^*$). This is because the presence of uncertain time-to-build reduces the expected profits from the investment and thereby increases the value of waiting. In terms of financial options, the time value of the option increases with the size of the investment lags. The decomposition of the option value into the intrinsic value (i.e., the payoff for immediately exercising the option) and the time value (i.e., the difference between the option value and intrinsic value) is also presented in Appendix B. We denote them by $V_0$, $V_0^{int}$, and $V_0^{tim}$, respectively, for the case with time-to-build. Each value with an overhead bar corresponds to the case without time-to-build. Figure  4c shows that both the option value and its intrinsic value strictly decrease with the size of the lags, which is a natural result considering that time-to-build negatively impacts the expected profits of the investment. However, the difference between them—namely, the time value of the option—strictly increases with the size of the time-to-build. Thus, the option’s time value is always higher in the presence of time-to-build than in the absence of the lags. This clarifies that the presence of time-to-build increases the value of waiting.

Figure 4b shows that the capacity choice is irrelevant to the presence of time-to-build (i.e., $\bar{Q}_0^*=Q_0^*$). Jeon (2021b) claimed that this is because the price elasticity of demand, which determines the capacity choice upon the investment, is irrelevant to exogenous demand shocks given the inverse demand function in (1).⁸ That is, the impact of time-to-build is fully absorbed by the adjustment of the investment timing when the firm has only a single investment.

Fig. 5

Comparative statics regarding expected time-to-build of the initial investment

The presence of the capacity expansion significantly alters the impact of time-to-build on the investment decisions. Figure 5a shows that the follow-up investment threshold in the presence of time-to-build is U-shaped and it can be lower than that in the absence of the lags (i.e., $X_{21}^*<\bar{X}_2^*$ for $1/\lambda _1<13.9$). Due to time-to-build, the firm does not make any instant profits after the initial investment. As demand grows further without generating any revenue, the option to invest in the follow-up project becomes more valuable than the case in which the investment yields instant revenue. In other words, the time-to-build of the initial investment undermines the value of waiting to invest in the follow-up project, advancing the timing of the capacity expansion. Intuitively, an asset becomes more valuable when it is more necessary, and the time-to-build of the initial project makes the firm favor the option of the capacity expansion more. This novel finding is in line with the observation of aggressive capacity expansion in the vaccine and semiconductor industries addressed in the introduction. The firms in those industries must have anticipated that it would take much time until they raise revenue from the investment, which would make them advance the timing of capacity expansion more than they otherwise would in the absence of the lags.

This argument can be verified by examining the time value of the capacity expansion. Appendix C presents the decomposition of the option value of the capacity expansion into its intrinsic value and time value. Note that the option value and its decomposition depend on whether it is before or after the initial capacity commences operations (i.e., $t<\hat{T}_1$ or $t\ge \hat{T}_1$). The values from the former are denoted by $V_{20}$, $V_{20}^{int}$, and $V_{20}^{tim}$, respectively, whereas those from the latter are denoted by $V_{21}$, $V_{21}^{int}$, and $V_{21}^{tim}$, respectively. For comparison, those without time-to-build are denoted by $\bar{V}_2$, $\bar{V}_2^{int}$, and $\bar{V}_2^{tim}$, respectively. Figures 5d and  5e show the decomposition of the capacity expansion option (i.e., $\hat{X}\in (X_1^*,X_{21}^*)$) before and after the initial capacity is in operation, respectively. Before the initial project is finished, the time value is higher in the presence of time-to-build, but it is not monotone with respect to the size of the lags (Fig. 5d). Recall that the firm can make the follow-up investment only after the initial project is finished. Note also that the investment threshold $X_{21}^*$ described in Fig. 5a is associated with the investment decision for $t\ge \hat{T}_1$. Thus, the time value of capacity expansion can be more accurately evaluated for $t\ge \hat{T}_1$, from which the firm can make the investment immediately if it is willing to.

After the initial capacity is in operation, the time value of capacity expansion begins decreasing as the initial project’s lags lengthen (Fig. 5e). This is because the impact of the appreciation of the expansion option dominates that of the decrease in the expected profits. This results in a decrease in the investment triggers for the capacity expansion (Fig. 5a). After the lags become significant (i.e., for $1/\lambda _1>6.9$), however, the impact of the decrease in the expected profits dominates that of the appreciation of the follow-up investment project, and the time value of the capacity expansion starts to increase with the size of the lags. This makes the investment triggers of the capacity expansion increase after the lags become significant (Fig. 5a). Note that the size of lags at which the time value of capacity expansion is minimized coincides with that at which the corresponding investment trigger is the lowest (i.e., $1/\lambda _1=6.9$), which clarifies that the value of waiting is a key determinant in this discussion. This argument becomes much clearer when the firm can make the follow-up investment before the initial project’s completion, which is discussed in detail in the Online Appendix.

It might seem implausible that the option value and intrinsic value begin increasing after the initial time-to-build exceeds a certain level in Fig. 5e, but recall that it represents the option value and its decomposition for $t\ge \hat{T}_1$. After the initial capacity is in place, the increase in time-to-build delays only the follow-up investment project, not the initial one. Thus, the negative impact of the delayed revenue from the follow-up project can be dominated by the positive impact of the increase in the initial capacity (Fig. 5b), which is in operation for $t\ge \hat{T}_1$.

We can also see from Fig. 5a that when investment lags are not substantial, not only the follow-up investment but also the initial investment can be made earlier in the presence of time-to-build than it would in the absence of the lags (i.e., $X_1^*<\bar{X}_1^*$ for $1/\lambda _1<8.9$). Since capacity expansion is conditional on the initial project’s completion, the firm accelerates the initial investment to allow the follow-up investments within a reasonable time. However, extremely long investment lags significantly decrease the value of investment projects, urging the firm to advance the timing for initial investment, only with a significant degree of learning by doing. This is discussed shortly.

The presence of capacity expansion also has a significant impact on capacity choice. Figure 5b shows that as time-to-build lengthens, the capacity of the follow-up investment dominates that of the initial project in most cases (i.e., $Q_1^*<Q_{21}^*$). This is in sharp contrast to the case of no time-to-build, in which the capacity of the initial investment dominates that of the follow-up project (i.e., $\bar{Q}_2^*<\bar{Q}_1^*$). This is because the follow-up project, which benefits from learning by doing, becomes more valuable as the initial project’s time-to-build lengthens and the firm places less weight on the initial investment. The capacity of the follow-up project, which can be greater in the presence of time-to-build (i.e., $\bar{Q}_2^*<Q_{21}^*$), should be read along with its investment timing, which can be advanced due to time-to-build (i.e., $X_{21}^*<\bar{X}_2^*$). These results imply that the firm can invest earlier in more capacity in the follow-up project in the presence of time-to-build than it would in its absence. The fact that the firm invests earlier not because it invests less but despite it invests more sheds light on the significance of the impact of time-to-build on the investment dynamics.

The capacity choice, however, is not monotone with respect to the size of the investment lags. After the lags become significant, the firm starts to raise its weight on the initial investment. That is, the capacity of the initial and follow-up projects starts to increase and decrease, respectively, after the lags exceed a certain level (i.e., for $1/\lambda _1>7.7$). This is because the initial time-to-build becomes so lengthy that the revenue from capacity expansion is expected to be generated in the distant future, even after considering learning by doing. Boonman and Siddiqui (2017) showed that longer lags lead to an increase in capacity, but there is a difference in both the modeling and the mechanism behind the result. They assumed operational flexibility with fixed lags after a one-shot investment; there are lags to resume the suspended operation but not in the suspension process. Because the suspension option truncates the downside risk of the investment without lags while revenues are expected to increase during the resumption’s lags, the capacity size increases with the lags. In contrast, our model shows that the capacity of the follow-up investment can increase with lags even when the lags are uncertain and the downside risk cannot be truncated by an abandonment option, mainly because of learning effects from the initial investment.

As Corollary 2 shows, we can decompose the firm’s option value into the value of each investment. Figure 5f shows that the value of the follow-up investment is inverted U-shaped, which is associated with the aforementioned findings. While the initial time-to-build is insignificant, the firm favors the expansion option and invests in more capacity as the lags lengthen. After the lags become significant, however, the effect of the decrease in the expected profits dominates that of the appreciation of the capacity expansion, and the firm’s capacity choice in the follow-up project decreases with the size of the lags. This amounts to the inverted U-shaped option value of capacity expansion. More specifically, we can see that the value of the capacity expansion triggered by hitting the threshold (i.e., $\Lambda _{21}(X)$) starts decreasing much earlier than that triggered by the initial project’s completion (i.e., $\hat{\Lambda }_{21}(X)$). This is a natural result considering that the former is less likely to occur as the initial project’s lags lengthen; this argument can be verified by the state prices of each scenario described in Fig. 5c.

Fig. 6

Comparative statics regarding the degree of learning by doing

Figure 6 presents the results of the comparative statics regarding the degree of learning by doing. Recall that $\phi =0$ and $\phi =1$ correspond to full and no learning by doing, respectively. Figure 6a shows that given a sufficient amount of learning by doing, both the initial and follow-up investment are made earlier in the presence of time-to-build than they would in the absence of the investment lags (i.e., $X_1^*<\bar{X}_1^*$ and $X_{21}^*<\bar{X}_2^*$ for $\phi <0.56$). This is in sharp contrast to the case of a single investment opportunity described in Fig. 4a, in which $\bar{X}_0^*<X_0^*$ always holds. As the degree of learning by doing increases, the initial project becomes more valuable as a source of learning. That is, the initial investment is made earlier not because the firm wants to generate revenue from it sooner but because the firm wants to learn from it earlier. This argument can be verified by the capacity choice described in Fig. 6b. When there is little learning from the previous investment, the initial capacity dominates the capacity of the follow-up project (i.e., $Q_{21}^*<Q_1^*$ for $\phi >0.67$), as in the case of no lags (i.e., $\bar{Q}_2^*<\bar{Q}_1^*$). However, this is reversed as learning by doing improves (i.e., $Q_{21}^*>Q_1^*$ for $\phi <0.67$). Combined with the findings shown in Fig. 6a, we can assert that when there is a significant amount of learning from the previous investment, the firm invests earlier not because it invests less but even if it invests more in the follow-up project.

These results are not only robust but also reinforced when we allow more flexibility in the timing of capital expansion. In the Online Appendix, we show that if the firm can expand its capacity either before or after the initial project is finished, the follow-up investment is made earlier in the presence of time-to-build than it would without the lags, even when there are no learning effects such that the expected time-to-build of the initial project and that of the subsequent one coincide.⁹

The seminal work of Bar-Ilan and Strange (1996) studied the impact of time-to-build on a firm’s investment decision and showed that the presence of time-to-build can hasten the investment. However, there is a difference in both the modeling and the mechanism that derives the result. They assumed fixed lags in a one-shot investment and allowed the option to abandon the project after it was completed. The lags increase uncertainty, and thus, the value of waiting, but the abandonment option truncates its downside risks. For this reason, longer lags increase the expected value of investment, and thus, result in earlier investment. In contrast, we assume that the firm faces uncertain time-to-build without the option to truncate the downside risks. Nevertheless, the time-to-build of the initial investment induces earlier follow-up investment while learning effects result in earlier initial investment.

4.2 Volatility of demand shocks

Fig. 7

Comparative statics regarding the volatility of demand shocks for a single investment

Fig. 8

Comparative statics regarding volatility of demand shocks

In this subsection, we discuss the comparative statics results of the volatility of demand shocks. Figures 7 and 8 present the benchmark case of a single investment and the main case of capacity expansion, respectively.

We can see from Fig. 7a that when a firm holds a single investment option, an increase in volatility delays the investment timing and that it is delayed further if the investment project involves time-to-build (i.e., $\bar{X}_0^*<X_0^*$). That is, the presence of uncertain lags amplifies the negative impact of uncertainty on investment timing. However, this is not the case when the firm holds the option to expand its capacity after the initial investment. Figure 8a shows that the investment thresholds for the initial and follow-up investment increase with the degree of volatility, which is in line with the conventional result from the real options literature [e.g., McDonald and Siegel (1986), Pindyck (1988, 1993)], but they increase at a slower rate in the presence of time-to-build. As a result, given substantial volatility, both investments are made earlier in the presence of time-to-build than they would be without the lags (i.e., $X_1^*<\bar{X}_1^*$ and $X_{21}^*<\bar{X}_2^*$). This implies that time-to-build and learning effects soften the negative impact of uncertainty on investment timing, and it can be interpreted as follows. We discussed in Sect. 4.1 that when the revenue is delayed due to time-to-build, the firm favors the expansion option more than it would in the absence of the lags, and volatile demand augments this effect. Given substantial volatility, market demand is likely to surge rapidly in a short period of time, which makes the firm further favor the option of capacity expansion. As the appreciation of capacity expansion increases, the firm also hastens the initial investment to exploit learning by doing from the follow-up investment. For this reason, investment is delayed as uncertainty increases, but the negative impact abates in the presence of time-to-build and learning by doing.

Recall that we have already seen from Fig. 6a that not only the follow-up investment but also the initial investment can be made earlier in the presence of time-to-build than in its absence (i.e., $X_1^*<\bar{X}_1^*$ and $X_{21}^*<\bar{X}_2^*$ for $\phi <0.56$). More specifically, the firm is willing to make the initial investment earlier when it can learn more from the initial project to ensure that the lags of the subsequent project are significantly reduced. Combining the findings shown in Figs. 6a and 8a, we can assert that the firm makes the initial investment earlier in the presence of time-to-build than it would without the lags when the degree of learning by doing and the volatility of market demand are substantial.

Figure 8b shows that the optimal capacities increase with the degree of volatility whether the investment involves time-to-build or not, and this is consistent with the conventional finding from the real options literature [e.g., Dangl (1999), Bar-Ilan and Strange (1999), and Seta et al. (2012)]. However, the presence of time-to-build has an influence on how much uncertainty affects the capacity size for each investment project. When the investment does not involve lags, the initial capacity increases with volatility at a much faster rate than the subsequent capacity. As a result, the latter dominates the former when volatility is insignificant (i.e., $\bar{Q}_1^*<\bar{Q}_2^*$ for $\sigma <0.14$) but this relation is reversed as uncertainty becomes more substantial (i.e., $\bar{Q}_2^*<\bar{Q}_1^*$ for $\sigma >0.14$). This is natural because market demand can surge rapidly with higher volatility, which makes the firm want to install a sufficient amount of capacity in the initial project. When the investment involves time-to-build, however, the capacities of both projects increase with volatility at a similar rate, and the follow-up capacity dominates the initial capacity regardless of the degree of volatility (i.e., $Q_1^*<Q_{21}^*$). This implies that the firm wants to exploit the benefit of learning by doing more than it wants to meet rapidly surging demand.

There are a few studies that show that the conventional results may not hold in the presence of time-to-build. For instance, Bar-Ilan and Strange (1996) showed that uncertainty can hasten investment in the presence of time-to-build. This is mainly because the downside risks of investment are truncated by the abandonment option, and they left the impact on investment size unanswered. Bar-Ilan et al. (2002) took both investment timing and its size into account in their discussion of the impact of volatility on investment in the presence of time-to-build, and they found mixed results; when the lags are short, uncertainty delays the investment yet increases its size, whereas, given significant lags, uncertainty hastens the investment and reduces its size. The unconventional finding in the latter case arises mainly because they assumed that excess capacity incurs costs, which naturally induces earlier investment in a smaller capacity. In contrast, our model shows that the conventional results from real options literature hold even in the presence of uncertain time-to-build and learning effects. However, we show that time-to-build and learning effects abate the impact of uncertainty on investment timing and the asymmetry between the size of uncertainty’s impact on the initial capacity and that on the follow-up capacity.

In a more volatile market, demand is more likely to reach the follow-up investment threshold and stay above it before the initial project’s completion. This can be clearly seen from Fig. 8c which describes the state prices for each scenario of capacity expansion. The state price of capacity expansion triggered by the initial project’s completion (i.e., $\hat{\psi }_{21}$) increases at a steeper rate as the volatility increases, whereas that triggered by hitting the threshold (i.e., $\psi _{21}$) starts decreasing after the volatility exceeds a certain level. As a result, we can see from Fig. 8d that the value of follow-up capacity in the former case (i.e., $\hat{\Lambda }_{21}(X)$) increases faster than that in the latter case (i.e., $\Lambda _{21}(X)$).

5 Conclusion

We investigated the impact of time-to-build on a firm’s investment dynamics from various perspectives. We assumed that the firm has the option of capacity expansion in addition to initial investment and that both projects involve uncertain time-to-build. Considering learning effects, we presumed that the lags of the follow-up project can be shorter than those of the initial project. First, we showed that the follow-up investment could be made earlier in the presence of time-to-build than it would in the absence of the lags. This is in sharp contrast to the case of a single investment, whose timing is always delayed by the lags. This is because the time-to-build of the initial project undermines the value of waiting to invest in the follow-up project. When learning effects are substantial, not only the follow-up investment but also the initial investment can be made earlier in the presence of time-to-build than it would in the absence of lags. This implies that the initial investment mainly serves as a source of learning rather than that of revenue if the size of the learning effects is substantial. We also found that the capacity in the subsequent project dominates that of the initial one in the presence of time-to-build, whereas the latter dominates the former in the absence of lags. Combining these findings, we can argue that the firm invests earlier in more capacity in the follow-up project in the presence of time-to-build than it would in the absence of lags. Lastly, we found that uncertainty delays investment yet increases its size, supporting the conventional result from the real options literature. However, time-to-build and learning effects soften the negative impact of uncertainty on investment timing and the asymmetry between the impact of uncertainty on the initial capacity and that on the subsequent capacity.

Several problems remain unsolved for future research. We described the learning effects by the decrease in time-to-build in the follow-up investment project. In general, marginal costs also decrease as the firm’s production experience accumulates, and the addition of this aspect of learning effects could enrich the discussion significantly. Seta et al. (2012) incorporated the learning effects by assuming the marginal costs to follow $c(t)=ce^{-\rho Z(t)}$ where $Z(t)=\int _0^t Q(s)\textrm{d}s$ denotes the cumulative output, and this setup can be easily incorporated for a single investment opportunity with time-to-build. With the option of capacity expansion, however, it harms the tractability of the model significantly because the follow-up investment decision depends on the amount of time that has elapsed since the initial capacity’s operation. That is, the investment decision of the follow-up project becomes time-dependent, and the solution, which should be described as a pair of (t, X(t)), can be found only by numerically solving a partial differential equation. The derivation and discussion of the initial investment strategy, which depends on the follow-up investment decision, become even more complicated and much harder to interpret. For this reason, Seta et al. (2012) made a strong assumption when extending the model to the case of the expansion option; they presumed a lower bound of learning effects and supposed that the follow-up investment is made when the marginal costs reach the lower boundary, thereby ruling out the timing decision of capacity expansion. Similar difficulties—and assumptions to circumvent them—can also be found in Grenadier and Weiss (1997). They investigated the investment strategy with technological innovation that arrives at a random time and assumed that the investment in the new technology can be made only at the arrival time of the new technology, whereas the investment in the existing technology can be optimally timed. This implicit assumption essentially eliminates the endogeneity of the investment timing in the new technology. With time-to-build as a key element, the timing decision is at the heart of our study’s discussion, and thus, exogenous investment timing harms the virtue of our framework significantly. Considering the technical difficulties and the volume of illustration necessary for the derivation of a solution, we believe that this extension deserves to be discussed in a separate study.

For an elaborate illustration of time-to-build, one can suppose that expected time-to-build decreases as time elapses after the investment is made. Hagspiel et al. (2021) examined a decision for green investment under time-dependent subsidy retraction risk and assumed that the timing of subsidy retraction follows an exponential distribution with intensity $\lambda (t):=\lambda t$, which increases with time. Evidently, the investment decision before the subsidy retraction becomes time-dependent, and thus, the solution—a pair of time and a state variable—can only be derived by numerically solving a partial differential equation as well. Their work clearly shows that the time-dependent intensity of exponential time can harm the tractability significantly, even when the firm holds only a single investment option. Undeniably, capacity expansion with time-dependent intensity of time-to-build would be very demanding from a technical perspective, but it deserves to be discussed with some assumptions that alleviate technical difficulties.

Moreover, we limited our analysis to a monopoly market for the sake of simplicity, but it is possible to introduce market competition and suppose a positive spillover of time-to-build. Specifically, future studies could suppose that a firm expects a shorter time-to-build if it invests after its competitor’s investment. This is directly associated with the empirical analysis by Salomon and Martin (2008), who found evidence from the global semiconductor industry that time-to-build decreases with not only the firm’s own experience but also with the industry’s experience. We hope that this study serves as a platform to investigate these problems in the future.

Appendices

A Proofs

1.1 A.1 Proof of Proposition 1

Suppose the firm invests in additional capacity $Q_2$ when the demand shock is X and the initial capacity $Q_1$ is operating. The firm value at the timing of investment, denoted by $\bar{V}_2(X,Q_1,Q_2)$, can be evaluated as follows:

$$\begin{aligned} \bar{V}_2(X,Q_1,Q_2)&=\mathbb {E}\Big [\int _0^\infty e^{-rt}(Q_1+Q_2)\left\{ X(t)\left( 1-\eta (Q_1+Q_2)\right) -c\right\} \textrm{d}t-\delta Q_2\Big |X(0)=X\Big ]\nonumber \\&=\frac{(Q_1+Q_2)\left( 1-\eta (Q_1+Q_2)\right) X}{r-\mu }-\frac{c(Q_1+Q_2)}{r}-\delta Q_2. \end{aligned}$$

(A.1)

Maximizing (A.1) with respect to $Q_2$ yields the following optimal capacity rule:

$$\begin{aligned} \bar{Q}_2^*(X,Q_1)=\frac{1}{2\eta }\left( 1-\frac{(c/r+\delta )(r-\mu )}{X}\right) -Q_1. \end{aligned}$$

(A.2)

Meanwhile, the firm value with the capacity $Q_1$ in operation and the option of capacity expansion, denoted by $\bar{F}_2(X,Q_1)$, should satisfy

$$\begin{aligned} r\bar{F}_2(X,Q_1)=\mathcal {L}\bar{F}_2(X,Q_1)+Q_1(1-\eta Q_1)X-cQ_1, \end{aligned}$$

(A.3)

subject to

$$\begin{aligned}&\bar{F}_2(\bar{X}_2^*,Q_1)=\bar{V}_2(\bar{X}_2^*,Q_1,Q_2), \end{aligned}$$

(A.4)

$$\begin{aligned}&\frac{\partial \bar{F}_2(X,Q_1)}{\partial X}\Big |_{X=\bar{X}_2^*}=\frac{\partial \bar{V}_2(X,Q_1,Q_2)}{\partial X}\Big |_{X=\bar{X}_2^*}, \end{aligned}$$

(A.5)

$$\begin{aligned}&\bar{F}_2(0,Q_1)=0, \end{aligned}$$

(A.6)

where the second-order partial differential operator is defined by

$$\begin{aligned} \mathcal {L}F(X,\cdot )=\mu X\frac{\partial F(X,\cdot )}{\partial X}+\frac{1}{2}\sigma ^2X^2 \frac{\partial ^2F(X,\cdot )}{\partial X^2}. \end{aligned}$$

(A.7)

A general solution of (A.3) with the boundary condition (A.6) is

$$\begin{aligned} \bar{F}_2(X,Q_1)=\frac{Q_1(1-\eta Q_1)}{r-\mu }-\frac{cQ_1}{r}+\bar{A}_2X^\beta , \end{aligned}$$

(A.8)

where $\beta$ is given by (9). Substituting (A.1) and (A.8) into (A.4) and (A.5) yields

$$\begin{aligned} \bar{X}_2^*(Q_1,Q_2)=\frac{\beta (c/r+\delta )(r-\mu )}{(\beta -1)(1-\eta Q_2-2\eta Q_1)}. \end{aligned}$$

(A.9)

From (A.2) and (A.9), we can obtain the results in Proposition 1.

1.2 A.2 Proof of proposition 2

Suppose the firm makes the initial investment in capacity $Q_1$ when the demand shock is X. The firm value at the timing of the investment, denoted by $\bar{V}_1(X,Q_1)$, is

$$\begin{aligned}&\bar{V}_1(X,Q_1)\nonumber \\ {}&\quad =\mathbb {E}\Big [\int _0^{T_2}e^{-rt}Q_1\{X(t)(1-\eta Q_1)-c\}\textrm{d}t-\delta Q_1\nonumber \\ {}&\qquad +\int _{T_2}^\infty e^{-rt}(Q_1+\bar{Q}_2^*(Q_1))\{X(t)(1-\eta (Q_1+\bar{Q}_2^*(Q_1)))-c\}\textrm{d} t-e^{-rT_2}\delta \bar{Q}_2^*(Q_1)\Big |X(0)=X\Big ]\nonumber \\&\quad =\frac{Q_1(1-\eta Q_1)X}{r-\mu }-\frac{cQ_1}{r}-\delta Q_1\nonumber \\ {}&\qquad +\Big [\frac{\bar{Q}_2^*(Q_1)(1-\eta \bar{Q}_2^*(Q_1)-2\eta Q_1)\bar{X}_2^*(Q_1)}{r-\mu }-\frac{c\bar{Q}_2^*(Q_1)}{r} -\delta \bar{Q}_2^*(Q_1)\Big ]\Big (\frac{X}{\bar{X}_2^*(Q_1)}\Big )^\beta . \end{aligned}$$

(A.10)

Substituting (10) and (11) into (A.10), we have

$$\begin{aligned} \frac{Q_1(1-\eta Q_1)X}{r-\mu }-\Big (\frac{c}{r}+\delta \Big )Q_1+\frac{(c/r+\delta )(1-2\eta Q_1)}{\eta (\beta +1)(\beta -1)}\Big (\frac{(\beta -1)(1-2\eta Q_1)X}{(\beta +1)(c/r+\delta )(r-\mu )}\Big )^\beta . \end{aligned}$$

(A.11)

By maximizing (A.11) with respect to $Q_1$, we obtain (16) from which we can implicitly derive the optimal capacity $\bar{Q}_1^*(X)$ for a demand shock X.

Meanwhile, the value of the initial investment option, denoted by $\bar{F}_1(X)$, should satisfy

$$\begin{aligned} r\bar{F}_1(X)=\mathcal {L}\bar{F}_1(X), \end{aligned}$$

(A.12)

subject to

$$\begin{aligned}&\bar{F}_1(\bar{X}_1^*)=\bar{V}_1(\bar{X}_1^*,Q_1), \end{aligned}$$

(A.13)

$$\begin{aligned}&\frac{\partial \bar{F}_1(X)}{\partial X}\Big |_{X=\bar{X}_1^*}=\frac{\partial \bar{V}_1(X,Q_1)}{\partial X}\Big |_{X=\bar{X}_1^*}, \end{aligned}$$

(A.14)

$$\begin{aligned}&\bar{F}_1(0)=0. \end{aligned}$$

(A.15)

A general solution of (A.12) with the boundary condition (A.15) is

$$\begin{aligned} \bar{F}_1(X)=\bar{A}_1X^\beta . \end{aligned}$$

(A.16)

Substituting (A.10) and (A.16) into (A.13) and (A.14) yields the results in Proposition 2.

1.3 A.3 Proof of proposition 3

Suppose the firm invests in capacity $Q_{21}$ which takes time-to-build when the demand shock is X and the initial capacity $Q_1$ is in operation. The firm value at the timing of investment, denoted by $V_{21}(X,Q_1,Q_{21})$, can be written as follows:

$$\begin{aligned}&V_{21}(X,Q_1,Q_{21}) \nonumber \\&=\mathbb {E}\Big [\int _0^{\tau _{21}}e^{-rt}Q_1\{X(t)(1-\eta Q_1)-c\}\textrm{d}t\nonumber \\&\quad \quad +\int _{\tau _{21}}^\infty e^{-rt}(Q_1+Q_{21})\{X(t)(1-\eta (Q_1+Q_{21}))-c\}\textrm{d}t-\delta Q_{21}\Big |X(0)=X\Big ]\nonumber \\&=\frac{Q_1(1-\eta Q_1)X}{r+\lambda _{21}-\mu }+\frac{\lambda _{21}(Q_1+Q_{21}) (1-\eta (Q_1+Q_{21}))X}{(r-\mu )(r+\lambda _{21}-\mu )}\nonumber \\&\quad \quad -\Big (\frac{cQ_1}{r+\lambda _{21}}+\frac{\lambda _{21}c(Q_1+Q_{21})}{r(r+\lambda _{21})}\Big )-\delta Q_{21}. \end{aligned}$$

(A.17)

Maximizing (A.17) with respect to $Q_{21}$ yields the following optimal capacity rule:

$$\begin{aligned} Q_{21}^*(X,Q_1)=\frac{1}{2\eta }\Big (1-\frac{\big (\frac{\lambda _{21}c}{r(r+\lambda _{21})} +\delta \big )(r-\mu )(r+\lambda _{21}-\mu )}{\lambda _{21}X}\Big )-Q_1. \end{aligned}$$

(A.18)

Meanwhile, the firm value with $Q_1$ in operation and the option of capacity expansion, denoted by $F_{21}(X,Q_1)$, should satisfy

$$\begin{aligned} rF_{21}(X,Q_1)=\mathcal {L}F_{21}(X,Q_1)+Q_1(1-\eta Q_1)X-cQ_1, \end{aligned}$$

(A.19)

subject to

$$\begin{aligned}&F_{21}(X_{21}^*,Q_1)=V_{21}(X_{21}^*,Q_1,Q_{21}), \end{aligned}$$

(A.20)

$$\begin{aligned}&\frac{\partial F_{21}(X,Q_1)}{\partial X}\Big |_{X=X_{21}^*}=\frac{\partial V_{21}(X,Q_1,Q_{21})}{\partial X}\Big |_{X=X_{21}^*}, \end{aligned}$$

(A.21)

$$\begin{aligned}&F_{21}(0,Q_1)=0. \end{aligned}$$

(A.22)

A general solution of (A.19) with the boundary condition of (A.22) is

$$\begin{aligned} F_{21}(X)=\frac{Q_1(1-\eta Q_1)X}{r-\mu }-\frac{cQ_1}{r}+A_{21}X^\beta . \end{aligned}$$

(A.23)

Substituting (A.17), (A.18), and (A.23) into (A.20) and (A.21) yields the results in Proposition 3.

1.4 A.4 Proof of proposition 4

Suppose $X\ge X_{21}$ and $t\in [T_{21},\hat{T}_{21})$. That is, the follow-up investment has been made but only the initial capacity is in operation at the moment. It is straightforward to calculate the firm value in this region, denote by $\bar{F}_{21}(X,Q_1,Q_{21})$, as follows:

$$\begin{aligned} \bar{F}_{21}(X,Q_1,Q_{21})&=\frac{Q_1(1-\eta Q_1)X}{r+\lambda _{21}-\mu }+\frac{\lambda _{21}(Q_1+Q_{21}) \{1-\eta (Q_1+Q_{21})\}X}{(r-\mu )(r+\lambda _{21}-\mu )}\nonumber \\ {}&\quad -\Big (\frac{cQ_1}{r+\lambda _{21}}+\frac{\lambda _{21}c(Q_1+Q_{21})}{r(r+\lambda _{21})}\Big ). \end{aligned}$$

(A.24)

Now let us suppose $X<X_{21}$ and $t\ge \hat{T}_1$. Namely, the initial project has been finished but the demand shock has not increased enough to trigger the capacity expansion of $Q_{21}$. The firm value with $Q_1$ in operation and the option of capacity expansion, denoted by $\underline{F}_{21}(X,Q_1)$, needs to satisfy (A.19) with boundary conditions (A.20) through (A.22), and the solution is given by the first row of (18).

In the region of $X<X_{21}$ and $t<\hat{T}_1$, the initial capacity $Q_1$ is not in operation and the firm has an option of capacity expansion. The firm value in this region, denoted by $\underline{F}_{20}(X,Q_1)$, switches to $\underline{F}_{21}(X,Q_1)$ as soon as the initial capacity $Q_1$ starts operation. Thus, the firm value should satisfy

$$\begin{aligned} r\underline{F}_{20}(X,Q_1)=\mathcal {L}\underline{F}_{20}(X,Q_1)+\lambda _1 \{\underline{F}_{21}(X,Q_1)-\underline{F}_{20}(X,Q_1)\}, \end{aligned}$$

(A.25)

subject to

$$\begin{aligned} \underline{F}_{20}(0,Q_1)=0, \end{aligned}$$

(A.26)

and other boundary conditions to be illustrated shortly. Given the solution of $\underline{F}_{21}(X,Q)$ in (18), a general solution of (A.25) with the boundary condition (A.26) is

$$\begin{aligned} \underline{F}_{20}(X,Q_1)=\Pi _1(X,Q_1)-\Gamma _1(Q_1)+\underline{A}_{20}X^{\beta _1} +A_{21}(Q_1)\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^\beta , \end{aligned}$$

(A.27)

where $\Pi _1(X,Q_1)$, $\Gamma _1(Q_1)$, and $\beta _1$ are given by (29), (30), and (33), respectively.

Now let us suppose $X\ge X_{21}$ and $t<\hat{T}_1$. In this region, the firm will make the follow-up investment in $Q_{21}$ as soon as the initial capacity starts operation. Thus, the firm value with $Q_1$ not in operation yet and the option of capacity expansion, denoted by $\bar{F}_{20}(X,Q_1)$, should satisfy

$$\begin{aligned} r\bar{F}_{20}(X,Q_1)=\mathcal {L}\bar{F}_{20}(X,Q_1) +\lambda _1\{\bar{F}_{21}(X,Q_1,Q_{21}^*(X,Q_1))-\delta Q_{21}^*(X,Q_1)-\bar{F}_{20}(X,Q_1)\}, \end{aligned}$$

(A.28)

subject to some boundary conditions to be illustrated shortly. Note that because the initial project is finished at a random time, the choice of capacity expansion will be $Q_{21}^* (X(\hat{T}_1),Q_1)$ with $Q_{21}^*(X,Q_1)$ in (A.18), not $Q_{21}^*(X_{21}^*(Q_1),Q_1)$ as in Proposition 3. A general solution of (A.28) is

$$\begin{aligned} \bar{F}_{20}(X,Q_1)=\Pi _1(X,Q_1)-\Gamma _1(Q_1) +\hat{A}_{21}(X,Q_1)+\bar{B}_{20}X^{\gamma _1} \end{aligned}$$

(A.29)

where $\hat{A}_{21}(X,Q_1)$ and $\gamma _1$ are given by (26) and (34), respectively. The equations (A.27) and (A.29) are subject to the following boundary conditions:

$$\begin{aligned}&\bar{F}_{20}(X_{21}^*,Q_1)=\underline{F}_{20}(X_{21}^*,Q_1), \end{aligned}$$

(A.30)

$$\begin{aligned}&\frac{\partial \bar{F}_{20}(X,Q_1)}{\partial X}\Big |_{X=X_{21}^*}=\frac{\partial \underline{F}_{20}(X,Q_1)}{\partial X}\Big |_{X=X_{21}^*}. \end{aligned}$$

(A.31)

From these conditions, we can derive the following results:

$$\begin{aligned}&\underline{A}_{20}=-\Big [A_{21}(Q_1)-\hat{A}_{21}(Q_1)-\{B_{21}(Q_1)-\hat{B}_{21}(Q_1)\}\Big ] \Big (\frac{1}{X_{21}^*(Q_1)}\Big )^{\beta _1}, \end{aligned}$$

(A.32)

$$\begin{aligned}&\bar{B}_{20}=\big \{B_{21}(Q_1)-\hat{B}_{21}(Q_1)\big \} \Big (\frac{1}{X_{21}^*(Q_1)}\Big )^{\gamma _1}, \end{aligned}$$

(A.33)

where $B_{21}(Q_1)$ and $\hat{B}_{21}(Q_1)$ are given by (27) and (28), respectively. Substituting (A.32) into (A.27), we have

$$\begin{aligned} \underline{F}_{20}(X,Q_1)&=\Pi _1(X,Q_1)-\Gamma _1(Q_1)+A_{21}(Q_1) \Big (\frac{X}{X_{21}^*(Q_1)}\Big )^\beta \nonumber \\&\quad -\Big [A_{21}(Q_1)-\hat{A}_{21}(Q_1)-\{B_{21}(Q_1)-\hat{B}_{21}(Q_1)\} \Big ]\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^{\beta _1}. \end{aligned}$$

(A.34)

Likewise, substituting (A.33) into (A.29), we have

$$\begin{aligned} \bar{F}_{20}(X,Q_1)=\Pi _1(X,Q_1)-\Gamma _1(Q_1)+\hat{A}_{21}(X,Q_1)+\big \{B_{21}(Q_1) -\hat{B}_{21}(Q_1)\big \}\Big (\frac{X}{X_{21}^*(Q_1)}\Big )^{\gamma _1}. \end{aligned}$$

(A.35)

1.5 A.5 Proof of proposition 5

At the timing of initial investment in $Q_1$, the firm value is

$$\begin{aligned} V_1(X,Q_1)=V_{20}(X,Q_1)-\delta Q_1, \end{aligned}$$

(A.36)

where $V_{20}(X,Q_1)$ is described in the first row of (25). Before making the investment, the initial option value, denoted by $F_1(X)$, needs to satisfy

$$\begin{aligned} rF_1(X)=\mathcal {L}F_1(X), \end{aligned}$$

(A.37)

subject to

$$\begin{aligned}&F_1(X_1^*)=V_1(X_1^*,Q_1), \end{aligned}$$

(A.38)

$$\begin{aligned}&\frac{\partial F_1(X)}{\partial X}\Big |_{X=X_1^*}=\frac{\partial V_1(X,Q_1)}{\partial X}\Big |_{X=X_1^*}, \end{aligned}$$

(A.39)

$$\begin{aligned}&F_1(0)=0. \end{aligned}$$

(A.40)

A general solution of (A.37) with the boundary condition of (A.40) is

$$\begin{aligned} F_1(X)=A_1X^\beta , \end{aligned}$$

(A.41)

and substituting (A.36) and (A.41) into (A.38) and (A.39) yields the results in Proposition 5.

B Single investment option

It is straightforward to derive the value function in the absence of time-to-build as follows:

$$\begin{aligned} \bar{V}_0(X)= {\left\{ \begin{array}{ll} \big (\bar{\Pi }_1(\bar{X}_0^*,\bar{Q}_0^*)-\bar{\Gamma }(\bar{Q}_0^*) -\delta \bar{Q}_0^*\big )\big (\frac{X}{\bar{X}_0^*}\big )^\beta ,&{}\text {if }X<\bar{X}_0^*,\\ \bar{\Pi }_1(X,\bar{Q}_0^*)-\bar{\Gamma }(\bar{Q}_0^*)-\delta \bar{Q}_0^*,&{}\text {if }X\ge \bar{X}_0^*, \end{array}\right. } \end{aligned}$$

(B.1)

where the optimal investment threshold and capacity are

$$\begin{aligned} \bar{X}_0^*&=\frac{(\beta +1)(c/r+\delta ) (r-\mu )}{\beta -1}, \end{aligned}$$

(B.2)

$$\begin{aligned} \bar{Q}_0^*&=\frac{1}{(\beta +1)\eta }. \end{aligned}$$

(B.3)

Although the firm optimally chooses its investment timing as $\bar{T}_0:=\inf \{t>0|X(t)\ge \bar{X}_0^*\}$, it can invest at any time before $\bar{T}_0$. The firm value with this immediate investment yields the intrinsic value as follows:

$$\begin{aligned} \bar{V}_0^{int}(X)=\bar{\Pi }_1(X,\bar{Q}_0^*(X))-\bar{\Gamma }(\bar{Q}_0^*(X))-\delta \bar{Q}_0^*(X), \end{aligned}$$

(B.4)

where

$$\begin{aligned} \bar{Q}_0^*(X)=\frac{1}{2\eta }\left( 1-\frac{(c/r+\delta )(r-\mu )}{X}\right) , \end{aligned}$$

(B.5)

and the time value of the option can be evaluated as $\bar{V}_0^{tim}(X):=\bar{V}_0(X)-\bar{V}_0^{int}(X)$ for $X<\bar{X}_0^*$.

Following the same argument, the value function in the presence of time-to-build is evaluated as

$$\begin{aligned} V_0(X)= {\left\{ \begin{array}{ll} \big (\Pi _1(X_0^*,Q_0^*)-\Gamma _1(Q_0^*)-\delta Q_0^*\big )\big (\frac{X}{X_0^*}\big )^\beta ,&{}\text {if }X<X_0^*,\\ \Pi _1(X,Q_0^*)-\Gamma _1(Q_0^*)-\delta Q_0^*,&{}\text {if }X\ge X_0^*, \end{array}\right. } \end{aligned}$$

(B.6)

where the optimal investment threshold and capacity are

$$\begin{aligned} X_0^*&=\frac{(\beta +1)(\frac{\lambda _1c}{r(r+\lambda _1)}+\delta )(r-\mu )(r+\lambda _1-\mu )}{(\beta -1)\lambda _1}, \end{aligned}$$

(B.7)

$$\begin{aligned} Q_0^*&=\frac{1}{(\beta +1)\eta }. \end{aligned}$$

(B.8)

The intrinsic value of the option with immediate investment is

$$\begin{aligned} V_0^{int}(X)=\Pi _1(X,Q_0^*(X))-\Gamma _1(Q_0^*(X))-\delta Q_0^*(X), \end{aligned}$$

(B.9)

where

$$\begin{aligned} Q_0^*(X)=\frac{1}{2\eta }\left( 1-\frac{(\frac{\lambda _1c}{r(r+\lambda _1)} +\delta )(r-\mu )(r+\lambda _1-\mu )}{\lambda _1X}\right) , \end{aligned}$$

(B.10)

and the time value of the option can be obtained as $V_0^{tim}(X):=V_0(X)-V_0^{int}(X)$ for $X<X_0^*$.

C Time value of capacity expansion

1.1 C.1 Without time-to-build

Given the optimal investment in the initial project, the option value before the follow-up project is $\bar{V}_2(X):=\bar{V}_2(X,\bar{Q}_1^*)$ with $\bar{V}_2(X,Q_1)$ in (4). Although it is optimal for the firm to invest at $\bar{X}_2^*$ as derived in Proposition 1, it can choose to invest at any time. The intrinsic value of capacity option with the immediate investment for $\hat{X}\in (\bar{X}_1^*,\bar{X}_2^*)$ is

$$\begin{aligned} \bar{V}_2^{int}(\hat{X})=\bar{\Pi }_1(\hat{X},\bar{Q}_1^*)+\bar{\Pi }_2(\hat{X},\bar{Q}_1^*, \bar{Q}_2^*(\hat{X},\bar{Q}_1^*))-\bar{\Gamma }(\bar{Q}_1^* +\bar{Q}_2^*(\hat{X},\bar{Q}_1^*))-\delta \bar{Q}_2^*(\hat{X},\bar{Q}_1^*), \end{aligned}$$

(C.1)

with $\bar{Q}_2^*(X,Q_1)$ in (A.2). Thus, the time value of capacity expansion in the absence of time-to-build for $\hat{X}\in (\bar{X}_1^*,\bar{X}_2^*)$ is $\bar{V}_2^{tim}(\hat{X}):=\bar{V}_2(\hat{X})-\bar{V}_2^{int}(\hat{X})$.

1.2 C.2 With time-to-build

Given the optimal investment in the initial project, the option value of capacity expansion before the initial capacity starts operating is $V_{20}(X):=V_{20}(X,Q_1^*)$ in (25); it is optimal to invest at $X_{21}^*$ after the initial project is finished. However, the firm can choose to invest as soon as the initial project is finished regardless of the level of demand shock, and thus, the intrinsic value of capacity option for $t<\hat{T}_1$ and $\hat{X}\in (X_1^*,X_{21}^*)$ is

$$\begin{aligned} V_{20}^{int}(\hat{X})&=\Pi _1(\hat{X},Q_1^*)-\Gamma _1(Q_1^*)+\hat{\Pi }_{21}(\hat{X},Q_1^*,Q_{21}^*(\hat{X},Q_1^*))\nonumber \\ {}&\quad -\hat{\Gamma }_{21}(Q_{21}^*(\hat{X},Q_1^*))-\frac{\lambda _1}{r+\lambda _1}\delta Q_{21}^*(\hat{X},Q_1^*), \end{aligned}$$

(C.2)

with $Q_{21}^*(X,Q_1)$ in (A.18). Thus, the time value of capacity expansion for $t<\hat{T}_1$ and $\hat{X}\in (X_1^*,X_{21}^*)$ is $V_{20}^{tim}(\hat{X}):=V_{20}(\hat{X})-V_{20}^{int}(\hat{X})$.

Meanwhile, after the initial capacity is in operation, the option value of capacity expansion is $V_{21}(X):=V_{21}(X,Q_1^*)$ in the first row of (18), and the intrinsic value of capacity option with the immediate investment for $\hat{X}\in (X_1^*,X_{21}^*)$ is

$$\begin{aligned} V_{21}^{int}(\hat{X}){} & {} =\bar{\Pi }_1(\hat{X},Q_1^*)-\bar{\Gamma }(Q_1^*)+\Pi _{21} (\hat{X},Q_1^*,Q_{21}^*(\hat{X},Q_1^*)) \nonumber \\{} & {} \quad -\Gamma _{21}(Q_{21}^*(\hat{X},Q_1^*))-\delta Q_{21}^*(\hat{X},Q_1^*), \end{aligned}$$

(C.3)

and thus, the time value of capacity expansion for $t\ge \hat{T}_1$ and $\hat{X}\in (X_1^*,X_{21}^*)$ is $V_{21}^{tim}(\hat{X}):=V_{21}(\hat{X})-V_{21}^{int}(\hat{X})$.