1 Introduction

Increasing globalization and outsourcing has meant greater emphasis on cooperation between organizations and their suppliers, more attention to supply chain management, and adherence to continuous improvement for maintaining long-term competitive advantage (Bai et al., 2021a, 2021b, 2021c; Charpin et al., 2021; Sting et al., 2019). Increasing stakeholder pressure to be environmental conscious and social responsibility has caused organizations and their suppliers to actively engage in supplier development (SD) efforts, especially those that introduce sustainable management principles (Bai and Sarkis, 2010; Liu et al., 2018; Saghiri & Mirzabeiki, 2021). Within this competitive context, sustainable supplier development (SSD) has become an increasingly important supplier management activity (Bai & Satir, 2022; Cole & Aitken, 2019).

Investigations have shown that SSD adoption can significantly affect other supply chain sustainability supportive processes (Bai & Satir, 2020; Sancha et al., 2015). An effective way for organizations to improve their suppliers’ operational capabilities and sustainability performance is by organizations investing in various sustainable supplier development practices (SSDPs) (Bai et al., 2021a, 2021b, 2021c).

SSDPs can involve a variety of dimensions, from sharing of transactional information to involvement of suppliers in top management decisions (Bai et al., 2016). Increasingly more research has addressed SSDPs evaluation issues in sustainable supply chain from a decision-method perspective (e.g. Bai and Sarkis, 2010; Fu et al., 2012; Dou et al., 2014; Trapp & Sarkis, 2016; Bai et al., 2021a, 2021b, 2021c). Effective SSDPs implementation not only significantly improves suppliers’ sustainable performance, such as safety and environmental concerns, but also creates competitive advantages for focal organizations (Awasthi & Kannan, 2016; Blome et al., 2014; Dou et al., 2014; Fu et al., 2012; Saghiri & Mirzabeiki, 2021; Sancha et al., 2015). Additionally, there exist cause-and-effect, interdependency relationships among SSDPs that will further change SSDPs performance or effectiveness (Fu et al., 2012; Blome et al., 2014; Dou et al., 2014; Powell and Coughlan, 2020).

When considering SSDPs adoption and implementation, organizations must consider allocation of limited resources and other operational constraints. This situation makes it unwise for haphazard SSDPs adoption by organizations (Bai et al., 2016; Zhao et al., 2022). Hence, organizations will need to choose the most appropriate and effective SSDPs and the resources allocated to these selected SSDPs to maintain competitiveness. SSDPs selection and investment allocation are strategic sustainable supply chain management decisions. A decision method aid to help in this strategic decision is valuable tool for guiding organizations in SSDPs planning. As far as we know, no such method is available that incorporates the various characteristics of allocation of resources amongst interrelated SSDPs.

Modeling selection of sustainable suppliers and order of allocation amongst them has been investigated, which is very similar to the problem in this paper, and both are the objects selection and resources allocation (e.g. Feng & Gong, 2020; Liu et al., 2022). These studies have conducted multidimensional research on supplier selection and order allocation (SSOA) problem from the perspectives of green, sustainable, gresilient, low-carbon and circular economy (Bai & Satir, 2022; Mohammed et al., 2021). Although SSOA problem is very similar to the SSDPs selection and investment allocation problem, these SSOA models cannot be directly used to solve it for the following two reasons. First, these models assume that suppliers act independently of each other and one supplier’s market share or activities do not affect those of other suppliers. In the SSD context, we must take in to account the synergy and/or counter-synergy caused by selected SSDPs. A set of selected SSDPs can complement each other such that their total effectiveness or performance exceed the sum of individual effectiveness. Alternatively, another set of SSDPs may interact is such a fashion that the total effectiveness is less than the sum. Therefore, organizations need to explicitly measure and consider interdependent SSDPs interactions in the selection and investment of desirable SSDPs. Second, above models always divided SSOA into sustainable supplier selection and order allocation two independent problems to solve. Therefore, the result of sustainable supplier selection decision will affect the result of order allocation, and then may produce a local optimal solution, especially when there has interdependency among these suppliers. The organizations need to consider the SSDPs selection and investment allocation at the same time, and find the global optimal solution. Therefore, this is a very complex problem, especially SSDPs have the synergy with each other. Therefore, this paper aims to solve the following research questions (RQ):

RQ1

What SSDPs can effectively improve the collaborative advantages of organization and its suppliers?

RQ2

What interdependency relationships exist between these SSDPs?

RQ3

How can an organization with limited capital select a set of SSDPs and invest them based on their interdependency to improve the collaborative advantages?

This study seeks to address the above research questions in sustainable supply chain planning where no previous works consider SSDPs interactions in their selection and resource allocation. This study includes the following contributions: (1) We study a novel SSDPs selection and investment allocation decision problem and methodology in sustainable supply chain. To our knowledge, this paper the first integration and consideration of a SSDPs selection and investment allocation problem in the field of sustainable supply chain. Previous studies only evaluated the performance of these SSDPs, few involve how to invest in these SSDPs, especially the integration of SSDPs selection decision and investment allocation decision (Saghiri & Mirzabeiki, 2021). (2) We develop a SSDPs framework from four groups based on relation view: sustainable product development (SPD), sustainable knowledge exchange (SKE), effective sustainable governance (ESG), and trust relationship (TR). The relational view is a good fit theoretical framework to explain how organization and its suppliers achieve collaborative advantages through SSDPs that could not be created by any single organization (Dyer and Singh, 1998). From the perspective of relational view, organization can improve the necessary knowledge and capabilities of its suppliers, and then seek support from these suppliers, rather than trying to overcome the challenges alone. This framework can comprehensively reflect the specific SSDPs that organization can invest in, and can also be used to evaluate the existing and cooperative relationship between the organization and its suppliers. (3) We propose a novel methodology that integrates established decision-analysis techniques of DEMATEL (Decision Making Trial and Evaluation Laboratory), the NK model and MOLP (multi-objective linear programming) model; which no previous supplier development study has adopted all three types of analysis tools (see Glock et al., 2017). The previous multi-objective model seldom considered the multiple complex influence relationship between the evaluation objects (Kaur & Singh, 2021). These techniques are innovatively integrated to evaluate the interdependency between SSDPs while seeking to optimize a company’s investment decisions. DEMATEL is applied to identify, segregate, and then evaluate the interdependency among the SSDPs. The NK model is used to select a set of SSDPs among the available set using an iterative process. MOLP, incorporating capital budgeting constraints, optimally allocates investment resources among the selected SSDPs; maximizing economic and environmental objectives. (4) We apply the methodology developed in the paper to data collected from an equipment manufacturing company in China helping to help evaluate the methodology in a practical context. Various policy, theoretical, managerial, and methodology insights for the organization are identified for optimal investments in SSDPs. In the remainder of this paper, we first provide a brief background on sustainable supplier development, supplier selection and order allocation research literature. Formal models in those areas are identified and a succinct overview is provided. We then provide a comparison between existing models and the methodology proposed in this paper with a table. The basic concepts associated with DEMATEL, the NK model are described. The general background information about the case company and proposed methodology that integrates DEMATEL and the NK model results with a multi-objective linear programming are then introduced. The field application is discussed, with policy, theoretical, managerial, and methodology implications and insights presented. We end the paper with major study findings, conclusions, and limitations. Directions for future research and some ideas about how the proposed framework and methodology might be improved are also presented in the final section.

2 Background

2.1 Sustainable supplier development and practices

The term “supplier development” has existed for decades (Leenders, 1966). SD is defined as buying organization (buyer) effort, in conjunction with its suppliers, to increase the performance and/or capabilities of the suppliers to meet the buyer’s needs (Charpin et al., 2021; Govindan et al., 2010; Jin et al., 2019; Wuttke et al., 2018; Zhou et al., 2022). Environmental regulations and community awareness of environmental issues have caused organizations to consider them for competitiveness reasons. Integrating environmental and social sustainability concerns into supplier development is a relatively recent phenomenon (Bai and Sarkis, 2010; Karaer et al., 2017; Chan et al., 2018; Govindan et al., 2018; Kumar et al., 2019; Powell and Coughlan, 2020) and has been termed “sustainable supplier development”.

SSD goes beyond just requiring supply chain partners to become sustainability; it involves an organization actively and strategically helping its suppliers to become sustainability (Bai & Satir, 2022; Sharma et al., 2022; Saghiri & Mirzabeiki, 2021). Recent occurrence of numerous serious incidents of environmental damage due to lack of responsible behavior and proactive action have made it necessary to promote supplier development and management from a sustainability perspective (Sancha et al., 2015). Organizations increasingly recognize that continuously improving supplier sustainable performance strengthens their own competitive advantage (Wagner, 2011), SSDPs as a collaborative strategy have received greater attention from both academia and practice (Bai et al., 2021a, 2021b, 2021c; Wu, 2017).

In recent years, organizations have implemented monitoring and collaborative SSDPs to ensure that suppliers can provide materials and services with high quality while adhering to environmental standards (Awasthi & Kannan, 2016; Bai & Satir, 2020; Dou et al., 2014; Sancha et al., 2015). SSDPs broadly include practices such as providing green technological advice, setting environmental improvement targets for suppliers, information sharing on environmental topics, transferring employees with environmental expertise to suppliers, investment in supplier capacity enhancement, requiring ISO14000 certification for suppliers, and obtaining top management commitment for suppliers for sustainable supply practices. SSDPs vary widely, and may be grouped into three categories (Bai and Sarkis, 2010): green knowledge transfer and communication, investment and resource transfer, and management and organizational practices.

The relational view is a theoretical framework to provide a good fit with the SSDPs studied for understanding the effects of SSDPs for gaining collaborative advantage to both suppliers and organizations, at least in a dyadic relationship (Zhao et al., 2022; Govindan et al., 2021; Dubey et al., 2020; Rodríguez et al., 2016). There are two differences between the relational view and other theories, such as resource-based view, transaction cost economics, dynamic capabilities (Bai & Satir, 2022). First, the unit of analysis in the relational view is a dyad or even a network of organizations, rather than a single organization. Second, instead of considering competitive advantage, the relational view considers the collaborative advantage that can be obtain by the support of the external organizations or partners. Collaborative advantage refers to the common benefits of both parties in rent-seeking behavior, while competitive advantage encourages individual rent-seeking behavior for its benefits. According the relational view, collaborative advantages can be obtained due to inter-firm specific assets, complementary resource endowments, exchange substantial knowledge, and effective governance (Bai et al., 2021a, 2021b, 2021c). To analyze the nature of the SSDPs as a collaborative advantage under sustainability, four groups of SSDPs are identified and shown in Table 1 based on the SSDPs literature review and relational view. SPD, which measures “complementary resource endowments”, refers to shared heterogeneous resources and capabilities among organization and its supplier to design, product, and purchase sustainable products. SKE, which measures “exchange substantial knowledge”, refers to shared critical sustainable information and knowledge among organization and its supplier through various ways. ESG, which measures “effective governance mechanisms”, is characterized by informal management systems, such as sustainable evaluation, sustainable verification, sustainable disclosure and report, carbon management, and so on. TR, which measures “inter-firm specific assets”, refers to trust or capital investments made by organization and its suppliers that are used to achieve consistent sustainable goals. A list of four SSDPs in each of the four major categories was developed from published literature (Chen et al., 2013; Bai and Sarkis, 2010; Hsu et al., 2013; Zhen, 2016; Liu et al., 2018; Bai et al., 2019a, 2019b; Govindan et al., 2021). These 16 SSDPs are used to identify and evaluate the characteristics of SSDPs in this study.

Table 1 A list of SSDPs
Full size table

Not all SSDPs contribute equally to improving supplier sustainable performance. Some SSDPs will be more effective if a certain subset of them is implemented simultaneously. For example, (1) assessing suppliers’ performance, and (2) feedback about evaluation results are two SSDPs that may need to be simultaneously implemented. Alternatively, other SSDPs subsets if deployed concurrently may diminish the effectiveness of individual SSDP. We attempt to quantify such vagaries and unique interactions, either, positive or negative, by DEMATEL in the SSDPs selection process. NK model and MOLP model is then integrated to optimally allocate resources given constrained investment funds among the selected SSDPs.

2.2 Optimal model for SSDPs

Literature on SSD using analytical decision-methods is relatively limited, although growing (Bai et al., 2019a, 2019b; Dou et al., 2014; Glock et al., 2017; Hosseini-Motlagh et al., 2019). Bai and Sarkis (2010) introduce an analytical model using rough set theory to investigate the relationships between organizational attributes, green supplier development programs (GSDPs), and performance outcomes. Fu et al. (2012) introduce a grey-based DEMATEL methodology for organizations to help evaluate the influence relationships amongst GSDPs. Blome et al. (2014) develop a structural equation model to test the relationship among top management commitment, and green supplier development. Dou et al. (2014) introduce a grey analytical network process-based model to identify the relation between the GSDPs and suppliers' performance. Akman (2015) applied fuzzy c-means and VIKOR methods to select suppliers for green supplier development programs. Awasthi and Kannan (2016) propose a fuzzy NGT-VIKOR based solution approach to evaluate the performance of GSDPs. Rashidi and Saen (2018) propose a data envelopment analysis (DEA)-based model to incorporate dynamic concept into gradual improvement approach to improve suppliers in sustainable supplier development. Bai and Satir (2020) developed a hybrid methodology by involving Grey-DEMATEL and Grey-ISM to identify the relationships among barriers and roles in the implementation of GSDPs under uncertainty.

Each of these studies uses some analytical technique to investigate SSDPs, especially the relationship amongst SSDPs or between SSDPs and other factors including supplier performance, organizational attributes and barriers. These techniques can aid in development and execution of SSDPs strategy. None of these studies provide a systemic methodology that can optimally allocate resources among SSDPs to arrive at the best performance. Few studies have focused on a comprehensive scrutiny of SSDPs interrelationships, their impact on total sustainability performance, and how to allocate SSDPs resources optimally while considering these interrelationships. It is within this context that this study seeks to make a research and practical contribution.

2.3 Supplier selection and order allocation

Supplier selection is a fundamental concern for strategic supply chain management and is closely related to SSDPs targeting and selection. It has received considerable attention in the supply chain management literature (Govindan et al., 2015; Kaur & Singh, 2021; Mota et al., 2018; Kannan, 2018; Sun et al., 2022). Two types of supplier selection problems typically exist: single sourcing and multiple sourcing (Setak et al., 2012). In single sourcing, the challenge is to select the best single supplier, which can satisfy all organization requirements (Bai et al., 2021a, 2021b, 2021c; Aditi et al., 2022). The second approach is about selecting an appropriate combination of suppliers when no single supplier can satisfy the organization requirements for a given source material. In the latter situation, management can split order quantities among suppliers, and may do so, as an example, for competitive or risk reasons (Sawik, 2014).

SSOA is a complex and multiple-criteria decision-making problem (Hu et al., 2018; Mohammed et al., 2021; Sun et al., 2022). It considers different tangible and intangible variables including price, quality, performance, technical capability, and delivery (Ghadimi, et al., 2018; Ho et al., 2010; Li et al., 2018a, 2018b). The scope of potential factors has expanded due to governmental legislation and greater societal awareness in social issues such as protecting the environment, which has caused a shift to green or sustainable SSOA (Govindan et al., 2015; Torabi et al., 2015; Jia et al., 2020).

Recent papers have employed several analytical methods in the supplier selection process. These methods include the analytic hierarchy process (AHP), analytic network process (ANP), technique for order performance by similarity to ideal solution (TOPSIS), potential support vector machine (P-SVM), preference programming (PP), fuzzy logic, and case-based reasoning (CBR), etc. (Govindan et al., 2015; Ho et al., 2010; Rezaei et al., 2020).

Supplier selection and order lot-sizing modeling studies have seen growth within the broader supplier selection literature. Much of this literature relies on various mathematical programming models (linear, mixed integer, goal and multi-objective) to investigate this issue (Aissaoui et al., 2007; Li, et al., 2018a, 2018b). When decision makers need to consider resource limitations and allocation in the supplier selection literature, mathematical programming models are generally preferred over AHP/ANP/TOPSIS methods (Setak et al., 2012). Generally, these mathematical programming models for joint supplier selection and order allocation are combined with other techniques to improve the range of application (Mafakheri et al., 2011). For example, Kannan et al. (2013) applied analytic hierarchy process and fuzzy techniques for order preference in the context of green supplier selection. We summarize the sustainable SSOA models in Table 2.

Table 2 Summary of literature for sustainable supplier selection and order allocation
Full size table

Through the comparative analysis in Table 2, we find that these models have three limitations, which can not effectively solve SSDPs selection and investment problem. First, a SSOA problem is divided into two independent problems: sustainable supplier selection and order allocation. The result of sustainable supplier selection decision will affect the result of order allocation. Therefore, they may produce a local optimal solution rather than a global optimal solution. Second, they all regard suppliers as independent individuals, and there is no interaction between these suppliers. Third, the most above order allocation models generate a set of Pareto solutions, but decision maker still needs to select a solution from this set of solutions. Furthermore, another method is needed to obtain the best Pareto solution.

In this paper we introduce an integrated methodology with DEMATEL, NK model and MOLP model to account for various constraints such as total investment, minimum and maximum investment desired, in addressing the selection and resource allocation issues for SSDPs.

2.4 Contributions of this research

The SSOA problem has received considerable attention in the literature, but few papers focus on and integrate multiple goals for the related SSDPs selection and resource allocation decision. A major shortcoming in the literature is the absence of interplay amongst various SSDPs. For example, let us say SSDP A enhances the effectiveness of SSDP B but adversely affects SSDP C effectiveness. Given this scenario, if SSDP B is selected then SSDP A should also be selected because the total positive impact of these two SSDPs together is synergistic, that is the benefit to both is greater than the sum of the benefits if both are separately funded at different times. The opposite will be true if SSDP C is selected with SSDP A. This phenomenon is common and well understood by practitioners.

Organization managers involved in making these decisions were interviewed concerning this situation. They had no difficulty in gauging these effects. However, it is difficult to describe the interdependency of SSDPs and quantifies it using only the traditional models in SSOA. Our paper considers the complex interdependency of SSDPs and quantifies it for an operational environment using DEMATEL, NK model method and MOLP model. First, DEMATEL method can be used to quantify the interdependency of SSDPs considered in decision making process, which supplements the NK and MOLP models. The managers can express their opinions about the interdependency relationships among SSDPs with higher efficiency. The interplay and interdependency information can serve as inputs to the NK and MOLP models. Second, NK and MOLP models integrate each other as a whole, and constantly seek the best performance investment strategy with the limited amount of capital. The NK model is used to select the set of SSDPs and MOLP is adopted to maximize economic and environmental objectives through optimally allocates investment resources among the selected SSDPs. The NK and MOLP models then can generate a fitness landscape which represents performance results corresponding to each combination of SSDPs. They use search strategies to navigate the fitness landscape to find the most suitable location, in this case the best performance strategy. Therefore, our augmented NK and MOLP models can obtain a global optimum solution without the need for complex computing processes. In summary, this study proposes a novel methodology that integrates DEMATEL and NK and MOLP models. This methodology can evaluate the interdependency between the SSDPs and simultaneously maximize economic and environmental objectives within constraints and optimizes resource (investment) allocation amongst the chosen SSDPs. An additional feature of this approach is that it allows for variation in the number of SSDPs that are considered. This variance will depend on the strength of interdependency.

3 The NK model and Dematel

3.1 The NK model

The NK model was initially developed for modelling biological evolution resulting from gene mutations and to describe how some gene mutations are more fit for long term survival (Kauffman, 1993). Let the N SSDPs of the sustainable supplier development system be represented by \(c = \{ c_{1} , \ldots ,c_{N} \}\). Each \(c_{i}\) can take the value 1 indicating implementation of SSDP i, or 0 otherwise. The index set \(I_{i}\), contains indices of the SSDPs that influence \(c_{i}\). If K = 3, then there are other 3 SSDPs that impact, for example, the effectiveness of \(c_{2}\). If those SSDPs are \(c_{4}\),\(c_{8}\), and \(c_{9}\) then \(I_{2} = \{ 4,_{{}} 8,_{{}} 9\}\). The effectiveness or performance of SSDP \(i\) is indicated by \(f_{i} (c_{i} ,\{ c_{j} :j \in I_{i} \} )\). This notation states that the effectiveness of \(c_{i}\) depends on itself and on other SSDPs in its index set \(I_{i}\). The average total effectiveness of all N SSDPs is given by:

$$F_{{}} = \frac{{\sum\nolimits_{i = 1}^{N} {f_{i} (c_{i} ,\{ c_{j} :j \in I_{i} \} } }}{N}$$
(1)

There are 65,536 different values that F can take, not all of them are necessarily distinct. In this problem context, the values of F create a hypersurface in N + 1 dimensions (since there are N variables in a configuration). The surface is called a fitness landscape, relating to the “survival of the fittest” notion. For each configuration, there is one value of F. Higher F values represent better species fitness. This fitness landscape consists of peaks and valleys. Species who reach the peaks from the valleys, due to beneficial mutation of genes, have a better chance of survival. Higher values of K create more and steeper peaks. The value of K varies from 0 to N−1; K = 0 indicates a system which has completely independent components, while K = N−1 means each component of the system affects every other in the system.

We will take another look at complexity created by higher K values. The number of distinct values of \(f_{i} (c_{i} ,\{ c_{j} :j \in I_{i} \} )\) is given by \(2^{K + 1}\) since there are K + 1 variables in the function and each variable is binary. This indicates that as K gets larger the function takes more different values, which creates greater differences in vertex values. Vertex values that differ significantly from each other create more peaks and valleys on the hypersurface.

3.2 DEMATEL

The Battelle Memorial Institute introduced DEMATEL method through its Geneva Research Centre (Gabus and Fontela, 1976). DEMATEL is used for identifying and analyzing indiscernible, causal relationships amongst a set of attributes using matrices or digraphs. The attributes can be criteria, objectives, or characteristics of an entity or a system. DEMATEL is simple to formulate, easy to understand, and useful in clarifying interrelationships amongst the components of a complex system. It has been successfully utilized in many practical problems and research areas including business process management, sustainable supplier selection, sustainable procurement (Kannan, 2021), and sustainable supply chain management (Govindan, 2023; Bai and Sarkis, 2013; Lin, 2013; Govindan and Arampatzis, 2023). This paper refines the version introduced by Fontela and Gabus (1976).

In this study DEMATEL is used to identify SSDPs interdependency. We want to know whether an SSDP’s implementation affects other SSDPs, how and to what extent. We use this information from DEMATEL to determine a set of K SSDPs that are influential in enhancing or diminishing the effectiveness of a given SSDP. In this case an SSDP that is diminishing effectiveness would be one that can be replaced by an SSDP with greater effectiveness. This information is used as input to the NK and MOLP models.

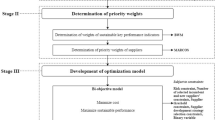
To construct an SSDPs selection and investment allocation decision methodology from empirical data, DEMATEL method and NK fitness landscapes model and the MOLP are integrated, and the calculation process is shown in Fig. 1. We have collected data from a case company and its SSDPs for this study. In the next section, we provide information about how we collected data for evaluating the information on SSDPs interdependency by the DEMATEL method and for estimating the SSDPs effectiveness and investment constraints. In the Sect. 5, the NK model and dynamic MOLP model are adopted to select different combinations of 16 SSDPs and allocate the investment among the selected SSDPs.

Fig. 1
figure 1

Flow chart of the calculation process

Full size image

4 Data collection

4.1 Sample case company characteristics

Over the past thirty years, China has gone through extraordinary rapid economic growth to become the second largest economy in the world. Along with benefits of rapid economic expansion came significant environmental and social degradation and its associated costs (Bai et al., 2015). In response to these concerns, and recognizing the importance and need for long-term, environmentally sustainable development, Chinese regulatory authorities have implemented a variety of policies to encourage sustainable modes of operations. These policies include, for example, the Circular Economy policies and incentives for a low-carbon economy.

Due largely to pressures from governments, customers, competitors, and various other stakeholders, many companies have adopted sustainability practices in their supply chains (Lu and Abeysekera, 2014). During the last decade, China’s corporations and academia have shown great interest in environmental sustainability (Bai et al., 2015). The company from which we collected the data on its supply chain system and policies is in industrialized northeast China. For this case investigation the case company reported some improved performance on economic and environmental dimensions after implementation of SSDPs. In order to comprehensively analyze this SSDPs implementation and performance, the study purposively targeted and selected a large-scale equipment manufacturing organizations in China. It may be viewed as a representative example of a manufacturer in China.

The company, a joint venture, is one of the largest home-appliance manufacturers in China. It, founded in 2003, is a state-level high-tech firm with a registered capital of 100 million yuan (Chinese currency unit) and more than 5000 employees. It covers an area of 20,000 M2, the plant area is 10000 M2. The company is a high-tech firm specialized in R&D and manufacturing of substation equipment and electrical equipment. The company has passed the ISO9000 quality management system certification, health certification, environmental certification, and obtained a number of national patent certificates.

Some of its suppliers are globally recognized companies. The company has cooperated and help these suppliers to develop environmentally sound technologies and products. This manufacturer is also interested in improving the environmental performance of the whole-life cycle of products it makes. Towards that end, it has helped and coached its suppliers to become sustainability since 2000.

To obtain the data presented in the Tables 3 and 5 and some additional information about SSDPs investment, we spoke with four company managers situated in a local division who were responsible for operations, finance, purchasing and environmental matters. First, the managers were informed about the study purpose, a brief overview of each method was presented and an introduction to the variables involved. In each session, managers were informed about the necessity for each variable to be measured. The managers discussed the issues involved before providing us with an individual perspective or a consensus as the situation warranted.

Table 3 The averages influence: direct-relationship matrix
Full size table

The first step in data collection was presenting a detailed list of possible SSDPs to the four managers for their local division operations. The four major categories include: involvement in SPD, SKE, ESG, TR. Table 1 lists the four SSDPs chosen under each of those categories. There is no significance in selecting exactly four SSDPs in each of the major supplier development areas. However, we wanted to make sure that the list was detailed enough to encompass the company’s activities and simultaneously not too long to overburden the managers with too much detail. Since this list forms the foundation of managerial responses to comparisons and judgements, we made sure that the managers had opportunities to discuss and obtain clear understanding of the SSDPs related to their operations.

4.2 Effectiveness of SSDPs

The effectiveness of an SSDP i, \(f_{i} (c_{i} ,\{ c_{j} :j \in I_{i} \} )\) depends on itself as well as other SSDPs implemented by the company. The other SSDPs could act to enhance or diminish the effectiveness of that SSDP. It depends upon the interdependency relationships. When NK model is used in practice, it is very rare to be able to obtain the effectiveness, or fitness, values for components of the system. This fact makes it difficult to study the hypersurfaces and determine optima (McCarthy & Tan, 2000). In such situations, the researchers often are limited to Monte Carlo simulation where the fitness values are assigned randomly, generally over the range from zero to one using uniform probability distribution. Such simulations can provide some general information about upper and lower bounds on system fitness or its performance with different values of N and K. Unfortunately, without specific effectiveness values for different system component states no specific system characteristics can be studied (Kaul, 2005; Wang et al., 2016).

We have the same quandary, it is difficult to determine the value of a SSDP’s effectiveness without knowing which SSDPs affect its performance and how to measure it. That is, how is the value of \(f_{i} (c_{i} ,\{ c_{j} :j \in I_{i} \} )\) determined? To overcome this problem, we propose a novel use of DEMATEL in conjunction with the NK model. The DEMATEL is described below in the context of SSDPs.

4.3 Data for DEMATEL

To obtain the information on SSDPs interdependency, the four managers were asked to rate the impact SSDP i on SSDP j on a five-gradation, Likert type scale described as from no influence (value 0) to very high influence (value 4). Each manager made an independent pairwise comparison of the impact of SSDP i on SSDP j. The four managerial values for a given SSDP relationship were averaged; the result is shown in the Table 3. The average influence numbers range from zero to 3.75.

DEMATEL helps extract and highlight the latent and intricate interdependency of components of complex systems with the total relationship matrix. However, in this study we are interested in a different aspect of the matrix. To achieve that, we first compute the mean value, \(\theta\), of the elements in the matrix T then subtract \(\theta\) from each element that matrix. The resulting interdependency matrix \(INF = \{ t_{ij} - \theta \}\) has the same information as the matrix T except the elements now indicate variations from the mean. Table 4 shows the INF matrix. We use the matrix to identify top K SSDPs that will affect a given SSDP.

Table 4 Interdependency matrix (INF)
Full size table

Let us define an index set S whose elements are the indices of the currently implemented SSDPs. For example, if SSDP 2, 5, 6, 10, 12, 13, and 16 were implemented then S = {2,5,6,10,12,13,16}. Note that each S set will correspond to and identify a vertex of the hypercube. Now if we want to find out, for example, the top 3 SSDPs out of the implemented ones that impact SSDP10 most then we examine column 10 of INF matrix for the impact values. Column 10 values are for SSDP 02 = − 0.029 or \(inf_{2,10} = - 0.029\). Similarly, we can find other interdependency values of interest as \(inf_{5,10} = + 0.023\), \(inf_{6,10} = + {0}{\text{.007}}\), \(inf_{12,10} = { - 0}{\text{.034}}\), \(inf_{13,10} = { + 0}{\text{.062}}\), \(inf_{16,10} = + {0}{\text{.066}}\). To find the top 3 SSDPs affecting SSDP 10, the SSDPs are ranked using the absolute values since we want to consider both positive and negative effect on effectiveness of SSDP 10. Those three SSDPs are 16, 13, 12, notation \(I_{10} = \{ 12,_{{}} 13,_{{}} 16\}\).

4.4 Data on SSDP effectiveness

As described earlier, many NK models do not progress beyond general analysis stage due to difficulty in obtaining the values of components effectiveness of a system. Let this direct effectiveness of SSDP i be indicated by \(g_{iB} (c_{i} )\) and \(g_{iE} (c_{i} )\) where the subscript B indicates business and E environmental effectiveness. To obtain the impact of interdependency on the effectiveness, we use information from DEMATEL’s INF matrix as follows:

$$f_{iB} (c_{i} ,\{ c_{j} :j \in I_{i} \} ) {=} \sum\limits_{{j \mathrel\backepsilon I_{i} }} {g_{iB} (c_{i} ) \times INF_{ji} } \quad f_{iE} (c_{i} ,\{ c_{j} :j \in I_{i} \} ) {=} \sum\limits_{{j \mathrel\backepsilon I_{i} }} {g_{iE} (c_{i} ) \times INF_{ji} }$$
(2)

To obtain \(g_{iB} (c_{i} )\) values for each SSDP, we asked the four managers to evaluate the effectiveness of SSDP i by itself on overall supply chain economic and environmental performance. The evaluation scale ranged from 0, which was not effective, to 1, which was pegged as highly effective. Economic or business effectiveness of a SSDP i, \(g_{iB} (c_{i} )\), refers mainly to business measures including cost, quantity, time and quality performance, whereas environmental effectiveness, \(g_{iE} (c_{i} )\) considers greenness of a supplier’s pollutant emissions, energy consumption and the recycling and reuse level of the products. Table 5 shows the evaluation of each SSDP by four managers on business and environmental effectiveness. We use the averages of the four values. We also asked the managers to estimate the minimum and maximum amounts, in percent terms, that should be spent on a given SSDP out of total budget, 100%, without considering any interactions among the SSDPs.

Table 5 Estimates of SSDP effectiveness and investment constraints
Full size table

5 NK model and dynamic MOLP model

The NK model is used to select different combinations of 16 SSDPs and determine their effectiveness using DEMATEL. Allocation of investment among the selected SSDPs is carried out using the dynamic MOLP model, which considers the effectiveness of the SSDPs based on their interdependency, and constraints on the investment. The objective function of dynamic MOLP includes a set of goals that should be satisfied while looking for pareto-optimal solution among the most efficient points (Chan & Lee, 2018; Mohebalizadehgashti et al., 2020).

5.1 The objective function

The objective function of the proposed MOLP model includes economic and environmental effectiveness. First, the economic and then the environmental component is considered; both have similar mathematical expressions.

Maximize:

$$F_{B} = \sum\limits_{i \in S} {\left[ {g_{iB} (c_{i} ) \cdot x_{i} + \omega \cdot \sum\limits_{{j \in I_{i} }}^{{}} {x_{j} \cdot x_{i} \cdot f_{iB} \left( {c_{i} ,\{ c_{j} :j \in I_{i} \} } \right)} } \right]}$$
(3)

where \(x_{i}\) is investment amount in SSDP i. The first term in expression (3) is the effectiveness of SSDP i investment without any interdependent impacts from other selected SSDPs. The index set S, it may be recalled, consists of all SSDPs currently implemented. The membership in set S changes as the search for an optimal SSDP set progresses. The second term provides the additional benefit or loss in investment effectiveness due to interdependency relationships of SSDP i and other SSDPs in the set \(I_{i}\). Note we include the investments \(x_{i}\) and \(x_{j}\) to include magnitude of investment in an SSDP j (from the set \(I_{i}\)) to account properly for its interdependency impact. The term \(\omega\) is used to normalize the second term; it is the average investment in an SSDP. If T is the amount of total investment then \(\omega = T/\) number of SSDPs implemented. The environmental part of the objective function (expression 4), follows the same logical reasoning as \(F_{B}\).

$$F_{E} = \sum\limits_{i \in S} {\left[ {g_{iE} (c_{i} ) \cdot x_{i} + \omega \cdot \sum\limits_{{j \in I_{i} }}^{{}} {x_{j} \cdot x_{i} \cdot f_{iE} \left( {c_{i} ,\{ c_{j} :j \in I_{i} \} } \right)} } \right]}$$
(4)

The above dynamic MOLP model can be converted into a single objective model by using a weighted additive function as proposed by (Amid et al., 2006). The weighted additive model is widely used in vector-objective optimization problems. The basic concept is to use a single utility function to express the overall preference of decision makers to draw out the relative importance of criteria (Lai and Hawang, 1994). The following single objective programming is equivalent to the above MOLP model:

$$\begin{array}{*{20}c} {\text{Maximize:}} & {} \\ \end{array} F = \lambda F_{B} + (1 - \lambda )F_{E}$$
(5)

where \(0 \le \lambda \le 1\) is the weighting coefficients that represent the relative importance given to economic performance.

5.2 Constraints

Budget/Investment Constraint: the capital budget limit is denoted by T. We set T = 100 instead of an actual budgeted amount.

$$\sum\limits_{i \in S}^{{}} {x_{i} } \le T$$
(6)

Limits on individual SSDP investment: some SSDPs may require some minimum investment to become operational. Some may also have an upper limit that indicates maximum amount that could be spent on it.

$$\min_{i} \le x_{i} \le \max_{i} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall i \in S$$
(7)

Investment is made in the selected SSDPs only:

$$\begin{gathered} x_{i} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall i \notin S; \hfill \\ x_{i} \ge 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall i \in S \hfill \\ \end{gathered}$$
(8)

5.3 The application

The complete procedure including the search algorithm is summarized in Fig. 2. The first four steps focus on data collection. Step 5 is the algorithm search initialization. The set S represents SSDPs implemented by the company. The membership of this set changes as the algorithm searches for other SSDPs that may provide better effectiveness. The different concurrent stages of this set are indicated by subscripts current and prior. We also use the subscripts for the objective function F.

Fig. 2
figure 2

Flowchart of the search algorithm

Full size image

In step 6, the interdependency index set Ii is determined for each currently implemented SSDPs (Scurrent). DEMATEL is used to identify the top K interacting SSDPs for a given SSDP. The interacting values are from the INF matrix in Table 4. The direct impact values for business and environmental effectiveness \(g_{iB} (C_{i} )\) and \(g_{iE} (C_{i} )\) are obtained from Table 5. The \(f_{iB} (C_{i} )\) and \(f_{iE} (c_{i} )\), which represent the change in the effectiveness SSDP i due to interactions with other SSDPs are computed from Eq. 2.

Step 7 solves the MOLP problem. The objective function is obtained based on values computed in step 6 by using Eqs. 3, 4, and 5. The value λ determines the relative importance attached to business and environmental objectives. As described in a later section, it is varied during the sensitivity analysis to obtain understanding of the impact of selection of SSDPs under these often-conflicting goals. At the end of this step, the objective function value Fcurrent is determined for one of the vertexes of the hypercube represented by indices in Scurrent.

In step 8, we check to see if we have made an improvement from the previous value of the objective function Fprior, which corresponds to vertex Sprior. We keep the better of the two effectiveness values and search for a higher effectiveness value amongst its neighboring vertexes. These neighboring vertexes are identified by selecting a random SSDP from 16 available. If it is already implemented we decommission it, on the other hand if the randomly selected vertex is not in the set, we implement it. Thus, a new set S is obtained, which now becomes the Scurrent. At this point we go back to step 6, re-compute all needed values so that a new objective function value can be computed and restart the search process for the best effectiveness value. The search process is iterated 100 times. The ending of the iterations is taken as the best value and corresponding values of xi are the most effective investments in SSDPs. The authors have developed a system of MATLAB software for the algorithm.

Based on the case data collected (Table 3 and 5) with K = 3 and λ=0.5, the optimal objective function results is: F = 91.0. This the total effectiveness of investment in the selected SSDPs. The economic part of the objective function is valued at 91.9 and the environmental part at 90.1, which are equally weighted. Four SSDPs were recommended for investment and with amounts of SSDP 13 = 20%, SSDP 14 = 30%, SSDP 15 = 23.6%, SSDP 16 = 26.4%. As mentioned before, the percentage values result from setting total investment, T, at 100%.

6 Sensitivity analysis

6.1 Coefficient \(\lambda\) variations

The results of this sensitivity analysis, with \(\lambda\) changed in increments of 0.1, are shown in Table 6 and Fig. 3.

Table 6 The SSDPs investment allocation results for different value \(\lambda\) (K set at 3)
Full size table
Fig. 3
figure 3

The SSDPs investment allocation and results for different value \(\lambda\) (K set at 3).

Full size image

When \(\lambda\)=0, the MOLP model becomes a single objective model focusing on the maximum environmental effectiveness. Same reason, the MOLP model become a single objective programming that get the maxim economic performance when \(\lambda\)=1. It is interesting to note that SSDPs 13 to 16 are in the selected set over the entire range of \(\lambda\). As may be seen from Table 1, these SSDPs are in the trust relationship group. This occurrence highlights the fact that it is important for the company to spend funds and effort building trust and confidence with its suppliers, maintain transparent and achievable goals, and be cognizant of suppliers’ interest in business relationship. Such a supply chain environment, it appears from our data, will provide economic and environmental benefits to the company.

The model allocates 20% and 30% to SSDP 13 and 14 respectively. The constant investment in these two SSDP across the entire range of \(\lambda\) highlights the importance of SSDP 13 and 14 from both economic and environmental perspectives. These two SSDPs emphasize consistent, competent, and effective sustainable goals and controls.

When SSDP 15 and 16 are considered, it appears that SSDP 15 becomes more important in terms of investment as more weight is given to business performance. SSDP 15 asks the company to be honest in business practices about sustainability. Investment direction in SSDP 16 is exactly opposite. As environmental factors increase in importance, more investment is allocated to SSDP 16, which requires the company to act in a partners’ best interest.

6.2 Interdependency parameter K variations

We select a K range from 0 to 5, in increments of 1. The results of this analysis are shown in Table 7 and Fig. 4.

Table 7 The SSDPs investment allocation results for different value K (\(\lambda\) set at 0.5)
Full size table
Fig. 4
figure 4

The SSDPs investment allocation results for different value K (\(\lambda\) set at 0.5)

Full size image

A low K value (e.g., K = 0) leads to a smoother hyperspace where the global optimum (or the highest peak) is easily searchable. With K=0, the model does not consider the interdependency relationship amongst the SSDPs. It only looks at the performance of the individual SSDPs, that is, the effectiveness of each SSDP is exactly as given in Table 5. It can be seen from that table that effectiveness level of SSDP 04, 01 and 02 are the top three, 0.9050, 0.9025 and 0.9025, respectively. The investment allocation to SSDP04 is at the upper limit 60 (Table 8). SSDP 01 and 02 have the same effectiveness hence the remaining 40 are distributed equally. When K > 0, the interdependency relationships displayed in Table 4 come into play. The effectiveness depends on both direct effectiveness values (Table 5), and on interaction between selected SSDPs (using Eq. 2).

Usually as K increases, the hyperspace becomes more uneven, displaying many peaks and valleys. In our example, however, that phenomenon is not evident. In Table 7, the results for all K>2 are the same. This is due to the investment constraint in the MOLP model. The interdependency amongst the SSDPs 13 to 16 is so strong (see SSDPs 13 to 16, and their columns and rows in Table 4) that most effective allocation of investment takes place when maximum investment is made into them. If there are no funds left then other SSDPs receive no investment, their \(x_{i}\) values are 0. Examination of Eqs. 3 and 4 makes it clear that other interactions do not play a role. Therefore, for any value K > 2, the investment allocation will be the same and the effectiveness of the SSDPs will be the same.

7 Results

7.1 Policy and theoretical implications

The implications for China are discussed first. China is facing domestic and international pressures to improve its environmental and sustainability performance and create awareness of social responsibility amongst its public and private organizatrions. First, in light of this situation, organizations should make investments in them suppliers to improve their sustainability performance (Bai et al., 2016). Therefore, the country should formulate relevant policies to not only encourage organizations to improve their sustainable performance, but also encourage them to improve the sustainable performance of their suppliers through SSD. Second, an organization may not be able to invest in all the SSDPs simultaneously; it may have to judiciously choose among the strategies and maximize the environmental and economic performance with limited resources and other restrictions arising out of operational considerations. Hence, it would be helpful to decision makers to identify how investment strategies affect the performance, which is strongly influenced by the SSDPs interdependency. The country can give more policy guidance and better play to the synergy of these SSDPs, so as to help organizations play a maximum role in SSD with limited capital.

The implications for theoretical research are also discussed. The SSDPs framework proposed in this study provides researchers and practitioners with some theoretical insights. First of all, in view of the increasing importance of collaborative advantage, the focus of competition has increasingly shifted from an inner-organization to strategic cooperation among supply chain partners. Therefore, investment in SSDPs must be based on the relational view to generate collaborative advantage by a dyad of buyer and its suppliers. Therefore, buyer and its suppliers can work together through SSDPs to greater common interests than acting alone. Second, it contains 4 key aspects: ISPD, SKE, ESG, and TR. These four aspects are the key aspects of establishing strategic cooperation and collaborative advantages. Based on 4 aspects of the relational view, this framework lets both researchers and practitioners think deeply and categorize various issues in SSDPs. Third, it includes 16 specific practices, which can be used as an initial list for practitioners to refer to and guide their specific practical activities. Through establishing a systematic framework to evaluate and select SSDPs, it may help buyer and its suppliers improve their sustainability through the SSDPs investment. This framework can also be used to evaluate the performance level of existing SSDPs investment or make decision analysis for future SSDPs investment. From this point of view, this study might help managers to obtain more efficient investment plans in sustainable development considering capital limitation.

7.2 Managerial implications

The methodology and its real-world application provided can provide insights for companies and suppliers alike. Professional and industrial organizations, and the government, can also benefit since the methodology developed in the paper will help them identify most effective sustainable and green environmental practices. In China, the implementation of sustainable supply chain management is still in the early stages of development; a methodology such as this can help organizations begin to determine best directions for adopting SSDPs. Analysis of the results in Tables 6 and 7 provide some insights into the investment strategies for sustainable supplier development practitioners and researchers.

7.2.1 The best practices for performance

SSDPs can be ranked according to the effectiveness level based on the results shown in the Table 5. Evaluating the contributions of each of these SSDPs can help identify which ones can be prioritized. SSDP01 and 04 are the most important for economic performance when those SSDPs separate implementation. SSDP02 is the most important for environmental performance when this SSDP separate implementation. This performance rank of these SSDPs can give an intuitive feeling to the case organization. Organizations can only consider these best activities if they only implement a single SSDP, but it is not suit for implementing a set of SSDPs.

7.2.2 The best practices for interdependency

To understand the implications of the interdependency among SSDPs, let's return to the DEMATEL results shown in Table 4. Using the final outcomes of DEMATAL, with the highest score of R + D, we can identify the most important (prominent) practices. SSDP16, 13, 14 and 15 are arranged in the first four. Organizations may gain a deeper understanding of investment practices. In our illustrative example, it was found that all trust relationship practices (SSDP 13—16) play a useful role in identifying good sustainable performance.

7.2.3 The investment allocation decision

For the illustrative example, the investment allocation result provides some insights and managerial implications into various sustainable supplier development investment and the performance outcomes. The model here mainly focuses on the estimated SSDP effectiveness values. It does not calculate the optimal total amount of investment that ought to be made in selected SSDPs. It prioritizes SSDPs for investment and indicates the proportion of the amount available that should be allocated to the selected SSDPs. SSDP 13–16, which are always selected for investment allocation for the entire range of \(\lambda\) are all practices of trust relationship. Not only that, but SSDPs 13 and 14, which refer to consistent sustainable goals and competent and effective in interactions, are always allocated the maximum proportion of the investment. For the company in our example, the trust relationship efforts will lead to greater performance improvements than other efforts. These managers feel that the company is still in the preliminary stages of supplier development and should first establish sound trust relationships with the suppliers. The matter of trust and support in business situations is very important in China. In many situations, however, trust may already be present, as the Guanxi relationship plays a large role (Tsang, 1998). It is felt that given these existing cooperative networks, building of trusting relationship with the suppliers would be easiest. In this scenario, although the performance level of the SSDP 01, 02 and 04 is the best, nothing is investment from them because of the low level relatiaonship of them lead to the not better effectiveness outcome. Although we set the parameter \(\omega\) of the relationship to a very small number 0.01, the interdependency among SSDPs still plays a very important role. It also proves that the SSDPs selection and investment allocation problem must be considered in inter-relationship to each other.

7.3 Methodology implications

An important contribution made by the methodology proposed in this paper can be highlighted by considering Table 5, which shows the effectiveness of each SSDP measured on an individual basis. Simply examining the table, one may draw the conclusion that SSDPs 01, 02, and 04 are the best suited for investment since they deliver higher performance. Our methodology, however, takes into account not only the individual performance, but it also considers and the interdependency among the SSDPs and finds the combined net effective impact. When such an impact is considered, we get entirely different set, SSDPs 13 to 16, provide the best outcome for investment.

We have proposed some resourceful improvements to the NK model, which may make the modified method even more useful in many areas of its application. The components of a system generally assume two discrete states (although the original method allows for more than 2). In the improvement proposed in the paper we allow each component to assume any continuous value greater than or equal to 0 by using the \(x_{i}\) variable for each component i as seen in Eq. 3. The DEMATEL method is used to account for interdependency among the components. This intermediate step allows for simple estimation of individual effectiveness of SSDPs without complications of impact of interdependency among them. Lastly, our use of term \(\omega /x_{i}\) in Eq. 3, for example, allows the model user additional flexibility in assigning weights to the performance of the components. All these modifications in the NK method make it more versatile.

Another important consideration is whether the highest peak among all the peaks on the hypersurface, that is, whether the optimum reached is indeed the global optimum. We check for such an optimum by starting at different vertex (in step 5, Fig. 1) and see if we reach the same optimum point.

Our integrated methodology did not experience the full impact of higher values of K due to the maximum investment constraints in MOLP. As described earlier, the results are the same for K > 2 in Table 7. In a pure straightforward application of the NK model, however, higher values of K would increase the occurrence that a local optimum was reached. All neighbor vertexes have lower performance values thus further improvement in performance (or fitness) is impossible. In these cases, it is possible to use a different vertex selection strategy and make a neighbors’ neighbor or a two-level jump. In such a jump two SSDPs are randomly changed instead of just one (steps 9a, 9b in Fig. 2). In our situation, this additional step was not warranted.

8 Conclusions

SSD has recently received considerable attention in supply chain management literature. Many organizations consider a well-designed and implemented SSD plan as an important tool that contributes greatly to overall competitiveness. Selection and allocation of investments to SSDPs is a complex problem. This is a multi-criteria decision problem that includes both qualitative and quantitative factors, which are often assessed with imprecise data and require subjective judgments. Our study examines this problem to provide guidance to organizations to enable them to effectively evaluate and implement SSDPs; seeking the best, or at least better, possible results.

This paper presents a comprehensive optimizing model, which integrates the DEMATEL method, the NK model, and MOLP model, for solving SSDPs selection and investment allocation decision problem, while considering both the economic and the environmental performance. The model is applied to a real-world situation and management implications are explored. Analysis of managerial implications shows that the proposed approach provides a systematic and effective decision tool for supply chain managers and practitioners. The result of the sensitivity analysis for varying parameters indicated that there are trade-offs and conflicts among decision variables and the performance of the system. The data required are easy to obtain and the methodology is rather straightforward to use making it suitable as part of a decision support system for practitioners. The framework presented in this paper can easily be extended to analyze other managerial decision-making problems that present complex interactions among components of a system.

We used subjective evaluation of SSDPs effectiveness based on the opinions of four managers in the organization. Although these managers were experienced experts in their field, some objective data based on historical performance of the suppliers in combination with expert evaluation would be valuable. This additional data would require an organization to maintain data bases on many aspects of the suppliers’ operations. We also should discuss the theory of decision-making process from the perspective of behavior decision, includes decision-maker behavior characteristics, prospect theory, regret theory, and so on. Application of fuzzy or grey methodologies would be another avenue to handle subjectivity of the collected data.

The framework we have built is based on the practical activities of both parties and lacks the relevant advanced technologies. Under the fourth industrial revolution, blockchain, artificial intelligence, the Internet of Things and other new generation of information technologies have attracted more and more attention. In future research, these disruptive technologies and related capabilities should be included in this framework, which extend the relational view. It will be interesting to see to what extent those concerns are similar to the concerns in the fourth industrial revolution. We have provided some directions, which we hope will foster further research in this important area.

We also believe that the methodology can be applied to a number of other settings where multiple criteria and complex relationships exist amongst programmatic selections. Investigating various applications of the general methodology can further determine its strengths and weaknesses, as well as its flexibility. Given the importance of supply chain sustainability and some of its complexities, we felt that this would be a good initial application.