Minimizing the makespan for the two-machine flow shop scheduling problem with random breakdown

Abstract

This paper studies a two-machine flow shop scheduling problem with availability constraints due to a breakdown on the first machine. The starting time of the breakdown is considered stochastic and follows a known probability distribution. A service-level constraint is introduced to model the guarantee with which the obtained schedule takes into account the stochastic nature of the breakdown’s starting time. The objective is to find a solution that minimizes the makespan while satisfying the desired service level. The studied problem is strongly NP-hard. We develop two mixed integer linear models that linearize the non-linear model. Using interval modeling of the breakdown, we propose lower bounds and a valid inequality that are used to strengthen both models. When the lower bounds and the valid inequality are applied, the performance of both models is greatly improved by reducing the gap and reaching optimality for more instances. We also introduced two heuristics that exploit the proposed interval modeling. The computational results indicate that both models are able to reach optimality for the 10-job instances. Moreover, the comparisons results between both models with the two heuristics showed their effectiveness.

1 Introduction

The deterministic scheduling problem consists in finding a job schedule which minimizes an objective function. Scheduling has been mostly investigated for the deterministic cases, in which all parameters are known in advance. Nevertheless, in real-world situations, events are frequently subject to uncertainties that can affect the decision-making process. Thus, it is important to study scheduling under uncertainties. Machine scheduling is subject to various disturbances deriving from data uncertainty and/or unexpected events.

Uncertainties can be due to several factors such as processing times (job processing times are random and follow a probability distribution function) and breakdowns (necessary time to repair a machine). There are three kinds of methods to deal with the uncertainties in scheduling (Aytug et al. 2005): the completely reactive scheduling, the predictive-reactive scheduling and the robust scheduling. In the completely reactive scheduling, no predictive schedule is generated before production. Once a machine becomes free, the job to be processed will be determined online according to priority dispatching rules. In the predictive-reactive scheduling, a predictive schedule is first generated to optimize some measure of performance without considering possible disruptions, and then the predictive schedule is rescheduled to maintain feasibility or improve performance when uncertainties occur during the execution. In the literature, we can identify two types of rescheduling methods: heuristic (Fahmy et al. 2009) and the metaheuristic algorithms (Hasan et al. 2011; Iwona and Bożena 2017; Sreekara Reddy et al. 2018). The methodology of robust scheduling can be applied to control the uncertainties, which generates predictive schedules that are insensitive to uncertainties. The robustness is used to indicate the insensitivity of the performance measure (for example makespan) to uncertainties.

Gourgand et al. (2000) and González-Neira et al. (2017) provided a structured review of stochastic scheduling according to two sources of uncertainties: processing times and machine breakdowns. Processing times have been considered to be random in several works. Portougal and Trietsch (2006) and Dauzère-Pérès et al. (2008) considered them probabilistic, Ng et al. (2009) and Sotskov et al. (2011) generated them in intervals whereas (Temİz and Erol 2004) generated them as fuzzy data. The first review of random processing times in scheduling problems can be found in Gourgand et al. (2000). Allahverdi and Mittenthal (1995) proposed a dominance rule based on Johnson’s rule to minimize the expected makespan for a two-machine flow shop scheduling problem. Mirabi et al. (2013) considered the random breakdown for a two-stage hybrid flow shop scheduling where the repair time is constant. Each machine may break down after processing each job and the probability of breakdown depends on the type of the job and the complexity of the operation.

Dauzère-Pérès et al. (2008) introduced the notion of service level in stochastic scheduling. The authors proposed two interesting research directions considering service levels: (1) finding a service level for a given schedule; and (2) finding a schedule that optimizes a service level. Inspired by the service level in lot sizing problems with backlogging, it can also be considered as a robust scheduling approach to generate a schedule insensitive to uncertainties under a desired value provided by decision makers.

In this paper, we consider that the uncertainty is related to the machine breakdown’s starting time in the case of a two-machine flow shop scheduling problem. In particular, we assume that the starting time of the breakdown on the first machine is not known in advance and derive thus a service level constraint to be satisfied. Processing times, however, are assumed deterministic. We define the service level in our problem as the guarantee with which the objective function of schedule is smaller (or larger) than (or equal to) a given value. We are inspired by studies cited before for the case of random processing times in order to introduce a new problem which, to the best of our knowledge, has never been introduced before.

We define this new problem as the stochastic scheduling problem under random unavailability due to a breakdown’s starting time on the first machine. The processing times are assumed deterministic. The objective is to minimize the makespan under a given service level. Several studies have considered the unavailability on the flow shop scheduling: Allaoui et al. (2006); Benttaleb et al. (2018, 2019); Hnaien et al. (2015); Kubzin et al. (2009); Lee (1997, 1999); Yang et al. (2008). All these works considered the deterministic case, i.e., the starting time and the duration of the unavailability are known in advance.

The contributions of this paper are fourfold. First, we introduce a new two-machine flow shop scheduling problem with breakdowns. The starting time of the breakdown is considered as a discrete random variable with a known probability distribution and the duration is deterministic and known. Moreover, a service level constraint has to be satisfied. Second, we model the problem using chance-constrained programming model and provide a linearization to obtain two mixed integer programs. The first is based on binary variables that limit the breakdown’s starting time whereas the second is based on interval modeling that allows to choose the best interval for the breakdown’s starting time. Third, we propose two heuristics that exploit the proposed interval modeling. Finally, we introduce a valid inequality and lower bounds and show that they greatly improve the performance of both models.

The remainder of the paper is as follows. In Sect. 2, we describe the problem and introduce the notations. In Sect. 3, the developed methods are presented. Section 4 is devoted to the computational results where we evaluate the effectiveness of the proposed methods. Conclusion and perspectives are reported in Sect. 5.

2 Problem description

We introduce the following notations (see Table 1):

Table 1 Notations

The considered problem can be stated as follows: We have a set of N independent jobs $i = {1,\ldots , N}$ to be performed on two machines. Each job i has to be processed first on machine 1 then on machine 2. Its corresponding processing time on machine m is $p_{i}^{m}$. Each machine m can perform only one job at a time. The first machine is considered unavailable during the period ($s^1$, $s^1+g^1$) due to a corrective maintenance. We assume that the preemption of an operation is not allowed. We also assume that jobs have to be performed under the non-resumable case (nr): a job has to be restarted if it was interrupted by a machine breakdown. The objective is to find a schedule that minimizes the makespan under a desired service level $1-\alpha$.

Fig. 1

An illustrative example of the probabilities of the different starting times of the breakdown

The interval of possible starting times of the breakdown is considered to be $s^1 \in \{L,\cdots ,U\}$. Given this interval (see Fig. 1), each possible starting time has a probability. In this example, the breakdown can start at $s^1 = 5$ with a probability of 0.2, at $s^1 = 6$ with a probability of 0.1 and at $s^1= 10$ with a probability of 0.1. When the desired service level is 0.8 ($1-\alpha = 0.8$), the obtained schedule must take into account all possible starting times such that the sum of their probabilities is greater or equal to the service level. For example, sets of starting times {5, 6, 7, 8, 9} and {6, 7, 8, 9, 10} satisfy the service level, among others.

$$\begin{aligned} \sum _{k = 5}^{9} Pr(s^1 = k) \ge 0.8 \\ \sum _{k = 6}^{10} Pr(s^1 = k) \ge 0.8 \end{aligned}$$

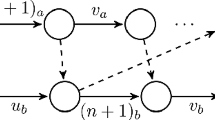
According to the above assumptions, the considered problem is denoted $F_2| nr-a(1), L\le s^1\le U| C_{max}$ (see Fig. 2), where nr (non-resumable case) and a(1) the availability constraint in first machine.

Fig. 2

$F_2| nr-a(1), L\le s^1\le U| C_{max}$

3 Developed methods

In this section, firstly, we present a mixed integer programming ($M_1$) model for solving optimally the problem. The second model ($M_2$) exploits the interval modeling that will be presented in Sect. 3.2. Each of these models is described below.

Property 1 We assume that $\displaystyle \sum \nolimits _{i=1,\ldots ,N}p_{i}^1>L$. For otherwise Johnson’s rule will be optimal.

3.1 The chance constrained programming model

In the following, the non-linear formulation of $F_2| nr-a(1), L\le s^1\le U| C_{max}$ is presented. We consider the following decision variables:

$$\begin{aligned} x_{i,j}= & {} \left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ job } j \text{ is } \text{ scheduled } \text{ immediately } \text{ after } \text{ job } i \text{ in } \text{ a } \text{ sequence } \\ 0 &{} \text{ otherwise. } \end{array} \right. \\ y_i= & {} \left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ job } i \text{ is } \text{ scheduled } \text{ before } \text{ breakdown } \\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

$C_{max}$: the maximum completion time (makespan)

$c_{i}^{m}$: the completion time of the job i on machine m

The starting time of the breakdown $s^1$ is a discrete random variable. The uncertainty of the breakdown’s starting time can be handled in the mathematical model by specifying a confidence level ($1 - \alpha$), where $\alpha \in [0,...,1]$ represents the threshold imposed for probabilistic constraints’ violation. By considering the defined decision variables and data parameters (see Table 1) introduced above, a chance-constrained programming model is expressed as follows:

$$\begin{aligned}&Min ~~~ C_{max} \end{aligned}$$

(1)

$$\begin{aligned}&c_{i}^1 \ge p_{i}^1 \ \quad \forall i=1,...,N \end{aligned}$$

(2)

$$\begin{aligned}&c_{i}^2 - c_{i}^1 \ge p_{i}^2\ \quad \forall i=1,...,N \end{aligned}$$

(3)

$$\begin{aligned}&Pr\left\{ \begin{array}{rl} c_{i}^1 - M \cdot (1 - y_{i}) \le s^1\ \forall i=1,...,N \\ c_{i}^1 +M \cdot y_{i} \ge s^1+g^1\ \forall i=1,...,N \end{array} \right\} \ge 1-\alpha \end{aligned}$$

(4)

$$\begin{aligned}&c_{j}^m - c_{i}^m +M \cdot (1 - x_{ij}) \ge p_{j}^m\ \quad \forall i,j=1,...,N; j< i; \forall m=1,2 \end{aligned}$$

(5)

$$\begin{aligned}&c_{i}^m - c_{j}^m + M \cdot x_{ij} \ge p_{i}^m\ \quad \forall i,j=1,...,N; j<i; \forall m=1,2 \end{aligned}$$

(6)

$$\begin{aligned}&C_{max}-c_{i}^2 \ge 0 \ \quad \forall i=1,...,N \end{aligned}$$

(7)

$$\begin{aligned}&C_{max}\ \text{ and } \ c_{i}^m \text{ integer } \quad \forall i=1,...,N, \forall m=1,2 \end{aligned}$$

(8)

$$\begin{aligned}&x_{ij}, y_{i}\in \{0,1\} \quad \forall i,j=1,...,N \end{aligned}$$

(9)

The objective is to minimize $C_{max}$ (see Constraint (1)). Constraints (2) specify that the completion time of job i is greater than or equal to its processing time. Constraints (3) state that the completion time of job i on machine 2 is not earlier than its completion time on machine 1 plus its processing time on machine 2. Constraint (4) ensures that the completion time of jobs before unavailability never exceed $s^1$. Otherwise, if it is scheduled after unavailability period, it specifies that the completion time of job i is greater than or equal to $s^1+g^1$. Constraints (5) and (6) ensure that only one job can be processed at the same time. Constraints (7) guarantee that the makespan is greater than or equal to the completion time of each job on machine 2. Constraints (8) define $C_{max}$ and $C_{i}^{m}$ as integer variables. Constraints (9) set up the binary restrictions for $x_{i,j} \text{ and } y_i$.

3.2 Modeling the breakdown starting times using intervals

The desired service level is enforced in $M_1$ using Constraint (4). We note that, to satisfy the desired service level, a set of breakdown’s starting times must be selected. Without loss of generality, we consider the example of Fig. 1 that we depicted in Fig. 3. We consider that the machine breakdown duration is 3 units of time (i.e. $g^1 = 3$).

When the service level to be satisfied is 0.8, one can choose different sets of starting times. A first choice can be the set $A_1$ of starting times $A_1 = \{5, 6, 7, 9\}$. Another choice would be set $A_2 = \{6, 7, 8, 9, 10\}$. Other choices of sets can also be made.

Fig. 3

The different starting times of the breakdown when $A_1$ is considered

Suppose that we choose $A_1$. This choice means that the schedule is valid for any starting time $s^1 \in A_1$. Therefore:

$$\begin{aligned} 5 \le s^1 \le 9. \end{aligned}$$

A feasible schedule must thus consider that the first machine is unavailable to process any job within the interval [5, 12]. It is important to notice that, even if starting time 8 is not considered and cannot be taken by $s^1$, the schedule has to take into account starting time 8 because starting time 9 must also be considered.

In the sequel, we consider that any set of different starting times is represented by an interval where the lower limit is the smallest starting time and the upper limit is the biggest starting time. Our two mathematical models exploit this modeling that allows to better represent the problem.

3.3 First mixed integer linear model: $M_1$

Finding the optimal solution that takes into account the breakdown can be transformed to a problem where one must find the best sequence of jobs and the interval that minimize the makespan and satisfy the desired service level. The proposed non-linear probabilistic mathematical model must be linearized in order to solve the problem using mixed integer programming. Using interval modeling, we linearize constraint (4) using the binary variables $\overline{z_{k}}$ and $\underline{z_{k}}$ and the integer variables $I_{min}$ and $I_{max}$ defined as follows:

$$\begin{aligned} \underline{z_k}= & {} \left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ the } \text{ lower } \text{ limit } \text{ of } \text{ the } \text{ chosen } \text{ interval } \text{ is } L+k \\ 0 &{} \text{ otherwise. } \end{array} \right. \\ \overline{z_k}= & {} \left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ the } \text{ upper } \text{ limit } \text{ of } \text{ the } \text{ chosen } \text{ interval } \text{ is } L+k \\ 0 &{} \text{ otherwise. } \end{array} \right. \\ I_{max}= & {} L + \sum _{k=0}^{U-L} k \overline{z_{k}} \\ I_{min}= & {} L + \sum _{k=0}^{U-L} k \underline{z_k} \end{aligned}$$

Integer variables $I_{min}$ and $I_{max}$ represent the lower and the upper limits of the chosen interval respectively.

In this manner, constraint (4) can be rewritten by the following deterministic constraints (4.1) to (4.9).

Proposition 1

The probabilistic constraint (4) can be expressed by the following linear constraints:

Proof

Constraint (4) can be rewritten as follows:

$$\begin{aligned}&Pr\left\{ \begin{array}{rl} c_{i}^1 - M \cdot (1 - y_{i}) \le s^1 \le c_{i}^1 +M \cdot y_{i}-g^1\ ; \forall i=1,...,N \end{array} \right\} \ge 1-\alpha \nonumber \\&Pr\left\{ \begin{array}{rl} \max \limits _{i=1,...,N} \left( c_{i}^1 - M \cdot (1 - y_{i}) \right) \le s^1 \le \min \limits _{i=1,...,N} \left( c_{i}^1 +M \cdot y_{i}\right) -g^1\ \end{array} \right\} \ge 1-\alpha \nonumber \\&\sum _{k=\max \limits _{i=1,...,N} \left( c_{i}^1 - M \cdot (1 - y_{i}) \right) }^{\min \limits _{i=1,...,N} \left( c_{i}^1 +M \cdot y_{i}\right) -g^1}Pr(s^1 =k) \ge 1-\alpha \end{aligned}$$

(10)

Let us introduce the auxiliary integer variables $I_{max}$ and $I_{min}$. Equation (10) can be replaced by the following constraints:

$$\begin{aligned}&\sum _{k=I_{min}}^{I_{max}}Pr(s^1 =k) \ge 1-\alpha \end{aligned}$$

(11)

$$\begin{aligned}&I_{max} \le c_{i}^1 +M \cdot y_{i}-g^1 \ \quad \forall i=1,...,N \end{aligned}$$

(12)

$$\begin{aligned}&I_{min} \ge c_{i}^1 - M \cdot (1 - y_{i}) \ \quad \forall i=1,...,N \end{aligned}$$

(13)

Constraints (11) can linearized as follows:

$$\begin{aligned} \sum _{k=I_{min}}^{I_{max}}Pr(s^1 =k)&= F(I_{max}) - F(I_{min}) + Pr(s^1 = I_{min}) \\&= F(L + \sum _{k=0}^{U-L} k \overline{z_{k}}) - F (L + \sum _{k=0}^{U-L} k \underline{z_{k}}) + Pr(s^1 = L + \sum _{k=0}^{U-L} k \underline{z_{k}}) \\&=\sum _{k=0}^{U-L} F(L+k) (\overline{z_{k}} - \underline{z_{k}}) + P(s^1 = L+k) \underline{z_{k}} \end{aligned}$$

Knowing that the probability of starting times outside interval [L, U] is equal to zero, Constraint (4) can be linearized as follows:

$\square$

The obtained linearized model $M_1$ is given by the following:

$$\begin{aligned}&Min ~~~ C_{max} \end{aligned}$$

(14)

$$\begin{aligned}&c_{i}^1 \ge p_{i}^1 \ \quad \forall i=1,...,N \end{aligned}$$

(15)

$$\begin{aligned}&c_{i}^2 - c_{i}^1 \ge p_{i}^2 \ \quad \forall i=1,...,N \end{aligned}$$

(16)

$$\begin{aligned}&\sum _{k=0}^{U-L} \left( F(L+k) (\overline{z_{k}} - \underline{z_{k}}) + P(s^1 = L+k) \underline{z_{k}}\right) \ge 1-\alpha \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{k=0}^{U-L} \overline{z_k} = 1 \quad \end{aligned}$$

(18)

$$\begin{aligned}&\sum _{k=0}^{U-L} \underline{z_k} = 1 \end{aligned}$$

(19)

$$\begin{aligned}&I_{max} = L + \sum _{k=0}^{U-L} k \overline{z_k} \end{aligned}$$

(20)

$$\begin{aligned}&I_{min} = L + \sum _{k=0}^{U-L} k \underline{z_k} \end{aligned}$$

(21)

$$\begin{aligned}&I_{max} \le c_{i}^1 +M \cdot y_{i}-g^1-p_{i}^{1} \ \quad \forall i=1,...,N \end{aligned}$$

(22)

$$\begin{aligned}&I_{min} \ge c_{i}^1 - M \cdot (1 - y_{i}) \quad \forall i=1,...,N \end{aligned}$$

(23)

$$\begin{aligned}&c_{j}^m - c_{i}^m + M \cdot x_{ij} \ge p_{j}^m\ \quad \forall \quad i,j=1,...,N; j< i; \forall m=1,2 \end{aligned}$$

(24)

$$\begin{aligned}&c_{i}^m - c_{j}^m + M \cdot (1 - x_{ij}) \ge p_{i}^m\ \quad \forall \quad i,j=1,...,N; j<i; \forall m=1,2 \end{aligned}$$

(25)

$$\begin{aligned}&C_{max}-c_{i}^2 \ge 0 \ \quad \forall i=1,...,N \end{aligned}$$

(26)

$$\begin{aligned}&C_{max}, I_{max}, I_{min}, \text{ and } \ c_{i}^m, \text{ integer } \ \ \ \quad \forall i=1,...,N, \forall m=1,2 \end{aligned}$$

(27)

$$\begin{aligned}&x_{ij}, y_{i}\in \{0,1\} \ \ \ \forall i,j=1,...,N \end{aligned}$$

(28)

$$\begin{aligned}&\overline{z_{k}}, \underline{z_k} \in \{0,1\} \ \ \ \forall k=0,...,U-L \end{aligned}$$

(29)

Constraints (14)–(16) and (24)–(26) are equivalent to constraints (1)–(3) and (5)–(9) respectively. Constraints (17)–(23) allow to linearize constraint (4).

3.4 Interval dominance

As we have seen before, the optimal schedule will contain an interval in which the breakdown arrives. We denote a feasible interval $I_v$ as the interval of starting times that satisfies the desired service level. $I_v$ is defined as follows:

$$\begin{aligned} I_v = \{x_v \in \{L, \cdots , U\} \quad | \quad \sum _{x_v} Pr(s^1 = x_v) \ge 1 - \alpha \} \end{aligned}$$

Proposition 2

Let $I^*$ be the chosen interval in which the breakdown arrives (i.e. $s_1 \in I^*$) in the optimal schedule. $I^*$ has a minimum length $L_{min}$ that can be computed according to the probability of the different starting times:

$$\begin{aligned} L_{min} = \min _{v} |I_v| \end{aligned}$$

Proof

We will prove this valid inequality by absurdity. Assume for the purpose of contradiction that there exists an interval $I'$ that is chosen in the optimal schedule and such that $|I'| < L_{min}$. By definition, if such interval exists, it is not a feasible interval that satisfies the desired service level. $\square$

Among all the feasible intervals, not all of them are of interest. Indeed, some intervals are dominated and do not need to be considered.

Definition 1

$I_v$ dominates $I_{v'}$ if they both satisfy the service level and $I_v \subset I_{v'}$.

We define thus non-dominated intervals as the intervals with the minimum length that are not included in other intervals. We show that it is sufficient to only consider the non-dominated intervals. We denote $\mathcal {I}$ the set of non-dominated intervals.

Proposition 3

$\forall \sigma$: $C_{max}(\sigma , I_v) \le C_{max}(\sigma , I_{v'})$ if $I_v$ dominates $I_{v'}$.

Proof

Since $I_v$ and $I_{v'}$ both satisfy the service level and $I_v \subset I_{v'}$, the length of the machine unavailability is smaller in the case of $I_v$ compared to that of $I_{v'}$. Therefore, from constraints (22) and (23), $I_{v'}$ generates more constraints on $\sigma$ than $I_v$ implying that the feasible region of $\sigma (I_{v'})$ is a subset of the feasible region of $\sigma (I_v)$. Therefore, $C_{max}(\sigma , I_v) \le C_{max}(\sigma , I_{v'})$. $\square$

Proposition 3 is a powerful property that can be exploited to derive a valid inequality for model $M_1$.

Proposition 4

Non-dominated intervals are solely considered for feasible solutions. Moreover, the following valid inequality can be added considered:

$$\begin{aligned} VC: \underline{z_k} = \left\{ \begin{array}{ll} \overline{z_{k'}} &{}\quad \forall I = [k, k'] \in \mathcal {I} \\ 0 &{}\quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

(30)

Proof

According to Proposition 3, dominated intervals have a bigger makespan compared to the non-dominated intervals’ makespan. Since $\underline{z_{k}}$ and $\overline{z_{k}}$ are binary variables that are used for the lower limit and the upper limit of the chosen interval, they are equal to one only for the limits of the chosen interval. For all other starting times, they must be equal to zero. $\square$

Proposition 5

When $F_2| nr-a(1), L\le s^1\le U| C_{max}$ has a unique non-dominated interval, the considered problem is equivalent to the $F_2 | nr-a(1) | C_{max}$. Moreover, an optimal solution can be obtained by partitioning the jobs into two subsets assigned before and after the breakdown respectively where each subset follows the Johnson’s rule (Lee 1999; Hnaien et al. 2015).

Proof

When $F_2| nr-a(1), L\le s^1\le U| C_{max}$ has a unique non-dominated interval, the machine is considered as unavailable during the interval and the execution of the breakdown. Therefore, the starting time of the breakdown is known (beginning of the interval). In this case, the breakdown can be considered as a planned maintenance as in $F_2 | nr-a(1) | C_{max}$. Lee (1999) proved that an optimal solution can be obtained for $F_2 | nr-a(1) | C_{max}$ by partitioning the jobs into two subsets assigned before and after the breakdown respectively where each subset follows the Johnson’s rule. $\square$

Corollary 1

Given multiple non-dominated intervals $I_v \in \mathcal {I}$ and their corresponding optimal solutions $\sigma _v$ (where the obtained makespan is denoted $C_{max}^{\sigma _v}$), the makespan of the optimal solution of $F_2| nr-a(1), L\le s^1\le U| C_{max}$ is given by $\underset{v}{\min } (C_{max}^{\sigma _v})$.

3.5 Second mixed-integer optimization model: $M_2$

Propositions 3, 4 and 5 can also be used to introduce another mixed integer optimization model. Since only non-dominated intervals should be considered and their length is known in advance (using a preprocessing based on Proposition 3), one can transform the problem to a choice of the best non-dominated one. As such, we introduce a binary variable $\lambda _v$ defined as follows:

$$\begin{aligned}&\lambda _v = \left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ interval } I_v = [\underline{I_v}, \overline{I_v}] \in \mathcal {I} \text{ is } \text{ chosen } \\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

(31)

$$\begin{aligned}&Min ~~~ C_{max} \end{aligned}$$

(32)

$$\begin{aligned}&c_{i}^1 \ge p_{i}^1 \ \quad \forall i=1,...,N \end{aligned}$$

(33)

$$\begin{aligned}&c_{i}^2 - c_{i}^1 \ge p_{i}^2\ \quad \forall i=1,...,N \end{aligned}$$

(34)

$$\begin{aligned}&\sum _{I_v \in \mathcal {I}} \lambda _v = 1 \end{aligned}$$

(35)

$$\begin{aligned}&\sum _{I_v \in \mathcal {I}} \overline{I_v} \cdot \lambda _v \le c_{i}^1 +M \cdot y_{i}-g^1-p_{i}^{1} \ \quad \forall i=1,...,N \end{aligned}$$

(36)

$$\begin{aligned}&\sum _{I_v \in \mathcal {I}} \underline{I_v} \cdot \lambda _v \ge c_{i}^1 - M \cdot (1 - y_{i}) \ \quad \forall i=1,...,N \end{aligned}$$

(37)

$$\begin{aligned}&c_{j}^m - c_{i}^m + M \cdot x_{ij} \ge p_{j}^m\ \quad \forall i,j=1,...,N; j< i; \forall m=1,2 \end{aligned}$$

(38)

$$\begin{aligned}&c_{i}^m - c_{j}^m + M \cdot (1 - x_{ij}) \ge p_{i}^m\ \quad \forall i,j=1,...,N; j<i; \forall m=1,2 \end{aligned}$$

(39)

$$\begin{aligned}&C_{max}-c_{i}^2 \ge 0 \ \quad \forall i=1,...,N \end{aligned}$$

(40)

$$\begin{aligned}&C_{max}\ \text{ and } \ c_{i}^m \text{ integer } \ \ \ \quad \forall i=1,...,N, \forall m=1,2 \end{aligned}$$

(41)

$$\begin{aligned}&x_{ij}, y_{i}, \lambda _v\in \{0,1\} \ \ \ \quad \forall i,j=1,...,N \end{aligned}$$

(42)

Constraints (32)–(34) and (38)–(42) are the same constraints used in $M_1$. Constraint (35) ensures that a single non-dominated interval is chosen. Constraints (36) and (37) ensure that no job is scheduled while the machine is unavailable due to the breakdown. These constraints are equivalent to constraints (17)–(23) in $M_1$.

3.6 Lower bounds

The lower bounds used in Hnaien et al. (2015) for the two-machine flow shop scheduling problem with preventive maintenance can be adapted to our problem while taking into account the minimum length of an interval.

Theorem 1

Let LB1 and LB2 be two lower bounds for the problem $F_2|nr-a(1), L\le s^1\le U| C_{max}$ and defined as follows:

$$\begin{aligned} LB1&= \sum _{i \in N}(p_{i}^1) + L_{min} + g^1 + \min _{j \in N}p_{j}^2 \end{aligned}$$

(43)

$$\begin{aligned} LB2&= \sum _{i \in N}(p_{i}^2) + \min _{j \in N}p_{j}^1 \end{aligned}$$

(44)

Proof

LB1 is an extension of the lower bound developed for the deterministic case (Hnaien et al. 2015). Since no schedule can take place during the interval of starting time, this period should also be considered in the schedule (i.e. $C_{max}$). Since $L_{min}$ represents the length of the shortest interval that can be chosen by any schedule, we add it to the lower bound. LB2 is a classical lower bound for $F_2 || C_{max}$. $\square$

3.7 Heuristic approaches

We propose two heuristics based on Johnson’s rule. These heuristics are derived by exploiting previous works of Lee (1999) and Hnaien et al. (2015) and Propositions 3, 4 and 5.

3.7.1 Interval Johnson order heuristic (IJO)

This heuristic is based on Johnson’s rule and Corollary 1. The pseudo-code of the heuristic is given in Algorithm 1. The heuristic starts by obtaining a sequence, denoted $\sigma$, according to Johnson’s order for a problem instance $\pi$. Next, a schedule is obtained by considering Johnson’s order and the unavailability on the first machine, given by an interval $I_v = [L_v, U_v] \in \mathcal {I}$. The obtained makespan is denoted $C_{max}^{\sigma _v}$. The heuristic chooses the schedule providing the minimium makespan.

3.7.2 Two-partition interval Johnson order (TPIJO)

This heuristic is derived from the heuristic proposed by Hnaien et al. (2015). As for IJO, the heuristic is applied for each non-dominated interval. The pseudo-code of the heuristic is given in Algorithm 2. The heuristic starts by building two sets $S_1$ (jobs having $p_{i}^1\le p_{i}^2$) and $S_2$ (jobs having $p_{i}^1 > p_{i}^2$) according to Johnson’s rule. Next, for each interval $I_v$, the HYM procedure proposed by Hnaien et al. (2015) is applied. Two sets are created A and B: set A represents the set of jobs assigned after the breakdown in the first machine and set B represents the set of jobs assigned before the breakdown in the first machine. Jobs in sets $S_1$ and $S_2$ are iteratively assigned to sets A and B according to whether jobs can be assigned before the breakdown or not.

Once the jobs are assigned to sets A and B, they might be an idle time after the jobs in set B on the first machine, since the breakdown can have a late arrival. To avoid such case, jobs of set A that can be inserted before the breakdown are shifted to set B. To determine which jobs to move from set A to set B, two criteria are used: (i) only jobs having a processing time smaller than the idle time and (ii) jobs are ordered in the Longest Processing Time (LPT) first to ensure that the breakdown is covered on the second machine. Once the jobs are shifted to B, the set is then sorted again according to Johnson’s rule.

3.8 An illustrative example

In order to illustrate the proposed study, an example is provided. Consider a 5-job scheduling problem with breakdown’s starting times in [6, 10] (i.e. $L=6$ and $U=10$). The breakdown’s duration $g^1=4$ and the jobs processing times are listed in Table 2. We use different probability distributions of the breakdown’s starting times. These probability distributions are truncated over the interval of the breakdown’s starting times. For this, we use the SciPy python library (Virtanen et al. 2020) to simulate the truncated distributions using the process proposed by Nadarajah and Kotz (2006). Starting times of the breakdown are assumed to follow the same distribution per instance where $\sigma ^2 = 2$ represents the variance, $\lambda _p=8$ denotes the rate parameter of the Poisson distribution, and ($k=1,\lambda _w=8$) are the (shape, scale) parameters characterizing the Weibull distribution.

Table 2 Jobs processing Time of the illustrative example

Four cases of probability distributions were obtained, based on $10^5$ random samples which follows respectively:

• 1. Uniform distribution:

  $P(s^1=6)$=0.200, $P(s^1=7)$=0.200, $P(s^1=8)$=0.200, $P(s^1=9)$=0.200, $P(s^1=10)$=0.200.

  Therefore, $E(s^1)=8.00$ and $\sigma ^2=2.00$.

• 2. Normal distribution:

  $P(s^1=6)$=0.068, $P(s^1=7)$=0.178, $P(s^1=8)$=0.288, $P(s^1=9)$=0.288, $P(s^1=10)$=0.178.

  Therefore, $E(s^1)=8.329$ and $\sigma ^2=1.343$.

• 3. Poisson distribution:

  $P(s^1=6)$=0.148, $P(s^1=7)$=0.196, $P(s^1=8)$=0.224, $P(s^1=9)$=0.224, $P(s^1=10)$=0.199.

  Therefore, $E(s^1)=8.034$ and $\sigma ^2=1.792$.

• 4. Weibull distribution:

  $P(s^1=6)$=0.252, $P(s^1=7)$=0.223, $P(s^1=8)$=0.197, $P(s^1=9)$=0.174, $P(s^1=10)$=0.153.

  Therefore, $E(s^1)=7.752$ and $\sigma ^2=1.960$.

The optimal solution satisfying the desired service level $1-\alpha$ is presented in Table 3. We can notice that as the service level decreases, the objective function decreases. This is an expected outcome as the service level is directly linked to the length of intervals.

Table 3 Optimal makespan for different distributions and service levels

4 Computational experiments and results

In this section, we present the results of our computational experiments of the two MIP formulations with the proposed lower bounds. The MIP models were coded in the C++ language, compiled using GCC 4.8.5 and solved using Cplex 12.10 solver. The default settings of the solver were used. The test problems were solved using a linux operating system running on an Intel(R) Xeon(R) Gold 5120 CPU @ 2.20GHz and 128GB of memory.

4.1 Problems data

For the experiments, we generated 10 instances for every combinations of parameters as follows:

• The number of jobs N was chosen in (10, 15, 20). For each number of jobs, the processing times on the first and second machines, the lower and upper limits (L, U) of the breakdown’s starting times and $\alpha$ are generated.

• Processing times are randomly generated following a discrete uniform distribution Uniform(1,100).

• In order to have a desired service level higher than $80\%$ ($1-\alpha \ge 0.80$), we generate $\alpha$ as follows: $\alpha \in \{0.05, 0.10, 0.15, 0.20\}$.

• We randomly generate four groups (Gw) of instances where the interval of the breakdown’s starting time varies as follows:

  • $L \in [\frac{w-1}{4}\sum _{i \in N }p_{i}^{1},\frac{w}{4}\sum _{i \in N }p_{i}^{1}[ \quad \quad w \in \{1, 2, 3, 4\}$

  • $U=\frac{w}{4}\sum _{i \in N }p_{i}^{1} \quad \quad \quad \quad \quad \quad \quad w \in \{1, 2, 3, 4\}$.

• The length of the unavailability period $g^1$ is defined as the average of the processing times on the first machine:

  $$\begin{aligned}\displaystyle g^{1}= \lceil *\rceil {\frac{\sum _{\begin{array}{c} i \in N \end{array}} p_{i}^{1} }{N}} \end{aligned}$$

• For each configuration (i.e. a set of parameters [Gw, $\alpha$, N]), ten different instances are randomly generated.

All the instances that have been generated can be found in scheduling.cc.

Fig. 4

The impact of the valid inequality on the average number of intervals for each instance size in Group 2

4.2 Impact of the valid inequality

To demonstrate the effects of the interval reduction obtained using Proposition 4, we display in Fig. 4, for each value of $\alpha$, the number of all possible intervals (I_P), the number of feasible intervals (I_F) and the number of intervals after applying the valid inequality (I_VC) on instances of Group 2. Similar results are obtained for the other groups.

As it can be seen, the number of intervals can be drastically reduced using the valid inequality. Moreover, when $\alpha$ increases, the number of non-dominated intervals increases as well due to the different possibilities that can be taken into account.

4.3 Results of $M_1$

Tables 4 and 5 summarize the results on the different instances solved using $M_1$. Each table is dedicated to two groups. In each table, four blocks that correspond to the values of $\alpha$ provide the average metrics for 10 different instances of a single configuration. Moreover, for each group, each table provides the number of optimal instances (#Optimal instances). The model is evaluated according to the average solver gap (Gap (%)) and the average CPU time (CPU(s)) for the 10 instances. For each configuration, the model is run without lower bounds and valid inequalities (rows “–"), with lower bounds (rows “LBs") and with both lower bounds and valid inequalities (rows “LBs-VC").

The model succeeds in solving all 10-job instances in all groups to optimality. Without taking into account the lower bounds (rows “-"), $M_1$ could not solve to optimality the 15- and 20-job instances and the Gap can exceed 50% for some instances regardless of the group. When taking into account lower bounds $LB_1$ and $LB_2$ (rows “LBs"), the gap is drastically reduced. Moreover, optimality is reached for most 15-job instances and for more than 50% of the 20-job instances.

The impact of the valid inequality VC can clearly be seen in all the results of the models. Indeed, in Group 4, thanks to VC, the number of 20-job instances solved to optimality increased from 14 to 19 instances. In addition, thanks to this valid inequality, the CPU-time has decreased in the majority of instances of all groups.

Table 4 Average metrics of $M_1$ for 10 different instances on Group 1 and Group 2

Table 5 Average metrics of $M_1$ for 10 different instances on Group 3 and Group 4

Table 6 Comparison between the results of $M_1$ and $M_2$ on instances of Group 1

Table 7 Comparison between the results of $M_1$ and $M_2$ on instances of Group 2

Table 8 Comparison between the results of $M_1$ and $M_2$ on instances of Group 3

Table 9 Comparison between the results of $M_1$ and $M_2$ on instances of Group 4

4.4 Comparison between $M_1$ and $M_2$

Tables 6, 7, 8, and 9 summarize a comparison between $M_1$ and $M_2$ on the four groups. We noticed that the models are equivalent when the lower bounds and the valid inequality are not applied. For each model, we only provide the results when the lower bounds and the valid inequality are applied. We recall that the valid inequality is only applied for $M_1$.

To compare the models, we use the same metrics, i.e. the number of optimal instances (# Optimal instances), the average gap (Gap (%)) and the average CPU time (CPU(s)) for each size (10, 15 and 20). We recall that each size comprises 10 instances.

Overall, the models are comparable and obtain similar performances on all groups. However, some differences can be noticed. For Groups 1, 3 and 4, model $M_1$ reaches optimality for a higher number of instances compared to $M_2$. This is not the case for Group 2 where $M_2$ performs better. For Group 2, model $M_1$ reaches optimality for all 15-job instances while model $M_2$ reaches optimality for all 15-job instances except for one.

It is worth noting that both models face greater difficulty for the instances of Group 4. The number of instances solved to optimality in the 15- and 20-job instances is far lower than compared to other groups.

Table 10 Gap (in %) between IJO and TPIJO and models $M_1$ and $M_2$ on all groups

4.5 Comparison of models with IJO and TPIJO heuristics

To better illustrate the results obtained by both models, we compared the best solutions obtained by $M_1$ and $M_2$ to the the solution obtained by IJO and TPIJO. Table 10 presents the average and the maximum gap obtained between the best solutions of $M_1$ and $M_2$ and the two heuristics agregated by the number of jobs. The gap is calculated according to Eq. (45). $S_{heuristic}$ represents the makespan of the solution obtained by the applied heuristic whereas $min(S_{M_1}, S_{M_2})$ represents the best makespan obtained by models $M_1$ and $M_2$. The results are displayed for each $\alpha$ and for each group.

$$\begin{aligned} G(heuristic, M_1/M_2) = \frac{S_{heuristic} - min(S_{M_1}, S_{M_2})}{S_{heuristic}} \end{aligned}$$

(45)

The results do not show the minimum average and the maximum gap as they are always equal to 0. The heuristics manage to reach the solutions obtained by the model for at least one instance for each group and instance size. It is noteworthy that the heuristics never obtained solutions that are better than those of both models. The results also show the effectiveness of the proposed heuristics. On average, the gap with the models does not exceed 5.8%.

Looking at Group 1, TPIJO yields the best results on average. However, the max gap grows for 10-job instances whereas for 15-job and 20-job instances, TPIJO’s max gap is better than IJO’s max gap except for the case when $\alpha = 0.05$ for 20-job instances. For Groups 2, 3 and 4, no dominance can be derived. TPIJO is generally better than IJO on average but some exceptions can be made. As running times are very short (within a second) for both heuristics, practitioners will be able to run both methods and choose the best approach.

5 Conclusions and perspective

This paper introduced a two-machine flow shop scheduling problem with machine breakdown on the first machine. The breakdown’s starting times are assumed to be stochastic and follow a known distribution. We introduced a service-level constraint that provides the guarantee with which the schedule is feasible regardless of the breakdown’s starting time. This constraint is equivalent to the service level in lot sizing problems with backlogging.

We proposed the stochastic mathematical model and provided two linearizations to obtain two mixed integer linear models. Based on interval modeling of the breakdown’s starting times, the first model is strengthened using a valid inequality that reduces the number of intervals to be considered. The second model takes advantage of the interval modeling to choose the best non-dominated interval that minimizes the makespan. Both models are enhanced with two lower bounds that are adapted from the deterministic flow shop scheduling problem. We further introduced two heuristics, Interval Johnson’s Order (IJO) and Two-Partition Interval Johnson Order (TPIJO) that exploit the proposed interval modeling. We tested all approaches on randomly generated instances that were adapted from existing instances in the literature and made them available for future works. Results show that both models are comparable and can be used interchangeably to achieve the best performance. Moreover, we compared the solutions obtained by both models with the two heuristics and showed their effectiveness.

Future research should investigate exact and approximate approaches to solve bigger instances that the models were not able to solve. We only considered a single breakdown on the first machine and the problem can be extended to multiple breakdowns on the first and/or the second machine. Besides, the breakdown duration can be considered to be stochastic or time dependent.