Perishable inventories with random input: a unifying survey with extensions

Abstract

This paper is devoted to the theory of perishable inventory systems. In such systems items arrive and stay ‘on the shelf’ until they are either taken by a demand or become outdated. Our aim is to survey, extend and enrich the probabilistic analysis of a large class of such systems. A unifying principle is to consider the so-called virtual outdating process $\textbf{V}$, where V(t) is the time that would pass from t until the next outdating if no new demands arrived after t. The steady-state density of $\textbf{V}$ is determined for a wide range of perishable inventory systems. Key performance measures like the rate of outdatings, the rate of unsatisfied demands and the distribution of the number of items on the shelf are subsequently expressed in that density. Some of the main ingredients of our analysis are level crossing theory and the observation that the $\textbf{V}$ process can be interpreted as the workload process of a specific single server queueing system.

1 Introduction

Background and motivation The theory of perishable inventory systems (PIS) deals with one of the classical topics of stochastic operations research: items of a certain type arrive at a collecting point from where they are taken away by incoming demands. If an item stays too long it can become unusable due to random deterioration or a predetermined maximum expiration time. The arrival intervals of items as well as those of demands may be random or deterministic, in either case a controller may try to govern them, and arrivals may also occur in batches. The standard real-world example is of course a storage place for commodities, but other applications include blood banks, spot markets for special goods, distribution sites for transplantation organs, or peer-to-peer lending agencies in the internet, where many individual lenders deposit money for a limited period, which can then be borrowed by debtors.

Our aim in this paper is to survey, extend and considerably supplement and enrich the probabilistic analysis of a large class of these PIS. Over the last four decades inventory models of this basic structure were treated in hundreds of articles, textbooks, and monographs. In many examples the system input is generated by replenishment orders of a controller who decides about the timing of the orders and their sizes. The great majority of papers studies optimization problems for this kind of systems, looking for optimal ordering policies; see for example the monograph by Nahmias (2012) and his earlier review (Nahmias, 1982). However, there is a second line of research dealing with PIS with random input (without involvement of a controller) and focusing on their stochastic analysis. That research is surveyed and expanded in this paper.

The survey (Karaesmen et al., 2011) contains a comprehensive section about the papers on PIS with random input that were published until 2011. The authors of the present paper were involved in many of the studies surveyed in Karaesmen et al. (2011) and since 2011 have extended the earlier results in several directions, contributing, jointly with various co-authors, more than 20 publications. This survey provides a unifying presentation of the published material and also develops several new model variants. Our approach also enables us to derive additional results for models studied in the past. In view of space constraints, the presentation of some of the new model variants necessarily is rather concise. We plan to elaborate on these discussions in an extended version of the present paper, accessible as a Eurandom report via https://www.eurandom.tue.nl/pre-prints/.

Even after having restricted ourselves to PIS with random input, there are topics that we largely ignore in order to present a methodologically coherent overview; for those topics we refer   to the valuable survey of Krishnamoorthy et al. (2020). An interesting line of research that will not be touched upon in the following sections is that of perishable inventory systems with common lifetime. In this type of PIS, which was first studied in Lian et al. (2005), it is assumed that all items of a batch of the same age fail at the same time. The topic was taken up by Chakravarthy (2010) and subsequently by Krishnamoorthy and collaborators (see e.g. Krishnamoorthy et al., 2016); several more references can be found in Section 6.2.5.1 of Krishnamoorthy et al. (2020), and a very recent one is Shajin et al. (2022).

Another interesting line of research that we do not discuss in the following sections is that of queueing/inventory systems with positive service times: If a demand arrives and an item is in stock, it may still require a non-negligible amount of time to take that item. Such systems are extensively surveyed by Krishnamoorthy et al. (2020). They sometimes give rise to a product form; often an asymptotic product form for the joint distribution of the number of waiting customers and the number of items in stock, or (cf. Otten et al., 2015 that considers a queueing system in a random environment) the joint distribution of the number of customers and the environment state—where the environment represents the inventory-replenishment structure. Some references in Table 6.1 and Subsection 6.2.1.1 of Krishnamoorthy et al. (2020) on such product form results in queueing-inventory systems also allow perishability; and again see (Shajin et al., 2022).

Finally, we also ignore PIS with retrials of demands. We refer to Section 6.2.4 of Krishnamoorthy et al. (2020) for references to queueing-inventory systems with retrials, and to Ko (2020) for a recent study on this topic with perishability of items.

Motivation The original motivation to consider PIS with external random input (without ordering policies) was formed by blood bank systems in which a random stream of blood donations serves as input and the output consists of satisfied demands, taking away blood units, and outdated blood units. Note that the maximum shelf life (sojourn time) of every blood unit is determined by some external authorities; that is, every country or province has its own health regulations regarding the expiration dates of the blood units. Organ transplantation sites (Boxma et al., 2011a) constitute another application area. Organs are removed from the bodies of just deceased people. In some countries this is possible either after receiving permission from the family or because the deceased had given permission while alive; in others it is mandated by law that every citizen is a potential donor. Both the (usually deterministic) shelf lifetimes of the organs and the random “impatience times” (lifetimes) of the waiting patients are finite. A spot market for perishable goods constitutes another PIS with random input; the flower market in The Netherlands may serve as a colorful example.

Methodology Our main focus is always on the analysis of the stationary (long-run) behavior of the PIS in question, often leading to closed-form expressions for the most relevant performance measures and functionals, or their transforms. The obtained explicit formulas can subsequently be used for numerical optimization of an objective (cost or profit) function. Cost functions usually involve the holding costs of items, which makes it important to study the distribution of the number of items in the system. Cost functions will also typically take into account penalties for unsatisfied demands and for outdatings of items.

Let us denote the above-mentioned number of items that are present in the system (“on the shelf”) at any time t by K(t). In general $\textbf{K} = \{K(t), t \ge 0\}$ is not a Markov process, since at any given time $t_0$ the distribution of $(K(t))_{t \ge t_0}$ usually depends on the evolution of the process before $t_0$ and not just on $K(t_0)$—indeed, the age of the items is important. One could try to use supplementary variables to retain the Markov property, but the resulting process would become too complex even for quite simple PIS. To overcome this difficulty, we now introduce a one-dimensional process that turns out to be Markovian in many PIS.

Let $\textbf{A}=\{A(t):t\in [0,\infty )\}$ where A(t) is the age of the oldest item on the shelf or, if the shelf is empty at time t, A(t) denotes a “negative age”, defined to be minus the time it takes until the next arrival at the shelf after time t. For simplicity assume that items expire at age 1. Then set $V(t)=1-A(t)$; cf. Fig. 1. A little reflection shows that V(t) is the time that would pass from t until the next outdating if no new demands arrived after t. This “virtual” process ${\textbf{V}}= \{V(t), t \ge 0\}$, the so-called Virtual Outdating Process (VOT), is closely related to $\textbf{K}$ provided that any newly arriving demand is always satisfied by the oldest item present, if at all. Indeed, the shelf is empty if and only if the age of the oldest item is negative ($A(t)<0$, so $V(t)>1$), and the number of items on the shelf equals n if and only if $n-1$ items have arrived during the age time interval of the oldest item.

Fig. 1

A typical sample path of the age process $\textbf{A}$ (top panel) and of the VOT process $\textbf{V}$ (bottom panel). $A_n$ ($D_n$) denotes the arrival time of the nth item (demand); $O_1$ denotes the first outdating, and $U_1$ the first unsatisfied demand; it coincides with $D_3$

For all PIS models in this survey $\textbf{V}$ turns out to be a key process. Under certain Poisson-type assumptions ${\textbf{V}}$ is a Markov process and, when the process is stationary, a regenerative process. When its steady-state distribution exists, it is characterized by an integral equation of the Pollaczek–Khintchine type. This integral equation, a Volterra integral equation of the second type, is for all $x \ge 0$ given by

$$\begin{aligned} r(x)f(x) = \int _{0}^{k(x)}\mu (w) [ 1-G\left( L(x)-L(w)\right) ] f(w)\textrm{d}w +f(0)[ 1-G( L(x))]. \end{aligned}$$

(1)

In (1) the function $f(\cdot )$ is the steady-state density of $\textbf{V}$ and the functions $r(\cdot ),L(\cdot ),G(\cdot ),\mu (\cdot )$ and $k(\cdot )$ are specific in every model variant. This equation can be obtained by deriving the Kolmogorov forward equation for the ${\textbf{V}}$ process. Typically one can also obtain it via application of the Level Crossing Theory (LCT) (Brill, 2008; Doshi, 1992). LCT observes and exploits the fact that, for the process ${\textbf{V}}$ in steady state, the long-run average number of downcrossings of any level x per time unit is equal to the long-run average number of upcrossings of that level per time unit.

For several model variants we shall show that the lefthand side of (1) equals the rate of downcrossings of level x, and the righthand side the rate of upcrossings of level x. In particular, we show this in some detail when proving Theorem 3. Solving the integral equation yields the steady-state density $f(\cdot )$ (or its Laplace transform). In several cases, we shall use that result to also determine the steady-state distribution of the number of items on the shelf.

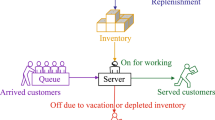
An important observation, suggested by Fig. 1 for the ${\textbf{V}}$ process, is that this process can be interpreted as the workload process of a specific single server queueing system. Here the jumps upward indicate service requirements of arriving customers, and the slope downward reflects the fact that a server is working (in the figure: at a constant speed of one unit of work per time unit). In addition, customers have a patience of length one; they do not enter the system if their waiting time would be larger than one (corresponding to unsatisfied demands). This observation allows us to make use of methods which have been developed, and results which have been obtained, for single server queues. It should be noticed that, in most queueing systems, when the system becomes empty it stays empty until the next arrival (an idle period); the graph for ${\textbf{V}}$ can be viewed as representing the workload in a queue after the idle periods have been removed and the busy periods have been glued together.

Structure of the paper In Sect. 2 we present a model description for a large class of PIS, and we also introduce some preliminary results, including a conservation law for the rate of the satisfied demands that is valid for all model variants. In Sect. 3 we introduce a class of PIS models in which the arrival processes of items and of demands are Poisson processes with rates that depend on the current value of the VOT process. This model is studied in detail in Sects. 3 and 4, along with several variants. In Sect. 5 we globally discuss PIS models in which the arrival process of items, or of demands, forms a renewal process. Section 6 contains a detailed analysis of three such models. Finally, Sect. 7 briefly mentions some model variants and problems which in our view are of considerable interest, but for which we lack the space to discuss them at length. This section also contains some open problems.

2 Model description and preliminaries

We consider a perishable inventory system with infinite storage capacity, in which input and demands are both random. Items arrive at the system according to a point process $\textbf{N}_I:= \{N_I(t), t \ge 0\}$. Each item has the same deterministic usable lifetime, which w.l.o.g. is assumed to be one time unit. Demands arrive according to a point process $\textbf{N}_D:= \{N_D(t), t \ge 0\}$. Upon arrival, a demand removes the oldest item in storage (‘on the shelf’), or leaves unsatisfied if the system is empty (but in Sect. 6.2 we shall also study a model in which demands are willing to wait). An item that has not been taken within one time unit of arrival becomes outdated and must be scrapped. The arrival processes of items and demands are assumed to be independent. We assume for simplicity that the system is empty at time 0.

The process of outdated items is denoted by $\textbf{N}_O:= \{N_O(t), t \ge 0\}$, and the process of unsatisfied demands is denoted by $\textbf{N}_U:= \{N_U(t), t \ge 0\}$. $\textbf{N}_O$ is a filtered process of $\textbf{N}_I$ and $\textbf{N}_U$ is a filtered process of $\textbf{N}_D$.

As will be seen in Theorem 2 below, if both $\textbf{N}_I$ and $\textbf{N}_D$ are Poisson processes, then both $\textbf{N}_O$ and $\textbf{N}_U$ are renewal processes. If $\textbf{N}_I$ is a renewal process but not Poisson, and $\textbf{N}_D$ is a Poisson process, then $\textbf{N}_O$ still is a renewal process but $\textbf{N}_U$ need not be a renewal process.

Let us assume that the following long-run arrival rates exist:

$$\begin{aligned} \begin{array}{c} \lambda \overset{def}{=}\ \lim _{t\rightarrow \infty }\frac{N_{I}(t)}{t} =\lim _{t\rightarrow \infty }\frac{EN_{I}(t)}{t}, \\ \mu \overset{def}{=} \lim _{t\rightarrow \infty }\frac{N_{D}(t)}{t}=\lim _{t\rightarrow \infty }\frac{EN_{D}(t)}{t}, \\ \lambda ^{*}\overset{def}{=} \lim _{t\rightarrow \infty }\frac{N_{O}(t)}{t} =\lim _{t\rightarrow \infty }\frac{EN_{O}(t)}{t}, \\ \mu ^{*}\overset{def}{=} \lim _{t\rightarrow \infty }\frac{N_{U}(t)}{t}=\lim _{t\rightarrow \infty }\frac{EN_{U}(t)}{t}. \end{array} \end{aligned}$$

The limits in the middle are almost-sure limits. $\lambda$ and $\mu$ are the arrival rates of items and of demands, respectively, while $\lambda ^*$ and $\mu ^*$ denote the outdating rate and the rate of unsatisfied demands. In all PIS considered in this paper these rates will be seen to exist due to the underlying regenerative structures.

Now let K(t) be the number of items in the system at time t. Clearly, K(t) is equal to the number of items that have arrived up to t minus the number of items that have left until then, which in turn is the sum of the number of outdatings and that of satisfied demands up to t. Hence,

$$\begin{aligned} K(t)=N_{I}(t)-[N_{O}(t)+N_{D}(t)-N_{U}(t)]. \end{aligned}$$

(2)

Dividing both sides of (2) by t and taking the limit as $t\rightarrow \infty$ yields the following conservation law.

Theorem 1

(Satisfied demand conservation law) Consider a PIS for which $\textbf{N}_{I}$ and $\textbf{N}_{D}$ are arbitrary counting processes and $\lambda , \lambda ^{^{*}}, \mu , \mu ^{*}$ exist. Then

$$\begin{aligned} \lambda -\lambda ^{*}=\mu -\mu ^{*}. \end{aligned}$$

(3)

The conservation law is intuitively clear: the left side represents the rate of items that do not become outdated, while the right side represents the rate of satisfied demands. The conservation law is very useful, e.g., when one out of $\textbf{N}_{I}$ or $\textbf{N}_{D}$ is a Poisson process and the second is a renewal process. Then, one process out of $\textbf{N}_{O}$ or $\textbf{N}_{U}$ is a renewal process while the second process is not, but at least its rate can be found by (3). The conservation law shows that the higher the outdating rate, the lower the rate of unsatisfied demands. Both a high outdating rate and a high unsatisfied demands rate have their drawback; the conservation law reflects the trade-off between the goals of efficient resource usage and customer satisfaction.

The conservation law (3) can be extended to the case in which either arrivals occur as batches or every demand is for a batch of items. In the latter case a demand can be either partially or fully satisfied. To see the generalization, suppose that the demand batch sizes are i.i.d. (independent, identically distributed) random variables with mean $\chi$. Then the balance equation (1) becomes

$$\begin{aligned} \lambda -\lambda ^{*}=\mu \chi -\mu ^{*}. \end{aligned}$$

(4)

Applications of (3) and (4) occur in later sections.

Remark 1

Keeping in mind the definition of the age process that was introduced in Sect. 1, it is readily seen that the following alternative representation of the number of items K(t) also holds:

$$\begin{aligned} K(t)=1+N_{I}(t)-N_{I }(t-A(t)), ~~~\forall ~t \ge 0. \end{aligned}$$

(5)

Note that $N_{I}(t)-N_{I }(t-A(t))$ is the number of items arriving during the age of the oldest item at t and that $\textbf{N}_{I}$ is right continuous. This identity is useful for determining the steady-state mean number of items on the shelf.

The case in which both $\textbf{N}_I$ and $\textbf{N}_D$ are Poisson processes is called the basic PIS. Recalling our remark above on the connection to queueing systems, one can view $\textbf{V}$ for the basic PIS as the workload process of a certain $M/M/1+D$ queue in which customers do not wait more than $D=1$ time unit for their service and the idle periods are deleted. The following theorem explores the probabilistic structure of the basic PIS, also allowing $\textbf{N}_I$ to be a renewal process.

Theorem 2

If for a PIS $\textbf{N}_I$ is a renewal process and $\textbf{N}_D$ is a Poisson process, the number of items process $\textbf{K}$, the VOT process $\textbf{V}$ and the age process $\textbf{A}$ are regenerative with the sequence of outdating times as regeneration points, and $\textbf{N}_O$ is a renewal process. For the basic PIS $\textbf{N}_U$ is also a renewal process.

Proof

Consider the system at a time T $\ (>1)$ of an outdating. Looking forward in time from T, the times until the next arrival of an item and until the next demand arrival do not depend on the prior history of the PIS and are independent of each other, the first having the distribution of an item interarrival time conditioned to be greater than 1 and the latter being exponentially distributed with parameter $\mu$, and they are also independent of T. Furthermore, the items that arrived in $[T-1,T)$ are still on the shelf, and their number is independent of the past, its distribution being equal to that of ${\ M } = \max \{ n: X_1+... +X_n<1 \}$, where the $X_i$ are i.i.d. item interarrival times (for the basic PIS this number is Poisson($\lambda$)-distributed). Altogether this implies that T is a regeneration time for the processes $\textbf{K}$, $\textbf{V}$ and $\textbf{A}$, and the times between successive outdatings are i.i.d. Hence $\textbf{N}_O$ is a renewal process.

At any arrival time of an unsatisfied demand the shelf is empty, so that for the basic PIS its future evolution depends only on the Poisson processes of future item arrivals and demand arrivals, which are independent of each other and, by their memoryless property, also independent of all past events. Thus $\textbf{N}_U$ is a renewal process for the basic PIS. $\square$

In the present paper we shall devote much attention to the following generalization that was instigated in Nahmias et al. (2004b). Let the item arrival rate and the demand arrival rate depend on the Virtual Outdating Time V(t), in the following way:

Given that $V(t)=x$, the probability of one item (respectively demand) arrival in the time interval $[t,t+\Delta t)$ equals $\lambda (x) \Delta t + o(\Delta t)$ (respectively $\mu (x) \Delta t + o(\Delta t)$), for $\Delta t \downarrow 0$; the probability of two or more such arrivals is $o(\Delta t)$.

It should be observed that one might be able to improve the performance of the system by adapting $\lambda (x)$ and $\mu (x)$, which may be done by varying the purchase price and the selling price. A controller might wish to choose these rates in order to stay away from VOT level 0 (too many outdatings) or level 1 (too many unsatisfied demands). Control based on the number of items on the shelf might also seem natural, but it has the disadvantage that $\textbf{K}$ is not a Markov process.

In Sect. 3 we shall study PIS with such Markovian Arrival Processes which we refer to as the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ model.

3 The $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ model

For the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ PIS model let us consider the VOT process $\textbf{V}$. Recall that items arrive with instantaneous rate $\lambda (x)$ when $V(t)=x$, demands arrive with instantaneous rate $\mu (x)$ when $V(t)=x$, demands arriving at an empty shelf leave unsatisfied, and any item that has not been taken within one time unit after arrival becomes outdated and must be scrapped. We note already here that for the calculation of the steady-state density of $\textbf{V}$ we may set $\mu (x)=0$ for $x > 1$, because a demand arriving at some time t when ${ V}(t )>1$ leaves unsatisfied and thus does not influence the virtual outdating time at t.

Also for this PIS the process $\textbf{V}$ is regenerative with outdating times as cycle beginnings. The proof of Theorem 2 works almost verbatim, since at any outdating time T the items on the shelf are the ones that arrived in $[T-1,T)$, the evolution of $\textbf{V}$ after T only depends on their ages and on item and demand arrivals after T.

The mean cycle length is finite. To see this, note that since the probability of no demand arrivals in $[T,T+1)$ is obviously positive, there is a positive probability, say $p> 0$, that the next outdating occurs before $T+1$, so that the time until the next outdating is bounded by a geometric random variable with parameter p. Hence, the mean cycle length is smaller than 1/p. It follows that $\textbf{V}$ is stable.

Alternatively to the VOT process of the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ PIS model, one could also speak of the workload process of a very specific M/M/1-type queueing system with state-dependent customer arrival rate $\mu (x)$ and state-dependent service rate $\lambda (x)$, in which a customer arriving when the current workload is w, say, causes the workload to jump upward to a new level that has distribution function

$$\begin{aligned} x \mapsto 1- \textrm{e}^{-[L(x)-L(w)]},~~~ x>w, \end{aligned}$$

where $L(x):= \int _0^x \lambda (y) \textrm{d}y$. There are no idle periods in this queue, because whenever the workload process hits zero, it immediately jumps upward to a new level that has distribution function $x \mapsto 1- \textrm{e}^{-L(x)}, x>0$. We denote the workload (or virtual waiting time, VWT) process of this queueing system by $\tilde{\varvec{V}}$. In the case $\mu (x)=0$ for $x>1$ there are no customer arrivals as long as the workload stays above 1. Then the queue workload process has the same law as the VOT process. This identity of distributions also occurs if we modify the queueing system by adding the feature that customers who upon their arrival encounter a workload larger than one do not enter the queue. View the bottom panel of Fig. 1 to see the equivalence between the PIS sample path and the familiar workload sample path in a single server queue.

For the queueing system we do not need the restriction $\mu \equiv 0$ on $(1, \infty )$. However, we make the following

Assumption (i) $\mu (x)$ is bounded and $\lim _{x\rightarrow \infty }\mu (x)=0$,

Assumption (ii) $0<a\le \lambda (x) \le b < \infty$ for some $a,b> 0$.

Then the arrival rate is for large x always smaller than the service rate minus a/2 (this ensures that $\lambda (x) - \mu (x)$ is bounded away from zero for large x, which will be needed in the proof of Theorem 4), and the marginal workload added at a customer arrival time is stochastically bounded by an $\exp (a)$ random variable. Hence the VWT process is a regenerative process, with the time periods between successive downcrossings of level 0 as cycles having finite mean cycle length. This implies that the VWT process $\tilde{\varvec{V}}$ is stable.

Next we derive an integral equation for the steady-state density $\tilde{f}(\cdot )$ of $\tilde{\varvec{V}}$, and use it to determine $\tilde{f}(\cdot )$ in closed form. Let $M(x):= \int _0^x \mu (w) \textrm{d} w$.

Theorem 3

Let $\tilde{f}(\cdot )$ be the steady-state density of the VWT process $\tilde{\varvec{V}}$. Then

$$\begin{aligned} \tilde{f}(x)=\int _{0}^{x}\mu (w) \textrm{e}^{-[L(x)-L(w)]}\tilde{f}(w)dw+\tilde{f}(0) \textrm{e}^{-L(x)}, ~~~~ x \ge 0. \end{aligned}$$

(6)

Proof

We use level crossing theory (LCT) to derive the Pollaczek-Khintchine type equation (6). According to LCT, the rate of downcrossing any level x equals the rate of upcrossing that level. It is readily seen that the downcrossing rate equals $\tilde{f}(x)$. We now show that the righthand side of (6) is equal to the corresponding upcrossing rate. Given that the state is $w\in (0,x)$, a jump occurs with instantaneous rate $\mu (w)$, and it upcrosses level x if and only if there were no item arrivals (in the PIS), while the VWT decreased from x to w (which happens with probability $\exp -\{L(x)-L(w)\}$), where the same $\tilde{f}(\cdot )$ appears both in the lefthand side and in the righthand side by PASTA. Level x can also be upcrossed just after $\tilde{\varvec{V}}$ hits level 0. In this case the probability to jump above x is $\exp \{-L(x)\}$. By LCT the rate of hitting level 0 is $\tilde{f}(0)$. The theorem is proved by deconditioning with respect to the position of $\tilde{\varvec{V}}$ just before the jump. $\square$

Remark 2

• (i) The application of PASTA (Poisson Arrivals See Time Averages) is here somewhat delicate, because the arrival rate is state-dependent. However, by taking $\bar{\mu }:= \textrm{sup}_{x \ge 0} \mu (x) < \infty$ we can rewrite the integral in (6) as $\bar{\mu } \int _0^x \frac{\mu (w)}{\bar{\mu }} \textrm{e}^{-[L(x)-L(w)]} \tilde{f}(w) \textrm{d}w$, thus we can assume that arrivals occur according to a Poisson process with constant rate $\bar{\mu }$, while an arrival at t is admitted to the system with probability $\mu (w)/\bar{\mu }$ when $\tilde{V}(t)=w$.

• (ii) Balance equations for the workload in single server queues with state-dependent arrival rate, service requirement rate and also service speed are discussed in detail in Section 3.2 of Bekker (2005). He uses Kolmogorov forward equations to derive such balance/integral equations. Apart from the technical issue of having deleted the idle periods, the above theorem follows from his Formula (3.2). See also Bekker et al. (2004) for the case of state-dependent arrival rate and service speed.

Theorem 4

The steady-state density $\tilde{f}(\cdot )$ of the VWT process $\tilde{\varvec{V}}$ in the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ model above is given by

$$\begin{aligned} \tilde{f}(x)=\dfrac{\textrm{e}^{-[L(x)-M(x)]}}{\int _{0}^{\infty }\textrm{e}^{-[L(y)-M(y)]}\textrm{d}y}, ~~~ x \ge 0. \end{aligned}$$

(7)

Proof

Multiplying both sides of (6) by $\textrm{e}^{L(x)}$ and introducing $g(x):= \tilde{f}(x) e^{L(x)}$, we obain the integral equation $g(x) = \int _0^x \mu (w) g(w) \textrm{d}w + g(0)$. Differentiation yields a first-order differential equation, and we readily find that

$$\begin{aligned} \tilde{f}(x)=\tilde{f}(0)\textrm{e}^{-[L(x)-M(x)]}. \end{aligned}$$

(8)

The normalizing condition $\int _0^{\infty } \tilde{f}(x) \textrm{d}x = 1$ gives (7). Note that, by Assumptions (i) and (ii), we have $\int _{0}^{\infty }\textrm{e}^{-[L(y)-M(y)]}\textrm{d}y < \infty$. $\square$

Now let us return to the VOT process of the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ PIS. Since demands arriving while ${ V}(t )>1$ have no bearing on the future evolution of $\textbf{V}$ we may replace the demand rate function $\mu (x)$ by $\tilde{\mu }(x)= \mu (x) 1_{(0, 1)}(x)$. Recall that this means that no demands enter the PIS as long as the shelf contains no items. (In the queueing interpretation in this case, customers who arrive and see a workload larger than one, i.e., would have a waiting time larger than one, do not join the queue—this behavior is called balking in queueing terminology.)

To derive the steady-state density of the VOT process, the only adaptation in the balance equation in Theorem 3 is that we have to replace the upper integration value x by $x \wedge 1$:

$$\begin{aligned} f(x)=\int _{0}^{x\wedge 1}\mu (w)e^{-[L(x)-L(w)]}f(w)dw+f(0)e^{-L(x)}, ~~~x \ge 0. \end{aligned}$$

(9)

This yields

Corollary 1

The steady-state density of the VOT process of the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ PIS is given by

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} ce^{-[L(x)-M(x)]}, &{} 0\le x\le 1 \\ ce^{-[L(x)-M(1)]}, &{} x>1 \end{array} \right. , \end{aligned}$$

(10)

where

$$\begin{aligned} c=\left[ \int _{0}^{1}e^{-[L(x)-M(x)]} \textrm{d}x+e^{M(1)}\int _{1}^{\infty }e^{-L(x)}\textrm{d}x\right] ^{-1}. \end{aligned}$$

This result immediately gives us the following key performance measures:

• (a) The long-run arrival rate of items is given by $\lambda = \int _0^{\infty } \lambda (x) f(x) \textrm{d}x$.

• (b) The long-run outdating rate equals $f(0)=c$.

• (c) The long-run arrival rate of demands is given by $\mu = \int _0^{\infty } \mu (x) f(x) \textrm{d}x$.

• (d) The long-run rate of unsatisfied demands equals $\int _1^{\infty } \mu (x) f(x) \textrm{d}x$, since all demands that find the shelf empty (i.e., the VOT above 1) depart unsatisfied.

Remark 3

The time between two successive outdatings of items is a busy period in the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}/1$ queue with customer balking when the waiting time exceeds 1. The lengths of successive busy periods, i.e., the times between successive downcrossings of level 0, are i.i.d.; the outdating times form a renewal process.

Remark 4

Consider a dual PIS (we speak of duality of type 1; later we also introduce a duality of type 2) in which every demand is willing to wait exactly one unit of time and an item that arrives and finds the waiting line in the PIS empty of waiting demands leaves immediately. The abandonment of items now is of the balking type, whereas the abandonment of the demands now is of the reneging type: each demand is admitted to the system, but it has a constant patience of length one and leaves unsatisfied when that patience runs out. A little reflection shows the following: (i) the instants of jumps are the times of item arrivals into the shelf, (ii) the jump sizes are the times between successive demand arrivals, (iii) a downcrossing of level 1 is a time of a first demand arrival into an empty waiting line, (iv) a downcrossing of level 0 is a time of a demand leaving unsatisfied, and (v) the abandonments of items occur when they arrive and find that $\textbf{V}>1$. From the above, we immediately conclude that in the dual model the times between unsatisfied demands have the same law as the times between outdatings in the primal PIS where $\lambda (x)$ and $\mu (x)$ are reversed.

We now consider a few special choices for $\lambda (x)$ and $\mu (x)$. In all examples, $f(\cdot )$ is the density of the VOT process, as given in Corollary  1.

Example 1

The case $\lambda (x)=\mu (x)$. In this case the constant c of the corollary becomes

$$\begin{aligned} c=\left[ 1+e^{L(1)}\int _{1}^{\infty }e^{-L(x)}\textrm{d}x\right] ^{-1}. \end{aligned}$$

The density f is constant on (0, 1). The steady-state distribution is a mixture with weights c and $1-c$ of the uniform distribution on (0, 1) and the distribution on $(1, \infty )$ having density $x \mapsto e^{-L(x)}/ \int _{1}^{\infty }e^{-L(u)}\textrm{d}u, \ \ x>1$.

Example 2

The basic PIS This special case was already treated in Kaspi and Perry (1983). From (10) we obtain for $\lambda \ne \mu$:

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} \dfrac{\lambda (\lambda -\mu )e^{-(\lambda -\mu )x}}{\lambda -\mu e^{-(\lambda -\mu )}}, &{} 0\le x\le 1 , \\ \dfrac{\lambda (\lambda -\mu )e^{-(\lambda x-\mu )}}{\lambda -\mu e^{-(\lambda -\mu )}}, &{} x>1. \end{array} \right. \end{aligned}$$

(11)

In the case $\lambda =\mu$ it follows from Example 1 that we get a mixture of the uniform distribution on (0, 1) and the distribution of $1+Y$ where Y is $\exp (\lambda )$-distributed. Once we know the steady-state density $f(\cdot )$, the rates $\lambda ^{*}$ and $\mu ^{*}$ are easily determined. The outdating rate is

$$\begin{aligned} \lambda ^{*}=f(0)=\dfrac{\lambda (\lambda -\mu )}{ \lambda -\mu e^{-(\lambda -\mu )}}, \end{aligned}$$

and by the conservation law

$$\begin{aligned} \mu ^{*}=\mu -\lambda +\dfrac{\lambda (\lambda -\mu )}{\lambda -\mu e^{-(\lambda -\mu )}}. \end{aligned}$$

The rate of unsatisfied demands $\mu ^{*}$ can also be obtained in an alternative way. By PASTA a demand is unsatisfied whenever it arrives at an empty system, which implies that $\mu ^{*}=\mu \int _{1}^{\infty }f(x) \textrm{d}x$.

One could also derive the distribution of the time between two successive outdatings by observing that this time is also the busy period in the M/M/1 queue with arrival rate $\mu$ and service rate $\lambda$, in which customers do not enter the system if they have to wait more than one time unit; this busy period has been studied in Kaspi and Perry (1983). In the dual model introduced in Remark 4, the same law holds with $\lambda$ and $\mu$ reversed.

We next derive the generating function of the steady-state number of items on the shelf. Use that

$$\begin{aligned} K(t)=\left\{ \begin{array}{ll} 0, &{} V(t)>1, \\ n, &{} V(t)\le 1\text { and }n-1\text { arrivals during the age of the oldest item.} \end{array} \right. \end{aligned}$$

Define K and V as the number of items on the shelf and the VOT in steady state. We have $\lim _{t\rightarrow \infty }{{\,\mathrm{\mathbb {P}}\,}}(V(t)>1)={{\,\mathrm{\mathbb {P}}\,}}(V>1)$ and (by dominated convergence) $\lim _{t\rightarrow \infty }{{\,\mathrm{\mathbb {E}}\,}}z^{K(t)}= {{\,\mathrm{\mathbb {E}}\,}}z^{K}, \ \ |z|<1$, so that

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}z^{K}={{\,\mathrm{\mathbb {P}}\,}}(V>1)+z\int _{0}^{1}e^{-\lambda (1-w)(1-z)}f(w) \textrm{d}w , \end{aligned}$$

(12)

and by substituting (11) we obtain (for $\lambda \ne \mu$)

$$\begin{aligned} \begin{array}{lll} {{\,\mathrm{\mathbb {E}}\,}}z^{K} &{} = &{} \dfrac{(\lambda -\mu )e^{-(\lambda -\mu )}}{ \lambda -\mu e^{-(\lambda -\mu )}}+z \int _{0}^{1}e^{-\lambda (1-w)(1-z)}\cdot \frac{\lambda (\lambda -\mu )e^{-(\lambda -\mu )w}}{\lambda -\mu e^{-(\lambda -\mu )}}\textrm{d}w \\ &{} = &{} \dfrac{(\lambda -\mu )e^{-(\lambda -\mu )}}{\lambda -\mu e^{-(\lambda -\mu )}}\ \dfrac{\lambda z \textrm{e}^{\lambda z - \mu } -\mu }{\lambda z - \mu }. \end{array} \end{aligned}$$

(13)

Formula (13) is not contained in Kaspi and Perry (1983).

In many inventory applications, younger items on the shelf are worth more than older items. In Nahmias et al. (2004a) the value of the inventory in steady state is determined from an actuarial point of view. A function R(x) is introduced that denotes the value of an item of age x. Let Z denote the steady-state total value of all items in the system. If $V>1$ then the total value is zero. Otherwise, if $V=w \in (0,1)$, let N denote the number of arrivals during the age $1-w$ of the oldest item, and denote their ages by $1-w-T_N,\dots ,1-w-T_1$ with $T_i$ the time between the arrival of the oldest item and the ith arrival. Then $Z = R(1-w) + \sum _{j=1}^N R(1-w-T_j)$. Since the item arrival process is Poisson, we can use a familiar property of the Poisson process: the arrival times of the N items are independent and uniformly distributed on $(0,1-w)$. Hence

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[\textrm{e}^{-\alpha Z}|V=w] = {{\,\mathrm{\mathbb {E}}\,}}[\textrm{e}^{-\alpha R(1-w)} G^N(\alpha ,1-w)], \end{aligned}$$

where

$$\begin{aligned} G(\alpha ,u):= \int _0^u \textrm{e}^{-\alpha R(y)} \frac{\textrm{d}y}{u}. \end{aligned}$$

A straightforward calculation now yields, with f(w) being given in (11):

$$\begin{aligned}{} & {} {{\,\mathrm{\mathbb {E}}\,}}[\textrm{e}^{-\alpha Z}] \nonumber \\= & {} {{\,\mathrm{\mathbb {P}}\,}}(V>1)+ \int _0^1 \textrm{e}^{-\alpha R(1-w)} \sum _{n=0}^{\infty } \textrm{e}^{-\lambda (1-w)} \dfrac{(\lambda (1-w))^n}{n!} G^n(\alpha ,1-w) ~f(w) \textrm{d}w \nonumber \\= & {} \dfrac{(\lambda - \mu ) \textrm{e}^{\mu - \lambda }}{\lambda - \mu \textrm{e}^{\mu -\lambda }} + \int _0^1 \textrm{e}^{-\alpha R(1-w) -\lambda (1-w)(1-G(\alpha ,1-w))} ~f(w) \textrm{d}w. \end{aligned}$$

(14)

Example 3

(See Nahmias et al., 2004b) Let $\lambda (x)=\lambda _{0}(x\wedge 1)^{a}$ and $\mu (x)=\mu _{0}[1-(1-x)^{+}]^{b}$, for some positive numbers $\lambda _{0}$, $\mu _{0}$, a and b. In this case we have for $0\le x\le 1$,

$$\begin{aligned} L(x)=\frac{\lambda _{0}x^{a+1}}{a+1},\ \ \ \ \ M(x)=\frac{\mu _{0}[1-(1-x)^{b+1}]}{b+1},\ \ \end{aligned}$$

so that (with c following by normalization)

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} c \exp \left\{ {\dfrac{\mu _{0}[1-(1-x)^{b+1}]}{b+1}-\dfrac{\lambda _{0}x^{a+1}}{a+1}}\right\} , &{} 0\le x\le 1, \\ c \exp \left\{ {\dfrac{\mu _{0}}{b+1}-\dfrac{\lambda _{0}}{a+1} - \lambda _0(x-1)}\right\} , &{} x>1. \end{array} \right. \end{aligned}$$

Example 4

Let $\lambda (x)=\lambda _{0}$ and $\mu (x)=\frac{\mu _{0}}{1+bx }$, for some constant $b>0$. Then $L(x)=\lambda _{0}x$ and $M(x)=\frac{\mu _{0}}{b}\ln (1+bx)$, so that

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} c(1+bx)^{{\mu _{0}}/{b}}\textrm{e}^{-\lambda _{0}x}, &{} 0\le x\le 1, \\ c(1+b)^{{\mu _{0}}/{b}}\textrm{e}^{-\lambda _{0}x}, &{} x>1. \end{array} \right. \end{aligned}$$

Example 5

Divide (0, 1) in N intervals, and for the kth interval take $\lambda (x) = \lambda _k$ and $\mu (x) = \mu _k$, $k=1,\dots ,N$. The expression for $f(\cdot )$ in (10) is easily evaluated. This might be relevant in the case of blood donations in a country or large city that is divided in a number of sections. In each section there are independent Poisson streams of blood donations and blood demands. By systematically adding and deleting sections a controller can adjust the effective arrival rates of blood items and of demands, to reduce the rates of outdated blood doses and of unsatisfied demand.

4 Applications

In this section we consider several variants of the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ PIS model.

4.1 Variant 1: Hysteretic control

This application is taken from Perry and Posner (1990).

Model variant We consider a $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ PIS model in which $\lambda (x) \equiv \lambda$, and in which the $\mu (x)$ function has the following special feature. There are two switchover levels a and b, such that $0<a<b<1$, and there are two possible demand rates: $\mu _{L}$ and $\mu _H > \mu _L$. Whenever a downcrossing of a occurs, the demand rate switches to $\mu _L$. It keeps that value until level b is upcrossed; it then switches back to $\mu _H$; etc. When one defines a cycle C as the period between two successive downcrossings of a, then each cycle consists of (first) a subcycle $C_L$ with demand rate $\mu _L$ and then a subcycle $C_H$ with demand rate $\mu _H$. See Fig. 2. The VOT process $\textbf{V}$ clearly is a regenerative process with regeneration epochs the successive downcrossing epochs of a. The difficulty in analyzing such a so-called hysteretic policy is that it is not a priori clear whether the demand rate is $\mu _L$ or $\mu _H$ when the VOT process takes a value between a and b.

Motivation A reason for using this policy could be that it will have fewer (possibly expensive) demand rate switches than if one would have no hysteresis but different demand rates in the three intervals (0, a), (a, b) and (b, 1). A possible application is found, e.g., in bloodbanks where a controller might wish to alternately include and exclude particular regions in submitting blood demands (and possibly also blood donations), in a hysteretic way.

The VOT process We construct two artificial regenerative processes from the VOT $\textbf{V}$ such that in each cycle V is split into two separate VOT processes, $\textbf{V}_{L}$ and $\textbf{V}_{H}$. $\textbf{V}_{L}$ (${\textbf{V}}_H$) is generated by deleting the $C_H$ ($C_L$) periods from C and gluing together the $C_L$ ($C_H$) periods.

Fig. 2

Hysteresis with two switchover levels. The demand rate is $\mu _L$ in $C_L$, an interval from a downcrossing of a until the next upcrossing of b. The demand rate is $\mu _H$ in $C_H$, an interval from such an upcrossing until the next downcrossing of a

Key performance measures We derive the steady-state proper (conditional) densities $f_L(\cdot )$ and $f_H(\cdot )$ by using LCT, and by weighing them appropriately we obtain $f(\cdot )$:

$$\begin{aligned} f(x)=\frac{EC_{L}}{EC_{L}+EC_{H}}f_{L}(x)+\frac{EC_{H}}{EC_{L}+EC_{H}} f_{H}(x). \end{aligned}$$

In the next lemma we first relate $EC_L$ and $EC_H$ to $f_H(a)$ and $f_L(\cdot )$, and then we derive integral equations for $f_L(x)$ and $f_H(x)$ which can be solved in a straightforward manner (first solving $f_L(x)$, then $f_H(x)$) and finally f(x) follows using normalization; we leave the details to the reader (see also Perry and Posner, 1990). Define the constant $\omega$ by

$$\begin{aligned} \omega :=\mu _{L}\int _{0}^{b}\textrm{e}^{-\lambda (b-w)}f_{L}(w)\textrm{d}w+\textrm{e}^{-\lambda b}f_{L}(0). \end{aligned}$$

(15)

Lemma 1

$$\begin{aligned} \frac{EC_{L}}{EC_{L}+EC_{H}}=\frac{f_{H}(a)}{f_{H}(a)+\omega }. \end{aligned}$$

(16)

$$\begin{aligned} f_{L}(x)=\left\{ \begin{array}{ll} \mu _{L}\int _{0}^{x}\textrm{e}^{-\lambda (x-w)}f_{L}(w)\textrm{d}w+\textrm{e}^{-\lambda x}f _{L}(0), &{} 0\le x\le a, \\ \mu _{L}\int _{0}^{x}\textrm{e}^{-\lambda (x-w)}f_{L}(w)\textrm{d}w+\textrm{e}^{-\lambda x} f _{L}(0)-\omega , &{} a<x\le b, \end{array} \right. \end{aligned}$$

(17)

and

$$\begin{aligned} f_{H}(x)=\ \ \left\{ \begin{array}{ll} \mu _{H}\int _{a}^{x}\textrm{e}^{-\lambda (x-w)}f_{H}(w)\textrm{d}w+ f_H(a), &{} a\le x\le b, \\ \mu _{H}\int _{a}^{x \wedge 1}\textrm{e}^{-\lambda (x-w)}f_{H}(w)\textrm{d}w + f_H(a) \textrm{e}^{-\lambda (x-b)}, &{} b<x. \\ \end{array} \right. \end{aligned}$$

(18)

Proof

We first prove (16). By LCT, $\omega$ is the rate of upcrossings of level b by $\textbf{V}_{L}$. However, level b is upcrossed only once at the end of the cycle $C_{L}$. Thus, by LCT $\omega =\frac{1}{EC_{L}}$. Similarly, level a is downcrossed only once at the end of the cycle $C_{H}$, so that $f_{H}(a)=\frac{1}{EC_{H}}$. By renewal theory, $\textbf{V}$ is a regenerative process whose successive cycles are composed of a $C_L$ period followed by a $C_H$ period. Thus, $\frac{EC_{L}}{EC_{L}+EC_{H}}$ and $\frac{EC_{H}}{ EC_{L}+EC_{H}}$ are the steady state probabilities of the $C_L$ and the $C_H$ periods, respectively. Formula (16) follows.

The first relation in (17) is a simple level crossing identity, but the second one is more subtle. Notice that for $x \in (a,b]$, with probability 1, the number of upcrossings in every cycle of $\textbf{V}_L$ minus the number of downcrossings equals 1, and that level b is upcrossed only once—at the end of $C_{L}$. By LCT the rate of downcrossings of level x is $f_{L}(x)$ and in steady state, the rate of upcrossings must be equal to the rate of upcrossings of level x minus $\omega$, which is the rate of upcrossings of level b. In terms of rates, we claim that during the L periods for every $a<x\le b$,

$$\begin{aligned} \{\text {downcrossing rate of}\, x\}= \{\text {upcrossing rate of}\, x\} -\{\text {upcrossing rate of}\, b\}. \end{aligned}$$

Note that as an intuitive consequence, the steady-state density $f_{L}(b)=0$ and by substituting $x=b$ this is what we get.

Next consider (18). During the $C_H$ periods there can be two types of upcrossings of level $x\ge a$. Firstly there are Poisson($\mu _{H}$) jumps; those jumps start at some level $w\ge a$. Secondly, at the start of each $C_H$ period there is exactly one jump above level b, that causes the transition from $C_L$ to $C_H$ period. The latter event has rate $f_H(a)$.

For the region $x>1$ the first integral runs until 1, since jumps are not admitted if they arrive to find $\textbf{V}_{H}$ above level 1. $\square$

4.2 Variant 2: Obsolescence

This section is mainly based on Perry and Stadje (2000b) (see also Perry, 1985); it extends the former paper by allowing state-dependent $\mu (\cdot )$ and by considering the joint distribution of the number of obsolescent and non-obsolescent items.

Model variant In this subsection we consider the $MPIS_{\mu (x)}/MPIS_{\lambda (x)}$ PIS model, where we restrict ourselves to $\lambda (x) \equiv \lambda$ while adding the following feature. So far, items that were not taken by a demand stayed on the shelf until reaching their fixed expiration age of 1. In the present subsection we also allow the possibility that an item becomes obsolete, i.e., is no longer of use for any demand, before the fixed unit expiration time. We assume that obsolescence depends on the age, occurring at rate s(x) if $V(t)=x$, for $0<x<1$. That is, if the lifetime distribution of an item is $H(\cdot )$ (ignoring the fact that an item that reaches age one is scrapped), then $s(x) = \frac{ \textrm{d}H(x)}{\textrm{d}x}/(1-H(x))$.

Motivation In many medical and food applications of PIS, an item can deteriorate while on the shelf.

The VOT process By LCT we derive the following integral equation, of Pollaczek-Khintchine type, for $f(\cdot )$:

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} \int _{0}^{x}[\mu (w)+s(1-w)]\textrm{e}^{-\lambda \int _{w}^{x}[1-H(1-y)]dy}f(w)\textrm{d}w &{} \\ \ \\ +f(0)\textrm{e}^{-\lambda \int _{0}^{x}[1-H(1-y)]\textrm{d}y}, &{} 0\le x<1, \\ c\textrm{e}^{-\lambda (x-1)}, &{} x\ge 1, ~~~ \end{array} \right. \end{aligned}$$

(19)

where the constant c can be found by the continuity condition $f(1-)=f(1+)$ and f(0) can be found by the normalizing condition $\int _{0}^{\infty }f(x)\textrm{d}x=1$.

To derive (19), suppose that $\textbf{V}$ is at level $w\in (0,1]$ at some time t, i.e. the oldest item in the system is of age $1-w$.

Fig. 3

A typical sample path of the VOT process $\textbf{V}$ in the case of random item lifetimes. $V(0)=v_0>1$ so that the first item arrives at time $v_0-1$. The jumps at times $t_1,t_2,t_3,t_5$ can be due to a demand or because the life of the oldest item present ends at that time. The item that arrived at $s_1$ becomes the oldest item after the jump at $t_2$. At $t_4$ the oldest item becomes outdated, leaving an empty shelf behind. A new item arrives at $s_2$, and it is removed at $t_5$ either by demand or because its life ends

Considering Fig. 3, it is easily seen that there is an instantaneous upcrossing of level x at time t if and only if the following two events occur:

• (i) The oldest item is removed either by an arriving demand or due to obsolescence. The rate of this to happen is $\mu (w)+s(1-w)$.

• (ii) None of the items that have entered the system during the time interval $(t-(x-w)-(1-x);t-(1-x)]$ is still present at time t (as otherwise V(t) would still be less than x after the jump, see Fig. 3). Conditioning on the number of arrivals in an interval, the arrival times are independent and uniformly distributed on an interval of length $x-w$, so that the probability that all these items are gone at time t is equal to

  $$\begin{aligned} \sum _{n=0}^{\infty } \textrm{e}^{-\lambda (x-w)} \frac{[\lambda (x-w)]^{n}}{n!}\left( \frac{\int _{0}^{x-w}H(1-w-u) \textrm{d}u}{x-w} \right) ^{n}=e^{-\lambda \int _{w}^{x}[1-H(1-y)]dy}. \end{aligned}$$

Key performance measures. Let us first determine $f(\cdot )$ from (19). Introducing $g(x):= f(x) ~ \textrm{exp}(\lambda \int _0^x [1-H(1-y)] \textrm{d}y)$ for $x \in [0,1)$, the first part of (19) reduces to

$$\begin{aligned} g(x) = \int _0^x [\mu (w) + s(1-w)] g(w) \textrm{d}w + g(0), ~~~0 \le x < 1. \end{aligned}$$

Differentiation w.r.t. x yields $g'(x) = [\mu (x) + s(1-x)] g(x)$, so

$$\begin{aligned} g(x) = g(0) \textrm{e}^{\int _0^x [\mu (y) + s(1-y)] \textrm{d}y}, \end{aligned}$$

and hence

$$\begin{aligned} f(x) = f(0) \textrm{e}^{\int _0^x [\mu (y) + s(1-y) - \lambda (1-H(1-y))] \textrm{d}y } , ~~~0 \le x < 1. \end{aligned}$$

(20)

For $x \ge 1$ it is clear that $f(x) = c \textrm{e}^{-\lambda (x-1)}$ $= f(1) \textrm{e}^{-\lambda (x-1)}$, as no jumps can occur in the VOT process for $x>1$. f(1) is expressed in f(0) via (20), and finally f(0) follows from the normalizing condition.

As in previous model variants, various performance measures can be obtained once $f(\cdot )$ is known. Firstly, the outdating rate equals f(0). Secondly we focus on the rate of unsatisfied demands. Using the conservation law (3) with $\mu = \int _0^{\infty } \mu (x) f(x) \textrm{d}x$ and $\lambda ^* = f(0)$, the unsatisfied demand rate is found to be $\mu ^* = \int _0^{\infty } \mu (x) f(x) \textrm{d}x - \lambda + f(0)$. Finally, we determine the (generating function of the) steady-state joint distribution of the number of non-obsolescent items $K_{NO}$ in the system and the number of items $K_O$ that, during the age of the oldest item, have left prematurely due to obsolescence. The reasoning in Sect. 3 leading to (12) is still valid: the system is empty at time t iff $V(t) > 1$, and if it is not empty and $V(t)=w \in (0,1)$, then the number of arrivals during the age $1-w$ of the oldest item is Poisson($\lambda (1-w)$). The latter Poisson process is split into two independent Poisson processes, with rates $\lambda \int _0^{1-w} (1-H(y)) \textrm{d}y$ for the ones that have not become obsolete and $\lambda \int _0^{1-w} H(y) \textrm{d}y$ for the ones that have become obsolete. Hence we have, with ${{\,\mathrm{\mathbb {P}}\,}}(V>1) = 1 -F(1)$:

$$\begin{aligned}{} & {} {{\,\mathrm{\mathbb {E}}\,}}[z_1^{K_{NO}}z_2^{K_O}] = 1-F(1) \nonumber \\{} & {} \quad + z_1 \int _0^1 \textrm{exp}[-\lambda (1-z_1)\int _0^{1-w} (1-H(y)) \textrm{d}y -\lambda (1-z_2) \int _0^{1-w} H(y) \textrm{d}y] f(w) \textrm{d}w.\nonumber \\ \end{aligned}$$

(21)

Notice that $z_1=z_2=1$ gives (12), and that there is a factor $z_1$ in front of the w-integral corresponding to the item with the oldest age (during whose lifetime the other items have arrived).

We end this subsection by briefly discussing some choices for $H(\cdot )$. For these choices, the above formulas may be somewhat simplified; in particular, s(x) and integrals like $\int _0^{1-w} H(y) \textrm{d}y$ can be evaluated.

• (i) If $H(\cdot )$ is uniform on (0, a) for some $a>1$, then $s(x) = 1/(a-x)$.

• (ii) If $H(x) = 1 - (1-x)^2$ for $0 \le x \le 1$ (triangular density), then $s(x) = 2/(1-x)$.

• (iii) If $H(x) = 1 - \textrm{e}^ {-\eta x}$, $x>0$, then $s(x) = \eta$.

• (iv) If $H(x) = x/(1+x)$, $x>0$ (Pareto), then $s(x) = 1/(1+x)$.

• (v) The case $H(x)=0$ for $x<0$, $H(x)=q$ for $0 \le x < a$ and $H(x)=1$ for $a \le x< b < 1$ is somewhat different. Here the maximum shelf life alternates between two constants a, b, with $0<a<b<1$. If an item has reached age a, it is inspected. With probability p it is found to be good and then $b-a$ time units are added to its expiration date. But with probability $q=1-p$ it is found to be unfit for issuance and it is removed from the shelf. Observe that no item stays longer than b in the system; we can now take $V(t) = b - A(t)$. We refer to Perry (1999) for a detailed discussion of this case, when $\mu (w) \equiv \mu$. In the case of general $\mu (\cdot )$, the balance equations are readily seen to be the following (notice that there are minor differences with Theorem 1 of Perry (1999), where in a few places a should have been replaced by $b-a$):

  $$\begin{aligned} f(x)= & {} \int _0^x \mu (w) \textrm{e}^{-\lambda p (x-w)} f(w) \textrm{d}w + f(0) \textrm{e}^{-\lambda p x}, ~~~0 \le x \le b-a, \nonumber \\ f(x)= & {} \int _0^{b-a} \mu (w) \textrm{e}^{-\lambda p (b-a-w) -\lambda (x-(b-a))} f(w) \textrm{d}w + f(0) \textrm{e}^{-\lambda p (b-a) -\lambda (x-(b-a))} \nonumber \\{} & {} + \int _{b-a}^{x \wedge b} \mu (w) \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w + q f((b-a)+) \textrm{e}^{-\lambda (x-(b-a))}, ~~~ x > b-a. \nonumber \\ \end{aligned}$$

  (22)

Notice that $b-a$ is a point of discontinuity for $\textbf{V}$, since $pf((b-a)+) = f((b-a)-)$. This is intuitive because the proportion between the downcrossing rates of levels $(b-a)-$ and $(b-a)+$ is p. The first equation is trivially solved by first multiplying both sides by $\textrm{e}^{\lambda p x}$ and then differentiating. The second equation is solved by distinguishing between $x\le b$ and $x>b$. In the latter case, $f(x)=C \textrm{e}^{-\lambda x}$ for some constant C. In the former case, multiplying both sides by $\textrm{e}^{\lambda x}$ and differentiating results in a simple first-order differential equation.

4.3 Variant 3: Risk management

An event of unsatisfied demand could have serious consequences, e.g., in organ transplant and blood bank settings. Hence a controller may want to avoid unsatisfied demands, or even risky situations, as much as possible. In this section we briefly discuss four possible strategies to accomplish this. In each case we assume that item arrivals (regular ones, see below) are Poisson ($\mu$) and demand arrivals are Poisson($\lambda$).

Model variant (i): Outsourcing; cf. Bar-Lev et al. (2005).

In this variant, the possibility of unsatisfied demands is excluded by introducing an alternative source of fresh items that is completely reliable and delivers with zero delay. When the shelf becomes empty, the controller places an order at this source, and it instantaneously delivers a batch of $n_0$ items. In the $\textbf{V}$ process, after each upcrossing of level 1, the next $n_0$ demands do not cause jumps in $\textbf{V}$ as long as the age of these items is less than 1. If some of the last of the $n_0$ items become outdated at age 1, the next demand does cause an exp($\lambda$) jump. However, if that jump happens to be larger than 1, it is cut off in the $\textbf{V}$ process by 1 and again $n_0$ items are ordered.

The VOT process A typical realization of the $\textbf{V}$ process is shown in the top panel of Fig. 4.

Fig. 4

A typical sample path of the VOT process $\textbf{V}$ (top panel), the age process $\textbf{A}$ (middle panel) and the transformation into the process $\textbf{W}$ (bottom panel), for the case of special deliveries with $n_0=4$. The dots correspond to demand arrivals that take one of the instant delivery items

Note that the demand process is a Poisson process with rate $\mu$, but the jump process of $\textbf{V}$ is not a Poisson process. In order to cope with this situation we apply a duality argument, called duality of type 2, in which we first look at the age process $\textbf{A}$, with $A(t) = 1-V(t)$. The original process (V(t) in the top panel of Fig.  4, with steady-state density $f(\cdot )$) is a regenerative process whose cycle is the time between two downcrossings of level 1. Construct a new process $\textbf{W}$, with steady-state density $f_W(\cdot )$, in the following way. Every trajectory of slope 1 in $\textbf{A}$ becomes a jump to the same level in $\textbf{W}$ and every negative jump in $\textbf{A}$ becomes a trajectory to the same level in $\textbf{W}$. Now, the $\textbf{A}$ process is a regenerative process whose cycles are the times between two successive downcrossings of level 0. The sample path of $\textbf{W}$ is the same as that of a finite dam (queueing) model in which the distribution of the first jump in a cycle is different from that of the other jumps. The first jump size is the sum of $n_0$ exp($\lambda$) distributed random variables, hence Erlang($n_0,\lambda$), but the jump is truncated (if necessary) at 1. All other jumps are exp($\lambda$) distributed. Also, the idle periods are deleted.

Key performance measures For the steady-state density $f(\cdot )$ of $\textbf{V}$ we have, for all $0\le x\le 1$:

$$\begin{aligned} f_W(x) = f(1-x) = \lambda \int _{0}^{x} \textrm{e}^{-\mu (x-w)}f_W(w)\textrm{d}w+f_W(0)\sum _{j=0}^{n_{0}-1}\frac{\textrm{e}^{-\mu x}(\mu x)^{j}}{j!} . \end{aligned}$$

(23)

By introducing $g(x):= \textrm{e}^{\mu x} f_W(x)$ and differentiating w.r.t. x, we obtain a simple first-order differential equation which is readily solved (we leave the details to the reader):

$$\begin{aligned} g'(x) = \lambda g(x) + f_W(0) \mu \sum _{j=1}^{n_0-1} \frac{(\mu x)^{j-1}}{(j-1)!}. \end{aligned}$$

Since $f(x) = f_W(1-x)$, we now also have $f(\cdot )$, and one can subsequently obtain other performance measures. In particular, the conservation law becomes

$$\begin{aligned} \mu =\lambda +n_{0}f(1)-f(0) {{\,\mathrm{\mathbb {E}}\,}}J, \end{aligned}$$

(24)

where J is the number of items that are outdated when $\textbf{V}$ reaches level 0, and this yields ${{\,\mathrm{\mathbb {E}}\,}}J$. The reasoning behind (24) is the following. Since there are no unsatisfied demands, the satisfied demand rate equals $\mu$. This should equal the item input rate $\lambda + n_0 f(1)$, minus the rate of outdated items.

Some interesting performance measures which were not discussed in Bar-Lev et al. (2005) are: (i) The distribution of the number of items which are on the shelf in steady state. Here there could be several oldest items. (ii) The distribution of the number of items that are outdated when $\textbf{V}$ reaches level 0. (iii) The distribution of the busy period; it can be obtained via a martingale argument.

Model variant (ii): Urgency Classes; cf.Bar-Lev et al. (2005).

In this variant it is not possible to place additional orders. The incoming demands are classified into different categories of urgency. For simplicity, assume that there are two such categories whose demand arrival times form independent Poisson processes of intensities $\mu _1(w)$ and $\mu _2(w)$, respectively; item arrivals are Poisson($\lambda$). One possible policy is to satisfy high-urgency (type 1) demands whenever possible (i.e., if the system is not empty) and less urgent demands (type 2) only if there are at least $m_{0}>1$ items on the shelf. An undesirable aspect of this policy is that it does not take the lifetime of the oldest item into account. For example, under this policy the oldest item will not be used for a less urgent demand even if its residual lifetime is very short, so its outdating is imminent. To avoid this drawback, we propose the following policy refinement. Fix $\gamma \in (0,1)$ and an integer $m_{0}>1$. A demand of type 1 is satisfied if and only if the system is not empty; a demand of type 2 is satisfied if and only if there are at least $m_{0}$ items in the system or the shelf age of the oldest item is at least $1-\gamma$. Any demand of type 1 or 2 that is not immediately satisfied is lost. This model was studied in Bar-Lev et al. (2005) for the case $\mu _1(w) \equiv \mu _1$, $\mu _2(w) \equiv \mu _2$.

The VOT process It is readily seen that the VOT density $f(\cdot )$ satisfies the following balance equations:

$$\begin{aligned} f(x)= & {} \int _0^x (\mu _1(w) + \mu _2(w)) \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w + f(0) \textrm{e}^{-\lambda x}, ~~~0 \le x< \gamma , \\ f(x)= & {} \int _0^x \mu _1(w) \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w + \int _0^{\gamma } \mu _2(w) \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w \\{} & {} + \sum _{i=m_0-1}^{\infty } \textrm{e}^{-\lambda (1-x)} \frac{(\lambda (1-x))^i}{i!} \int _{\gamma }^x \mu _2(w) \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w + f(0) \textrm{e}^{-\lambda x}, ~~~\gamma \le x < 1, \\ f(x)= & {} \int _0^1 \mu _1(w) \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w + \int _0^{\gamma } \mu _2(w) \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w + f(0) \textrm{e}^{-\lambda x}, ~~~ x \ge 1. \end{aligned}$$

The first equation can be solved easily by multiplying both sides by $\textrm{e}^{\lambda x}$ and differentiating. The third equation shows that $f(x) = c \textrm{e}^ {-\lambda x}$ with c some constant. The second equation can be formally solved via the technique of Picard iteration; this method is discussed in some detail in Sect. 5. In the, not unrealistic, case that the ratio $\mu _1(w)/\mu _2(w)$ is constant, the equation can be solved more explicitly, using the same approach as for the first equation.

Possible extensions which were not treated in Bar-Lev et al. (2005) are: (i) the distribution of the number of items on the shelf; taking lead times for special orders into account.

Model variant (iii): Risk of an empty shelf. In this third model variant (which has not been considered before) we assume that the controller carries out the following policy. When only one item is on the shelf when a demand arrives, the condition of that demand (e.g., a person requiring blood or an organ) is inspected. The demand is diagnosed with probability p as urgent, and then the demand is immediately satisfied. If it is diagnosed as non-urgent, the demand is released unsatisfied.

The VOT process The balance equation in this case is easily seen to be

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} \begin{array}{l} \mu p\left[ \int _{0}^{x}\textrm{e}^{-\lambda (1-w)}f(w)\textrm{d}w+\lambda (1-x)\int _{0}^{x}\textrm{e}^{-\lambda (1-w)}f(w)\textrm{d}w\right] \\ +\mu \int _{0}^{x}[\textrm{e}^{-\lambda (x-w)}-\textrm{e}^{-\lambda (1-w)}]f(w) \textrm{d}w +f(0)\textrm{e}^{-\lambda x}, \end{array} &{} 0\le x\le 1, \\ \mu p\int _{0}^{1}\textrm{e}^{-\lambda (x-w)}f(w)\textrm{d}w+f(0)\textrm{e}^{-\lambda x}, &{} x>1. \end{array} \right. \end{aligned}$$

Indeed, for $0 \le x\le 1$ let S be the jump size, which is the generic time between arrivals at the shelf. By conditioning on both $V=w$ and on the number $N_I$ of items seen by the arriving demand we get for $0 \le x \le 1$:

$$\begin{aligned} f(x)= & {} \mu p\int _{0}^{x} {{\,\mathrm{\mathbb {P}}\,}}(S>1-w\mid N_{I}(1-w)=0){{\,\mathrm{\mathbb {P}}\,}}(N_{I}(1-w)=0)f(w)\textrm{d}w \\{} & {} + \mu p\int _{0}^{x}{{\,\mathrm{\mathbb {P}}\,}}(x-w\le S<1-w\mid N_{I}(1-w)=1){{\,\mathrm{\mathbb {P}}\,}}(N_{I}(1-w)=1)f(w)\textrm{d}w \\{} & {} + \mu \int _{0}^{x}\sum \limits _{n=2}^{\infty }{{\,\mathrm{\mathbb {P}}\,}}(x-w\le S<1-w\mid N_{I}(1-w)=n){{\,\mathrm{\mathbb {P}}\,}}(N_{I}(1-w)=n)f(w)\textrm{d}w. \end{aligned}$$

The first conditional probability given $N_{I}(1-w)=0$ is equal to 1, since the events $\{N_{I}(1-w)=0\}$ and $\{S>1-w\}$ are equivalent events. In the second line S, given $\{N_{I}(1-w)=1\}$, is uniformly distributed on $(0,1-w)$ and in the third line S given $\{N_{I}(1-w)=n\}$ (for $n\ge 2$) is stochastically equal to the minimal order statistic taken from a uniform distribution on $(0,1-w)$. Note that the second and the third lines are separated from each other, since the demand rates are $\mu p$ and $\mu$ respectively. The above equation thus becomes, for $0 \le x \le 1$:

$$\begin{aligned} \begin{array}{lll} f(x) &{} = &{} \mu p\int _{0}^{x}\textrm{e}^{-\lambda (1-w)}f(w)\textrm{d}w +\mu p\int _{0}^{x}\frac{1-x}{1-w}\textrm{e}^{-\lambda (1-w)}\lambda (1-w)f(w)\textrm{d}w \\ &{}&{}+ \mu \int _{0}^{x}\sum \limits _{n=2}^{\infty }\left( \frac{1-x}{ 1-w}\right) ^{n-1}\frac{\textrm{e}^{-\lambda (1-w)}[\lambda (1-w)]^{n-1}}{(n-1)!} f(w)\textrm{d}w. \end{array} \end{aligned}$$

The proof is completed after some simple algebra and the fact that for $x>1$ an upcrossing means that an arriving demand sees only one item on the shelf and is satisfied by it.

Remark 5

A weakness of the policy is that it does not take the age of the oldest item on the shelf into account. Suppose that, when a demand arrives, the age of the oldest item is close to 1. If the demand is not satisfied by the oldest item, the item will become obsolete very soon anyway. Thus, it would be reasonable to issue the item regardless of the demand’s condition. Accordingly, it is natural to fix a certain switchover level, say a, such that if the age of the item is greater than $1-a$ (alternatively, $V< a$), the demand will be satisfied even if it is the only item present on the shelf. We distinguish between two cases: if just before a moment of demand arrival, there is one item on the shelf the demand is satisfied by the item with probability $p_{1}$ and the shelf becomes empty. But if just before a moment of demand arrival, there are at least two items on the shelf the demand is satisfied by the oldest item with probability $p_{2}$ and immediately after the issuance only one item is left on the shelf. It is not hard to derive the integral equation for density $f(\cdot )$ for this adaptation.

Finally we refer to Balcioglu et al. (2008) for a risk management study of a basic PIS with a demand rate that is either high or low depending on the value of $\textbf{V}$.

Model variant (iv): Optional shelf life In some cases, it might be disastrous to have an unsatisfied demand. Keeping the blood bank example in mind, one can imagine that there are situations in which it is opportune to slightly extend the fixed maximum shelf life time when the alternative—an unsatisfied demand—is likely to have worse consequences. Accordingly, we propose a model variant in which the system controller is allowed to lengthen the expiration date of items under certain conditions. Our easy-to-apply control policy consists of the following simple rules.

• (1) When the oldest item on the shelf is the only item on the shelf and reaches age 1, an additional amount of time a is added to its life time.

• (2) If in the next a time units a demand arrives, before a fresh item, then the item with extended life time satisfies this demand.

• (3) If in the next a time units a fresh item arrives on the shelf, before a demand, then the item with extended life time is removed from the shelf.

• (4) If in the next a time units no demand and no fresh item arrive, then the item with extended life time is removed from the shelf.

It is readily verified that this gives rise to the following balance equations for the VOT, when we assume Poisson($\lambda$) item arrivals and Poisson($\mu$) demand arrivals; see also Fig. 5.

$$\begin{aligned} f(x)= & {} (\lambda +\mu ) F(x) + f(0), ~~~0 \le x< a, \nonumber \\ f(x)= & {} (\lambda + \mu )F(a) + f(0) + \mu \int _a^x \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w \nonumber \\{} & {} + f(a+) [\textrm{e}^{-\lambda (x-a)} - \textrm{e}^{-\lambda }], ~~~a \le x < 1+a, \nonumber \\ f(x)= & {} \mu F(a) \textrm{e}^{-\lambda (x-a-1)} + f(0) \textrm{e}^{-\lambda (x-a-1)} \nonumber \\+ & {} \mu \int _{a}^{1+a} \textrm{e}^{-\lambda (x-w)} f(w) \textrm{d}w, ~~~x \ge 1+a. \end{aligned}$$

(25)

The three terms on the right in the first line of (25) correspond respectively to the following events, when the oldest item has age $\in (1,1+a]$: (i) a fresh item arrives (cf. $t_4$ in the figure), (ii) a demand arrives (cf. $t_5$); and (iii) outdating of the oldest item occurs (cf. $t_6$). The term in the third line also deserves to be mentioned. It represents the event in which a is reached from above but not downcrossed; the oldest item reaches age 1 and is removed because there is a younger item on the shelf (cf. $t_2$ in the figure). In the fourth line we have a term $\mu F(a) \textrm{e}^{-\lambda (x-a-1)}$ instead of an integral from 0 to a, because any jump from below a will exceed level $a+1$ and then continue for an exp($\lambda$) distributed amount, regardless of the precise level it jumped from. Similarly for the f(0) term. The other terms are self-explanatory and/or the same as in the case $a=0$.

Finally we observe that it is straightforward to determine $f(\cdot )$ from (25) (in particular, f(x) is proportional to $\textrm{e}^{(\lambda + \mu )x}$ for $x \in [0,a)$ and to $\textrm{e}^{-\lambda x}$ for $x\ge 1+a$); we leave the details to the reader.

Remark 6

It should be noticed that the density $f(\cdot )$ has two points of discontinuity: (i) $f(a+) = f(a-) \textrm{e}^{\lambda }$ (cf. $t_2$) and (ii) $f((a+1)+) - f((a+1)-) = - \lambda F(a)$ (cf. $t_4$).

The conservation law For the present model variant, we have

$$\begin{aligned} \lambda - f(0) - [f(a+)-f(a-)] - [f((a+1)-) - f((a+1)+)] = \mu F(a+1). \end{aligned}$$

Both sides represent the rate of the satisfied demands. This is obvious for the righthand side. The lefthand side is the arrival rate $\lambda$ minus the rate of the three outdating components: f(0) for items that become outdated at age $1+a$; $f(a+)-f(a-) = f(a+)[1 - \textrm{e}^{-\lambda }]$ for items that are removed at age 1 and left a non-empty shelf; and $f((a+1)-)-f((a+1)+) = \lambda F(a)$ for items that are removed at an age between 1 and $1+a$ due to the arrival of a fresh item.

Fig. 5

A typical sample path of the VOT process $\textbf{V}$ in the case of optional shelf life a. $t_1$ is the time of a demand arrival; it is satisfied by the oldest item, whose age is less than 1. $t_2$ is a time at which a is reached from above. The age of the oldest item reaches 1 and it is removed because it is not the only item on the shelf. $t_3$ is another time at which a is reached from above; now it is downcrossed, because the oldest item is the only item present. $t_4$ marks the arrival of a fresh item, that instantaneously replaces the oldest (and outdated) item. $t_5$ is the arrival time of a demand that is satisfied by an item with age $>1$; subsequently the shelf becomes empty. $t_6$ is the time of outdating of an item with age $1+a$

Model variant (v): Secondary products In some real-world applications items are not scrapped when reaching their formal, preset expiration age, but are taken for secondary use. In a blood bank, expired blood portions that are no longer suitable for transfusions could be processed to other medical products; similarly, in a PIS for certain foodstuff, e.g. fruits, products that are not any more considered to be marketable could be transformed into others, e.g. juice or jam.

A first attempt at modeling this situation is a PIS with two storage places, say the upper shelf and the lower shelf for the primary and the secondary items, respectively. Let the maximal shelf life of the primary product again be 1. When an item reaches this age it is immediately transferred to the lower shelf where its maximal shelf age is b. There are two independent Poisson arrival streams of demands with rates $\mu _{0}$ and $\mu _{1}$, respectively. This and more refined models were analyzed in Perry and Stadje (2000a).

In this PIS there are two coupled VOT processes, one for the upper shelf and one for the lower shelf. A typical sample path is shown in Fig. 6.

Fig. 6

A typical sample path of the two VOT processes in the case of primary and secondary products

The times $t_i$ are the times of a removal in the upper VOT (times of outdatings, hence transfers from the upper to the lower shelf), and the intervals between these times are also the jump sizes in the lower (bold) VOT. Note that when the lower shelf is empty, there is only one common VOT for both the upper and the lower shelves.

It is easy to conclude that the upper VOT has the same law as the workload process in the $M/M/1+D$ ($D=1$) queue in which the idle periods are deleted (this is the VOT of the basic model), while the lower VOT behaves like the workload process in the $M/G/1+D$ ($D=b$) queue in which the idle periods are deleted and G denotes the distribution of inter-outdating times of the upper shelf. The marginal laws of both systems can be determined; the analysis of the $M/M/1+D$ case is described in the basic PIS above and that of the $M/G/1+D$ case in Sect. 5 below.

Another interpretation of this PIS with two shelves is an inventory subject to two types of demands: normal demands and urgent demands. The urgent demands have priority over the normal ones and require young items. Accordingly, the controller prepares an infrastructure of two shelves such that the items on the upper shelf are young and are supposed to satisfy only the urgent demands, while the items on the lower shelf are older and are supposed to satisfy only the normal demands. Whenever an item on the upper shelf reaches its maximum admissible age, it is moved to the lower shelf. In case a normal demand arrives at an empty lower shelf, it leaves unsatisfied even if the upper shelf is not empty. (The rationale behind this policy is that the controller wants to keep young items for potential future arrivals of urgent demands.) This model clearly coincides mathematically with the PIS above for primary and secondary products.

5 PIS Models with renewal arrival processes

This section is devoted to the $MPIS_{\mu (x)}/G$ PIS, a model in which the item arrival process is a renewal process, while the demand arrival process is a Poisson process with rate $\mu (x)$ when the age is $1-x$. Let $G(\cdot )$ denote the distribution of the i.i.d. item interarrival times. As before, we assume that each item has a usable lifetime of one time unit and that, upon arrival, a demand removes the oldest item on the shelf—leaving unsatisfied if the shelf is empty. An item that has not been taken within one time unit of arrival becomes outdated. Finally, the arrival processes of items and demands are again assumed to be independent.

This model is studied in Kaspi and Perry (1984), for the case $\mu (w) \equiv \mu$. In the present section we first derive an integral equation for the steady-state density $f(\cdot )$ of the VOT process $\textbf{V}$ for general $\mu (\cdot )$, and we subsequently outline its solution. Thereafter, we restrict ourselves to $\mu (w) \equiv \mu$, in which case the solution of the integral equation becomes more explicit. We also express the distribution of the number of items on the shelf into $f(\cdot )$. Three natural applications of MPIS/G and M/G PIS models will be discussed in Sect. 6.

Again consider the age process $\textbf{A}$ and, in particular, the VOT process $\textbf{V}$, where $V(t) = 1-A(t)$. Since we allow no patience of demands, the steady-state density $f(\cdot )$ of $\textbf{V}$ always exists. To determine it, we can again take $\mu (w)=0$ for $w>1$, because a demand arriving at some time t when $V(t)>1$ leaves unsatisfied and thus does not influence the virtual outdating time at t. A level crossing argument readily yields that $f(\cdot )$ satisfies the following integral equation:

$$\begin{aligned} f(x) = \int _0^{x \wedge 1} \mu (w) (1-G(x-w)) f(w) \textrm{d}w + f(0)(1-G(x)), ~~~ x \ge 0. \end{aligned}$$

(26)

Notice that the case $G(x) = 1 - \textrm{e}^{-\lambda x}$ was treated in Corollary 1 (in fact, we there allowed $\lambda (\cdot )$); for that exponential case, a straightforward solution procedure is to multiply both sides by $\textrm{e}^{\lambda x}$, after which differentiation results in a simple first-order differential equation. That approach breaks down for general $G(\cdot )$. However, there is a standard (albeit somewhat formal) solution procedure, Picard iteration, for such Volterra integral equations of the second kind (see, e.g., Chapter I of Mikhlin (1957)). We now outline that procedure. Let $K(x,w):= \mu (w) (1-G(x-w))$ for $0 \le w \le x$. Then (26) becomes: $f(x) = \int _0^x K(x,w) f(w) \textrm{d}w + cK(x,0)$, where $c:= f(0)/\mu (0)$. Iteration yields:

$$\begin{aligned} f(x)= & {} cK(x,0) + c \int _0^x K(x,w) K(w,0) \textrm{d}w\nonumber \\{} & {} + c \int _0^x K(x,w) \int _0^w K(w,y) K(y,0) \textrm{d}y \textrm{d}w + \cdots \end{aligned}$$

(27)

Introducing $K_1(x,w):= K(x,w)$ and $K_n(x,w):= \int _w^x K_{n-1}(x,z) K(z,y) \textrm{d}z$ for $n=2,3,\dots$, one can verify that f(x) is given by the following convergent sum:

$$\begin{aligned} f(x) = c \sum _{n=1}^{\infty } K_n(x,0) , ~~~x \ge 0. \end{aligned}$$

(28)

Now take $\mu (w) \equiv \mu$ for $0 \le w \le 1$, and $\mu (w)=0$ otherwise. Kaspi and Perry (1984) exploit the fact that the VOT process now coincides with the above-mentioned workload process in an M/G/1 queue with restricted accessibility (an $M/G/1+D$ queue) and deleted idle periods. Using a result of Daley (1964) for the so-called finite dam, they find the distribution $F(x) = \int _0^x f(w) \textrm{d}w$. With $1/\lambda$ the mean of $G(\cdot )$ and $n*$ denoting an n-fold convolution, their Formula (3.21) states that

$$\begin{aligned} F(x)= & {} \frac{\frac{\lambda }{\mu } \sum _{n=0}^{\infty } \int _{0+}^x \frac{[-\mu (x-u)]^n}{n!} ~ \textrm{e}^{\mu (x-u)} \textrm{d}G^{n*}(u)}{\sum _{n=0}^{\infty } \int _{0-}^1 \frac{[-\mu (1-u)]^n}{n!} ~ \textrm{e}^{\mu (1-u)} \textrm{d}G^{n*}(u)}, ~~~0 < x \le 1, \nonumber \\ F(x)= & {} \mu \int _{y=0}^x \int _{u=0}^1 (1-G(y-u)) f(u) \textrm{d}u \textrm{d}y, ~~~x > 1. \end{aligned}$$

(29)

When $G(\cdot ) \sim \textrm{exp}(\lambda )$, this expression is readily seen to simplify to (11).

Repeating an argument that was already used for that exponential $G(\cdot )$ case, we can also find the distribution of the steady-state number of items on the shelf:

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}(K=n)= & {} \int _0^1 [G^{(n-1)*}(1-w) - G^{n*}(1-w)] f(w) \textrm{d}w, ~~~~ n=1,2,\dots , \nonumber \\ {{\,\mathrm{\mathbb {P}}\,}}(K=0)= & {} 1-F(1). \end{aligned}$$

(30)

Remark 7

It would also be interesting to study PIS models in which the item arrival process is Poisson but the demand arrival process is not Poisson but a renewal process. The LCT approach now breaks down: jumps do not occur according to a Poisson process, so PASTA does not hold and the VOT at a jump epoch is not the same as the steady-state VOT. We briefly sketch an approach that one can follow in this case. Just like in Sect. 4.3, see in particular Fig. 4, one could construct a new process $\textbf{W}$ from $\textbf{A}$ by replacing upward trajectories with slope 1 by upward jumps to the same level, and downward jumps by downward trajectories of slope $-1$ to the same level. This so-called duality of type 2 results in an artificial MPIS/G process $\textbf{W}$ with the same steady-state law as $\textbf{V}$. The balance equations for that MPIS/G model can be derived using LCT.

6 Renewal arrivals: Three variants

In this section we discuss three PIS models that may be viewed as special cases of MPIS/G models. In Sect. 6.1 we consider PIS models with batch arrivals of either items or demands. Sect. 6.2 is devoted to the case in which demands are willing to wait. In Sect. 6.3 we take a closer look at intervals between successive outdatings and intervals between successive unsatisfied demands when item arrivals follow a renewal process.

6.1 Batch arrivals

In this subsection we briefly discuss three different cases in which items and/or demands arrive in batches.

Case 1: Poisson$(\lambda )$ item arrivals and Poisson$(\mu (x))$ demand arrivals; demands arrive in batches (cf. Kaspi & Perry, 1984). Let $\theta _n$ be the probability that the demand batch size equals n, $n=1,2,\dots$, with generating function $J(\cdot )$. This case basically is a special version of the M/G model studied in Sect. 5, with the jump sizes being a random sum of exp($\lambda$) random variables with distribution $G(x) = \int _0^x \sum _{n=1}^{\infty } \theta _n \lambda \textrm{e}^{-\lambda t} \frac{(\lambda t)^{n-1}}{(n-1)!} \textrm{d} t$. There are two exceptions to this: (i) if the jump size is above level 1 then the overflow above 1 is always just one exp($\lambda$) phase; and (ii) the jump from zero is also exp($\lambda$), since such a jump is not due to a demand. In passing we observe that $G(\cdot )$ is a phase-type distribution, with LST $J(\frac{\lambda }{\lambda + \alpha })$. We also observe that a batch demand can alternatively be viewed as a single demand for a random number of items.

The balance equations for the density $f(\cdot )$ of the VOT process are given by

$$\begin{aligned} f(x)= & {} \int _0^x \mu (w) [1-G(x-w)] f(w) \textrm{d}w + f(0) \textrm{e}^{-\lambda x}, ~~~0 \le x \le 1, \nonumber \\ f(x)= & {} \int _0^1 \mu (w)[1-G(1-w)] \textrm{e}^{-\lambda (x-1)} f(w) \textrm{d}w + f(0) \textrm{e}^{-\lambda x}, ~~~x>1. \end{aligned}$$

(31)

One could solve the first equation using the Picard iteration outlined in Sect. 5, while the second equation immediately translates into $f(x) =c \textrm{e}^{-\lambda x}$ for some constant c. If $\theta _n = (1-a)a^{n-1}$ for $n=1,2,\dots$ (i.e., geometric batch sizes), then $1-G(x) = \textrm{e}^{-(1-a)x}$, and it is straightforward to determine $f(\cdot )$ more explicitly.

Remark 8

If items arrive according to a renewal process with distribution $S(\cdot )$ and demands arrive in batches according to a Poisson process, then the above phase-type $G(\cdot )$ is replaced by a more general $G(\cdot )$ with density $g(\cdot )$. Formula (31) becomes

$$\begin{aligned} f(x)= & {} \int _0^x [1-G(x-w)] f(w) \textrm{d}w + f(0)[1-S(x)], ~~~0 \le x \le 1,\\ f(x)= & {} \int _0^1 \int _{y=w}^1 \sum _{n=0}^{\infty } g^{n*}(y-w) [1-S(x-y)] \textrm{d}y f(w) \textrm{d}w + f(0) [1-S(x)], ~~~x > 1. \end{aligned}$$

Here $g^{n*}$ denotes the n-fold convolution of the density $g(\cdot )$, and $g^{0*}(\cdot )=1$. The resulting integral equation can again be solved via Picard iteration.

Case 2: Poisson($\lambda$) item arrivals and Poisson($\mu$) demand arrivals; items arrive in batches. Successive item batch sizes $J_1,J_2,\dots$ are i.i.d., with generating function $J(\cdot )$. In Fig. 7 we display the VOT process $\textbf{V}$ and the age process $\textbf{A}$ in the top and middle panel. All the dots in those two panels occur at times of satisfied demands—except for the dot at $A(t)=1$. In the figure we have $J_1=4$, $J_2=2$, $J_3=6$ and $J_4 \ge 3$; observe that $J_4$ may have been larger than 3, because the VOT jumps up from 0 at an outdating, and if $J_4>3$ then more than 3 items are simultaneously outdated. The jump process is not a Poisson process, since only the last item in the batch is accompanied by a jump.

Fig. 7

A typical sample path of the VOT process $\textbf{V}$ (top panel), the age process $\textbf{A}$ (middle panel) and the transformation into the process $\textbf{W}$ (bottom panel), for the case of batch arrivals of items

Just like in Sect. 4.3 we apply the duality of type 2: every negative jump in A(t) becomes a trajectory with decreasing slope of rate 1 in W(t) and every trajectory with increasing slope of rate 1 in A(t) becomes a positive jump in W(t) (cf. Fig. 7). LCT implies that the processes $\textbf{A}$ and $\textbf{W}$ have the same steady-state law, since by the above construction the numbers of up- and downcrossings of every level $x>0$ in both processes are the same for every realization. The process $\textbf{W}$ describes a finite dam model with Poisson arrivals of rate $\lambda$ and the jump sizes have a phase-type distribution $G(\cdot )$ with LST $J(\frac{\mu }{\alpha +\mu })$. That is, the LST of the jump size is the generating function of a random sum of exp($\mu$) random variables. Also note that the emptiness period in $\textbf{W}$ is exactly the time during which the shelf is empty in $\textbf{A}$. We can now apply LCT to the $\textbf{W}$ process and thus get the following balance equation for its steady-state density $f_W(\cdot )$:

$$\begin{aligned} f_{W}(x)=\lambda \int \limits _{0}^{x}[1-G(x-w)]f_{W}(w)\textrm{d}w+\pi \textrm{e}^{-\lambda x}, ~~~ 0 \le x \le 1, \end{aligned}$$

(32)

where the probability of an empty dam

$$\begin{aligned} \pi =\frac{1/\lambda }{1/\lambda +1/f_{W}(0)}=\frac{f_{W}(0)}{ f_{W}(0)+\lambda }. \end{aligned}$$

In principle (32) can be solved via Picard iteration. One additional equation is provided by the normalizing condition:

$$\begin{aligned} \int _{0}^{1}f_{W}(x)\textrm{d}x=1-\pi . \end{aligned}$$

Finally, by the duality construction of W(t) from V(t) we get the density $f(\cdot )$ of $\textbf{V}$ from $f_W(\cdot )$: $f(x)=f_{W}(1-x)$ for $0 \le x\le 1$ and $f(x)=\pi e^{-\lambda (x-1)}$ for $x>1$ (recall that the overflow above level 1 in $\textbf{V}$ is exp($\lambda$)).

Case 3: Poisson arrivals of item batches and Poisson arrivals of demand batches. We assume independence of the arrival processes and of the various batch sizes. Furthermore, item batch sizes are geometric($\gamma _I$) distributed, and demand batch sizes geometric($\gamma _D$); i.e., a generic item batch size $B_I$ has distribution ${{\,\mathrm{\mathbb {P}}\,}}(B_I=n) = \gamma _I (1-\gamma _I)^{n-1}$, $n=1,2,\dots$, and similarly for a generic demand batch size. This case was discussed in Goh et al. (1993); they focus on the busy period, and not on the steady-state analysis of $\textbf{V}$. A generic item batch size $B_I$ is smaller than or equal to a generic demand batch size $B_D$ with probability $\rho$, where it is readily verified that $\rho = \frac{\gamma _I}{\gamma _I + \gamma _D - \gamma _I \gamma _D}$. Hence a demand arrival epoch is with probability $1-\rho$ not accompanied by a jump. By the memoryless property of the geometric distribution, the residual size of the partially taken item batch again is geometric($\gamma _I$) distributed, and so forth. Similarly, if the demand batch size is strictly larger than the item batch size, then the batch demand is only partially satisfied and the residual size of the demand batch again is geometric($\gamma _D$) distributed, and so forth. A conclusion from the above is that we again almost have the basic PIS, in which now jumps upward form a Poisson process with rate $\mu \rho$ and the jump sizes are independent and exp($\lambda (1-\rho )$) distributed. The two exceptions are: (i) a jump size from 0 (after an outdating) is exp($\lambda$) distributed and (ii) the overflow is also exp($\lambda$). Accordingly, we get the balance equations

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} \int _{0}^{x}\mu \rho e^{-\lambda (1-\rho )(x-w)}f(w)dw+f(0)e^{-\lambda x}, &{} 0\le x\le 1, \\ \int _{0}^{1}\mu \rho e^{-\lambda (1-\rho )(1-w)-\lambda (x-1)}f(w)dw+f(0)e^{-\lambda x}, &{} x>1. \end{array} \right. \end{aligned}$$

f(x) can be easily determined from these equations (again multiplying both sides of the first equation by $\textrm{e}^{\lambda x}$ and then differentiating).

Conservation law of satisfied demand We have

$$\begin{aligned} \frac{\lambda -f(0)}{\gamma _I }=\frac{\mu F(1)-f(1)(1-\gamma _D)}{\gamma _D}. \end{aligned}$$

Indeed, the lefthand side represents the rate of not outdated items. The righthand side is the rate of all the demands that arrive when the VOT is below level 1, with one correction: An upcrossing of level 1 means that a residual amount of the arriving demand batch (which is still geometric($\gamma _D$)) is unsatisfied, except if $B_D$ exactly equals $B_I$. The probability of the latter event is $\rho (1-\gamma _D)$. Hence $\frac{{{\,\mathrm{\mathbb {P}}\,}}(B_D>B_I)}{{{\,\mathrm{\mathbb {P}}\,}}(B_D \ge B_I)} = 1-\gamma _D$.

6.2 Demands that are willing to wait

Model variant Perishable items arrive at the shelf according to a renewal process with interrenewal time distribution $G(\cdot )$, having mean $1/\lambda$. Demands for items arrive according to a Poisson process with rate $\mu$, independent of the item arrival times. A demand that upon its arrival finds the shelf of items not empty is satisfied immediately by the oldest item present. Demands that arrive at an empty shelf join the line of waiting demands; newly arriving items are assigned on the spot to waiting demands on a first-come-first-served basis. It should be observed that the main difference with all previously discussed models is that here demands are willing to wait.

Each demand possesses its own random patience time. Denoting by $P_{n}$ the patience time of the nth arriving demand, we assume that $P_1,P_2,\ldots$ is a sequence of i.i.d. positive random variables which are independent of the arrival times of items and demands. $P_1$ has distribution $H(\cdot )$, with mean $1/\eta$. If the waiting time of the nth demand exceeds its patience, then it abandons the waiting line without receiving an item. The shelf lifetime of the stored items, i.e., their maximum usage time, is (as before) set to 1. Thus, each item is stored until it either satisfies some demand or, after one time unit on the shelf, is outdated (and then scrapped).

Motivation This type of model occurs, e.g., when persons demand an organ, or a portion of blood. In both cases, the demanded item can only be stored for a limited amount of time. The organ transplantation problem and the blood transfusion process have been captured in various stochastic models. For further references see (Zenios et al., 2000) for an excellent introduction to the modeling of live organ transplantations by means of a waiting list, see (Perry & Stadje, 1999) for another paper on PIS with demands that are willing to wait, and see the paper (Boxma et al., 2011a) on which the present subsection is based. The model that we discuss here captures the essential aspects of the organ transplantation process, while ignoring some aspects which are relevant in the blood transfusion process (like the fact that not all types of blood are of use for a patient).

The VOT process Again let A(t) denote the age of the oldest item on the shelf at time t, and let $V(t) = 1 - A(t)$. The VOT process $\textbf{V}$ again is a Markov process. It can also be interpreted as the workload process in an $M/G/1+G$ queue—a queue with Poisson($\mu$) arrivals, service requirements with distribution $G(\cdot )$ and patience time $1+P_n$. If the idle periods in such a queue are deleted and the busy periods are glued together, a workload process results which has the same law as $\textbf{V}$. See Fig. 8 for a graphical representation of the age and the VOT process.

Fig. 8

a typical sample path of A(t) and the corresponding sample path of the VOT. $A_n$ ($D_n$) denotes the arrival time of the nth item (demand); $P_n$ denotes the patience time of the nth demand, and $O_n$ the time of the nth outdating

Once again applying LCT, it follows that the stationary density $f(\cdot )$ of $\textbf{V}$ satisfies the integral equations

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} \begin{array}{l} \mu \int _0^x [1-G(x-w)]f(w)\ \textrm{d}w +f(0)[1-G(x)], ~~~0 < x \le 1, \end{array} \\ \ \\ \begin{array}{l} \mu \int _0^1 [1-G(x-w)]f(w)\ \textrm{d}w +f(0)[1-G(x)] \\ \\ +\mu \int _{1}^{x}[1-G(x-w)][1-H(w-1)]f(w)\ \textrm{d}w, ~~~~ x > 1. \end{array} \end{array} \right. \end{aligned}$$

(33)

If the arrival times of items form a Poisson($\lambda$) process, then the VOT is the workload process in an $M/M/1+G$ queue with deleted idle periods. Solving for $f(\cdot )$ in (33) with $1-G(x)$ being replaced by $\textrm{e}^{-\lambda x}$, we obtain (see also Section IV of Baccelli et al. (1981))

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} k_{0}e^{-(\lambda -\mu )x}, &{} 0<x\le 1, \\ k_{1} \exp \left\{ -[\lambda x-\mu \int _1^x (1-H(z-1)) \textrm{d}z] \right\} , &{} x>1, \end{array} \right. \end{aligned}$$

(34)

for certain constants $k_{0}$ and $k_{1}$. To find $k_{0}$ and $k_{1}$ note that f(x) is continuous at 1. We get $k_{0}=k_{1}e^{\mu }$ and $k_0$ can be easily calculated via the normalizing condition for $f(\cdot )$:

$$\begin{aligned} k_0=\bigg [ \int _{0}^{1} e^{-(\lambda -\mu )x} \textrm{d}x+ e^{\mu } \int _{1}^{\infty }\exp \left\{ -[\lambda x-\mu \int _1^x (1-H(z-1)) \textrm{d}z]\right\} \textrm{d}x \bigg ]^{-1}. \end{aligned}$$

The workload density $f(\cdot )$ for general $G(\cdot )$ and $H(\cdot )$ can be obtained from (33) in the following way: (i) solve the integral equation (33) in the interval [0, 1] via Picard iteration (in terms of an infinite series of convolutions and the constant f(0)); (ii) insert this solution in the equation for $x\in (1,\infty )$, which can then also be solved in terms of an infinite series of convolutions in which the first series occurs as under the integral sign; and (iii) determine f(0) from the normalization condition $\int _0^\infty f(x)\ \textrm{d}x = 1$. We refer to Section 4 of Boxma et al. (2011a) for a different approach. There $\textbf{V}$ is decomposed into two processes, which are constructed by deleting the time periods in which $\textbf{V} > 1$ respectively $\textbf{V} \le 1$. The first process is then related to a so-called finite dam, and the second process, decreased by one, represents the workload in an $M/G/1+G$ queue with deleted idle periods in which the first service time of a busy period has a different distribution. The densities of those two processes are subsequently determined.

Key performance measures The rate of item outdatings is given by $\lambda ^{*} = f(0)$. The rate of unsatisfied demands equals $\mu ^{*} = \mu -\lambda + f(0)$. By LCT, the rate of item arrivals at an empty system equals f(1).

We next focus on the steady-state number of items K on the shelf. This number is zero when $\textbf{V} > 1$, and otherwise it equals one plus the number of item arrivals during the age of the oldest item. Hence

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}z^{K}&= \int _{1}^{\infty }f(x)\ \textrm{d}x + \int _0^1 \sum _{n=1}^\infty z^n {{\,\mathrm{\mathbb {P}}\,}}(n-1 \text{ arrivals } \text{ in } ~ 1-x) f(x)\ \textrm{d}x \nonumber \\&= \int _{1}^{\infty }f(x)\ \textrm{d}x + \int _0^1 \sum _{n=1}^\infty z^n (G^{(n-1)*}(1-x) - G^{n*}(1-x)) f(x)\ \textrm{d}x . \end{aligned}$$

(35)

When items arrive according to a Poisson($\lambda$) process, the sum over n becomes $z \textrm{e}^ {-\lambda (1-z)(1-x)}$. We refer to Boxma et al. (2011a) for a study of the steady-state waiting time of demands, of the long-run fraction of time the shelf is empty, and of the outdating process. The number of waiting demands has been studied in the setting of the $M/G/1+G$ queue, cf. Boxma et al. (2011b).

6.3 Outdating and unsatisfied demands in the M/G PIS model

Model variant In this subsection we again have Poisson($\mu$) demand arrivals while item arrivals form a renewal process with renewal distribution $G(\cdot )$. As before, we assume that each item has a usable lifetime of one time unit and that, upon arrival, a demand removes the oldest item on the shelf—leaving unsatisfied if the shelf is empty. An item that has not been taken within one time unit of arrival becomes outdated. Finally, the arrival processes of items and demands are again assumed to be independent.

We already know how to obtain the density $f(\cdot )$ of the VOT process, but in this subsection we shall exploit its knowledge only in a few places. We shall mainly focus on the following three performance measures, and on some useful techniques for analyzing them: The time between two successive outdatings, the time between two successive unsatisfied demands, and the shelf emptiness period.

The distribution of the time between two successive outdatings. As observed before, the time between successive outdatings is a busy period in the $M/G/1+D$ queue. Its distribution has been derived in Perry et al. (2000). As the analysis in that paper, and the end result, are very complicated, we here present a different approach that is applicable when $G(\cdot )$ has a phase-type distribution or, more specifically, a mixture of Erlang distributions with the same mean for all exponential phases. This class of distributions is known to lie dense in the class of all probability distributions of nonnegative random variables (cf. Section III.4 of Asmussen (2003)). To explain the approach, we restrict ourselves here even further to the case that $G(\cdot )$ is an Erlang distribution with two exponential phases: $G(x) = \int _0^x \lambda ^2 t \textrm{e}^{-\lambda t} \textrm{d}t$ (note that the mean item interarrival time now is $2/\lambda$). A key quantity in the analysis is the stopping time

$$\begin{aligned} \tau =\min \{t:V(t)=0\ \ \textrm{or}\ \ V(t)\ge 1\},\ \ \end{aligned}$$

when starting in some state x. We use the abbreviation ${{\,\mathrm{\mathbb {E}}\,}}_{x}={{\,\mathrm{\mathbb {E}}\,}}(\cdot \mid V(0)=x)$. The conditional joint LST ${{\,\mathrm{\mathbb {E}}\,}}_x\left( \textrm{e}^{-\alpha V(\tau )-\beta \tau }{\vert }V(\tau )>1\right)$ of the overflow and the time of the overflow given that an overflow occurred is not easy to obtain for general $G(\cdot )$ due to the dependence between $V(\tau )$ and $\tau$. However, when the item interarrival times are Erlang distributed, $V(\tau )$ and $\tau$ are conditionally independent given the number of exponential phases of the overflow above level 1. We now first show how it can be obtained in the Erlang($2,\lambda$) case. Defining the events $I=${level 1 is upcrossed by the second phase of the jump} and $II=${level 1 is upcrossed by the first phase of the jump}, we have for $Q=I,II$:

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_x\left( \textrm{e}^{-\alpha V(\tau )-\beta \tau }{\vert }V(\tau )>1, Q \right) ={{\,\mathrm{\mathbb {E}}\,}}_x\left( \textrm{e}^{-\alpha V(\tau )}{\vert }V(\tau )>1, Q \right) {{\,\mathrm{\mathbb {E}}\,}}_x\left( \textrm{e}^{-\beta \tau }{\vert }V(\tau )>1, Q \right) , \end{aligned}$$

(36)

and

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_x\left( \textrm{e}^{-\alpha V(\tau )-\beta \tau }{1}_{{ \{V(\tau )>1\}} }\right)= & {} {{\,\mathrm{\mathbb {E}}\,}}_x\left( \textrm{e}^{-\alpha V(\tau )-\beta \tau }{ 1}_{{ \{V(\tau )>1, I \}} }\right) +{{\,\mathrm{\mathbb {E}}\,}}_x\left( \textrm{e}^{-\alpha V(\tau )-\beta \tau }{ 1}_{{ \{V(\tau )>1, II \}} }\right) \nonumber \\= & {} \textrm{e}^{-\alpha }\frac{\lambda }{\lambda +\alpha } {{\,\mathrm{\mathbb {E}}\,}}\left( \textrm{e}^{-\beta \tau }{ 1}_{{ I}}\right) + \textrm{e}^{-\alpha } \left( \frac{\lambda }{\lambda +\alpha }\right) ^{2} {{\,\mathrm{\mathbb {E}}\,}}\left( \textrm{e}^{-\beta \tau }{ 1}_{{ II}}\right) .\nonumber \\ \end{aligned}$$

(37)

Then, for $0<x\le 1$ we get

$$\begin{aligned} \begin{array}{lll} {{\,\mathrm{\mathbb {E}}\,}}_{x}\textrm{e}^{-\alpha V(\tau )-\beta \tau }= & {} \phi _{0}(\beta ;x)+\textrm{e}^{-\alpha } \frac{\lambda }{\lambda +\alpha }\phi _{I}(\beta ;x)+\textrm{e}^{-\alpha }\left( \frac{\lambda }{\lambda +\alpha }\right) ^{2}\phi _{II}(\beta ;x), \end{array} \end{aligned}$$

where $\phi _{0}(\beta ;x)$, $\phi _{I}(\beta ;x)$ and $\phi _{II}(\beta ;x)$ are the partial LSTs of $\tau$ such that

$$\begin{aligned} \begin{array}{l} \phi _{0}(\beta ;x):={{\,\mathrm{\mathbb {E}}\,}}_x\textrm{e}^{-\alpha V(\tau )-\beta \tau }{ 1}_{{ \{V(\tau )=0\}}} = {{\,\mathrm{\mathbb {E}}\,}}_x\textrm{e}^{-\beta \tau } { 1}_{\{V(\tau )=0\}} , \\ \phi _{I}(\beta ;x):={{\,\mathrm{\mathbb {E}}\,}}_x\textrm{e}^{-\beta \tau }{ 1}_{{ I}}, \\ \phi _{II}(\beta ;x):={{\,\mathrm{\mathbb {E}}\,}}_x\textrm{e}^{-\beta \tau }{ 1}_{{ II }}. \end{array} \end{aligned}$$

(38)

Note that $\phi _{0}(0;x)$, $\phi _{I}(0;x)$ and $\phi _{II}(0;x)$ are the probabilities of the event $\{V(\tau )=0\}$, the event I and the event II, respectively. To find $\phi _{0}(\beta ;x)$, $\phi _{I}(\beta ;x)$ and $\phi _{II}(\beta ;x)$ consider the following process M(s) which is a Kella-Whitt martingale (cf. Kella and Whitt 1992):

$$\begin{aligned} M(s):= \left[ \alpha -\mu \left( 1-\left( \frac{\lambda }{\lambda +\alpha }\right) ^{2}\right) -\beta \right] \int _{0}^{s}\textrm{e}^{-\alpha V(t)-\beta t} \textrm{d}t + \textrm{e}^{-\alpha x} - \textrm{e}^{-\alpha V(s) -\beta s}. \end{aligned}$$

Now use the optional sampling theorem with stopping time $\tau$ to obtain ${{\,\mathrm{\mathbb {E}}\,}}M(\tau )=0$, i.e., the following fundamental identity:

$$\begin{aligned}{} & {} \left[ \alpha -\mu \left( 1-\left( \frac{\lambda }{\lambda +\alpha }\right) ^{2}\right) -\beta \right] {{\,\mathrm{\mathbb {E}}\,}}_{x}\int _{0}^{\tau }\textrm{e}^{-\alpha V(t)-\beta t}\textrm{d}t =-\textrm{e}^{-\alpha x} \nonumber \\{} & {} \quad +\phi _{0}(\beta ;x)+\textrm{e}^{-\alpha }\frac{\lambda }{\lambda +\alpha }\phi _{I}(\beta ;x)+\textrm{e}^{-\alpha }\left( \frac{\lambda }{\lambda +\alpha }\right) ^{2}\phi _{II}(\beta ;x). \end{aligned}$$

(39)

The term between square brackets in the lefthand side has three zeroes (which actually are real), while the ${{\,\mathrm{\mathbb {E}}\,}}_x$ term must be finite for finite $\alpha$; hence we get three linear equations for the three unknowns $\phi _{0}(\beta ;x)$, $\phi _{I}(\beta ;x)$ and $\phi _{II}(\beta ;x)$.

Remark 9

Briefly consider the case that $G(\cdot )$ is a mixture of Erlang distributions with the same mean for all exponential phases. Its LST is given by $b(\alpha ) = \sum _{k=1}^n p_k (\frac{\lambda }{\lambda +\alpha })^k$, with all $p_k>0$ and summing to one. We then have to distinguish between n instead of two events, corresponding to the number of phases of overshoots above 1. The Kella-Whitt martingale now yields a generalization of (39) with $n+1$ unknown functions of x in the righthand side, while the term between square brackets in the lefthand side is replaced by $\alpha - \mu (1-b(\alpha )) - \beta$. This is a familiar term in the study of the transient behavior of the M/G/1 queue, cf. p. 259 and p. 548 of Cohen (1982). The term has $n+1$ zeroes in our case; Rouché’s theorem can be used to prove that one of them lies in the righthalf plane, but the zeroes are not necessarily real. It is also not a priori clear how to prove that the resulting $n+1$ linear equations for the $n+1$ unknowns are independent.

We are now ready to obtain the LST of T, the time between two successive outdatings. We have

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}\textrm{e}^{-\beta T}=\int _{0}^{1}\lambda ^{2}xe^{-\lambda x}{{\,\mathrm{\mathbb {E}}\,}}_{x}\textrm{e}^{-\beta T}\textrm{d}x+{{\,\mathrm{\mathbb {E}}\,}}_{1}\textrm{e}^{-\beta T}\left[ \lambda \textrm{e}^{-\lambda }\frac{\lambda }{\lambda +\beta }+\textrm{e}^{-\lambda }\left( \frac{\lambda }{\lambda +\beta }\right) ^{2} \right] . \end{aligned}$$

(40)

To solve for ${{\,\mathrm{\mathbb {E}}\,}}\textrm{e}^{-\beta T}$ we first have to find ${{\,\mathrm{\mathbb {E}}\,}}_{x}\textrm{e}^{-\beta T}$for $0<x\le 1$. Observe that the factor $\lambda \textrm{e}^{-\lambda }$ is the probability that the first phase of the item arrival interval does not exceed 1, but the sum of the two phases does exceed 1, and that the factor $\textrm{e}^{-\lambda }$ is the probability that the first phase of the item arrival interval exceeds 1. We have

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{x}e^{-\beta T}=\phi _{0}(\beta ;x)+\phi _{I}(\beta ;x)\frac{\lambda }{ \lambda +\beta }{{\,\mathrm{\mathbb {E}}\,}}_{1}e^{-\beta T}+\phi _{II}(\beta ;x)\left( \frac{\lambda }{ \lambda +\beta }\right) ^{2}{{\,\mathrm{\mathbb {E}}\,}}_{1}e^{-\beta T}, \end{aligned}$$

and by substituting $x=1$ we obtain the LST of the time between two successive outdatings:

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{1}e^{-\beta T}=\frac{\phi _{0}(\beta ;1)}{1-\phi _{I}(\beta ;1)\frac{ \lambda }{\lambda +\beta }-\phi _{II}(\beta ;1)\left( \frac{\lambda }{ \lambda +\beta }\right) ^{2}}. \end{aligned}$$

The time between two successive unsatisfied demands Consider an upcrossing of level 1 of the VOT process $\textbf{V}$. Because of the Erlang($2,\lambda$) item arrival intervals, such an upcrossing is either with one or with two exp($\lambda$) phases. If the next demand occurs before an arrival of an item on the shelf, it is unsatisfied. The unsatisfied demand process is not a renewal process. However, we can find the LST of the time U between two successive unsatisfied demands by distinguishing whether an upcrossing of level 1 occurs with one or two exp($\lambda$) phases. Let $\Psi ^{(i)}(\beta )$ denote the LST of the time from such an upcrossing until the next unsatisfied demand, if that upcrossing is with i phases, $i=1,2$. We have, with ${{\,\mathrm{\mathbb {E}}\,}}_1 \textrm{e}^{-\beta U}$ the conditional LST of the remaining length of U, from the moment that level 1 is downcrossed:

$$\begin{aligned} \Psi ^{(1)}(\beta )=\frac{\mu }{\mu +\lambda +\beta }+\frac{\lambda }{\mu +\lambda +\beta }{{\,\mathrm{\mathbb {E}}\,}}_{1}\textrm{e}^{-\beta U}, \end{aligned}$$

and

$$\begin{aligned} \Psi ^{(2)}(\beta )=\frac{\mu }{\mu +\lambda +\beta }+\frac{\lambda }{\mu +\lambda +\beta }\Psi ^{(1)}(\beta ). \end{aligned}$$

To compute ${{\,\mathrm{\mathbb {E}}\,}}_{1}\textrm{e}^{-\beta U}$, and more generally ${{\,\mathrm{\mathbb {E}}\,}}_x\textrm{e}^{-\beta U}$, the LST of the time until the next unsatisfied demand when starting from level x, we distinguish between the three possibilities that stopping time $\tau$ first occurs via an upcrossing of level 1 with one phase, or with two phases, or that it occurs by reaching level zero:

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{x}\textrm{e}^{-\beta U}= & {} \phi _{I}(\beta ;x)\Psi ^{(1)}(\beta )+\phi _{II}(\beta ;x)\Psi ^{(2)}(\beta ) \nonumber \\{} & {} +\phi _{0}(\beta ;x)\left[ \int _{0}^{1}\lambda ^{2}y \textrm{e}^{-\lambda y}{{\,\mathrm{\mathbb {E}}\,}}_{y}\textrm{e}^{-\beta U}dy+\lambda \textrm{e}^{-\lambda }\Psi ^{(1)}(\beta )+\textrm{e}^{-\lambda }\Psi ^{(2)}(\beta )\right] . \nonumber \\ \end{aligned}$$

(41)

To solve for ${{\,\mathrm{\mathbb {E}}\,}}_{x}e^{-\beta U}$ multiply both sides of (41) by $\lambda ^{2}x \textrm{e}^{-\lambda x}$, integrate and introduce

$$\begin{aligned} \Omega (\beta ):=\int _{0}^{1}\lambda ^{2}x\textrm{e}^{-\lambda x}{{\,\mathrm{\mathbb {E}}\,}}_{x}\textrm{e}^{-\beta U}\textrm{d}x. \end{aligned}$$

Then we get

$$\begin{aligned} \Omega (\beta )= & {} \Psi ^{(1)}(\beta ) \int _{0}^{1}\lambda ^{2} x\textrm{e}^{-\lambda x}\phi _{I}(\beta ;x)\textrm{d}x \\{} & {} +\Psi ^{(2)}(\beta ) \int _{0}^{1}\lambda ^{2}x\textrm{e}^{-\lambda x}\phi _{II}(\beta ;x)\textrm{d}x \\{} & {} +[\Omega (\beta ) + \lambda \textrm{e}^{-\lambda } \Psi ^{(1)}(\beta ) + \textrm{e}^{-\lambda } \Psi ^{(2)}(\beta )] \int _{0}^{1}\lambda ^{2}x\textrm{e}^{-\lambda x}\phi _{0}(\beta ;x)\textrm{d}x, \end{aligned}$$

so that

$$\begin{aligned} \Omega (\beta )= & {} \frac{\Psi ^{(1)}(\beta ) \int _{0}^{1}\lambda ^{2}x \textrm{e}^{-\lambda x}\phi _{I}(\beta ;x)\textrm{d}x +\Psi ^{(2)}(\beta ) \int _{0}^{1}\lambda ^{2}x\textrm{e}^{-\lambda x}\phi _{II}(\beta ;x)\textrm{d}x}{1-\int _{0}^{1}\lambda ^{2}x \textrm{e}^{-\lambda x}\phi _{0}(\beta ;x)\textrm{d}x} \nonumber \\{} & {} + \frac{ [\lambda \textrm{e}^{-\lambda } \Psi ^{(1)}(\beta ) + \textrm{e}^{-\lambda } \Psi ^{(2)}(\beta )] \int _0^1 \lambda ^2 x \textrm{e}^{-\lambda x} \phi _0(\beta ;x) \textrm{d}x}{1-\int _{0}^{1}\lambda ^{2}x \textrm{e}^{-\lambda x}\phi _{0}(\beta ;x)\textrm{d}x}. \end{aligned}$$

Now observe that this expression for $\Omega (\beta )$ still contains (hidden in $\Psi ^{(1)}(\beta )$) the unknown ${{\,\mathrm{\mathbb {E}}\,}}_1 \textrm{e}^{-\beta U}$. By taking $x=1$ in (41) we obtain a second linear equation between $\Omega (\beta )$ and ${{\,\mathrm{\mathbb {E}}\,}}_1 \textrm{e}^{-\beta U}$, and thus both functions can be determined.

Remark 10

We emphasize that the time periods between unsatisfied demands are neither independent nor identically distributed, but they are conditionally independent given the number of phases of the overshoot above level 1. It is also of relevance to determine the probability $\zeta$ that an overshoot above level 1 is one phase. $\zeta$ can be determined by observing that 1/f(1) is the mean time between successive unsatisfied demands, and that hence the fraction of time above level 1 can be written as

$$\begin{aligned} 1-F(1)=f(1)\left[ \frac{\zeta }{\lambda }+\frac{2(1-\zeta )}{\lambda } \right] =f(1)\frac{2-\zeta }{\lambda }. \end{aligned}$$

Hence

$$\begin{aligned} \zeta =\frac{\lambda [\lambda -2f(1)]}{f(1) } (\frac{1}{2\mu } - \frac{1}{\lambda }). \end{aligned}$$

Incidentally, that factor $(2-\zeta )/\lambda$ is not only the expected overshoot above level 1, but of course it is also the expected length of the emptiness period.

The emptiness period: The general case Earlier we already emphasized the analogy between the $M/G/1+D$ queue and the PIS model with Poisson demand arrival process and with a renewal arrival process of items. In particular, the workload process of the latter queue, with the idle periods deleted, agrees with the VOT process of the PIS. However, different quantities are of interest in the queue and PIS setting. For example, the amount of overflow above level 1 is not of that much relevance in the $M/G/1+D$ queue, but it represents the important emptiness period of the shelf in the PIS. We study it below. For this, we need the steady-state density $f(\cdot )$ of the VOT $\textbf{V}$. In Sect. 5 we have discussed how $f(\cdot )$ can be obtained by solving (26) via Picard iteration. Using this knowledge about $f(\cdot )$ we obtain the distribution $B(\cdot )$ of the overshoot above level 1. The following lemma has been introduced in Boxma et al. (2011a), with a different motivation, and for the case of constant $\mu (\cdot )$.

Lemma 2

$$\begin{aligned} B(x)=1-\frac{f(x+1)}{f(1)}, ~~~x \ge 0, \end{aligned}$$

where $f(\cdot )$ is the solution of (26).

Proof

On the one hand, $b_{e}(x):=\frac{f(x+1)}{1-F(1)}$ for $x>0$ is the conditional steady-state density of $\textbf{V}$ given that the shelf is empty. On the other hand, by deleting the time periods in which $\textbf{V} \le 1$ and gluing together the time periods in which $\textbf{V}>1$ we see that above level 1 the behavior of the VOT $\textbf{V}$ is stochastically equal to that of the equilibrium forward recurrence time associated with $B(\cdot )$, so that $b_{e}(x)=\frac{1-B(x)}{\int _{0}^{\infty }[1-B(y)]dy}$. From the argument above, $\int _{0}^{\infty }[1-B(y)]dy=\frac{1-F(1)}{f(1)}$. Thus, by equating $\frac{f(x+1)}{1-F(1)}$ with $\frac{1-B(x)}{ \int _{0}^{\infty }[1-B(y)]dy}$, the lemma follows. $\square$

We end this section by briefly mentioning Cohen’s approach (Cohen, 1976, Chapter III) to the workload distribution in the $M/G/1+D$ queue, with buffer size $D=1$. Note that this immediately translates into results for the M/G PIS model. Cohen derives $\xi (x):= {{\,\mathrm{\mathbb {P}}\,}}_x(V(\tau )=0) = 1 - {{\,\mathrm{\mathbb {P}}\,}}_x(V(\tau ) \ge 1)$, for the case of general $G(\cdot )$, as well as the steady-state workload distribution. Note that $\xi (x)$ is the probability that the shelf becomes empty before an outdating when the starting state is x. This probability is of importance from an operational research point of view, since outdating (perishability) and emptying the shelf involve costs of an opposite type that should be optimally balanced. Cohen introduces $\tilde{G}(x):= \rho \int _0^x (1-G(y)) \textrm{d}y$, with $\rho := \lambda {{\,\mathrm{\mathbb {E}}\,}}G$, and a parameter $\delta$ which is zero if $\rho \le 1$ and which otherwise is the unique positive zero of $\int _0^{\infty } \textrm{e}^{-xy} \textrm{d} \tilde{G}(y) - 1$. He then proves that, with $\hat{G}(x):= \int _0^x \textrm{e}^{-\delta y} \textrm{d}\tilde{G}(y)$ and with

$$\begin{aligned} \tilde{V}(x) := \int _{0-}^x \textrm{e}^{\delta y} \textrm{d} \sum _{n=0}^{\infty } \hat{G}^{n*}(y), ~~~x \ge 0, \end{aligned}$$

(42)

one has the following expression for the steady-state distribution of the workload $V^{(1)}$ in the finite dam $M/G/1+D$ with buffer of size $D=1$:

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}(V^{(1)}< x) = \frac{\tilde{V}(x)}{\tilde{V}(1)}, ~~~0 < x \le 1. \end{aligned}$$

(43)

See also (29) for another representation, up to a multiplicative constant. For $\rho < 1$ the steady-state workload distribution of the ordinary M/G/1 queue exists, and $\tilde{V}(x)$ is proportional to that distribution, with proportionality factor $1/(1-\rho )$; and it is a well-known result that the steady-state distribution of the finite dam ($M/G/1+D$) for $\rho < 1$ is proportional to the steady-state workload distribution in the infinite dam (M/G/1); see, e.g., Hooghiemstra (1987) for an elegant sample-path proof.

Cohen (1976) subsequently obtains the following expression for the probability $\xi (x)$ that the workload process hits level 0 before hitting level 1, when starting from level x:

$$\begin{aligned} \xi (x) = \frac{\tilde{V}(1-x)}{\tilde{V}(1)}, ~~~0 \le x < 1. \end{aligned}$$

(44)

Such exit probability results have later been obtained in much greater generality for Lévy processes, typically expressing these exit probabilities in terms of so-called scale functions (cf. Section 8.2 of Kyprianou, 2006).

7 Conclusion and suggestions for further research

In this paper we have surveyed, extended and enriched the probabilistic analysis of a large class of perishable inventory systems. We have emphasized that a unifying principle is to consider the so-called virtual outdating process $\textbf{V}$, where V(t) equals one minus the age of the oldest item on the shelf at time t. The steady-state density of $\textbf{V}$ was shown to be the main vehcle to obtain key performance measures like the rate of outdatings, the rate of unsatisfied demands and the distribution of the number of items on the shelf.

Through the years, we have devoted a significant part of our research efforts towards the probabilistic analysis of perishable inventory systems, and we hope to inspire others to also study them at length. There are many interesting methods and fascinating open problems in this area. Moreover, perishable inventory systems have huge societal relevance, and there is an abundance of practically relevant variants of the basic PIS that we have described in Sect. 2. Some such variants and generalizations have been described and analyzed in the present paper, but neither did we have the space to discuss them exhaustively, nor were we able to treat all the major variants. Below we mention a few more interesting PIS problems.

• FIFO versus LIFO. In the PIS literature, it is commonly assumed that items are issued First-In-First-Out (FIFO). One exception is Parlar et al. (2011), where the Last-In-First-Out (LIFO) issuance policy is studied for the basic PIS. Under LIFO, the shelf sojourn time of an item is shown to be distributed as the minimum of 1 and the busy period of an M/M/1 queue with arrival rate $\lambda$ and service rate $\mu$. This result is used to derive several other performance measures. Subsequently FIFO and LIFO are compared according to some cost criterion. Interestingly, while FIFO performs better in most cases, LIFO is better when the holding costs of items are high. It would be interesting to study other issuance policies like a random selection policy. For the secondary products/emergency demands model discussed at the end of Sect. 4.3, it could be natural to assume that in the upper shelf (items for emergency demands) the issuance policy is LIFO.

• Disasters. In Perry and Stadje (2001), the basic PIS is studied with the following additional feature: at Poisson epochs, all items become obsolete (e.g., because of a power failure). The steady-state density of the VOT is derived using LCT and solving a second-order homogeneous differential equation. In an extended version of this paper, we intend to treat this model for the case of renewal arrivals of items.

  In Perry and Stadje (2001) the system is also studied in heavy traffic. Under those conditions, the system is only instantaneously empty. Between disasters, the VOT evolves like reflected Brownian motion on [0, 1]. At disasters, it restarts at 1. Using the theory of reflected Brownian motion (cf. Chapter 5 of Harrison (1985)), several cost functionals are determined.

• Heavy traffic. Another heavy-traffic study of a PIS is performed in Perry (1997). It proposes a diffusion approximation for a basic PIS with the additional feature of hysteresis (cf. also Sect. 4.1). A reflected Brownian motion between barriers 0 and 1 is obtained, with the special feature that the drift becomes $\gamma _L$ when the process downcrosses a level a, and becomes $\gamma _H$ the first time that the process subsequently upcrosses some level $b>a$. The stationary law of the process is analysed by using a martingale, and the total expected discounted costs are evaluated. This heavy-traffic approach seems to have potential for a wider class of PIS, and could be explored further.

• Two systems with one-way substitution.Liu et al. (2022) study two PIS that are correlated through a so-called one-way substitution of demands. If the shelf of PIS II is empty when it receives a type-II demand, then that demand is redirected to PIS I. However, if the shelf of PIS I is empty when it receives a type-I demand, then that demand cannot be redirected. This problem is inspired by blood banks, in which persons of a particular blood type can or cannot use blood of another type. The mathematical analysis of PIS II is straightforward, but that of PIS I gives rise to a modulated Poisson demand process in a non-Markovian environment, for which Liu et al. develop an approximation method. The study of correlated systems of PIS still is almost unexplored territory.

• Lead times. In many real-life inventory systems, there is an item ordering policy, under which one or more items are ordered when the number of items in stock decreases to a certain level; and typically there is a lead time involved in such a replenishment order. We refer to Berk and Gürler (2008) for the study of a PIS with the so-called (Q, r) replenishment policy with lead times.

• Positive service times. As mentioned in Sect. 1, there is an interesting line of research regarding PIS with positive service times: if a demand arrives and finds an item in stock, it takes a positive amount of time to take that item. It would be interesting to explore whether the VOT approach can shed light on such PIS models.

Finally, we would like to point out that the transient behavior of PIS has hardly received attention so far. Also, it would be useful to have sharp approximations and bounds for key performance measures in cases for which it is too hard to obtain explicit expressions for the steady-state density of the VOT.