Fuzzy clustering with entropy regularization for interval-valued data with an application to scientific journal citations

Abstract

In recent years, the research of statistical methods to analyze complex structures of data has increased. In particular, a lot of attention has been focused on the interval-valued data. In a classical cluster analysis framework, an interesting line of research has focused on the clustering of interval-valued data based on fuzzy approaches. Following the partitioning around medoids fuzzy approach research line, a new fuzzy clustering model for interval-valued data is suggested. In particular, we propose a new model based on the use of the entropy as a regularization function in the fuzzy clustering criterion. The model uses a robust weighted dissimilarity measure to smooth noisy data and weigh the center and radius components of the interval-valued data, respectively. To show the good performances of the proposed clustering model, we provide a simulation study and an application to the clustering of scientific journals in research evaluation.

1 Introduction

In recent years, the research of statistical methods to analyze complex structures of data has increased. In particular, a lot of attention has been focused on the interval-valued data (Denoeux & Masson, 2000; D’Urso & De Giovanni, 2014; D’Urso & Leski, 2016).

In the literature on data analysis, a great deal of attention is paid to statistical methods to treat interval-valued data, in different research areas (Coppi et al., 2006; Denoeux & Masson, 2000; D’Urso & Giordani, 2005; Giordani & Kiers, 2004; D’Urso & Leski, 2016; D’Urso & De Giovanni, 2014).

In a classical cluster analysis framework, a variety of interesting methods have been suggested. In particular, Gowda and Diday (1991) hinted a clustering method for symbolic data; Guru et al. (2004) proposed a similarity measure to compare interval-valued data and a modified agglomerative method for clustering symbolic data. De Carvalho and Lechevallier (2009) proposed a partitional dynamic clustering method for interval data based on adaptive Hausdorff distances; De Carvalho et al. (2006) suggested clustering methods for interval data based on single adaptive distances.

An interesting line of research has focused on the clustering of interval-valued data based on fuzzy approaches, where the weighting exponent m controls the extent of membership sharing between fuzzy clusters (De Carvalho & Tenório, 2010; Denoeux & Masson, 2000; D’Urso et al., 2015b; D’Urso & Giordani, 2006a; D’Urso et al., 2017). Li and Mukaidono (1995) remarked that this unusual parameter is unnatural and doesn’t have a physical meaning. The parameter m may be removed in the objective function of the clustering model; when this is the case, the procedure cannot generate the membership update equations (Coppi & D’Urso, 2006). For this purpose, Li and Mukaidono (1995, 1999) suggested a new approach to fuzzy clustering by proposing the so-called Maximum Entropy Inference Method. The underlying idea is presented in the paper by Miyamoto and Mukaidono (1997), where the trade-off between fuzziness and compactness is dealt with by introducing a unique objective function reformulating the maximum entropy method in terms of regularization of the Fuzzy c-Means (FCM) function.

In the literature, many authors proposed the entropy-based approach as a regularization in fuzzy clustering modeling. In particular, Yao et al. (2000) proposed an entropy-based fuzzy clustering method which automatically identifies the number and initial locations of cluster centers. Successively, it removes all data points having dissimilarity larger than a threshold with the chosen cluster center; the procedure is repeated until all data points are removed. Ichihashi (2000) and Miyagishi et al. (2000) suggested a generalized objective function with additional variables. These authors consider a covariance matrix and show an equivalence between their Kullback–Leibler (KL) fuzzy clustering and the Gaussian mixture model. The method of fuzzy clustering using the KL information is called entropy-based method of FCM. Ménard and Eboueya (2002) suggested an axiomatic derivation of the Maximum Entropy Inference (and also of the possibilistic) clustering approach, based on a unifying principle of physics, that of Extreme Physical Information (EPI) defined by Frieden and Binder (2000). Coppi and D’Urso (2006) suggested fuzzy unsupervised clustering models based on Shannon entropy regularization to classify time-varying data. Zarinbal et al. (2014) proposed a new fuzzy clustering method based on FCM and the relative entropy is added to the objective function as a regularization function to maximize the dissimilarity between clusters. Kahali et al. (2019) presented an entropy-based FCM segmentation method that incorporates the uncertainty of classification of individual pixels within the classical framework of FCM. Gao et al. (2019) showed a novel method considering noise intelligently based on the existing FCM approach, called adaptive-FCM and its extended version (adaptive-REFCM) in combination with relative entropy. More recently, Ashtari et al. (2020) proposed an entropy-based regularization approach to fuzzify the partition and to weight features, enabling the method to capture more complex patterns, identify significant features, and yield better performance facing high-dimensional data.

Note that the models cited above utilizing entropy-based regularization regard ordinary point data.

Following this line of research, in this paper a new robust fuzzy clustering model for interval-valued data with entropy as a regularization function is proposed. The model is named Robust Entropy-based Fuzzy c-Medoids clustering for interval-valued data (EFCMd-ID).

The paper is organized as follows. In Sect. 2.1, the basic notation and the family of robust dissimilarity measures for interval-valued data are described; in Sect. 2.2, the motivation of the use of the Shannon entropy regularization in fuzzy clustering is discussed. Then in Sect. 2.3, the modeling details and the algorithm of the proposed EFCMd-ID model for interval-valued data along with the Robust Entropy-based Fuzzy c-Means clustering variant (EFCM-ID) are presented. In Sect. 3, a detailed simulation study and comparison with other fuzzy and not fuzzy clustering models for interval-valued data is proposed. In Sect. 4, the results obtained by the application of the EFCMd-ID model on empirical data are shown. In Sect. 5, some concluding remarks and the lines for future research are provided.

2 Robust entropy-based fuzzy c-medoids clustering for interval-valued data (robust EFCMd-ID model)

2.1 Robust dissimilarity measure for interval-valued data

An interval-valued datum can be formalized as $x_{ij}=[\underline{x}_{ij},\overline{x}_{ij}],\,i=1,\ldots ,I;\, j=1,\ldots ,J$, where $x_{ij}$ indicates the j-th interval-valued variable observed on the i-th object; $\underline{x}_{ij}$ and $\overline{x}_{ij}$ denote, respectively, the lower and upper bounds of the interval, i.e., they represent the minimum and maximum values of the j-th interval-valued variable with respect to the i-th object. Each object is represented geometrically by a hyper-rectangle in $\mathfrak {R}^j$ having $2^J$ vertices. All the $2^J$ vertices correspond to all the possible (lower bound, upper bound) combinations. In particular, in $\mathfrak {R}\,\, (J=1)$ the generic object is represented by a segment; in $\mathfrak {R}^2\,\, (J=2)$, it is represented by a rectangle with $2^2=4$ vertices, and so on (Cazes et al., 1997).

Then, assuming J interval-valued variables are observed on I objects, the entire dataset can be stored in the so-called interval-valued matrix as follows:

$$\begin{aligned} \textbf{X}\equiv \{x_{ij}=[\underline{x}_{ij},\overline{x}_{ij}]:\,i=1,\ldots ,I;\, j=1,\ldots ,J\}. \end{aligned}$$

(1)

By denoting with

$$\begin{aligned} \textbf{M}\equiv \left\{ m_{ij}=\frac{\overline{x}_{ij}+\underline{x}_{ij}}{2}:\,i=1,\ldots I;\, j=1,\ldots ,J\right\} , \end{aligned}$$

(2)

the midpoint matrix (center matrix), where $m_{ij}$ is the midpoint (center) of the associated interval value for $i=1,\ldots ,I$ and $j=1,\ldots ,J$, and with

$$\begin{aligned} \textbf{R}\equiv \left\{ r_{ij}=\frac{\overline{x}_{ij}-\underline{x}_{ij}}{2}:\,i=1,\ldots ,I;\, j=1,\ldots ,J\right\} , \end{aligned}$$

(3)

the radius matrix, where $r_{ij}$ is the radius (spread) of the associated interval for $i=1,\ldots ,I$ and $j=1,\ldots ,J$, we can reformulate the interval-valued matrix (1) as follows:

$$\begin{aligned} {\tilde{\textbf{X}}}\equiv \{\tilde{x}_{ij}=[m_{ij},r_{ij}]:\,i=1,\ldots ,I;\, j=1,\ldots ,J\}=\{{\tilde{\textbf{x}}}_{i}=[\textbf{m}_{i},\textbf{r}_{i}]:\,i=1,\ldots ,I\}. \end{aligned}$$

(4)

where $\textbf{m}_{i}$ and $\textbf{r}_{i}$ denote, respectively, the i-th row of $\textbf{M}$ and $\textbf{R}$.

Then, $\tilde{x}_{ij}=[m_{ij},r_{ij}]$ represents an alternative formalization of the interval-valued datum $x_{ij}=[\underline{x}_{ij},\overline{x}_{ij}]$. In this way, the lower and upper bounds of the interval-valued datum can be obtained as $\underline{x}_{ij}=m_{ij}-r_{ij}$ and $\overline{x}_{ij}=m_{ij}+r_{ij}$, respectively.

The generic interval-valued datum pertaining to the i-th object with respect to the j-th interval-valued feature can be shown as the pair ($m_{ij}$,$r_{ij}$), $i={1,\dots , I}$ and $j={1,\dots , J}$, where $m_{ij}$ denotes the midpoint and $r_{ij}$ denotes the radius of the interval.

In the literature, several metrics have been suggested for interval-valued data. In this paper, we adopt a robust weighted dissimilarity measure.

The robustness of the dissimilarity measure for interval-valued data is obtained by considering the exponential version (Wu & Yang, 2002; Zhang & Chen, 2004) of the distance measure for interval-valued data proposed by D’Urso and Giordani (2004) and successively adopted by D’Urso et al. (2017).

The dissimilarity measure is weighted as the dissimilarity between each pair of objects is measured by separately considering the midpoints and the radii of the interval-valued data and using a suitable weighting system for such components (D’Urso & Giordani, 2006b).

In formula, the robust weighted dissimilarity measure between objects i and $i'$ is:

$$\begin{aligned} \begin{aligned} d^2_{exp}({\tilde{\textbf{x}}}_{i},{\tilde{\textbf{x}}}_{i'})=\left\{ 1-exp \left[ -\beta [w_m^2d^2(\textbf{m}_{i},\textbf{m}_{i'}) +w_r^2d^2(\textbf{r}_{i},\textbf{r}_{i'})\right] \right\} \end{aligned} \end{aligned}$$

(5)

where $d^2(\textbf{m}_{i},\textbf{m}_{i'})=\left\| \textbf{m}_{i}-\textbf{m}_{i'}\right\| ^2$ is the squared Euclidean distance between the midpoints and $d^2(\textbf{r}_{i},\textbf{r}_{i'})=\left\| \textbf{r}_{i}-\textbf{r}_{i'}\right\| ^2$ is the squared Euclidean distance between the radii, while $w_m$ and $w_r$ are the weights for the midpoint component and the radius component, respectively, and $\beta >0$.

The exponential dissimilarity measure (5) assigns small weights to noisy objects and large weights to those objects that are more compact in the data set (Wu & Yang, 2002), and it is superiorly bounded by 1.

Following Wu and Yang (2002), $\beta$ is set as the inverse of the variability of the data:

$$\begin{aligned} \beta = \left( \frac{\sum _{i=1}^{I}d^2(\textbf{m}_{i},\textbf{m}_{q})+d^2(\textbf{r}_{i},\textbf{r}_{q})}{I} \right) ^{- 1} \end{aligned}$$

(6)

where $\textbf{m}_{q}, \textbf{r}_{q}$ is the unit closest to all other units.

See Wu and Yang (2002), D’Urso et al. (2015a) and D’Urso et al. (2017) for further insights on the robustness of the exponential distance and on the role of $\beta$.

Moreover, we assume the following conditions: (i) $w_m+w_r=1$ (normalization condition) and (ii) $w_m\ge w_r\ge 0$ (coherence condition).

The coherence condition excludes that the radius component, which represents the uncertainty around the midpoint of the interval-valued data, has more importance than the midpoint component.

The normalization condition assesses, in a comparative fashion, the contributions of the midpoint and radius components to the dissimilarity measure computation.

2.2 Shannon entropy regularization in a fuzzy clustering framework

We focus on the entropy regularization approach in a fuzzy clustering framework. It is known that the maximum entropy principle, as applied to fuzzy clustering, provides a new perspective on facing the problem of fuzzifying the clustering of the objects, whilst ensuring the maximum compactness of the obtained clusters (Coppi & D’Urso, 2006; Gao et al., 2019). The first objective is achieved by maximizing the entropy (and, therefore, the uncertainty) of the assignment of the objects into the clusters. The Shannon entropy measure is employed in the objective function of the Fuzzy c-Medoids or Fuzzy c-Means model to deal with the uncertainty of the clustering. The second objective is obtained by minimizing the overall distance of the objects from the cluster prototypes (i.e. to maximize cluster compactness).

The trade-off between fuzziness and compactness is dealt with by introducing a unique objective function reformulating the maximum entropy method in terms of “regularization” of the Fuzzy c-Means objective function (Miyamoto & Mukaidono, 1997; Kahali et al., 2019) and of the Fuzzy c-Medoids objective function.

The novelty of the proposal is the use of entropy regularization for fuzzy clustering of interval-valued data.

Additionally, given the nature of the data (i.e., interval-valued), a weighted dissimilarity measure proposed by D’Urso and Giordani (2006b) is adopted. Here, the dissimilarity between each pair of objects is measured by separately considering the midpoints and the radii of the interval-valued data and using a suitable weighting system for such components.

2.3 Modeling

2.3.1 Robust entropy-based fuzzy c-medoids clustering (EFCMd-ID) model

Let $\textbf{X}$ be an $I\times J$ interval-valued data matrix. Given the dissimilarity measure shown in Eq. (5), in which we assume that the weights (i.e., ${w_m}$ and $w_r$) are objectively computed during the clustering process. We have set $w_m=(1-w)$ and $w_r=w$. In this way, the normalization condition is satisfied and the coherence condition turns to $0\le w\le 0.5$. Following a Partitioning Around Medoid (PAM) approach (Kaufmann & Rousseeuw, 1987), the Robust Entropy-based Fuzzy c-Medoids clustering (EFCMd-ID) model is characterized as follows:

$$\begin{aligned} \begin{aligned}&\text {min: }{}{J_{EFCMd-ID}(\textbf{U},{\tilde{\textbf{X}}},w)}=\sum _{i=1}^I \sum _{c=1}^Cu_{ic}d_{exp}^2({\tilde{\textbf{x}}}_{i},{\tilde{\textbf{x}}}_{c}) +p\sum _{i=1}^I\sum _{c=1}^Cu_{ic}log(u_{ic})=\\&\quad \sum _{i=1}^I\sum _{c=1}^Cu_{ic}\left\{ 1-exp \left[ -\beta [(1-w)^2d^2(\textbf{m}_{i},\tilde{\textbf{m}}_{c}) +w^2d^2(\textbf{r}_{i},\tilde{\textbf{r}}_{c})\right] \right\} +{}{} p\sum _{i=1}^I\sum _{c=1}^Cu_{ic}log(u_{ic})\\&\quad \sum _{c=1}^Cu_{ic}=1, u_{ic}\ge 0\\&\quad 0\le w\le 0.5 \end{aligned} \end{aligned}$$

(7)

where $u_{ic}$ indicates the membership degree of the i-th unit in the c-th cluster and $\textbf{U}$ is the related $I \times C$ matrix; $d_{exp}^2({\tilde{\textbf{x}}}_i, {\tilde{\textbf{x}}}_c)$ is the squared version of Eq. (5) between the i-th unit and the medoid in the c-th cluster; $\textbf{m }_{i}$ and $\textbf{r}_{i}$ are the midpoints and radii of the i-th unit, respectively; ${\tilde{\textbf{m}}}_{c}$ and ${\tilde{\textbf{r}}}_{c}$ are the medoids of the midpoints and radii in the c-th cluster, respectively; $p\sum _{i=1}^I\sum _{c=1}^Cu_{ic}log(u_{ic})$ is the fuzzy entropy function; p is a factor called degree of fuzzy entropy that represents the extent of fuzziness uncertainty of the partition (Coppi & D’Urso, 2006; Li & Mukaidono, 1995, 1999).

By solving the constrained quadratic minimization problem shown in Eq. (7) via the Lagrangian multiplier method, we obtain the optimal solutions $u_{ic}$ and w. In particular, by considering the following Lagrangian function:

$$\begin{aligned} L_m(u_{ic}, \lambda , w)&=\sum _{i=1}^I\sum _{c=1}^Cu_{ic}\left\{ 1-exp \left[ -\beta [(1-w)^2d^2(\textbf{m}_{i},{\tilde{\textbf{m}}}_{c}) +w^2d^2(\textbf{r}_{i},{\tilde{\textbf{r}}_{c}})\right] \right\} +\nonumber \\&\quad +p\sum _{i=1}^I\sum _{c=1}^Cu_{ic}log(u_{ic})-\lambda \left( \sum _{c=1}^Cu_{ic}-1\right) \end{aligned}$$

(8)

and setting the first partial derivatives with respect $u_{ic}$ and $\lambda$ equal to zero, we obtain:

$$\begin{aligned}{} & {} \frac{\partial L_m(u_{ic}, \lambda , w)}{\partial u_{ic}}=0 \Leftrightarrow 1-exp\left[ -\beta [(1-w)^2d^2(\textbf{m}_{i},{\tilde{\textbf{m}}}_{c}) +w^2d^2(\textbf{r}_{i},{\tilde{\textbf{r}}}_{c})\right] ]\nonumber \\{} & {} \quad +p(log(u_{ic})+1)-\lambda =0 \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \frac{\partial L_m(u_{ic}, \lambda , w)}{\partial \lambda }=0 \Leftrightarrow \sum _{c=1}^Cu_{ic}-1=0. \end{aligned}$$

(10)

From Eq. (9), we obtain:

$$\begin{aligned} log(u_{ic})=\frac{1}{p}\left[ \lambda -\left\{ 1-exp\left[ -\beta [(1-w)^2d^2(\textbf{m}_{i}, {\tilde{\textbf{m}}}_{c})+w^2d^2(\textbf{r}_{i},{\tilde{\textbf{r}}}_{c})]\right] \right\} -1\right] \end{aligned}$$

(11)

and then

$$\begin{aligned} u_{ic}=\exp \left\{ \frac{\lambda }{p}-\frac{1}{p}\left\{ 1-exp \left[ -\beta [(1-w)^2d^2(\textbf{m}_{i},{\tilde{\textbf{m}}}_{c}) +w^2d^2(\textbf{r}_{i},{\tilde{{\textbf{r}}}_{c}})]\right] \right\} -1\right\} . \end{aligned}$$

(12)

By considering Eq. (10):

$$\begin{aligned} exp\left( \frac{\lambda }{p}-1\right) =\frac{1}{\sum _{c=1}^C exp \left[ -\frac{1}{p}[1-exp[-\beta [(1-w)^2d^2(\textbf{m}_{i},{\tilde{\textbf{m}}}_{c}) +w^2d^2(\textbf{r}_{i},{\tilde{\textbf{r}}}_{c})]]\right] } \end{aligned}$$

(13)

and by replacing Equation (13) in Equation (12), we obtain:

$$\begin{aligned} u_{ic}=\frac{exp\left[ -\frac{1}{p}[1-exp[-\beta [(1-w)^2d^2(\textbf{m}_{i}, {\tilde{\textbf{m}}}_{c})+w^2d^2(\textbf{r}_{i},{\tilde{\textbf{r}}}_{c})]]\right] }{\sum _{c'=1}^C\exp \left[ -\frac{1}{p}[1-exp[-\beta [(1-w)^2d^2(\textbf{m}_{i}, {\tilde{\textbf{m}}_{c'}})+w^2d^2(\textbf{r}_{i},{\tilde{\textbf{r}}}_{c'})]]\right] }. \end{aligned}$$

(14)

The normalization condition for w is implicitly satisfied. To take into account the coherence condition, we derive with respect to w and select the minimum between the obtained value and 0.5:

$$\begin{aligned}{} & {} \frac{\partial L_m(u_{ic}, \lambda , w)}{\partial w}=0\nonumber \\{} & {} \quad w=\frac{\sum _{i=1}^I\sum _{c=1}^Cu_{ic}d^2(\textbf{m}_{i},{\tilde{\textbf{m}}}_{c}) exp\left[ -\beta [(1-w)^2 d^2(\textbf{m}_{i},{\tilde{\textbf{m}}}_{c})+w^2d^2(\textbf{r}_{i},{\tilde{\textbf{r}}}_{c})]\right] }{\sum _{i=1}^I\sum _{c=1}^Cu_{ic}(d^2(\textbf{m}_{i},{\tilde{\textbf{m}}}_{c})+d^2(\textbf{r}_{i}, {\tilde{\textbf{r}}}_{c}))exp\left[ -\beta [(1-w)^2 d^2(\textbf{m}_{i},{\tilde{\textbf{m}}}_{c})+w^2d^2(\textbf{r}_{i},{\tilde{\textbf{r}}}_{c})]\right] }.\nonumber \\ \end{aligned}$$

(15)

Note that (15) can be solved only using an iterative method.

The fuzzy clustering algorithm that minimizes (7) is built by adopting an estimation strategy based on the Fu and Albus heuristic algorithm (Fu & Albus, 1977; Krishnapuram et al., 1999, 2001). Indeed, the alternating optimization estimation procedure cannot be adopted because the necessary conditions cannot be derived by differentiating the objective function in (7) with respect to the medoids. The fuzzy clustering procedure is illustrated in Algorithm 1.

2.3.2 Robust entropy-based fuzzy c-means clustering (EFCM-ID) model

The Robust Entropy-based Fuzzy c-Means clustering (EFCM-ID) model is characterized as follows:

$$\begin{aligned} \begin{aligned}&\text {min: }{}{}{J_{EFCM-ID}(\textbf{U},\tilde{\textbf{X}},w)}=\\&\qquad \sum _{i=1}^I\sum _{c=1}^ku_{ic}\left\{ 1-exp\left[ -\beta [(1-w)^2d^2(\textbf{m}_{i}, \textbf{m}_{c})+w^2d^2(\textbf{r}_{i},\textbf{r}_{c})\right] \right\} \\&\qquad + {p\sum _{i=1}^I\sum _{c=1}^Cu_{ic}log(u_{ic})}\\&\qquad {\sum _{c=1}^Cu_{ic}=1, u_{ic}\ge 0}\\&\qquad {0\le w\le 0.5} \end{aligned} \end{aligned}$$

(16)

where $\textbf{m}_{c}$ and $\textbf{r}_{c}$ are the centroids of the midpoints and radii in the c-th cluster.

The optimal solutions for $u_{ic}$ and w are obtained as in the EFMd-ID model.

The centroids for the midpoints and radii are obtained by minimizing the objective function with respect to $\textbf{m}_{c}$ and $\textbf{r}_{c}$ component-wise, respectively:

$$\begin{aligned}{} & {} \textbf{m}_{c}=\frac{\sum _{i=1}^Iu_{ic}exp\left[ -\beta [(1-w)^2d^2(\textbf{m}_{i}, \textbf{m}_{c})+w^2d^2(\textbf{r}_{i},\textbf{r}_{c})]\right] \textbf{m}_{i}}{\sum _{i=1}^Iu_{ic}exp\left[ -\beta [(1-w)^2d^2(\textbf{m}_{i},\textbf{m}_{c}) +w^2d^2(\textbf{r}_{i},\textbf{r}_{c})]\right] } \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \textbf{r}_{c}=\frac{\sum _{i=1}^Iu_{ic}exp\left[ -\beta [(1-w)^2d^2(\textbf{m}_{i}, \textbf{m}_{c})+w^2d^2(\textbf{r}_{i},\textbf{r}_{c})]\right] \textbf{r}_{i}}{\sum _{i=1}^Iu_{ic}exp\left[ -\beta [(1-w)^2d^2(\textbf{m}_{i},\textbf{m}_{c}) +w^2d^2(\textbf{r}_{i},\textbf{r}_{c})]\right] } \end{aligned}$$

(18)

Note that Eqs. (17) and (18) can be solved only using an iterative method.

The fuzzy clustering procedure is illustrated in Algorithm 2.

2.3.3 Other models

As variants of the proposed fuzzy clustering models (7) and (14) other related models can be suggested, either fuzzy entropy-based not robust or fuzzy not entropy-based.

In particular:

• - Entropy-based Fuzzy c-Medoids clustering model for interval-valued data with (not robust) weighted dissimilarity measure (not robust version of EFCMd-ID).

• - Entropy-based Fuzzy c-Means clustering model for interval-valued data with (not robust) weighted dissimilarity measure (not robust version of EFCM-ID).

• - Robust Fuzzy c-Medoids clustering model for interval-valued data (FCMd-ID with exponential weighted dissimilarity measure 5) (D’Urso et al., 2016): fixing p=0 (removing the entropy term) and considering the fuzziness exponent m for the membership degrees in (7).

• - Robust Fuzzy c-Means clustering model for interval-valued data (FCM-ID with exponential weighted dissimilarity measure 5): fixing p=0 (removing the entropy term) and considering the fuzziness exponent m for the membership degrees in (16).

The models are summarized in Table 1.

Table 1 Variants of the proposed fuzzy clustering models (7) and (16)

3 Simulation study

The performances of the proposed Robust Entropy-based Fuzzy c-Medoids clustering model for interval-valued data with weighted dissimilarity measure, i.e. the EFCMd-ID model, have been evaluated by carrying out a simulation study. The proposed model has been compared with the Robust Entropy-based Fuzzy c-Means clustering model for interval-valued data with weighted dissimilarity measure i.e. the EFCM-ID model, with the Robust Fuzzy c-Medoids clustering model for interval-valued data (FCMd-ID with exponential weighted dissimilarity measure) and with its EFCMd-ID not robust version.

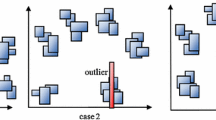
Eighty objects ($I=80$), two interval-valued variables ($J=2$) and three percentages of noisy data in the dataset (0% to 15% step 5%) have been considered. Two clusters ($C=2$) are generated in each simulation. Five values of the degree of fuzzy entropy p (0.05 to 0.30 step 0.05) for the entropy-based models and four values of the fuzziness parameter m ($m=1.0, 1.3, 1.5, 2.0$) have been considered.

In the data generation scheme the midpoints and the radii of the interval-valued data belonging to the first cluster (I/2 observations) are all randomly generated from U[0, 1], whereas the midpoints and the radii belonging to the second cluster (I/2 observations) from U[1.5, 2.5].

To evaluate the robustness of the proposed model in presence of noisy data, $0.05 \cdot I$ to $0.15 \cdot I$ noisy objects have been added to the 80 objects. The midpoints and the radii of the noisy objects are generated from a Gaussian distribution N(4.5, 2). Each data generation scheme has been replicated 100 times.

The data generation is summarized in Table 2.

Table 2 Data and noisy data generation scheme

The simulated scenario is presented in Fig. 1.

Fig. 1

Simulated midpoint-radius scenario. The midpoints are presented in the left figure, the radii in the right figure

To assess the robustness with respect to misclassification in the presence of noisy data, an extension of the Adjusted Rand Index (ARI) for fuzzy partitions based on the Normalized Degree of Concordance (D’Ambrosio et al., 2021) has been used. The index allows the comparison of the hard partition in two clusters with the fuzzy partition obtained as a result of the robust model. The normalized degree of concordance varies between 0 and 1, and it always equals 1 when comparing a fuzzy partition with itself. The index has been then averaged over the 100 simulation runs.

The boxplots of the values of the extended ARI over 100 simulations are presented in Figs. 2, 3, 4 and 5, along with the boxplots of the values of the weight of the radii.

Fig. 2

Robust EFCMd-ID. The extended ARI is shown in the left panel, while the weight of the radii is on the right panel. From top to bottom, there are scenarios with 0%, 5%, 10% and 15% of noisy data, respectively. Five values of the degree of fuzzy entropy p (0.05 to 0.30 step 0.05) are considered

Fig. 3

Robust EFCM-ID. The extended ARI is shown in the left panel, while the weight of the radii is on the right panel. From top to bottom, there are scenarios with 0%, 5%, 10% and 15% of noisy data, respectively. Five values of the degree of fuzzy entropy p (0.05 to 0.30 step 0.05) are considered

Fig. 4

FCMd-ID with exponential weighted dissimilarity measure. The extended ARI is shown in the left panel, while the weight of the radii is on the right panel. From top to bottom, there are scenarios with 0%, 5%, 10% and 15% of noisy data, respectively. Four values of the fuzziness parameter m (1.0, 1.3, 1.5, 2.0) are considered

Fig. 5

Not robust EFCMd-ID. The extended ARI is shown in the left panel, while the weight of the radii is on the right panel. From top to bottom, there are scenarios with 0%, 5%, 10% and 15% of noisy data, respectively. Five values of the degree of fuzzy entropy p (0.05 to 0.30 step 0.05) are considered

Some comments follow, with respect to the boxplots of the extended ARI.

The model FCMd-ID is less robust to the presence of noisy data than the other models. Considering the three robust models, EFCMd-ID presents better performances than EFCM-ID and FCMd-ID, in particular as the percentage of noisy data increases, especially for small values of the degree of fuzzy entropy. The weights of the radii are in the region of 0.5, always below, as expected.

4 Application: robust clustering of scientific journals

In this Section, an application of the proposed EFCMd-ID model to the clustering of scientific journals in the field of research evaluation is presented.

Institutional bodies in many countries evaluate the quality of the outcomes of the research of the universities and research institutes providing an up-to-date assessment of the state of research in the various scientific fields, in order to promote the improvement of research quality in the assessed institutions and to allocate the Ordinary Financing Fund for the University system on a performance basis.

To define the quality profiles of the research outputs, the peer review method is adopted. When considered appropriate to the characteristics of the field, peer review can be informed by the use of international citation indicators.

The Journal Citation Report$^{\text {TM}}$ (JCR) from Clarivate provides transparent, publisher-neutral data and statistics needed to make confident decisions in the evolving scholarly publishing landscape. Publishers and editors can make confident business decisions - understand how journals are performing and benchmark them against others. Librarians can make confident collection management decisions - understand which journals are the most important to the institution’s and researchers’ success. Researchers can make confident decisions about where to submit manuscripts - using Journal Citation Reports as a definitive list and guide to discover and select the most appropriate journals to read and publish research findings.

Among the indicators proposed by JCR, the 5-Year Journal Impact Factor (5-Year JIF) and the Immediacy Index$^\text {TM}$ have been considered in the application.

The Journal Impact Factor$^{\text {TM}}$ is the average number of times articles from the journal published in the past two years have been cited in the JCR year. The Impact Factor is calculated by dividing the number of citations in the JCR year by the total number of articles published in the two previous years. Citing articles may be from the same journal; most citing articles are from different journals.

The 5-year Journal Impact Factor is the average number of times articles from the journal published in the past five years have been cited in the JCR year. It is calculated by dividing the number of citations in the JCR year by the total number of articles published in the five previous years. The 5-Year Impact Factor is available only in JCR 2007 and subsequent years.

The Immediacy Index is the average number of times an article is cited in the year it is published. The journal Immediacy Index indicates how quickly articles in a journal are cited. The Immediacy Index is calculated by dividing the number of citations to articles published in a given year by the number of articles published in that year. Because it is a per-article average, the Immediacy Index tends to discount the advantage of large journals over small ones. However, frequently issued journals may have an advantage because an article published early in the year has a better chance of being cited than one published later in the year. Many publications that publish infrequently or late in the year have low Immediacy Indexes. For comparing journals specializing in cutting-edge research, the Immediacy Index can provide a useful perspective.

Journals are organized into categories and groups. Groups are used to organize the 254 categories of JCR into broad discipline areas. Groups in JCR have no associated metrics and aren’t used for rankings. Categories may be in more than one group.

The category “Health Care Sciences & Services” in the group “Clinical Medicine” has been considered. Health Care Sciences & Services covers resources on health services, hospital administration, health care management, health care financing, health policy and planning, health economics, health education, history of medicine, and palliative care.

The units (objects) are 74 journals, the variables 5-Year JIF and Immediacy index (J = 2). The variables have been collected in the period 2017–2021 and the minimum and maximum value in the period has been computed for each variable. The reformulation with midpoint and radius has been used. The data are presented in Fig. 6 and Table 4. We observe that the two indexes give different information as expected. The EFCMd-ID model has been run over five values of the degree of fuzzy entropy p (p = 0.05$-$ 0.30 step 0.05) and C = 2, 3, 4, 5, 6 clusters.

Remark 1 Cluster validity. Because of its particularly satisfactory results in recognizing the true number of clusters [for a reference, see the extensive simulations carried out in Arbelaitz et al. (2013)], we select the optimal C according to the Fuzzy Silhouette criterion (Campello & Hruschka, 2006), that is a fuzzy version of the Average Silhouette Width (ASW) criterion (Kaufman & Rousseeuw, 1990). The Fuzzy Silhouette index (FS) measures cohesion and separation of a partition. This index represents the weighted average of individual silhouettes width, $\lambda _i$, with weights derived from the fuzzy membership matrix $\textbf{U}=\{u_{ic}:\;i=1,\ldots ,I;\,c=1,\ldots ,C\}$:

$$\begin{aligned} \text {FS}=\frac{\sum _{i=1}^{I}(u_{ip}-u_{iq})^{\alpha }\cdot \lambda _i}{\sum _{i=1}^{I}(u_{ip}-u_{iq})^{\alpha }}, \qquad \lambda _i=\frac{(b_i-a_i)}{\max \{b_i,a_i\}} \end{aligned}$$

(19)

where $a_{i}$ is the average distance between the i-th unit and the units belonging to the cluster p ($p=1$,...,C) with which i is associated with the highest membership degree; $b_{i}$ is the minimum (over clusters) average distance of the i-th unit to all units belonging to the cluster q with $q\ne p$; $(u_{ip}-u_{iq})^{\alpha }$ is the weight of each $\lambda _i$ calculated upon $\textbf{U}$, where p and q are, respectively, the first and second best clusters (according to the membership degree) to which the i-th unit is associated; $\alpha \ge 0$ is an optional user defined weighting coefficient. The traditional Silhouette coefficients is obtained by setting $\alpha =0$.

The higher the value Fuzzy Silhouette index, the better the assignment of the units to the clusters simultaneously obtaining the minimization of the intra-cluster distance and the maximization of the inter-cluster distance.

Remark 2 Fuzzy membership. An empirical rule for selecting a suitable cut-off point of the highest membership values has been suggested by Dembélé and Kastner (2003) and also used by Belacel et al. (2004). Dembélé and Kastner (2003) and Belacel et al. (2004) studied the cut-off point of the highest membership value with the fuzziness parameter in a fuzzy clustering framework. In particular, Dembélé and Kastner (2003) proposed a new method which enabled the computation of the upper bound value for m and showed that Fuzzy c-Means clustering of microarray data, combined with threshold-based gene selection, offers a convenient way of defining subsets of gene which are more tightly associated with a given cluster. In our paper, the aim is not to investigate the relationship between m and the cut-off for the membership degrees. Hence, the chosen cut-off point of 0.7 for a partition in two clusters for the membership degrees is compatible with the indications suggested in literature; i.e., for the simulation studies, see D’Urso and Maharaj (2009) and Maharaj et al. (2010), and for the applications see Dembélé and Kastner (2003) and D’Urso and Giordani (2006b).

The results are presented in Table 3 - Fuzzy Silhouette.

Fig. 6

Midpoints and radii of the variables 5-year JIF and Immediacy index. The midpoints are presented in the left figure, the radii in the right figure

Table 3 Fuzzy Silhouette for different values of the number of clusters C and of the degree of fuzzy entropy p

Table 4 Fuzzy memberships

The optimal number of clusters is $C=2$, the degree of fuzzy entropy $p=0.20$. The cluster numerosity is 30, 22 and 22 journals have a fuzzy membership. The medoids are journal 39: “Journal of interprofessional care” and journal 8: “Supportive care in cancer” (highlighted in bold in Table 4).

Considering the midpoints (Fig. 6, left and Fig. 7 ), two clusters represent, respectively, journals with small values of the midpoint of the 5-Year JIF and medium-high values of the midpoint of the Immediacy index (medoid: “Journal of interprofessional care”); and journals with high values of the midpoint of the 5-Year JIF and medium-high values of the midpoint of the Immediacy index (medoid: “Supportive care in cancer”), for some journals smaller than in the other cluster.

The 22 fuzzy journals (in italic in Table 4) show either the values of the midpoints of the two variables greater than the cluster with medoid “Supportive care in cancer”, in particular journals 1, 4, 5, 10, 11, 25, 36; or the values of the midpoint of the 5-Year JIF greater than the cluster with medoid “Supportive care in cancer”, in particular journals 3, 7, 12, 13, 30; or the values of the midpoints of the two variables in the middle with respect to the medoids of the two clusters. The memberships demonstrate the ability of the model to smooth the presence of noisy journals, without altering the medoids.

Considering the radii (Fig. 6, right and Fig. 7, greater dispersion is observed with respect to the Immediacy index. Noisy also with respect to the radii are journals 4, 11, 5, 36 (high 5-Year JIF and Immediacy radius), journals 3, 7, 13, 25 (high 5-Year JIF radius). Journal 74 is a singleton as it shows a high radius of 5-Year JIF and a small radius of the Immediacy index.

The value of the weight of the radius component is always greater than 0.5, demonstrating the smaller variability of the radii, resulting in a weight equal to 0.5.

Fig. 7

Midpoints and radii of the variables 5-year JIF and Immediacy index. The midpoints are presented in the left figure, the radii in the right figure. The journals in the two clusters are coloured red and black, respectively, the fuzzy journals grey

5 Final remarks

In this paper, a robust entropy-based fuzzy c-Medoids clustering model for interval-valued data is suggested. In particular, by considering a suitable weighted measure, we propose a robust fuzzy clustering model with an entropy regularization and Partition Around Medoid approach, the EFCMd-ID model. An important advantage of the use of the entropy regularization approach in a fuzzy clustering framework is the maximum entropy principle that provides the fuzzy clusterization of the observations while ensuring the maximum compactness of the obtained clusters (Coppi & D’Urso, 2006; Gao et al., 2019; Kahali et al., 2019). Robustness to noisy observations is obtained by the use of the exponential trasformation. The simulations have shown the ability of the model to tune properly the weight of the center and radius components of the interval-valued data and the degree of fuzzy entropy, besides robustness to noisy data, in a comparative assessment. An application to the clustering of scientific journals in the field of research evaluation is provided, useful for Institutional bodies to evaluate the quality of the outcomes of the research of the universities and research institutes, in order to promote the improvement of research quality in the assessed institutions and to allocate the Ordinary Financing Fund for the University system on a performance basis.