Scheduling operating rooms of multiple hospitals considering transportation and deterioration in mass-casualty incidents

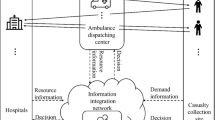
Abstract

In mass casualty incidents, patients need to be evacuated to nearby hospitals as soon as possible, and a surge in demand for emergency medical services then occurs. It would result in ambulance offload delays, i.e., no emergency operating room is available when the ambulance arrives at a hospital, and thus the patients cannot be treated immediately. In this paper, we aim to solve a combinatorial problem of patient-to-hospital assignment and patient surgery sequence considering patient deterioration and ambulance offload delay during a mass casualty incident. A mixed-integer programming model is proposed. The objective is to minimize the completion time of all patients’ surgeries. For solving such a problem, some structural properties of our studied problem are derived, and a heuristic is developed to solve the single operating room scheduling problem considering ambulance offload delay and patient deterioration based on these structural properties. A hybrid Firefly Algorithm-Variable Neighborhood Search algorithm incorporating the heuristic method is proposed to solve it. Our proposed algorithm can solve the problem within a short computation time, and the computational results demonstrate the superiority of our proposed algorithm over the compared algorithms.

Appendix

In this appendix, the proof of Lemma 2 in Sect. 4.2 is presented.

Proof

Given that an operating room has been assigned a set of patients, there exist two schedules for the operating room. We assume that ${\pi }^{*}$ is an optimized schedule where patient i precedes patient j to start the surgery, while in ${\pi }^{^{\prime}}$ schedule, patient j precedes patient i to start the surgery. That is, ${\pi }^{*}=(\dots ,{I}_{A},{I}_{i},{I}_{j},{I}_{B},\dots )$, and ${\pi }^{^{\prime}}=(\dots ,{I}_{A},{I}_{j},{I}_{i},{I}_{B},\dots )$.

For ${\pi }^{*}$ and ${\pi }^{^{\prime}}$ schedule, the surgery start time of patient A is given as ${S}_{A}({\pi }^{*})={S}_{A}({\pi }^{^{\prime}})={S}_{A}$, and the surgery duration of patient A is ${p}_{A}^{*}={p}_{A}^{^{\prime}}={p}_{A}$, and thus the complete time of patient A is ${C}_{A}({\pi }^{*})={C}_{A}({\pi }^{^{\prime}})={C}_{A}$.

For ${\pi }^{*}$, ${S}_{i}({\pi }^{*})=\mathrm{max}\{{S}_{A}({\pi }^{*})+{T}_{h},{C}_{A}({\pi }^{*})\}=\mathrm{max}\{{S}_{A}+{T}_{h},{C}_{A}({\pi }^{*})\}$. There exist two situations: (1) ${T}_{h}>{p}_{A}$; (2) ${T}_{h}<{p}_{A}$.

• (1) In situation (1), ${\mathrm{T}}_{\mathrm{h}}>{\mathrm{p}}_{\mathrm{A}}$:

  ${S}_{i}\left({\pi }^{*}\right)={S}_{A}+{T}_{h}$, ${C}_{i}\left({\pi }^{*}\right)={S}_{i}\left({\pi }^{*}\right)+{p}_{i}^{*}= {S}_{i}\left({\pi }^{*}\right)+\left(\overline{{p }_{i}}+\upbeta {S}_{i}\left({\pi }^{*}\right)\right) =\left(1+\upbeta \right){S}_{i}\left({\pi }^{*}\right)+\overline{{p }_{i}}=\left(1+\upbeta \right)\left({S}_{A}+{T}_{h}\right)+\overline{{p }_{i}}$, and ${S}_{j}({\pi }^{*})=\mathrm{max}\{{S}_{i}({\pi }^{*})+{T}_{h}, {C}_{i}({\pi }^{*})\}=\mathrm{max}\{{S}_{A}+2{T}_{h},\left(1+\upbeta \right)\left({S}_{A}+{T}_{h}\right)+\overline{{p }_{i}}\}$. There are two cases:

  • (a) When ${T}_{h}>\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-\upbeta }$:

  ${S}_{j}\left({\pi }^{*}\right)={S}_{A}+2{T}_{h}$, ${C}_{j}\left({\pi }^{*}\right)={S}_{j}\left({\pi }^{*}\right)+{p}_{j}^{*}={S}_{j}\left({\pi }^{*}\right)+\left(\overline{{p }_{j}}+\upbeta {S}_{j}\left({\pi }^{*}\right)\right)=\left(1+\upbeta \right){S}_{j}\left({\pi }^{*}\right)+\overline{{p }_{j}}=\left(1+\upbeta \right)({S}_{A}+2{T}_{h})+\overline{{p }_{j}}$. Then ${S}_{B}({\pi }^{*})=\mathrm{max}\{{S}_{j}({\pi }^{*})+{T}_{h},{C}_{j}({\pi }^{*})\}=\mathrm{max}\{{S}_{A}+3{T}_{h},(1+\upbeta )( {S}_{A}+2T) +\overline{{p }_{j}}\}$. If ${T}_{h}>\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-2\upbeta }$,${S}_{B}({\pi }^{*})={S}_{A}+3{T}_{h}$. Otherwise, ${S}_{B}^{*}=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{j}}$.

  • (b) When ${T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-\upbeta }$:

    ${S}_{j}({\pi }^{*})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}$, ${C}_{j}\left({\pi }^{*}\right)={S}_{j}\left({\pi }^{*}\right)+{p}_{j}^{*}={S}_{j}\left({\pi }^{*}\right)+\left(\overline{{p }_{j}}+\upbeta {S}_{j}\left({\pi }^{*}\right)\right)=\left(1+\upbeta \right){S}_{j}\left({\pi }^{*}\right)+\overline{{p }_{j}}=\left(1+\upbeta \right)\left[\left(1+\upbeta \right)\left( {S}_{A}+{T}_{h}\right)+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$. Then ${S}_{B}({\pi }^{*})=\mathrm{max}\{{S}_{j}({\pi }^{*})+{T}_{h},{C}_{j}({\pi }^{*})\}=\mathrm{max}\{(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}+{T}_{h}, (1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}\right] +\overline{{p }_{j}}\}$. If ${T}_{h}>\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{i}}+\overline{{p }_{j}}}{1-\upbeta -{\upbeta }^{2}}$, ${S}_{B}({\pi }^{*})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}+{T}_{h}$. Otherwise, ${S}_{B}({\pi }^{*})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$.

• (2) In situation (2),${\mathrm{T}}_{\mathrm{h}}<{\mathrm{p}}_{\mathrm{A}}$:

  ${S}_{i}({\pi }^{*})={C}_{A}$,${C}_{i}({\pi }^{*})={S}_{i}({\pi }^{*})+{p}_{i}^{*}={S}_{i}({\pi }^{*})+\left(\overline{{p }_{i}}+\upbeta {S}_{i}\left({\pi }^{*}\right)\right) =(1+\upbeta ){S}_{i}({\pi }^{*})+\overline{{p }_{i}}=(1+\upbeta ){C}_{A}+\overline{{p }_{i}}$, and ${S}_{j}({\pi }^{*})=\mathrm{max}\{{S}_{i}^{*}+{T}_{h},{C}_{i}({\pi }^{*})\}=\mathrm{ max}\{{C}_{A}+{T}_{h},(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\}$. There are two cases:

  • (a) When ${T}_{h}>\upbeta {C}_{A}+\overline{{p }_{i}}$:

    ${S}_{j}({\pi }^{*})={C}_{A}+{T}_{h}$, ${C}_{j}({\pi }^{*})={S}_{j}({\pi }^{*})+{p}_{j}^{*}=(1+\upbeta ){S}_{j}({\pi }^{*})+\overline{{p }_{j}}=(1+\upbeta )({C}_{A}+{T}_{h})+\overline{{p }_{j}}$. Then ${S}_{B}({\pi }^{*})=\mathrm{max}\{{S}_{j}({\pi }^{*})+{T}_{h}, {C}_{j}({\pi }^{*})\}=\mathrm{max}\{{C}_{A}+2{T}_{h},(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{j}}\}$. If ${T}_{h}>\frac{\upbeta {C}_{A}+\overline{{p }_{j}}}{1-\upbeta }$, ${S}_{B}({\pi }^{*})={C}_{A}+2{T}_{h}$. Otherwise, ${T}_{h}<\frac{\upbeta {C}_{A}+\overline{{p }_{j}}}{1-\upbeta }$,${S}_{B}({\pi }^{*})=(1+\upbeta )( {C}_{A}+T) +\overline{{p }_{j}}$

  • (b) When ${T}_{h}<\upbeta {C}_{A}+\overline{{p }_{i}}$,

    ${S}_{j}({\pi }^{*})=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}$, ${C}_{j}({\pi }^{*})={S}_{j}({\pi }^{*})+{p}_{j}^{*}=(1+\upbeta ){S}_{j}({\pi }^{*})+\overline{{p }_{j}}=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$. Then ${S}_{B}({\pi }^{*})=\mathrm{max}\{{S}_{j}({\pi }^{*})+{T}_{h}, {C}_{j}({\pi }^{*})\}=\mathrm{max}\{(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}, (1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\right] +\overline{{p }_{j}}\}$. If ${T}_{h}>\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{i}}+\overline{{p }_{j}}$, ${S}_{B}({\pi }^{*})=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}$. Otherwise, ${T}_{h}<\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{i}}+\overline{{p }_{j}}$,${S}_{B}({\pi }^{*})=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$.

Similarly, we can obtain that for ${\pi }^{^{\prime}}$:

• (1) In situation (1),${T}_{h}>{\mathrm{p}}_{\mathrm{A}}$

  • (a) When ${T}_{h}>\mathrm{max}\{\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta },\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-2\upbeta }\}$, ${S}_{B}({\pi }^{^{\prime}})={S}_{A}+3{T}_{h}$.

  • (b) When $\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta }<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-2\upbeta }$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{i}}$.

  • (c) When $\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}}{1-\upbeta -{\upbeta }^{2}}<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta }$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}+{T}_{h}$.

  • (d) When ${T}_{h}<\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}}{1-\upbeta -{\upbeta }^{2}}$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$.

• (2) In situation ${T}_{h}<{\mathrm{p}}_{\mathrm{A}}$, there are four cases:

  • (a) When ${T}_{h}>\mathrm{max}\{\upbeta {C}_{A}+\overline{{p }_{j}},\frac{\upbeta {C}_{A}+\overline{{p }_{i}}}{1-\upbeta }\}$, ${S}_{B}({\pi }^{^{\prime}})={C}_{A}+2{T}_{h}$.

  • (b) When $\upbeta {C}_{A}+\overline{{p }_{j}}<{T}_{h}<\frac{\upbeta {C}_{A}+\overline{{p }_{i}}}{1-\upbeta }$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{i}}$.

  • (c) When $\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{j}}+\overline{{p }_{i}}<{T}_{h}<\upbeta {C}_{A}+\overline{{p }_{j}}$, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}+{T}_{h}$.

  • (d) When ${T}_{h}<$ min{$\upbeta {C}_{A}+\overline{{p }_{j}}, \left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{j}}+\overline{{p }_{i}}$}, ${S}_{B}({\pi }^{^{\prime}})=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$

By the analysis above, we conclude 14 cases in total:

• (1) When ${T}_{h}>\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-2\upbeta }$, ${S}_{B}({\pi }^{*})= {S}_{B}({\pi }^{\mathrm{^{\prime}}})={S}_{A}+3{T}_{h}$

• (2) When $\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-2\upbeta }<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-2\upbeta }$,${S}_{B}({\pi }^{*})={S}_{A}+3T$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=\left(1+\upbeta \right)\left( {S}_{A}+2{T}_{h}\right)+\overline{{p }_{i}}$

• (3) When $\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-\upbeta }<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-2\upbeta }$, ${S}_{B}({\pi }^{*})=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{j}}$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{i}}$

• (4) When $\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta }<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{i}}}{1-\upbeta }$, ${S}_{B}({\pi }^{*})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}+{T}_{h}$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )( {S}_{A}+2{T}_{h}) +\overline{{p }_{i}}$

• (5) When $\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{i}}+\overline{{p }_{j}}}{1-\upbeta -{\upbeta }^{2}}<{T}_{h}<\frac{\upbeta {S}_{A}+\overline{{p }_{j}}}{1-\upbeta }$, ${S}_{B}({\pi }^{*})=\left(1+\upbeta \right)\left( {S}_{A}+{T}_{h}\right)+\overline{{p }_{i}}+{T}_{h}, {S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}+T$

• (6) When $\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}}{1-\upbeta -{\upbeta }^{2}}<{T}_{h}<\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{i}}+\overline{{p }_{j}}}{1-\upbeta -{\upbeta }^{2}}$, ${S}_{B}({\pi }^{*})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}+{T}_{h}$

• (7) When ${\mathrm{p}}_{\mathrm{A}}<{T}_{h}<\frac{\left({\upbeta }^{2}+\upbeta \right){S}_{A}+(1+\upbeta )\overline{{p }_{j}}+\overline{{p }_{i}}}{1-\upbeta -{\upbeta }^{2}}$,${S}_{B}({\pi }^{*})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$, ${S}_{B}({\pi }^{\mathrm{^{\prime}}})=(1+\upbeta )\left[(1+\upbeta )( {S}_{A}+{T}_{h})+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$

• (8) When $\frac{\upbeta {C}_{A}+\overline{{p }_{i}}}{1-\upbeta }<{T}_{h}<{\mathrm{p}}_{\mathrm{A}}$, ${S}_{B}^{*}={S}_{B}^{\mathrm{^{\prime}}}={C}_{A}+2{T}_{h}$

• (9) When $\frac{\upbeta {C}_{A}+\overline{{p }_{j}}}{1-\upbeta }<{T}_{h}<\frac{\upbeta {C}_{A}+\overline{{p }_{i}}}{1-\upbeta }$, ${S}_{B}^{*}={C}_{A}+2{T}_{h}$, ${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{i}}$

• (10) When $\upbeta {C}_{A}+\overline{{p }_{i}}<{T}_{h}<$ $\frac{\upbeta {C}_{A}+\overline{{p }_{j}}}{1-\upbeta }$, ${S}_{B}^{*}=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{j}}$, ${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{i}}$

• (11) When $\upbeta {C}_{A}+\overline{{p }_{j}}<{T}_{h}<\upbeta {C}_{A}+\overline{{p }_{i}}$, ${S}_{B}^{*}=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}$,${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )( {C}_{A}+{T}_{h}) +\overline{{p }_{i}}$

• (12) When $\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{j}}+\overline{{p }_{i}}<{T}_{h}<\upbeta {C}_{A}+\overline{{p }_{j}}$, ${S}_{B}^{*}=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}$,${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}+{T}_{h}$

• (13) When $\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{i}}+\overline{{p }_{j}}<{T}_{h}<\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{j}}+\overline{{p }_{i}}$,${S}_{B}^{*}=(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}+{T}_{h}$,${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$

• (14) When ${T}_{h}<\left({\upbeta }^{2}+\upbeta \right){C}_{A}+\upbeta \overline{{p }_{i}}+\overline{{p }_{j}}$, ${S}_{B}^{*}=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{i}}\right] +\overline{{p }_{j}}$,${S}_{B}^{\mathrm{^{\prime}}}=(1+\upbeta )\left[(1+\upbeta ) {C}_{A}+\overline{{p }_{j}}\right] +\overline{{p }_{i}}$

These 14 cases can be summarized as shown in Table 3 in the main body of the paper.