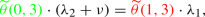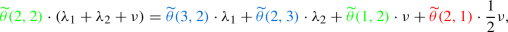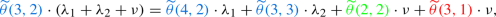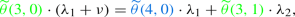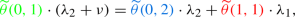Load balancing in a network of queueing-inventory systems

Abstract

We study a supply chain consisting of production-inventory systems at several locations which are coupled by a common supplier. Demand of customers arrives at each production system according to a Poisson process and is lost if the local inventory is depleted (“lost sales”). To satisfy a customer’s demand a server at the production system needs raw material from the associated local inventory. The supplier manufactures raw material to replenish the local inventories, which are controlled by a continuous review base stock policy. The routing of items depends on the on-hand inventory at the locations with the aim to obtain “load balancing”. We show that the stationary distribution has a product form of the marginal distributions of the production subsystem and the inventory-replenishment subsystem. For the marginal distribution of the production subsystem we derive an explicit solution and for the marginal distribution of the inventory-replenishment subsystem we deduce an explicit solution or a recursive algorithm for some special cases.

1 Introduction

We consider a supply chain consisting of production-inventory systems at several locations which are coupled by a common supplier. Demand of customers arrives at each production system and is lost if the local inventory is depleted. To satisfy a customer’s demand a server at the production system takes exactly one unit of raw material from the associated local inventory. The supplier manufactures raw material to replenish the local inventories, which are controlled by a continuous review base stock policy. We focus on the research of the network’s behaviour, where the supplier consists only of one machine (single server) and replenishes the inventories at all locations. The items of raw material are indistinguishable (exchangeable). The routing of items depends on the on-hand inventory at the locations with the aim to obtain “load balancing”. More precisely, we consider strict priorities, i.e. the finished item of raw material is sent to the location(s) with the highest difference between the on-hand inventory and the capacity of the inventory.

Although we describe our system in terms of production and manufacturing, there are other applications where our model can be used, e.g. distributed retail systems where customers’ demand has to be satisfied from the local inventories and delivering the goods to the customers needs a non-negligible amount of time; the replenishment for the local retail stations is provided by a production network. Another setting is a distributed set of repair stations where spare parts are needed to repair the brought-in items which are held in local inventories. Production of the needed spare parts and sending them to the repair stations is again due to a production network.

We use queueing theory and inventory theory to analyse the above-described production-inventory-replenishment system. Queueing theory and inventory theory are fields of Operations Research with different methodologies to optimise e.g. production processes and inventory control. In classical Operations Research, queueing theory and inventory theory are often considered as disjoint areas of research. On the other side, the emergence of complex supply chains calls for integrated queueing-inventory models, where, as usual, the production systems are modelled by queueing systems and the inventories are modelled by classical inventories with replenishment policies. These integrated queueing-inventory models are the focus of our present research. In particular, we develop a Markovian stochastic model of the production-inventory-replenishment system.

We are able to prove that the stationary distribution has a product form. This means that the steady states of the production network and the inventory-replenishment complex decouple asymptotically and the equilibrium for the production subsystem decomposes in true independent coordinates. This product form structure of the joint stationary distribution is often characterised as the global process being “separable”. Separability is an important (but rather rare) property of complex systems.

The paper is organised as follows. In Sect. 2, we describe the related literature. In Sect. 3, we introduce our integrated model for production and inventory management. To model our production-inventory-replenishment system as a queueing network, we make a number of simplifying assumptions. This enables us to compute the stationary distribution and to show in Sect. 4 that it is of product form. In Sect. 5 we show some structural properties of the stationary inventory-replenishment subsystem.

2 Related literature and own contributions

Relevant for our research are queueing theory and inventory control, in particular integrated queueing-inventory models.

Literature on queueing theory is overwhelming, so we point only to the most relevant sources for our present investigation. Our production systems are classical $M/M/1/\infty$ queueing systems which constitute a network of parallel queues connected to the central supplier queue, cf. Kelly (1979) and Chao et al. (1999) for general networks of queues.

Special queueing networks, which model multi-station maintenance and repair systems, are investigated by Ravid et al. (2013) and Daduna (1990) and references therein. In these systems, circulating items are “exchangeable”. This feature will occur in our model as well.

Literature on inventory theory is, similar to that on queueing theory, overwhelming, so we only point to some references closely related to our investigations. There are two extreme cases of arriving customers’ reactions in the situation that inventory is depleted when demand arrives [cf. Silver et al. (1998)]: Either backordering, which means that customers are willing to wait for their demands to be fulfilled, or lost sales, which means that demand is lost when no inventory is available on hand.

In classical inventory theory it is common to assume that excess demand is backordered (Silver et al., 1998; Zipkin 2000, p. 40; Axsäter 2000). However, studies by Gruen et al. (2002) and Verhoef and Sloot (2006) analyse customers’ behaviour in practice and show that in many retail settings most of the original demand can be considered to be lost in case of a stockout.

For an overview of the literature on systems with lost sales we refer to Bijvank and Vis (2011). They present a classification scheme for the replenishment policies most often applied in literature and practice, and they review the proposed replenishment policies, including the base stock policy. According to Donselaar (2013) “Their literature review confirms that there are only a limited number of papers dealing with lost sales systems and the vast majority of these papers make simplifying assumptions to make them analytically tractable.”

Rubio and Wein (1996) and Zazanis (1994) investigated classical single item and multi-item inventory systems. Similar to our approach they used methods and models from queueing theory to evaluate the performance of base stock control policies in complex situations.

Reed and Zhang (2017) study a single item inventory system under a base stock policy with backordering and a supplier who consists of a multi-server production system. Their aim is to minimise a combination of capacity, inventory and backordering costs. They develop a square-root rule for the joint decision. Furthermore, they justify the rule analytically in a many-server queue asymptotic framework.

Because we consider queueing-inventory systems where inventories are controlled by base stock policies, we mention here that Tempelmeier (2005, p. 84) argued that base stock control is economically reasonable if the order quantity is limited because of technical reasons.

The base stock policy is “(...) more suitable for item with low demand, including the case of most spare parts” (Rego & Mesquita, 2011, p. 661).

Morse (1958, p. 139) investigated (pure) inventory systems that operate under a base stock policy. He gives a very simple example where the concept “re-order for each item sold” is useful: Items in inventory are bulky, and expensive (automobiles or TV sets¹). He uses queueing theory to model the inventory systems, analogously to Reed and Zhang (2017), etc.

Literature on integrated queueing-inventory models (i.e. queueing theory in combination with inventory theory) is also overwhelming. For a recent review we refer to Krishnamoorthy et al. (2021).

In this paper, we analyse an extension of the complex supply chain from Otten et al. (2016), where routing of items depends on the on-hand inventory at the locations with the aim to obtain “load balancing”. It can be differed between two load balancing policies. In Otten (2017, Section 3.4) we consider weak priorities, i.e. the finished item of raw material is sent with greater probability to the location with higher difference between the on-hand inventory and the capacity of the inventory. In this paper, we focus on strict priorities, i.e. the finished item of raw material is sent to the location(s) with the highest difference between the on-hand inventory and the capacity of the inventory. Therefore, we mention here some

Literature about load balancing policies with strict priorities:

The research of such systems is motivated by state-dependent routing/branching of customers. “The purpose of introducing flexible state-dependent routing strategies is to optimally utilize network resources and to minimise network delay and response times” (Daduna, 1987, p. 1) and “Unfortunately it turned out that introducing state-dependent routing into product form networks usually destroys the product-form of the steady state probabilities” (Daduna, 1987, p. 1). Product form solutions under state-dependent routing are, for example, found in Pittel (1979), Hordijk and Dijk (1984) and Schassberger (1984).

Several other stock allocation policies can, for example, be found in the article of Abouee-Mehrizi et al. (2014). They consider a two-echelon inventory system with a capacitated centralized production facility and several distribution centres. We will not go into any greater detail in this allocation policies.

Daduna (1985, p. 624) and Towsley (1980, pp. 327f.) argued that an optimal routing/branching policy for systems with identical peripheral processors is by intuitive reasoning: “Customers enter the peripheral processor with the shortest queue”. This is equivalent to our strict priorities for load balancing policy.

Chow and Kohler (1977, 1979) analyse the performance of two-processor distributed computer systems under several dynamic load balancing policies. They compare the performance and their results indicate that a simple load balancing policy can significantly improve the performance (turnaround time) of the system. In (Chow & Kohler, 1977) they analyse the performance of homogeneous (i.e. identical) two-processor distributed computer systems under several dynamic load balancing policies. Their analysis is based on the recursive solution technique, which was first suggested by Herzog et al. (1975) for queueing problems. Their strategy “join the shorter queue without channel transfer” in Chow and Kohler’s Model B  (Chow & Kohler, 1977, pp. 42f.) is equivalent to our strict load balancing policy. Additionally, they allow a channel transfer in Model C  (Chow & Kohler, 1977, pp. 42f.).

Flatto and McKean (1977) study also Chow and Kohler’s Model B and derive by the generating function approach a complicated closed form solution (cf. Flatto & McKean, 1977, Section 3, p. 261), where the interarrival times of customers are exponentially distributed with rate 1.

Chow and Kohler (1979) present a generalization of the recursive solution technique. They apply the method to non-homogeneous ($=$ heterogeneous) two-processor systems with special properties in Chow and Kohler (1979, Section IV, pp. 358f.) and present a sample system using the algorithm in  Chow and Kohler (1979, Appendix, pp. 360f.). They mention that the generalization of recursive solution “(...) technique for three or more processors does not appear to be straightforward” (Chow & Kohler, 1979, p. 359).

Our main contributions are the following:

We extend the network of queueing-inventory systems from Otten et al. (2016) by load balancing. For the system with strict priorities for load balancing policy we develop a Markov process. We prove that the stationary distribution has a product form of the marginal distributions of the production subsystem and of the inventory-replenishment subsystem. We derive an explicit solution for the marginal distribution of the production subsystem. Furthermore, for the special case with base stock levels equal to one we have derived an explicit solution for the marginal distribution of the inventory-replenishment subsystem. For systems with base stock levels greater than one the marginal distribution of the inventory-replenishment subsystem with two locations can be obtained by a recursive method which is described by an algorithm. On the other hand, our work is an extension of the investigations of Chow and Kohler (1977, 1979): Their study is limited to two processors ($=$ our inventories without production systems). For the heterogeneous case, our load balancing policy is slightly different from that of Chow and Kohler (1979, Section IV, pp. 358f.) (for more details see Remark 6). Therefore, we construct a new algorithm.

Notations and conventions:

• ${\mathbb {N}}:=\left\{ 1,2,3,\ldots \right\}$, ${\mathbb {N}}_{0}:=\{0\}\cup {\mathbb {N}}$.

• The vector $\textbf{0}$ is a row vector of appropriate size with all entries equal to 0. The vector $\textbf{e}$ is a column vector of appropriate size with all entries equal to 1. The vector is a vector of appropriate dimension.

• The notation $\subset$ between sets means “subset or equal” and $\subsetneq$ means “proper subset”. For a set A we denote by $\vert A\vert$ the number of elements in A.

• $1_{\left\{ expression\right\} }$ is the indicator function which is 1 if expression is true and 0 otherwise.

• Empty sums are 0, and empty products are 1.

• Throughout this article it is assumed that all random variables are defined on a common probability space $(\Omega ,{{\mathcal {F}}},P)$. Furthermore, by Markov process we mean time-homogeneous continuous-time strong Markov process with discrete state space ($=$ Markov jump process). Without further mentioning all Markov processes are assumed to be regular and have cadlag paths, i.e. each path of a process is right-continuous and has left limits everywhere. We call a Markov process regular if it is non-explosive (i.e. the sequence of jump times of the process diverges almost surely), its transition intensity matrix is conservative (i.e. row sums are 0) and stable (i.e. all diagonal elements of the transition intensity matrix are finite).

3 Description of the general model

The supply chain of interest is depicted in Fig. 1. We have a set of locations $\overline{J}:=\left\{ 1,2,\dots ,J\right\}$, $J>1$. Each of the locations consists of a production system with an attached inventory. The inventories are replenished by a single central supplier, which is referred to as workstation $J+1$ and manufactures raw material for all locations. The items of raw material are indistinguishable (exchangeable).

Fig. 1

Supply chain with base stock policies and load balancing policies

Facilities in the supply chain. Each production system $j\in \overline{J}$ consists of a single server (machine) with infinite waiting room that serves customers on a make-to-order basis under a FCFS regime. Customers arrive one by one at the production system j according to a Poisson process with rate $\lambda _{j}>0$ and require service. To satisfy a customer’s demand the production system needs exactly one item of raw material, which is taken from the associated local inventory. When a new customer arrives at a location while the previous customers’ order is not finished, this customer will wait. If the inventory is depleted at location j, the customers who are already waiting in line will wait, but new arriving customers at this location will decide not to join the queue and are lost (“local lost sales”).

The service requests at the locations are exponentially distributed with mean 1. All service requests constitute an independent family of random variables which are independent of the arrival streams. The service at location $j\in \overline{J}$ is provided with local queue-length-dependent intensity. If there are $n_{j}>0$ customers present at location j, either waiting or in service (if any), and if the inventory is not depleted, the service intensity is $\mu _{j}(n_{j})>0$. If the server is ready to serve a customer who is at the head of the line, and the inventory is not depleted, the service immediately starts. Otherwise, the service starts at the instant of time when the next replenishment arrives at the local inventory.

The inventory at location $j\in \overline{J}$ is controlled by prescribing a local base stock level $b_{j}\ge 1$, which is the maximal size of the inventory there, we denote ${{\textbf{b}}}:=\left( b_{j}:j\in \overline{J}\right)$.

The central supplier (which is referred to as workstation $J+1$) consists of a single server (machine) and a waiting room under FCFS regime. At most $\sum _{j\in \overline{J}}b_{j}-1$ replenishment orders are waiting at the central supplier. Service times at the central supplier are exponentially distributed with parameter $\nu >0$.

Routing in the supply chain. A served customer departs from the system immediately after service and the associated consumed raw material is removed from the inventory and an order of one item is placed at the central supplier at this time instant (“base stock policy”).

A finished item of raw material departs from the central supplier immediately and is sent with probability $p_{j}(\textbf{k})$, independent of the network’s history, to location j, $j\in \overline{J}$, if the state of the inventory-replenishment subsystem is $\textbf{k}:=(k_{1},\dots ,k_{J},k_{J+1})$, i.e. $k_j$ is the size of the inventory at location $j\in \overline{J}$ and $k_{J+1}$ the number of replenishment orders at the central supplier. We consider the following load balancing policy with strict priorities: The finished item of raw material is sent to location $j\in \overline{J}$ with probability

$$\begin{aligned} p_{j}(\textbf{k})={\left\{ \begin{array}{ll} 1, &{} \ \text {if }\{j\}=\underset{i\in \overline{J}}{\arg \max }(b_{i}-k_{i}),\\ \frac{1}{\vert \underset{i\in \overline{J}}{\arg \max }(b_{i}-k_{i})\vert }<1, &{} \ \text {if }\{j\}\subsetneq \underset{i\in \overline{J}}{\arg \max }(b_{i}-k_{i}),\\ 0, &{} \ \text {if }j\notin \underset{i\in \overline{J}}{\arg \max }(b_{i}-k_{i}), \end{array}\right. } \end{aligned}$$

i.e. to the location(s) with the highest difference between the on-hand inventory and the capacity of the inventory ($=$ base stock level), if the inventory is not full at this/these location(s) (this means that the on-hand inventory level at this/these location(s) is lower than the base stock level). The routing probabilities out of the central supplier must sum to one if there is at least one order at the central supplier.

It is assumed that transmission times for orders are negligible and set to zero and that transportation times between the central supplier and the local inventories are negligible. The usual independence assumptions are assumed to hold as well.

To obtain a Markovian process description of the integrated queueing-inventory system, we denote by $X_{j}(t)$ the number of customers present at location $j\in \overline{J}$ at time $t\ge 0$, either waiting or in service (queue length). By $Y_{j}(t)$ we denote the size of the inventory at location $j\in \overline{J}$ at time $t\ge 0$. By $W_{J+1}(t)$ we denote the number of replenishment orders at the central supplier at time $t\ge 0$, either waiting or in service (queue length).

We define the joint queueing-inventory process of this system by

$$\begin{aligned} Z=\left( \left( X_{1}(t),\ldots ,X_{J}(t),Y_{1}(t),\ldots ,Y_{J}(t),W_{J+1}(t)\right) \,:\,t\ge 0\right) . \end{aligned}$$

Then, due to the usual independence and memoryless assumptions Z is a homogeneous Markov process, which we assume to be irreducible and regular. The state space of Z is $E=\left\{ \left( \textbf{n},\textbf{k}\right) :\textbf{n}\in {\mathbb {N}}_{0}^{J},\,\textbf{k}\in K\right\}$ with

$$\begin{aligned} K&:=\Big \{(k_{1},\dots ,k_{J},k_{J+1})\vert 0\le k_{j}\le b_{j},\,j=1,\dots ,J,\,k_{J+1}=\sum _{j=1}^{J}(b_{j}-k_{j})\Big \}\\&\subset {\mathbb {N}}_{0}^{J+1}. \end{aligned}$$

Note the redundancy in the state space: $W_{J+1}(t)=\sum _{j\in \overline{J}}b_{j}-\sum _{j\in \overline{J}}Y_{j}(t)$. We prefer to carry all information explicitly with because the dynamics of the system are easier visible.

Discussion of the modelling assumptions

We have imposed several simplifying assumptions on the production-inventory-replenishment system to obtain explicit and simple-to-calculate performance metrics of the system, which give insights into its long-time and stationary behaviour. This enables a parametric and sensitivity analysis that is easy to perform.

First, the assumption of exponentially distributed inter-arrival and service times are standard in the literature and are the best first-order approximations. The locally state-dependent service rates are also common and give quite a bit of flexibility. The lead time is composed of the waiting time plus the production time at the central supplier. Therefore, it is more complex than exponential, constant or even zero lead times (which are often assumed in standard inventory literature). Zero lead times in our systems would result in almost trivial extensions of the queueing systems.

Second, we assume that the local base stock levels are positive (i.e. $b_{j}\ge 1$ at location j). This assumption can be made without loss of generality. Otherwise, all customers at location j would be lost, which is the same as excluding location j from the production-inventory-replenishment system.

Third, the assumption of zero transportation times can be removed by inserting special (virtual) $M/G/\infty$ workstations into the network.

4 Limiting and stationary behaviour

The queueing-inventory process Z has an infinitesimal generator $\textbf{Q}=\left( q(z;\tilde{z}):z,\tilde{z}\in E\right)$ with the following transition rates for $(\textbf{n},\textbf{k})\in E$:

$$\begin{aligned} q\left( (\textbf{n},\textbf{k});(\textbf{n}+\textbf{e}_{i},\textbf{k})\right)&=\lambda _{i}\cdot 1_{\left\{ k_{i}>0\right\} },{} & {} i\in \overline{J},\\ q\left( (\textbf{n},\textbf{k});(\textbf{n}-\textbf{e}_{i},\textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1})\right)&=\mu _{i}(n_{i})\cdot 1_{\left\{ n_{i}>0\right\} }\cdot 1_{\left\{ k_{i}>0\right\} },{} & {} i\in \overline{J},\\ q\left( (\textbf{n},\textbf{k});(\textbf{n},\textbf{k}+\textbf{e}_{i}-\textbf{e}_{J+1})\right)&=\nu \cdot p_{i}(\textbf{k})\cdot 1_{\left\{ k_{i}<b_{i}\right\} },{} & {} i\in \overline{J}. \end{aligned}$$

Note that $k_{J+1}>0$ holds if $k_{i}<b_{i}$ for some $i\in \overline{J}$.

Furthermore, $q(z;\tilde{z})=0$ for any other pair $z\ne \tilde{z}$, and

$$\begin{aligned} q\left( z;z\right) =-\sum _{\begin{array}{c} \tilde{z}\in E,\\ z\ne \tilde{z} \end{array}}q\left( z;\tilde{z}\right) \qquad \forall z\in E. \end{aligned}$$

Proposition 1

There exists a strictly positive measure $\widetilde{\theta }=(\widetilde{\theta }(\textbf{k}):\textbf{k}\in K)$, which will be provided below, such that the measure $\textbf{x}:=\left( x\left( \textbf{n},\textbf{k}\right) :\left( \textbf{n},\textbf{k}\right) \in E\right)$ with

$$\begin{aligned} x\left( \textbf{n},\textbf{k}\right) =\widetilde{\xi }(\textbf{n})\cdot \widetilde{\theta }\left( \textbf{k}\right) , \end{aligned}$$

(1)

where

$$\begin{aligned} \widetilde{\xi }(\textbf{n})=\prod _{j\in \overline{J}}\widetilde{\xi }_{j}(n_{j}), \qquad \qquad \widetilde{\xi }_{j}(n_{j})=\prod _{\ell =1}^{n_{j}}\frac{\lambda _{j}}{\mu _{j}(\ell )}, \quad n_{j}\in {\mathbb {N}}_{0},\ j\in \overline{J}, \end{aligned}$$

(2)

solves the global balance equations $\textbf{x}\cdot \mathbf {Q=0}$ and is therefore stationary for Z. Consequently, $\textbf{x}$ is strictly positive.

Proof

The global balance equations $\textbf{x}\cdot \mathbf {Q=0}$ of the stochastic queueing-inventory process Z are given for $\left( \textbf{n},\textbf{k}\right) \in E$ by

$$\begin{aligned}&x\left( \textbf{n},\textbf{k}\right) \cdot \Big (\sum _{i\in \overline{J}}\lambda _{i}\cdot 1_{\left\{ k_{i}>0\right\} }+\sum _{i\in \overline{J}}\mu _{i}(n_{i})\cdot 1_{\left\{ n_{i}>0\right\} }\cdot 1_{\left\{ k_{i}>0\right\} }+\sum _{i\in \overline{J}}\nu \cdot p_{i}(\textbf{k})\cdot 1_{\left\{ k_{i}<b_{i}\right\} }\Big )\\&\quad =\sum _{i\in \overline{J}}x\left( \textbf{n}-\textbf{e}_{i},\textbf{k}\right) \cdot \lambda _{i}\cdot 1_{\left\{ n_{i}>0\right\} }\cdot 1_{\left\{ k_{i}>0\right\} }\\&\quad +\sum _{i\in \overline{J}}x\left( \textbf{n}+\textbf{e}_{i},\textbf{k}+\textbf{e}_{i}-\textbf{e}_{J+1}\right) \cdot \mu _{i}(n_{i}+1)\cdot 1_{\left\{ k_{i}<b_{i}\right\} }\\&\quad +\sum _{i\in \overline{J}}x\left( \textbf{n},\textbf{k}-\textbf{e}_{i} +\textbf{e}_{J+1}\right) \cdot \nu \cdot p_{i}(\textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1})\cdot 1_{\left\{ k_{i}>0\right\} }. \end{aligned}$$

It has to be shown that the stationary measure from Proposition 1 satisfies these global balance equations.

Substitution of (1) and (2) into the global balance equations directly leads to

$$\begin{aligned}&\left( \prod _{j\in \overline{J}}\widetilde{\xi }_{j}(n_{j})\right) \cdot \widetilde{\theta }\left( \textbf{k}\right) \\&\quad \cdot \Big (\sum _{i\in \overline{J}}\lambda _{i}\cdot 1_{\left\{ k_{i}>0\right\} } +\sum _{i\in \overline{J}}\mu _{i}(n_{i})\cdot 1_{\left\{ n_{i}>0\right\} }\cdot 1_{\left\{ k_{i}>0\right\} } +\sum _{i\in \overline{J}}\nu \cdot p_{i}\cdot 1_{\left\{ k_{i}<b_{i}\right\} }\Big )\\&\quad =\sum _{i\in \overline{J}}\left( \prod _{{j\in \overline{J}\backslash \left\{ i\right\} }}\widetilde{\xi }_{j}(n_{j})\right) {\widetilde{\xi }_{i}(n_{i}-1)}\cdot \widetilde{\theta }\left( \textbf{k}\right) \cdot {\lambda _{i}}\cdot 1_{\left\{ n_{i}>0\right\} } \cdot 1_{\left\{ k_{i}>0\right\} }\\&\quad +\sum _{i\in \overline{J}}\left( \prod _{j\in \overline{J}\backslash \left\{ i\right\} }\widetilde{\xi }_{j}(n_{j})\right) \cdot \widetilde{\xi }_{i}(n_{i}+1)\cdot \widetilde{\theta }\left( \textbf{k}+\textbf{e}_{i}-\textbf{e}_{J+1}\right) \cdot \mu _{i}(n_{i} +1)\cdot 1_{\left\{ k_{i}<b_{i}\right\} }\\&\quad +\sum _{i\in \overline{J}}\left( \prod _{j\in \overline{J}}\widetilde{\xi }_{j}(n_{j})\right) \cdot \widetilde{\theta } \left( \textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1}\right) \cdot \nu \cdot p_{i}\cdot 1_{\left\{ k_{i}>0\right\} }. \end{aligned}$$

By substitution of (2) we obtain

$$\begin{aligned}&\left( \prod _{j\in \overline{J}}\widetilde{\xi }_{j}(n_{j})\right) \cdot \widetilde{\theta }\left( \textbf{k}\right) \\&\quad \cdot \Big (\sum _{i\in \overline{J}}\lambda _{i}\cdot 1_{\left\{ k_{i}>0\right\} } +\sum _{i\in \overline{J}}\mu _{i}(n_{i})\cdot 1_{\left\{ n_{i}>0\right\} }\cdot 1_{\left\{ k_{i}>0\right\} } +\sum _{i\in \overline{J}}\nu \cdot p_{i}\cdot 1_{\left\{ k_{i}<b_{i}\right\} }\Big )\\&\quad =\sum _{i\in \overline{J}}\left( \prod _{j\in \overline{J}}\widetilde{\xi }_{j}(n_{j})\right) \cdot \widetilde{\theta } \left( \textbf{k}\right) \cdot \mu _{i}(n_{i})\cdot 1_{\left\{ n_{i}>0\right\} }\cdot 1_{\left\{ k_{i}>0\right\} }\\&\quad +\sum _{i\in \overline{J}}\left( \prod _{j\in \overline{J}}\widetilde{\xi }_{j}(n_{j})\right) \cdot \widetilde{\theta } \left( \textbf{k}+\textbf{e}_{i}-\textbf{e}_{J+1}\right) \cdot \lambda _{i}\cdot 1_{\left\{ k_{i}<b_{i}\right\} }\\&\quad +\sum _{i\in \overline{J}}\left( \prod _{j\in \overline{J}}\widetilde{\xi }_{j}(n_{j})\right) \cdot \widetilde{\theta } \left( \textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1}\right) \cdot \nu \cdot p_{i}\cdot 1_{\left\{ k_{i}>0\right\} }. \end{aligned}$$

Cancelling $\left( \prod _{j\in \overline{J}}\widetilde{\xi }_{j}(n_{j})\right)$ and the sums with the terms $\mu _{i}(n_{i})\cdot 1_{\left\{ n_{i}>0\right\} }\cdot 1_{\left\{ k_{i}>0\right\} }$ on both sides of the equation leads to

$$\begin{aligned}&\widetilde{\theta }\left( \textbf{k}\right) \Big (\sum _{i\in \overline{J}}\lambda _{i}\cdot 1_{\left\{ k_{i}>0\right\} } +\sum _{i\in \overline{J}}\nu \cdot p_{i}(\textbf{k})\cdot 1_{\left\{ k_{i}<b_{i}\right\} }\Big )\nonumber \\&\quad =\sum _{i\in \overline{J}}\widetilde{\theta }\left( \textbf{k}+\textbf{e}_{i}-\textbf{e}_{J+1}\right) \cdot \lambda _{i} \cdot 1_{\left\{ k_{i}<b_{i}\right\} }\nonumber \\&\quad +\sum _{i\in \overline{J}}\widetilde{\theta }\left( \textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1}\right) \cdot \nu \cdot p_{i}(\textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1}) \cdot 1_{\left\{ k_{i}>0\right\} }.\qquad \end{aligned}$$

(3)

An inspection of the system (3) reveals that it is a “generator equation”, i.e. the global balance equation $\widetilde{\theta }\cdot \textbf{Q}_{red}=0$ for a suitably defined ergodic Markov process on state space K with “reduced generator” $\textbf{Q}_{red}=\left( q_{red}(\textbf{k};\widetilde{\textbf{k}}):\textbf{k},\widetilde{\textbf{k}}\in K\right)$ with the following transition rates for $\textbf{k}\in K$:

$$\begin{aligned} q_{red}\left( \textbf{k};\textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1}\right)&=\lambda _{i}\cdot 1_{\left\{ k_{i}>0\right\} },{} & {} i\in \overline{J},\\ q_{red}\left( \textbf{k};\textbf{k}+\textbf{e}_{i}-\textbf{e}_{J+1}\right)&=\nu \cdot p_{i}(\textbf{k})\cdot 1_{\left\{ k_{i}<b_{i}\right\} },{} & {} i\in \overline{J}. \end{aligned}$$

The Markov process generated by $\textbf{Q}_{red}$ is irreducible on K and therefore (3) has a solution which is unique up to a multiplicative constant, which yields $\widetilde{\theta }$. $\square$

Remark 1

In Sect. 4.1.1, the marginal measure $\widetilde{\theta }$ is derived in explicit form for the special case with base stock levels $b_{j}=1$, $j\in \overline{J}$.

For systems with two locations and base stock levels greater than one ($b_{j}>1$, $j\in \overline{J}$), the marginal measure $\widetilde{\theta }$ can be obtained by a recursive method which is described by the algorithm given in Sect. 4.1.2.

Recall that the system is irreducible and regular. Therefore, if Z has a stationary and limiting distribution, this is uniquely defined.

Definition 1

For the queueing-inventory process Z on state space E, whose limiting distribution exists, we define

$$\begin{aligned} \pi :=\left( \pi \left( \textbf{n},\textbf{k}\right) :\left( \textbf{n},\textbf{k}\right) \in E\right) , \quad \pi \left( \textbf{n},\textbf{k}\right) :=\lim _{t\rightarrow \infty }P\left( Z(t)=(\textbf{n},\textbf{k})\right) \end{aligned}$$

and the appropriate marginal distributions

$$\begin{aligned} \xi:= & {} \left( \xi \left( \textbf{n}\right) :\textbf{n}\in {\mathbb {N}}_{0}^{J}\right) ,\quad \xi \left( \textbf{n}\right) :=\lim _{t\rightarrow \infty }P\left( \left( X_{1}(t),\ldots ,X_{J}(t)\right) =\textbf{n}\right) ,\\ \theta:= & {} \left( \theta \left( \textbf{k}\right) :\textbf{k}\in K\right) ,\quad \theta \left( \textbf{k}\right) :=\lim _{t\rightarrow \infty }P\left( \left( Y_{1}(t),\ldots ,Y_{J}(t),W_{J+1}(t)\right) =\textbf{k}\right) . \end{aligned}$$

Theorem 2

The queueing-inventory process Z is ergodic if and only if for $j\in \overline{J}$

$$\begin{aligned} \sum _{n_{j}\in {\mathbb {N}}_{0}}\prod _{\ell =1}^{n_{j}}\frac{\lambda _{j}}{\mu _{j}(\ell )}<\infty . \end{aligned}$$

If Z is ergodic, then its unique limiting and stationary distribution is

$$\begin{aligned} \pi \left( \textbf{n},\textbf{k}\right) =\xi (\textbf{n})\cdot \theta \left( \textbf{k}\right) , \end{aligned}$$

(4)

with

$$\begin{aligned} \xi (\textbf{n})=\prod _{j\in \overline{J}}\xi _{j}(n_{j}),\qquad \qquad \xi _{j}(n_{j})=C_{j}^{-1}\prod _{\ell =1}^{n_{j} }\frac{\lambda _{j}}{\mu _{j}(\ell )},\quad n_{j}\in {\mathbb {N}}_{0},\ j\in \overline{J}, \end{aligned}$$

(5)

and normalisation constants

$$\begin{aligned} C_{j}=\sum _{n_{j}\in {\mathbb {N}}_{0}}\prod _{\ell =1}^{n_{j}}\frac{\lambda _{j}}{\mu _{j}(\ell )} \end{aligned}$$

and $\theta$ is the probabilistic solution of (3).

Proof

Z is ergodic if and only if the strictly positive measure $\textbf{x}$ of the global balance equation $\textbf{x}\cdot \textbf{Q}=\textbf{0}$ from Proposition 1 can be normalised (i.e. $\sum _{\textbf{n}\in {\mathbb {N}}_{0}}\sum _{\textbf{k}\in K}x(\textbf{n},\textbf{k})<\infty$). Because of Proposition 1 it holds

$$\begin{aligned} \sum _{\textbf{n}\in {\mathbb {N}}_{0}}\sum _{\textbf{k}\in K}x(\textbf{n},\textbf{k}) =\sum _{\textbf{n}\in {\mathbb {N}}_{0}}\widetilde{\xi }(\textbf{n})\cdot \sum _{\textbf{k}\in K} \widetilde{\theta }\left( \textbf{k}\right) =\left( \prod _{j\in \overline{J}}\sum _{n_{j}\in {\mathbb {N}}_{0}} \prod _{\ell =1}^{n_{j}}\frac{\lambda _{j}}{\mu _{j}(\ell )}\right) \cdot \sum _{\textbf{k}\in K}\widetilde{\theta }\left( \textbf{k}\right) . \end{aligned}$$

Hence, since K is finite, the measure $\textbf{x}$ from Proposition 1 can be normalised if and only if $\sum _{n_{j}\in {\mathbb {N}}_{0}}\prod _{\ell =1}^{n_{j}}\frac{\lambda _{j}}{\mu _{j}(\ell )}<\infty$ for all $j\in \overline{J}$.

Consequently, if the process is ergodic, the limiting and stationary distribution $\pi$ is given by

$$\begin{aligned} \pi (\textbf{n},\textbf{k})=\frac{x(\textbf{n},\textbf{k})}{\sum _{\textbf{n}\in {\mathbb {N}}_{0}}\sum _{\textbf{k}\in K}x(\textbf{n},\textbf{k})}, \end{aligned}$$

where $x(\textbf{n},\textbf{k})$ is given in Proposition 1. $\square$

Remark 2

The expression (4) shows that the two-component production-inventory-replenishment system is separable, the steady states of the production network and the inventory-replenishment complex decouple asymptotically.

Representation (5) shows that the equilibrium for the production subsystem decomposes in true independent coordinates. A product structure of the stationary distribution as

$$\begin{aligned} \xi (\textbf{n})=\prod _{j\in \overline{J}}\xi _{j}(n_{j})=\prod _{j\in \overline{J}}C_{j}^{-1}\prod _{\ell =1}^{n_{j}}\frac{\lambda _{j}}{\mu _{j}(\ell )} \end{aligned}$$

is commonly found for standard Jackson networks (cf. Jackson (1957)) and their relatives. In Jackson networks servers are “non-idling”, i.e. they are always busy as long as customers are present at the respective node. In our production network, however, servers may be idle while there are customers waiting because a replenishment needs to arrive first. Consequently, the product form (4) has been unexpected to us.

Our production-inventory-replenishment system can be considered as a “Jackson network in a random environment” in  Krenzler et al. (2016, Section 4). We can interpret the inventory-replenishment subsystem, which contributes via $\theta$ to Theorem 2, as a “random environment” for the production network of nodes $\overline{J}$, which is a Jackson network of parallel servers. Taking into account the results of  Krenzler et al. (2016, Theorem 4.1) we conclude from the hindsight that decoupling of the queueing process $\left( X_{1},\dots ,X_{J}\right)$ and the process $\left( Y_{1},\dots ,Y_{J},W_{J+1}\right)$, i.e. the formula (4), is a consequence of that Theorem 4.1.

Our direct proof of Proposition 1 is much shorter than embedding the present model into the general framework of Krenzler et al. (2016).

Structural properties of the integrated system

The investigations in this section rely on the fact that the product form of the stationary distribution ($=$ separability) makes structures easily visible that are hard to detect by simulations or by direct numerical investigations. As a byproduct we demonstrate the power of product form calculus.

Ergodicity:

As shown in Theorem 2, ergodicity is determined by $\sum _{n_{j}\in {\mathbb {N}}_{0}}\prod _{\ell =1}^{n_{j}}\frac{\lambda _{j}}{\mu _{j}(\ell )}<\infty$, $j\in \overline{J}$, because K is finite. Hence, ergodicity is determined by the parameters of the isolated queueing system without the inventory system at the locations. For instance, if ${\mu _{j}(\ell )}=\mu _{j},\forall \ell$, then $\lambda _{j}<\mu _{j},\forall j$, is the correct condition for stabilizing the entire system.

Noteworthy is that the extra idle times of the servers at the production systems do not destroy ergodicity due to the necessary replenishments. The reason behind this is that the local lost sales at the individual servers at these locations automatically balance a possible bottleneck behaviour of the central supplier.

Insensitivity and robustness:

Sensitivity analysis is an important topic in classical inventory theory and is often hard to perform. In our model the stationary distribution $\pi \left( \textbf{n},\textbf{k}\right) =\left( \prod _{j\in \overline{J}}\xi _{j}(n_{j})\right) \cdot \theta \left( \textbf{k}\right)$ reveals strong insensitivity properties of the system which make sensitivity analysis amenable: The steady state behaviour of the subnetwork consisting of inventories and the central supplier does not change when the service rates at the locations are changed as long as the global system remains ergodic. Therefore $\theta$ is robust against the estimation errors in determining the $\mu _{j}(\cdot )$. Vice versa, the distribution $\xi _{j}(n_{j})$ is robust against changes in the inventory-replenishment network as long as the demand intensity and the service rates are maintained.

Remark 3

A cost analysis can be performed as for the model without load balancing in Otten et al. (2016, pp. 11f.). Note a corrected version of the definition of the cost function can be found in Otten (2017, Section 2.5, pp. 25f.).

4.1 Calculation of $\widetilde{\theta }$

4.1.1 Special case: $b_{j}=1$, $j\in \overline{J}$

In this section, we will solve the global balance equation $\widetilde{\theta }\cdot \textbf{Q}_{red}=\textbf{0}$ for the special case with base stock levels $b_{j}=1$, $j\in \overline{J}$. In this special case, our model with strict priorities is identical to the model with weak priorities in Otten (2017, Section 3.4), where the finished item of raw material is sent with a greater probability to the location with higher difference between the on-hand inventory and the capacity of the inventory. For the sake of completeness we present the proof here.

We recall the notation for the inventory-replenishment subsystem

$$\begin{aligned} \widetilde{\theta }(\overbrace{k_{1},k_{2},\ldots ,k_{J}}^{\begin{array}{c} \text {inventories}\\ \text {at locations} \end{array}},\overbrace{k_{J+1}}^{\text {supplier}}). \end{aligned}$$

Furthermore, in this special case it holds $p_{i}(\textbf{k})=\frac{1}{J-\sum _{j\in \overline{J}}k_j}$ if $k_i=0$, $i\in \overline{J}$.

Proposition 3

The strictly positive measure $\widetilde{\theta }=\left( \widetilde{\theta }(\textbf{k}):\textbf{k}\in K\right)$ of the inventory-replenishment subsystem with base stock levels $b_{1}=\cdots =b_{J}=1$ is given by

$$\begin{aligned} \widetilde{\theta }(\textbf{k})=\widetilde{\theta }(k_{1},k_{2},\ldots ,k_{J},k_{J+1})&=\left( \prod _{\ell =0}^{(\sum _{j\in \overline{J}}k_{j})-1}\frac{1}{J-\ell }\right) \cdot \left( \prod _{j\in \overline{J}}\left( \frac{1}{\lambda _j}\right) ^{k_{j}}\right) \cdot \left( \frac{1}{\nu }\right) ^{k_{J+1}} \end{aligned}$$

(6)

Remark 4

As we have mentioned before (3) has a solution which is unique up to a multiplicative constant, which yields $\widetilde{\theta }$. In Otten (2017, Proposition 3.3.6, p. 50) another stationary measure $\widetilde{\theta }_1$ is presented which differs from our stationary measure up to a multiplicative constant, i.e.  $\widetilde{\theta }=\left( \tfrac{1}{\nu }\right) ^{J}\cdot \widetilde{\theta }_1$.

Proof

It has to be shown that the stationary measure (6) satisfies the global balance equations $\widetilde{\theta }\cdot \textbf{Q}_{red}=\textbf{0}$, which are given for $\textbf{k}\in K$ by

$$\begin{aligned}&\widetilde{\theta }\left( \textbf{k}\right) \cdot \Big (\sum _{i\in \overline{J}}\lambda _{i}\cdot 1_{\left\{ k_{i}=1\right\} } +\sum _{i\in \overline{J}}\nu \cdot p_{i}(\textbf{k})\cdot 1_{\left\{ k_{i}=0\right\} }\Big )\\&\quad =\sum _{i\in \overline{J}}\widetilde{\theta }\left( \textbf{k}+\textbf{e}_{i}-\textbf{e}_{J+1}\right) \cdot \lambda _{i}\cdot 1_{\left\{ k_{i}=0\right\} }\\&\quad +\sum _{i\in \overline{J}}\widetilde{\theta }\left( \textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1}\right) \cdot \nu \cdot p_{i}(\textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1})\cdot 1_{\left\{ k_{i}=1\right\} }\\&\Leftrightarrow \widetilde{\theta }\left( \textbf{k}\right) \cdot \Big (\sum _{i\in \overline{J}}\lambda _{i}\cdot 1_{\left\{ k_{i}=1\right\} } +\sum _{i\in \overline{J}}\nu \cdot p_{i}(\textbf{k})\cdot 1_{\left\{ k_{i}=0\right\} }\Big )\\&\quad =\sum _{i\in \overline{J}} \underbrace{\left( \prod _{\ell =0}^{(\sum _{j\in \overline{J}}k_{j})-1}\frac{1}{J-\ell }\right) \cdot \left( \prod _{j\in \overline{J}}\left( \frac{1}{\lambda _j}\right) ^{k_{j}}\right) \cdot \left( \frac{1}{\nu }\right) ^{k_{J+1}}}_{\widetilde{\theta }\left( \textbf{k}\right) }\\&\quad \cdot \underbrace{\frac{1}{J-\sum _{j\in \overline{J}}k_{j}}}_{=p_i(\textbf{k})} \cdot \frac{1}{\lambda _{i}}\cdot \nu \cdot \lambda _{i}\cdot 1_{\left\{ k_{i}=0\right\} }\\&\quad +\sum _{i\in \overline{J}} \underbrace{\left( \prod _{\ell =0}^{(\sum _{j\in \overline{J}}k_{j})-1}\frac{1}{J-\ell }\right) \cdot \left( \prod _{j\in \overline{J}}\left( \frac{1}{\lambda _j}\right) ^{k_{j}}\right) \cdot \left( \frac{1}{\nu }\right) ^{k_{J+1}}}_{\widetilde{\theta }\left( \textbf{k}\right) }\\&\quad \cdot \underbrace{\left( J+1-\sum _{j\in \overline{J}}k_{j}\right) }_{=\frac{1}{p_{i}(\textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1})}} \cdot \lambda _i \cdot \frac{1}{\nu } \cdot \nu \cdot p_{i}(\textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1})\cdot 1_{\left\{ k_{i}=1\right\} } \end{aligned}$$

The right hand-side of the last equation is

$$\begin{aligned} \sum _{i\in \overline{J}}\widetilde{\theta }\left( \textbf{k}\right) \nu \cdot p_{i}(\textbf{k})\cdot 1_{\left\{ k_{i}=0\right\} } +\sum _{i\in \overline{J}}\widetilde{\theta }\left( \textbf{k}\right) \lambda _{i}\cdot 1_{\left\{ k_{i}=1\right\} }. \end{aligned}$$

$\square$

Remark 5

We make a distinction between homogeneous and heterogeneous locations.

We mean by homogeneous locations that the inventories have identical base stock levels $b_{1}=b_{2}=\cdots =b_{J}$ and identical arrival rates $\lambda _{1}=\lambda _{2}=\cdots =\lambda _{J}>0$. Service rates $\mu _{j}(\cdot )>0$, $j\in \overline{J}$, obey no such restrictions.

We mean by heterogeneous locations that there may be different arrival rates $\lambda _{j}>0$, $j\in \overline{J}$ (and any service rate $\mu _{j}(\cdot )>0$, $j\in \overline{J}$) and for the base stock levels hold $b_{1}\ge b_{2}\ge \cdots \ge b_{J}$.

As a consequence of the preceding Proposition 3 the following symmetry property for homogeneous locations with base stock levels $b_{1}=b_{2}=\cdots =b_{J}=1$ is valid.

For all permutations $\sigma$ of $\left\{ 1,\ldots ,J\right\}$ it holds

$$\begin{aligned} \widetilde{\theta }(\overbrace{k_{1},k_{2},\ldots ,k_{J}}^{\begin{array}{c} \text {inventories}\\ \text {at locations} \end{array} },\overbrace{k_{J+1}}^{\text {supplier}})=\widetilde{\theta }(\overbrace{k_{\sigma (1)},k_{\sigma (2)}, \ldots ,k_{\sigma (J)}}^{\begin{array}{c} \text {inventories}\\ \text {at locations} \end{array} },\overbrace{k_{\sigma J+1}}^{\text {supplier}}). \end{aligned}$$

For $b_{1}=b_{2}=\cdots =b_{J}>1$ the global balance equations (3) reveal directly that this symmetry property holds in this case as well.

4.1.2 Special case: two locations and $b_{j}>1$, $j\in \overline{J}$

In this section, we assume that there are two heterogeneous locations with base stock levels $b_{1}\ge b_{2}$, where $b_{1}, b_{2}>1$ and arrival rates $\lambda _{1},\lambda _{2}, \nu >0$. The state transition diagram for such a system is presented in Fig. 2.

Fig. 2

State transition diagram of a system with two heterogeneous locations

To obtain $\widetilde{\theta }(\textbf{k})$, $\textbf{k}\in K$, from the global balance equations $\widetilde{\theta }\cdot \textbf{Q}_{red}=\textbf{0}$ (cf. Eq. (3)) we use the recursive solution technique. This technique uses the fact that the steady state probabilities of the system can sometimes be expressed in terms of other steady state probabilities. Consequently, this leads to a reduction of the number of unknowns in the global balance equations. For our system the recursive method is described by the following algorithm.

$\kappa$ is a variable which represents a temporarily unknown probability and GBE is used to denote a global balance equation. We will henceforth use an abbreviated notation because $k_{J+1}=\sum _{j=1}^{J}(b_{j}-k_{j})$ and the base stock levels $b_{j}$, $j\in \overline{J}$, are fixed parameters:

$$\begin{aligned} \widetilde{\theta }\Big (\overbrace{\ \,k_{1},\ \ k_{2}}^{\begin{array}{c} \text {inventories}\\ \text {at locations} \end{array} }\Big ):=\widetilde{\theta }\Big (\overbrace{\ \,k_{1},\ \ k_{2},}^{\begin{array}{c} \text {inventories}\\ \text {at locations} \end{array} }\overbrace{k_{3}}^{\text {supplier}}\Big ) \end{aligned}$$

and hence,

$$\begin{aligned} p_{i}(\textbf{k}-\textbf{e}_{i}) :=p_{i}(\textbf{k}-\textbf{e}_{i}+\textbf{e}_{J+1}),\qquad p_{i}(\textbf{k}+\textbf{e}_{i}) :=p_{i}(\textbf{k}+\textbf{e}_{i}-\textbf{e}_{J+1}),\ i\in \overline{J}. \end{aligned}$$

A few steps of the algorithm are visualised in the state transition diagram in Fig. 3 and the algorithm is illustrated by an example in Appendix A, which is motivated by the computational example in  Chow and Kohler (1979, Appendix, pp. 360f.). Furthermore, a detailed explanation of the algorithm can be found in Otten (2017, Appendix C.1, pp. 275–311).

Remark 6

Chow and Kohler apply a recursive solution technique to non-homogeneous (= heterogeneous) twoprocessor systems with special properties in (Chow & Kohler, 1979, Section IV, pp. 358f.). One special property of the load balancing policy that enables to use their technique for the two-processor heterogeneous systems is that the policy line ($=$ continuous chain of arrival transitions starting at state (0, 0) given that no departure occurs) partitions the states of the state transition rate diagram into two regions. Our load balancing policy is slightly different from that of Chow and Kohler because of $\frac{1}{2}\nu$ (since if both inventories have the same difference between the on-hand inventory and the capacity of the inventory, it enters either with equal probability) as can be seen in the state transition diagram in Fig. 2.

Fig. 3

Visualisation of a few steps of the algorithm

Special case: two homogeneous locations

Our algorithm for two locations can also be applied to obtain $\widetilde{\theta }$ for a system with two homogeneous locations, i.e. where the inventories have identical base stock levels $b_{1}=b_{2}>1$ and identical arrival rates $\lambda _{1}=\lambda _{2}>0$ (and any service rates $\mu _{1},\mu _{2}>0$). The state transition diagram for such a system is presented in Fig. 4. However, the algorithm can be simplified for the case of two homogeneous locations, since in the state transition diagram of a system with two homogeneous locations is symmetric about the diagonal elements $(k_{1},k_{2})$. Hence, the state transition diagram can be folded to obtain a triangle as shown in Fig. 4. Consequently, it holds $\widetilde{\theta }(k_{1},k_{2})=\widetilde{\theta }(k_{2},k_{1})$.

Fig. 4

State transition diagram (left) and folded state transistion diagram (right) of a system with two homogeneous locations

We can extend our model with two locations by a channel transfer and obtain a stationary distribution of product form. Then, the inventories at the locations are connected through a transfer channel. The transfer time of the channel is exponentially distributed with rate $\beta >0$. If the difference between the number of items in location i and the number of items at location j is equal to or greater than two ($=$ disbalance condition), then the transfer channel initiates a transfer from items from location i to location j. There can be only one transfer at a time and the transfer of an item is discontinued if the disbalance condition changes before the transfer is completed. The state transition diagram can still be folded into a triangle, so that the symmetry property holds. Second, because the channel transfer leads to a further summand on the left side of the GBE (flow into the state). The state transition diagram as well as the folded state transition diagram for such a system with two locations are presented in Fig. 5.

Fig. 5

State transition diagram (left) and folded state transition diagram (right) of a system with two homogeneous locations and transfer channel

5 Structural properties of the stationary inventory-replenishment subsystem

In this section, we assume that the queueing-inventory process Z is ergodic. We make again a distinction between homogeneous and heterogeneous locations. Furthermore, in this section, we will use an abbreviated notation because $k_{J+1}=\sum _{j=1}^{J}(b_{j}-k_{j})$ and the base stock levels $b_{j}$, $j\in \overline{J}$, are fixed parameters:

$$\begin{aligned} \theta (\overbrace{k_{1},k_{2},\ldots ,k_{J}}^{\begin{array}{c} \text {inventories}\\ \text {at locations} \end{array} }):=\theta (\overbrace{k_{1},k_{2},\ldots ,k_{J}}^{\begin{array}{c} \text {inventories}\\ \text {at locations} \end{array} },\overbrace{k_{J+1}}^{\text {supplier}}). \end{aligned}$$

Homogeneous locations

Let $(Y_{1},Y_{2},\ldots Y_{J},W_{J+1})$ be a random variable which is distributed according to the marginal steady state probability for the inventory-replenishment subsystem.²

Proposition 4

For the inventory process holds

$$\begin{aligned}&P\left( Y_{1}=\ell \right) =P\left( Y_{j}=\ell \right) ,\quad j\in \overline{J}\setminus \left\{ 1\right\} ,\ \ell \in \{0,\ldots ,b_{1}\},\nonumber \\&P\left( Y_{1}=\ell \right) \cdot \lambda _{1}\nonumber \\&\quad =P\left( Y_{j}=\ell -1\ \text {for }j\in \overline{J}\right) \cdot \frac{\nu }{J}\nonumber \\&\quad +\sum _{i=1}^{J-1}P\left( Y_{j}=\ell -1\ \text {for }j=1,\ldots ,i\ \text {and }\ell -1<Y_{k}\le b_{k}\ \text {for }k=i+1,\ldots ,J\right) \nonumber \\&\quad \cdot \left( {\begin{array}{c}J-1\\ i-1\end{array}}\right) \cdot \frac{\nu }{i}, \qquad \qquad \qquad \ell \in \{1,\ldots ,b_{1}\}. \end{aligned}$$

(7)

Proof

It holds

$$\begin{aligned} P\left( Y_{1}=\ell \right) =P\left( Y_{j}=\ell \right) ,\quad j\in \overline{J}\setminus \left\{ 1\right\} ,\ \ell \in \{0,\ldots ,b_{1}\} \end{aligned}$$

because of the symmetry property for homogeneous locations (see Remark 5) and because

$$\begin{aligned} P\left( Y_{1}=\ell \right) =\sum _{k_{2}=0}^{b_{2}}\cdots \sum _{k_{J}=0}^{b_{J}}\theta (\ell ,k_{2},\ldots ,k_{J}). \end{aligned}$$

The Eq. (7) can be proven by the cut-criterion for positive recurrent processes (see Kelly, 1979, Lemma 1.4, p. 8).

For $\ell \in \left\{ 1,\ldots ,b_{1}\right\}$, it can be proven by a cut, which divides E into complementary sets according to the size of the inventory at location 1 that is less than or equal to $\ell -1$ or greater than $\ell -1$, i.e. into the sets

$$\begin{aligned}{} & {} \Big \{(k_{1},k_{2},\ldots ,k_{J}):k_{1}\in \{0,1,\ldots ,\ell -1\},\,k_{j}\in \{0,\ldots ,b_{j}\},\ j \in \left\{ 2,\ldots ,J\right\} \Big \},\\{} & {} \quad \left\{ (\widetilde{k}_{1},\widetilde{k}_{2},\ldots ,\widetilde{k}_{J}):\widetilde{k}_{1} \in \{\ell ,\ldots ,b_{1}\},\,\widetilde{k}_{j}\in \{0,\ldots ,b_{j}\},\ j\in \left\{ 2,\ldots ,J\right\} \right\} , \ \ell \in \left\{ 1,\ldots ,b_{1}\right\} . \end{aligned}$$

Then, it follows for $\ell \in \left\{ 1,\ldots ,b_{1}\right\}$

$$\begin{aligned}&\sum _{k_{1}=0}^{\ell -1}\sum _{k_{2}=0}^{b_{2}}\cdots \sum _{k_{J}=0}^{b_{J}}\ \sum _{\widetilde{k}_{1}=\ell }^{b_{1}}\sum _{\widetilde{k}_{2}=0}^{b_{2}}\cdots \sum _{\widetilde{k}_{J}=0}^{b_{J}} \theta (k_{1},k_{2},\ldots ,k_{J})\nonumber \\&\quad \cdot q_{red}\left( (k_{1},k_{2},\ldots ,k_{J});(\widetilde{k}_{1},\widetilde{k}_{2}, \ldots ,\widetilde{k}_{J})\right) \nonumber \\&\quad =\sum _{\widetilde{k}_{1}=\ell }^{b_{1}}\sum _{\widetilde{k}_{2}=0}^{b_{2}}\cdots \sum _{\widetilde{k}_{J}=0}^{b_{J}}\ \sum _{k_{1}=0}^{\ell -1}\sum _{k_{2}=0}^{b_{2}}\cdots \sum _{k_{J}=0}^{b_{J}}\theta (\widetilde{k}_{1},\widetilde{k}_{2}, \ldots ,\widetilde{k}_{J})\nonumber \\&\quad \cdot q_{red}\left( (\widetilde{k}_{1},\widetilde{k}_{2},\ldots , \widetilde{k}_{J});(k_{1},k_{2},\ldots ,k_{J})\right) \nonumber \\ \nonumber \\&\Leftrightarrow \quad \theta (\ell -1,\ell -1,\ldots ,\ell -1)\cdot \frac{\nu }{J} \end{aligned}$$

(8)

$$\begin{aligned}&\quad +\sum _{i=1}^{J-1}\sum _{k_{i+1}=\ell }^{b_{i+1}}\cdots \sum _{k_{J}=\ell }^{b_{J}} \theta (\ell -1,\ell -1,\ldots ,\ell -1,k_{i+1},\ldots ,k_{J})\cdot \left( {\begin{array}{c}J-1\\ i-1\end{array}}\right) \cdot \frac{1}{i}\cdot \nu \nonumber \\&\quad =\sum _{\widetilde{k}_{2}=0}^{b_{2}}\cdots \sum _{\widetilde{k}_{J}=0}^{b_{J}}\theta (\ell , \widetilde{k}_{2},\ldots ,\widetilde{k}_{J})\cdot \lambda _{1}. \end{aligned}$$

(9)

The only possible transitions from the set, where the size of the inventory at location 1 is less than or equal to $\ell -1$, to the set, where the inventory at location 1 is greater than $\ell -1$, are transitions according to a replenishment. In particular, transitions from $\Big \{(\ell -1,k_{2},\ldots ,k_{J}):k_{j}\in \{\ell -1,\ldots ,b_{j}\},\ j\in \left\{ 2,\ldots ,J\right\} \Big \},$ to $\left\{ (\ell ,\widetilde{k}_{2},\ldots ,\widetilde{k}_{J}):\widetilde{k}_{j}\in \{\ell -1,\ldots ,b_{j}\},\ j\in \left\{ 2,\ldots ,J\right\} \right\} ,\ \ell \in \left\{ 1,\ldots ,b_{1}\right\} .$

A replenishment at location 1 is only possible if $\{1\}\subseteq \underset{j\in \overline{J}}{\arg \max }(b_{j}-k_{j})$. This means that there is no other location with higher difference between the on-hand inventory and the capacity of the inventory ($=$ base stock level). Consequently, all possible states where the other locations have $\ell -1$ items or more items in the inventory have to be considered.

In Eq. (8) all locations have exactly $\ell -1$ items in the inventory and in Eq. (9) i states how many locations have exactly $\ell -1$ items in the inventory. This results in the factor $\frac{1}{i}$, which is the probability that the finished item is sent to location i. The symmetry property leads to the factor $\left( {\begin{array}{c}J-1\\ i-1\end{array}}\right)$.

Hence, we have shown for $\ell \in \left\{ 1,\ldots ,b_{1}\right\}$

$$\begin{aligned}&P\left( Y_{1}=\ell \right) \cdot \lambda _{1}\\&\quad =P\left( Y_{j}=\ell -1\ \text {for }j\in \overline{J}\right) \cdot \frac{\nu }{J}\\&\quad +\sum _{i=1}^{J-1}P\left( Y_{j}=\ell -1\ \text {for }j=1,\ldots ,i\ \text {and }\ell -1<Y_{k}\le b_{k}\ \text {for }k=i+1,\ldots ,J\right) \\&\qquad \cdot \left( {\begin{array}{c}J-1\\ i-1\end{array}}\right) \cdot \frac{\nu }{i}. \end{aligned}$$

$\square$

Heterogeneous locations

Let $(Y_{1},Y_{2},W_{3})$ be a random variable which is distributed according to the marginal steady state probability for the inventory-replenishment subsystem.³

Remark 7

From Eq. (10) in the following proposition follows

$$\begin{aligned} P(Y_{1}=\ell _{1})=P(Y_{1}=0)\cdot \left( \frac{\nu }{\lambda _{1}}\right) ^{\ell _{1}}, \qquad \ell _{1}\in \left\{ 1,\ldots ,b_{1}-b_{2}\right\} . \end{aligned}$$

Proposition 5

For the inventory process holds for $\ell _{1}=1,\ldots ,b_{1}-b_{2}$

$$\begin{aligned} P(Y_{1}=\ell _{1})\cdot \lambda _{1}=P(Y_{1}=\ell _{1}-1)\cdot \nu , \end{aligned}$$

(10)

for $\ell _{1}=b_{1}-b_{2}+1,\ldots ,b_{1}-1$

$$\begin{aligned} P(Y_{1}=\ell _{1})\cdot \lambda _{1}&=P(Y_{1}=\ell _{1}-1,Y_{2}=\ell _{1}-1-b_{1}+b_{2})\cdot \frac{1}{2}\nu \nonumber \\&\quad +P(Y_{1}=\ell _{1}-1,Y_{2}>\ell _{1}-1-b_{1}+b_{2})\cdot \nu , \end{aligned}$$

(11)

for $\ell _{1}=b_{1}$

$$\begin{aligned} P(Y_{1}=b_{1})\cdot \lambda _{1}&=P(Y_{1}=b_{1}-1,Y_{2}=b_{2}-1)\cdot \frac{1}{2}\nu \qquad \qquad \nonumber \\&\quad +P(Y_{1}=b_{1}-1,Y_{2}=b_{2})\cdot \nu , \end{aligned}$$

(12)

for $\ell _{2}=1,\ldots ,b_{2}$

$$\begin{aligned} P(Y_{2}=\ell _{2})\cdot \lambda _{2}&=P(Y_{1}=b_{1}-b_{2}+\ell _{2}-1,Y_{2}=\ell _{2}-1)\cdot \frac{1}{2}\nu \nonumber \\&\quad +P(Y_{1}>b_{1}-b_{2}+\ell _{2}-1,Y_{2}=\ell _{2}-1)\cdot \nu . \end{aligned}$$

(13)

Proof

The equations can be proven by the cut-criterion for positive recurrent processes (see Kelly, 1979, Lemma 1.4, p. 8).

For $\ell _{1}\in \left\{ 1,\ldots ,b_{1}-b_{2}\right\}$, Eq. (10) can be proven by a cut, which divides E into complementary sets according to the size of the inventory at location 1 that is less than or equal to $\ell _{1}-1$ or greater than $\ell _{1}-1$, i.e. into the sets

$$\begin{aligned}{} & {} \Big \{(k_{1},k_{2}):k_{1}\in \{0,1,\ldots ,\ell _{1}-1\},\,k_{2}\in \{0,\ldots ,b_{2}\}\Big \},\\{} & {} \quad \left\{ (\widetilde{k}_{1},\widetilde{k}_{2}):\widetilde{k}_{1}\in \{\ell _{1},\ldots ,b_{1}\},\, \widetilde{k}_{2}\in \{0,\ldots ,b_{2}\}\right\} ,\quad \ell _{1}\in \left\{ 1,\ldots ,b_{1}-b_{2}\right\} . \end{aligned}$$

Then, it follows for $\ell _{1}\in \left\{ 1,\ldots ,b_{1}-b_{2}\right\}$

$$\begin{aligned}&\sum _{k_{1}=0}^{\ell _{1}-1}\sum _{k_{2}=0}^{b_{2}}\ \sum _{\widetilde{k}_{1}=\ell _{1}}^{b_{1}} \sum _{\widetilde{k}_{2}=0}^{b_{2}}\theta (k_{1},k_{2})\cdot q_{red}\left( (k_{1},k_{2});(\widetilde{k}_{1},\widetilde{k}_{2})\right) \\&\quad =\sum _{\widetilde{k}_{1}=\ell _{1}}^{b_{1}}\sum _{\widetilde{k}_{2}=0}^{b_{2}}\ \sum _{k_{1}=0}^{\ell _{1}-1} \sum _{k_{2}=0}^{b_{2}}\theta (\widetilde{k}_{1},\widetilde{k}_{2})\cdot q_{red}\left( (\widetilde{k}_{1}, \widetilde{k}_{2});(k_{1},k_{2})\right) \\&\Leftrightarrow \quad \underbrace{\sum _{k_{2}=0}^{b_{2}}\theta (\ell _{1}-1,k_{2})}_{=P(Y_{1}=\ell _{1}-1)} \cdot \nu =\underbrace{\sum _{\widetilde{k}_{2}=0}^{b_{2}}\theta (\ell _{1},\widetilde{k}_{2})}_{=P(Y_{1}=\ell _{1})}\cdot \lambda _{1}. \end{aligned}$$

Hence, we have shown for $\ell _{1}\in \left\{ 1,\ldots ,b_{1}-b_{2}\right\}$

$$\begin{aligned} P(Y_{1}&=\ell _{1}-1)\cdot \nu =P(Y_{1}=\ell _{1})\cdot \lambda _{1}. \end{aligned}$$

For $\ell _{1}\in \left\{ b_{1}-b_{2}+1,\ldots ,b_{1}-1\right\}$, Eq. (11) can be proven by a cut, which divides E into complementary sets according to the size of the inventory at location 1 that is less than or equal to $\ell _{1}-1$ or greater than $\ell _{1}-1$, i.e. into the sets

$$\begin{aligned}{} & {} \left\{ (k_{1},k_{2}):k_{1}\in \{0,1,\ldots ,\ell _{1}-1\},\,k_{2}\in \{0,\ldots ,b_{2}\}\right\} ,\\{} & {} \left\{ (\widetilde{k}_{1},\widetilde{k}_{2}):\widetilde{k}_{1}\in \{\ell _{1},\ldots ,b_{1}\},\, \widetilde{k}_{2}\in \{0,\ldots ,b_{2}\}\right\} ,\quad \ell _{1}\in \left\{ b_{1}-b_{2}+1,\ldots ,b_{1}-1\right\} . \end{aligned}$$

Then, it follows for $\ell _{1}\in \left\{ b_{1}-b_{2}+1,\ldots ,b_{1}-1\right\}$

$$\begin{aligned}&\sum _{k_{1}=0}^{\ell _{1}-1}\sum _{k_{2}=0}^{b_{2}}\ \sum _{\widetilde{k}_{1}=\ell _{1}}^{b_{1}} \sum _{\widetilde{k}_{2}=0}^{b_{2}}\theta (k_{1},k_{2})\cdot q_{red}\left( (k_{1},k_{2});(\widetilde{k}_{1},\widetilde{k}_{2})\right) \\&\quad =\sum _{\widetilde{k}_{1}=\ell _{1}}^{b_{1}}\sum _{\widetilde{k}_{2}=0}^{b_{2}}\ \sum _{k_{1}=0}^{\ell _{1}-1} \sum _{k_{2}=0}^{b_{2}}\theta (\widetilde{k}_{1},\widetilde{k}_{2})\cdot q_{red}\left( (\widetilde{k}_{1},\widetilde{k}_{2});(k_{1},k_{2})\right) \\&\Leftrightarrow \quad \underbrace{\sum _{k_{2}=b_{2}-(b_{1}-\ell _{1})}^{b_{2}} \theta (\ell _{1}-1,k_{2})\cdot }_{=P(Y_{1}=\ell _{1}-1,Y_{2}>b_{2}-\left( b_{1}-(\ell _{1}-1)\right) }\nu +\underbrace{\theta (\ell _{1}-1,b_{2}-\left( b_{1}-(\ell _{1}-1)\right) )}_{=P(Y_{1} =\ell _{1}-1,Y_{2}=b_{2}-\left( b_{1}-(\ell _{1}-1)\right) }\cdot \frac{1}{2}\nu \\&\quad =\underbrace{\sum _{\widetilde{k}_{2}=0}^{b_{2}}\theta (\ell _{1},\widetilde{k}_{2})}_{=P(Y_{1} =\ell _{1})}\cdot \lambda _{1}. \end{aligned}$$

Hence, we have shown for $\ell _{1}\in \left\{ b_{1}-b_{2}+1,\ldots ,b_{1}-1\right\}$

$$\begin{aligned} P(Y_{1}=\ell _{1})\cdot \lambda _{1}&=P(Y_{1}=\ell _{1}-1,Y_{2}=b_{2}-\left( b_{1}-(\ell _{1}-1)\right) )\cdot \frac{1}{2}\nu \\&\quad +P(Y_{1}=\ell _{1}-1,Y_{2}>b_{2}-\left( b_{1}-(\ell _{1}-1)\right) )\cdot \nu \\&=P(Y_{1}=\ell _{1}-1,Y_{2}=\ell _{1}-1-b_{1}+b_{2})\cdot \frac{1}{2}\nu \\&\quad +P(Y_{1}=\ell _{1}-1,Y_{2}>\ell _{1}-1-b_{1}+b_{2})\cdot \nu .\\ \end{aligned}$$

For $\ell _{1}=b_{1}$, Eq. (12) can be proven by a cut, which divides E into complementary sets according to the size of the inventory at location 1 that is less than or equal to $b_{1}-1$ or greater than $b_{1}-1$, i.e. into the sets

$$\begin{aligned}{} & {} \Big \{(k_{1},k_{2}):k_{1}\in \{0,1,\ldots ,b_{1}-1\},\,k_{2}\in \{0,\ldots ,b_{2}\}\Big \},\\{} & {} \quad \left\{ (\widetilde{k}_{1},\widetilde{k}_{2}):\widetilde{k}_{1}=b_{1},\,\widetilde{k}_{2}\in \{0,\ldots ,b_{2}\}\right\} . \end{aligned}$$

Then, it follows for

$$\begin{aligned}&\sum _{k_{1}=0}^{b_{1}-1}\sum _{k_{2}=0}^{b_{2}}\ \sum _{\widetilde{k}_{1}=b_{1}}^{b_{1}} \sum _{\widetilde{k}_{2}=0}^{b_{2}}\theta (k_{1},k_{2})\cdot q_{red}\left( (k_{1},k_{2}); (\widetilde{k}_{1},\widetilde{k}_{2})\right) \\&=\sum _{\widetilde{k}_{1}=b_{1}}^{b_{1}}\sum _{\widetilde{k}_{2}=0}^{b_{2}}\ \sum _{k_{1}=0}^{b_{1}-1} \sum _{k_{2}=0}^{b_{2}}\theta (\widetilde{k}_{1},\widetilde{k}_{2})\cdot q_{red}\left( (\widetilde{k}_{1}, \widetilde{k}_{2});(k_{1},k_{2})\right) \\&\Leftrightarrow \quad \underbrace{\theta (b_{1}-1,b_{2})}_{=P(Y_{1}=b_{1}-1,Y_{2}=b_{2})}\cdot \nu +\underbrace{\theta (b_{1}-1,b_{2}-1)}_{=P(Y_{1}=b_{1}-1,Y_{2}=b_{2}-1)}\cdot \frac{1}{2}\nu =\underbrace{\sum _{\widetilde{k}_{2}=0}^{b_{2}}\theta (b_{1},\widetilde{k}_{2})}_{=P(Y_{1}=b_{1})}\cdot \lambda _{1}. \end{aligned}$$

Hence, we have shown

$$\begin{aligned} P(Y_{1}=b_{1})\cdot \lambda _{1}&=P(Y_{1}=b_{1}-1,Y_{2}=b_{2}-1)\cdot \frac{1}{2}\nu +P(Y_{1}=b_{1}-1,Y_{2}=b_{2})\cdot \nu . \end{aligned}$$

For $\ell _{2}\in \left\{ 1,\ldots ,b_{2}\right\}$, Eq. (13) can be proven by a cut, which divides E into complementary sets according to the size of the inventory at location 2 that is less than or equal to $\ell _{2}-1$ or greater than $\ell _{2}-1$, i.e. into the sets

$$\begin{aligned}{} & {} \Big \{(k_{1},k_{2}):k_{1}\in \{0,\ldots ,b_{1}\},\,k_{2}\in \{0,1,\ldots ,\ell _{2}-1\}\Big \},\\{} & {} \quad \left\{ (\widetilde{k}_{1},\widetilde{k}_{2}):\widetilde{k}_{1}\in \{0,\ldots ,b_{1}\},\, \widetilde{k}_{2}\in \{\ell _{2},\ldots ,b_{2}\}\right\} ,\quad \ell _{2}\in \left\{ 1,\ldots ,b_{2}\right\} . \end{aligned}$$

Then, it follows for $\ell _{2}\in \left\{ 1,\ldots ,b_{2}\right\}$

$$\begin{aligned}&\sum _{k_{1}=0}^{b_{1}}\sum _{k_{2}=0}^{\ell _{2}-1}\ \sum _{\widetilde{k}_{1}=0}^{b_{1}} \sum _{\widetilde{k}_{2}=\ell _{2}}^{b_{2}}\theta (k_{1},k_{2})\cdot q_{red}\left( (k_{1},k_{2});(\widetilde{k}_{1},\widetilde{k}_{2})\right) \\&\quad =\sum _{\widetilde{k}_{1}=0}^{b_{1}}\sum _{\widetilde{k}_{2}=\ell _{2}}^{b_{2}}\ \sum _{k_{1}=0}^{b_{1}} \sum _{k_{2}=0}^{\ell _{2}-1}\theta (\widetilde{k}_{1},\widetilde{k}_{2})\cdot q_{red}\left( (\widetilde{k}_{1},\widetilde{k}_{2});(k_{1},k_{2})\right) \\&\Leftrightarrow \quad \underbrace{\theta (b_{1}-\left( b_{2}-(\ell _{2}-1)\right) ,\ell _{2}-1)}_{=P(Y_{1}=b_{1}-\left( b_{2}-(\ell _{2}-1)\right) ,Y_{2}=\ell _{2}-1)}\cdot \frac{1}{2}\nu \underbrace{\sum _{k_{1}=b_{1}-(b_{2}-\ell _{2})}^{b_{1}}\theta (k_{1},\ell _{2}-1)}_{=P(Y_{1}>b_{1}-\left( b_{2}-(\ell _{2}-1)\right) ,Y_{2}=\ell _{2}-1)}\cdot \nu \\&\quad =\underbrace{\sum _{\widetilde{k}_{1}=0}^{b_{1}}\theta (\widetilde{k}_{1},\ell _{2})}_{=P(Y_{2}=\ell _{2})}\cdot \lambda _{2}. \end{aligned}$$

Hence, we have shown for $\ell _{2}\in \left\{ 1,\ldots ,b_{2}\right\}$

$$\begin{aligned} P(Y_{2}=\ell _{2})\cdot \lambda _{2}&=P(Y_{1}=b_{1}-\left( b_{2}-(\ell _{2}-1)\right) ,Y_{2}=\ell _{2}-1)\cdot \frac{1}{2}\nu \\&\quad +P(Y_{1}>b_{1}-\left( b_{2}-(\ell _{2}-1)\right) ,Y_{2}=\ell _{2}-1)\cdot \nu \\&=P(Y_{1}=b_{1}-b_{2}+\ell _{2}-1,Y_{2}=\ell _{2}-1)\cdot \frac{1}{2}\nu \\&\quad +P(Y_{1}>b_{1}-b_{2}+\ell _{2}-1,Y_{2}=\ell _{2}-1)\cdot \nu . \end{aligned}$$

$\square$

6 Conclusion

The paper investigated a supply chain where routing of items depends on the on-hand inventory at the locations with the aim to obtain “load balancing”. The main result of the paper is to prove that the stationary distribution has a product form. This means that the steady states of the production network and the inventory-replenishment complex decouple asymptotically, and the equilibrium for the production subsystem decomposes in true independent coordinates. For the marginal distribution of the production subsystem an explicit solution was derived and for the marginal distribution of the inventory-replenishment subsystem an explicit solution or a recursive algorithm were deduced for some special cases.

To extend the results to queueing-inventory systems with other replenishment policies is part of our ongoing research. First results for queueing-inventory systems with (r, S)-policy with location specific items can be found in Otten (2017, Chapter 7).

Appendix A Computational example

Motivated by the computational example in  Chow and Kohler (1979, Appendix, pp. 360f.) we consider an example with two locations, base stock levels $b_{1}=4$, $b_{2}=3$ and arrival rates $\lambda _{1},\ \lambda _{2}>0$. The state transition diagram is presented in Fig. 6.

Fig. 6

State transition diagram of a system with two locations and $b_{1}=4$, $b_{2}=3$ and $\lambda _{1},\lambda _{2}>0$

Inside the following equations, we use colour for the expressions which are known independent of $\kappa$, colour for the expressions which are known as a function of $\kappa$ and colour for the expressions which are unknown.

The solution steps for this system using the algorithm follow:

• $\blacktriangleright$ Set $\widetilde{\theta }(4,0)=1$.

• $\blacktriangleright$ For $k_{2}=3$:

(1)(a):

Set $\widetilde{\theta }(0,3)=\kappa$.

(b):

For $\ell =0$: Use the GBE of state (4, 0) to find an expression for $\widetilde{\theta }(4,1)$ independent of $\kappa$:

which is equivalent to

$$\begin{aligned} \widetilde{\theta }(4,1)=\frac{\lambda _{1}+\nu }{\lambda _{2}}=:c^{(4,1)}\left( \lambda _{1},\lambda _{2},\nu \right) . \end{aligned}$$

For $\ell =1$: Use the GBE of state (4, 1)

to find an expression for $\widetilde{\theta }(4,2)$ independent of $\kappa$:

which is equivalent to

$$\begin{aligned} \widetilde{\theta }(4,2)=\frac{(\lambda _{1}+\lambda _{2}+\nu )}{\lambda _{2}}\cdot c^{(4,1)}\left( \lambda _{1},\lambda _{2},\nu \right) =:c^{(4,2)}\left( \lambda _{1},\lambda _{2},\nu \right) . \end{aligned}$$

(c):

For $k_{1}=0$: Use the GBE of state (0, 3)

to find an expression for $\widetilde{\theta }(1,3)$ as a function of $\kappa$:

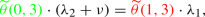
which is equivalent to

$$\begin{aligned} \widetilde{\theta }(1,3)=\frac{\lambda _{2}+\nu }{\lambda _{1}}\cdot \kappa =:c^{(1,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa . \end{aligned}$$

For $k_{1}=1$: Use the GBE of state (1, 3)

to find an expression for $\widetilde{\theta }(2,3)$ as a function of $\kappa$:

which is equivalent to

$$\begin{aligned} \widetilde{\theta }(2,3)&=\frac{\widetilde{\theta }(1,3)\cdot (\lambda _{1} +\lambda _{2}+\nu )-\widetilde{\theta }(0,3)\cdot \nu }{\lambda _{1}}\\&=\frac{c^{(1,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot (\lambda _{1}+\lambda _{2}+\nu )-\nu }{\lambda _{1}}\cdot \kappa =:c^{(2,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa . \end{aligned}$$

For $k_{1}=2$: Use the GBE of state (2, 3)

to find an expression for $\widetilde{\theta }(3,3)$ as a function of $\kappa$:

which is equivalent to

$$\begin{aligned} \widetilde{\theta }(3,3)&=\frac{\widetilde{\theta }(2,3)\cdot (\lambda _{1}+\lambda _{2}+\nu ) -\widetilde{\theta }(1,3)\cdot \nu }{\lambda _{1}}\\&=\frac{c^{(2,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot (\lambda _{1}+\lambda _{2}+\nu )-c^{(1,3)} \left( \lambda _{1},\lambda _{2},\nu \right) \cdot \nu }{\lambda _{1}}\cdot \kappa \\&=:c^{(3,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa . \end{aligned}$$

(d):

Use the GBE of state (4, 3)

to find an expression for $\widetilde{\theta }(4,3)$ as a function of $\kappa$:

which is equivalent to

$$\begin{aligned} \widetilde{\theta }(4,3)&=\frac{\widetilde{\theta }(3,3)\cdot \nu +\widetilde{\theta }(4,2)\cdot \nu }{\lambda _{1}+\lambda _{2}} =\frac{c^{(3,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \nu }{\lambda _{1}+\lambda _{2}}\cdot \kappa +\frac{c^{(4,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \nu }{\lambda _{1}+\lambda _{2}}\\&=:c_{1}^{(4,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa +c_{2}^{(4,3)}\left( \lambda _{1},\lambda _{2},\nu \right) . \end{aligned}$$

(e):

For $k_{1}=3$: Use the GBE of state (3, 3)

to find an expression for $\widetilde{\theta }(3,2)$ as a function of $\kappa$:

which is equivalent to

$$\begin{aligned}&\widetilde{\theta }(3,2) \\&=\frac{\widetilde{\theta }(3,3)\cdot (\lambda _{1}+\lambda _{2}+\nu ) -\widetilde{\theta }(4,3)\cdot \lambda _{1}-\widetilde{\theta }(2,3)\cdot \nu }{\frac{1}{2}\cdot \nu }\\&=\frac{c^{(3,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot (\lambda _{1}+\lambda _{2}+\nu ) -c_{1}^{(4,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \lambda _{1}-c^{(2,3)}\left( \lambda _{1},\lambda _{2}, \nu \right) \cdot \nu }{\frac{1}{2}\cdot \nu }\cdot \kappa \\&\quad -\frac{c_{2}^{(4,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \lambda _{1}}{\frac{1}{2}\cdot \nu }\\&=:c_{1}^{(3,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa +c_{2}^{(3,2)}\left( \lambda _{1},\lambda _{2},\nu \right) . \end{aligned}$$

(f):

Use the GBE of state (4, 2) to solve for $\kappa$.

which is equivalent to

$$\begin{aligned}&\quad c^{(4,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \left( \lambda _{1}+\lambda _{2}+\nu \right) \\&\quad =\left( c_{1}^{(4,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa +c_{2}^{(4,3)} \left( \lambda _{1},\lambda _{2},\nu \right) \right) \cdot \lambda _{2}\\&\quad +\left( c_{1}^{(3,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa +c_{2}^{(3,2)} \left( \lambda _{1},\lambda _{2},\nu \right) \right) \cdot \frac{1}{2}\cdot \nu +c^{(4,1)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \nu \\&\quad \Leftrightarrow c_{1}^{(4,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa \cdot \lambda _{2}+c_{1}^{(3,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \kappa \cdot \frac{1}{2}\cdot \nu \\&\quad =c^{(4,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \left( \lambda _{1}+\lambda _{2}+\nu \right) -c^{(4,1)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \nu \\&\quad -c_{2}^{(3,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \frac{1}{2}\cdot \nu -c_{2}^{(4,3)} \left( \lambda _{1},\lambda _{2},\nu \right) \cdot \lambda _{2}\\&\quad \Leftrightarrow \kappa =\left[ c^{(4,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \left( \lambda _{1}+\lambda _{2}+\nu \right) -c^{(4,1)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \nu \right. \\&\qquad \left. -c_{2}^{(3,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \frac{1}{2} \cdot \nu -c_{2}^{(4,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \lambda _{2}\right] \\&\qquad \cdot \frac{1}{c_{1}^{(4,3)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \lambda _{2} +c_{1}^{(3,2)}\left( \lambda _{1},\lambda _{2},\nu \right) \cdot \frac{1}{2}\cdot \nu } \end{aligned}$$

if the denominator is not equal to zero.

(g):

Substitute the value of $\kappa$ into the equations in the above steps (1)(a) and (1)(c)–(e).

• $\blacktriangleright$ For $k_{2}=2$:

(2)(a):

Set $\widetilde{\theta }(0,2)=\kappa$.

(b)(i):

For $k_{1}=0$: Use the GBE of state (0, 2)

to find an expression for $\widetilde{\theta }(1,2)$ as a function of $\kappa$ ($\widetilde{\theta }(0,3)$ is known independent of $\kappa$ from step (1)):

which is equivalent to

For $k_{1}=1$: Use the GBE of state (1, 2)

to find an expression for $\widetilde{\theta }(2,2)$ as a function of $\kappa$ ($\widetilde{\theta }(1,3)$ is known independent of $\kappa$ from step (1)):

which is equivalent to

(b)(ii):

For $k_{1}=2$: Use the GBE of state (2, 2)

to find an expression for $\widetilde{\theta }(2,1)$ as a function of $\kappa$ ($\widetilde{\theta }(3,2)$ and $\widetilde{\theta }(2,3)$ are known independent of $\kappa$ from step (1)):

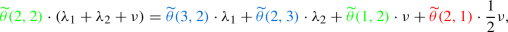
which is equivalent to

(c):

For $\ell =2$: Use the GBE of state (3, 2)

to find an expression for $\widetilde{\theta }(3,1)$ as a function of $\kappa$ ($\widetilde{\theta }(3,2)$, $\widetilde{\theta }(4,2)$ and $\widetilde{\theta }(3,3)$ are known independent of $\kappa$ from step (1)):

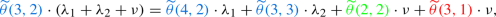
which is equivalent to

For $\ell =1$: Use the GBE of state (3, 1) to find an expression for $\widetilde{\theta }(3,0)$ as a function of $\kappa$ ($\widetilde{\theta }(4,1)$ and $\widetilde{\theta }(3,2)$ are known independent of $\kappa$ from step (1)):

which is equivalent to

(d):

Use the GBE of state (3, 0) to solve for $\kappa$

($\widetilde{\theta }(4,0)$ is known independent of $\kappa$ from step (1)):

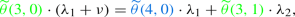
which is equivalent to

if the denominator is not equal to zero.

(e):

Substitute the value of $\kappa$ into the equations in the above steps (2)(a)–(c).

(3)(a):

Set $\widetilde{\theta }(0,1)=\kappa$.

(b)(i):

For $k_{1}=0$: Use the GBE of state (0, 1) to find an expression for $\widetilde{\theta }(1,1)$ as a function of $\kappa$ ($\widetilde{\theta }(0,2)$ is known independent of $\kappa$ from step (2)):

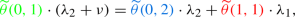
which is equivalent to

(b)(ii):

For $k_{1}=1$: Use the GBE of state (1, 1) to find an expression for $\widetilde{\theta }(1,0)$ as a function of $\kappa$ ($\widetilde{\theta }(2,1)$ and $\widetilde{\theta }(1,2)$ are known independent of $\kappa$ from step (2)):

which is equivalent to

For $k_{1}=2$: Use the GBE of state (2, 1) to find an expression for $\widetilde{\theta }(2,0)$ as a function of $\kappa$ ($\widetilde{\theta }(2,1)$, $\widetilde{\theta }(3,2)$ and $\widetilde{\theta }(2,2)$ are known independent of $\kappa$ from steps (1) and (2)):

which is equivalent to

(c):

For $k_{1}=1$: Use the GBE of state (1, 0) to find an expression for $\widetilde{\theta }(0,0)$ as a function of $\kappa$:

which is equivalent to

(d):

Use the GBE of state (2, 0) to solve for $\kappa$ ($\widetilde{\theta }(3,0)$, $\widetilde{\theta }(2,1)$ are known independent of $\kappa$ from steps (2)):

if the denominator is not equal to zero.

(e):

Substitute the value of $\kappa$ into the equations in the above steps (3)(a)–(c).

• $\blacktriangleright$Normalise all $\widetilde{\theta }(k_{1},k_{2})$ by setting

  $$\begin{aligned} \widetilde{\theta }(k_{1},k_{2})\leftarrow \frac{\widetilde{\theta }(k_{1},k_{2})}{\sum _{k_{1}=0}^{b_{1}} \sum _{k_{2}=0}^{b_{2}}\widetilde{\theta }(k_{1},k_{2})} \end{aligned}$$