A decision support system for reducing the strategic risk in the schedule building process for network carrier airline operations

Abstract

This study addresses the evaluation of schedule time window of a new frequency for a network carrier airline. The ideal schedule for an airline can involve various criteria that consist of commercial and operational constraints. This study proposes a new integrated Best–Worst Method and Technique for Order Preference by Similarity to Ideal Solution based on heterogeneous decision making approach for determining the most suitable schedule. This approach combines the advantages of multi-expert multi-criteria decision analysis, which yields heterogeneous information, with a developed decision making model. In addition, a sensitivity analysis is performed to observe the robustness of the proposed approach. To illustrate the efficiency of the proposed approach, a real world problem at a network carrier airline in Turkey is presented. The results indicate that the flexibility and applicability of the proposed approach can address real-world problems.

1 Introduction

Airline companies have many optimization and decision-making problems. They have been using Operations Research techniques to solve these problems since 1950 (Barnhart & Talluri, 1997). These problems include both long term, high cost and high uncertainties, such as fleet planning and short term, more certain, i.e., crew resource planning which is optimal crew planning level suitable for the next 1-month period. The fundamental airline problems can be categorized as planning or operational problems (Bazargan, 2016). The planning problems generally consist of flight scheduling (Çiftçi & Özkır, 2020), fleet assignment (Wei et al., 2020; Yan et al., 2020), aircraft routing (Chen et al., 2020; Cacchiani and Salazar-Gonzalez, 2020), and crew paring (Deveci & Demirel, 2018) and rostering (Quesnel et al., 2020). The operational problems comprise of revenue management (Yazdi et al., 2020), new destination study (Deveci et al., 2017), gate assignments (Xiao et al., 2020), and irregular operations.

The most valuable asset of an airline is its aircraft, and the most important product is its schedule. The revenue-generating activity of airlines is not the number of aircraft, destinations, or its in-flight design. What makes money for airlines is the seats they offer to the market. While inefficient schedule can cost millions of dollars, an efficient aircraft usage and schedule structure reduces the impact of fixed expenses (fixed and overhead costs) on production, resulting in increased gains. Many constraints and factors play critical role in schedule creation process. This process also varies according to the business model of the airline. The schedule planning of low cost airlines (LCC), and hub and spoke (HS) carriers are different from each other. While HS carriers optimize their schedule by considering connected flights and wide geographic areas and many destinations, LCCs consider individual routes and no connections are provided. HS carriers prefer high daily frequency, LCCs generally flies with lower frequency (Cook & Goodwin, 2008). In addition, the schedule structure that is suitable for the potential passengers of a city A, regardless of the airline, may not be suitable for another city B (Belobaba et al., 2015).

In airlines, schedule planning is generally done by network or schedule planner. Network planning can be defined as the managing passenger flow and flight connections at the hub and spoke system. Network planners are responsible for carrying out the economic evaluation of various new route options while independently assessing various business risks such as demand planning, competitive landscape, cost implications and financial exposures. They also consistently review route network performance in order to identify profitability issues and provide forewarning to the senior management and executive teams along with detailed recommendations to improve route profitability and strategy going forward. Network planning includes evaluation of the strategic opportunities in the product planning, such as aircraft redeployment scenarios and new schedule design by providing improvements in network (fleet, schedule and routing) deployment to maximize network profitability (cost efficiencies and revenue potential). A typical network planner starts analyzing the market data and identifying patterns for potential routes in order to optimize airline schedule and network profitability (Bazargan, 2016).

Creating a new schedule is a complex process that requires the contribution of internal and external stakeholders from different departments. Examples of internal stakeholders are operational departments, crew planning, revenue management etc., and external stakeholders are passengers, civil aviation authorities, airport slot planning departments, ground handling firms etc. Experts always evaluate more than one alternative schedule for the new frequencies and destinations. Therefore, a Multi-Expert Multi-Criteria Decision Analysis (MEMCDA) process is necessary to perform this complex selection process. It should consider different points of view from internal and external stakeholders and multiple conflicting criteria that might be quantitative or qualitative. This implies a heterogeneous decision framework (Herrera et al., 2005; Palomares et al., 2013) able to deal with different kind of information and the imprecision of the experts involved in the problem.

In order to select the new frequency for an airline company different Multi-Criteria Decision Making (MCDM) models introduced in the literature (Chen & Hwang, 1992; Kahraman et al., 2015) such as, AHP, TOPSIS, VIKOR etc., could be used to solve this decision problem. Nevertheless, due to the interdisciplinary of this decision process that implies the necessity of using a heterogeneous framework, as far as we know there is not any previous model that can straight to solve this MCDM problem.

The purpose of this study is to propose a new and specific MEMCDA approach able to deal with different kinds of information and to decide on the ideal schedule structure for a new frequency by using commercial and operational constraints within existing network. Among the different MCDM models that can be applied to solve this problem, in this contribution we will use fuzzy TOPSIS because it is one of the most widely used models in MCDM to solve different problems obtaining satisfactory results (Behzadian et al., 2012; Sang et al., 2015) because of its advantages regarding other MCDM models (Ishizaka & Nemery, 2013; Shih et al., 2007): (i) it has a sound logic that represents the rationale of human choice, (ii) a scalar value that considers the best and worst alternatives at the same time, (iii) a simple computation algorithm and a (iv) minimal number of inputs from experts.

On the other hand, as the criteria considered to select the new frequency have different importance, we will use the Best Worst Method (BWM) (Rezaei, 2015) to obtain the criteria weights because it reduces the inconsistency in experts’ preferences in comparison with other methods as AHP (Kahraman et al., 2015). Moreover, the dependencies among criteria are studied and taken into account by using the Trapezoidal Fuzzy Number Weighted Extended Bonferroni Mean (Dutta et al., 2019) which reflects the criteria importance.

Therefore, the main novelties of the proposal are the following ones:

• To define a new MEMCDA to model different kinds of information and able to provide the best schedule for a new frequency according to commercial and operational constraints.

• To use the BWM to obtain the criteria weights by means of the experts’ opinions.

• To study the relations among criteria and use a suitable aggregation operator able to capture such relations and consider the criteria weights.

• To evaluate a new frequency for a network carrier airline between Istanbul and Stockholm applying the proposed MEMCDA model.

• To show the robustness of the solution by a sensitivity analysis.

The rest of paper is organized as follows: Sect. 2 introduces the factors taken into account to choose a schedule and the operational constraints. It makes also a short review about fuzzy MCDM methods related to transport problems. Section 3 proposes the MEMCDA able to deal with heterogeneous information to select a new frequency for a network carrier airline. Section 4 presents a real case study to show the performance and feasibility of the proposal. It also includes a sensitivity analysis to study the robustness of the solution obtained, and finally Sect. 5 points out some conclusions.

2 Background

This section revises the general factors considered to choose a schedule for a new frequency in a network carrier airline, explains the operational and commercial constraints and shows different fuzzy MCDM approaches that have been used to manage air transport problems.

2.1 General factors for schedule planning

There are models that evaluate the schedules and forecast its market shares while developing and calibrating models that quantifies the passenger choice on the picking up the airline for their itinerary. These models are generally called quality service index (QSI) models. It is a method to evaluate different options (airlines and flights) in front of the consumer (passenger). It starts determining the factors that affect passengers’ choice when choosing a flight among the others. Passenger utility is a value that is calculated by these models and it assumes that is going to be maximised with rationale choices of experts. General factors that have been used to the selection are the following ones (Belobaba et al., 2015):

2.1.1 Number of stops

How many stops/connections occur in the itinerary? Some lucky city pairs in the world have direct flights (IST-JFK, LAX-DXB etc.), however given 10 K airports in the world, there are many more indirectly connected city pairs (ADB-BCN, ESB-LHR etc.) with at least 1 or more stops. Passenger utility decreases while providing an increase of the number of stops in the travel.

2.1.2 Aircraft type

Which aircraft type is going to operate the flights? This factor is important especially for the jet and turboprop aircraft types. There is a less preference on the turboprops over the jet aircrafts. In most cases, passengers are not aware of different aircraft types involved in a given itinerary. However, with help of the advertisement, airlines can make more revenues; becoming the first airline to operate the newest aircraft type (e.g. Airbus 380, Boeing 787) or the being the airline with the youngest fleet.

Aircraft type is also important in terms of its capacity (available seat) provided to route. High capacity attracts more market share.

2.1.3 Flight frequency

Just like aircraft type, more frequent services provide more capacity and attract more market share. It is also important to have at least daily services (one flight per each day in a week) in order to cover all the demand around the week.

2.1.4 Detour

Comparison (ratio) of the direct routing and indirect routing in terms of distance. Nonstop itineraries detour is 1. In general, detour factor up to 1.4 is acceptable for the itineraries that have intermediate stops. Although, passengers do not prefer high detours, they are obliged in some cases due to insufficient itinerary options. There can be only one flight to some airports and they do not have any option to select (Burghouwt & Wit, 2005).

2.1.5 Travel time

Elapse time or travel time can be defined as total trip time that is required from origin city to destination city of itinerary including connection times at the intermediate stops. Longer itineraries are less attractive compared to shorter ones.

2.1.6 Time of day preference

Morning and evening times are important for business travellers. It is also important to match hotel check-in and check-out timings for leisure travellers. Night schedules, especially after the midnight, are less preferable due to less transportation opportunities between airports and city centres, inconvenient departure and arrival times of the flight. Destinations with high local share are scheduled according to their time-of-day preferences in order to ensure market acceptance and exploit market potential.

2.1.7 Day of week preference

Mondays and Fridays are important for business travellers in general. It is important to have schedule on weekends due to high demand for leisure travellers. In some Muslim countries in the Middle East, Friday and Saturday are weekends, therefore airlines should be careful and aware of this fact while they plan their schedule to these destinations.

A typical schedule consists of the following information (see Table 1); airline code, flight number, departure time, arrival time, aircraft type, block time and departure day.

Table 1 Example of an airline schedule

2.2 Operational and commercial constraints

Flight scheduling has a strong impact on all of the activities of the airlines (Bazargan, 2016). Operations, revenue management, crew planning, profitability are affected by the schedule structure. Building a perfect schedule is constrained by both economic and operational constraints. A schedule is successful when it is commercial profitable as well as operationally feasible. Thus, it is convenient to consider some operational and commercial constraints.

Operational constraints:

• Block times of the flight legs and Ground times at the stations should be validated by the operational departments.

• Departure and arrival times of the schedule should be in line with the meteorological analysis. Destinations that have airport curfews and do not allow night operations should be planned according to their respective airport curfews.

• Minimum connection time between flights that are required for transferring passengers at the hub station must be considered when the schedule is planned.

• Departure and arrival slots at the congested spoke airports must be satisfied.

• Crew planning department should validate the duty times of the schedule.

Commercial constraints:

• Fleet should be available and should be rotated for given schedule. Local departure and arrival times should be reasonable for passengers. Market potentials are used to identify the ideal capacity allocation for the destinations. Historical market data, growth rates and the level of competition are used to determine the market potential for each destination. Together with passenger demand, potential of the belly cargo contribution of the destinations should be considered when feasibility studies are evaluated.

• Fleet assignment should be in line with the market potential and passenger preference. Passenger spill is minimized by re-distributing aircraft capacity in order to capture full potential of passengers. Seat capacity for seasonal destinations should be adjusted through the year in order to reflect demand variability.

• A minimum service level of frequency per week should be defined in order to guarantee product quality. Frequency rights should be utilized accordingly, however frequency or capacity cannot exceed the defined right in the bilateral air service agreement to allow international commercial air transport services between countries.

• Schedule of the codeshare partner airlines should be considered for codeshare connecting passengers.

2.3 Fuzzy MCDM approaches in air transport management

There have been studies investigating different methods for various air transport management problems over the last decade as presented in Table 2. The acronyms are defined as follow: AHP is Analytic Hierarchy Process, ANP is Analytic Network Process, TOPSIS is Technique for Order Preference by Similarity To An Ideal Solution, VIKOR is VIseKriterijumska Optimizacija I Kompromisno Resenje, DEMATEL is DEcision MAking Trial and Evaluation Laboratory, GRA is Grey Relational Analysis, QFD is Quality Function Deployment, WASPAS is Weighted Aggregated Sum Product Assessment, ARAS is Additive Ratio ASsessment, and COPRAS is COmplex PRoportional Assessment.

Table 2 Overview of the studies on air transport managements using different fuzzy MCDM approaches

A variety of fuzzy MCDM approaches have been applied to air transport management problems by using different fuzzy extensions to model the uncertainty and vagueness of the information. For instance, Tsaur et al. (2002) proposed an approach based on AHP and TOPSIS to evaluate the service quality of airline using fuzzy sets, Kuo (2011) used interval-valued fuzzy sets based VIKOR and GRA, Percin (2018) introduced another fuzzy approach based on DEMATEL, ANP and VIKOR, and Deveci et al. (2018) used interval type-2 hesitant fuzzy sets to model the uncertainty and defined a new MCDM model.

Some researchers defined new fuzzy MCDM approaches to evaluate the quality of airports: fuzzy sets based TOPSIS (Wang & Lee, 2007), and VIKOR and GRA (Kuo & Liang, 2011). Liou et al. (2011), and Garg (2016) presented a novel approach based on ANP, and AHP based TOPSIS, respectively, dealing with fuzzy sets for strategic alliance partner selection problems. Torlak et al. (2011) applied fuzzy TOPSIS approach to rank air carriers according to business competition. Deveci et al. (2017) studied airline new route selection between Turkey- North American region destinations using interval type-2 fuzzy sets based TOPSIS.

3 A heterogeneous decision making approach

This section proposes a selection process based on a fuzzy TOPSIS method that provides a rank of frequencies to include a new one in the schedule planning for airlines. It will be able to deal with heterogeneous contexts in which linguistic and numerical values are used to evaluate the criteria. Additionally, the criteria weights are obtained by means of the BWM. This selection process consists of six phases (see Fig. 1) which are explained in further detail below.

Fig. 1

Scheme of the heterogeneous decision making approach

3.1 Definition of the framework

A set of experts $E=\{{e}_{1},\dots ,{e}_{m}\}$ provides their preferences over a set of alternatives $X=\{{x}_{1},\dots ,{x}_{n}\}$ that are defined by a set of main criteria $C=\{{c}_{1},\dots ,{c}_{r}\}$ where each main criterion is defined by a set of sub-criteria ${c}_{i}=\left\{{c}_{i1},\dots {c}_{it}\right\}, {c}_{i}\in C$.

The experts’ preferences ${e}_{k}\in E$ over the alternatives ${x}_{l}\in X$ and sub-criteria ${c}_{ij}\in C$ are represented by preferences vectors: $({p}_{ij}^{kl},\dots ,{p}_{rt}^{kl})$ with $i\in \left\{1,\dots ,r\right\}$ and $j\in \left\{1,\dots ,t\right\}$. In this proposal the preferences ${p}_{ij}^{kl}$ can be elicited by means of different expression domains (linguistic terms and numerical values) according to their nature. Therefore,

$${p}_{ij}^{kl}\in \left\{\begin{array}{c}S=\{{s}_{0},\dots {s}_{g}\}\\ \gamma \in R\end{array}\right.$$

The main criteria and sub-criteria weights are obtained from experts’ opinions by using the BWM and they are represented by vectors: $({w}_{1}^{k},\dots ,{w}_{r}^{k})$ and $\left({w}_{i1}^{k},\dots ,{w}_{it}^{k}\right)$.

3.2 Gathering of information

Once the framework has been defined, experts ${e}_{k}\in E$ involved in the selection process elicit their preferences about the alternatives ${x}_{l}\in X$ and sub-criteria ${c}_{ij}\in C$ by using linguistic terms or numerical values according to the criteria nature and provide their opinions about the criteria importance by using a scale of values that is used by the BWM to obtain the criteria weights. This method is explained in the following phase.

3.3 Applying BWM to obtain the criteria weights

The criteria and sub-criteria weights are computed through the BWM (Labella et al., 2021; Rezaei, 2015). The BWM is a MCDM technique aims to derive the prioritization of different decision elements by means of pairwise comparisons. The method consists of comparing the best and worst element with the remainder, as opposed to other proposals where all elements are compared with each other. These comparisons are so-called reference comparisons in BWM. In this way, the number of reference comparisons is reduced and, in turn, the emergence of inconsistency in experts’ preferences that appears when the number of comparisons is too large. The BWM steps are described below:

• 1. To choose a set of decision criteria. In our proposal, such criteria are described in Sect. 4.

• 2. To select the best criterion ${C}_{B}$ and the worst criterion ${C}_{W}$. If there are several best and/or worst criteria, they are selected randomly.

• 3. To make pairwise comparisons among ${C}_{B}$ and the rest of the criteria, by obtaining the Best to Others (BO) vector, $BO=\left\{{a}_{B1},{a}_{B2},\dots ,{a}_{Br}\right\}$, where ${a}_{Bi}$ represents the preference degree of ${C}_{B}$ over the criterion ${C}_{i}$ and ${a}_{B1}\ge 1, i=1, 2,\dots ,r, i\ne B$.

• 4. To make pairwise comparisons among the rest of the criteria and ${C}_{W}$, by obtaining the Others to Worst (OW) vector, $OW=\left\{{a}_{1W},{a}_{2W},\dots ,{a}_{rW}\right\}$, where ${a}_{iW}$ represents the preference degree of the criterion ${C}_{i}$ over ${C}_{W}$ and ${a}_{iW}\ge 1, i=1, 2,\dots ,r, i\ne B or W$.

• 5. To compute the criteria weights by using an optimization model. For each reference comparison, the optimal criteria weights must satisfy ${w}_{B}/{w}_{i}={a}_{Bi}$ and ${w}_{i}/{w}_{W}={a}_{iW}$. Hence, the maximum absolute differences ${|w}_{B}/{w}_{i}-{a}_{Bi}|$ and ${|w}_{i}/{w}_{W}-{a}_{iW}|$ should be minimized (see (M-1)).

$$\mathit{min}\varepsilon $$

$$s.t=\left\{\begin{array}{c}\left|\frac{{w}_{B}}{{w}_{i}}-{a}_{Bi}\right|\le \varepsilon \\ \left|\frac{{w}_{i}}{{w}_{W}}-{a}_{iW}\right|\le \varepsilon \\ \sum\limits_{i=1}^{r}{w}_{i}=1\\ {w}_{i}\ge 0 \quad \forall i=\mathrm{1,2},\dots ,r\end{array}\right.$$

where ε refers to the maximum absolute deviation between the reference comparisons provided by the experts and the computed criteria weights $\left({w}_{1},{w}_{2},\dots ,{w}_{r}\right)$ by the model (M-1).

A key aspect in the BWM is related to the experts’ preferences consistency. Obviously, experts’ preferences should make sense and not be provided in an illogical or random way. For this reason, in (Rezaei, 2015) was introduced a consistency ratio to measure the level of inconsistency in experts’ opinions. According to Rezaei, perfect consistency is achieved when ${a}_{Bi} x {a}_{iW}={a}_{BW}$. From this assumption, the consistency ratio is computed as follows:

$$Consistency\, Ratio= \frac{{\varepsilon }^{*}}{Consistency\, Index}$$

where ${\varepsilon }^{*}$ represents the maximum absolute difference between the optimal weights obtained from the model (M-1) and the reference comparisons provided by the experts. Consistency index is a numerical vale obtained from ${a}_{BW}$ and several experiments carried out by Rezaei (see Rezaei (2015) for further detail). The consistency ratio provides a value in [0, 1], where 0 represents perfect consistency.

3.4 Unification process

The heterogeneous information provided by experts must be transformed into a common expression domain to facilitate the computations. We use a fuzzy domain to model the uncertainty and carry out the computations in a precise way. This unification process is reached by means of different equations according to the type of information.

• Linguistic terms: The linguistic terms $S=\{{s}_{0},\dots ,{s}_{g}\}$ are transformed into trapezoidal fuzzy numbers which are represented as $\widetilde{Z}=(a,b,c,d)$.

• Numerical values: The numerical values are normalized into $[\mathrm{0,1}]$ and then transformed into trapezoidal fuzzy numbers by the following function $F$.

$$\begin{aligned} &\qquad\quad\qquad F:\left[\mathrm{0,1}\right]\to \widetilde{Z} \\ & F\left(\gamma \right)=\widetilde{Z}=\left(\gamma ,\gamma ,\gamma ,\gamma \right), \gamma \in [\mathrm{0,1}]\end{aligned}$$

(1)

For sake of clarity the experts’ preferences ${{\varvec{p}}}_{{\varvec{i}}{\varvec{j}}}^{{\varvec{k}}{\varvec{l}}}$ transformed into trapezoidal fuzzy numbers are represented as ${\widetilde{{\varvec{p}}}}_{{\varvec{i}}{\varvec{j}}}^{{\varvec{k}}{\varvec{l}}}$.

3.5 Aggregation process

Once the criteria weights are computed by the BWM, they are used to obtain the overall values for the main criteria and alternatives. This process is divided into two phases:

• Criteria aggregation: Experts’ preferences ${\widetilde{p}}_{ij}^{kl}$ over the sub-criteria ${c}_{ij}\in C$ for each alternative ${x}_{l}\in X$ are fused by means of a fuzzy aggregation operator to obtain an overall value ${\widetilde{p}}_{i}^{kl}$. We suggest using the Trapezoidal Fuzzy Number Weighted Extended Bonferroni Mean (TFNWEBM) (Dutta et al., 2019) because it allows capturing heterogeneous relations among the input (in this paper sub-criteria) and reflects the criteria importance. This operator classifies the input into two categories $U$ and $V$, where every input of $U$ is related to the remaining inputs, i.e., ${E}_{i}\subset a\backslash \{{a}_{i}\}$ and the inputs of $V$ are not related among them.

Definition 1

(Dutta et al., 2019): Let $\left({\widetilde{Z}}_{1},\dots ,{\widetilde{Z}}_{n}\right)$ be a vector of trapezoidal fuzzy numbers, which are interrelated. For any $p,q\ge 0$ with $p+q>0$ and the weighting vector $({w}_{1},\dots ,{w}_{n})$ such that ${w}_{i}>0$ and $\sum_{i=1}^{n}{w}_{i}=1$, the aggregated value by the TFNWEBM is a fuzzy number and it is given as follows:

$$\begin{aligned} & TFNWEB{M_{p,q}}\left( {{{\tilde Z}_1}, \ldots ,{{\tilde Z}_n}} \right) = (WEBM\left( {{a_1},{a_2}, \ldots ,{a_n}} \right),WEBM\left( {{b_1},{b_2}, \ldots ,{b_n}} \right),\\ & \quad WEBM\left( {{c_1},{c_2}, \ldots ,{c_n}} \right),WEBM\left( {{d_1},{d_2}, \ldots ,{d_n}} \right))\end{aligned}$$

(2)

$\widetilde{Z}=(a,b,c,d)$ is a trapezoidal fuzzy number for all $i=1,\dots ,n$. The ${WEBM:[\mathrm{0,1}]}^{n}\to [\mathrm{0,1}]$

$${WEBM}_{p,q}\left({a}_{1},{a}_{2},\dots ,{a}_{n}\right) ={\left({\left(1-\sum_{i\in {I}{{^{\prime}}}}{w}_{i}\right)\left(\sum_{i\notin {I}{{^{\prime}}}}\frac{{w}_{i}}{1-\sum_{i\in {I}{{^{\prime}}}}{w}_{i}}{a}_{i}^{p}\left(\frac{1}{\left|{I}_{i}\right|}\sum_{j\in {I}_{i}}\frac{{w}_{j}}{\sum_{j\in I}{w}_{j}}{a}_{j}^{q}\right)\right)}^{\frac{p}{p+q}} \oplus \sum_{i\in {I}{{^{\prime}}}}{w}_{i}\left(\sum_{i\in I{^{\prime}}}\frac{{w}_{i}}{\sum_{i\in I{^{\prime}}}{w}_{i}}{a}_{i}^{p}\right)\right)}^{\frac{1}{p}}$$

(3)

where ${I}_{i}, {E}_{i}$ is the set of indices of the elements of , $I{^{\prime}}$ is the set of indices of the inputs of $V$ and $|{I}{^{\prime}}|$ is the cardinality of the set $I{^{\prime}}$. The empty sum of fuzzy numbers is set as fuzzy zero (with the representation (0,0,0,0) following the classic convention for crisp system (for further details see Dutta et al. (2019)

• Experts aggregation: The overall values ${\widetilde{p}}_{i}^{kl}$ obtained in the previous step are fused by using the fuzzy weighted aggregation operator to obtain a global value for each main criteria and alternative ${\widetilde{p}}_{i}^{l}$. We propose this aggregation operator because it allows to assign different weights to the experts involved in the MCDM problem according to this knowledge or experience.

$${\widetilde{p}}_{i}^{l}=\sum_{k=1}^{m}{w}_{k}*{\widetilde{p}}_{i}^{kl}$$

(4)

where ${w}_{k}$ is the weight assigned to the expert ${e}_{k}$, ${w}_{k}>0$ and $\sum_{k=1}^{m}{w}_{k}=1$where is the weighted form of Extended Bonferroni Mean aggregation operator given by))

3.6 Applying Fuzzy TOPSIS

Finally, in order to obtain a ranking of frequencies and select the best one for the airline, the fuzzy TOPSIS method (Chen & Hwang, 1992) is used. It is explained in short as follows:

• i. To create the fuzzy normalized decision matrix $\widetilde{D}={({\widetilde{p}}_{i}^{l})}_{nxr}$ by means of the global values obtained in the previous phase.

• ii. To compute the weighted fuzzy normalized decision matrix $\widetilde{R}={({\widetilde{v}}_{i}^{l})}_{nxr}$ being ${\widetilde{v}}_{i}^{l}={\widetilde{p}}_{i}^{l}*{w}_{i}$, with ${w}_{i}$ the main criteria weight and ${w}_{i}>0$, $\sum_{i=1}^{r}{w}_{i}$= 1.

• iii. To define the positive ideal solution (PIS) ${\widetilde{Z}}^{+}=\left({\widetilde{z}}_{1}^{+},\dots ,{\widetilde{z}}_{r}^{+}\right)$, and the negative ideal solution (NIS) ${\widetilde{Z}}^{-}=\left({\widetilde{z}}_{1}^{-},\dots ,{\widetilde{z}}_{r}^{-}\right)$, being ${\widetilde{z}}_{i}^{+}=\left(\mathrm{1,1},\mathrm{1,1}\right)$ and ${\widetilde{z}}_{i}^{-}=\left(\mathrm{0,0},\mathrm{0,0}\right)$.

• iv. To compute the distance for each alternative from ${\widetilde{Z}}^{+}$ to ${\widetilde{Z}}^{-}$.

$${d}^{l+}=\sum_{i=1}^{r}d({\widetilde{v}}_{i}^{l},{\widetilde{z}}_{i}^{+}) {d}^{l-}=\sum_{i=1}^{r}d({\widetilde{v}}_{i}^{l},{\widetilde{z}}_{i}^{-})$$

(5)

where $d(\bullet ,\bullet )$ is the distance between two trapezoidal fuzzy numbers and $l=\{1,\dots ,n\}$.

• v. To compute the closeness coefficient ${{\varvec{C}}{\varvec{C}}}^{{\varvec{l}}}$ for each alternative:

$${CC}^{l}=\frac{{d}^{l-}}{{d}^{l+}+{d}^{l-}}$$

(6)

• vi. Finally, the alternatives (new frequencies) are ordered according to ${{\varvec{C}}{\varvec{C}}}^{{\varvec{l}}}$ to select the best one.

4 Case study

This section describes a real case study to include a new frequency in the route Istanbul and Stockholm that is solved by using the proposed heterogeneous decision making approach. Moreover, a sensitive analysis is introduced to show the robustness of the decision.

4.1 Selection of new frequency

Four alternatives are identified for selecting the most appropriate new frequency. Table 3 presents the current flight schedule (in local times) of airline that operates between Istanbul and Stockholm on daily three basis. The proposed 4 new frequency alternatives are given in Table 4. The visualization of current and new frequencies is shown in Fig. 2. While current schedule departure and arrival times are shown in red colour, new schedules are represented in blue colour. 3 black horizontal axes represent the 24 clock hour in one day for Istanbul and Stockholm. If a flight is below the horizontal axis, it means that it is an arrival flight. If a flight is above the horizontal axis it means that it is a departure flight.

Table 3 Current schedule between IST-ARN

Table 4 New frequency proposals between IST-ARN

Fig. 2

Current and alternative schedules on timeline

The new frequency alternatives are described by twelve evaluation sub-criteria under four main criteria including passenger preference, competition, slot availibiliy and connection. These main criteria and sub-criteria have been determined and defined by airline company experts. Figure 3 presents a schematic overview of the qualitative and quantitative criterias that are used in the study.

Fig. 3

Scheme of the main criteria, sub-criteria and their kinds of information for prioritizing new frequencies

The main criteria and sub-criteria are defined as follows:

• (1) Passenger schedule preference (C₁): It is defined as the time preference of the passenger for an alternative schedule. The departure time and days preference are examined in Fig. 4a, b for criterion C₁₁ and C₁₃. Both figures present a preference coefficient on the vertical axis which creates a curve over the day of a sample week. These values are calculated from historical market data with the help of experts using statistic tools.

  C₁₁: Hub local departure time: Scheduled time of departure of a flight from hub which shows the doors closing time at the gate.

C₁₂: Dest local arrival time: Scheduled time of arrival of a flight to spoke which shows the doors opening time at the gate.

C₁₃: Dest local departure time: Scheduled time of departure of a flight from spoke airport which shows the doors closing time at the gate.

C₁₄: Hub local arrival time: Scheduled time of arrival of a flight to hub which shows the doors opening time at the gate.

Fig. 4

Departure time and day preference for criterion C₁₁ and C₁₃

• (2) Competition (C₂): Competition criterion reflects the effects of the other schedules on the same city pair. Other schedule could belong a competitor airline or it could be the current schedule of the examined airline Schedule (see Table 5).

  C₂₁: Schedule time of competitor airlines: The aim of this criterion is to present the competitiveness of the alternative schedule by comparing with other airlines' schedule that serves the same city pair (IST-ARN-IST route).

  C₂₂: Cannibalization effect current schedule: The aim of this criterion is to show the deterioration of the alternative schedules by comparing with current schedule of the case airline on the IST-ARN route. ie, Case airline has 3 flights on IST ARN route. Alternative schedule will have effect on the local and transfer passenger demand on the other flights of the examined airline. Alternative flights will have its own demand and it will also steal market share from competitors and current schedule of the airline. Fig. 5 shows the seat load factor loss of the alternative schedules on the current schedule of the examined airline. These values are calculated by schedule experts using airline planning simulation tools.

  Fig. 5

  

  Cannibalization impact of the alternative schedules on the current flights

• (3) Slot availability (C₃): Slot is defined as a landing and departing permission from airport authority to use the airport, runway and terminal for a specific time range. Slot availibility is shown in Fig. 6. which illustrates the probability of getting a slot for alternative schedules. These values are provided by airport authorities to the airline schedule planners.

  C₃₁: Hub slot availability: Probability of having a slot at the hub airport (IST) at planned schedule time.

  Fig. 6

  

  Slot availability of alternative schedules

  C₃₂: Dest slot availability: Probability of having a slot at the spoke airport (ARN) at planned schedule time.

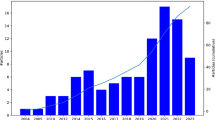
• (4) Connection (C₄): Connection criterion is a measure for connectivity of the alternative schedule at the IST airport and ARN airport within a time window. This time window starts with minimum connection time (1 h) until 12 h for a connection. High number of connections creates more demand for the planned schedule, therefore it is very important for a profitable schedule. Figure 7 presents the number of connections for alternative schedule on bar charts as primary axis on the left. Black curve represents the passenger volume on the connections which is secondary axis on the right. Number of connection values are calculated on the schedule by simply counting the flight legs that have sufficient connection time. Passenger volumes are the market figures that are flown in the last one year.

  Fig. 7

  

  Number of connection opportunities and passenger potentials of the alternative schedules

  C₄₁: # of weekly ınbound connection: An Inbound connection is that flights are arriving to hub and feeding the connection of the specified destination in terms of passenger volume.

  C₄₂: # of weekly outbound connection: An Outbound connection is that flights are departing from hub and defeeding the connection of the specified arrival in terms of passenger volume.

  C₄₃: # of weekly codeshare connectivity: A codeshare connection is a connection that has at least a carrier change and a flight change in the itinerary with a codeshare partner airline.

  C₄₄: dep + arr connection potential: Total number of O&D market volume in terms of passenger.

It is necessary to consider that in this case study experts involved in the problem point out that some sub-criteria are related (see Fig. 8). The sub-criterion ${c}_{12}$ is dependent of ${c}_{11}$ and sub-criterion ${c}_{14}$ is dependent of ${c}_{13}$.

Fig. 8

Dependency among sub-criteria

4.2 Applying the novel heterogeneous decision making approach

The case study introduced in the previous section is solved by using the MEMCDA approach presented in Sect. 3. To facilitate the understanding of the case study resolution, the different steps of the proposal applied to it are described in detail in the following subsections. Note that the resolution of the case study has been carried out by using the decision support system FLINTSTONES (Estrella et al., 2014).

4.2.1 Definition of the framework

Six experts from network planning and scheduling department of an airline company evaluate the four possible new frequencies between Istanbul and Stockholm over 4 criteria and 12 sub-criteria. These experts are specialized in network planning and scheduling and each of them have at least 5 years’ experience. Both alternatives, criteria and sub-criteria have been described in Sect. 4.

4.2.2 Gathering of information

This case study is composed by quantitative and qualitative criteria. The experts do not need to provide their opinions over the quantitative criteria, since they represent objective information related to different aspects of the new frequencies (see Table 6) as they have been explained for each criterion. However, the experts should provide their opinions over the criterion Competition and its sub-criteria related to the effects of the other schedules on the same city pair. To evaluate such criterion and sub-criteria, the experts provide qualitative assessments by making use of the following linguistic terms set S = {Nothing (N), Very low (VL), Low (L), Medium (M), High (H), Very high (VH), Excellent (E)}. The qualitative preferences are shown in Table 7. Additionally, the experts provide their opinions over the criteria importance by means of pairwise comparisons, which will be used to derive the weights by using the BWM. Such pairwise comparisons are presented in Tables 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 in Appendix. Note that these opinions were obtained from a questionnaire which was sent to the experts via email. The structure of this questionnaire follows the BWM approach thus, after a brief description of the problem and the criteria, the experts were asked to choose the best and worst criteria according to their expertise to lately compare these with the remainder. They had to make this selection for both the main criteria and the sub-criteria which belong to each one. An example of this questionnaire can be found at the following link https://sinbad2.ujaen.es/sites/default/files/2022-07/Survey__Experts.pdf.

Table 5 Competitor airline schedule

Table 6 The values of quantitative criteria

Table 7 The values of Competition criterion

4.2.3 Applying BWM to obtain the criteria weights

From the pairwise comparisons given in Tables 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, the criteria and sub-criteria weights are derived by using the BWM, particularly the optimization model (M-1). Table 8 presents the resulting weights for all the criteria and sub-criteria together the consistency of the experts’ opinions. Note that, according to (Liang et al., 2020), all the experts’ preferences are consistent.

Table 8 The weights of criteria and sub-criteria

4.2.4 Unification process

The heterogeneous information about the new frequencies implies the need of transforming such information into a unique expression domain in order to accomplish the computations in the next step. The unification process defined in Eq. (1) provides a fuzzy representation of each expert’s assessment for NA₁ (see Table 9). The calculations for the rest of the alternatives (NA₂, NA₃, and NA₄) are presented in Tables 25, 26, 27 in Appendix.

Table 9 Unified assessments for alternative NA₁

4.2.5 Aggregation process

First, for each expert, the sub-criteria are aggregated by means of the TFNWEBM operator in order to obtain an aggregated value for each criterion. In this step, the criteria and sub-criteria weights derived from the BWM are used. The experts’ decision matrices obtained from this aggregation step are shown in Table 10.

Table 10 Decision matrices by expert

Afterwards, each expert’s decision matrix is aggregated by using the Weighted Average Mean operator in order to obtain a collective decision matrix (see Table 11). In this step, the experts’ weights are derived from the years of experience of each expert (see Table 12).

Table 11 Collective decision matrix

Table 12 Experts’ weights according to their experience

4.2.6 Applying Fuzzy TOPSIS

Finally, the ranking of the alternatives is obtained by applying the fuzzy TOPSIS approach revised in Sect. 3.6 (see Table 13).

Table 13 Ranking of the alternatives

According to the results obtained from our proposal, the best frequency is NA₃.

Therefore, we have proved that the proposal is useful to solve real-world MEMCDA problems such as the one presented in the case study. The unification process allows transforming the heterogeneous information provided by the experts into a single format that facilitates computations. Then, the BWM derives the weights for criteria and sub-criteria by using an optimization model that guarantees the most representative weights according to the experts’ opinions. Afterwards, the aggregation process takes into account the relations between criteria and their importance by using the TFNWEBM operator and the different importance for the experts according to their level of expertise by using the Weighted Average Mean. Finally, taking advantage of the fuzzy representation, the fuzzy TOPSIS method is applied to obtain the ranking of the alternatives.

4.3 Sensitivity analysis

The robustness of the given solution is analyzed by means of a sensitive analysis (Triantaphyllou, 2000). This sensitive analysis consists of identifying the most critical criterion, which is the one that, with the smallest change in its weight, implies a change in the ranking of the alternatives. Table 14 shows the necessary changes in the criteria weights to modify the position between each pair of alternatives, which are graphically represented in Fig. 9. According to the results, the most critical criterion is C₂ since, an increment of the 45.04% (highlighted bold in the table) on its weight would provoke an exchange of positions between the alternatives NA₃ and NA₄. The remainder criteria need very high changes on their weights to provoke the same situation and, in some cases, the exchange of positions between specific pair of alternatives never happens (represented as Non Feasible (N/F)). Therefore, the results presented in Table 14 indicate that our solution is completely robust being necessary to modify the weights more than 45% to change the ranking of the alternatives.

Table 14 Most critical criterion

Fig. 9

Sensitive analysis for each criterion

5 Conclusions

This study aims to propose a new and specific MEMCDA model based on heterogeneous information for solving the selection problem of a new frequency for a network carrier airline in Turkey. The main advantages of this proposal are:

• It is able to deal with different kind of information to evaluate the criteria

• It provides the best schedule for a new frequency according to commercial and operational constraints.

• It uses the BWM to obtain the criteria weights by means of the experts’ opinions.

• It studies the relations among criteria and use a suitable aggregation operator able to capture such relations and consider the criteria weights.

Our study helps airline network and schedule planners to manage the potential risks through at the strategic planning phases of the schedule building process. Thanks to considering the slot availability criteria, experts considers the runway and gate congestion at the airports and they are able to enhance the robustness and resilience of the airline schedules at the operational phase.

The limitations of this study are as follows: (i) profitability evaluation of the alternative schedule is not possible due to confidentiality issues. Therefore, we cannot conclude that the best alternative is also the best profitable one. There might be revenue differences on the different time of days due to the different mix of passengers and its volume. (ii) it has been pre-assumed that alternative schedules are operationally feasible in terms of meteorological conditions and airport operations. In case of the non-compliance with these constraints, schedules cannot be operable. Additionally, regarding the MEMCDA approach, (iii) the results are represented both with a numerical and fuzzy representation but a linguistic representation closer to the experts’ way of thinking may facilitate even more their readability from the experts’ point of view.

As future works, the proposal of a new MEMCDA approach able to obtain easy-to interpret linguistic results may be interesting. Additionally, a consensus reaching process may be included in the resolution scheme of the MEMCDA approach with the aim of detecting and smoothing possible disagreements in the experts’ preferences and obtain agreed solutions. At the same time, the model can be made more effective by using operation research techniques. We can study the application of dynamic methods that allow the experts in the process consider the evolution across time to select a new frequency for a network carrier airline.

Appendix

See Tables 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27

Table 15 Best to others comparisons for general criteria

Table 16 Others to worst comparisons for general criteria

Table 17 Best to others comparisons for Passenger schedule preference

Table 18 Others to worst comparisons for passenger schedule preference

Table 19 Best to others comparisons for competition

Table 20 Others to worst comparisons for competition

Table 21 Best to others comparisons for slot availability

Table 22 Others to worst comparisons for slot availability

Table 23 Best to others comparisons for connection

Table 24 Others to worst comparisons for connection

Table 25 Unified assessments for alternative NA₂

Table 26 Unified assessments for alternative NA₃

Table 27 Unified assessments for alternative NA₄

.