Abstract
Time-relaxed sports timetables use more time slots than strictly needed, and are particularly popular in amateur (indoor) leagues. However, due to unexpected events, a considerable number of games may not be played as initially planned before the start of the tournament, leading to a potentially very different realized timetable. This study focuses on dealing with these uncertain events in time-relaxed round-robin sports timetabling, and how to mitigate their effect on the quality of the timetable. We use three quality measures to evaluate the time-relaxed timetables, namely, the games played difference index, the rest difference index and the number of cancelled games. We present several combined proactive and reactive approaches taking into account venue and team availability. Proactive strategies determine the position of time slots that are used as a buffer, while reactive strategies reschedule matches to these buffers in terms of the quality measures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Sports timetables determine when teams will play against each other and in which venue, and come in two kinds: time-constrained (or compact) and time-relaxed timetables. Time-constrained timetables use the minimum number of time slots required to play all games. In contrast, there are (often many) more time slots than necessary in time-relaxed timetables, which is the setting we focus on in this paper. While in professional sports leagues time-constrained timetables are prevalent (e.g. nowadays all European professional (association) football timetables are compact (Goossens & Spieksma, 2012)), time-relaxed timetables are commonly used in amateur leagues, such as indoor football (Van Bulck & Goossens, 2020a; Van Bulck et al., 2019) and table tennis (Knust, 2010; Schönberger et al., 2004). In the USA, general professional sports such as the National Basketball Association (NBA) are scheduled in time-relaxed format. In these sports, where the availability of teams and venues is limited, having a surplus of time slots offers the league organizer extra flexibility.
During a tournament, unexpected events such as for instance bad weather conditions, conflicts with other competitions, or defective infrastructure may prevent games from being played as planned. These unexpected events can affect the implementation of the so-called initial timetable, which is usually published before the start of the tournament, and may lead to the postponement, or even cancellation of matches. The matches as they are effectively played is referred to as the realized timetable, which becomes apparent only at the end of the season. According to Yi et al. (2020), \(1.36\%\) of the matches in 10 main professional (time-constrainted) European football leagues were not played as initially scheduled. Although this seems a small fraction, the authors report that this has had a profound impact on the quality of the realized timetables.
In (time-relaxed) amateur sports leagues, team members have other obligations such as work or family, preventing them from being constantly available for their sport. Furthermore, players can be absent because of injuries or otherwise indisposed, such that some teams cannot gather enough players to compete. Besides, teams usually share their venues with other clubs or sports disciplines, and are not in full control of other events taking place there. Overall, this leads to a much higher proportion of postponed games, compared to professional sports. We collected data from a Norwegian indoor football league (“Norges Itrettsforbund”), where more than \(13\%\) of the games were not played as initially planned in season 2018-19. Moreover, a Belgian indoor football league (“LZV Cup”, see also Van Bulck et al. (2019)), reported that in season 2018–19, nearly 10.9% of the 7528 matches had been postponed, and another 7.2% was cancelled. Although data from amateur leagues is hard to come by, it seems safe to say that the problem of postponed and cancelled games is substantial. Obviously, these figures date from before the COVID-19 outbreak, whose impact was such that most amateur competitions (and several professional leagues as well) were simply aborted mid-season.
Despite numerous contributions on sport scheduling (see e.g. (Rasmussen & Trick, 2008; Wright, 2009; Kendall et al., 2010; Ribeiro, 2012) and Durán (2021) for surveys and applications, Van Bulck et al. (2020) for a problem classification and data format, the literature on dealing with uncertainty in sports scheduling is thin. Schauz (2016) studies an online scheduling setting to deal with unannounced absences of players. Generally speaking, in this setting, games are scheduled round by round, as information about unavailabilities becomes available right before the start of each round. The author presents bounds on the number of rounds needed to complete the tournament in the worst case. Yi et al. (2020) focus on the issue of dealing with uncertainty in time-constrained sports leagues. They insert so-called catch-up rounds into the initial timetable in order to create buffers for rescheduling postponed games. This proactive strategy is then complemented with a reactive policy, which determines for each game that cannot be played as planned to which catch-up slot it should be rescheduled. In a follow-up paper, Yi and Goossens (2021) develop a stochastic programming approach to determine where to position the catch-up rounds in order to maintain the quality of the schedule. Both approaches are however not well suited for a time-relaxed setting. First, they focus on quality measures such as avoiding consecutive home games, whereas in time-relaxed (amateur) tournaments, this is usually of little importance. On the other hand, they do not consider differences in rest times, since every team plays on every round in a time-constrained schedule (if the number of teams is even). Second, the catch-up slots in time-constrained timetables are limited in number, but useful to all teams. On the other hand, in time-relaxed timetables, there are already (many) more time slots available than required, which can be viewed as catch-up slots. However, due to highly restrictive venue and team availabilities, each catch-up slot is typically only useful for a small subset of the teams. The idea of having buffers in time-relaxed timetables has also been mentioned by Durán et al. (2019), who schedule for a professional basketball league where so-called rest weeks can be used a posteriori for any reschedulings that may be required due to unforeseen circumstances. However, the authors consider the position of these rest weeks as given, and the rescheduling process not discussed either.
Building on the work of Yi et al. (2020), we develop combined proactive and reactive policies specially designed for time-relaxed timetables. We first devise initial timetables with good quality, which can accommodate postponed games. Next, we reschedule the postponed games, striving to maintain the quality of the realized timetable. Although other approaches for dealing with unexpected events (e.g. robust optimization, stochastic programming) are conceivable too, (combined) proactive and reactive optimization have the advantage that (i) they do not require probabilistic knowledge of the uncertain events, (ii) they look beyond avoiding some worst-case scenarios and feasibility issues, and (iii) their implementation is relatively easy, making it more accessible for practitioners. Another contribution is that our work is based on quality measures that are relevant for time-relaxed timetables, for various sports. As teams do not play on each slot, making sure that opponents are either fully rested, or receive a similar rest period is crucial. We propose an integer programming formulation for minimizing such rest difference index, which has, to the best of our knowledge, not been provided before in the literature. We also acknowledge that in order to have a fair ranking and to avoid match fixing incentives, teams need to have played as much as possible the same number of games at each point in the season. Finally, we study the impact of team and venue availabilities, and the number of games that cannot be played as planned on the performance of the developed policies.
The rest of our paper unfolds as follows. We introduce and explain the terminology and problem description, and discuss related research on time-relaxed round-robin timetabling in Sect. 2. Three quality measures for evaluating time-relaxed timetables are introduced in Sect. 3. Next, we discuss several proactive and reactive policies in Sect. 4. We design our experiment and discuss the simulation results in the following two sections, respectively, before concluding in Sect. 7.
2 Time-relaxed sports timetabling
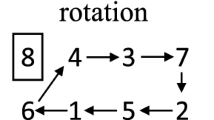
We denote the set of teams by \(T=\{1,2,...,n\}\), playing a double round-robin tournament in a set of time slots \(S=\{1,2,...,s\}\). A game (or match) is an ordered pair of teams, denoted as \(i-j\), meaning that team i plays at home, i.e., it uses its own venue (stadium) for that game against team j; we say that team j plays away. In a round-robin tournament, each team meets each other team t times (for a double round-robin tournament, \(t=2\)). We say that a team has a bye in a given time slot if it does not play in that slot. In a compact timetable with an odd number of teams, each team only has one bye during the whole season. In contrast, a team can have several byes in a row in a time-relaxed timetable. In any timetable, multiple matches can be played on the same time slot, however, each team can play at most once on a slot. An example of a double round robin (2RR) time-relaxed timetable with 4 teams is illustrated in Fig. 1.
In the time-relaxed availability constrained double round-robin tournament, known as RAC-2RR (Van Bulck & Goossens, 2020a), each team \(i \in T\) provides a venue availability set \(H_{i} \subseteq S\) with time slots on which its home venue is available (the team’s home games can only be played on such time slots). Furthermore, each team specifies a team unavailability set \(F_{i} \subseteq S\) with time slots on which it cannot play a game. Since every team has to play \(n-1\) home games in a double round-robin tournament, we assume that \(|H_{i}| \geqslant n-1, \forall i \in T\). Thus, every team has \(|H_{i}| - (n-1)\) extra home slots. We also assume that \(H_{i} \cap F_{i} = \varnothing , \forall i \in T\) as slots in the venue availability set that are included in the team unavailability set can never serve their purpose. As a result, a feasible timetable should assign teams to time slots such that:
-
Each team plays a home game against each other team exactly once (C1),
-
The venue availability \(H_{i} (i \in T )\) is respected for all teams, i.e., no game \(i-j\) is planned on a time slot \(s \notin H_i\) (C2),
-
The team unavailability \(F_{i} (i \in T )\) is respected for all teams, i.e., no game \(i-j\) or \(j-i\) is planned on a time slot \(s \in F_{i}\) (C3),
-
Each team plays at most one game per time slot (C4).
Van Bulck and Goossens (2020a) show that RAC-2RR is NP-hard, even if venues are always available. This problem forms the core of a number of real-life sports timetabling applications. Schönberger et al. (2004) discuss the timetabling problem faced by a regional non-professional table-tennis association in Germany, where, on top of venue availability and team unavailability constraints, the season is subdivided into six time intervals and the number of matches that each team should play in each of these intervals is constrained. Besides, the teams also specify the number of time slots they want between two successive games. Following up on this research, Knust (2010) considers additional hard constraints, like weekday constraints and fixed matches. She models the problem as a multi-mode resource-constrained project scheduling problem with partially renewable resources. Van Bulck et al. (2019) describe and solve a sports timetabling problem for the LZV Cup, a non-professional indoor football league with both venue and team availabilities. The authors balance each team’s games over the season, in the sense that there should be no close succession of games involving the same team.
Suksompong (2016) studies an extreme case of time-relaxed timetabling, the so-called asynchronous round-robin tournament. In this setting, only one game can be played on each time slot, allowing spectators to follow all the games live. He also introduces a number of quality measures for time-relaxed timetables (see Sect. 3). A fundamental problem in time-relaxed timetabling is whether one can obtain a feasible timetable, given the set of time slots for each team on which it plays a game. This problem is known as the game-off-day pattern set feasibility problem. Van Bulck and Goossens (2020b) provide a discussion of the computational complexity of this problem, as well as a number of necessary conditions.
We conclude this non-exhaustive overview with mentioning that there are also professional leagues that use time-relaxed timetables. For instance the National Hockey League (NHL) (Costa, 1995; Ferland & Fleurent, 1991; Fleurent & Ferland, 1993), the National Basketball Association (NBA) (Bao, 2009; Bean & Birge, 1980), the World Cup cricket (Armstrong & Willis, 1993), and the Australian State cricket (Willis & Terrill, 1994). Furthermore, there are a number of papers that focus on minimizing traveling distance in time-relaxed timetables (Bao & Trick, 2010; Bean & Birge, 1980; Brandão & Pedroso, 2014), similar to the well-know traveling tournament problem for compact schedules. However, travel distance falls outside the scope of this paper.
3 Quality measures for time-relaxed timetables
There are many ways to assess the quality of a sports timetable. Van Bulck et al. (2020) mention five criteria that have frequently been used in the literature as an objective function, and the most popular of them (minizing the weighted sum of violated constraints) has been implemented in many ways. For their study on time-constrained timetables, Yi et al. (2020) use quality measures related to the home advantage such as the number of breaks (i.e., two consecutive home or two consecutive away matches for the same team), k-balancedness (see Nurmi et al. (2010)), and g-balancedness (see Goossens and Spieksma (2012)). However, in time-relaxed timetables the home advantage is typically not so important, as they are mostly used for amateur competitions where the impact of spectators is negligible. In this section, we suggest 3 general quality measures that are relevant for time-relaxed timetables in various sports.
Since no team plays on every slot in a time-relaxed timetable, the number of games played may vary considerably between the teams throughout the season. This may result in an intermediate ranking that does not reflect the strength of the teams, and it may also provide extra information to the teams that played fewer matches. Indeed, this could give them a competitive advantage, such as knowing when they could settle for a draw or when a win is crucial, and even provide incentives for match fixing. In his study of asynchronous round-robin tournaments, Suksompong (2016) proposes the games-played difference index (GPDI). Following the idea, we have a first quality measure defined as below.
Measure 1
(GPDI, based on Suksompong (2016)) The games-played difference index of a sports timetable is the minimum integer g such that at any point in the timetable, the difference between the number of games played by any two teams is at most g.
A timetable with a low GPDI avoids that at any point in the season, some team will have played many more matches than some other team. For a time-constrained timetable the GPDI is zero if the number of teams is even, and one if the number of teams is odd. However, in a time-relaxed k-round-robin tournament with n teams, the GPDI can amount to \(k(n-2)\), i.e., all teams except a single team have played k times against all other teams, and that single team has played no game at all. An IP formulation for minimizing the GPDI for the time-relaxed availability constrained double round robin tournament can be found in the Van Bulck and Goossens (2020a).
Another issue with time-relaxed timetables is that there can be a varying number of time slots without a match between two consecutive games of a team. A team may suffer mentally as well as physically from fatigue without enough rest time. Furthermore, the rest time that opponents of a match have been granted by the timetable can be significantly different. Several researchers (e.g. Bengtsson et al. (2013), Dupont et al. (2010), Hägglund et al. (2013)) find a relation between having a close succession of matches and higher injury rates. Scoppa (2015) finds that more rest time in professional football positively impacts the performance of the team, when at least one of the two teams enjoys a very short period of rest. No impact is found when the rest time of both teams is sufficiently long: Scoppa (2015) shows that the impact of extra rest days becomes negligible when teams have four days or more between consecutive matches. This is in line with a study by Ispirlidis et al. (2008) on post-game effects (inflammatory responses and anaerobic performance) of a football match, which can last for 72 hours.
Making the rest time of two opponents roughly the same before their game is not easily achievable. Çavdaroğlu and Atan (2020) study the problem of minimizing the total rest difference among opposing teams to find the matchdays for an announced opponent schedule. Atan and Çavdaroğlu (2018) refer to the occurrence of a difference in the rest periods of opponent teams in a game as a rest mismatch. They develop two integer linear formulations and a constraint programming formulation for a time-relaxed round robin tournament (without availability constraints) where the goal is to minimize the number of rest mismatches. Suksompong (2016) defines the rest difference index (RDI) for asynchronous round-robin tournaments such that for any game in the timetable, if one team has not played in \(i_1\) consecutive time slots and the other team has not played in \(i_2\) consecutive time slots since their last games, respectively, the RDI is no less than \(|i_1-i_2|\). For any time-relaxed tournament with at least three teams, the RDI is at least one.
In this study, motivated by the findings by Scoppa (2015), we impose a cut-off point on the RDI: we say that a team has completely recovered from its last game if it rested at least \(\tau \) time slots. Hence, rest differences are ignored if both of the teams in a game have at least \(\tau \) rest slots
Measure 2
(RDI, based on Suksompong (2016)) The rest difference index of a sports timetable is the minimum integer r such that for any game in the timetable, if one team has not played in \(i_1\) consecutive time slots since its last game and the other team has not played in \(i_2\) consecutive time slots since its last game, then \(|\min (i_1, \tau )-\min (i_2,\tau )| \leqslant r\), where \(\tau \) is a given positive integer.
It follows from the definition that the rest difference index will never be larger than \(\tau \). We give an illustration of calculating the RDI for the time-relaxed timetable in Fig. 1.
-
If \(\tau = 5\), RDI = 4
In slot 8, team 2 has no rest as it also plays in slot 7 while team 3 has 4 slots for rest since it last game; since this is the maximal difference, and it does not exceed \(\tau \) slots, the rest difference in this case equals 4.
-
If \(\tau = 3\), RDI = 3
Team 3 has enough rest for recovery in slot 8 (\(4 > \tau \)), which means the rest difference for its match against team 2, which played on round 7 is restricted to \(\tau \) slots. This truncation also applies to the match between team 2 and 4 on time slot 7, but this has no impact on the RDI value.
In addition to the GPDI and RDI, a third important quality measure is the number of games that cannot be played on its originally planned timeslot, and for which no suitable time slot can be found to reschedule the game to. Obviously, cancellations are to be avoided, since they invalidate the final ranking. This measure was also used by Yi et al. (2020). We assume that in the initial timetable, all matches can be planned. If not, the team and or venue availabilities are not feasible, and we expect league organizers to negotiate new options with their teams. Consequently, we can attribute the number of cancelled games to the realized timetable, and in particular, to the effectivity of the scheduling policy with respect to handling uncertainty.
Measure 3
(Number of cancelled games) The number of cancelled games corresponds to the number of matches in the initial schedule that could not be played in the realized schedule.
4 Proactive and reactive policies
In order to alleviate the negative effects of unexpected events on the quality of time-relaxed round-robin timetables, we propose combined proactive and reactive policies to handle games that need to be postponed. We use proactive policies to devise initial timetables of good quality (i.e., with a small GPDI or small RDI), which offer possibilities to accommodate unexpected events. On the other hand, we apply reactive policies for rescheduling postponed games without much impact on the quality measures.
4.1 Proactive policies
An initial timetable is generated and strengthened according to a proactive policy, which anticipates the realization of unexpected events during the season. First of all, a high initial quality with respect to GPDI or RDI is desired. While a timetable with GPDI equal to 0 also has RDI equal to 0, the reverse is not true and moreover, a small positive value for GPDI may result in a high value for RDI. Hence, we develop separate proactive policies for obtaining a small GPDI (G-) and a small RDI (R-) value. As a first step, we develop integer programming formulations from which we can learn the best possible value for GPDI (\(g^*\)), and RDI (\(r^*\)) for a given problem instance.
Let \(p_{i,j,s}\) be the decision variable, which is 1 if team \(i \in T\) plays a home game against team \(j \in T\) on time slot \(s\in S\). Making use of a variable \(g_{i,s}\) which represents the number of games played by team \(i\in T\) up to and including slot \(s\in S\), a formulation for minimizing the GPDI (represented by g) for a time-relaxed availability constrained double round robin tournament is given as follows by Van Bulck and Goossens (2020a).
Constraints (1a) enforce that each team plays a home game against each other team exactly once, taking into account the venue and team availabilities. Constrains (1b) make sure that each team plays at most one game per slot. The next sets of constraints (1c) and (1d) calculate the number of games played by team i on the first and subsequent slots, respectively. Constraints (1e) calculate the GPDI value, which is minimized in the objective function. The remaining constraints settle the domain of the decision variables.
In order to minimize the RDI value, in addition to the p-variables, the following decision variables are used. For each team \(i \in T\) and slot \(s \in S\), a variable \(w_{i,s}\) is 1 if team i has a game on slot s, and 0 otherwise. Moreover, the value of variable \(a_{i,s,t} \) is one if team \(i \in T\) has consecutive games on slots s and t within \(\tau \) time slots. Besides, we also have variables \(r_{i,j}\), representing the rest time difference between the opponents of a home team \(i \in T\) and away team \(j \in T\). The rest time difference index is represented by r and minimized in the following model.
Constrains (2b) allow the w variables to keep track of when each team plays. The values of the \(a_{i,s,t}\) variables are regulated in constraints (2c) and (2d): they get value 1 if team i plays on slots s and t without another game of that team in between; the rest time between slots s and t is less than \(\tau \). Constraints (2e)–(2g) calculate the rest time differences between the home team and away team in each match. More specifically, constraints (2e) calculate the difference when both teams play consecutive games and rest less than \(\tau \) time slots, and constraints (2f) and (2g) calculate the difference when one of the opponents gets less than \(\tau \) time slots rest while the opponent rests \(\tau \) time slots or more. Note that when both opponents receive at least rest time needed for full recovery (\(\tau \)), the rest time difference can be set to 0. Finally, Constraints (2h) define the RDI, while Constraints (2i)–(2l) give the range of decision variables.
Once we know the best quality that can be achieved with respect to GPDI (i.e., \(g^*\) from model 1) and RDI (i.e., \(r^*\) from model 2), we create an initial timetable with that quality that offers flexibility for handling unexpected events. Notice that we use both models independently. Indeed, since we are not sure how RDI affects GPDI exactly, we focus on optimizing either RDI or GPDI, and avoid interactions between both measures. Since teams can only play home games on slots from their venue availability sets, it is important to carefully select which of these slots to use in the initial schedule and which to leave unused to accommodate postponed games. We develop three different strategies to accomplish this.
For the first proactive strategy, we define for each time slot s a degree \(dg_{s}\), which corresponds to the number of times it occurs in the venue availability sets of all teams. An illustration of this concept for 4 teams and their venue availability sets is shown in Fig. 2. For example, only team 1 can play a home game on slot 4, hence the degree of slot 4 is one; all teams can play home games on slot 11, which has a degree of 4. The smaller the degree of a time slot, the fewer teams can play a home game on this slot and the more relatively isolated this time slot is.
Since teams only have limited options for playing a home game, and they cannot be matched with a team that is already playing in some other game on that slot, relatively isolated time slots increase the number of opportunities to reschedule games. Indeed, if a slot with degree one is left unused in the initial schedule, we can use it to reschedule any home game of the team that has this slot in its home availability set. Hence, our first strategy is to keep as many relatively isolated slots as possible unused in the initial timetable. We do this by replacing Constraints (1e) with
in the Proactive GPDI model, and Constraints (2h) with
in the Proactive RDI model. Furthermore, in both formulations, we replace the objective function by
to obtain the proactive policies where we maximize the unused relatively isolated slots throughout the whole season (G-ISO, R-ISO), and by
to obtain the proactive policies where we maximize the unused relatively isolated slots in the second half of the season (G-ISO2, R-ISO2). The latter is motivated by the idea that more information with respect to the matches that need to be postponed is revealed as the season progresses.
The second strategy is also based on the idea that slots in the home availability set are scarce resources. Because away games can be played on any slot which does not belong to the team unavailability set, another way of saving home slots for postponed games is trying not have a team play an away match on a slot on which its home venue is available. We achieve this by using as an objective function
to obtain the proactive policies where we minimize the number of venue availability slots used for away games throughout the whole season (G-H4A, R-H4A), and
for proactive policies that only focus on the second half of the season (G-H4A2, R-H4A2).
The third strategy simply tries to schedule the matches as early as possible in the season, in order to keep as many slots from the venue availability set near the end of the season unused. We refer to these policies as G-tail and R-tail. We implement them by using the following objective, where usunsed venue availability slots receive a higher weight as they are closer to the end of the season:
4.2 Reactive policies
Reactive policies revise the initial schedule after an unforeseen event has occurred, instead of strengthening the initial timetable as proactive policies do. More specifically, after each slot, it becomes clear which games from that slot have not been played as scheduled. Reactive policies will determine to which available slot these games should be postponed, however, taking into account that no slot can have more than one match involving the same team, and also considering venue and team availability constraints. Note that, in line with common practice, we do not allow to make changes to other matches from the initial schedule, and matches that cannot be played as planned can only be moved to a later date. We consider the following three reactive policies:
-
Reschedule a postponed game to the first available time slot (FA),
-
Reschedule a postponed game to the best available time slot with respect to GPDI (BG),
-
Reschedule a postponed game to the best available time slot with respect to RDI (BR).
The first available (FA) reactive policy is easy to implement: it suffices to check the upcoming slots one by one to verify if the postponed match can be played there, taking into account (C1)–(C4), until a suitable slot is found. The other two reactive policies are a bit more involved, and we propose an integer programming formulation for each of them.
We denote the set of postponed games by D, with \(D_{i} \subseteq D\) referring to the set of postponed games that feature team \(i \in T\). We define the decision variable \(x_{d,s}\) which is 1 if postponed match \(d \in D\) is rescheduled to the slot \(s \in S\), and 0 otherwise. Let \(s_{d}\) refer to the initial slot of the postponed match \(d \in D\), and \(h_d\) (\(a_d\)) refer to its home (away) team. Next, \(w_{i,s}\) is 1 if team \(i \in T\) has a game in slot s that can be played as initially planned, and 0 otherwise, \(\forall i \in T\) and \(s\in S\). Notice that \(w_{i,s}\) is a parameter in the reactive models, whereas it was a variable in the proactive models. We also define \(z_{i,s}\) to be 1 if team \(i \in T\) plays a game in slot \(s \in S\), and 0 otherwise. For games that can be played as scheduled, the corresponding \(z_{i,s}\) of related teams is determined by the initial timetable. Variable \(y_{d}\) is 1 if postponed match \(d \in D\) is cancelled, and 0 otherwise. For each cancelled game, a penalty \(p_{c}\) will be charged. Following is the formulation for the BG reactive policy, where the GPDI is represented by g.
The objective function aims at minimizing the GPDI, and avoid cancellations at the same time. Constraints (5a) set the number of games played by team i up to slot s to the appropriate value. Constraints (5b) define the GPDI, i.e., the differences on the number of games played by every team should be at most g. With Constraints (5c), we regulate that a postponed game can only be rescheduled to a slot after its original slot that satisfies the relevant team and venue availabilities. Moreover, Constraints (5d) enforce that each postponed game can only be rescheduled once. According to Constraints (5e), a postponed game is cancelled if there is no available slot to reschedule it to. Constraints (5f) explain the relations between \(z_{i,s}\) and \(x_{d,s}\), and enforce that postponed games cannot be rescheduled to a slot where an involved team already has a game. Finally, Constraints (5g)–(5j) specify the range of the decision variables. Note that integrality of the \(g_{i,s}\) variables follows from the fact that the \(z_{i,s}\) variables are binary.
The third reactive policy (BR), which focusses on minimizing the RDI, also uses variable \(a_{i,s,t}\) as the proactive RDI model. From the initial timetable and the information on the postponed games, we can set \( p_{i,j,s}\) equal to 1 if home team i plays as initially planned against away team j on slot s, and 0 otherwise (e.g. in case this match cannot be played as planned on round s). Note that \(p_{i,j,s}\) is a parameter in this model. A binary variable \(k_{i,j,s}\) is 1 if team i and j play each other at i’s venue on slot s. For the games that are not postponed, the value of \(k_{i,j,s}\) is equal to \(p_{i,j,s}\).
Constraints (6a) and (6b) regulate the value of \(a_{i,s,t}\), making sure that it is set to one if team i plays a game on slot s and has its next game on slot t, at most \(\tau \) time slots later. Constraints (6c) calculate the rest difference between the opponents in a game if they both rest less than \(\tau \) time slots. Constraints (6d) and (6e) calculate the rest difference if one of the opponents is sufficiently rested while the other team is not. Constraints (6f) define the RDI value, represented by r. Constraints (6g) make sure that all games that can be played as planned, remain on their initially scheduled slot. Constraints (6h) imply that games that cannot be played as planned are either rescheduled or cancelled. Finally, constraints (6i)–(6k) specify the range of the decision variables.
5 Experimental design
Our experimental design is based on a double round-robin tournament with 10 teams and 50 time slots. This problem size is in line with the amateur table-tennis problem described by Schönberger et al. (2004), although we acknowledge that larger leagues exist in amateur (e.g. indoor football, 13–15 teams, see Van Bulck et al. (2019) as well as professional (e.g. NBA, 30 teams) competitions. The instance generation process with respect to the team and venue availability sets is based on the procedure described by Van Bulck and Goossens (2020a), except that we assume that the sizes of these sets do not differ between the teams. As each team has to play one home game against each other team, every team must have at least 9 venue availability slots. We consider 5, 10, and 15 extra venue availability slots for each team, and a size of 0, 5, and 10 for the team unavailability set. For each combination of these sizes, 5 different problem instances are generated. To be able to assess the impact of the size of the team and venue availability set, we opt to stick to the slots already in these sets as they grow larger. For instance, the venue availability set with 10 extra slots consists of the same slots as the one with 5 extra slots, and 5 additional venue availability slots. Scoppa (2015) mentions that teams have on average 4.27 days of rest between 2 consecutive games in FIFA and UEFA tournaments, and 4 days of rest is adequate for recovering in football. In line with this, we set the cut-off point \(\tau = 5\). Thus, the RDI can be at most 5. Moreover, since both g and r are relative small value, a very large value of \(p_{c}\) would force the model to avoid cancelling a game and small changes of g and r may have no influence on the objective value. Cancelling a game would definitely make two teams play one game less after the involved slots and they may have more rest, which can further affect the GPDI and RDI. Based on these considerations, the value for \(p_{c}\) is set to 1.
We generate a set D of games that cannot be played as planned, with a size ranging from 5 to 20, in steps of 5. Note that for instances with different combinations of team and venue availability set sizes, even if these sets are kept similar as described above, team pairs can play each other on different slots in the resulting schedules. This holds the risk that the evaluation of the initial schedules generated with different proactive methods is based on very different sets of games that cannot be played as planned. To mitigate this heterogeneity, it is reasonable to generate these games with respect to the index of the game for the home team. More specifically, in order to generate a postponed game d, we randomly pick a home team \(h_d\) and a home game index \(k_d\). Consequently, the \(k_d\)th home game of team \(h_d\) is postponed in each problem instance. The away team \(a_d\) and the time slot \(s_d\) that correspond to this postponed game d will however depend on the instance and its initial schedule.
In summary, we have 3 different sizes for both the set of extra venue availability slots and the set of team unavailability slots, and 5 instances per combination, resulting in \(3\times 3\times 5\) instances. For each such instance, an initial schedule is generated according to the 3 proactive strategies. These initial schedules are then confronted with sets of postponed games, with size 5, 10, 15, and 20. The reactive policies are applied under two settings: (i) fixed setting: each postponed game should be rescheduled to a feasible slot immediately and this arrangement is permanent; (ii) flexible setting: a postponed game is rescheduled to a feasible slot temporarily, i.e., this assignment can be adjusted after obtaining more information. These settings have been introduced by Yi et al. (2020).
All simulations were implemented on a MacOS 10.13.6 system with 8 GB memory and an Intel Core i5 processor, running at 2.3 GHz. All IP-formulations were programmed in Xcode 10.1 (C++), configured with and solved by IBM ILOG CPLEX 12.71. In order to have a good idea of the quality in terms of GPDI and RDI that can be achieved in the initial schedule, we first solve formulations (1) and (2) respectively. As these models are computationally expensive, we set a time limit of 400 seconds for each instance. Nevertheless, we managed to obtain the optimal GPDI value for all instances, which is 1. For the RDI, we are able to solve at least 2 out of the 45 instances to optimality (\(RDI=1\)); 26 instances obtained \(RDI=2\) and the other instances result in \(RDI=3\). When implementing the various proactive policies, we make use of constraints (3) and (4) to fix these values for GPDI and RDI respectively, hence ensuring that the initial timetables obtained with each policy have the same good quality. The average quality of the initial timetables is shown in Table 1. Among the G- strategies, the best RDI is achieved with the tail proactive policy, whereas among the R- strategies, the best results for GPDI are obtained by the ISO proactive policy. Finally, after the realization of the matches that need to be postponed, each reactive policy is executed on each initial schedule.
6 Simulation result and discussion
Tables 2, 3 and 4 present, for each combination of proactive and reactive policies, results for the quality of the realized schedules in terms of GPDI, RDI, and the number of cancelled games, respectively. Note that each entry represents the average of 45 instances, based on 9 combinations of team and venue availability set sizes, and 5 instances per such combination. The tables have the best performances colored in red; values in blue are the second-best and values in green are ranked third. This ranking was found using a student’s t-test: if we can find a significant difference between the performances of two combined policies, the policy with smaller average value has the better ranking, otherwise, the policies are considered equivalent. Because of the cut-off (\(\tau \)) applied on the RDI, this value is not normally distributed, and hence we used the paired Wilcoxon signed-rank test to check wether differences are significant in Table 3.
In general, the policies perform much better under a flexible setting than under a fixed setting, which confirms the findings reported earlier by Yi et al. (2020). In particular with respect to the number of cancelled games, this difference is significant for every combination of proactive and reactive strategies. Furthermore, proactive policies that focus on GPDI (G-) always result in a smaller GPDI compared to the proactive policies that focus on RDI (R-), regardless of the reactive policy. The latter always score better with respect to RDI. In that sense, the results for the realized schedule are in line with the quality of the initial schedules in Table 1, and selecting the appropriate type of proactive policy is crucial. In fact, for the G-policies, the realized GPDI values are still better than the initial GPDI values with which the R-policies started.
Leaving more home venue availability slots unused at the end of the season (tail) profoundly reduces the number of cancelled games, regardless of the reactive policy. Moreover, focussing on the second half of the season also has a beneficial impact on the number of cancellations, except for the R-H4A/R-H4A2 policies, which do not seem to behave well in this regard. On the other hand, when considering GPDI, there is a clear increase from ISO to ISO2, and from H4A to H4A2; the G-tail policy has an even worse GPDI. Hence, there is a trade-off between the games played difference index and the number of cancellations. Indeed, having several rescheduling options near the end of the season will increase the chance that a match can be postponed rather than cancelled, but as it will be postponed near the end of the season, the involved teams will have played one match fewer than the other teams for much of the remainder of the season.
Adding buffers in the second half of the season does however not have an adverse effect on the RDI. This can be explained by the fact that if relatively few matches are scheduled towards the end of the season, it is easier to postpone a match to this period in a way that both teams can enjoy sufficient rest time, hence without worsening the RDI. In terms of not using home slots for scheduling away games (H4A2), the added value of focussing on the second half of the season is negligible with respect to reducing the RDI. The deterioration with respect to GPDI, however, is still there. Free space in the schedule in the second half of the season can be exploited for balancing the differences in rest time, provided that there is enough flexibility (ISO2), however postponing matches for a long period increases the games played difference index.
Overall, the G-ISO proactive policy is the best choice with respect to GPDI. In a flexible setting, the reactive policy BG (which aims at minimizing the GPDI) works better in terms of GPDI for G-policies. However, if rescheduling decisions are irrevocable (fixed setting), the BG reactive policy loses its edge, and the first available reactive policy is slightly better. With respect to RDI, all R-policies obtain their best results when combined with the BR reactive policy, regardless of whether a fixed or flexible setting applies. Particularly the flexible BR policy, combined with either tail, ISO2 (or even ISO) gives the best values for RDI. In terms of avoiding cancelled games, the tail proactive policy is by far the best option (again performing better under a flexible rather than a fixed setting), regardless of the reactive policy. Figs. 3, 4 and 5 provide detailed picture of the behaviour of the best combined policies for each quality measure, showing the impact of the size of the team and venue availability sets, as well as the number of games that cannot be played as planned.
As shown in Fig. 3, if there are 10 or more matches that cannot be played as planned, even the best combined policy does not perform well with respect to GPDI if only 5 extra venue availabilities are given per team. There is a clear improvement if each team has 10 extra venue availability slots rather than 5, however, increasing the size of the venue availability set with another 5 slots hardly yields further effect, even if 20 matches need to be postponed. The impact of the size of the team unavailability set is much less pronounced.
Fig. 4 indicates a similar impact of the number of matches that cannot be played as planned and the size of the team unavailability set. It is interesting though that having a higher venue availability may actually worsen the performance with respect to RDI. The reason behind this is associated with the number of cancelled games. More cancelled games create a less congested schedule for the involved teams, creating more options to reduce the RDI.
As for the number of cancelled games, Fig. 5 shows that tail-first available policy succeeds very well in avoiding cancellations. Cancellations occur only in case of lots of matches that need postponing and a large team unavailability set, however, if each team provides 10 extra venue availability slots, cancelled games can be completely avoided.
In addition to Figs. 3, 4 and 5, we conducted several generalized linear regression analyses to assess the impact of venue and team availability, and the number of games that need to be postponed on the quality of the resulting schedule. The results were obtained using RStudio (Version 1.0.153) and are given in Table 5. In general, if a team is more frequently unavailable, the GPDI, RDI and the number of cancelled games increase significantly, while more venue availabilities improve the quality of the realized timetable. These effects are very similar in size, except with respect to cancellations, where a venue availability on average adds more to the quality than a team unavailability takes away. When only the results for specific policies are included, however, the regression yields somewhat different results. The best combined policy for GPDI, i.e., G-ISO-BG is not sensitive to the size of team unavailability set with respect to GPDI. On the other hand, the size of the venue availability has no impact on the performance of R-ISO2-BR with respect to RDI (and GPDI). Both results confirm what we remarked earlier with Figs. 3 and 4. As for the R-tail-FA policy, which is best for avoiding cancelled games, we can see that the size of venue and team availability sets both play an important role. All three policies are sensitive to the number of postponed games for all three studied quality aspects.
7 Conclusions
We studied the impact of uncertainty on the quality of time-relaxed round-robin tournaments with availability constraints on the team and the venue. These type of timetables are common in (indoor) amateur sports, which makes that our approach can be useful for designing and maintaining good quality timetables for practitioners in various sports, like indoor football, table tennis, and so on. We proposed several (combined) proactive and reactive strategies for anticipating and handling matches that need to be postponed. We focussed on minimizing the rest difference between the opponents (RDI), having a ranking in which all teams have played as much as possible the same number of games at any point in the season (GDPI), and avoiding cancelled games, as three distinct quality measures.
We found that there is no strategy that performs best on all quality characteristics. In particular, a preference for RDI or GDPI should be reflected in a corresponding choice for the proactive policy. We found G-ISO-BG to work best for managing the games played difference index, and R-ISO2-BR to be one of the best choices to avoid rest differences. If avoiding cancelled games is the only priority, then one should try to avoid scheduling games towards the end of the season in the initial schedule, and rescheduling postponed games to the earliest available slot. Overall, not using slots on which a team’s venue is available to schedule an away game of that team is a rather mediocre policy, which gives no clear advantage. In any case, it pays off to maintain flexibility with the rescheduling process in the sense that games that have been postponed to a later date can still be rescheduled to yet another date, as long as they have not been played.
Provided that the best proactive-reactive strategy is applied, asking each team to provide 50% more slots on which they have their home venue availability than strictly needed to schedule the tournament can largely avoid cancellations and mitigate problems with rest differences. This will, however, typically not be sufficient with respect to GPDI, where we advise to have twice as many venue availability slots as strictly needed. Having these buffers should be enough to adequately handle a situation with up to 20% of the matches that need to be postponed, which does not seem an exceptional number in amateur sports. Restricting the number of time slots on which a team can indicate that they are not available does not seem to contribute much to the quality of the realized schedules.
The fact that no strategy appears to be the best choice for all of the quality characteristics, suggests that there is a trade-off to be made between RDI, GDPI, and avoiding cancelled games. While we have optimized for each measure separately in this text, it may be a valuable area for future research to study this from a multi-objective angle, and for instance, try to construct a Pareto front of solutions from which the league organizer could pick one, based on a well-informed trade-off.
Finally, while the presented approach works well for leagues with up to 10 teams, the use of integer programming in time-relaxed timetabling (in particular for minimizing the rest difference index) does not seem to scale very well. Recent work by Van Bulck and Goossens (2022) suggests that larger instances can be solved with a decomposed approach using logic-based Benders cuts, at least if number of time slots is not more than twice the number of games per team. It will be an interesting line of future research to figure out whether such approach can also be useful for mitigating the effect of uncertain events on the quality of the timetable. Naturally, it would be of great added value if our strategies for dealing with uncertainty in time-relaxed sports timetabling. could be tested and applied in real-world leagues.
References
Armstrong, J., & Willis, R. J. (1993). Scheduling the cricket world cup—a case study. Journal of the Operational Research Society, 44(11), 1067–1072.
Atan, T., & Çavdaroğlu, B. (2018). Minimization of rest mismatches in round robin tournaments. Computers & Operations Research, 99, 78–89.
Bao R (2009) Time relaxed round robin tournament and the NBA scheduling problem. PhD thesis, Cleveland State University.
Bao, R., & Trick, M. A. (2010) The relaxed traveling tournament problem. In: Proceedings of the 8th international conference on the practice and theory of automated timetabling PATAT 2010, pp 167–178.
Bean, J. C., & Birge, J. R. (1980). Reducing travelling costs and player fatigue in the national basketball association. Interfaces, 10(3), 98–102.
Bengtsson, H., Ekstrand, J., & Hägglund, M. (2013). Muscle injury rates in professional football increase with fixture congestion: An 11-year follow-up of the uefa champions league injury study. British Journal of Sports Medicine, 47(12), 743–747.
Brandão, F., & Pedroso, J. (2014). A complete search method for the relaxed traveling tournament problem. EURO Journal on Computational Optimization, 2, 77–86.
Çavdaroğlu, B., & Atan, T. (2020). Determining matchdays in sports league schedules to minimize rest differences. Operations Research Letters, 48(3), 209–216.
Costa, D. (1995). An evolutionary tabu search algorithm and the NHL scheduling problem. INFOR: Information Systems and Operational Research, 33(3), 161–178.
Dupont, G., Nedelec, M., McCall, A., McCormack, D., Berthoin, S., & Wisløff, U. (2010). Effect of 2 soccer matches in a week on physical performance and injury rate. The American Journal of Sports Medicine, 38(9), 1752–1758.
Durán, G. (2021). Sports scheduling and other topics in sports analytics: A survey with special reference to Latin America. Top, 29(1), 125–155.
Durán, G., Durán, S., Marenco, J., Mascialino, F., & Rey, P. A. (2019). Scheduling Argentina’s professional basketball leagues: A variation on the travelling tournament problem. European Journal of Operational Research, 275(3), 1126–1138.
Ferland, J. A., & Fleurent, C. (1991). Computer aided scheduling for a sport league. INFOR: Information Systems and Operational Research, 29(1), 14–25.
Fleurent, C., & Ferland, J. A. (1993). Allocating games for the NHL using integer programming. Operations Research, 41(4), 649–654.
Goossens, D., & Spieksma, F. C. (2012). Soccer schedules in Europe: An overview. Journal of Scheduling, 15(5), 641–651.
Hägglund, M., Waldén, M., Magnusson, H., Kristenson, K., Bengtsson, H., & Ekstrand, J. (2013). Injuries affect team performance negatively in professional football: An 11-year follow-up of the UEFA Champions League injury study. British Journal of Sports Medicine, 47(12), 738–742.
Ispirlidis, I., Fatouros, I. G., Jamurtas, A. Z., Nikolaidis, M. G., Michailidis, I., Douroudos, I., Margonis, K., Chatzinikolaou, A., Kalistratos, E., Katrabasas, I., et al. (2008). Time-course of changes in inflammatory and performance responses following a soccer game. Clinical Journal of Sport Medicine, 18(5), 423–431.
Kendall, G., Knust, S., Ribeiro, C., & Urrutia, S. (2010). Scheduling in sports: An annotated bibliography. Computers and Operations Research, 37, 1–19.
Knust, S. (2010). Scheduling non-professional table-tennis leagues. European Journal of Operational Research, 200(2), 358–367.
Nurmi, K., Goossens, D., Bartsch, T., Bonomo, F., Briskorn, D., Duran, G., Kyngäs, J., Marenco, J., Ribeiro, C. C., Spieksma, F., et al. (2010). A framework for scheduling professional sports leagues. AIP Conference Proceedings, American Institute of Physics, 1285, 14–28.
Rasmussen, R. V., & Trick, M. A. (2008). Round robin scheduling-a survey. European Journal of Operational Research, 188(3), 617–636.
Ribeiro, C. C. (2012). Sports scheduling: Problems and applications. International Transactions in Operational Research, 19(1–2), 201–226.
Schauz, U. (2016). The tournament scheduling problem with absences. European Journal of Operational Research, 254(3), 746–754.
Schönberger, J., Mattfeld, D. C., & Kopfer, H. (2004). Memetic algorithm timetabling for non-commercial sport leagues. European Journal of Operational Research, 153(1), 102–116.
Scoppa, V. (2015). Fatigue and team performance in soccer: Evidence from the fifa world cup and the uefa european championship. Journal of Sports Economics, 16(5), 482–507.
Suksompong, W. (2016). Scheduling asynchronous round-robin tournaments. Operations Research Letters, 44(1), 96–100.
Van Bulck, D., & Goossens, D. (2020). Handling fairness issues in time-relaxed tournaments with availability constraints. Computers & Operations Research, 115, 104856.
Van Bulck, D., & Goossens, D. (2020). On the complexity of pattern feasibility problems in time-relaxed sports timetabling. Operations Research Letters, 48, 452–459.
Van Bulck, D., & Goossens, D. (2022). Optimizing rest times and differences in games played: An iterative two-phase approach. Journal of Scheduling, 7, 1–11.
Van Bulck, D., Goossens, D., & Spieksma, F. C. (2019). Scheduling a non-professional indoor football league: A tabu search based approach. Annals of Operations Research, 275(2), 715–730.
Van Bulck, D., Goossens, D., Schönberger, J., & Guajardo, M. (2020). RobinX: A three-field classification and unified data format for round-robin sports timetabling. European Journal of Operational Research, 280(2), 568–580.
Willis, R. J., & Terrill, B. J. (1994). Scheduling the Australian state cricket season using simulated annealing. Journal of the Operational Research Society, 45(3), 276–280.
Wright, M. (2009). 50 years of OR in sport. Journal of the Operational Research Society, 60(sup1), S161–S168.
Yi, X., & Goossens, D. (2021). A stochastic-programming approach for scheduling catch-up rounds in round-robin sport leagues. IMA Journal of Management Mathematics, 32(4), 425–449.
Yi, X., Goossens, D., & Nobibon, F. T. (2020). Proactive and reactive strategies for football league timetabling. European Journal of Operational Research, 282(2), 772–785.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Yi, X., Goossens, D. Strategies for dealing with uncertainty in time-relaxed sports timetabling. Ann Oper Res 320, 473–492 (2023). https://doi.org/10.1007/s10479-022-04957-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-022-04957-0